Protein Flexibility and Dissociation Pathway Differentiation Can Explain Onset Of Resistance Mutations in Kinases

Abstract

Understanding how mutations render a drug ineffective is a problem of immense relevance. Often the mechanism through which mutations cause drug resistance can be explained purely through thermodynamics. However, the more perplexing situation is when two proteins have the same drug binding affinities but different residence times. In this work, we demonstrate how all-atom molecular dynamics simulations using recent developments grounded in statistical mechanics can provide a detailed mechanistic rationale for such variances. We discover dissociation mechanisms for the anti-cancer drug Imatinib (Gleevec) against wild-type and the N368S mutant of Abl kinase. We show how this point mutation triggers far-reaching changes in protein’s flexibility and leads to a different, much faster, drug dissociation pathway. We believe that this work marks an efficient and scalable approach to obtain mechanistic insight into resistance mutations in biomolecular receptors that are hard to explain using a structural perspective.

Graphical Abstract

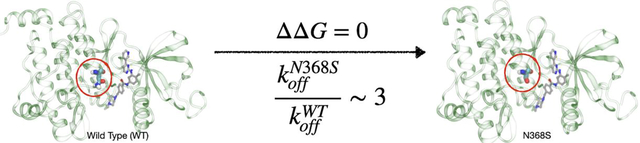
Gleevec has same binding affinity yet different dissociation times against Wild-Type and N368S mutated Abl kinase. Our all-atom enhanced molecular dynamics simulations explain why.

Introduction

Protein kinases are dynamic molecules that serve as signaling enzymes to catalyze the transfer of γ-phosphate of an ATP molecule to the hydroxyl group of Ser, Thr, or Tyr residues,^1–5 acting as switches that control key cellular signaling pathways. Over the years, the importance of kinases as drug targets and efforts to develop therapeutic agents for modulating kinase activity have been well established. ^5–7 The development of kinase inhibitors is how- ever challenging because of the high sequence conservation of the kinase ATP-binding site, the major site targeted by these small molecules. However, despite the challenges, progress in the field of kinase-based drug design was made with the discovery of Imatinib (Gleevec)^8,9 as a potent Abl kinase inhibitor. Gleevec is highly efficacious in the treatment of early-stage chronic myeloid leukemia (CML).^8,9 Unfortunately, a large fraction of late-stage CML patients suffer from cancer relapse due to the onset of drug resistance.^10–13

Understanding the molecular basis of the effects of these oncogenic mutations on the efficacy of cancer drugs is the first step in solving the problem of drug resistance. From a molecular view, the mutations can be classified as either orthosteric i.e., in the inhibitor binding site directly affecting Imatinib binding or allosteric wherein these mutations modulate drug resistance indirectly.¹⁴ In the past, multiple studies^10,14–17 have tried to explain the resistance by either pointing to direct abrogation of H-bonding interactions or steric effects in the reduction of the binding affinity. The well-studied T315I mutation in Abl kinase is such an example.^15,18,19 Although alchemical methods^20,21 to a certain degree have been able to quantify the effects of resistant mutations on inhibitor binding free energies, it remains un- tenable to use them for allosteric mutations that rely mainly on modulating conformational dynamics of the kinase. A recent study of 94 mutations²² associated with clinical resistance to Imatinib showed, that only approximately one-third of mutations weakened the inter- action with Imatinib by more than 2-fold compared to Abl wild-type (WT). Interestingly, several mutations changed the dissociation kinetics of Imatinib from Abl much more than the affinity. Since drug residence time is a strong predictor of drug efficacy, it is tempting to speculate that these mutations cause resistance via a kinetic mechanism related to the pharmacodynamics of the drug. However, currently, there is very limited mechanistic understanding of how mutations could alter the residence time. Despite the importance of kinetic measurements in understanding drug efficacy,^23–25 such measurements either computationally or experimentally have remained challenging. In the context of drug-receptor binding, experimental methods have been useful in the elucidation of drug-bound states, however, they have lacked in the description of short-lived metastable and transition states that could determine drug dissociation kinetics. While the association of drugs to their binding sites has been studied computationally before, ²⁶ the challenge for the computational study of dissociation kinetics lies in the extremely slow dissociation times, often minutes or slower.

Our specific interest in this work pertains to a recent discovery made by Lyczek et al,²² who have characterized the N368S mutant of Abl to which Imatinib (Gleevec) binds with a similar binding affinity as it does to WT. However, they find that Imatinib dissociates three times faster from the mutant than from WT. In this work, we use recent statistical mechanics based all-atom resolution methods^27–29 to provide a mechanistic rationale for this perplexing finding. Our method provides quantitative estimates for the dissociation rate constant k_off for both WT and mutant Abl. In addition we also obtained similar binding affinities for both the systems using free energy perturbation calculations. The estimates are within an order of magnitude of the experimentally determined values and capture their relative magnitudes. Going even beyond reproducing k_off values, our calculations directly pinpoint the varied dissociation pathways adopted by Imatinib in both variants of Abl kinase. Our key mechanistic finding can be summarized as follows: We find that there are two distinct Imatinib dissociation pathways for the WT and the mutant Abl. Furthermore, we explain the order of magnitude difference between WT and mutant Imatinib unbinding kinetics by invoking varied structural rearrangements required to allow distinct dissociation pathways in WT and mutant Abl.

To perform such mechanistically insightful simulations, in principle one could use computational methods like molecular dynamics (MD). These have the potential to not just quantify k_off, but also give a direct atomistic understanding of metastable states along with drug binding/unbinding pathways which have remained elusive through experiments. However, even with highly specialized hardware, MD has been limited to at best a fraction of a millisecond.^30,31 On the other hand, numerous enhanced sampling algorithms^32–42 have been employed for k_off calculations with reasonable computational costs and the ability to achieve pharmacologically relevant timescales of seconds, and slower. Here we use one such method “infrequent metadynamics” that has been employed to obtain unbiased estimates of dissociation kinetics in numerous systems.^27,39,40,43 The reliability of such calculations⁴⁴ is closely linked to the ability to design an appropriate reaction coordinate (RC) that describes the dissociation and that can be used to construct the low-dimensional biasing potential. In general, learning such an RC is a difficult problem especially for rare events such as drug dissociation, wherein any framework used to learn the RC depends on the quality of the sampling, while accurate sampling itself can not be achieved without having a reasonable RC. In this work, we make use of recently developed machine learning and statistical mechanics- based methods^27–29 that tackle the above chicken-versus-egg problem through systematically iterating between sampling and RC optimization in a nearly automated manner (see Fig. 7 in Supplementary Information (SI) for a flowchart of the overall protocol). Once a reliable RC is obtained, infrequent metadynamics can be performed along it to calculate k_off estimates with error bars⁴³ and directly observe the entire dissociation pathway with all-atom and femtosecond resolution.

Results and discussion

Abl-kinase structure

For the sake of completeness, we begin by summarizing some well-known structural details. Abl kinase has a typical bilobal kinase domain, consisting of a smaller N-terminal lobe (N-lobe) and a larger C-terminal lobe (C-lobe). The ATP binding site is located between the N-lobe and the C-lobe of the catalytic domain, distinguished by conserved structural features like the phosphate-positioning loop (P-loop), the activation loop (A-loop), the αC helix, and the conserved Asp-Phe-Gly (DFG) motif (Fig. 1). As evidenced by biophysical experiments^45–48 in addition to computational^49–57 and structural studies, ^{11,15,47,58–60} Abl-kinase exists in a dynamic equilibrium between multiple conformations: active, inactive and multiple intermediate states interspersing these. These states are characterized by the conformational flexibility of evolutionarily preserved kinase motifs such as the A-loop, DFG motif and the αC-helix (Fig. 1). Abl-kinase in its active conformation is characterized by the “DFG-in” and “αC-in” state. In this state the D381 residue of the DFG loop points towards the active site, ready to coordinate with ATP and the Mg²⁺ ion. The αC helix swings in towards the binding site adopting the “αC-in” conformation and allowing for ion-pair interaction between the conserved E286 on αC helix with conserved K271 in the β3 strand. At the same time, the A-loop adopts an extended conformation allowing space for the substrate to dock. The conserved E286, in turn, interacts with the α and β phosphates of ATP. In contrast to this very specific characterized active state, a kinase can also adopt one of many inactive conformations. ^61–64 One such often-mentioned conformation is the so-called “DFG-out” conformation, where the D381 switches its position with the phenylalanine F382, pointing away from the ATP binding site. Type II inhibitors such as Imatinib are suspected to selectively target this “DFG-out” inactive state. ^17,65 Imatinib is stabilized in the ATP binding site predominately via hydrophobic interactions with V256 and F382 along with hydrogen bonding interactions with side chain hydroxyl of the gatekeeper residue T315, E286 sidechain on αC-helix, backbone-NH of D381 on the DFG loop and backbone-NH of M318 on hinge. Furthermore, the terminal 4-methylpiperazine ring interacts with backbone carbonyl of I360 (SI Fig. 10).

Figure 1:

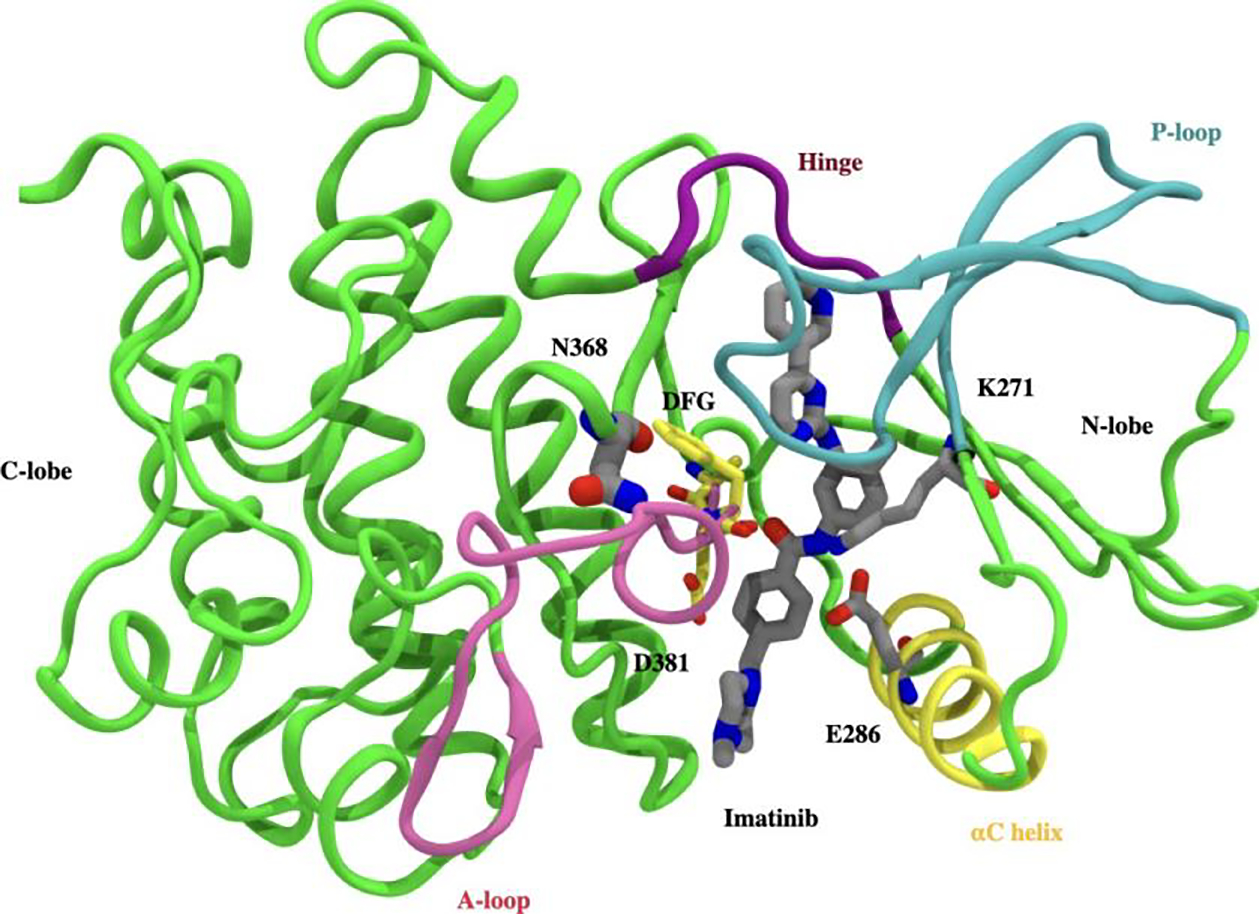
Crystallographic binding mode: Imatinib (gray) bound to the catalytic domain of Abl kinase (PDB id 1OPJ). Kinase domain is divided into N-terminal lobe (N-lobe) and C-terminal lobe (C-lobe), with the inhibitor (Imatinib) binding site located between the lobes. Abl-kinase has conserved structural features like A-loop (pink ribbon), P-loop (blue ribbon), αC helix (yellow ribbon), hinge (purple ribbon), and DFG motif (yellow sticks). D381 in the DFG motif, and the salt bridge involving E286 in the αC helix, and K271 cover and block the binding tunnel in front. The site of mutation (N368) lies behind the DFG motif and is shown in a gray stick representation.

Finally, we note here that alchemical free energy perturbation calculations (see Supplementary Information (SI)) reproduce the lack of binding affinity difference displayed by Imatinib against WT and N368S Abl kinase.

Infrequent metadynamics simulations reveal two distinct pathways

In this work, our central aim is to use all-atom MD simulations to understand the molecular determinants that speed up dissociation of Imatinib from N386S 3-fold relative to WT. Due to the extremely slow timescales of the dissociation process relative to what can be achieved in MD simulations, here we use a combination of enhanced sampling methods as mentioned in the Introduction and detailed in the Methods section. The first step in the k_off calculation for Imatinib is the description of a low-dimensional reaction coordinate (RC) that can suitably describe biological processes of interest, in this case, the dissociation of Imatinib from WT/mutant Abl kinase. Briefly, we perform 100 ns long unbiased MD simulation on Imatinib bound with WT and mutant Abl kinase respectively. By employing the method AMINO²⁹ (Methods) on these trajectories we learned non-redundant trial order parameters (OPs) that describe Imatinib dissociation (Fig. 2 A-B). Starting from a total possible 84 OPs corresponding to different possible kinase-Imatinib heavy-atom contacts, AMINO identified 5 OPs to be sufficient for the WT and the mutant complexes respectively shown in Fig. 2 A-B. See Table 2 in SI for a summary of OPs. These OPs are expressed as distances between Cα atoms of highlighted residues and centers of mass of two halves of Imatinib. These two halves are labeled p2a (blue stick), which is initially solvent exposed, and p2b (orange stick) which is the buried half. In the case of WT, AMINO derived OPs measure the distance between p2a and the Cα atoms of residues Y232, Y253 along with the distance between p2b and Cα atoms of residues E238 and S229. In comparison, OPs for Abl N368S are defined by the distance between p2a and the Cα atoms of residues I313, K274 along with the distance between p2b and Cα atoms of residues D325, Y253, F283. Along with these OPs, the common OPs for mutant and WT are the distances between CαCβ atoms of T315 shown in red spheres and the N3 and N4 atoms of Imatinib shown in blue spheres. Subsequently, multiple rounds of maximum caliber-based SGOOP optimization^28,66 are performed to construct an even lower-dimensional RC from these OPs shown in Fig. 2 C-D. Finally, 11 independent trials of infrequent metadynamics were performed starting from the bound crystal pose and biasing the aforementioned RC, stopping when the ligand was fully solvated. Through these, we generated an ensemble of ligand dissociation pathways along with the associated protein conformational changes and culminating in the k_off calculation (Fig. 2 E) through the procedure of Ref.^27,43

Figure 2:

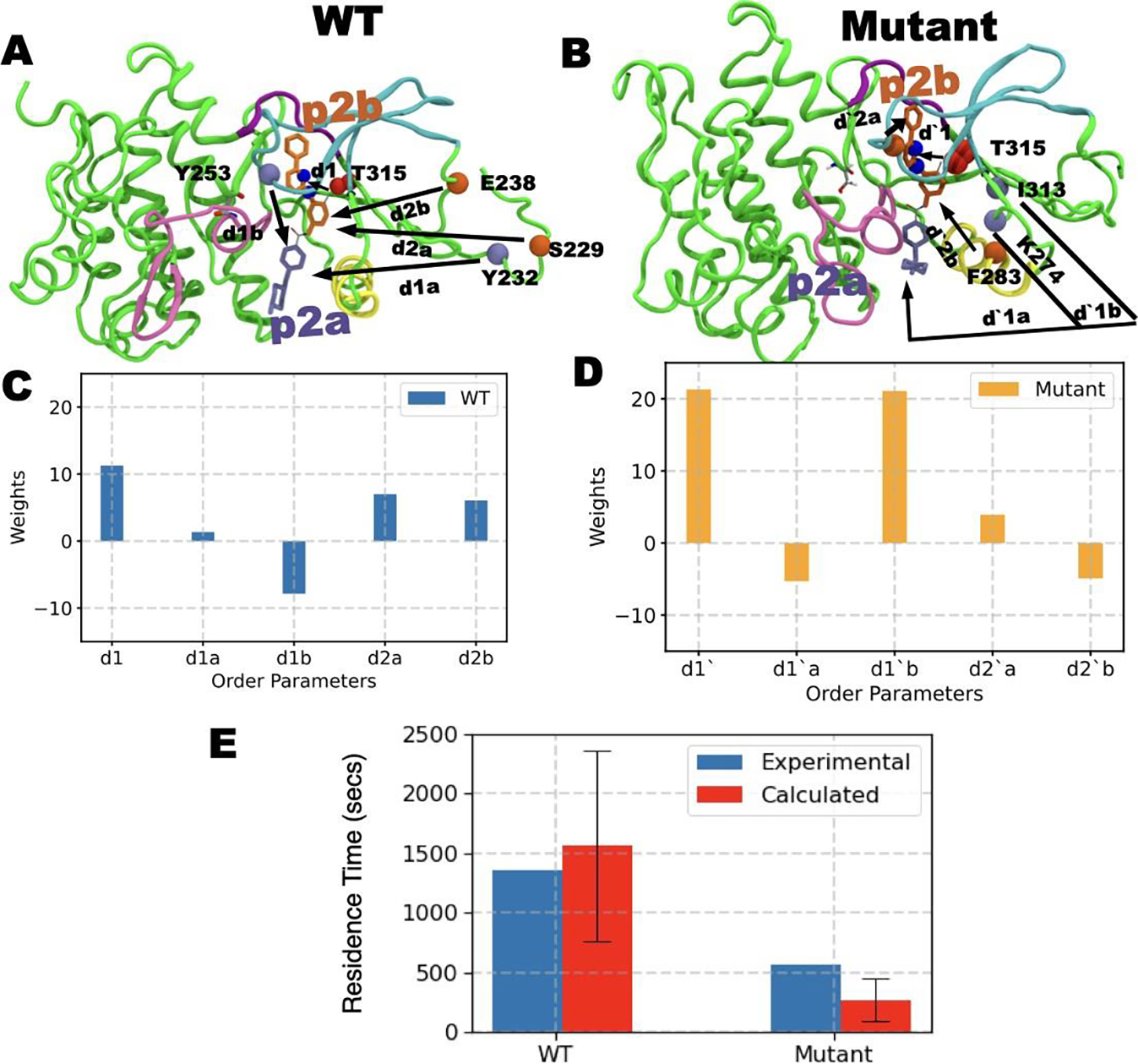
A) and B) show order parameters OPs obtained through AMINO for WT and mutant respectively. C) and D) show the respective RC constructed from these OPs through SGOOP. E) shows the residence times (red bar) obtained by biasing the respective RC for WT and mutant system compared against experimental measurements (blue bars). The red bars represent the fitted residence time⁴³ while the standard deviation is shown as a black error bar. See main text for further details of the OPs.

We would like to comment here on using different RCs for the two systems. Metadynamics and other sampling methods for more than a decade followed the strategy of biasing the same variable for different systems. However over the last few years consensus started to emerge that different systems can have different slow processes and if the biasing variable misses out on those, then the sampling could be incorrect or misleading.⁶⁷ Recent machine learning and statistical physics based methods such as the ones used in this work and others⁶⁸ have now made it possible to learn such system-specific RC, starting from a short unbiased MD trajectory which thereby makes the protocol robust and takes the guesswork out of the process.

In the infrequent metadynamics simulations, depending upon the protein, WT or mutant, two distinct Imatinib release pathways were observed. The two pathways as shown in Fig. 3 A (left/right upper panel), can be described as: (i) exit under the P-loop closer to the αC helix (i.e., through the hydrophobic pocket), henceforth named as the αC pathway, or (ii) exit through a pathway closer to the P-loop and the kinase hinge, named as the hinge pathway. These two pathways can be more quantitatively characterized by projecting them onto a 2-D space spanned by the two distances between the Imatinib center of mass and the centers of mass (i) of the alpha carbons of the hinge, and (ii) of the αC helix. Evidently, as can be seen in Fig. 3 A (upper/bottom left panel), in the WT dissociation trajectory, the hinge pathway is the dominant pathway. Quantitatively, Imatinib during its dissociation comes as close as 3.8±1 Å to the hinge region while not getting closer than 9±0.5 Å from the αC helix. Sharply contrasted to this, for dissociation from N368S we find that Imatinib does not get closer than 8±0.5 Å to the hinge region while it comes as close as 6±0.5 Å to the αC helix. These distances are the averaged values over the different independent trajectories with error bars shown in Fig. 3.

Figure 3:

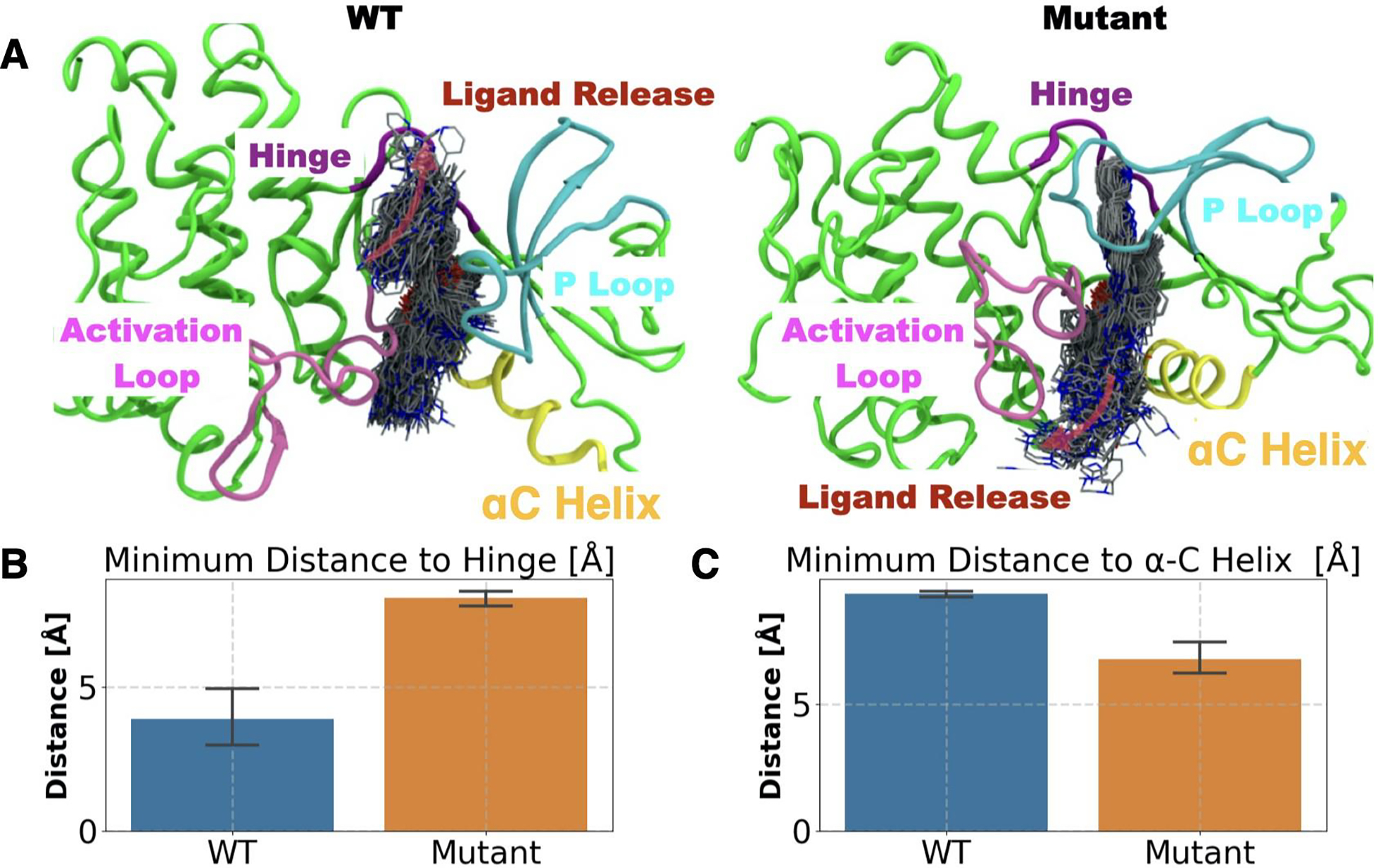
Mutational effect on the substrate release pathway (red arrows in the top panel): A) WT (top left) and mutant (top right) panels. Ligand dissociation trajectory is depicted by ligands in licorice representation sampled every 100 ps. The overall direction of the substrate release is depicted by transparent pink arrows. Bar plot and the error bar representing the mean and standard deviation of the closest distance between the center of mass of Imatinib and B) hinge and C) αC helix for WT (blue bar) and mutant (orange bar) trajectories.

Together these observations give mechanistic insight into the different dissociation time scales for Imatinib from WT Abl and from N368S Abl. A single point mutation results in divergent pathways for Imatinib dissociation, opening up the possibility to take a much quicker release route for the drug and thus lowering its residence time. In the next section, we provide calculated residence times from our simulations for both systems along with experimental benchmarks, following which we provide an atomistic underpinning for the observed differences in the WT and mutant dissociation pathways and k_off values.

Overall kinetics of the dissociation process

In order to determine the kinetics of the dissociation process, we first define the dissociated state of the ligand as when Imatinib has reached the solvent-exposed surface of the protein. We find that starting here there could be other “trap states” on the surface where Imatinib could bind with much weaker strength, but we ignore the kinetics corresponding to these as they can be expected to contribute much less relative to the time Imatinib takes to dissociate from the main binding site. More quantitatively, Imatinib is considered to be dissociated if the distance between the ligand center of mass and the binding site (defined as the heavy atoms of the residues within 5 of the ligand) exceeds 15 Å. As stated in the previous section, ligand dissociation was observed in each of the 11 infrequent metadynamics simulations for the WT and for the mutant. By fitting the respective 11 observations of the residence time to a Poisson distribution as per the protocol in Ref.^40,43 and described further in Supplementary Information (SI), we calculate the residence times τ for both systems along with k_off = 1/τ. We also perform a p-value analysis (Table 3 and Fig. 9 in SI) for both which indicate that the residence time calculations meet the reliability threshold from Ref.^40,43 The residence time for Imatinib in WT Abl was 1600±800 sec, in excellent agreement with the experimentally determined residence time of 1200±120 sec. On the other hand, we find a shorter residence time for Imatinib in the mutant Abl kinase, equalling 300±200 sec and again in excellent agreement with the experimentally measured value of 370±37 sec. Thus as can be seen in Fig. 2 E, qualitatively and quantitatively we are successful in recapitulating the experimentally observed residence times, with Imatinib k_off for mutant Abl being around an order of magnitude faster than WT. More importantly, apart from having a qualitative agreement in predicting the order of magnitude difference in Imatinib k_off for mutant vs WT Abl, the absolute values of the calculated residence time and k_off are well within the same order of magnitude as the experimentally determined values (Fig. 2 E). In the next section, the different dissociation pathways are explored in detail, describing the structural features distinguishing the two main pathways and finally culminating in providing a mechanistic explanation for the observed difference in Imatinib k_off values between WT and N368S Abl kinase.

Mechanistic underpinning of mutational effects on dissociation path

In the previous sections, we established that Imatinib unbinds from WT-Abl and N368-Abl dominantly via the hinge pathway and the αC pathway respectively and that our enhanced sampling approach is based on AMINO, SGOOP and infrequent metadynamics can return quantitatively accurate residence times for Imatinib in WT and N368S Abl kinase. We now provide further mechanistic analysis joining the results of the previous sections. For this, we approximately classify the Imatinib-Abl kinase system in three states, on the basis of the distance d between the Imatinib center of mass and the binding site. These are the (i) starting state (crystal structure), (ii) pre-release state (d ≤ 4.5 within Å) and (iii) the dissociated state (d≥15 Å).

We observe that for Imatinib in complex with the WT-Abl system (Fig. 4 A), the substrate release pathway is enclosed by a triad of interactions between the P-loop, hinge, and the DFG loop. In this state, residue Y253 from the P-loop forms a hydrogen bond with N322 from the hinge. Furthermore, Y253 packs against F382 from the DFG loop stabilized by the CH–π interaction. Subsequently, as Abl kinase transits to the pre-release state, P-loop moves away from the hinge and the DFG loop, resulting in the loss of the Y253-N322 hydrogen bond. The resultant pre-release state is characterized by weakened P-loop hinge interaction and an open pathway for substrate release. Consistent with this, for the WT Abl-Imatinib system by averaging over all 11 independent dissociation trajectories, we find (Fig. 4 A, C) the minimum attained distance between P-loop and the hinge region to be 8.7±3.1 Å, at the point of Imatinib release implying an open pathway for the substrate release proximal to the P-loop-hinge region. In contrast for the N368S Abl system, the corresponding minimum distance between P-loop and Hinge region (Fig. 4 C) is 6±3.73 Å, signifying a relatively occluded release pathway as compared to WT Abl. In the case of N368S mutant Abl, αC pathway is blocked by the packing of αC helix against the DFG motif and Imatinib. Particularly, the residue K271 from the K271–E286 of the prototypical ionic lock interacts with the backbone carbonyl (Fig. 4 B) of the residue D381 from the DFG motif. Furthermore, the backbone N-H of the F382 from the DFG motif stabilizes the binding of Imatinib. As mu- tant Abl transits to the pre-released state, the major conformational change that we observe involves (Fig. 4 B) the outward motion of αC helix from the αC helix-in state. As a direct consequence of the αC helix outward motion, we observe diminished K271-DFG interaction resulting in the formation of an open the αC helix pathway. Consistently, in the N368S Abl-Imatinib system by averaging over all 11 independent dissociation trajectories, we find (Fig. 4 D) the K271-D381 distance to be 7.9±1 Å in the pre-released state. Comparatively, for WT Abl-Imatinib, the average K271-D381 distance was 5±3 Å, signifying an open αC helix pathway for Imatinib release.

Figure 4:

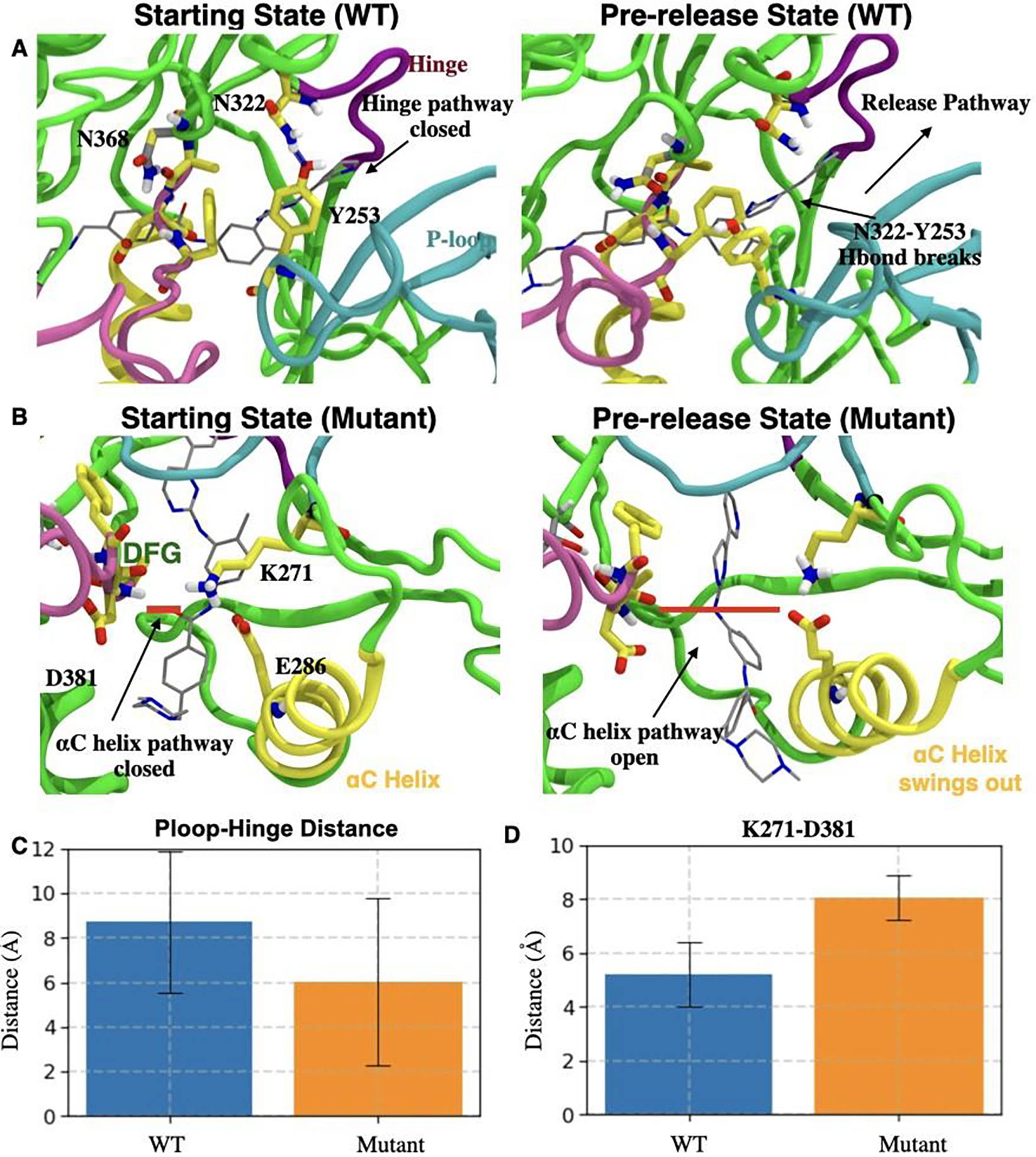
A) Left: Starting state of WT Abl (Crystal structure). H-bond between Y253 (P-loop) and N322 (hinge) is shown as a blue dashed line. Right: Abl conformation transiting to the pre-release state involves disrupted H-bond between Y253 and N322 forming an open ligand release pathway depicted by a black arrow. B) Left: H-bond between D381 from the DFG motif and Imatinib (gray sticks) in N368S Abl is shown as a thick red line. Right: Conformational changes in N368S Abl as it transits to the pre-released state involve the disruption of the interaction network of E286, K271, Imatinib, and DFG motif. C) and D) respectively show the closest distance (with error bars) between C) Cα atoms of Y253 and N322 for WT Abl (blue) and N368S Abl (orange); and D) Cα atoms of K271 and D381 for WT Abl (blue) and N368S Abl (orange).

In order to further understand the molecular basis of distinct Imatinib release pathways for WT and N368S Abl and the resulting differences in dissociation kinetics, we also analyze the effect of mutation on the conformational dynamics of the DFG motif. We observe (Fig. 5 A (left panel)) that the residue N368 in WT Abl forms hydrogen bonds with the backbone of residue A380 which is one residue upstream of D381 from the DFG motif. However, in N368S Abl, the mutated residue Serine with a smaller side-chain than the original Asparagine in the WT Abl has diminished propensity (Fig. 5 A (right panel)) to form the aforementioned hydrogen bonding interaction. Evidently, by averaging over all independent 11 WT dissociation trajectories prior to the substrate release, we observe (Fig. 5 B) that on average N368 forms 0.8±0.5 hydrogen bonds with backbone A380. On the other hand, by averaging over all independent 11 trajectories, the average number of hydrogen bonds between S368 and DFG motif was observed to be only 0.3±0.5. As a direct consequence of impaired hydrogen bonding interactions, we observe that the DFG motif has an elevated conformational flexibility (Fig. 5 B) in mutant Abl as compared to WT. Consistently, we observe that on an average in the N368S Abl-Imatinib trajectories, the mean root mean square deviation (RMSD) of the DFG motif from the crystal structure was observed to be 2.8 Å in comparison to 2.2 Å for the WT trajectories.

Figure 5:

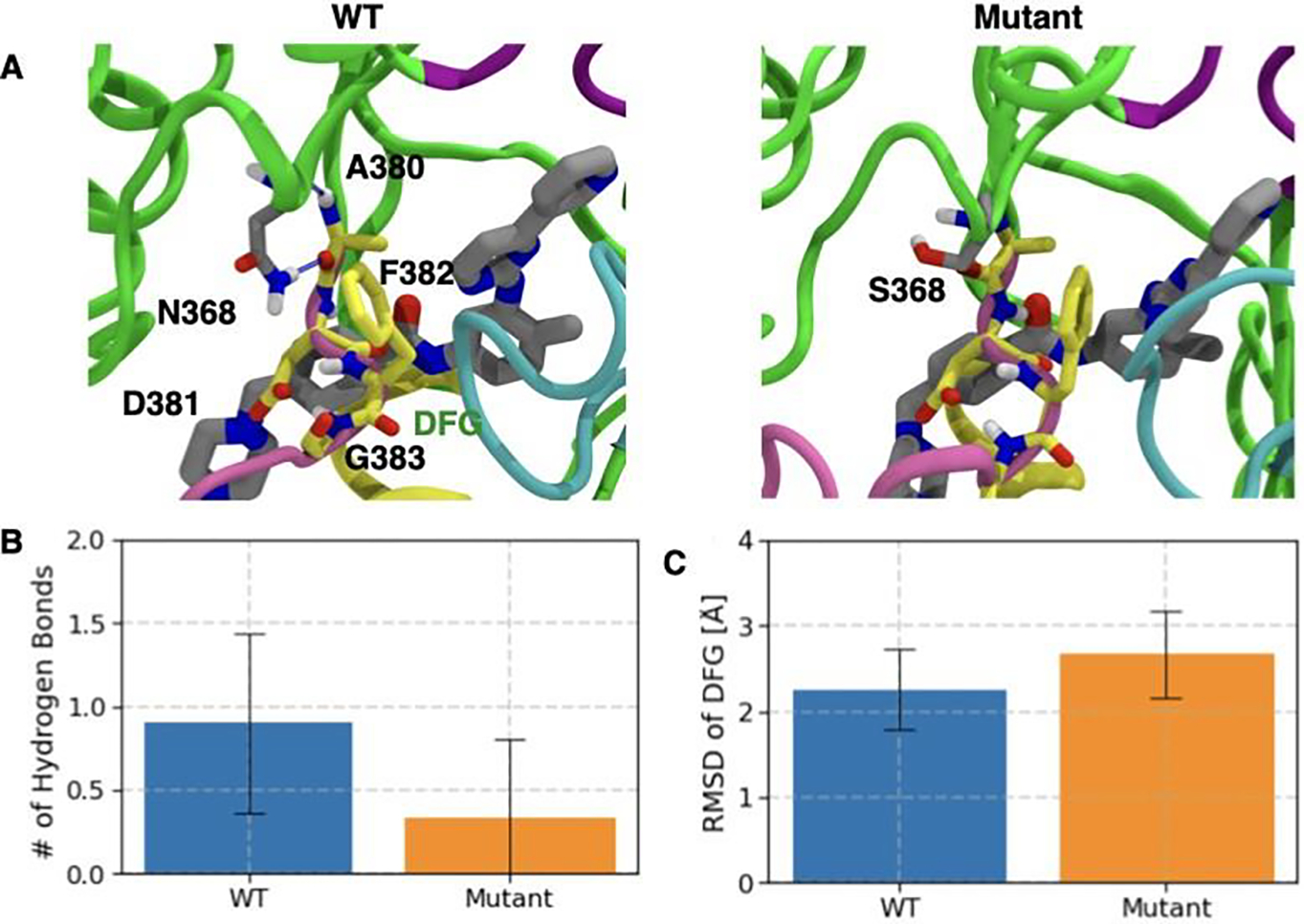
Flexibility of DFG motif is modulated by H-bond interaction of N368 and the DFG loop. A) Crystal structure pose of Imatinib (gray licorice representation) in WT (left panel) and N368S (right panel). DFG motif is represented by yellow licorice. H-bond between N368 (gray licorice) and A380 is shown as blue dashed line. Bar plot and the error bar representing the mean and standard deviation of B) N368 and DFG motif for WT Abl (blue bar) and N368S Abl (orange bar) C) Root mean square deviation (RMSD) of DFG motif from the crystal structure position for WT Abl (blue bar) and N368S Abl (orange bar).

We hypothesize that the increased flexibility of the DFG motif in the mutated N368S Abl kinase correlates with the diminished interaction between K271 and the DFG backbone, thereby allowing for the outward αC helix motion. This outward αC helix motion results in an open Imatinib release pathway proximal to αC helix. However, the P-loop and hinge interaction in mutant Abl remains unaffected and hence the pathway proximal to the hinge remains closed. In comparison to WT Abl, the DFG motif has diminished conformational flexibility, and thus the K271 DFG interaction is conserved. As a result, the αC helix remains packed against the DFG motif effectively blocking the αC helix proximal pathway. At the same time, we observe that in WT Abl instead of the outward αC helix motion, the P-loop and hinge interaction is weakened by the outward motion of the P-loop from the binding site. The outward P-loop motion contributes to opening up the substrate release pathway proximal to the hinge rather than the αC helix. It is worth pointing out here that as reported in Ref.²² the drug Dasatinib dissociates from wild-type and N368S Abl with near-identical and overall slower kinetics (43.2 and 43.8 minutes respectively). It is tempting to speculate here that this observation could also be qualitatively explained in light of our findings. In its bound structure Dasatinib is much closer to the hinge region, whereas Imatinib occupies the whole pocket. This could make Dasatinib more likely to dissociate through the hinge region, and thus less sensitive to the N368S mutation. Interestingly such a dissociation pathway was reported for Dasatinib from c-Src kinase previously where it took the hinge pathway during dissociation.⁷⁰

Conclusion

Drug resistance remains a major factor in the failure of anticancer therapeutic treatments. In this work, we describe an efficient formalism to characterize the molecular determinants of the resistance mutations. Particularly, we focus on the N368S Abl kinase mutation that results in a three times faster k_off for Imatinib against mutated Abl versus wild-type Abl, while the Imatinib binding affinity remains unchanged.⁶⁹ We systematically employ a combination of information theory (AMINO)²⁹ and statistical mechanics based (SGOOP)²⁸ methods to determine an optimum reaction coordinate (RC) that describes Imatinib unbinding mechanism from the WT and N368 Abl. The RC is optimized by iterating between rounds of SGOOP and metadynamics simulations and then used in independent rounds of infrequent metadynamics²⁷ to obtain dissociation kinetics.

We observe that Imatinib dissociates from WT and N368S Abl through two distinct pathways. The predominant Imatinib dissociation pathway from WT Abl is through the kinase hinge region, while against N368S Abl Imatinib dissociates via the αC helix region. Subsequently, comparing the Imatinib unbinding from the N368S and WT infrequent metadynamics trajectories, we observe a diminished propensity of the mutated serine at N368 to form an H-bond with the backbone carbonyl of A380 which is one residue upstream from D381 of the DFG motif. In comparison, in the WT Abl aforementioned H-bonding interaction is conserved. Furthermore, the reduced H-bonding interaction between N368S and the DFG motif gets manifested in increased flexibility of the DFG motif. We hypothesize that the increased DFG motif flexibility as observed in N368S Abl results impairs the interaction of K271 and the DFG backbone, facilitating an outward αC helix motion, thus allowing for Imatinib release via the αC helix pathway. The increased flexibility of N368S relative with WT is consistent with experimental observations. ⁶⁹ In comparison, in WT Abl Imatinib unbinding requires a drastic conformational change involving disruption of the H-bonding interaction of N322 from the hinge and Y253 from the P-loop, creating a pathway for Ima- tinib to release via the hinge pathway. We reason that comparatively larger conformational change in the Abl resulting in Imatinib release from WT as compared to N368S Abl assists in faster k_off for N368S as compared to WT Abl. This work thus demonstrates the potential to perform such investigations in the future for diverse systems using all-atom simulations that can access pharmacologically relevant timescales with minimum human intervention and prior bias.

Table 1:

Summary of Imatinib dissociation kinetics, comparing the residence time/k_off of WT and mutant Abl as measured in this work against experiments in Ref. ⁶⁹

System	Infreq Metad residence time (sec)	Infreq. Metad. koff (sec−1)	Experimental residence time (sec)	Experimental koff (sec−1)	p-value
Wild-type	1600± 800	6± 3 e-04	1200± 120	8.3± .83 e-04	0.11
N368S	300± 200	4± 2 e-03	370± 37	2.7± .27 e-03	0.23.

Data Availability Statement

The data supporting this work is available upon request. Software used in this work is available at github.com/tiwarylab