Characterization and parametric optimization of additive manufacturing process for enhancing mechanical properties

Abstract

Additive manufacturing (AM), also known as 3D printing, is a cutting-edge industrial production technique that enables the creation of lighter, stronger components and systems. Fused deposition modeling (FDM) is a popular AM process for creating prototypes and functional components out of common engineering polymers. The mechanical characteristics of printed items are dramatically altered as a result of various process factors. As a result, it is critical to examine the impact of printing settings on the quality of the printed item. In terms of flexural strength, this study presents an experimental examination into the quality analysis of parameters on printed components utilizing FDM. By adjusting process factors such as layer height, raster width, raster angle, and orientation angle, the experiment was carried out utilizing Taguchi's L18 mixed orthogonal array approach. The UNITEK-94100 universal testing equipment was used to evaluate the flexural strength of Acrylonitrile butadiene styrene (ABS) specimens that had been conditioned as per ASTM D790 standard. The impacts of parameters on experimental results were examined and optimized using the hybrid genetic algorithm with response surface methods, response surface approach, and Taguchi method. When the optimal solutions of each technique were studied, the response surface approach and Taguchi methods were determined to be less promising than the genetic algorithm method.

Highlights

• This study contains the following remarkable contents:

• •Fused deposition modeling is a popular Additive manufacturing process for creating prototypes and functional components out of common engineering polymers.
• •Fused deposition modeling was considered in this study.
• •The genetic algorithm, response surface methodology, and Taguchi method were employed for multi-objective optimization of printing component characteristics.
• •The considered operational parameters are layer height, raster width, raster angle, and orientation angle.
• •Flexural strength is considered output response.

Additive manufacturing; Fused deposition modeling; Flexural strength; Genetic algorithm; Response surface method; Taguchi method.

1. Introduction

Additive manufacturing (AM), commonly known as 3D printing is a cutting-edge technology that produces a product directly from a CAD file using a layer-based manufacturing approach. In additive manufacturing, data computer-aided design (CAD) software or 3D object scanners are used to direct machines to deposit material in precise geometric patterns, successive layers. AM is a relatively new technology that is swiftly gaining momentum in the marketplace. This technology is increasingly being used for product customization and for the manufacturing of any type of complicated design in the industries of agriculture, healthcare, automobiles, and aviation. There are different types of technologies under additive manufacturing like Material extrusion, Material jetting, Powder bed fusion, Vat photopolymerization, Sheet lamination, Binder jetting, Directed energy deposition [1, 2, 3]. ABS, PLA, polycarbonate, Ultem, PEEK, and fiber-reinforced thermoplastics are some of the thermoplastic polymers and reinforced materials that can be printed with FDM [4, 5, 6]. FDM-produced components are increasingly displacing conventional components in a diversity of industries, including the locomotive, aviation, and health sectors. The mechanical features of FDM printed components are strongly prejudiced by the process variables and their settings [7, 8, 9, 10, 11]. As a result, examining the impacts of input factors and anticipating outcomes by utilizing appropriate process parameters is critical for enhance the mechanical characteristics of printed components.

Many of the reported studies attempted to improve the production parameters of fused deposition modelling for printing high-quality parts. For instant Srinivasan et al. [12] employ response surface methodology to anticipate and optimize the impact of process parameters (infill concentration, infill design, and layer height) on tensile properties in FDM-produced ABS components. Using Taguchi's mixed model fractional factorial design, Hikmat et al. [13] investigated the effect of various printing parameters on tensile strength using PLA filament, including build orientation, raster orientation, nozzle diameter, extruder temperature, infill density, shell number, and extruding speed. The findings revealed that build orientation, nozzle diameter, and infill density all had a substantial impact on component strength, with build orientation having the biggest impact. Rayegani and Onwubolu [14] utilize differential evolution and group method for data handling to anticipate and optimize the connection between input factors (part alignment, raster orientation, raster width, and orientation angle) and tensile strength for FDM parts. According to Enemuoh et al. [15], infill density, followed by layer height, print speed, and fill pattern, has high potential on the tensile strength of the FDM component. Christiyan et al. [16] examined the effect of process factors (layer height and printing speed) on the mechanical features of 3D-printed ABS composite. They discovered low production speed and small layer height resulted in the material's optimal tensile and flexural strength. Gebisa and Lemu [17] looked examined the influence of process on the tensile characteristics of components made with the FDM method and ULTEM 9085 polymeric material. According to their findings, the raster angle has a substantial impact on tensile characteristics.

The mechanical characteristics of FDM-produced components are highly impacted by process parameters, according to the literature. It was also vital to examine the combined effects of FDM parameters on the mechanical features of the produced components. As a result, As a result, the present study examined the impact of four key process factors on the flexural strength of ABS components printed using an FDM printer, including layer height, raster width, raster angle, and orientation angle. The remaining parameters are left at their default values. In Minitab software, the Taguchi L18 mixed orthogonal array design of experimental sets was used to organize the trials. The flexural specimens were built in accordance with the ASTM D790 standard. Taguchi analysis, analysis of variance, and factorial plots were used to explore the impact of each performance characteristic. The genetic algorithm hybrid with response surface methods, response surface approach, and Taguchi method were used to optimize the output response. Furthermore, the optimal results of each method were compared to identify the best optimizing method.

2. Materials and methods

2.1. Additive manufacturing machine and printing materials

The specimens in this investigation were printed using a Flash Forge Guider II 3D printer. The printer's build envelope measures 280 × 250 × 300 mm³ and it can produce components with an accuracy of ±0.2 mm. ABS (Acrylonitrile Butadiene Styrene), the most commonly used 3D printing polymer, is employed to create the components in this research. ABS is a popular thermoplastic with the chemical formula (C8H8• C4H6•C3H3N). ABS is a copolymer composed of styrene and acrylonitrile polymerized with polybutadiene [18].

2.2. Experimental design

This study takes into account four primary Flash Forge Guider II 3D printer settings in order to improve and assess the relationship between these parameters and the suggested response characteristics. Inputs like Layer height, raster width, raster angle, and orientation angle were chosen as a result. Layer height is the height of the deposited layer measured along the Z-axis following extrusion from the nozzle tip (or the vertical direction of the FDM machine). It is usually less than the diameter of the extruder nozzle tip [19]. The width of the beads deposited along the extruder tool path is referred to as raster width (which forms the raster). It is mostly determined by the diameter of the extruder nozzle tip [20]. The direction of material beds in relation to the build platform's x-axis is defined as raster angle. It's the angle of the raster pattern in relation to the X-axis [21]. The orientation angle characterizes how the component is positioned (oriented) within the build platform in relation to the FDM machine's x-, y-, and z-axes, as well as the angle at which the part will be produced [22, 23]. The input factors were chosen based on the specification of the machine and the remaining parameters are left at their default values. The input parameters and their ranges that were investigated for this research are listed in Table 1. A design of experiments matrix was generated using Taguchi L18 mixed orthogonal array based on specified input components and their levels, as shown in Table 2.

Table 1.

Process parameters to be controlled and its range.

S.No.	Process parameters	Units	Level 1	Level 2	Level 3
	Layer height	mm	0.15	0.25
	Raster width	mm	0.4064	0.4364	0.4664
	Raster angle	˚	0	22.5	45
	Orientation angle	˚	0	15	30

Table 2.

L18 orthogonal array Taguchi experimental design matrix and measured responses.

Exp. Trials	Layer height (mm)	Raster width (mm)	Raster angle (˚)	Orientation angle (˚)	Flexural Strength (MPa)	S/N ratio
1.	0.15	0.4064	0.0	0	15.34	23.7165
2.	0.15	0.4064	22.5	15	22.79	27.1549
3.	0.15	0.4064	45.0	30	22.13	26.8996
4.	0.15	0.4364	0.0	0	22.82	27.1663
5.	0.15	0.4364	22.5	15	28.14	28.9865
6.	0.15	0.4364	45.0	30	29.83	29.4931
7.	0.15	0.4664	0.0	15	20.29	26.1456
8.	0.15	0.4664	22.5	30	31.24	29.8942
9.	0.15	0.4664	45.0	0	18.79	25.4785
10.	0.25	0.4064	0.0	30	14.09	22.9782
11.	0.25	0.4064	22.5	0	22.12	26.8957
12.	0.25	0.4064	45.0	15	31.64	30.0047
13.	0.25	0.4364	0.0	15	18.81	25.4878
14.	0.25	0.4364	22.5	30	27.92	28.9183
15.	0.25	0.4364	45.0	0	30.69	29.7399
16.	0.25	0.4664	0.0	30	13.45	22.5744
17.	0.25	0.4664	22.5	0	27.78	28.8746
18.	0.25	0.4664	45.0	15	25.04	27.9727

2.3. Specimen fabrication

According to the specifications, CATIA V5 software was used to create a 3D model of the test specimen. The stereo lithography (STL) type is used to save the CAD file. The File format is then passed via the slicer, which separates it into the needed number of layers. Flash print slicing program is also used to add printing settings. The slicer then transforms the STL file to a G-code data, which the printers use to begin layer-by-layer fabrication of the specimen. The flexural specimens were built in accordance with the ASTM D790 (127 mm × 25.4 mm x 6.35 mm) standard as shown in Figure 1. Test sample fabricated for the experiments are shown in Figure 2.

Figure 1.

The ASTM D790 - flexural test (size: mm).

Figure 2.

Flexural test specimens.

2.4. Experimental producers

The UNITEK-94100 universal testing equipment was used to evaluate the flexural strength of ABS specimens that had been conditioned as per ASTM D790 standard. The test sample with the necessary length was supported from below by two supports, and the load was given from above with a radius of 5 mm edge, as illustrated in Figure 3. The loading rate in the experiment was 2.54 mm/min (0.1 in/min). To prevent sample loosely positioned between the supports, and ensure that the specimens were in good contact with the supports, 10N preload was applied at middle of span length using a loading pin. When the ultimate flexural strength is reached, the samples are broken by a fracture that runs from the bottom to the top. The test was halted when the sample achieved 5 percentage strains, as indicated by the standard, for those test samples that did not breakdown even at extreme load. The experimental flexural strength values are shown in Table 2.

Figure 3.

Experimental setup of flexural test.

2.5. Hybrid GA-RSM optimization

Natural selection inspired the genetic algorithm, which is a powerful evolutionary technique. It implements bio-inspired procedures such population initiation, selection, recombination, and crossover to realize the idea of survival of the fittest. By integrating the GA fitness function with the mathematical equation, the GA optimization is created [24, 25] In this work, the multi-objective hybrid GA-RSM was employed as an optimal algorithm in MATLAB 2019a. The fitness function for GA is loaded with the RSM equation to construct the GA-RSM model. Variation of the GA parameter functions during successive trials yields the optimal fitness value. Table 3 lists the parameter functions and values that were utilized in this investigation in GA. To get an optimum solution using the Genetic algorithm, Eq. (1) was employed as objective functions.

Table 3.

GA parameter setting and its value.

Population type	Double vectors
Population size	200
Creation function	Feasible population
Fitness scaling function	Rank
Selection function	Tournament
Tournament size	4
Reproduction	Default values
Elite count	1.5 (0.05∗ Population size)
Crossover fraction	0.8
Mutation function	Adaptive feasible
Crossover function	Constraint dependent
Number of generations	400
Function tolerance	1e-6
Constraint tolerance	1e-3

2.6. Response surface methods optimization

The response surface method (RSM) is a mathematical and statistical technique for determining the relationships between response and input parameters (independent variables). RSM entails choosing an experimental method to investigate the parameters and using empirical statistical modelling to establish a link between the variables and the outcomes [26]. Using Minitab 18 software, regression mathematical models for interaction between process parameter and flexural strength were created in this study. The proposed mathematical model employs factors with a prob > F smaller than 0.05, and these models may be used to estimate flexural strength experimental outcomes using any combination of printing parameters. Table 4 shows the ANOVA results for the tensile strength with 95% confedence of interval. The additional adequacy metrics R², Adjusted R², and projected R² are also shown in the same tables. It is noteworthy that the experimental outcome is better and more consistent with the model as it approaches unity. The mathematical model in Eq. (1) connects the output response with the input printing settings. The RSM methods have also been used to increase the flexural strength of FDM ABS printing products.

$$FlexuralStrength=-935+332A+4163B+0.327C+1.06D-4492B\ast B-0.00828C2+0.00149D2-825A\ast B+2.86A\ast C-1.97A\ast D-0.95B\ast C-1.56B\ast D+0.00317C\ast D$$ (1)

Where A is layer height, B is raster width, C is raster angle and D is orientation angle.

Table 4.

ANOVA for flexural strength.

Source	DF	Adj SS	Adj MS	F-Value	P-Value
Regression	13	552.090	42.4684	3.95	0.097
A	1	12.115	12.1150	1.13	0.348
B	1	69.462	69.4617	6.47	0.064
C	1	1.177	1.1767	0.11	0.757
D	1	5.895	5.8946	0.55	0.500
B∗B	1	60.712	60.7116	5.65	0.076
C∗C	1	58.752	58.7520	5.47	0.079
D∗D	1	0.374	0.3741	0.03	0.861
A∗B	1	14.920	14.9204	1.39	0.304
A∗C	1	60.594	60.5940	5.64	0.076
A∗D	1	12.832	12.8316	1.19	0.336
B∗C	1	2.383	2.3831	0.22	0.662
B∗D	1	2.821	2.8207	0.26	0.635
C∗D	1	3.708	3.7085	0.35	0.588
Error	4	42.966	10.7416
Total	17	595.056

2.7. Taguchi methods optimization

Dr. Genichi Taguchi, a Japanese engineer, created the Taguchi technique, which is based on orthogonal arrays (OA). To arrange the process's parameters and the levels at which they should be adjusted, Taguchi's experimental design employs orthogonal arrays [27]. The trial findings should be converted into signal-to-noise ratio (S/N ratios) to assure the quality of the production process. There are three basic types of S/N ratios: smaller-is-better, nominal-is-best, and larger-is-better. For this study flexural strength, the larger one is best chosen. The signal-to-noise ratio (S/N) is a performance metric used in the development of noise-sensitive products and processes. The greatest signal-to-noise ratio process parameter choices always produce the best quality with the least amount of contrast [28, 29]. To select the best configuration, Minitab V 18 software was utilised Taguchi methods in this paper.

3. Results and discussion

3.1. Impact of process parameters on flexural strength

The Taguchi analysis technique was used to examine the flexural strength outcomes. Table 5 illustrations the relative impact of numerous factors to relative changes in flexural strength. The most critical element impacting flexural strength is raster angle, followed by raster width, orientation angle, and layer height, according to our findings.

Table 5.

Response table for flexural strength.

Levels	Layer height mm	Raster width mm	Raster angle º	Orientation angle º
1	23.49	21.35	17.47	22.92
2	23.50	26.37	26.67	24.45
3		22.77	26.35	23.11
Delta	0.02	5.02	9.20	1.53
Rank	4	2	1	3

The results of the flexural strength test (UTS) were evaluated using ANOVA to identify critical parameters impacting performance metrics. The average tensile strength (UTS) ANOVA findings for each 95 % confidence interval are shown in Table 6. To validate the significance, the F and P values in the ANOVA table are employed. The F-test and P-test are based on the premise that the higher the F- value ​and lower the P - ​value of a parameter, the greater the impact of changing that process parameter on performance characteristics. If the P-value is less than 0.0500 (that is, = 0.05, or a 95 percent confidence level), the term process parameter is important. The P-values for the raster angle in the ​ANOVA tables are less than 0.05, indicating that the raster angle is a substantial factor affecting flexural strength.

Table 6.

ANOVA for flexural strength.

Source	DF	Adj SS	Adj MS	F-Value	P-Value
Layer height	1	0.002	0.002	0.00	0.993
Raster width	2	80.297	40.148	2.24	0.157
Raster angle	2	327.359	163.679	9.14	0.006
Orientation angle	2	8.341	4.171	0.23	0.796
Error	10	179.057	17.906
Total	17	595.056

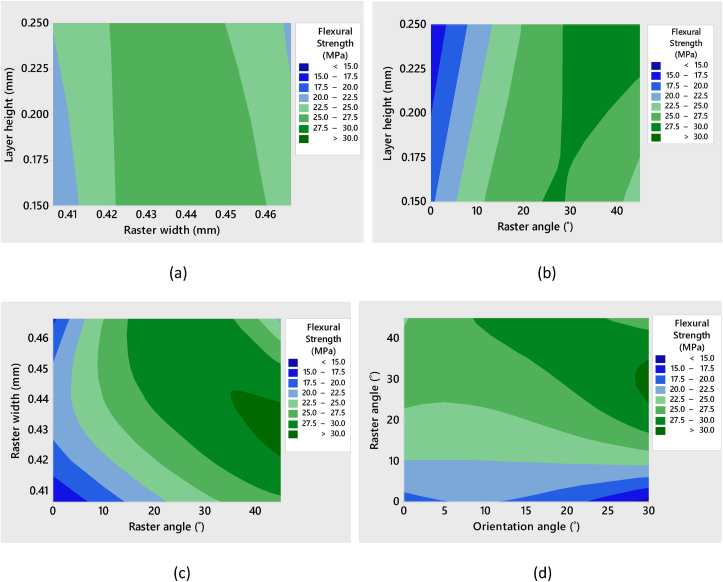
Figure 4 illustrates the contour plot graphs that demonstrate the relationship between ABS component flexural strength and process variables. Layer height (or also known as layer thickness) is important factor that could influence the flexural properties. As clear shown in Figure 4(a) and (b), increasing layer height has insignificant impact on the flexural strength. Raster width is another important factor that could influence the flexural strength. As it can be clearly shown in Figure 4(a) and (c), 043 mm of raster width have given the highest flexural strength. Raster angle (or also known as raster orientation) is another important factor that could influence the mechanical properties of the specimen. As it can be clearly shown in Figure 4(b) and (c), 45° of raster angle has given the highest flexural strength of the specimen. Effect of orientation angle (or also known as building orientation) on flexural strength was clearly shown in Figure 4(d). From the figure, it is clear that the flexural strength tends to rise slightly when the orientation angle increases.

Figure 4.

Contour plots of flexural strength with process parameters.

Figure 5 illustrates factorial plots for flexural strength, which show how flexural strength varies with input parameters. The layer height, raster width, and orientation angle all have negligible effects on flexural strength, as shown by these factorial graphs. The raster angle has the largest influence on flexural strength, and as the raster angle increases, so does the flexural strength.

Figure 5.

Factorial plots for flexural strength and inputs parameters.

3.2. Hybrid GA-RSM optimization results

The most optimum outcome was reached using the genetic algorithm after 102 rounds, which is a rather quick process. The average spread in each generation is shown in Figure 6 as a function of the number of repetitions. The input parameters have been fine-tuned to provide the highest possible flexural strength. The best input parameters were 0.25 mm layer height, 0.432mm raster width, 43.871 raster angle, and 29.991 orientation angle, which were employed in a multi-objective evolutionary algorithm in MATLAB 2019a to reach a maximum flexural strength of 33.096 MPa Table 7 shows the optimal values for flexural strength using the GA, RSM, and Taguchi techniques. When compared to RSM and Taguchi approaches, it can be seen that GA-based methodology has been successful in modeling, simulating, and optimizing process parameters for maximum flexural strength.

Figure 6.

Average spread as a function of iteration number for flexural strength.

Table 7.

GA, RSM, and Taguchi methods optimized response parameters.

Optimization methods	Optimum setting				Optimum flexural strength (MPa)
	Layer height (mm)	Raster width (mm)	Raster angle (˚)	Orientation angle (˚)
Hybrid GA-RSM optimization	0.25	0.432	43.871	29.991	33.096
Response surface methods (RSM) optimization	025	0.4306	43.6364	30	33.315
Taguchi methods optimization	0.25	0.4064	45	15	31.640

3.3. Response surface methods optimization results

According to the optimization plot Figure 7, the flexural strength individual desirability and optimal results are 1.000 and 33.315 MPa, respectively. 0.25 mm layer height, 0.4306 mm raster width, 43.6364 raster angle, and 30 orientation angle are the best settings. Using the RSM Approaches, Table 7 gives the best flexural strength values.

Figure 7.

Optimization of response parameters using RSM.

3.4. Taguchi methods optimization results

When applying the Taguchi technique, there are three prerequisites for improvement. Smaller is preferable, nominal is preferable, and greater is preferable. For this study, flexural strength, the larger one, was best chosen. The signal-to-noise ratio (SNR) is a performance metric used in the development of noise-sensitive products and processes. The process parameter selections with the highest signal-to-noise ratio always yield the best quality with the least amount of contrast. According to S/N analysis, the best flexural strength value in this investigation is 31.64 MPa with a signal to noise ratio of 30.0047. The results obtained from Taguchi techniques reveal the optimal setup parameters as 0.25 mm layer height, 0.4064 mm raster width, 45 raster angle, and 15 orientation angle. Table 7 displays the Taguchi methods' ideal flexural strength values.

4. Conclusions

For enhancing the flexural strength of components created on FDM flash dreamer II machines, this work proposes genetic algorithms, response surface approaches, and Taguchi methods. For the L18 mixed orthogonal matrix experiment, the Taguchi design was employed. Taguchi analysis, bar charts, and factorial plots were used to examine the impacts of process factors such as layer height, raster width, raster angle, and orientation angle using Minitab V18.1 software. To attain a maximum flexural strength, a multi-objective hybrid GA-RSM in MATLAB 2019a was employed, whereas response surface techniques and Taguchi methods used MintabV18.1. The optimal setting of Taguchi method was determined using the resultant signal-to-noise ratio. From the study we can conclude Raster angle has significant impact on flexural strength, whereas raster width, orientation angle, and layer height have negligible effect. The optimal flexural strength obtained using hybrid GA-RSM are 33.096 MPa at .25 mm layer height, 0.432mm raster width, 43.871 raster angle, and 29.991 orientation angle. According to the RSM study, 0.25 mm layer height, 0.4306 mm raster width, 43.6364 raster angle, and 30 orientation angle produce the best flexural strength of 33.315 MPa with a desirability of 1.00. The best setup settings, according to Taguchi, are 0.25mm layer height, 0.4064mm raster width, 45 raster angle, and 15 orientation angle. The optimal FDM values for flexural strength, according to Taguchi optimization techniques, are 31.64 MPa with a maximum ratio of S/N = 30.0047. The findings also show that the Taguchi and response surface methods are less promising than the GA-RSM.

Declarations

Author contribution statement

Amanuel Diruba Tura: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Hana Beyene Mamo: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Funding statement

Amanuel D. Tura was supported by Jimma Institute of Technology under Mega Project Code: JiT_2021_22, Ref. No: RPD/JiT/329/14 dated 07/02/2022.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.