Abstract
Background
Genome-wide Association Studies (GWAS) aims to uncover the link between genomic variation and phenotype. They have been actively applied in cancer biology to investigate associations between variations and cancer phenotypes, such as susceptibility to certain types of cancer and predisposed responsiveness to specific treatments. Since GWAS primarily focuses on finding associations between individual genomic variations and cancer phenotypes, there are limitations in understanding the mechanisms by which cancer phenotypes are cooperatively affected by more than one genomic variation.
Results
This paper proposes a network representation learning approach to learn associations among genomic variations using a prostate cancer cohort. The learned associations are encoded into representations that can be used to identify functional modules of genomic variations within genes associated with early- and late-onset prostate cancer. The proposed method was applied to a prostate cancer cohort provided by the Veterans Administration’s Million Veteran Program to identify candidates for functional modules associated with early-onset prostate cancer. The cohort included 33,159 prostate cancer patients, 3181 early-onset patients, and 29,978 late-onset patients. The reproducibility of the proposed approach clearly showed that the proposed approach can improve the model performance in terms of robustness.
Conclusions
To our knowledge, this is the first attempt to use a network representation learning approach to learn associations among genomic variations within genes. Associations learned in this way can lead to an understanding of the underlying mechanisms of how genomic variations cooperatively affect each cancer phenotype. This method can reveal unknown knowledge in the field of cancer biology and can be utilized to design more advanced cancer-targeted therapies.
Keywords: Genome-wide Association Study, Network Representation Learning, Machine Learning
Introduction
Genome-wide Association Studies (GWAS) correlate specific genomic variations with phenotypes. They are being actively applied in cancer biology to investigate the link between an individual’s genomic variations and cancer phenotypes, including susceptibility to certain types of cancer or predisposed responsiveness to treatments. GWAS has identified many common genomic variants associated with cancer phenotypes. A recent review study by Sud et al. [1] highlighted hundreds of loci associated with increased cancer risk in a variety of cancer tissues, including breast, prostate, lung, colorectal, pancreatic, gastric, renal, and bladder cancers.
Cancer phenotypes, such as early-onset and late-onset, can be understood as a result of the accumulation of abnormal gene functions, where each gene function can be compromised by genomic variants within each gene [2]. The implications of individual genomic variants on gene function have been actively investigated using genomic data. Substantial amounts of genomic variants have been identified with the potential to affect gene function in a variety of mechanisms, including premature stop, splice site, frameshift insertion and deletion (InDel), missense, untranslated region (UTR), promoter, proximal enhancer, protein binding sites, and RNA binding sites [3].
A collection of genomic variants within each gene can cooperatively alter the expression level of a gene [4] and the structure of its gene product [5]. This implies that cancer phenotypes can be cooperatively influenced by two or more genomic variations within genes that interact with each other [2]. The widespread linkage disequilibrium (LD) of the human genome also suggests that there may be unknown functional associations among individual genomic variations within genes [6]. To understand how genomic variations cooperatively affect specific cancer phenotypes, it is required to first identify associations among them.
There are some challenges in identifying associations among genomic variants within each gene. First, there are no metrics available that can encompass both the co-occurrence between variations and the correlation between the co-occurrence and a given cancer phenotype. This makes it difficult to generate machine learning models that require quantifiable features that well represent associations among genomic variants within each gene. Second, there is no effective and unbiased way to learn associations from pairwise relationships between variations. A computational framework capable of extracting usable representations from data with a graph structure is required, where each node is each variant, and the edge is the degree of association between the two variants. Lastly, there is no systematic way to test how robust these learned associations are.
Biological networks have been actively used to learn associations between biological entities, such as protein-protein interaction (PPI) networks and gene co-expression networks. Many studies have used these network approaches to capture biologically meaningful subgroups or gene subsystems in which genes interact with each other [7–9]. In this study, we consider the individual genomic variations within each gene as entities and extend the biological networks approach to learn associations between them from data.
One of the most effective ways to extract information from a network is to use a network representation learning technique such as DeepWalk [10] and GloVe [11]. DeepWalk is a graph embedding algorithm that uses a deep learning architecture. It learns vector representations from a given graph structure, where the representation encodes relationships between nodes [10]. It first generates a document-like input by sampling the nodes with random walks, and then uses natural language processing (NLP) techniques on the input data to generate vector representations. The learned representation space reflects the relative distance between nodes. GloVe takes the input structure as a global matrix and applies matrix factorization to get vector representations [11]. DeepWalk relies on local contexts to learn representation while GloVe uses global statistics. Both approaches are known to have good performances in NLP tasks such as word analogy inference [10, 11].
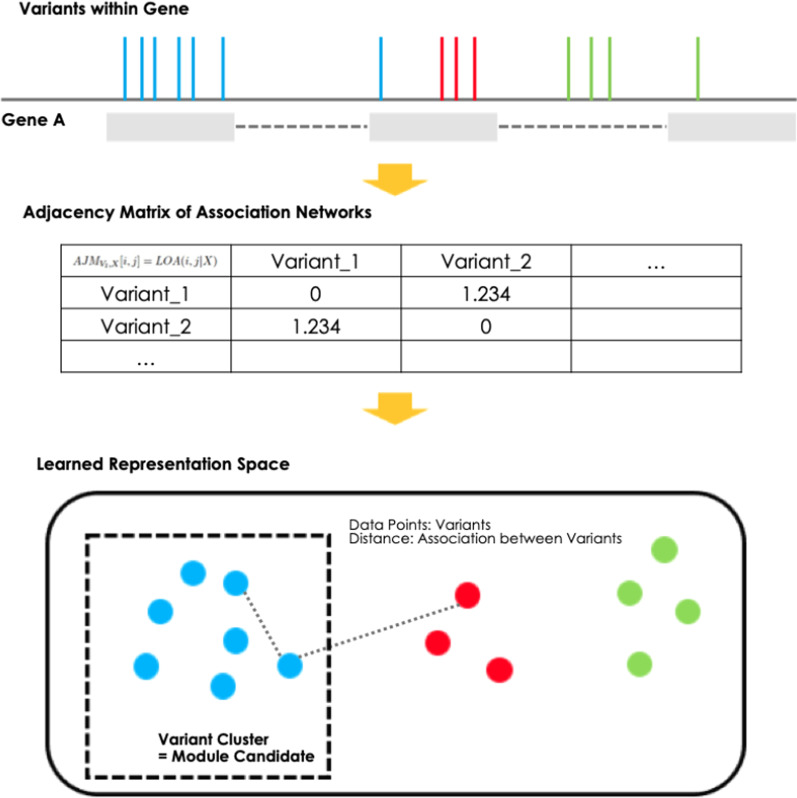
We devised a computational framework for identifying associations among variants by learning network representations. Here, we define the association between two variants by two criteria: (1) the two variants must co-occur frequently, and (2) this co-occurrence must be correlated with a given cancer phenotype. We devised a metric that can quantify both criteria at once to define the level of association (LOA) between two variants for a given cancer phenotype. By measuring the LOA for every pair of variants within a gene, it is possible to construct an association network where each node is each variant and the edge weights are the LOAs between them (Fig. 1). It is possible to infer modules of variants in a data-driven manner using representations learned from the constructed network.
Fig. 1.
Identification of functional module candidates within a gene. First, the proposed method generates an association network by calculating the LOA between each variant within a gene. It then learns the associations from the network to produce a representation that can be used to identify module candidates
Prostate Cancer (PC) is the leading cancer diagnosis in U.S. men with an estimated 191,930 new cases expected in 2020 and the second most common cause of cancer deaths in U.S. men, accounting for about 33,330 deaths in 2020 [12]. PC is known to be a heterogeneous disease that includes both a chronic phenotype of old age and an aggressive phenotype such as clinically advanced early-onset PC. High-throughput sequencing technology offers opportunities to elucidate biomarkers at the molecular level [13]. However, the clinical and molecular characteristics of early-onset PC still have not been well described [14]. This creates an opportunity for large-scale machine learning genomics approaches to contribute to elucidating the mechanisms of early-onset PC at the molecular level.
We applied the proposed approach to the prostate cancer cohort provided by the Veterans Administration’s (VA) Million Veteran Program (MVP) to identify intragenic functional modules associated with early-onset prostate cancer. Our cohort had 33,159 PC patients (3,181 early-onset and 29,978 late-onset). Note that the scope of the study included only early and late-onset patients with prostate cancer and that the methodology was also evaluated using only the prostate cancer cohort.
The following sections describe (1) how to define associations between genomic variations for a given cancer phenotype, (2) how to learn representations from defined association networks between variations, and (3) how to identify sets of genomic variations within each gene as candidates for functional modules associated with a given cancer phenotype and (4) how to evaluate the proposed method.
Materials and methods
Our study used DNA samples and phenotypic data from Million Veterans Project (MVP). The MVP program recruited individuals aged 18 to >100 years old from 63 Veterans Affairs Medical Centers across the United States. We used MVP release 19.2 for this analysis [15]. This approach was applied to a cohort with 33,159 prostate cancer patients (3,181 early-onset and 29,978 late-onset). We identified 2,146,891 genomic variations within 5,298 genes. Note that variants here include only single nucleotide variations (SNVs) and InDels.
Our project was approved by the VA Central IRB. All participants enrolled in the MVP have signed an Informed Consent document allowing the use of their data by approved researchers in accordance with the MVP data access policy.
Terminology
A genomic variation, variation, genomic variant, or variant refers to individual SNVs and InDels at specific genomic locations.
Association refers to the co-occurrence between two genomic variations or a correlation between a specific variation and a phenotype.
An intragenic functional module or module within a gene refers to a set of genomic variants located within each gene, where members co-affect the structure or function of the gene product.
A module candidate refers to a set of variants within a gene that is inferred from the data as potential candidates for a module.
A phenotype associated module refers to a module candidate identified as having a statistically significant association with a given phenotype.
Defining associations between genomic variations
Identifying genomic variations that are associated with each other starts with defining what is association. There are two different aspects of associations to be considered in this context: (1) Co-occurrence between two genomic variations and (2) Correlations between the co-occurrence and a given cancer phenotype. We addressed this by defining the level of association between two variations A and B for a given phenotype X as the following Eqs. (1a, 1b).
| 1a |
| 1b |
LOA(A, B|X) represents the level of association between the two variations A and B for a given phenotype X. is the Jaccard similarity [16] of the two variations A and B when X is k. Where k is 0 or 1. Where represents the sample with the given phenotype X, and is vice versa. represents the intersection of samples with phenotype values of k and both A and B variations, whereas indicates the union. Hence, JCS is the ratio of intersection to the union, which is how frequently the two variations co-occur. LOA represents the log ratio of JCS for samples with a given phenotype to samples without the phenotype. Thus, a positive LOA indicates a positive association between two variations for a given phenotype, a negative LOA indicates the opposite, and a value of 0 indicates no association. By defining a metric in this way, it is possible to measure how differentially two variants co-occur in samples with different phenotypes.
Constructing association networks of intragenic variations
After annotation, each genomic variation is assigned to the gene in which it is located. We then computed the LOA between all pairwise variations (Eq. 1a) to construct a graph structure represented by the adjacency matrix AJM (Eq. 2). Each node in the constructed graph or association network is a genomic variation and the edge weight represents the level of association between the two variations.
| 2 |
For i and , where is the set of all genomic variations identified in gene l. The edge weight between two nodes or variations i and j for a given phenotype X can be defined as LOA(i, j|X), which is also the value of the adjacency matrix . Since the metric is symmetric, equals .
Representation learning for the defined association networks
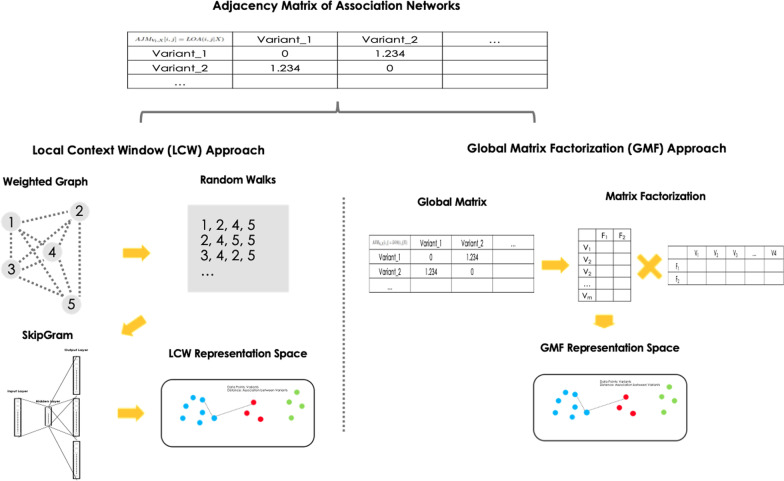
The constructed association network contains valuable information about how each genomic variation in each gene is associated with each other. There are two major approaches to learning associations between entities, (1) Local context window approaches such as DeepWalk [10], (2) Global matrix factorization approaches such as GloVe [11]. In the task of learning associations between genomic variations, there was no systematic comparison of which approach worked better, so we implemented both methods to suit our problem and compared the results. Hereafter, the local context window approach will be referred to as the LCW approach and the global matrix factorization approach will be referred to as the GMF approach.
Both approaches have a similar input/output structure that takes a pairwise adjacency matrix (Eq. 2) and then learns a vector representation for each variant (Fig. 2). LCW takes a matrix as a weighted graph where each node is a variant. Then it samples a weighted random walk starting at each node as a corpus of words (Fig. 2). This approach uses Word2Vec (i.e. SkipGram) [17] to learn the representation of each variant in the corpus by processing it as a word in the document. GMF takes the matrix then applies matrix factorization to produce a vector representation (Fig. 2). It extracts a representation by decomposing a given adjacency matrix into two low-dimensional rectangular matrices. Principal component analysis (PCA) [18] and non-negative matrix factorization (NMF) [19] were used for the decomposition.
Fig. 2.
Description of sub-approaches to learning representations of an association network. The first sub-approach is to use SkipGram, the other is to use global matrix factorization
Identifying module candidates using the learned representations
After learning the representation space from the data, we applied a general data mining technique, hierarchical clustering [20] to extract variant clusters that can be considered module candidates. The optimal number of clusters k was determined using the silhouette score [21] (Fig. 1). For each gene, the optimal number of variant clusters was found by choosing the k that maximizes the silhouette score. Then each cluster was considered a module candidate.
Measuring the association between module candidates and cancer phenotypes
To assess the significance of each module candidate, we established a metric that measures how strongly the module candidate is associated with a given phenotype. The metric computes the correlation between each patient’s module status and phenotype. Here, we defined the status of each module for each patient as either activated or inactivated. For a given threshold thr between 0 and 1, if the module activation level MAL of patient p for module m exceeds thr, then the module activation status MAS of patient p for module m is set to activated (Eqs. 3a, 3b, 3c).
| 3a |
| 3b |
| 3c |
MAL(p, m) represents the module activation level of patient p for module m, where is the set of variants in module m and is the set of variants that are found in patient p. MAS(p, m) represents the module activation status of patient p for module m for a given threshold value for module m, thr(m), where 1 indicates activated and 0 indicates the opposite. the(m) is computed as the mean MAL(p, m) for all patients, where L is the set of all patients in the data.
For the confusion matrix described in Table 1, we defined as the one-sided p value of Fisher’s exact test [22] and Defined as the prior odds ratio (Eq. 4). Here, is the set of patients with MAL activated and early onset phenotype. is the set of patients with MAL activated and late-onset phenotypes. is the set of patients with MAL inactivated and early onset phenotype. is the set of patients with MAL inactivated and late-onset phenotype. Note that is defined as a positive one-sided Fisher’s exact test, meaning that it only measures the significance of the positive correlation between module activation and the early onset phenotype.
| 4 |
Table 1.
Confusion matrix for calculating positive one-sided Fisher’s exact test
| Early-onset | Late-onset | |
|---|---|---|
| Module activated | ||
| Module inactivated |
is the prior odds ratio of Fisher’s exact test between module activation status and the early-onset prostate cancer phenotype for module m. A higher value indicates a greater positive correlation between activation of the module m and the given phenotype , which is the early-onset phenotype in this case, and a lower indicates a greater positive correlation.
Evaluation of the approach
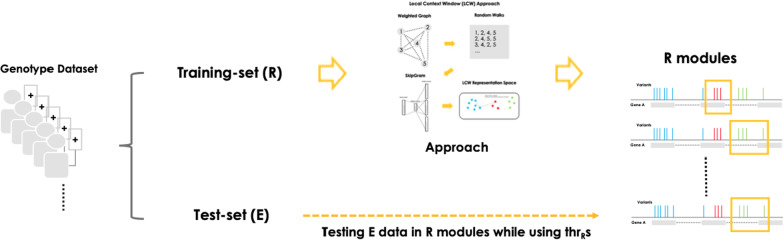
One of the main challenges in analyzing genomics data with machine learning approaches is overfitting. It occurs when the model memorizes the training data and the results are not reproduced in other datasets. We measured the robustness of our approach as the model’s ability to handle noise and prevent overfitting, which is measurable through the level of reproducibility of the results between two separate datasets. We divided the data set into training and test datasets to test reproducibility. Here, the training-set contains 16,579 prostate cancer samples (1590 early-onset, 14,989 late-onset) and the test-set contains 16,580 samples (1591 early-onset, 14,989 late-onset) (Fig. 3).
Fig. 3.
Description of the evaluation scheme. It aims to evaluate the robustness of each sub-approach by measuring reproducibility
Three sub-approaches with different implementations were prepared for evaluation: (1) LCW approach using SkipGram (LCW-SG), (2) GMF approach using PCA (GMF-PCA), and 3) GMF approach using NMF (GMF-NMF). In addition, two alternative approaches were prepared as controls: (1) the individual variant approach (CTRL-INV) and (2) the gene-level aggregation approach (CTRL-GLA). CTRL-INV is a control approach that evaluates the performance of individual variants instead of modules, which can show whether it is useful to infer associations between variants. CTRL-GLA is a control approach in which all variants within each gene are considered a single module, which can show whether it is useful to infer modules from the data. A total of five approaches were evaluated in terms of robustness (Fig. 3).
The evaluation process is performed for each sub-approach as follows (Fig. 3). (1) identify module candidates using each sub-approach, (2) measure FEP with training data for each module candidate, (3) identify phenotype associated modules with a p value threshold of 0.05, (4) measure FEP with test data for each phenotype associate module, and (5) calculate the reproduction rate by applying a p value threshold of 0.05. For example, if the LCW-SG approach identifies 1000 module candidates from the training data, 100 of them are found to have FEPs greater than 0.05. And if nine of them are found to have FEPs greater than 0.05 in the test data, then the reproduction rate is 9%. Since the test data were not used to define module candidates, the reproduction rate reflects the expected reproducibility when using the approach on one dataset and validating it on another dataset.
Implementation of the sub-approaches
As stated, LCW-SG, GMF-PCA, and GMF-NMF are the network representation learning approaches we aim to evaluate, while CTRL-INV and CTRL-GLA are the control approaches that provide a baseline for evaluation.
CTRL-INV is an approach that measures the reproduction rate of individual variants. It calculates the p value of the Fisher-exact test to measure the correlation between the early onset phenotype and each variant instead of a module candidate. It does not use any algorithms, models, or parameters. Thus, the reproduction rate here reflects the innate bias between the training and test datasets, meaning that this is a target that an ideal algorithm can achieve. CTRL-GLA is an approach that considers all variants within a gene to constitute a single module, thus it represents a passive algorithm that does not actively identify modules among variants. It can be used to quantify the usefulness of approaches using active algorithms such as LCW-SG, GMF-PCA, and GMF-NMF compared to a passive algorithm.
LCW-SG, GMF-PCA, and GMF-NMF approaches use network representation learning approaches to identify module candidates from given data (Fig. 2). The aforementioned approaches take AJM as input, learn vector representations for each variant, and then identify module candidates using hierarchical clustering [20] in the learned representation space, where the optimal number of clusters is determined using the silhouette score [21]. Their difference lies in how the network representation is learned from AJM.
In the case of LCW-SG, it starts at each node (i.e. each variant) and extracts 10 weighted random walks of length 10 each to learn the network representation. For example, if a gene has 100 variants, AJM represents a graph of 100 nodes, where the edge weights between nodes A and B represent the LOA between variants A and B. Since the edge weight reflects the level of association between two variants (Eq. 1a), the weighted random walk contains association information between variants. Therefore, by applying the SkipGram algorithm to the extracted random walk, associations between variants can be encoded into a vector representation.
GMF-PCA learns the vector representation by applying PCA [18] to AJM via two-dimensional reduction, whereas GMF-NMF uses NMF [19] with the same number of dimensions. Note that the matrix AJNM (Eq. 5) used in GMF-NMF was a matrix with an exponential value for each value of AJM, because NMF requires the matrix to be non-zero.
| 5 |
Results
As shown in the Table 2, the three approaches identified 14,000–20,000 module candidates in 5270 genes (variants in 28 genes were missing in the training data). LCW-SG identified 20,045 module candidates, of which 517 were found to be phenotype associated in the training data (acceptance rate 2.58%), of which 59 were found to be phenotype associated in the test data (reproduction rate 11.41%). Next, GMF-NMF identified 14,985 module candidates, of which 1728 were identified as having a phenotype association in the training data (acceptance rate 11.53%), of which 257 were identified as being phenotype associated in the test data (reproduction rate 14.87%). Lastly, GMF-PCA identified 20,369 module candidates, of which 2465 were found to be phenotype associated in the training data (acceptance rate 12.10%), of which 342 were identified as phenotype associated in the test data (reproduction rate 13.87%).
Table 2.
Reproducibility test results with a p value threshold of 0.05
| Approaches | #_of_module_candidates | pR < 0.05 | Ratio | pE < 0.05 | Ratio |
|---|---|---|---|---|---|
| LCW-SG | 20,045 | 517 | 0.0258 | 59 | 0.1141 |
| GMF-NMF | 14,985 | 1,728 | 0.1153 | 257 | 0.1487 |
| GMF-PCA | 20,369 | 2,465 | 0.1210 | 342 | 0.1387 |
| CTRL-GLA | 5,270 | 67 | 0.0127 | 4 | 0.0597 |
| CTRL-INV | 1,887,981 | 305,106 | 0.1616 | 188,369 | 0.6174 |
CTRL-GLA identified 5270 module candidates for each gene (Table 2), of which 67 were found to be phenotypes associated in the training data (acceptance rate 1.27%), of which 4 were found to be phenotype associated in the test data (reproduction rate 5.97%). This means that all three approaches, LCW-SG, GMF-NMF, and GMF-PCA, performed better in terms of reproduction rate, with the best approach being GMF-NMF, which is 2.49 times larger than CTRL-GLA. This means that GMF-NMF is 2.49 times more reproducible than a passive algorithm. CTRL-INV identified 1,887,981 individual variants as module candidates, of which 305,106 were identified as having a phenotype association in the training data (acceptance rate 16.16%), of which 188,369 were identified as being a phenotype associated in the test data (reproduction rate 61.74%). As shown in Table 2, the reproduction rate of GMF-NMF was 24.09% of CTRL-INV, which is the target value that an ideal algorithm can achieve. This means that the robustness level of the network representation learning approach is as good as 24.09% of the ideal target value.
Discussion
GMF-NMF showed the best performance in terms of reproduction rate among the three approaches based on network representation learning (NRL). All three approaches were found to outperform CTRL-GLA. This means that the NRL approach can improve reproducibility when identifying functional modules within genes, regardless of implementation.
Limitations of the approach
As can be seen from the comparison with CTRL-INV, the best of the three NRL approaches performed 24.09% compared to the control, implying that substantial overfitting still remains. These limitations can be explained in part by the use of primitive algorithms to identify phenotype associated modules. Since our goal was to measure the effectiveness of the NRL method itself, we did not use techniques to reduce overfitting such as data augmentation [23] and regularization [24] in this evaluation. This means that there is room to improve the performance of the approaches by deploying more sophisticated machine learning approaches such as deep neural network architectures and XGBoost [25] that can leverage the aforementioned techniques.
However, as indicated by the reproduction rate of the CTRL-INV approach, even the non-parameterized approach did not achieve 100% reproducibility. In other words, the data is inherently biased and prone to false discoveries. Since these innate biases reside in the data itself, it cannot be addressed by more sophisticated machine learning approaches or other techniques to avoid overfitting. To address these challenges, there is an alternative to improving machine learning approaches by adopting prior knowledge of the associations and interactions between biological entities. In a recent study by Kim et al. [9], an external source of information such as a PPI network was adopted in addition to the given input data so that the model can learn more generalized and reproducible patterns to avoid overfitting.
Unfortunately, it is not easy to apply the aforementioned idea directly to our problem because there is not enough information about the functional associations among variants. As discussed in the Introduction section, the functional and structural associations among variants within a gene are not yet fully understood. We believe that advances in deep neural networks (DNNs) and artificial intelligence (AI) technologies in genomics studies could be a solution to the problem. To the best of our knowledge, there are no viable methods that can identify associations among variants within a gene in terms of implications for protein function and structure. Therefore, this leaves us with two interesting topics for future research. First, to develop a method to learn functional associations between variants by adopting external information, such as linkage disequilibrium (LD) among variants [26, 27], or a method to learn functional associations directly from genomic sequences using AI techniques. Next, to integrate the learned associations between variants with our network representation learning framework.
Limitations in the cohort selection
Due to the MVP enrollment protocols, and the overall demographics of the VA population, the data used for this study is biased towards individuals who survive to the date of enrollment in the MVP program. Most of the subjects with both early and later onset prostate cancer enrolled in MVP after their diagnosis of Prostate Cancer (92% of early-onset and 83% of later onset). This suggests the possibility of survival bias in both groups, particularly in the early-onset group. However, our paper focuses on methods development, and the intragenic GWAS approach described in this paper is generalizable to other association studies.
Novelty of learning associations among genomic variations
Learning associations between biological entities have been widely used in the biomedical field, not only in genomics data [9] but also in other clinical data such as electronic health records [28]. However, to our knowledge, no approach has been found that can actively learn associations among genomic variations to target variables such as early and late-onset phenotypes. Therefore, the proposed approach can be of great benefit for further studies pursuing specific target phenotypes.
Future works
We identified associations between variations within genes. Since the underlying biological mechanisms for each association have not yet been investigated, it is not easy to present the outcomes as meaningful results. For example, suppose we found an association between a particular variant A and B. To reasonably interpret the results, we should also be able to provide actual evidence to support a functional association between them. It could be a linkage related to protein structure or other regulatory implications it may have, such as transcription factor (TF) and microRNA (miRNA) binding sites. Therefore, to evaluate and annotate learned associations in terms of clinical and biological significance, a more systematic framework is needed to evaluate these implications by integrating heterogeneous data sources such as biological networks and sequences.
Conclusion
This work proposes a network representation learning (NRL) approach and evaluates its utility in the identification of intragenic functional modules of genomic variation within a gene to facilitate understanding of the link between genomic variation and cancer phenotype. This approach was applied to the MVP prostate cancer cohort, which included 33,159 prostate cancer patients, 3,181 early-onset, and 29,978 late-onset. The NRL approach was evaluated in terms of reproducibility. The GMF-NMF approach showed 2.49 times higher reproduction rate than CTRL-GLA using a passive algorithm, while 24.09% compared to CTRL-INV, indicating that there is still substantial overfitting to improve.
To our knowledge, this is the first attempt to use the NRL approach to identify associations between genomic variations within genes. This study made it clear that the NRL approach can improve model performance in terms of reproducibility. Moreover, it opens up ways to study associations among variants to facilitate the understanding of the underlying biological mechanisms of how variants affect cancer phenotypes, which could lead to more advanced therapeutic targets for anticancer therapies.
Acknowledgements
This research is based on data from the Million Veteran Program, Office of Research and Development, Veterans Health Administration, and was supported by award MVP017. This publication does not represent the views of the Department of Veteran Affairs or the United States Government. This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. This research used resources of the Knowledge Discovery Infrastructure at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725 and the Department of Veterans Affairs Office of Information Technology Inter-Agency Agreement with the Department of Energy under IAA No. VA118-16-M-1062. The authors also wish to acknowledge the support of the larger partnership. Most importantly, the authors would like to thank and acknowledge the veterans who chose to get their care at the Veterans Affairs.
VA Million Veteran Program Yan Sun1, Rachel McArdle2, Louis Dellitalia3, Brady Stephens4, Kelly Cho4, Saiju Pyarajan4, Kristin Mattocks5, John Harley6, Jeffrey Whittle7, Roy Mathew8, Jean Beckham9, River Smith10, John Wells11, Salvador Gutierrez12, Kimberly Hammer13, Pran Iruvanti14, Zuhair Ballas15, Stephen Mastorides16, Jonathan Moorman17, Saib Gappy18, Jon Klein19, Nora Ratcliffe20, Ana Palacio21, Olaoluwa Okusaga22, Maureen Murdoch23, Peruvemba Sriram24, Dean P. Argyres25, Todd Connor25, Gerardo Villareal26, Scott Kinlay26, Shing Shing Yeh27, Darshana Jhala28, Neeraj Tandon28, Kyong-Mi Chang29, Samuel Aguayo30, David Cohen31, Satish Sharma32, Mark Hamner33, Suthat Liangpunsakul34, Michael Godschalk35, Kris Ann Oursler36, Mary Whooley37, Jennifer Greco38, Sunil Ahuja39, Joseph Constans40, Paul Meyer41, Michael Rauchman42, Richard Servatius43, Rachel Ramoni44, Sumitra Muralidhar44, J. Michael Gaziano45, Melinda Gaddy46, Agnes Wallbom47, James Norton48, Timothy Morgan49, Todd Stapley50, Peter Liang51, Sujata Bhushan52, Frank Jacono53, Daryl Fujii54, Philip Tsao54, Donald E. Humphries55, Grant Huang55, James Breeling55, Jennifer Moser55, Jessica V. Brewer55, Juan P. Casas55, Kelly Cho55, Lori Churby55, Luis E. Selva55, Mary T. Brophy55, Nhan Do55, Philip S. Tsao55, Shahpoor Alex Shayan55, Stacey B. Whitbourne55, Patrick Strollo56, Edward Boyko57, Jessica Walsh57, Saiju Pyarajan58, Elizabeth Hauser58, Scott L. DuVall58, Samir Gupta59, Mostaqul Huq60, Joseph Fayad61, Adriana Hung62, Junzhe Xu63, Kathrina Alexander64, Robin Hurley65, Jack Lichy66, Hongyu Zhao67, Peter Wilson67, Brooks Robey68, and Prakash Balasubramanian69.
1Atlanta VA Medical Center, Decatur, GA, USA. 2Bay Pines VA Healthcare System, Bay Pines, FL, USA. 3Birmingham VA Medical Center, Birmingham, AL, USA. 4Canandaigua VA Medical Center, Canandaigua, NY, USA. 5Central Western Massachusetts Healthcare System, Leeds, MA, USA. 6Cincinnati VA Medical Center, Cincinnati, OH, USA. 7Clement J. Zablocki VA Medical Center, Milwaukee, WI, USA. 8Columbia VA Health Care System, Columbia, SC, USA. 9Durham VA Medical Center, Durham, NC, USA. 10Eastern Oklahoma VA Health Care System, Muskogee, OK, USA. 11Edith Nourse Rogers Memorial Veterans Hospital, Bedford, MA, USA. 12Edward Hines, Jr. VA Medical Center, Hines, IL, USA. 13Fargo VA Health Care System, Fargo, ND, USA. 14Hampton VA Medical Center, Hampton, VA, USA. 15Iowa City VA Health Care System, Iowa City, IA, USA. 16James A. Haley Veterans’ Hospital, Tampa, FL, USA. 17James H. Quillen VA Medical Center, Mountain Home, TN, USA. 18John D. Dingell VA Medical Center, Detroit, MI, USA. 19Louisville VA Medical Center, Louisville, KY, USA. 20Manchester VA Medical Center, Manchester, NH, USA. 21Miami VA Health Care System, Miami, FL, USA. 22Michael E. DeBakey VA Medical Center, Houston, TX, USA. 23Minneapolis VA Health Care System, Minneapolis, MN, USA. 24N. FL/S. GA Veterans Health System, Gainesville, FL, USA. 25New Mexico VA Health Care System, Albuquerque, NM, USA. 26New Mexico VA Health Care System, S.E. Albuquerque, NM, USA. 27Northport VA Medical Center, Northport, NY, USA. 28Overton Brooks VA Medical Center, Shreveport, LA, USA. 29Philadelphia VA Medical Center, Philadelphia, PA, USA. 30Phoenix VA Health Care System, Phoenix, AZ, USA. 31Portland VA Medical Center, Portland, OR, USA. 32Providence VA Medical Center, Providence, RI, USA. 33Ralph H. Johnson VA Medical Center, Charleston, SC, USA. 34Richard Roudebush VA Medical Center, Indianapolis, IN, USA. 35Richmond VA Medical Center, Richmond, VA, USA. 36Salem VA Medical Center, Salem, VA, USA. 37San Francisco VA Health Care System, San Francisco, CA, USA. 38Sioux Falls VA Health Care System, Sioux Falls, SD, USA. 39South Texas Veterans Health Care System, San Antonio, TX, USA. 40Southeast Louisiana Veterans Health Care System, New Orleans, LA, USA. 41Southern Arizona VA Health Care System, Tucson, AZ, USA. 42St. Louis VA Health Care System, St. Louis, MO, USA. 43Syracuse VA Medical Center, Syracuse, NY, USA. 44US Department of Veterans Affairs, Washington, DC, USA. 45VA Boston Healthcare System, Boston, MA, USA. 46VA Eastern Kansas Health Care System, Leavenworth, KS, USA. 47VA Greater Los Angeles Health Care System, Los Angeles, CA, USA. 48VA Health Care Upstate New York, Albany, NY, USA. 49VA Long Beach Healthcare System, Long Bea.ch, CA, USA. 50VA Maine Healthcare System, Augusta, ME, USA. 51VA New York Harbor Healthcare System, New York, NY, USA. 52VA North Texas Health Care System, Dallas, TX, USA. 53VA Northeast Ohio Healthcare System, Cleveland, OH, USA. 54VA Pacific Islands Health Care System, Honolulu, HI, USA. 55VA Palo Alto Health Care System, Palo Alto, CA, USA. 56VA Pittsburgh Health Care System, Pittsburgh, PA, USA. 57VA Puget Sound Health Care System, Seattle, WA, USA. 58VA Salt Lake City Health Care System, Salt Lake City, UT, USA. 59VA San Diego Healthcare System, San Diego, CA, USA. 60VA Sierra Nevada Health Care System, Reno, NV, USA. 61VA Southern Nevada Healthcare System, North Las Vegas, NV, USA. 62VA Tennessee Valley Healthcare System, South Nashville, TN, USA. 63VA Western New York Healthcare System, Buffalo, NY, USA. 64Veterans Health Care System of the Ozarks, Fayetteville, AR, USA. 65W.G. Bill Hefner VA Medical Center, Salisbury, NC, USA. 66Washington DC VA Medical Center, Washington, D.C., USA. 67West Haven VA Medical Center, West Haven, CT, USA. 68White River Junction VA Medical Center, White River Junction, VT, USA. 69William S. Middleton Memorial Veterans Hospital, Madison, WI, USA.
Author contributions
MK developed methods, performed evaluations, interpreted results, and wrote the manuscript. The manuscript was reviewed by JH, AJ, IG, and GA. ID supervised the project and revised the manuscript. All authors read and approved the final manuscript.
Funding
This project is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725 and the Department of Veterans Affairs Office of Information Technology Inter-Agency Agreement with the Department of Energy under IAA No. VA118-16-M-1062.
Availability of data and materials
Full GWAS summary statistics can be found in dbGaP (https://www.ncbi.nlm.nih.gov/gap/) under the Million Veteran Program accession phs001672.
Declarations
Ethics approval and consent to participate
Approved researchers, such as researchers of this study, agree to follow the Million Veteran Program data use Rules of Behavior, including not trying to re-contact Million Veteran Program participants. All data analysis is completed within secure, Veterans Affairs-approved work environments. Our project was approved by the Veterans Affairs Central Institutional Review Boards. All participants enrolled in the Million Veteran Program have signed an Informed Consent document allowing the use of their data by approved researchers in accordance with the Million Veteran Program data access policy.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Minsu Kim, Email: kimm@orgnl.gov.
Jennifer E. Huffman, Email: Jennifer.Huffman2@va.gov
Amy Justice, Email: amy.justice2@va.gov.
Ian Goethert, Email: goethertid@ornl.gov.
Greeshma Agasthya, Email: agasthyaga@ornl.gov.
Ioana Danciu, Email: danciui@ornl.gov.
VA Million Veteran Program:
Yan Sun, Rachel McArdle, Louis Dellitalia, Brady Stephens, Kelly Cho, Saiju Pyarajan, Kristin Mattocks, John Harley, Jeffrey Whittle, Roy Mathew, Jean Beckham, River Smith, John Wells., Salvador Gutierrez, Kimberly Hammer, Pran Iruvanti, Zuhair Ballas, Stephen Mastorides, Jonathan Moorman, Saib Gappy, Jon Klein, Nora Ratcliffe, Ana Palacio, Olaoluwa Okusaga, Maureen Murdoch, Peruvemba Sriram, Dean P. Argyres, Todd Connor, Gerardo Villareal, Scott Kinlay, Shing Shing Yeh, Darshana Jhala, Neeraj Tandon, Kyong-Mi Chang, Samuel Aguayo, David Cohen, Satish Sharma, Mark Hamner, Suthat Liangpunsakul, Michael Godschalk, Kris Ann Oursler, Mary Whooley, Jennifer Greco, Sunil Ahuja, Joseph Constans, Paul Meyer, Michael Rauchman, Richard Servatius, Rachel Ramoni, Sumitra Muralidhar, J. Michael Gaziano, Melinda Gaddy, Agnes Wallbom, James Norton, Timothy Morgan, Todd Stapley, Peter Liang, Sujata Bhushan, Frank Jacono, Daryl Fujii, Philip Tsao, Donald E. Humphries, Grant Huang, James Breeling, Jennifer Moser, Jessica V. Brewer, Juan P. Casas, Kelly Cho, Lori Churby, Luis E. Selva, Mary T. Brophy, Nhan Do, Philip S. Tsao, Shahpoor Alex Shayan, Stacey B. Whitbourne, Patrick Strollo, Edward Boyko, Jessica Walsh, Saiju Pyarajan, Elizabeth Hauser, Scott L. DuVall, Samir Gupta, Mostaqul Huq, Joseph Fayad, Adriana Hung, Junzhe Xu, Kathrina Alexander, Robin Hurley, Jack Lichy, Hongyu Zhao, Peter Wilson, Brooks Robey, and Prakash Balasubramanian
References
- 1.Sud A, Kinnersley B, Houlston RS. Genome-wide association studies of cancer: current insights and future perspectives. Nat Rev Cancer. 2017;17(11):692–704. doi: 10.1038/nrc.2017.82. [DOI] [PubMed] [Google Scholar]
- 2.Han J, Hankinson SE, Zhang SM, De Vivo I, Hunter DJ. Interaction between genetic variations in DNA repair genes and plasma folate on breast cancer risk. Cancer Epidemiol Prev Biomark. 2004;13(4):520–524. doi: 10.1158/1055-9965.520.13.4. [DOI] [PubMed] [Google Scholar]
- 3.Lappalainen T, MacArthur DG. From variant to function in human disease genetics. Science. 2021;373(6562):1464–1468. doi: 10.1126/science.abi8207. [DOI] [PubMed] [Google Scholar]
- 4.Ackermann M, Sikora-Wohlfeld W, Beyer A. Impact of natural genetic variation on gene expression dynamics. PLoS Genet. 2013;9(6):1003514. doi: 10.1371/journal.pgen.1003514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Glusman G, Rose PW, Prlić A, Dougherty J, Duarte JM, Hoffman AS, Barton GJ, Bendixen E, Bergquist T, Bock C, et al. Mapping genetic variations to three-dimensional protein structures to enhance variant interpretation: a proposed framework. Genome Med. 2017;9(1):1–10. doi: 10.1186/s13073-017-0509-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Joiret M, John JMM, Gusareva ES, Van Steen K. Confounding of linkage disequilibrium patterns in large scale DNA based gene–gene interaction studies. BioData Min. 2019;12(1):1–23. doi: 10.1186/s13040-019-0199-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lim S, Park Y, Hur B, Kim M, Han W, Kim S. Protein interaction network (pin)-based breast cancer subsystem identification and activation measurement for prognostic modeling. Methods. 2016;110:81–89. doi: 10.1016/j.ymeth.2016.06.015. [DOI] [PubMed] [Google Scholar]
- 8.Park J, Hur B, Rhee S, Lim S, Kim M-S, Kim K, Han W, Kim S. Information theoretic sub-network mining characterizes breast cancer subtypes in terms of cancer core mechanisms. J Bioinform Comput Biol. 2016;14(05):1644002. doi: 10.1142/S0219720016440029. [DOI] [PubMed] [Google Scholar]
- 9.Kim M, Lee S, Lim S, Lee DY, Kim S. Subnetwork representation learning for discovering network biomarkers in predicting lymph node metastasis in early oral cancer. Sci Rep. 2021;11(1):1–12. doi: 10.1038/s41598-020-79139-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Perozzi B, Al-Rfou R, Skiena S. Deepwalk: online learning of social representations. In: Proceedings of the 20th ACM SIGKDD international conference on knowledge discovery and data mining; 2014. pp. 701–710.
- 11.Pennington J, Socher R, Manning CD. Glove: global vectors for word representation. In: Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP); 2014. pp. 1532–1543.
- 12.Henley SJ, Ward EM, Scott S, Ma J, Anderson RN, Firth AU, Thomas CC, Islami F, Weir HK, Lewis DR, et al. Annual report to the nation on the status of cancer, part I: national cancer statistics. Cancer. 2020;126(10):2225–2249. doi: 10.1002/cncr.32802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Alkhateeb A, Rezaeian I, Singireddy S, Cavallo-Medved D, Porter LA, Rueda L. Transcriptomics signature from next-generation sequencing data reveals new transcriptomic biomarkers related to prostate cancer. Cancer Inform. 2019;18:1176935119835522. doi: 10.1177/1176935119835522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Salinas CA, Tsodikov A, Ishak-Howard M, Cooney KA. Prostate cancer in young men: an important clinical entity. Nat Rev Urol. 2014;11(6):317–323. doi: 10.1038/nrurol.2014.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gaziano JM, Concato J, Brophy M, Fiore L, Pyarajan S, Breeling J, Whitbourne S, Deen J, Shannon C, Humphries D, et al. Million veteran program: a mega-biobank to study genetic influences on health and disease. J Clin Epidemiol. 2016;70:214–223. doi: 10.1016/j.jclinepi.2015.09.016. [DOI] [PubMed] [Google Scholar]
- 16.Jaccard P. The distribution of the flora in the alpine zone. 1. New Phytol. 1912;11(2):37–50. doi: 10.1111/j.1469-8137.1912.tb05611.x. [DOI] [Google Scholar]
- 17.Mikolov T, Chen K, Corrado G, Dean J. Efficient estimation of word representations in vector space.2013. arXiv:1301.3781.
- 18.Wold S, Esbensen K, Geladi P. Principal component analysis. Chemom Intell Lab Syst. 1987;2(1–3):37–52. doi: 10.1016/0169-7439(87)80084-9. [DOI] [Google Scholar]
- 19.Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401(6755):788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- 20.Johnson SC. Hierarchical clustering schemes. Psychometrika. 1967;32(3):241–254. doi: 10.1007/BF02289588. [DOI] [PubMed] [Google Scholar]
- 21.Rousseeuw PJ. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math. 1987;20:53–65. doi: 10.1016/0377-0427(87)90125-7. [DOI] [Google Scholar]
- 22.Fisher RA. On the interpretation of χ2 from contingency tables, and the calculation of p. J R Stat Soc. 1922;85(1):87–94. doi: 10.2307/2340521. [DOI] [Google Scholar]
- 23.Van Dyk DA, Meng X-L. The art of data augmentation. J Comput Graph Stat. 2001;10(1):1–50. doi: 10.1198/10618600152418584. [DOI] [Google Scholar]
- 24.Ghojogh B, Crowley M. The theory behind overfitting, cross validation, regularization, bagging, and boosting: tutorial.2019. arXiv:1905.12787.
- 25.Chen T, He T, Benesty M, Khotilovich V, Tang Y, Cho H, et al.: Xgboost: extreme gradient boosting. R Package version 0.4-2.2015;1(4):1–4.
- 26.Weir BS. Inferences about linkage disequilibrium. Biometrics. 1979;35:235–54. [PubMed]
- 27.Reich DE, Cargill M, Bolk S, Ireland J, Sabeti PC, Richter DJ, Lavery T, Kouyoumjian R, Farhadian SF, Ward R, et al. Linkage disequilibrium in the human genome. Nature. 2001;411(6834):199–204. doi: 10.1038/35075590. [DOI] [PubMed] [Google Scholar]
- 28.Hasan SS, Kim M, Park BH, Jones MM, Ward M, Nebeker J. A knowledge network-based approach to facilitate annotation of clinical pathway component clusters. In: 2021 IEEE EMBS international conference on biomedical and health informatics (BHI). IEEE; 2021. pp. 1–4.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Full GWAS summary statistics can be found in dbGaP (https://www.ncbi.nlm.nih.gov/gap/) under the Million Veteran Program accession phs001672.