Abstract
Many voice disorders are the result of intricate neural and/or biomechanical impairments that are poorly understood. The limited knowledge of their etiological and pathophysiological mechanisms hampers effective clinical management. Behavioral studies have been used concurrently with computational models to better understand typical and pathological laryngeal motor control. Thus far, however, a unified computational framework that quantitatively integrates physiologically relevant models of phonation with the neural control of speech has not been developed. Here, we introduce LaDIVA, a novel neurocomputational model with physiologically based laryngeal motor control. We combined the DIVA model (an established neural network model of speech motor control) with the extended body-cover model (a physics-based vocal fold model). The resulting integrated model, LaDIVA, was validated by comparing its model simulations with behavioral responses to perturbations of auditory vocal fundamental frequency (fo) feedback in adults with typical speech. LaDIVA demonstrated capability to simulate different modes of laryngeal motor control, ranging from short-term (i.e., reflexive) and long-term (i.e., adaptive) auditory feedback paradigms, to generating prosodic contours in speech. Simulations showed that LaDIVA’s laryngeal motor control displays properties of motor equivalence, i.e., LaDIVA could robustly generate compensatory responses to reflexive vocal fo perturbations with varying initial laryngeal muscle activation levels leading to the same output. The model can also generate prosodic contours for studying laryngeal motor control in running speech. LaDIVA can expand the understanding of the physiology of human phonation to enable, for the first time, the investigation of causal effects of neural motor control in the fine structure of the vocal signal.
Author summary
With the incorporation of a physiologically relevant vocal fold model into a computational speech motor control framework, LaDIVA is a neurocomputational model that includes realistic laryngeal activity. The proposed model has demonstrated capability to simulate different modes of laryngeal motor control, ranging from short-term (i.e., reflexive) and long-term (i.e., adaptive) auditory feedback paradigms, to generating prosodic contours in speech. LaDIVA displays properties of motor equivalence, i.e., it robustly generates similar compensatory responses to auditory perturbations for all simulations regardless of the variety in initial laryngeal muscle activation levels tested. LaDIVA can be used to expand the understanding of the physiology of human phonation to enable, for the first time, the investigation of causal effects of neural motor control in the fine structure of the vocal signal.
Introduction
Voice disorders are a common and recurring occupational health disorder, affecting 7% of the U.S. population and causing severe mental, physical, and emotional repercussions, as well as adverse consequences on job performance [1]. Fifty percent of teachers report voice problems during their career [2] and 2.5 billion dollars each year are spent on treatments and sick leave for voice disorders in the U.S. [3]. Many voice disorders are the result of intricate neural and biomechanical impairments that are poorly understood [4]. Effective clinical management of many of these voice pathologies is hampered by the limited knowledge of their etiology and pathophysiological mechanisms, as well as overlapping symptoms among multiple disorders [5,6]. Identification of the pathophysiology of voice impairments and decoupling the neural and biomechanical aspects of the pathology may provide new directions for clinical intervention.
Speech production is a complex motor skill involving a multitude of neuromuscular executions in respiratory, laryngeal, and articulatory muscles [7]. Simultaneously, the neural motor controllers integrate sensory information from multiple feedback modalities (i.e., auditory and somatosensory feedback) to monitor the accuracy of the acoustic output [8]. Neurocomputational models of speech are designed to systematically unify available knowledge on speech motor control, to simulate behavior, and test hypotheses related to speech motor control architecture [9–12]. Likewise, computational models of voice production have improved our understanding of typical and pathological phonation by providing access to relevant features that are difficult, if not impossible, to directly measure [13–16]. However, current models do not yet integrate physiologically relevant models of phonation into computational models of neural motor control, which would allow for investigation of auditory and somatosensory processing in voice production. Thus, despite the contribution of these models to enhance the clinical assessment of vocal function, their capacity to study laryngeal motor control is lacking.
Neurocomputational models use mathematical representations and/or neural networks to abstract components of brain function in a straightforward manner [17]. Of current biologically plausible neural network models of speech production [18,19], the Directions into Velocities of Articulators model (DIVA; [8, 20]) is possibly the most thoroughly defined and physiologically validated neurocomputational model for articulatory speech motor control to date. The DIVA model incorporates detailed neuroanatomical and neurophysiological information into a unified platform, making it well-suited to generate simulations of speech production for meaningful, quantitative comparisons with experimental observations [8,20–22]. DIVA is a neural network model whose components correspond to regions of the cerebral cortex and cerebellum, including premotor, motor, auditory, and somatosensory cortical areas. Although DIVA does not provide a complete account of the cortical and cerebellar mechanisms involved, the mathematical model has been able to replicate behavioral and neural responses via simulations of simple syllable productions. The model uses decades of behavioral and neuroimaging data to tie the components of the mathematical framework to neural substrates particularly related to articulation. The DIVA model was developed to replicate human speech produced at behavioral, neurological, and developmental levels [8,11,20,23,24]. It consists of a hybrid control system combining three main control components related to speech articulation: 1) a feedforward controller that utilizes internally stored motor programs to produce sound, 2) an auditory feedback controller that detects errors between actual acoustic output and acoustic feature targets, and 3) a somatosensory feedback controller that detects errors between actual somatosensory (i.e., kinesthetic or proprioceptive) output and somatosensory feature targets. The DIVA model has been successfully used in conjunction with brain imaging and behavioral experiments to refine our understanding of the neural control of speech and generate hypotheses for further behavioral studies [8,12,23–25]. However, the neuromuscular control of laryngeal function is an important aspect of speech production that is not addressed in the DIVA model [25]. Key acoustic features of voice production, such as vocal fundamental frequency (fo), vocal sound pressure level (SPL), and voice signal quality are modulated via laryngeal motor control in humans [26,27], and prior research suggests that disorders such as spasmodic dysphonia, vocal hyperfunction, spastic dysarthria, and vocal tremor may be related to abnormal laryngeal motor control [28–33]. Incorporating laryngeal motor control to models of speech motor control will enhance the ability to understand these disorders.
Characterizing laryngeal function in phonation requires a detailed understanding of the underlying physiology, biomechanics, and neuromuscular control. The neural motor control and biomechanical mechanisms of typical and disordered laryngeal function involved in vocal production, and the interaction between them are poorly understood, partly due to the invasive nature of assessment and characterization of laryngeal function (i.e., laryngeal electromyography: [34–39], laryngeal endoscopy: [40,41], contact pressure probes:[42]). The geometry and mechanical properties of the vocal folds (VFs) exhibit a great deal of variability as a function of intrinsic muscle activation, voicing conditions, sex, age, and individual anatomical features, and complex physical interactions occur between VF tissue, airflow, and sound [43,44]. Thus, it is crucial to investigate these components and their variability to better understand laryngeal function in typical and pathologic conditions. Low-order models of phonation such as lumped-element VF models with acoustic and aerodynamic modules offer a simple yet physiologically relevant framework for investigating biomechanical aspects of voice production while remaining computationally efficient [45]. For instance, the well-established body-cover model (BCM; [46–48]) can control supra and subglottal tract features such as subglottal pressure (Ps), and neuromuscular activation of the cricothyroid (CT), thyroarytenoid (TA), lateral cricothyroid (LCA), and posterior cricothyroid (PCA; [48]) intrinsic laryngeal muscles [47–49]. Models extending the long-standing BCM have been broadly used to predict complex physical phenomena in voice production in humans, such as irregular vibration in VF nodules [50], contact mechanics [13,51], compensatory responses in vocal hyperfunction [14,49], chaotic vibration in unilateral VF paralysis [52,53], and dynamic mechanisms of atypical vocal fold vibration in vocal tremor [54]. As higher order three-dimensional finite element models [43,54–56] are computationally demanding to account for neural motor control effects, low-order models are most suitable to comprehensive parametric stimulations of laryngeal motor control. The extended body cover model selected in the current study (hereafter referred to as extended BCM; [49]) is an extension of the BCM by Story and Titze (46), with the addition of a posterior glottal opening, and model parameters selected to simulate a male modal voice using muscle activation principles defined in Titze and Story (48). See the original paper for the equations for the motion of vocal folds in the extended BCM model [46]. The extended BCM was specially selected considering its simplicity as well as scalability for future iterations of LaDIVA. In summary, combining a low-order biomechanical model with models of neural laryngeal motor control will provide an integrated framework to simulate vocal productions that are comparable to outputs of behavioral study data collected from individuals with and without voice disorders [57–60].
Behavioral studies are often conducted with the aim of understanding and quantifying responses of the speech motor control system to erroneous feedback stimuli. Prior research has behaviorally characterized laryngeal motor control with externally imposed short-term (i.e. reflexive) and long-term (i.e. adaptive) alterations of auditory feedback of laryngeal features (i.e., vocal fo, vocal SPL, duration). Reflexive paradigms targeting vocal fo (the physical quantity underlying the perceptual feature of pitch) present sudden, unpredictable alterations to auditory fo feedback to measure the feedback-based error detection, correction, and incorporation to real-time motor production (commonly termed pitch reflex; [61–64]). Adaptive vocal fo paradigms present predictable, sustained perturbations to auditory fo feedback over time to measure the speaker’s ability to correct errors in subsequent feedforward motor commands [65–67]. Behavioral studies of these types have been performed with those with typical voices [68] as well as speakers with neurological and/or voice disorders (e.g., Parkinson’s disease [PD; 69] and vocal hyperfunction [57,70,71]). Studies using auditory feedback perturbations in vocal fo have indicated that individuals with PD have a higher reliance on the auditory feedback subsystem for vocal motor control [72–75], and impaired auditory-motor integration in terms of feedforward motor control [69]. Similar studies have also provided evidence that individuals with vocal hyperfunction demonstrate potential signs of a motor speech disorder [57,70,71] with difficulty using auditory feedback to update their feedforward control subsystems. Moreover, these studies also observed larger individual variability in the vocal responses of individuals with vocal hyperfunction compared to speakers with typical speech. Overall, the outcomes of these studies suggest there are possible vocal motor control impairments related to vocal fo in specific populations with voice disorders. These experimental data have been replicated via a simple three-parameter model of speech and vocal production: simpleDIVA [76]. Although simpleDIVA successfully abstracts the DIVA architecture to model both articulatory and laryngeal motor control, the simplification of DIVA to three mathematical equations has its own limitations; namely, it implicitly assumes a laryngeal system that will perfectly achieve commanded movements. A neurocomputational model of laryngeal motor control equipped with biomechanical mechanisms of laryngeal function would allow comprehensive investigation via repeated simulations of numerous experimental conditions, that may be exhaustive to participants during behavioral experimentation, or inaccessible to conduct/assess due to technical limitations in experimentation (e.g., voice quality perturbation, combined perturbations, running speech perturbation). Model simulations of laryngeal motor control would be particularly valuable to address these limitations and to better understand typical and atypical laryngeal motor control behaviors.
In this paper, we introduce the laryngeal DIVA model (LaDIVA), a neurocomputational model that integrates biomechanics of phonation and neural laryngeal motor control in a single computational framework. The novel model is based on two widely accepted existing models, the DIVA model for the neural laryngeal motor control component [8] and the extended BCM [49] for the biomechanical component. The combined model, LaDIVA, is able to dynamically control the intrinsic laryngeal muscles of the extended BCM by assessing the resultant acoustic output based on auditory feedback and feedforward mechanisms. LaDIVA will significantly expand the capabilities and potential of current VF modeling tools, particularly for investigating voice disorders in which neuropathy related to auditory and/or somatosensory systems is suspected. In addition, LaDIVA can be used to predict variations in underlying feedforward and feedback control mechanisms between typical vocal production and disordered voice production, which could motivate future behavioral study designs to investigate laryngeal function in voice disorders.
In the following sections, we describe the construction of LaDIVA and the initial simulations performed to validate the model using behavioral data. The Model Overview summarizes the architecture and the computational implementation of LaDIVA, which currently enables vocal fo and vocal SPL (the physical quantity underlying the perceptual feature of loudness) control. In the Results, we evaluate LaDIVA to show that it can replicate human laryngeal motor control qualitatively and quantitatively. Data collected from a previous behavioral experiment [68] from adults with typical speech were used to validate LaDIVA.
Model overview
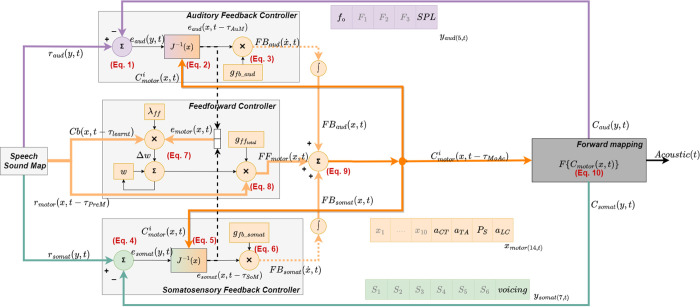
LaDIVA is a neurocomputational laryngeal control model, combining two well-established and physiologically validated models describing different aspects of speech production. DIVA [8], a neurocomputational model of speech, and the extended BCM [49], a biomechanical model of phonation. Fig 1 illustrates a simplified version of LaDIVA architecture with adapted modules from DIVA shaded in light grey and adapted modules from the extended BCM shaded in dark grey. The controlled variables of the model are listed in Table 1.
Fig 1. LaDIVA model architecture.
Modules in light grey are adapted from the DIVA model and the module in dark grey represents the larynx, mathematically modeled via the extended body-cover model for vocal folds. Mobility space variables are denoted by x, and task space variables are denoted by y. Pathways denoted in auditory task space are purple. Pathways denoted in somatosensory task space are green. Pathways denoted by motor mobility space are orange. See Materials and Methods for annotated equations.
Table 1. LaDIVA Model Parameters.
| DIVA component → | BCM component | ||
|---|---|---|---|
| Mobility Space (xmotor) | Articulatory dimensions (10) | Ten vocal tract shapes | N/A |
| Source dimensions (4) | Cricothyroid Muscle Activation (aCT), Thyroarytenoid Muscle Activation (aTA), Subglottal Pressure (PS) | Input Parameters | |
| Glottal constriction dimension | Voiced state handled via BCM (aLC) | ||
| DIVA component ← | BCM component | ||
| Auditory Task Space ( y aud ) | Source dimensions (2) | Vocal Fundamental Frequency (fo), Vocal Sound Pressure Level (SPL) | Output Parameters (derived via glottal flow signal; Ug) |
| Articulatory dimensions (3) | First Formant (F1), Second Formant (F2), Third Formant (F3) | N/A | |
| Somatosensory Task Space ( y somat ) | Articulatory dimensions (6) | Place of constriction in vocal tract: Labial, Alveolar/Dental, Palatal, Velar, Uvular, Pharyngeal | N/A |
| Source dimensions (1) | Glottal constriction dimension | Voiced state handled via BCM (aLC) | |
In DIVA [8], there are multi-dimensional goal regions defined for controlled variables. These regions are termed targets and are expressed in task space and mobility space variables. The relevant task space variables in DIVA required to define laryngeal movement are vocal fo for auditory tasks pace and vocal SPL for somatosensory task space (see Table 1: in LaDIVA, vocal SPL is modified to be an auditory task space variable). The motor planning layer of DIVA contains the speech sound map, an expansive list of speech sounds composed of phonemes, syllables, or word sounds. Each speech sound is mapped to a three-component representation of controlled variables. The first component is an articulatory trajectory (i.e., generally referred to as motor trajectories) that defines the mobility space targets of a specific speech sound (i.e., the information related to the position of a particular articulator; represented in orange in Fig 1). The other two are distinct target trajectories in auditory and somatosensory task spaces (represented in purple and green respectively in Fig 1). These three types of target trajectories constitute the reference signals for the feedforward controller, auditory feedback controller, and somatosensory feedback controller in DIVA, respectively.
At the beginning of a speech sound production, the speech sound map for that sound is activated, leading to a readout from memory of a learnt set of motor target trajectories for that specific sound. The feedforward controller compares these motor targets with the current motor control signal (Cimotor(x, t); dark orange arrows) and generates a feedforward motor control signal (FFmotor(x,t); light orange arrows). In the feedback controllers, auditory and somatosensory feedback error between the sensory outputs and desired sensory targets are inversely transformed (i.e., J-1(x)) from tasks space variables to mobility space variables, and the resultant feedback error correction signals (i.e., FBaud(x,t) and FBsom(x,t); dotted light orange arrows), are incorporated to the feedforward control signal to generate the subsequent motor control signal (Ci+1motor(x, t); i.e., dark orange arrows). DIVA then uses a forward transformation (i.e., F{~}) to generate the subsequent auditory and somatosensory outputs relevant to the motor control signal.
DIVA primarily controls movements of the supralaryngeal vocal tract articulators. These articulators define the shape of the vocal tract “tube”, which is used in combination with a simplified glottal wave model [77] to convert vocal tract articulatory mobility space trajectories into auditory and somatosensory task space trajectories [78]. Ten different articulatory position dimensions are used to define articulatory mobility space trajectories. The forward transformation of these articulatory trajectories results in sensory trajectories with three auditory task space dimensions (i.e., F1, F2, F3) and seven somatosensory task space dimensions (i.e., six places of constriction in the vocal tract and a glottal constriction). The model also includes three voicing-related output variables (i.e., for VF tension, subglottal pressure, and voicing), but values for these are specified directly by the user rather than computed by the model’s feedforward and feedback control system interactions.
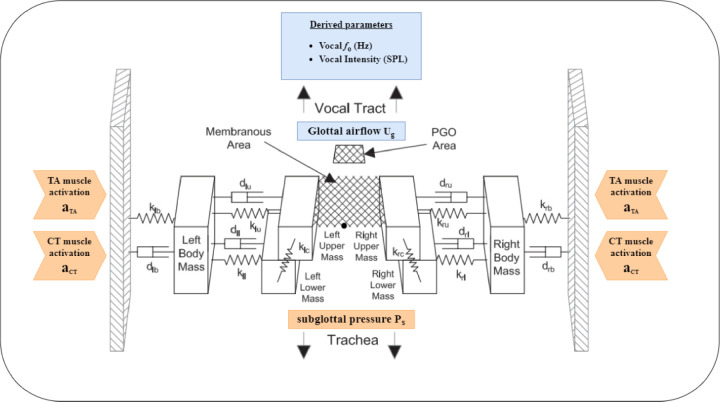
In contrast, in LaDIVA, the extended BCM is used to convert VF mobility space trajectories (i.e., laryngeal trajectories) to changes in auditory and somatosensory task space trajectories. Three different VF mobility space dimensions are used, namely, 1) activation level of cricothyroid muscle (aCT), 2) activation level of thyroarytenoid muscle (aTA), and 3) subglottal pressure level (Ps). These laryngeal mobility space trajectories are then converted into sensory task space trajectories consisting of two auditory dimensions (vocal fo and SPL). With this inclusion, both laryngeal and vocal tract articulatory components of the speech sound are controlled via the feedforward-feedback control architecture of LaDIVA. The extended BCM model is shown in Fig 2. A more detailed technical description of LaDIVA is provided in Materials and Methods. Note that the current implementation of LaDIVA does not contain a somatosensory task space representation for laryngeal mobility space variations due to the limited somatosensory task space representation in DIVA for laryngeal motor control.
Fig 2. Extended Body-Cover Model.
Vocal fold mobility variables input from or output to the DIVA model are shown in orange and blue shaded regions, respectively. Reproduced from Zañartu, Galindo [49] (https://doi.org/10.1121/1.4901714), with the permission of the Acoustical Society of America.
Results
Here we present an evaluation of LaDIVA’s ability to simulate human laryngeal motor control. A series of model simulations were carried out to validate the model qualitatively and quantitatively.
Model response to reflexive and adaptive auditory perturbations
We used data collected from a previous behavioral experiment [68] to validate LaDIVA. A series of model simulations replicating vocal fo reflexive and adaptive perturbation paradigms were conducted. LaDIVA simulation responses were comparable with behavioral responses to vocal fo reflexive and vocal fo adaptive perturbations of auditory feedback of laryngeal features (i.e., vocal fo) collected in adults with typical speech [68]. Fig 3 shows the simulation responses in LaDIVA in comparison with the mean group response (20 young adults with typical speech) of the behavioral dataset.
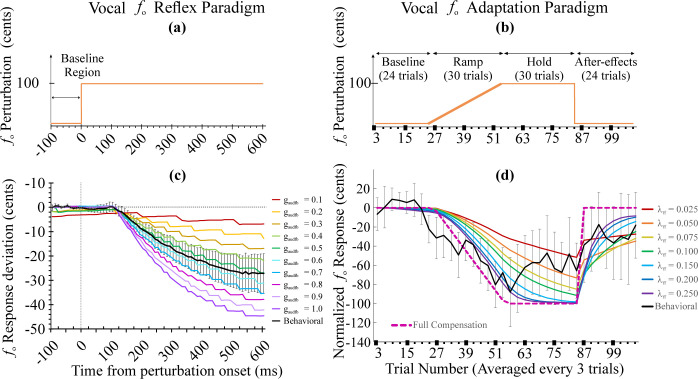
Fig 3. Simulation responses of LaDIVA compared with the mean group response (20 adults with typical speech) of the behavioral dataset.
(a) Applied fo perturbation for a perturbed trial in the vocal fo reflexive paradigm. (b) Vocal fo perturbation across all 108 trials of the vocal fo adaptive paradigm. (c) Simulation response for vocal fo reflexive paradigm. (d) Simulation response for vocal fo adaptation paradigm. All simulations in panel (c) and (d) were conducted under initial laryngeal muscle activation settings (Case B: aCT = 0.169, aTA aTA = 0.175, and Ps = 800 Pa). Group mean response of behavioral dataset in black with 95% CI error bars).
In LaDIVA we focused on five tunable parameters for the simulations: two parameters from DIVA and three from the extended BCM. These were defined within physiologically relevant ranges and tuned to best match behavioral data from the previous study [68]. The DIVA parameters are auditory feedback gain (gaudfb), and feedforward learning rate (λff). See Materials and Methods for parameter incorporation via mathematical equations. The extended BCM parameters are the mobility space targets for CT muscle activation (aCT), TA muscle activation (aTA), and subglottal pressure (Ps). All other parameters in DIVA and extended BCM were set to replicate male VFs as described in Story and Titze Body-Cover Models [46,48], with a baseline vocal fo of 134 Hz [79] and a vocal intensity represented by a radiated sound pressure level of 75 dB SPL at 30 cm from the lips.
The auditory feedback gain (gaudfb) was determined using a reflexive paradigm simulation. The vocal fo of the auditory feedback signal fed into the model was artificially shifted by +100 cents (1 semitone) after 500 ms from vocal onset (see Fig 3A: only 100 ms before perturbation onset is shown) and the perturbation was sustained until the end of the utterance. LaDIVA was used to replicate the real-time response for the utterance of a target vowel /ɑ/, with the added auditory perturbation. The LaDIVA auditory state indicates the current auditory feedback the model receives, which is comparable to the headphone signal a participant hears in an experimental session. See Eq 10B in Materials and Methods for details. Thus, the system response to the auditory perturbation can be calculated as the difference between the current auditory state and the applied auditory perturbation. Normalized vocal fo responses for vocal fo reflexive paradigm simulations are provided in Fig 3C for varied auditory feedback gains (gaudfb ranging from 0.1–1.0). The model simulation results were overlaid with the behavioral data of the reflexive group mean fo response, and the best fit for feedback gain was selected. With the lowest RMSE and difference between area under the curves, gaudfb = 0.5 provided the best fit for the behavioral mean vocal fo reflexive response (RMSE = 0.91, R2 = 1.0; See Table 2). Note that the feedforward learning rate parameter (λff) was kept constant for the auditory feedback gain parameter exploration as reflexive paradigms are designed to avoid learning effects by avoiding the presentation of sustained and predictable perturbations to auditory feedback that may cause persistent auditory feedback errors.
Table 2. Goodness-of-fit statistics for behavioral dataset for vocal fo reflexive paradigm explained by model simulations.
AUC = area under the curve.
| Feedback Gain | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| R-squared | -0.40 | 0.19 | 0.62 | 0.87 | 0.98 | 0.97 | 0.83 | 0.59 | 0.24 | -0.17 |
| RMSE | 12.67 | 9.63 | 6.61 | 3.90 | 1.49 | 1.95 | 4.41 | 6.87 | 9.32 | 11.62 |
| Absolute Difference AUC | 596.06 | 473.42 | 312.46 | 161.15 | 15.79 | 93.14 | 235.85 | 375.19 | 513.57 | 645.51 |
The feedforward learning rate parameter (λff) was determined through the use of a vocal fo adaptive paradigm simulation (gaudfb was kept constant). The vocal fo of the auditory feedback signal fed into the model was perturbed according to four ordered phases; 1) Baseline: no perturbations, 2) Ramp: vocal fo shift increasing by +3.3. cents in each adjacent trial, 3) Hold: vocal fo shifted by +100 cents, and 4) Aftereffect: no perturbation applied. See Material and Methods: Behavioral study dataset section for more details. For perturbed trials, the vocal fo of the auditory feedback signal fed into the model was shifted before vocal utterance onset and the perturbation was sustained until the end of the utterance in the simulation. The model simulation was run for 108 adjacent simulations (i.e., trials) to replicate 108 trials of target vowel /ɑ/ utterances, with added auditory perturbation in specified phases. The vocal response is a combination of the feedforward and feedback motor commands acting on current vocal production. See Material and Methods Eq 9 for more details. In order to extract the acoustic response driven by feedforward motor commands alone, an analysis window from 40 ms to 120 ms after the vocal onset was selected. This analysis window was selected to target the feedforward motor command based response as auditory feedback is assumed to affect current vocal productions with a latency of 120 ms [63]. The initial 40 ms of the response signal was discarded to avoid vocal onset variability generally present in human vocal production. The mean response fo for the analysis window of each trial was calculated to represent the adaptive response per each trial. Note that in the model simulations, the analysis window captures pure feedforward signals as the modeled auditory feedback signal latency is 120 ms. Although this analysis window is identical to the behavioral data analysis, in behavioral data from human speech motor control systems, there could be somatosensory feedback signals (i.e., with feedback latency 65–75 ms; [80]) present and affecting the speech signal in the selected analysis window. Normalized vocal fo responses per each trial for the adaptive paradigm simulations are provided in Fig 3D for the preselected auditory feedback gain via vocal fo reflexive simulations (gaudfb = 0.5) and for different feedforward learning rates (λff ranging from 0–0.25). Although an ideal fit was not observed, with the lowest RMSE and difference between area under the curves, λff = 0.1 provided a consistent fit for the behavioral mean vocal fo adaptive response (RMSE = 21.57, R2 = 0.32; See Table 3).
Table 3. Goodness-of-fit statistics for behavioral dataset for vocal fo adaptive paradigm explained by model simulations.
AUC = area under the curve.
| Feedforward learning rate | 0.025 | 0.050 | 0.075 | 0.100 | 0.150 | 0.200 | 0.250 |
|---|---|---|---|---|---|---|---|
| R-squared | 0.16 | 0.33 | 0.33 | 0.32 | 0.26 | 0.21 | 0.20 |
| RMSE | 24.02 | 21.44 | 21.43 | 21.57 | 22.55 | 23.24 | 23.41 |
| Absolute Difference AUC | 545.85 | 227.93 | 52.90 | 27.58 | 131.07 | 184.41 | 203.94 |
Motor equivalence in simulated vocal productions
The initial biomechanical conditions of the VFs define how the compensatory responses to auditory perturbations are handled in dimensions that are acoustically less important. This is known as motor equivalence [20]. Based on this theory, we carried out two sets of simulations to characterize LaDIVA’s behavior. Initial laryngeal mobility space variables aCT, aTA, and Ps were preset parameters for the extended BCM. We used these parameters to characterize the model behavior in a controlled manner to understand how differences in CT and TA muscle activations affect the acoustic outcomes of the system. We confirmed that a variety of combinations of aCT and aTA parameters could produce the same vocal fo while subglottal pressure is kept constant (i.e., Ps = 800 Pa). See Fig 4A Muscle Activation Map for vocal fo (fo = 134 Hz contour line). Vocal SPL also remained fairly constant during these simulations (range: 71–76 dB SPL), which is consistent with in vivo work that observed minimal change in SPL in the lower register (i.e., including modal phonation) when Ps is kept constant [81]. See Fig 4B Muscle Activation Map for vocal SPL. Four combinations of initial aCT and aTA levels were used to simulate four different initial conditions in phonation (see Table 4 and Fig 4A and 4B cases). For each of these cases, a simulation of a vocal fo reflexive paradigm was carried out and the model outputs of each paradigm were compared across cases (see Fig 4). We observed that, although aCT and aTA trajectories varied across the simulations (Fig 4C and 4D), the vocal fo responses (i.e., the acoustic output) were comparable to the behavioral dataset across cases (Fig 4E). For very small values of aCT, we see aTA dominance in fo control (shown in case A in Fig 4). For the rest of the cases, aCT takes precedence in controlling vocal fo and aTA plays a less dominant role. This is consistent with prior literature that suggests antagonistic relationships between vocal fo and aCT and aTA across the chest register [55,82,83]. The vocal SPL target range was maintained at 68–80 dB for the simulations to mimic the vocal SPL outputs expected in the behavioral study (i.e., participants were instructed to speak in their typical speaking voice). As we maintained a constant subglottal pressure through all simulations, in the range of aCT and aTA considered, the change in vocal SPL output was less than 1 dB SPL. Thus, the vocal SPL outputs did not exceed the target range, and no corrective feedback signals modifying SPL output were generated. As a result, no deviations in vocal SPL were observed for the simulations. For all simulations in Cases A through D, the auditory feedback gain and feedforward learning rate were kept constant (i.e., gaudfb = 0.5 and gff = 0.1).
Fig 4. Simulation responses of LaDIVA for four different initial laryngeal muscle activation levels.
(a-b) Cases A, B, C, and D muscle activation levels are indicated by dots on the fo = 134 Hz solid line, with subglottal pressure (Ps) = 800 Pa. (a) shows fo contours (Hz units) and (b) shows SPL contours (dB units). (c) Cricothyroid muscle activation level trajectory over the simulation for all initial conditions. (d) Thyroarytenoid muscle activation level trajectory over the simulation for all initial conditions. (e) Vocal fo simulation response for vocal fo reflexive paradigm in comparison with mean group response (20 adults with typical speech) of behavioral dataset marked in black with 95% CI error bars. Note: vocal SPL output deviation was zero as the SPL target range was set to 68–80 dB and all cases remained within target range.
Table 4. Initial laryngeal intrinsic muscle activation levels applied for simulations.
aLC was kept fixed at 0.5 for all simulations.
| Case A | Case B | Case C | Case D | |
|---|---|---|---|---|
| aCT and aTA relationship | aCT > aTA | aCT = aTA | aCT < aTA | aCT << aTA |
| aCT level | 0.300 | 0.169 | 0.202 | 0.256 |
| aTA level | 0.050 | 0.175 | 0.400 | 0.600 |
| Subglottal Pressure (P s ) | 800 | 800 | 800 | 800 |
| Vocal fo output (Hz) | 134.20 | 133.98 | 133.96 | 133.97 |
| Sound Pressure Level (dB SPL) | 76 | 74 | 71 | 71 |
Prosodic contour simulations
Auditory perturbations have been carried out to understand the vocal motor control mechanisms for control of vocal fo and SPL in a task-dependent manner during the production of suprasegmental features (e.g., stress, intonation) in running speech [84–86]. Different prosodic contours are generated by participants for running speech utterances and vocal fo perturbations are carried out at different stages of the utterance to investigate the task-relevance of compensatory responses to these perturbations. To model these dynamic perturbations, as an initial step, speech production models should be able to generate running speech utterances with different vocal fo contours. So far, the DIVA model has been unable to simulate dynamic vocal fo perturbations as vocal fo and SPL were not controlled variables in the model. As an initial step to assess and showcase the LaDIVA model’s ability to conduct dynamic vocal fo perturbations, we carried out a series of model simulations incorporating four intonation patterns to a single base statement. These examples showcase that the LaDIVA model can be used to embed different prosodic contours in phrases as vocal fo is a controlled component. We expect that this methodology can be used in the future to generate stimuli for auditory vocal fo perturbations of running speech.
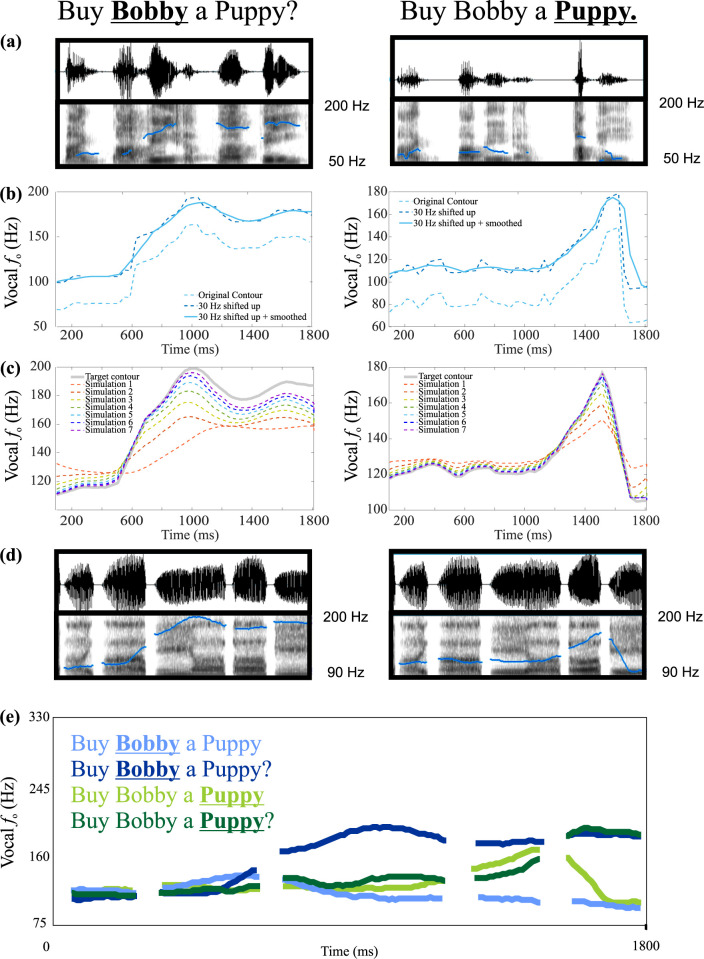
LaDIVA contains an acoustic synthesizer that is adapted from DIVA and modified to accommodate the extended BCM. See Materials and Methods for more information on the acoustic synthesizer. The prosodic contour simulations can also be used to assess the function of the acoustic synthesizer and the naturalness of the acoustic outputs generated. See S1 Audio for audio recordings of original and LaDIVA-synthesized utterances. The statement “Buy Bobby a Puppy” was recorded from one of the authors (F.H.G.) with four different prosodic contours, providing different intonation patterns, and thus, different contextual information. The sentence was also synthesized in the model by defining auditory and somatosensory targets in the articulatory domain such that a monotonic production of the sentence was produced. The simulated sentence duration was 1815 ms. Original recordings were time-normalized by warping each recording in the time domain to match the model production. From each time-warped recording, the pitch contour was extracted. Initial aCT and aTA levels of case B were used to conduct all pitch contour simulations, resulting in an initial vocal fo of 134 Hz. A baseline vocal fo increase of 30 Hz was applied to all extracted pitch contours to match the original recordings (i.e., of a male with 100 Hz vocal fo) to model production that has a baseline fo of 134 Hz. The pitch contours were then smoothed using a 5-point moving-average, before being fed to the model as vocal fo target contours. A series of simulations was carried out until the output of each vocal fo pitch contour converged to the target contour. The number of iterations required for contour convergence was determined be faster or slower based on the model parameters used. The model parameters were set as following for the simulations shown in Fig 5 (gfb_aud = 1; λff = 0.5). See Fig 5 for time-warped versions of the original pitch contours of the four different intonations patterns plotted against synthesized versions of the same contours from LaDIVA. These results showcase LaDIVA’s potential to perform simulations for studies incorporating intonation, tonal languages, and running speech fo perturbations [85, 86].
Fig 5. Prosodic Contours of “Buy Bobby a Puppy”.
Fig 5A–5D Vocal fo contour extraction, transformation, model simulation, and model synthesis output shown for two intonation patterns. (a) Original recordings recorded from author F.H.G. (male 100 Hz vocal fo). (b) A baseline vocal fo increase of 30 Hz was applied to all extracted pitch contours to match case B model mean vocal fo of 134 Hz. The pitch contours were smoothed using a 5-point moving-average. (c) Transformed pitch contours were then fed as vocal fo target contours to the model and a sequence of simulations were carried out until the output vocal fo contour matched the target contour. (d) output signal and vocal fo contour produced by LaDIVA acoustic synthesizer. (e) Simulated vocal fo contours of four different intonation patterns of producing the sentence ‘Buy Bobby a Puppy’ time warped to be the same duration in time. Bolded and underlined sections highlight stressed words. Note: model parameters were set as following for these simulations (learning rate = 0.5; feedback gain = 1). The contour convergence process can be faster or slower based on the parameters used.
Discussion
In the current study, we introduced LaDIVA, a neurocomputational model of laryngeal motor control. LaDIVA extends the well-established neurocomputational model DIVA, incorporating a biomechanical VF model for dynamic adjustment of laryngeal function. Model performance was validated via empirical evidence from a behavioral study on adults with typical speech involving reflexive and adaptive vocal fo auditory feedback perturbation paradigms. Through the application of LaDIVA, we were able to successfully replicate both the reflexive and adaptive auditory vocal fo responses observed in the behavioral data. The simulations also provided CT and TA laryngeal muscle activation levels across time for the paradigms. However, these predicted muscle activations remain to be experimentally validated via behavioral studies. Intrinsic laryngeal muscle activity is difficult to obtain in behavioral settings due to its invasive recording procedures using laryngeal electromyography techniques [34,35,37]. Only one previous study measured laryngeal electromyography responses to a vocal fo auditory feedback reflexive perturbation paradigm [36]. The paradigms conducted in that study with conversational speech did not elicit observable patterns in CT and TA muscle activation levels and the authors speculated that the muscle activation levels were not detectable due to high levels of underlying neuromuscular signal noise. Nonetheless, the current model results are supported by a prior study conducted using graded muscle simulations on an in vivo canine larynx that observed general laryngeal motor equivalence, i.e., the ability of the larynx to produce same vocal fo and SPL outputs with multiple combinations of intrinsic laryngeal muscle activations [81]. Thus, modeling efforts could be an effective way to investigate intrinsic laryngeal muscle activity related to vocal fo reflexive paradigms further in future.
Auditory feedback gain and feedforward learning rate in LaDIVA are model parameters that can be modified to represent neural motor control impairments related to neurological (i.e., Parkinson’s disease; PD) or functional voice disorders (i.e., vocal hyperfunction). Hyperactive auditory feedback responses in persons with PD who are off medication have been noted by multiple altered auditory feedback behavioral studies for vocal fo [72–75] and for vocal SPL [73]. Reduced adaptive responses were also observed in several studies carried out with persons with PD (vocal fo: [69], vocal SPL: [87]). Overall, these studies suggest that persons with PD have hyperactive auditory feedback and weakened auditory-motor integration that causes impaired feedforward motor control. Thus, the vocal motor control deficits in PD can be modeled using LaDIVA by increasing the auditory feedback gain and decreasing the feedforward learning rate. Altered auditory feedback behavioral studies have also indicated that there is a possible auditory-motor phenotype for individuals with vocal hyperfunction in which atypical vocal motor control is observed [57,70,71]. Deficits in auditory motor integration has been identified via adaptive vocal fo studies conducted in individuals with vocal hyperfunction [57,70]. Thus, the suspected vocal motor control deficits in vocal hyperfunction can be modeled using LaDIVA by decreasing the feedforward learning rate. However, vocal hyperfunction has not been sufficiently investigated to conclude if the origins are neurological, anatomical, or has components from both neural control and biomechanical control. The objective of LaDIVA was to combine a neurocomputational model of vocal motor control and a biomechanical model of the peripheral laryngeal apparatus, thus providing a comprehensive model of voice motor control. We can manipulate the model’s neurocomputational as well as biomechanical parameters to investigate and gather insight on how the respective changes affects the vocal motor outcomes of the system.
An interesting finding of the current study was that LaDIVA yielded similar acoustic outputs to a reflexive paradigm across different initial muscle activation conditions. Based on VF physiology, laryngeal muscle activations vary across individuals with typical laryngeal function based on sex, age, and different voicing conditions [88]. These observations might be instrumental in understanding how similar acoustic outputs are achieved despite individual variability in internal neuromuscular activations. LaDIVA can be used with individualized parameters to reflect physiological changes in VFs due to age or sex, and the variability in laryngeal muscle activations can be quantified, using simulation outcomes such as vocal fo reflexive responses. These quantitative results may be instrumental in identifying what degree of variability is due to variations in laryngeal physiology. At the same time, these results caution us against using only the acoustic vocal fo response measures in characterizing neural laryngeal motor control function, specifically in individuals with voice disorders characterized by increased laryngeal muscle tension. For example, individuals with vocal hyperfunction are thought to exhibit higher laryngeal muscle activation [89,90]. However, a recent study found no significant differences in vocal fo reflexive responses in individuals with vocal hyperfunction compared to individuals without vocal hyperfunction [57]. Thus, individuals with vocal hyperfunction seem to be generating similar acoustic outcomes as individuals without vocal hyperfunction, but presumably with higher intrinsic muscle activation levels. This could be a possible explanation for the clinical observations of low vocal efficiency in individuals with vocal hyperfunction [90,91].
We note that LaDIVA’s adaptive paradigm simulations are not as well-fit to the behavioral data as reflexive paradigm simulations. There could be multiple reasons for this observation, including: 1) vocal motor variability not being a modeled characteristic in LaDIVA, 2) somatosensory feedback not being a modeled component, 3) a single parameter (i.e., feedforward learning rate) defining adaptive behavior in LaDIVA, and 4) identical feedback error contributions being used for feedforward and feedback motor control. Trial-to-trial noise in speech acquisition, production, and learning are inherent characteristics in empirical data related to speech motor control [92–94]. However, the current implementation of LaDIVA contains no model characteristic defining vocal motor production or perception variability. Behavioral responses used in the current study clearly show the trial-to-trial noise variations whereas the model simulations are noise-free and smooth across trials. See S2 Text for production noise related variations observed in simulated adaptive paradigm outputs when varying levels of production noise are included in the LaDIVA model. Adding noise-based variability at production, perception, and/or learning levels will be carried out in future iterations as it requires qualitative and quantitative specification of noise characteristics via behavioral paradigms. Somatosensory feedback of the model remains unchanged during auditory feedback perturbations and would cause the feedforward control system to correct for accumulated somatosensory errors over time. Thus, the overall effect would yield a lower fo magnitude for the simulated adaptive response. In addition, identical feedforward learning rates are chosen for the incorporation of auditory and somatosensory feedback to feedforward controller in LaDIVA. As somatosensory feedback contributions are set to zero in the current iteration of LaDIVA, this assumption does not affect the overall adaptive response simulations. Furthermore, a recent study examined the error sensitivity of feedforward and feedback motor control systems using adaptive paradigms in first and second vowel formants and the state-space model [95]. The study provided initial evidence that feedforward and feedback control systems may function independently, with higher error sensitivity in feedback control compared to feedforward control. These recent findings are in contrast to the DIVA model assumption that the feedback and feedforward motor controllers share identical error sensitivity. LaDIVA shares this assumption, which could be a possible explanation for poorer simulation fits for the adaptive paradigm compared to reflexive paradigm.
In this validation study, we have demonstrated LaDIVA’s capability to simulate both adaptive and reflexive paradigms of sustained vowels as well as its capability to handle running speech utterances (see Results section on prosodic contours). LaDIVA provides the flexibility to observe feedback- and feedforward-based fo contours across the time span of a trial, as well as to focus on specific time windows. Thus, LaDIVA can be used to replicate and study characteristics of feedback and feedforward responses separately (i.e., via late and early time windows in each trial) using adaptive paradigm simulations [95]. The capability to simulate running speech utterances embedded with laryngeal motor control gives LaDIVA the unique capability to model vocal fo perturbation studies in running speech, which has so far not been modeled to the best of our knowledge. Thus, LaDIVA may allow for the generation of better hypotheses for behavioral studies related to vocal fo perturbations in running speech. We have carried out parameter fitting for auditory feedback gain and feedforward learning rate parameters in the current study as a validation of the model’s capability to model instances of laryngeal motor control with hyperactive auditory motor control mechanisms and weak auditory-motor integration capabilities. Thereby, we showcase LaDIVA’s capability to replicate vocal motor control deficits that have been documented in voice disorders related to PD and vocal hyperfunction. Thus, the parametric fitting carried out in the validation of LaDIVA serves a larger purpose than merely showcasing that the model can fit data. It sheds light to the neurobiological control of vocal fo.
Comparisons with simpleDIVA
SimpleDIVA is a 3-parameter model recently developed to fit average data from different cohorts under different auditory and somatosensory adaptive paradigms. It can be used to predict auditory and somatosensory feedback gains, as well as the feedforward learning rates used by each behavioral dataset [76]. SimpleDIVA can be used to predict the outcome fo contours of specific adaptive auditory feedback paradigms based on prior assumptions about feedback gains and the feedforward learning rate. SimpleDIVA is a powerful modeling tool due to its simplicity leading to unique solutions with limited degrees of freedom. Although simpleDIVA successfully abstracts the DIVA architecture to model both articulatory and laryngeal motor control, its simplification of DIVA to three mathematical equations has its own limitations.
SimpleDIVA and LaDIVA are radically different in both their architecture and more importantly, their intent. LaDIVA is a control model of vocal and supralaryngal production that is capable of learning. Moreover, LaDIVA is capable of simulating acoustic responses and brain activations to behavioral paradigms. SimpleDIVA is, conversely, a way to fit a set of equations to time-series data to estimate gain parameters. Thus, LaDIVA can complement simpleDIVA in studying laryngeal motor control. LaDIVA can be used to support the development of hypotheses that can be tested empirically in behavioral studies to ultimately advance the field of laryngeal motor control. LaDIVA increases the predictive power in hypotheses by incorporating biomechanical and physiological restrictions of the VFs in producing vocalizations. A biologically relevant neural model of laryngeal motor control provides a unique platform to model voice disorders that are hypothesized to have neurological origins.
The availability of multiple degrees of freedom in LaDIVA can be a disadvantage due to the large number of non-unique solutions the data fits could provide. However, the inclusion of the VF model provides its own physiologically valid restrictions on laryngeal motor control function of LaDIVA and thus safeguards LaDIVA from resulting in biologically infeasible solutions. Moreover, due to the large number of defined biomechanical control parameters, LaDIVA possesses the ability to carry out subject-specific simulations. This feature is inherited to LaDIVA from the extended BCM, which has been successfully used to conduct subject-specific modeling in individuals with vocal hyperfunction [14,96]. Although simulating subject-specific data is out of scope for the current investigation, this is a potential area of future expansion of LaDIVA.
Auditory acuity and auditory target size
Vocal fo acuity can be assessed via the minimum noticeable difference in vocal fo, commonly referred to as the Just Noticeable Difference (JND; inversely related to vocal fo acuity) between two frequencies in behavioral paradigms. In LaDIVA, vocal fo acuity is a preset parameter. See Materials and Methods: targets section for more detail. The JND for vocal fo in LaDIVA was set during all simulations to be significantly smaller compared to the maximum perturbation magnitude utilized in the perturbation paradigms (here, vocal fo JND = 5 cents << maximum perturbation magnitude = 100 cents). Here, a five-cent JND threshold was selected to reflect a model with excellent fo acuity, since prior studies have indicated that participants respond to fo shifts as small as 10 cents in reflexive paradigms [97,98]. However, vocal fo acuity has been previously shown to differ across individuals and thus could be varied as a parameter in future versions of LaDIVA [99–101]. Prior studies have provided evidence that participants with better vowel formant acuity generate larger compensatory response magnitudes to adaptive vowel formant perturbation paradigms [102–104]. A single study using DIVA was able to replicate this relationship for simulated participant responses, with vowel formant target sizes modeled using Gaussian distributions with varying distribution variances (i.e., vowel formant acuity was inversely related to distribution variance; [104]). However, in terms of laryngeal motor control, there have been conflicting prior study observations about the relationship between auditory feedback perturbation magnitudes and corresponding vocal fo acuity, suggesting that there could be a complex relationship (or lack thereof) between generating corrective feedback for auditory feedback errors and perceiving those feedback errors [68,98,105,106]. Including vocal fo acuity as a variable parameter will allow for modeling intra-speaker fo acuity variability in LaDIVA, helping to interpret these recent findings.
Limitations
The current implementation does not include physical tissue-aero-acoustic interactions at the glottis (i.e., the modification of VF dynamics due to acoustic and aerodynamic feedback; [81]). The DIVA model provides a modified Maeda model [78] based vocal tract, which is integrated in LaDIVA. When coupling effects due to vocal tract acoustics are neglected, the laryngeal adjustments resulting from the coordinated control of VF stiffness, geometry, and position do not adequately model the effects on the source intensity or vocal quality. This is backed by laryngeal, physical, or computational models of phonation [107]. The effect of laryngeal adjustments on vocal intensity becomes more relevant in the presence of an interactive vocal tract model [14]. DIVA currently contains an articulatory synthesizer that incorporates simplified, custom source-filter interactions that are mathematically defined. However, a more physiologically relevant source-filter interaction can be modeled using biomechanical VF models with vocal tract interactions. The Maeda model used for vocal tract modeling in DIVA is compatible with any biomechanical VF model. Moreover, an added advantage specific to Maeda’s model is that it allows simulation of vocal tract elongation/shortening, which is perceptually important for speech simulation [78,108,109]. Thus, a possible future modification that can be implemented in LaDIVA is to incorporate the tissue-aero-acoustic interaction at the glottis using the extended BCM, and the acoustic effects due to subglottal tract dynamics by interconnecting the BCM with the Maeda model, making LaDIVA to be more physiologically relevant.
Currently, LaDIVA focuses mainly on the auditory feedback controller and auditory feedback perturbations. We kept the somatosensory feedback controller offline for the current version by setting the somatosensory feedback gain to zero. However, laryngeal motor control is reliant on feedforward motor commands and sensory feedback provided via both auditory and somatosensory feedback subsystems [110,111]. Thus, the contributions of the somatosensory feedback controller cannot be ignored completely. Many auditory sensorimotor adaptation studies in vowel formants as well as vocal fo showcase that the amount of adaptation plateaus well before reaching full compensation [66,68,69,104,112]. This partial compensation is explained in the DIVA model as being driven by the competition between counteracting auditory and somatosensory feedback signals. At the beginning of a trial when auditory feedback is artificially modified, the somatosensory feedback controller does not find any discrepancies between somatosensory feedback received (unaltered) and desired somatosensory targets. As the system starts compensating for the artificial auditory feedback alterations by modifying subsequent feedforward motor commands and producing altered speech sounds, the somatosensory feedback also starts to be altered, causing errors between somatosensory feedback and desired somatosensory targets. These counteracting feedback signals eventually cause the compensatory response to plateau, before it fully compensates for the altered auditory feedback. This reasoning may explain why LaDIVA’s adaptive simulations do not produce fo contours that fit empirical data as well as its reflexive simulations.
With regard to reflexive vocal fo paradigms (i.e., where real-time feedback error correction is investigated) there are also behavioral observations of partial compensation [113–117]. These compensatory magnitudes are explained in the DIVA model as being driven by the competition between feedforward and feedback control systems, as well as the competition between auditory and somatosensory feedback mechanisms. Since the corrective auditory feedback-driven motor command is (weighted and) summed with the feedforward command to produce the final speech signal, theoretically the system can maximally produce a partial compensation of 50% (see Eq 9). This is a strong prediction of the model and can be observed via the reflexive paradigm simulations (see Fig 3C and Fig A in S1 Text). In these simulations, setting the total feedforward gain to 1, the auditory feedback gain to 1, and the somatosensory feedback gain to 0 results in a partial compensation of 50 cents for a 100 cent- reflexive perturbation of auditory feedback, which converts to a 50% (partial) compensation. With non-zero somatosensory feedback contributions, the partial compensation will be even less, as observed in literature [113–117].
In LaDIVA, the glottal constriction is the only parameter for somatosensory representation of vocal motor function and it was not controlled by the extended BCM in the current version (i.e., it was predefined as constant values for voiced and unvoiced portions of productions and not dependent on LCA or PCA muscle activity in the extended BCM). Better understanding of the somatosensory feedback controller contribution to laryngeal motor control needs to be obtained to define accurate somatosensory representations for vocal features. For example, it remains unknown whether vocal fold collision and tactile feedback during voicing onset and offsets are monitored via the same somatosensory feedback mechanisms as those that monitor vocal fo control via VF vibratory activity during sustained phonation. Thus, more information about the types of somatosensory feedback (i.e., tactile, vibratory, and proprioceptive) used in laryngeal motor control needs to be acquired to define multiple somatosensory representations for laryngeal motor control in LaDIVA. Prior research suggests that somatosensory feedback provides prephonatory information about the intrinsic laryngeal musculature and the length of the VF (i.e., proprioceptive feedback), prior to the onset of the vocalization [118,119]. This may indicate that auditory and somatosensory feedback controllers operate over different time scales when providing corrective signals for laryngeal motor control. Finally, individual variability in the sensitivity to or reliance on somatosensory feedback may be important. Women have shown exhibited increased sensitivity to somatosensory feedback manipulations relative to men, suggesting a higher density of mechanoreceptors in women compared to men due to anatomical differences [120]. Furthermore, prior work using vowel formants suggests that there is a sensory preference in the articulatory domain for either auditory and somatosensory feedback that varies across individuals [121,122]. In sum, there are many factors affecting the contribution of somatosensory feedback to laryngeal motor control, which should be incorporated into future modeling efforts.
When repeated vocal productions are carried out (e.g., via adaptive paradigms), vocal fatigue increases vocal fold tension, which in turn causes the mean vocal fo for each trial to drift upwards in later trials [123–125]. In behavioral data analysis, a control experiment with the same number of trials as an adaptive experiment is carried out and each trial mean adaptive fo magnitude is subtracted from the adaptive experiment responses to account for this drift [68,69]. In contrast, LaDIVA does not simulate accumulated vocal fatigue over multiple trial repetitions. For each trial, LaDIVA simulated VF dynamics starting from the same initial conditions and there were no carry over components of VF characteristics related to vocal fatigue. In future versions of LaDIVA, the VF model could incorporate features that represent effects accumulated muscle fatigue (i.e., increased tension in intrinsic VF musculature).
Future directions
LaDIVA can be used to expand the understanding of the physiology of human phonation and to elucidate the origins of specific disorders affecting voice that have or are speculated to have neurological origins (i.e., laryngeal dystonia, hypokinetic dysarthria, vocal hyperfunction). The improvements introduced in LaDIVA provide practical benefits for the investigation of key aspects of the auditory-motor function involved in human phonation. We foresee the application of LaDIVA to simulate behavior of laryngeal motor control for speakers with typical vocal function as well as speakers with voice disorders. LaDIVA can thus provide informative clinical insights for generating hypotheses for future behavioral studies. Moreover, LaDIVA can be used to fit individual participant data. This subject-specific parameterization can provide better understanding of different conditions and individual variability seen in previous behavioral studies [69,70].
Behavioral data collected from cohorts with voice disorders can be used to validate the hypothesis-driven modeling efforts for voice disorders, in a manner similar to the simulations carried out in our model validation. One such example is modeling unilateral VF paralysis (UVFP). UVFP is classically viewed as an isolated peripheral motor condition [126,127]. However, a recent pilot study carried out in a cohort with UVFP has suggested that this isolated peripheral injury to the larynx may have important consequences that impact central auditory processing [58]. Individuals with UVFP were found to generate significantly smaller compensatory responses to reflexive vocal fo perturbations, compared to responses from adults with typical speech. However, the study findings are challenged by the sex-mismatch in the group of individuals with UVFP and control participants (i.e., the majority of participants in UVFP group were female and the majority of participants in control group were male). Unfortunately, sex is an external factor affecting vocal fo control, and male speakers have been observed to produce significantly larger vocal fo responses in prior work [128]. Thus, there is not sufficient evidence to conclude whether the group difference found was due to a sex-mismatch or due to an underlying impairment in vocal motor control in individuals with UVFP. LaDIVA’s incorporation of both neural motor control and biomechanical mechanisms of vocal production could allow for a deeper understanding of UVFP. The extended BCM could be modified to mimic the physiology of a larynx with UVFP in LaDIVA. A patient-specific UVFP-based LaDIVA model, with an asymmetric VF model with reduced/null motor control signaling to one VF, may provide insights about the laryngeal motor control of the disorder [49,53,129]. The model could provide simulated patterns of CT and TA muscle activations and subglottal pressure in the process of simulating responses to reflexive fo auditory perturbations, which would be helpful in understanding the underlying mechanisms of UVFP.
The main objective of the current implementation of LaDIVA was to assess the validity of a computational model of neural control of laryngeal function with neural and biomechanical components. We have opted to use a combination with minimal computational complexity, providing near real-time simulations of vocalizations. Thus, LaDIVA uses a low-order lumped-element model to describe the biomechanics of phonation that does not model the complexities of three-dimensional geometry characteristics of the VFs provided by higher-order VF models [81]. In future iterations of LaDIVA we hope to incorporate more accurate models that could increase the accuracy of VF modeling of LaDIVA. Another simplification in LaDIVA was maintaining subglottal pressure at 800 Pa through all simulations. This was an intention choice to characterize the effects of different laryngeal muscle activation configurations on vocal fo and SPL outputs in a controlled manner. However, future work should be carried out to improve the forward model solution optimization to handle instances in which multiple vocal fo and SPL output solutions are available for a selected combination of aCT, aTA, and Ps in a way that does not cause discontinuities in vocal fo values across time steps in model simulations. Currently, there is a future implementation underway considering additional inputs and outputs to extend the scope of the model to incorporate all five intrinsic muscle activation variations (i.e., CT, TA, LCA, PCA, and IA) and vocal quality-based modifications.
Conclusion
In this study, we have introduced and validated LaDIVA, a new neurocomputational model with physiologically based laryngeal motor control. LaDIVA combines the DIVA model for neural motor control with a lumped-element physics-based vocal fold model. LaDIVA simulations were qualitatively and quantitatively compared and contrasted against adaptive and reflexive behavioral responses to vocal fo auditory feedback perturbations collected in individuals with typical speech. In addition, simulations of different natural intonation patterns for a running speech utterance were successfully performed. LaDIVA allows for investigation of comprehensive parameter variations, complex stationary and dynamic perturbations that are difficult to assess psychophysically, and causal effects, thus providing a tool for advancing the understanding of typical and disordered voice production.
Materials and methods
Notation
Mobility space () represents positions and changes in positions of a physical structure being controlled. In LaDIVA, mobility space is defined by 14 variables (see Fig 1; mobility space pathways denoted in orange). Ten variables are used to represent the vocal tract, each variable defining a specific vocal tract articulatory composition (x1−x10). Three variables represent the larynx, each variable defining activation levels of three intrinsic laryngeal muscles (aCT, aTA, aLC). One variable represents the respiratory system, defining the subglottal pressure applied on the larynx via the lungs (Ps). The first ten variables representing the vocal tract are preserved from DIVA model, and the variables representing the larynx and respiratory system are modified in LaDIVA. More details are provided in the Extended Body-Cover Model section. Mobility space variables are represented by 1) the symbol x if referring to a mobility space state, and 2) the symbol if referring to the change in the mobility space state.
Task space () represents sensory inputs in auditory and somatosensory domains. In LaDIVA, auditory task space is represented by five variables (see Fig 1; auditory task space pathways denoted in purple). Three variables represent the vocal tract and are defined as the first three resonant frequencies of the vocal tract. These are referred to as first, second, and third vowel formants (F1, F2, and F3). Two variables represent the larynx and are defined as the vocal fundamental frequency (fo; the acoustic correlate of vocal pitch), and the vocal sound pressure level (SPL; the acoustic correlate of loudness). In LaDIVA, somatosensory task space is represented by seven variables, which are preserved from DIVA (see Fig 1; somatosensory task space pathways denoted in green). Six variables represent the vocal tract and are defined as constriction levels of six different places of constriction along the vocal tract (S1−S6). One variable represents the larynx and is defined as the constriction at the glottis (referred to as the glottal constriction in DIVA) in somatosensory task space. Task space variables are generally represented by 1) the symbol y if referring to a task space state, and 2) the symbol if referring to the change in task space state. More specifically, auditory and somatosensory task space variables are referred to as yaud and ysomat, respectively.
Targets rα(β, t), where α = {motor, aud, somat} and β = {x, y}, represent the specific references for each sound unit, provided in the speech sound map in the brain (see Fig 1; outputs of speech sound map). Targets are defined as auditory and somatosensory task space reference targets for a given speech sound. The initial states of mobility state variables are set to zero for untuned targets. Through several iterations of simulations, the mobility space variables can be tuned to produce the desired auditory and somatosensory task space outcomes. The tuning process involves identifying the auditory and somatosensory feedback errors from desired auditory and somatosensory targets and produced auditory and somatosensory outputs of the system in current iteration and incorporating corrective motor programs to subsequent productions from the system using inverse mapping capabilities. See Inverse Mapping subsection for more details. These tuned targets can be saved as mobility space variables. As reference targets vary over time, they are defined as time series of minimum and maximum target values that each domain variable can operate within (e.g., raudmin(y,t) and raudmax(y,t)). From these maximum and minimum values, the value closest to the domain variable at each time step is considered the target for the purpose of error calculation.
In LaDIVA, similar to DIVA, targets are specified in auditory and somatosensory task space variables when initially loaded for simulations. For all simulations using the sustained vowel /a/, the vowel /a/ was tuned to obtain the desired auditory and somatosensory reference targets by tuning the mobility space variables. For the sustained vowel /a/, the vocal fo target maximum and minimum are defined to be + 5 and—5 cents from baseline fo value of production. For the sentence ‘Buy Bobby a puppy’, first the sentence was tuned to obtain the desired auditory and somatosensory reference targets in articulatory domain by setting the vocal fo target to be monotonic (i.e., fo = 134 Hz) across the utterance. Then, for each of the four prosodic contours, the sentence was separately tuned to obtain the desired auditory reference target defining each prosodic contour. For prosodic contours, both vocal fo target maximum and minimum were set to the baseline fo contour of each intonation pattern, thus a point trajectory was considered instead of a region.
In the current version of LaDIVA, the perceptual acuity (i.e., measured by just noticeable difference (JND) between two values in a task space variable) is considered to be identical to the reference target of that task space variable. For example, for the sustained vowel /a/, the vocal fo target maximum and minimum are defined to be + 5 and—5 cents from the baseline fo value of the production. Thus, an error larger than 5 cents from baseline vocal fo will be detected and corrected by the control system. The just noticeable difference is also set to be 5 cents. In future versions of LaDIVA, acuity in each task space can be differed to provide additional variability to the targets.
Intrinsic delays τvariable, represent the intrinsic delay parameters defined in DIVA to mimic neural and biomechanical processing delays. The propagation delay of signal transmission in cortico-cortical connections between premotor cortex and motor cortex as well as between auditory/somatosensory areas and motor cortex is set to 5 ms. The time it takes for a motor command to have effects on articulatory mechanisms is set to 50 ms. The time it takes an acoustic signal transduced by cochlear to make its way to the auditory cortical areas (i.e., superior temporal cortex; auditory state map in DIVA) is set to 50 ms. The time it takes for somatosensory feedback from peripheral regions to reach higher order somatosensory cortical areas (i.e., inferior parietal cortex; somatosensory state map in DIVA) is set to 20 ms. The rest of the delays in DIVA correspond to ‘learned’ or ‘necessary’ delays for accurate representation of neural signal calculations. The learned delays between premotor cortex (speech sound map in DIVA) and auditory and somatosensory areas (auditory and somatosensory error maps) are set to 55 ms and 25 ms, respectively, to make the auditory and somatosensory expectation signals arrive at the error maps at the same time that the corresponding auditory and somatosensory state signals do, such that the error signals are computed correctly. The learned delays between premotor cortex and motor cortex (for the pathway through the cerebellum) are similarly set to 55 ms and 25 ms, respectively for auditory and somatosensory components, to make the learning signals arrive at the motor cortex at the same time that the corresponding feedback corrective signal such that the correct portion of the feedforward command is adapted. These ‘learned’ delays are necessary for the correct behavior of the model but they could be implemented in many different ways (e.g., differentially delaying the auditory and somatosensory areas’ projections to motor cortex to make the somatosensory and auditory error signals arrive at the same time despite different intrinsic delays, so that the rest of the ‘learned’ delays to the motor cortex need not differentiate between the auditory and somatosensory signals). The equations in the following sections include delay parameters discussed above in more detail. Note that the delays above are those specified in the DIVA Simulink version (2017), which were used for implementation of LaDIVA. Please refer to Guenther, Ghosh [21] for a detailed description of DIVA intrinsic delays and the neurobiological literature supporting the selections.
Control Modules in LaDIVA
Auditory feedback controller
In LaDIVA, the auditory feedback controller calculates the difference between the reference auditory target, raud(y,t), and the current auditory output, Caud(y), to calculate the auditory error signal, eaud(y) (Eq 1). The Jacobian inverse mapping, J(x)−1, translates the auditory error from auditory task space to mobility space (i.e., eaud(y)→eaud(x); Eq 2). A fraction of the translated error is then carried forward as the output of the auditory feedback controller, , to be added as a corrective command to the feedforward controller. To achieve this fractional addition, the translated error is multiplied by a gain factor (auditory feedback gain; 0<gfb_aud<1). See Eq 3.
| (1) |
| (2) |
| (3) |
Here, reference auditory target = raud(y,t), current auditory output = Caud(y,t), auditory error signal in auditory task space = eaud(y,t−τAuM), auditory error signal in mobility space = eaud(x,t−τAuM), Jacobian inverse mapping = J(x)−1, auditory feedback gain = gfb_aud and output of the auditory feedback controller = . τAuM (set to 5 ms) is the long range cortico-cortical signal transmission delay between superior temporal cortex (i.e., auditory error map) and motor cortex (i.e., articulatory velocity position map). Note that is a 14-n array containing the rate of change in mobility space variables. Thus, the exact corrective command, .
Somatosensory feedback controller
Similarly, the somatosensory feedback controller in LaDIVA calculates the difference between the reference somatosensory target, rsomat(y,t), and the current somatosensory output, Csomat(y), to calculate the somatosensory error signal, esomat(y) (Eq 4). The Jacobian inverse mapping, J(x)−1, translates the somatosensory error from somatosensory task space to mobility space (i.e., esomat(y)→esomat(x); Eq 5). A fraction of the translated error is then carried forward as the output of the somatosensory feedback controller to be added as a corrective command to the feedforward controller. To achieve this fractional addition, the translated error is multiplied by a gain factor (somatosensory feedback gain; 0<gfb_somat<1). See Eq 6.
| (4) |
| (5) |
| (6) |
Here, reference somatosensory target = rsomat(y,t), current somatosensory output = Csomat(y,t), somatosensory error signal in somatosensory task space = esomat(y,t−τSoM), somatosensory error signal in mobility space = esomat(x,t−τSoM), Jacobian inverse mapping = J(x)−1, somatosensory feedback gain = gfb_somat, and output of the somatosensory feedback controller = τSoM (set to 5 ms) is the long range cortico-cortical signal transmission delay between inferior parietal cortex (i.e., somatosensory error map) and motor cortex (i.e., articulatory velocity position map). Note that the exact corrective command, .
Feedforward controller
In LaDIVA, the feedforward controller calculates the feedforward motor command FFmotor(x,t) by multiplying the reference mobility target, rmotor(x,t) by a weighting parameter wmotor(x) and the total feedforward gain . See Eq 8. The weighting parameter wmotor(x) is calculated by considering a fraction of the corrective motor commands from auditory and somatosensory feedback controllers (i.e., eaud(x,t)+esomat(x,t)). See Eq 7A. The feedforward learning rate is defined to quantify the fraction of feedback corrective commands incorporated into subsequent motor output (Feedforward learning rate; 0<λff<1). See Eq 7B. Note that the original DIVA model has an additional gain parameter defined to represent total feedforward gain (total feedforward gain; ) that should not be confused with λff. Given that an adult system should possess fully tuned motor programs, the feedforward gain was set to its maximum value (gff = 1). Unless there is an anatomical change or sensory deficit that affects speech production, the feedforward gain is not expected to differ across time courses relevant to behavioral paradigms [8]. The current motor output is a combination of the feedforward motor command FFmotor(x,t) and a fraction of the corrective motor commands from auditory and somatosensory feedback controllers. See Eq 9. The total feedback gain is defined to quantify the fraction of the combined auditory and somatosensory feedback corrective commands incorporated into subsequent motor output (total feedback gain; ). For LaDIVA simulations, was set to 1.
| (7A) |
| (7B) |
| (7C) |
| (8) |
| (9) |
Here reference mobility target = rmotor(x,t), subsequent motor output = , feedforward motor command error = emotor(x,t), output of the feedforward motor controller = FFmotor(x,t), output of the auditory feedback controller = output of the somatosensory feedback controller = . For LaDIVA, auditory task space variables: fo and SPL, mobility space variables: aCT, aTA, aLC, and Ps, and the somatosensory task space variable: glottal constriction, are the relevant parameters. The learned delays τlearnt between premotor cortex and motor cortex (for the pathway through the cerebellum) are set to 55 ms and 25 ms, respectively, for auditory and somatosensory components to make the learning signals arrive at the motor cortex at the same time that the corresponding feedback corrective signal such that the correct portion of the feedforward command is adapted. τPreM (set to 5 ms) is the long range cortico-cortical signal transmission delay between premotor cortex (i.e., speech sound map) and motor cortex (i.e., articulatory velocity position map).
Forward mapping F{x}
The forward model in LaDIVA, denoted by F{~}, predicts the auditory consequences, Caud(y,t), of the CT and TA laryngeal muscle activations and subglottal pressure buildup due to respiratory function. See Eq 10. Although somatosensory consequences of motor commands, Csomat(y,t), can also be predicted, the current version of LaDIVA focuses on auditory consequences. The forward mapping is a consolidation of 1) conversion of current motor output Cmotor(x,t−τMoAc), to positions of the articulators Artic(x,t), 2) the conversion of positions of the articulators to the resultant to acoustic output Acoustic(t) as derived by the acoustic synthesizer in DIVA, and 3) the conversion of the acoustic signal to the current auditory output at the cochlear Caud(y,t). Thus, Eq 10 can be further broken down to three equations. See Eqs 10A–10C.
| (10) |
| (10A) |
| (10B) |
| (10C) |
If any auditory perturbation is added to the system, it will be added to the acoustic signal as per Eq 10B. Here, τMoAc is the time it takes for the motor command to have its effects on the articulatory mechanisms. τAcAu is the time it takes an acoustic signal transduced by the cochlea to make its way to the auditory cortical areas.
Jacobian Inverse Mapping J(x)−1
The Jacobian inverse mapping in LaDIVA, denoted by J(x)−1, converts the auditory error signals from auditory task space to mobility space (i.e., Caud(y,t) to Caud(x,t)). Similarly, somatosensory error signals in somatosensory task space are converted to mobility task space (i.e., Csomat(y,t) to Csomat(x,t)). In the current version of LaDIVA, we focus on auditory error signals. Eqs 11 – 14 summarize the computations involved in generating the Jacobian inverse mapping required to convert the auditory error signals from auditory task space to mobility space corrective motor commands.
| (11) |
| (12) |
| (13) |
| (14) |
| (2) |
Here, F{~} = forward model in LaDIVA, Caud(y,t) = current auditory consequences, I(x) = identity matrix, γ = Jacobian regularization factor, ξ = Jacobian step size, Cmotor(x,t) = current motor command, Δx = Jacobian step size change in mobility space, = auditory task space change for a Jacobian step size change in mobility space, J(y) = Jacobian matrix, J(x)−1 = Jacobian inverse mapping, [~]+ = Moore Penrose pseudo inverse, eaud(y,t) = auditory error signal in auditory task space, eaud(x,t) = auditory error signal in mobility space. τlearned is the delay within the motor cortex between the current motor position signal and the Jacobian inverse-map. τlearned is set to 55 ms make the current articulator position signal arrive at the inverse-map at the same time that the corresponding error signals such that the inverse projection is computed based on the motor configuration of the articulators at the time of the error generating production.
Modification to extended BCM
Overview of extended BCM
To incorporate motor control of glottal function into DIVA, biomechanical low-dimensional lumped-element modeling of vocal fold (VF) oscillations was applied. For this, an extended version of the well-established body-cover model (BCM) developed by Story and Titze [46] resembling internal layered tissue structure in the VFs was chosen. The extended version of the BCM introduced by Zañartu, Galindo [49], which contains the original BCM mathematical equations as well as added features including a revised glottal flow model with a posterior glottal gap, was used. The BCM formulation allows for accurate description and simulation of many fundamental aspects of vocal function, at a low computational cost [45]. These include flow-induced self-sustained oscillations, the vertical mucosal surface wave, and fold collision during the closed phase [43,130]. It further considers the three-way interaction at the glottis between sound, flow, and VF tissue; and is compatible with acoustic wave propagation schemes for modeling vocal tract articulation [131]. In the extended BCM model, the effects of a posterior gap on the VF tissue dynamics are also taken into account, which is crucial for modeling vocal hyperfunction [49].
For the implementation in this paper, the DIVA acoustic synthesizer was applied to generate the acoustic signal outputs of the model (see Materials and Methods: acoustic synthesizer section). However, it should be noted that DIVA does not contain biomechanically-relevant source-filter interactions in its acoustic synthesizer. Intrinsic laryngeal muscles control the VF configurations in the BCM. The thyroarytenoid (TA) muscle comprises the body of the VFs and contributes to changing the tension and length of the VFs. The cricothyroid (CT) muscle tilts the thyroid cartilage forward, which in turn tightens and stretches the VFs. The interarytenoid (IA) and lateral cricoarytenoid (LCA) muscles work in conjunction to adduct the glottis. The opposite action is performed by the posterior cricoarytenoid (PCA) muscle solely. Intrinsic laryngeal muscles also control VF posturing and tissue properties. In the BCM, VF adjustment (i.e., controlled modification of geometrical and biomechanical model parameters) is obtained using a simplified muscle activation scheme based upon a set of physiological rules [46,48]. The defined set of rules allow for capturing the essential effects on vocal function during phonation due to the activation of intrinsic musculature. The rules consider normalized activation levels of CT (aCT) and TA (aTA) muscles, whereas the resulting adductor effect due to both the LCA and PCA is represented through a single activation level (aLC). Subglottal pressure (Ps) is not controlled by the rules and it is a separate input parameter that controls the driving force of the self-sustained model and affects the resulting amplitude and pitch. In the current implementation of LaDIVA we have mainly focused on the activations of CT and TA intrinsic muscles for the production of acoustic outcomes. LCA, PCA, and IA muscle activation is kept constant at an adducted state to simulate voice production via the extended BCM for LaDIVA. Unvoiced productions are handled via the noise generator in DIVA acoustic synthesizer. In future iterations we hope to incorporate all five intrinsic laryngeal muscles (i.e., CT, TA, LCA, PCA, IA) and their activations in LaDIVA.
Combining DIVA and extended BCM
The extended BCM requires CT and TA muscle activations (aCT, aTA) and subglottal pressure (Ps) as inputs. These were linked from DIVA vocal fold mobility trajectories. For all simulations, the initial mass, position, velocity, and acceleration of the VFs were specified as per the original BCM formulation [46]. The main output of the extended BCM is the glottal area waveform. However, DIVA requires auditory task space variables as sensory inputs. To generate the auditory targets compatible with DIVA, vocal fo and radiated SPL signals were generated from the glottal area waveform provided by the extended BCM. Vocal fo was generated from the glottal area waveform using an autocorrelation algorithm. Radiated SPL at glottis was calculated as 20log10[rms(Zv*(dUg/dt)/(2x10-5)], where impedance constant Zv was set to 45000 kg.m-4 and Ug was the glottal flow signal [132]. These derived outputs were used as sensory inputs to DIVA.
Generating forward maps
The control loop in the DIVA implementation operates iteratively over 5-ms non-overlapping windows. At each 5-ms time step of an utterance, the motor representations are converted to auditory and somatosensory representations via the forward maps and error signals are calculated and inverse mapped to motor presentations. Thus, connecting DIVA and extended BCM together with a set of auditory task space parameters and motor mobility space parameters at their connection interface meant that simulations were required to be run every 5 ms across the two systems. Firstly, this limited the near real-time simulations of LaDIVA. Secondly, a 5-ms simulation in extended BCM was not sufficient to generate a glottal airflow signal stable enough to calculate a vocal fo (i.e., due to vocal variability at the start of production in extended BCM). See Acoustic Synthesizer section below fo more details. Thus, we generated a forward mapping for all combinations of motor mobility space variables (i.e., aCT, aTA, and Ps) to auditory task space variables (vocal fo and SPL), using model simulations of the extended BCM for all possible combinations of input parameters; aCT (range: 0–1, initial step size: 0.02, smoothed step size: 0.001), aTA (range: 0–1, initial step size: 0.02, smoothed step size: 0.001), and Ps (range 10–2010 Pa, initial step size: 100 Pa, smoothed step size: 5 Pa). Linear interpolation was used to smooth the forward map outputs. This forward mapping was connected to the DIVA model to replicate vocal fold biomechanical parameters in the feedforward controller (see Fig 1). In a similar manner, the Jacobian inverse functions were modified to refer to the new forward mapping added for vocal fold parameters in order to conduct the inverse mapping required in the error correction processes in the auditory and somatosensory feedback controllers [22] (See Fig 1).
Behavioral study dataset
In order to validate LaDIVA, an experimental dataset previously collected from 20 female adults with typical speech and no neurological, speech, or hearing disorders was used [68]. The participants underwent reflexive and adaptive vocal fo perturbation paradigms, and the group responses for each paradigm were considered as the reference standard in the current study to fit the simulated responses generated via the new model implementation. For both vocal fo reflexive and adaption paradigms, participants were asked to repeatedly produce the sustained vowel /ɑ/ for 108 trials. For the vocal fo reflexive paradigm, auditory feedback for the vocal production was delivered unaltered for 75% of the trials. For a randomly selected 25% of the trials, auditory feedback presented via headphones to the participants was altered in real-time. The vocal fo was increased by +100 cents using pitch shifting hardware (Eclipse V4 Harmonizer; Eclipse, Little Ferry, NJ), and presented with a jittered perturbation onset of 500–1000 ms from vocal onset (see Fig 3A). For the vocal fo adaptive paradigm, the first 24 trials of the paradigm (termed baseline phase) had unperturbed auditory feedback provided to the participant. The next 30 trials of the paradigm (termed ramp phase) had each trial’s auditory feedback shifted by an increasing step size of 3.33 cents from 0 to +100 cents. For the next 30 trials (termed hold phase), the auditory feedback perturbation was held steady at +100 cents in each trial. The last 24 trials (termed after effect phase) contained unperturbed auditory feedback (see Fig 3B). The vocal fo of the auditory feedback signal was shifted prior to vocal onset and the perturbation was sustained until the end of the trial.
Model simulations
LaDIVA was implemented in MATLAB based on the DIVA implementation using the Simulink platform. All simulations for LaDIVA were carried out via MATLAB scripts and Simulink (Mathworks, Natick, MA, Version R2018a). Reflexive and adaptive vocal fo perturbation paradigms identical to those in the behavioral dataset were simulated for LaDIVA with initial muscle activations and subglottal pressure set to replicate a male voice with vocal fo = 134 Hz (achieved via four initial cases of laryngeal muscle activation levels; see Table 4).
Acoustic synthesizer
The incorporation of the extended BCM in LaDIVA follows the same principle in order to be compatible with the DIVA control loop and acoustic synthesizer. See Fig 1 and Table 1 for the LaDIVA control loop architecture and controlled parameter list, respectively. The control loop in the DIVA implementation is decoupled from its acoustic synthesizer such that the control loop operates iteratively over 5 ms non-overlapping windows. At each 5-ms time step, the motor representations are converted to auditory and somatosensory representations via the forward maps and error signals are calculated and inverse mapped to motor presentations. See Eq 10 in the Forward mapping section above. At the end of the full simulation (e.g., an utterance of total duration of 3050 ms for the sustained vowel /a/), the motor representation time series is applied to the acoustic synthesizer to generate the time varying acoustic signal. See Eqs 10A and 10B.
The reasoning for not calculating the acoustic signal per each 5 ms time window is as follows. According to the source-filter theory, the glottal air volume velocity (glottal air flow) is the source of phonation [133]. The glottal airflow signal is filtered through the vocal tract model for modulating the spectral information (e.g., enhancing spectral formant regions or deemphasizing anti-formant regions; [47]). In the latest version of the DIVA model (dated Oct 22, 2017), a static signal for the glottal air flow is simulated via the glottal function in Liljencrantz-Fant glottal flow model [77], which is filtered via the time-varying vocal tract filter of DIVA speech synthesizer. For the LaDIVA implementation, we inputted trajectories of CT and TA muscle activation and subglottal pressure signals as control signals to the extended BCM to simulate VF dynamics for a full speech utterance (i.e., 3050 ms duration) that in turn generated a time-varying glottal area waveform. The derivative of this waveform is calculated to generate the glottal airflow signal, that is then filtered by the time-varying DIVA vocal tract filter to generate the resulting acoustic output of LaDIVA. The VF dynamics require initial kinematics of VFs (i.e., position, velocity, and acceleration) to be defined at the beginning of simulation and outputs end kinematics of VFs at the end of each simulation. If the muscle activations and subglottal pressure were fed to extended BCM every 5 ms, the simulation would reset the VF kinematics to initial state at the beginning of each 5 ms, which would generate discontinuities in VF movement and thereby discontinuities in the derived glottal airflow signal. Moreover, a 5 ms window is not sufficient for the extended BCM to generate a stable glottal airflow signal to calculate vocal fo. Thus, for the purposes of acoustic synthesis, the glottal area waveform is not derived for 5 ms time steps of the vocal utterance and parsed together. Instead, the glottal area and air flow signals for a complete vocal utterance are generated via the extended BCM by providing a time series of muscle activations and subglottal pressure and simulating VF dynamics and thereby a glottal airflow waveform for the total utterance.
Supporting information
(RAR)
S1 Text: Simulation responses of the LaDIVA model for the vocal fo reflexive paradigm plotted over a longer period of time.
(DOCX)
(DOCX)
Acknowledgments
We acknowledge Alfonso Nieto-Castañón and Jason Tourville for providing support related to original DIVA model source code. We acknowledge Rodrigo Manríquez for contributing to the software in the generation of vocal fo outputs from glottal airflow signals.
Data Availability
The source code of LaDIVA model is available at https://sites.bu.edu/guentherlab/software/diva-source-code/.
Funding Statement
This research was supported by the National Institutes of Health (NIH; https://www.nih.gov/) National Institute on Deafness and Other Communication Disorders (NIDCD;https://www.nidcd.nih.gov/) through Grants No. P50 DC015446(C.E.S, M.Z), F31 DC014872(G.C), F32 DC017637(G.C), R01 DC016270(C.E.S, F.H.G), and R01 DC002852(F.H.G), and by the Agencia Nacional de Investigación y Desarrollo (ANID;https://www.anid.cl/) through Grants Nos. FONDECYT 1191369 (M.Z) and BASAL FB0008(M.Z). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.
References
- 1.Roy N, Merrill RM, Thibeault S, Gray SD, Smith EM. Voice disorders in teachers and the general population. Journal of Speech, Language, and Hearing Research. 2004. [DOI] [PubMed] [Google Scholar]
- 2.Mattiske JA, Oates JM, Greenwood KM. Vocal problems among teachers: a review of prevalence, causes, prevention, and treatment. Journal of voice. 1998;12(4):489–99. doi: 10.1016/s0892-1997(98)80058-1 [DOI] [PubMed] [Google Scholar]
- 3.Verdolini K, Ramig LO. Occupational risks for voice problems. Logopedics Phoniatrics Vocology. 2001;26(1):37–46. [PubMed] [Google Scholar]
- 4.American Speech-Language-Hearing Association. Voice Disorders: (Practice Portal); n.d. [cited n.d.]. Available from: www.asha.org/Practice-Portal/Clinical-Topics/Voice-Disorders/.
- 5.Stemple JC, Roy N, Klaben BK. Clinical voice pathology: Theory and management: Plural Publishing; 2018. [Google Scholar]
- 6.Verdolini K, Rosen CA, Branski RC. Classification manual for voice disorders-I: Psychology Press; 2014. [Google Scholar]
- 7.Hixon TJ, Weismer G, Hoit JD. Preclinical speech science: Anatomy, physiology, acoustics, and perception: Plural Publishing; 2018. [Google Scholar]
- 8.Guenther FH. Neural control of speech: Mit Press; 2016. [Google Scholar]
- 9.Houde JF, Chang EF. The cortical computations underlying feedback control in vocal production. Current opinion in neurobiology. 2015;33:174–81. doi: 10.1016/j.conb.2015.04.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Houde JF, Nagarajan SS. Speech production as state feedback control. Frontiers in human neuroscience. 2011;5:82. doi: 10.3389/fnhum.2011.00082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Parrell B, Lammert AC, Ciccarelli G, Quatieri TF. Current models of speech motor control: A control-theoretic overview of architectures and properties. The Journal of the Acoustical Society of America. 2019;145(3):1456–81. doi: 10.1121/1.5092807 [DOI] [PubMed] [Google Scholar]
- 12.Perkell JS. Five decades of research in speech motor control: what have we learned, and where should we go from here? Journal of Speech, Language, and Hearing Research. 2013. [DOI] [PubMed] [Google Scholar]
- 13.Erath BD, Zañartu M, Peterson SD. Modeling viscous dissipation during vocal fold contact: The influence of tissue viscosity and thickness with implications for hydration. Biomechanics and modeling in mechanobiology. 2017;16(3):947–60. doi: 10.1007/s10237-016-0863-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Galindo GE, Peterson SD, Erath BD, Castro C, Hillman RE, Zañartu M. Modeling the pathophysiology of phonotraumatic vocal hyperfunction with a triangular glottal model of the vocal folds. Journal of Speech, Language, and Hearing Research. 2017;60(9):2452–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Alzamendi GA, Manríquez R, Hadwin PJ, Deng JJ, Peterson SD, Erath BD, et al. Bayesian estimation of vocal function measures using laryngeal high-speed videoendoscopy and glottal airflow estimates: An in vivo case study. The Journal of the Acoustical Society of America. 2020;147(5):EL434–EL9. doi: 10.1121/10.0001276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ibarra EJ, Parra JA, Alzamendi GA, Cortés JP, Espinoza VM, Mehta DD, et al. Estimation of subglottal pressure, vocal fold collision pressure, and intrinsic laryngeal muscle activation from neck-surface vibration using a neural network framework and a voice production model. Frontiers in Physiology. 2021:1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rouat J, Loiselle S, Pichevar R. Towards neurocomputational speech and sound processing. Progress in Nonlinear Speech Processing: Springer; 2007. p. 58–77. [Google Scholar]
- 18.Morasso P, Sanguineti V, Frisone F. Cortical maps as topology-representing neural networks applied to motor control. Plausible neural networks for biological modelling: Springer; 2001. p. 189–218. [Google Scholar]
- 19.Westermann G, Miranda ER. A new model of sensorimotor coupling in the development of speech. Brain and language. 2004;89(2):393–400. doi: 10.1016/S0093-934X(03)00345-6 [DOI] [PubMed] [Google Scholar]
- 20.Guenther FH. A neural network model of speech acquisition and motor equivalent speech production. Biological cybernetics. 1994;72(1):43–53. doi: 10.1007/BF00206237 [DOI] [PubMed] [Google Scholar]
- 21.Guenther FH, Ghosh SS, Tourville JA. Neural modeling and imaging of the cortical interactions underlying syllable production. Brain and language. 2006;96(3):280–301. doi: 10.1016/j.bandl.2005.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guenther FH, Hampson M, Johnson D. A theoretical investigation of reference frames for the planning of speech movements. Psychological review. 1998;105(4):611. doi: 10.1037/0033-295x.105.4.611-633 [DOI] [PubMed] [Google Scholar]
- 23.Miller HE, Guenther FH. Modelling speech motor programming and apraxia of speech in the DIVA/GODIVA neurocomputational framework. Aphasiology. 2020:1–18. doi: 10.1080/02687038.2020.1765307 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Terband H, Maassen B, Guenther FH, Brumberg J. Auditory–motor interactions in pediatric motor speech disorders: Neurocomputational modeling of disordered development. Journal of Communication Disorders. 2014;47:17–33. doi: 10.1016/j.jcomdis.2014.01.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tourville JA, Guenther FH. The DIVA model: A neural theory of speech acquisition and production. Language and cognitive processes. 2011;26(7):952–81. doi: 10.1080/01690960903498424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dichter BK, Breshears JD, Leonard MK, Chang EF. The control of vocal pitch in human laryngeal motor cortex. Cell. 2018;174(1):21–31. e9. doi: 10.1016/j.cell.2018.05.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Simonyan K, Horwitz B. Laryngeal motor cortex and control of speech in humans. The Neuroscientist. 2011;17(2):197–208. doi: 10.1177/1073858410386727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Aronson AE, Winholtz WS, Ramig LO, Silber SR. Rapid voice tremor, or “flutter,” in amyotrophic lateral sclerosis. Annals of Otology, Rhinology & Laryngology. 1992;101(6):511–8. [DOI] [PubMed] [Google Scholar]
- 29.Darley FL, Aronson AE, Brown JR. Motor speech disorders: WB Saunders Company; 1975. [Google Scholar]
- 30.Izdebski K. Symptomatology of adductor spasmodic dysphonia: a physiologic model. Journal of Voice. 1992;6(4):306–19. [Google Scholar]
- 31.Ludlow CL, Yamashita T, Schulz GM, Deleyiannis FW-B. Abnormalities in long latency responses to superior laryngeal nerve stimulation in adductor spasmodic dysphonia. Annals of Otology, Rhinology & Laryngology. 1995;104(12):928–35. doi: 10.1177/000348949510401203 [DOI] [PubMed] [Google Scholar]
- 32.Schwartz MF. The core of the stuttering block. Journal of Speech and Hearing Disorders. 1974;39(2):169–77. doi: 10.1044/jshd.3902.169 [DOI] [PubMed] [Google Scholar]
- 33.Wyke B. Phonatory reflex mechanisms and stammering. Folia Phoniatrica et Logopaedica. 1974;26(5):321–38. [PubMed] [Google Scholar]
- 34.Force ALET. Laryngeal electromyography: an evidence-based review. Muscle & nerve. 2003;28(6):767–72. [DOI] [PubMed] [Google Scholar]
- 35.Heman-Ackah YD, Barr A. The value of laryngeal electromyography in the evaluation of laryngeal motion abnormalities. Journal of Voice. 2006;20(3):452–60. doi: 10.1016/j.jvoice.2005.04.009 [DOI] [PubMed] [Google Scholar]
- 36.Liu H, Behroozmand R, Bove M, Larson CR. Laryngeal electromyographic responses to perturbations in voice pitch auditory feedback. The Journal of the Acoustical Society of America. 2011;129(6):3946–54. doi: 10.1121/1.3575593 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sataloff RT. Laryngeal electromyography: Plural Publishing; 2017. [Google Scholar]
- 38.Watson BC, Schaefer SD, Freeman FJ, Dembowski J, Kondraske G, Roark R. Laryngeal electromyographic activity in adductor and abductor spasmodic dysphonia. Journal of Speech, Language, and Hearing Research. 1991;34(3):473–82. doi: 10.1044/jshr.3403.473 [DOI] [PubMed] [Google Scholar]
- 39.Yin SS, Qiu WW, Stucker FJ. Major patterns of laryngeal electromyography and their clinical application. The Laryngoscope. 1997;107(1):126–36. doi: 10.1097/00005537-199701000-00024 [DOI] [PubMed] [Google Scholar]
- 40.Mehta DD, Hillman RE. Current role of stroboscopy in laryngeal imaging. Current opinion in otolaryngology & head and neck surgery. 2012;20(6):429. doi: 10.1097/MOO.0b013e3283585f04 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rosen CA, Murry T. Diagnostic laryngeal endoscopy. Otolaryngologic Clinics of North America. 2000;33(4):751–7. doi: 10.1016/s0030-6665(05)70241-3 [DOI] [PubMed] [Google Scholar]
- 42.Mehta DD, Kobler JB, Zeitels SM, Zañartu M, Ibarra EJ, Alzamendi GA, et al. Direct Measurement and Modeling of Intraglottal, Subglottal, and Vocal Fold Collision Pressures during Phonation in an Individual with a Hemilaryngectomy. Applied Sciences. 2021;11(16):7256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhang Z. Mechanics of human voice production and control. The journal of the acoustical society of america. 2016;140(4):2614–35. doi: 10.1121/1.4964509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Manríquez R, Peterson SD, Prado P, Orio P, Galindo GE, Zañartu M. Neurophysiological muscle activation scheme for controlling vocal fold models. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2019;27(5):1043–52. doi: 10.1109/TNSRE.2019.2906030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Erath BD, Zanartu M, Stewart KC, Plesniak MW, Sommer DE, Peterson SD. A review of lumped-element models of voiced speech. Speech Communication. 2013;55(5):667–90. [Google Scholar]
- 46.Story BH, Titze IR. Voice simulation with a body-cover model of the vocal folds. The Journal of the Acoustical Society of America. 1995;97(2):1249–60. doi: 10.1121/1.412234 [DOI] [PubMed] [Google Scholar]
- 47.Titze IR. Parameterization of the glottal area, glottal flow, and vocal fold contact area. The Journal of the Acoustical Society of America. 1984;75(2):570–80. doi: 10.1121/1.390530 [DOI] [PubMed] [Google Scholar]
- 48.Titze IR, Story BH. Rules for controlling low-dimensional vocal fold models with muscle activation. The Journal of the Acoustical Society of America. 2002;112(3):1064–76. doi: 10.1121/1.1496080 [DOI] [PubMed] [Google Scholar]
- 49.Zañartu M, Galindo GE, Erath BD, Peterson SD, Wodicka GR, Hillman RE. Modeling the effects of a posterior glottal opening on vocal fold dynamics with implications for vocal hyperfunction. The Journal of the Acoustical Society of America. 2014;136(6):3262–71. doi: 10.1121/1.4901714 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pelorson X, Hirschberg A, Van Hassel R, Wijnands A, Aurégan Y. Theoretical and experimental study of quasisteady-flow separation within the glottis during phonation. Application to a modified two-mass model. The Journal of the Acoustical Society of America. 1994;96(6):3416–31. [Google Scholar]
- 51.Serry MA, Stepp CE, Peterson SD. Physics of phonation offset: Towards understanding relative fundamental frequency observations. The Journal of the Acoustical Society of America. 2021;149(5):3654–64. doi: 10.1121/10.0005006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Herzel H, Berry D, Titze I, Steinecke I. Nonlinear dynamics of the voice: signal analysis and biomechanical modeling. Chaos: An Interdisciplinary Journal of Nonlinear Science. 1995;5(1):30–4. doi: 10.1063/1.166078 [DOI] [PubMed] [Google Scholar]
- 53.Erath BD, Zañartu M, Peterson SD, Plesniak MW. Nonlinear vocal fold dynamics resulting from asymmetric fluid loading on a two-mass model of speech. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2011;21(3):033113. [DOI] [PubMed] [Google Scholar]
- 54.Zhang Y, Jiang JJ. Nonlinear dynamic mechanism of vocal tremor from voice analysis and model simulations. Journal of sound and vibration. 2008;316(1–5):248–62. doi: 10.1016/j.jsv.2008.02.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chhetri DK, Neubauer J, Sofer E, Berry DA. Influence and interactions of laryngeal adductors and cricothyroid muscles on fundamental frequency and glottal posture control. The Journal of the Acoustical Society of America. 2014;135(4):2052–64. doi: 10.1121/1.4865918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Geng B, Pham N, Xue Q, Zheng X. A three-dimensional vocal fold posturing model based on muscle mechanics and magnetic resonance imaging of a canine larynx. The Journal of the Acoustical Society of America. 2020;147(4):2597–608. doi: 10.1121/10.0001093 [DOI] [PubMed] [Google Scholar]
- 57.Abur D, Subaciute A, Kapsner-Smith M, Segina RK, Tracy LF, Noordzij JP, et al. Impaired auditory discrimination and auditory-motor integration in hyperfunctional voice disorders. Scientific Reports. 2021;11(1):1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Naunheim ML, Yung KC, Schneider SL, Henderson-Sabes J, Kothare H, Mizuiri D, et al. Vocal motor control and central auditory impairments in unilateral vocal fold paralysis. The Laryngoscope. 2019;129(9):2112–7. doi: 10.1002/lary.27680 [DOI] [PubMed] [Google Scholar]
- 59.Thomas A, Mirza N, Eliades SJ. Auditory Feedback Control of Vocal Pitch in Spasmodic Dysphonia. The Laryngoscope. 2020. doi: 10.1002/lary.29254 [DOI] [PubMed] [Google Scholar]
- 60.Ziethe A, Petermann S, Hoppe U, Greiner N, Brüning M, Bohr C, et al. Control of fundamental frequency in dysphonic patients during phonation and speech. Journal of Voice. 2019;33(6):851–9. doi: 10.1016/j.jvoice.2018.07.001 [DOI] [PubMed] [Google Scholar]
- 61.Burnett TA, Freedland MB, Larson CR, Hain TC. Voice F0 responses to manipulations in pitch feedback. J Acoust Soc Am. 1998;103(6):3153–61. Epub 1998/06/24. doi: 10.1121/1.423073 . [DOI] [PubMed] [Google Scholar]
- 62.Burnett TA, Senner JE, Larson CR. Voice F0 responses to pitch-shifted auditory feedback: a preliminary study. J Voice. 1997;11(2):202–11. Epub 1997/06/01. doi: 10.1016/s0892-1997(97)80079-3 . [DOI] [PubMed] [Google Scholar]
- 63.Hain TC, Burnett TA, Kiran S, Larson CR, Singh S, Kenney MK. Instructing subjects to make a voluntary response reveals the presence of two components to the audio-vocal reflex. Experimental Brain Research. 2000;130(2):133–41. doi: 10.1007/s002219900237 [DOI] [PubMed] [Google Scholar]
- 64.Larson CR, Burnett TA, Kiran S, Hain TC. Effects of pitch-shift velocity on voice F 0 responses. The Journal of the Acoustical Society of America. 2000;107(1):559–64. doi: 10.1121/1.428323 [DOI] [PubMed] [Google Scholar]
- 65.Jones JA, Keough D. Auditory-motor mapping for pitch control in singers and nonsingers. Experimental brain research. 2008;190(3):279–87. doi: 10.1007/s00221-008-1473-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Jones JA, Munhall KG. Remapping auditory-motor representations in voice production. Current biology. 2005;15(19):1768–72. doi: 10.1016/j.cub.2005.08.063 [DOI] [PubMed] [Google Scholar]
- 67.Keough D, Hawco C, Jones JA. Auditory-motor adaptation to frequency-altered auditory feedback occurs when participants ignore feedback. BMC neuroscience. 2013;14(1):1–11. doi: 10.1186/1471-2202-14-25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lester-Smith RA, Daliri A, Enos N, Abur D, Lupiani AA, Letcher S, et al. The Relation of Articulatory and Vocal Auditory–Motor Control in Typical Speakers. Journal of Speech, Language, and Hearing Research. 2020;63(11):3628–42. doi: 10.1044/2020_JSLHR-20-00192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Abur D, Lester-Smith RA, Daliri A, Lupiani AA, Guenther FH, Stepp CE. Sensorimotor adaptation of voice fundamental frequency in Parkinson’s disease. PLoS One. 2018;13(1):e0191839. doi: 10.1371/journal.pone.0191839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Stepp CE, Lester-Smith RA, Abur D, Daliri A, Pieter Noordzij J, Lupiani AA. Evidence for Auditory-Motor Impairment in Individuals With Hyperfunctional Voice Disorders. J Speech Lang Hear Res. 2017;60(6):1545–50. Epub 2017/06/08. doi: 10.1044/2017_JSLHR-S-16-0282 ; PubMed Central PMCID: PMC5544411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ziethe A, Petermann S, Hoppe U, Greiner N, Bruning M, Bohr C, et al. Control of Fundamental Frequency in Dysphonic Patients During Phonation and Speech. J Voice. 2019;33(6):851–9. Epub 2018/08/26. doi: 10.1016/j.jvoice.2018.07.001 . [DOI] [PubMed] [Google Scholar]
- 72.Chen X, Zhu X, Wang EQ, Chen L, Li W, Chen Z, et al. Sensorimotor control of vocal pitch production in Parkinson’s disease. Brain Research. 2013;1527:99–107. doi: 10.1016/j.brainres.2013.06.030 [DOI] [PubMed] [Google Scholar]
- 73.Liu H, Wang EQ, Metman LV, Larson CR. Vocal responses to perturbations in voice auditory feedback in individuals with Parkinson’s disease. PloS one. 2012;7(3):e33629. doi: 10.1371/journal.pone.0033629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Mollaei F, Shiller DM, Baum SR, Gracco VL. Sensorimotor control of vocal pitch and formant frequencies in Parkinson’s disease. Brain research. 2016;1646:269–77. doi: 10.1016/j.brainres.2016.06.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Mollaei F, Shiller DM, Baum SR, Gracco VL. The relationship between speech perceptual discrimination and speech production in Parkinson’s disease. Journal of Speech, Language, and Hearing Research. 2019;62(12):4256–68. doi: 10.1044/2019_JSLHR-S-18-0425 [DOI] [PubMed] [Google Scholar]
- 76.Kearney E, Nieto-Castañón A, Weerathunge HR, Falsini R, Daliri A, Abur D, et al. A simple 3-parameter model for examining adaptation in speech and voice production. Frontiers in psychology. 2020;10:2995. doi: 10.3389/fpsyg.2019.02995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Fant G, Liljencrants J, Lin Q-g. A four-parameter model of glottal flow. STL-QPSR. 1985;4(1985):1–13. [Google Scholar]
- 78.Maeda S. A digital simulation method of the vocal-tract system. Speech communication. 1982;1(3–4):199–229. [Google Scholar]
- 79.Hirano M. Morphological structure of the vocal cord as a vibrator and its variations. Folia Phoniatrica et Logopaedica. 1974;26(2):89–94. doi: 10.1159/000263771 [DOI] [PubMed] [Google Scholar]
- 80.Sapir S, Baker KK, Larson CR, Ramig LO. Short-latency changes in voice F0 and neck surface EMG induced by mechanical perturbations of the larynx during sustained vowel phonation. Journal of Speech, Language, and Hearing Research. 2000;43(1):268–76. doi: 10.1044/jslhr.4301.268 [DOI] [PubMed] [Google Scholar]
- 81.Chhetri DK, Park SJ. Interactions of subglottal pressure and neuromuscular activation on fundamental frequency and intensity. The Laryngoscope. 2016;126(5):1123–30. doi: 10.1002/lary.25550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Movahhedi M, Geng B, Xue Q, Zheng X. Effects of cricothyroid and thyroarytenoid interaction on voice control: Muscle activity, vocal fold biomechanics, flow, and acoustics. The Journal of the Acoustical Society of America. 2021;150(1):29–42. doi: 10.1121/10.0005275 [DOI] [PubMed] [Google Scholar]
- 83.Geng B, Movahhedi M, Xue Q, Zheng X. Vocal fold vibration mode changes due to cricothyroid and thyroarytenoid muscle interaction in a three-dimensional model of the canine larynx. The Journal of the Acoustical Society of America. 2021;150(2):1176–87. doi: 10.1121/10.0005883 [DOI] [PubMed] [Google Scholar]
- 84.Chen SH, Liu H, Xu Y, Larson CR. Voice F 0 responses to pitch-shifted voice feedback during English speech. The Journal of the Acoustical Society of America. 2007;121(2):1157–63. doi: 10.1121/1.2404624 [DOI] [PubMed] [Google Scholar]
- 85.Hilger A, Cole J, Kim JH, Lester-Smith RA, Larson C. The effect of pitch auditory feedback perturbations on the production of anticipatory phrasal prominence and boundary. Journal of Speech, Language, and Hearing Research. 2020;63(7):2185–201. doi: 10.1044/2020_JSLHR-19-00043 [DOI] [PubMed] [Google Scholar]
- 86.Patel R, Niziolek C, Reilly K, Guenther FH. Prosodic adaptations to pitch perturbation in running speech. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Senthinathan A, Adams S, Page AD, Jog M. Speech Intensity Response to Altered Intensity Feedback in Individuals With Parkinson’s Disease. J Speech Lang Hear Res. 2021;64(6S):2261–75. Epub 2021/04/09. doi: 10.1044/2021_JSLHR-20-00278 . [DOI] [PubMed] [Google Scholar]
- 88.Patel RR, Awan SN, Barkmeier-Kraemer J, Courey M, Deliyski D, Eadie T, et al. Recommended Protocols for Instrumental Assessment of Voice: American Speech-Language-Hearing Association Expert Panel to Develop a Protocol for Instrumental Assessment of Vocal Function. Am J Speech Lang Pathol. 2018;27(3):887–905. Epub 2018/06/30. doi: 10.1044/2018_AJSLP-17-0009 . [DOI] [PubMed] [Google Scholar]
- 89.Casper JK, Leonard R. Understanding voice problems: A physiological perspective for diagnosis and treatment: Lippincott Williams & Wilkins; 2006. [Google Scholar]
- 90.Hillman RE, Stepp CE, Van Stan JH, Zañartu M, Mehta DD. An Updated Theoretical Framework for Vocal Hyperfunction. American Journal of Speech-Language Pathology. 2020:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Espinoza VM, Zañartu M, Van Stan JH, Mehta DD, Hillman RE. Glottal aerodynamic measures in women with phonotraumatic and nonphonotraumatic vocal hyperfunction. Journal of Speech, Language, and Hearing Research. 2017;60(8):2159–69. doi: 10.1044/2017_JSLHR-S-16-0337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Cumbers BA. Perceptual correlates of acoustic measures of vocal variability: The University of Wisconsin-Milwaukee; 2013. [Google Scholar]
- 93.Dhawale AK, Smith MA, Ölveczky BP. The role of variability in motor learning. Annual review of neuroscience. 2017;40:479–98. doi: 10.1146/annurev-neuro-072116-031548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Scheerer NE, Jones JA. The relationship between vocal accuracy and variability to the level of compensation to altered auditory feedback. Neuroscience letters. 2012;529(2):128–32. doi: 10.1016/j.neulet.2012.09.012 [DOI] [PubMed] [Google Scholar]
- 95.Daliri A. A Computational Model for Estimating the Speech Motor System’s Sensitivity to Auditory Prediction Errors. Journal of Speech, Language, and Hearing Research. 2021:1–14. doi: 10.1044/2021_JSLHR-20-00484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Alzamendi GA, Peterson SD, Erath BD, Hillman RE, Zañartu M. Triangular body-cover model of the vocal folds with coordinated activation of five intrinsic laryngeal muscles with applications to vocal hyperfunction. arXiv preprint arXiv:210801115. 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Liu H, Larson CR. Effects of perturbation magnitude and voice F 0 level on the pitch-shift reflex. The Journal of the Acoustical Society of America. 2007;122(6):3671–7. doi: 10.1121/1.2800254 [DOI] [PubMed] [Google Scholar]
- 98.Scheerer NE, Jones JA. Detecting our own vocal errors: An event-related study of the thresholds for perceiving and compensating for vocal pitch errors. Neuropsychologia. 2018;114:158–67. doi: 10.1016/j.neuropsychologia.2017.12.007 [DOI] [PubMed] [Google Scholar]
- 99.Kishon-Rabin L, Amir O, Vexler Y, Zaltz Y. Pitch discrimination: Are professional musicians better than non-musicians? Journal of basic and clinical physiology and pharmacology. 2001;12(2):125–44. doi: 10.1515/jbcpp.2001.12.2.125 [DOI] [PubMed] [Google Scholar]
- 100.Tervaniemi M, Just V, Koelsch S, Widmann A, Schröger E. Pitch discrimination accuracy in musicians vs nonmusicians: an event-related potential and behavioral study. Experimental brain research. 2005;161(1):1–10. doi: 10.1007/s00221-004-2044-5 [DOI] [PubMed] [Google Scholar]
- 101.Troche J, Troche MS, Berkowitz R, Grossman M, Reilly J. Tone discrimination as a window into acoustic perceptual deficits in Parkinson’s disease. 2012. doi: 10.1044/1058-0360(2012/11-0007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Martin CD, Niziolek CA, Duñabeitia JA, Perez A, Hernandez D, Carreiras M, et al. Online adaptation to altered auditory feedback is predicted by auditory acuity and not by domain-general executive control resources. Frontiers in Human Neuroscience. 2018;12:91. doi: 10.3389/fnhum.2018.00091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Villacorta V, Perkell J, Guenther F. Relations between speech sensorimotor adaptation and perceptual acuity. The Journal of the Acoustical Society of America. 2005;117(4):2618–9. [DOI] [PubMed] [Google Scholar]
- 104.Villacorta VM, Perkell JS, Guenther FH. Sensorimotor adaptation to feedback perturbations of vowel acoustics and its relation to perception. The Journal of the Acoustical Society of America. 2007;122(4):2306–19. doi: 10.1121/1.2773966 [DOI] [PubMed] [Google Scholar]
- 105.Alemi R, Lehmann A, Deroche ML. Adaptation to pitch-altered feedback is independent of one’s own voice pitch sensitivity. Scientific reports. 2020;10(1):1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Murray ESH, Stepp CE. Relationships between vocal pitch perception and production: A developmental perspective. Scientific reports. 2020;10(1):1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Tanaka S, Tanabe M. Glottal Adjustment for Regulating Vocal Intensity An Experimental Study. Acta oto-laryngologica. 1986;102(3–4):315–24. doi: 10.3109/00016488609108682 [DOI] [PubMed] [Google Scholar]
- 108.Birkholz P, Martin L, Xu Y, Scherbaum S, Neuschaefer-Rube C. Manipulation of the prosodic features of vocal tract length, nasality and articulatory precision using articulatory synthesis. Computer Speech & Language. 2017;41:116–27. [Google Scholar]
- 109.De Boer B, Tecumseh Fitch W. Computer models of vocal tract evolution: An overview and critique. Adaptive Behavior. 2010;18(1):36–47. [Google Scholar]
- 110.Larson CR, Altman KW, Liu H, Hain TC. Interactions between auditory and somatosensory feedback for voice F 0 control. Experimental brain research. 2008;187(4):613–21. doi: 10.1007/s00221-008-1330-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Mallard A, Ringel R, Horii Y. Sensory contributions to control of fundamental frequency of phonation. Folia Phoniatrica et Logopaedica. 1978;30(3):199–213. doi: 10.1159/000264125 [DOI] [PubMed] [Google Scholar]
- 112.Houde JF, Jordan MI. Sensorimotor adaptation in speech production. Science. 1998;279(5354):1213–6. doi: 10.1126/science.279.5354.1213 [DOI] [PubMed] [Google Scholar]
- 113.Burnett TA, Larson CR. Early pitch-shift response is active in both steady and dynamic voice pitch control. The Journal of the Acoustical Society of America. 2002;112(3):1058–63. doi: 10.1121/1.1487844 [DOI] [PubMed] [Google Scholar]
- 114.Burnett TA, McCurdy KE, Bright JC. Reflexive and volitional voice fundamental frequency responses to an anticipated feedback pitch error. Experimental brain research. 2008;191(3):341–51. doi: 10.1007/s00221-008-1529-z [DOI] [PubMed] [Google Scholar]
- 115.Donath TM, Natke U, Kalveram KT. Effects of frequency-shifted auditory feedback on voice F 0 contours in syllables. The Journal of the Acoustical Society of America. 2002;111(1):357–66. [DOI] [PubMed] [Google Scholar]
- 116.Kiran S, Larson CR. Effect of duration of pitch-shifted feedback on vocal responses in patients with Parkinson’s disease. 2001. [DOI] [PubMed] [Google Scholar]
- 117.Sivasankar M, Bauer JJ, Babu T, Larson CR. Voice responses to changes in pitch of voice or tone auditory feedback. The Journal of the Acoustical Society of America. 2005;117(2):850–7. doi: 10.1121/1.1849933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Wyke B. Neuromuscular control systems in voice production. Vocal fold physiology: Contemporary research and clinical issues. 1983:71–6. [Google Scholar]
- 119.Wyke BD. Laryngeal myotatic reflexes and phonation. Folia Phoniatrica et Logopaedica. 1974;26(4):249–64. [DOI] [PubMed] [Google Scholar]
- 120.Hammer MJ, Krueger MA. Voice-related modulation of mechanosensory detection thresholds in the human larynx. Experimental brain research. 2014;232(1):13–20. doi: 10.1007/s00221-013-3703-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Feng Y, Gracco VL, Max L. Integration of auditory and somatosensory error signals in the neural control of speech movements. Journal of neurophysiology. 2011;106(2):667–79. doi: 10.1152/jn.00638.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Lametti DR, Nasir SM, Ostry DJ. Sensory preference in speech production revealed by simultaneous alteration of auditory and somatosensory feedback. Journal of Neuroscience. 2012;32(27):9351–8. doi: 10.1523/JNEUROSCI.0404-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Hunter EJ, Titze IR. Quantifying vocal fatigue recovery: dynamic vocal recovery trajectories after a vocal loading exercise. Annals of Otology, Rhinology & Laryngology. 2009;118(6):449–60. doi: 10.1177/000348940911800608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Sander EK, Ripich DE. Vocal fatigue. Annals of Otology, Rhinology & Laryngology. 1983;92(2):141–5. doi: 10.1177/000348948309200209 [DOI] [PubMed] [Google Scholar]
- 125.Welham NV, Maclagan MA. Vocal fatigue: current knowledge and future directions. Journal of voice. 2003;17(1):21–30. doi: 10.1016/s0892-1997(03)00033-x [DOI] [PubMed] [Google Scholar]
- 126.Havas T, Lowinger D, Priestley J. Unilateral vocal fold paralysis: causes, options and outcomes. Australian and New Zealand journal of surgery. 1999;69(7):509–13. doi: 10.1046/j.1440-1622.1999.01613.x [DOI] [PubMed] [Google Scholar]
- 127.Misono S, Merati AL. Evidence-based practice: evaluation and management of unilateral vocal fold paralysis. Otolaryngologic Clinics of North America. 2012;45(5):1083–108. doi: 10.1016/j.otc.2012.06.011 [DOI] [PubMed] [Google Scholar]
- 128.Chen Z, Liu P, Jones JA, Huang D, Liu H. Sex-related differences in vocal responses to pitch feedback perturbations during sustained vocalization. J Acoust Soc Am. 2010;128(6):EL355–60. Epub 2011/01/12. doi: 10.1121/1.3509124 . [DOI] [PubMed] [Google Scholar]
- 129.Erath BD, Peterson SD, Weiland KS, Plesniak MW, Zañartu M. An acoustic source model for asymmetric intraglottal flow with application to reduced-order models of the vocal folds. PloS one. 2019;14(7):e0219914. doi: 10.1371/journal.pone.0219914 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Smith SL, Titze IR. Vocal fold contact patterns based on normal modes of vibration. Journal of biomechanics. 2018;73:177–84. doi: 10.1016/j.jbiomech.2018.04.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Zanartu M, Mongeau L, Wodicka GR. Influence of acoustic loading on an effective single mass model of the vocal folds. The Journal of the Acoustical Society of America. 2007;121(2):1119–29. doi: 10.1121/1.2409491 [DOI] [PubMed] [Google Scholar]
- 132.Tanaka S, Gould WJ. Relationships between vocal intensity and noninvasively obtained aerodynamic parameters in normal subjects. The Journal of the Acoustical Society of America. 1983;73(4):1316–21. doi: 10.1121/1.389235 [DOI] [PubMed] [Google Scholar]
- 133.Titze IR. Nonlinear source–filter coupling in phonation: Theory. The Journal of the Acoustical Society of America. 2008;123(4):1902–15. doi: 10.1121/1.2832339 [DOI] [PMC free article] [PubMed] [Google Scholar]