Preferred synonymous codons are translated more accurately: Proteomic evidence, among-species variation, and mechanistic basis

Abstract

A commonly stated cause of unequal uses of synonymous codons is their differential translational accuracies. A key prediction of this long-standing translational accuracy hypothesis (TAH) of codon usage bias is higher translational accuracies of more frequently used synonymous codons, which, however, has had no direct evidence beyond case studies. Analyzing proteomic data from Escherichia coli, we present direct, global evidence for this prediction. The experimentally measured codon-specific translational accuracies validate a sequence-based proxy; this proxy provides support for the TAH from the vast majority of over 1000 taxa surveyed in all domains of life. We find that the relative translational accuracies of synonymous codons vary substantially among taxa and are strongly correlated with the amounts of cognate transfer RNAs (tRNAs) relative to those of near-cognate tRNAs. These and other observations suggest a model in which selections for translational efficiency and accuracy drive codon usage bias and its coevolution with the tRNA pool.

Preferred codons are decoded more accurately, and accurate codons vary across species due to the variation of the tRNA pool.

INTRODUCTION

Eighteen of the 20 amino acids are each encoded by more than one codon, but the synonymous codons are usually used unequally in a genome (1, 2). Among the synonymous codons of an amino acid, those used more often than the average are referred to as preferred codons, while the rest are designated unpreferred. This phenomenon of codon usage bias (CUB), initially discovered more than four decades ago from the first few determined gene sequences (3–6), is a result of the joint forces of mutation, genetic drift, and natural selection, but the specific selective agents have not been fully deciphered (1, 2). One long-standing hypothesis, known as the translational accuracy hypothesis (TAH), asserts that synonymous codons are translated with different accuracies and that CUB results at least in part from natural selection for translational accuracy (7). The importance of accurate protein translation cannot be overstated, because mistranslation may lead to the loss of normal protein functions and gain of cellular toxicity (8) and cause severe diseases including cancer and neurodegenerative diseases (9). Several cellular mechanisms to ensure the overall fidelity of protein synthesis have been discovered. For example, conformational changes of the ribosome decoding center can be more efficiently induced by cognate codon-anticodon interactions than near-cognate codon-anticodon interactions (10), allowing discrimination against incorrect decoding. In addition, the accuracy of many steps in translation, such as tRNA aminoacylation (10) and codon-anticodon matching, is enhanced by the energy-consuming kinetic proofreading (11).

The TAH of CUB comprises the following two elements: (i) Translational accuracy varies among synonymous codons, and (ii) CUB is at least in part due to selection for translational accuracy. These two elements together make two predictions. First, preferred codons are translated more accurately than unpreferred synonymous codons. In an early study, Precup and Parker (12) used site-directed mutagenesis followed by peptide sequencing to show that AAT, an unpreferred codon of Asn, is misread as Lys four to nine times more often than is AAC, a preferred codon of Asn, at a particular position of the coat protein gene of the bacteriophage MS2 under Asn starvation. Similarly, Kramer and Farabaugh (13) observed that AAT has a significantly higher rate of mistranslation to Lys than AAC at a particular position of a reporter gene in Escherichia coli. Nonetheless, Kramer and Farabaugh (13) also observed that the unpreferred Arg codons of CGA and CGG and the preferred Arg codons of CGT and CGC exhibited similar rates of mistranslation to Lys (13). While the above experiments directly tested the first prediction of the TAH, they were each based on the investigation of one amino acid site of one protein, so the genome-wide generality of their findings is unknown.

The second prediction of the TAH was formulated by Akashi (7), who reasoned that the benefit of using relatively accurate codons should be greater at functionally more constrained amino acid sites than at less constrained sites when the expression level is controlled; hence, the TAH predicts a higher usage of preferred codons at evolutionarily conserved than unconserved sites of the same protein. Akashi’s test (7) based on genomic data is positive for several species investigated (7, 14, 15).

It is important to recognize that the two predictions of the TAH are complementary to each other. Specifically, evidence for the first prediction alone does not prove selection for translational accuracy, because synonymous codons differ in multiple properties including the translational elongation speed (16, 17), and selection for translational efficiency (18) might also lead to a higher usage of more accurate codons (see Discussion). Hence, confirming the second prediction when the first prediction is true could exclude the possibility of no selection for translational accuracy (7). Conversely, evidence for the second prediction supports the TAH only when the first prediction is true, because if preferred codons are not found by sensitive methods to be more accurately decoded than unpreferred codons under relevant conditions, then evidence for the second prediction becomes difficult to interpret. Therefore, in the presence of global evidence for the second prediction in a few species (7, 14, 15), global evidence for the first prediction is needed to validate the TAH.

Capitalizing on a proteome-wide probe of mistranslation in E. coli (19), we here show that preferred codons are generally translated more accurately than unpreferred synonymous codons, confirming the first prediction of the TAH. We then use the E. coli data to validate a sequence-based proxy for relative translational accuracies of synonymous codons. Using this proxy and Akashi’s test (7), we show that the TAH is supported in the vast majority of over 1000 diverse taxa surveyed, but that the relative translational accuracies of synonymous codons vary substantially among taxa. We find that the relative translational accuracy of a synonymous codon is strongly correlated with its cognate tRNA abundance relative to near-cognate tRNA abundance, offering a mechanistic insight into the translational accuracy variations across synonymous codons and species. These and other results suggest a model in which selections for translational efficiency and accuracy drive the CUB and its coevolution with the tRNA pool.

RESULTS

Preferred synonymous codons are more accurately decoded than unpreferred ones

Testing the first prediction of the TAH requires comparing the mistranslation rate among synonymous codons. Using mass spectrometry, Mordret et al. (19) quantified mistranslations at individual sites of the E. coli proteome. After removing sites and codons where mistranslation rates cannot be quantified because of technical reasons (see Materials and Methods), we grouped mistranslation events according to the identities of their original codons. We then computed the absolute mistranslation rate of a codon as the ratio of the total intensity of mistranslated peptides to that of all peptides mapped to the codon. Last, we computed the relative mistranslation rate (RMR) of a codon by dividing its absolute mistranslation rate by the mean absolute mistranslation rate of all codons coding for the same amino acid. RMR >1 means that the codon has a higher mistranslation rate than the average among all codons for the same amino acid, whereas RMR <1 means the opposite. Codon usage was assessed by the relative synonymous codon usage (RSCU). The RSCU of a codon equals its frequency in the genome relative to the average frequency of all codons for the same amino acid (20). A codon with RSCU >1 is preferred, while a codon with RSCU <1 is unpreferred.

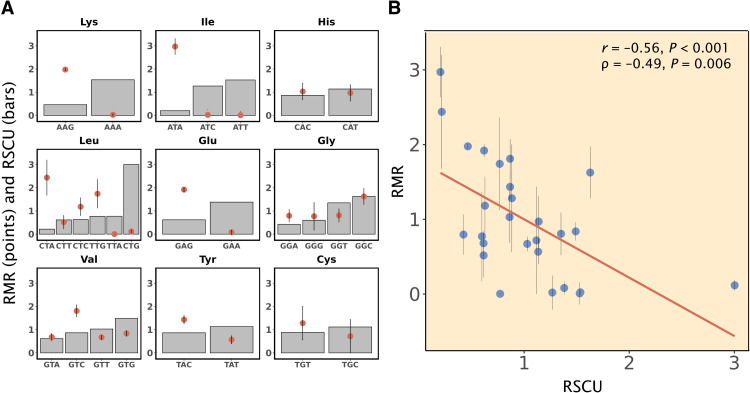
We were able to estimate the RMR for 27 codons of nine amino acids (Fig. 1A). Except for Gly, the most preferred synonymous codon of an amino acid shows an RMR <1, providing a significant support for the first prediction of the TAH (P = 0.02, one-tailed binomial test). Similarly, except for Gly and Val, the least prevalent synonymous codon of an amino acid shows an RMR >1 (P = 0.09, one-tailed binomial test). Because both RSCU and RMR of a codon are relative to the mean of all codons for the same amino acid, they can be compared among codons of different amino acids. A strong negative correlation was observed between RSCU and RMR among the 27 codons [Pearson’s correlation coefficient (r) = −0.56, P < 0.001, permutation test; Spearman’s ρ = −0.49, P = 0.006, permutation test; Fig. 1B]. Together, these findings from the proteomic data of E. coli demonstrate that preferred codons tend to have lower mistranslation rates, confirming the first prediction of the TAH.

Fig. 1. More frequently used synonymous codons tend to be decoded more accurately in E. coli.

(A) Comparison of RSCU (bars) and RMR (dots) among synonymous codons for nine amino acids with proteome-based RMR estimates. (B) A significant negative correlation between RSCU and RMR across the 27 codons in (A). The red line is the linear regression. In both panels, error bars represent 1 SE estimated by the bootstrap method. The SE of RSCU estimated by the bootstrap method is negligible because of the large number of occurrences of each codon in the genome, and so is not shown. P values are based on permutation tests.

Relative translational accuracies of synonymous codons vary across taxa

How do certain synonymous codons achieve higher translational accuracies than others? There are two general possibilities. In the first possibility, referred to as the constant accuracy hypothesis hereinafter, the translational accuracy is intrinsically higher for a synonymous codon than another because of their different chemical nature that affects codon-anticodon interactions. Consequently, the relative translational accuracies of synonymous codons should be more or less the same in different species. For instance, a higher translational accuracy of AAA (Lys) than AAG (Lys), evident in E. coli (Fig. 1A), should hold in all species. Hershberg and Petrov (21) observed some general patterns of codon usage across species after controlling the genomic GC content. However, whether these generalities reflect intrinsic accuracies of different synonymous codons is unknown. Alternatively, relative translational accuracies of synonymous codons may be greatly influenced by species-specific factors such as the tRNA pool. Under this possibility, referred to as the variable accuracy hypothesis hereinafter, the relative accuracies of synonymous codons vary across species. That is, AAA is more accurate than AAG in many species, but the opposite is true in many other species.

Measuring the relative translational accuracies of synonymous codons in a large number of species will allow differentiating between the above two hypotheses, which will, in turn, help understand the mechanism underlying the translational accuracy differences among synonymous codons. Because codon-specific, proteome-based translational accuracies have not been measured beyond E. coli, we resort to a sequence-based proxy referred to as the odds ratio (OR) that originated from Akashi’s test (7). Specifically, the OR of synonymous codon X that encodes amino acid Y in a gene is the number of times that X is used at invariant Y sites relative to the number of times that X is not used at invariant Y sites, divided by the number of times that X is used at variant Y sites relative to the number of times that X is not used at variant Y sites (Fig. 2A). Here, invariant and variant Y sites refer to Y sites in the focal species whose counterparts in the ortholog from a related species have Y and non-Y, respectively. The OR values computed from individual genes can be combined to yield a single OR using the Mantel-Haenszel procedure (see Materials and Methods). While OR was originally developed for preferred codons, it can be computed for any codon of the 18 amino acids that have multiple synonymous codons (18). On the basis of Akashi’s test (7), OR has been used as a proxy for the relative translational accuracy of a codon (18). To verify the relationship between OR and relative translational accuracy, we computed OR values by aligning E. coli genes with their Salmonella enterica orthologs at the genomic scale. For the 27 codons with RMR estimates, OR and RMR are strongly negatively correlated (r = −0.63, P < 0.001; ρ = −0.43, P = 0.01; Fig. 2B), confirming that the OR of a codon is a valid proxy for its relative translational accuracy (OR >1 indicates a higher-than-average translational accuracy among synonymous codons and vice versa).

Fig. 2. Variation of relative translational accuracies of synonymous codons across taxa.

(A) Diagram explaining the calculation of OR of the codon CAT that serves as a proxy for its relative translational accuracy. Shown here is a hypothetical alignment of orthologous proteins (and the underlying coding sequences) between the focal species and a related species. (B) OR is negatively correlated with RMR across codons in E. coli. P values are based on permutation tests. The red line shows the linear regression. (C) Frequency distribution of Pearson’s correlation between RSCU and OR in 1197 bacterial taxa. Ninety-five percent of these taxa show positive correlations. (D) ln(OR) of codon CAT for each of 118 bacterial taxa, one per order, arranged according to their phylogeny shown in the middle. (E) Violin plots showing frequency distributions of ln(OR) of individual codons across 1197 bacterial taxa.

To examine whether the relative translational accuracies of synonymous codons vary across species, we took advantage of a recently built phylogenetic tree of 10,575 microbial taxa (22). Because most taxa (9867) in the tree are from the domain Bacteria, we first focused our analysis on Bacteria. We picked all 1197 pairs of sister bacterial taxa from the tree and aligned their orthologous genes (see Materials and Methods). We randomly assigned one taxon in each pair as the focal taxon and computed OR for each codon as described above. A positive correlation between RSCU and OR across codons was observed in 95% of the taxa examined (Fig. 2C), demonstrating an overwhelming support for the TAH of CUB in Bacteria.

We computed ln(OR) to make its distribution relatively symmetric to aid visualization and examined, as an example, ln(OR) for codon CAT (His) in each of the focal taxa arranged according to the bacterial tree (one taxon per order is presented in Fig. 2D). We found ln(OR) to vary greatly from negative values to positive values, with a high density near 0 (Fig. 2E). Furthermore, the extreme values of ln(OR) (orange and blue in Fig. 2D) are scattered across the tree rather than concentrated in a few clades, suggesting that the relative translational accuracy of CAT has changed substantially and frequently in evolution. The inter-taxon variation of OR indicates that CAT is the relatively inaccurate one of the two synonymous codons of His in many taxa (blue in Fig. 2D) but the relatively accurate one in many other taxa (orange), supporting the variable accuracy hypothesis. From Fig. 2E, which shows the 18 amino acids each with multiple codons, it is clear that the pattern observed for CAT applies to all codons. Furthermore, every codon has an OR >1 in at least 8.9% of the taxa examined (fig. S1A). These results thus support the variable accuracy hypothesis for all synonymous codons. The above observations of OR variation among taxa are not primarily caused by sampling error, because a similar pattern was detected when we analyzed a subset of taxa for each amino acid where the number of occurrences of each synonymous codon considered in OR estimation is at least 1000 per taxon (fig. S1B). They are not mainly caused by genetic drift either, because a similar pattern was found when we analyzed a subset of taxa with strong signals of selection for translational accuracy (correlation between RSCU and OR exceeding 0.5) (fig. S1C). Note that, despite the general support for the variable accuracy hypothesis, for a minority of codons such as ATA (Ile), AGA (Arg), and AGG (Arg), the distribution of ln(OR) is strongly skewed toward negative values (Fig. 2E), suggesting that their relative translational accuracies are somewhat constrained in evolution, although not invariable. For these codons, the constant accuracy model may have merit, and future studies should attempt to identify the mechanistic basis of these codons’ relatively constant accuracies.

To investigate whether the above observations from Bacteria are generalizable to the other two domains of life, we first expanded our analysis to Archaea represented in the large phylogeny previously mentioned (22). We found that the correlation between RSCU and OR is positive in 90% of taxa examined and that ln(OR) varies greatly across taxa for each codon (fig. S2), further supporting the TAH and the variable accuracy hypothesis. For Eukaryota, we analyzed five commonly used model organisms: human, mouse, roundworm, fly, and budding yeast (see Materials and Methods). In each of these species, the correlation between RSCU and OR is significantly positive (table S1), supporting the TAH. Except for the two mammal species, which are closely related, the ORs estimated from one species are not well correlated with those estimated from another species (fig. S3). Furthermore, the correlation in OR generally declines with the divergence time between the two species (fig. S3), consistent with the variable accuracy hypothesis. Together, our results show that the TAH is generally supported in all domains of life, but the relative translational accuracies of synonymous codons vary across taxa.

Mechanistic basis of among-codon and across-taxon variations of translational accuracies

The empirical support for the variable accuracy hypothesis strongly suggests that the determinants of the RMRs of synonymous codons vary among species. In the aforementioned study of Kramer and Farabaugh (13), the authors found that artificially increasing the expression level of the cognate tRNA for Arg codons AGA and AGG reduces their mistranslations to Lys, and so proposed that the competition between cognate and near-cognate tRNAs determines the mistranslation rate of a codon. Here, the cognate tRNA is the tRNA whose anticodon pairs with the codon correctly (allowing wobble pairing), whereas the near-cognate tRNA corresponds to a different amino acid and has an anticodon that mismatches the codon at one position. Consistent with the above proposal, Mordret et al. (19) inferred that most of the mistranslation events in E. coli arose from the mispairing between codons and near-cognate tRNAs. They further noted that, for certain types of mistranslation, there is a negative correlation across growth phases between the mistranslation rate and the ratio (R_c/nc) in abundance between cognate and near-cognate tRNAs, although the correlation was rarely statistically significant (19). On the basis of these past observations, we hypothesize that the relative translational accuracy of a synonymous codon increases with its relative R_c/nc, or RR_c/nc, which is R_c/nc divided by the mean R_c/nc of all codons coding for the same amino acid (see Materials and Methods). We further hypothesize that, because the tRNA pool varies substantially across species (23), the across-species variation of relative translational accuracies arises from the across-species variation in RR_c/nc.

To test the above hypotheses, we computed RR_c/nc for each codon using published tRNA expression levels in E. coli (19). We observed a significant negative correlation between RR_c/nc and RMR (r = −0.54, P = 0.003; ρ = −0.56, P = 0.002; Fig. 3A) and a significant positive correlation between RR_c/nc and OR (r = 0.51, P = 0.02; ρ = 0.68, P = 0.01; Fig. 3B) across codons, supporting the hypothesis that the relative ratio of cognate to near-cognate tRNA abundances is a major determinant of a codon’s relative translational accuracy in E. coli. Note that the relative cognate tRNA abundance alone is not significantly correlated with RMR (r = −0.24, P = 0.2; ρ = 0.03, P = 0.5; fig. S4A), supporting the role of competition between cognate and near-cognate tRNAs in determining RMR. As previously reported (18), the relative cognate tRNA level is highly correlated with RSCU (r = 0.78, P < 0.001; ρ = 0.47, P < 0.001; fig. S4B), which is likely a result of selection for high translational efficiency (i.e., more codons translated per unit time per cell), because balanced codon usage relative to cognate tRNA concentrations maximizes translational efficiency (18).

Fig. 3. The relative ratio of cognate tRNA concentration to near-cognate tRNA concentration (RR_c/nc) is a major determinant of a codon’s relative translational accuracy.

(A) RMR is negatively correlated with RR_c/nc across codons in E. coli. (B) OR is positively correlated with RR_c/nc across codons in E. coli. (C) RMR is negatively correlated with RR_c/nc computed using tRNA gene copy numbers instead of tRNA concentrations in E. coli. (D) Frequency distribution of Pearson’s correlation between OR and RR_c/nc computed using tRNA gene copy numbers in bacterial taxa with >80 tRNA genes. Ninety-two percent of the taxa show a positive correlation. All P values are based on permutation tests. In (A) to (C), the red line is the linear regression.

We next investigated whether the above finding in E. coli applies to other bacterial taxa surveyed in Fig. 2. Because tRNA expression levels are unknown for the vast majority of these taxa, we used the gene copy number of each tRNA species as a proxy for the total expression level of the tRNA species (24). E. coli RR_c/nc computed from tRNA gene copy numbers is highly correlated with that computed from tRNA expression levels (r = 0.80, P = 4 × 10⁻⁷; ρ = 0.91, P = 4 × 10⁻¹¹). Furthermore, E. coli RR_c/nc computed from tRNA gene copy numbers is significantly correlated with RMR (Fig. 3C), confirming the validity of using this proxy. We obtained the tRNA gene annotations for 1094 of the 1197 focal bacterial taxa examined in Fig. 2. However, in many of these taxa, there is little tRNA gene redundancy or variation in cognate tRNA gene copy number among synonymous codons despite considerable CUB; in these taxa, the tRNA gene copy number is unlikely a good proxy for tRNA abundance (25). Because the tRNA gene copy number is a good proxy for tRNA abundance in E. coli, which has 85 tRNA genes, we decided to filter out taxa with fewer than 81 tRNA genes to strike a balance between the noise level and number of taxa in our analysis. This filtering left us with 59 taxa, in each of which we correlated the OR of a codon with its RR_c/nc computed from tRNA gene copy numbers. The vast majority (92%) of these taxa show a positive correlation (Fig. 3D), supporting the generality of our hypothesis on the role of RR_c/nc in determining the relative translational accuracy of a codon in Bacteria.

To investigate whether the above finding is generalizable to other domains of life, we analyzed tRNA genes in Archaea taxa and Eukaryotic model organisms. Unfortunately, no Archaea taxa examined have more than 80 tRNA genes. For each of the five eukaryotes (human, mouse, fly, roundworm, and yeast), the correlation between OR and RR_c/nc computed from tRNA gene copy numbers is significantly positive for linear or rank correlation (table S2). Together, our findings support that, in the diverse taxa surveyed, the ratio of cognate tRNA abundance to near-cognate tRNA abundance is generally a major determinant of the relative translational accuracy of a codon. Hence, the across-species variation of the tRNA pool can explain the across-species variation of the relative translational accuracies of synonymous codons.

DISCUSSION

Analyzing the published proteomic data from E. coli, we found that preferred codons are generally decoded more accurately than unpreferred synonymous codons, providing global evidence for the first prediction of the TAH. After validating Akashi’s OR as a proxy for the measured translational accuracy in E. coli, we applied Akashi’s test (7) to thousands of species across all three domains of life and found evidence for the second prediction of the TAH in the vast majority of the species examined, substantially expanding such evidence previously collected in a few species (7, 14, 15). Using the OR of a codon as a proxy for its translational accuracy, we discovered that the relative translational accuracies of synonymous codons vary substantially among species, supporting the variable accuracy hypothesis. Inspired by the qualitative observations of Kramer and Farabaugh (13) and Mordret et al. (19), we obtained quantitative evidence that the ratio of the cognate tRNA abundance to the near-cognate tRNA abundance is a major determinant of a codon’s relative translational accuracy. Hence, the inferred across-species variation in a codon’s translational accuracy is mechanistically explained by the across-species variation of the tRNA pool.

As mentioned in the Introduction, mistranslation could be deleterious because it lowers the fraction of protein molecules with normal functions and/or generates toxic molecules. When the mistranslation rate is given, the number of toxic molecules (but not the fraction of molecules with normal functions) rises with the number of protein molecules synthesized, so selection for translational accuracy is expected to be stronger in more highly expressed genes if minimizing toxicity is an important cause of the selection. Results from Akashi’s test (7) in a few species (14) and the proteomic data of E. coli (19) both support that the mistranslation rate is lower for more highly expressed genes. Notwithstanding, signals of selection for translational accuracy were found even in lowly expressed genes in some species (7, 26, 27), suggesting the possibility that minimizing the loss of proteins with normal functions is also behind the selection for translational accuracy.

Our findings, together with the previous report on the selection for translational efficiency (18), suggest a model in which the tRNA pool and codon usage coevolve to improve both translational efficiency and accuracy (Fig. 4A). Specifically, mutation and drift can alter both codon frequencies and tRNA concentrations. The cellular translational efficiency is maximized when (transcriptomic) codon frequencies equal relative cognate tRNA concentrations (18), whereas the translational accuracy of a codon is maximized when the ratio of its cognate tRNA concentration to near-cognate tRNA concentration is maximized. Under this model, selections for translational efficiency and accuracy are related but not perfectly aligned, which could introduce trade-offs between translational efficiency and accuracy (28). Our simulation of a simple genetic system with two amino acids, each encoded by two synonymous codons (Fig. 4B), found that imposing a selection for translational accuracy can lower translational efficiency (Fig. 4C).

Fig. 4. Selections for translational efficiency and accuracy shape the tRNA pool and codon usage.

(A) A model for the coevolution of the tRNA pool and codon usage driven by selections for translational efficiency and accuracy. (B) A toy model with two amino acids, each encoded by two synonymous codons. A dotted line connects a codon with its near-cognate tRNA. (C) Simulation of evolution shows that translational efficiency is significantly lower in the presence of selection for translational accuracy than in the absence of this selection. (D) The absolute difference between the RSCU of 00 (RSCU₀₀) and that of 11 (RSCU₁₁) is smaller under the selection for translational accuracy than without this selection. With the selection, codon usage for aa₀ and that for aa₁ become coupled, because the selection disfavors the cognate tRNA of the common codon of aa₀ to become the near-cognate tRNA of the common codon of aa₁ and vice versa. In (C) and (D), each box plot shows the distribution from 200 replicates. The lower and higher edges of a box represent the first (qu₁) and third (qu₃) quartiles, respectively; the horizontal line inside the box indicates the median (md); the whiskers extend to the most extreme values inside inner fences, md ± 1.5(qu₃ − qu₁); and the dots are outliers. *0.01 ≤ P < 0.05, Wilcoxon rank sum tests; **0.001 ≤ P < 0.01; ***P < 0.001.

The above model also implies that, even in the absence of selection for translational accuracy, the positive correlation between synonymous codon frequency and cognate tRNA concentration resulting from selection for translational efficiency (18) may render the cognate tRNA concentration relative to near-cognate tRNA concentration higher for more frequently used synonymous codons. Consequently, the positive correlation between the relative codon frequency and relative translational accuracy may arise in the absence of selection for translational accuracy. In E. coli, for 15 of the 18 amino acids with multiple synonymous codons, the codon with the highest cognate tRNA concentration has the highest RR_c/nc. Upon randomly shuffling the expression levels among tRNA species, we found that, for over 50% of the 18 amino acids, the codon with the highest cognate tRNA concentration has the highest RR_c/nc. This was true in each of the 1000 shufflings. Nevertheless, in only 6 of these 1000 shufflings did all 18 amino acids exhibit the above feature. Thus, a high but imperfect concordance between translational efficiency and accuracy is expected, confirming the notion in Introduction that the first prediction of the TAH could be true even in the absence of selection for translational accuracy. In other words, the correlation in Fig. 1B alone does not prove selection for translational accuracy. However, the combination of this correlation and that between RSCU and OR (i.e., evidence for the second prediction of the TAH) demonstrates that evolutionarily conserved sites tend to use preferred synonymous codons, which tend to be relatively accurately translated. Therefore, the role of selection for translational accuracy in causing CUB is established, and the TAH is validated.

How codon usage and the tRNA pool evolve under the joint forces of selections for translational efficiency and accuracy in addition to mutation and drift is quite complex. For instance, because any tRNA is simultaneously a cognate tRNA for one or more codons and a near-cognate tRNA for some other codons, increasing the translational accuracy of a particular codon might be at the expense of that of another codon. A previous study showed that artificially increasing the cognate tRNA expression levels for Arg codons can result in proteotoxic stress (29). This subtle trade-off could cause nonindependent uses of codons of different amino acids, which were evident in the aforementioned simulation (Fig. 4D). Future modeling work with realistic parameters might shed more light on this issue. In addition to affecting translational efficiency and accuracy, synonymous mutations also affect mRNA folding (30), mRNA stability (31), mRNA concentration (31–33), pre-mRNA splicing (34), and cotranslational protein folding (35, 36); thus, additional selective factors may shape CUB and its evolution.

Our study has several caveats. First, in our calculation of a codon’s mistranslation rate, we lumped all mistranslations of the codon regardless of the erroneous amino acid it is translated to. Because different mistranslations of the same codon likely have differential fitness costs and because selection for translational accuracy likely minimizes the total fitness reduction caused by mistranslation instead of the mistranslation rate per se, properly weighting different mistranslations in RMR calculation will likely strengthen its correlation with RSCU. Second, when calculating the ratio of cognate tRNA concentration to near-cognate tRNA concentration, we did not consider the difference in interaction strength between different codons and anticodons (37). Future research that takes into account this interaction under physiological conditions may significantly improve the signal in the correlation analysis of Fig. 3. Third, our analysis in Fig. 3D was limited to taxa with >80 tRNA genes. Future research using tRNA expression levels (25), when they become available, can confirm if the same pattern holds for taxa with fewer tRNA genes. Last, because of the data limitation, we did not consider variations in tRNA expression across environments, cell cycle stages, or tissues (38). In the future, it would be interesting to study how such variations simultaneously affect translational efficiency and accuracy.

Our results might help design organisms with expanded code tables (39). Expanding the code table is realized by introducing unnatural tRNAs that are charged with noncanonical amino acids. The introduction of these tRNAs often leads to fitness defects due to mistranslation of normal codons (40). Our findings suggest that one way to alleviate the proteotoxic stress is to identify potential near-cognate codons that could be mistranslated by the unnatural tRNA and adjust the natural tRNA pool to minimize the impact.

MATERIALS AND METHODS

Estimating RMRs of synonymous codons from E. coli proteomic data

The proteomic data analyzed came from table S1 in Mordret et al. (19). The authors separately measured mistranslation events from high-solubility and low-solubility proteins using mass spectrometry, and both groups of events were considered in our analysis. We focused on the data from the wild-type strain BW25113 in the Mops complete medium, because (i) this dataset was the largest among datasets from all strain-medium combinations, and (ii) no artificial perturbation such as mutation, drug, or amino acid depletion was applied (19). We first removed sites that cannot be traced to a unique original codon. We also filtered out sites showing an intensity of “NaN” for the unmodified (also known as base) peptide or mistranslated (also known as dependent) peptide. Because different synonymous codons tend to generate different mistranslations by mispairing with different near-cognate tRNAs, if these different mistranslations have different detection probabilities, then the comparison between synonymous codons would be unfair. Unfortunately, some mistranslations produce mass shifts indistinguishable from posttranslational modifications, and so cannot be reliably identified through mass spectrometry (19), causing unfair comparisons among synonymous codons in some cases. Therefore, we removed amino acids with undetectable mistranslations except for Leu and Ile. We kept these two amino acids because the only undetectable mistranslations for them are Leu to Ile and Ile to Leu; both can be considered benign because of the high physicochemical similarity between Leu and Ile (41). Considering the structure of the genetic code table, we found that the underestimation of the mistranslation rate due to the negligence of mistranslations between Leu and Ile is more severe for unpreferred than preferred codons, suggesting that the actual strength of evidence for higher mistranslation rates of unpreferred than preferred synonymous codons is stronger than what is shown in Fig. 1. We then computed each codon’s absolute mistranslation rate by dividing the total intensity of mistranslated (i.e., dependent) peptides by that of all (i.e., dependent + base) peptides mapped to the codon. We divided each codon’s absolute mistranslation rate by the mean absolute mistranslation rate of all codons coding for the same amino acid to obtain the codon’s RMR. We removed an amino acid if any of its synonymous codons lacked data, because calculating RMR requires having data for all synonymous codons of the amino acid. In total, we computed RMR for 27 codons of nine amino acids.

RSCU, OR, and RR_c/nc for E. coli

Peptide and cDNA sequences of E. coli (genome assembly: ASM584v2) and S. enterica (genome assembly: ASM78381v1) were downloaded from Ensembl Bacteria (42). We computed RSCU of codon j of amino acid i from all coding sequences of E. coli by ${\text{RSCU}}_{i,j}=\frac{n_i{x}_{i,j}}{{\displaystyle {\sum }_{j=1}^{n_i}}{x}_{i,j}}$, where n_i is the number of synonymous codons of amino acid i and x_i,j is the number of occurrences of codon j of amino acid i in all coding sequences (20). Conventionally, RSCU is computed from highly expressed genes (20). However, because of the lack of gene expression information from most of the species analyzed, we computed RSCU from all genes. This should not qualitatively affect our analysis, because RSCU computed from highly expressed genes (e.g., the top 20% of genes) is nearly perfectly correlated with that computed from all genes (e.g., in E. coli, r = 0.96, P < 2.2 × 10⁻¹⁶).

To calculate the OR of each codon, we first identified one-to-one orthologous proteins between E. coli and S. enterica using OrthoFinder (43). Next, we aligned these one-to-one orthologs using MUSCLE (44), separating all amino acid sites into invariant and variant sites. For a focal codon in gene i, we tabulated a_i, number of occurrences of the focal codon at invariant amino acid sites; b_i, number of occurrences of the focal codon at variant sites; c_i, total number of occurrences of the focal codon’s synonymous codons at invariant sites; and d_i, total number of occurrences of the focal codon’s synonymous codons at variant sites. Here, the focal codon’s synonymous codons do not include itself. OR for gene i equals (a_id_i)/(b_ic_i). Using the Mantel-Haenszel procedure, we combined the ORs of the focal codon from individual genes into one OR (7) by $\text{OR}=\frac{{\sum }_i\frac{a_i{d}_i}{(a_i+b_i+c_i+d_i)}}{{\sum }_i\frac{b_i{c}_i}{(a_i+b_i+c_i+d_i)}}$.

To compute RR_c/nc of a codon, we tabulated the cognate tRNAs and near-cognate tRNAs of the codon. Cognate tRNAs are all tRNAs that can pair with the focal codon, allowing wobble pairing at the third codon position, while near-cognate tRNAs are tRNAs coded for a different amino acid but can pair with the focal codon with one base pair mismatch (allowing wobble pairing at the third codon position). We then weighted each tRNA by their average relative expression levels across three growth stages in the Mopes complete media (Gene Expression Omnibus number: GSE128812). Last, we normalized the ratio for each codon by the average ratio of all codons coding for the same amino acid.

RSCU, OR, and RR_c/nc for other species

RSCU, OR, and RR_c/nc were calculated for non–E. coli taxa as for E. coli, with the differences noted below. For the non–E. coli prokaryotic taxa, we downloaded the phylogenetic tree of 10,575 taxa from the Web of Life (https://biocore.github.io/wol/) (22) and identified sister taxa from the tree. In brief, each pair of sister taxa are each other’s single closest relative in the tree. For each pair of sister taxa, we downloaded from the same website their protein-coding DNA sequences, protein sequences, and tRNA gene copy numbers. For eukaryotic model organisms, we downloaded protein-coding DNA sequences and protein sequences of human (Homo sapiens), mouse (Mus musculus), fly (Drosophila melanogaster), roundworm (Caenorhabditis elegans), and budding yeast (Saccharomyces cerevisiae) from the National Center for Biotechnology Information (NCBI) Reference Sequence (RefSeq) database (45). We further downloaded the protein sequences of Macaca mulatta (as a relative of H. sapiens), Rattus norvegicus (as a relative of M. musculus), Drosophila erecta (as a relative of D. melanogaster), Caenorhabditis briggsae (as a relative of C. elegans), and Saccharomyces paradoxus (as a relative of S. cerevisiae) from the NCBI RefSeq database. The tRNA gene annotations in the five model organisms were downloaded from GtRNAdb (23). RR_c/nc was computed using tRNA gene copy numbers instead of tRNA expression levels.

Statistical analysis

Many of the quantities estimated in our work, such as RMR, RR_c/nc, RSCU, and OR, are not independent among synonymous codons. To deal with this nonindependence in statistical tests, we applied permutation tests. Specifically, in Fig. 1B, we generated 1000 permuted samples by shuffling the absolute mistranslation rates among all codons and then re-estimated RMR values. We then computed the correlation between RMR and RSCU in each permuted sample while holding the RSCU value of each codon unchanged. P equals the fraction of permuted samples with the correlation coefficient more negative than that observed in the original sample. Similarly, when testing the correlation between RMR and OR (Fig. 2B), we shuffled the absolute mistranslation rate among all codons and recomputed RMR while holding the OR for each codon unchanged. When testing the correlation between RMR (or OR) and RR_c/nc (Fig. 3), we shuffled the absolute mistranslation rates among codons and the expression levels (or gene copy numbers) among tRNAs. Last, when testing the correlation between RMR (or RSCU) and relative cognate tRNA concentration (fig. S4), we shuffled the absolute mistranslation rate among codons and the expression level among tRNAs.

To estimate the SE of the RMR of each codon, we constructed 1000 bootstrap samples by resampling the sites in the original data with replacement. Similarly, we estimated the SE of the OR of each codon by constructing 1000 bootstrapped E. coli genomes via resampling its genes that have one-to-one orthologs in S. enterica.

Simulation

To assess the impact of selections for translational accuracy and efficiency on codon usage, we built a toy model with two amino acids, aa₀ and aa₁. Amino acid aa₀ is encoded by synonymous codons 00 and 01, while aa₁ is encoded by synonymous codons 10 and 11 (Fig. 4B). Codon-anticodon pairing follows the rule that 0 pairs with 1 and vice versa. The cognate tRNA of a codon has an anticodon that pairs perfectly with the codon, while the near-cognate tRNA has an anticodon that pairs with the codon with exactly one mismatch and carries the other amino acid.

We considered a unicellular organism with one gene consisting of n codons. We assumed that the mRNA level of the gene does not change in the evolution simulated and that ribosomes are in shortage. We defined the organismal fitness as follows

$$\begin{array}{c}\text{Absolute fitness}=\text{Function}-\text{Cost}, \text{where}\\ \text{Function}=\text{TE} \times {\displaystyle {\sum }_{i=1}^n}{f}_i \text{and} \text{Cost}={\sum }_{i=1}^n{c}_i\end{array}$$

Here, f_i and c_i are the function and cost of codon i, respectively. We set f_i = F_i if codon i encodes the prespecified optimal amino acid at the codon; otherwise, f_i = 0. For each i, F_i is a random variable sampled from an exponential distribution with the mean equal to 1 (46). Following a previous study (18), we set the expected codon selection time per amino acid aa₀ during translation at t₀ = p₁²/q₁ + p₂²/q₂, where p₁ and p₂ = 1 − p₁ are the fractions of amino acid aa₀ encoded by codon 00 and 01, respectively, and q₁ and q₂ = 1 − q₁ are the fractions of corresponding cognate tRNAs among all tRNAs of aa₀, respectively. We similarly set the expected codon selection time per amino acid aa₁ and computed the total codon selection time of all codons. Translational efficiency, TE, which is the number of codons translated per unit time, is the inverse of the total codon selection time. We set c_i = C_i × TE if codon i does not encode the prespecified optimal amino acid at the codon; otherwise, $c_i=C_i\times \text{TE}\times \frac{1}{{\mathrm{RR}}_{\mathrm{c}/\text{nc}}}$. When there is no selection for translational accuracy, C_i = 0; otherwise, C_i for codon i is a random variable sampled from an exponential distribution with mean equal to 1. Note that C_i and F_i are independent from each other. RR_c/nc is computed as described in Results, and the inverse of RR_c/nc measures the mistranslation rate.

We started the simulation with a coding sequence of 200 nucleotides, coding for 100 amino acids. Each site had a 50% chance to be 0 or 1. For simplicity, we assumed that the initial amino acid sequence is optimal such that the evolution in our simulation is primarily about synonymous codon usage. For each of the four different tRNAs (with anticodons of 00, 01, 10, and 11, respectively), we sampled its initial copy number from 1 to 3 with equal probabilities.

Next, we simulated the coevolution between the tRNA pool and codon usage following a strong selection, weak mutation regime. We first generate a mutation. With a probability of 0.02, it alters the copy number of a tRNA. In this case, we randomly pick a tRNA species to change its copy number by +1 or −1 with equal probabilities unless the copy number is 1, in which case it is +1. With a probability of 0.98, the mutation is a random point mutation at a randomly picked site of the coding sequence. The fitness of the mutant is then computed following the above fitness definition. The mutation is fixed with a probability of $\frac{1-r^{-1}}{1-r^{-N}}$, where r is the ratio of the absolute fitness of the mutant to that of the wild type and N is the population size (47). The above mutation-selection process was repeated for 100,000 rounds in each simulation to reach an equilibrium. For each N, we simulated 200 times with and 200 times without selection for translational accuracy.

Supplementary Materials

This PDF file includes:

Tables S1 and S2

Figs. S1 to S4

Other Supplementary Material for this manuscript includes the following:

Data file S1

View/request a protocol for this paper from Bio-protocol.