Biomechanical evaluations of the long-term stability of dental implant using finite element modeling method: a systematic review

Abstract

PURPOSE

The aim of this study is to summarize various biomechanical aspects in evaluating the long-term stability of dental implants based on finite element method (FEM).

MATERIALS AND METHODS

A comprehensive search was performed among published studies over the last 20 years in three databases; PubMed, Scopus, and Google Scholar. The studies are arranged in a comparative table based on their publication date. Also, the variety of modeling is shown in the form of graphs and tables. Various aspects of the studies conducted were discussed here.

RESULTS

By reviewing the titles and abstracts, 9 main categories were extracted and discussed as follows: implant materials, the focus of the study on bone or implant as well as the interface area, type of loading, element shape, parts of the model, boundary conditions, failure criteria, statistical analysis, and experimental tests performed to validate the results. It was found that most of the studied articles contain a model of the jaw bone (cortical and cancellous bone). The material properties were generally derived from the literature. Approximately 43% of the studies attempted to examine the implant and surrounding bone simultaneously. Almost 42% of the studies performed experimental tests to validate the modeling.

CONCLUSION

Based on the results of the studies reviewed, there is no "optimal" design guideline, but more reliable design of implant is possible. This review study can be a starting point for more detailed investigations of dental implant longevity.

INTRODUCTION

The use of dental implants has become a common procedure in dentistry. However, there is always a risk of failure due to structural and functional defects. The success of an implant depends on its stability, which is influenced by the biomechanical conditions of the bone-implant interface.¹ With the advent of computer-aided modeling technology and software packages such as ABAQUS and ANSYS, the design and analysis techniques of implants have undergone a new approach.² Fracture resistance is the most important property of implant components.³ Static fracture tests are usually simulated to determine the strength of implant components. However, verification of the actual performance of implants should be investigated with intermittent and prolonged loading.⁴

An important aspect to consider in implant biomechanics is the size of the implant and its components. Considering the anatomy of the jawbone in terms of geometry and the mechanical and physiological properties of the cortical and cancellous bone, it can be concluded that there are fundamental limitations to implant design, particularly diameter and length.⁵ After implantation, bone adapts its structure to the mechanical loads through remodeling processes.⁶ In order to achieve optimal longevity of dental implants, careful selection of the implant structure considering the bone characteristics is recommended.⁷ The choice of material and geometric design of other components such as abutment, screws, and threads also influence the stress distribution in the implant and the surrounding bone and thus the results of long-term stability. Therefore, attempts to improve stress distribution have been the subject of some research in this area.⁸ Some studies have evaluated stress distribution patterns in the bone-implant interface by investigating stress shielding and remodeling to estimate implant function and potential defects.⁹ However, many studies have investigated the durability of implants rather than the bone-implant complex.¹⁰

Loading of implants is based on replicating the in vivo loading conditions in the oral cavity and includes the magnitude and direction of the applied load. Different loading angles are set with respect to the longitudinal axis of the implant, resulting in a combination of axial, bending, and torsional loads.¹¹

Studies show that stress concentration leads to bone tissue resorption. Moreover, if the load is too low, bone loss will occur. Therefore, the issue of uniform stress distribution during long-term operation is very important and requires the proper design of implants.¹² It can be concluded that a partial and asymmetric type of bone repair around the implant poses a potential risk to implant reliability.¹³

After implant placement, the initial stability of the implant depends on the amount of surrounding cortical and trabecular bone.¹⁴ However, predicting the long-term stability of dental implants is more complicated. The long-term stability of dental implants can be divided into two main aspects: 1) stability of the implant-bone complex, 2) fatigue resistance of the implant and its components.¹⁵ First, implants are subjected to different masticatory loads over time, and the remodeling process simultaneously changes the surrounding medium. This affects the stability of the implant-bone complex. Secondly, the long-term stability of the dental implant itself (rather than the implant-bone complex) is highly dependent on the fracture strength under cyclic masticatory forces and is usually evaluated by fatigue testing. Studies on the fatigue behavior of dental implants are conducted using the criteria of Goodman, Soderberg, and Gerber. The results show that these criteria can be effective in evaluating the failure of dental prostheses.¹⁶ Experimental tests conducted by researchers in this field are often based on ISO 14801 (Dynamic fatigue test for endosseous dental implants).⁴,⁵ The loading and boundary conditions of many finite element method (FEM) are also derived from this standard.¹⁷

Accurate investigation of dental implants embedded in the jawbone under oral cavity conditions such as temperature fluctuations, humidity, and masticatory loading require in vivo testing. However, due to the difficulties involved, researchers often use the finite element method to simulate implants and bone. However, there are limitations when it comes to modeling all conditions in the oral cavity in the software. In conclusion, the finite element method allows the simulation of real conditions of biomechanical structures with an acceptable approximation.¹⁸

So far, many studies have been presented in the field of dental implant design and analysis. This has led to the creation of geometric diversity in order to obtain implants with long-term functions.¹⁹ Due to the variety of geometric parameters involved in implant design such as length, diameter, thread form, helix angle, etc., the importance of statistical methods such as sensitivity analysis and reliability to achieve optimal geometry in different implant models seems greater than before.²⁰ In the problems of geometric optimization of dental implants, the mentioned geometric parameters of the model are selected as input variables. The stress distribution pattern in the form of maximum Von-Mises stress and/or strain or other failure criteria as output is included to optimize the geometry and increases the reliability of dental implants.²¹

Another recently proposed solution to improve stress distribution is the use of porous structures. Porous implants can act as a porous scaffold and improve ossification around the implant.²² Moreover, if geometric parameters are defined for a porous geometric pattern, it would be possible to use optimization methods.²³

In this study, a summary of the efforts to evaluate the long-term stability of dental implants is given and different categories are extracted and classified in the comparison tables. The details of experimental data and statistical analysis are also tabulated. Then various aspects of these studies including methodology and shortcomings are discussed. Here, the use of statistical approaches and comparison of modeling with experimental results are considered as qualitative measurement criteria in the study of the long-term stability of dental implants. Now it is possible to compare the methods and results of the studies and to get an overview of the different approaches of the articles to each extracted category.

MATERIALS AND METHODS

Search strategy

In order to obtain a comprehensive biomechanical overview of dental implant stability, the first step of the careful review involved a thorough search of articles published in databases such as PubMed, Scopus, and Google Scholar over the last 20 years up to November 2021. Terms such as “dental implant + longevity + FEM”, “dental implant + reliability + FEM”, “dental implant + stability + FEM”, and “dental implant + fatigue + FEM” were searched. These terms represent the study of various biomechanical aspects of dental implant stability by researchers. A manual search was also performed through the reference list of studies found. A total of 174 articles were found.

Screening the title

The initial screening was based on the titles of the found articles. The titles of the articles were studied in detail by both authors to confirm the purpose and relevance of each investigation to the content of our manuscript (long-term stability of dental implants from a biomechanical point of view). After reading their titles, those that met the qualification were selected for a more accurate processing.

Inclusion and exclusion criteria

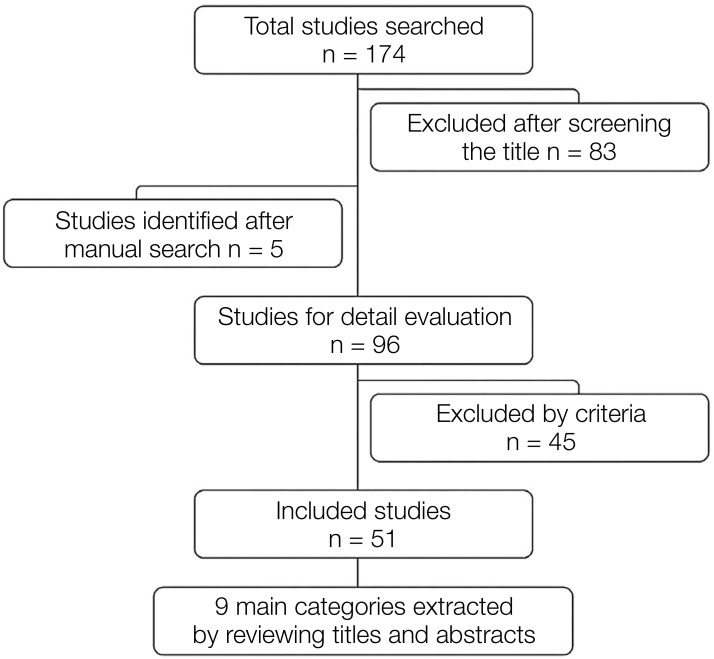
In this study, the main criteria for evaluating dental implant stability methods are long-term evaluations (dynamic tests) using the finite element method. Therefore, studies that satisfied the initial stability and/or static tests to predict the long-term behavior of dental implants without performing dynamic loading were excluded. Finally, 51 articles that were most relevant to the main content were selected. Figure 1 shows the review process in the form of a flow chart.

Fig. 1. Flow chart of the review procedure.

Category selection

In the second step, the authors carefully reviewed the abstracts of the selected papers to examine the similarities. Nine main categories were selected including, implant materials, bone-implant interface, type of loading, element shape, parts in the finite element model, boundary conditions, failure criteria, statistical analyses, and comparison of results with experimental data. By comparing the studies using these categories, it is possible to understand the strengths and weaknesses of each study, which finally led to determine the necessary future attempts in this area. The collected articles are compared in Table 1 based on the date of publication, and then each category was discussed separately.

Table 1. Summary of articles reviewed: implant materials, studies focusing on bone or implant, type of loading, element shape, boundary conditions, failure criteria, parts of the finite element model, statistical analyses, and comparison with experimental results.

Author (Year)	Implant Material	Study Focus on Bone and/or Implant	Type of Loading	Element Shape	Boundary Condition	Failure Criteria	Parts of Finite Element Model	Statistical Analyses	Comparison with Experimental
Kunavisarut et al.24 (2002)	Titanium	Both	Static Overload	-	-	Von misses	7 Parts: Crown, Gold Screw, Abutment, Screw, Implant, Cortical Bone, Cancellous Bone	-	No
Perriard et al.25 (2002)	Titanium	Implant	Static, Dynamic (Fatigue)	Tetrahedron	-	-	5 Parts: Implant, Abutment, Screw, Loading Cap, Resin Block	Yes	Yes
Genna26 (2003)	Titanium	Implant	Dynamic (Fatigue)	-	-	-	4 Parts: Abutment, Implant, Screw, Epoxy Resin as Fixture	-	Yes
Kayabasi et al.27 (2006)	Ti-6Al-4V	Both	Static, Dynamic (Fatigue)	4-Node Tetrahedron	Bottom Surface of Mandible Fixed	Von Mises	6 Parts: Implant, Abutment, Metal Framework, Occlusal Material, Cortical Bone, Trabecular Bone	-	No
Wierszycki et al.28 (2006)	Titanium	Implant	Dynamic (Fatigue)	-	Different Levels of Osseointegration	The factor of strength	4 Parts: Implant, Abutment, Screw, Bone	-	Yes
Yang et al.29 (2007)	Functionally Graded Biomaterial	Both	Static and Harmonic Occlusal	10-Node Tetrahedron	-	Von Mises	5 Parts: Abutment, Screw, Cortical Bone, Trabecular Bone, FGM Implant	-	No
Kong et al.30 (2009)	Titanium	Both	Immediate Loading	10-Node Tetrahedron/20-Node Hexahedron	-	Von Mises	4 Parts: Implant, Cortical Bone, Cancellous Bone, Porcelain	Yes	No
Hasan et al.31 (2010)	Titanium	Both	Immediate Loading	4-Node Tetrahedron	End Faces Constrained	Von Mises	2 Parts: Implant, Bone Block	-	No
Pérez32 (2012)	Titanium	Implant-bone Interface	Dynamic	Tetrahedron	Bone Sides and Bottom Fixed	Von Mises	2 Parts: Implant, Bone	Yes	No
Hasan et al.33 (2012)	Titanium	Implant	Immediate Loading	Tetrahedron	Bone Sides and Bottom Fixed	Equivalent stress	3 Parts: Implant, Cortical Bone, Cancellous Bone	Yes	Yes
Tsai et al.34 (2012)	Titanium	Implant	Static, Dynamic (Fatigue)	-	-	Von Mises, Soderberg, Goodman & Gerber	4 Parts: Implant, Abutment, Loading Cap, Holder	Yes	Yes
Lee et al.35 (2012)	Titanium	Both	Static, Dynamic	Tetrahedron	Bone Fixed at Mesio-Distal Ends/Implant Fully Bonded Bone	Strain Energy Density/Von Mises	4 Parts: Implant, Abutment, Cortical Bone, Trabecular Bon	-	No
Ali et al.36 (2013)	Titanium	Both	Dynamic/Dynamic (Over Load)	-	Bottom Surface of Jaw Fixed	Von Mises	5 Parts: Implant, Crown, Abutment, Cancellous Bone, Cortical Bone	-	No
Covani et al.37 (2013)	Titanium	Implant	Dynamic	Tetrahedral	Bone Constrained	Von Mises	4 Parts: Implant, Abutment, Bone, Screw	-	No
Geringer et al.38 (2014)	Titanium	Both	Static, Fatigue	Tetrahedral	Base Displacements Set to Zero in 3 Dimensions	Von Mises	4 Parts: Implant, Crown, Abutment, Resin Block	-	No
Ayllón et al.39 (2014)	Titanium	Implant	Dynamic (Fatigue)	10-Node Tetrahedron	Null Displacement on The Crests of External Thread	Von Mises	5 Parts: Implant, Screw, Pillar, Loading Cap, Fixed Support	-	Yes
Bulaqi et al.40 (2015)	Titanium	Both	Dynamic (Fatigue)	Tetrahedral	Bone Bounded	Von Mises	8 Parts: Implant, Direct Abutment, Screw, Metal Frame, Porcelain, Resin, Cortical Bone, Trabecular Bone	-	No
Hernandez et al.41 (2015)	Cobalt-Chrome Alloy	Implant	Dynamic (Fatigue)	10-Node SOLID 187 3 Degrees of Freedom	Down Base and Lateral Bone Faces Restricted in 3 Longitudinal and Rotational Directions	Von Mises, Goodman, Soderberg, and Gerber	8 Parts: Crown Inner, Crown Outer, Fixation's Screw, Abutment's Screw, Abutment, Single Implant, Cancellous Bone, Cortical Bone	-	No
Hernandez-Rodriguez et al.42 (2015)	Ti-6Al-4V	Implant	Static, Dynamic (Fatigue)	Tetrahedron	Holder Constrained by a Fixed Support	Von Mises	5 Parts: Loading Cap, Abutment, Implant, Screw, Holder	-	Yes
Prados-Privado et al.43 (2015)	Ti-6Al-4V	Implant	Static, Dynamic (Fatigue)	-	Displacements Restrained, Only Normal to The Surface Allowed	Goodman, Soderberg, Gerber	1 Part: Implant	Yes	No
Toyoshima et al.44 (2015)	Ti-6Al-4V	Implant	Static, Dynamic (Fatigue)	8-Node Tetrahedron	Holder Constrained by a Fixed Support	Von Mises	3 Parts: Implant, Cancellous Bone, Cortical Bone	-	Yes
Bicudo et al.45 (2016)	Titanium	Both	Static, Dynamic (Fatigue)	SOLID187	Constrained Lateral Faces of Epoxy and Saw bone	Von Mises	3 Parts: Implant, Epoxy Resin layer, Saw Bone	-	Yes
Szajek et al.46 (2016)	Titanium	Implant	Static, Dynamic (Fatigue)	8-Node Linear Brick	Fixed Implant Root	Von Mises	3 Parts: Abutment, Screw, Fixture	-	No
Bicudo et al.47 (2016)	Titanium	Both	Dynamic (Fatigue)	SOLID187	Constrained Lateral Faces of Epoxy and Saw Bone	Von Mises	3 Parts: Implant, Epoxy Resin layer, Saw bone	-	Yes
Prados-Privado et al.48 (2016)	Titanium	Implant	Dynamic (Fatigue)	-	-	Von Mises	3 Parts: Implant, Abutment, Crown	Yes	No
Wu et al.49 (2017)	Titanium, Ti-6Al-4V	Both	Dynamic (Fatigue)	-	Constrained Cuboid Bone Surface	Von Mises	6 Parts: Implant, Abutment, Fixation Screw, Crown, Cortical Bone, Cancellous Bone	Yes	Yes
Geramizadeh et al.50 (2017)	Titanium	Both	Static Dynamic (Fatigue)	4-Node Tetrahedron	Mandible Base Fixed	Von Mises, Goodman	4 Parts: Implant, Abutment, Cortical Bone, Cancellous Bone	-	No
Bordin et al.51 (2017)	Titanium	Implant	Dynamic (Fatigue)	Tetrahedron	Full Constrain of Model	Von Mises	4 Parts: Implant, Abutment, Crown, PVC Tube Holder	-	Yes
Prados-Privado et al.52 (2017)	Titanium	Implant	Dynamic (Fatigue)	-	Inferior Border of Cortical Bone Restrained/Mesial/Distal Borders of End, Bone Section Was Constrained	Von Mises	3 Parts: Implant, Cortical Bone, Trabecular Bone	Yes	No
Castolo et al.53 (2018)	Titanium	Implant	Static, Dynamic (Fatigue)	Triangular Elements for Surface/Tetrahedral Elements For Volume	Implant Root Embedded in Fixture	Von Mises	5 Parts: Dental Implant, Connecting Screw, Hemispherical Member, Connecting Part, Holding Element	-	Yes
Yamaguchi et al.54 (2018)	Titanium	Implant	Dynamic (Fatigue)	-	-	-	5 Parts: Implant, Abutment, Screw, Cortical Bone, Trabecular Bone	Yes	Yes
Cinel et al.55 (2018)	Titanium/Titanium-Zirconium	Both	Static, Dynamic (Fatigue)	8-Node Tetrahedral	Mandible Lower Border, Maxilla Upper Border Fixed	Von Mises, Goodman, Soderberg, Gerber	7 Parts: Implant, Crown, Metal Framework, Screw, Abutment, Cortical Bone, Trabecular Bone	-	No
Cervino et al.56 (2018)	Titanium, Ti-6Al-4V	Both	Dynamic	SOLID 186/SOLID 187	Ideal Osseointegration with Total Contact Surface Between Implant/Bone	Von Mises	5 Parts: Implant, Abutment, Screw, Cortical Bone, Trabecular Bone	-	No
Geramizadeh et al.57 (2018)	Titanium	Both	Static, Dynamic (Fatigue)	4-Node Tetrahedron	Mandible Base Fixed	Von Mises	4 Parts: Implant, Abutment, Cortical Bone, Trabecular Bone	Yes	No
Topkaya et al.58 (2018)	Ti-6Al-4V	Implant	Dynamic (Fatigue)	10-node Tetrahedron 6 Degrees of Freedom	All Edges, Area of Substructure Constrained	Von Mises	5 Parts: Implant, Abutment, Screw, Cortical Bone, Trabecular Bone	-	Yes
Abasolo et al.59 (2018)	Ti-6Al-4V Cobalt-Chrome Alloy	Implant	Dynamic (Fatigue)	High/low order Hexahedral 3 Degrees of Freedom	Both Ends of The Mandible Are Clamped	Goodman	8 Parts: Implant, Abutment, Lower Screw, Cortical and Trabecular Bone, Lower-Upper Screw, Framework	-	No
Duan et al.60 (2018)	Titanium	Implant	Dynamic (Fatigue)	4- Nodes Tetrahedron	Constrained Bottom Surface of The Holder Block	Von Mises	5 Parts: Implant Body, Abutment, Abutment Screw, Cylindrical Base, Hemispherical Loading Cap	Yes	Yes
Bayata et al.61 (2018)	Titanium	Both	Dynamic (Fatigue)	10-Node Tetrahedron	Lateral Surface of Holder Fixed	Von Mises, Goodman	3 Parts: Implant, Abutment, Holder Block	-	No
Prados-Privado et al.62 (2018)	Ti-6Al-4V	Implant	Dynamic (Fatigue)	-	Bottom/Lateral Surface of Bone Restrained	Von Mises	4 Parts: Implant, Loading Cap, Abutment, Cylindrical Bone	-
Lee et al.63 (2019)	Titanium	Both	Dynamic (Fatigue)	4-Nodes Tetrahedron	Both Ends of Bone Block Fixed in All Directions	Von Mises	8 Parts: Crown, Cement layer, Abutment, Screw, Implant, Cortical Bone, Trabecular Bone, Nerve Canal	-	No
Wang et al.64 (2019)	Commercially pure Titanium	Both	Dynamic (Fatigue)	-	Bone/Implant Perfectly Bonded	Von Mises	5 Parts: Implant, Loading Cap, Abutment, Cortical Bone, Cancellous Bone	-	Yes
Bataineh et al.65 (2019)	Ti-6Al-4V	Both	Dynamic (Fatigue)	-	Bone Fixed	Von Mises, Maximum Principle Stress/Strain	5 Parts: Implant, Crown, Abutment, Cortical Bone, Cancellous Bone	-	No
Manea et al.66 (2019)	Ti-6Al-4V	Implant	Static Dynamic (Fatigue)	Tetrahedron	Complete Immobilization of Implant Exterior Part/Outer Surface Blocked	Von Mises	8 Parts: Implant, Cushioning Mechanism, Abutment, Locking Pins, Implant Screw, O-Ring, Loading Cap, Bone Block	Yes	Yes
Prados-Privado et al.67 (2019)	Titanium	Implant	Dynamic (Fatigue)	-	Degrees of Freedom in Bottom/Lateral Surfaces in Resin Block Restrained	-	3 Parts: Implant, Metallic Crown, Resin Block	-	No
Zhang et al.68 (2020)	Ti-6Al-4V	Implant	Static Dynamic (Fatigue)	-	Good Osseointegration Between Implant/Alveolar Bone	Von Mises	6 Parts: Implant, Abutment, Central Screw, Loading Cap, Cortical Bone, Cancellous Bone	-	Yes
Sahin69 (2020)	Titanium/Titanium-Zirconium	Both	Static Dynamic (Fatigue)	Tetrahedron	Inferior Edge of Mandible, Superior Edge of Maxilla, Lateral Region of Jaw Fixed	Von Mises	7 Parts: Implant, Crown, Substructure Part, Abutment, Screw, Cortical Bone, Cancellous Bone	-	No
Nokar et al.70 (2020)	Ti-6Al-4V	Both	Static Dynamic (Fatigue)	Tetrahedron	Bone Segment Fixed From The Mesial/Distal	Von Mises	7 Parts: Implant, Crown, Abutment, Frame Work, Porcelain, Cortical, Cancellous Bone	-	No
Armentia et al.71 (2020)	Commercially Pure Titanium Ti-6Al-4V	Implant	Static Dynamic (Fatigue)	-	Holder Fixed	-	4 Parts: Implant, Abutment, Screw, Specimen Holder	-	Yes
Bayata et al.72 (2020)	Ti-6Al-4V	Implant	Dynamic (Fatigue)	10-Node Tetrahedron	Lateral Surface of Implant Holder Fixed	Von Mises	3 Parts: Implant, Abutment, Holder Block	-	No
Lee et al.73 (2021)	Ti-6Al-4V	Implant	Dynamic (Fatigue)	Tetrahedron	Bone Block Fixed Along All Axes	Von Mises	9 Parts: Crown, Cement, Screw, Abutment, Implant, Cortical Bone, Cancellous Bone, Cylindrical Part, Nerve Canal	Yes	No
Bergamo et al.74 (2021)	Ti-6Al-4V	Implant	Dynamic (Fatigue)	-	Bottom Surface of Abutment Fixed	Maximum Principal Stress/Strain	4 Parts: Implant, Abutment, Resin Matrix, Ceramic Crown	Yes	Yes

Cells marked with ((-)) indicate that the case was not mentioned in the article.

^*Ti-6Al-4V refers to the chemical composition of the alloy of almost 90% titanium, 6% aluminum, 4% vanadium.

RESULTS

Implant material

It was found that most of the studies mainly used titanium (Ti) and its alloys such as Ti-6Al-4V (the alloy of almost 90% titanium, 6% aluminum, 4% vanadium) as implant material. Due to the biocompatibility of titanium and its physical and mechanical properties, implants are highly successful. Various studies have shown that titanium has considerable long-term stability.⁷⁵ The main alloys used in the manufacture of commercial implants are pure titanium and Ti-6Al-4V. The fatigue strength of Ti-6Al-4V has been reported to be better. However, there are concerns about the biological effects of the very small amounts of aluminum and vanadium that enter the body. Despite these concerns, there is ample empirical evidence that both alloys have good biocompatibility and the ability to osseointegrate.⁷⁶

Other implant parts such as the abutments or abutment screws are made of different alloys such as gold, cobalt, or chromium.⁷⁷ In biomechanical simulations of dental implants, the main focus is usually on the mechanical behavior of material, alloys, and structural components. Other biocompatibility parameters such as surface modification and roughness and their effects on bone remodeling and physiology are not a priority in such studies.⁷⁸ Based on the reviewed studies, Titanium and its alloys are commonly used in the evaluation of long-term stability when selecting materials, and the variety of materials used in this field is small.

The focus of the study on bone and/or implant

In 53% of the articles reviewed, the focus was only on the implant and the components embedded in a restrained fixture, but other studies considered the surrounding bone as an important part to be studied under different loading conditions, such as a fatigue test. In the studies investigated, the surrounding bone was modeled as a continuous medium, taking into account the different mechanical properties of cortical and cancellous bone, without focusing on the complicated geometry of cancellous bone. However, three-dimensional reconstructed models of bone based on micro-computed tomography (micro CT scanning) provide more accurate geometry for FE analyses.⁷⁹,⁸⁰

In the reviewed studies, the contact surface between the bone and the implant is often considered as a complete connection. 47% of the reviewed studies investigated the distribution of stress in this area. The biomechanical modeling of the bone-implant interface is of particular importance. Recent studies have been performed on the biomechanical aspects of this area.⁸¹

Loading

Implant and bone must be considered under the following loading conditions: static and dynamic. Dynamic loading is usually derived from the standard ISO 14801,¹⁷ which represents the loading conditions for the implant during mastication. The loading should represent a simple case, but the worst possible case. The oblique orientation is often considered biologically justified because it causes an accumulation of bending and pressure on the implant components.⁸² Many modeling studies in the field of dental implants have only investigated implants under static loading, while fewer studies have investigated implants under dynamic loading.⁸³ Since satisfactory static behavior is not necessarily a guarantee of long-term implant performance, this review focused on articles that investigated the dynamic test as a representative of long-term implant behavior.⁸⁴

Recent studies show that the success rate of dental implants in immediate loading depends on factors such as bone quality, implant dimensions, implant components, and force.⁸⁵

Shape of elements

To perform FE analysis, the model must be discretized into small elements in the spatial dimension so that the software can construct a mesh of the objects. In the studied articles, a frequently used element is tetrahedron (in some studies the element shape was not mentioned). The accuracy of the result in finite element analysis depends on the element shape, the number of nodes and the degrees of freedom. These factors were explicitly mentioned in some studies. Higher-order elements were used for complex geometries.⁸⁶ Some studies only specified the element type. The degrees of freedom in each element are also an important feature in FEM. However, very few articles mentioned the number of degrees of freedom of elements. The most widely used software packages for FE analysis are ANSYS and ABAQUS, although not all studies mentioned their software.

The property of the FEM to obtain an accurate solution by mesh improvement and corrections for error minimization is called “convergence”. After appropriate meshing and achieving suitable finite element network, one will obtain the desired number of elements and degrees of freedom. The main variable to be considered for the solution convergence is the field variable in FEA (e.g. the maximum stress or displacement, etc.). Usually, by increasing the number of elements to an optimum number, an agreement will be grasped between the convergence time and the number of elements. It is important to realize that increasing the number of elements does not necessarily conclude to higher accuracy of the solution, but increases the computational cost.⁸⁷

Although optimization of the mesh size and convergence of the results is one of the most important issues in the application of the FEA and it is necessary to gain acceptable solution accuracy, most of the reviewed studies mention the number of elements, the type of elements and, in some cases, the number degrees of freedom.

Boundary conditions

Due to the complexity of the bone-implant interface area, modeling this region is difficult and always involves assumptions. The structure of the bone changes over time due to the remodeling process. Moreover, due to the different elastic modulus of the implant and the surrounding bone, as well as the mechanical behavior of the individual parts, the local occurrence of complex multiaxial stresses is predictable. On the other hand, the rate of bone repair varies in different parts of the bone-implant interface (BII) region.⁸⁸ In some studies, different stages of bone repair were considered as contact boundary conditions. In the present study, based on paper reviewed, different boundary conditions were investigated and considered in different modeling cases. Most of the boundary conditions aim to restrain the displacements of the jaw bone or the implant root attachment.

Failure criteria

In the studies reviewed, various criteria were considered to evaluate the risk of failure of the implant and/or surrounding bone. In the evaluation of stress distribution, the Von-Mises stress criterion was considered in the analysis of the models. The Goodman, Gerber, and Soderberg criteria were used in the fatigue studies.

Although these criteria are mainly used in articles, recent studies show that the onset of bone remodeling is more closely related to strain energy density. Mechanical parameters that are closely related to the onset of the remodeling response are strain energy density, longitudinal shear stress, and principal tensile stress.⁸⁹

Parts of the model

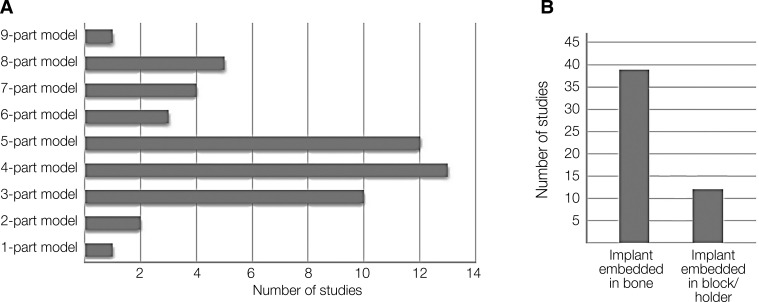
As shown in Table 1, in the reviewed studies, the modeling related to dental implants varies in terms of the components of the finite element model. Modeling from one-part to nine-part modeling is given in the comparison table with details. For example, one of the models includes implants, abutments, screw abutments, and a model of the jaw bone containing cortical and cancellous bone. In some of the reviewed studies, dental implants are embedded in resin blocks (holders). As shown in Figure 2, the authors are more inclined to 4-part and 5-part modeling.

Fig. 2. Classification of modeling based on the number of model components and the tendency of researchers for each (A), number of models with implant embedded in block/holder or bone (B).

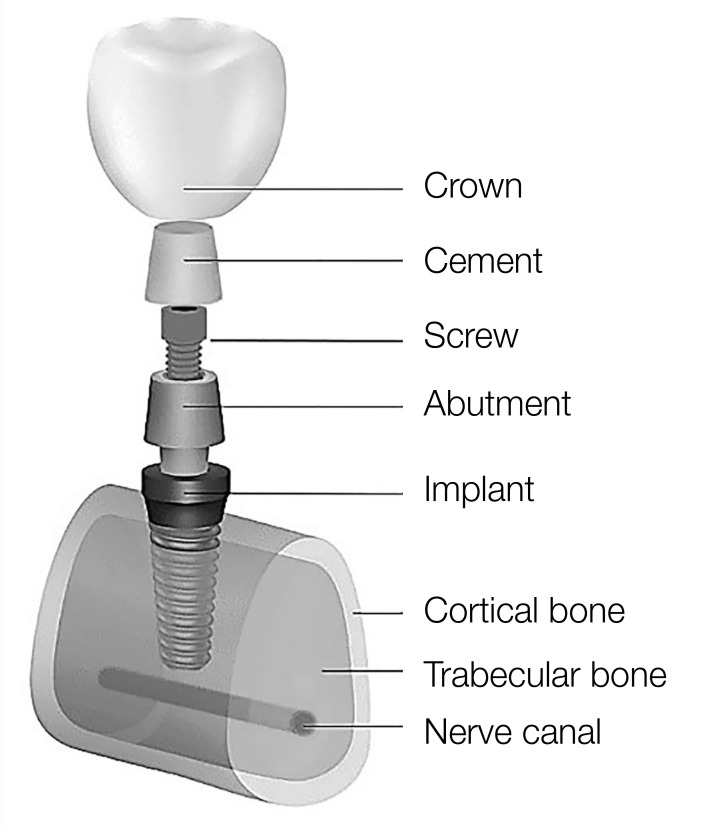
The number of components of the finite element model can determine the accuracy of modeling and its greater adaptation to real conditions. For this reason, in some models, more details including implants, abutments, screw abutments, crowns, cement layer, and even the nerve canal inside the jaw bone have been modeled (Fig. 3). In modeling, the crown (ceramic) is often modeled as a rigid body. As can be seen in Figure 2, in most models (77%), the implant is embedded in the bone, while in a number of studies (23%), the implant is placed inside a resin block (or holder).

Fig. 3. Schematic representation of the different parts of a finite element model.

Aside from discussing the quality and accuracy of dental implant modeling and components of each finite element model, it is important to examine which component(s) are specially targeted. Table 2 shows the main topic of each of the studies regarding the component of the implant set. Since dental implants are made up of a number of components that are in contact and interconnected, when discussing the long-term stability of the implant, the strength and durability of each component affect the success of the implant placement. In addition, the stress distribution between the components and in the bone-implant set should be optimal. The study of long-term stability has been conducted in several areas, including the study of the effects of component material, geometric optimizations, the study and comparison of the stability of commercial implants, sudden or overloaded implants, and the study of fatigue. These topics are summarized in Table 2.

Table 2. Summary of the main themes of the studies and topics.

Author	Main Issue of study						Study Subject
	Crown	Metal Framework	Abutment Screw	Abutment	Implant	Bone
Kunavisarut et al.24	*		*	*	*	*	Misfit of Parts
Perriard et al.25			*	*			Abutment Connectors Fatigue
Genna26			*	*	*		Cyclic Transversal Force
Kayabasi et al.27	*	*	*		*		Dental Implant Fatigue
Wierszycki et al.28					*	*	Dental Implant Fatigue
Yang et al.29					*	*	Functionally Graded Material
Kong et al.30			*		*	*	Immediate Load
Hasan et al.31					*	*	Short Dental Implant
Pérez32					*		Dental Implant Fatigue
Hasan et al.33			*				Design Abutment Influence
Tsai et al.34			*		*		Dental Implant Fatigue
Lee et al.35					*		Dental Implant Fatigue
Ali et al.36	*		*		*	*	Overloading In Mastication
Covani et al.37			*	*	*		Implant-Abutment Connect
Geringer et al.38			*				Zirconia Abutment
Ayllón et al.39					*		Fatigue Life Estimation
Bulaqi et al.40	*	*	*	*	*	*	Stress In Bone-Implant
Hernandez et al.41	*		*	*	*	*	Dental Implant Fatigue
Hernandez-R et al.42			*		*		Failure Analysis
Prados-Privado et al.43					*		Dental Implant Fatigue
Toyoshima et al.44					*		Load Limit Mini-Implant
Bicudo et al.45					*	*	Mechanical Behavior
Szajek et al.46			*	*	*		Fatigue life
Bicudo et al.47					*	*	Performance Evaluation
Prados-Privado et al.48			*				Random Fatigue
Wu et al.49			*				Effect of Lubricant
Geramizadeh et al.50					*	*	Dental Implants Threads
Bordin et al.51			*		*		Narrow Dental Implants
Prados-P et al.52					*		Dental Implant Fatigue
Castolo et al.53			*		*		Mechanical Strength
Yamaguchi et al.54			*	*	*		Fixture/Abutment Joint
Cinel et al.55					*	*	Narrow Diameter Implants
Cervino et al.56			*	*	*		Structural Components
Geramizadeh et al.57					*		Optimization, Sensitivity
Topkaya et al.58					*		Implant Dimension/Fatigue
Abasolo et al.59			*				Misfit/Screw Fatigue
Duan et al.60			*	*	*	*	Fatigue Lifetime Prediction
Bayata et al.61					*	*	Mechanical Behaviors
Prados-Privado et al.62					*		External Hexagonal
Lee et al.63			*		*	*	Short Dental Implants
Wang et al.64					*	*	Porous Dental Implant
Bataineh et al.65	*					*	Biocompatible Implant
Manea et al.66					*		Shock Absorbers
Prados-P et al.67					*		Fatigue Behavior
Zhang et al.68			*	*	*		Statics/Fatigue Analysis
Sahin69					*	*	Narrow Diameter Implants
Nokar et al.70			*		*	*	Stress in Bone/Abutment
Armentia et al.71			*	*	*		Fatigue Design
Bayata et al.72			*		*		Design Parameters Effects
Lee et al.73			*	*	*		Diameter, Connection Type
Bergamo et al.74	*						Survival of Implant

^*Means that the study contains the items listed.

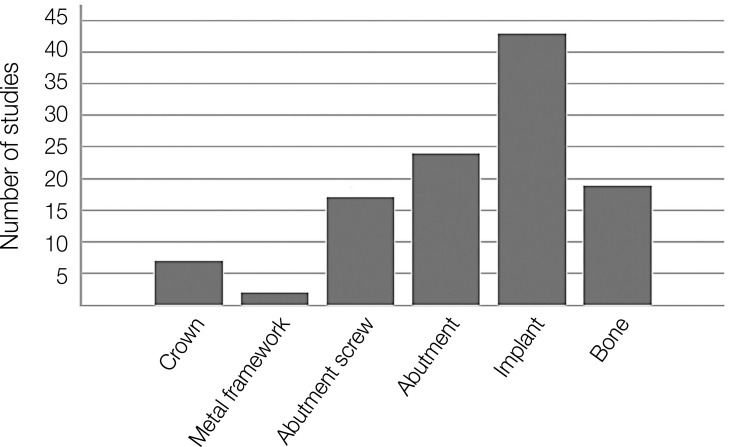
From the graph in Figure 4, it can be seen that implants (roots) and abutments have received the most attention from researchers over the past twenty years when it comes to long-term stability. Many studies have investigated the contact properties and stress distribution between implants and abutments as a part of the discussion on long-term stability. However, the role of the screw connection is also important and the subject of several studies in this field.

Fig. 4. The extent of each part of the implant-bone set as the main subject of the studies.

As shown in Table 2 and Figure 4, the study of components such as the crown or the metal framework has received the least attention. In 97% of the reviewed studies, the framework was ignored. Due to the fact that the crown is made of ceramic, it is modeled as a rigid element in most studies. Furthermore, in many models, a rigid spherical metal cap was used to apply force instead of the implant crown.

Statistical analyses

A few studies used statistical methods in which multiple statistical analyses were performed to assess the significance of the difference between the modeling approach and the results obtained. The characteristics of these analyses, including sample size, methodologies, mean and variance of stresses resulting from modeling, reliability, and sensitivity analyses are summarized in Table 3.

Table 3. The summary of the statistical analyses performed to assess results.

Author	Number of Samples	Details
Perriad et al.25	9 Specimens to Adjust Machine Settings, 20 Specimens for O-O Combination 10 For Both The S-S and O-S Pairs	Standard Deviation Computed
Kong et al.30	9 Samples	Response Surface Construction and Sensitivity Analysis
Pérez32	-	Mean Value and Monte Carlo Sampling
Hasan et al.33	30 Samples	Differences of Mean Implant Displacements and Rotations Analysed Using Mann-Whitney Test
Tsai et al.34	4 Samples	Regression Analysis Method
Prados-Privado et al.43	Several Taylor Expansions Done Around Every Random Variable, Instead of Generating Samples	PFEM have been chosen (perturbation method)
Prados-Privado et al.48	-	Mean Value and Variance, Perturbation Method
Wu et al.49		One-way analysis of variance (ANOVA) with Fisher's PLSD test was used to compare the differences (P < .05)
Prados-Privado et al.52	-	Mean Value and Variance to Estimate The Fatigue Life and Probability of Failure
Yamaguchi et al.54	Mild: n = 3 Moderate: n = 2 Aggressive: n = 1	Two-Way ANOVA P < .001
Geramizadeh et al.57	3 Candidate Points of 1000 Iteration Extracted	Sensitivity Analysis
Duan et al.60	-	Fatigue Lifetime Statistics of Physical Specimens Were Estimated in a Reliability Analysis Software (ALTA PRO)
Manea et al.66	10 Samples	U Test, Mann-Whitney, and Wilcoxon Test For Paired Samples
Lee et al.73	12 Samples	Statistical Analysis Performed with SPSS 20.0 Software (IBM)/Analysis for Normal Distribution With The Shapiro-Wilk Test. Kruskal-Wallis One-Way And Mann-Whitney U Tests
Bergamo et al.74	n = 9 in the mild, n = 6 in the moderate, n = 3 in the aggressive loading	Reliability Analyses, Weibull Beta Parameter Calculation

The cells indicated by ((-)) means that the case has not been mentioned in the article.

One of the most important applications of statistics to represent the behavior of phenomena is found in “reliability theory”. This theory is mainly used in cases such as engineering and determining the lifetime of systems. Reliability can be considered as the ability to determine the lifetime of a system based on its components. Therefore, based on probability theory, the degree of reliability can be considered as the probability of failure (probability of longevity).⁹⁰ In recent studies, the method of sensitivity and reliability analysis is considered as a new approach to estimate the lifetime of implants and their sensitivity to changes in various parameters as input.⁵⁷

Comparison between FEM and experimental results

Comparing the results of FEM with the experimental results, one could conclude that some results of FEM have been validated. About 42% of the studied articles have performed experimental studies to compare with the computational results, while 5% of the articles have performed this comparison using the experimental results from the literature. The rest of the studied articles have been satisfied with computational analyses. The summary of the experimental methods performed by some authors is summarized in Table 4.

Table 4. The summary of the experimental results performed to validate finite element modeling.

Author	Test Details
Perriad et al.25	Implant Under Servohydraulic Fatigue Tester
Genna26	Implant Immersed in Resin Cylinder
	Transversal Cyclic Test
Wierszycki et al.28	Radiograph Case Report of Patient
Hasan et al.33	Immediate Loading Condition on The Implant
Tsai et al.34	Fatigue Test/5*106 Cycles
Ayllón et al.39	Implant Locked in Fixture/Test According to ISO 14801/5*106 Cycles
Hernandez-Rodriguez et al.42	Dental Implant with Fixed Clamping Device
	Visual Inspection, Chemical Analysis, Metallography, Micro Hardness
Toyoshima et al.44	Fatigue Test According to ISO 14801/5*106 Cycles
Bicudo et al.45	Two Types of Implants Embedded in Polyurethane Foam/Fatigue Test According to ISO 14801
Bicudo et al.47	Two Types of Implants Embedded in Polymeric Foam/Fatigue Test According to ISO 14801
Wu et al.49	Fatigue Test According to ISO-FDIS 14801 /5*106 Cycles
Bordin et al.51	Implant Embedded in Cylinder PVC Tube/105 Cycles
Castolo et al.53	Fatigue Test According to ISO 14801/106 Cycles
Yamaguchi et al.54	Implants Embedded in Resin/Fatigue Test
Topkaya et al.58	Fatigue Test According to ISO 14801/103 – 106 Cycles
Duan et al.60	Fatigue Test According to ISO 14801/5*106 Cycles
Prados-Privado et al.62	Static and Fatigue Tests
Wang et al.64	Fatigue Test According to ISO 14801/5*106 Cycles
Manea et al.66	Static and Dynamic Test/2*105 Cycles
Zhang et al.68	Fatigue Test of Dental Implant/6*105 Cycles
Armentia et al.71	46 Experimental Tests According to ISO 14801
Bergamo et al.74	Stereomicroscope Micrographs of Cracks in Loading Areas

DISCUSSION

In this study, various research aspects of the biomechanical evaluation of long-term stability of dental implants were investigated including modeling and/or laboratory methods. To understand the significance of studying the long-term stability of dental implants using the finite element method, it is worth stating that, in addition to the variety of modeling, this method also allows the application of different boundary conditions.¹ Since several factors play a role in the study of the long-term stability of dental implants, it is possible to apply a variety of boundary and loading conditions simultaneously. Another advantage of the FEM is that it is inexpensive compared to laboratory methods. It is possible to identify the pattern of stress distribution and stress shielding in complex geometric structures.⁸⁸ The ability to use higher-order elements to improve the accuracy of the results can increase the accuracy of the modeling solutions.⁸⁶ It is also possible to study the stress pattern at the implant-bone interface region, which can predict the mechanical and physiological response of bone to implant over time. Evaluating the bone biological response to the implant required in vivo testing, which is limited, expensive, and time-consuming. Finally, FEA has the capability to adapt to new approaches such as optimization and reliability analysis to achieve optimal geometric structures and increase the long-term stability of dental implants.⁵⁷

Although many studies have been conducted on the design and fabrication of dental implants, less attention has generally been paid in the literature to long-term evaluation, including fatigue test analysis and reliability. The evaluation of the long-term stability of dental implants is not limited to biomechanical aspects. Other researchers have attempted to investigate various aspects of this topic from other perspectives such as biology, tissue engineering, and the interaction between implants and biological tissues.⁹¹

It has been shown that the structure of the implant strongly influences the stress distribution at the implant-bone interface. Therefore, proper choice of the implant could allow more realistic stress transmission at the interface and stress distribution in the surrounding bone.⁹² This avoids stress shielding and stress concentration, which is beneficial for the long-term performance and stability of the implant.⁹³

The choice of material as the first step in selecting a dental implant is of particular importance. Although most dental implants are made of titanium, other alloys can be modeled in this manner. Based on the fact that titanium alloys have acceptable fatigue strength, in most studies reviewed, these alloys were used as the basis for implants. However, less attention has been paid to the properties of other materials, such as functionally graded biomaterials, when it comes to long-term stability.⁷⁵,⁷⁸

It is necessary that dental implants to be examined separately according to existing standards (ISO 14801, 2007). However, there is always a need to examine the implant and bone collection to observe stress distribution, stress concentration, and shielding after implant placement.

Static loading is commonly used to evaluate the initial stability of a dental implant. But simulating the loading in masticatory mode can be an accurate assessment of the loading status of the implant. When applying FEA to the model, it is important to consider not only axial loads and horizontal forces (moment-inducing loads) but also a combined load (oblique occlusal force). Although the study of static and dynamic loads is performed according to the existing standards (ISO 14801, 2007), the modeling of excessive and impact loads in implant performance can be performed as an approach in the discussion of long-term stability.

In finite element modeling, the choice of element type depends on the geometric complexity of the model structure. The type of elements, the number of nodes per element, and the degrees of freedom of each node directly affect the accuracy and precision of the results. For more complex geometries, elements with higher orders such as 10-node tetrahedron are recommended.⁵⁸

Usually, the cancellous mandibular bone is considered as a continuum and uniform. Considering that the structure of cancellous bone is heterogeneous and has a complex geometry, the three-dimensional reconstruction of the mandibular bone based on micro-CT scans seems to give a more accurate model.⁹⁴

Several assumptions were made in the development of the finite element models in the studies reviewed. For example, the model components are homogeneous and isotropic and have linear elastic properties. In several studies, the thickness of the applied cement layer was ignored. In addition, the bone-implant interface region is generally assumed to be fully osseointegrated, which does not necessarily correspond to clinical conditions. Despite all the advantages of using FEM to evaluate dental implants, studies do not consider the physiology of bone as an important factor in modeling. As the bone heals after implant placement, the environment surrounding the implant changes. Therefore, some studies have considered different stages of osseointegration.²⁸ Because bone density differs between men and women, the validity of modeling must be categorized by gender.⁹⁵

In reviewed studies, the Von Mises stress criterion is often used to discuss the quality of stress distribution in the structures. Criteria such as Goodman are also used to study the fatigue behavior of structures. The choice of failure criterion is one of the most important issues when analyzing the results of FEM. Depending on the nature of the question, consideration of other failure criteria such as strain energy density may be helpful in modeling implants and bone remodeling.⁸⁹

In most of the studies, the focus of the investigation was on the implant, whereas the presence of other components and the diversity of their material and geometry may affect the overall distribution of stress in the bone and implant complex and may impact long-term stability. Given the differences in modeling and case studies, it was pointed out that each model consists of several parts. For example, some of the modeling studies have investigated one-piece implants,³⁹ while others have investigated implants that contain some components such as abutment, abutment screw, crown, and implant, as shown in Figure 3.

None of the studies reviewed discuss how much the number of components in a model affects the accuracy of the responses. The physical parameters involved in the design of each component, the material of each part, and their effects on the long-term stability of the implant may be the subject of case studies. New methods such as sensitivity analysis can be used to accurately determine the effects of the individual components.⁵⁷

In the studies reviewed, the diversity of modeling in terms of the number of components of the model and the subject matter of each study has led to different outcomes in the discussion of the long-term stability of dental implants, making it difficult to compare the results. Due to the breadth of the discussion, there is no consistent trend in the studies examined regarding the long-term stability of dental implants.

In the reviewed studies, there is little literature that deals with the statistical analysis of dental implants. Moreover, the studies in this field have a limited sample size and more attention has been paid to modeling aspects such as the number of fatigue cycles, loading devices, loading variables. Obviously, this is a matter of selecting an appropriate sample size depending on the problem variables. For example, implant geometry and mechanical and physical properties, and the simultaneous effect of these variables need many case studies that require accurate statistical analysis to investigate the significance of the differences.⁵⁷ The method of sensitivity and reliability analysis is recommended as a new approach to evaluating the long-term performance of dental implants, which is less common in the reviewed studies. In other words, there is a way to change the inputs of a statistical model in an organized manner that can predict more realistic effects of these changes on the output of the model. Design sensitivity analysis plays an important role in inverse studies and identification as well as numerical optimization and reliability analysis. The main purpose of sensitivity analysis is to inform about the significance of the input parameters.⁹⁰

The accuracy of the computational results of FEM depends on several factors, such as material properties, boundary conditions, bone-implant interface conditions, and modeling precision. The finite element models presented in previous studies always represent an approximation of the clinical condition. Therefore, laboratory and clinical tests are always required to evaluate the agreement of the results with the model. As can be seen in Table 1, of the studies conducted, fewer experimental tests were performed to validate the data obtained from FEM. A few experimental tests were performed based on ISO 14801,¹⁷ where the implant is placed in a metal fixator and not in the bone. Importantly, the exact level of stress that triggers biological responses such as bone resorption and remodeling is not fully known.⁶ Therefore, loading data obtained from finite element analysis must be compared with data from clinical studies. In vivo tests can be used to evaluate dental implants over time.

One of the methods used in engineering to validate the results of finite element analysis is the photoelastic test. In this method, by placing the dental implant in a transparent block made of resin, a load is applied, and light radiation creates a colored contour in the interface areas of the implant and the holder. By interpreting the colors and the relevant calculations, the amount and pattern of stress distribution can be obtained. This method has been used in only one study.⁵⁷

Recently, another solution has been proposed to increase the long-term stability of dental implants based on the use of porous implants. By reducing the effects of the mismatch between bone and implant hardness, more adaptive biomechanical properties are created compared to conventional screws. The size, morphology, and porosity of the medium that cause bone ingrowth directly affect biological adaptability. This leads to an overall mechanical interlock, resulting in higher reliability of the bone-implant complex.⁹⁶ In addition, more regular pores exhibited a higher elastic modulus than pores in a random arrangement.⁹⁷ In addition, the porous structure within a certain range of porosity and pore size can create strong adhesions between bone and implants, resulting in better ossification.⁹⁸

CONCLUSION

This study could be a starting point for a more detailed investigation of the fatigue life of dental implants. In general, finite element models have their limitations because the mechanical properties and nonlinear behavior of biological tissues cannot be accurately and exactly modeled. The evaluation of implant stability is difficult because it depends on several factors, such as the mechanical design and the topography and the geometry of the implant, bone quality, applied loads, and the implant-bone interface. Also, a common problem with fatigue testing is that it must be performed in multidimension, over a long period of time which makes it very costly. The use of porous implants can be an effective way to improve the bone-implant interaction and increase the biological adaptivity of dental implants. New methods such as geometry optimization based on sensitivity analysis and dental implant reliability can be used for optimal implant designs at a reasonable time and cost.