Evaluating the performance of random forest and iterative random forest based methods when applied to gene expression data

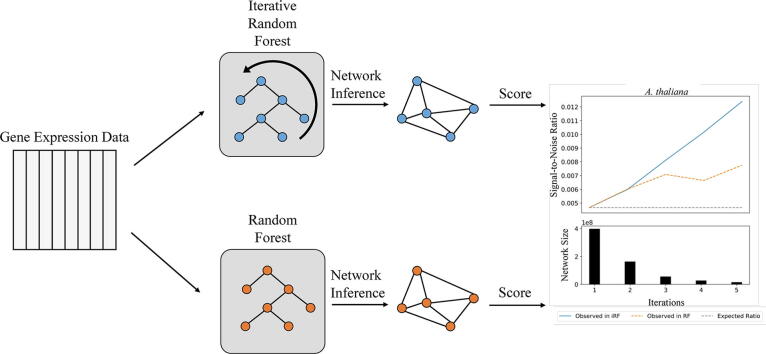
Graphical abstract

Abstract

Gene-to-gene networks, such as Gene Regulatory Networks (GRN) and Predictive Expression Networks (PEN) capture relationships between genes and are beneficial for use in downstream biological analyses. There exists multiple network inference tools to produce these gene-to-gene networks from matrices of gene expression data. Random Forest-Leave One Out Prediction (RF-LOOP) is a method that has been shown to be efficient at producing these gene-to-gene networks, frequently known as GEne Network Inference with Ensemble of trees (GENIE3). Random Forest can be replaced in this process by iterative Random Forest (iRF), which performs variable selection and boosting. Here we validate that iterative Random Forest-Leave One Out Prediction (iRF-LOOP) produces higher quality networks than GENIE3 (RF-LOOP). We use both synthetic and empirical networks from the Dialogue for Reverse Engineering Assessment and Methods (DREAM) Challenges by Sage Bionetworks, as well as two additional empirical networks created from Arabidopsis thaliana and Populus trichocarpa expression data.

1. Introduction

Gene Regulatory Networks (GRNs) are crucial to understanding biological systems since they show the regulatory relationships between transcription factors and target genes. A GRN can be predicted from an input gene expression matrix (a data set with samples as rows and genes as columns measuring expression levels of each gene) using a variety of algorithms such as Weight Gene Correlation Network Analysis (WGCNA) [1] and BackWard Elimination Random Forest (BWERF) [2]. A conceptual expansion on the GRN is the Predictive Expression Network (PEN). While typical GRNs tend to be focused on transcription factor-to-gene relationships, PENs can capture expression-based relationships beyond regulation by transcription factors. Unlike GRNs, algorithms that produce PENs utilize all genes in the input data, creating an all genes-to-all other genes network. This all-to-all network provides additional information not found in a standard GRN, since these non-transcription factor edges can reveal additional biological relationships, such as genes interacting together in a biosynthetic pathway, or genes that encode proteins that form larger complexes. However, due to the increased number of input genes involved, inferring a PEN can be computationally expensive and challenging to implement on larger datasets. The most common approach, typified by WGCNA, is to calculate a pairwise correlation between all genes and then threshold the results. While this is computationally efficient for large datasets, the simplistic model only accurately reflects relationships where one gene influences another gene in a linear manner and absent of influence from any other genes. In reality, it is possible that a gene’s expression is jointly influenced by many other genes, possibly in a non-linear manner, and a better model should account for this.

Random Forest (RF) [3] is a supervised learner that makes few assumptions about the relationships between variables and is able to capture complex interactions between variables that are common in biological systems. The core of RF is the binary decision tree, which progressively splits the samples into two child nodes to maximize the variance explained of the dependent variable. Individual decision trees tend to over-fit the data, so RF counters this by using an ensemble of trees (a forest) where each tree uses a random sample of the data (rows), while only a subset of all features (columns) is assessed for each node split. RF is explainable, in that features are scored according to how influential they are in generating the trees in the forest, thus producing a ranked list of feature importance for predicting the dependent variable.

RF provides a good base learner for the purposes of gene regulatory inference. One may fit an RF model to predict the expression of a target gene by using the expression of all other genes across all samples as model features. The result is a bipartite network with directional edges between predictor genes (features) with high importance in the model, and the regulatory target gene. This approach can be extended with RF-Leave One Out Prediction (RF-LOOP), which performs this process for every gene in the gene expression matrix. If there are n genes in the expression matrix then n RF models are produced. Each gene is used as the dependent variable once, resulting in n bipartite networks. When the bipartite networks from all n models are merged, it produces an all-to-all PEN. RF-subLOOP is a modification of RF-LOOP, in which the features used in each individual RF model are limited to a subset of all possible features (e.g. known transcription factors), while the dependent variables selected are the potential regulatory target genes. This produces a traditional GRN containing only TF-to-target edges.

Several implementations of RF-LOOP and RF-subLOOP exist, the best known being GEne Network Inference with Ensemble of trees (GENIE3) [4]. GENIE3 was the overall winner of the DREAM4 and DREAM5 competitions, proving the robustness of the RF-LOOP approach to inferring gene-to-gene connectivity based on expression data [4], [5].

Iterative Random Forest (iRF) [6] provides a potential improvement to the RF base learner used by GENIE3 and several other GRN inference methods. In iRF, a standard Random Forest is initially run where every feature is given equal weighting in the randomized feature sampling process. The feature importance scores from the forest are then used as weights in the feature sampling process in a new random forest. This process continues for a set number of iterations. At each iteration, some features may have their importance reduced to zero and are effectively eliminated from the model, while other features have their importance boosted. For expression network inference, iRF provides improvements that would not be achieved by simply increasing the number of trees in a single random forest, such as removing spurious edges from the network completely (when their importance is zero) and boosting important edges in the final edge ranking list. Furthermore, this iterative process also improves the robustness of downstream path analysis algorithms [6], such as Random Intersection Trees (RIT) [7], which determine sets of features that jointly affect the dependent variable. In the context of gene expression data, applying RIT to each iRF model has the potential to identify regulatory influences by sets of genes that form complex conditional relationships.

Here we compare the performance of RF and iRF in producing GRNs and PENs from gene expression data by comparing the networks resulting from using RF-LOOP (via GENIE3) or iRF-LOOP and iRF-subLOOP or RF-subLOOP (via GENIE3). Using both synthetic and experimental data, we find that iRF outperforms RF on various metrics, producing more accurate predictions, smaller networks with improved signal-to-noise ratio, and higher quality top ranked edges.

We have included an in depth analysis of the top ranked PEN edges produced by iRF-LOOP on Arabidopsis thaliana gene expression data as well as the top sets of interacting genes produced by RIT on the resulting iRF tree paths. This analysis shows that the predictive power available using iRF can reveal interactions beyond TF-driven interactions. Additionally, we have included an analysis comparing the resulting biological pathways in PENs produced by GENIE3 and iRF-LOOP on A. thaliana and Populus trichocarpa expression data. Overall, this study shows that iRF provides meaningful biological information that would not have been obtained using a RF based method.

2. Methods

In order to compare iRF-LOOP versus GENIE3, we used multiple synthetic datasets and two empirical datasets for evaluation. Synthetic datasets were provided by Sage Bionetworks in the form of their Dialogue for Reverse Engineering Assessment and Methods (DREAM) Challenges, in particular DREAM4 and DREAM5 challenges for inferring PENs and GRNs from population-scale expression data.

We also compare iRF-LOOP and GENIE3 in creating PENs from real gene expression data available for A. thaliana from 1001 Genomes [8], [9] and for P. trichocarpa from the NCBI SRA database [10]. The GRNs and PENs generated for each dataset were evaluated against a gold standard network, which is a known network of confirmed true positive and true negative edges expected in the inferred network.

The computational resource used to run both the HPC implementation of iRF-LOOP [11] and GENIE3 was Summit. Summit is a supercomputer at Oak Ridge Leadership Computing Facility (OLCF) located at Oak Ridge National Laboratory. Summit is an IBM system that contains 4,608 nodes, each with two POWER9 processors and six NVIDIA Tesla V100 GPUs. Each POWER9 processor contains 22 cores that contains 4 threads each for a total of 176 threads per node. Each node contains 512 GB of DDR4 memory.

2.1. RF-LOOP and iRF-LOOP

Both RF-LOOP and iRF-LOOP use an input matrix of features measured in a population of samples to produce all-to-all predictive networks. For example, for an input matrix of n gene expression features, RF-LOOP and iRF-LOOP will produce n models where the expression of $n-1$ genes are predicting the expression of the $i^{\mathit{th}}$ gene, and $i\in \{1\dots n\}$. The importance scores for the $i^{\mathit{th}}$ model determine the strength of the edges from the predictor genes to the $i^{\mathit{th}}$ dependent gene. However, importance scores across each of the n models are not comparable, so they must be normalized before they are merged into one final network. The network that results from applying RF-LOOP or iRF-LOOP to a gene expression matrix is a Predictive Expression network (PEN). We used five iterations as the default number of iterations for iRF-LOOP and iRF-subLOOP. The iterations occur within each individual iRF model, and remains the major difference between RF-LOOP and iRF-LOOP.

The latest version of GENIE3 [12] is used throughout this analysis as an implementation of RF-LOOP, in which the importance scores for each generated random forest are normalized by the total variance of the dependent variable (Y vector) for that forest. By contrast, in the High Performance Computing (HPC) implementation of iRF used for iRF-LOOP, the importance scores of each generated iterative random forest are normalized by the sum of the importance scores in that iRF model. This HPC version of iRF is parallelized across compute nodes and is capable of running large datasets of hundreds of thousands of features [11].

2.2. RF-subLOOP and iRF-subLOOP

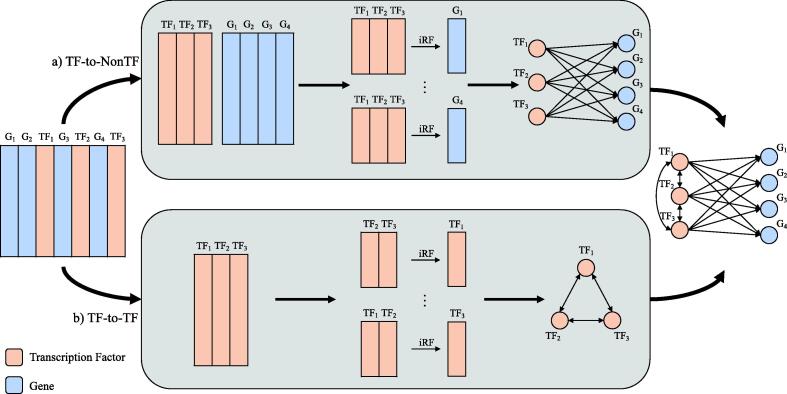
For cases in which a known list of regulatory genes exists, a transcription factor-to-all other genes network (GRN) can be created instead of an all-to-all network (PEN) using the RF-subLOOP algorithm. This requires subsetting the genes used as independent features to only the known regulatory genes [Fig. 1]. RF-subLOOP is implemented in the GENIE3 software by using the regulators argument, denoting the regulators to be used as predictors. This use is recommended by the authors due to the computational complexity of performing RF-LOOP for large datasets. Our iRF-LOOP implementation, however, does not have this same capability, so in order to implement the subLOOP functionality we used two separate types of iRF runs [Fig. 1]. The first run (a) separates all the feature columns into two matrices, one of all transcription factors and one of all other non-transcription factor genes. For every gene in the non-transcription factor matrix, the given gene is used as the dependent variable and the entire matrix of transcription factors is used as model features. This produces a TF-to-NonTF network. The second run (b) is similar to iRF-LOOP, but only the transcription factors are used as model features and as dependent variables. This produces a TF-to-TF network. Combining these two networks creates an overall TF-to-All network. This separation is crucial - if iRF-LOOP is run on all genes instead and the NonTF-to-All edges are simply dropped from the final network, the resulting paths of the trees would include these unwanted features and impact the final importance scores, making it incomparable to the GENIE3 implementation of RF-subLOOP.

Fig. 1.

This diagram shows the process of creating a transcription factor-to-all other genes GRN using the iRF-subLOOP algorithm. The overall algorithm contains two types of iRF runs. The first run type (a) creates a TF-to-NonTF network by partitioning the expression matrix into TF and NonTF parts. The TFs are then used as the features predicting each of the individual genes in the NonTF matrix. The second run type (b) creates a TF-to-TF network, similar to iRF-LOOP but instead of all genes being used as the input features, only the TFs are used. The resulting networks from (a) and (b) are merged to create a TF-to-All GRN.

2.3. Dream challenge datasets

The DREAM4 In Silico Size 100 Multifactorial sub challenge provides five small synthetic expression data sets of 100 samples and 100 genes to predict five networks [4]. GENIE3 and iRF-LOOP were used to create PENs from each of the DREAM4 expression datasets. For DREAM4 datasets, GENIE3 used 1000 trees for each RF model, while iRF-LOOP used 1000 trees for five iterations, yielding 5000 trees total for each iRF model. GENIE3 was also run with 5000 trees per RF model to ensure that any improvement shown in iRF-LOOP was due to the iterative process, not the increase in trees.

The DREAM5 Network Inference challenge provides one synthetic and two experimental expression data sets, of a varying number of samples and genes, to predict three networks [5]. Network 1, the synthetic dataset, contains 1,643 total genes and 805 samples. Networks 3 and 4, empirical datasets from E. coli and S. cerevisiae, contain 4,511 total genes and 805 samples and 5,950 total genes and 536 samples respectively. In each of these datasets, a subset of genes were flagged as known transcription factors (195, 334, and 333 transcription factors for networks 1, 3, and 4 respectively) and the expectation of the DREAM5 competition was that TF-to-target GRNs would be inferred for each dataset Therefore, RF-subLOOP (via GENIE3 with the known transcription factors used as regulators) and iRF-subLOOP were used to create GRNs from the DREAM5 expression datasets. For DREAM5, GENIE3 was run with 1000 trees only, while iRF-subLOOP was run with 1000 trees at each iteration for five iterations.

2.4. A. thaliana and P. trichocarpa PEN inference

We compared the performance of GENIE3 and iRF-LOOP for inferring PENs from real A. thaliana and P. trichocarpa gene expression data from leaf tissues. For A. thaliana, SRA data were obtained from Kawakatsu, et al. [8], totaling 6,584 FASTQ files from 728 samples and 38,186 genes. STAR [13] was used to map reads to the TAIR 10.1 A. thaliana reference genome. 15 samples and 186 corresponding runs were removed from the resulting raw counts matrix since the corresponding runs did not have a GSM sample ID and could not be tied to genotypes. Raw counts per gene were summed for each sample. Two more samples, GSM2135743 and GSM2136308, were removed due to low overall counts. Genes with less than 50 reads in at least 10% of samples were then removed, removing 18,199 genes. Raw counts were converted to gene length corrected Trimmed Mean of M-value (geTMM) [14]. The resulting X matrix for iRF-LOOP contained 711 samples and 19,987 genes. For P. trichocarpa, a similar process was applied. The RNAseq data was obtained from SRA (see Yates, et al. [15] Supplementary Table 11 for SR IDs). Reads were aligned with STAR, using the Populus trichocarpa v.3.0 reference genome [10], totaling 470 samples and 41,335 genes. Genes with less than 50 reads in 10% or more of the samples were removed. The rest were converted to geTMM, resulting in a genotype-transcript matrix with 15,205 genes across 470 samples. For both A. thaliana and P. trichocarpa, GENIE3 was run with 1000 trees and iRF-LOOP was run with 1000 trees at each iteration for five iterations.

2.5. Performance evaluation

The competing models were evaluated by scoring their ability to generate PENs and GRNs that contain correct (gold) edges using several metrics. For the synthetic DREAM4 challenges, gold standard networks are provided and, because these data are simulated, the gold edges contain 100% of the truth with total accuracy. The gold standard networks provided for the five DREAM4 datasets contained both true positives and true negatives, where 1 denoted a positive edge, and 0 denoted a negative edge, for all 9,900 possible PEN edges that can be inferred from all 100 unique input genes. The number of true edges (1’s) per network ranged from 176 to 249, meaning that each gold network is heavily imbalanced towards negative edges.

For the DREAM5 challenges, the gold standard networks and expression datasets are also provided with some caveats. These gold standard networks are not complete with 100% accuracy, and for the two empirical gold standard networks only the high confidence regulatory interactions are included. The DREAM5 datasets were considerably bigger than the DREAM4 challenge datasets. The synthetic dataset (DREAM5 Network 1) contained 1,643 unique genes and transcription factors. The gold network contains 178 unique transcription factors connecting to 1,565 target genes. Since the DREAM5 goal was to infer a GRN rather than a PEN, the gold network contains 278,392 TF-to-target edges rather than all-to-all edges, of which 4,012 are positives (1’s) and 274,380 are negatives (0’s). The empirical E. coli gold network (DREAM5 Network 3) contains 152,280 edges connecting 141 unique transcription factors to 1,081 target genes. 2,066 of these edges are positives and 150,214 of these edges are negatives. The positive edges only include interactions in which there existed ”strong evidence” in RegulonDB [16], [5]. The empirical S. cerevisiae gold network (DREAM5 Network 4) contained 227,202 edges connecting 114 transcription factors to 1,994 target genes. 3,940 of these edges are positives and 223,262 of these edges are negatives. The positive edges are based on an analysis of ChIP data and TF binding motifs with a stringent threshold to only consider edges with high confidence [17], [18], [5].

For evaluating the A. thaliana and P. trichocarpa PENs, we assembled gold standard networks using only verified true positive edges of known TF-to-gene and gene-to-gene relationships. The gold standard network for A. thaliana was manually constructed using two different sets of edges: a literature curated transcription factor to target network [19] and a gene to gene network constructed from AraCyc [20] reactions where two genes are connected if they share a common metabolite substrate or product. Using only the transcription factor to target edges as the gold network would neglect to score non-TF driven relationships that could be observed in a PEN inferred from all genes. Gold edges that linked to genes that were not in the original expression matrix were subsequently dropped from the gold network. The gold TF-to-gene network contained 231 unique transcription factors, 469 unique target genes for a total of 948 directed edges, and the gene to gene network contained 2,383 unique genes and 17,715 directed edges. Thus, the overall A. thaliana PEN gold standard network contained 18,663 directed edges between 2,864 unique genes. The gold network for P. trichocarpa was constructed similarly. The literature curated transcription to target network from A. thaliana was mapped to P. trichocarpa using orthologs, and the gene to gene network was constructed from PoplarCyc reactions via the Plant Metabolic Network [21] similar to A. thaliana. Again, edges contained only genes that were found in the input expression matrix. The transcription to target network contained 96 unique transcription factors, 163 unique target genes for a total of 379 directed edges. The gene to gene network contained 1505 unique genes and 8889 directed edges. The overall P. trichocarpa PEN gold standard network contained 9268 directed edges for 1690 unique genes.

It is worth noting that these real-world gold standard networks are incomplete since they do not contain any true negative edges, are missing many known non-metabolic and non-TF driven relationships, are missing hitherto unknown biological relationships that may indeed be evident in the input data, and probably contain several biologically false positive relationships.

Sage Bionetworks provides scoring methods for both DREAM4 (as a python package) and DREAM5 (as a MATLAB script) that calculates the Area Under the Precision Recall curve (AUPR), the Area Under the Receiver Operator Characteristic curve (AUROC), and p-values for AUPR and AUROC. The p-values represent the probability that the AUPR or AUROC that is achieved is better than a random permutation of the network edges that have been submitted to the official DREAM challenge. For DREAM4, all of the 9,900 network edges are used in the random permutation for each of the five networks, but in DREAM5 only the network edges of the submitted challenge networks are used. In the final scoring for DREAM4 all submitted edges are scored. For DREAM5 only the top ranked 100,000 edges are scored and the remaining edges are assumed to occur at random.

In order to summarize scores across all five DREAM4 networks, Sage Bionetworks provides an overall score, defined as

$$\mathit{overall}\mathit{score}=-0.5{\log }_{10}(p_1{p}_2)$$

where $p_1$ is the geometric mean of the five AUPRC p-values and $p_2$ is the geometric mean of the five AUROC p-values. The submissions to the official DREAM4 challenge are ranked based on the highest overall score. Similarly, for the DREAM5 networks, the overall score is defined as

$$\mathit{AUPR}\mathit{score}=\frac{1}{3}{\displaystyle \sum _{i=1}^3}-{\mathit{log}}_{10}(p_{\mathit{AUPR},i})$$

$$\mathit{AUROC}\mathit{score}=\frac{1}{3}{\displaystyle \sum _{i=1}^3}-{\mathit{log}}_{10}(p_{\mathit{AUROC},i})$$

$$\mathit{overall}\mathit{score}=\frac{\mathit{AUPR}\mathit{score}+\mathit{AUROC}\mathit{score}}{2}$$

where $p_{\mathit{AUPR},i}$ is the AUPR p-value for network i, and $p_{\mathit{AUROC},i}$ is the AUROC p-value for network i. Like DREAM4, the submissions to the official DREAM5 challenge are ranked based on the highest overall score. Although Sage Bionetworks has provided leaderboards for these two challenges, GENIE3 was rerun on these data sets to verify results with the updated codebase.

Implementing AUPR and AUROC comes with some caveats. AUPR and AUROC will penalize a false positive edge that does not appear in the gold standard network, but it is possible for edges to be ranked highly due to an uncharacterized yet true relationship between the two genes that is present in the dataset at hand. Since a 100% complete gold standard network is not possible in real empirical datasets, AUPR and AUROC are not ideal to use in these scenarios. Additionally, precision and recall at threshold k do not take into consideration the ranking of each edge. For example, it is possible at threshold k two networks can have the same number of true edges and false edges corresponding to the same precision and recall values, but the rank order of these edges can be wildly different. In addition to calculating the AUPR and AUROC of the empirical datasets, normalized Discounted Cumulative Gain (nDCG) [22] was calculated for every edge from one to k, where k is the number of true positive values in the gold standard network. This is defined as follows:

$${\mathit{nDCG}}_{\mathit{network},k}=\frac{{\mathit{DCG}}_{\mathit{network},k}}{{\mathit{IDCG}}_{\mathit{gold}\mathit{standard},k}}$$

$${\mathit{DCG}}_{\mathit{network},k}={\displaystyle \sum _{i=1}^k}\frac{x}{{\log }_2(i+1)}$$

$$x=\left\{\begin{array}{cc}1\hfill & \text{if edge is a true positive}\hfill \\ 0\hfill & \text{if edge is a false positive}\hfill \end{array}\right)$$

$${\mathit{IDCG}}_{\mathit{gold}\mathit{standard},k}={\displaystyle \sum _{i=1}^k}\frac{1}{{\log }_2(i+1)}$$

Using nDCG accounts for how early the true positive edges are found. If a true positive edge is found at a higher rank in the network than another true positive edge, the higher rank edge boosts the score more than the lower ranked true positive edge. This yields a better score if the true positive edges are found earlier in the ranking versus spread out across the whole list. Usually, the resulting networks are large and are thresholded before use, thus capturing true positive edges earlier in the ranking is necessary to retain them after thresholding.

To emphasize the biological significance of iterative RF in network prediction, we included an analysis of two select biological pathways from AraCyc and PlantCyc for A. thaliana and P. trichocarpa respectively, produced by GENIE3 and iRF-LOOP.

2.6. Random Intersect Trees (RIT)

The algorithm RIT [7] works by mining the node-split pathways in the forests resulting from iRF to find sets of features that occur consecutively along the pathways more than expected by chance. This suggests that the model uses those features in conjunction with each other in a potentially non-linear manner. RIT is able to efficiently discover feature interactions of any order if their joint importance is high enough. We ran RIT on the resulting forests from the A. thaliana iRF-LOOP and identified a sample of highly prevalent sets of interacting genes.

3. Results and discussion

3.1. Replacing RF with iRF improves overall DREAM scores

For the synthetic DREAM4 overall score metric, iRF-LOOP using 1000 trees per iteration (40.521) outperformed RF-LOOP as implemented by either the original GENIE3 or by the updated GENIE3 code [Table 1]. This was the case whether GENIE3 was run with 1000 trees, or with 5000 trees to match the total number of trees produced by iRF-LOOP. This suggests that the addition of iterations of random forest improves the overall quality of PENs inferred from these datasets, and that the increase in overall score observed for iRF-LOOP is not simply due to the increase in overall number of trees from 1000 to 5000.

Table 1.

This table depicts the overall scores for the DREAM4 In Silico Size 100 Multifactorial and DREAM5 Network Inference networks using the DREAM scoring system. The iRF based algorithms outperform all three RF based algorithms. This table also shows that simply increasing the number of trees in an RF based model to match the total number of trees used in an iRF based model does not account for the overall score increase seen in iRF-LOOP. Raw AUPR and AUROC values as well as their p-values can be found in Supplementary Table A.4, Table A.5, Table A.6, Table A.7.

DREAM Challenge	Base Learner	Algorithm	Number of Trees Per Iteration	Overall Score
DREAM4	RF	GENIE3 (original)	1000	37.428
DREAM4	RF	GENIE3 (new)	1000	39.375
DREAM4	RF	GENIE3 (new)	5000	39.446
DREAM4	iRF	iRF-LOOP	1000	40.521
DREAM5	RF	GENIE3 (original)	1000	40.279
DREAM5	RF	GENIE3 (new)	1000	43.329
DREAM5	iRF	iRF-subLOOP	1000	65.466

The DREAM5 results showed a similar, but more dramatic improvement in the overall DREAM score metric when using iRF in place of RF for inferring GRNs with the subLOOP algorithm. iRF-subLOOP obtained a score over 50% greater than the best performing GENIE3 score [Table 1]. For synthetic Network 1 data, iRF-subLOOP produced a GRN with a p-value of 3.8e-269, while GENIE3 produced a GRN with a p-value of 6.1e-121 [Supplementary Table A.6, Table A.7]. This resulted in an overall AUPR score of 91.829 for iRF-subLOOP and 47.097 for GENIE3. However, for the empirical datasets (DREAM5 Network 3 and DREAM5 Network 4) the raw AUPR and AUROC values for GRNs generated by GENIE3 and iRF-subLOOP were highly similar [Supplementary Table A.4, Table A.5]. Thus the improvement of iRF-subLOOP over GENIE3 was primarily driven by the AUPR p-value component of the DREAM scoring metric for the synthetic DREAM5 Network 1 dataset.

3.2. iRF-LOOP on A. thaliana and P. trichocarpa Improves Early nDCG and AUnDCG

Since the DREAM scoring system does not adequately capture the rankings of the edges within the networks, applying nDCG to these DREAM networks and observing the changes over iterations may be more beneficial to determining whether iterations in random forests provides an improvement for all types of network prediction.

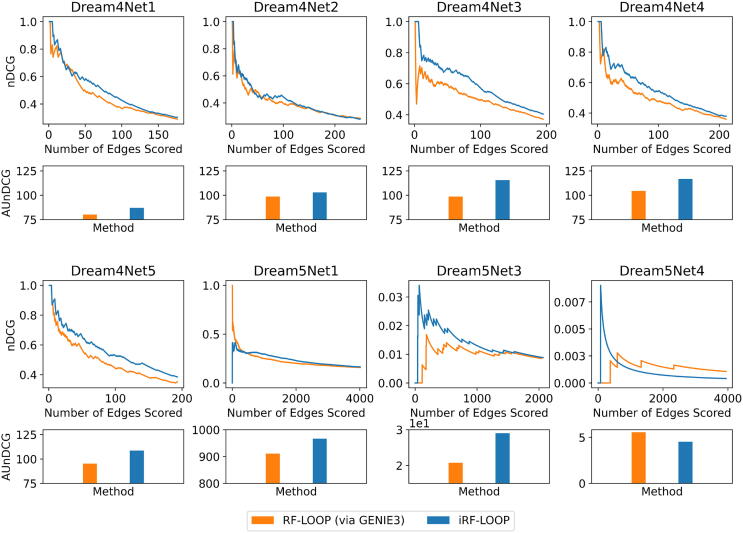
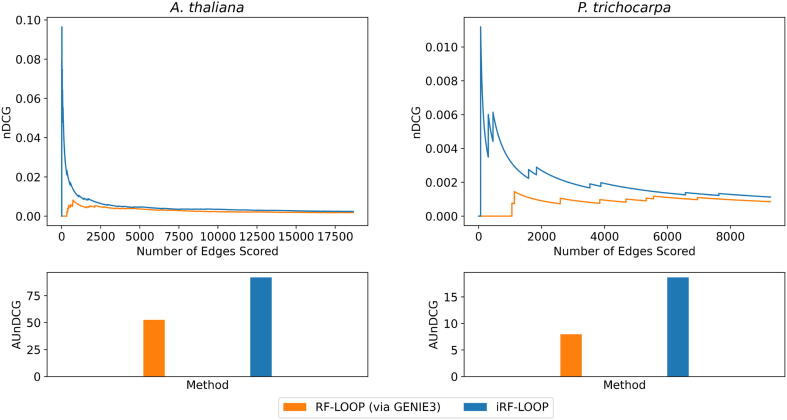
The nDCG scores for both GENIE3 and iRF-LOOP were calculated at every value of k from zero to the number of true positive values in the gold standard network, 18,663 for A. thaliana and 9,268 for P. trichocarpa. For the DREAM4 networks, this ranges from 176 to 249 edges. For the DREAM5 networks, this ranges from 2,066 to 4,012 edges. When we scored the DREAM4 and DREAM5 networks with nDCG, we found that the AUnDCG was greater in iRF-LOOP than GENIE3 for all expression networks except for DREAM5 Network 4 [Supplemental Fig. A.7]. For A. thaliana, iRF-LOOP obtained an AUnDCG of 91.897, which is a 1.75-fold increase over GENIE3’s AUnDCG of 52.694 [Fig. 2]. The improvement in AUnDCG when using iRF-LOOP instead of GENIE3 was even more pronounced in the P. trichocarpa networks where iRF-LOOP scored a 18.672, a 2.5-fold increase over GENIE3. Thus, iRF-LOOP is more likely to rank true positive edges more highly than GENIE3. Furthermore, iRF-LOOP tends to have a higher early nDCG, i.e., the nDCG for the higher ranked edges of the network, than GENIE3.

Fig. A.7.

This figure depicts the nDCG scores for all of the DREAM4 and DREAM5 networks for both GENIE3 and iRF-LOOP as the number of edges scored, k, increases. The maximum k for each network depends on the number of true positive values in the corresponding gold standard network, ranging from 176 to 249 edges for the DREAM4 networks and 2,066 to 4,012 edges for the DREAM5 networks. For all networks except the DREAM5 Network 4, the AUnDCG for iRF-LOOP is higher than the AUnDCG for GENIE3, this suggests that iRF-LOOP outperforms GENIE3.

Fig. 2.

This figure depicts the nDCG scores for both A. thaliana and P. trichocarpa for both GENIE3 and iRF-LOOP as k, the number of edges scored, increases. The maximum k for each organism is equal to the size of the gold standard network. For both A. thaliana and P. trichocarpa, the early nDCG is higher in iRF-LOOP than GENIE3, and the overall AUnDCG for both organisms is also higher in the iRF based algorithm. For A. thaliana, AUnDCG for iRF-LOOP and GENIE3 were 91.897 and 52.694 respectively. For P. trichocarpa, AUnDCG for iRF-LOOP and GENIE3 were 18.672 and 7.972 respectively. This suggests that iRF-LOOP outperforms GENIE3.

3.3. iRF boosts important edges and improves feature selection

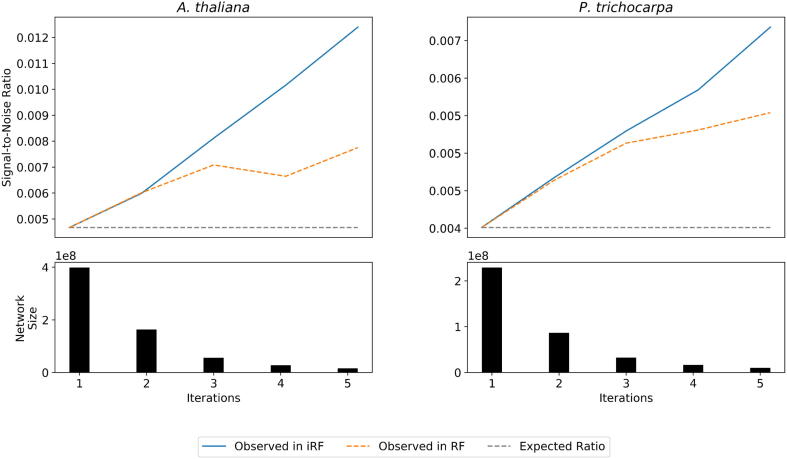
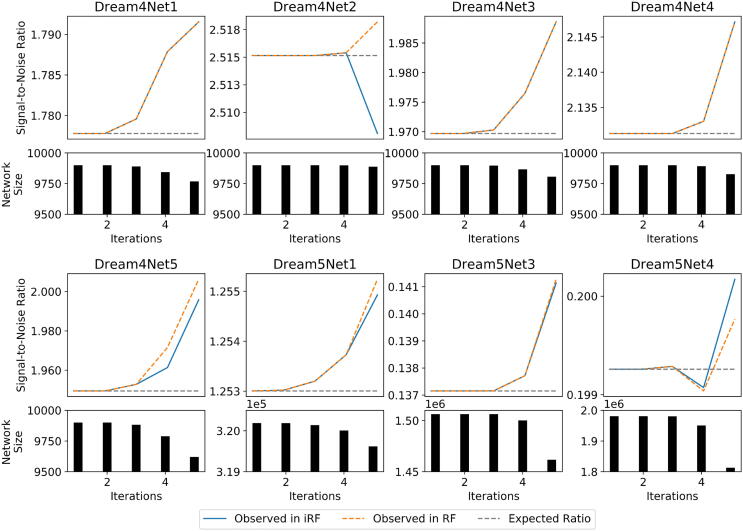
Adding iterations to RF-LOOP provides two major advantages. First is feature selection, which comes from the feature culling performed at each iteration. In Fig. 3, the A. thaliana and P. trichocarpa networks both see a twofold reduction in the resulting network sizes at each iteration as certain genes are deemed to have zero importance in the model predicting the target gene. The networks from the DREAM4 and DREAM5 challenges also see a decrease in network sizes, but with the smaller data sets used in this challenge this effect is not as extreme [Supplementary Fig. A.8]. With this decrease in network size comes an increase in the signal-to-noise ratio, where the percentage of edges kept that are true positive edges increases over iterations. This culling of noisy edges is a form of unsupervised thresholding. When comparing the effectiveness of this unsupervised thresholding in iRF-LOOP to manually removing the same number of lowest ranked edges from the GENIE3 network, it performs best in larger networks and data sets, such as the A. thaliana and P. trichocarpa networks [Fig. 3].

Fig. 3.

In this figure, the blue line depicts the truly observed signal-to-noise ratio for each network as the number of iterations in iRF increases. As the iterations increase, a number of edges are dropped from consideration due to their importance scores equaling zero. To confirm that the improvement in signal-to-noise ratio is not due to simply thresholding the networks, the RF network is thresholded to match the network size of the iRF network at each iteration and is depicted as the orange dashed line. For both A. thaliana and P. trichocarpa, the observed signal-to-noise ratio in iRF is greater than both what is expected from random and if the RF network is simply thresholded. This shows that the unsupervised thresholding from iRF provides an improvement over a simple manual thresholding.

Fig. A.8.

This figure depicts the true signal-to-noise ratio for each iteration of iRF-LOOP for the DREAM challenges as the blue line. The orange line is the corresponding GENIE3 network thresholded to match the same number of edges as the iRF-LOOP network, used to confirm that the unsupervised thresholding contributes to the improvement in signal-to-noise ratio. Unlike the larger empirical networks shown in Fig. 3, these DREAM networks are too small to make a considerable difference when thresholdi.ng the networks.

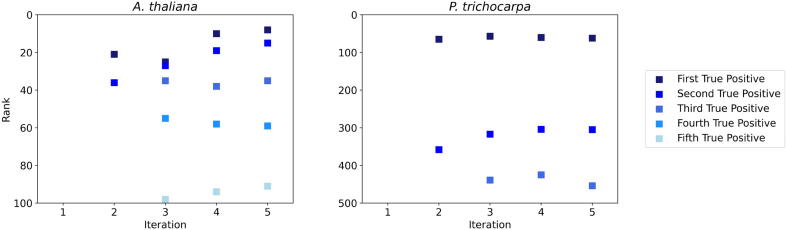
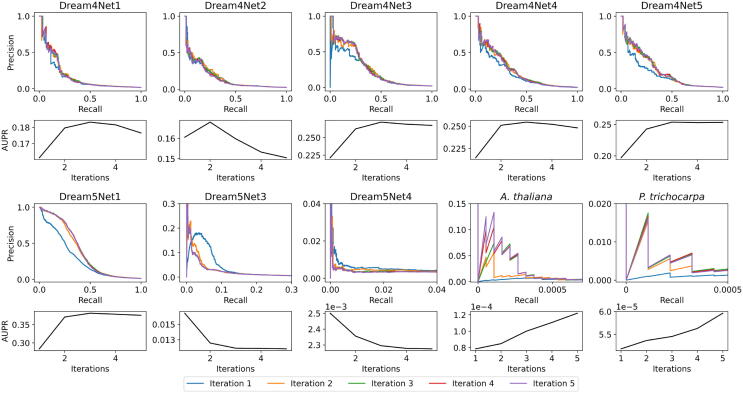
The second major advantage of the iterative approach to RF is the boosting of important edges after each iteration. Since resulting networks are typically thresholded for use, it is imperative that true positive edges are ranked higher in the network than false edges. In Fig. 4, the true positive edges within the first 100 and 500 ranked edges and their ranking per iteration are shown for A. thaliana and P. trichocarpa respectively (where a rank of 1 is the best possible). The improvement in ranking of true positive edges can clearly be seen for A. thaliana. There are no true positives in the first 100 edges after one iteration and the first true positive edge was not found until rank 325. After the second iteration, two true positives were found in the top 100 ranks, and as iterations increase these true positives shift up in the rankings and more true positives move into the top 100 edges. A similar pattern can be observed in P. trichocarpa, where there are no true positives in the first 500 edges after one iteration and the first true positive edge was found at rank 965. As more iterations are added, the true positives shift up the ranks, boosting the true edges to the higher rankings in the final network. This boosting of important edges can also be seen in the Precision-Recall curves, since the AUPR values increase over iterations for the A. thaliana and P. trichocarpa networks [Supplementary Fig. A.9]. While this effect is not as obvious for some of the smaller networks in the DREAM challenges, there is an overall trend of AUPR increasing as the number of iterations increases [Supplementary Fig. A.9].

Fig. 4.

This figure shows the true positive edges, depicted as a square, for the top ranked 100 edges and 500 edges across each iteration for A. thaliana and P. trichocarpa respectively. For iteration 1 in A. thaliana, the first true positive edge is not discovered until rank 325. For iteration 1 in P. trichocarpa, the first true positive edge is not discovered until rank 965. The shifting of the true positive edges towards earlier rankings indicates the true positive edges moving up in the ranks of the final edge list and are more likely to be retained when thresholded.

Fig. A.9.

This figure depicts the Precision-Recall curves and the corresponding AUPR values for each iteration in the networks used in this analysis. For many of the synthetic DREAM networks, the improvement in AUPR plateaus after 2 or 3 iterations, which may be due to the size of the networks. This may suggests that iterations improve RF, but larger networks are needed to verify this. The Precision-Recall curves themselves show minimal improvement after the second iteration for the empirical networks. However, the AUPR value increases as the number of iterations increases, even after the second iteration. Thus this shows that the addition of iterations to RF improves the AUPR values for the two empirical data sets used in this study.

3.4. PEN edges and RIT sets capture complex biological relationships in A. thaliana

Table 2 contains the top five ranked edges from the iRF-LOOP network on A. thaliana. None of these five edges are found in the gold standard network. However, many of these edges describe a relationship that is not as simple as gene-to-gene or regulator-to-target. For example, third ranked edge show connections between extensin genes and are associated with functions in the cell wall [25]. The edges ranked second and fourth represent the relationship between two genes with two different directionalities, and both are involved in the Aminoacyl-tRNA biosynthesis pathway [24]. The edge ranked fifth shows connections between the two genes CruA (AT5G44120) and CruC (AT4G28520), which both contribute to hexamer formation via an intermediary gene CruB. In the pathway CruA regulates CruB which regulates CruC [26], [27]. Of the five top edges that were not found in the gold network, all five of these edges had some sort of biological relationship shown in the literature. It is apparent that not only do PENs capture regulatory information in a biological system, but also capture other complex biological relationships.

Table 2.

This table depicts the top five ranked edges from the PEN created using iRF-LOOP on A. thaliana expression data. None of the edges were true positive edges in the gold standard network, but have some existing biological relationship. This table shows that PENs produced with iRF-LOOP capture relationships beyond simple gene regulation.

Rank	Impor-tance Score	Start Gene – End Gene ID	Start Gene – End Gene Function	Relationship
1	0.970	AT5G05430 — AT5G05420	RNA-binding protein — FKBP-like peptidyl-prolyl cis–trans isomerase family protein	Endosperm specific genes [23]
2	0.962	ArthCt101 — ArthCt092	Transfer RNA — Transfer RNA	Noncoding transfer RNAs, both in Aminoacyl-tRNA biosynthesis pathway [24]
3	0.959	AT3G28550 — AT1G23720	Proline rich extensin like family protein — Proline rich extensin like family protein	EXT genes in cell wall [25]
4	0.949	ArthCt092 — ArthCt101	Transfer RNA — Transfer RNA	Noncoding transfer RNAs, both in Aminoacyl-tRNA biosynthesis pathway [24]
5	0.941	AT5G44120 — AT4G28520	RmlC-like cupins superfamily protein — Cruciferin 3	Seed storage proteins that are down and up regulated together, both contribute to hexamer formation [26], [27]

Table 3 contains a sample of three highly prevalent sets from the RIT analysis on the resulting trees from the iRF-LOOP A. thaliana run. These three sets were chosen based on the three highest prevalence scores, which is dependent on the target gene and thus not comparable across iRF models. Duplicate sets were removed. None of the three sets existed as edges in the gold standard network. All three sets existed as edges in the iRF-LOOP network, both as Gene A to Gene B and Gene B to Gene A, though some had low importance scores. RIT was able to identify all three highly prevalent sets of genes as having some known biological relationship, such as existing in the same pathway or having the same classification. This shows that RIT combined with iRF-LOOP can yield new information that would not have been possible previously, and sheds light on higher order sets of interacting genes. Supplementary Table A.8, Table A.9 contains two samples of higher order sets, one of size four and one of size five, where known biological relationships were recovered among the sets.

Table 3.

This table depicts a sample of three highly prevalent sets determined using RIT on the resulting paths from iRF-LOOP on A. thaliana expression data. All three of these sets have been found to have some known biological relationship. None of these sets were found in the gold standard network, while some were found in the iRF-LOOP PEN as edges with low importance scores. This shows that RIT combined with iRF-LOOP can be used to discover or validate gene to gene relationships in sets.

Prev-alence	Gene ID	Function	Target	Target Function	Relation-ship
0.966	AT3G44630 – AT3G44400	Both disease resistance protein (TIR-NBS-LRR class) family	AT3G44480	Encodes a TIR-NB-LRR R-protein RPP1 that confers resistance to Peronospora parasitica	All three encode disease resistant proteins, regulation is linked in some experiments [28]
0.964	AT3G28550 – AT3G54590	Proline-rich extensin-like family protein – Hydroxy-proline-rich glycoprotein	AT3G54580	Proline-rich extensin-like family protein	EXT genes in cell wall [25]
0.957	AT3G44480 – AT3G44630	Both disease resistance protein (TIR-NBS-LRR class) family	AT3G44400	Disease resistance protein (TIR-NBS-LRR class) family	All three encode disease resistant proteins

3.5. Replacing RF with iRF captures more members of metabolic reaction pathways

To compare GENIE3 and iRF-LOOP on the A. thaliana and P. trichocarpa expression data in this section, the GENIE3 PEN is thresholded to match the size of the iRF-LOOP PEN which was automatically reduced in size due to the culling of edges of zero importance per iteration. For A. thaliana this is 15,719,197 edges and for P. trichocarpa this is 10,180,484 edges.

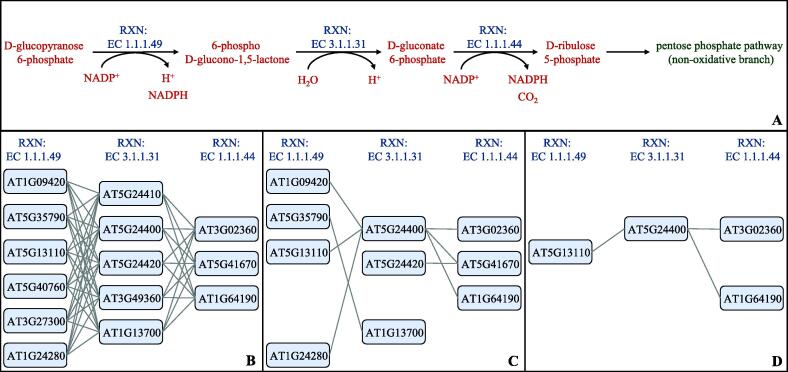
There are 1,996 unique RXN-to-RXN pathways found in the gold standard AraCyc gene-to-gene edges. 535 of these pathways were discovered using GENIE3 on the A. thaliana expression data, comprising 1,076 edges in the network. For iRF-LOOP 688 RXN-to-RXN pathways were discovered comprising 1,776 edges in the network. This increase shows that the true positive edges were elevated in the rankings. Additionally, the average percentage of edges discovered for each RXN-to-RXN pathway in GENIE3 was 8.279%, where the percentage in iRF-LOOP is 12.878%. Fig. 5 shows this improvement in edges discovered in a pathway in A. thaliana. The pentose phosphate pathway is shown in Fig. 5A, containing 2 RXN-to-RXN pathways, EC 1.1.1.49 to EC 3.1.1.31 and EC 3.1.1.31 to EC 1.1.1.44. Fig. 5B shows the gold edges expected in this pathway, and Fig. 5C shows the edges discovered using iRF-LOOP compared to Fig. 5D which shows the edges discovered using GENIE3. While not all edges from the gold standard pathway are discovered in iRF-LOOP, it is possible that iRF-LOOP is discovering the most important edges. Additionally, iRF-LOOP discovers more edges than GENIE3 does.

Fig. 5.

This figure depicts the compounds, RXNs, and genes included in the pentose phosphate pathway in A. thaliana, and the genes that are recovered by GENIE3 and iRF-LOOP. The resulting PEN from GENIE3 was thresholded to match the same size as the iRF-LOOP PEN. A) Steps in the pathway encompassing the three RXNs according to AraCyc. B) All of the possible edges between the known genes in neighboring steps in the pathway. C) The edges recovered by iRF-LOOP. D) The edges recovered by GENIE3.

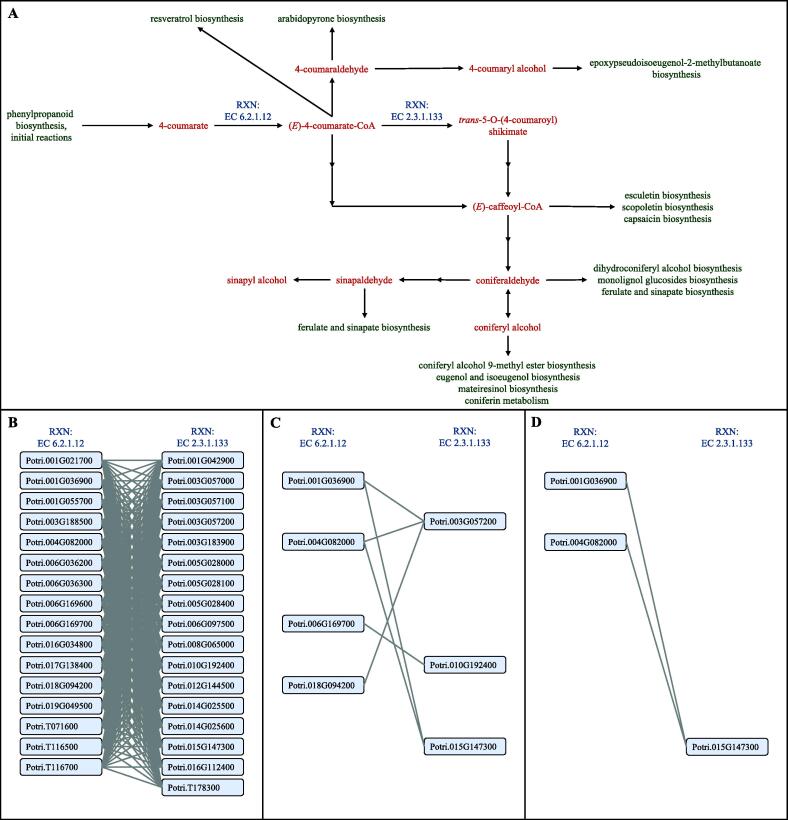
There are 1,075 unique RXN-to-RXN pathways found in the gold standard PlantCyc gene-to-gene edges used for the P. trichocarpa analysis. Similar to the A. thaliana pathways, GENIE3 discovered 244 RXN-to-RXN pathways using 523 edges, while iRF-LOOP discovered 269 RXN-to-RXN pathways using 625 edges, again showing the boosting of true positive edges. The average percentage of edges discovered for each pathway also increased from GENIE3 to iRF-LOOP, from 5.270% to 6.357%. Fig. 6 contains the Phenylpropanoid biosynthesis pathway, an important pathway used in bioenergy research. Since only a little over half of the total possible pathways were discovered using iRF-LOOP, Fig. 6B only shows the single RXN-to-RXN pathway discovered in iRF-LOOP, EC 6.2.1.12 to EC 2.3.1.133. Fig. 6C shows the edges discovered by iRF-LOOP and Fig. 6D shows the edges discovered by GENIE3. Again, not all edges are discovered in iRF-LOOP, but it is possible that only the most important edges are discovered, and it is clear that iRF-LOOP discovers more edges than GENIE3.

Fig. 6.

This figure depicts the compounds, and a selection of RXNs and genes that are included in the phenylpropanoid biosynthesis pathway in P. trichocarpa. This figure also depicts the genes that are recovered by GENIE3 and iRF-LOOP in the EC 6.2.1.12 and EC 2.3.1.133 RXNs within the phenylpropanoid biosynthesis pathway. For comparison, in this figure the GENIE3 PEN is thresholded to match the same network size as the PEN created by iRF-LOOP. A) The entire phenylpropanoid pathway in P. trichocarpa is shown with the two RXNs of interest shown in blue. B) All of the theoretically possible edges between the known genes associated with the two RXNs. C) The genes and edges recovered by iRF-LOOP. D) The genes and edges recovered by GENIE3.

4. Conclusion

The use of whole networks in biology is unwieldy, an all-to-all directed network of tens of thousands of genes quickly becomes hundreds of millions of edges. Typically either only the top k edges or top n percent of edges are selected to be used in further studies or computational analysis. The value to use for thresholding is often difficult to discern, the goal being capturing high quality edges and culling noise [29]. To determine whether to use a network created by one method over another, the chosen network must have the correct edges found higher in the ranking of all edges than the network not chosen. The better algorithm must boost the true edges up in the ranking so that they are retained after thresholding. Culling noisy and true negative edges from the network entirely helps to ameliorate the thresholding problem.

The A. thaliana and P. trichocarpa empirical networks were many orders of magnitude larger than the DREAM challenge networks, thus the effect of this unsupervised thresholding can be observed. At the end of each iteration in the empirical networks around half of the edges were dropped entirely from the network, removing noisy edges from the final network. When comparing the final network after five iterations of iRF to the network resulting from one iteration of RF, a higher number of total RXN pathways were discovered in the iRF network, as well as a higher percentage of the individual RXN pathways being discovered. This process of discovering pathways is comparable to nDCG, where iRF ranks the true positive edges higher in the network than RF.

PENs serve a different purpose than GRNs. GRNs focus on primarily regulatory relationships while PENs capture directional gene to gene relationships other than the direct regulation of one gene on another. RIT as applied to iRF tree paths can be used to create new layers in addition to PENs and GRNs and captures unique set relationships beyond gene to gene that are likely quite common in biological systems. PENs and other non-regulatory layers can provide expanded functional content for graph learning algorithms and other downstream applications such as Random Walk with Restart and other lines of evidence methods [30]. iRF can be used successfully in contexts beyond gene expression analysis. RF-LOOP tools such as GENIE3 have been a benchmark for other network inference problems, such as networks of transcriptomic and proteomic data [31]. iRF can be used beyond building networks, since RF has also shown to be effective in classification problems [32]. iRF contains a multitude of advantages that could replace the use of RF in biology and beyond.

Data availability

The A. thaliana and P. trichocarpa iRF-LOOP networks have been made available at https://doi.org/10.25983/1871691.

Funding

This work was supported by the Center for Bioenergy Innovation (CBI) and the Secure Ecosystem Engineering and Design (SEED) project. CBI is a U.S. Department of Energy Bioenergy Research Center supported by the Office of Biological and Environmental Research in the DOE Office of Science. The Secure Ecosystem Engineering and Design (SEED) (https://seed-sfa.ornl.gov/) project is funded by the Genomic Science Program of the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research (BER) as part of the Secure Biosystems Design Science Focus Area (SFA).

CRediT authorship contribution statement

Angelica M. Walker: Conceptualization, Investigation, Formal analysis, Visualization, Writing - original draft, Writing - review & editing. Ashley Cliff: Formal analysis, Software. Jonathon Romero: Formal analysis, Software. Manesh B. Shah: Data curation, Writing - review & editing. Piet Jones: Data curation, Writing - review & editing. Joao Gabriel Felipe Machado Gazolla: Data curation, Writing - review & editing. Daniel A Jacobson: Funding acquisition, Project administration, Supervision, Writing - review & editing. David Kainer: Conceptualization, Funding acquisition, Project administration, Supervision, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary figures and tables

Table A.4, Table A.5, Table A.6, Table A.7, Table A.8, Table A.9, Fig. A.7, Fig. A.8, Fig. A.9.

Table A.4.

This table contains the AUPR values for the networks within the DREAM4 and DREAM5 challenges.

DREAM Challenge	Base Learner	Algorithm	Number of Trees Per Iteration	Net 1	Net 2	Net 3	Net 4	Net 5
DREAM4	RF	GENIE3 (Official Scores)	1000	0.154	0.155	0.231	0.208	0.197
DREAM4	RF	GENIE3	1000	0.165	0.158	0.237	0.218	0.213
DREAM4	RF	GENIE3	5000	0.161	0.158	0.249	0.220	0.213
DREAM4	iRF	iRF-LOOP	1000	0.177	0.150	0.267	0.248	0.253
DREAM5	RF	GENIE3 (Official Scores)	1000	0.291	–	0.093	0.021	–
DREAM5	RF	GENIE3	1000	0.303	–	0.095	0.020	–
DREAM5	iRF	iRF-subLOOP	1000	0.387	–	0.070	0.020	–

Table A.5.

This table contains the AUROC values for the networks within the DREAM4 and DREAM5 challenges.

DREAM Challenge	Base Learner	Algorithm	Number of Trees Per Iteration	Net 1	Net 2	Net 3	Net 4	Net 5
DREAM4	RF	GENIE3 (Official Scores)	1000	0.745	0.733	0.775	0.791	0.798
DREAM4	RF	GENIE3	1000	0.755	0.738	0.786	0.802	0.801
DREAM4	RF	GENIE3	5000	0.758	0.739	0.784	0.800	0.805
DREAM4	iRF	iRF-LOOP	1000	0.743	0.711	0.775	0.794	0.792
DREAM5	RF	GENIE3 (Official Scores)	1000	0.815	–	0.617	0.518	–
DREAM5	RF	GENIE3	1000	0.816	–	0.617	0.516	–
DREAM5	iRF	iRF-subLOOP	1000	0.816	–	0.614	0.516	–

Table A.6.

This table contains the AUPR p-values for the networks within the DREAM4 and DREAM5 challenges.

DREAM Challenge	Base Lear-ner	Algorithm	Number of Trees Per Iteration	Net 1	Net 2	Net 3	Net 4	Net 5	P-Value
DREAM4	RF	GENIE3 (Official Scores)	1000	3.3e-34	7.9e-54	1.8e-54	5.5e-47	4.6e-44	1.0e-46
DREAM4	RF	GENIE3	1000	7.7e-37	3.5e-55	4.8e-56	1.3e-49	6.8e-48	4.1e-49
DREAM4	RF	GENIE3	5000	5.5e-36	4.8e-55	9.3e-57	5.7e-50	8.5e-48	4.1e-49
DREAM4	iRF	iRF-LOOP	1000	9.5e-40	1.5e-51	8.3e-64	5.6e-57	1.2e-57	6.1e-54
DREAM5	RF	GENIE3 (Official Scores)	1000	1.60e-104	–	5.15e-20	1.58e-01	–	41.295
DREAM5	RF	GENIE3	1000	6.18e-121	–	3.54e-21	2.34e-01	–	47.097
DREAM5	iRF	iRF-subLOOP	1000	3.81e-269	–	1.32e-07	6.473e-01	–	91.829

Table A.7.

This table contains the AUROC p-values for the networks within the DREAM4 and DREAM5 challenges.

DREAM Challenge	Base Lear-ner	Algorithm	Number of Trees Per Iteration	Net 1	Net 2	Net 3	Net 4	Net 5	P-Value
DREAM4	RF	GENIE3 (Official Scores)	1000	3.3e-18	1.1e-28	9.7e-34	6.7e-33	1.9e-34	1.4e-29
DREAM4	RF	GENIE3	1000	3.1e-19	7.1e-30	2.6e-36	5.2e-35	5.2e-35	4.4e-31
DREAM4	RF	GENIE3	5000	1.3e-19	4.1e-30	8.4e-36	1.2e-34	5.8e-36	3.1e-31
DREAM4	iRF	iRF-LOOP	1000	6.6e-18	3.0e-24	1.1e-33	1.3e-33	2.7e-33	1.5e-28
DREAM5	RF	GENIE3 (Official Scores)	1000	3.06e-106	–	5.00e-11	1.06e-02	–	39.263
DREAM5	RF	GENIE3	1000	1.19e-107	–	3.65e-11	4.78e-02	–	39.561
DREAM5	iRF	iRF-subLOOP	1000	6.39e-108	–	1.75e-09	4.40e-02	–	39.103

Table A.8.

This table depicts a sample fourth order gene set that were discovered using RIT on the resulting paths from iRF-LOOP on A. thaliana expression data. This set had a prevalence of 0.331. This set contains a mix of both known and unknown gene to gene relationships.

Gene ID	Function	Target	Target Function	Relationship
AT3G10040 – AT5G39890 – AT1G12805 – AT5G15120	Hypoxia Response Attenuator 1 (HRA1) – Plant Cysteine Oxidase 2 (PCO2), Hypoxia Response Unknown Protein 43 (HUP43) – Nucleotide binding protein – Plant Cysteine Oxidase 1 (PCO1), Hypoxia Response Unknown Protein 29 (HUP29)	AT3G27220	Hypoxia Response Unknown Protein 6 (HUP6)	HUP43, HUP29, and HUP6 are all Hypoxia – Responsive Unknown Proteins (HUPs). HRA1 interacts with RAP2.12, RAP2.12 binds to PCO1 promoters in the Hypoxia-Responsive Promoter Element regions, which includes HUP6. RAP2.12 also binds to HUP29 and HUP43 [33], [34], [35].

Table A.9.

This table depicts a sample fifth order gene set that were discovered using RIT on the resulting paths from iRF-LOOP on A. thaliana expression data. This set had a prevalence of 0.153. This set contains a mix of both known and unknown gene to gene relationships.

Gene ID	Function	Target	Target Function	Relation-ship
AT4G3860 – AT3G50370 – AT1G80070 – AT3G02260 – AT1G55860	Ubiquitin-Protein Ligase 3 (UPL3) – Hypothetical protein – Encodes a factor that influences pre-mRNA splicing and is required for embryonic development – Calossin-like protein required for polar auxin transport – Ubiquitin-Protein Ligase 1 (UPL1)	AT1G70320	Ubiquitin-Protein Ligase 2 (UPL2)	UPL1, UPL2, UPL3 are all ubiquitin protein ligases