Abstract

The pyrolysis of endothermic hydrocarbon fuel plays a vital role in regenerative cooling channels. Based on previous experiments and mechanism models of n-decane, and considering the impact of the secondary reaction at high conversion, the present work establishes a cracking reaction model of n-decane containing 16 species and 26 reactions. One-dimensional plug flow reactor simulation verifies that the model has high accuracy in predicting species distribution. The high-accuracy model is applied to the computational fluid dynamics (CFD) simulation of the supercritical cracking heat transfer, and compared with the results of a one-step global model as the chemistry model. The results show that the high-accuracy model is more accurate in terms of fuel conversion, temperature, and product distribution. Furthermore, the reasons for the difference of the two chemistry models in the CFD simulation are analyzed from the perspective of chemical kinetics. The new model generates more products of small molecules due to the consideration of secondary reactions. However, for the one-step model, it mainly cracked into large molecules even at high conversion. The product distribution affects the chemical endotherm and then the fuel temperature, which in turn affects the reaction rate and finally the conversion of the fuel. In addition, pyrolysis affects the properties of the fuel, which in turn affects the convective heat transfer. Among the several influencing factors of heat transfer, the correction factor of isobaric specific heat, which is the ratio of the specific heat of fluid to the average specific heat, can well reflect the changing trend of the convective heat transfer coefficient. The present work demonstrates the important role of the kinetic model in the simulation of the supercritical cracking heat transfer process, and the corresponding methods can be used in the design of regenerative cooling systems.
1. Introduction
The combustor of a supersonic aircraft has an extremely harsh thermal environment.1−4 The regenerative cooling method is one of the best cooling technologies for rescuing this problem.5,6 The coolant flows through cooling channels to cool the combustor walls before it is pumped into the combustion chamber.7,8 Endothermic hydrocarbon fuels with high density and heat sink capacity due to endothermic reactions of the fuels, such as JP-7, JP-8, JP-10, and RP-3, are applied as the primary coolant.9−11 Moreover, the endothermic cracking process of n-decane, as a representative component and model fuel,12 has attracted much attention from researchers.13,14 During the cooling process, fuels undergo heat transfer coupled with thermal cracking and turbulent flow in a supercritical pressure state (4 MPa or higher15). To accurately determine the supercritical cracking heat transfer performance of fuels in cooling channels, it is necessary to study the interaction of flow and chemical reactions.
Computational fluid dynamics (CFD) simulation is an effective tool to pore over this coupling process. To explore the impact of pyrolysis on heat transfer and flow characteristics, the chemical reaction mechanism is indispensable in CFD simulation. However, due to the limitation of the number of computations, most numerical simulation studies on the cracking process of hydrocarbon fuels including aviation kerosene, n-dodecane, and n-decane use global mechanism models, and the secondary reactions are not always considered in the existing literature.
Ward et al.16,17 developed a one-step global model of 19 species for n-decane pyrolysis based on proportional product distribution (PPD). This model was applied to numerous studies.18−26 Tao et al.24 used this model to study the effect of n-decane thermal cracking under supercritical conditions on heat transfer characteristics and flow resistance and suggested that cracking can enhance heat transfer and improve heat transfer deterioration. Feng et al.25 established a numerical model with the PPD chemical model to analyze the effect of turbulence on pyrolysis. Their result indicated that with increasing turbulence intensity, the radial distribution of conversion is more uniform. Lei et al.26 also applied this model to study the effect factors of convective heat transfer and then modified the Dittus–Boelter correlation, which is suitable for conversion less than 23% of rectangular tubes. According to the experimental measurements from Ward,16,17 Ruan et al. proposed a global pyrolytic reaction model with 18 species for n-decane,18 which was employed in CFD simulation.27 A differential global reaction (DGR) model proposed by Jiang et al.28 was implemented in CFD simulation to predict n-decane cracking coupled with heat transfer, flow, and wall thermal conduction. Wang et al.29 and Liu et al.30 pointed out that pressure has an effect on the pyrolysis of n-decane, so Wang29 developed a novel global model of 38 species with secondary reactions suitable for both low and high pressures. Jiao et al.31 proposed a model extrapolation method based on activated volume, which allows the kinetic model to be extrapolated to a wider range of pressure conditions. In addition, many researchers proposed the global reaction model for aviation fuel cracking. Jiang et al.32 developed a one-step model of 15 species for fuels HF-II with n-alkanes, isoalkanes, naphthenes, and aromatics. The corresponding CFD simulation shows that when the conversion is less than 25%, the simulation results are in good agreement with the experiment. A pyrolysis mechanism model of aviation kerosene RP-3 with two reactions proposed by Jiao et al.33 was used in CFD simulation to study the cracking effect on heat transfer in the different regions through two aspects including heat absorption and fuel properties.
The traditional global mechanism as a practical solution for CFD simulation does not require a large number of computations, while accurately predicting fuel thermal cracking behavior, heat transfer, and flow characteristics under mildly-cracked conditions of low conversion. There is a big deviation in the prediction of the flow field at high fuel conversion as a result of secondary reactions.13,14,17,34 To consider the impact of the secondary reactions in the framework of one global reaction, the DGR model29 was constructed for n-decane with the stoichiometric coefficients related to the conversion and pressure. Because the format of DGR is different from the commonly used mechanism, it is necessary to configure complex user-defined functions (UDFs) when implemented in CFD simulation. Therefore, some researchers used skeletal mechanisms in CFD applications to break the limitations that global mechanisms cannot be used for high fuel conversion. Xu et al.35 used a molecular kinetic model36,37 for aviation kerosene, including 18 species and 24 reactions in the numerical study of fuel cracking and heat transfer. Zhao et al.38 also utilized this cracking mechanism to study the pressure effect on fuel cracking, and the results indicated that the conversion of fuel is proportional to the pressure. Li et al.39 applied improved kinetics of the aviation kerosene HF-140 in a CFD model to the coupling mechanism of heat transfer and thermal cracking. The results pointed out that increasing heat flux leads to local heat transfer deterioration. However, when the framework mechanism model is applied to numerical simulations, there are still few studies to analyze the mechanism performance from the perspective of chemical kinetics. Therefore, it is necessary to develop a cracking mechanism model under high conversion and then apply it to numerical simulations to reveal the interaction between flow and chemical reaction.
The focus of the present work is to conduct a comprehensive study on the cracking heat transfer process of n-decane under supercritical pressure to reveal the interaction between flow and chemical reaction. Based on previous experimental data and mechanism models, a high-accuracy multi-step cracking reaction model is established and incorporated into a CFD model. Compared with the one-step model, the multi-step mechanism better describes the reaction flow process. Furthermore, the reasons for the difference in the convective heat transfer coefficient prediction of the two reaction models in the CFD simulation are analyzed from heat absorption capacity and thermophysical properties. Among the several influencing factors of heat transfer, the correction factor of isobaric specific heat can well reflect the changing trend of the convective heat transfer coefficient. The present work demonstrates the important role of the mechanism model in the simulation of the supercritical cracking heat transfer process, and provides guidance for the selection of the chemical reaction model in CFD simulation.
2. Chemical Kinetic Model
2.1. Model Construction
In previous work, Wang et al. proposed a descriptive chemical kinetic model for n-decane thermal cracking based on their experimental results of product distributions.41 The model contains one primary reaction and 21 secondary reactions to describe the product distributions from low to high conversion of n-decane. However, in the descriptive model, the non-aromatic main products with more than four carbons and the aromatic species are lumped as C5+ and CnH2n-6, respectively. Although the incomplete model cannot be used directly in CFD simulation, it provides a foundation to obtain a high-accuracy model suitable for a wide range of conditions. C5+ is mainly composed of olefins, paraffin, and a small number of cyclo-olefins. Aromatics are mainly benzene and toluene. The average molecular weight of C5+ and CnH2n-6 are 84.5 and 134 g/mol, respectively. Based on the molecular weight and the yield of the main products, the present work embodied C5+ as C6H12, namely 1-hexene, and embodied CnH2n-6 as C10H14, which is butylbenzene. The Benson group contribution method42 was adopted to calculate thermodynamic data of the species C10H14 and C6H12, and transport data were calculated from the critical parameters of the species.43 The property data of other species, mainly came from previous work.41 The detailed thermodynamic and transport data of species are provided in the Supporting information (SI). And then, according to the law of conservation of mass and the yield of the products, the primary reaction was obtained as follows
| 1 |
The corresponding structures to the species involved in the primary reaction are given in the Supporting information. The pre-exponential factor is 6.209 × 1015 s–1, and the activation energy is 59.35 kcal/mol. Table 1 shows the kinetic model of n-decane cracking. The kinetic parameters of partial secondary reactions come from the literature44−46 in Arrhenius form. Moreover, the pre-exponential factor and activation energy of some secondary reactions have been adjusted to improve the predictions of the model on species distribution of typical cracking products including methane, ethane, ethylene, propylene, benzene, and toluene-based on the simulation results of the Chemkin program.47 The adjusted reactions were labeled in Table 1. The present kinetic model, hereafter referred to as a multi-step model, was derived from the experimental results, it does not consider the coking process that should occur when the fuel temperature is above 700 °C.
Table 1. Kinetic Model for the Thermal Cracking of n-Decane.
| reaction | Ea (kcal/mol) | A (s–1) | source | |
|---|---|---|---|---|
| (1) |  |
59.35 | 6.21E + 15 | a |
| (2) |  |
65.21 | 4.65E + 13 | (17) |
| (3) | 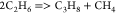 |
50.25 | 3.75E + 12 | a |
| (4) | 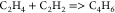 |
41.26 | (1.03E + 12)b | (17) |
| (5) |  |
60.43 | (7.08E + 13)b | (17) |
| (6) | 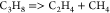 |
50.60 | 4.69E + 10 | (17) |
| (7) | 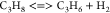 |
51.29 | 5.89E + 10 | (17) |
| (8) | 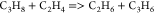 |
59.06 | (2.54E + 13)b | (41) |
| (9) | 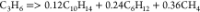 |
54.49 | 1.42E + 13 | a |
| (10) | 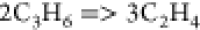 |
59.39 | 7.39E + 11 | (41) |
| (11) |  |
55.80 | 7.28E + 16 | a |
| (12) | 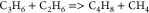 |
56.20 | (1.00E + 16)b | (41) |
| (13) |  |
59.64 | 7.00E + 12 | (17) |
| (14) | 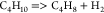 |
62.06 | 1.64E + 12 | (17) |
| (15) | 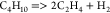 |
70.68 | 7.00E + 14 | (17) |
| (16) | 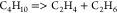 |
61.31 | 4.10E + 14 | a |
| (17) |  |
50.00 | 1.00E + 10 | (17) |
| (18) |  |
53.56 | 1.11E + 11 | a |
| (19) | 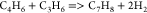 |
36.90 | 9.74E + 13b | a |
| (20) |  |
52.20 | (1.36E+15)b | (41) |
| (21) |  |
36.60 | 1.08E + 14b | a |
| (22) |  |
55.07 | 2.35E + 12 | a |
| (23) | 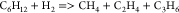 |
55.07 | 4.00E + 12 | a |
| (24) |  |
57.07 | 9.10E + 12 | a |
| (25) |  |
59.64 | 7.00E + 16 | a |
| (26) |  |
44.08 | 1.80E + 13 | a |
Kinetic parameters redressed by authors.
Units: m3/(mol ·s).
2.2. Model Validation
The model validation has been conducted against the pyrolysis experiments41 from low conversion to high conversion of n-decane in an electrical heating tube under a pressure of 4 MPa and temperature range of 480–740 °C. Table 2 shows the three experimental operating conditions from run1 to run3. According to the fuel temperature distribution of the heating tube obtained from the experiments as shown in Figure 1, a one-dimensional plug flow reactor (PFR) was used to simulate the reaction process using the Chemkin program.47
Table 2. Three Operation Conditions in PFR Experiments.
| |
test
section |
|||
|---|---|---|---|---|
| run no. | qm (g/s) | p (MPa) | L (m) | Tout (°C) |
| 1 | 1.00 | 4.0 | 0.55 | 719.6 |
| 2 | 1.00 | 4.0 | 0.50 | 728.7 |
| 3 | 1.00 | 4.0 | 0.46 | 740.1 |
Figure 1.

Fuel temperatures along the test tube reactor. The data from ref (41).
The experimental data used in this paper are from the work of Wang et al.41 Wang et al. carried out experiments in a two-stage fuel heating and cracking system. The detailed local chemical compositions and temperatures of the reactor tube were obtained by the electric heating tube method. The tube (2 mm inner diameter) was placed horizontally and heated by resistive heating. Consistent with the actual working conditions in the engine’s cooling channel, the pressure was set to 4.0 MPa, and the mass flow rate was 1.00 g/s. The pyrolysis experiments were conducted from low conversion to high conversion of n-decane. A detailed description of the experimental system can be found in the previous work of Lei et al.22 The fluid temperatures were measured using a thermocouple with an accuracy of ±0.5%. The relative uncertainty of the measured mass flow rate of the inlet fuel was less than 0.1%, and the uncertainties of the measured mass fraction for all species were less than 2.5%.
Figure 2 shows the comparisons between simulated and experimental yields of typical cracked products of n-decane along the test tube reactor. Methane, ethane, ethylene, and propylene are the gas-phase products with higher yields. Benzene and toluene are important products of the secondary reaction.41 Therefore, these six products were selected as components for comparison of the errors between simulations and experiments. As shown in Figure 2, the predicted yields of methane, ethane, and ethylene are consistent with the experimental values in a wide range. When the conversion exceeds 70%, the predicted values of methane and ethane are slightly lower than experiments and the maximum relative error is within 15%. The predicted values of ethylene under run1 and run2 conditions are only slightly lower than the experiment at 0.45–0.55 m. Under run3 conditions, when the cracking rate of n-decane is greater than 65%, the maximum relative error reaches 24%. The simulated values of propylene under the three operating conditions are all greater than the experimental values, indicating that the reaction kinetics related to the formation of propylene may be greatly overestimated. The yields of benzene and toluene obtained by the simulation are in good agreement with the experimental results under the operating conditions of run2 and run3, and both are higher than the experimental values under the operating conditions of run1. The deviation of some points should be ascribed to the uncertainty of the cracking experiment of n-decane and the analysis uncertainty of the complex components, and to the kinetic model with limited components and reactions.
Figure 2.
Simulation and experimental yields of typical products along the test tube reactor PFR. (a) Methane, (b) ethane, (c) ethylene, (d) propylene, (e) benzene, and (f) toluene (lines, simulated data; points, experimental data41).
The simulation results of fuel density and corresponding residence time are compared with experimental results as shown in Figure 3. As the heating distance increases, the fuel density drops from 95.2 to 17.0 kg/m3 in the experiment, while the simulated value decreases from 84.5 to 17.0 kg/m3. The relative error of 13% is obtained at the entrance, which should be attributed to estimating the thermophysical properties of the fuel with the ideal gas equation of state, which is different from the real fuel properties. The results show that the residence time increases rapidly at the beginning attributed to the relatively high density of the unreacted n-decane, and then the residence time gradually increases because the fuel density decreases sharply resulting from the heating, phase transition, and thermal cracking of n-decane. Finally, the maximum calculated fuel residence time of 0.075 s is obtained at the exit of run1. Overall, the developed multi-step kinetic model has high accuracy in predicting the typical product yields, density, and residence time. After the above validation from chemical kinetics, the developed model can be used in the following numerical simulations.
Figure 3.

Simulation and experimental results along the test tube reactor PFR. (a) Density and (b) residence time (lines, simulated data; points, experimental data41).
2.3. One-Step Kinetic Model for Comparison
The one-step global model proposed by Ward17 was used for comparative study in the following part of the numerical simulation. The one-step model with 19 species is expressed as follows
 |
2 |
Its pre-exponential factor is 1.6 × 1015 s–1, and the activation energy is 63 kcal/mol. The corresponding chemical names of the species involved in the model are included in the Supporting information. The one-step global model is widely used for low fuel conversion, so it can be used to compare the performance of the multi-step model and the one-step model in the front section of the reaction tube. Under the condition of high fuel conversion, the comparison of the two reaction models can illustrate the effect of the secondary reactions on fuel cracking.
3. CFD Model
3.1. Computational Model and Mesh
Based on experimental conditions,41 a two-dimensional axisymmetric model of the horizontal circular tube was established for the CFD simulation, as shown in Figure 4. The radius was 1 mm, and the length of the uniformly heated section was 550 mm. At the inlet, an adiabatic section of 150 mm was adopted with the purpose of the complete development of the flow. While at the outlet, an adiabatic section of 150 mm was also included to avoid the outflow boundary effects. There are detailed fuel conversion, fluid temperature, and species distribution along the electrical heating tube reactor for operation condition 1, so these conditions were selected as boundary conditions of numerical simulations. The mass flow rate was set as 1 g/s, operating pressure was 4 MPa, inlet temperature was 753 K, the wall heat flux was 640 kW/m2, and gravitational acceleration was 9.8 m/s2. To verify the reasonability of the two-dimensional axisymmetric model, three-dimensional simulations are performed for the same operating conditions, and the comparisons are given in Figures S1–S3 of the SI. The slight temperature difference demonstrate that the flow can be considered as axisymmetric under the present conditions.
Figure 4.
Schematic diagram of the physical model.
The mesh independence was first studied to ensure the accuracy of the mesh before conducting a detailed numerical study. The axial and radial direction mesh size was determined as 850 × 40. To ensure the wall y+ is less than 1, the first layer mesh height was 0.001 mm, and the mesh growth rate was 1.2.
3.2. Governing Equations and Solution Method
For the two-dimensional (2D) axisymmetric geometry, the equations for conservation of continuity, momentum, energy, and species could be written as follows48
| 3 |
 |
4 |
 |
5 |
| 6 |
| 7 |
where
| 8 |
And x is the axial coordinate, r is the radial coordinate, vx is the axial velocity and vr is the radial velocity, Sh is the energy source representing the heat of the chemical reaction, Yi is the mass fraction of species i, J⃗i is the diffusion flux of species i, and Ri is the net rate of production of species i.
The turbulence kinetic energy k and its rate of dissipation ε, were obtained from the following transport equations
| 9 |
 |
10 |
The turbulent viscosity μt was computed as follows
| 11 |
where Gk represents the generation of turbulence kinetic energy due to the average velocity gradients and Cμ, C1ε, C2ε, σk, and σε are constant, and they were 0.09, 1.44, 1.92, 1.0, and 1.3, respectively.
The steady-state conservation equations were solved using commercial software ANSYS Fluent 14.5. The standard k-ε model was employed to simulate the turbulent flow. The “enhanced wall treatment” was used for the near-wall treatment. The Eddy-dissipation concept (EDC) model was utilized to consider the interaction between turbulence and chemical reactions. The SIMPLEC algorithm was adopted for the coupling of pressure–velocity, and the second-order upwind scheme was utilized for the discretization of the convection terms. The convergence criterion was that the residuals of the continuity, energy, and other equations were less than 10–3, 10–6, and 10–5, respectively. The difference in mass flow rate between the inlet and outlet was less than 10–3, the outlet temperature and velocity were stable.
3.3. Fluid Properties
The thermophysical properties of the fuel are calculated based on the method of Li et al.49 The specific heat, and enthalpy and entropy of n-decane, and its cracked products were provided by thermodynamic data, as listed in Table S3. Table S4 lists the transport data of thermal conductivity and viscosity of species. According to Supertrapp,50 the linear interpolation of density with respect to temperature was obtained. Correspondingly, the density, specific heat, thermal conductivity, and viscosity of the mixture were calculated by the volume-weighted mixing law, mixing law, mass-weighted mixing law, and mass-weighted mixing law, respectively.
3.4. Parameter Definition for Analysis
The conversion of n-decane was defined as
| 12 |
where the mass fraction of n-decane YC10H22 was computed as follows
| 13 |
The definition of heat transfer coefficient h, Nusselt number Nu, Reynolds number Re, Prandtl number Pr, and correction factor for specific heat Cp,ave/Cp,f used to analyze the effect of convective heat transfer were as follows
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
where qw is the wall heat flux, Tw is the wall temperature, d is the diameter, λ is the thermal conductivity, ρ is the density, μ is the dynamic viscosity, Cp,f is the specific heat of fluid, Cp,ave is the average specific heat, Hw is the enthalpy of the wall temperature, and Hf is the enthalpy of the fluid temperature. Fluid temperature Tf was computed as follows
| 19 |
The total heat absorbed by fuel Qtotal consists of sensible heat sink and chemical heat absorption.51 The total heat absorption is calculated from the difference between the absolute enthalpy of the fuel at the inlet of the tube (Habs,inlet) and the absolute enthalpy of the mixture at any tube length l (Habs,l),37,41 as shown by eq 20
| 20 |
where Habs,inlet is the sum of the formation enthalpy of n-decane and the sensible enthalpy of inlet temperature (Tinlet), the formula is as follows
| 21 |
The sensible heat sink Qsen,l can be calculated by the temperature integration of specific heat of the pyrolysis fuel.51,52 The chemical heat sink Qchem,l was obtained based on the difference of Qtotal,l and Qsen,l.
4. Results and Discussion
Although the simulation conditions are the same, the results of the flow field are different for the multi-step kinetic model and one-step kinetic model, which indicates the importance of the mechanism in the CFD simulation. The simulation results of the two models are discussed in the following sections.
4.1. Fuel Conversion and Temperature
Figure 5a illustrates the results of n-decane conversion. Compared with the one-step model, the conversion predicted by the multi-step kinetic model is more consistent with the experimental data. The occurrence of pyrolysis in the multi-step model is earlier than the one-step model. More specifically, the multi-step model begins to crack at about 190 mm, where the conversion is 0.78%, while the one-step model begins to crack at about 290 mm, where the conversion is 0.56%. This phenomenon is related to the reaction rate constant. Figure 6 shows the rate constant K of the primary reaction of the two models. The inlet temperature of the two models is the same at 753 K, but the K of the multi-step model is larger than that of the one-step model, so the multi-step model cracks earlier, which leads to a greater conversion in the front section of the tube. Then, at 250 and 350 mm for the multi-step model and the one-step model, the slopes of the conversion indicate that the reaction rate of n-decane has become larger, which suggests that the fuel enters the severe cracking zone. Eventually, the conversion of the multi-step model is lower than that of the one-step model. The conversion at the exit of the multi-step model is 86.65%, and the relative error from the experiment is 1.1%. In contrast, n-decane in the one-step model has completely cracked at 690 mm. Compared with the experimental data, the relative error at the exit is 16.7%. This is related to the temperature as shown in Figure 5b, the temperature of the multi-step model is much lower than that of the one-step model, which leads to a smaller reaction rate. Consequently, the conversion of the multi-step model is lower than that of the one-step model.
Figure 5.

Comparison of numerical simulation results between the two different kinetic models. (a) Conversion εn-decane and (b) fuel temperature Tf. Experimental data from ref (41).
Figure 6.

Rate constants of the primary reaction of the multi-step model and the one-step model.
Figure 5b presents the results of the fuel temperature Tf. Compared with the one-step model, the temperature predicted by the multi-step mechanism model is more consistent with the experimental data. And the temperature of the multi-step model is lower than that of the one-step model, which is related to the heat absorption capacity of n-decane. Before about 190 mm, the multi-step model has not cracked, and its variation tendency of temperature is generally in agreement with the one-step model. But after that, the two models show obvious discrepancies due to the occurrence of different pyrolysis reactions. Figure 7 gives the chemical endotherm due to pyrolysis of n-decane as the difference value between the total heat absorption capacity and sensible heat sink. As exhibited in Figure 7, the heat absorption capacity provided by chemical reactions of the multi-step model is always larger than that of the one-step model in the entire reaction zone. Accordingly, the temperature change rate of the multi-step model is smaller than that of the one-step model, which results in a lower temperature. In the front section about 190 mm of the reaction tube, the multi-step model enters the slow cracking state earlier than the one-step model. The heat absorption capacity mainly contains a sensible heat sink in this region, consequently, the temperature increases rapidly for the two models. After about 250 mm, the reaction of the multi-step model is violent with more chemical endotherm, which reduces the change rate in temperature. At the exit, the chemical endotherm of the multi-step model and the one-step model are 1.46 and 0.87 MJ/kg, respectively, accounting for 40 and 25.6% of the total value. The fuel heats up to 988.1 and 1141 K at the exit, respectively, and the relative errors from the experiment are 0.47 and 15%.
Figure 7.

Heat absorption capacities of n-decane.
4.2. Product Distributions
The differences in chemical heat sink as described above come from the different products predicted by the two reaction models. Therefore, it is necessary to analyze the distribution of cracked products from the level of the reaction mechanism. Figure 8 depicts the yield of 6 typical products along the flow direction. For the simulation results based on the one-step model, the species yield is zero in the front part of the tube since no cracking reaction takes place. Although the conversion of n-decane becomes higher in the later stage, it mainly cracks into large molecules, some small molecules, and no aromatic hydrocarbons due to the absence of secondary reactions. Finally, at the exit of the reactor tube, the three most abundant products of the one-step model are 1-hexene, 1-heptene, and 1-octene, and their mass fractions are 11.52, 11.65, and 11.98%, respectively. In contrast, there are more products of small molecules for the simulation results with the multi-step model, such as ethylene, 1-propene, and 1-butene, with mass fractions of 12.99, 18.36, and 12.55%, respectively. Additionally, the contribution of large molecules to the heat absorption is small, and the formation of small molecules results in more chemical heat sink, which are responsible for the reason why the chemical heat sink of the one-step model is less than the multi-step model. As shown in Figure 8, as the cracking progresses for the multi-step model, aromatic hydrocarbon (C6H6, C7H8), and the species (CH4, C2H6, C2H4) with one and two carbon atoms are gradually lower than the experimental measurements, and the species (C3H6) with three carbon atoms are slightly higher than the experiment. At the exit, the relative errors of CH4, C2H6, C2H4, C3H6, C6H6, and C7H8 of the multi-step model are 29.74, 23.18, 24.37, 12.64, 5.04, and 36.21%, respectively. Moreover, the comparison of the yields of all products obtained based on the two chemical kinetic models and experimental results at the exit are provided in the Supporting information.
Figure 8.
Comparisons of CFD simulation results of typical product yields using the multi-step model and the one-step model. (a) Methane, (b) ethane, (c) ethylene, (d) propylene, (e) benzene, and (f) toluene. Experimental data from ref (41).
The comparison of one-dimensional simulation results and two-dimensional simulation results can provide some understanding of the coupling between turbulence and reaction. In the second half of the reactor tube, the product yield obtained by the multi-step model in the CFD simulation is lower than the corresponding one-dimensional value described in Section 2.2. This could be ascribed initially to the lower conversion of n-decane of the two-dimensional simulation, as shown in Figure S4. In view of the solution method of EDC, it assumes basically that the flow in a grid can be divided into large-scale turbulent coherent structures and small-scale fine structures, and reactions occur within small fine scales.44 This is different from the one-dimensional laminar flow simulation in which reactions can occur in the entire grid. The consideration of the coupling between turbulence and chemical reactions in the CFD simulation gives more accurate results on the pyrolysis process of hydrocarbon fuels.
4.3. Convective Heat Transfer
The present work discusses the performance of the two kinetic models in the calculation of convective heat transfer in this section. Convective heat transfer coefficient h is a crucial parameter to estimate the heat transfer efficiency, while Nusselt number Nu is the criterion number to represent h.53 In the process of cracking flow, the main influencing factors of heat transfer include heat absorption capacity through pyrolysis, the fluid physical properties depicted by Pr, the fluid flow state depicted by Re, and the correction factor of isobaric-specific heat (Cp,ave/Cp,f). The chemical endotherm is beneficial for heat transfer.33 From the convective heat transfer correlation proposed by Jackson and Hall54 (J–H correlation) (22), it is known that Pr, Re, and Cp,ave/Cp,f are all positively correlated with Nu.
| 22 |
Figure 9a presents the simulation results of h. In the front section of the tube, h predicted by the multi-step model and one-step model increase steadily to 5802 W/(m2·K) at 410 mm and 4614 W/(m2·K) at 370 mm, respectively. The conversion of n-decane calculated by the multi-step model in the front section of the tube is greater than that by the one-step model, resulting in more chemical endotherms, which is beneficial for heat transfer. As displayed in Figure 9b, the Cp,ave/Cp,f of the multi-step model is larger and more conducive to heat transfer than the one-step model. The Pr shown in Figure 9c reveals the changes in fuel properties caused by cracking. The multi-step model predicts that the conversion at 410 mm has reached 33%. Therefore, the gradually decreasing Pr is not conducive to heat transfer. On the simulation results using the one-step model, the obvious cracking starts at 350 mm with the conversion of 6%, so the Pr hardly changes in the front section of the tube. As demonstrated in Figure 9c, the Re values of the two models both decrease gradually, which is not advantageous to heat transfer. Among the above four influencing factors, the chemical endotherm and the increasing Cp,ave/Cp,f are dominant over the influence of decreasing Pr and Re. Finally, h increases steadily in the front section of the tube, and the prediction of the multi-step model is greater than that of the one-step model. In the end section of the tube, the variation trend of h are different from that of the front. The increased rate of h predicted by the multi-step model becomes slow, and the one-step model does not increase but slightly decreases. For the multi-step model, as the reaction progresses, Pr and Re are reduced gradually, and they drop to 0.9355 and 25 726 at the exit, respectively. The simulation results of Cp,ave/Cp,f show a fluctuation trend, which makes h to fluctuate from 410 mm, increasing slightly. For the one-step model, Pr and Re decrease to 0.9568 and 26 717 at the exit. Due to the increase in the chemical endotherm caused by the violent cleavage reaction, Cp,ave/Cp,f decreases sharply from the position of 370 mm to the exit. Under the combined action of the four influencing factors, h appears an inflection point at the position of 370 mm of the tube.
Figure 9.
CFD simulation results of (a) h and Nu, (b) Cp,ave/Cp,f, (c) Pr and Re using the multi-step model and the one-step model, respectively.
As illustrated in Figure 9a, the simulation results of Nu based on different kinetic models are distinct. The Nu of the multi-step model is always greater than that of the one-step model. The correlation of (22) is further studied and developed by others.55,56 Based on the vertical tube experiment, Zhang57 proposed a correlation suitable for forced convection heat transfer of RP-3. Lei26 developed a n-decane correlation suitable for its conversion less than 23%. Figure 10 exhibits the comparison of Nu between the J–H correlation and the simulation results. It can be seen that the correlation does not elucidate the trend of Nu well, and the numerical results are larger than the correlation. The maximum relative errors of Nu between the correlation and the two models reach 31 and 13%, respectively. For the one-step model, the changes in the chemical endotherm, Pr and Cp,ave/Cp,f induced by the cracking reactions are smaller than that of the multi-step model. Consequently, the results predicted by the one-step model are slightly close to the results of J–H correlation. From the above discussion, the chemical endotherm and the changes in physical properties attributed to fuel cracking play an essential role in the convective heat transfer process, especially the parameter of Cp,ave/Cp,f, which can well reflect the changing trend of the h. The coincidence of key inflection points for these two variables illustrates the conclusion.
Figure 10.

Comparisons between the J–H correlation and the CFD simulation results of the multi-step model and the one-step model.
5. Conclusions
The present work performs numerical investigations on the kinetic models for n-decane pyrolysis in a horizontal tube under supercritical conditions. Considering the high conversion of n-decane, a multi-step chemical model including secondary reactions is developed and applied in the CFD simulations in comparison with the corresponding results of the one-step global model. After careful analysis and comparison, the main summaries are as follows:
-
(1)
The multi-step model with high accuracy gives better prediction results on temperature, conversion, and product distributions. Compared with the experimental data and the simulation results of the multi-step model, the one-step model demonstrated a lower conversion of n-decane in the initial section of the tube, which is contributing to its slower rate constant than that of the primary reaction of the multi-step model. In the entire reaction zone, the chemical endotherm of the multi-step model is larger than that of the one-step model. Accordingly, the temperature change rate of the multi-step model is smaller than that of the one-step model, which results in lower temperature and conversion at the back section of the reactor tube. Moreover, from the yield of typical six products along the flow direction, one can see that the multi-step model generates more products of small molecules due to the consideration of secondary reactions. However, for the one-step model, it mainly cracked into large molecules even at high conversion. Overall, the multi-step model reproduces the flow field well even at high conversion.
-
(2)
On the correlations of convective heat transfer, the existing correlations are limited to the cases of relatively low conversion of fuels. In the supercritical cracking heating transfer process, the chemical endotherm and the changes in physical properties attributed to fuel cracking play an essential role in the convective heat transfer process, especially the parameters of Cp,ave/Cp,f. While the chemical endotherm and fluid properties are directly determined by the pyrolysis products, which are related to the kinetic models. Consequently, the choice of the chemical kinetic model is extremely imperative to pore over the cracking heat transfer process. As shown in Sections 4.1 and 4.2, the multi-step model with high accuracy gives better prediction results on temperature, conversion, and product distributions, which is more conducive to the study of the heat transfer process with thermal cracking and then construct the corresponding correlation of supercritical hydrocarbon fuels.
Acknowledgments
This work was supported by the National Science and Technology Major Project (2017-I-0004-0004).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c01178.
Species involved in the two chemical kinetic models, the thermodynamic file, the transport property file, comparison of the yields of all products obtained based on the two chemical kinetic models and experimental results at the exit of the reactor tube, the verification of the constructed two-dimensional axisymmetric model, conversion of n-decane obtained from the two-dimensional simulation and one-dimensional simulation with the multi-step reaction model (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Yang Y. Z.; Yang J. L.; Fang D. N. Research Progress on Thermal Protection Materials and Structures of Hypersonic Vehicles. J. Appl. Math. Mech. 2008, 29, 51–60. 10.1007/s10483-008-0107-1. [DOI] [Google Scholar]
- Yan X.; Wen-Jun F.; Wen-Jie X.; et al. Thermal Cracking and Heat Sink Measurement of Model Compounds of Endothermic Hydrocarbon Fuels under Supercritical Conditions. Acta Chim. Sin. 2008, 2243–2247. [Google Scholar]
- Giraudot T.; Massot A.; Boselli L.; Talbot B. Dual-fueled advanced high-speed ramjets: students paper. AIAA Paper 2002, 5214. [Google Scholar]
- Song K. D.; Choi S. H.; Scotti S. J. Transpiration Cooling Experiment for Scramjet Engine Combustion Chamber by High Heat Fluxes. J. Propul. Power 2006, 22, 96–102. 10.2514/1.11300. [DOI] [Google Scholar]
- Sobel D. R.; Spadaccini L. J. Hydrocarbon fuel cooling technologies for advanced propulsion. J. Eng. Gas Turbines Power 1997, 119, 344–351. 10.1115/1.2815581. [DOI] [Google Scholar]
- Gilani N.; Haghighi; Poshtiri A. Heat Exchanger Design of Direct Evaporative Cooler Based on Outdoor and Indoor Environmental Conditions. J. Therm. Sci. Eng. Appl. 2014, 6, 041016 10.1115/1.4028179. [DOI] [Google Scholar]
- Gascoin N.; Abraham G.; Gillard P. Synthetic and jet fuels pyrolysis for cooling and combustion applications. J. Anal. Appl. Pyrolysis 2010, 89, 294–306. 10.1016/j.jaap.2010.09.008. [DOI] [Google Scholar]
- Dinda S.; Vuchuru K.; Konda S.; Uttaravalli A. N. Heat Management in Supersonic/Hypersonic Vehicles Using Endothermic Fuel: Perspective and Challenges. ACS Omega 2021, 6, 26741–26755. 10.1021/acsomega.1c04218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell O. A.; Edwards J. T.; Norris R. B.; Numbers K. E.; Pearce J. A. Development of Hydrocarbon-Fueled Scramjet Engines: The Hypersonic Technology (HyTech) Program. J. Propul. Power 2001, 17, 1170–1176. 10.2514/2.5891. [DOI] [Google Scholar]
- Liu P.; Zhang T.; Zhou L.; Chen Z.; Zhu Q.; Wang J.; Li X. Experimental and numerical analysis on flow characteristics and pyrolysis mechanism of hydrocarbon fuel with a novel online hybrid method. Energy Convers. Manage. 2019, 198, 111817 10.1016/j.enconman.2019.111817. [DOI] [Google Scholar]
- Huang H.; Spadaccini L. J.; Sobel D. R. Fuel-Cooled Thermal Management for Advanced Aeroengines. J. Eng. Gas Turbines Power 2004, 126, 284–293. 10.1115/1.1689361. [DOI] [Google Scholar]
- Li S.; Yang Q.; Ye L.; Du H.; Zhang Z.; Huang X.; Xu J. Effect of Nanoparticle Concentration on Physical and Heat-Transfer Properties and Evaporation Characteristics of Graphite/n-Decane Nanofluid Fuels. ACS Omega 2022, 7, 3284–3292. 10.1021/acsomega.1c05343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y.; Peng W.; Xu R.; Jiang P. Review on active thermal protection and its heat transfer for airbreathing hypersonic vehicles. Chin. J. Aeronaut. 2018, 31, 1929–1953. 10.1016/j.cja.2018.06.011. [DOI] [Google Scholar]
- Yu J.; Eser S. Thermal Decomposition of C10–C14 Normal Alkanes in Near-Critical and Supercritical Regions: Product Distributions and Reaction Mechanisms. Ind. Eng. Chem. Res. 1997, 574–584. 10.1021/ie960392b. [DOI] [Google Scholar]
- Chen Y.; Lei Z.; Zhang T.; Zhu Q.; Bao Z.; Zhang Q.; Li X. Y. Flow distribution of hydrocarbon fuel in parallel minichannels heat exchanger. AIChE J. 2018, 64, 2781–2791. 10.1002/aic.16086. [DOI] [Google Scholar]
- Ward T. A.; Ervin J. S.; Zabarnick S.; Shafer L. Pressure Effects on Flowing Mildly-Cracked n-Decane. J. Propul. Power 2005, 21, 344–355. 10.2514/1.6863. [DOI] [Google Scholar]
- Ward T. A.; Ervin J. S.; Striebich R. C.; Zabarnick S. Simulations of Flowing Mildly-Cracked Normal Alkanes Incorporating Proportional Product Distributions. J. Propul. Power 2004, 20, 394–402. 10.2514/1.10380. [DOI] [Google Scholar]
- Ruan B.; Meng H.; Yang V. Simplification of pyrolytic reaction mechanism and turbulent heat transfer of n-decane at supercritical pressures. Int. J. Heat Mass Transfer 2014, 69, 455–463. 10.1016/j.ijheatmasstransfer.2013.10.045. [DOI] [Google Scholar]
- Qin J.; Zhang S.; Bao W.; Zhou W.; Yu D. Thermal management method of fuel in advanced aeroengines. Energy 2013, 49, 459–468. 10.1016/j.energy.2012.10.050. [DOI] [Google Scholar]
- Feng Y.; Qin J.; Zhang S.; Bao W.; Cao Y.; Huang H. Modeling and analysis of heat and mass transfers of supercritical hydrocarbon fuel with pyrolysis in mini-channel. Int. J. Heat Mass Transfer 2015, 91, 520–531. 10.1016/j.ijheatmasstransfer.2015.07.095. [DOI] [Google Scholar]
- Bao W.; Zhang S.; Qin J.; Zhou W.; Xie K. Numerical analysis of flowing cracked hydrocarbon fuel inside cooling channels in view of thermal management. Energy 2014, 67, 149–161. 10.1016/j.energy.2014.01.044. [DOI] [Google Scholar]
- Lei Z.; Liu B.; Huang Q.; He K.; Bao Z.; Zhu Q.; Li X. Thermal cracking characteristics of n-decane in the rectangular and circular tubes. Chin. J. Chem. Eng. 2019, 27, 2876–2883. 10.1016/j.cjche.2019.01.034. [DOI] [Google Scholar]
- Zhang S.; Feng Y.; Jiang Y.; Qin J.; Bao W.; Han J.; Haidn O. J. Thermal behavior in the cracking reaction zone of scramjet cooling channels at different channel aspect ratios. Acta Astronaut. 2016, 127, 41–56. 10.1016/j.actaastro.2016.05.015. [DOI] [Google Scholar]
- Tao Z.; Hu X.; Zhu J.; Wu H. Numerical investigation of pyrolysis effects on heat transfer characteristics and flow resistance of n-decane under supercritical pressure. Chin. J. Aeronaut. 2018, 31, 1249–1257. 10.1016/j.cja.2018.03.015. [DOI] [Google Scholar]
- Feng Y.; Liu S.; Qin J.; Cao Y.; Jiang Y.; Zhang S. Numerical study on the influence of turbulence on the pyrolysis of hydrocarbon fuel in mini-channel. Int. J. Heat Mass Transfer 2018, 119, 768–776. 10.1016/j.ijheatmasstransfer.2017.12.002. [DOI] [Google Scholar]
- Lei Z.; He K.; Huang Q.; Bao Z.; Li X. Numerical study on supercritical heat transfer of n-decane during pyrolysis in rectangular tubes. Appl. Therm. Eng. 2020, 170, 115002 10.1016/j.applthermaleng.2020.115002. [DOI] [Google Scholar]
- Hu X.; Tao Z.; Zhu J.; Li H.. Numerical Study of Pyrolysis Effects on Supercritical-Pressure Flow and Conjugate Heat Transfer of N-Decane in the Square Channel. In Turbo Expo: Power for Land, Sea, and Air, American Society of Mechanical Engineers, 2017; Vol. 50879, p V05AT11A008. [Google Scholar]
- Jiang P-X.; Wang Y.; Zhu Y. Differential Global Reaction Model with Variable Stoichiometric Coefficients for Thermal Cracking of n-Decane at Supercritical Pressures. Energy Fuels 2019, 33, 7244–7256. 10.1021/acs.energyfuels.9b01505. [DOI] [Google Scholar]
- Wang Y.; Jiang P-X.; Zhu Y. A novel global reaction modeling approach considering the effects of pressure on pyrolysis of n-decane at supercritical pressures. Fuel 2021, 287, 119416 10.1016/j.fuel.2020.119416. [DOI] [Google Scholar]
- Wang H.; Gong S.; Liu G. Atmospheric and high pressures pyrolysis study of n-decane in a flow reactor with online GC-MS/FID analysis: Experiments and modeling. J. Anal. Appl. Pyrolysis 2021, 155, 105065 10.1016/j.jaap.2021.105065. [DOI] [Google Scholar]
- Jiao S.; Li S.; Pu H.; Dong M.; Shang Y. Investigation of Pressure Effect on Thermal Cracking of n-Decane at Supercritical Pressures. Energy Fuels 2018, 32, 4040–4048. 10.1021/acs.energyfuels.7b03865. [DOI] [Google Scholar]
- Jiang P.; Yan J.; Yan S.; Lu Z.; Zhu Y. Thermal Cracking and Heat Transfer of Hydrocarbon Fuels at Supercritical Pressures in Vertical Tubes. Heat Transfer Eng. 2019, 40, 437–449. 10.1080/01457632.2018.1432026. [DOI] [Google Scholar]
- Jiao S.; Li S.; Pu H.; Dong M.; Shang Y. Investigation of pyrolysis effect on convective heat transfer characteristics of supercritical aviation kerosene. Acta Astronaut. 2020, 171, 55–68. 10.1016/j.actaastro.2020.02.049. [DOI] [Google Scholar]
- Yu J.; Eser S. Kinetics of Supercritical-Phase Thermal Decomposition of C10–C14 Normal Alkanes and Their Mixtures. Ind. Eng. Chem. Res. 1997, 36, 585–591. 10.1021/ie9603934. [DOI] [Google Scholar]
- Xu K.; Meng H. Numerical study of fluid flows and heat transfer of aviation kerosene with consideration of fuel pyrolysis and surface coking at supercritical pressures. Int. J. Heat Mass Transfer 2016, 95, 806–814. 10.1016/j.ijheatmasstransfer.2015.12.050. [DOI] [Google Scholar]
- Xu K.; Meng H. Modeling and Simulation of Supercritical-Pressure Turbulent Heat Transfer of Aviation Kerosene with Detailed Pyrolytic Chemical Reactions. Energy Fuels 2015, 29, 4137–4149. 10.1021/acs.energyfuels.5b00097. [DOI] [Google Scholar]
- Jiang R.; Liu G.; Zhang X. Thermal Cracking of Hydrocarbon Aviation Fuels in Regenerative Cooling Microchannels. Energy Fuels 2013, 27, 2563–2577. 10.1021/ef400367n. [DOI] [Google Scholar]
- Zhao G.; Song W.; Zhang R. Effect of pressure on thermal cracking of china RP-3 aviation kerosene under supercritical conditions. Int. J. Heat Mass Transfer 2015, 84, 625–632. 10.1016/j.ijheatmasstransfer.2015.01.059. [DOI] [Google Scholar]
- Li Z.; Liu G.; Zhang R. Heat transfer to supercritical hydrocarbon fuel in horizontal tube: Effects of near-wall pyrolysis at high heat flux. Chem. Eng. Sci. 2021, 229, 115994 10.1016/j.ces.2020.115994. [DOI] [Google Scholar]
- Li Z.; Wang H.; Jing K.; Wang L.; Li Y.; Zhang X.; Liu G. Kinetics and modeling of supercritical pyrolysis of endothermic hydrocarbon fuels in regenerative cooling channels. Chem. Eng. Sci. 2019, 207, 202–214. 10.1016/j.ces.2019.06.019. [DOI] [Google Scholar]
- Wang Y.; Zhao Y.; Liang C.; Chen Y.; Zhang Q.; Li X. Molecular-level modeling investigation of n-decane pyrolysis at high temperature. J. Anal. Appl. Pyrolysis 2017, 128, 412–422. 10.1016/j.jaap.2017.08.009. [DOI] [Google Scholar]
- Sidney W. B.ThermoChemical Kinetics—Methods for the Estimation of Thermochemical Data and Rate Parameters; WILEY, 1968. [Google Scholar]
- Holley A. T.; You X. Q.; Dames E.; Wang H.; Egolfopoulos F. N. Sensitivity of propagation and extinction of large hydrocarbon flames to fuel diffusion. Proc. Combust. Inst. U.S.A. 2009, 32, 1157–1163. 10.1016/j.proci.2008.05.067. [DOI] [Google Scholar]
- Sundaram K. M.; Froment G. F. Modeling of thermal cracking kinetics—I. Chem. Eng. Sci. 1977, 32, 609–617. 10.1016/0009-2509(77)80226-1. [DOI] [Google Scholar]
- Pant K. K.; Kunzru D. Pyrolysis of methylcyclohexane: Kinetics and modelling. Chem. - Eng. J. 1997, 67, 123–129. 10.1016/S1385-8947(97)00023-5. [DOI] [Google Scholar]
- Kumar P.; Kunzru D. Modeling of naphtha pyrolysis. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 774–782. 10.1021/i200030a043. [DOI] [Google Scholar]
- CHEMKIN-PRO 15112, Reaction design, San Diego
- ANSYS 14.5 FLUENT User’s Guide; ANSYS Inc: Canonsburg, PA, USA, 2013. [Google Scholar]
- Li Y.; Wang J.; Xie G.; Sunden B. Effect of thermal pyrolysis on heat transfer and upward flow characteristics in a rectangular channel using endothermic hydrocarbon fuel. Chem. Eng. Sci. 2021, 244, 116806 10.1016/j.ces.2021.116806. [DOI] [Google Scholar]
- NIST Standard Reference Database 4-NIST Thermophysical Properties of Hydrocarbon Mixtures Database, Version 3.2, National Institute of Standards and Technology Standard Reference Data Program Gaithersburg, MD, 200720899.
- Jiao S.; Li S.; Pu H.; Dong M.; Shang Y. Experimental investigation on thermal cracking and convective heat transfer characteristics of aviation kerosene RP-3 in a vertical tube under supercritical pressures. Int. J. Therm. Sci. 2019, 146, 106092 10.1016/j.ijthermalsci.2019.106092. [DOI] [Google Scholar]
- Sobel D. R.; Spadaccini L. J. Hydrocarbon Fuel Cooling Technologies for Advanced Propulsion. J. Eng. Gas Turbines Power 1997, 119, 344–351. 10.1115/1.2815581. [DOI] [Google Scholar]
- Chen M. H.; Pan H. L.; Qi M. Z.. Principles of Chemical Engineering: Fewer Hours; East China University of Science and Technology Press, 2008. [Google Scholar]
- Hall W. B.; Jackson J. D.; Watson A.. Paper 3: A Review of Forced Convection Heat Transfer to Fluids at Supercritical Pressures. In Proceedings of the Institution of Mechanical Engineers, Conference Proceedings; England: SAGE Publications: Sage UK: London, 1967; pp 10–22 10.1243/PIME_CONF_1967_182_262_02. [DOI]
- Hua Y.-X.; Wang Y.-Z.; Meng H. A numerical study of supercritical forced convective heat transfer of n-heptane inside a horizontal miniature tube. J. Supercrit. Fluids 2010, 52, 36–46. 10.1016/j.supflu.2009.12.003. [DOI] [Google Scholar]
- Wang Y.-Z.; Hua Y.-X.; Meng H. Numerical Studies of Supercritical Turbulent Convective Heat Transfer of Cryogenic-Propellant Methane. J. Thermophys. Heat Transfer 2010, 24, 490–500. 10.2514/1.46769. [DOI] [Google Scholar]
- Zhang B.; Zhang C. B.; Deng H. W.; Xu G. Q.; Zhu K. Heat transfer characteristics of hydrocarbon fuel at supercritical pressure in vertical circular tubes. J. Aerosp. Power 2012, 03, 595–603. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.






