Abstract

Ultrasonic flotation is useful for fine low-rank coal purification; however, the efficiency of ultrasonic flotation still needs to be improved. Because the dynamic behavior of flotation bubbles has significant effects on their flotation efficiency, it was investigated under different gas input conditions with and without ultrasound using the volume of fluid method and h-speed imaging. The results indicated that the gas input method can influence the final kinetic behavior of the flotation bubbles by changing the morphology of the initial bubble. With an increase in the size and aspect ratio of the bubble, the bubble deformation and velocity increased, and the range of motion of the bubble increased and then decreased. Meanwhile, the size of the bubble increased with an increase in the thickness of the vibrating plate of the ultrasonic transducer owing to the aggregation of the bubbles under the influence of ultrasound.
1. Introduction
Flotation is an effective method for upgrading fine-grained minerals and coal particles by increasing the differences in their hydrophobicity and floatability.1−4 Ultrasonic flotation technology has several advantages in the separation and purification of complex ores, in which the dynamic behavior of flotation bubbles has an important influence on the improvement in flotation efficiency.4−7 Because flotation efficiency is closely related to the dynamic behavior of flotation bubbles, investigating the dynamic properties of flotation bubbles is important.
Several studies have reported that the recovery of particles (1–10 μm in diameter) increases with the decrease in bubble size,8−10 mainly because of the capture efficiency.11,12 Tripathi et al.13 investigated the kinetic properties of bubbles in the stationary liquid phase using the volume of fluid (VOF) method and determined that bubbles undergo axially symmetric, skirting, sawtooth/spiral, peripheral fragmentation and five central modes of bubble behavior in water; the mechanism of bubble motion under several different flow conditions was revealed using this model.14−16 Hoque et al. experimentally analyzed the fluidity around rising bubbles of different diameters in a stationary medium and determined the effect of the bubble size on the kinetic energy distribution.17
Sarhan et al. studied the effect of gas–liquid two-phase physical parameters such as density on bubble generation and kinetic properties using CFD methods.18 Chen et al.19,20 investigated the differences in the collisional adhesion processes between mineral particles, oil bubbles, and conventional bubbles and explored the enhancement effect of oil bubbles on the flotation mineralization process.
Meanwhile, the effect of ultrasonic excitation of flotation bubbles on the enhancement of flotation efficiency has received considerable attention. Ozkan reported that ultrasonic cavitation can increase more uniformity and produce fine bubbles.21 Ultrasonic cavitation produces a large number of cavitation bubbles to improve the stability of the flotation froth layer and the mineralization efficiency between the coal particles and bubbles. Mitra et al. investigated the role of cavitation bubbles in the dynamics of bubble-particle interactions using high-speed imaging and discovered that cavitation bubbles facilitated the formation of stable bubble-particle aggregates22 and discovered that the sound field can improve the collision and adhesion efficiency of bubbles and particles.23
Ye et al. developed a dual-frequency ultrasonic bubble dynamics model by considering thermal effects and obtained numerical solutions for the dynamic evolution processes of bubble radius, pressure, energy, temperature, and number of water vapor molecules inside the bubble.24 Jin et al. explored the effect of standing wave ultrasound on flotation efficiency using a high-speed camera technique and discovered that the ultrasonic frequency had a significant effect on bubble aggregation and the number of small bubbles under the Bjerknes force.25
Recently, the cleaning effect of ultrasound on particle surfaces has been experimentally verified.26,27 Hong et al. revealed that ultrasonic treatment significantly affects the contact angle of the graphite surface.28 Xu et al.29 investigated the effect of ultrasonic pretreatment time on the flotation of oxidized coal and discovered that ultrasound effectively removed the hydrophilic oxide layer on the coal surface and improved the floatability and recovery of oxidized coal. Ozuna et al.30 found that ultrasonic pretreatment had a significant effect on the recovery of trap-free flotation of oxidized pyrite, with a recovery of 50% after 60 min of ultrasonic treatment.
Peng et al.31 applied ultrasound to the slurry phase in a high-ash lignite flotation process and demonstrated that ultrasound produced several microbubbles, which played a bridging role in the bubble-coal particle attachment process and improved the floatability of lignite. Cilek and Ozgen investigated the effect of ultrasound on the flotation efficiency in a complex sulfide ore flotation process and applied ultrasound to the froth phase. The authors discovered that had a positive effect on the flotation performance under medium to high flow rate conditions.32
Ultrasound also has a positive effect on the flotation desulfurization of high sulfur coal.33,34 In addition, ultrasonic treatment has provided good results for flotation and ash removal from oil shale.35 As ultrasonic treatment has both oscillation and cavitation effects, surface cleaning and treatment can be achieved to pretreat the minerals. Kang et al.36 noticed an increase in the hydrophobicity of coal and hydrophilicity of pyrite after the ultrasonic treatment. Aldrich and Feng37 observed that ultrasonic pretreatment increased the hydrophobicity of sulfides and hydrophilicity of silicates. Chen et al.38,39 treated mineral particles using standing wave ultrasound and discovered that coal particles were aggregated and adsorbed by large bubbles, which increased the recovery rate.
The effect of ultrasound on flotation bubbles is receiving an increasing amount of attention. However, many studies have investigated the kinetic properties of bubble-particle aggregates in ultrasound fields, and we focus on the changes in the kinetic properties of flotation bubbles under the influence of gas input methods and ultrasound. In this study, the effects of ultrasound and gas input methods on the motion characteristics of flotation bubbles during their ascent were investigated in a liquid–gas system using a high-speed camera, and the effect of bubble input methods on the initial bubble morphology was analyzed using the VOF method. Finally, the dynamic behavior of the rising motion of bubbles in the ultrasonic field was investigated to elucidate the influence of the initial morphology of bubbles and ultrasound on the dynamic behavior of flotation bubbles. The results of this study are expected to provide guidance for effective ultrasonic flotation engineering.
2. Experimental Section
2.1. Ultrasonic Transducer
The ultrasonic transducer is the key device of the experimental system, and the theoretical research and practical application of the bolt-fastening ultrasonic transducer are extensive. Therefore, this study designed a bolt-fastening ultrasonic transducer based on the piezoelectric principle. Figure 1 illustrates the structure of the bolt-fastening ultrasonic transducer used in this study. The back-end cover, piezoelectric ceramic, and amplitude rod were fixed together using pre-tightened bolts. The piezoelectric ceramic converted the high-frequency voltage excitation into a mechanical vibration output, and high-frequency vibration was transmitted to the vibration plate through the amplitude rod to generate ultrasonic waves. Moreover, the ultrasonic performance was affected by the thickness and shape of the vibration plate. Therefore, analyzing and discussing the thickness and shape of the vibration plate on the ultrasonic transducer was necessary.
Figure 1.
Schematic diagram of the structure of the bolt-fastening ultrasonic transducer.
The thickness and shape of the vibration plate influenced the performance of the ultrasonic transducer system. Figure 2 shows the relationship between the thickness of the vibrating plate and resonant frequency of the ultrasonic transducer. As the thickness of the vibration plate increased, the resonance frequency of the ultrasonic transducer first increased and then decreased, thereby indicating that the change in the thickness of the vibrating plate affects the structure of the ultrasonic transducer and was the main factor affecting the resonance frequency of the ultrasonic transducer.
Figure 2.

Effect of vibration plate thickness on ultrasonic resonance frequency.
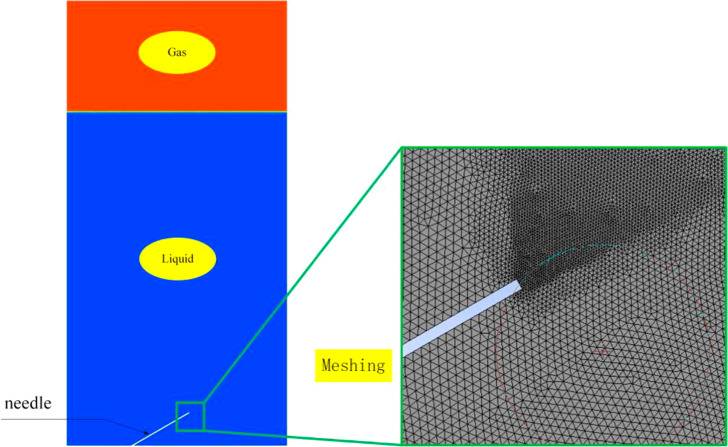
As shown in Figure 3, the finite element method is used to build and mesh the piezoelectric transducer model for modal analysis, and the influence of the shape of the vibrating plate on the vibration characteristics of the piezoelectric transducer is studied. A fixed constraint is applied at the flange of the model and a voltage is applied at the end face of the piezoelectric ceramic, and the Block Lanczos method is applied to solve the vibration mode of the piezoelectric transducer model.
Figure 3.
Modal analysis model and meshing of piezoelectric transducer: (a) model and (b) meshing.
Meanwhile, Figure 4 shows that the change in the shape of the vibration plate changes the transmission of the vibration generated by the piezoelectric ceramic on the vibration plate, thereby resulting in the differences in the vibration mode of the ultrasonic transducer system according to different shapes of the vibration plates. When the vibration plate was circular, the amplitude of the vibration plate was small, whereas the amplitude of vibration on the square vibration plate was large and the distribution of the vibration direction on the vibration plate was more dispersed, which is conducive to the uniform transmission of ultrasonic waves in the medium.
Figure 4.
Effect of the shape of the vibrating plate on the vibration mode of the ultrasonic transducer: (a) modal analysis diagram and (b) displacement vector diagram.
2.2. Experimental System
The experimental system is shown in Figure 5 and consists of a micro syringe pump, syringe, flat-tipped needle, flotation column, ultrasonic transducer, signal controller, power amplifier, and high-speed camera. The flotation column possessed the dimensions of 130 mm × 70 mm × 200 mm and was made of acrylic, which enabled the high-speed camera to capture the changes in the kinetic behavior of the bubbles in the liquid.
Figure 5.
Experimental device for the ultrasonic flotation bubble, (a) schematic diagram of the experimental apparatus, and (b) physical diagram of the experimental apparatus.
The experiments were conducted at room temperature and atmospheric pressure in a gas–liquid system. Gas was supplied by pushing the syringe through a microinjection pump during the entire experiment, and bubbles were subsequently generated by release through a flat-ended needle. The movement of bubbles in the flotation column was observed using a high-speed camera when the bubble output was stabilized, and the change in bubble movement was observed by replacing the inner diameter of the flat-ended needle and changing the angle of the needle tilt. When ultrasound was introduced, the effect of ultrasound was changed by replacing the vibration plate on the ultrasound transducer to observe the effect of ultrasound on the kinetic behavior of flotation bubbles. The dimensions of the flat-ended needles used in the experiments are listed in Table 1. The diameters of the flat-ended needles were 0.2, 0.3, 0.4, and 0.6 mm; the thicknesses of the vibrating plates were 0.6, 0.8, 1.0, and 1.2 mm; and the shapes of the vibrating plates were round and square.
Table 1. Needle Size.
| needle number | outer diameter (mm) | inner diameter (mm) |
|---|---|---|
| 1 | 0.9 | 0.6 |
| 2 | 0.71 | 0.41 |
| 3 | 0.55 | 0.3 |
| 4 | 0.41 | 0.19 |
3. Numerical Model
3.1. Model Construction and Meshing
As shown in Figure 6, the model calculation area was divided using unstructured meshing, and the mesh was locally encrypted. The total number of meshes divided by the model was approximately 4 × 105. The bottom and two boundaries of the calculation region were set as the no-slip interface, air holes were set as the velocity inlet boundary conditions, and top boundary is set as the free outflow boundary, and the gas–liquid two-phase region at the initial moment was divided by initializing the calculation region.
Figure 6.
Numerical analysis model and mesh division of bubble movement in water.
3.2. Numerical Methods
The VOF model can trace the gas–liquid interface; therefore, the VOF model was used to perform numerical analysis of the bubble motion. In addition, based on the experimental environment, the following assumptions were made: (1) the fluid inside and outside the bubble was a continuous and incompressible Newtonian fluid; (2) the bubble motion environment was isothermal and adiabatic; and (3) the gas–liquid two-phase flow system separated by the interface was a single-phase flow system. Based on the above assumptions, the mass and momentum equations in the control equation are expressed as follows
| 1 |
| 2 |
where  and
and  are the velocity of the flow field
in the
are the velocity of the flow field
in the  and
and  directions, respectively, ρ
is the
fluid density,
directions, respectively, ρ
is the
fluid density,  and
and  are the distances of movement
in the
are the distances of movement
in the  and
and  directions,
directions,  is the pressure,
is the pressure,  is the dynamic viscosity, g is the acceleration of gravity, and
is the dynamic viscosity, g is the acceleration of gravity, and  is
the volume force.
is
the volume force.
The VOF model introduces the phase volume fraction as a function to chieve the track the gas and liquid interfaces according to the following equation
| 3 |
where  denotes the gas volume fraction.
The volume
fraction
denotes the gas volume fraction.
The volume
fraction  indicates
that the grid cell contains only
one fluid phase, that is, the liquid phase;
indicates
that the grid cell contains only
one fluid phase, that is, the liquid phase;  indicates
that the cell table contains
only one fluid phase, that is, the gas phase; and
indicates
that the cell table contains
only one fluid phase, that is, the gas phase; and  indicates that there is a gas–liquid
interface in the cell grid. The sum of the volume fractions of all
phases in each calculation grid was 1.
indicates that there is a gas–liquid
interface in the cell grid. The sum of the volume fractions of all
phases in each calculation grid was 1.
To analyze the effect
of bubble motion on the perturbation of liquid
flow, the standard  turbulence model was applied, and the control
equation is as follows
turbulence model was applied, and the control
equation is as follows
| 4 |
 |
5 |
where  and
and  are the terms for the generation
of turbulent
energy k caused by the mean velocity gradient and
buoyancy,
are the terms for the generation
of turbulent
energy k caused by the mean velocity gradient and
buoyancy,  is the turbulent viscosity,
is the turbulent viscosity,  ,
,  , and
, and  are empirical
constants,
are empirical
constants,  is the Prandtl number
corresponding to
the turbulent kinetic energy k, and
is the Prandtl number
corresponding to
the turbulent kinetic energy k, and  and
and  are source items.
are source items.
3.3. Calculation Conditions
The numerical analysis simulation used the PISO algorithm to couple the relationship equation between pressure and velocity. The velocity inlet was used for the gas phase inlet, the wall was set to the no-slip wall boundary condition, and the pressure outlet is used for the top outlet of the liquid phase. The physical parameters of the gas and liquid phases are presented in Table 2.
Table 2. Physical Parameters of the Gas and Liquid Phases.
| liquid density/(kg/m3) | gas density/(kg/m3) | liquid dynamic viscosity/(pa·s) | gas dynamic viscosity/(pa·s) | surface tension/(N/s) | gravitational acceleration/(m/s2) |
|---|---|---|---|---|---|
| 998 | 1.225 | 0.89 × 10–3 | 1.79 × 10–5 | 0.072 | 9.81 |
3.4. Verification of the Correlation between Experimental Results and Those Obtained Using Numerical Analysis
The results obtained experimentally for the three stomatal input angles were compared with those obtained numerically, and Figure 7 shows that the shapes and trajectories of the bubbles during the generation and rising motion of the bubbles in the experimental and numerical analysis diagrams are similar. Therefore, the numerical analysis model can be concluded to provide good reproduction of the experimental process.
Figure 7.
Comparison diagram of the simulation results and experimental results: (a) θ = 30°, (b) θ = 45°, and (c) θ = 60°.
4. Results and Discussion
4.1. Analysis of the Factors Influencing the Motion of Hydrostatic Bubbles
4.1.1. Effect of the Inner Diameter of the Stomata and Angle of Inclination on the Motion of the Bubbles
Figure 8 shows the effect of the gas input mode on the motion of flotation bubble motion under the hydrostatic conditions, thereby revealing the influence of different inner diameters and tilt angles on the motion characteristics of the flotation bubbles. The trajectory of the bubbles in the process of movement is linear, as shown in Figure 8. For the convenience of the subsequent description, this series of moving bubbles is denoted as a bubble chain. The bubble chains generated by the needle with different inner diameters and inclination angles were “S” shaped, and the bubbles oscillated along a zigzag path because of the uneven influence of liquid resistance, pressure, and buoyancy. The bubbles were flattened owing to the pressure imbalance on the upper and lower surfaces during movement.
Figure 8.
Schematic diagram of the movement of the flotation bubble under static water condition: (a) θ = 30°, (b) θ = 45°, and (c) θ = 60°.
Figure 8a shows that the number of bubbles in the bubble chain increases with an increase in the inner diameter of the needle when the gas input angle is 30°. The constant input air velocity resulted in a small air flow at the orifice per unit time when the inner diameter of the needle was small; thus, fewer bubbles were generated. As shown in Figure 8b, the range of bubble chain motion increases significantly when the gas input angle is 45°. When the gas input angle was 60°, the shape of the bubble generated by the 0.4–0.6 mm needles converted from a spherical cap to an ellipsoid with large deformations, which can be clearly observed in Figure 8c. This demonstrated that the bubble motion was mainly affected by the tilt angle of the needle when the inner diameter of the air hole was large.
Figure 9 shows the principle of bubble aggregation in an ultrasonic field. Leighton et al. proposed a mathematical formula to explain the bubble aggregation phenomenon in an ultrasonic field based on the Bjerknes force theory. The ultrasonic field changes the ambient pressure of the liquid, and the change in volume of the gas at the varying pressure of the liquid is given by40
| 6 |
where R0 is the radius of the bubble at equilibrium; P0 is the hydrostatic pressure; Pv is the vapor pressure; ρ, σ, and μ are the density, surface tension, and viscosity of the liquid, respectively; κ is the multivariability index of the gas inside the bubble; and P(t) is the time-varying sound pressure.
Figure 9.
Mechanism of bubble aggregation in an ultrasonic field.
The resonant frequency of the bubble is given by
| 7 |
where ωr is the resonant frequency when the resonant bubble size is R0.
Whether the intrinsic frequency of the resonant bubbles is greater than the driving frequency is determined by the following equation41
| 8 |
where vr is the linear resonant frequency.
The equation of motion of the bubble along the pressure gradient is
| 9 |
The bubbles in the ultrasonic field oscillated under the influence of the acoustic pressure field during their motion. If the acoustic pressure gradient was not zero, it was coupled with bubble oscillation to produce the main Bjerknes force that affected the bubble flat motion. The ultrasonic frequency vibration of the vibrating plate caused ultrasonic waves to be transferred in the liquid medium, and the Bjerknes force in the acoustic field was the strongest driving force affecting bubble motion in still water. Under the action of the acoustic field, bubbles with frequencies higher than the resonant frequency moved toward the wave node under the influence of the acoustic pressure gradient, and the bubble aggregation occurred in the ultrasonic field.40,42,43
The variation in the gas input mode significantly affected the trajectory of the bubbles under hydrostatic conditions. Figure 10a–c shows the changes in the bubble trajectories under hydrostatic conditions with different needle tilt angles and inner diameters. The trajectory range of the bubble chain tended to increase and then decrease with an increase in the inner diameter of the needle. However, the trajectory of the bubbles showed a different pattern with an increase in the inner diameter of the needle when the tilting angle of the needle changed. Under the same input air velocity, the lateral motion offset range of the bubble chain increased gradually with an increase in the inner diameter of the orifice, and the lateral offset range of the bubble chain starts to decrease when the inner diameter of the orifice exceeds a certain value. Therefore, a maximum value of the lateral motion of the bubble chain existed with a change in the stomatal inner diameter, and the maximum value increased with an increase in the stomatal inclination angle. The maximum values of the lateral range of motion of the bubble chain were 0.3, 0.4, and 0.4 for each stomatal tilt angle in Figure 10.
Figure 10.
Trajectory diagram of the flotation bubbles under static water conditions: (a) θ = 30°, (b) θ = 45°, and (c) θ = 60°.
4.1.2. Effect of Ultrasound on the Motion of the Bubbles
The motion of the bubbles generated by the needles with different inner diameters and tilt angles under the influence of ultrasound is given shown in Figure 11. Compared with Figure 9, for the bubbles exposed to ultrasound, the bubble aggregation occurred during the motion, thereby forming bubble clusters of different sizes and shapes. As shown in Figure 11, when the inner diameter of the needle is small (0.2–0.3), the bubbles are aggregated to form bubble clusters under the action of ultrasound. Additionally, the number of bubbles in the bubble cluster was large, and the bubble size was small and easily affected by ultrasound. When the inner diameter of the stomata was large (0.4–0.6), tilt angles were 30 and 45° (Figure 11), inner diameters of the needle were small (0.2–0.3), the bubbles gathered under the action of ultrasound to form a bubble cluster, and the number of bubbles in the bubble cluster was large. Furthermore, when the tilt angle was 60°, the bubbles were close to each other; however, the bubble spacing was large. This indicated that the effect of ultrasound on bubbles decreased with an increase in needle diameter because the bubble movement was governed by the liquid resistance. Moreover, as shown in Figure 11, the bubbles were mainly clustered in the lateral direction to form bubble clusters, which indicated that the influence of ultrasound on the flotation bubble movement in the lateral direction was dominant.
Figure 11.
Effect of ultrasound on bubble motion under different pore diameters and inclination angles: (a) θ = 30°, (b) θ = 45°, and (c) θ = 60°.
Figure 12 shows the relationship between the bubble trajectory and the thickness of the vibrating plate in the ultrasonic field excited by the two types of vibrating plate-shaped ultrasonic transducer systems. As shown in Figure 12a, when the vibrating plate was square, the horizontal displacement of the bubble trajectory changed periodically, the moving range of the bubble in the ultrasonic field is smaller. As the thickness of the vibrating plate increased, the moving range of the bubble in the horizontal direction first decreased and then increased. When the thickness of the square vibrating plate was 0.8 mm, the moving distance of the bubble in the horizontal direction was the minimum. As shown in Figure 12b, when the vibrating plate is round, the displacement of bubbles in the horizontal direction under the action of ultrasound showed no obvious change, unlike that of the bubbles transmitted by the square vibrating plate in an ultrasonic field. However, but the displacement of bubbles in the horizontal direction did not show a regular change, and the displacement distance of the bubbles gradually decreased with the increase in the rising height of the bubbles.
Figure 12.
Effect of the thickness of the vibration plate on the trajectory of the bubbles in the ultrasonic field for different vibration plate shapes (d0 = 0.3 mm and θ = 45°): (a) square vibration plate and (b) circular vibration plate.
4.1.3. Effect of the Gas Input Method on Bubble Velocity
The variation law of the bubble motion velocity with time under different needle inner diameters and tilt angles is shown in Figure 13. When the bubble was in ascending motion, the change in speed of this motion was divided into three phases: acceleration, deceleration, and uniform motion. From Figure 13, it is revealed that when the bubble is first generated, the velocity of motion increases rapidly and then starts to decrease after reaching the maximum value with time; subsequently, it levels off and finally reaches a near constant terminal velocity. Meanwhile, the bubble is generated when the speed is low and the liquid resistance is small, and the bubble speed increases dramatically. With the acceleration of the bubble, the bubble is subject to changes in the force, the liquid resistance increases when the speed of movement increased to a certain value, and then, the bubble began to reduce the speed, the bubble shape tends to stabilize, the forces tend to balance, and the bubble speed also tends to a constant value.
Figure 13.
Schematic diagram of the changes in the bubble rising speed with time under different pore diameters and inclination angles: (a) θ = 30°, (b) θ = 45°, and (c) θ = 60°.
As shown in Figure 13, the final velocity of the bubble motion increases with an increase in the inner diameter. The increase in the inner diameter of the needle increases the gas flow rate, which resulted in an increase in the frequency of bubbles produced by the orifice plate, thereby resulting in a decrease in the apparent viscosity within the bubble channel. Additionally, the final velocity increased as the bubble viscosity resistance decreased. However, as shown in Figure 13a,b, when the needle is tilted at an angle of 30–45°, the deceleration time of the bubble is short and the final velocity of the bubble increases with the inner diameter of the needle in the uniform velocity phase. From Figure 13c, the deceleration time of bubble motion is observed to be long when the air hole tilt angle is 60° and the difference in bubble velocity is pronounced at low and high needle diameters.
4.1.4. Effect of Ultrasound on Bubble Velocity
The ultrasonic field has a significant effect on the velocity of the rising bubbles. Figure 14 shows the effect of the thickness of the vibrating plate on the rising velocity of the bubble when the bubble in the ultrasonic field was in the uniform velocity phase. From Figure 14, the ultrasonic field was observed to significantly reduce the rising velocity of the bubble, and the bubble is affected by the acoustic pressure gradient during motion, which prolongs the motion of the bubble in the ultrasonic field. As the thickness of the vibration plate increased, the bubble velocity first increased and then decreased. Meanwhile, the bubble motion velocity was lower when the shape of the vibration plate was square, which indicated that there was a close relationship between the amplitude of the vibration plate and bubble motion velocity.
Figure 14.

Effect of vibration plate thickness on bubble motion velocity (d0 = 0.3 mm and θ = 45°).
4.2. Effect of Gas Input Method on the Initial Bubble Morphology
To analyze the dynamic behavior of flotation bubbles under hydrostatic conditions from a microscopic point of view, kinetic parameters that cannot be obtained from experiments, such as the variation in bubble motion velocity in the liquid, were obtained using CFD methods. Additionally the VOF method was used to study the influence of the initial bubble morphology on the bubble motion.
The variation in the initial morphology of the bubble generation process affected the trajectory and final velocity of the bubble during the upward motion. Therefore, we investigated the initial morphology of the bubbles in combination with the multiple morphologies of these bubbles during motion, and the differences in the morphology, trajectory, and velocity of the bubbles generated using needles with different inner diameters were investigated. Figure 15 shows the numerical analysis images of bubble generation at the orifice, thereby reflecting the morphological characteristics of the bubbles generated using needles with different inclination angles and internal diameters when bubbles leave the orifice. There were two typical bubble shapes when a bubble detached from the orifice. When the surface tension was the main influence, the bubble shape was often in the shape of a ball cap. In contrast, the bubble was mushroom-shaped when it oscillated owing to the breakage of the bubble tail during the process of bubble release from the orifice.
Figure 15.
Morphological characteristics of bubbles formed by different pore inclination angles and inner diameters: (a) θ = 30°, (b) θ = 45°, and (c) θ = 60°.
Figure 16 shows the trend of the aspect ratio of the flotation bubbles with respect to the diameter and inclination angle of the needle. The aspect ratio of a bubble is the ratio of its longitudinal distance to its transverse distance, which characterizes the degree of deformation of the bubble during its movement. Here, the closer the aspect ratio is to 1, the more the shape of the bubble tends to be round, and the closer the aspect ratio is to 0, the flatter the shape of the bubble tends to be. As shown in Figure 16, the aspect ratio of the bubble gradually increases with an increase in the stomatal tilt angle, and the aspect ratio of the bubble shows a gradually decreasing trend when the needle diameter increases, and the bubble shape becomes increasingly flat. When the needle diameter was small, the bubble aspect ratio was influenced by the tilt angle of the needle, and the bubbles were affected by the shear force of the wall in the process of bubble generation when the needle was tilted. This resulted in the shape of the bubble gradually changing from near-spherical to a ball-cap with an increase in the needle tilt angle. The bubble velocity vector at the orifice varies with the diameter of the needle, as shown in Figure 17. When the needle diameter was small, the airflow velocity was observed to be mainly along the needle direction and the component of the airflow velocity in the direction of bubble motion was small. However, as the needle diameter increased, the component of the orifice velocity in the direction of bubble motion gradually increased, and the bottom velocity vector of the bubble also increased; thus, the bubble aspect ratio gradually decreased.
Figure 16.

Schematic diagram of the relationship between the initial bubble aspect ratio, pore inclination angle, and inner diameter.
Figure 17.

Initial bubble velocity vector at the orifice with different needle diameters: (a) d0 = 0.2 mm, (b) d0 = 0.3 mm, (c) d0 = 0.4 mm, and (d) d0 = 0.6 mm.
Figure 18 shows the effect of needle diameter and tilt angle on the initial bubble size. The bubble diameter increased with an increase in the needle diameter. However, the magnitude of the increase varied with the change in the needle tilt angle, and the bubble diameter showed a trend of first increasing and then decreasing with the increase in the needle tilt angle. Furthermore, when the needle diameter d0 = 0.2–0.3 mm, the bubble diameter was less affected by the needle tilt angle, and the difference between the bubble diameter was not pronounced when the needle diameter is the same, and when the needle diameter gradually increases (d0 = 0.4–0.6 mm), the bubble is subject to the shear force of the needle as well as the buoyancy force, which leads to a larger effect of the needle tilt angle on the bubble diameter.
Figure 18.

Effect of the needle tilt angle and diameter on the initial bubble size.
In this study, the VOF 2D model is used to analyze the trajectory and velocity change of bubbles in the process of movement, but there are limitations in the deformation analysis of bubbles in the process of movement. In the future research, a 3D model will be built to further study the bubble movement.
4.3. Effect of Initial Bubble Morphology on the Upward Motion of the Bubble
The relationship between the initial state and kinetic behavior of the bubbles was investigated using experiments and numerical simulations. The size and aspect ratio of the bubble are important for its motion characteristics during ascent when it leaves the orifice.
4.3.1. Effect of the Initial Aspect Ratio of the Bubble on Its Upward Motion
Figure 19 presents the motion of the ascending bubble when the needle diameter is 0.2 mm, which reflects the effect of the aspect ratio on the kinetic characteristics of the bubble. When the needle diameter was 0.2 mm, the difference in bubble diameter of the bubble (d = 1.68–1.75 mm) was small and the aspect ratio varied widely under different air hole tilt angles; therefore, the effect of this aspect ratio on the bubble motion characteristics can be explored. As shown in Figure 19, when the aspect ratio of the bubble was E < 0.73, the shape of the bubble was flat. Furthermore, during movement in the presence of liquid resistance, the surface of the bubble constantly oscillated, such that the bubble under the influence of inertial force oscillation increases. Thus, the smaller the aspect ratio of the bubble, the greater the oscillation amplitude. Nevertheless, when E = 0.83, the shape of the bubble was nearly spherical, and the bubble trajectory was roughly straight. Simultaneously, the bubble is less disturbed by the liquid during motion, and the free energy of the bubble surface is small. These behaviors were owing to the predominant effect of the viscous drag force over the inertial force.
Figure 19.
Effect of aspect ratio of the bubble on bubble motion in the absence of ultrasound: (a) E = 0.58, (b) E = 0.73, and (c) E = 0.83.
The effect of the aspect ratio of the bubble on the bubble motion characteristics under ultrasonic intervention is investigated, as shown in Figure 20. When ultrasound was introduced under the conditions shown in Figure 19, the bubbles changed their aggregation behavior from a loose state to an aggregated state under the action of ultrasound. Meanwhile, the bubbles with aspect ratios E < 0.73 formed “wrapped clusters” or “chain-like” bubble aggregates in the process of motion, and the velocity of the bubble motion decreased under the action of ultrasound. Additionally, these bubbles collided with the rising bubbles behind to form bubble clusters, thereby resulting in an increase in the number of bubbles in the ultrasound zone. When the aspect ratio of the bubble was 0.83, the bubbles fused under the action of ultrasound, which increased the sizes and decreased the number of bubbles. This indicated that the near spherical bubbles were more likely than the bubble of other shapes to fuse and form large bubbles under the influence of ultrasound.
Figure 20.
Effect of the initial aspect ratio of the bubbles on the bubble motion under the influence of ultrasound: (a) E = 0.58, (b) E = 0.73, and (c) E = 0.83.
4.3.2. Effect of the Initial Size of the Bubbles on Their Upward Motion
Figure 21 illustrates the effect of the different sizes of the initial bubbles on the bubble motion, and each image shows the motion trajectory of the bubble in the steady-state. Here, the initial aspect ratio of the bubbles fluctuated in the range of 0.58–0.63, and the difference had a small effect on the bubble motion; thus, the initial aspect ratio of the bubbles was concluded to be constant. Figure 21 shows that in the case of the same initial aspect ratio, the bubble trajectory is “S” shaped when the bubble diameter d < 2.68 mm. The bubble is subject to greater resistance by the liquid with the increase of bubble diameter, resulting in an increase in the range of bubble motion and more violent oscillation. However, when the bubble diameter d = 3.32 mm, the bubble trajectory showed a chaotic rise. The bubble volume was large at this time, bubble surface deformation was irregular during the motion, motion speed was large, and inertial force enhanced the oscillation of the bubble interface. Therefore, the bubble rose in a disorderly manner during the motion.
Figure 21.
Effect of the initial size of the bubble on the bubble motion in the absence of ultrasound: (a) d = 1.92 mm, (b) d = 2.68 mm, and (c) d = 3.32 mm.
Figure 22 illustrates the relationship between the bubble motion and initial size of the bubble under the influence of ultrasound. Notably, the initial size of the bubble has a significant effect on the bubble motion under the action of ultrasound. For the bubble diameter d = 1.92 mm, we observed that the bubbles gathered and formed different shapes and sizes of “wrapped clusters” aggregates in the rising process and the distribution of bubble is more dispersed. In contrast, for a bubble of diameter d = 2.68 mm, the bubbles begin to fuse (Figure 23) and collided with each other under the action of ultrasound, thereby resulting in an increase in the bubble diameter and a decrease in the number of bubbles. Moreover, when the bubble diameter d = 3.32 mm, the range of motion of the bubbles increased under the influence of acoustic radiation force, and the bubbles clustered with each other. However, no collision occurred to form bubble aggregates, thereby indicating that ultrasound had an effect on the motion trajectory of the bubbles with large diameters and had little effect on the clustering behavior of the bubbles.
Figure 22.
Effect of initial size of the bubble on bubble motion under ultrasonic action: (a) d = 1.92 mm, (b) d = 2.68 mm, and (c) d = 3.32 mm.
Figure 23.
Effect of ultrasound on bubble coalescence: (a) t = 0 s, (b) t = 0.2 s, (c) t = 0.5 s, and (d) t = 0.7 s.
Typically, a change in the gas input method is an important factor that affects the initial size and aspect ratio of the bubble. A change in the needle tilt angle will generate bubbles in the orifice when the left and right forces are nonuniform. Therefore, different degrees of bubble deformation affected the initial aspect ratio of the bubble. The increase in the needle diameter increased the size of the initial bubble generated at the orifice, which caused the bubble to oscillate on the surface during the rising process and affected the rising motion of the bubble. Therefore, the gas input method significantly affected the rising motion of the bubble by changing the morphological parameters of the initial bubble.
5. Conclusions
In this study, the VOF method and experimental analyses were used to study the initial state of the bubble and its influence on the dynamic behavior of the bubble during the rise of the flotation column. Moreover, the dynamic interactions between the bubbles and the structural parameters of the ultrasonic transducer were assessed. The following conclusions were drawn:
First, the relationship between the motion of the bubble and gas input method was shown. When the diameter of the needle was increased, the bubble size increased, and the lateral movement range of the bubble first increased and then decreased. In addition, the speed of the bubble motion increased with time, subsequently decreased, and finally stabilized. Additionally, the bubble speed increased with the increase in needle diameter in the uniform velocity phase. However, bubble agglomeration and coalescence occurred during the motion of the bubble under ultrasonic action, and the bubble size increased with the thickness of the vibrating plate.
The diameter of the needle and the tilt angle were important factors that affected the initial aspect ratio of the bubble. As the tilt angle and inner diameter of the air hole decreased, the aspect ratio of the bubble decreased, degree of deformation increased, and the bubble was typically mushroom-shaped and ball-cap-shaped. Furthermore, as the needle diameter increased, the initial bubble diameter increased. Additionally, the bubble diameter tended to increase and then decrease with the increase in the stomatal tilt angle.
Finally, the initial parameters of the bubble had a significant effect on its dynamic behavior. Under the static water conditions, the bubble oscillated during the rising process, and the lateral oscillation range of the bubble increased. Subsequently, the range decreased with an increase of the aspect ratio and, finally, rose vertically. Meanwhile, with the increase in the initial bubble diameter, the bubble motion trajectory changed from “S” shaped to a disorderly and chaotic rise. Nevertheless, with an increase in the initial aspect ratio of the bubble, aggregates were formed under the influence of ultrasound. Additionally, the bubbles began to fuse, which increased the size of the bubbles. Furthermore, the increase in the initial bubble diameter resulted in bubble coalescence.
Acknowledgments
This study was supported by the National Natural Science Foundation of China (52104258) and Natural Science Foundation of Shandong Province (ZR2021ME016).
The authors declare no competing financial interest.
References
- Shi K.; Wang J.; Wang S.; Yu Z.; Chen P.; Li S. Improving the flotation performance of coking coal using the reverse-direct flotation process. Energy Sources, Part A 2018, 40, 2886–2894. 10.1080/15567036.2018.1512686. [DOI] [Google Scholar]
- Zhou Y.; Albijanic B.; Tadesse B.; Wang Y.; Yang J. Investigation of bubble-particle attachment interaction during flotation. Miner. Eng. 2019, 133, 91–94. 10.1016/j.mineng.2018.12.023. [DOI] [Google Scholar]
- Li Y.; Chen J.; Shen L. Flotation Behaviors of Coal Particles and Mineral Particles of Different Size Ranges in Coal Reverse Flotation. Energy Fuel. 2016, 30, 9933–9938. 10.1021/acs.energyfuels.6b01516. [DOI] [Google Scholar]
- Wang A.; Yan X.; Wang L.; Cao Y.; Liu J. Effect of cone angles on single-phase flow of a laboratory cyclonic-static micro-bubble flotation column: Ply measurement and CFD simulations. Sep. Purif. Technol. 2015, 149, 308–314. 10.1016/j.seppur.2015.06.004. [DOI] [Google Scholar]
- Gungoren C.; Ozdemir O.; Wang X.; Ozkan S. G.; Miller J. D. Effect of ultrasound on bubble-particle interaction in quartz-amine flotation system. Ultrason. Sonochem. 2019, 52, 446–454. 10.1016/j.ultsonch.2018.12.023. [DOI] [PubMed] [Google Scholar]
- Kang W.; Li H. Enhancement of flaky graphite cleaning by ultrasonic treatment. R. Soc. Open Sci. 2019, 6, 191160. 10.1098/rsos.191160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen A. V.; Phan C. M.; Evans G. M. Effect of the bubble size on the dynamic adsorption of frothers and collectors in flotation. Int. J. Miner. Process. 2006, 79, 18–26. 10.1016/j.minpro.2005.11.007. [DOI] [Google Scholar]
- Nguyen A. V.; George P.; Jameson G. J. Demonstration of a minimum in the recovery of nanoparticles by flotation: theory and experiment. Chem. Eng. Sci. 2002, 61, 2494–2509. 10.1016/j.ces.2005.11.025. [DOI] [Google Scholar]
- Waters K. E.; Hadler K.; Cilliers J. J. The flotation of fine particles using charged microbubbles. Miner. Eng. 2008, 21, 918–923. 10.1016/j.mineng.2008.04.011. [DOI] [Google Scholar]
- Miettinen T.; Ralston J.; Fornasiero D. The limits of fine particle flotation. Miner. Eng. 2010, 23, 420–437. 10.1016/j.mineng.2009.12.006. [DOI] [Google Scholar]
- Nguyen A. V.; Evans G. M. Attachment interaction between air bubbles and particles in froth flotation. Exp. Therm. Fluid Sci. 2004, 28, 381–385. 10.1016/j.expthermflusci.2002.12.001. [DOI] [Google Scholar]
- Sarrot V.; Huang Z.; Legendre D.; Guiraud P. Experimental deter-mination of particles capture efficiency in flotation. Chem. Eng. Sci. 2007, 62, 7359–7369. 10.1016/j.ces.2007.08.028. [DOI] [Google Scholar]
- Tripathi M. K.; Sahu K. C.; Govindarajan R. Dynamics of an initially spherical bubble rising in quiescent liquid. Nat. Commun. 2015, 6, 6268. 10.1038/ncomms7268. [DOI] [PubMed] [Google Scholar]
- Sahu K. C. Double-diffusive instability in core–annular pipe flow. J. Fluid Mech. 2016, 789, 830–855. 10.1017/jfm.2015.760. [DOI] [Google Scholar]
- Premlata A. R.; Tripathi M. K.; Sahu K. C. Dynamics of rising bubble inside a viscosity-stratified medium. Phys. Fluids 2015, 27, 072105. 10.1063/1.4927521. [DOI] [Google Scholar]
- Premlata A. R.; Tripathi M. K.; Karri B.; Sahu K. C. Dynamics of an air bubble rising in a non-Newtonian liquid in the axisymmetric regime. J. Non-Newtonian Fluid Mech. 2017, 239, 53–61. 10.1016/j.jnnfm.2016.12.003. [DOI] [Google Scholar]
- Hoque M. M.; Moreno-Atanasio R.; Doroodchi E.; Joshi J. B.; Evans G. M.; Mitra S. Dynamics of a single bubble rising in a quiescent medium. Exp. Therm. Fluid Sci. 2022, 132, 110546. 10.1016/j.expthermflusci.2021.110546. [DOI] [Google Scholar]
- Sarhan A. R.; Naser J.; Brooks G. CFD modeling of bubble column: influence of physico-chemical properties of the gas/quid phases properties on bubble formation. Sep. Purif. Technol. 2018, 201, 130–138. 10.1016/j.seppur.2018.02.037. [DOI] [Google Scholar]
- Chen S.; Tao X.; Wang S.; Tang L.; Liu Q.; Li L. Comparison of air and oily bubbles flotation kinetics of long-flame coal. Fuel 2019, 236, 636–642. 10.1016/j.fuel.2018.08.131. [DOI] [Google Scholar]
- Chen S.; Wang S.; Li L.; Qu J.; Tao X.; He H. Exploration on the mechanism of enhancing low-rank coal flotation with cationic surfactant in the presence of oily collector. Fuel 2018, 227, 190–198. 10.1016/j.fuel.2018.04.003. [DOI] [Google Scholar]
- Ozkan S. G. Further investigations on simultaneous ultrasonic coal flotation. Minerals 2017, 7, 177. 10.3390/min7100177. [DOI] [Google Scholar]
- Mitra S.; Mainul Hoque M.; Evans G.; Nguyen A. V. Direct visualisation of bubble-particle interactions in presence of cavitation bubbles in an ultrasonic flotation cell. Miner. Eng. 2021, 174, 107258. 10.1016/j.mineng.2021.107258. [DOI] [Google Scholar]
- Yasmin D.; Mitra S.; Evans G. M. Analysis of dynamic interactions in a bubble-particle system in presence of an acoustic field. Miner. Eng. 2019, 131, 111–123. 10.1016/j.mineng.2018.11.008. [DOI] [Google Scholar]
- Ye L.; Zhu X.; Liu Y. Numerical study on dual-frequency ultrasonic enhancing cavitation effect based on bubble dynamic evolution. Ultrason. Sonochem. 2019, 59, 104744. 10.1016/j.ultsonch.2019.104744. [DOI] [PubMed] [Google Scholar]
- Jin L.; Wang W.; Tu Y.; Zhang K.; Lv Z. Effect of ultrasonic standing waves on flotation bubbles. Ultrason. Sonochem. 2021, 73, 105459. 10.1016/j.ultsonch.2020.105459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grzybek T.; Pietrzak R.; Wachowska H. The influence of oxidation with air in comparison to oxygen in sodium carbonate solution on the surface composition of coals of different ranks. Fuel 2006, 85, 1016–1023. 10.1016/j.fuel.2005.09.017. [DOI] [Google Scholar]
- Mao Y.; Bu X.; Peng Y.; Tian F.; Xie G. Effects of simultaneous ultrasonic treatment on the separation selectivity and flotation kinetics of high-ash lignite. Fuel 2020, 259, 116270. 10.1016/j.fuel.2019.116270. [DOI] [Google Scholar]
- Hong S.-J.; Li Y.-F.; Hsiao M.-J.; Sheng Y.-J.; Tsao H.-K. Anomalous wetting on a superhydrophobic graphite surface. Appl. Phys. Lett. 2012, 100, 121601. 10.1063/1.3697831. [DOI] [Google Scholar]
- Xu M.; Xing Y.; Gui X.; Cao Y.; Wang D.; Wang L. Effect of Ultrasonic Pretreatment on Oxidized Coal Flotation. Energy Fuel. 2017, 31, 14367–14373. 10.1021/acs.energyfuels.7b02115. [DOI] [Google Scholar]
- Ozuna S.; Hassasa B. V.; Millera J. D. Collectorless Flotation of Oxidized Pyrite. Colloids Surf., A 2019, 561, 349–356. 10.1016/j.colsurfa.2018.10.064. [DOI] [Google Scholar]
- Peng Y.; Mao Y.; Xia W.; Li Y. Ultrasonic flotation cleaning of high-ash lignite and its mechanism. Fuel 2018, 220, 558–566. 10.1016/j.fuel.2018.02.049. [DOI] [Google Scholar]
- Cilek E. C.; Ozgen S. Effect of ultrasound on separation selectivity and efficiency of flotation. Miner. Eng. 2009, 22, 1209–1217. 10.1016/j.mineng.2009.06.007. [DOI] [Google Scholar]
- Kang W.; Xun H.; Hu J. Study of the effect of ultrasonic treatment on the surface composition and the flotation performance of high-sulfur coal. Fuel Process. Technol. 2008, 89, 1337–1344. 10.1016/j.fuproc.2008.06.003. [DOI] [Google Scholar]
- Zhang H.-X.; Hou X.-Y.; Xu S.-X.; Li Z.-L.; Yu H.-F.; Shen X.-H. Enhanced desulfurizing flotation of coal using sonoelectrochemical method. Ultrason. Sonochem. 2013, 20, 1176–1181. 10.1016/j.ultsonch.2013.02.007. [DOI] [PubMed] [Google Scholar]
- Altun N. E.; Hwang J.-Y.; Hicyilmaz C. Enhancement of flotation performance of oil shale cleaning by ultrasonic treatment. Int. J. Miner. Process. 2009, 91, 1–13. 10.1016/j.minpro.2008.10.003. [DOI] [Google Scholar]
- Kang W.-z.; Xun H.-x.; Chen J.-t. Study of enhanced fine coal de-sulphurization and de-ashing by ultrasonic flotation. J. China Univ. Min. Technol. 2007, 17, 358–362. 10.1016/s1006-1266(07)60105-9. [DOI] [Google Scholar]
- Aldrich C.; Feng D. Effect of ultrasonic preconditioning of pulp on the flotation of sulphide ores. Miner. Eng. 1999, 12, 701–707. 10.1016/s0892-6875(99)00053-9. [DOI] [Google Scholar]
- Wang W.; Liu D.; Tu Y.; Jin L.; Wang H. Enrichment of residual carbon in entrained-flow gasification coal fine slag by ultrasonic flotation. Fuel 2020, 278, 118195. 10.1016/j.fuel.2020.118195. [DOI] [Google Scholar]
- Chen Y.; Ni C.; Xie G.; Liu Q.. Toward efficient interactions of bubbles and coal particles induced by stable cavitation bubbles under 600 kHz ultrasonic standing waves. Ultrason. Sonochem. 2020, 64. 10.1016/j.ultsonch.2020.105003. [DOI] [PubMed] [Google Scholar]
- Leighton T. G.; Walton A. J.; Pickworth M. J. W. Primary Bjerknes forces. Eur. J. Phys. 1990, 11, 47–50. 10.1088/0143-0807/11/1/009. [DOI] [Google Scholar]
- Minnaert M. XVI.On musical air-bubbles and the sounds of running water. Phil. Mag. 1933, 16, 235–248. 10.1080/14786443309462277. [DOI] [Google Scholar]
- Leighton T. G.; Pickworth M. J. W.; Walton A. J.; Dendy P. P. Studies of the cavitational effects of clinical ultrasound by sonoluminescence: 1. Correlation of sonoluminescence with the standing wave pattern in an acoustic field produced by a therapeutic unit. Phys. Med. Biol. 1988, 33, 1239–1248. 10.1088/0031-9155/33/11/002. [DOI] [Google Scholar]
- Maksimov A. O.; Leighton T. G. Acoustic radiation force on a parametrically distorted bubble. J. Acoust. Soc. Am. 2018, 143, 296–305. 10.1121/1.5020786. [DOI] [PubMed] [Google Scholar]