Analysis of natural convection for a Casson-based multiwall carbon nanotube nanofluid in a partially heated wavy enclosure with a circular obstacle in the presence of thermal radiation

Graphical abstract

Highlights

• •Casson Sodium alginate based MWCNT nanofluid is considered in a wavy enclosure for the first time.
• •Natural convection is analyzed in the presence of adiabatic/hot/cold obstacle.
• •The dimensional velocities, streamlines and isotherms are discussed thoroughly.
• •FEM simulations are done with thermal radiation.

Abstract

Introduction

Nanofluids are considered a better alternative to conventional fluids in many industrial situations and unfolding new opportunities for various applications owing to the optical and thermal properties of additive nanosized materials.

Objectives

In this study, the thermal and hydraulic characteristics of a Casson-based (sodium alginate) multiwall carbon nanotube (MWCNT) nanofluid were computationally investigated inside a wavy square enclosure containing a circular-shaped obstacle. The square enclosure comprised two cooled vertical walls and a wavy adiabatic top wall. The central part of the bottom wall comprised a heated wavy structure, and the remaining parts exhibited a flat and adiabatic structure.

Methods

The Navier–Stokes (N–S) equations and boundary conditions were established using the non-Newtonian Casson fluid model and Rosseland thermal radiation. The present problem was numerically simulated using the Galerkin finite element method for three types of obstacles, namely, adiabatic, hot, and cold. The impacts of Casson parameter (0.001 ≤ β ≤ 0.1), Rayleigh number (10³ ≤ Ra ≤ 10⁶), nanoparticle volume fraction (0.01 ≤ φ ≤ 0.1) and radiation parameter (1 ≤ Rd ≤ 4) are analysed. A numerical code validation was performed using the available benchmark results.

Results

The characteristics of the convective radiation heat transport were clearly analyzed through the stream function and isotherm plots. For all types of obstacles, the mean Nusselt number along the heated wavy wall increased with the Casson parameter, MWCNT volume fraction, Rayleigh number, and radiation parameter. Conclusion: The heat and flow characteristics of a Casson-based MWCNT nanofluid inside a wavy square enclosure were investigated. The mean Nusselt number was higher (lower) in the presence of cold (hot) obstacles.

Nomenclature

x, y

distance along the x and y coordinates (m)

X, Y

dimensionless distance along the x and y coordinates

u, v

x and y components of velocity (m/s)

U, V

x and y components of dimensionless velocity

L

length of the enclosure (m)

T

temperature (K)

$\left(\rho C_p\right)$

specific heat capacitance (kJ/ Km³)

$q_{r1}\text{and}{q}_{r2}$

Rosseland approximations

$k$

thermal conductivity (W m⁻¹ K⁻¹)

Pr

Prandtl number

$\mathit{Gr}$

Grashof number

$\mathit{Ra}$

Rayleigh number

$\mathit{Rd}$

radiation parameter

$N{u}_{\mathit{loc}}$

local Nusselt number

$N{u}_m$

mean Nusselt number

Greek symbols

$\beta$

Casson parameter

γ

coefficient of mean absorption

σ

Stefan–Boltzmann constant

$\rho$

density (kg m⁻³)

ν

kinematic viscosity (m² s⁻¹)

$\mu$

dynamic viscosity (kg m⁻¹ s⁻¹)

π_ct

critical value dependent on the fluid model

ψ

stream function

φ

volume fraction of MWCNT

Subscript and superscript

x

differentiation with respect to x

y

differentiation with respect to y

f

properties of the base fluid

nf

properties of the nanofluid

c

cold

h

hot

SA

properties of sodium alginate

MWCNT

properties of multiwall carbon nanotubes

Introduction

In many mechanical and industrial tools, including various heat exchangers, the most common working fluids are ethylene glycol, water, and engine oil, which exhibit a very low thermal conductivity. Even minor developments in the thermal characteristics of these working fluids will lead to considerable savings in terms of energy and cost. Numerous practical and theoretical experiments have been conducted to achieve advancements in the thermal properties of such working fluids. Initial research investigations have suggested the suspension of millimeter- or micrometer-sized particles in common working fluids. However, the practical implementation of this suggestion has various drawbacks, such as an increased pressure drop, component erosion owing to abrasion, and particle settlement. Because of numerous difficulties with millimeter- and micrometer-sized particles, Choi [1] pioneered a study on nanometer-sized particles within the working fluids and achieved an effective heat transfer performance. He proposed suspending nanometer-sized particles in the working fluids to overcome their typical poor thermal performance and achieve remarkable thermal efficiency. These novel fluids, known as nanofluids, are produced by incorporating nanosized metallic particles, carbon nanotubes (CNTs), or metallic oxides in the base fluids, such as water, engine oil, and ethylene glycol. Nanofluids have various applications in the cooling of equipment in engineering processes, nuclear reactors, imaging and sensing, drug delivery, fuel cells, microchips, etc. [2], [3], [4], [5].

The current research is primarily focused on CNTs and Casson-based sodium alginate nanofluids. CNTs were first popularized by Iijima in 1991 [6]. Ajayan and Iijima [7] used CNTs as a filler in nanocomposites owing to their excellent thermal, electrical, and mechanical properties. Based on their structure, CNTs are classified into single-wall carbon nanotubes (SWCNTs) and multiwall carbon nanotubes (MWCNTs). SWCNTs and MWCNTs exhibit both similar and contrasting properties. SWCNTs and MWCNTs have significant impacts on applied sciences, energy processes, manufacturing, and fabric sciences because of their flexibility, chemical and thermal stabilities, high conductivity, and strength [8]. Compared with Newtonian fluids, the non-Newtonian behavioral characteristics of rheological fluids are more suitable in food processing, drilling operations, petroleum products, and bioengineering processes. Understanding all the properties of non-Newtonian fluids using a single mathematical model is challenging. Researchers have proposed numerous complex models for non-Newtonian fluids, such as the second power-law model [9], Jeffrey fluid model [10], Maxwell fluid model [11], and viscoplastic fluid model. The Casson fluid model [12] is a viscoplastic fluid model. Casson fluids behave like a solid when the stress generated within the fluids is greater than the shear stress. These types of fluids have applications in many food processing industries. Some examples of Casson fluids include tomato sauce, honey, chocolate, blood, soup, and jelly. The present work focuses on sodium alginate-based nanofluids. Sodium alginate is a natural Casson fluid, which was discovered by Stanford in 1881 [13], [14]. It is extracted from brown algae and is generally used in various applications, such as cosmetics, textiles, pharmaceuticals, and food manufacturing. The flow characteristics of sodium alginate have been discussed in recent studies [15], [16], [17], [18], [19], [20], [21].

The nanofluid flow and related heat transfer process driven by natural convection inside wavy and complex geometries play an important role in many engineering and medical systems. The analysis of such processes is crucial in solar collectors, grain storage, heat radiators, refrigerator condensers, heat exchangers, diagnostic tests, cancer treatments, etc. The complex geometry of an enclosure can significantly affect the flow and thermal behaviors of the fluid inside the enclosure. Owing to the increasing number of applications of these nanofluids in various fields in which the enclosure geometry plays an important role, researchers from mechanical, chemical, and biomechanical engineering and applied mathematics fields have devoted their attention to such nanofluids in the recent years [22], [23], [24]. Oztop et al. [25] examined a Newtonian fluid flow inside a wavy enclosure with heat generation and reported that the amplitude of the wavy wall had a significant impact on the heat transfer rate. Sheremet et al. [26] performed heat transfer and entropy generation analyses of single-phase nanofluids inside a wavy enclosure. The natural convection of silver-water and alumina water nanofluids inside an inclined wavy enclosure with discrete isoflux boundary condition was investigated by Hussein et al. [27]. They successfully implemented heat lines and heat function techniques to describe heat transfer inside wavy enclosure. Oztop et al. [28] investigated CuO–water nanofluids in a partially heated wavy lid-driven enclosure using MHD effects. Several studies have [29], [30], [31], [32], [33], [34], [35], [36], [37], [38] reported various Newtonian nanofluid flows inside a wavy enclosure. Pop and Sheremet [39] studied the thermal radiation and viscous dissipation effects of a Casson fluid on heat transfer in a regular square enclosure with heated and cooled side walls and adiabatic top and bottom walls. They concluded that the heat transfer rate is suppressed with Eckert number. Mehmood et al. [40] investigated the non-Newtonian Casson fluid flow inside a square enclosure with a grid resolution of 128 × 128 using the finite volume method. Their study mainly focused on obtaining a numerical scheme for the Casson fluid square-enclosure problem. The investigation of a Casson fluid flow in a trapezoidal-shaped enclosure was reported by Hamid et al. [41]. They found that the Casson fluid parameter with lower values significantly impacts the heat transfer rate. The natural convection inside a porous square box with a Casson fluid was explored by Aneja et al. [42]. This porous square box comprised a partially heated bottom wall and cooled vertical walls. Alzahrani et al. [43] performed a numerical simulation to understand the behavior of entropy generation in a Casson fluid-filled rectangular enclosure with heated and cooled walls placed vertically. Recently, Khan et al. [44] conducted a numerical study on the flow of a Casson fluid inside a square enclosure with “Y”-shaped heated fin. They demonstrated that the presence of heated fin is beneficial for enhancing the heat transfer rate in the enclosure. All the aforementioned studies considered the general Casson fluid model with regular geometries.

To the best of the author’s knowledge, no investigations have been conducted on a particular Casson fluid inside a wavy square geometry. Hence, in the present computational study, the heat transfer behavior of a particular Casson (i.e., sodium alginate)-based MWCNT nanofluid flowing in a square enclosure with complex wavy walls and a circular obstacle was analyzed. As mentioned earlier, this type of problem has potential applications in heat exchangers, solar collectors etc. The model is explained in detail in the next section. Computational results for the governing Navier–Stokes (N–S) equations were obtained using the Galerkin finite element method (FEM). Finally, a thorough flow and heat transfer analysis was performed using streamlines, isotherms, dimensionless velocities, and Nusselt number plots.

Model of the geometry

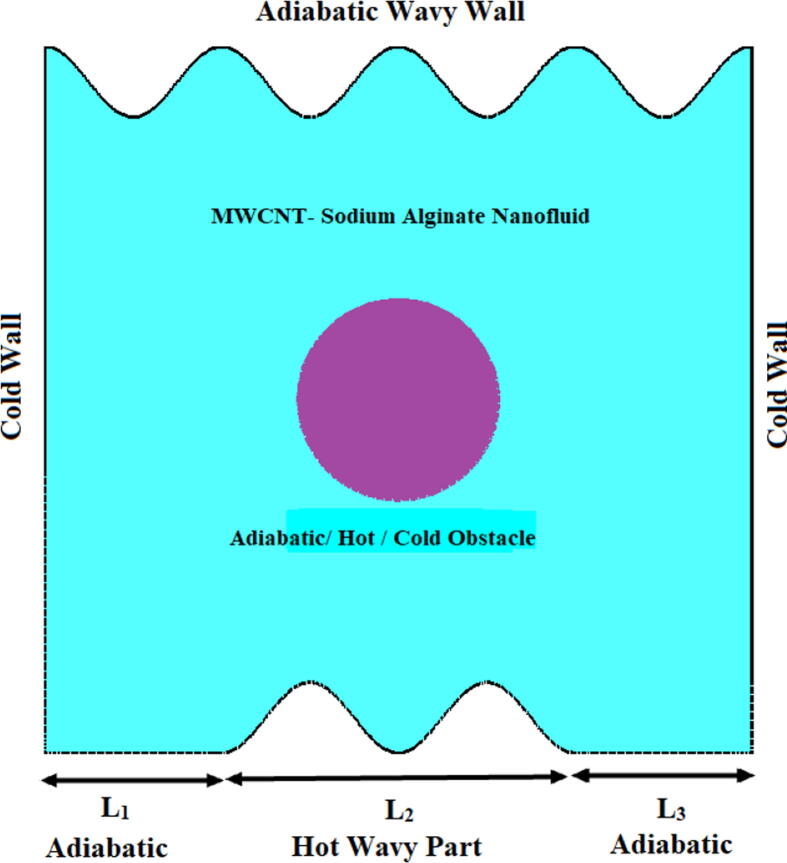
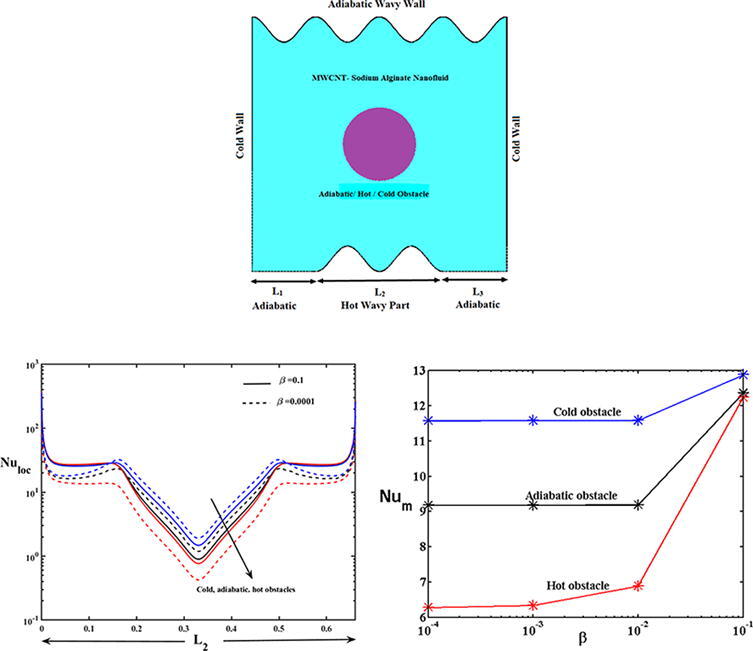
The physical layout of the present problem is presented in Fig. 1. Let us consider the flow of the sodium alginate-based MWCNT nanofluid inside an enclosure of length L and height H where L = H. The flow of this nanofluid was considered to be laminar, steady, incompressible, and radiative. The shape of the enclosure was assumed to be square. The fluid flow was cooled using two cooled side walls, and the temperature at these walls was T_c. No heat transfer occurred along the top wavy wall, here referred to as adiabatic. The bottom of the enclosure contained two adiabatic flat parts [L₁ (0 < x < 0.25L) and L₃ (0.75 L < x < 1L)] and a heated wavy part [L₂ (0.25L < x < 0.75L)]. The bottom and top wavy walls of the enclosure were modeled using the mathematical functions $y=A(1-cos(8\pi x/L))$ and $y=1-A(1-cos(8\pi x/L))$ respectively, where A = 0.5. The length of the heated wavy part (0.25 L < L₂ < 0.75L) was set as 0.5 L, and the temperature at L₂ was T_h.. A circular-shaped obstacle of radius 0.1 L was placed at the central part of the enclosure. The thermo physical properties of MWCNT and sodium alginate are given in Table 1.

Fig. 1.

Physical configuration.

Table 1.

Thermo physical properties of MWCNT and sodium alginate-based Casson fluid.

	ρ (kg/m3)	Cp (J/kg K)	k (W/m K)	Pr
Sodium alginate (C6H9NaO7)	989	4175	0.6376	6.45
Multiwall carbon nanotubes (MWCNTs)	1600	796	3000	–

The present geometry was analyzed using the following three cases:

• (i)Enclosure containing an adiabatic circular obstacle;
• (ii)Enclosure containing a hot circular obstacle;
• (iii)Enclosure containing a cold circular obstacle.

The x and y axes were fixed to be parallel and perpendicular to the bottom wall, respectively, and u and v denote the components of the velocity along the x and y axes, respectively. The sodium alginate-based Casson solution and MWCNT nanoparticles were assumed to be in thermal equilibrium. The thermal radiation was mathematically implemented using the Rosseland approximation.

Theoretical formulation

Casson fluid model

The rheological model of the Casson fluid is expressed as follow [12], [21]:

$${\tau }_{\mathit{lm}}=\left\{\begin{array}{c}2{\rho }_{\mathit{lm}}\left({\mu }_C+\frac{r_y}{{\left(2\pi \right)}^{0.5}}\right),\pi >{\pi }_{\mathit{ct}},\\ 2{\rho }_{\mathit{lm}}\left({\mu }_C+\frac{r_y}{{\left(2{\pi }_{\mathit{ct}}\right)}^{0.5}}\right),\pi <{\pi }_{\mathit{ct}},\end{array}\right)$$ (1)

where μ_C, ${\rho }_{\mathit{lm}}$, π_ct, and $r_y=\left(\frac{{\mu }_C{\left(2\pi \right)}^{0.5}}{\beta }\right)$ denote the plastic dynamic viscosity, (l, m)^th constituent of the rate of deformation, critical value, which depends on the fluid model, and yield stress, respectively. Furthermore, $\pi =\left({\rho }_{\mathit{lm}}{\rho }_{\mathit{lm}}\right)$. For Casson non-Newtonian fluid case, the dynamic plastic viscosity can be expressed as $\mu =\left({\mu }_C+\frac{r_y}{{\left(2\pi \right)}^{0.5}}\right),\left(\pi >{\pi }_{\mathit{ct}}\right).$ Now using the yield stress expression, the kinematic viscosity of the casson fluid can be derived as $\nu ={\mu }_C{\rho }^{-1}\left(1+{\beta }^{-1}\right),$ where β is casson parameter.

For the sodium alginate casson based MWCNT nanofluid, the kinematic viscosity can be written as ${\nu }_{\mathit{nf}}={\mu }_{\mathit{nf}}{\rho }_{\mathit{nf}}^{-1}\left(1+{\beta }^{-1}\right).$

Using Boussinesq approximation and the above assumptions, the governing equations can be expressed as follows:

$$v_y=-u_x,$$ (2)

$$u{u}_x+\frac{1}{{\rho }_{\mathit{nf}}}{p}_x={\mu }_{\mathit{nf}}{\left({\rho }_{\mathit{nf}}\right)}^{-1}\left(1+{\beta }^{-1}\right)\left(u_{\mathit{yy}}+u_{\mathit{xx}}\right)-v{u}_y,$$ (3)

$$u{v}_x+\frac{1}{{\rho }_{\mathit{nf}}}{p}_y+v{v}_y={\mu }_{\mathit{nf}}{\left({\rho }_{\mathit{nf}}\right)}^{-1}\left(1+{\beta }^{-1}\right)\left(v_{\mathit{yy}}+v_{\mathit{xx}}\right)+g\left(T-T_c\right){\beta }_{\mathit{nf}},$$ (4)

$$u{T}_x+T_{y}v=k_{\mathit{nf}}{\left({\left(\rho C_p\right)}_{\mathit{nf}}\right)}^{-1}\left(T_{\mathit{yy}}+T_{\mathit{xx}}\right)-{\left(q_{r1}\right)}_x{\left({\left(\rho C_p\right)}_{\mathit{nf}}\right)}^{-1}-{\left(q_{r2}\right)}_y{\left({\left(\rho C_p\right)}_{\mathit{nf}}\right)}^{-1}.$$ (5)

The corresponding boundary conditions are listed:

• (1)Square enclosure:

T = T_c, on the two vertical walls (0 < y < 1L),

T = T_h, on L₂ (0.25 L < x < 0.75L, $y=\frac{(1-cos(8\pi (x/L)\left)\right)}{2}$),

T_n = 0, on the top wavy wall, L₁ (0 < x < 0.25L) and L₃ (0.75L < x < 1L).

• (2)Obstacle:

$$\begin{array}{c}{T}_n=0,\left(\mathrm{adiabatic}\mathrm{circular}\mathrm{obstacle}\right),\hfill \\ T=T_h,\left(\mathrm{hot}\mathrm{obstacle}\right),\hfill \\ T=T_c,\left(\mathrm{cold}\mathrm{obstacle}\right),\hfill \end{array}$$ (6)

where ${\rho }_{\mathit{nf}}$, ${\mu }_{\mathit{nf}}$, ${\beta }_{\mathit{nf}}$, $k_{\mathit{nf}}$, ${\left(\rho C_p\right)}_{\mathit{nf}}$, and $\beta$ are the density, kinematic viscosity, thermal expansion coefficient, thermal conductivity, specific heat capacitance, and Casson parameter of the sodium alginate-based MWCNT nanofluids, respectively. The aforementioned properties can be characterized as follows [8]:

$${\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}=\left(1-\phi \right)+\phi {\rho }_{\mathit{MWCNT}}{\rho }_{\mathit{SA}}^{-1},$$ (7)

$${\mu }_{\mathit{nf}}{\mu }_{\mathit{SA}}^{-1}={\left(1-\phi \right)}^{-5/2},$$ (8)

$${\beta }_{\mathit{nf}}{\beta }_{\mathit{SA}}^{-1}=\left(1-\phi \right)+\phi {\beta }_{\mathit{MWCNT}}{\beta }_{\mathit{SA}}^{-1},$$ (9)

$$k_{\mathit{nf}}{k}_{\mathit{SA}}^{-1}=\frac{\left(1-\phi \right)+2\phi \left(k_{\mathit{MWCNT}}/\left(k_{\mathit{MWCNT}}-k_{\mathit{SA}}\right)\right)\left[ln\left(k_{\mathit{MWCNT}}+k_{\mathit{SA}}\right)-ln\left(2k_{\mathit{SA}}\right)\right]}{\left(1-\phi \right)+2\phi \left(k_{\mathit{SA}}/\left(k_{\mathit{MWCNT}}-k_{\mathit{SA}}\right)\right)\left[ln\left(k_{\mathit{MWCNT}}+k_{\mathit{SA}}\right)-ln\left(2k_{\mathit{SA}}\right)\right]},$$ (10)

$${\left(\rho C_p\right)}_{\mathit{nf}}=\left(1-\phi \right){\left(\rho C_p\right)}_{\mathit{SA}}+\phi {\left(\rho C_p\right)}_{\mathit{MWCNT}}.$$ (11)

The thermal radiation terms $q_{r1}\text{and}{q}_{r2}$ are expressed using the Rosseland approximation:

$$q_{r1}=\frac{-4\sigma }{3\gamma }{T}_x^4,q_{r2}=\frac{-4\sigma }{3\gamma }{T}_y^4.$$ (12)

Expanding T⁴ as $T^4\approx 4T_c^{3}T-3T_c^4$ (Taylor series of T_c and omitting the higher-order terms), we obtain

$$q_{r1}=-\frac{16\sigma T_c^3}{3\gamma }{T}_x,q_{r2}=-\frac{16\sigma T_c^3}{3\gamma }{T}_y.$$ (13)

Here, σ is the Stefan–Boltzmann constant and γ is the coefficient of mean absorption.

The following dimensionless variables can be defined as

$$\mathit{YL}=y,XL=x,V{\alpha }_{\mathit{SA}}=vL,U{\alpha }_{\mathit{SA}}=uL,{\rho }_{\mathit{SA}}{\alpha }_{\mathit{SA}}^{2}P=p{L}^2\text{and}\left(T_h-T_c\right)\theta =T-T_c$$ (14)

Using Eqs. (6), (7), (8), (9), (10), (11), (12), (13), the Eqs. (2), (3), (4), (5) and the boundary conditions in Eq. (5) can be converted into the following dimensionless expressions:

$$V_Y=-U_X,$$ (15)

$$U{U}_X+\frac{P_X}{{\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}}+V{U}_Y=\frac{{\mu }_{\mathit{nf}}{\mu }_{\mathit{SA}}^{-1}{Pr}_{\mathit{SA}}}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\left(U_{\mathit{YY}}+U_{\mathit{XX}}\right)\left(1+{\beta }^{-1}\right),$$ (16)

$$U{V}_X+\frac{P_Y}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}+V{V}_Y=\frac{{\mu }_{\mathit{nf}}{\mu }_{\mathit{SA}}^{-1}{Pr}_{\mathit{SA}}}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\left(V_{\mathit{YY}}+V_{\mathit{XX}}\right)\left(1+{\beta }^{-1}\right)+\left({\beta }_{\mathit{nf}}{\beta }_{\mathit{SA}}^{-1}\right)RaP{r}_{SA}\theta ,$$ (17)

$$U{\theta }_X+V{\theta }_Y=\left[\frac{\left(k_{\mathit{nf}}{k}_{\mathit{SA}}^{-1}\right)}{\left({\left(\rho C_p\right)}_{\mathit{nf}}{\left(\rho C_p\right)}_{\mathit{SA}}^{-1}\right)}\right]\left(1+\frac{4Rd}{3\left(\left(k_{\mathit{nf}}{k}_{\mathit{SA}}^{-1}\right)\right)}\right)\left({\theta }_{\mathit{YY}}+{\theta }_{\mathit{XX}}\right).$$ (18)

The converted boundary conditions are listed:

• (1)Square enclosure:

$$V=U=0,\theta =0,\text{on vertical walls (0 < Y < 1)}$$

$$V=U=0,\theta =1,{\text{on L}}_2\left(\text{Bottom wavy part}\right)\text{,}$$

$$V=U=0,{\theta }_n=0,{\text{on top wavy wall, L}}_2{\text{and L}}_3.$$

• (2)Obstacle:

$$\begin{array}{c}V=U=0,\theta =0.\left(\mathrm{adiabatic}\mathrm{obstacle}\right)\hfill \\ V=U=0,\theta =1.\left(\mathrm{hot}\mathrm{obstacle}\right)\hfill \\ V=U=0,\theta =0.\left(\mathrm{cold}\mathrm{obstacle}\right)\hfill \end{array}$$ (19)

${Pr}_{\mathit{SA}}=\frac{v_{\mathit{SA}}}{{\alpha }_{\mathit{SA}}}$ is the Prandtl number, $\mathit{Gr}=\frac{{\beta }_{\mathit{SA}}\left(T_h-T_c\right)L^3}{g^{-1}{v}_{\mathit{SA}}^{}}$ is the Grashof number, $\mathit{Ra}={Pr}_{\mathit{SA}}Gr$ is the Rayleigh number, and $\mathit{Rd}=\frac{4\sigma T_c^3}{k_{\mathit{SA}}\gamma }$ is the radiation parameter.

The heat transport coefficient along the heated wavy bottom part (L₂) can be analyzed using the following quantities:

$$N{u}_{\mathit{loc}}=-\left(\left(k_{\mathit{nf}}{k}_{\mathit{SA}}^{-1}\right)\right)\left(\left(1+\frac{4Rd}{3\left(\left(k_{\mathit{nf}}{k}_{\mathit{SA}}^{-1}\right)\right)}\right)\right){\left({\theta }_n\right)}_{n=0},\left(\text{local Nusselt number}\right)$$

$$\text{and}N{u}_m={\int }_{L_2}^{}N{u}_{\mathit{loc}}dn,\left(\text{mean Nusselt number}\right)$$

where n is the coordinate normal to the surface.

Numerical methodology

The numerical simulation was performed using Galerkin FEM [45], [46], [47], [48], [49], [50]. The pressure and the velocity are the unknown variables in the governing equations (16), (17). The penalty finite element method is used to solve the Eqs (16), (17) with the corresponding boundary conditions in Eq(19). The mass balance equation (15) is utilized as a constraint to obtain the pressure distribution. The pseudo-constitutive relation $P=-\mathrm{\Gamma }\left(V_Y+U_X\right)$ is used to eliminate the pressure. Since the equation (15) holds for large penalty parameter Γ, it was fixed in the range 10⁶–10⁸ [45], [46], [47]. The detailed numerical procedure can be assessed in [46], [47]. After removing the pressure the term, Eqs (16), (17) become

$$U{U}_X-\frac{\mathrm{\Gamma }\left(V_Y+U_X\right)}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}+V{U}_Y=\frac{{\mu }_{\mathit{nf}}{\mu }_{\mathit{SA}}^{-1}{Pr}_{\mathit{SA}}}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\left(U_{\mathit{YY}}+U_{\mathit{XX}}\right)\left(1+{\beta }^{-1}\right),$$ (20)

$$U{V}_X-\frac{\mathrm{\Gamma }\left(V_Y+U_X\right)}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}+V{V}_Y=\frac{{\mu }_{\mathit{nf}}{\mu }_{\mathit{SA}}^{-1}{Pr}_{\mathit{SA}}}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\left(V_{\mathit{YY}}+V_{\mathit{XX}}\right)\left(1+{\beta }^{-1}\right)+\left({\beta }_{\mathit{nf}}{\beta }_{\mathit{SA}}^{-1}\right)RaP{r}_{SA}\theta .$$ (21)

The unknown velocity and temperature are approximated by the basis function ${\left\{{\mathrm{H}}_k\right\}}_{k=1}^N$ as follow [41], [42], [43], [44], [45], [46]

$$V\approx \sum _{k=1}^N{V}_k{\mathrm{H}}_k\left(X,Y\right),U\approx \sum _{k=1}^N{U}_k{\mathrm{H}}_k\left(X,Y\right),\theta \approx \sum _{k=1}^N{\theta }_k{\mathrm{H}}_k\left(X,Y\right)$$ (22)

With the help of Galerkin FEM and the above approximations, we obtain the following non-residual equations at the internal domain nodes

$$\begin{array}{c}{R}_i^{(U)}=\sum _{k=1}^N{U}_k{\int }_{\mathrm{\Omega }}\left[\left(\sum _{k=1}^N{U}_k{\mathrm{H}}_k\right)\frac{\partial {\mathrm{H}}_k}{\partial X}+\left(\sum _{k=1}^N{V}_k{\mathrm{H}}_k\right)\frac{\partial {\mathrm{H}}_k}{\partial Y}\right]{\mathrm{H}}_{i}dXdY+\frac{\mathrm{\Gamma }}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\ast \\ \left[\sum _{k=1}^N{U}_k{\int }_{\mathrm{\Omega }}\frac{\partial {\mathrm{H}}_i}{\partial X}\frac{\partial {\mathrm{H}}_k}{\partial X}dXdY+\sum _{k=1}^N{V}_k{\int }_{\mathrm{\Omega }}\frac{\partial {\mathrm{H}}_i}{\partial X}\frac{\partial {\mathrm{H}}_k}{\partial Y}dXdY\right]\\ +\frac{{\mu }_{\mathit{nf}}{\mu }_{\mathit{SA}}^{-1}{Pr}_{\mathit{SA}}\left(1+{\beta }^{-1}\right)}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\left[\sum _{k=1}^N{U}_k{\int }_{\mathrm{\Omega }}\left[\frac{\partial {\mathrm{H}}_i}{\partial X}\frac{\partial {\mathrm{H}}_k}{\partial X}+\frac{\partial {\mathrm{H}}_i}{\partial Y}\frac{\partial {\mathrm{H}}_k}{\partial Y}\right]dXdY\right],\end{array}$$ (23)

$$\begin{array}{c}{R}_i^{\left(V\right)}=\sum _{k=1}^N{V}_k{\int }_{\mathrm{\Omega }}\left[\left(\sum _{k=1}^N{U}_k{\mathrm{H}}_k\right)\frac{\partial {\mathrm{H}}_k}{\partial X}+\left(\sum _{k=1}^N{V}_k{\mathrm{H}}_k\right)\frac{\partial {\mathrm{H}}_k}{\partial Y}\right]{\mathrm{H}}_{i}dXdY+\frac{\mathrm{\Gamma }}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\ast \\ \left[\sum _{k=1}^N{U}_k{\int }_{\mathrm{\Omega }}\frac{\partial {\mathrm{H}}_i}{\partial Y}\frac{\partial {\mathrm{H}}_k}{\partial X}dXdY+\sum _{k=1}^N{V}_k{\int }_{\mathrm{\Omega }}\frac{\partial {\mathrm{H}}_i}{\partial Y}\frac{\partial {\mathrm{H}}_k}{\partial Y}dXdY\right]\\ +\frac{{\mu }_{\mathit{nf}}{\mu }_{\mathit{SA}}^{-1}{Pr}_{\mathit{SA}}\left(1+{\beta }^{-1}\right)}{\left({\rho }_{\mathit{nf}}{\rho }_{\mathit{SA}}^{-1}\right)}\left[\sum _{k=1}^N{V}_k{\int }_{\mathrm{\Omega }}\left[\frac{\partial {\mathrm{H}}_i}{\partial X}\frac{\partial {\mathrm{H}}_k}{\partial X}+\frac{\partial {\mathrm{H}}_i}{\partial Y}\frac{\partial {\mathrm{H}}_k}{\partial Y}\right]dXdY\right]\\ -\left({\beta }_{\mathit{nf}}{\beta }_{\mathit{SA}}^{-1}\right)Ra{Pr}_{\mathit{SA}}{\int }_{\mathrm{\Omega }}\left(\sum _{k=1}^N{\theta }_k{\mathrm{H}}_k\right){\mathrm{H}}_{i}dXdY,\end{array}$$ (24)

$$R_i^{(\theta )}=\sum _{k=1}^N{\theta }_k{\int }_{\mathrm{\Omega }}\left[\left(\sum _{k=1}^N{U}_k{\mathrm{H}}_k\right)\frac{\partial {\mathrm{H}}_k}{\partial X}+\left(\sum _{k=1}^N{V}_k{\mathrm{H}}_k\right)\frac{\partial {\mathrm{H}}_k}{\partial Y}\right]{\mathrm{H}}_{i}dXdY+\left[\frac{\left(k_{\mathit{nf}}{k}_{\mathit{SA}}^{-1}\right)}{\left({\left(\rho C_p\right)}_{\mathit{nf}}{\left(\rho C_p\right)}_{\mathit{SA}}^{-1}\right)}\right]\left(1+\frac{4Rd}{3\left(\left(k_{\mathit{nf}}{k}_{\mathit{SA}}^{-1}\right)\right)}\right)\left[\sum _{k=1}^N{\theta }_k{\int }_{\mathrm{\Omega }}\left[\frac{\partial {\mathrm{H}}_i}{\partial X}\frac{\partial {\mathrm{H}}_k}{\partial X}+\frac{\partial {\mathrm{H}}_i}{\partial Y}\frac{\partial {\mathrm{H}}_k}{\partial Y}\right]dXdY\right].$$ (25)

The bi-quadratic triangular elements with six nodes are used to divide the computational domain Ω. The above system of nonlinear algebraic equations is solved using the reduced integration and Newton–Raphson approach. At each iteration, a system of $3N\times 3N$ equations was obtained:

$$J\left(a^n\right)\left[a^n-a^{n+1}\right]=R(a^n).$$ (26)

Here, $J\left(a^n\right)$ and $R(a^n)$ are the Jacobian matrix and residual vector, respectively. The iterative process is terminated with the convergence criterion ${\left[\sum {\left(R_i^{(j)}\right)}^2\right]}^{0.5}⩽{10}^{-6}.$ The relationship between the velocities and stream functions for this flow problem is expressed as

$${\psi }_Y=U,-{\psi }_X=V,$$ (27)

which assumes the following form:

$${\psi }_{\mathit{YY}}+{\psi }_{\mathit{XX}}=-V_X+U_Y.$$

To investigate the stream function ψ, it is expanded into the basis set ${\left\{H_k\right\}}_{k=1}^N$:

$$\begin{array}{c}{R}_i^{(U)}=\sum _{k=1}^N{U}_k{\int }_{\mathrm{\Omega }}{H}_i\frac{\partial H_k}{\partial Y}dXdY-\sum _{k=1}^N{V}_k{\int }_{\mathrm{\Omega }}{H}_i\frac{\partial H_k}{\partial Y}dXd\\ +\sum _{k=1}^N{\psi }_k{\int }_{\mathrm{\Omega }}\left[\frac{\partial H_i}{\partial X}\frac{\partial H_k}{\partial X}+\frac{\partial H_i}{\partial Y}\frac{\partial H_k}{\partial Y}\right]dXdY,\end{array}$$ (28)

and ψ is obtained by solving the above N linear residual equations.

Steps associated with FEM

The steps associated with FEM can be explained briefly as follows.

• •Discretization of the computational domain (enclosure with obstacle) into triangular elements.
• •Derivation and assembly of element equations.
• •Implementation of boundary conditions and solution of assembled equations
• •Post processing of results.

Grid refinement test

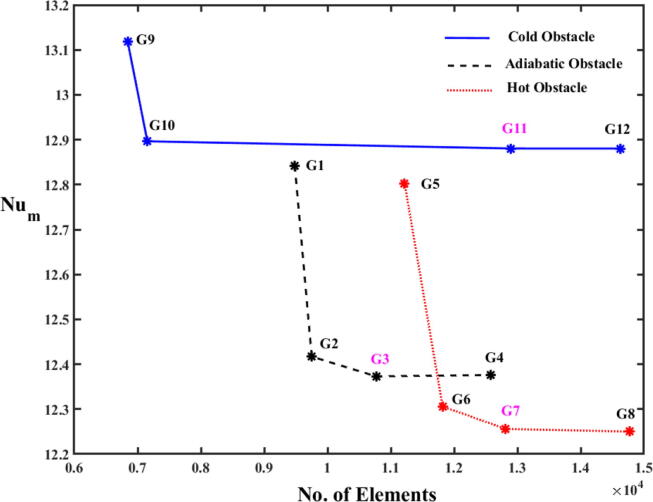
Before using the abovementioned numerical procedure, an appropriate mesh for the geometry must be selected; here, this was achieved using a grid independence test. The calculated mean Nusselt number values at various grids are plotted in Fig. 2. and listed in Table 2. The test was conducted for the adiabatic, hot, and cold obstacles (Fig. 2. and Table 2) with φ = 0.1, β = 0.1, Rd = 1, Ra = 10⁶, and Pr_SA = 6.45. The computations were performed using G3 (elements = 10769, nodes = 20607), G7 (elements = 12816, nodes = 24619), and G11 (elements = 12901, nodes = 24860)) grids for adiabatic, hot, and cold obstacles, respectively. These grid types were selected according to the accuracy of the mean Nusselt numbers and computational time.

Fig. 2.

Grid sensitivity test.

Table 2.

Grid sensitivity test with φ = 0.1, β = 0.1, Rd = 1, and Pr_SA = 6.45.

Type of Obstacle	Grid Type	No. of Nodes	No. of Cells	Num
Adiabatic	G1	9484	18,417	12.842
	G2	9752	18,842	12.417
	G3	10,769	20,607	12.373
	G4	12,582	23,827	12.376
Hot	G5	11,219	21,835	12.803
	G6	11,819	22,885	12.306
	G7	12,816	24,619	12.256
	G8	14,769	28,032	12.250
Cold	G9	6843	13,247	13.1199
	G10	7155	13,780	12.8924
	G11	12,901	24,860	12.88040
	G12	14,625	27,948	12.88024

Validation

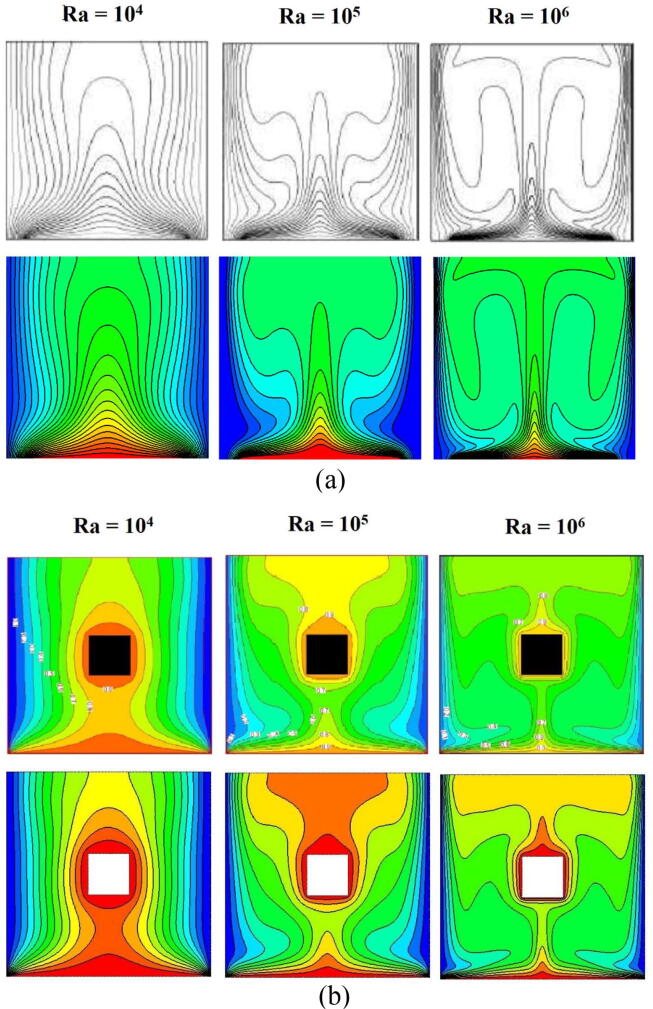
To validate the proposed code, simulations were conducted for the problem previously considered by De Vahl Davis [51]. A benchmark solution for the natural convection of an air-filled enclosure with adiabatic top and bottom walls and heated and cooled side walls was obtained by De Vahl Davis [51] for different Rayleigh numbers (Ra = 10³, 10⁴, 10⁵, etc). In the case of nanofluids, the same geometry was analyzed by Khanafer et al. [52] using the finite volume approach. They compared their findings with those of De Vahl Davis and presented their results. In this work, the mean Nusselt number values for Ra = 10³, 10⁴, and 10⁵ were calculated and compared with those reported in the studies of Khanafer el al. [52] and De Vahl Davis [51] (Table 3). Additionally, the patterns of the isotherms were compared with the results obtained by Calcagni et al. [53] and Rahmati and Tahery [54]. The free convective heat transfer in a square enclosure was experimentally and numerically analyzed by Calcagni et al. [53] using a bottom heater with different lengths. Rahman and Tahery [54] investigated the free convection flow of TiO₂-water nanofluid in a bottom heated enclosure with hot square obstacle and presented the results for at various Rayleigh numbers (Ra = 10⁴, 10⁵ and 10⁶) with 4% percentage of nanoparticle volume fraction and Pr = 6.2. To validate the pattern, the code implemented herein was run for the cases of Calcagni et al. [53] (a bottom heater of length Ɛ = 4/5 with Ra = 10⁴, 10⁵ and 10⁶) and Rahman and Tahery [54] and the corresponding isotherm graphs are plotted in Fig. 3. Based on the excellent agreement between the results, the proposed code is inferred to be suitable to be applied to the present problem.

Table 3.

Comparison results of Nu_m for Pr_f = 0.71.

Ra		Num
	Present	Khanafer et al.[52] and (Error %)	De Vahl Davis [51] and (Error %)
103	1.1178	1.118 (0.0179)	1.118 (0.0179)
104	2.2450	2.245 (0.0)	2.243 (0.0892)
105	4.5232	4.522 (0.0265)	4.519 (0.0929)

Fig. 3.

Comparison of isotherms with available literature. (a) Calcagni et al. [53] with Pr = 0.71 (b) Rahman and Tahery [54] with Pr = 6.2 and φ = 0.04 (First rows of (a) and (b) correspond to Calcagni et al. [53] and Rahman and Tahery [54] results respectively, Second rows of (a) and (b) correspond to present results).

Results and discussion

The numerical procedure explained in the numerical methodology section was employed to simulate the nanofluid flow. The following values were constant throughout the investigation: φ = 0.1, Ra = 10⁶, Rd = 1, β = 0.1, and Pr_SA = 6.45. The impact of each individual parameter is described in corresponding graphs. The stream function, isotherms, the horizontal velocity along horizontal mid axis, the vertical velocity along vertical mid axis, the local Nusselt number and mean Nusselt number are plotted in the Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15.

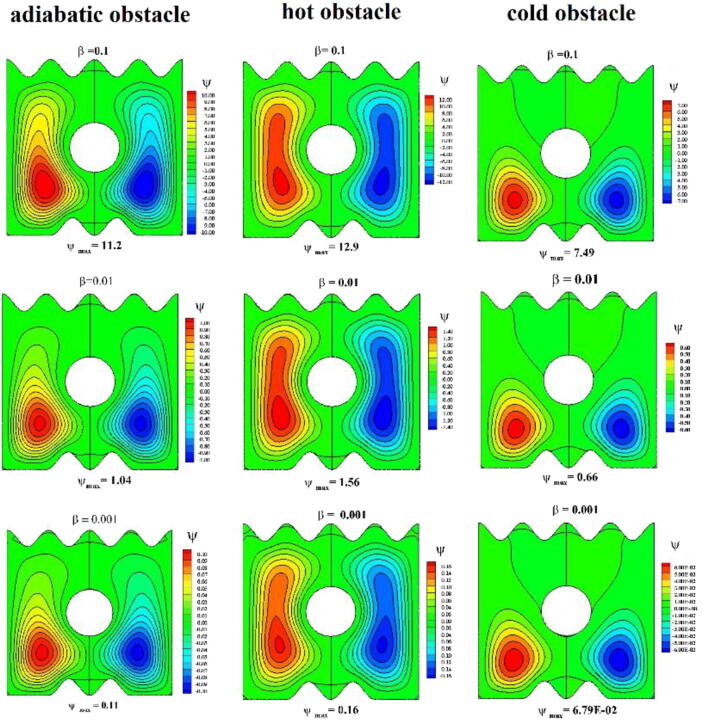
Fig. 4.

Impact of the Casson parameter (β) on the streamlines of the sodium alginate-based MWCNT nanofluid with φ = 0.1, Ra = 10⁶, Rd = 1, and Pr_SA = 6.45.

Fig. 5.

Impact of the Casson parameter (β) on the isotherms of the sodium alginate-based MWCNT nanofluid with φ = 0.1, Ra = 10⁶, Rd = 1, and Pr_SA = 6.45.

Fig. 6.

Impact of the Casson parameter (β) with φ = 0.1, Ra = 10⁶, Rd = 1, and Pr_SA = 6.45 on (a) the variation in velocity U (b) the variations in velocity V (c) local Nusselt number along the heated wavy bottom, and (d) mean Nusselt number along the heated wavy bottom.

Fig. 7.

Impact of the nanoparticle volume fraction (φ) on the streamlines of the sodium alginate-MWCNT nanofluid with β = 0.1, Ra = 10⁶, Rd = 1, and Pr_SA = 6.45.

Fig. 8.

Impact of the nanoparticle volume fraction (φ) on the isotherms of the sodium alginate-based MWCNT nanofluid with β = 0.1, Ra = 10⁶, Rd = 1, and Pr_SA = 6.45.

Fig. 9.

Impact of the nanoparticle volume fraction (φ) with β = 0.1, Ra = 10⁶, Rd = 1, and Pr_SA = 6.45 on (a) the variation in velocity U (b) the variations in velocity V (c) local Nusselt number along the heated wavy bottom, and (d) mean Nusselt number along the heated wavy bottom.

Fig. 10.

Impact of the Rayleigh number (Ra) on the streamlines of the sodium alginate-based MWCNT nanofluid with β = 0.1, Rd = 1, and Pr_SA = 6.45.

Fig. 11.

Impact of the Rayleigh number (Ra) on the isotherms of the MWCNT-sodium alginate nanofluid with β = 0.1, Rd = 1, and Pr_SA = 6.45.

Fig. 12.

Impact of the Rayleigh number (Ra) with β = 0.1, Rd = 1, and Pr_SA = 6.45 on (a) the variation in velocity U (b) the variations in velocity V (c) local Nusselt number along the heated wavy bottom, and (d) mean Nusselt number along the heated wavy bottom.

Fig. 13.

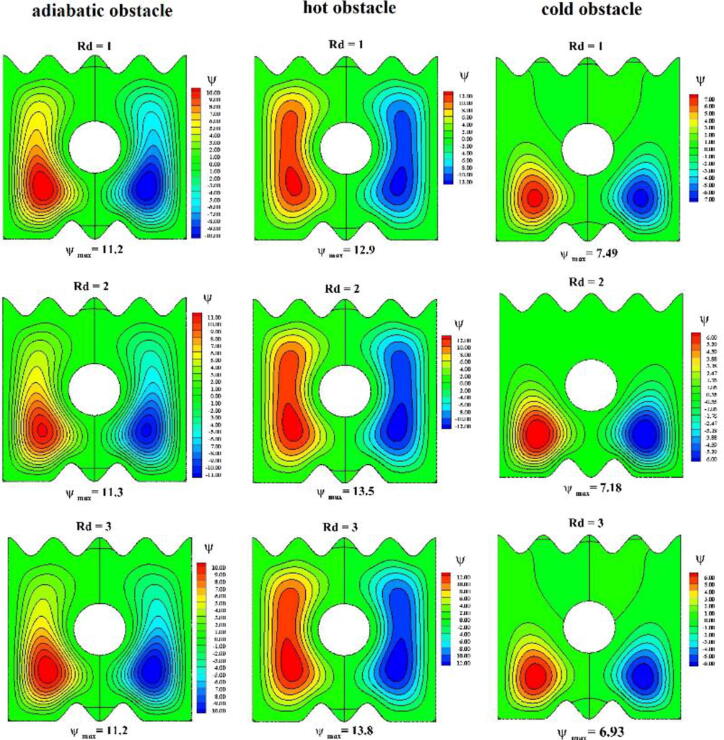
Impact of the radiation parameter (Rd) on the streamlines of the sodium alginate-based MWCNT nanofluid with β = 0.1, Ra = 10⁶, Rd = 1, and Pr_SA = 6.45.

Fig. 14.

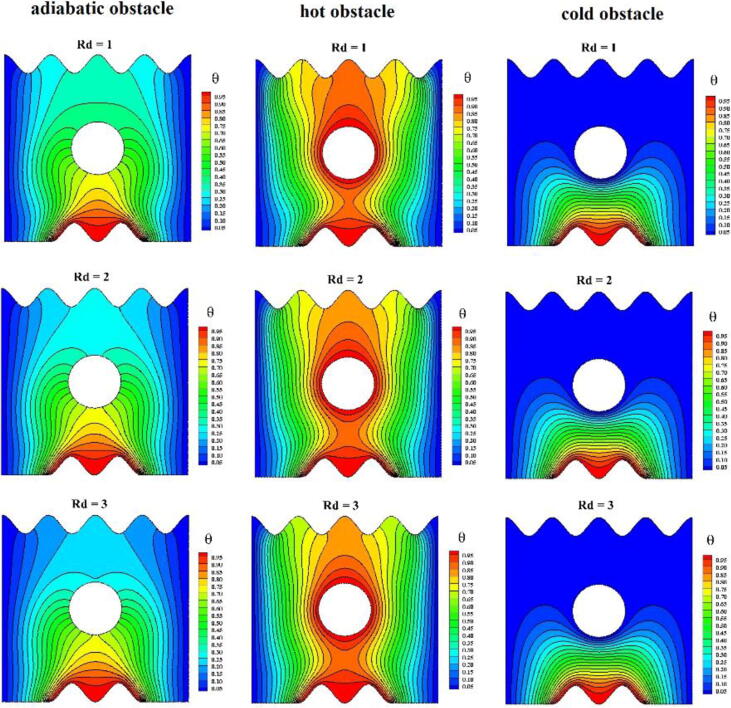
Impact of the radiation parameter (Rd) on the isotherms of the sodium alginate-based MWCNT nanofluid with β = 0.1, Ra = 10⁶ and Pr_SA = 6.45.

Fig. 15.

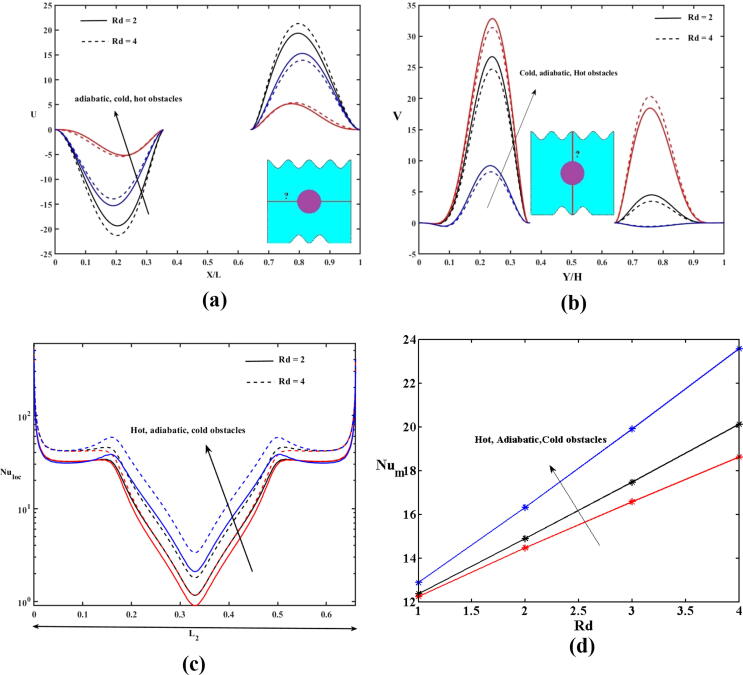
Impact of the radiation parameter (Rd) with β = 0.1, Ra = 10⁶, and Pr_SA = 6.45 on (a) the variation in velocity U (b) the variations in velocity V (c) local Nusselt number along the heated wavy bottom, and (d) mean Nusselt number along the heated wavy bottom.

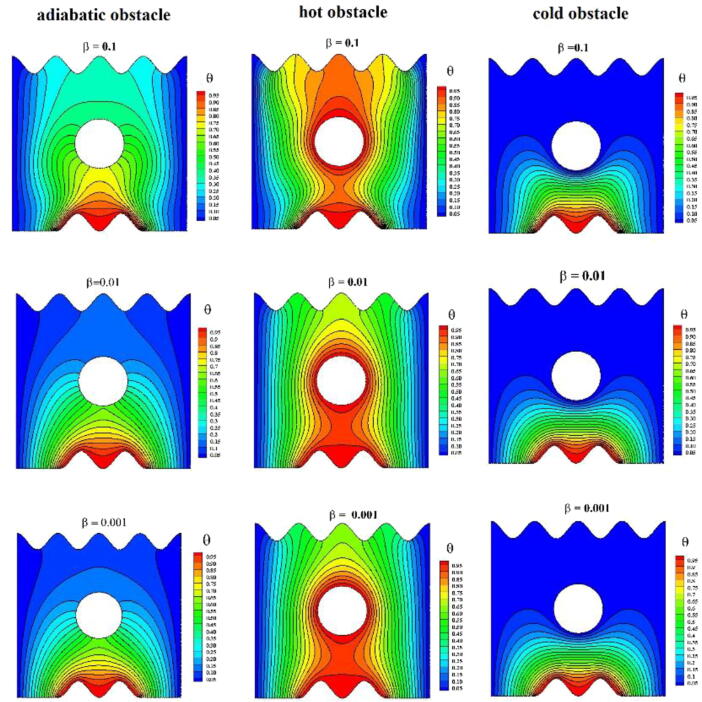
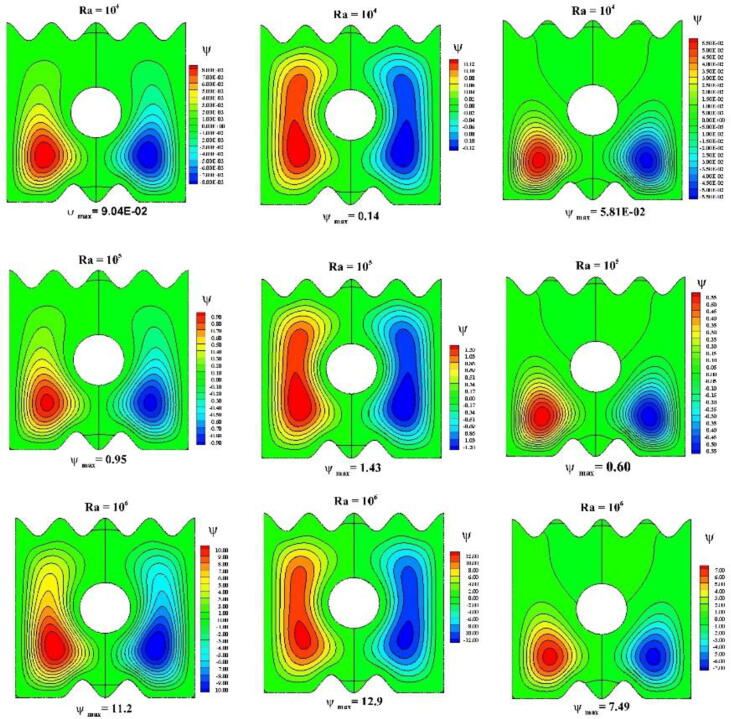
The impact of the Casson parameter (β = 0.1, 0.01, and 0.001) on the stream function and isotherms of the sodium alginate-based MWCNT nanofluid inside the enclosure is shown in Fig. 4, Fig. 5 for the adiabatic, hot, and cold obstacles. A symmetric behavior was observed in both the stream functions and isotherms for all types of obstacles. A pair of rotating cells was formed inside the enclosure. In the case of hot and adiabatic obstacles, these rotating cells filled the entire enclosure (β = 0.1) because of the heat provided by the heated wavy part and reduced density owing to buoyancy; the fluid raised up and the density of the moving fluid improved because of the heat absorption of the cold walls. Then, the fluid moved in a circular trajectory. The adiabatic obstacle acted as a barrier in the fluid motion; hence, the fluid formed laminar boundary layers around the obstacle. The hot obstacle also acted as a barrier in the fluid motion; however, it provided additional heat to the moving nanofluid. Thus, the fluid further raised up because of this additional energy and moved in a circular trajectory. The circular trajectories are elongated upward in the enclosure containing the hot obstacle. Consequently, the streamlines are more intense in the enclosure containing the hot obstacle compared with the enclosure containing the adiabatic obstacle. However, in the case of the cold obstacle, the fluid raised up because of the heated wavy part and was cooled by the walls and obstacle. Thus, the fluid moved in a circular trajectory only in the lower part of the enclosure, i.e., below the obstacle. The streamline intensity was significantly lower in the enclosure containing the cold obstacle. The central part of the cells is located below the obstacle.

The impact of the Casson parameter on the streamlines can be observed in Fig. 4. An increase in the Casson parameter (β = 0.001, 0.01, and 0.1) strengthened the streamlines of the sodium alginate-based MWCNT nanofluid inside the enclosure containing all types of obstacles. Weaker streamlines were observed for β = 0.001; this result was observed because the viscosity of the Casson fluid decreased as the Casson parameter increased. Hence, the fluid moved faster for higher Casson parameter values. A notable result was observed in the enclosure containing the adiabatic obstacle the occupancy of the streamlines inside the enclosure increased as the Casson parameter value increased.

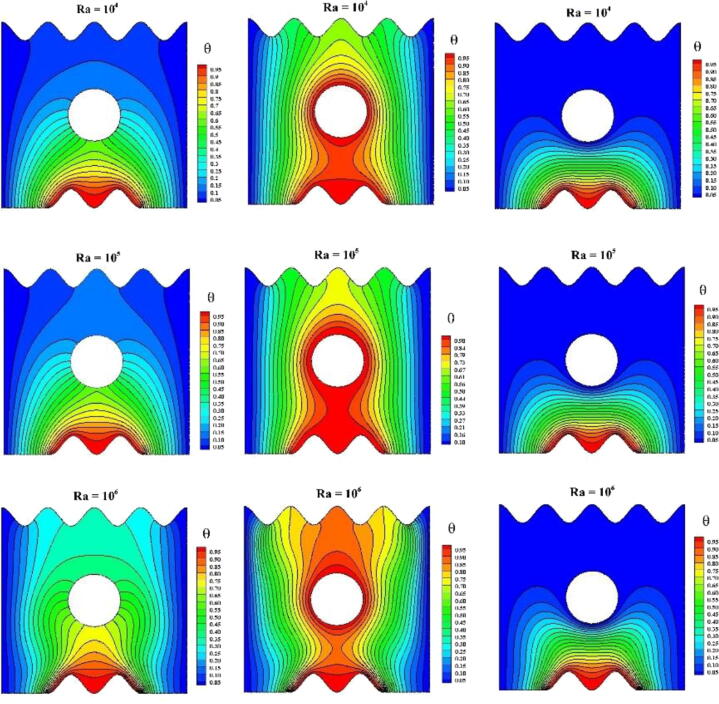
The isotherms of the sodium alginate-based MWCNT nanofluid are plotted in Fig. 5. The heat transfer inside the enclosure can be analyzed using the isotherms. In the case of the hot/adiabatic obstacle, the isotherms occupied the entire enclosure. The stronger isotherms were observed only below the cold obstacle. The thermal boundary layers grew from the wavy bottom of the enclosure in cases of adiabatic and cold obstacles. Conversely, in the case of the hot obstacle, the thermal boundary layers grew from both the wavy bottom part and the hot obstacle. The temperature inside the enclosure decreased with decreasing values of β. A decreasing β value indicates an increase in the nanofluid viscosity. The fluid viscosity decreased when β = 0.1 and increased for β = 0.01 and 0.001. For β = 0.1, the nanofluid moved faster because of the low viscosity and inertial force; thus, the transfer of heat from the heated wavy part propagated to the entire enclosure containing the adiabatic obstacle. A plum-shaped isotherm can be observed in the heated wavy part and was obstructed by the adiabatic obstacle. Some isotherms were parallel to the cooled side walls, which developed from the adiabatic bottom part. The growth of all the isotherms was obstructed by the cold obstacle, and the heat energy did not disperse in the entire region in this case. In the enclosure containing the hot obstacle, the isotherms were parallel to the side walls. A plum-shaped isotherm can be observed above the hot obstacle, and the isotherms were concentrated at the top corners of the enclosure. The thermal boundary layers were very thin at the initial and end points of the wavy part when β = 0.1. By decreasing β, the temperature gradient decreased inside the enclosure; this is because decreasing β increases the inertial forces, which arrest the velocity of the moving fluid and nanotubes. Hence, the transfer of heat via convection decreases, and conduction remains the dominant mechanism for heat transfer inside the enclosure.

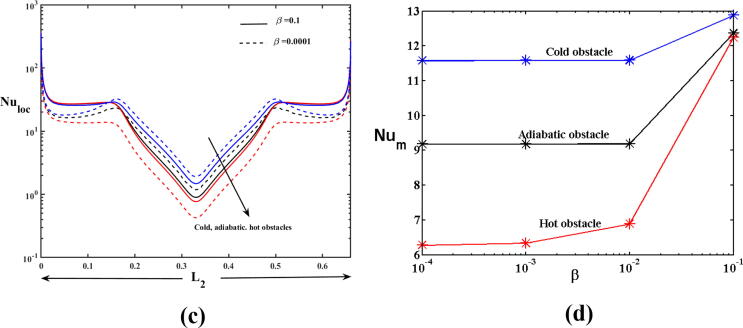
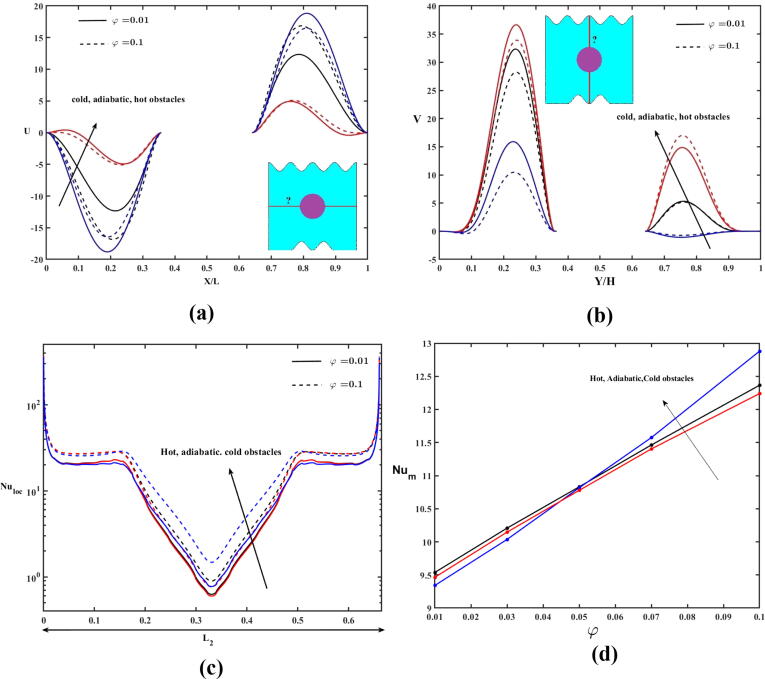
The variations in the dimensionless velocities (U and V) and local and mean Nusselt numbers are presented in Fig. 6. It is observed that ‘U’ is minimum between left wall and the obstacle while maximum between obstacle and the right wall in all cases with all parameters (See Fig. 6, Fig. 9, Fig. 12, Fig. 15). The increasing values of β decreased the velocity ‘U’ in the interval 0 < X/L < 0.4 and increased in the interval 0.6 < X/L < 1. The velocity ‘U’ was higher in the enclosure with hot obstacle in between the left wall and the obstacle and an opposite impact was observed in between the obstacle and right wall (Fig. 6(a)). The vertical velocity ‘V’ increased with β, below and above the obstacle in the enclosure with hot and adiabatic obstacles. In the case of cold obstacle, ‘V’ increased below the obstacle and decreased above the obstacle. The velocity was higher in the enclosure with adiabatic obstacle (Fig. 6(b)). The impact of the Casson parameter on the local and mean Nusselt numbers along the heated wavy bottom part of the enclosure is presented in Fig. 6(c) and (d). The local Nusselt number reached its minimum value in the central part of L₂ and its maximum value at the initial and end points of wavy part of the enclosure. Furthermore, the local Nusselt number increased with an increase in the Casson parameter value near the left and right edges of the heated wavy L₂ part in all the three obstacle cases but an opposite behavior is noted at the central part of L₂ in the adiabatic and cold obstacle cases. The mean Nusselt number also increased as a function of the Casson parameter; it was higher in the enclosure containing the cold obstacle and lower in the enclosure containing the hot obstacle.

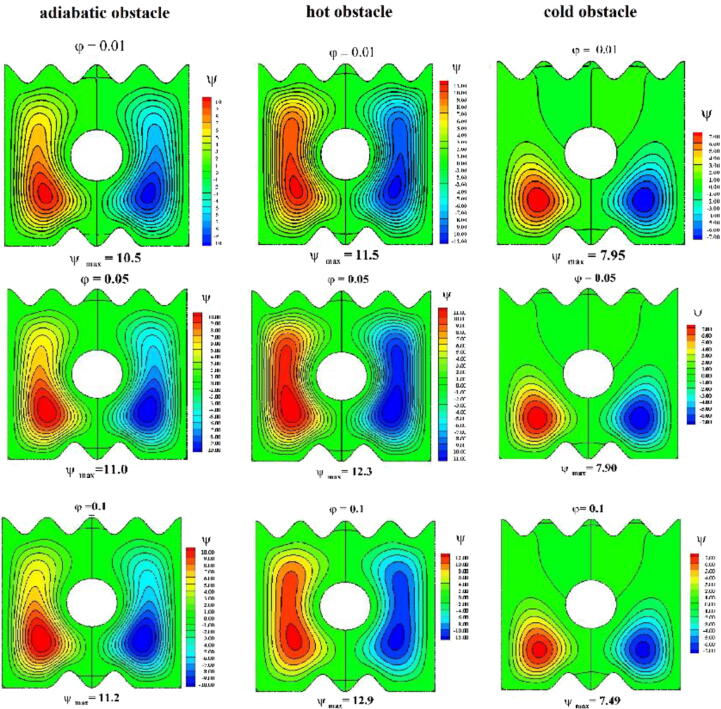
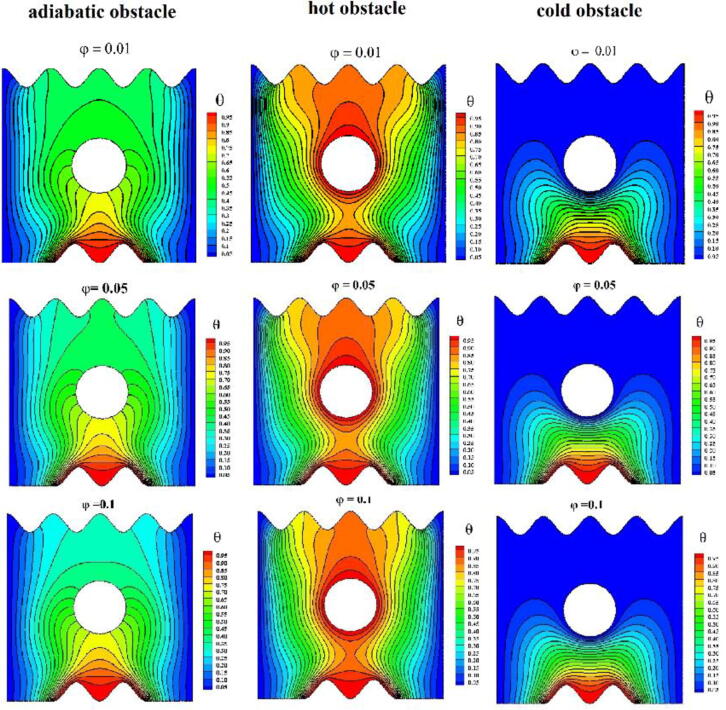
The streamlines and isotherms for different values of the MWCNT volume fraction are presented in Fig. 7, Fig. 8. The flow and thermal patterns are similar to those already discussed in Fig. 4, Fig. 5 for β = 0.1. The MWCNT volume fraction in the sodium alginate solution had a significant impact on the inside of the enclosure containing the hot obstacle. The figures are plotted for φ in the range of 0.01–0.1. Increasing the volume fraction increased the strength of the streamlines in the enclosure containing the adiabatic/ hot obstacle and decreased in the case of cold obstacle. The effect of the volume fraction was not significant in the flow patterns inside the enclosure containing the hot and adiabatic obstacles.

A slight change can be observed in the isotherms with different volume fraction values inside the enclosure. Increasing the volume fraction of MWCNTs in the sodium alginate-based Casson fluid provided an additional resistance to the motion of the Casson fluid. Moreover, because of the increased buoyancy force, the motion of the nanofluid with a higher MWCNT volume fraction decreased. From the color bars of the isotherms, it can be observed that for a higher solid volume fraction, the dimensionless temperature decreased above the hot/adiabatic obstacle. Conversely, the volume fraction did not have a considerable impact on the isotherms in the enclosure containing the cold obstacle.

The impact of the volume fraction on U, V, and local and mean Nusselt numbers is shown in Fig. 9(a)–(d). The velocity U decreased with nanoparticle volume fraction between the left wall and the obstacle and increased between the obstacle and the right wall in the enclosure with hot and adiabatic obstacles (Fig. 9(a)). The nanoparticle volume fraction shows an interesting result in the enclosure containing cold obstacle. The increased values of φ increased ‘U’ in the interval 0 < X/L < 0.4 and decreased in 0.6 < X/L < 1. The horizontal velocity ‘U’ was higher in the enclosure with hot obstacle and lower in the enclosure with cold obstacle between the left wall and obstacle and a reverse trend can be observed between the obstacle and the right wall. The vertical velocity ‘V’ decreased below the obstacle with the increase of nanoparticle volume fraction in the enclosure with all types of obstacles (Fig. 9(b)). But the nanoparticle volume fraction parameter showed an opposite impact above the hot obstacle. The variation in the local Nusselt number along L₂ was similar to the variation described in Fig. 9(c). The local and mean Nusselt number increased as a function of φ along the wavy bottom part. This is because the increasing volume fraction of the MWCNTs increased the convection, as heat was carried along the base fluid. The mean Nusselt number was higher in adiabatic obstacle and lower in cold obstacle for the range 0.01 < φ < 0.05. But in the range of 0.05 < φ < 0.1, the mean Nusselt number was higher for cold obstacle and lower for hot obstacle (Fig. 9(d)).

Fig. 10, Fig. 11 show the impact of the Rayleigh number on the streamlines and isotherms of the sodium alginate-based MWCNT nanofluid. The strength of the streamlines was low for Ra = 10⁴ and increased as the Rayleigh number increased. The strength of the streamlines was high for Ra = 10⁶ because the buoyancy force increased as the Rayleigh number increased. Hence, the flow velocity increased with the buoyancy force and induced a stronger circular trajectory inside the enclosure containing all types of obstacles. Additionally, the stream lines occupied the entire enclosure only when the Rayleigh numbers were high (10⁵ and 10⁶). Based on the nature of the isotherms at high Rayleigh numbers, convection was the dominant mode of heat transfer for all types of obstacles. At Ra = 10⁵, the isotherms developed from the heated wavy part and spread toward the cooled walls in the enclosure containing the adiabatic obstacle. The isotherms spread toward the cooled walls from both the hot obstacle and heated wavy part, which were parallel to the cooled vertical walls. At Ra = 10⁶, a plum-shaped isotherm developed from the heated wavy part; this isotherm was obstructed by the adiabatic obstacle and spread through the entire enclosure. The density of the isotherms was higher at the top corners of the enclosure containing the adiabatic obstacle. In the enclosure containing the hot obstacle, two plum-shaped isotherms developed—one originated from the heated part and the other from the upper part of the hot obstacle. This is because of the higher buoyancy and faster movement of the nanofluid, as natural convection became the dominant mode of heat transfer.

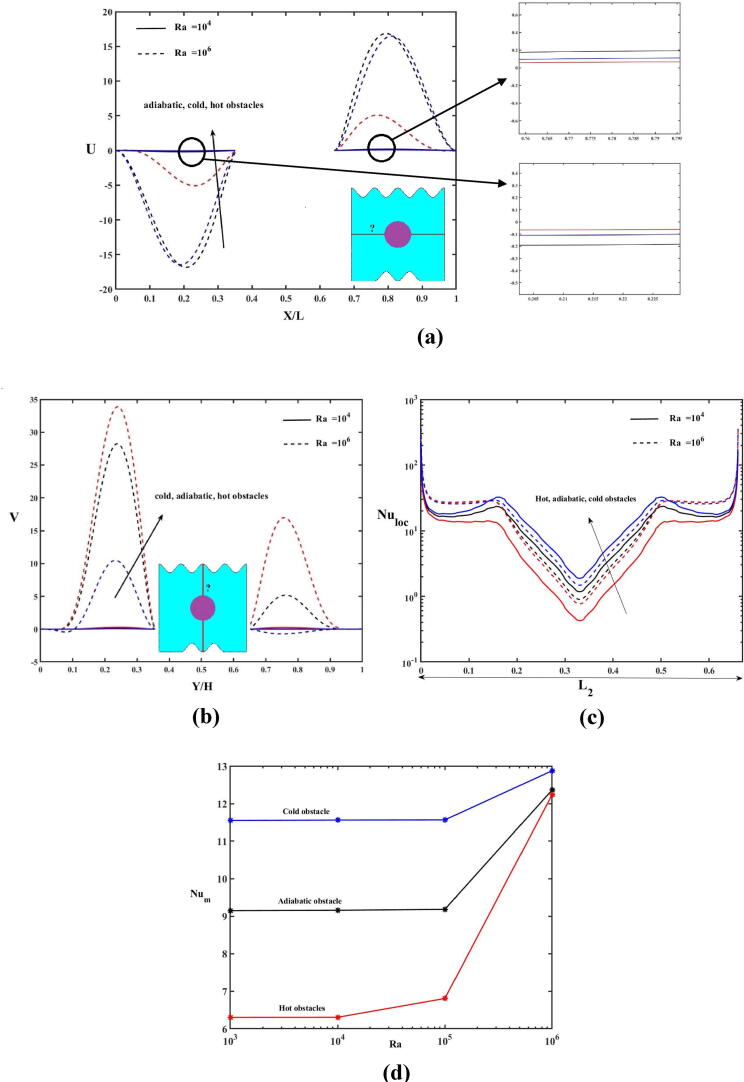
The Rayleigh number had a significant influence on the dimensionless velocities (U and V) and local and mean Nusselt numbers (Fig. 12(a)–(d)). The increased value of Rayleigh number diminished the velocity ‘U’ in 0 < X/L < 0.4 while enhanced in 0.6 < X/L < 1. The horizontal velocity was maximum in the enclosure with hot obstacle between left wall and obstacle with higher Raleigh number while it was minimum between the obstacle and right wall of the enclosure (Fig. 12(a)). The vertical velocity raised with Rayleigh number above\below obstacle in the cases of enclosure with hot and adiabatic obstacles. But in the case of cold obstacle, the vertical velocity ‘V’ decreased with higher Rayleigh number above the obstacle (Fig. 12(b)). The local Nusselt number increased with an increase in the Rayleigh number in the enclosure with hot and adiabatic obstacles and decreased with Rayleigh number in the enclosure containing cold obstacle in 0.15 < X/L < 0.5 of heated wavy part. The increased value of Rayleigh number increased the local Nusselt number in the intervals 0 < X/L < 0.15 and 0.5 < X/L < 0.65. The local Nusselt number attained maximum and minimum values at the edges and in the center of L₂, respectively (Fig. 12(c)). The mean Nusselt number also increased as a function of the Rayleigh number (Fig. 12(d)).

The influence of the radiation parameter on the streamlines and isotherms of the sodium alginate-based MWCNT nanofluid is shown in Fig. 13, Fig. 14. The radiation parameter had a limited impact on the stream function inside the enclosure containing the adiabatic obstacle. However, the strength of the stream function increased with Rd in the enclosure containing the hot obstacle, whereas it decreased in the enclosure containing the cold obstacle. A slight variation in the isotherms can be observed in the enclosure containing the adiabatic and hot obstacles. The temperature gradient near the top wavy adiabatic wall and below the obstacle decreased as the radiation parameter increased. For a lower radiation parameter, the isotherms were widely spread near the top wavy wall in the enclosure containing the hot obstacle. The impact of the radiation parameter on the isotherms of the enclosure containing the cold obstacle was negligible because of the occurrences of radiation heat transfer. In the mode of radiation heat transport, the MWCNTs in the sodium alginate base liquid absorbed and emitted the heat energy; hence, the heat diffused from the heated parts to cooled parts.

The impact of the radiation parameter on the dimensionless velocities and local and mean Nusselt numbers is shown in Fig. 15 (a)-(d). The increased radiation parameter decreased the velocity ‘U’ between the left wall and obstacle and enhanced the velocity between the obstacle and right wall (Fig. 15(a)). The vertical velocity is decreased with higher radiation parameter below the hot\adiabatic obstacle (Fig. 15(b)). It is enhanced above the hot obstacle with radiation parameter. Both the local and mean Nusselt numbers increased with the radiation parameter for all types of obstacles (Fig. 15(c) and (d)).

In addition, the correlations for the mean Nusselt number with the impacts of pertinent parameters (0.001 ≤ β ≤ 0.1, 10³ ≤ Ra ≤ 10⁶_, 0.01 ≤ φ ≤ 0.1 and 1 ≤ Rd ≤ 4) are obtained as follows

$$\begin{array}{c}N{u}_{\mathit{avg}}=\text{4.4873}+\text{0.4479}\beta \text{+ 0.44873}\phi -\text{4.5103}\times {\text{10}}^{-6}Ra+\text{4.4873 Rd}+\text{0.044888}{\beta }^2\\ +\text{0.045266}{\phi }^2\text{+ 3.6039}\times {\text{10}}^{-12}R{a}^2+\text{0.031399}{\text{Rd}}^2+\text{0.044873}\beta \phi +\text{3.2091}\times {10}^{-5}\beta Ra\\ +\text{0.44873}\beta \text{Rd}+\text{3.0292}\times {10}^{-5}\phi Ra+\text{0.44873}\phi R\text{d}-\text{2.1501}\times {10}^{-6}Ra\text{Rd}.\left(\text{Adiabatic obstacle}\right)\end{array}$$

$$\begin{array}{c}N{u}_{\mathit{avg}}=\text{3.0956}+\text{0.30899}\beta \text{+ 0.30956}\phi -\text{2.8728}\times {\text{10}}^{-6}Ra+\text{3.0956 Rd}+\text{0.030967}{\beta }^2\\ +\text{0.031232}{\phi }^2+\text{7.7364}\times {\text{10}}^{-13}R{a}^2{\text{- 0.043507 Rd}}^2+\text{0.030956}\beta \phi +\text{5.9132}\times {10}^{-5}\beta Ra\\ +\text{0.30956}\beta \text{Rd}+\text{2.9881}\times {10}^{-5}\phi Ra+\text{0.30956}\phi R\text{d}-\text{8.182}\times {10}^{-7}Ra\text{Rd}.\left(\text{Hot obstacle}\right)\end{array}$$

$$\begin{array}{c}N{u}_{\mathit{avg}}=\text{5.6568}+\text{0.56464}\beta \text{+}\text{0.56568}\phi -\text{3.0873}\times {\text{10}}^{-6}Ra+\text{5.6568 Rd}+\text{0.056587}{\beta }^2\\ +\text{0.057062}{\phi }^2+\text{1.7478}\times {\text{10}}^{-12}R{a}^2+{\text{0.051774 Rd}}^2+\text{0.056568}\beta \phi +\text{1.2015}\times {10}^{-5}\beta Ra\\ +\text{0.56568}\beta \text{Rd}+\text{3.8579}\times {10}^{-5}\phi Ra+\text{0.56568}\phi R\text{d}-\text{2.45}\times {10}^{-6}Ra\text{Rd}.\left(\text{Cold obstacle}\right)\end{array}$$

Conclusions

In this work, the flow characteristics of the sodium alginate-based MWCNT nanofluids were investigated inside a square wavy enclosure using the Galerkin FEM. The enclosure comprised (i) two cooled vertical walls, (ii) an adiabatic top wavy wall, (iii) a bottom wavy wall with a heated central part, and (iv) a circular obstacle (adiabatic, hot, and cold). Additionally, the thermal radiation impacts were considered. Numerical simulations were performed to analyze the impact of the Casson parameter, MWCNT volume fraction, Rayleigh number, and radiation parameter on the streamlines and isotherms of the fluid. The main findings of the study can be summarized as follows:

Both the streamlines and isotherms were symmetrical about the central part of the bottom wall. The presence of a circular obstacle obstructed both the streamlines and isotherms. The streamlines were more intense in the enclosure containing the hot obstacle than in the enclosure containing the cold obstacle.

The streamlines of the MWCNT nanofluids occupied the entire enclosure in the presence of the adiabatic and hot obstacles, exhibiting two rotating cells. The stronger streamlines are observed only the lower part of the enclosure the cold obstacle case.

The strength of the streamlines increased with the Casson parameter and Rayleigh number. A considerable variation was observed in the isotherms with a higher Casson parameter, MWCNT volume fraction, Rayleigh number, and radiation parameter in the enclosure containing the adiabatic and hot obstacles.

The dimensionless temperature increased with the increasing values of Casson parameter and Rayleigh number inside the enclosure, whereas it decreased with the MWCNT volume fraction and radiation parameter inside the enclosure above the hot and adiabatic obstacles.

The local Nusselt number along the heated wavy part decreased below all types of obstacles inside the enclosure.

The mean Nusselt number along the heated wavy bottom wall increased with the Casson parameter, Rayleigh number, and radiation parameter for all types of obstacles. Further, it was higher in the presence of the cold obstacle than that of the hot obstacle when 0.05 < φ < 0.1. The mean Nusselt number was higher in adiabatic obstacle and lower in cold obstacle for the range 0.01 < φ < 0.05.

These results obtained for the Nusselt number and isotherms patterns agreed well with the theoretical and experimental benchmark solutions.

The steady state results presented in the study are valid for 10³ ≤ Ra ≤ 10⁶. To predict the flow and thermal patterns for higher Rayleigh number (Ra ≥ 10⁷), one should solve the governing equations in transient form.

Future directions

Since the geometry of the enclosure, non-Newtonian behavior of base fluids and the thermal boundary conditions may led to semi-symmetric flow and heat transport in the enclosure. Hence the study on the natural convection due to various non-Newtonian based nanofluids with higher Rayleigh numbers can be investigated in future works.

Compliance with Ethics Requirements

This article “Analysis of natural convection for a Casson-based multiwall carbon nanotube nanofluid in a partially heated wavy enclosure with a circular obstacle in the presence of thermal radiation” does not contain any studies with human or animal subjects.

CRediT authorship contribution statement

N. Vishnu Ganesh: Conceptualization, Data curation, Formal analysis, Funding acquisition, Software, Investigation, Writing – original draft. Qasem M. Al-Mdallal: Conceptualization, Data curation, Formal analysis, Funding acquisition, Software, Investigation, Writing – original draft. Hakan F. Öztop: Conceptualization, Supervision, Data curation, Formal analysis, Validation, Writing – review & editing. R. Kalaivanan: Formal analysis, Validation, Visualization, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.