Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 May 30;22(7):4431–4436. doi: 10.1021/acs.cgd.2c00378

Calcite Kinetics for Spiral Growth and Two-Dimensional Nucleation

Robert Darkins †,*, Yi-Yeoun Kim ‡, David C Green ‡, Alexander Broad †, Dorothy M Duffy †, Fiona C Meldrum ‡, Ian J Ford †
PMCID: PMC9264354  PMID: 35818387

Abstract

graphic file with name cg2c00378_0005.jpg

Calcite crystals grow by means of molecular steps that develop on {10.4} faces. These steps can arise stochastically via two-dimensional (2D) nucleation or emerge steadily from dislocations to form spiral hillocks. Here, we determine the kinetics of these two growth mechanisms as a function of supersaturation. We show that calcite crystals larger than ∼1 μm favor spiral growth over 2D nucleation, irrespective of the supersaturation. Spirals prevail beyond this length scale because slow boundary layer diffusion creates a low surface supersaturation that favors the spiral mechanism. Sub-micron crystals favor 2D nucleation at high supersaturations, although diffusion can still limit the growth of nanoscopic crystals. Additives can change the dominant mechanism by impeding spiral growth or by directly promoting 2D nucleation.

Short abstract

The growth kinetics of calcite are determined for both spiral growth and 2D nucleation as a function of the surface supersaturation. These kinetics reveal the dominant growth mechanism and the role of solute diffusion in single crystal growth.

1. Introduction

Calcite (CaCO3) is used as a model system to study how additives control crystallization kinetics and incorporate into crystals.1−11 Generally, these studies aim to understand either how biological organisms use additives to tailor the properties of biominerals or how we can use similar strategies to create new bio-inspired composites. A model that could predict the growth kinetics of calcite over a wide range of conditions could help to interpret these experimental studies and therefore help to design new strategies for growth inhibition and additive incorporation.

An obstacle in developing such a model is measuring the surface-controlled kinetics of calcite growth. The preeminent method for probing crystal growth processes in solution is flow-through atomic force microscopy (AFM). This method has been used extensively to study how supersaturation,12−14 stoichiometry,15−17 pH,16 and additives18−20 affect the growth of calcite. It had long been believed on the basis of variable flow rate tests that calcite growth was limited by surface reaction during flow-through AFM.21 It is now known, to the contrary, that variable flow rate tests are inconclusive and that the bulk supersaturation does not extend all the way to the surface of calcite under typical flow rates.22 Nevertheless, for AFM studies that report both the step velocities and the step densities of spiral hillocks, it remains possible to recover the surface-controlled kinetics using theory. Specifically, the step velocities and the step densities can be used to compute the critical step length, which provides an indicator of the surface supersaturation and therefore a means of characterizing mass transport in the experiment.22

In this paper, we determine the surface-controlled kinetics of calcite for both spiral growth and two-dimensional (2D) nucleation by applying the critical step length indicator22 to past AFM data.12 We relate our results to real-world crystallization by examining two issues: (i) how the mechanism (spiral growth versus 2D nucleation) and the limiting kinetics (reaction versus diffusion) depend on crystal size and bulk supersaturation and (ii) how additives might change the mechanisms and kinetics.

2. Results and Discussion

2.1. Surface-Controlled Kinetics

The growth kinetics of calcite depend on the supersaturation

2.1. 1

where {x} is the activity of species x and Ksp is the solubility product of calcite. We will use subscripts to distinguish the supersaturation at the crystal surface, Ssurf, from the bulk solution, Sbulk (see Figure 1a).

Figure 1.

Figure 1

Open in a new tab

(a) Illustration of a calcite crystal growing via 2D nucleation (green islands) and a spiral hillock. The surface supersaturation Ssurf, bulk supersaturation Sbulk, crystal size L, and normal growth rate R are depicted. (b) The surface-controlled growth rate of calcite obtained from theoretical fits to AFM data with mass transport accounted for. The shaded areas represent uncertainty in the models. (c) Dominant growth mechanism derived by plugging the surface-controlled kinetics into a model of solute diffusion. (d) Ssurf as a function of L and Sbulk. The black line corresponds to the Damköhler number Da = 1. We had to estimate some model parameters to produce this plot, see Section 4.1.2. (e) Relative growth rate of 2D nucleation and spiral growth. The growth rates are very similar for Sbulk ≳ 2.5 and L ≳ 1 μm because the growth is diffusion-dominated. (b–e) The dashed lines show the predictive limits of the model.

The kinetics of spiral growth for calcite have previously been measured as a function of Sbulk using flow-through AFM.12 The same study also reported growth by 2D nucleation at Sbulk = 1.5. However, the surface-controlled kinetics of a crystal must be characterized by the supersaturation at the crystal surface, Ssurf. To compute the growth kinetics for both spiral growth and 2D nucleation from these same AFM data,12 but as a function of Ssurf, we used the critical step length indicator22 to determine Ssurf and classical growth theory to extrapolate the results to a wider range of supersaturations. Full details can be found in Section 4.1.

The resulting growth rates are shown in Figure 1b as a function of Ssurf, where the shaded areas represent uncertainty in the model. At low supersaturations (Ssurf ≲ 2.2), spiral growth is faster because 2D nucleation is hindered by a large activation barrier. At higher supersaturations (Ssurf ≳ 3.0), 2D nucleation is faster. We cannot determine the faster mechanism in the intervening supersaturations (2.2 ≲ Ssurf ≲ 3.0) due to the uncertainty in the model. The reason 2D nucleation was observed under AFM at Ssurf < Sbulk = 1.5, in apparent conflict with our model (Figure 1b), is because the crystal surface had not achieved a steady state in the experiment: the expanding spiral hillocks had not been allowed sufficient time to reach the probed region of the surface.

Since step kinetics are sensitive to the solution conditions,16 the kinetic curves in Figure 1b will be specific to the solution conditions in the AFM experiment (stoichiometry of {Ca}/{CO3} = 1.04 ± 0.01, ionic strength fixed between 0.105 and 0.111 M using NaCl, and a pH of 8.50 maintained with a NaOH buffer). However, the relative speed of 2D nucleation and spiral growth will depend on the relative step density of these two modes, which is principally a function of the supersaturation. The supersaturation reported here that marks the transition between the two growth modes is therefore expected to hold over a much wider range of solution conditions.

2.2. Crystals of Finite Size

Since the surface supersaturation Ssurf of a crystal is difficult to measure experimentally and is therefore seldom known, it can be more useful to characterize the growth kinetics in terms of the bulk supersaturation Sbulk and the crystal size L. To this end, we combined the surface-controlled kinetics from the previous section with a simple model of solute diffusion to determine the growth kinetics as a function of the pair (L, Sbulk). Full details can be found in Section 4.2.

According to this model, 2D nucleation only dominates over spiral growth when the bulk supersaturation is high (Sbulk ≳ 3) and the crystal size is small (L ≲ 1 μm), see Figure 1c. Significantly, spiral growth is predicted to dominate over 2D nucleation for crystals larger than ∼1 μm, irrespective of the bulk supersaturation. At the super-micron length scale, slow boundary layer diffusion creates a low Ssurf that favors spiral growth. These predictions (Figure 1c) are supported by experimental evidence: intrasectoral zoning, which is a signature of spiral growth,23,24 has been observed in calcite crystals for (L ∼10 μm, Sbulk = 3.9)11 and (L ∼100 μm, Sbulk = 4.5).25

The surface supersaturation surrounding a calcite crystal is shown in Figure 1d as a function of L and Sbulk (we had to estimate some model parameters to produce this plot). The black line in Figure 1d divides the plot into two regimes where growth is limited mainly by (i) surface reaction or (ii) boundary layer diffusion. Strictly speaking, crystal growth is always limited by the surface reaction; however, the surface reaction depends on the surface supersaturation, which is limited by diffusion. We say that growth is limited mainly by diffusion when the Damköhler number Da > 1 (see Section 4.2). In the diffusion-dominated regime, Ssurf has a weak dependence on Sbulk due to a feedback mechanism that attenuates any change in Ssurf. Specifically, an increase in Ssurf produces faster crystal growth that acts to decrease Ssurf. For this same reason, the crystal growth rate has a weak dependence on the growth mechanism in most of the diffusion-dominated regime; the relative growth rate of 2D nucleation and spiral growth varies by less than a factor of 2 when L ≳ 1 μm and Sbulk ≳ 2.5 (Figure 1e).

Figure 2 summarizes the above discussion by showing the predicted time evolution of a single crystal in a solution with a constant bulk supersaturation. As the crystal grows, the growth rate decreases due to increasingly slow boundary layer diffusion. When Sbulk ≳ 3, the growth rate depends only weakly on Sbulk, and the growth mechanism undergoes a transition from 2D nucleation to spiral growth as L exceeds ∼1 μm. It would take more than 1 week for the crystal to reach 100 μm in size when Sbulk = 3, whereas it would take a matter of hours if growth was always reaction-limited.

Figure 2.

Figure 2

Open in a new tab

Time evolution of the size, growth rate, and growth mechanism of a single crystal of calcite in a solution with a constant bulk supersaturation, starting from a size L = 10 nm.

2.3. Additives Can Change the Dominant Growth Mechanism

In pure solution, 2D nucleation is predicted to dominate over spiral growth only when the supersaturation is high (Sbulk ≳ 3) and the crystal size is small (L ≲ 1 μm). This account, however, is not necessarily accurate when additives are introduced to the solution. We identify four ways that an additive might change the dominant growth mechanism.

First, an additive could immobilize the screw dislocations by changing the crystal morphology. Calcite has a rhombohedral morphology in pure solution (Figure 3a), but additives can cause steps to pile up to form pseudo-faces.26 By increasing the additive concentration, pseudo-faces can become expressed in the morphology to an almost arbitrary degree; for example, very little remains of the {10.4} faces when calcite is precipitated in the presence of a high concentration of Asp (Figure 3b). Since a pseudo-face must engulf any dislocation in its way, the residual {10.4} faces might be free of dislocations and have no option but to grow by 2D nucleation.

Figure 3.

Figure 3

Open in a new tab

Scanning electron micrographs of three synthetic calcite crystals. (a) The equilibrium morphology in pure solution is a rhombohedron composed of {10.4} faces. (b) Aspartic acid can change the morphology by creating pseudo-faces. These pseudo-faces can engulf the dislocation sources, forcing the residual {10.4} faces to grow by 2D nucleation. (c) Seeded calcite growth in the presence of Congo red produces strongly partitioned surfaces. Growth must occur via 2D nucleation since a dislocation in one partition would be unable to supply steps to its neighboring partitions.

Second, an additive could isolate the dislocation sources by partitioning the surface. Poorly soluble additives may aggregate on the crystal surface to form assemblies that are too large to be overgrown.6,27 By blocking growth, the assemblies partition the surface such that any dislocation source in one partition would be unable to supply steps to the neighboring partitions, forcing them to grow by 2D nucleation. To illustrate this partitioning effect, Figure 3c shows a calcite crystal overgrown in a solution containing the dye Congo red.

Third, the additive could enhance the 2D nucleation rate, e.g., by providing a site for heterogeneous nucleation, thus shifting the kinetics in favor of 2D nucleation. This effect has not been observed in calcite to the best of our knowledge.

Fourth, imagine a crystal in pure solution within the diffusion-dominated regime. If an inhibitor was introduced to slow down the crystal growth, then Ssurf would increase, shifting the kinetics in favor of 2D nucleation. For example, if Sbulk = 4, then a crystal will transition from 2D nucleation to spiral growth at a crystal size of approximately 1 μm in pure solution. If, however, the solution included an inhibitor that slowed crystal growth by 50%, then spiral growth would begin to dominate at approximately 2 μm. At 90% inhibition, the transition would occur at approximately 10 μm. In this way, an additive could have a significant effect on the dominant growth mechanism but only at very high inhibitions.

In all four cases, the additive promotes 2D nucleation over spiral growth. Note that, if L ≳ 1 μm and Sbulk ≳ 2.5, then an additive-induced transition from spiral growth to 2D nucleation might not produce a significant change in the overall growth rate since the growth is diffusion-limited (see Figure 1e).

3. Conclusions

Boundary layer diffusion can play a critical role in determining the growth rate and growth mechanism of calcite. Additives can complicate the story by immobilizing growth spirals or by reducing the significance of diffusion through growth inhibition. Diffusion might therefore be an important and under-investigated aspect of how additives and even confinement28 control the growth and polymorphism of CaCO3.

4. Methods

4.1. Surface-Controlled Kinetics

Calcite growth kinetics have previously been measured as a function of Sbulk using flow-through AFM.12 In this section, we recast those AFM-derived kinetics as a function of Ssurf.

4.1.1. Spiral Growth

The step velocities (v±) and terrace widths (λ±) of the acute (−) and obtuse (+) steps of calcite are reported in Table 2 of ref (12) as a function of Sbulk. For each of these measurements, the critical step length can be determined and used as an indicator of the surface supersaturation to establish the true surface-controlled kinetics. We summarize this procedure here. The reader will find a more detailed account elsewhere.22

The average critical length can be computed from the experimental step velocities and terrace widths

4.1.1. 2

where

4.1.1. 3

measures the angle between adjacent spiral turns. From ⟨Lc⟩, the obtuse critical length Lc follows from the empirical relationship13

4.1.1. 4

If the step free energy ϕ was known, then the surface supersaturation Ssurf could be determined from Lc

4.1.1. 5

In this way, each experimental measurement of the step velocity (Sbulk, v) could be mapped to its surface-controlled analogue (Ssurf, v). The acute and obtuse step velocities v±(Ssurf; ϕ) could then be obtained through linear fits to these new surface-controlled measurements (Ssurf, v), where the obtuse step velocity is fitted subject to the constraint v+(Ssurf = 1; ϕ) = 0.

Finally, the normal growth rate of the spiral hillock is

4.1.1. 6

where v±(Ssurf; ϕ) refers to the linear fits and λ±(Ssurf; ϕ) is evaluated using eqs 2–5. The step free energy ϕ is estimated to fall in the range of 2.5 ≤ ϕ/kBT ≤ 3.5.22 Sampling this range of ϕ produces the range of growth rates shown in Figure 1b.

The role of mass transport in the AFM measurements can be characterized by a boundary layer thickness δ. Since the normal growth rate of the surface R(Ssurf)/ω will balance with the net flux of solutes across the boundary layer, Dγ–1Ksp1/2(Sbulk – Ssurf)/δ, we get

4.1.1. 7

where ω is the molar volume of calcite, D is the ion diffusion coefficient, Ksp is the solubility product of calcite, and γ is the activity coefficient. If the crystal surface structure has fully reconstructed to achieve a steady state, then R in eq 7 will correspond to Rspiral(Ssurf; ϕ) in eq 6. In ref (22), three AFM measurements were identified as corresponding to a fully reconstructed surface: (Sbulk, Lc) = (1.674,14.64 nm), (1.819,12.99 nm), and (2.036,12.28 nm). From these three data points, it is possible to determine δ for any given ϕ: If δ was known, then eq 7 could be solved numerically to obtain Ssurf for a given Sbulk, and Lc would then follow from Ssurf via eq 5. In this way, the value of δ can be optimized for a given ϕ to produce a least squares fit to the three (Sbulk, Lc) data points above.

4.1.2. 2D Nucleation

The kinetics of a calcite surface growing by 2D nucleation, R2D, has never been recorded. However, in the AFM study analyzed in the previous section, a single in situ micrograph (Figure 3c of ref (12)) was presented showing a calcite surface growing by 2D nucleation at Sbulk = 1.5. The growth rate of the crystal surface in this micrograph, R2D*, can be determined using the step velocities and boundary layer thickness established in the previous section. We will use an asterisk, e.g., R2D, to denote any quantity that is specific to the micrograph.

We measured the average dimensionless step density in the micrograph to be ρ* = 0.00039. This is equivalent to an average step spacing of 821 nm. If the surface supersaturation Ssurf* was known, then R2D could be computed with an accuracy dependent on how well ϕ is known

4.1.2. 8

where v±(Ssurf; ϕ) are the linear fits from the previous section. It follows from eq 7 that

4.1.2. 9

where the boundary layer thickness δ(ϕ) was established in the previous section to characterize the mass transport in the system. Equation 9 can be solved numerically to find Ssurf*, and R2D then follows from eq 8.

This datum (Ssurf*(ϕ), R2D(ϕ)) can be extrapolated to other surface supersaturations using classical nucleation theory29

4.1.2. 10

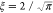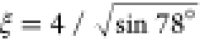where k is a kinetic coefficient and ξ is a shape factor defined as the ratio of the perimeter of the critical nucleus to the square root of its area. We sample the same step free energy range as in the previous section, 2.5 ≤ ϕ/kBT ≤ 3.5, and assume the shape factor to fall between that of a circle (Inline graphic) and that of a calcite rhombohedron (Inline graphic). The shape of the post-critical islands in the AFM micrograph fell within this range (we measured ξ* ≈ 3.8). For each combination of (ξ, ϕ), the prefactor k is fixed by the datum (Ssurf*(ϕ), R2D(ϕ)) according to eq 10.

The classical nucleation theory that we use to extrapolate the results (eq 10) implicitly assumes that islands only interact with other islands after exceeding the critical size. This is not possible when the supersaturation is so high that the average step spacing (v– + v+)/(2R2D) is comparable to the critical nucleus size Lc = 2ϕ/(kBT ln Ssurf). Therefore, in constructing Figure 1b, we only explored Ssurf for each parameter set (k, ξ, ϕ) up until (v– + v+)/(2R2D) = Lc. Furthermore, in constructing Figures 1d,e and 2, we estimated ϕ = 3kBT and ξ = 3.8, and we only explored crystal sizes L > 2Lc as it is unclear what the spiral kinetics would be for smaller crystals.

4.2. Transform (L, Sbulk) to Ssurf

The previous section derived the growth kinetics of calcite as a function of surface supersaturation Ssurf. The kinetics can alternatively be characterized as a function of crystal size L and bulk supersaturation Sbulk.

In the steady state, the supersaturation field surrounding a crystal will satisfy the diffusion equation ∇2S = 0 subject to two boundary conditions: (i) the solute flux −D ∇ S must balance with the growth rate R of the crystal at each point on the surface and (ii) S = Sbulk in the far-field. To solve this equation analytically, the rhombohedral calcite crystal of length L can be approximated as a sphere with an equivalent surface area, i.e., with a radius 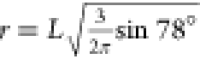Inline graphic. In this case, the diffusion equation solves to

4.2. 11

This equation can be solved numerically to find Ssurf for any L, Sbulk, and any growth mechanism encapsulated in R. Setting R = max (Rspiral, R2D) captures the faster of the two growth modes. From Ssurf, the growth kinetics and dominant growth mechanism can be identified as before.

Within this model, the relative significance of surface reaction and solute diffusion can be quantified by the Damköhler number, Da. This quantity is defined as the ratio of the crystal growth rate under reaction control to the crystal growth rate under diffusion control,

4.2. 12

When Da ≪ 1, crystal growth is limited by the surface reaction, and when Da ≫ 1, growth is limited by diffusion. The curve Da = 1 therefore divides these two growth regimes, as shown in Figure 1d.

4.3. Calcite Crystal Examples

Figure 3 features three synthetic calcite crystals grown from three different solutions.

Figure 3a shows a calcite crystal grown from pure solution using the ammonium diffusion method.30 Aqueous solution containing [CaCl2] = 10 mM was placed in a plastic Petri dish containing a glass slide. The dish was covered with a perforated Parafilm and placed for 2 days in a desiccator previously charged with 5 g of freshly crushed (NH4)2CO3 powder. Full details can be found elsewhere.2

Figure 3b shows a calcite crystal grown using the above method except the solution also contained [Asp] = 50 mM.

Figure 3c shows a calcite crystal that was initially a ∼50 μm seed. It was subsequently overgrown for 3 days in a solution comprising [CaCl2] = [NaHCO3] = 10 mM and [Congo red] = 20 μM. Full details can be found elsewhere.6

Acknowledgments

This work was supported by an Engineering and Physical Sciences Research Council (EPSRC) Programme Grant (EP/R018820/1).

The authors declare no competing financial interest.

References

  1. Karaseva O. N.; Lakshtanov L. Z.; Okhrimenko D. V.; Belova D. A.; Generosi J.; Stipp S. L. S. Biopolymer control on calcite precipitation. Cryst. Growth Des. 2018, 18, 2972–2985. 10.1021/acs.cgd.8b00096. [DOI] [Google Scholar]
  2. Kim Y. Y.; Carloni J. D.; Demarchi B.; Sparks D.; Reid D. G.; Kunitake M. E.; Tang C. C.; Duer M. J.; Freeman C. L.; Pokroy B.; Penkman K.; Harding J. H.; Estroff L. A.; Baker S. P.; Meldrum F. C. Tuning hardness in calcite by incorporation of amino acids. Nat. Mater. 2016, 15, 903–910. 10.1038/nmat4631. [DOI] [PubMed] [Google Scholar]
  3. Nahi O.; Kulak A. N.; Kress T.; Kim Y. Y.; Grendal O. G.; Duer M. J.; Cayre O. J.; Meldrum F. C. Incorporation of nanogels within calcite single crystals for the storage, protection and controlled release of active compounds. Chem. Sci. 2021, 12, 9839–9850. 10.1039/D1SC02991F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Nielsen A. R.; Jelavic S.; Murray D.; Rad B.; Andersson M. P.; Ceccato M.; Mitchell A. C.; Stipp S. L. S.; Zuckermann R. N.; Sand K. K. Thermodynamic and kinetic parameters for calcite nucleation on peptoid and model scaffolds: A step toward nacre mimicry. Cryst. Growth Des. 2020, 20, 3762–3771. 10.1021/acs.cgd.0c00029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Lang A.; Mijowska S.; Polishchuk I.; Fermani S.; Falini G.; Katsman A.; Marin F.; Pokroy B. Acidic monosaccharides become incorporated into calcite single crystals. Chemistry–A European Journal 2020, 26, 16860–16868. 10.1002/chem.202003344. [DOI] [PubMed] [Google Scholar]
  6. Green D. C.; Darkins R.; Marzec B.; Holden M. A.; Ford I. J.; Botchway S. W.; Kahr B.; Duffy D. M.; Meldrum F. C. Dichroic calcite reveals the pathway from additive binding to occlusion. Cryst. Growth Des. 2021, 3746. 10.1021/acs.cgd.1c00068. [DOI] [Google Scholar]
  7. Weiner S.; Addadi L. Crystallization pathways in biomineralization. Annu. Rev. Mater. Res. 2011, 41, 21–40. 10.1146/annurev-matsci-062910-095803. [DOI] [Google Scholar]
  8. Elhadj S.; De Yoreo J. J.; Hoyer J. R.; Dove P. M. Role of molecular charge and hydrophilicity in regulating the kinetics of crystal growth. Proc. Natl. Acad. Sci. 2006, 103, 19237–19242. 10.1073/pnas.0605748103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Marzec B.; Green D. C.; Holden M. A.; Coté A. S.; Ihli J.; Khalid S.; Kulak A.; Walker D.; Tang C.; Duffy D. M.; Kim Y. Y.; Meldrum F. Amino acid assisted incorporation of dye molecules within calcite crystals. Angew. Chem., Int. Ed. 2018, 57, 8623–8628. 10.1002/anie.201804365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bracco J. N.; Grantham M. C.; Stack A. G. Calcite growth rates as a function of aqueous calcium-to-carbonate ratio, saturation index, and inhibitor concentration: Insight into the mechanism of reaction and poisoning by strontium. Cryst. Growth Des. 2012, 12, 3540–3548. 10.1021/cg300350k. [DOI] [Google Scholar]
  11. Green D. C.; Ihli J.; Thornton P. D.; Holden M. A.; Marzec B.; Kim Y. Y.; Kulak A. N.; Levenstein M. A.; Tang C.; Lynch C.; Webb S. E. D.; Tynan C. J.; Meldrum F. C. 3D visualization of additive occlusion and tunable full-spectrum fluorescence in calcite. Nat. Commun. 2016, 7, 1–13. 10.1038/ncomms13524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Teng H. H.; Dove P. M.; De Yoreo J. J. Kinetics of calcite growth: surface processes and relationships to macroscopic rate laws. Geochim. Cosmochim. Acta 2000, 64, 2255–2266. 10.1016/S0016-7037(00)00341-0. [DOI] [Google Scholar]
  13. Teng H. H.; Dove P. M.; Orme C. A.; De Yoreo J. J. Thermodynamics of calcite growth: baseline for understanding biomineral formation. Science 1998, 282, 724–727. 10.1126/science.282.5389.724. [DOI] [PubMed] [Google Scholar]
  14. Teng H. H.; Dove P. M.; DeYoreo J. J. Reversed calcite morphologies induced by microscopic growth kinetics: insight into biomineralization. Geochim. Cosmochim. Acta 1999, 63, 2507–2512. 10.1016/S0016-7037(99)00103-9. [DOI] [Google Scholar]
  15. Stack A. G.; Grantham M. C. Growth rate of calcite steps as a function of aqueous calcium-to-carbonate ratio: independent attachment and detachment of calcium and carbonate ions. Cryst. Growth Des. 2010, 10, 1409–1413. 10.1021/cg901395z. [DOI] [Google Scholar]
  16. Hong M.; Teng H. H. Implications of solution chemistry effects: Direction-specific restraints on the step kinetics of calcite growth. Geochim. Cosmochim. Acta 2014, 141, 228–239. 10.1016/j.gca.2014.06.023. [DOI] [Google Scholar]
  17. Sand K. K.; Tobler D. J.; Dobberschutz S.; Larsen K. K.; Makovicky E.; Andersson M. P.; Wolthers M.; Stipp S. L. S. Calcite growth kinetics: dependence on saturation index, Ca2+: CO32– activity ratio, and surface atomic structure. Cryst. Growth Des. 2016, 16, 3602–3612. 10.1021/acs.cgd.5b01792. [DOI] [Google Scholar]
  18. Orme C. A.; Noy A.; Wierzbicki A.; McBride M. T.; Grantham M.; Teng H. H.; Dove P. M.; De Yoreo J. J. Formation of chiral morphologies through selective binding of amino acids to calcite surface steps. Nature 2001, 411, 775–779. 10.1038/35081034. [DOI] [PubMed] [Google Scholar]
  19. Astilleros J. M.; Fernández-Díaz L.; Putnis A. The role of magnesium in the growth of calcite: An AFM study. Chem. Geol. 2010, 271, 52–58. 10.1016/j.chemgeo.2009.12.011. [DOI] [Google Scholar]
  20. Elhadj S.; Salter E. A.; Wierzbicki A.; De Yoreo J. J.; Han N.; Dove P. M. Peptide controls on calcite mineralization: Polyaspartate chain length affects growth kinetics and acts as a stereochemical switch on morphology. Cryst. Growth Des. 2006, 6, 197–201. 10.1021/cg050288+. [DOI] [Google Scholar]
  21. Fan C.; Chen J.; Chen Y.; Ji J.; Teng H. H. Relationship between solubility and solubility product: The roles of crystal sizes and crystallographic directions. Geochim. Cosmochim. Acta 2006, 70, 3820–3829. 10.1016/j.gca.2006.06.011. [DOI] [Google Scholar]
  22. Darkins R.; McPherson I. J.; Ford I. J.; Duffy D. M.; Unwin P. R. Critical step length as an indicator of surface supersaturation during crystal growth from solution. Cryst. Growth Des. 2022, 982. 10.1021/acs.cgd.1c01249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Paquette J.; Reeder R. J. New type of compositional zoning in calcite: Insights into crystal-growth mechanisms. Geology 1990, 18, 1244.. [DOI] [Google Scholar]
  24. Shtukenberg A. G.; Lee S. S.; Kahr B.; Ward M. D. Manipulating crystallization with molecular additives. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 77–96. 10.1146/annurev-chembioeng-061312-103308. [DOI] [PubMed] [Google Scholar]
  25. Paquette J.; Reeder R. J. Relationship between surface structure, growth mechanism, and trace element incorporation in calcite. Geochim. Cosmochim. Acta 1995, 59, 735–749. 10.1016/0016-7037(95)00004-J. [DOI] [Google Scholar]
  26. De Yoreo J. J.; Dove P. M. Shaping crystals with biomolecules. Science 2004, 306, 1301–1302. 10.1126/science.1100889. [DOI] [PubMed] [Google Scholar]
  27. Momper R.; Nalbach M.; Lichtenstein K.; Bechstein R.; Kuhnle A. Stabilization of polar step edges on calcite (10.4) by the adsorption of Congo Red. Langmuir 2015, 31, 7283–7287. 10.1021/acs.langmuir.5b01043. [DOI] [PubMed] [Google Scholar]
  28. Meldrum F. C.; O’Shaughnessy C. Crystallization in confinement. Adv. Mater. 2020, 32, 2001068. 10.1002/adma.202001068. [DOI] [PubMed] [Google Scholar]
  29. Tilbury C. J.; Doherty M. F. Modeling layered crystal growth at increasing supersaturation by connecting growth regimes. AIChE J. 2017, 63, 1338–1352. 10.1002/aic.15617. [DOI] [Google Scholar]
  30. Ihli J.; Bots P.; Kulak A.; Benning L. F.; Meldrum F. C. Elucidating mechanisms of diffusion-based calcium carbonate synthesis leads to controlled mesocrystal formation. Adv. Funct. Mater. 2013, 23, 1965–1973. 10.1002/adfm.201201742. [DOI] [Google Scholar]

Articles from Crystal Growth & Design are provided here courtesy of American Chemical Society

RESOURCES