Abstract
This paper introduces new methods of modeling and analyzing social networks that emerge in the context of disease spread. Four methods of constructing informative networks are presented, two of which use. static data and two use temporal data, namely individual citizen mobility observations taken over an extensive period of time. We show how the built networks can be analyzed, and how the numerical results can be interpreted, using network permutation-based surprise analysis. In doing so, we explain the relationship of surprise analysis with conventional network hypothesis testing and Quadratic Assignment Procedure regression. Surprise analysis is more comprehensive, and can be without limitation performed with any form(s) of network subgraphs, including those with multiple nodal attributes, weighted links, and temporal features. To illustrate our methodological work in application, we put them to use for interpreting networks constructed from the data collected over one year in an observational study in Buffalo and Erie counties in New York state during the 2016–2017 influenza season. Even with the limitations in the data size, our methods are able to reveal the global (city- and season-wide) patterns in the spread of influenza, taking into account population mobility and socio-economic factors.
Keywords: Influenza spread, Social network analysis, Surprise analysis, Permutation testing
1. Introduction
The need to understand and control the transmission of communicable diseases has been an acute challenge, presented to society by the dangers of epidemic outbreaks of potentially deadly viruses such as the 1918 influenza virus, H1N1 virus of 2009, and the currently active Ebola and COVID-19 viruses [1,13,22,25]. Viruses such as influenza, or flu, that activate seasonally offer an opportunity for observational research, as their resurgence is periodic.
Empirical studies that take a detailed view on disease propagation present an invaluable source of knowledge about the predictors of epidemics, particularly in densely populated areas. However, such studies are extremely rare due to high costs and resource needs.
Indeed, while hospitals and doctor offices track both the number of patients treated and the severity of proliferating viruses, preparation for and management of an epidemic requires an understanding of how the day-to-day behavior of potential patients affects their propensity of catching a virus. In order to back up any policy-making insights with real world, up-to-date empirical evidence, there is a need to track the dissemination of contagious diseases before they reach an epidemic level, and also, the need for methods that enable statistically valid analyses of complex datasets. On the data side, federal funding agencies, and in particular NIH, have begun to support large-scale data collection endeavors, capable of capturing individual mobility-based trends in disease transmission. However, given the high complexity of such datasets – longitudinal nature coupled with the obvious “network” type, – special analysis approaches are needed to fully unlock their potential to generate insights, both predictive and policy-making oriented ones.
Social network analysis offers a set of modeling and methodological approaches that can help study the transmission of flu-like illnesses. The network perspective on events and behavior can be useful at the individual level (individual-centric) as well as the spatial level (location-centric), to capture the relationship between disease spread and human mobility [3,6,9,28]. However, as this science is still fairly new, it keeps offering room for further innovation with each newly explored application and with the added data complexity-dependent challenges.
This paper enriches the methodological toolbox for complex temporal data analysis, in particular in social network analysis, to allow one to reveal evidence-based insights about the correlations between the dynamics of disease spread over city regions and the socio-economic descriptors of these regions.
Our contributions take place in three areas, with the main methodological advances rooted in the creative uses of network formation and permutation testing principles. First, given the travel paths of individuals, we present four ways for building/defining network links, two of which construct links temporally. Second, we explain and expand permutation-based network hypothesis testing methodology, called surprise analysis, to allow for simultaneously testing multiple network hypotheses, on both static and temporal, directed and undirected weighted networks featuring multiple attributes. This new type of multi-hypothesis testing capitalizes on seeing which hypotheses hold at the same time, thus allowing for interesting and convincing interpretations of results. Lastly, we illustrate how these methods can be used to evaluate the impact of population mobility-based and socio-economic factors on influenza proliferation.
In addition to extensive methodological explorations, where we present new, application-oriented data processing – network-building – methods, and statistical analysis methods in theory, we also showcase the applied potential of these methods through working with a recently collected real-world dataset. Specifically, we use the data from a large-scale observational study conducted in Erie and Niagara counties in Western New York during the 2016–2017 influenza season. The collected high-resolution, i.e., individual-level, data on the transmission of flu-like illnesses and human mobility, achieved through sophisticated tracking coupled with population surveys, were post-processed to inform the construction of a weighted attributed network of Census block groups. Both the observed travel patterns and publicly available Census data were used to express the relationships between a set of Census block groups within the city of Buffalo, NY. We report the insights from the analyses of a number of static networks, as well as a series of time-periodic networks that comprehensively elucidate the global patterns of an epidemic influenza proliferation through a city within a full influenza season.
More specifically, our statistical analysis focuses on income and illness indicators as they relate to mobility patterns. We gathered Census data of block group income levels, as well as race and health insurance information. These data, coupled with the survey data, allow us to explore relationships between block group level attributes and travel to assess disease dissemination in Erie and Niagara counties in Western New York. An example of a hypothesis we test is, “The frequency of travel tends to be greater between block groups with the same level of illness.” Hypotheses in this form enable us to explore the relationship between human mobility and block group attributes to infer their effect on disease propagation.
This paper is structured as follows. Section 2 provides a review of relevant literature, specifically literature pertaining to epidemics and pandemics, dissemination of communicable diseases, permutation testing, and surprise analysis. Section 3 details the data processing methodology, which is divided into two parts: data manipulation and network-building. Section 4 presents our analytical methodology developments, focusing on surprise analysis. Section 5 presents the results from our illustrative explorations, organized by methodology type with surprise analysis at the core, and followed by interpretative discussions. Section 6 concludes the paper, offering directions for further research.
2. Literature review
Influenza-like illnesses affect a vast majority of people, across many countries and social-demographics. In order to mitigate the harmful effects of such illnesses, both active and passive research studies in the United States continue to be conducted at the transnational, national, and state levels. Datasets created by the Census Bureau, Sentinel Surveillance System and individual research project surveys allow for flu-like illness spread to be evaluated as a network process. A number of methods to analyze the dependencies between processes on networks, and network node and edge characteristics fall under a broad umbrella of permutation-based analysis. Here, permutation or re-sampling of network elements can enable hypothesis testing, regression modeling and more ad-hoc types of analysis exploiting the concept of surprise. This prompts a review of the following topics: epidemics and pandemics, dissemination of communicable diseases, permutation-based analysis, and surprise analysis. Thus, this section is divided into four parts: Section 2.1 provides a overview of the literature on epidemics and pandemics, Section 2.2 covers dissemination of communicable diseases, Section 2.3 reviews permutation testing, and Section 2.4 describes the roots of surprise analysis.
2.1. Epidemics and pandemics
A lack of intervention and control over the dissemination of communicable diseases throughout a community can lead to the occurrence of epidemics, which can lead to pandemics if proper measures are not executed. Throughout history, we have witnessed a multitude of fervent disease spread cases at both the epidemic and pandemic levels, which has deservedly attracted much research attention. Most notable have been the influenza pandemics of 1918 and the H1N1 virus in 2009, the Ebola epidemic in Africa, and COVID-19 coronavirus pandemic in 2020 [1,13,22,25]. Historical, biological, chemical, and statistical studies have been conducted to better understand pandemics of the past (how they spread and what causes them) to inform future policy and intervention protocol in order to prevent similar disasters.
A study by Smith et al. [25] reveals that three of the most recent pandemics may have resulted from a sequence of reassortments among viruses previously found in humans and viruses that originate in the fauna, namely, in birds and swine [25]. Smith et al. conclude that pandemic level viruses are forming in stages through reassortment for years, before their existences come to affect people. They propose taking preventative measures to protect human society from such diseases. In the same vein, Gomes et al. perform a statistical analysis of the most recent Ebola epidemic and create projections for disease spread in Africa as well as other countries that have yet to be affected [13].
The objective of the above mentioned studies is to inform policy makers on the potential value of intervention protocols. There is much value in enriching this body of work, as it is foundational for preventive efforts.
2.2. Dissemination of communicable diseases
The dissemination of communicable diseases is studied both passively and actively, with the investigative efforts taking place at the state, national, and international levels. Such studies consider geographic, socio-demographic, and temporal factors as they relate to human interaction and mobility.
At the national level, observational studies on the effect of mobility in the spread of disease have been conducted worldwide, e.g., in China [28] and France [4]. In an observational (aka. passive, non-experimental) study, Charaudeau et al. use data from the French Census to explore the affects of mobility on the spread of flu like illnesses [4]. Home and work locations as well as travel times are used to describe mobility patterns. They find that the peak flu season cases are clustered in densely populated areas and that commuter travel flows are highly correlated with the spatial spread of disease. However, their work does not consider socio-demographic factors and their effects. Similarly, Zhong and Bian observe the effects of mobility and human interaction on the dynamics of an epidemic in Midwestern China [28]. They adopt a social network analysis approach for analyzing these dynamics at the level of residential units rather than working with individual travelers.
Lee et al. compare flu spike surveillance systems at the state and county levels, accounting for functions of climate-related and socio-environmental factors including humidity, pollution, and population density over large spatial zones [17]. They find that state surveillance models underestimate the disease proliferation in counties that are at high risk; meanwhile, the same indicators are overestimated in counties that are at low risk for epidemics. They speak in favor of surveying the flu spread at finer spatial scales in future work, so as to better understand the mechanisms of flu propagation.
In another relevant work, Cauchemez et al. model the spread of the H1N1 virus through a social network to analyze the effect that classroom relationships have on the spread of the virus in schools [3]. They find that students are likely to pass the disease onto classmates of the same sex and within the same grade, however, only one in five students transfer the illness to those members of their households that are above the age of 18. As schools are a hotbed for disease spread, understanding how these human interactions affect the spread allows for potential control and mitigating interventions in the future.
The purpose of studying the dissemination of communicable diseases is to express and quantify the dynamics of human interaction, mobility patterns, and disease spread at specific geographic levels. As suggested by Lee et al., there is an opportunity to study these dynamics at a finer spatial scale. Collecting detailed data at this scale may open new doors for supporting policy-making.
2.3. Permutation-based analyses on networks
Due to the complexity of data that reflect the impact of social mobility and interactions on disease spread, special attention must be paid to the analytical methods permitting static and longitudinal analyses of network data. This section delves into the review of the key idea most commonly used for traditional social network analysis – permutation-based analysis.
The fundamental analytical method that deserves to be discussed first is permutation-based hypothesis testing, or simply permutation tests. Permutation tests are resampling- or randomization-based methods used when distributions of variables under study are unknown and potentially dependent.
Fig. 1 displays an example “Observed Network” and two example permutations based on it. Network permutation can be performed on the nodes or the edges; a Node-Based Permuted Network and an Edge-Based Permuted Network are shown in Fig. 1. The buildings are nodes (also referred to as actors) and they are connected by edges (also referred to as links). In a practical sense, a network can be viewed as a neighborhood, in this case a small one, with only four buildings (nodes), two residential and two corporate. The buildings are connected by a set of roads (edges). The car shapes on the roads represent the characteristics of travel between buildings; technically, numerical characteristics are typically referred to as edge weights. To understand how permutation testing is done, consider the Node-Based Permuted Network, it has the same set of four nodes, but they are now (co-)located differently. The roads, or edges, remain fixed, as do the edge weights. The Edge-Based Permuted Network also has the same set of nodes and edges as the Observed Network, however, the edge weights (car shapes of respective colors) have been shuffled and redistributed across the edges. Note, in edge-based permutation, the structure of the network, i.e., the placement of the nodes and edges, remains constant. This allows us to analyze network dependencies and the likelihood of links forming between any two nodes.
Fig. 1.
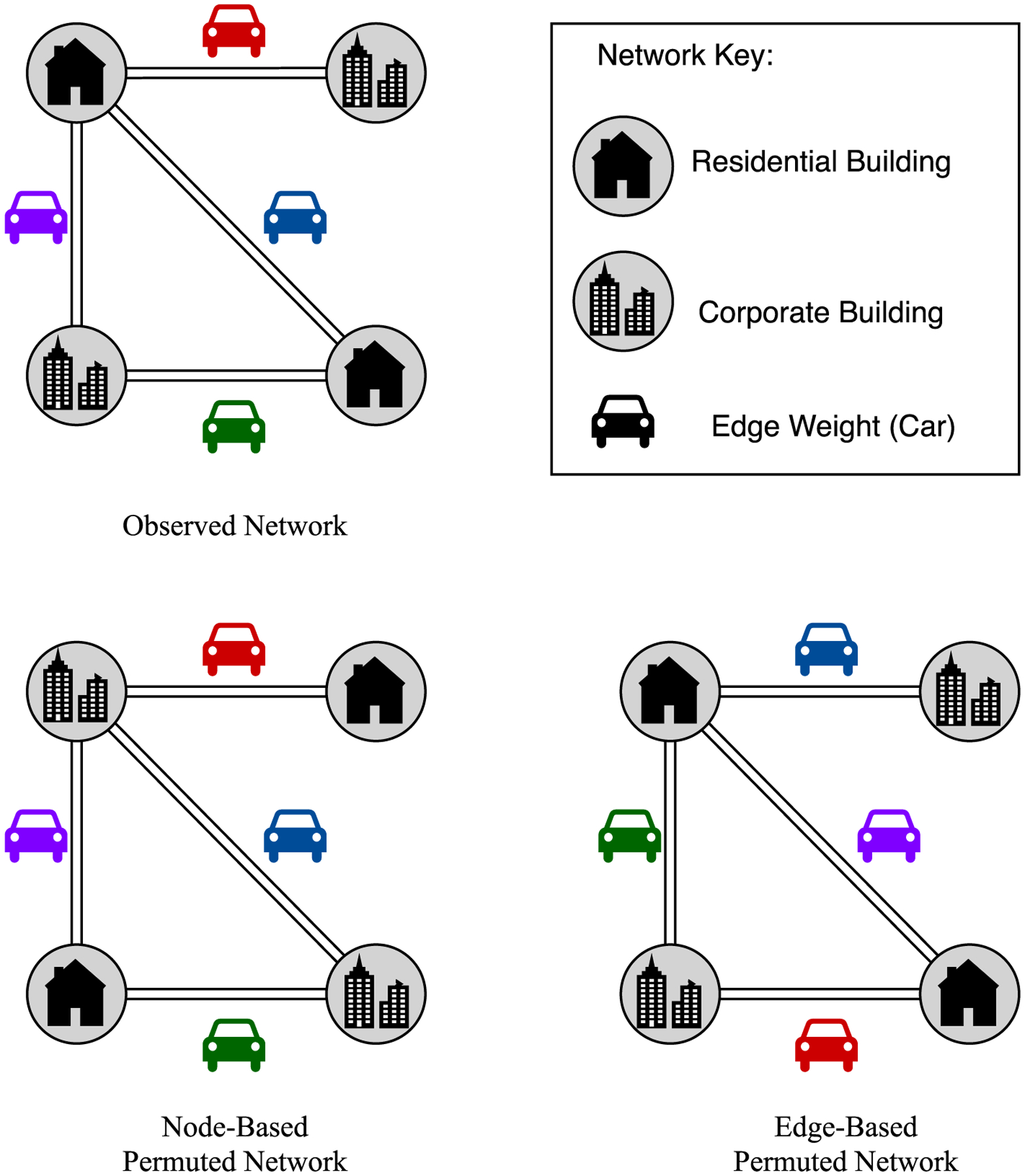
An example of an Observed Network, a Node-based Permuted Network, and an Edge-Based Permuted Network. Each network is comprised of residential/corporate building nodes, linked together by roadways, and the colored car shapes represent edge characteristics/weights.
The illustrative example in Fig. 1 is helpful for conceptual understanding of key terms used to discuss permutation testing. If we ignore the cars on the edges in the Observed Network, it becomes a binary weighted network. A binary weighted network is one where edges are binary weighted, that is, either present (weight of 1) or not present (weight of 0). A pair of nodes connected by a link is referred to as a dyad or dyadic structure. Focus on the top left and right nodes of the Observed Network: they are connected by an edge, forming a dyad. A dyad is one type of subgraph. A subgraph of a particular type, with all attributes fixed, is referred to as a feature. Note that the use of terms “subgraph” and “feature” is ubiquitous in probabilistic graphical modeling for social network analysis [10] but is not as widespread in statistical analysis of networks. The three dyad-based features one can define in the Observed Network are: (1) residential building connected to a corporate building, (2) residential building connected to a residential building, and (3) a corporate building connected to a corporate building. We may use the counts of instances of a particular feature in a network to analyze different subgraphs that may have practical meaning. For example, the count of the residential building to corporate building feature is three, the count of the residential building to residential building feature is one, and the count of the corporate to corporate building feature is zero. In permutation testing, the counts of each feature in the Observed Network are compared against the aggregate of the corresponding feature counts of the Permuted Networks.
In network-based permutation testing, where the dependence is induced and implicitly expressed by the observed structure of the network in the data collected, the edge- and/or node-based labels are reshuffled to produce multiple permutations (which can be thought of as permuted “clones”) of the original network, to test whether the count of a selected subgraph-based feature in the original network is extreme, i. e., too high or too low, compared to the same counts in the permuted networks. The verdict of a test states whether an outside-of-average, or surprising, observation is statistically significant to claim the tested effect and support the hypothesis that implies this effect.
The other permutation-based method, widely used for multivariate analyses and implemented in the most popular software for social network analysis UCINET, is called Quadratic Assignment Procedure (QAP) regression [8,16,21]. QAP regression employs permutation logic to test the significance of the inferred regression coefficients. Both permutation tests and QAP regression are traditionally performed on nodes, links or dyads within a single observed (aka. original) network. Note that, being more complex than a node or a link, a dyad is itself a special case of an even more complex general network element – subgraph.
The level of significance to use and number of permutations to be executed in QAP are at the discretion of the researcher. North et al. suggest performing at least permutations, where α is the desired level of significance, in order to control precision [23].
To report a few relevant use cases, Lusseau et al. perform edge-based permutation tests to explain group formation among the actors embedded into a network with weighted edges. More specifically, they analyze clustering effects in certain animal species [19]. Croft et al. conduct edge-based, as well as node-based, permutation tests for describing animal social behaviors [7]. Similar to Lusseau et al., they strongly argue for the use of weighted networks for describing relationships, as it is difficult to confidently assign an edge weight of zero within a binary weighted network. Thus, any analyses performed on networks with binary weighted edges should be interpreted with caution.
Bavaud et al. develop a way of using permutation testing for explaining spatial auto-correlation in weighted networks [2]. They employ this method to analyze the effect that linguistic barriers have on the migration patterns of Swiss cantons. The regions they study vary in size and economical value, so they introduce an extension to standard permutation testing that can capture such differences and their effects. They incorporate an auxiliary variable that provides information on multiple spatial attributes. This single value variable is applied to each given node or region, providing rich information about the region, e.g., the number of cars per inhabitant, or average income over a certain spatial area. Their investigations provide insights into system dynamics based on multiple attributes and maintain the simplicity of single attributed permutation testing.
These developments provide a foundation for the analysis of multiple nodal attributes within weighted networks that can be used as a launch pad for similar studies with temporal aspects. Note also that permutation testing can be used as a stand-alone method, or in conjunction with other tools for statistical analysis.
2.4. Surprise analysis
Surprise analysis is a permutation-based tool which can be used to test multiple hypotheses simultaneously. Surprise analysis can be viewed as a generalization of the idea of permutation-based network hypothesis testing to the effect that multiple subgraph-based features defined on the same network are analyzed simultaneously. The concept of surprise analysis was introduced by Leskovec et al., in 2010 [18] and further extended by Guo et al., in 2011 [14]. The metric “surprise” is formally defined as the number of standard deviations by which the count of a studied feature differs from the count expected from purely random (re)shuffling. However, when using surprise analysis to test hypotheses, rather than to just make observations, it may be advantageous to transform the metric to be akin to a p-value. When performing surprise analysis, approximately 10,000 permutations are aggregated and compared to the counts in the Observed Network. Looking again at the Node-Based Permuted Network example in Fig. 1, we see that the count of the feature residential building to residential building is one in the Observed Network, and zero in the Permuted Network. Though this is a small network with only four nodes and four links, it provides a context for what it means to compare counts between observed and permuted networks.
Indeed, network label reshuffling can be applied to many network structure elements including nodes, edges, and node/edge labels. Traditional statistical tools consider one structure at a time, e.g., taking a dyad as a subgraph of interest. Meanwhile, surprise analysis can be used to analyze subgraphs of more diverse forms, using pre-defined features on these subgraphs; the latter can be complex structures such as attributed triads. To recap, surprise analysis goes beyond the binary determination (hypothesis verdict) adopted in traditional analysis of statistical significance in hypothesis investigations or analysis of relationships between dependent and independent network-based variables, e.g., as is the case with QAP regression. Importantly, surprise analysis enables the testing of multiple hypotheses at once and reports how strong a particular effect is, instead of just stating if the effect exists or not at a pre-selected level of significance. For example, if standard hypothesis testing were used to analyze the dyadic features in the Observed Network of Fig. 1, it would require three separate tests, one for each of the features previously described. However, surprise analysis enables us to analyze all three features with the same set of permutations and not have to state any hypothesis in advance. At a larger scale, the number of features increases exponentially as the number of nodal attributes increases, all of which can be analyzed in an application of surprise analysis. Thus, surprise analysis provides a more holistic outlook of the processes/relationships that the studied networks express, and produces more comprehensive insights than those acquired through other, more traditional methods such as individual hypothesis-based permutation tests.
Because our paper will advance and apply surprise analysis in a new context, it is worth looking at its prior use case in greater detail. In their original work [18], Leskovec et al. use surprise analysis to analyze the triads (a triad is a structure consisting of three connected nodes) formed by humans within signed networks, which is a special and practically useful case of weighted networks [11]. Leskovec et al. evaluate the evidence in support of Heider’s Balance Theory and of their own newly proposed Status Theory for explaining the formation of signed ties between actors that socially interact with each other. They use surprise analysis to determine the likelihood of appearance of particular triads in trust networks, and then, propose a theoretical explanation to their observations. The analyses are conducted with the excerpts of large online social networks, namely, Epinions, Slashdot, and Wikipedia [5, 14,15]. They take a network, and analyze the counts of different triad types in the network, in comparison to the counts of these triads in the permuted variations of the same network. The surprise analysis does this for all the types of triads at once, and reports the levels of positive/negative surprise detected. By tracking both undirected and directed triads, Leskovec et al. find weaknesses in the Heider’s Balance Theory and motivate their newly proposed Status Theory.
While the work of the Leskovec’s group focuses on finding the right theory to explain network observations, the “surprise analysis” research direction can be generalized, e.g., expanded from triads to any subgraphs of interest, including attributed dyads, attributed triads, etc., to detect complex dependencies. One could employ surprise analysis to analyze the nodal attributes within subgraphs together with the edge-based attributes. One could use surprise analysis to analyze networks with temporal aspects as well, and the temporal dimension could be applied to detect a deeper meaning implied by both the attributes and the network structure. This paper seizes the opportunity to investigate the promise of these new forms of surprise analysis.
3. Advances in network building methodology
Before any analytical inquiries can be conducted, a key step is to determine how to transform unprocessed data into a network which can be analyzed. Individually collected, i.e. unprocessed, survey or tracking data may imply a network structure, but how exactly to extract it leaves much room for creativity.
In this section we demonstrate how to manipulate a data structure to obtain a network, depending on how the unprocessed information is interpreted: network nodes are clearly defined and methods for edge construction are described. Indeed, we show multiple ways to achieve it, with each method having its own pros and cons.
To more precisely explain what is meant by “unprocessed data”, think of an outcome of an observational study (i.e., a data collection exercise) that comes in the form of individual trip records. Referring to a set of pre-indexed “from/to” locations, the recorded data thus reflect the daily movement of travelers over multiple days or over more granular time windows.
Links between actors in a network can be defined based upon acquaintance, information/disease spread, travel between locations, etc. In this section, we present four approaches for constructing links within both static and longitudinal networks. An example of the data structure from which networks can be derived is displayed in the table in Fig. 2. The data consist of user ID’s, origin locations, destination locations, and time period designations (detailed temporal information becomes available if movement of travelers is captured over multiple time periods, e.g., on each day). Consider the travel of the subject with user ID “2”: within one time period, they travel from Home to Point 1, Point 1 to Work, Work to Point 2 and finish by returning to Home. This produces a travel path for each user, as depicted as Network I in Fig. 2.
Fig. 2.
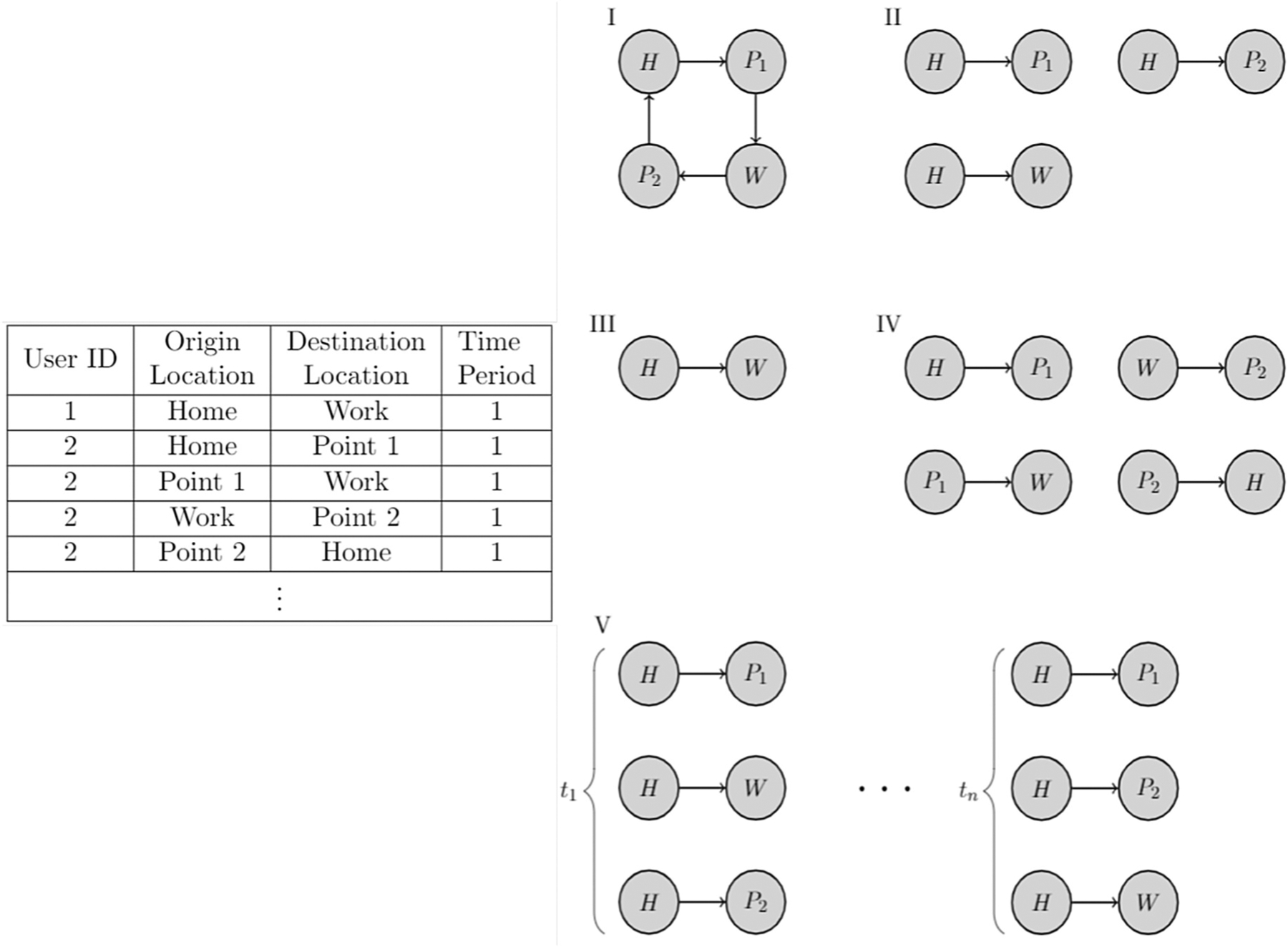
The table presents an example dataset that demonstrates the structure from which Networks of types I through V can be constructed. This particular dataset form contains information on subjects and their travel patterns. The five networks represent the types that can be built from the dataset. Types of networks: Network I – original path of travel, II – links with home locations used as origin points, III – home to work links, IV – temporal links with each point in the original path creating a new origin point, and V – temporal links based upon time periods with home locations used as origin points. Note that the node labels “H”, “W”, “P1”, and “P2” correspond to the locations Home, Work, Point 1 and Point 2, respectively, in the table.
Given an original observed travel path of an individual, four types of directed links can be defined en route to creating a local network for this individual. Per conventional terminology, a local network is comprised of one focal actor node and the adjacent nodes (those within 1-hop away) around it [24]. More simply, a local network is comprised of a focal actor node, that is the central node, and its incoming/outgoing links. We call these four types of local networks, respectively: “star” network, “home-work” network, “temporal network based on paths”, and “temporal network based upon time periods”. Fig. 2 provides a table with example data and the corresponding travel path of user 2, with the four types of directed links that can be derived from these data. Additionally, the local networks for multiple individuals can be overlaid to create a larger network that contains weighted links between two locations that are traversed by multiple users. In this case, edge weights could be integer or between 0 and 1: an integer edge weight represents the amount of subjects traversing between two locations and a decimal edge weight represents the proportion of all travel that occurs between two locations. Thus, location-centric data can inform the creation of several different networks. The main focus of the methodology here is on constructing, i.e., defining, links between actor locations.
Fig. 2 contains a table with an example dataset, an original travel path (Network I) of user 2, and four local networks derived from Network I. Each of the four networks derived from Network I has its own advantages as different network types emphasize different link types. Network II is referred to as the star network. The star network builds links from the home location to each of the locations that are traveled within the original path. Given the original path in Network I, creating links using the star network approach produces three edges, all with the generative node Home. The advantage to using Network II is that all generative nodes are Home, which places the emphasis on a subject’s home location, as it is presumably the geographic location in which they spend the most time. Network III is termed the home-work network, in which links are built between each of the Home and Work locations that are traversed. In this case, the observed path informs the creation of a single directed link within the home-work network. Network III is advantageous because it focuses on the travel between only a subject’s home and work locations, which is where the greatest proportion of travel occurs. Network IV is a temporal network based upon paths such that one link is created between each locale traversed within the original path. This temporal network approach creates four directed links. The advantage of using Network IV to create links is that it captures all travel, similarly to Network II, however, unlike Network II, the links are created based upon the sequence of travel. Lastly, Network V is a temporal network based on time periods that creates n separate networks where n is the number of time periods. Within each of the networks, links are created similarly to the star network, using the home location as the origin of each directed pair. Network V is advantageous as it incorporates a temporal element allowing for time periods to be visualized and analyzed separately as opposed to in aggregate. To recap, four distinct methods of creating links can be applied to produce different meaningful networks from one local network of recorded travel of one individual.
By overlaying a multitude of local networks, a larger network containing the information of multiple individuals can be created. Thus, larger weighted networks can be built using each of the four methods outlined above. The weighted networks are then used for statistical analyses, as described in the following sections.
4. Analytical methods with disease spread-based networks
In social network analysis, statistical tests analyze the number, i.e. the count, of specific network structures. These structures, termed subgraphs, are comprised of nodes and links and may take different forms. In this Section 4, we will be mainly concerned with dyadic structures. An example of a dyad is shown in the Observed Network in Figure ??: to simplify the presentation we disregard empty dyads and say that the nodes labeled 1 and 2 form a dyadic subgraph, whereas nodes 2 and 6 do not. A subgraph with particular values of random variables, e.g., nodal attributes, involved in it is referred to as a feature. Features are used to conduct hypothesis testing on subgraphs. For example, they are useful for capturing pairwise agreements or (dis)similarities (homophily) between nodes. The concept of defining features on a dyadic subgraph is further illustrated in part (c) of Fig. 4. The remainder of this section explores the use of analytical methods—permutation testing, hypothesis testing, and QAP regression—on mobility-based social networks.
Fig. 4.
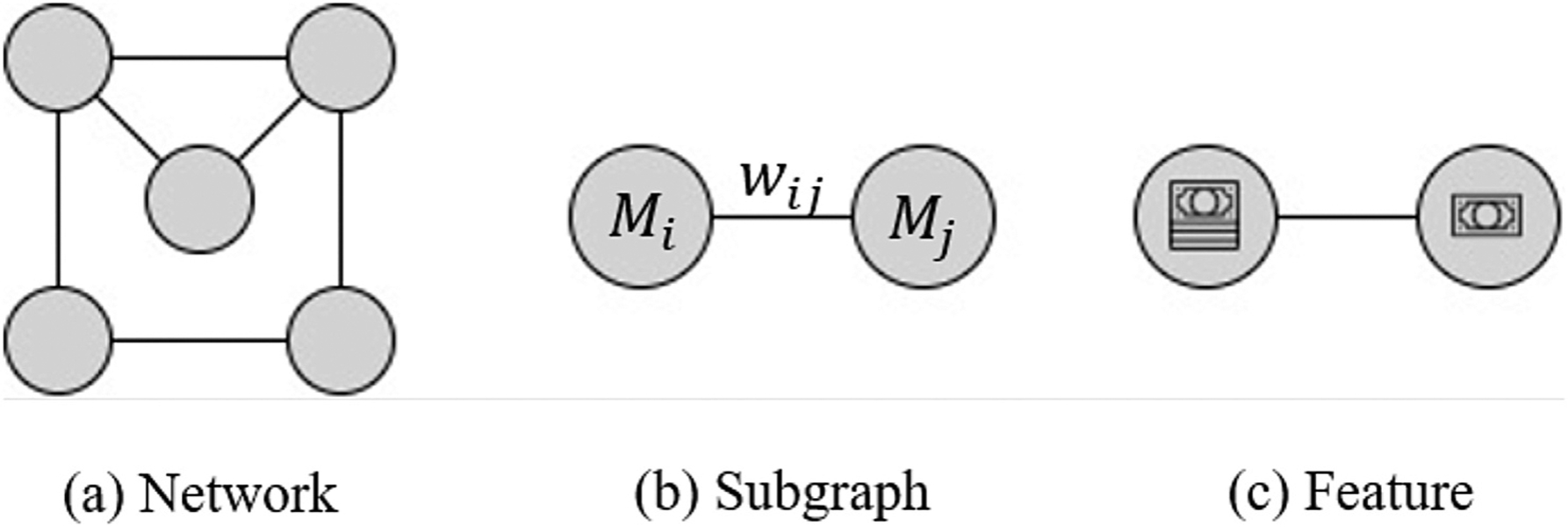
(a) A schematic network structure. (b) An example of a dyadic subgraph structure with nodal attributes Mi indicating the ‘income’ level of actor i and edge weight wij for edge eij. (c) An example of a feature type which can be derived from the subgraph in (b). This feature represents the frequency of travel in both directions (the link is undirected, with no attribute on it) between two nodes with differing ‘income’ levels.
4.1. Network-based hypothesis testing
Hypothesis testing on networks, though very similar to standard hypothesis testing, is conducted through permutation testing. Permutation testing is a resampling method for social network analysis that allows one to quantitatively assess the prevalence of a certain pattern within a network. In this resampling method, either nodes (or nodal labels) or edges (or edge labels) are reshuffled multiple times to test whether the frequency of appearance of a feature of interest in an observed network significantly deviates from its expectation per the distribution of the same frequencies across permuted networks.
Most useful for our application – mobility-based network data – is an extension of permutation testing at the nodal level. In order to conduct a nodal permutation test, a large number of possible network realizations (node rearrangements) are taken in aggregate to create the distribution of the count of appearance of a pre-defined feature in them. Fig. 1 provides an example of an Observed Network and a single node-based permutation of that network. As stated, our application makes use of mobility-based network data, so consider a neighborhood with four buildings connected by four roads, this can be represented as a network with four nodes and four edges. Notice that the nodes, or buildings, in the Node-Based Permuted Network are not in the same position as the buildings in the Observed Network, this is because the nodal labels have been shuffled, or permuted. However, the edges maintain the same structure. Permutation testing allows us to test whether the node relationships/connections in the Observed Network exhibit a pattern that is unlikely to have occurred at random.
Our method incorporates weighted edges and multiple nodal attributes into permutation testing, as well. Fig. 3 demonstrates a single permutation of an Observed Network with multiple nodal attributes and weighted edges. Similarly to Fig. 1, the edge structure of the network following a permutation remains the same, including the weights on the edges, represented by cars in the previous example. The sets of nodal attributes, termed nodal bundles, are permuted: each bundle is kept together as a unit and is uniformly randomly placed into a “placeholder”. Placeholder here is best described as a node circle in a graph, without any object/node label in it; placeholders are not shuffled while their contents are. Fig. 3 shows how network elements are denoted using only mathematical notations (and no pictures). To understand it in the same context as Fig. 1, imagine that each node is a building filled with people. Buildings are shuffled with all the people inside, the people are not moved individually. As such, each building is treated as a single piece: this is how nodal bundles work. A single nodal attribute, a1 for example, cannot be permuted alone, it must be permuted as part of the nodal bundle A, containing the set of attributes {a1, …, an}. In the context of Fig. 1, a1 could represent an attribute of the people within the buildings, such as level of illness. This attribute is attached to the building, or node, and permuted with it. In the case of Fig. 3, a1 is a single attribute in the nodal bundle A, so it is permuted as a group with the other attributes in A. Within the Observed Network, the placeholders of nodes A and C are connected; this is one type of a dyadic subgraph, for which the network-based hypothesis testing, as well as the methods described in the following subsections, come useful.
Fig. 3.
(a) The Observed Network contains nodal bundles A, B, …, E with attributes {1, 2, …, n}, and edge weights wij for nodes i and j. (b) The Permuted Network is an example of one permutation of the Observed Network. It maintains the same structure as the Observed Network, but the nodal bundles are reshuffled.
To better understand network hypothesis testing we will explore two possible testing templates, demonstrated in Figs. 5 and 6. Setting the stage for these structures and those illustrated in Sections 4.2 and 4.3, we will consider an example network dataset. The data consists of nodes which represent geographic locations, more specifically Census block groups, and network edges establishing travel between two nodes. Table 1 presents the attributes of the dataset which provide the basis for hypotheses.
Fig. 5.
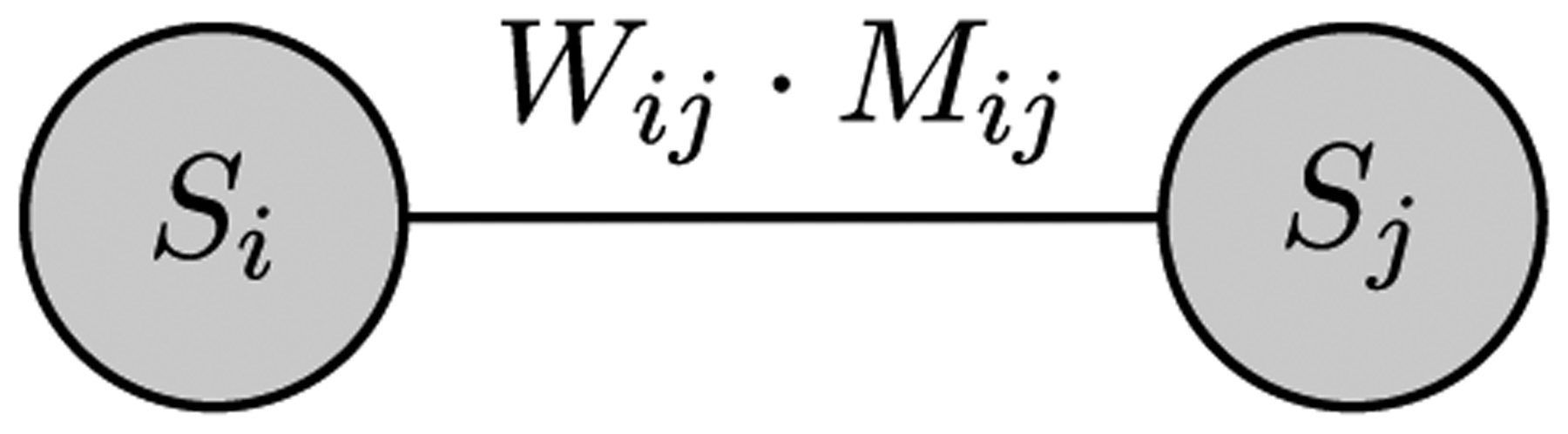
A hypothesis testing template of a dyadic subgraph with an undirected weighted and attributed edge and nodal attribute. This subgraph has nodal attribute S (‘illness’ level), edge weight wij and edge attribute M (‘income’ level).
Fig. 6.
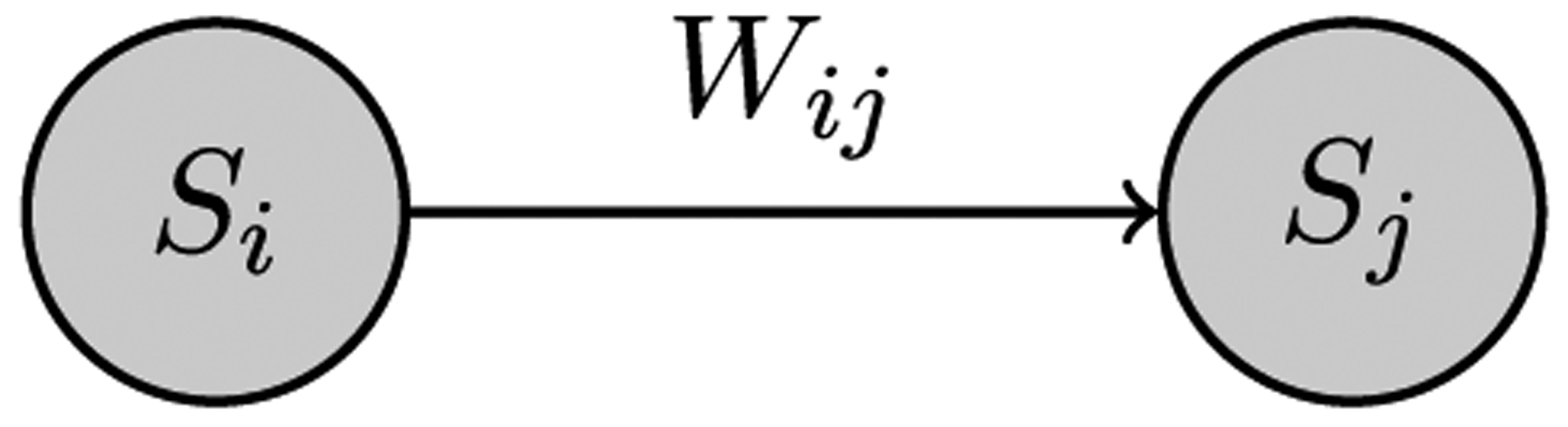
A hypothesis testing template of a dyadic subgraph with a directed weighted edge and nodal attribute. This subgraph has nodal attribute S (‘illness’ level) and edge weight wij.
Table 1.
Descriptions of Census block group nodal attributes F, S, and M which are used in the testing setups illustrated in Figs. 5, 6, and 8 through 10.
| Attribute | Description |
|---|---|
| F | Percentage of block group who received the flu shot |
| S | Average percentage of all participants within a block group who reported having symptoms during the survey |
| M | Median income of the block group |
Fig. 4 gives an example of a dyadic subgraph with nodal attributes and weighted undirected edges. Fig. 4 (c) gives an example of one of the four possible features that can be defined on this subgraph. Importantly, edge weight is not considered part of the definition of a feature. Take variable Mi as the ‘income’ level designation at location (node) i (a low ‘income’ level is represented by a small money bundle ($), a high ‘income’ level is represented by a large money bundle ($$)). The edge weights will represent travel frequencies between location pairs, and will determine the contribution of each appearance of the same feature in a network. The sum of these weights will first be taken in the Observed Network, and then, compared against the distribution of these sums across multiple permuted networks. As is typical for the binary edge weights, we will still refer to the sum of non-binary weights as “feature count”. An in depth example of how feature counts are tallied is provided in Fig. 7 in Section 4.2, but for context consider part (c) of Fig. 4. Part (c) represents a feature with the attribute ‘income’. To determine the count of this feature within the network, each instance of a low ‘income’ level node connected to a high ‘income’ level node is counted, and the final tally is referred to as the “feature count”. The feature in Fig. 4(c), defined on the subgraph in Fig. 4(b), can be useful for testing different network hypotheses, e.g., the hypothesis: “In the original (observed) network, travel tends to occur at a lower frequency between locations with differing (polar) levels of average income”.
Fig. 7.
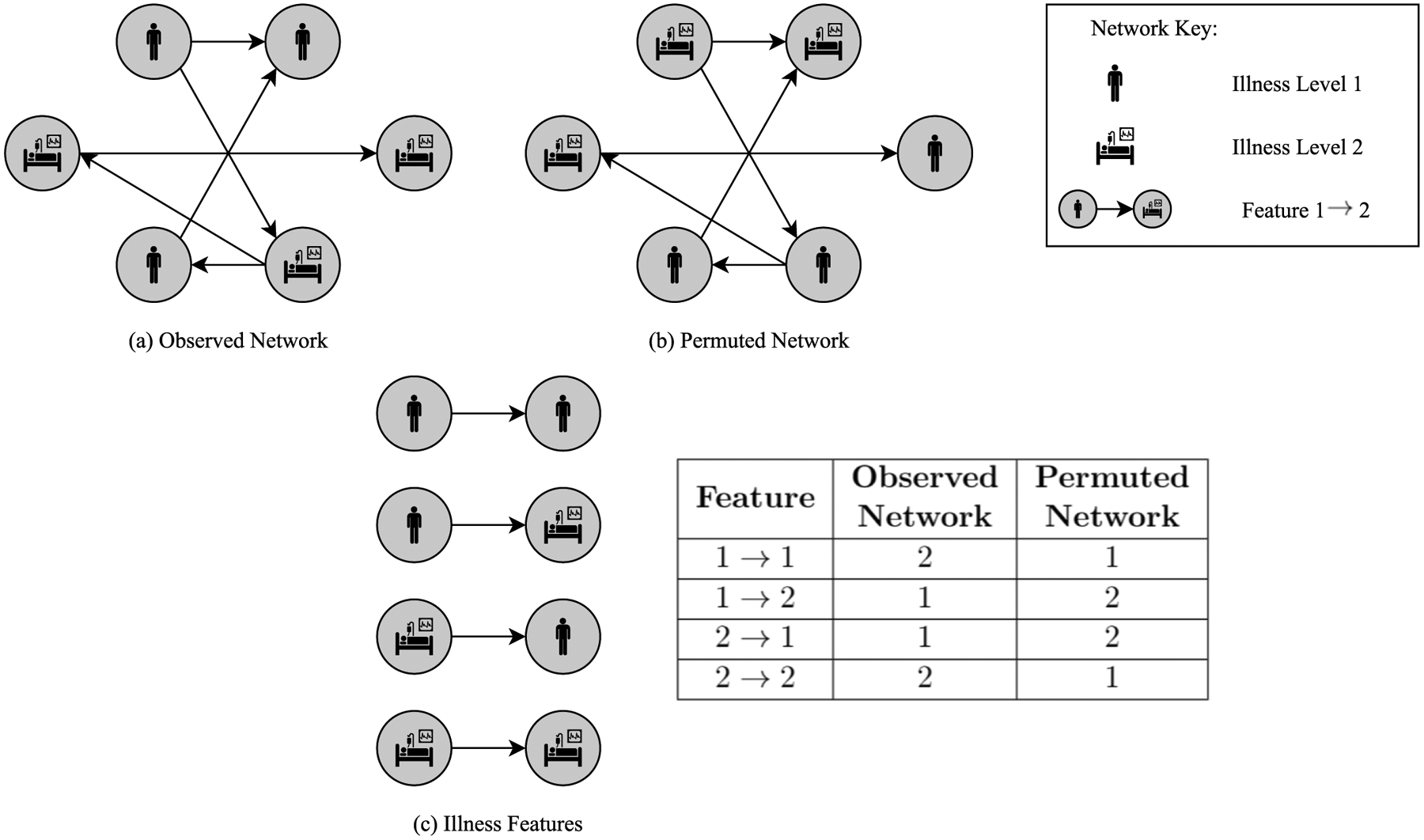
Features can be used to quantitatively describe the structure of a network. Four examples of possible directed features with the nodal attribute ‘illness’ level, (S), are given. Once one generates a permutation (a Permuted Network) of an original Observed Network, both these networks can be described by the counts of the defined features, as shown in the table.
The idea of permuting information “bundles” on networks is used widely both to conduct hypothesis testing and QAP regression on networks. Using a defined testing structure, we are able to construct sixteen possible setups to use for hypothesis testing, surprise analysis, and QAP regression. Generalizing the example given in this section, any testing structure must contain the following four components: network-based variables of interest (node- and/or edge-based, binary or real), a hypothesis, a subgraph (suitable to provide hypothesis-driven evidence), and analysis type (network hypothesis test or network regression). Sections 4.2 through 4.3 explore the use of permutation testing on networks with specific testing structures.
The attributes introduced in Table 1 provide context for the two testing setups displayed in Figs. 5 and 6. Both of the templates employ a permutation based approach. The first template is based on a weighted, undirected subgraph, which incorporates nodal and edge-based attributes, specifically ‘median income’ level and ‘illness’ level, as shown in Fig. 5. This structure can be used to test a variety of hypothesis; one hypothesis that can be tested is, “The greater the frequency of travel between two block groups in the same income bracket, the more likely it is that the two block groups exhibit the same ‘illness’ level”.
The second set up is based on a weighted, directed subgraph with the single nodal attribute S, level of ‘illness’, as shown in Fig. 6. A sample of a hypothesis that can be tested on this subgraph is,“The greater the frequency of travel from one block group to another, the more likely it is that the two block groups exhibit the same level of illness”.
The weighted, attributed subgraphs displayed in Figs. 5 and 6 are templates for a multitude of possible hypotheses, however, standard hypothesis testing only allows for a single hypothesis to be tested at a time. The following section illuminates a method, surprise analysis, which enables the simultaneous test multiple hypotheses which can be drawn from the set of features derived from each subgraph template which provides more robust results and deeper insights.
4.2. Surprise analysis
Surprise analysis allows us to test multiple hypotheses at once, without having to a-priori focus on any one in particular, by looking at all the features based on the same subgraph of interest. In particular, it facilitates an in-depth exploration of how attributes that are part of a nodal bundle interact with one another in affecting disease spread. For example, an analyst might want to use surprise analysis to evaluate how common it is to observe specific patterns in travel between multiple geographic locations that are characterized by certain average ‘income’ levels and ‘illness’ levels (the latter measured at a particular point in time, e.g., during the same week).
Continuing with the example dataset introduced in Section 4.1, the logic of surprise analysis will be explained in reference to Fig. 7. Fig. 7, the bottom left, shows four features defined on a directed dyadic subgraph, with the (trivial) nodal bundles comprised of only one attribute S (‘illness’ level). The Observed Network contains six nodes in total, three of which represent a low level of ‘illness’ (S = 1) at these locations, visually depicted by a figure of a person, the remaining three nodes represent a high level of ‘illness’ (S = 2) at the respective locations, depicted by a person in a hospital bed. The Permuted Network (b) in Fig. 7 is one example permutation of the Observed Network (a). The edge structure remains constant (i.e., node placeholders do not move), but node bundles are shuffled. Of course, the number of nodes with each particular value of S in the network remains the same upon shuffling, that is, in both the Observed Network and the Permuted Network there are three nodes representing a low level of ‘illness’ and three nodes representing a high level of ‘illness’. The table in Fig. 7 contains the counts of each feature within the two networks; note that the feature labeled 1→2 represents the directed dyad in which the generative node (one from which the directed edge emanates) has attribute value S = 1 and the receptive node has attribute value S = 2, representing travel from a block group with a low level of ‘illness’ to a block group with a high level of ‘illness’. As exhibited in the table, the count of each feature became different in the Permuted Network, compared to the Observed Network, as a result of the performed permutation.
The goal of surprise analysis is to determine if the count of any feature(s) within the original real-world network significantly differs from the expected value of the feature(s). The expected count for each feature is calculated by permuting the observed network thousands of times and building the empirical probability mass function of the counts over all these permutations. Determining the significance of the extremity is done by calculating the proportion of permutations in which the observed count is less than the permuted count. Mathematically speaking, this is calculated as . Note that P is the number of Permuted Networks in which the count of a specified feature is less than the corresponding feature count in the Observed Network, and T is the total number of permutations performed. For example, suppose we concentrate on the ‘illness’ feature 1→2, and, in some observed network let this feature count equal 200. Suppose 10,000 permutations are performed, in 1200 of these permuted networks the feature count is less than 200, then the proportion less than is calculated as . If the feature proportion is less than or equal to 0.20 (think of this as the conventional p-value), then the feature in the original network is said to appear significantly less often than expected; as usual, it is up to the analyst to set the critical significance level. On the other hand, if we wanted to determine if a feature appears significantly more often than expected, then the proportion less than would be considered significant if it was greater than 0.8, capturing the right tail of the permutations-based distribution of the feature count.
In addition to this type of evaluation, which is typical for conventional hypothesis testing, in surprise analysis we can also compute how many standard deviations separate the original observed feature count from its mean; both the mean and standard deviation are taken for the distribution of the respective feature count across multiple permutations. This enables us to establish the extremity of observation – surprise – for every feature within the original network. The power of this methodology is illustrated in the practical example in Section 5.
4.3. QAP regression
QAP regression is useful when analyzing dyadic datasets or the relationship between nodal pairings – dyads – in a network. For instance, this method would be useful in answering the question, “How does travel intensity between a pair of block groups explain (affect) the similarity in their illness levels?”. As usual, regression analysis works to explain a part of variation in a dependent variable through the observable values of a number of independent variables, including temporal variables. We first define a unit of analysis – namely dyads – and determine the dependent variable, which can be edge-based or, for larger subgraphs, node-based. When a dependent variable is edge-based it means the dependent variable is on the edge, as shown in Fig. 8, and in these cases the structure being evaluated is a dyad. When the dependent variable is node-based it means the dependent variable is on the central node, as shown in Fig. 10, in this case the structure consists of a node and all its adjacent nodes. The following four examples displayed in Fig. 8 through 10 are a sample of templates for QAP regression. Again, the context for these setups is provided by Table 1.
Fig. 8.
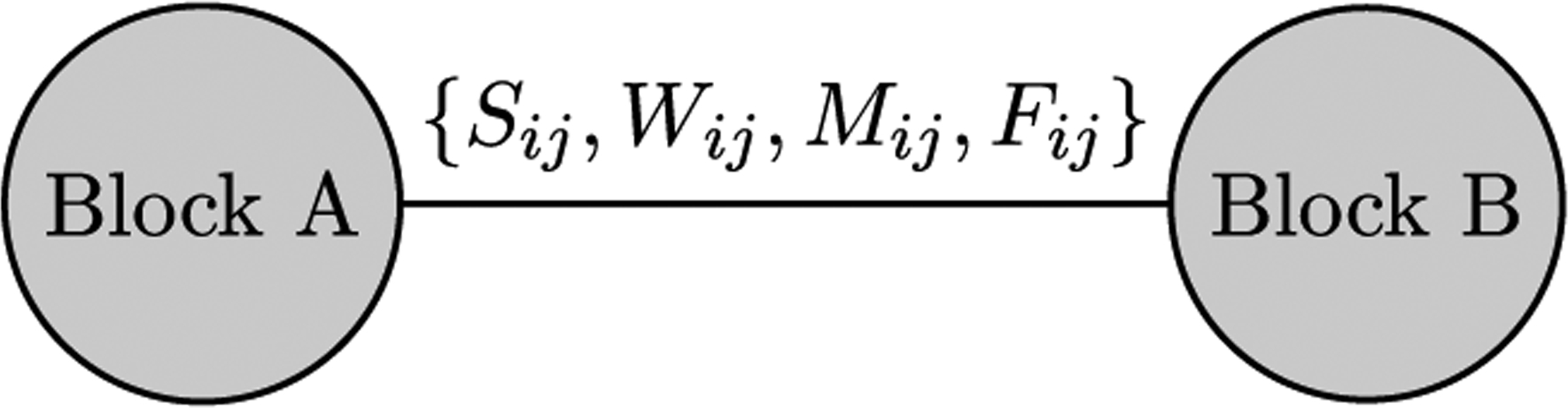
A QAP regression template of a dyadic subgraph with edge-based dependent variable. This subgraph undirected and weighted with an attributed edge. Specifically, the edge attributes are S, W, and F, as described in Table 2 and edge weight W.
Fig. 10.
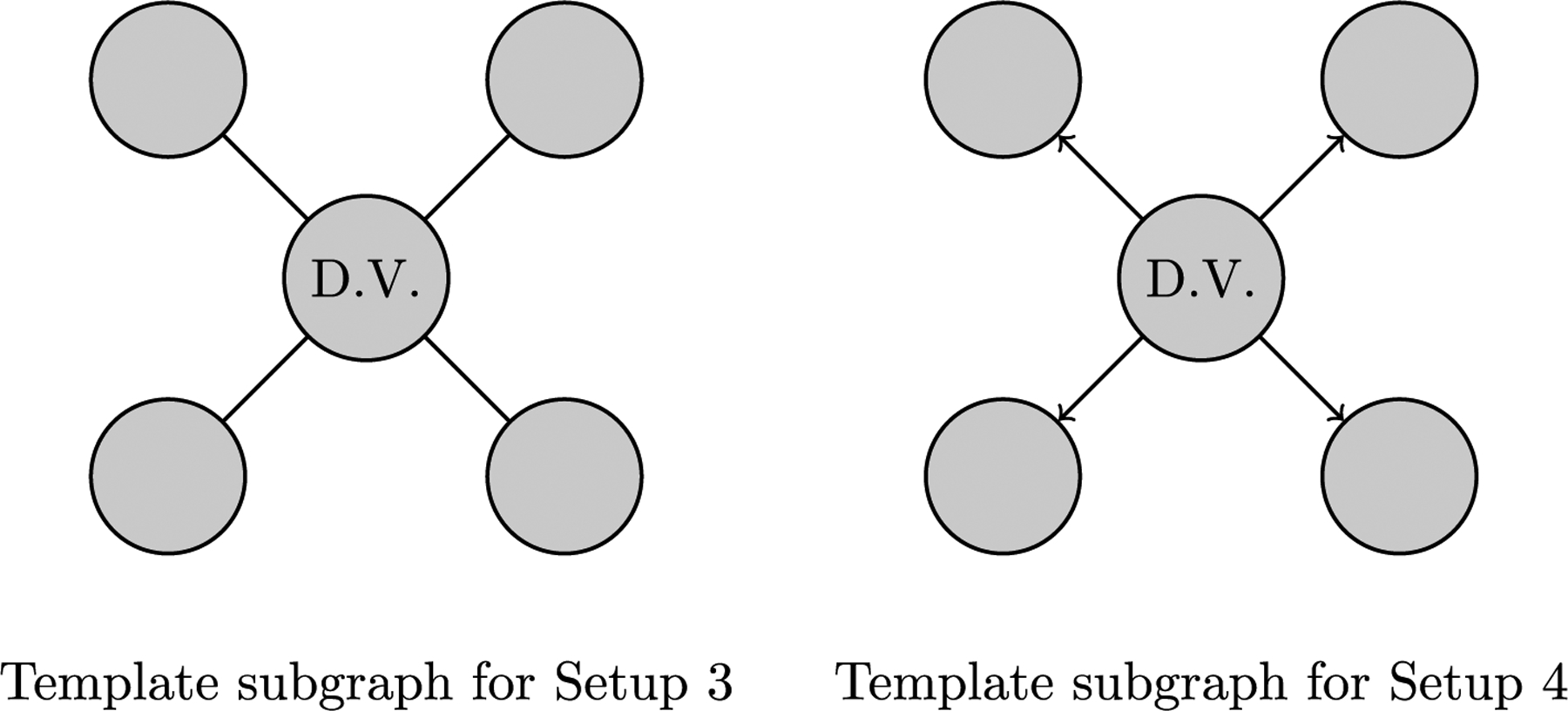
QAP regression setups: (a) under Setup 3, the unit of analysis is an undirected subgraph with the dependent variable in the central node and the independent variables in the adjacent nodes; (b) under Setup 4, the unit of analysis is an directed subgraph with the dependent variable in the central node and the independent variables in the out-neighbors of the central node.
The first two setups are tested using QAP regression for edge-based dependent variables. The first template, displayed in Fig. 8, is based on a weighted, undirected subgraph with edge-based attributes. The attribute bundle contains the variables S, M, and F. The following hypothesis can be tested using this setup, “Illness index similarity is dependent upon travel frequency, income similarity indication, and flu shot similarity indicators”.
The second setup adds a temporal element to the edge-based attributes. Fig. 9 illustrates a weighted, undirected subgraph with a temporal ‘illness’ level attribute and weight. The temporal element is based upon time periods within the study and allows us to test hypotheses such as, “Illness index similarity is dependent upon travel frequency so many, e. g. 2, time periods ago”.
Fig. 9.
A QAP regression template of a dyadic subgraph with edge-based dependent variable. This subgraph is directed and weighted with a temporally attributed edge. Specifically, the edge attributes are S, W, and F, as described in Table 2 for time period t and edge weight W.
The third and fourth QAP regression setups are used to test hypotheses with node based dependent variables. Both setups incorporate the nodal attributes, ‘illness’ level (S), ‘median income’ (M), and rate of flu shot reception (F) and test the hypothesis, “Illness level of a block group is dependent upon the incomes and flu shot rate of the block groups between which there is travel.” However, the third setup features a subgraph with undirected edges and the fourth setup features a subgraph with directed edges, shown in Fig. 10. Both setups can be used to test a variety of hypotheses, including those with a temporal element.
QAP regression enables nodal and edge based inference. Methodological approaches which allow for incorporating temporal elements are useful when analyzing longitudinal datasets, as demonstrated in the illustrative example in Section 5.
5. Illustrative results: a case of flu spread in Western New York
This section provides an in depth example of the use of the methods detailed in Sections 3 and 4. The case data preparation involved organizing the survey responses and identifying links for network building, and calculating the values of attributes for each of the actors that were used to create networks, as shown in Section 3. These data were then used to conduct hypothesis tests, surprise analysis, and QAP regression. The section is divided into subsections based on the methodology that was implemented. A variety of tests were performed on different network types in order to demonstrate the versatility of permutation testing and surprise analysis.
5.1. Data preparation
An observational study was conducted in Erie and Niagara counties in Western New York during the 2016–2017 influenza season. Over 2000 people were recruited to participate in the study and respond to surveys. Participants filled out an initial survey that gathered general demographic data, including home and work place addresses. Following the initial survey, they used a smart phone application to complete a weekly questionnaire concerning their health status, as well as the status of other members of the household, and their mobility.
Concurrently, GPS records were collected from iPhone users. iPhones detect locations and distance traveled between previous location and current location, thus, the GPS locations captured via iPhone would track every new location to which a participant traveled. Since the iPhones record location every time a participant moves 500+ meters, many of the records were retrieved during travel. In order to eliminate such points, the notion of a (visited) place was introduced. A place is defined as a GPS location in which the time spent by a study participant meets or exceeds 30 min. Amount of time spent was calculated by finding the difference in time between two consecutive GPS records for the same participant. All records of the locations that did not meet the requirements to be a place were eliminated.
Each set of place coordinates was mapped to their Census block group ID. Additionally, the self reported home and work locations were assigned their corresponding block group ID. Geographically, a block group spans 2–2.5 miles in diameter. Since GPS locations for iPhones are accurate within 500 m, the entire geographic span will be contained within a single block group.
Every week the participants filled out a survey with questions concerning their travel and health status. Their responses were used to calculate attributes for the block groups. There were five attributes obtained from the survey information: P, R, F, G, and S, described in Table 2. The attributes R, F, G, and S were calculated to be continuous factors, but were then encoded to be categorical variables in the set {1, 2}. The values corresponded to a bin in which the continuous factor belonged, illustrated in Table 3.
Table 2.
Description of all attributes obtained from the survey and Census data. These attributes represent nodal information for Census block groups. Census data from: https://factfinder.census.gov/faces/nav/jsf/pages/index.xhtml.
| Attribute | Description |
|---|---|
| Survey | |
| P | Number of participants residing in the block group |
| R | Percentage of block group who reported taking reactionary measures |
| F | Percentage of block group who received the flu shot |
| G | Percentage of block group who identifies as male |
| S | Average percentage all participants within a block group reported having symptoms during the survey |
| Census | |
| M | Median income of the block group |
| E | Predominant race(s) within the block group |
| I | Percentage of the block group over the age of 18 who are insured |
There are a total of eight attributes collected from the survey and Census data, however, R, E and I were excluded from testing as all block groups had values too similar to warrant analysis. The remaining five attributes – P, F, G, S, and M, – were used in the analyses explored in the remainder of the paper.
Table 3.
Categorical encoding for the continuous survey attributes described in Table 2.
| Categorical Value | Continuous Range |
|---|---|
| 1 | |
| 2 |
Additionally, the Census collects data and a multitude of it is publicly available at the block group level. Census data was collected from the American Factfinder on median household income, race, and health insurance status.
As shown in Table 3, the continuous range of each variable is split into two categorical bins using the average value as a cut-off point, or threshold. Researchers must decide the number of levels of each attribute, the number of levels is dependent upon the data being analyzed. For our purposes, each attribute has two possible levels, creating a binary designation. This decision was made for three reasons: (1) using the average value for an attribute as the threshold is a natural way to create levels and makes the distinction between levels easily interpretable (i.e. above average or below average), (2) our data are sparse, so if we were to include more than two levels for each attribute, then there would not be enough subjects per block group at each level for robust analysis, and (3) the number of possible features increases exponentially as the number of levels increases. For the purposes of our application, using only two levels is advantageous, however, we acknowledge that the number of levels and determination of thresholds may affect the results.
5.2. Hypothesis testing and QAP regression
The network building methodology of Section 3 was implemented to create a series of networks based on the data obtained from the observational study outlined in Subsection 5.1.
Test Set-Up 1: Standard Hypothesis Testing and QAP Regression.
To start, we construct a star network (see Network II in Fig. 2) in which links are created between the home location and each place a subject visited. The star network includes all visited places whilst emphasizing subjects’ home locales. Of immediate interest to us is the relationship between frequency of travel and a subset of key attributes as it provides in-depth insight on our data to inform the next step of analysis. For example, making use of the attribute S (‘illness’ level), one can formulate the hypothesis, “The frequency of travel tends to be greater between block groups with the same level of illness.” Other hypotheses may explore the relationships between frequency of travel and the following attributes: ‘illness’ level (S), ‘median income’ level (M), ‘gender’ (G), and ‘flu shot’ reception (F), as shown in Table 4.
Table 4.
Results from a series of hypothesis tests and QAP regression analysis on Network II from Fig. 2. Two of the hypotheses produced significant results for a significance level of α = 0.10. Note that in column 3, the labels “Level 1” and “Level 2” refer to the illness/income measure being at a low or high level, respectively.
| Hypothesis | Approach | Result |
|---|---|---|
| The frequency of travel tends to be greater between block groups with the same level of illness. | Hypothesis Testing (Homophily) | Level 1: p = 0.0954 Level 2: p = 0.0228 |
| The frequency of travel tends to be greater between block groups within the same income bracket. | Hypothesis Testing (Homophily) | Level 1: p = 0.0614 Level 2: p = 0.1382 |
| The frequency of travel tends to be greater between block groups with the same gender distribution. | Hypothesis Testing (Homophily) | Not Significant |
| The frequency of travel tends to be greater between block groups with the same percentage of flu shot reception. | Hypothesis Testing (Homophily) | Not Significant |
| Illness similarity is dependent upon frequency of travel. | QAP – Edge Based | Not Significant |
Test 1 Results.
Standard network hypothesis testing and QAP regression are utilized to test the six hypotheses in Table 4. The hypotheses that tested to statistically significant outcomes turned out to be, “The frequency of travel is likely to be greater between block groups with the same level of illness”, and “The frequency of travel is likely to be greater between block groups in the same income bracket.” However, when we implemented QAP regression to analyze the dependence of ‘illness’ (S) and ‘income’ (M) similarity, separately, upon frequency of travel, the produced results were not significant.
Test 1 Observed Insights.
There is evidence to support the hypotheses that there tends to be a higher volume of travel between block groups with the same level of ‘illness’ or between block groups belonging to the same income bracket. In a practical sense, the trends are justified by the nature of disease propagation. We would expect that two block groups with a high frequency of travel between them would have similar levels of ‘illness’. Furthermore, it would be unlikely for there to be a high volume of travel between a block group with a low level of ‘illness’ and a block group with a high level of ‘illness’ because the disease would spread between the two block groups. Additionally, the majority of travel occurred between subjects’ home and work locations, thus we would expect to see high volumes of travel between block groups with a similar level of ‘income’. If a subject resides in a high ‘income’ block group, then it is more probable that they work in a high ‘income’ block group, this logic follows for subjects residing in low ‘income’ block groups. These results demonstrate a need for policy intervention targeting high need areas. Specifically, we see a high volume of travel between block groups with the same level of ‘illness’, thus these block groups would be good locations to intervene, for example, by employing contact-tracing policies. Similarly, we see frequent travel between block groups with the same level of ‘income’. Since there is more travel between these block groups, it would make them attractive targets for relevant health insurance campaigns or subsidy programs.
However, there is not sufficient evidence to support the claim, “Illness similarity is dependent upon frequency of travel”, nor to determine the relationship between income similarity and frequency of travel. These findings provoke further exploration using surprise analysis.
5.3. Surprise analysis
The insights discussed in Section 5.2 motivate our use of surprise analysis as this method provides a more holistic view on the dependencies between the network structure and attributes of interest. To extend our analysis to another network type, we reorganize the data to build the “Home-Work” network (Network III in Fig. 2). Travel between home and work locations was observed to remain constant throughout the study, thus the element of time is inconsequential for Network III. The results from the hypothesis testing and QAP regression suggest two contradictory outcomes: (1) that there is interdependence of travel frequency and level of ‘illness’ as well as level of ‘income’, and (2) that similarity of ‘illness’/’income’ levels between block groups is not significantly dependent upon frequency of travel between them.
Test 2 Set-Up: Network III with Single-Attributes Nodes.
Surprise analysis allows us to more deeply analyze the interdependence of multiple nodal attributes. As demonstrated in Fig. 11, we are able to differentiate between the four possible features derived from a dyadic subgraph with signed, directed edges and nodal attributes ‘illness’ and ‘income’. We now build a network where an edge labeled with (+) signifies travel from a block group with a low ‘income’ or ‘illness’ level to a block group with a higher level of ‘income’ or ‘illness’, respectively. Similarly, an edge labeled with (−) signifies travel from a block group with a high level of ‘income’ or ‘illness’ to one with a lower level. If the two block groups have the same label, the edge is labeled with (0).
Fig. 11.
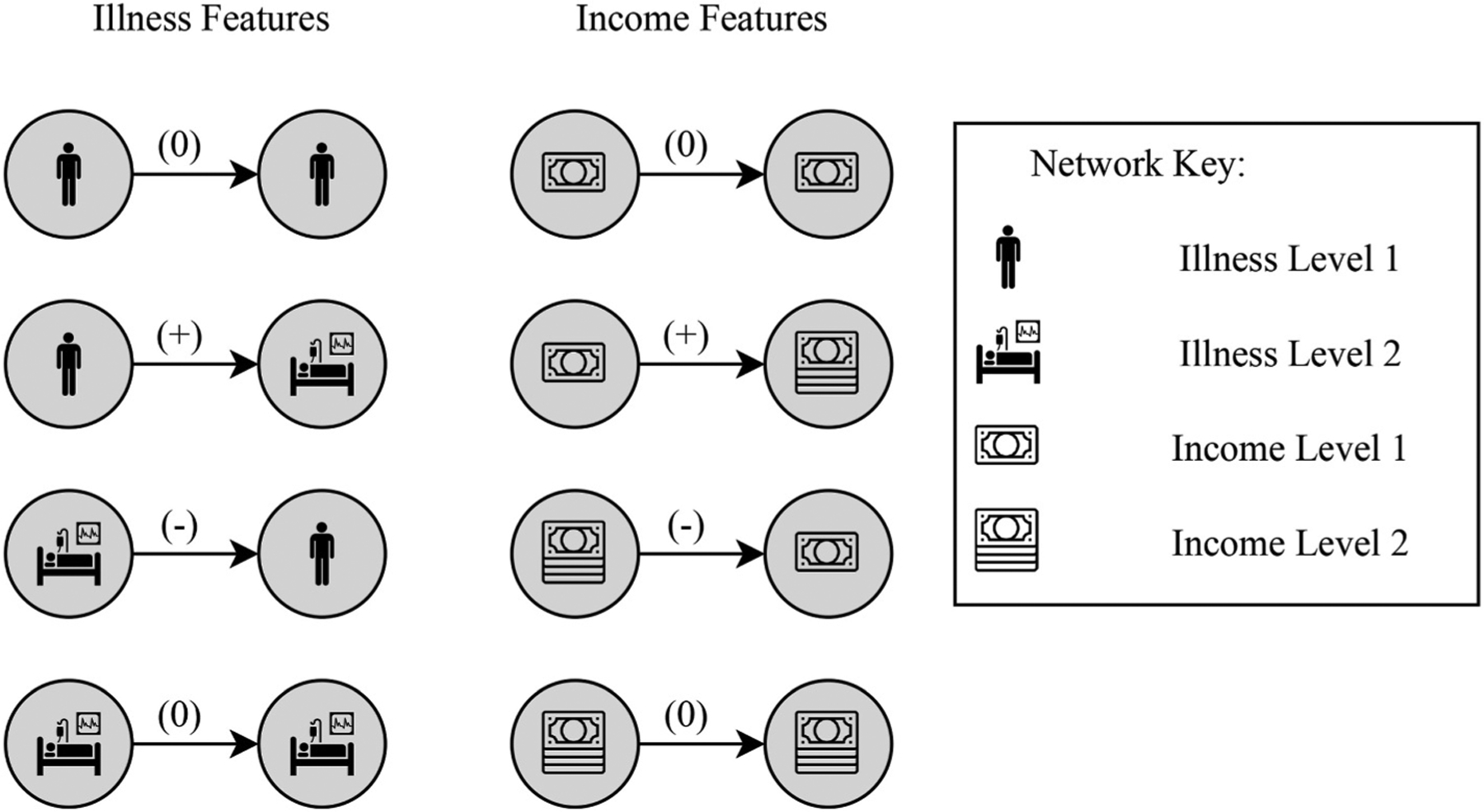
(a) The four possible features derived from a dyadic subgraph with signed, directed edges and nodal attribute S = 1 for a low level of ‘illness’ and S = 2 for a high level of ‘illness’. (b) The four possible features derived from a dyadic subgraph with signed, directed edges and nodal attribute M = 1 for a low ‘income’ level and M = 2 for a high ‘income’ level.
In order to test at once multiple hypotheses of the form “The frequency of travel tends to be greater between block groups with the same level of illness” via surprise analysis, all possible features with nodal attribute ‘illness’ must be defined. Fig. 11 depicts all possible features involving ‘illness’ and ‘income’ nodal attributes. We conduct surprise analysis by aggregating the outputs from 10,000 network permutations, and tallying the counts of features produced from dyadic subgraphs with ‘illness’ and ‘income’ nodal attributes in Fig. 11.
Test 2 Results.
The results for the surprise analysis applied for analyzing directed dyads with ‘illness’ and ‘income’ nodal data are shown in Tables 5 and 6, respectively. Each table displays the Observed Value, Expected Value, and the Proportion Less Than (proportion of permuted networks with counts less than the observed value) numbers for each of the four features. The Expected Value of each feature is the aggregate of the counts of that feature across all permuted networks. If the Expected Value is greater than the Observed Value, the feature appears more than expected in the permutated networks, and vice versa for features in which the Expected Value is less than the Observed Value. In the tables, the column labeled 1→2 contains the results for the features representing travel from a low ‘illness’/’income’ level block group to high ‘illness’/’income’ level block group. Note that the values in the Observed Value row are highlighted indicating that the observed value is less than the expected value (red) or the observed value is greater than the expected value (green).
Table 5.
The observed and expected values for the ‘illness’ based features presented in Fig. 11 and their respective p – values. Given a significance level of 0.2, features 1→1, 1→2, and 2→1 had a prevalence that was significantly extreme in the observed network. The values highlighted in medium grey produced significant results.
| 1 → 1 | 1 → 2 | 2 → 1 | 2 → 2 | |
|---|---|---|---|---|
| Observed Value | 749 | 326 | 421 | 198 |
| Expected Value | 690.0542 | 391.4836 | 389.3635 | 223.0987 |
| Prop. Less Than | 0.8485 | 0.0934 | 0.8100 | 0.2309 |
Table 6.
The observed and expected values for the ‘income’ based features presented in Fig. 11 and their respective p – values. Given a significance level of 0.2, none of the features in the observed network had a prevalence that was significantly extreme.
| 1 → 1 | 1 → 2 | 2 → 1 | 2 → 2 | |
|---|---|---|---|---|
| Observed Value | 357 | 430 | 423 | 484 |
| Expected Value | 384.2575 | 421.6094 | 421.1001 | 467.033 |
| Prop. Less Than | 0.2798 | 0.5585 | 0.5194 | 0.6303 |
Table 5 displays the surprise analysis results for the directed dyads with ‘illness’ level nodal data. There are four features deserving discussion; of these, features 1→2 and 2→2 have expected values greater than their respective observed values, while features 1→1 and 2→1 appear more than expected in the observed network. In the observed network, features 1→1, 1→2, and 2→1, had observed counts which significantly differed from the expected counts.
Table 6 displays the results for the surprise analysis test employed to analyze directed dyads with ‘income’ nodal data. Here, features 1→2, 2→1, and 2→2 have the observed counts that were greater than their corresponding expectations, whereas the count of feature 1→1 is less than its expected value. However, none of the four features have counts which differ significantly between the observed and permuted networks.
Test 2 Observed Insights.
Our quantitative analysis shows that the subjects in the study traveled to block groups with a lower level of ‘illness’ more frequently than they traveled to block groups with higher levels of ‘illness’. Recall that all these destinations are workplace locations (this is how Network III is constructed). There is significantly more travel to block groups with a low level of ‘illness’, which could mean workplace locations are in regions with a low level of ‘illness’. This could be because some workplace locations are in non-residential block groups. Similarly, the counts of features 1→2 and 2→2 in the observed network are less than their corresponding expected values, which suggests that subjects tend to travel to block groups with high ‘illness’ levels less often. In other words, since the destinations are workplace locations, this provides evidence to support the notion that workplace locales are located in non-residential, low ‘illness’ level block groups. Though many workplaces are located in non-residential, less densely populated areas, they are traveled to frequently. Gibson et al. conducted a study examining distance traveled to receive care at a mobile clinic and found that the vast majority of people who visited these clinics traveled five miles or less for care [12]. Our study identifies high traffic areas, and thus, these geographic areas would be prime locations for mobile clinics as people are traveling to these places already.
Test 3 Set-Up: Network III with Multiple Nodal Attributes.
So far, we looked separately at the features produced from the dyadic subgraphs with nodal attributes ‘illness’ and ‘income’. However, to understand how these attributes interact, it is desirable to work with features that simultaneously include both the attributes. Surprise analysis, unlike standard network hypothesis testing, enables the testing of features with multiple nodal attributes, as shown in Fig. 12.
Fig. 12.
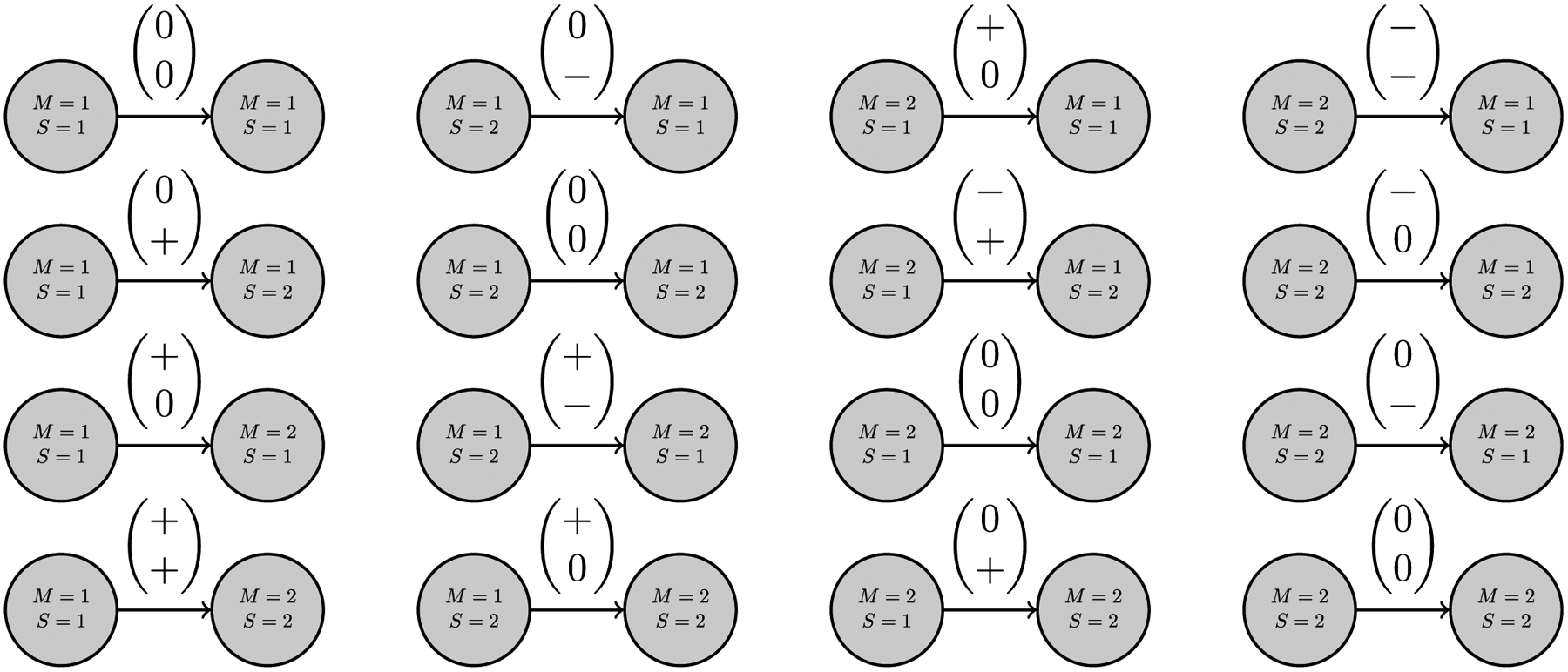
The sixteen possible features derived from a dyadic subgraph with signed, directed edges, and nodal attributes S and M that can take the values 1 or 2 to represent a low or high level, respectively. The edge tuple contains signs indicating status determined by the node attribute M on top and S on bottom.
Note that it is possible to use the same method even with the features comprised of both ‘income’ and ‘illness’ attributes, to analyze the ‘income’- and ‘illness’-based features simultaneously, however, this may not be advantageous. Evaluating multiple attributes individually by performing surprise analysis on combined features produces muddy results. For example, the ‘illness’ feature 1→1 would be split across four features: {11}→{11}, {11}→{21}, {21}→{11}, and {21}→ {21}. Unless the goal is to study how ‘income’- and ‘illness’-based features interact, it is best to test them separately.
In Fig. 12, similarly to Fig. 11, M represents the block groups’ ‘income’ level and S represents the block groups’ ‘illness’ level. The edges are labeled such that the top value indicates the ‘income’ status difference between the nodes and the bottom value indicates the ‘illness’ status difference between the nodes. To better understand Fig. 12, consider one feature, specifically the feature in row one, column two. The generative node has attributes M = 1 and S = 2 signaling that the block group it represents has a low ‘income’ level and a high ‘illness’ level. The receptive node has attributes M = 1 and S = 1 signaling both a low ‘income’ level and a low level of ‘illness’. Both the generative and receptive nodes have a low ‘income’ level resulting in the top value of (0) in the edge label. However, the ‘illness’ level for the generative node is high, and for the receptive node it is low, resulting in the bottom value of (−) in the edge label. The other fifteen features can be interpreted in a similar fashion.
Test 3 Results.
The results of the surprise analysis conducted with the sixteen features in Fig. 12 are shown in Table 7. The feature {12}→{11} represents the feature in row one, column two of Fig. 12, as described in detail above. Similarly to Tables 5 and 6, Table 7 contains the Observed Value, Expected Value, and Proportion Less Than for each of the sixteen features with significant results highlighted in grey. The counts of three of the features are significantly extreme. Two of the three features, {11}→{12} and {12}→{12} have counts that are lower than expected in the observed network, whereas there is a higher prevalence of feature {12}→{21} in the observed network.
Table 7.
The observed and permuted counts of the sixteen features presented in Fig. 12 containing both ‘income’ and ‘illness’ nodal data. Three of the sixteen features, {11}→{12}, {12}→{12} and {12}→{21} have significantly extreme counts in the observed network. Features with significant counts are highlighted in grey.
| Feature | Observed Value | Expected Value | Prop. Less Than |
|---|---|---|---|
| {11} → {11} | 173 | 158.9006 | 0.7087 |
| {11} → {12} | 66 | 88.0504 | 0.1091 |
| {11} → {21} | 154 | 171.504 | 0.2692 |
| {11} → {22} | 97 | 98.918 | 0.5203 |
| {12} → {11} | 80 | 87.7958 | 0.3254 |
| {12} → {12} | 38 | 49.8753 | 0.1570 |
| {12} → {21} | 115 | 95.6615 | 0.8603 |
| {12} → {22} | 64 | 55.1384 | 0.7606 |
| {21} → {11} | 192 | 171.4591 | 0.7610 |
| {21} → {12} | 80 | 95.9102 | 0.2394 |
| {21} → {21} | 187 | 188.288 | 0.5071 |
| {21} → {22} | 113 | 107.9723 | 0.6427 |
| {22} → {11} | 104 | 98.5469 | 0.6402 |
| {22} → {12} | 47 | 55.2645 | 0.2788 |
| {22} → {21} | 118 | 107.6252 | 0.7200 |
| {22} → {22} | 66 | 63.0898 | 0.6175 |
Features with multiple nodal attributes can be divided into single-attributed sub-features. This allows us to interpret the interaction between the attributes and to analyze the contribution of each attribute individually. Figs. 13 and 14 demonstrate how features with multiple attributes can be broken down into single-attributed sub-features.
Fig. 13.
The leftmost dyadic feature consists of a nodal bundle with attributes S and M and directed, signed edges. This displays how a ‘income-illness’ feature with an extreme observed value can be broken down into its respective income and ‘illness’ sub-features to demonstrate how the attributes interact with one another.
Fig. 14.
The leftmost dyadic feature consists of a nodal bundle with attributes S and M and directed, signed edge. This displays how an ‘income-illness’ feature that is not extreme can be broken down into its respective ‘income’ and ‘illness’ sub-features to demonstrate how the attributes interact with one another.
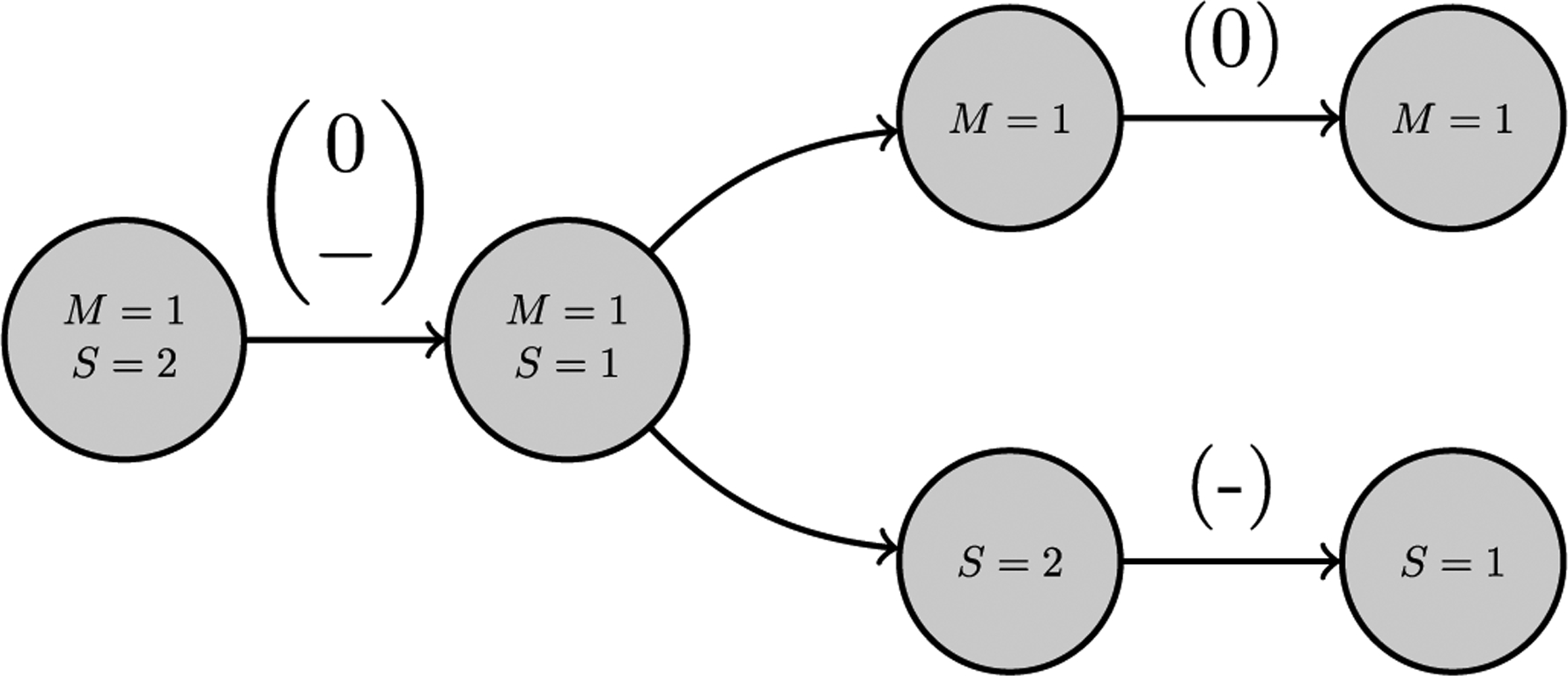
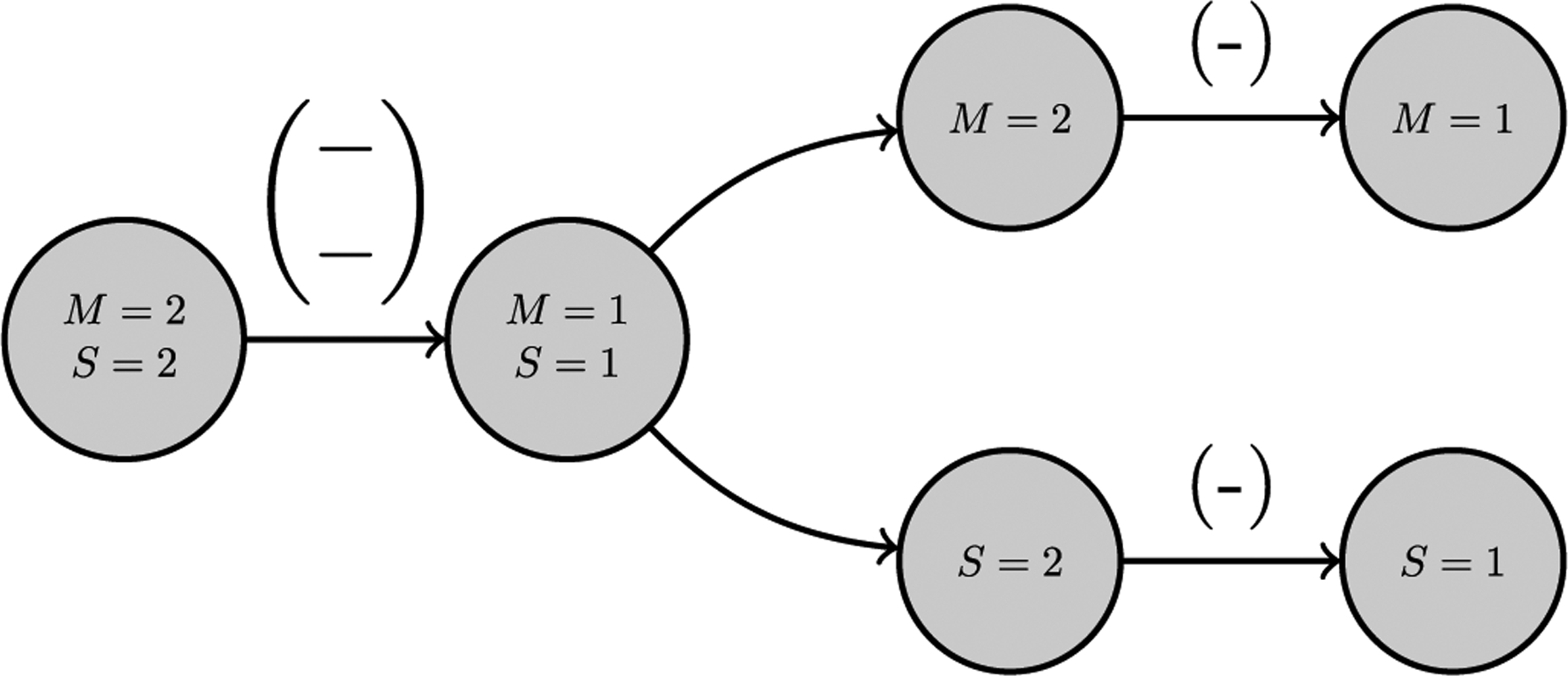
Fig. 13 exhibits the breakdown of feature {11}→{12}, which is occurs in the observed network much more often than could be expected at random. Examining the values of the ‘income’ and ‘illness’ attributed features in Tables 5 and 6, we find that the observed counts for these features is less than the corresponding expected values, and that the observed count of the ‘illness’ attributed feature differed significantly from the expected value. Similarly, the ‘income’ and ‘illness’ sub-features of the remaining two features with extreme counts, {12}→{12} and {12}→{21}, coincide, signaling that if the count of the complete feature is extreme, then both of its ‘income’ and ‘illness’ sub-features occur less or more often than expected.
In a contrasting manner, a majority of the features which do not occur with significant frequency are comprised of ‘income’ and ‘illness’ sub-features in which one is less prevalent and one is more prevalent in the observed network, as displayed in Fig. 14. Additionally, its ‘income’-attributed sub-feature occurs more than expected whereas its ‘illness’-attributed sub-feature occurs less than expected in the observed network.
The evaluation of these two features provides support for the notion that in order for a feature consisting of multiple attributes to have extreme counts, it is necessary for the representation of the sub-features to coincide. In the same vein, this means that one attribute cannot determine the representation of a feature containing multiple attributes.
Test 3 Observed Insights.
The quantitative results for Test 3 can be explained by closely examining the results we gathered in Test 2. Test 2 provides sufficient evidence to support the claim that there is a higher volume of travel to destinations with a low ‘illness’ level. Additionally, there is some evidence to support the notion that there is less travel between two block groups with a low ‘income’ level. Keeping this in mind, when we analyze the results in Table 7 we see a similar pattern form. On the whole, there is more travel between block groups with a low ‘illness’ level and less travel between block groups with a low level of ‘income’, these results are consistent with those found in Test 2. Of the results displayed in Table 7, only two features produced surprising results, {11}→{21} and {21}→{21}. The first feature represents travel from a low ‘income’ and ‘illness’ block group to a high ‘income’, low ‘illness’ block group. The second feature represents travel originating in a high ‘income’, low ‘illness’ block group to a high ‘income’, low ‘illness’ block group. In both cases, we would expect there to be a higher volume of travel as both block groups have low ‘illness’ levels. However, the difference between the observed and expected counts in these instances were insignificant.
Test 4 Set-Up: Exploration of Single-Attributed Temporal Networks.
So far we have demonstrated how surprise analysis can be implemented to analyze static networks, however, as the data were collected through a longitudinal study, methods to evaluate temporal networks are of particular interest. The temporal network based upon time periods, Network V, builds links in the same way as the star network (Network II), i.e., home locations serve as origin points of all travel, however, to construct this network, the GPS records were divided into two-week periods which created fourteen networks corresponding to specific time periods. Fig. 15 shows the four types of directed subgraphs that can be created using the nodal attribute ‘illness’, in this new context. Each network is labeled with the first week from which the data were derived, i.e., Week_0 contains the travel data from week 0, the start of the study, and week 1. Note that networks Week_14 and Week_16 contain the travel data from the peak period of the influenza season.
Fig. 15.
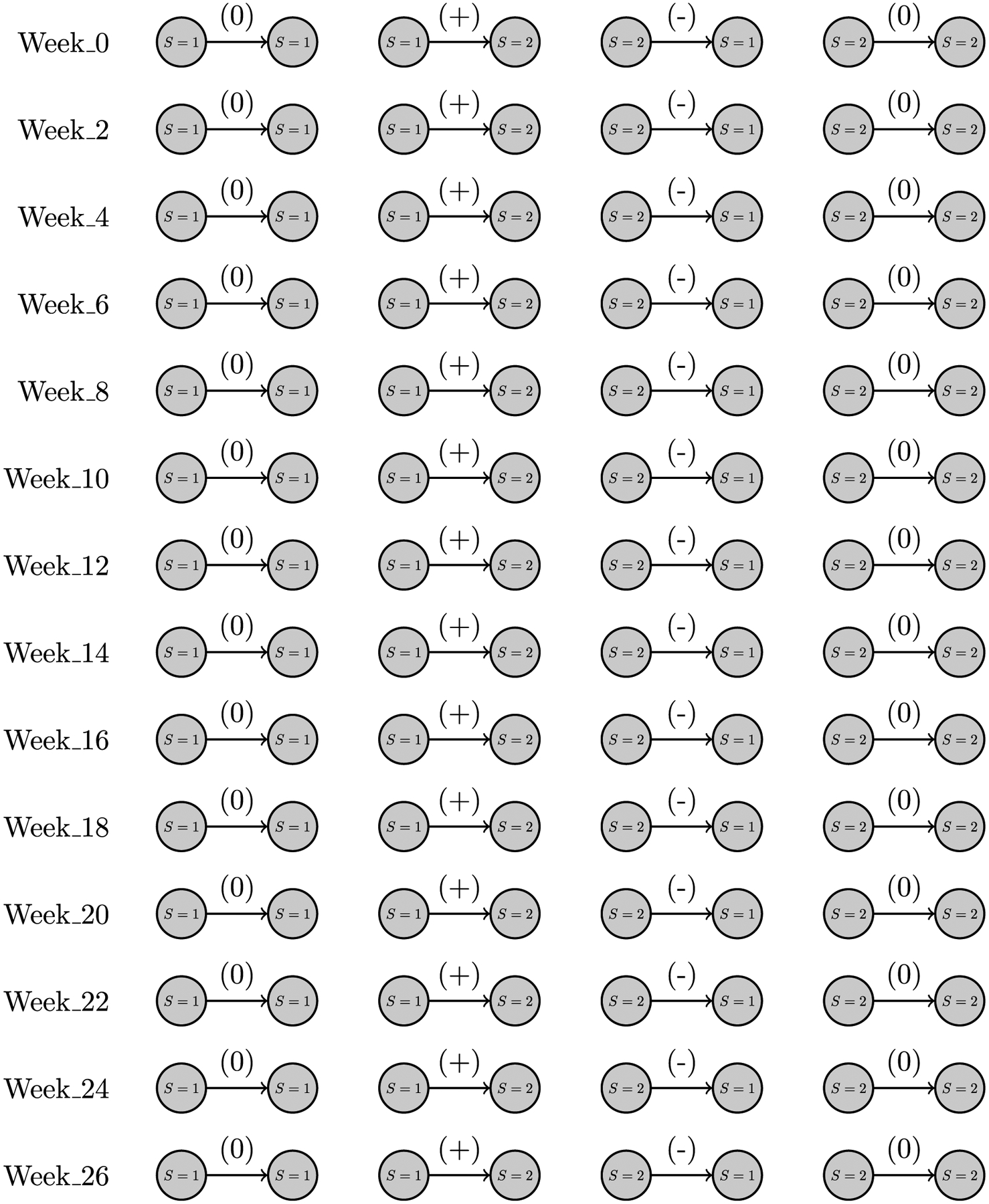
An example of features present in a network with the structure of Network V in Fig. 2. Week_0 through Week_26 are networks constructed from time periods of two weeks. Each network has four possible features. The features are directed, signed, dyads with node attribute S, ‘illness’.
Test 4 Results.
Surprise analysis was implemented to evaluate the biweekly temporal networks present in Fig. 15. The results are displayed in Tables 8 and 9. The Observed and Expected Value of each of the four features across all fourteen networks are provided in Table 8. Observed values highlighted in red indicate features whose observed counts are less than the expected counts and values highlighted in green indicate features whose observed counts are greater than the corresponding expected counts.
Table 8.
The observed and permuted counts of the four features in each of the fourteen time periods displayed in Fig. 15. Observed values, highlighted in red, appeared less than expected and values highlighted in green appeared more than expected in the permuted network.
| Observed Value | Expected Value | |||||||
|---|---|---|---|---|---|---|---|---|
| Features | 1 → 1 | 1 → 2 | 2 → 1 | 2 → 2 | 1 → 1 | 1 → 2 | 2 → 1 | 2 → 2 |
| Week_0 | 25 | 51 | 72 | 316 | 133.4057 | 82.1893 | 89.916 | 158.489 |
| Week_2 | 26 | 104 | 203 | 597 | 267.4617 | 165.2756 | 183.8470 | 313.4157 |
| Week_4 | 99 | 178 | 318 | 587 | 337.6947 | 208.9106 | 235.3290 | 400.0657 |
| Week_6 | 46 | 159 | 297 | 795 | 369.2047 | 223.754 | 265.8359 | 438.2054 |
| Week_8 | 184 | 247 | 352 | 497 | 363.5309 | 229.3759 | 258.6104 | 428.4828 |
| Week_10 | 162 | 243 | 358 | 503 | 359.1563 | 220.7937 | 259.9480 | 426.1020 |
| Week_12 | 220 | 269 | 375 | 500 | 380.8585 | 237.2562 | 284.6681 | 461.2172 |
| Week_14 | 415 | 332 | 334 | 296 | 392.6428 | 239.5582 | 286.7702 | 458.0288 |
| Week_16 | 557 | 333 | 263 | 164 | 372.2968 | 230.9279 | 269.8036 | 443.9717 |
| Week_18 | 79 | 196 | 242 | 811 | 379.0608 | 228.4776 | 272.7187 | 447.7429 |
| Week_20 | 800 | 238 | 152 | 79 | 359.9355 | 218.4159 | 263.1858 | 427.4628 |
| Week_22 | 890 | 246 | 159 | 89 | 389.0809 | 237.5807 | 288.7515 | 468.5869 |
| Week_24 | 845 | 229 | 158 | 34 | 361.0754 | 220.3165 | 261.1503 | 423.4578 |
| Week_26 | 856 | 255 | 173 | 44 | 371.7338 | 231.4841 | 275.3467 | 449.4354 |
Table 9.
The results of the surprise analysis test on the temporal networks displayed in Fig. 15 for 10,000 permutations. There are many significant results for significance level α = 0.20. Significant results are highlighted in red and green to represent feature counts which are less than or greater than the expected value, respectively.
| Prop. Less Than | ||||
|---|---|---|---|---|
| Feature | 1 → 1 | 1 → 2 | 2 → l | 2 → 2 |
| Week_0 | 0.0112 | 0.0014 | 0.0242 | 1.0000 |
| Week_2 | 0.0003 | 0.0027 | 0.8007 | 0.9982 |
| Week_4 | 0.0343 | 0.0147 | 0.9704 | 0.8966 |
| Week_6 | 0.0000 | 0.0010 | 0.6394 | 0.9999 |
| Week_8 | 0.4215 | 0.1361 | 0.9580 | 0.4345 |
| Week_10 | 0.0191 | 0.0720 | 0.9498 | 0.9150 |
| Week_12 | 0.0077 | 0.0620 | 0.8672 | 0.9909 |
| Week_14 | 0.3705 | 0.5118 | 0.5392 | 0.6275 |
| Week_16 | 0.7449 | 0.8022 | 0.1873 | 0.1810 |
| Week_18 | 0.0084 | 0.0207 | 0.1630 | 0.9989 |
| Week_20 | 0.9920 | 0.3603 | 0.0066 | 0.0947 |
| Week_22 | 0.9892 | 0.3108 | 0.0066 | 0.2218 |
| Week_24 | 0.9891 | 0.5031 | 0.0328 | 0.0014 |
| Week_26 | 0.9212 | 0.7157 | 0.0631 | 0.0179 |
Table 9 displays the Proportion Less Than results for each of the fourteen temporal networks. Similarly to Table 8, highlighted cell values indicate extreme observed counts of corresponding features. Note that the majority of the features across all fourteen time periods occur with frequency that is significantly different from the expectation based upon 10,000 permutations.
Test 4 Observed Insights.
Examining the results in Table 8, an interesting pattern reveals itself, specifically if we focus on features 1→1 and 2→2. In the first seven time periods, feature 1→1 consistently has observed values which are less than the expectation and feature 2→2 consistently has observed values which are greater than expected. One interpretation of this pattern is that participants had a high rate of illness during the first half of the study, but still chose to travel. However, the travel between block groups with a low level of ‘illness’ occurred less than expected, presumably not because they did not travel, but because the general rate of illness was higher during this time. These results also illuminate specific time periods when policy intervention would be most helpful, i.e., prior to the peak and decrease in travel. This is because the best preventative action for influenza is flu shot, which is proactive rather than reactive. The results gathered from the fourth test break down the influenza season into biweekly periods, which allows policy makers to visualize the peak of the season as well as travel patterns. This may informs intervention timing, and recommend locations to target based on frequency of travel, so as to protect the largest number of patients.
In network Week_14, none of the feature counts are extreme. Week_14 contains the travel information from the beginning of the peak of influenza season, thus subjects are just starting to fall seriously ill, so the frequency of travel between block groups with a high rate of illness begins to fall as people refrain from traveling. In Week_16 we see that the features 1→2, 2→1, and 2→2 have extreme observed counts. Interestingly, travel between low ‘illness’ block groups occurs more than expected whereas travel originating from a high ‘illness’ block groups occurs less than expected, presumably because seriously ill people are not traveling. In Week_18 we see a spike in the travel between block groups with high levels of ‘illness’, which shows that a large fraction of the studied population likely remained ill, however, as the subjects chose not to travel in the prior weeks they could no longer remain home, which produced a higher rate of travel between ill block groups.
In the other networks we built, feature 1→1 consistently has significantly higher counts than expected and features 2→1 and 2→2 consistently have significantly lower counts suggesting that the ‘illness’ level of block groups has decreased as travel between block groups with a low level of ‘illness’ has increased. These networks contain the travel data from after the peak of the influenza season so we would expect there to be a lower level of ‘illness’ and a higher rate of travel between healthy block groups. The data analysis supports these expectations.
As demonstrated throughout this section, surprise analysis enables the testing of a multitude of hypotheses at once providing more robust and deeper insights than hypothesis testing. Similarly to QAP regression, surprise analysis permits analysis of networks with temporal elements. This methodological approach incorporates the attractive characteristics of both hypothesis testing and QAP regression and allows us to test a myriad of hypotheses at once.
6. Discussion and conclusion
Monitoring of travel environment becomes more and more valuable resource for collecting data about population mobility patterns in general [26,27] and decease spread in particular [9,20]. The contributions of this paper to the use of social network analysis with city-limits mobility data are both methodological and practically informative. First, we illustrate how surprise analysis allows for creatively analyzing static and longitudinal networks, by studying subgraphs with multiple nodal or edge-based attributes simultaneously, which is not possible with conventional network hypothesis testing. Second, we specify multiple ways to construct both directed and undirected weighted networks from travel data. Finally, these developments feed into the detailed analysis of complex data to shed insights into the dynamics of large-scale flu spread over time, as a function of population mobility and socio-economic indicators.
Note that the socio-economic indicators, or variables, used were transformed from continuous to categorical variables. The continuous range is split into two categorical bins using the average value as a cut-off point, or threshold. Using averages is a natural way to create levels; it also creates easily interpretable categories, i.e., below average or above average. However, the choice of cut-off point(s), as well as the number of bins, is at the discretion of the researcher. Using two levels effectively creates a binary designation and limits the number of possible features. As the number of levels increases, the number of possible features increases exponentially. Thus, two levels were used to keep the number of features manageable and possible to visualize. We acknowledge that the determination of a threshold(s) may affect the results, thus future researchers must pay special attention to how they make these decisions.
There are many methods that could be employed for construction of networks. In this paper, we introduced four different methods for building links with mobility data, including two link definitions that account for a temporal element.
Permutation testing is a popular method in social network analysis. Using surprise analysis produces results than presents a more holistic picture of the variable dependencies, compared to standard testing individual hypotheses in a one-by-one manner.
Last but not the least, the methods we presented enable the analysis of networks containing weighted edges and nodes with multiple attributes.
It is important to note that in any predictive analysis, such as the analysis explored in this paper, one has to be cautious about unobservable covariates. Unobservable covariates are those which have an effect on the measured response, or dependent variable, and may be correlated with the independent variable. If these covariates are ignored or incorrectly estimated, it can lead to spurious results. The type and effect of unobserved covariates varies depending upon the data being analyzed. Researchers have to independently consider the observed and unobserved variables in their data to ensure accuracy when implementing the methods outlined in this paper.
Combining the data processing and analytical methodology efforts will allow researchers to perform more robust analysis on similar networks. Our investigations confirm that it is possible to produce meaningful insights from building individual-centric networks where all subjects residing within one geographic unit are treated as a single network actor, block group in our analysis. Given a dataset with a greater level of representation within each geographic unit, these methods could of course enable further, deeper exploration of associations.
Acknowledgments
This work was funded in part by the US National Institutes of Health (grant no. 5R01GM108731-04).
Biographies
Courtney Burris: Courtney Burris is a PhD candidate in the Department of Industrial and Systems Engineering at the University at Buffalo. She has a B.S. from Elmira College in mathematics, and a M.S. from the University at Buffalo in Industrial and Systems Engineering. She is interested in engineering education, curricular analytics, and social network analysis.
Alexander Nikolaev: Alexander Nikolaev is an Associate Professor in the Department of Industrial and Systems Engineering at the University at Buffalo. He has a B.Sc. from Moscow Institute of Physics and Technology, and M.S. from the Ohio State University and PhD from University of Illinois at Urbana-Champaign (both in Industrial Engineering). Dr. Nikolaev’s interests and expertise are in resource allocation under uncertainty, social network analysis, causal inference, and decision-making that supports pro-health, pro-environmental and educational programs. He has (co-)authored 50s publication in archival journals and referred proceedings, and was a (co-)recipient of University at Buffalo Teaching Innovation Award and INFORMS Impact Prize.
Shiran Zhong: Shiran Zhong is a PhD candidate in the Department of Geography, University at Buffalo, The State University of New York, Amherst, NY 14261. His research interests include individual-based epidemiological modeling, forecasts of influenza epidemics, spatial networks, and deep learning.
Ling Bian: Dr. Bian is a Professor in the Department of Geography at the State University of New York of Buffalo and the director of National Center for Geographical Information Analysis. Her research interests are in the integration of GIS with environmental modeling. Her current research projects are in two areas: (1) Individual-based epidemiological modeling, and (2) Inter-operable environmental models. She teaches courses in GIS, remote sensing, geostatistics, GIS for environmental modeling, and a seminar on objects and fields.
Footnotes
CRediT author statement
Courtney Burris: Formal analysis, Roles/Writing - original draft.
Alexander Nikolaev: Supervision, Writing - review & editing.
Shiran Zhong: Data curation.
Ling Bian: Funding Acquisition, Supervision.
References
- [1].Bajardi P, Poletto C, Ramasco JJ, Tizzoni M, Colizza V, Vespignani A. Human mobility networks, travel restrictions, and the global spread of 2009 H1N1 pandemic. PloS One 2011;6(1). e16591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Bavaud F Testing spatial autocorrelation in weighted networks: the modes permutation test. In Spatial Econometric Interaction Modelling. Springer; 2016. p. 67–83. [Google Scholar]
- [3].Cauchemez S, Bhattarai A, Marchbanks TL, Fagan RP, Ostroff S, Ferguson NM, Swerdlow D, Group PHW, et al. Role of social networks in shaping disease transmission during a community outbreak of 2009 H1N1 pandemic influenza. Proc Natl Acad Sci Unit States Am 2011;108(7):2825–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Charaudeau S, Pakdaman K, Böelle P-Y. Commuter mobility and the spread of infectious diseases: application to influenza in France. PloS One 2014;9(1). e83002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Chiang K-Y, Hsieh C-J, Natarajan N, Dhillon IS, Tewari A. Prediction and clustering in signed networks: a local to global perspective. J Mach Learn Res 2014;15(1): 1177–213. [Google Scholar]
- [6].Christley RM, Pinchbeck G, Bowers R, Clancy D, French N, Bennett R, Turner J. Infection in social networks: using network analysis to identify high-risk individuals. Am J Epidemiol 2005;162(10):1024–31. [DOI] [PubMed] [Google Scholar]
- [7].Croft DP, Madden JR, Franks DW, James R. Hypothesis testing in animal social networks. Trends Ecol Evol 2011;26(10):502–7. [DOI] [PubMed] [Google Scholar]
- [8].Dekker D, Krackhardt D, Snijders T. Multicollinearity robust QAP for multiple regression. In: 1st annual conference of the north American association for computational social and organizational science. vols. 22–25. NAACSOS; 2003. [Google Scholar]
- [9].Eubank S, Guclu H, Kumar VA, Marathe MV, Srinivasan A, Toroczkai Z, Wang N. Modelling disease outbreaks in realistic urban social networks. Nature 2004;429 (6988):180. [DOI] [PubMed] [Google Scholar]
- [10].Farasat A, Nikolaev A, Srihari SN, Blair RH. Probabilistic graphical models in modern social network analysis. Social Netw Anal Min 2015;5(1):1–18. [Google Scholar]
- [11].Farasat A, Nikolaev AG. Signed social structure optimization for shift assignment in the nurse scheduling problem. Soc Econ Plann Sci 2016;56(3–13). [Google Scholar]
- [12].Gibson BA, Ghosh D, Morano JP, Altice FL. Accessibility and utilization patterns of a mobile medical clinic among vulnerable populations. Health Place 2014;28: 153–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Gomes MF, Piontti A P y, Rossi L, Chao D, Longini I, Halloran ME, Vespignani A. Assessing the international spreading risk associated with the 2014 west African Ebola outbreak. PLoS Curr 2014;6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Guo S, Wang M, Leskovec J. The role of social networks in online shopping: information passing, price of trust, and consumer choice. In: Proceedings of the 12th ACM conference on Electronic commerce. ACM; 2011. p. 157–66. [Google Scholar]
- [15].Khodadadi A, Jalili M. Sign prediction in social networks based on tendency rate of equivalent micro-structures. Neurocomputing 2017;257:175–84. [Google Scholar]
- [16].Labianca G, Brass DJ, Gray B. Social networks and perceptions of intergroup conflict: the role of negative relationships and third parties. Acad Manag J 1998;41 (1):55–67. [Google Scholar]
- [17].Lee EC, Arab A, Goldlust SM, Viboud C, Grenfell BT, Bansal S. Deploying digital health data to optimize influenza surveillance at national and local scales. PLoS Comput Biol 2018;14(3). e1006020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Leskovec J, Huttenlocher D, Kleinberg J. Signed networks in social media. In: Proceedings of the SIGCHI conference on human factors in computing systems. ACM; 2010. p. 1361–70. [Google Scholar]
- [19].Lusseau D, Whitehead H, Gero S. Incorporating uncertainty into the study of animal social networks. 2009. arXiv preprint arXiv:0903.1519 [Google Scholar]
- [20].Ma F, Zhong S, Gao J, Bian L. Influenza-like symptom prediction by analyzing self-reported health status and human mobility behaviors. In: Proceedings of the 10th ACM international conference on bioinformatics, computational biology and health informatics; 2019. p. 233–42. [Google Scholar]
- [21].Martin JL. A general permutation-based QAP analysis approach for dyadic data from multiple groups. Connections 1999;22(2):50–60. [Google Scholar]
- [22].Mills CE, Robins JM, Lipsitch M. Transmissibility of 1918 pandemic influenza. Nature 2004;432(7019):904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].North B, Curtis D, Cassell P, Hitman G, Sham P. Assessing optimal neural network architecture for identifying disease-associated multi-marker genotypes using a permutation test, and application to calpain 10 polymorphisms associated with diabetes. Ann Hum Genet 2003;67(4):348–56. [DOI] [PubMed] [Google Scholar]
- [24].O’malley AJ, Marsden PV. The analysis of social networks. Health Serv Outcome Res Methodol 2008;8(4):222–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Smith GJ, Bahl J, Vijaykrishna D, Zhang J, Poon LL, Chen H, Webster RG, Peiris JM, Guan Y. Dating the emergence of pandemic influenza viruses. Proc Natl Acad Sci Unit States Am 2009;106(28):11709–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Wu L, Kang JE, Chung Y, Nikolaev A. Monitoring multimodal travel environment using automated fare collection data: data processing and reliability analysis. J Big Data Anal Transport 2019;1(2):123–46. [Google Scholar]
- [27].Wu L, Kang JE, Chung Y, Nikolaev A. Inferring origin-destination demand and user preferences in a multi-modal travel environment using automated fare collection data. Omega 2020;102260. [Google Scholar]
- [28].Zhong S, Bian L. A location-centric network approach to analyzing epidemic dynamics. Ann Assoc Am Geogr 2016;106(2):480–8. [DOI] [PMC free article] [PubMed] [Google Scholar]


