Translating Dosimetry of Dibenzo[def,p]chrysene (DBC) and Metabolites Across Dose and Species Using Physiologically Based Pharmacokinetic (PBPK) Modeling

Abstract

Dibenzo[def,p]chrysene (DBC) is an environmental polycyclic aromatic hydrocarbon (PAH) that causes tumors in mice and has been classified as a probable human carcinogen by the International Agency for Research on Cancer. Animal toxicity studies often utilize higher doses than are found in relevant human exposures. Additionally, like many PAHs, DBC requires metabolic bioactivation to form the ultimate toxicant, and species differences in DBC metabolism have been observed. To understand the implications of dose and species differences, a physiologically based pharmacokinetic model (PBPK) for DBC and major metabolites was developed in mice and humans. Metabolism parameters used in the model were obtained from experimental in vitro metabolism assays in mice and human hepatic microsomes. PBPK model simulations were evaluated against mice dosed with 15 mg/kg DBC by oral gavage and human volunteers orally microdosed with 29 ng of DBC and. DBC and its primary metabolite DBC-11,12-diol were measured in blood of mice and humans, while in urine, the majority of DBC metabolites were conjugated DBC-11,12-diol, conjugated DBC tetrols, and unconjugated DBC tetrols. The PBPK model was able to predict the time course concentrations of DBC and DBC-11,12-diol, and other DBC metabolites in blood and urine of human volunteers and mice with reasonable accuracy. The agreement between the simulations of our model and measured pharmacokinetic data in mice and human studies demonstrate the success and versatility of our model for interspecies extrapolation and applicability for different doses. Furthermore, our simulations show that internal dose metrics used for risk assessment do not necessarily scale allometrically, and that PBPK modeling provides a reliable approach to appropriately account for interspecies differences in metabolism and physiology.

Introduction

Dibenzo[def,p]chrysene (DBC) belongs to a class of hydrocarbons called polycyclic aromatic hydrocarbons (PAHs), which are formed as a byproduct of incomplete combustion of organic matter (1). DBC is a persistent environmental contaminant because of its high lipophilicity, low volatility, and high molecular weight. Up to 70% of PAH exposure for non-smoking humans is associated with diet and oral route of exposure in non-occupational settings (2–4). Primary dietary sources include cereals, oils, vegetables, and food cooked over an open flame (5). Human dietary exposure to DBC is estimated to be ≥9 ng/d (6). As such, we focused oral absorption of DBC as the primary route of exposure.

Human exposure to DBC is a concern because researchers observed it to be highly carcinogenic in several laboratory studies. Dermal exposure to DBC has been shown to cause skin tumors in mice (7–10). Likewise, intramammary exposure of DBC in mice has been shown to promote mammary tumors and lung and liver cancer in mice exposed intraperitoneally (11, 12). In fact, a study has found DBC to be 100 times more potent than benzo[a]pyrene (B[a]P) in producing lung adenomas (12). More recently, DBC has been shown to cross the placenta in B6129F1/J mice and cause T-cell lymphoma, lung adenoma and liver lesions in offspring of mothers exposed to DBC (13, 14). The International Agency for Research on Cancer (IARC) has classified DBC as class 2B, a suspected carcinogen for humans (1).

DBC can be metabolized by both phase I and II enzymes primarily located in the liver. DBC is oxidized by cytochrome P450 (CYP) enzymes forming DBC epoxides or DBC hydroxides (Figure 1). DBC epoxides can be hydrolyzed, typically by epoxide hydrolase, forming various DBC-trans-diols (15–17). The primary DBC epoxide and corresponding diol metabolites are DBC-11,12-epoxide and DBC-11,12-diol, but CYP can also act on other sites, leading to the formation of other DBC epoxides, diols, and hydroxides. For example, as noted in a study by Devanesan et al., in addition to the primary DBC epoxide and diol metabolites, hepatic metabolism of DBC also produces DBC-8,9-diol and DBC-7-OH (18). DBC-diols can undergo further oxidation and hydroxylation reactions forming various compounds such as DBC-diol-epoxides, DBC-quinones, and DBC-tetrols. Hydroxyl moieties on DBC metabolites can undergo phase II conjugation, increasing the water solubility of these compounds and facilitating excretion, which is the crucial detoxification mechanism for these DBC-metabolites (19–21). Additionally, other metabolites of DBC, such as DBC-dione, DBC-phenols and others can also be formed.

Figure 1:

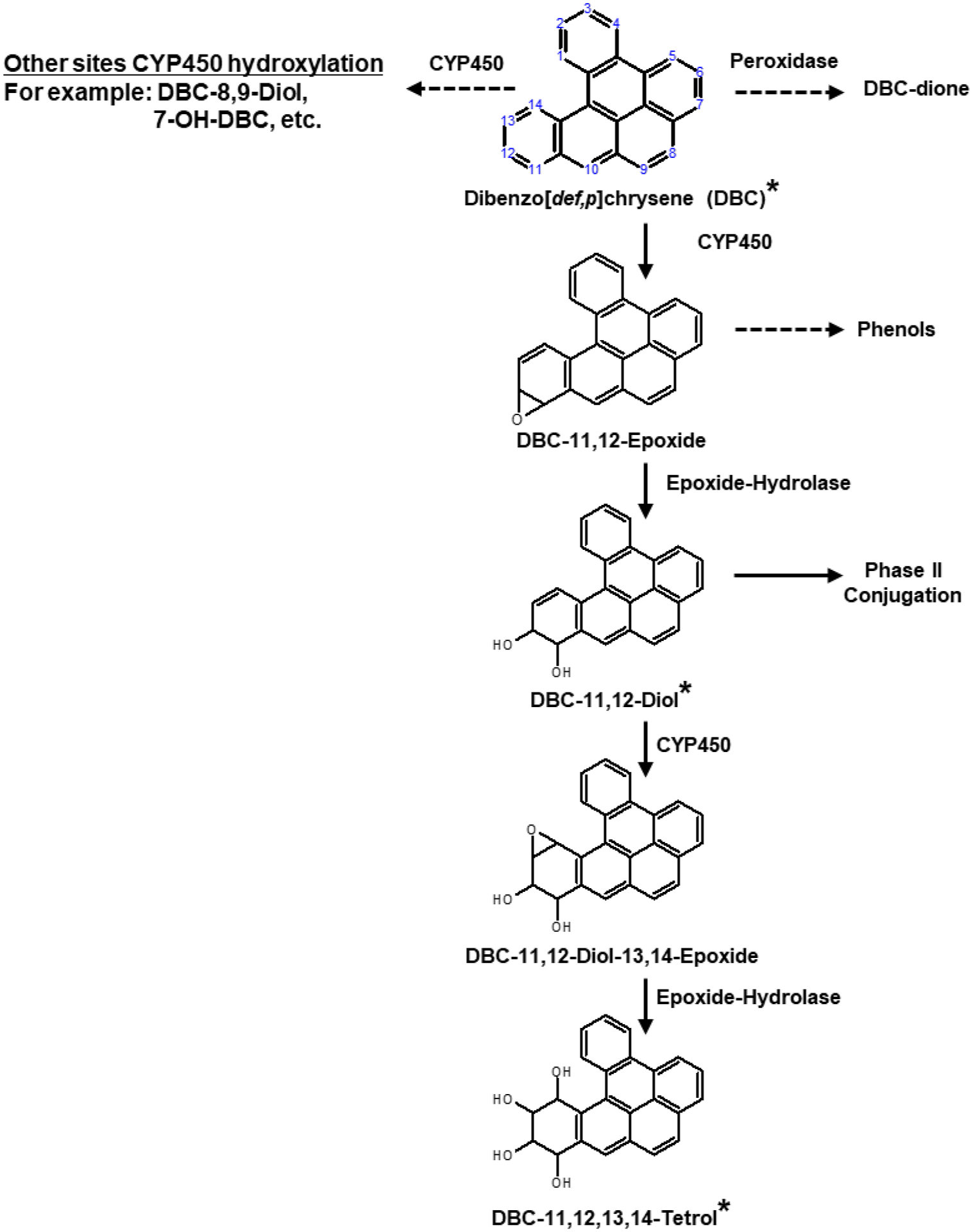
Simplified metabolic pathway of dibenzo[def,p]chrysene (DBC). Solid arrows indicate the primary metabolic pathway that is modeled in our physiologically based pharmacokinetic (PBPK) model, whereas dashed arrows indicate other secondary pathways that are not accounted for in our PBPK model. Compound names with asterisks are the chemical species that are explicitly modeled in our PBPK model.

Physiological based pharmacokinetic (PBPK) models provide a useful method to quantitatively extrapolate chemical dosimetry from animal models to humans. In recent years, PBPK modeling has found successful applications in drug discovery and development and to support human risk assessment at regulatory agencies (22). Despite the pervasiveness and toxicity of PAHs, only a handful of PBPK models have been developed for PAHs and metabolites, particularly for high molecular weight compounds such as DBC. This is partly because of the experimental challenges associated with their high lipophilicity, and complex metabolism that presents both analytical and modeling challenges. These challenges are even greater in the context of human studies, where performing exposure studies with a suspected carcinogen, such as DBC, requires extremely low doses and thereby presents a significant challenge in measuring low-levels of the parent compound, and even lower levels of metabolites in plasma and urine. This is perhaps why so few PBPK models exist for high molecular weight PAHs in general, and DBC in particular. In fact, even for a compound as well-studied as B[a]P, PBPK models only validated in rodents have been developed (23), and the only models developed for humans have not been substantially compared against pharmacokinetic data (24, 25).

Recently, Madeen et al. reported the application of a novel “moving wire” accelerator mass spectroscopy (AMS) technique coupled with ultraperformance liquid chromatography (UPLC) that allowed for the measurement of extremely low doses of DBC and its metabolites in humans (6). Using this technique, Madeen et al. were able to detect and quantify parent DBC and its metabolites in femtomolar amounts in blood in humans orally microdosed with extremely low dose (29 ng; 5 nCi) of DBC. This study provided the data necessary to successfully develop and validate a PBPK model of DBC in humans.

In the current study, we expanded a previously published basic PBPK model for DBC (26) to include the disposition of DBC-11,12-diol, a major metabolite, and updated parameter values. Metabolism parameters in our model were updated using experimentally in vitro metabolism assays in mice and human hepatic microsomes. We compared PBPK model simulations to measured levels of DBC, DBC-11,12-diol, and other DBC metabolites in blood and urine of mice over time following oral administration of DBC. Inter-species extrapolation of the model was tested by validating the human model against data obtained from extremely low-dose exposure studies performed on human volunteers using ultrasensitive measurement techniques to detect femtomolar levels of DBC and its metabolites in plasma and urine samples (6, 27).

Materials and Methods

Chemicals

Acetone, benzo[a]pyrene (BaP), ethyl acetate, acetonitrile, methanol, sodium sulfate, sulfuric acid, potassium phosphate salts (dibasic and monobasic), phosphate buffered saline (PBS), trifluoroacetic acid, sodium ascorbate, and copper sulfate were purchased from Sigma-Aldrich (St. Louis, MO, USA). Drs. Shantu Amin and Arun Sharma (Pennsylvania State University (State College, PA, USA)) synthesized dibenzo[def,p]chrysene (DBC), dibenzo[def,p]chrysene-11,12 diol (DBC diol), dibenzo[def,p]chrysene-11,12,13,14-tetraol (DBC tetrol), benzo[a]pyrene-7,8-dihydrodiol (BaP diol), benzo[a]pyrene-7,8,9,10-tetraol (BaP tetrol) according to previous methods (28–30).

Dosing and Sample Collection

Animals

Our group has utilized female B6129SF1/J mice as an animal model in prior PAH carcinogenicity, toxicokinetic, and in vitro metabolism studies (26, 31–34). We developed physiologically based pharmacokinetic models (PBPK) to better interpret various models of PAH toxicity and translate results in animal models to humans (26, 35). As such, we used this animal model to maintain consistency and relevancy with our previous work.

Adult female B6129SF1/J mice were purchased from The Jackson Laboratory (Bar Harbor, ME, USA). Mice were group-housed (3 per cage) in solid bottom cages using alpha cellulose bedding (Shepherd’s™ ALPHA-dri®, Animal Specialties, Inc., Hubbard, OR, USA) under standard laboratory conditions (temperature ranged 20–24 C, humidity ranged 30–70%, 12 hr light-12 hr dark cycle). LabDiet Certified Rodent Diet rodent chow 5002 (LabDiet, St. Louis, MO, USA) and water were available ad libitum. All procedures involving animals were in accordance with protocols established in the NIH/NRC Guide and Use of Laboratory Animals (NIH/NRC) and were approved by Pacific Northwest National Laboratories Institutional Animal Care and Use Committee (PNNL ICUAC). Mice were dosed by oral gavage of 15 mg/kg of DBC dissolved in corn oil (0.2 mL/kg of body weight). We selected this dose based on previous toxicity studies of DBC in mice (13, 26, 32). This dose also allows quantification of DBC and metabolites in blood using an HPLC. Blood samples were obtained at 0.5, 1, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 6.0, 12.0, 24.0, and 48.0 hour post-exposure by euthanizing subgroups of three mice by CO₂ asphyxiation followed by exsanguination through vena cava. All urine voided during 0–8, and 8–16 hour intervals were collected in glass containers for analytical measurements of cumulative urinary elimination of metabolites. Animals designated for 48 h sacrifice were individually housed in all-glass metabolism cages for separate collection of urine and feces over dry ice.

Analyte quantification

Analyte extraction and quantification were performed as previously described (31). Urine samples were prepared with and without treatment with β-glucuronidase (100 units/sample or 0.4–1.0 units/mg) at 37°C for 22 h to determine total amounts of DBC-diol and DBC-diol glucuronide. BaP, BaP diol, and BaP tetrol was added to each sample to serve as internal standards. Na₂SO₄ (~250 mg) was added to each blood or urine sample followed by 0.5 mL ethyl acetate. Each sample was vortexed for 5 seconds and centrifuged for 10 min at 4°C and 1600 × g. Using a glass pipette, supernatants were removed and placed in a new glass vial. The extraction was then repeated, and ethyl acetate from the combined supernatants was evaporated under a stream of nitrogen. Dried extracts were reconstituted in 0.5 mL methanol. Analytes were quantified in extracts using reverse phase HPLC using an Agilent 1100 HPLC system equipped with a fluorescence detector (Santa Clara, CA, USA). Twenty μL of sample was injected into an Ascentis 25 cm × 4.6 mm, 5 μm C18 column (Sigma-Aldrich, St. Louis, MO, USA). A gradient of water and acetonitrile from 55:45 to 0:100 was employed from 0 to 10 min and then was held at 100% acetonitrile until 22 min at a flow rate of 0.95 mL/min. Excitation and emission wavelengths were 360 nm and 430 nm for DBC-diol and B[a]P-diol, 235 nm and 430 nm for DBC and B[a]P, and 245 nm and 430 nm for DBC tetrols and B[a]P tetrols, respectively. Quantification was accomplished using a linear regression fit to an external calibration curve. The calibration curve was made by spiking known analyte amounts into control blood or urine and processed simultaneously with samples. Approximate limits of reliable quantitation (LOQ) for DBC and DBC diol were ~0.04 μM.

Humans: DBC

Madeen et al. measured the pharmacokinetics of orally administered DBC in human volunteers (6, 27). Overnight fasted human volunteers (Table 1) were administered a capsule dose of radiolabeled [¹⁴C]-DBC, comprising 29 ng of DBC and 5 nCi [¹⁴C]. Blood was drawn at 0, 0.25, 0.5, 0.75, 1.0, 1.5, 2.0, 2.5, 3.0, 4.0, 8.0, 12.0, 24.0, 48.0, and 72.0 hour post consumption and collected into glass vacutainer tubes containing EDTA to prevent coagulation. Similarly, all urine voided during 0–6, 6–12, 12–24, 24–48, and 48–72 hour intervals were collected in glass containers for homogenized sampling and volume record by interval. Further details of sample collection can be found in Madeen et al. (6, 27).

Table 1:

Body weight (BW), height (Ht), Body Mass Index (BMI), age, gender, and availability of various data for the six volunteers used in the study (6).

	BW (kg)	Ht (cm)	BMI	Age	Gender	Total C14 (Plasma)	Total C14 (Urine)	Plasma (DBC, DBC-Diol)	Urine (DBC-Diol, Tetrol)
V5	86	158	34	65	F		✓	✓	✓
V6	94	196	24	47	M	✓	✓		✓
V8	78	180	24	26	M	✓	✓	✓	✓
V9	78	156	32	56	F	✓	✓	✓	✓
V10	71	174	23	20	M	✓	✓		✓
V13	124	191	34	36	M	✓	✓	✓

Sample Preparation and Analysis

Total [¹⁴C]-DBC concentrations were obtained by analyzing blood and urine samples from volunteers using accelerator mass spectroscopy (AMS). Following the method of Ognibene et al. (36), the extracted samples were evaporated, flame-sealed, and combusted in a quartz tube to produce graphite, which was subsequently loaded into an aluminum sample holder for AMS analysis conducted on the 1 MV AMS at the Lawrence Livermore National Laboratory (LLNL). Specific details for DBC and BaP measurements can be found in Madeen et al. (27) and Hummel et al. (37), respectively.

For measuring DBC and DBC metabolites’ concentrations, blood and urine samples were extracted using liquid-liquid extraction and DBC and metabolites were subsequently measured using high performance liquid chromatography (HPLC) as described in (6).

PBPK Model

Model structure

The DBC PBPK model structure was based on a previously published preliminary PBPK model for PAHs (26), including DBC (Figure 2). In our model, only the primary metabolic pathway (DBC→DBC-11,12-diol→DBC-11,12,13,14-tetrol) and the corresponding metabolites (solid arrows in Figure 1, and compounds marked with an asterisk (*)) are explicitly modeled. To account for DBC metabolites, we included a parallel model describing the disposition of DBC-11,12-diol. DBC absorption was modeled through the oral route as a two-compartment theoretical gut using first order kinetics to describe the transfer between the two-compartments and reabsorption into the liver (26). We included a fractional absorption term in the model to account for different extents of observed bioavailability in various studies. Likewise, a fractional metabolism ratio factor was also included to account for the proportion of primary DBC-11,12-diol and its subsequent metabolites generated via the primary metabolic pathway compared to other metabolites that are formed by CYP hydroxylation at sites other than the primary 11,12 site of DBC. Like Crowell et al. (26), all compartments except fat were modeled as flow limited. Fat, which acts as a depot for lipophilic PAHs, was modeled as diffusion limited. The liver was the site of Phase 1 metabolism of DBC to DBC-11,12-diol and DBC-11,12-diol to DBC-tetrol. Phase II uridine 5’-diphospho-glucuronosyltransferase (UGT) metabolism of DBC-11,12-diol to conjugated DBC-11,12-diol was also modeled in the liver. Elimination was facilitated as urinary excretion of DBC-11,12-diol, conjugated DBC-11,12-diol, and DBC-tetrol. The PBPK model was coded in Magnolia, Version 1.2.2 (Magnolia Sciences, LLC, Orlando, Florida), which is a publicly available software for mathematical modeling and simulation.

Figure 2:

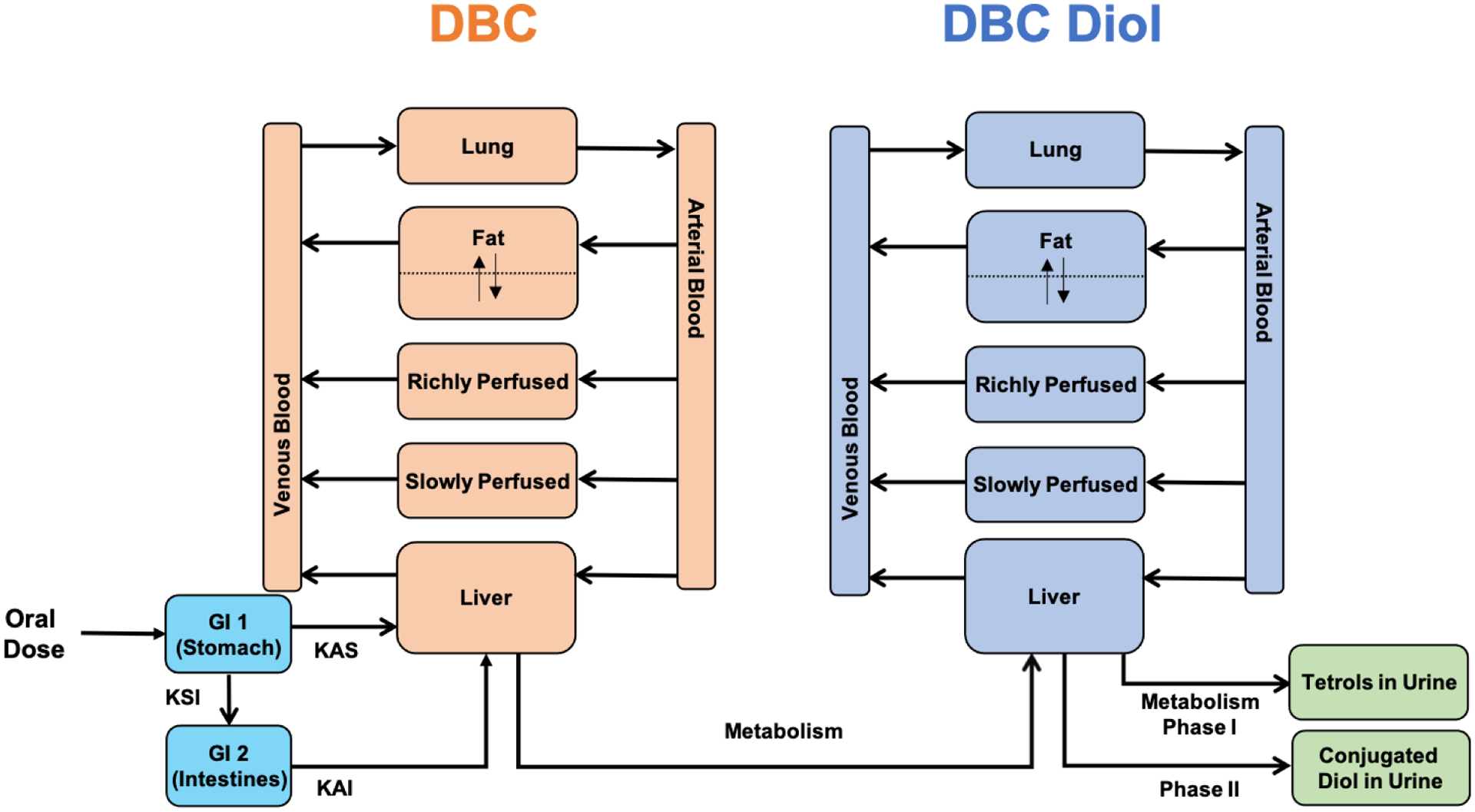
Schematic of the physiologically based pharmacokinetic (PBPK) model incorporating metabolism of dibenzo[def,p]chrysene (DBC). We expanded a previously published basic PBPK model for DBC (26) shown in orange, to include a parallel model, shown in blue, describing the disposition of the diol metabolite of DBC. Oral absorption of DBC to a theoretical two-compartment GI tract (GI 1 and GI2) is modeled by selecting appropriate values for absorption parameters (KAS, KAI, KSI; see Table 7 for further details).

Model parametrization

Compartmental volumes and blood flows were defined from standard published sources of physiological data for mice and humans. For mice, compartment volumes were expressed as a fraction of body weight (Table 2). Regional blood flows to the four compartments, namely, the fat, liver, poorly perfused, and richly perfused compartments in mice were calculated based on the blood distribution to these compartments expressed as a fraction of the mean total cardiac output (Table 3), which was estimated to be 14.6 mL/min by using the allometric relationship described in Arms and Travis (39). For humans, the compartment volumes for each volunteer were calculated based on the volunteer-specific physiological measurements of body weight, height, and age (40) (Table 4). Blood flow to each organ was calculated using a perfusion rate per tissue volume (Table 5). For simulations of average observed DBC and metabolite levels in human volunteers, we utilized parameters corresponding to an average male weighing 88.5 kg (average weight of all volunteers in our study).

Table 2:

Organ-specific weights expressed as a fraction of body weight for mice (38).

Organ/Tissue	Percent BW
Blood	4.9
Arteries	0.25 × Blood
Veins	0.75 × Blood
Fat	7
Liver	5.5
Lung	0.7
Slowly Perfused (Skin + Muscle)	54.9
Rapidly Perfused (Heart + Kidney + Brain + GI + Other Organs)	10.6

Table 3:

Regional blood flow distribution expressed as a percent of cardiac output (38).

Organ/Tissue	Percent BW
Blood	4.9
Arteries	0.25 × Blood
Veins	0.75 × Blood
Fat	7
Liver	5.5
Lung	0.7
Slowly Perfused (Skin + Muscle)	54.9
Rapidly Perfused (Heart + Kidney + Brain + GI + Other Organs)	10.6

^*Value for mice unavailable, used rat value instead

Table 4:

Organ-specific weights for humans expressed in terms of physiological measurements of body weight, height, and age ((40), unless noted otherwise)

Organ	Male	Female
Blood	(13.1*H + 18.05*W – 480)/572.3	(35.5*H + 2.27*W – 3382)/617.8
Fat	(1.20*BMI + 0.23*A – 16.2)*W/0.923/100	(1.20*BMI + 0.23*A – 5.4)*BW/0.923/100
Muscle	FFM*54/100/1.04	FFM*48.9/100/1.04
Skin*	3300/1.04/1000	2300/1.04/1000
Liver	1.0728*SA – 0.3457	1.0728*SA – 0.3457
Heart	(155.18*((H0.725)*(W0.425)*71.84/10000)1.29)/1.04/1000	(124.13*((H0.7763)*(W0.4081)*71.84/10000)1.242)/1.04/1000
Spleen	6.516*BW0.797/1.04/1000	6.516*BW0.797/1.04/1000
Kidneys	(5.04 + 2.53*A + 1.31*W + 1.36*H – 255.7)*2/1000	(5.04*2 + 2.53*A + 1.31*W + 1.36*H – 255.7)*2/1000
Brain**	1.2875	1.1585
Lungs	0.021*FFM/1.04	0.019*FFM/1.04
GI	0.021*FFM/1.04	0.027*FFM/1.04
Pancreas	0.0017*FFM/1.04	0.002*FFM/1.04
Thyroid	0.00034*FFM/1.04	0.00043*FFM/1.04
Others^	1453.03/1.04/1000	1524.88/1.04/1000

H = Height in cm; W = Weight in kg; A = Age in years; BMI = Body Mass Index in kg/m²

FFM = W – Fat mass = Fat Free Mass in kg; SA = W^0.5378 *H^0.3964*0.024265 = Surface Area in m²

^*Ref (42). Tissue density of 1.04 kg/L assumed

^**Estimated as the mean of White and African American populations (40)

^{^}Based on the sum of (gender-specific) all remaining rapidly-perfused organs (40)

Table 5:

Average perfusion rates of different compartments for humans (40)

Organ/Tissue	Average Perfusion Rate (mL/min/mL)
	Male	Female
Fat	0.02	0.03
Liver	0.84	1.0
Slowly Perfused (Skin + Muscle)	0.04	0.04
Rapidly Perfused (Heart + Kidney + Brain + Others)	0.98	0.96

Tissue:blood partition coefficients for DBC and DBC-11,12-diol (Table 6) were estimated using an algorithm, which estimates partitioning using chemical constants (e.g. octanol:water partitioning) and tissue composition (41). We assumed that mice and humans have the same partitioning coefficient.

Table 6:

Partition coefficients used in the model

Organ/Tissue	Partition Coefficient
Fat	158.33
Liver	9.38
Lung	1.13
Slowly Perfused*	7.49
Rapidly Perfused**	10.37

^*Value for muscle,

^**Average of brain and kidney

First order rate constants for absorption from the stomach (KAS) and the intestines (KAI) as well as the gastric emptying rate (KSI) were manually optimized to obtain satisfactory fits to the early phase of the kinetics of DBC concentration in blood (Table 7). For the mouse model, a value of 15 mg/kg (oral bolus dose administered to the animals) for nominal dose was used. The percent of administered dose absorbed by the animal was included in the model as a parameter, and was set equal to 0.311, which is the amount of dose recovered in urine.

Table 7:

Biochemical parameters (all first order rate constants with units 1/min) for mice and humans used in PBPK model

Parameter	Symbol^	Mouse	Human
Absorption rate from stomach to liver	KAS	0.001†	0.0001
Absorption rate from intestines to liver	KAI	0.008†	0.1
Gastric emptying rate	KSI	0.01	0.02

^{^}See Figure 2

^†Ref (26)

For humans, a nominal oral dose of 29ng was assumed and the fraction absorbed for each volunteer was optimized by fitting model prediction for total DBC urinary elimination kinetics to the measured total [¹⁴C]-DBC elimination kinetics data. The optimized values for fraction absorbed are shown in Table 9.

Table 9:

Nominal dose administered to volunteers, total urinary elimination, and optimized percent absorption used in the model.

	Eliminated Total (ng 14C-DBCeq)A	Oral Dose DBC (ng)	% Excreted	Optimized percent absorbed
V5	0.532	25.2	2.11	2.71
V6	0.441	29.8	1.48	1.92
V8	0.285	23.9	1.20	1.42
V9	0.200	28.5	0.70	0.93
V10	0.494	25.6	1.93	2.65
V13	0.263	28.5	0.92	1.34
Average			1.39	1.51

^ASum of all DBC metabolites excreted in urine.

Metabolism parameters of DBC used in the model were obtained from in vitro metabolism studies in hepatic microsomes of mice and humans (31, 33) (Table 8). Metabolism of DBC and Phase II UGT metabolism of DBC-11,12-diol in liver were implemented using a Michaelis-Menten function for saturable kinetics. Phase I metabolism of DBC-11,12-diol was modeled using an intrinsic clearance equation since saturation was not observed in vitro. Metabolic parameters were scaled from microsomal level to the organism level using 30 mg microsomal protein/g liver tissue (31, 33).

Table 8:

Metabolism parameters for mice and humans used in PBPK model

Substrate	Species	Best Fit Model	Clint (mL/min/mg)	Vmax (nmol/min/mg)	Km (μM)
DBC†	Mouse	MM		19.38	6.63
	Human	MM		0.27	0.915
DBC-Diol* (Phase I)	Mouse	First Order	11.58
	Human	First Order	0.54
DBC-Diol* (Phase II)	Mouse	MM		26.49	29.7
	Human	MM		7.74	25.9

^†Ref (31)

^*Ref (33)

Sensitivity Analysis

A local sensitivity analyses was performed to identify the most important parameters for estimating concentrations of DBC and DBC-11,12-diol in blood in for both mouse and human models, following an oral bolus dose equal to the nominal doses used in our experiments, i.e., 15 mg/kg for mouse model and 29 ng for human model. Normalized sensitivity coefficients were calculated for a 1% change in a given model parameter when all other parameters were held fixed. The sensitivity coefficients were classified as low (values less than 0.15), medium (values between 0.15 and 0.5), or high (values 0.5 and higher) based on a previously published criteria by Teeguarden et al. (43).

Comparison of PBPK Modeling Predictions with Allometric Scaling

Allometric scaling as a power (e.g. ¾) of body weight is traditionally used for interspecies extrapolation of external dose, especially for compounds that are cleared by metabolism. Although widely used in the risk assessment process, the validity of this approach remains dependent on metabolism rates scaling by the same factor (body weight^3/4) across species. To test the validity of allometric scaling in the context of DBC internal dosimetry, we compared the simulated concentrations of DBC and DBC-11,12-diol in blood in an average mouse PBPK model, assuming an external oral bolus animal dose (AD) of 1 mg/kg-body weight and compared it with the simulated concentrations of the same compounds in an average human PBPK model, assuming an allometrically scaled human equivalent dose (HED) estimated to be 0.2419 mg/kg-body weight, based on the following equation: $\text{HED}=\text{AD}*{\left[{\text{BW}}_{\text{mouse}}/{\text{BW}}_{\text{human}}\right]}^{1-0.75}$, where BW_mouse is the mouse body weight, which was set equal to 25 g (38)and BW_human is the human weight, which was set to 73 kg the average weight of a male reference human (42). The compartment volumes and blood flows for these average weight values for the two species were estimated based on relationships described earlier. The fractional absorption and metabolism ratio factor was set to 1.0, and simulations were run for a period of 72 hours. Dose metrics were compared between mouse and human simulations.

Results

PBPK model predictions of DBC orally administered to mice.

We measured levels of DBC and DBC-11,12-diol in blood following oral administration with 15 mg/kg of DBC in mice. DBC and DBC-11,12-diol concentrations in blood rapidly increased post dosing and peaked between 3–5 hr (Figure 3A). Peak concentrations of DBC measured in blood was around 3.5 μM, while peak DBC-11,12-diol concentration was approximately 0.05 μM. Concentrations of both DBC and DBC-11,12-diol decreased from their respective peak concentrations to approximately 0.0075 μM at 48 hr post dosing, indicating a faster clearance rate of DBC compared to DBC-11,12-diol.

Figure 3:

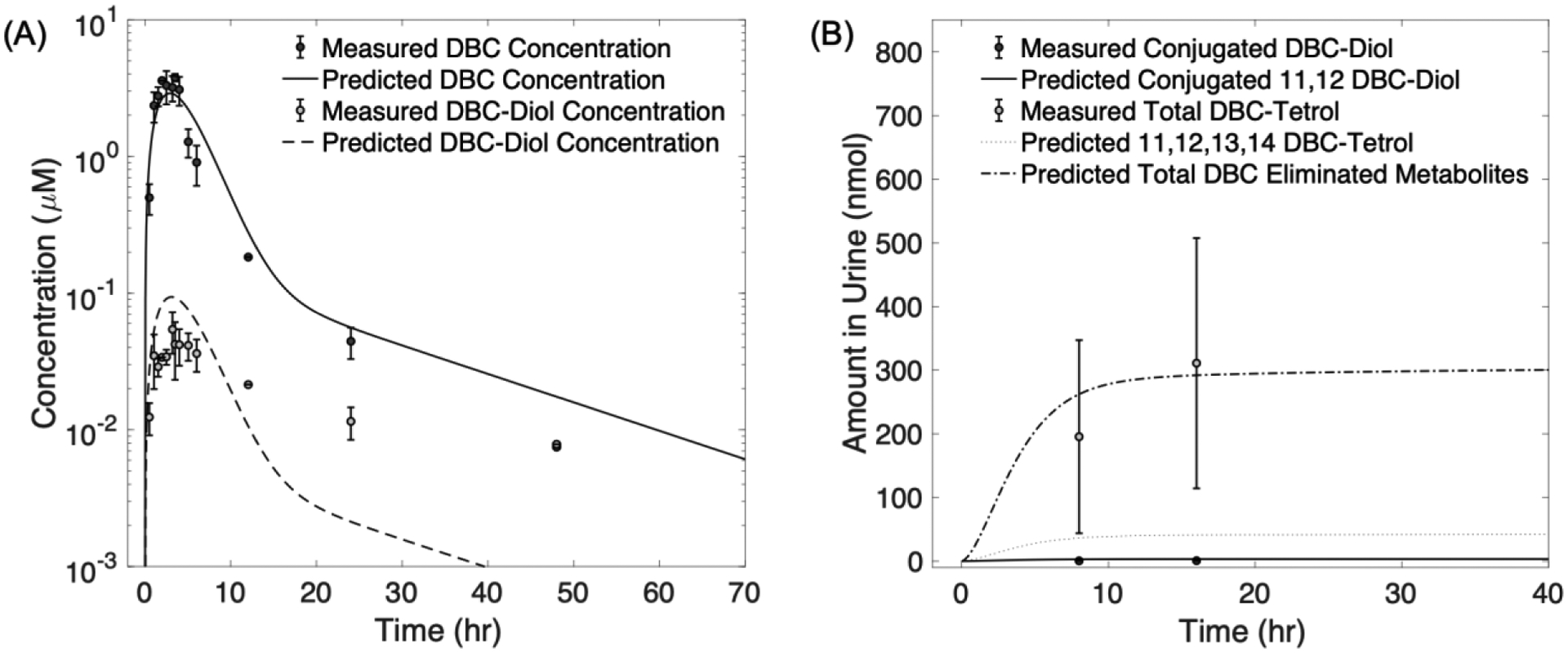
Measured concentrations of dibenzo[def,p]chrysene (DBC) and DBC metabolites in blood and urine of mice following an oral dose of 15 mg/kg. Data points represent mean measured levels of DBC and its metabolites in plasma (A) and urine (B). Error bars represent standard deviations. Lines represent physiologically based pharmacokinetic (PBPK) model simulations of data.

Only trace levels of DBC and DBC-11,12-diol were detected in urine. Conjugated DBC-11,12-diol and DBC-tetrols were first detected during the 0–16 hr collection interval, with mean DBC-tetrols amount in that interval being 98.9 times higher than the conjugated DBC-11,12-diol level in the same time interval, mirroring rapid blood clearance of DBC-11,12-diol (Figure 3B).

The PBPK model simulated observed PAH levels in blood reasonably well. The PBPK predicted measured concentrations of DBC in blood within a factor of 2, except for the last time point at 48 hours for which the predicted DBC level was 2.5 times higher than the observed level. Likewise, the PBPK model predicted DBC-11,12-diol levels within a factor of 2.5 of measured concentrations in blood, except for last two time points (24 and 48 hr).

The PBPK model slightly overpredicted conjugated DBC-11,12-diol in urine, with the predicted values being around 3–4 times higher than the measured levels (Figure 3B). The overprediction of conjugated diol urine suggests that the model predicts a faster urinary elimination for DBC-11,12-diol, which is also suggested by the model’s underprediction of DBC-11,12-diol in blood during the elimination phase at later time points.

PBPK model predictions for the amount of total tetrols in urine were reasonably accurate with the predicted values being within the error bounds of the measured levels of total tetrols in urine. The predicted values for tetrols formed from only the primary detoxification pathway (Figure 3B) were lower than the measured tetrols in urine suggesting more than one pathway for tetrol formation.

PBPK model predictions of DBC orally administered to humans.

Average Human Data

Averaged pharmacokinetic data for DBC and DBC-11,12-diol in blood in human volunteers, administered with an oral dose of 29 ng of DBC (Figure 4A) indicates a rapid increase in concentrations of both DBC and DBC-11,12-diol, with both compounds peaking at around 1 hr post dosing before decreasing during the distribution and excretion phases. Peak DBC concentration of 74.8 fM was 10 times higher than peak DBC-11,12-diol concentration, which was measured to be 7.4 fM.

Figure 4:

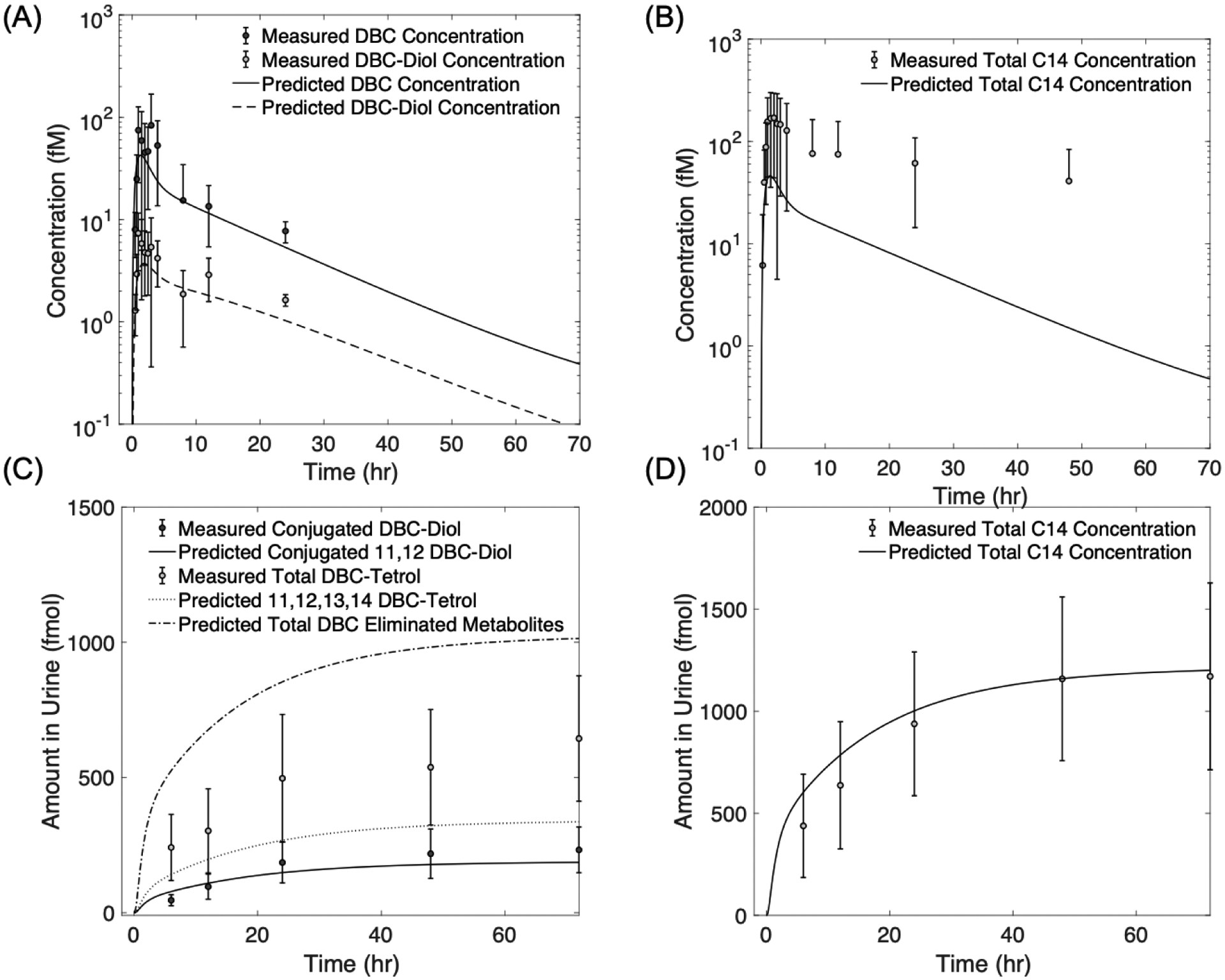
Measured vs. concentrations of dibenzo[def,p]chrysene (DBC) and DBC metabolites in plasma (A-B) and urine (C-D), averaged across six human volunteers orally administered with an oral dose of 29 ng of DBC. Lines are physiologically based pharmacokinetic (PBPK) model simulations of data (6).

The PBPK model was able to predict both DBC and DBC-11,12-diol concentrations in blood with high accuracy. PBPK model predictions being within one standard deviation of the mean measured values (Figure 4A). The averaged concentration of total [¹⁴C]-DBC in blood (Figure 4B) followed a similar trend as DBC and DBC-11,12-diol of rapid increase during the early time points but had a significantly slower rate of decrease during later time points. Additionally, peak total [¹⁴C]-DBC concentration in blood was almost twice the sum of peak concentrations of DBC and DBC-11,12-diol in blood, suggesting the presence of additional DBC-metabolites other than the primary DBC-11,12-diol that contribute to the higher total [¹⁴C]-DBC concentration, and moreover, also persist in blood for a longer time than the parent compound and the primary DBC-11,12-diol. As such, the PBPK model consistently underpredicted total [¹⁴C]-DBC concentration in blood at all time points since it only predicted DBC and DBC-11,12-diol in blood and other metabolites may be contributing to the total measured [¹⁴C]-DBC.

The amount of total tetrols detected in urine were 2.5 to 5 times higher than the conjugated diol (Figure 4C). Moreover, total [¹⁴C]-DBC in urine (Figure 4D) was more than the sum of measured conjugated DBC-11,12-diol and tetrol indicating that DBC metabolites measured in urine comprised possibly of metabolites formed from additional detoxification pathways other than the primary diol to tetrol route.

The model accurately predicted the conjugated DBC-11,12-diol levels in urine (Figure 4C), with model predictions being within one standard deviation of the measured levels. The predicted values for tetrol formed from DBC-11,12-diol were slightly less than the total tetrol measured in urine (Figure 4C), which suggests that urinary tetrols comprised of tetrols not only formed from the primary DBC-11,12-diol but perhaps also from other diols. However, the simulated values of non-diol metabolites in urine (Figure 4C) that comprises tetrol from DBC-11,12-diol and any other metabolites that are excreted in urine, were slightly higher than the total tetrol measured in urine indicating the presence of non-tetrol metabolites in urine.

Simulated total [¹⁴C]-DBC amount in urine were within the error bounds of the measured total [¹⁴C]-DBC values (Figure 4C) indicating that the fractional absorption coefficient term in our model, which is determined based on the ratio of nominal oral dose to the total DBC eliminated in urine, successfully captures the overall bioavailability of DBC.

Human Data for Volunteers 8 and 9

Pharmacokinetic data for DBC and DBC-11,12-diol in blood for volunteers 8 and 9 show similar overall trends (Figure 5). Peak concentrations of DBC and DBC diol were measured at ~100 and 10 fM, respectively, for both volunteers. Moreover, concentrations for both DBC and DBC-11,12-diol in blood peaked between 1–2 hours post dosing, followed by a gradual decrease at subsequent time points. Total [¹⁴C]-DBC measured in blood also followed similar trends for the two volunteers, showing a rapid increase in concentration before reaching peak concentration at around 1 hour after dosing, much like the concentration profiles of DBC and DBC-11,12-diol in blood but a much slower decrease in concentration subsequently.

Figure 5:

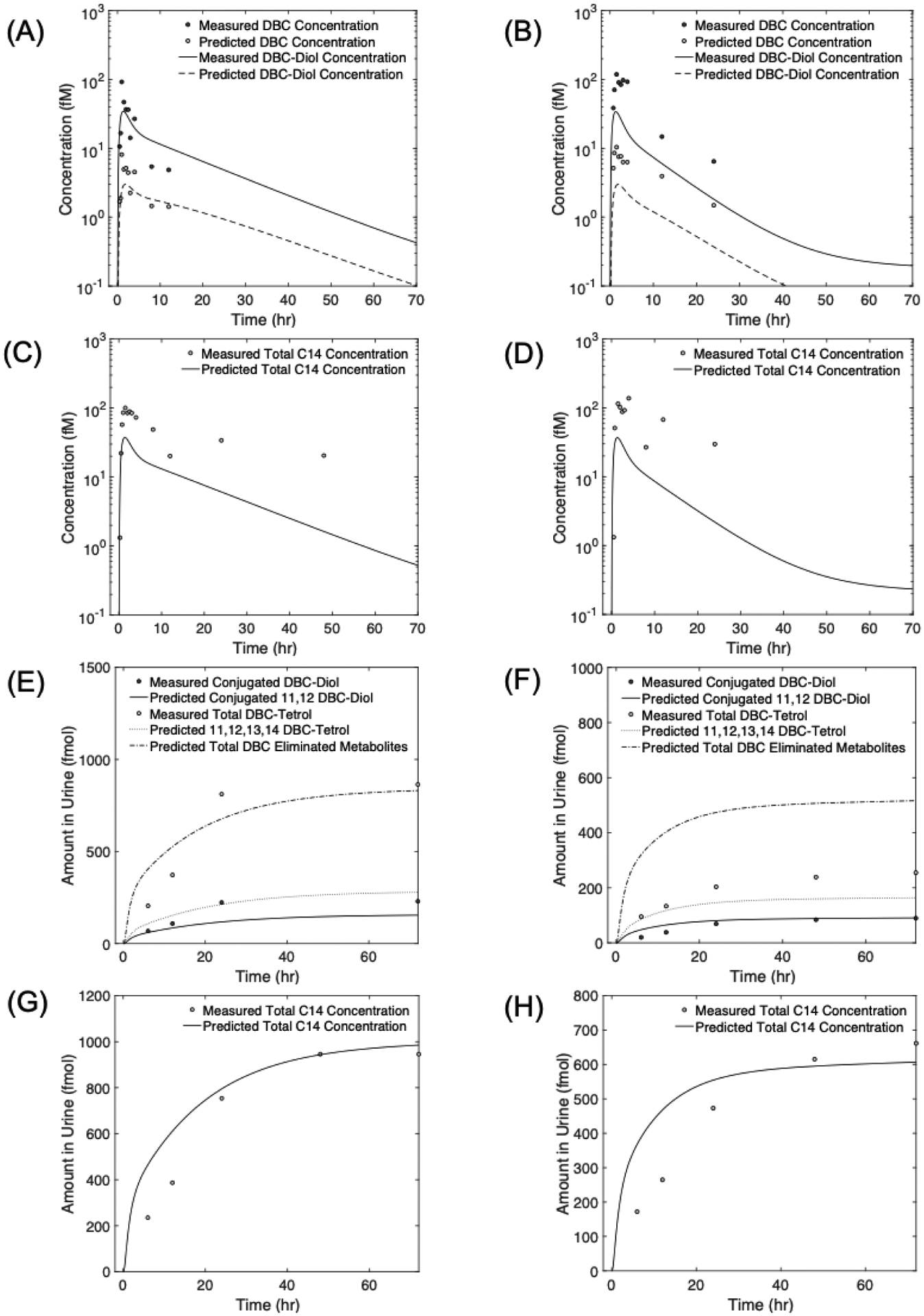
Measured concentrations of dibenzo[def,p]chrysene (DBC) and DBC metabolites in plasma (A -D) and urine (E - H), for two human volunteers: Volunteer 8 (left panel), and Volunteer 9 (right panel), orally administered with an oral dose of 29 ng of DBC. Lines are physiologically based pharmacokinetic (PBPK) model simulations of data.

Model predictions for DBC and DBC-11,12-diol concentrations in blood more accurately predicted measured values of Volunteer 8 than Volunteer 9. For DBC, model predictions for Volunteer 8 were mostly within two-fold deviation from the measured blood concentration, whereas for Volunteer 9 model predictions deviated 3 to 5 times from measured values. Model predictions for DBC-11,12-diol also followed the same pattern of mostly being within two-fold deviation from measured concentration for Volunteer 8 but varying between 3- to 4-fold for Volunteer 9. A plausible reason for this could be the inaccuracy in measured metabolite concentration values due to the uncertainty in extraction efficiency. While an aggregate extraction efficiency was quantified, it was not quantified or controlled with an internal standard for each individual sample. This could possibly explain why the model had better predictions for Volunteer 8 than Volunteer 9.

As with the data averaged among all volunteers, total [¹⁴C]-DBC levels in blood were consistently underpredicted by the model for Volunteers 8 and 9. While the peak values were underpredicted by a factor of approximately 2 for Volunteer 8, and 3 for Volunteer 9, the prediction for the distribution and excretion phases (time > 5h) deviated significantly from the measured values, with the predicted kinetics showing a much more rapidly decreasing trend for total [¹⁴C]-DBC concentrations than the measured levels. The larger discrepancy between model predictions and measured total [¹⁴C]-DBC concentration at later time points, indicates the possibility of loss of material during extraction and/or the presence of additional persistent metabolites that were not measured using the UPLC accelerator mass spectrometry and consequently not accounted for in the model. This hypothesis is further supported by the observation that the sum of measured concentrations of DBC and DBC-11,12-diol does not equal the measured total [¹⁴C]-DBC levels in blood during later time points (> 5h).

Similar to the concentrations of DBC and its metabolites in blood, measurements of urinary metabolites for volunteers 8 and 9 also showed similar overall trends, with tetrol amount in urine being 2–5 times higher than the conjugated-diol levels for both volunteers (Figure 5 E–F). Moreover, as in the case of total [¹⁴C]-DBC levels in blood, the total [¹⁴C]-DBC measured in urine (Figure 5 G–H) was not equal to the sum of the two main urinary metabolites, namely the conjugated DBC-11,12-diol and tetrols. In fact, while the total [¹⁴C]-DBC amount detected in urine for Volunteer 8 was on average 0.78 times smaller than the sum of amounts of individual urinary metabolites, it was on average 1.4 times higher for Volunteer 9. This observation further supports the possibility of measured metabolite concentration values being affected by extraction efficiency.

The PBPK model predicted the conjugated-diol and total [¹⁴C]-DBC amounts in urine with reasonable accuracy for both volunteers, with model predictions and measured values being within a factor of two for both volunteers (solid lines in Figure 5 E–H)). Simulated levels of tetrol formed via the 11,12-diol detoxification pathway were lower than the measured tetrol in urine for both volunteers, suggesting additional pathways for tetrol formation. For volunteer 8, model predictions for all non-diol metabolites (all tetrols and other non-diol metabolites) had better agreement with total tetrol measurements (dash-dotted line in Figure 5E), with the average deviation of model prediction from measured total tetrol values being 1.4 fmol. For volunteer 9 though, the average deviation of model predictions for all non-diol metabolites was 2.5 fmol (dash-dotted line in Figure 5F).

Sensitivity Analysis

Several common patterns in sensitivity coefficients were observed between mouse and human model parameters (Table 10). The most sensitive parameters for both models for DBC concentration and DBC-11,12-diol concentration in blood were associated with protein binding fractions of DBC and DBC-11,12-diol, respectively. Fractional oral absorption also had high sensitivity for both models for both endpoints, which is expected as this parameter is an important determinant of the bioavailability of DBC. Similarly, several parameters related to the liver, including the volume of the liver compartment, flow to the liver, blood:tissue partitioning coefficient for DBC in the liver, and the liver metabolism rates of DBC, all had high sensitivity for both end-points, suggesting the importance of metabolism in the liver in determining the disposition of DBC and DBC-11,12-diol. Additionally, parameters specific to DBC-11,12-diol were observed to have high sensitivity for DBC-11,12-diol concentration in both models. For example, the fractional metabolism parameter that determines the fraction of DBC that gets metabolized through the primary DBC--DBC--diol--DBC-tetrol pathway had high sensitivity for DBC-11,12-diol concentration in blood, whereas low sensitivity for DBC concentration in blood. A similar trend was observed in both models for the blood:tissue partitioning coefficient for DBC-11,12-diol in the liver.

Table 10:

Sensitivity analysis for parameters of dibenzo[def,p]chrysene (DBC) physiologically based pharmacokinetic (PBPK) model. Sensitivity coefficients were categorized as “Low” (absolute value of sensitivity coefficient < 0.1), “Medium” (absolute value of sensitivity coefficient > 0. 1 and < 0.5), and “High” (absolute value of sensitivity coefficient > 0.5).

Parameter	Symbol	Sensitivity Category		Sensitivity Category
		Mouse Model		Human Model
		DBC Concentration in Blood	DBC-Diol Concentration in Blood	DBC Concentration in Blood	DBC-Diol Concentration in Blood
Metabolism
Maximum rate of reaction for DBC metabolism	vmlpc	High	High	High	High
Michaelis constant for DBC metabolism	kmlp	High	High	High	High
First order rate for Phase 1 metabolism of DBC-Diol	cllmlc	Low	High	Low	High
Maximum rate of reaction for Phase II metabolism of DBC-Diol	vml2mlc	Low	Low	Low	Medium
Michaelis constant for Phase II metabolism of DBC-Diol	km 12ml	Low	Low	Low	Medium
Absorption
Absorption rate from stomach to liver	kas	High	High	Low	Low
Absorption rate from intestines to liver	ksi	High	High	High	High
Gastric emptying rate	kai	High	High	High	High
Compartment Volumes
Arterial blood	vac	Low	Low	Low	Low
Venous blood	wc	High	High	High	High
Fat	vfc	High	High	Medium	High
Liver	vie	High	High	High	High
Lung	vlngc	Low	Low	Low	Low
Rapidly Perfused	vrc	Medium	Medium	Medium	Medium
Slowly Perfused	vsc	Medium	High	High	High
Blood Flows
Fat	qfc	High	High	Medium	Medium
Liver	qlc	High	High	High	High
Rapidly Perfused	qrc	Medium	Medium	Medium	Medium
Alowly Perfused	qsc	Medium	Medium	Medium	Medium
Partition Coefficients (DBC)
Fat	pfp	High	High	Medium	Low
Liver	pip	High	High	High	High
Slowly perfused	psp	High	Medium	High	High
Rapidly perfused	prp	Medium	Low	Medium	Medium
Lung	plngp	Low	Low	Low	Low
Partition Coefficients (DBC-Diol)
Fat	pfml	Low	High	Low	Low
Liver	plml	Low	High	Low	High
Slowly perfused	psml	Low	Medium	Low	High
Rapidly perfused	prml	Low	Medium	Low	Medium
Lung	plngml	Low	Low	Low	Low
Other
Fractional oral absorption	per_abs	High	High	High	High
Fractional metabolism factor	fracl	Low	High	Low	High
Fractional protein binding (DBC)	fbp	High	Medium	High	High
Fractional protein binding (DBC-Diol)	fbml	Low	High	Low	High

Comparison of PBPK Modeling Predictions with Allometric Scaling

A comparison of model predictions for DBC and DBC-11,12-diol in an average mouse model assuming an oral bolus dose of 1 mg/kg-body weight and a human model with an allometrically scaled equivalent dose (0.2419 mg/kg-body weight) show that the kinetics of these two compounds do not scale allometrically (Figure 6). The peak concentration of DBC in blood for humans was 3.47 times higher than mice, whereas for DBC-11,12-diol it was 2.22 times in humans than mice. Likewise, the area under the curve (AUC) for DBC and DBC-11,12-diol concentrations were 5.47 and 6.84 times higher for humans than mice. Furthermore, our simulations predict that >99% of DBC is eliminated in mice after 72 hours, while in humans about 80% in eliminated in same time frame. Moreover, the model predicts that significantly more amount of DBC gets eliminated via Phase I route (almost 93%) compared to Phase II in mice, compared to only 54% eliminated via Phase I in humans.

Figure 6:

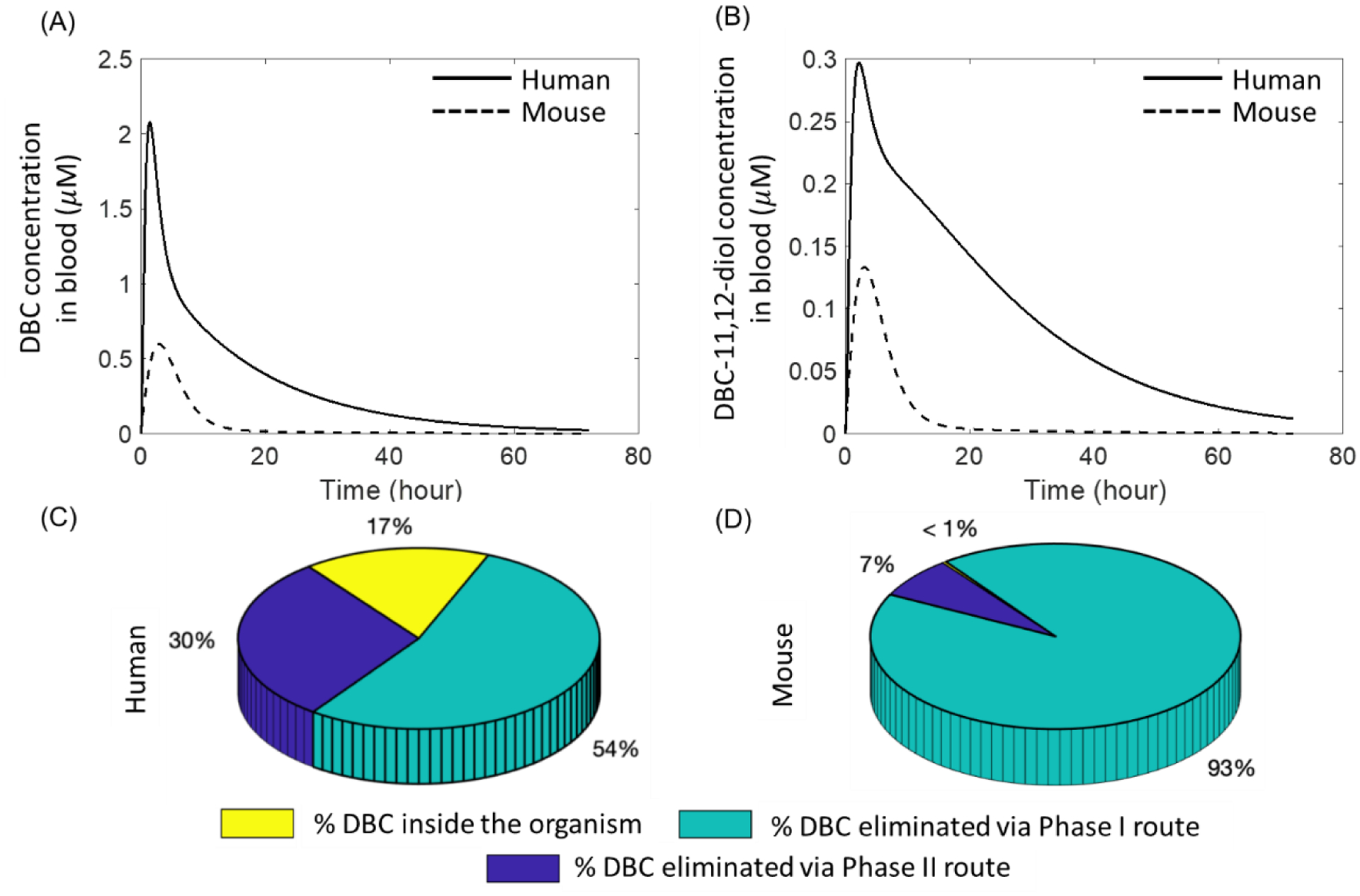
Simulated kinetics of (A) Dibenzo[def,p]chrysene (DBC) and (B) DBC-11,12-diol in mouse (dashed line) and human (solid line) physiologically based pharmacokinetic (PBPK) model for an oral bolus dose of 1 mg/kg-body weight in mouse and the corresponding human equivalent dose of 0.2419 mg/kg-body weight. Predictions for the disposition of (DBC) after 72 hours of oral administration estimated from the (C) human and (D) mouse model.

Discussion

A PBPK model for DBC was developed to predict the disposition of DBC and its metabolites in mice and humans. The model was first evaluated against in vivo plasma and urine measurements of DBC and DBC-metabolites in mice, and subsequently against in vivo human pharmacokinetic data, by appropriately scaling the physiological and biochemical parameters. The model was an extension of the preliminary model previously developed by our group (26). In the current model, the previously developed model for the parent compound was integrated with a similar model to account for the disposition of the diol metabolite of DBC. This is an important step towards the development of a more comprehensive PBPK model, and is particularly relevant, because for most PAHs, including DBC, carcinogenesis is more strongly correlated with the reactive metabolites than the parent compound. The metabolic parameters used in our model were experimentally obtained through in vitro experiments performed in mice and human hepatic microsomes. Moreover, the inter-species extrapolation from mice to humans and validation against in vivo plasma and urine pharmacokinetic measurements obtained from extremely low-dose exposure, which is representative of true environmental exposure, was made possible by using a novel ultrasensitive “moving wire” interface between ultraperformance liquid chromatography and accelerator mass spectrometry, which is capable of measuring concentrations in the femtomolar range.

Traditionally used interspecies extrapolation methods rely on simple approaches like using a 10-fold default uncertainty factor (UF) (44) or allometric scaling based on body weight or surface area (45), primarily due to the lack of enough toxicokinetic data. Metabolic rates do not necessarily scale allometrically between species, as observed by Smith et al., for DBC and DBC 11,12 diol (33). After scaling to body weight to the ¾ power, compared to humans, mice displayed 3-fold faster DBC metabolism, 6.5-fold faster CYP oxidation of DBC 11,12 diol, and equivalent rates of UGT conjugation of DBC 11,12 diol (33). Standard extrapolation approaches do not capture these measured differences. It is for this reason that traditionally used allometry-based approaches for extrapolating external dose to produce the same internal dose in different species might not be the most appropriate approach. In our simulations comparing the predictions from mouse and human PBPK models with those expected from an allometry-based approach demonstrated this point (Figure 6), where it can be seen that the internal concentrations of DBC and DBC-11,12-diol in blood in the two species are not similar, which would have been the case based on the assumption of allomeric scaling of external doses. Moreover, the amount of difference between the concentrations of the two compounds in mice and humans is dependent on the choice of internal dose metric, i.e., if the peak concentration is chosen as the dose-metric then the ratio of human to mouse values is higher for DBC than DBC-diol (1.85 vs. 1.35), whereas, for the AUC metric, the same ratio is lower for DBC than DBC-11,12-diol (2.66 vs. 3.46). This suggests that not only do internal dose metrics not scale allometrically in different species, but also that the scaling factor is dependent on the choice of dose metric. The differences between predictions for metabolic disposition of DBC based on allometric scaling vs. PBPK modeling is even more stark when we compare the fractions of DBC eliminated via Phase I and Phase II pathways. Based on our PBPK model, we see that a higher proportion of DBC gets eliminated via bioactivation route (Phase I) than detoxification route (Phase II) in mice (93% vs. 7%), which contrasts with predictions from the human model, where a smaller proportion of DBC gets eliminated via Phase I than Phase II route (54% vs. 30%) thereby implying that for allometrically determined equivalent external exposures, humans are less susceptible to DBC than mice, which is contrary to what one would expect based on allometric scaling.

Successful development of a PBPK model is the first step towards using the model for risk assessment. As noted in several guidance documents and reports (22, 46) the use of PBPK models for risk assessment offers the advantage of reducing the uncertainty in cross-species extrapolation of relative potency factor (RPF) and also in risk assessment of mixtures by considering species-dependent differences in pharmacokinetics, including differences in metabolic rates for the parent PAH and PAH metabolites. The RPF approach provides a method of cancer risk estimation for PAH mixtures by summing doses of component PAHs in a mixture after scaling the doses with RPFs relative to the potency of BaP. Although the RPF approach provides an accepted method of estimating toxicity of mixtures, it relies on several assumptions, such as dose additivity and proportionality of ADME characteristics for mixture constituents, that are not always true for environmentally relevant mixtures (47, 48). Moreover, since RPFs are estimated based on animal experiments, for human risk assessment, an interspecies extrapolation is required, which is challenging because of the differences and uncertainties in the exposure scenarios with respect to the route of administration and various species-dependent absorption and metabolic rates that need to be considered and accounted for appropriately (49, 50). These limitations of existing approaches for RPF and risk assessment for mixtures toxicity can be overcome by using a PBPK model for interspecies extrapolation of doses across species, which is currently being investigated by our group as a part of the future work.

In conclusion, we developed a PBPK model to simulate internal dosimetry of DBC and its primary metabolites in plasma and urine. The model was performance was evaluated against in vivo plasma and urine measurements of DBC and DBC-metabolites in mice, following which, it was validated against in vivo human pharmacokinetic data, by appropriate inter-species scaling of the physiological and biochemical parameters. The agreement between the simulations of our model and measured pharmacokinetic data in average mice and human studies demonstrate the success and versatility of our model for interspecies extrapolation and applicability for different doses. The model’s success is even more noteworthy considering that during model development and parametrization, we added only as much complexity as needed to explain the available pharmacokinetic data and optimized only a few parameters. Most model parameters were derived by using either published mathematical relationships (compartment volumes, blood flows, and partition coefficients) or values reported in prior studies, such as metabolic rates for that were obtained from in vitro studies. Additionally, our simulations showed the striking differences between internal dose metrics determined via allometric scaling vs. using a PBPK model, highlighting the importance of using PBPK models for risk assessment. In the future, we envision the application of our model in the simulating internal dosimetry and metabolic interactions between different PAHs in a complex mixture, which is more representative of environmentally relevant exposure scenario. In this respect, the success of the current model provides a promising foundation for such future endeavors.