Factor Retention Using Machine Learning With Ordinal Data

Abstract

Determining the number of factors in exploratory factor analysis is probably the most crucial decision when conducting the analysis as it clearly influences the meaningfulness of the results (i.e., factorial validity). A new method called the Factor Forest that combines data simulation and machine learning has been developed recently. This method based on simulated data reached very high accuracy for multivariate normal data, but it has not yet been tested with ordinal data. Hence, in this simulation study, we evaluated the Factor Forest with ordinal data based on different numbers of categories (2–6 categories) and compared it to common factor retention criteria. It showed higher overall accuracy for all types of ordinal data than all common factor retention criteria that were used for comparison (Parallel Analysis, Comparison Data, the Empirical Kaiser Criterion and the Kaiser Guttman Rule). The results indicate that the Factor Forest is applicable to ordinal data with at least five categories (typical scale in questionnaire research) in the majority of conditions and to binary or ordinal data based on items with less categories when the sample size is large.

Introduction

Determining the number of factors in exploratory factor analysis (EFA) is arguably the most crucial decision a researcher has to face when conducting the analysis. Since often little is known in advance about the factorial structure underlying a set of variables in the context of EFA, no theoretical assumptions about the dimensionality can be made and the number of factors has to be estimated based on the empirical data set. Over the years, several so-called factor retention criteria have been developed to tackle this issue. However, even though there are simulation studies (e.g., Velicer et al., 2000; Zwick & Velicer, 1986) showing the poor performance of several simple heuristic rules like the Kaiser–Guttman rule (KG, Kaiser, 1960), researchers tend to rely heavily on inaccurate criteria instead of using new approaches (Fabrigar et al., 1999; Goretzko et al., 2019). This is problematic as extracting too few factors (underfactoring) or too many (overfactoring) can deteriorate the EFA results (De Winter & Dodou, 2012; Fabrigar et al., 1999; Fava & Velicer, 1996).

Although researchers who conduct an EFA should make educated decisions and apply more sophisticated methods than KG or the completely outdated Scree test (Cattell, 1966), it can be challenging to select an appropriate criterion due to the varying accuracy of these methods under different data conditions. Auerswald and Moshagen (2019) conducted a comprehensive simulation study comparing different criteria and showed that none of them can be seen as superior throughout all conditions. Therefore, they suggested combining parallel analysis (PA, Horn, 1965) ¹ —which is often seen as a gold-standard (e.g., Fabrigar et al., 1999; Goretzko et al., 2019) as it has been shown to be superior to simple heuristic rules (e.g., Peres-Neto et al., 2005; Zwick & Velicer, 1986) and robust against distributional assumptions (Dinno, 2009)—with new approaches like comparison data (CD, Ruscio & Roche, 2012), the hull method proposed by Lorenzo-Seva et al. (2011) or the empirical Kaiser criterion (EKC, Braeken & Van Assen, 2017) which is a descendant of KG.

Both Fabrigar et al. (1999) and Goretzko et al. (2019) also recommend consulting several factor retention criteria and compare their results. This can be a rather complex and challenging task for practitioners and hence may not be the way to go for the majority of EFA users. For this reason, Goretzko and Bühner (2020) proposed a new criterion that promises an easy application and a high accuracy without having to compare different criteria. The new approach combines extensive data simulation that covers all data conditions reflecting the application context with training a machine learning (ML) algorithm that “learns” the relations between the true number of factors in the data generating process and data characteristics that can be observed (or calculated) for empirical data. Since Goretzko and Bühner (2020) trained and evaluated the ML model on multivariate normal data, further research has to evaluate how robust their method is against varying distributional assumptions. In their article, the authors suggested training different models for different distributional contexts. ² However, before simulating data for each new and slightly different context (especially with regard to distributional assumptions) and training several separate models, it should be evaluated how the initial model based on multivariate normality can deal with discretized data (ordinal data that are collected using questionnaires with Likert-type items while the underlying latent factors are assumed to be continuous and normally distributed) which is arguably the more common application context of EFA (compared with actual continuous data). For this reason, a simulation study was conducted investigating the accuracy of the new method (called Factor Forest)—or rather the pre-trained Factor Forest model provided by Goretzko and Bühner (2020)—as well as several common approaches in conditions with ordinal questionnaire items (that reflect normally distributed latent variables) varying the number of categories between two (dichotomous or binary items) and six (Likert scales often have five or six levels).

The Factor Forest

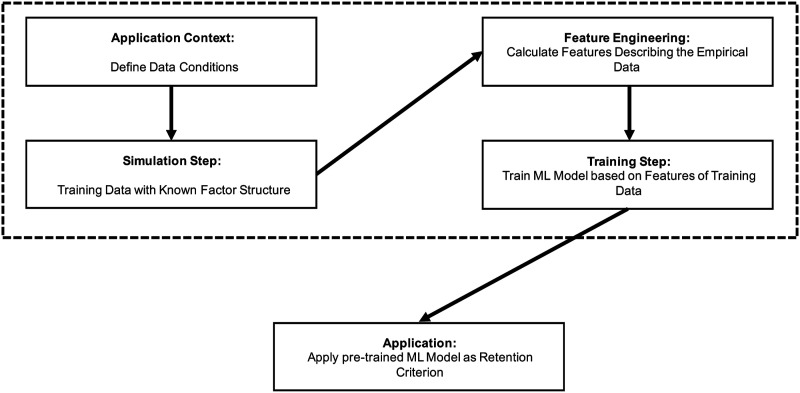
In the following, the general approach of the Factor Forest and the basic concepts of the respective modeling idea are described. The new approach developed by Goretzko and Bühner (2020) is based on two major steps (see Figure 1). First, a data basis that reflects “typical” data conditions of the application context has to be simulated. The trained ML model that the authors provided covers data conditions with k ∈ {1, …, 8} true underlying factors, p ∈ {4, …, 80} manifest variables, different communalities, and sample sizes of N ∈ {200, …, 1000}. Then features that merely describe the correlation matrix of the manifest variables are extracted for each simulated data set. Goretzko and Bühner (2020) used 184 features for the final model that was deployed online—the eigenvalues of the empirical correlation matrix; the eigenvalues of the reduced correlation matrix (based on the initial communality estimates of the common factor model); the sample size; the number of indicators; the number of eigenvalues greater than one (Kaiser–Guttman rule); the number of eigenvalues that are greater than 0.7; the relative proportions of the first, the first two and the first three eigenvalues, respectively; the standard deviation of all eigenvalues; the number of eigenvalues that account for 50% variance as well as the number of eigenvalues that account for 75% variance; the L₁-norm, the Frobenius-norm, the maximum norm and the spectral-norm of the correlation matrix; the average of the off-diagonal elements of the correlation matrix; the number of correlations smaller or equal to 0.1 (or rather the respective absolute values); the average initial communality estimates; the determinant of the correlation matrix; the measure of sampling adequacy; two inequality measures (Kolm measure and Gini-coefficient) applied to the correlation matrix; and the suggested number of factors from PA, EKC, and CD. They found the eigenvalues of the reduced correlation matrix based on the factor model and the inequality measures to be the most important features for their initial model without PA, EKC, and CD. Adding these features (and tuning the ML algorithm) improved the predictive performance substantially, which is why it can be assumed that they are also quite important for the final model’s predictions. Based on these extracted features, an ML model is trained (the authors used an xgboost model, Chen et al., 2018) that models the relation between the extracted features and the true number of factors which is known for the simulated data sets. The xgboost algorithm is a complex ML algorithm that is based on the idea of (gradient) boosting. Boosting is a method to create an ensemble of several relatively “weak” or less complex ML models. Usually, decision trees are combined by fitting each tree to the residuals of the previous ones—in contrast to other tree-ensembles such as random forests where each tree is fitted separately to a different bootstrap sample of the data. Since subsequently fitting single trees to the residuals of the model enables the model to quickly reach perfect accuracy on all training instances which poses a great risk of overfitting, it is important to “slow down” the way each tree updates the model’s predictions by adjusting a so-called learning rate (a hyperparameter in boosting models). This learning rate is flexible in gradient boosting and is adjusted in each step (Friedman, 2001). The very flexible and therefore extremely powerful xgboost algorithm is a state-of-the-art implementation of gradient boosting which has several ways to optimize the predictive power and to prevent overfitting (e.g., regularization measures on tree- and node-level, subsampling of observations and features).

Figure 1.

General idea of the factor forest.

The idea of FF is that the ML model—in the current implementation the xgboost model—“learns” the relationship between observable indicators (i.e., the extracted features such as, for example, the maximum norm of the correlation matrix of the manifest variables or the second eigenvalue of this matrix) that can be calculated for each empirical data set and the number of underlying factors that should be retained in an EFA. The trained ML model as provided by Goretzko and Bühner (2020) is a (complex) prediction model that is able to predict the number of factors given this set of extracted features as input variables and that can be applied to empirical data if the particular empirical data set fits its “application context” (i.e., the data context the ML model is trained on). In the present study, the pre-trained model which was trained on multivariate normal data and has been provided by Goretzko and Bühner (2020) is evaluated on ordinal data with underlying continuous latent variables.

Common Factor Retention Criteria

In the following, the four common factor retention criteria that were used for comparison in the evaluation study are briefly introduced.

Kaiser Criterion or Kaiser–Guttman Rule (KG)

The Kaiser criterion or Kaiser–Guttman rule (Kaiser, 1960) is one of the oldest ways to determine the number of factors in EFA. The idea is simply to retain all factors for which the corresponding eigenvalue is greater than one since a factor should explain more variance than a single variable. While this rationale seems to be appealing and quite meaningful on the population level, sampling error can deteriorate KG’s results as it often overfactors (Zwick & Velicer, 1986).

Empirical Kaiser Criterion (EKC)

The empirical Kaiser criterion is a descendant of KG which takes the sample size and the impact of strong major factors into account (Braeken & Van Assen, 2017). Instead of comparing the empirical eigenvalues to one, reference eigenvalues are calculated considering the sample size N, the number of manifest variables p, and the size of all previous eigenvalues. The reference value $l_j^{REF}$ for the j-th empirical eigenvalue λ _j is determined via

$$l_j^{REF}=max\left(\frac{p-{\displaystyle {\sum }_{k=0}^{j-1}{\lambda }_k}}{p-j+1}{\left(1+\sqrt{\frac{p}{N}}\right)}^2,1\right)$$

if only factors with eigenvalues greater one should be considered (restricted EKC to avoid low-reliability factors) and simply

$$l_j^{REF}=\frac{p-{\displaystyle {\sum }_{k=0}^{j-1}{\lambda }_k}}{p-j+1}{\left(1+\sqrt{\frac{p}{N}}\right)}^2$$

if no such restriction is made. In this study, we only present the results of the restricted EKC as the unrestricted EKC suggested too many factors most of the time and performed considerably worse than the restricted version.

Parallel Analysis (PA)

Parallel analysis was developed by Horn (1965) and became one of the most popular ways to determine the number of factors (e.g., Goretzko et al., 2019). The idea of this approach is to compare the sequence of empirical eigenvalues with eigenvalues of simulated (or resampled) data sets. In the traditional implementation of PA, S random data sets are simulated and the eigenvalues of the correlation matrix are calculated. Then the first empirical eigenvalue is compared to the mean of the S first random eigenvalues and the factor is retained if the empirical eigenvalue is greater. Analogously, the second empirical eigenvalue is compared to the mean of the S second random eigenvalues and so on until the empirical eigenvalue is smaller than the reference value. Other implementations of PA use the 95%-quantile of the random eigenvalues, are based on resampled instead of simulated data, or focus on eigenvalues of a reduced correlation matrix (based on the common factor model) rather than calculating eigenvalues of the empirical correlation matrix. A comparison of these different PA methods can be found at Auerswald and Moshagen (2019) or Lim and Jahng (2019). In this study, we chose PA based on the common factor model with squared multiple correlations as communality estimates and the 95%-quantile of the random eigenvalue distribution which is the default in the R package psych (Revelle, 2018).

Comparison Data (CD)

The comparison data approach (Ruscio & Roche, 2012) can be seen as an extension of PA that applies the model testing perspective of structural equation modeling to the issue of factor retention. The iterative method consists of non-parametric significance tests that compare two subsequent factor solutions with regard to the deviation of the eigenvalues of the reproduced correlation matrix (based on a particular number of factors) from the empirical eigenvalues. First, so-called comparison data sets are simulated that reproduce the correlation matrix based on a single factor. The eigenvalues of these comparison data sets are then compared to the empirical eigenvalues by calculating the RMSE for each comparison data set. Then, a Mann–Whitney-U-test is applied to compare the RMSE distribution of the single-factor solution with the RMSE distribution of the two-factor solution. If the test is significant, the procedure continues with the two-factor and three-factor solution, then with the three-factor and four-factor solution, and so on until no significant improvement is detected. The CD approach has several parameters that can be set by the researcher (i.e., the size of the simulated population, the number of comparison data sets drawn from each population and the α-level of the internal significance test). For this study, we used the values suggested by Ruscio and Roche (2012)—namely, α = .30, 500 comparison data sets per factor solution as well as a population size of 10,000 (the size of the population from which the comparison data sets are sampled). The unusual α-level of 30% is recommended by Ruscio and Roche (2012) as the best trade-off between under- and overfactoring (as a type-I error would result in overfactoring and a type-II error in underfactoring). This seems to be reasonable, especially since underfactoring is seen as more severe compared to extracting too many factors (e.g., Fabrigar et al., 1999).

Evaluation

Since we wanted to find out how robust the Factor Forest is against distributional assumptions, a simulation study was conducted that covers similar data conditions compared to Goretzko and Bühner (2020; who chose the simulation conditions based on other simulation studies, for example, Auerswald & Moshagen, 2019 and real data contexts, Goretzko et al., 2019) but relied on ordinal indicators instead of continuous data. In doing so, the simulation conditions reflect data conditions that are typical for psychological research reported in review studies (e.g., Fabrigar et al., 1999; Goretzko et al., 2019). We simulated data with 250 or 1000 observations, based on one, four, or six latent factors, different loading magnitudes for primary and cross-loadings (same loading patterns ³ as Goretzko & Bühner, 2020), orthogonal or oblique factor structures (all inter-factor correlations set to 0.3) and different numbers of manifest variables (using four or seven indicators per latent variable). For the specific application context (continuous latent variables and ordinal manifest indicators), we first simulated multivariate normal data using the mvtnorm package (Genz et al., 2018) and then discretized the data either using symmetrical thresholds or asymmetrical thresholds (conditions with skewed item distributions) according to the procedure described by Yang and Xia (2015). Table A1 in the electronic supplemental material (https://osf.io/bcfvs/) presents the thresholds used in the different data conditions. In this process, ordinal indicators were created with different numbers of categories (2, 3, 4, 5, 6) while the set of underlying latent variables was normally distributed. In total, we simulated data for 1520 different conditions with 500 replications each (760,000 data sets). To be more precise, 2 (sample sizes) × 2 (numbers of variables per factor) × 3 (numbers of latent variables) × 2 (levels of inter-factor correlations) × 3 (levels of primary loadings) × 3 (levels of cross-loadings) × 2 (types of thresholds) × 5 (numbers of categories) = 2160 conditions were simulated. Since inter-factor correlations and cross-loadings are irrelevant for conditions with only one latent factor k = 1, we excluded all conditions (600 in total) with k = 1 and inter-factor correlations rho ≠ 0 as well as conditions with cross-loadings and k = 1. We further excluded 40 conditions with high standardized primary loadings, medium-sized cross-loadings, inter-factor correlations ρ = 0.3 and k = 6 as these conditions imply impossible communalities that exceed one. Hence, 2160 − 600 − 40 = 1520 conditions were used in the evaluation study.

In this evaluation study, we compared the Factor Forest, the trained xgboost model (retrieved from https://osf.io/mvrau/) to the exact same common factor retention criteria used in Goretzko and Bühner (2020) - PA, CD, EKC, KG - with regard to their accuracy as well as tendencies of under- or overfactoring. As ordinal indicators were used, polychoric correlations replaced Pearson correlations when calculating the features for the predictions of the Factor Forest or when applying PA, EKC, or KG. The R-code of this evaluation study and an example on how to apply the Factor Forest are provided at https://osf.io/bcfvs/. The data generation and all statistical analyses were performed with R. The psych package (Revelle, 2018) was used to conduct parallel analysis, to calculate eigenvalues and to compute polychoric correlations. The evaluation study was set up using the batchtools package (Bischl et al., 2015) and for the Factor Forest implementation, the packages mlr (Bischl et al., 2016), ineq (Zeileis, 2014), and purrr (Henry & Wickham, 2020) provided helpful functionalities. In the online repository, interested readers can also find preliminary results for additional simulation conditions evaluating all five factor retention criteria when minor factors are present as well as on a finer grid regarding the sample size. For the evaluation, we focused on two metrics, the accuracy and the bias of each method. The accuracy is simply the proportion of cases where the number of factors was correctly identified by the respective method, while we refer to the mean deviation of the true number of factors as bias ( $\widehat{Bia{s}_k}=\overline{\widehat{k}}-k$ , for each k).

Results

Overall, across all conditions considered in the study, the Factor Forest (FF, the trained xgboost model) reached the highest accuracy with 85.2% correctly identified cases. PA showed the second-highest overall accuracy (76.8%), followed by CD (66.2%), EKC (64.7%), and KG (52.5%). 89% of these conditions can be considered to be well-scalable (the number of eigenvalues of the population correlation matrix that were greater than one and the true number of factors was the same, which means that no minor or weak factors were present), while approximately 11% of the data sets were based on respective weak factors. In well-scalable conditions, all methods performed better and reached slightly higher overall accuracies (Acc _FF = 87.9%, Acc _PA = 83.0%, Acc _CD = 72.8%, Acc _EKC = 72.7%, and Acc _KG = 57.8%). In the following sections, the evaluation results are presented in greater detail and separately for conditions with symmetric and asymmetric thresholds.

Ordinal Data with Symmetric Thresholds

Table 1 shows the averaged accuracy over all conditions with ordinal indicators and symmetric thresholds as well as the accuracy and the bias of the five factor retention criteria for data conditions with different numbers of categories separately. FF yielded the highest accuracy for ordinal indicators with symmetric thresholds independently of the number of item categories. With dichotomous data (two levels), it performed worse (Acc_FF.2 = 0.80) than with ordinal data with more levels (Acc_FF.>2 ≥ 0.89). PA reached the second-highest accuracy for ordinal data with symmetric thresholds and also performed better when items had more than two levels. The more categories there were, the more accurate CD was as well. Contrary, for KG and EKC no clear pattern was found as both methods yielded the lowest accuracies on average and seemed not to benefit from an increase of categories. All common factor retention criteria showed signs of bias—PA, CD, and EKC tended to underfactor (negative bias: suggesting too few factors), while KG was prone to overfactoring (positive bias: suggesting too many factors). FF was (virtually) unbiased for all numbers of categories. The rates of under- and overfactoring are presented in an additional table in the online supplemental material (https://osf.io/bcfvs/).

Table 1.

Accuracy and Bias of the Factor Retention Criteria for Ordinal Indicators, Symmetric Thresholds and Different Numbers of Categories.

Method	Acc	Acc 2−Cat	Bias 2−Cat	Acc 3−Cat	Bias 3−Cat	Acc 4−Cat	Bias 4−Cat	Acc 5−Cat	Bias 5−Cat	Acc 6−Cat	Bias 6−Cat
FF	0.891	0.803	0.021	0.888	0.027	0.913	0.029	0.924	0.034	0.929	0.033
PA	0.807	0.727	−0.538	0.803	−0.412	0.828	−0.369	0.838	−0.350	0.842	−0.342
CD	0.692	0.550	−1.654	0.693	−1.006	0.730	−0.839	0.743	−0.727	0.746	−0.654
EKC	0.647	0.645	−0.812	0.651	−0.996	0.647	−1.031	0.645	−1.049	0.645	−1.057
KG	0.550	0.434	1.675	0.532	1.046	0.576	0.843	0.596	0.744	0.610	0.690

Note. Acc stands for accuracy - so Acc_2−Cat stands for the accuracy in conditions based on ordinal indicators with two levels (and symmetric thresholds). Bias describes the mean deviation of the suggested number of factors from the true number of factors in the respective conditions.

FF = Factor Forest; CD = Comparison Data; EKC = empirical Kaiser criterion; KG = Kaiser–Guttman rule.

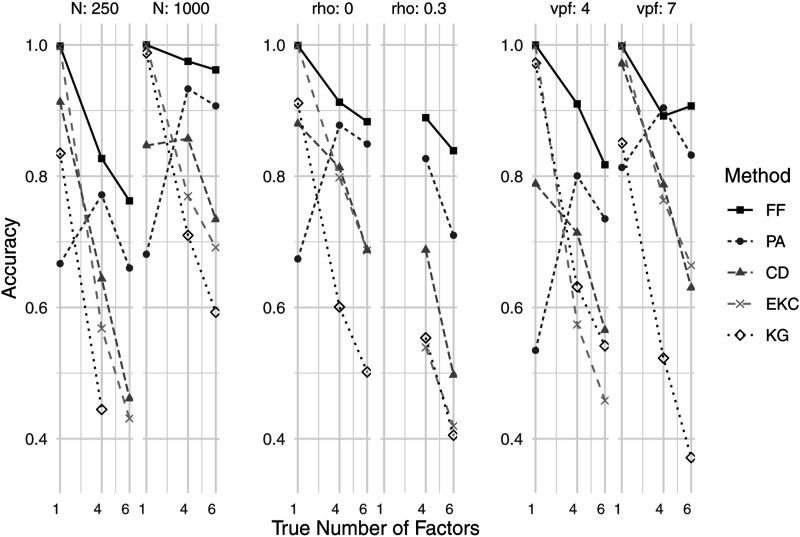
In data conditions with N = 1000, FF was able to achieve nearly perfect accuracy (overall: Acc _FF = 0.97/with at least four categories: Acc_FF.>3 = 0.99), while being superior to the other criteria when N = 250. FF showed also the highest accuracy for both uncorrelated and correlated factor structures as well as for different degrees of overdetermination (PA performed comparably well for data conditions with seven indicators per latent variable). In Figure 2, the results of the different ordinal data conditions are presented in more detail. One can see that EKC shows nearly perfect accuracy for unidimensional data, but failed to retain the correct number of factors with increasing dimensionality. While this pattern (less accuracy with an increasing number of factors) was also observable for CD and KG (as well as for FF on a higher level), PA showed peak performance in conditions with k = 4 and was not able to correctly identify unidimensionality comparably well.

Figure 2.

Ordinal data with symmetric thresholds: Accuracy of factor retention for different true numbers of factors as well as for different sample sizes (N), inter-factor correlations (rho) and variables per factor (vpf).

Both EKC and KG showed a worse performance when factors were correlated—a tendency that was also found for CD, while FF reached almost the same accuracy for correlated as for uncorrelated (orthogonal) factors. The accuracy of PA was also lower for correlated factors, yet when k = 4, PA had almost the same accuracy in correlated-factor conditions as in conditions with no between-factor correlations.

While all methods benefited from greater sample sizes, a higher overdetermination improved the accuracy of the factor retention process only for FF, PA, EKC, and CD, but not for KG, which tended to overfactor much more strongly in conditions with seven manifest indicators per factor (overall bias in conditions with seven indicators per factor: Bias _KG ._vpf=7 = 1.93 vs. overall bias in conditions with four indicators per factor: Bias _KG ._vpf=4 = 0.07).

One major factor influencing the accuracy of the factor retention process was the true loading pattern. The higher primary loadings were, the more accurately each method was able to determine the number of factors. As expected, deviations from simple structure harmed the accuracy of the factor retention process, that is, higher cross-loadings impaired the performance of all five factor retention criteria. This result pattern was also found for data conditions with asymmetric thresholds. Interested readers find the respective results in the online supplemental material (https://osf.io/bcfvs/).

Ordinal Data with Asymmetric Thresholds

Table 2 shows the averaged accuracy over all conditions with ordinal indicators and asymmetric thresholds as well as the accuracy and the bias of the five factor retention criteria for data conditions with different numbers of categories separately. All factor retention criteria except EKC performed worse compared to conditions with symmetric thresholds. Accordingly, skewed item distributions negatively affected the factor retention process for all methods, but EKC.

Table 2.

Accuracy and Bias of the Factor Retention Criteria for Ordinal Indicators, Asymmetric Thresholds and Different Numbers of Categories.

Method	Acc	Acc 2−Cat	Bias 2−Cat	Acc 3−Cat	Bias 3−Cat	Acc 4−Cat	Bias 4−Cat	Acc 5−Cat	Bias 5−Cat	Acc 6−Cat	Bias 6−Cat
FF	0.812	0.737	0.054	0.803	0.056	0.829	0.065	0.842	0.072	0.848	0.074
PA	0.729	0.646	−0.548	0.721	−0.418	0.747	−0.377	0.761	−0.356	0.768	−0.352
CD	0.632	0.515	−1.759	0.603	−1.362	0.658	−1.125	0.686	−1.006	0.699	−0.944
EKC	0.648	0.633	−0.702	0.654	−0.939	0.652	−0.986	0.651	−1.005	0.649	−1.015
KG	0.501	0.394	1.902	0.493	1.300	0.523	1.098	0.542	0.995	0.553	0.937

Note. Acc stands for accuracy - so Acc_2−Cat stands for the accuracy in conditions based on ordinal indicators with two levels (and asymmetric thresholds). Bias describes the mean deviation of the suggested number of factors from the true number of factors in the respective conditions.

FF = Factor Forest; CD = Comparison Data; EKC = empirical Kaiser criterion; KG = Kaiser–Guttman rule.

Again, as in conditions with symmetric thresholds, FF yielded the highest accuracy independently of the number of item categories. It reached at least 80% accuracy for all conditions, except from those based on dichotomous data where it performed worse (Acc_FF.2 = 0.74). With more levels, FF reached accuracies between (Acc_FF.3 = 0.80) and (Acc_FF.6 = 0.85). PA reached the second-highest accuracy for ordinal data with asymmetric thresholds and also performed better with an increasing number of item categories. KG and CD also performed better the more levels the items had reaching only accuracies of Acc_CD.2 = 0.52 and Acc_KG.2 = 0.39 for dichotomous items. As for symmetric thresholds, all common factor retention criteria showed signs of bias. While PA and EKC showed virtually the same tendency of underfactoring, this tendency of suggesting too few factors increased for CD (especially when items had more than two levels—compare Table 1 and 2). KG was prone to overfactoring (suggesting too many factors in 40.25% of the cases) and showed a stronger bias than in conditions with symmetric thresholds and non-skewed item distributions. Even though FF showed a slight tendency to overfactor (a tendency that became stronger as the number of categories increased), it can be marked as “quasi-unbiased” in comparison to all four other criteria. The specific rates of under- and overfactoring are presented in an additional table in the online supplemental material (https://osf.io/bcfvs/).

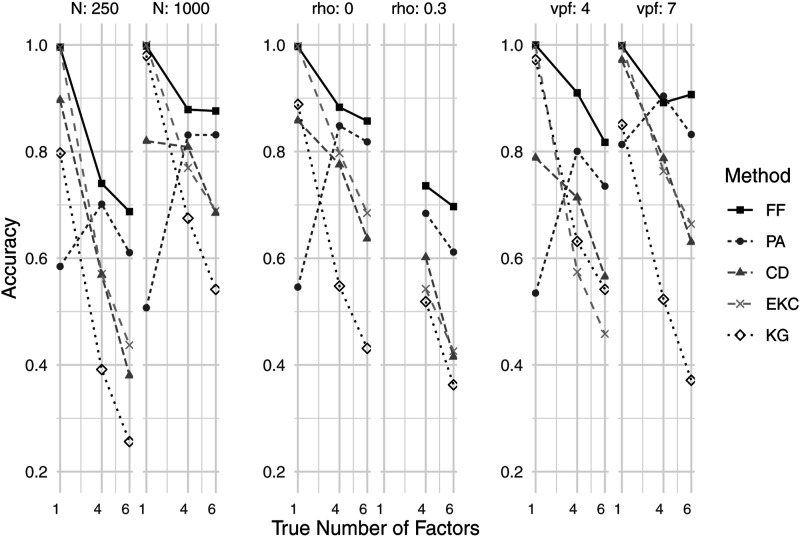
In Figure 3, the results are presented in greater detail for different numbers of factors, sample sizes, levels of overdetermination, and for correlated and uncorrelated factors separately. The general patterns are quite similar to the result patterns for ordinal items based on symmetric thresholds (Figure 2). The greater the sample size was, the more accurate each factor retention became. The only exception to this rule was PA in single-factor conditions in which its performance slightly dropped when N increased (this finding was accompanied by the general weak performance of PA in conditions with only one underlying factor).

Figure 3.

Ordinal data with asymmetric thresholds: Accuracy of factor retention for different true numbers of factors as well as for different sample sizes (N), inter-factor correlations (rho) and variables per factor (vpf).

Again, the factor retention was less accurate when between-factor correlations were present (contrary to ordinal data with symmetric thresholds, FF also performed substantially worse in conditions with correlated factors than in orthogonal conditions). On average, EKC and KG reached an accuracy of less than 50% in these conditions, while CD (Acc _CD . _cor = 0.51) was not able to identify the number of factors correctly in almost every second case. Higher overdetermination (more indicators per factor) fostered the accuracy of all methods except KG (as already observed for ordinal data with symmetric thresholds).

Applicability of the Factor Forest to Ordinal Data

As Tables 1 and 2 as well as Figures 2 and 3 show, FF is able to handle ordinal data (i.e., ordinal manifest variables and continuous latent variables) better than common factor retention criteria (namely PA, EKC, CD, or KG). When the number of categories increased, its performance increased as well (reaching a roughly eight percentage points higher accuracy than PA—a performance gap that was rather constant across conditions with different numbers of categories). Contrary to the other factor retention criteria evaluated in this study, FF showed no substantial bias (not even in conditions with skewed item distributions due to asymmetric thresholds). In conditions with N = 1000, FF reached an accuracy of Acc_FF.2 = 0.88 for dichotomous items and an accuracy above 92% when items had at least three categories (e.g., Acc_FF.3 = 0.92). In smaller samples (N = 250), while being consistently superior to all common methods, the accuracy of FF dropped (between Acc_FF.2 = 0.66 and Acc_FF.6 = 0.82). However, in conditions with four or more categories and N = 250, FF was the only method to reach an accuracy of 80% or higher. When the item distributions were not skewed (symmetric thresholds), FF even reached an 80%+ accuracy with three categories in these small sample conditions. On the other hand, when sample sizes were high, FF had substantially higher accuracies even in conditions with skewed item distributions (e.g., Acc_FF.2 = 0.84 for binary items and Acc_FF.5 = 0.91 for typical five-point scale items). Accordingly, FF trained on normal data seems to be applicable to data with ordinal manifest variables if sample sizes are high or in small sample conditions when the item distributions are not skewed. Besides, when the number of categories is comparably high (e.g., five or six categories), its performance is also acceptable for manifest variables with skewed item distributions. Besides, in less favorable conditions (e.g., small sample sizes, skewed item distributions due to asymmetric thresholds, correlated factors, and/or small levels of overdetermination), FF still reached higher accuracies than all common criteria. For these conditions—a newly trained model that “knows” ordinal data from the training data might be more accurate, but compared to other methods that are currently applied to social-scientific data (which are often questionnaire data and therefore of ordinal nature) the trained xgboost model provided by Goretzko and Bühner (2020) seems to be preferable.

Discussion

In comparison to the study of Goretzko and Bühner (2020) where FF, PA, CD, EKC, and KG were evaluated in data conditions based on multivariate normality, all methods performed substantially worse in our study focusing on ordinal data. PA reached only slightly lower overall accuracy than in the study of Goretzko and Bühner (2020)—which may be explainable by its robustness against distributional assumptions of the simulated data used for comparison in the analysis (Dinno, 2009). As mentioned above (and discussed by other authors, e.g., Lim & Jahng, 2019), there are several different implementations of PA (we used the default implementation of the psych package by Revelle, 2018 to ensure comparability with Goretzko & Bühner, 2020). Besides these different implementations of PA, it is also debated whether to rely on Pearson correlations or polychoric correlations when applying PA to ordinal data (e.g., Timmerman & Lorenzo-Seva, 2011); however, polychoric correlations seem to be preferable (Garrido et al., 2013), so our implementation of PA based on polychoric correlations is unlikely to have disadvantaged PA in this evaluation study. Our study indicates that while being able to handle ordinal data with symmetric thresholds quite well in general, PA is less accurate when variables are dichotomous or when asymmetric thresholds are present (skewed item distributions) which is line with the findings of Yang and Xia (2015). CD also benefited from increasing the number of categories and was able to handle ordinal data with symmetric thresholds better than data with skewed item distributions. Its weaker performance compared to PA contrasts the findings of Ruscio and Roche (2012) who also evaluated both methods with ordinal data, but unlike this study did not assume the underlying factors to be continuous. However, since other studies (e.g., Auerswald & Moshagen, 2019; Goretzko & Bühner, 2020) with similar data conditions (but normal data) found CD not to outperform PA, we would argue that conditions in which all methods reach lower accuracies, CD seems to be inferior to PA. As CD has several parameters (e.g., the α-level of the internal significance tests or the number of comparison data sets drawn for each factor solution, see also Ruscio & Roche, 2012), it might be necessary to select other parameters for this special setting (comparably to other implementations of PA) to reach higher accuracy. EKC performed very well in conditions with a single underlying factor—which is in line with its strong performance in comparable settings with normal data (e.g., Auerswald & Moshagen, 2019; Goretzko & Bühner, 2020) and theoretical expectations (Braeken & Van Assen, 2017). With more than one underlying factor its performance decreased rapidly—especially when overdetermination was small—a tendency that was also found for normal data (e.g., Auerswald & Moshagen, 2019) but that was considerably stronger in this study. The number of categories had almost no impact on both EKC and KG (the latter slightly improved with an increase in categories) which might be explainable by the relative stability of the eigenvalues of polychoric correlation matrices over different degrees of discretization (e.g., Yang & Xia, 2015), while the rather weak performance of the EKC (compared to its performance with normal data, see, for example, Goretzko & Bühner, 2020) can be explained (to some extent) by the approximation of the correction term that is added to KG to address sampling errors. The derivation of this correction term is based on normal data (Braeken & Van Assen, 2017), so for ordinal data, the reference eigenvalues may be slightly off. In general, all methods were less accurate when the item distributions were skewed (asymmetric thresholds) which was also reported by Yang and Xia (2015). Auerswald and Moshagen (2019), though, reported almost no effects of skewness, but their results were based on non-normal continuous data and rather small skewness.

Goretzko and Bühner (2020) suggested using the xgboost model that they provided (here called FF) only in contexts with normal data because the training data solely consisted of multivariate normally distributed data sets and argued that a new model has to be trained on newly simulated data for different distributional assumptions. However, this study shows that the pre-trained xgboost model is able to deal with ordinal data quite well (at least better than PA and other common factor retention criteria)—especially in conditions with larger sample sizes (and when typical five-level items are used). Hence, we would argue that in these cases where FF yielded an overall accuracy above 80% (often above 90%), the evaluated model is still trustworthy. When the empirical item distributions are not skewed (symmetric thresholds) and/or the sample size is very large, it seems reasonable to apply the provided model, otherwise, it is necessary to question its predictions. Since the current evaluation study solely focused on positive loading patterns (no negative cross-loadings or negative inter-factor correlations), the results have to be interpreted with caution and further research has to specifically investigate respective data conditions. However, as Goretzko and Bühner (2020) found the trained xgboost model to perform equally well on normal data that were based on a factor model with both positive and negative loadings, it seems reasonable to believe that the performance of FF does not differ in data conditions with negative loading patterns and ordinal data as well. That is, we would assume that the results of this study can be transferred to data conditions equal to those investigated here but based on negative loading patterns (or negative inter-factor correlations). Nonetheless, future research should focus on different loading patterns (i.e., loading patterns with negative cross-loadings, different degrees of overdetermination for each factor instead of a constant number of variables per factor, etc.) to evaluate the generalizability of our findings. In doing so, data conditions not covered in this study (or in Goretzko and Bühner (2020)) with a focus on population matrices that are approximately rank deficient, for example, in multitrait-multimethod models (e.g., Grayson & Marsh, 1994), should be investigated as well. Beauducel and Hilger (2021) recently evaluated different implementations of PA under these conditions providing first insights on how to handle this issue.

Further research could also investigate the performance of FF (and other factor retention methods) on actual ordinal data without assuming an underlying normally distributed latent variable, even though the respective data would not be in line with common EFA but would be more appropriate for specific ordinal factor models. More importantly, further research should also investigate data settings where the underlying continuous latent variables are not normally distributed (which can be quite challenging, Grønneberg & Foldnes, 2019) since the respective conditions are probably more difficult for an ML model trained on normally distributed data.

For skewed ordinal data conditions, especially in small sample size settings, the performance of the pre-trained FF model decreased. Hence, a separate ML model has to be trained on respective training data to reach higher accuracy for this kind of data. For the time being, researchers have to consult different factor retention criteria as no single criterion was superior throughout all data conditions with asymmetric thresholds, yet FF may be more trustworthy than the approaches it was compared with as it reached the highest overall accuracy in these cases. It has to be stated that the accuracy of all factor retention criteria could be even lower when the underlying latent variables are not normally distributed. Nevertheless, for many application contexts in social-scientific research (relying on five-point Likert scales and more than 250 observations—the sample size median of EFA applications is around 400, see Goretzko et al., 2019) where an assumption of normally distributed latent variables is appropriate, the current version of FF may yield acceptable or even quite good results.

ORCID iD

David Goretzko https://orcid.org/0000-0002-2730-6347