Simultaneous confidence bands for functional data using the Gaussian Kinematic formula

Abstract

We propose a construction of simultaneous confidence bands (SCBs) for functional parameters over arbitrary dimensional compact domains using the Gaussian Kinematic formula of t-processes (tGKF). Although the tGKF relies on Gaussianity, we show that a central limit theorem (CLT) for the parameter of interest is enough to obtain asymptotically precise covering even if the observations are non-Gaussian processes. As a proof of concept we study the functional signal-plus-noise model and derive a CLT for an estimator of the Lipshitz–Killing curvatures, the only data-dependent quantities in the tGKF. We further discuss extensions to discrete sampling with additive observation noise using scale space ideas from regression analysis. Our theoretical work is accompanied by a simulation study comparing different methods to construct SCBs for the population mean. We show that the tGKF outperforms state-of-the-art methods with precise covering for small sample sizes, and only a Rademacher multiplier-t bootstrap performs similarly well. A further benefit is that our SCBs are computational fast even for domains of dimension greater than one. Applications of SCBs to diffusion tensor imaging (DTI) fibers (1D) and spatio-temporal temperature data (2D) are discussed.

1. Introduction

In the past three decades functional data analysis has received increasing interest due to the possibility of recording and storing data collected with high frequency and/or high resolution in time and space. Many methods have been developed to study these complex data objects; for overviews of some recent developments in this fast growing field we refer the reader to the review articles Cuevas (2014) and Wang et al. (2016) and books among others Ferraty and Vieu (2006) and Ramsay and Silverman (2007).

Despite the success of functional data analysis, only recently quantification of uncertainty with simultaneous confidence bands has received increasing attention. The existing methods for construction of simultaneous confidence bands (SCBs) split into three groups. The first group is based on functional central limit theorems (fCLTs) in the Banach space of continuous functions endowed with the maximum metric and evaluation of the maximum of the limiting Gaussian field often using Monte-Carlo simulations with an estimate of the limiting covariance structure, cf. Bunea et al. (2011), Degras (2011, 2017), Cao et al. (2012) and Cao et al. (2014). The second group is based on the bootstrap, among others (Cuevas et al., 2006; Chang et al., 2017; Wang et al., 2019) and Belloni et al. (2018). Thirdly, recently the use of a generalized Kac Rice formula for fast construction of SCBs for one dimensional functional data has been proposed in Liebl and Reimherr (2019), which is similar to our proposal, but limited to one dimensional domains.

Except for Liebl and Reimherr (2019) the mentioned methods are computationally expensive, since they either simulate from an estimated limiting field or require to draw many bootstrap samples. This hinders their use for domains of dimension greater than one. Moreover, they often perform poorly on small samples.

In order to construct precise and efficiently computable SCBs for functional parameters over arbitrarily dimensional domains, we propose to use random field theory (RFT). RFT was studied extensively in Adler (1981) and Adler and Taylor (2009), and has been successfully used in the neuroimaging community to control the FWER of statistical 3D images, among others (Worsley et al., 1996, 2004). More precisely we use the so called Gaussian kinematic formula (GKF) for pointwise t-distributed random fields (Taylor, 2006; Taylor and Worsley, 2007).

In a nutshell GKFs express the expected Euler characteristic (EEC) of the excursion set of a Gaussian related random field F(Z₁, … , Z_N), $F\in {\mathcal{C}}^2\left({ℝ}^N,ℝ\right)$ in terms of a finite linear combination of D known functions, called Euler characteristic (EC) densities. Here Z₁, … , Z_N ~ Z are i.i.d. zero-mean, unit-variance Gaussian fields with twice differentiable sample paths over a nice compact subset of ${ℝ}^D$. The linear coefficients in this formula are called Lipshitz–Killing curvatures (LKCs) and depend solely on the domain and the covariance structure of the derivative of Z. Remarkably, the only difference between GKFs for different Gaussian related fields is that the EC densities change, see Adler and Taylor (2009, p.315, (12.4.2)). Takemura and Kuriki (2002) have shown that the GKF for Gaussian fields is closely related to the Volume of Tubes formula dating all the way back to Working and Hotelling (1929). The latter has been applied for SCBs in nonlinear regression analysis, e.g., Johansen and Johnstone (1990), Krivobokova et al. (2010) and Lu and Kuriki (2017). In this sense the GKFs of Taylor (2006) can be interpreted as a generalization of the volume of tube formula for repeated observations of functional data.

Our main contributions are the following. In Theorem 2 we show based on the main result in Taylor et al. (2005) that, asymptotically, the error in the covering rate of SCBs for a function-valued population parameter based on the tGKF can be bounded and is small, if the targeted covering probability of the SCB is sufficiently high. This requires neither Gaussianity nor stationarity of the observed fields. It only requires that the estimator of the targeted function-valued parameter fulfills an fCLT in the Banach space of continuous functions with a sufficiently regular Gaussian limit field. Moreover, it requires consistent estimators for the LKCs. The latter have been studied in Taylor and Worsley (2007) and Telschow et al. (2020). We illustrate the general approach for the special case of SCBs of the population mean curve and the difference of population means for functional signal-plus-noise models, where we allow the error fields to be non-Gaussian. Especially we derive for such models defined over sufficiently regular domains $S\subset {ℝ}^D$, D = 1, 2, consistent estimators for the LKCs and derive CLTs for them. In order to deal with observation noise we discuss SCBs for scale spaces. In Theorem 8 we give sufficient conditions to have weak convergence of a scale space field to a Gaussian limit extending the results from Chaudhuri and Marron (2000) from regression analysis to repeated observations of functional data. Additionally, we prove that the LKCs of this limit field can be consistently estimated and therefore Theorem 2 can be used to bound the error in the covering rate for SCBs of the population mean of a scale space field.

Scale spaces are not the only way to deal with the observation noise and discrete sampling. For example local polynomial estimators can be used to estimate the population mean (Zhang et al., 2007; Degras, 2011; Zhang et al., 2016). Our proposed construction of SCBs is applicable in these cases provided that the LKCs can be consistently estimated and a bias correction is introduced. Note that in the ultra dense sampling case (Zhang et al., 2016) our developed theory for the SCBs of signal-plus-noise models can be directly used, since the bias introduced by the smoother is negligible. For less dense sampling schemes a bias correction and consistent estimates of the LKCs need to be derived, yet Theorem 2 can then still be applied.

The theory is accompanied by a simulation study using the Rpackage SIRF (Spatial Inference for Random Fields), which can be found on https://github.com/ftelschow/SIRF, and demonstrate the use of SCBs on two different data applications. In the simulation study we compare the performance of the tGKF approach to SCBs for different error fields mainly with bootstrap approaches and conclude that the tGKF approach does not only often give better coverings for small sample sizes, but outperforms bootstrap approaches computationally. Moreover, the average width of the tGKF confidence bands is lower for large sample sizes. As a first application we demonstrate the use of SCBs for scale spaces on a diffusion tensor imaging (DTI) experiment to detect differences in population means between healthy subjects and patients. The second application constructs simultaneous confidence bands for the expected increase in mean summer and winter temperatures over North America obtained from NARCAP simulations (Mearns et al., 2013).

Organization of the article.

Section 2.1 introduces necessary notations and definitions. In Section 2.2 and Section 2.3 we describe the general idea of construction of SCBs for functional parameters using the tGKF. In Section 2.4 we prove a theorem establishing that the SCBs from the tGKF give accurate covering rates. Applications to the functional signal-plus-noise model are given in Section 3. Especially, we provide consistent estimators of the LKCs and prove consistency and a CLT for them in Section 3.2. SCBs for scale space models are discussed in Section 3. In Section 4 we compare the tGKF approach in different simulations to competing state of the art methods to construct SCBs for functional signal-plus-noise models. Section 5 applies these ideas to real data.

2. Simultaneous confidence bands

2.1. Preliminary definitions and notations

Definition 1.

A random field G is a random function from a parameter space S to $ℝ$. The function $G_{\omega }:S\to ℝ$, where ω ∈ Ω is an element of the underlying probability space, is called a sample path. Moreover, G is called Gaussian random field, if for all (s₁, … , s_M) ∈ S^M, $M\in \mathbb{N}$, the random vector (G(s₁), … , G(s_M)) has a multivariate Gaussian distribution.

A detailed treatment of random fields can be found in Adler and Taylor (2009). Another important quantity, which we need is the Euler characteristic (EC) of a set A ⊆ S denoted by χ(A). The EC of a topological space is an invariant that can be rigorously defined using homology groups of a topological space (Bredon, 2013) or it can be defined using triangulations (Flegg, 2001). Intuitively, the EC of $A\subset {ℝ}^D$ is the number of connected components for D = 1, the number of connected components minus the number of holes for D = 2 and the number of connected components minus the number of holes plus the number of hollows (for example the hole in the 2-sphere) for D = 3.

Classical results on functional central limit theorems (fCLTs), which we will use later, make use of semi-metrics (Jain and Marcus, 1975). Hence we recall the definition:

Definition 2.

A semi-metric on a topological space S is a map $\delta :S\times S\to ℝ$ such that (1.) δ(s, s′) ≥ 0, (2.) δ(s, s′) = 0 if and only if s = s′, (3.) δ(s, s′) = δ(s′, s). This implies that each metric is a semi-metric. A semi-metric is called continuous with respect to the topology of S, if it is a continuous function in the product topology of S × S.

To improve readability we abbreviate higher order partial derivatives using the following notation

$$f^I=\frac{{\partial }^{|I{|}_f}}{\partial s_{d_1}\dots \partial s_{d_K}},$$

where K = |I| denotes the number of elements in the multi-index I = (d₁, … , d_K). We denote with $\mathcal{C}(S)$ the space of continuous functions from S to $ℝ$ and with “⇒” weak convergence in $\mathcal{C}(S)$ endowed with the maximum norm ‖f‖_∞ = max_s∈S|f(s)|. Moreover, a letter in Fraktur font, for example $\mathfrak{r}$, will always denote the covariance function of a random field.

2.2. SCBs for functional parameters

We describe a general well-known scheme for construction of simultaneous confidence bands (SCBs) for a functional parameter s ↦ θ(s), s ∈ S, where $S\subset {ℝ}^D$ is compact. Hereafter, we assume that all functions of s ∈ S belong to $\mathcal{C}(S)$.

Let $s\mapsto {\widehat{\theta }}_N(s)$ and $s\mapsto {\widehat{\varsigma }}_N(s)$ be estimators of functional parameters θ, ς respectively, fulfilling

$${\tau }_N\frac{{\widehat{\theta }}_N-\theta }{\varsigma }\stackrel{N\to \infty }{\Rightarrow }G,$$ (E1)

$$\mathbb{P}\left(\underset{N\to \infty }{\text{lim}}{\Vert {\widehat{\varsigma }}_N-\varsigma \Vert }_{\infty }=0\right)=1.$$ (E2)

Here G is a zero-mean Gaussian field with covariance function $\mathfrak{r}$ satisfying $\mathfrak{r}(s,s)=1$ for all s ∈ S, τ_N → ∞ is a sequence of positive numbers. Under (E1) and (E2) Slutzky’s Lemma implies

$${\tau }_N\frac{{\widehat{\theta }}_N-\theta }{{\widehat{\varsigma }}_N}\stackrel{N\to \infty }{\Rightarrow }G.$$ (1)

Thus, it is easy to verify that the collection of intervals

$$SCB\left(s,q_{\alpha ,N}\right)=\left[{\widehat{\theta }}_N(s)-q_{\alpha ,N}\frac{{\widehat{\varsigma }}_N(s)}{{\tau }_N},{\widehat{\theta }}_N(s)+q_{\alpha ,N}\frac{{\widehat{\varsigma }}_N(s)}{{\tau }_N}\right]$$ (2)

form (1 − α)-simultaneous confidence bands of θ, i.e.

$$\mathbb{P}\left(\forall s\in S:\theta (s)\in SCB\left(s,q_{\alpha ,N}\right)\right)=1-\alpha ,$$

provided that

$$\mathbb{P}\left(\underset{s\in S}{\text{max}}{\tau }_N\left|\frac{{\widehat{\theta }}_N(s)-\theta (s)}{{\widehat{\varsigma }}_N(s)}\right|q_{\alpha ,N}\right)=\alpha .$$ (3)

The quantiles q_α,N are in general unknown and need to be estimated.

To the best of our knowledge there are two approaches for this. Limit approximations try to estimate q_α,N by estimation of the asymptotic covariance function and simulations of sample paths from the corresponding Gaussian field (Degras, 2011, 2017). Better performances for small samples can be achieved by bootstrap approaches such as the parametric bootstrap proposed in Degras (2011) or the multiplier bootstrap (Chang et al., 2017). Compare also Appendix A.

2.3. Estimation of the quantile using the tGKF

In this section we propose to use the Gaussian kinematic formula for t-fields (tGKF) as proven in Taylor (2006) to approximate the quantiles q_α,N.

2.3.1. The Gaussian Kinematic Formula for t-fields

Let $G_1,\dots ,G_N\stackrel{i.i.d.}{~}G$ be zero-mean, unit-variance Gaussian fields. The field T satisfying

$$T(s)=\frac{\sqrt{N}{G}_N(s)}{\sqrt{\frac{1}{N-1}{\sum }_{n=1}^{N-1}{G}_n{(s)}^2}},$$

is called a t_N−1-field. We pose the following assumptions on G:

• (G1)G has almost surely ${\mathcal{C}}^2$-sample paths.
• (G2)The joint distribution of the derivative fields (G^(d)(s), G^(d,l)(s)) is nondegenerate for all s ∈ S and d, l = 1, … , D.
• (G3)
  There is an ϵ > 0 such that

  $$\mathbb{E}\left[{\left(G^{(d,l)}(s)-G^{(d,l)}\left(s^{\prime }\right)\right)}^2\right]\le K{\left|\text{log}\Vert s-s^{\prime }\Vert \right|}^{-(1+\gamma )}$$

  for all d, l = 1, … , D and for all |s − s′| < ϵ. Here K > 0 and γ > 0 are finite constants.
• (G4)$\mathbb{E}\left[G(s)G\left(s^{\prime }\right)\right]=1$ if and only if s = s′.

Remark 1.

Assumptions (G1)-(G3) imply (cf., Adler and Taylor (2009, Thm 11.3.3)) that the paths of G are almost surely Morse functions. This is necessary since the proof of the GKF is based on the classical Morse theorem for Whitney-stratified manifolds (Goresky and MacPherson, 1988). Thus, (G2) is necessary to ensure that almost surely all critical points are nondegenerate. Assumption (G3) is satisfied for any field G having almost surely ${\mathcal{C}}^3$-sample paths and all third derivatives have a finite second $\mathcal{C}\left(S\right)$-moment, see Definition 3. In particular, this holds true for any Gaussian field with ${\mathcal{C}}^3$-sample paths. For completeness the argument is carried out in more detail in Appendix B.1. Condition (G4) excludes, for example, periodic fields.

Under these assumptions the tGKF is an exact, analytical formula of the expectation of the Euler characteristic χ of the excursion sets A(T, u) = {s ∈ S | T(s) > u} of T. This formula as proven in Taylor (2006) or Adler and Taylor (2009) is

$$\mathbb{E}[\chi (A(T,u))]=\sum _{d=0}^D{L}_d(S,G){\rho }_d^{t_{N-1}}(u),D\in \mathbb{N},$$ (4)

where ${\rho }_d^{t_{N-1}}$, d = 0, … , D, is the d-th Euler characteristic density of a t_N−1-field (Taylor and Worsley, 2007), usually known, and L_d denotes the d-th Lipshitz–Killing curvature, which only depends on G and the parameter space S. Note that L₀(S, G) = χ(S) and hence is usually known.

Eq. (4) is useful, since by the expected Euler characteristic heuristic (EECH) (Taylor et al., 2005), we expect

$$\frac{1}{2}\mathbb{P}\left(\underset{s\in S}{\text{max}}|T(s)|>u\right)\le \mathbb{P}\left(\underset{s\in S}{\text{max}}T(s)>u\right)\approx \mathbb{E}[\chi (A(T,u))],$$ (5)

to be a good approximation for large thresholds u. In the case that $S\subset ℝ$ this approximation is always from above. This is due to the fact that the Euler characteristic of one-dimensional sets is always non-negative and hence using the Markov-inequality we obtain

$$\frac{1}{2}\mathbb{P}\left(\underset{s\in S}{\text{max}}|T(s)|>u\right)\le \mathbb{P}(\chi (A(T,u))\ge 1)\le \mathbb{E}[\chi (A(T,u))].$$

The same argument is heuristically valid for high enough thresholds in any dimension, since the excursion set will with high probability consist mostly of simply-connected sets. This heuristic has been rigorously proven in Taylor et al. (2005) for T being a Gaussian field.

2.3.2. The tGKF-estimator of q_α,N

Let ${\widehat{L}}_d(S,G)$ be consistent estimators of the LKCs L_d(S, G) for d = 1, … , D, then combining the tGKF (4) and the EEC heuristic Eq. (5) yields the natural plug-in estimator ${\widehat{q}}_{\alpha ,N}$ of the quantile q_α,N defined in Eq. (3) as the largest solution u of

$${\widehat{EEC}}_{t_{N-1}}(u)=L_0(S){\rho }_0^{t_{N-1}}(u)+\sum _{d=1}^D{\widehat{L}}_d(S,G){\rho }_d^{t_{N-1}}(u)=\frac{\alpha }{2}.$$ (6)

The following result is important for the proof of the accuracy of the SCBs derived using the tGKF estimator of q_α,N.

Theorem 1.

Assume that ${\widehat{L}}_d^N(S,G)$ is a consistent estimator of L_d(S, G). Then ${\widehat{q}}_{\alpha ,N}$ given by (6) converges almost surely for N tending to infinity to the largest solution ${\widehat{q}}_{\alpha }$ of

$$EE{C}_G(u)=L_0(S){\rho }_0(u)+\sum _{d=1}^D{L}_d(S,G){\rho }_d(u)=\frac{\alpha }{2},$$ (7)

where ρ_d are the Euler characteristic densities of a Gaussian field, which can be found in Adler and Taylor (2009, p.315, (12.4.2)).

Remark 2.

Estimation of LKCs is not widely studied yet. For stationary random fields this has been done in Kiebel et al. (1999). For non-stationary random fields over domains in arbitrary dimensions, consistent estimators based on residuals have been introduced in Taylor and Worsley (2007) and Telschow et al. (2020). The former uses a warping to stationary transform, while the latter uses projections onto Hermite polynomials. For signal-plus-noise models and D ≤ 2 we take a more direct approach based on normalized residuals in Section 3.2.

2.4. Asymptotic covering rates

This section discusses the accuracy of the SCBs obtained using the tGKF. Since the expected Euler characteristic of the excursion sets is only an approximation of the excursion probabilities, there is no hope to prove that the covering of these confidence bands is exact. Especially, if α is large the approximation fails badly and usually will lead to confidence bands that are too wide. However, for values of α < 0.1 typically used for confidence bands, the EEC approximation works astonishingly well. Theoretically, this has been made precise for Gaussian fields in Theorem 4.3 of Taylor et al. (2005), which is the main ingredient in the proof of the next result. Additionally, it relies on the fCLT (1) and the consistency of ${\widehat{q}}_{\alpha ,N}$ for ${\widehat{q}}_{\alpha }$ proved in Theorem 1.

Theorem 2.

Assume (E1–E2) and assume that the limiting Gaussian field G satisfies (G1–G3). Moreover, let ${\widehat{L}}_d^N$ be a sequence of consistent estimators of L_d for d = 1, … , D. Then there exists an α′ ∈ (0, 1) such that for all α ≤ α′ we have that the SCBs defined in Eq. (2) fulfill

$$\underset{N\to \infty }{\text{lim}}\left|1-\alpha -\mathbb{P}\left(\forall s\in S:\eta (s)\in SCB\left(s,{\widehat{q}}_{\alpha ,N}\right)\right)\right|\le e^{-\left(\frac{1}{2}+\frac{1}{2{\sigma }_c^2}\right){\tilde{q}}_{\alpha }^2}<e^{-\frac{{\tilde{q}}_{\alpha }^2}{2}},$$

where ${\sigma }_c^2$ is the critical variance of an associated field of G, ${\widehat{q}}_{\alpha ,N}$ is the quantile estimated using Eq. (6) and ${\tilde{q}}_{\alpha }$ is defined in Theorem 1.

Typically, in our simulations we have that, for α = 0.05, the quantile ${\tilde{q}}_{\alpha }$ is about 3 leading to an upper bound of ≈ 0.011, if we use the weaker bound without the critical variance.

3. Application to the functional signal-plus-noise model

As it is an important example, we discuss in depth SCBs for the population mean in the functional signal-plus-noise model given by

$$Y(s)=\mu (s)+\sigma (s)Z(s),\text{ for }s\in S.$$ (8)

Here μ, σ are continuously differentiable functions on a compact domain $S\subset {ℝ}^D$ and Z is a stochastic process with zero mean and covariance function $\text{cov}\left[Z(s),Z\left(s^{\prime }\right)\right]=\mathfrak{c}\left(s,s^{\prime }\right)$ for s, s′ ∈ S satisfying $\mathfrak{c}\left(s,s^{\prime }\right)=1$ if and only if s = s′. Additionally, we will need regularity conditions based on Definition 3 to guarantee that an i.i.d. sample of (8) fulfills a functional central limit theorem.

Definition 3.

1. We say a random field Z with domain S is $\left({\mathcal{L}}^p,\delta \right)$-Lipshitz, if there exists a (semi)-metric δ on S, continuous in the standard topology of ${ℝ}^D$, and a random variable A satisfying $\mathbb{E}\left[|A{|}^p\right]<\infty$ such that

   $$\left|Z(s)-Z\left(s^{\prime }\right)\right|\le A\delta \left(s,s^{\prime }\right)\text{ for all }s,s^{\prime }\in S$$ (9)

   and ${\int }_0^1{H}^{1/2}(S,\delta ,ϵ)dϵ<\infty$, where H(S, δ, ϵ) denotes the metric entropy function of the (semi)-metric space (S, δ), e.g., Adler and Taylor (2009, Def. 1.3.1.).

2. We say a random field Z has finite pth $\mathcal{C}(S)$-moment, if $\mathbb{E}\left[\parallel Z{\parallel }_{\infty }^p\right]<\infty$.

Proposition 1.

Any $\left({\mathcal{L}}^p,\delta \right)$-Lipshitz field over a compact set S has finite pth $\mathcal{C}(S)$-moment if $\mathbb{E}\left[|Z(s){|}^p\right]<\infty$ for some s ∈ S.

Remark 3.

1. Any $\left({\mathcal{L}}^p,\delta \right)$-Lipshitz field Z has necessarily almost surely continuous sample paths. Moreover, this property is the main ingredient in the version of a CLT in $\mathcal{C}(S)$ proven in Jain and Marcus (1975) or Ledoux and Talagrand (2013, Section 10.1).

2. Since any continuous Gaussian field satisfies the finite pth $\mathcal{C}(S)$-moment condition, cf. Landau and Shepp (1970), it is possible to prove a reverse of Proposition 1 for continuously differentiable Gaussian fields. Moreover, finite pth $\mathcal{C}(S)$-moment conditions are often assumed, when uniform consistency of estimates of the covariance function are required, e.g., Hall et al. (2006) and Li et al. (2010).

3.1. Asymptotic SCBs for the one and two sample case

As an application of Theorem 2 we derive SCBs for the population mean and the difference of population means in one and two sample scenarios of the signal-plus-noise model. We base our assumptions on the $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz property.

Theorem 3 (Asymptotic SCBs for the Signal-plus-noise Model).

Let $Y_1,\dots ,Y_N\stackrel{i.i.d.}{~}Y$ be a sample of model (8) and assume Z is an $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz field. Define Y(s) = (Y₁(s), … , Y_N(s)).

1. Then the estimators

   $${\widehat{\mu }}_N(s)=\overline{Y}(s)=\frac{1}{N}\sum _{n=1}^{N}Y(s),{\widehat{\sigma }}_N^2(s)={\widehat{\text{var}}}_N[Y(s)]=\frac{1}{N-1}\sum _{n=1}^N{\left(Y_n(s)-\overline{Y}(s)\right)}^2,$$

   fulfill the conditions (E1–2) with ${\tau }_N=\sqrt{N}$, θ = μ, ς = σ and $\mathfrak{r}=\mathfrak{c}$.
2. Let ${\widehat{L}}_1,\dots ,{\widehat{L}}_D$ be consistent estimators of the LKCs of G. Additionally, assume that the $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz field Z has almost surely ${\mathcal{C}}^3$-sample paths, that all partial derivatives up to order 3 of Z are $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz and that G fulfills the non-degeneracy condition (G2). Then the accuracy result of Theorem 2 holds true for the SCBs

   $$SCB\left(s,{\widehat{q}}_{\alpha ,N}\right)={\widehat{\mu }}_N(s)\pm {\widehat{q}}_{\alpha ,N}\frac{{\widehat{\sigma }}_N(s)}{\sqrt{N}}$$

   with ${\widehat{q}}_{\alpha ,N}$ given in Theorem 1.

Remark 4.

1. Under the assumptions on Z and G in (ii), the warping estimator (Taylor and Worsley, 2007), the Hermite Projection estimator (Telschow et al., 2020) and the estimators discussed in Section 3.2 are all consistent estimators of the LKCs of G. Hence the first assumption in (ii) is not restrictive.

2. A simple condition on Z to ensure that G fulfills the non-degeneracy condition (G2) is that for all d, l ∈ {1, … , D} we have that cov [(Z^(l)(s), Z^(d,l)(s))] has full rank for all s ∈ S. A proof is provided in Lemma 13 in the Appendix.

Theorem 4 (Asymptotic SCBs for Difference of Means of Two Signal-plus-noise Models).

Let $Y_1,\dots ,Y_N\stackrel{i.i.d.}{~}Y$ and $X_1,\dots ,X_M\stackrel{i.i.d.}{~}X$ be independent samples, where

$$Y(s)={\mu }_Y(s)+{\sigma }_Y(s)Z_Y(s)\mathit{\text{and}}X(s)={\mu }_X(s)+{\sigma }_X(s)Z_X(s),$$

with Z_Y, Z_X both $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz fields and assume that c = lim_N,M→∞ N/M. Then

1. Condition (E1) is satisfied, i.e.

   $$\frac{\sqrt{N+M-2}\left(\overline{Y}-\overline{X}-{\mu }_Y+{\mu }_X\right)}{\sqrt{\left(1+c^{-1}\right){\widehat{\sigma }}_N{(Y)}^2+(1+c){\widehat{\sigma }}_N{(X)}^2}}\stackrel{N,M\to \infty }{\Rightarrow }G=\frac{\sqrt{1+c^{-1}}{\sigma }_Y{G}_Y-\sqrt{1+c}{\sigma }_X{G}_X}{\sqrt{\left(1+c^{-1}\right){\sigma }_Y^2+(1+c){\sigma }_X^2}},$$

   where G_Y, G_X are Gaussian fields with the same covariance structures as X and Y and the denominator converges uniformly almost surely, i.e. condition (E2) is satisfied.
2. If there are consistent estimators of the LKCs L_d of G and Z_X, Z_Y have ${\mathcal{C}}^3$-sample paths, fulfill the non-degeneracy condition (G2) and all their partial derivatives are $\left({\mathcal{L}}^p,\delta \right)$-Lipshitz fields with finite $\mathcal{C}(S)$-variances, then the accuracy result of Theorem 2 holds for the sets

   $$SCB\left(s,{\widehat{q}}_{\alpha ,N}\right)={\widehat{\mu }}_N(s)\pm {\widehat{q}}_{\alpha ,N}\frac{\sqrt{\left(1+c^{-1}\right){\sigma }_Y^2+(1+c){\sigma }_X^2}}{\sqrt{N+M}}$$

   with ${\widehat{q}}_{\alpha ,N}$ given in Theorem 1.

3.2. Estimation of LKCs

For D ≤ 2, we can obtain consistent estimators of the LKCs by directly implementing their definitions. These estimators are conceptually easier to understand than existing estimators (Taylor and Worsley, 2007; Telschow et al., 2020). Additionally, they allow for simple proofs of their consistency and fulfill a CLT.

For a zero-mean, unit-variance Gaussian field G, the LKCs L_d(S, G) are intrinsic volumes of S with respect to the pseudo-Riemannian metric Λ given in standard coordinates of ${ℝ}^D$ as

$${\Lambda }_{dl}(G,s)={\Lambda }_{dl}(s)=\text{cov}\left[G^{(d)}(s),G^{(l)}(s)\right],d,l=1,\dots ,D.$$ (10)

Using this notation the general expression of the LKCs (Adler and Taylor, 2009, Definition 10.7.2) for D = 1 yields

$$L_1(S,G)={\text{vol}}_1(S,\Lambda )={\int }_S\sqrt{\text{var}\left[\frac{dG}{ds}(s)\right]}ds.$$ (11)

In the case of $S\subset {ℝ}^2$ with piecewise ${\mathcal{C}}^2$-boundary ∂S parametrized by a piecewise ${\mathcal{C}}^2$-function $\gamma :[0,1]\to {ℝ}^2$ the LKCs are given by

$$\begin{gathered} L_1=\frac{1}{2}\text{length(}\partial S,\Lambda )=\frac{1}{2}\underset{0}{\overset{1}{\int }}\sqrt{\frac{d{\gamma }^T}{dt}(t)\Lambda (\gamma (t))\frac{d\gamma }{dt}(t)}\Vert \frac{d\gamma }{dt}(t)\Vert dt \\ {L}_2={\text{vol}}_2(S,\Lambda )={\int }_S\sqrt{\text{det}(\Lambda (S))}d{s}_{1}d{s}_2. \end{gathered}$$ (12)

An application of the chain rule shows that L₁ is independent of the parametrization γ of S.

These formulas allow to estimate the unknown LKCs from a sample Y₁, … , Y_N ~ Y of model (8). The estimators are built on the normalized residuals

$$R_n(s)=\left(Y_n(s)-\overline{Y}(s)\right)/{\widehat{\sigma }}_N(s),s\in S,n=1,\dots ,N.$$ (13)

To abbreviate the following formulas we define R(s) = (R₁(s), … , R_N(s)). In view of Eq. (11) a natural estimator of L₁ for D = 1 is given by

$${\widehat{L}}_1^N={\int }_0^1\sqrt{\widehat{\text{Var}}\left[\frac{d}{ds}(R(s))\right]}ds,$$ (14)

and Eqs. (12) suggest the estimators

$$\begin{gathered} {\widehat{L}}_1^N=\frac{1}{2}{\int }_0^1\sqrt{\frac{d{\gamma }^T}{dt}(t){\widehat{\Lambda }}_N(\gamma (t))\frac{d\gamma }{dt}(t)}dt \\ {\widehat{L}}_2^N={\int }_S\sqrt{\text{det}\left({\widehat{\Lambda }}_N(s)\right)}d{s}_{1}d{s}_2, \end{gathered}$$ (15)

for D = 2. Here ${\widehat{\Lambda }}_N(s)={\widehat{\text{var}}}_N[\nabla R(s)]$ is the empirical covariance matrix of the sample ∇R₁, … , ∇R_N consisting of the gradients of the normed residuals. In order to prove consistency of the LKC estimates, we establish that ${\widehat{\Lambda }}_N$ converges uniformly almost surely to Λ.

Theorem 5.

If Z and Z^(d) for d = 1, … , D are $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz fields, then

$$\mathbb{P}\left(\underset{N\to \infty }{\text{lim}}{\widehat{\Lambda }}_N=\Lambda \right)=1.$$

If Z and Z^(d) for d = 1, … , D are even $\left({\mathcal{L}}^4,\delta \right)$-Lipshitz, we obtain

$$\sqrt{N}\left(\iota \left({\widehat{\Lambda }}_N\right)-\iota (\Lambda )\right)\stackrel{N\to \infty }{\Rightarrow }G(0,\mathfrak{t})$$

with $\iota :\text{Sym}(2)\to {ℝ}^3$ mapping

$$\left(\begin{array}{cc}a& b\\ b& c\end{array}\right)\mapsto (a,b,c)$$

and the matrix valued covariance function $\mathfrak{t}:S\times S\to \text{Sym}(3)$ is given componentwise by

$${\mathfrak{t}}_{dl}\left(s,s^{\prime }\right)=cov\left[Z^{(d)}(s)Z^{(l)}(s),Z^{(d)}\left(s^{\prime }\right)Z^{(l)}\left(s^{\prime }\right)\right]$$ (16)

for all s, s′ ∈ S and d, l = 1, … , D.

This theorem is the backbone in the proof of consistency and the CLT for the estimators (14) and (15).

Theorem 6 (Consistency of LKCs).

Under the setting of Theorem 3(ii) it follows for d = 1, 2 that

$$\mathbb{P}\left(\underset{N\to \infty }{\text{lim}}{\widehat{L}}_d^N=L_d\right)=1.$$

Remark 5.

Our proposed sample estimator of Λ through residuals is only one viable possibility. In general consistent estimation of the LKCs can be achieved by any estimator of Λ, which converges uniformly almost surely to Λ. Especially, this means that it is not necessary to observe complete fields as our residual approach suggests.

Theorem 7 (CLT for LKCs).

Assume Z and Z^(d) for d = 1, 2 are $\left({\mathcal{L}}^4,\delta \right)$-Lipshitz fields. Then, if $S\subset ℝ$,

$$\sqrt{N}\left({\widehat{L}}_1^N-L_1\right)\to \frac{1}{2}{\int }_S\frac{G(S)}{\sqrt{\Lambda (S)}}ds,$$

and, if $S\subset {ℝ}^2$, we obtain

$$\sqrt{N}\left(\left({\widehat{L}}_1^N,{\widehat{L}}_2^N\right)-\left(L_1,L_2\right)\right)\to (\frac{1}{2}{\int }_0^1\frac{1}{\sqrt{{\gamma }^{\prime }{(s)}^T\Lambda (\gamma (s)){\gamma }^{\prime }(s)}}tr(\Lambda (\gamma (s))\iota (G(\gamma (s))))ds,{\int }_S\frac{1}{\sqrt{\text{det}(\Lambda (s))}}\text{tr}(\Lambda (s)\iota (\text{diag}(1,-1,1)G(s)))ds).$$

where G(s) is a Gaussian field with zero-mean and covariance function $\mathfrak{t}$ as in Theorem 5 and γ is a parametrization of the boundary ∂S.

Corollary 1.

Assume additionally to the Assumptions of Theorem 7 that Z is Gaussian with covariance function $\mathfrak{c}$ and $S\subset ℝ$. Then, we have the simplified representation

$$\sqrt{N}\left({\widehat{L}}_1^N-L_1\right)\stackrel{N\to \infty }{\Rightarrow }\mathcal{N}\left(0,{\tau }^2\right),$$

where

$${\tau }^2=\frac{1}{2}{\int }_S{\int }_S\frac{\dot{\mathfrak{c}}{\left(s,s^{\prime }\right)}^2}{\sqrt{\dot{\mathfrak{c}}\left(s,s^{\prime }\right)\dot{\mathfrak{c}}\left(s,s^{\prime }\right)}}dsd{s}^{\prime }\mathit{\text{with}}\dot{\mathfrak{c}}\left(s,s^{\prime }\right)=\frac{{\partial }^2\mathfrak{c}}{\partial s\partial s^{\prime }}\left(s,s^{\prime }\right)$$

Estimation of LKCs in the scenario of two independent samples can be achieved along the same lines as in the one sample case. Here the independence of the samples implies that the covariance matrix Λ of the partial derivatives of the limiting field in Theorem 4(i) splits into a sum of covariance matrices depending on G_X and G_Y, i.e.,

$$\Lambda (G)=\Lambda \left(\frac{\sqrt{1+c^{-1}}{\sigma }_Y{G}_Y}{\sqrt{\left(1+c^{-1}\right){\sigma }_Y^2+(1+c){\sigma }_X^2}}\right)+\Lambda \left(\frac{\sqrt{1+c}{\sigma }_X{G}_X}{\sqrt{\left(1+c^{-1}\right){\sigma }_Y^2+(1+c){\sigma }_X^2}}\right).$$

Under the assumptions of Theorem 4(ii) these summands can be separately consistently estimated using the respective normalized residuals

$$R_n^Y=\frac{\sqrt{1+M/N}\cdot \left(Y_n-\overline{Y}\right)}{\sqrt{(1+M/N){\widehat{\sigma }}_N(Y)+(1+N/M){\widehat{\sigma }}_N(X)}}$$

$$R_n^X=\frac{\sqrt{1+N/M}\cdot \left(X_n-\overline{X}\right)}{\sqrt{(1+M/N){\widehat{\sigma }}_N^2(Y)+(1+N/M){\widehat{\sigma }}_N^2(X)}}$$

and the sum of these estimators is a uniformly almost surely consistent estimator of Λ(G). Thus it yields a consistent estimator of the LKCs in the two sample scenario.

3.3. Discrete sampling and additive noise: A scale space approach

In applications data of a signal-plus-noise model is usually observed on a discrete grid with possible additive measurement noise yielding the model

$$Y\left(s_p\right)=\mu \left(s_p\right)+\sigma \left(s_p\right)Z\left(s_p\right)+\epsilon \left(s_p\right),\text{ for }p=1,\dots ,P,$$ (17)

where $S=\left(s_1,\dots ,s_p\right)\in S\subset {ℝ}^{D\times P}$ is a random (or deterministic) sampling of the domain S, ε is a random field on S with finite second $\mathcal{C}(S)$-moment representing the observation noise and covariance function $\mathfrak{e}$ and ε, Z and S are mutually independent.

A generic way to estimate μ and perform inference on it is via local polynomial smoothers. Degras (2011) discussed construction of SCBs for these estimators. Since he proved that local linear smoothers under certain conditions similar to ours satisfy a fCLT, it is easy to extend our previous results of the signal plus noise model to his setup. However, there is no satisfactory solution to the question of choosing a data-driven bandwidth for finite sample sizes. Therefore, we consider scale spaces and their SCBs for inference on the population mean μ instead. This concept was originally introduced for regression in Chaudhuri and Marron (1999, 2000). Our goal is to construct SCBs for the smoothed population mean simultaneously across different bandwidths. For simplicity we restrict ourselves to the Priestley–Rao smoothing estimator. Extensions to local polynomial or other appropriate linear smoothers are possible.

Definition 4 (Scale Space Field).

We define the Scale Space field with respect to a continuous kernel function $K:\tilde{S}\times \left[h_0,h_1\right]\to ℝ$ with $\tilde{S}\supset S$ and 0 < h₀ < h₁ < ∞ corresponding to Model (17) as

$$\tilde{Y}(s,h)=\frac{1}{P}\sum _{p=1}^{P}Y\left(s_p\right)K\left(s-s_p,h\right)$$

with mean

$$\tilde{\mu }(s,h)=\frac{1}{P}\sum _{p=1}^P\mu \left(s_p\right)K\left(s-s_p,h\right).$$

In order to apply the previously presented theory we have to obtain first a functional CLT. The version we present is similar to Theorem 3.2 of Chaudhuri and Marron (2000) with the difference that we consider the limit with respect to the number of observed curves and include the case of possibly having the (random) measurement points depend on the number of samples, too. The regression version in Chaudhuri and Marron (2000) treats the limit of observed measurement points going to infinity for one noisy observed function.

Theorem 8.

Let $Y_1,\dots ,Y_N\stackrel{i.i.d.}{~}Y$ be a sample from Model (17), where P is allowed to depend on N and assume that Z has finite second $\mathcal{C}(S)$-moment. Further assume max_s∈S σ(s) ≤ B < ∞ and

$$\mathfrak{r}\left((s,h),\left(s^{\prime },h^{\prime }\right)\right)=\underset{N\to \infty }{\text{lim}}\frac{1}{P^2}\sum _{p,p^{\prime }=1}^P\mathbb{E}\left[\left(\sigma \left(s_p\right)\sigma \left(s_{p^{\prime }}\right)\mathfrak{c}\left(s_p,s_{p^{\prime }}\right)+\mathfrak{e}\left(s_p,s_{p^{\prime }}\right)\right)K\left(s-s_p,h\right)K\left(s^{\prime }-s_{p^{\prime }},h^{\prime }\right)\right]$$ (18)

exists for all (s, h), $\left(s^{\prime },h^{\prime }\right)\in S\times \mathcal{H}$, where the expectation is w.r.t. the sampling distribution of S = (s₁, … , s_P). Finally, assume that the smoothing kernel (s, h) ↦ K(s, h) is α-Hölder continuous. Then in $\mathcal{C}(S\times \mathcal{H})$

$$\sqrt{N}\left(N^{-1}\sum _{n=1}^N{\tilde{Y}}_n(s,h)-\mathbb{E}[\tilde{\mu }(s,h)]\right)\stackrel{N\to \infty }{\Rightarrow }G(0,\mathfrak{r}).$$

Remark 6.

Suppose S ⊂ [0, 1] is non-random. If P independent of N and s_p = (p − 0.5)/P for p = 1, … , P for all n = 1, … , N and $\epsilon \left(s_1\right),\dots ,\epsilon \left(s_P\right)\stackrel{i.i.d.}{~}\mathcal{N}\left(0,{\eta }^2\right)$, then Assumption (18) is trivially satisfied. If instead P → ∞ as N → ∞ it is sufficient that the following integral exists and is finite for all (s, h), $\left(s^{\prime },h^{\prime }\right)\in S\times \mathcal{H}$

$$\mathfrak{r}\left((s,h),\left(s^{\prime },h^{\prime }\right)\right)={\int }_S{\int }_S\left(\sigma (\tau )\sigma \left({\tau }^{\prime }\right)\mathfrak{c}\left(\tau ,{\tau }^{\prime }\right)+\mathfrak{e}\left(\tau ,{\tau }^{\prime }\right)\right)K(s-\tau ,h)K\left(s^{\prime }-{\tau }^{\prime },h^{\prime }\right)d\tau d{\tau }^{\prime },$$

in order to have Assumption (18) satisfied. For example, this is the case if $\mathfrak{c}$ and $\mathfrak{e}$ are continuous.

In order to use Theorem 2 it remains to show that the LKCs can be consistently estimated and the assumptions of the GKF from Section 2.3 are satisfied.

Proposition 2.

Under the setting of Theorem 8 assume additionally that the kernel $K\in {\mathcal{C}}^3(S\times \mathcal{H})$. Define

$$\widehat{\tilde{\mu }}(s,h)=\frac{1}{N}\sum _{n=1}^N{\tilde{Y}}_n(s,h)and\widehat{\tilde{\sigma }}(s,h)=\sqrt{\frac{1}{N}\sum _{n=1}^N{\left({\tilde{Y}}_n(s,h)-\widehat{\tilde{\mu }}(s,h)\right)}^2}$$

and assume that $\mathfrak{r}$ has continuous partial derivatives up to order 3 and the covariance matrices of

$$\underset{N\to \infty }{\text{lim}}\frac{1}{P}\sum _{p=1}^P\left(\sigma \left(s_p\right)Z\left(s_p\right)+\epsilon \left(s_p\right)\right)\left(\frac{\partial K\left(s-s_p,h\right)}{\partial x},\frac{{\partial }^{2}K\left(s-s_p,h\right)}{\partial s\partial h}\right),x=sorh,$$

have rank 2. Then $\widehat{\tilde{\mu }}(s,h)$ and $\widehat{\tilde{\sigma }}(s,h)$ satisfy Assumptions (L), (E2) and (G3). Thus, all assumptions of Theorem 2 are satisfied.

Remark 7.

Assume the situation of Remark 6. Then the assumption that $\mathfrak{r}$ has continuous partial derivatives up to order 3 follows directly from the assumption $K\in {\mathcal{C}}^3(S\times \mathcal{H})$.

4. Simulations

All simulations are based on 5000 Monte Carlo simulations in order to estimate the covering rate of the SCBs. We compare SCBs constructed using the tGKF, the non-parametric bootstrap-t (Boots-t) and the multiplier-t with Gaussian (gMult-t) or Rademacher (rMult-t) multipliers. For the Gaussian simulations we include the fast and fair bands (ffscb) from Liebl and Reimherr (2019). Bootstrap methods are based on 5000 bootstrap replicates.

4.1. Coverage: Smooth Gaussian case

This first set of simulations deals with the most favorable case for the tGKF method. We simulate samples from the following smooth signal-plus-noise models (8)

$$\text{Model}\text{A}(1D)\text{ : }{Y}^A(s)=\text{sin}(8\pi s)\text{exp}(-3s)+\frac{{(0.6-s)}^2+1}{6}\cdot \frac{a^T{K}^A(s)}{{\Vert K}^A(s)\Vert },s\in [0,1]$$

$$\text{Model}\text{B}(1D):Y^B(s)=\text{sin}(8\pi s)\text{exp}(-3s)+\frac{{(0.6-s)}^2+1}{6}\cdot \frac{b^T{K}^B(s)}{{\Vert K}^B(s)\Vert },s\in [0,1]$$

$$\text{Model}\text{C} (2D):Y^C(s)=s_1{s}_2+\frac{s_1+1}{s_2^2+1}\cdot \frac{c^T{K}^C(s)}{{\Vert K}^C(s)\Vert },s=\left(s_1,s_2\right)\in {[0,1]}^2$$

with $a~\mathcal{N}\left(0,I_{7\times 7}\right)$, $b~\mathcal{N}\left(0,I_{21\times 21}\right)$ and $c~\mathcal{N}\left(0,I_{36\times 36}\right)$. The vector K^A(s) has entries $K_i^A(s)=\left(\begin{array}{l}6\hfill \\ j\hfill \end{array}\right)s^i{(1-s)}^{6-i}$, the (i, 6)-th Bernstein polynomial for i = 0, … , 6, K^B(s) has entries $K_i^B(s)=\text{exp}\left(-\frac{{\left(s-x_i\right)}^2}{2h_i^2}\right)$ with x_i = i/21, h_i = 0.04 for i < 10, h₁₁ = 0.2 and h_i = 0.08 for i > 10 and K^C(s) is the vector of all entries from the 6 × 6-matrix $K_{ij}(s)=\text{exp}\left(-\frac{{\Vert s-x_{ij}\Vert }^2}{2h^2}\right)$ with x_ij = (i, j)/6 with h = 0.06. Examples of sample paths of the signal-plus-noise models and the error fields, are shown in the top two rows of Fig. 1.

Fig. 1.

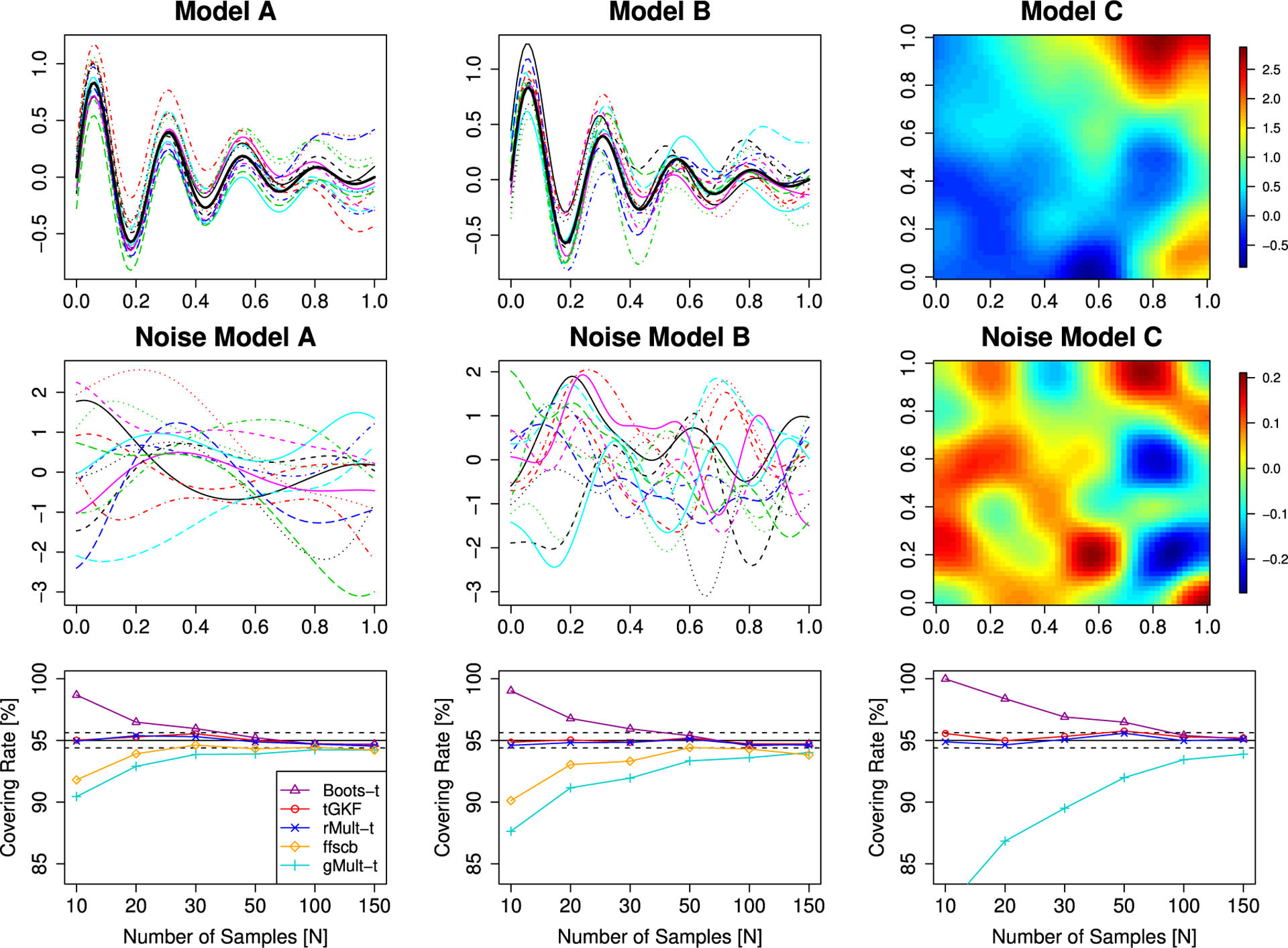
Simulation results for smooth Gaussian fields. Top row: samples from the signal-plus-noise models. Middle row: samples from the error fields. Bottom row: simulated covering rates. The solid black line is the targeted level of the SCBs and the dashed black line is twice the standard error for a Bernoulli random variable with p = 0.95.

We simulated samples from Model A and B on an equidistant grid of 200 points of [0, 1]. Model C was simulated on an equidistant grid with 50 points in each dimension.

According to the results of this simulation, shown in the bottom row of Fig. 1, the tGKF and the rMult-t method perform best since they are close to nominal level for all considered sample sizes; ffscb converges to the nominal level, too. Table 1 summarizes the computation times of the compared methods. It shows that the tGKF SCBs do not only provide the correct covering rates, it is also approximatively 20 times faster than its competitors. That ffscb has similar computation times as bootstrap methods is surprising. Personal communication with the authors suggests that their R-code needs to be optimized.

Table 1.

Comparison of the runtime for different methods to construct SCBs. The reported runtime is the average over 1000 calls to construct a SCB for a sample of size N = 50 from Model A in 1D and Model C in 2D.

	tGKF	ffscb	Boots-t	gMult-t	rMult-t
Model A (1D)	4.2 s	115.2 s	88.4 s	86.6 s	83.9 s
Model C (2D)	92.8 s	-	2039.6 s	1858.4 s	1864.9 s

4.2. Coverage: Smooth non-Gaussian case

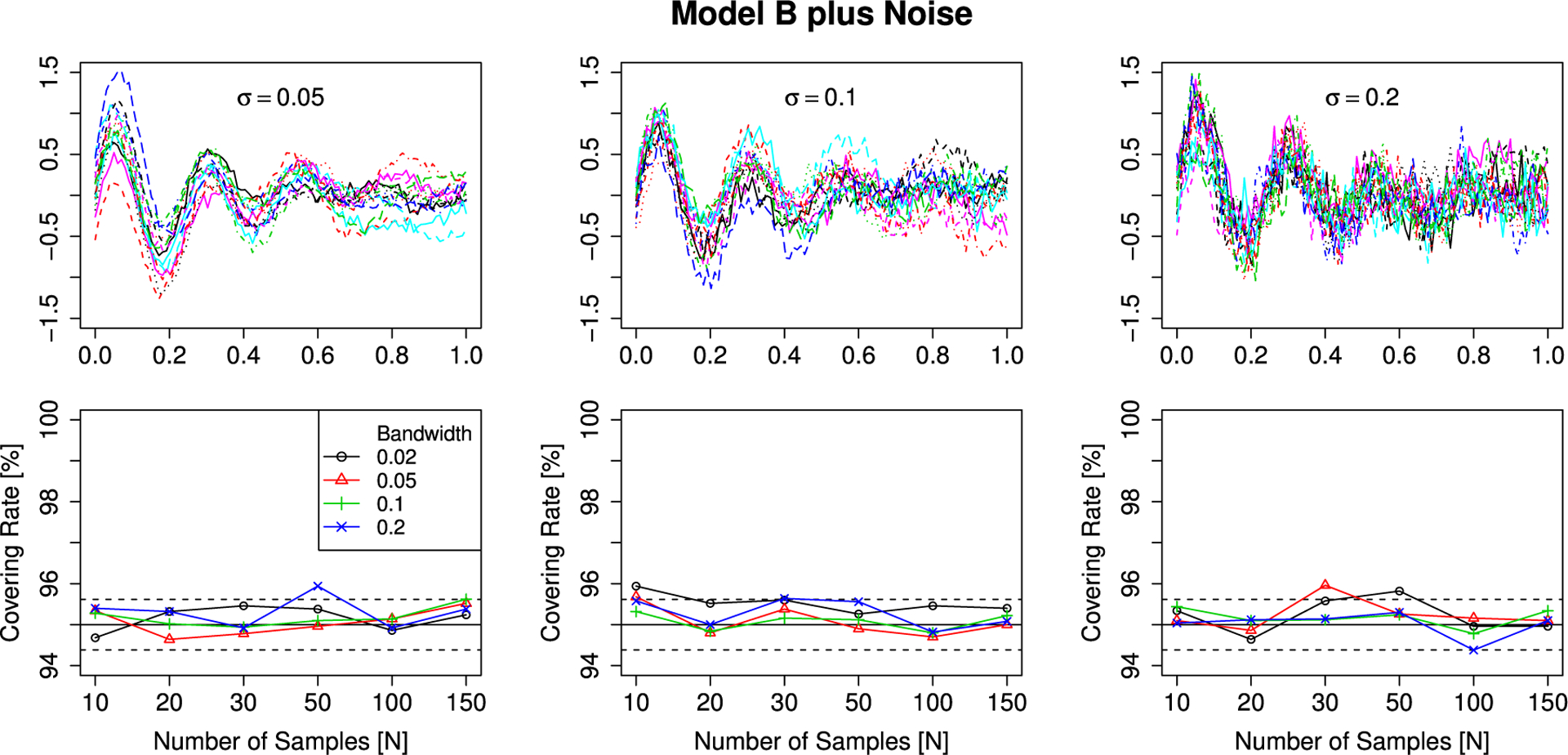
The tGKF method is based on a formula valid for Gaussian fields only. However, we have seen in Section 2.4 that under appropriate conditions the covering is expected to be good asymptotically even if this condition is not fulfilled. For the simulations here we use Model A with the only change that a has i.i.d. entries of a Student’s $t_3/\sqrt{3}$ random variable, which is non-Gaussian, but still symmetric. A second simulation study tackles asymmetry of the noise distribution and increasing similarity to Gaussianity. Here we use Model B where b has i.i.d. entries of $\left({\chi }_v^2-v\right)/\sqrt{2v}$ random variables for different parameters of ν. These random variables are non-symmetric, but for ν → ∞ they converge to a standard normal.

Fig. 2 shows that in the symmetric distribution case of Model A the tGKF has some over coverage for small sample sizes, but eventually it is in the targeted region for 95% coverage. For the particular process used in this simulation, ffscb seems to converge faster to nominal than tGKF SCBs. A possible explanation might be that the slight undercovering, which was present in the Gaussian case, is compensated due to the non-Gaussianity. A careful comparison of these cases will be part of future research. For this symmetric non-Gaussian distribution the rMult-t still works well. This is probably because it preserves all moments up to the fourth. The case of non-symmetric distributions produces usually undercovering for the tGKF. However, as predicted by Theorem 3 eventually for large N it gets close to the targeted covering. In this case, the bootstrap-t converges faster to the correct covering rate because it does not require symmetry (see Fig. 3).

Fig. 2.

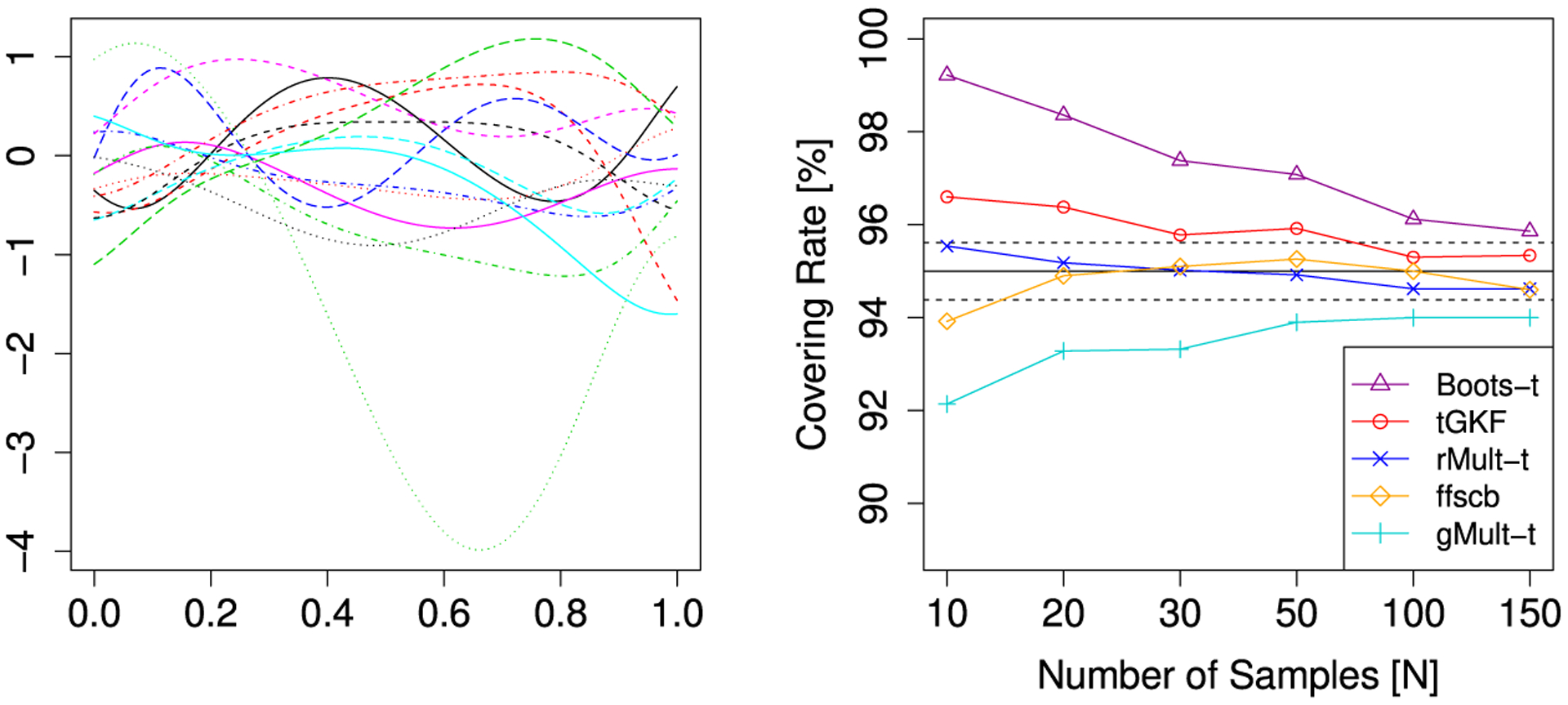
Simulation results for smooth non Gaussian fields (Model A). Left: samples from the error fields. Right: simulated covering rates. The solid black line is the targeted level of the SCBs and the dashed black line is twice the standard error for a Bernoulli random variable with p = 0.95.

Fig. 3.

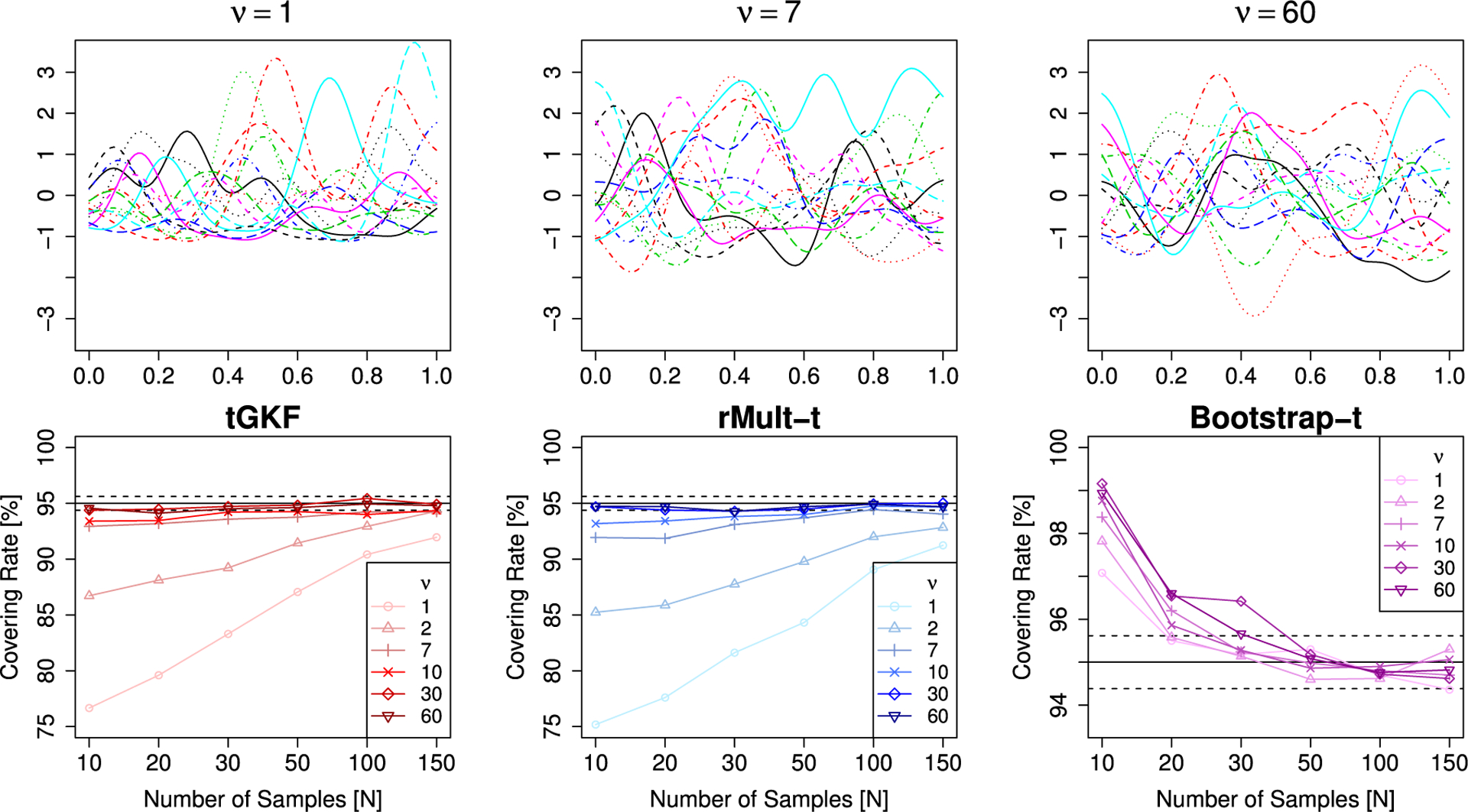
Simulation results for smooth non Gaussian fields (Model B). Left: samples from the error fields. Right: simulated covering rates. The solid black line is the targeted level of the SCBs and the dashed black line is twice the standard error for a Bernoulli random variable with p = 0.95.

4.3. Average width and variance of different SCBs

An important feature of confidence bands is its pointwise width averaged over the domain and the variance of this average width over repeated experiments. It is preferable to have the smallest possible width that still has the correct coverage. Moreover, the width of a SCB should remain stable, meaning that its variance should be small.

Here we focus on the estimation of the quantile ${\widehat{q}}_{N,\alpha }$, which for all methods except for ffscb is closely related to the width of the confidence band averaged over the domain. We decided to present this estimate, since it can be compared to its theoretical value and is easier to interpret. We simulate estimates of the quantile ${\widehat{q}}_{N,\alpha }$ obtained from different methods for the Gaussian Model B and the non-Gaussian Model B with ν = 7. The optimal quantile q_α is simulated using a Monte-Carlo simulation with 50,000 replications. Since the ffscb method from the R-package ffscb is not based on the quantile q_α we instead compute for this method

$${\widehat{q}}_{N,\alpha }^{\text{ffscb }}(s)=\sqrt{N}\frac{\text{ ffscb.up }(s)-\text{ ffscb.low }(s)}{2{\widehat{\sigma }}_N(s)}$$

and report its average value over S. This quantity is comparable to the quantile ${\widehat{q}}_{N,\alpha }$ from the other methods and closely related to the average width of the ffscb.

We compare ffscb from the R-package ffscb, Degras’ asymptotic method from the R-package SCBmeanfd, SCBs based on the GKF and the tGKF, the non-parametric bootstrap-t, multiplier-t, non parametric bootstrap and a simple multiplier bootstrap. Here the latter two methods use the variance of the original sample instead of its bootstrapped version, compare Appendix A.

Tables 2 and 3 show the simulation results. We can draw two main conclusions from these tables. First, the tGKF method has the smallest standard deviation among the compared methods in the quantile while still having good coverage (at least asymptotically in the non-Gaussian case). Second, the main competitor – the bootstrap-t – has a much higher standard error in the width, but its coverage converges faster in the highly non-Gaussian and asymmetric case. This shows that the tGKF method is the most stable among the compared methods.

Table 2.

Bias of average estimate of ${\widehat{q}}_{0.05,N}$ and twice its standard error for different methods of SCBs and the Gaussian Model B. The simulations are based on 1000 Monte Carlo simulations.

N	10	20	30	50	100	150
true	4.118	3.382	3.211	3.081	2.993	2.960
tGKF	−0.140 ± 0.033	−0.016 ± 0.011	−0.008 ± 0.007	+0.003 ± 0.004	+0.007 ± 0.002	+0.013 ± 0.001
GKF	−1.190 ± 0.016	−0.459 ± 0.008	−0.289 ± 0.005	−0.159 ± 0.003	−0.072 ± 0.002	−0.039 ± 0.001
Degras	−1.252 ± 0.021	−0.500 ± 0.011	−0.324 ± 0.007	−0.191 ± 0.005	−0.100 ± 0.003	−0.063 ± 0.003
Boots	−1.427 ± 0.023	−0.569 ± 0.012	−0.360 ± 0.010	−0.202 ± 0.007	−0.096 ± 0.005	−0.058 ± 0.004
Boots-t	+ 1.701 ± 0.604	+0.226 ± 0.050	+0.083 ± 0.019	+0.027 ± 0.009	+0.006 ± 0.005	+0.010 ± 0.004
gMult	−1.121 ± 0.159	−0.460 ± 0.031	−0.297 ± 0.016	−0.168 ± 0.009	−0.080 ± 0.005	−0.048 ± 0.004
gMult-t	−0.688 ± 0.046	−0.292 ± 0.017	−0.200 ± 0.011	−0.121 ± 0.007	−0.060 ± 0.005	−0.035 ± 0.004
rMult	−1.428 ± 0.179	−0.616 ± 0.032	−0.403 ± 0.015	−0.232 ± 0.009	−0.111 ± 0.005	−0.067 ± 0.004
rMult-t	−0.018 ± 0.122	−0.000 ± 0.023	−0.009 ± 0.013	−0.003 ± 0.008	+0.001 ± 0.005	+0.005 ± 0.004
ffscb	−0.530 ± 0.055	−0.181 ± 0.027	−0.111 ± 0.018	−0.057 ± 0.013	−0.022 ± 0.009	−0.048 ± 0.007

Table 3.

Bias of average estimate of ${\widehat{q}}_{0.05,N}$ and twice its standard error for different methods of SCBs and the non-Gaussian Model B with ν = 7. The simulations are based on 1000 Monte Carlo simulations.

N	10	20	30	50	100	150
true	4.532	3.628	3.373	3.190	3.048	3.004
tGKF	−0.558 ± 0.040	−0.262 ± 0.014	−0.170 ± 0.008	−0.106 ± 0.004	−0.048 ± 0.002	−0.031 ± 0.001
GKF	−1.606 ± 0.019	−0.705 ± 0.010	−0.451 ± 0.006	−0.268 ± 0.004	−0.127 ± 0.002	−0.083 ± 0.001
Degras	−1.666 ± 0.022	−0.749 ± 0.011	−0.488 ± 0.008	−0.301 ± 0.005	−0.156 ± 0.003	−0.108 ± 0.003
Boots	−1.835 ± 0.025	−0.809 ± 0.013	−0.516 ± 0.010	−0.307 ± 0.007	−0.147 ± 0.005	−0.099 ± 0.004
Boots-t	+ 1.618 ± 0.699	+0.218 ± 0.098	+0.080 ± 0.042	+0.023 ± 0.016	+0.006 ± 0.006	+0.001 ± 0.004
gMult	−1.471 ± 0.205	−0.703 ± 0.036	−0.457 ± 0.018	−0.278 ± 0.009	−0.135 ± 0.005	−0.091 ± 0.004
gMult-t	−1.104 ± 0.047	−0.544 ± 0.018	−0.371 ± 0.012	−0.240 ± 0.008	−0.128 ± 0.005	−0.090 ± 0.004
rMult	−1.763 ± 0.234	−0.870 ± 0.039	−0.574 ± 0.018	−0.352 ± 0.009	−0.175 ± 0.005	−0.116 ± 0.004
rMult-t	−0.422 ± 0.133	−0.278 ± 0.027	−0.194 ± 0.015	−0.130 ± 0.009	−0.064 ± 0.005	−0.044 ± 0.004
ffscb	−0.947 ± 0.053	−0.427 ± 0.026	−0.274 ± 0.018	−0.166 ± 0.013	−0.077 ± 0.008	−0.092 ± 0.006

4.4. The influence of observation noise

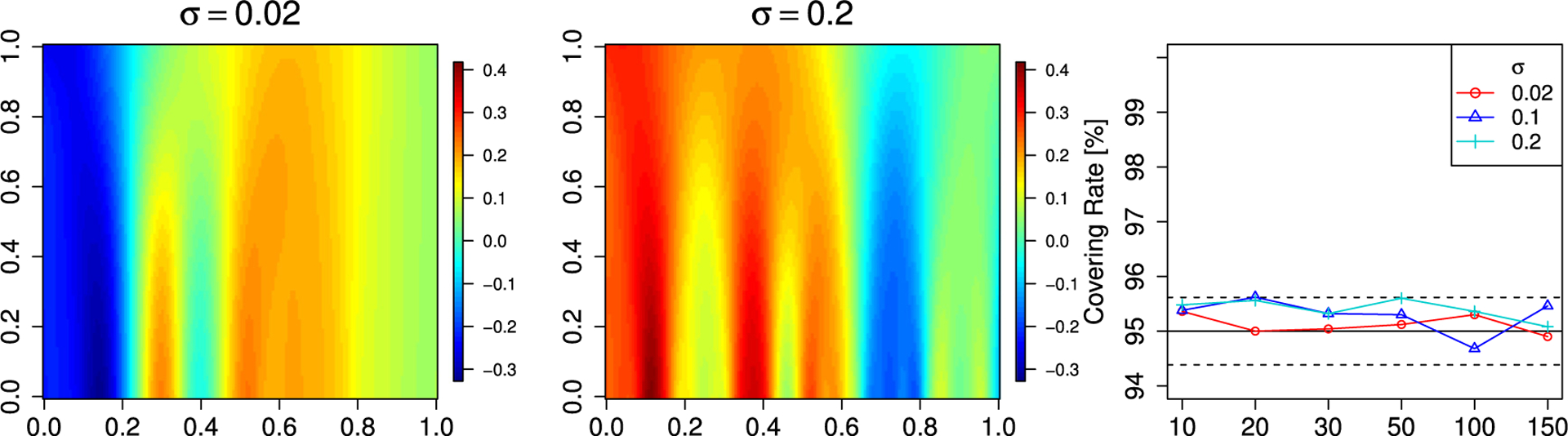
In order to study the influence of observation noise, we evaluate the dependence of the covering rate of the smoothed mean of a signal-plus-noise model with added i.i.d. Gaussian observation noise on the bandwidth used in a local linear smoother (Degras, 2011) and the standard deviation of the observation noise. For the simulations we generate samples from the Gaussian Model A and Model B on an equidistant grid of [0, 1] with 100 points and add $\mathcal{N}(0,\sigma )$-distributed independent observation noise with σ ∈ {0.02, 0.1, 0.2}. Afterwards we smooth the samples with a Gaussian kernel with bandwidths h ∈ {0.02, 0.03, 0.05, 0.1}. The smoothed curves are evaluated on an equidistant grid with 400 points. The results of these simulations are shown in Figs. 4 and 5. In most cases the nominal covering is achieved independent of N. Only for small smoothing bandwidths and large standard deviation of the observation errors a slight overcoverage is present. This might be a problem with the estimation of LKCs, since they depend on numerical derivatives of the sample paths, which are in these particular scenarios highly variable.

Fig. 4.

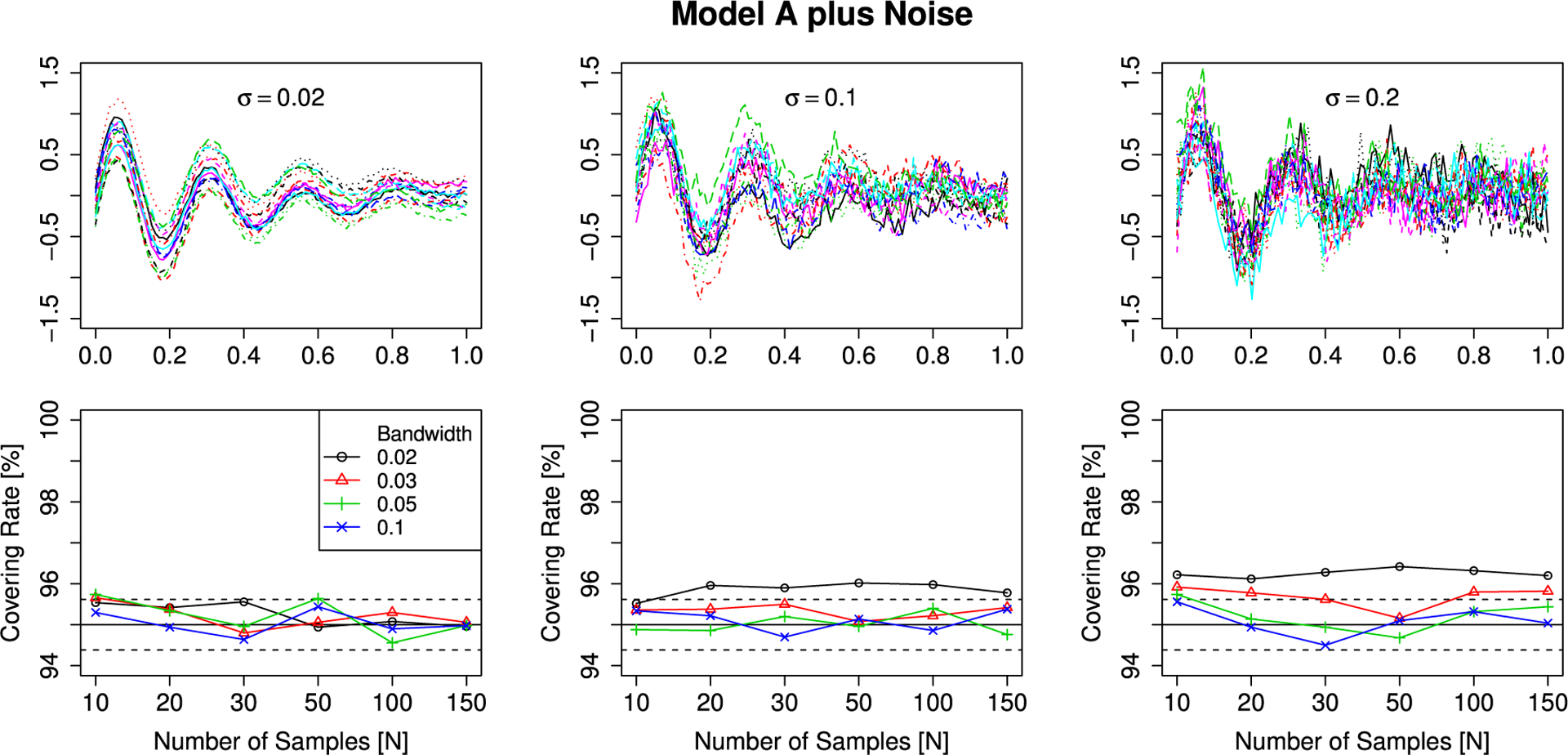
Simulation results for Gaussian fields (Model A) with observation noise. Top row: samples from the error fields. Bottom row: simulated covering rates. The solid black line is the targeted level of the SCBs and the dashed black line is twice the standard error for a Bernoulli random variable with p = 0.95.

Fig. 5.

Simulation results for Gaussian fields (Model B) with observation noise. Top row: samples from the error fields. Bottom row: simulated covering rates. The solid black line is the targeted level of the SCBs and the dashed black line is twice the standard error for a Bernoulli random variable with p = 0.95.

We also study the covering rate of the population mean of the scale space field of Model B. The generation of the samples is the same as for the previous simulations. The only difference is that instead of smoothing with one bandwidth we construct the scale space field. Here we use a equidistant grid of 100 points of the interval [0.02, 0.1]. The results can be found in Fig. 6 and show that the covering rate of the tGKF SCB is close to nominal.

Fig. 6.

Simulation results for the scale space field from the Gaussian fields of Model B with added observation noise. Left two panels: samples from the error fields. Right panel: simulated covering rates. The solid black line is the targeted level of the SCBs and the dashed black line is twice the standard error for a Bernoulli random variable with p = 0.95.

4.5. SCBs for the difference of population means of two independent samples

Since the single sample scenario was studied in great detail, we only present the case of one dimensional smooth Gaussian noise fields in the two sample scenario. Moreover, we only report the results for the tGKF approach. The previous observations regarding the other methods carry over to this scenario.

The simulations are designed as follows. We generate two samples of sizes N and M such that N/M = c ∈ {1, 2, 4}. We are interested in four different scenarios. The first scenario is the most favorable having the same correlation structure and the same variance function. Here we use for both samples the Gaussian Model A from Section 4.1. In all remaining scenarios one of the samples will always be this error field. In order to check the effect of the two samples having different correlation structures, we use Gaussian Model B as the second sample from Section 4.1. For dependence on the variance, while the correlation structure is the same, we change the variance function in the Gaussian Model A to σ²(s) = 0.04 for the second sample. As an example field where both the correlation and the variance are different we use Gaussian Model B with the modification that the error field has pointwise variance σ²(s) = 0.04. The results of these simulations are shown in Fig. 7 and show that, except for very unbalanced sample sizes between the two groups, the covering rate of the tGKF SCB is close to nominal.

Fig. 7.

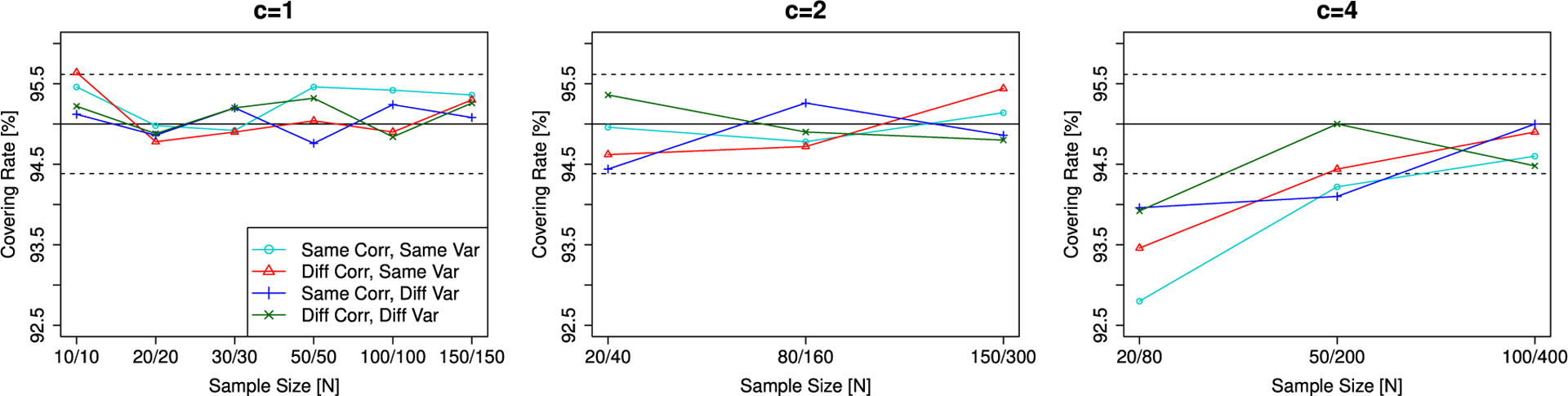
Simulation results for the SCBs of the difference between mean curves of two samples of smooth Gaussian fields for varying c = M/N. The solid black line is the targeted level of the SCBs and the dashed black line is twice the standard error for a Bernoulli random variable with p = 0.95.

5. Applications

5.1. DTI fibers

Our first data example (1D) concerns the impact of the eating disorder anorexia nervosa on white-matter tissue properties during adolescence in young females. The experimental setup and a different methodology to statistically analyze the data using pointwise testing and permutation tests can be found in the original article (Travis et al., 2015). The data set consists of a control group of 15 healthy subjects and 15 patients. For each subject 27 different neural fibers were extracted. The data for each fiber consists of fractional anisotropy values sampled on an equidistant grid of length 100.

In order to locate differences in the DTI fibers between the two groups, we computed for each fiber defined on the domain S = [0, 100] the two-sample 95%-SCBs for the difference of the population mean of the control group and the patients as explained in Section 3. Robustness of detected differences across scales is tested by computing the SCBs for the corresponding scale space fields, see Section 3. For the latter we used a Gaussian smoothing kernel and the considered bandwidth range $\mathcal{H}=[1.5,10]$ was sampled at 200 equidistant bandwidths.

The results for the three fibers for which we find significant differences are shown in Fig. 8. Our results are mostly consistent with the results from Travis et al. (2015) in the sense that both approaches find significant differences at similar locations in the right thalamic radiation and the left superior longitudinal fasciculus (SLF). Additionally, SCBs detect significant differences in the right cingulum hippocampus. Travis et al. (2015) claim further significant findings. However, these belong to criteria, which do not take simultaneous testing along the fibers into account. Therefore SCBs might not be able to detect them, since they correct for multiplicity along the fiber.

Fig. 8.

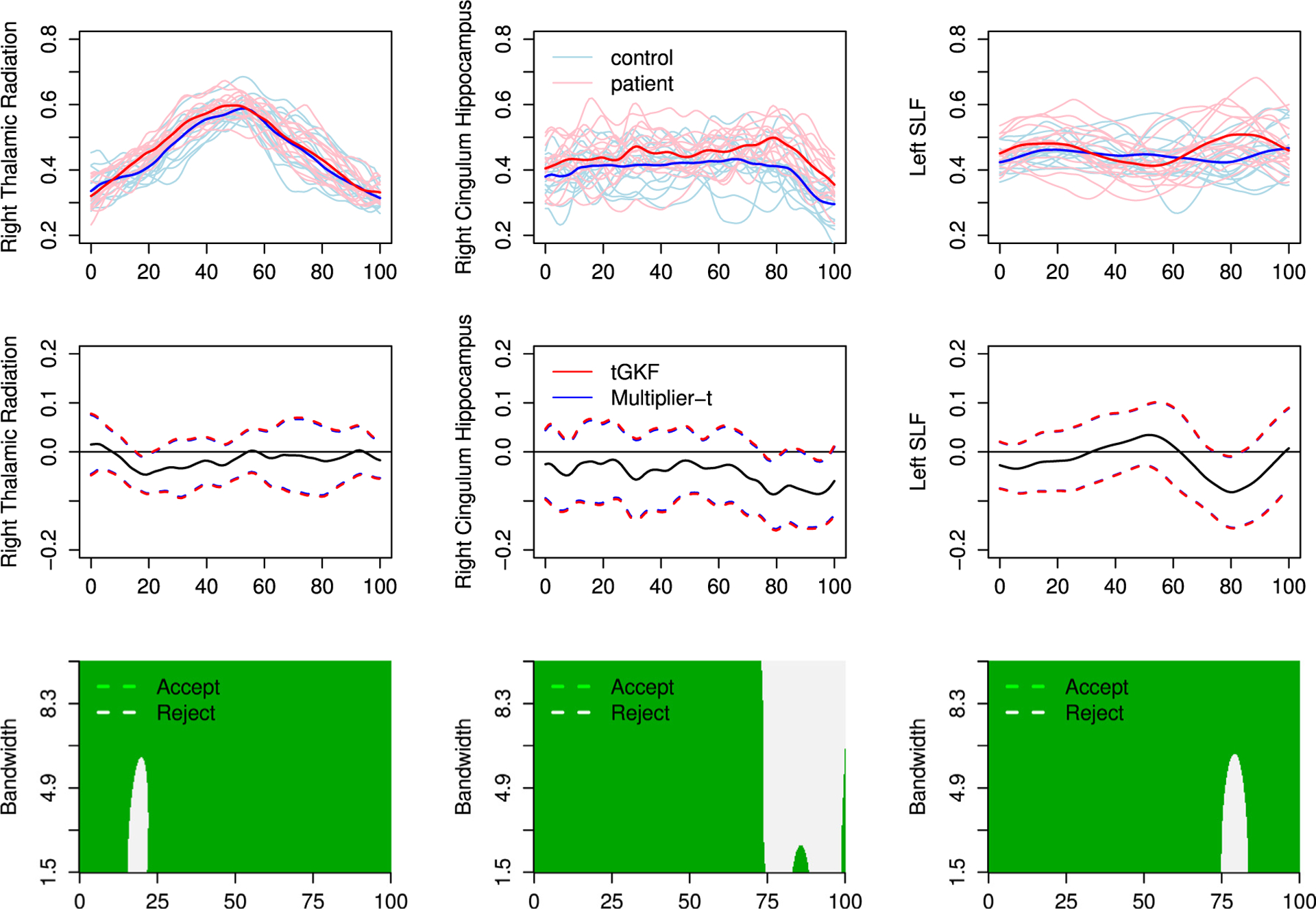
DTI fibers with significant differences in the mean function. Top row: data and sample means. Middle row: estimated difference of the mean function and 95%-SCBs constructed using the tGKF and the Multiplier-t. Bottom row: areas where the confidence bands for the difference in the mean function for the scale field do not include 0.

5.2. Climate data

Our second data example (2D) concerns the change in temperature over North America within the next century. The data was obtained from the North American Regional Climate Change Assessment Program (NARCCAP) project (Mearns et al., 2013). It consist of two sets of 29 spatially registered arrays of mean seasonal temperatures for summer (June–August) and winter (December–February) evaluated at a fine grid of fixed locations 0.5 degrees apart in geographic longitude and latitude over the time periods 1971–1999 and 2041–2069. Sommerfeld et al. (2018) analyzed this data set with the aim to detect regions at risk of exceeding a 2 °C temperature increase. To complement their analysis, we use their model and data processing and provide 90% SCBs for the estimated difference of mean temperatures between the two time periods assuming that the two samples have the same covariance structure.

Our results are shown in Fig. 9. From the 2 °C contour lines (yellow) of the lower bound for the SCBs we conclude that there is likely an increase of at least 2 °C in the time period 2041–2069 compared to 1971–1999 during the summer months in the region of the Rocky Mountains and the Sierra Madre Occidental mountains of Mexico, since in this region the lower bound of the SCBs is here larger than 2 °C. Similarly we obtain that for mean winter temperatures, small regions around the Hudson Bay and in the Canadian Shield are at risk of having an increase of more than 2 °C. The area enclosed by the 2 °C contour lines for the upper bound of the SCBs show that during summer large areas in Canada and Alaska as well as smaller patches at the Hudson Bay and the Gulf of Mexico are not at risk experiencing an temperature increases of more than 2 °C. For winter mean temperature there are only small regions for which we are certain that the temperature does not rise above 2 °C.

Fig. 9.

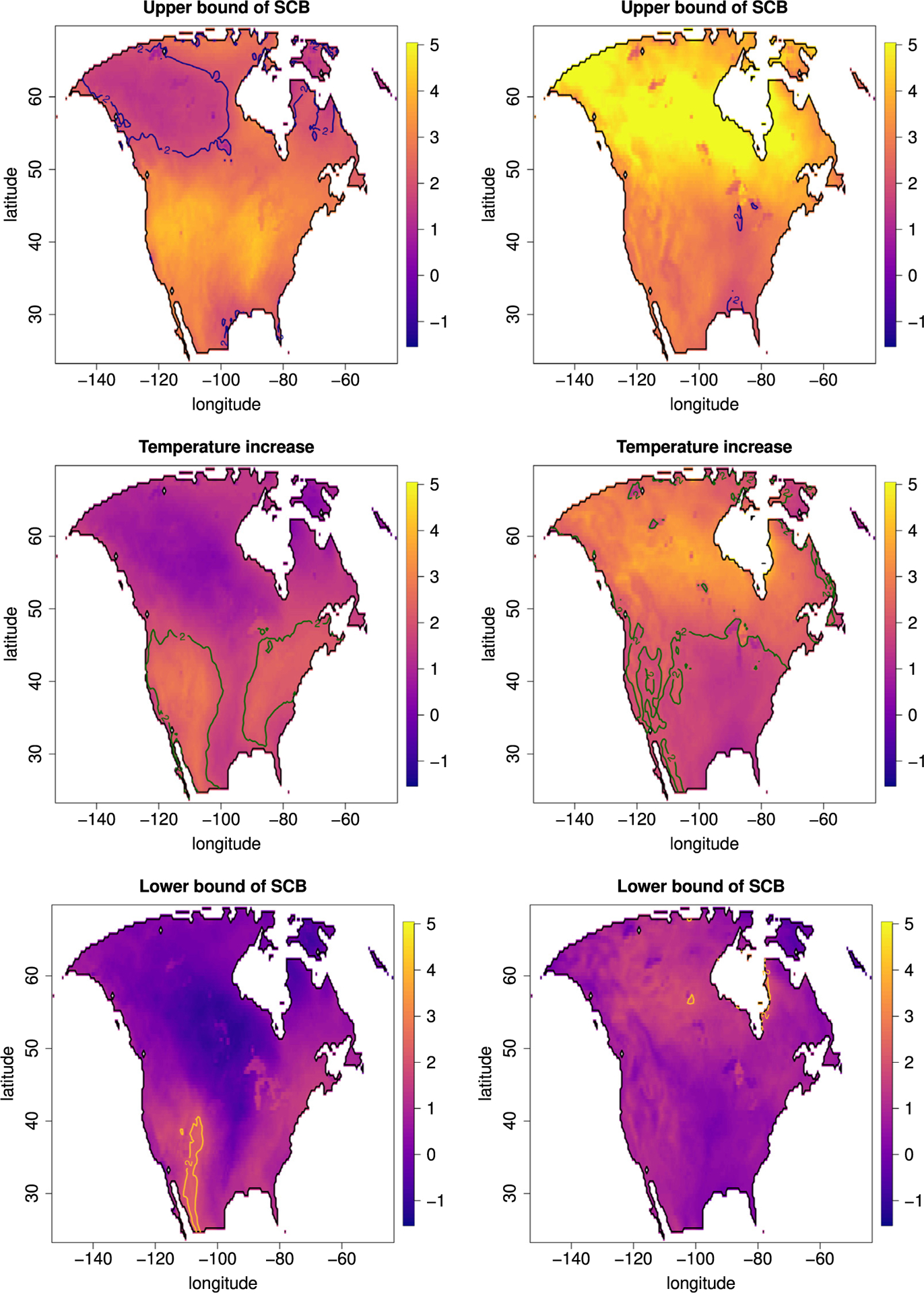
Visualization of the difference of mean temperatures in summer (left) and winter (right) of the time periods 2041–2069 and 1971–1999. To visualize regions at risk to experience an increase of more than 2 °C we report in each figure the 2 °C contour line. Top row: upper bound of the SCBs. Middle row: point estimate. Bottom row: lower bound of SCBs.

The aforementioned areas within the contour lines of the lower and upper bounds of the SCBs are similar to the COverage Probability Excursion (CoPE) sets introduced in Sommerfeld et al. (2018). CoPE sets are a pair ${\widehat{\mathcal{A}}}^{+}\subset {\widehat{\mathcal{A}}}^{-}$ of data driven random sets, for which ${\widehat{\mathcal{A}}}^{-}$ completely contains with a preset probability the true excursion set, while the set ${\widehat{\mathcal{A}}}^{+}$ is completely contained in the true excursion set.

The interior of the yellow contour lines, i.e., thresholding of the lower bound of the SCB yields a set similar to ${\widehat{\mathcal{A}}}^{+}$, while thresholding the upper bound can be compared to ${\widehat{\mathcal{A}}}^{-}$. In fact, we believe thresholding SCBs can be interpreted as conservative CoPE sets, explaining why our analysis is comparable to the results in Sommerfeld et al. (2018). Exploring this connection between CoPE sets and SCBs will be future research.

Appendix A. Bootstrap methods

Parametric bootstrap-t for q_α,N (Degras, 2011).

Assume that the estimators $s\mapsto {\widehat{\eta }}_N(s)$ and $s\mapsto {\widehat{\varsigma }}_N(s)$ are obtained from a sample $Y_1,\dots ,Y_N\stackrel{i.i.d.}{~}Y$ of random functions, then the parametric bootstrap-t estimator of q_α,N is obtained as follows:

1. Resample from Y₁, … , Y_N with replacement to produce a bootstrap sample $Y_1^{*},\dots ,Y_N^{*}$.

2. Compute ${\widehat{\eta }}_N^{*}$ and ${\widehat{\varsigma }}_N^{*}$ using the sample $Y_1^{*},\dots ,Y_N^{*}$.

3. Compute $T^{*}={\text{max}}_{s\in S}{\tau }_N\left|{\widehat{\eta }}_N^{*}(s)-{\widehat{\eta }}_N(s)\right|/{\widehat{\varsigma }}_N^{*}(s)$.

4. Repeat steps 1 to 3 many times to approximate the conditional law ${\mathcal{L}}^{*}=\mathcal{L}\left(T^{*}\mid Y_1,\dots ,Y_N\right)$ and take the (1 − α) · 100% quantile of ${\mathcal{L}}^{*}$ to estimate q_α,N.

Remark 8.

Note that the variance in the denominator is also bootstrapped, which corresponds to the standard bootstrap-t approach for confidence intervals, cf. DiCiccio and Efron (1996). This is done in order to mimic the l.h.s. in (1) and improves the small sample coverage.

According to our simulations in Section 4 this estimator works well only for large enough sample sizes, although Degras (2011) introduced it especially for small sample sizes. Moreover, it is well known that confidence intervals for finite dimensional parameters based on the bootstrap-t have highly variable end points for small sample sizes, cf., Good (2005, Section 3.3.3). Evidence that this remains the case in the functional world is provided in Tables 2 and 3.

Multiplier-t bootstrap for q_α,N.

The second bootstrap method builds on residuals and a version of the multiplier (or wild) bootstrap as introduced in Chang et al. (2017). Here we assume that we can construct residuals $R_n^N$ for n = 1, … , N satisfying $\sum R_n^N=1$ and $\sum R_n^N(s)R_n^N\left(s^{\prime }\right)\to \mathfrak{r}$ as N → ∞ uniformly almost surely. For example for the signal-plus-noise model the residuals $R_n^N=\sqrt{\frac{N}{N-1}}\left(Y_n-{\widehat{\mu }}_N\right)$ do satisfy these conditions, if the error field Z is $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz and has finite second $\mathcal{C}(S)$-moment. Here as before ${\widehat{\eta }}_N={\widehat{\mu }}_N$ and ${\widehat{\varsigma }}_N={\widehat{\sigma }}_N$ denote the pointwise sample mean and the pointwise sample standard deviation. Algorithmically, the multiplier bootstrap estimates q_α,N are as follows:

1. Compute residuals $R_1^N,\dots ,R_N^N$ and multipliers $g_1,\dots ,g_N\stackrel{\text{i.i.d.}}{~}g$ with $\mathbb{E}[g]=0$ and var[g] = 1

2. Compute ${\widehat{\sigma }}_N^{*}(s)$, i.e. the sample standard deviation of $g_1{R}_1^N(s),\dots ,g_N{R}_N^N(s)$.

3. Compute $T^{*}(s)=\frac{1}{\sqrt{N}}{\sum }_{n=1}^N{g}_n\frac{R_n^N(s)}{{\widehat{\sigma }}_N^{*}(s)}$.

4. Repeat steps 1 to 3 many times to approximate the conditional law ${\mathcal{L}}^{*}=\mathcal{L}\left(T^{*}\mid Y_1,\dots ,Y_N\right)$ and take the (1 − α) · 100% quantile of ${\mathcal{L}}^{*}$ to estimate q_α,N.

In our simulations we use Gaussian and Rademacher multipliers. The latter perform much better for small sample sizes than Gaussian multipliers. This is the reason why they probably have been used in Chang et al. (2017).

Appendix B. Proofs

B.1. Proof of Claim in Remark 1

Using the multivariate mean value theorem and the Cauchy–Schwarz inequality yields

$${\left|G^{(d,l)}(s)-G^{(d,l)}\left(s^{\prime }\right)\right|}^2\le \underset{t\in S}{\text{max}}{\Vert \nabla G^{(d,l)}(t)\Vert }^2{\Vert s-s^{\prime }\Vert }^2.$$

Applying the expectation to both sides and then taking the maximum of the resulting sums we obtain

$$\mathbb{E}\left[{\left|G^{(d,l)}(s)-G^{(d,l)}\left(s^{\prime }\right)\right|}^2\right]\le D\underset{k=1,\dots ,D}{\text{max}}\mathbb{E}\left[\underset{t\in S}{\text{max}}{\left|G^{(d,l,k)}(t)\right|}^2\right]{\Vert s-s^{\prime }\Vert }^2.$$

The proof follows now from the following two observations. Firstly, by Remark 3 each of the expectations we take the maximum of is finite (Landau and Shepp, 1970, Thm 5), since all components of the gradient of ∇G^(d,l) are Gaussian fields with almost surely continuous sample paths. Secondly, |log‖x‖|⁻² ≥ x² for all 0 < x < 1.

B.2. Proof of Theorem 1

Lemma 9.

Let the function ${\widehat{f}}_N(u)$ and its first derivative ${\widehat{f}}_N^{\prime }(u)$ be uniformly consistent estimators of the function f(u) and its first derivative f′(u), respectively, where both are uniformly continuous over $u\in ℝ$. Assume there exists an open interval I = (a, b) such that f is strictly monotone on I and there exists a unique solution u₀ ∈ I to the equation f(u) = 0. Define ${\widehat{u}}_N=\text{sup}\left\{u\in I:{\widehat{f}}_N(u)=0\right\}$. Then $\widehat{u}$ is a consistent estimator of u₀.

Proof.

Assume w.l.o.g. that f is strictly decreasing on I. Thus, for any ε > 0 we have f(u₀ − ε) > 0 > f(u₀ + ε) by f(u₀) = 0. The assumption that ${\widehat{f}}_N(u)$ is a consistent estimator of f(u) yields

$$\mathbb{P}\left({\widehat{f}}_N\left(u_0-\epsilon \right)>0>{\widehat{f}}_N\left(u_0+\epsilon \right)\right)\to 1,$$

which implies that with probability tending to 1, there is a root of $\widehat{f}$ in I_0,ε = (u₀ − ε, u₀ + ε). On the other hand the monotonicity of f guarantees the existence of an δ > 0 such that inf{|f(u)| : u ∈ I \ I_0,ε } > δ. Moreover, by the uniform consistency of $\widehat{f}$, we have that

$$\mathbb{P}\left(\underset{u\in I}{\text{sup}}\left|{\widehat{f}}_N(u)-f(u)\right|<\delta /2\right)\to 1.$$

Therefore, using the inequality

$$\underset{u\in I\backslash I_{0,\epsilon }}{\text{inf}}\left|{\widehat{f}}_N(u)\right|\ge \underset{u\in I\backslash I_{0,\epsilon }}{\text{inf}}|f(u)|-\underset{u\in I\backslash I_{0,\epsilon }}{\text{sup}}\left|{\widehat{f}}_N(u)-f(u)\right|,$$

we can conclude that

$$\begin{gathered} \mathbb{P}\left(\underset{u\in I\backslash I_{0,\epsilon }}{\text{inf}}\left|{\widehat{f}}_N(u)\right|>\delta /2\right)\ge \mathbb{P}\left(\underset{u\in I\backslash I_{0,\epsilon }}{\text{inf}}|f(u)|-\underset{u\in I\backslash I_{0,\epsilon }}{\text{sup}}\left|{\widehat{f}}_N(u)-f(u)\right|>\delta /2\right) \\ =\mathbb{P}\left(\underset{u\in I\backslash I_{0,\epsilon }}{\text{sup}}\left|{\widehat{f}}_N(u)-f(u)\right|<\underset{u\in I\backslash I_{0,\epsilon }}{\text{inf}}|f(u)|-\delta /2\right)\to 1, \end{gathered}$$

which implies that with probability tending to 1, there is no root of ${\widehat{f}}_N$ outside I_0,ε. Hence from the definition of ${\widehat{u}}_N$, it is clear that ${\widehat{u}}_N$ is the only root of ${\widehat{f}}_N$ in I with probability tending to 1. As an immediate consequence we have that

$$\mathbb{P}\left[\left|{\widehat{u}}_N-u_0\right|<\epsilon \right]=\mathbb{P}\left[{\widehat{u}}_N\in I_{0,\epsilon }\right]\to 1,$$

which finishes the proof that $\widehat{u}$ is a consistent estimator of u₀.

Lemma 10.

Let ${\widehat{L}}_d^N$ be a consistent estimator of L_d and EEC_G(u) given in Eq. (7).

1. ${\Vert {\text{EEC}}_G(u)-{\widehat{\text{EEC}}}_{t_{N-1}}(u)\Vert }_{\infty }\stackrel{N\to \infty }{\to }0$ almost surely.

2. ${\Vert {\text{EEC}}_G^{\prime }(u)-{\widehat{{\text{EEC}}^{\prime }}}_{t_{N-1}}(u)\Vert }_{\infty }\stackrel{N\to \infty }{\to }0$ almost surely.

Proof.

Part 1.:

This is a direct consequence of the consistency of the LKC estimates and the observation that the EC densities ρ^tν of a t_ν-field with ν = N − 1 degrees of freedom converges uniformly to the EC densities of a Gaussian field ρ^G as N tends to infinity, i.e.

$$\underset{v\to \infty }{\text{lim}}\underset{u\in ℝ}{\text{max}}\left|{\rho }^{t_{\nu }}(u)-{\rho }^G(u)\right|=0.$$

The latter follows from Worsley (1994, Theorem 5.4), which implies that the uniform convergence of EC densities is implied by the uniform convergence of

$$\underset{v\to \infty }{\text{lim}}\underset{u\in ℝ}{\text{max}}\left|{\left(1+\frac{u^2}{v}\right)}^{-\frac{v-1}{2}}-e^{-\frac{u^2}{2}}\right|=0.$$

To see this, note that the distance

$$h_v(u)={\left(1+\frac{u^2}{v}\right)}^{-\frac{v-1}{2}}-e^{-\frac{u^2}{2}}\ge 0,\text{ for }u\in ℝ$$

fulfills lim_{u→ ± ∞} h_ν(u) = 0. Thus, there is a $C_v={\text{max}}_{u\in ℝ}\left|h_v(u)\right|$ by continuity of h_ν. Moreover, note that h_ν(u) ≥ h_ν+1(u) for ν ≥ 1, all $u\in ℝ$ and lim_ν→∞ h_ν(u) = 0. Hence, C_ν converges to zero for ν → ∞.

Part 2.:

This follows similar by the same arguments as above applied to the derivatives of the EC densities.

Proof of Theorem 1.

In order to prove the almost sure convergence ${\widehat{q}}_{\alpha ,N}\stackrel{N\to \infty }{\to }{\tilde{q}}_{\alpha }$, note that for u large enough u ↦ EEC_G(u) is strictly monotonically decreasing and therefore combining Lemmas 9 and 10 yields the claim.

B.3. Proof of Theorem 2

By Taylor et al. (2005, Theorem 4.3) we have for $\mathcal{Z}$ a zero-mean Gaussian field over a parameter set $\mathcal{T}$ that

$$\underset{u\to \infty }{\text{lim}\text{inf}}-u^2\text{log}\left|\mathbb{P}\left(\underset{t\in \mathcal{T}}{\text{max}}\mathcal{Z}(t)\ge u\right)-{\text{EEC}}_{\mathcal{Z}}(u)\right|\ge \frac{1}{2}\left(1+\frac{1}{2{\sigma }_c^2}\right),$$

where ${\sigma }_c^2$ is a variance depending on an associated field to $\mathcal{Z}$. This implies that there is a $\tilde{u}$ such that for all $u\ge \tilde{u}$ we have that

$$\left|\mathbb{P}\left(\underset{t\in \mathcal{T}}{\text{max}}\mathcal{Z}(t)\ge u\right)-{\text{EEC}}_{\mathcal{Z}}(u)\right|\le e^{-{\left(\frac{1}{2}+\frac{1}{2{\sigma }_c^2}\right)}^{u^2}}.$$ (19)

Equipped with this result using the definition M = max_s∈S G(s) and |M| = max_s∈S|G(s)| we compute

$$\begin{gathered} \left|1-\alpha -\mathbb{P}\left(\forall s\in S:\eta (s)\in SCB\left(s,{\widehat{q}}_{\alpha ,N}\right)\right)\right|\le \left|-\alpha +\mathbb{P}\left(\underset{s\in S}{\text{max}}\left|{\tau }_N\frac{{\widehat{\eta }}_N(s)-\eta (s)}{{\widehat{\varsigma }}_N(s)}\right|>{\widehat{q}}_{\alpha ,N}\right)\right| \\ \le \left|\mathbb{P}\left(\left|M\right|>{\widehat{q}}_{\alpha ,N}\right)-\alpha \right|+\left|\mathbb{P}\left(\underset{s\in S}{\text{max}}\left|{\tau }_N\frac{{\widehat{\eta }}_N(s)-\eta (s)}{{\widehat{\varsigma }}_N(s)}\right|>{\widehat{q}}_{\alpha ,N}\right)-\mathbb{P}\left(\left|M\right|>{\widehat{q}}_{\alpha ,N}\right)\right|=I+II. \end{gathered}$$

Here II converges to zero for N tending to infinity by the fCLT for ${\widehat{\eta }}_N$ and the consistent estimation of ${\widehat{\varsigma }}_N$ from (E1–2). Therefore it remains to treat I.

To deal with this summand, note that

$$\mathbb{P}\left(\left|M\right|>{\widehat{q}}_{\alpha ,N}\right)=\mathbb{P}\left(\underset{s\in S}{\text{max}}|G(s){|}^2>{\widehat{q}}_{\alpha ,N}^2\right)=\mathbb{P}\left(\underset{(s,v)\in S\times S^0}{\text{max}}\mathcal{Z}(s,v)>{\widehat{q}}_{\alpha ,N}\right),$$

where the Gaussian random field $\mathcal{Z}$ over $\mathcal{T}=S\times S^0$, where S⁰ = {1, −1}, is defined by $\mathcal{Z}(s,v)=v\cdot \mathcal{G}(s)$.

Using the above equality, ${\widehat{\text{EEC}}}_{t_{N-1}}\left({\widehat{q}}_{\alpha ,N}\right)=\alpha /2$, i.e. the definition of our estimator ${\widehat{q}}_{\alpha ,N}$ from Eq. (6) and Lemma 10 we have that

$$\begin{gathered} I=\left|\mathbb{P}\left(\underset{s\in S\times S^0}{\text{max}}\mathcal{Z}(s,v)>{\widehat{q}}_{\alpha ,N}\right)-2{\widehat{\text{EEC}}}_{t_{N-1}}\left({\widehat{q}}_{\alpha ,N}\right)\right| \\ \stackrel{N\to \infty }{\to }\left|\mathbb{P}\left(\underset{(s,v)\in S\times S^0}{\text{max}}\mathcal{Z}(s,v)>{\tilde{q}}_{\alpha }\right)-2{\text{EEC}}_G\left({\tilde{q}}_{\alpha }\right)\right|. \end{gathered}$$

Thus, using the fact that $L_d(\mathcal{T},\mathcal{Z})=L_0\left(S^0\right)L_d(S,G)=2L_d(S,G)$ and (19) and the observation that ${\tilde{q}}_{\alpha }$ is monotonically increasing in α for α small enough, we can bound I by

$$I=\left|\mathbb{P}\left(\underset{(s,v)\in S\times S^0}{\text{max}}\mathcal{Z}(s,v)>{\tilde{q}}_{\alpha }\right)-{\text{EEC}}_{\mathcal{Z}}\left({\tilde{q}}_{\alpha }\right)\right|\le e^{-\frac{1}{2+2{\sigma }_c^2}{\tilde{q}}_{\alpha }^2}$$

for all α smaller than some α′, which finishes the proof.

Remark 9.

The specific definition of σ_c associated with the Gaussian field $\mathcal{Z}$ can be found in Taylor et al. (2005).

B.4. Proof of Proposition 1

Assume that Z is $\left({\mathcal{L}}^p,\delta \right)$-Lipshitz, then using convexity of |·|^p we compute

$$\begin{gathered} \mathbb{E}\left[\Vert Z{\Vert }_{\infty }^p\right]\le 2^{p-1}\mathbb{E}\left[\underset{s\in S}{\text{max}}{\left|Z(s)-Z\left(s^{\prime }\right)\right|}^p\right]+2^{p-1}\mathbb{E}\left[\underset{s\in S}{\text{max}}{\left|Z\left(s^{\prime }\right)\right|}^p\right] \\ \le 2^{p-1}\mathbb{E}\left[|A{|}^p\right]\underset{s\in S}{\text{max}}\delta {\left(s,s^{\prime }\right)}^p+2^{p-1}\mathbb{E}\left[{\left|Z\left(s^{\prime }\right)\right|}^p\right]<\infty . \end{gathered}$$

Hence Z has also a finite pth $\mathcal{C}(S)$-moment.

B.5. Proofs of Theorems 3 and 4

The following Lemma provides almost sure uniform convergence results and will be used often in the following proofs.

Lemma 11.

Assume that $X_1,\dots ,X_N\stackrel{i.i.d.}{~}X$ and $Y_1,\dots ,Y_N\stackrel{i.i.d.}{~}Y$ are $\left({\mathcal{L}}^1,\delta \right)$-Lipshitz, Then $\overline{X}\stackrel{N\to \infty }{\to }\mathbb{E}[X]$ uniformly almost surely. If X and Y are $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz, then ${\widehat{\text{cov}}}_N[X,Y]\stackrel{N\to \infty }{\to }\text{cov}[X,Y]$ uniformly almost surely.

Proof.

First claim:

Using the generic uniform convergence result in Davidson (1994, Theorem 21.8), we only need to establish strong stochastical equicontinuity (SSE) of the random function $\overline{X}-\mathbb{E}[X]$, since pointwise convergence is obvious by the SLLNs. SSE, however, can be easily established using Davidson (1994, Theorem 21.10 (ii)), since

$$\left|N^{-1}\sum _{n=1}^N\left(X_n(s)-X_n\left(s^{\prime }\right)\right)-\mathbb{E}\left[X(s)-X\left(s^{\prime }\right)\right]\right|\le \left(N^{-1}\sum _{n=1}^N{A}_n+\mathbb{E}[A]\right)\delta \left(s,s^{\prime }\right)=C_N\delta \left(s,s^{\prime }\right)$$

for all s, s′ ∈ S. Here $A_1,\dots ,A_N\stackrel{\mathit{\text{ i.i.d. }}}{~}A$ denote the random variables from the $\left({\mathcal{L}}^1,\delta \right)$-Lipshitz property of the X_n’s and X and hence the random variable C_N converges almost surely to the constant $2\mathbb{E}[A]$ by the SLLNs.

Second claim:

Adapting the same strategy as above and assuming w.l.o.g. $\mathbb{E}[X]=\mathbb{E}[Y]=0$, we compute

$$\begin{gathered} \left|\frac{1}{N}\sum _{n=1}^N{X}_n(s)Y_n(s)-X_n\left(s^{\prime }\right)Y_n\left(s^{\prime }\right)\right|\le \left(\frac{1}{N}\sum _{n=1}^N{\Vert X_n\Vert }_{\infty }{B}_n+{\Vert Y_n\Vert }_{\infty }{A}_n\right)\delta \left(s,s^{\prime }\right) \\ \le \left(\sqrt{\sum _{n=1}^N\frac{{\Vert X_n\Vert }_{\infty }^2}{N}}\sqrt{\sum _{n=1}^N\frac{B_n^2}{N}}+\sqrt{\sum _{n=1}^N\frac{{\Vert Y_n\Vert }_{\infty }^2}{N}}\sqrt{\sum _{n=1}^N\frac{A_n^2}{N}}\right)\delta \left(s,s^{\prime }\right), \end{gathered}$$

where $\Vert X{\Vert }_{\infty }={\text{max}}_{s\in S}|X(s)|$ and $B_1,\dots ,B_N\stackrel{i.i.d.}{~}B$ denote the random variables from the $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz property of the Y_n’s and Y. Again by the SLLNs the random Lipshitz constant converges almost surely and is finite, since X and Y have finite second $\mathcal{C}(S)$-moments and are $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz.

Lemma 12.

Let $\mathfrak{c}$ be a covariance function. Then

1. If $\mathfrak{c}$ is continuous and has continuous partial derivatives up to order K, then the zero-mean Gaussian field with covariance $\mathfrak{c}$ has ${\mathcal{C}}^K$-sample paths with almost surely uniform and absolutely convergent expansions

   $$G^I(s)=\sum _{i=1}^{\infty }\sqrt{{\lambda }_i}{A}_i{\phi }_i^I(s),$$

   where λ_i, φ_i are the eigenvalues and eigenfunctions of the covariance operator of Z and ${\left\{A_i\right\}}_{i\in \mathbb{N}}$ are i.i.d. $\mathcal{N}(0,1)$.

2. If Z and all its partial derivatives Z^I with |I| = K′ ≤ K, $K\in \mathbb{N}$, are $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz fields with finite $\mathcal{C}(S)$-variances, then $\mathfrak{c}$ is continuous and all partial derivatives ${\partial }^{|I|+\left|I^{\prime }\right|}\mathfrak{c}\left(s,s^{\prime }\right)/\partial s^I\partial {s^{\prime }}^{I^{\prime }}$ for |I|, |I′| ≤ K exist and are continuous for all s, s′ ∈ S.

Proof.

1. Since $\mathfrak{c}$ is continuous the field G is mean-square continuous. Hence there is a Karhunen–Loéve expansion of the form

   $$G(s)=\sum _{i=1}^{\infty }\sqrt{{\lambda }_i}{A}_i{\phi }_i(s),$$

   with λ_i, φ_i are the eigenvalues and eigenfunctions of the covariance operator associated with $\mathfrak{c}$ and ${\left\{A_i\right\}}_{i\in \mathbb{N}}$ are i.i.d. $\mathcal{N}(0,1)$. From Ferreira and Menegatto (2012, Theorem 5.1) we have that ${\phi }^I\in {\mathcal{C}}^K(S)$. Moreover, it is easy to deduce from their equation (4.3) that

   $$G^I(s)=\sum _{i=1}^{\infty }\sqrt{{\lambda }_i}{A}_i{\phi }^I(s),$$

   is almost surely absolutely and uniformly convergent.
2. The continuity is a simple consequence of the $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz property and the finite $\mathcal{C}(S)$-variances. Let X be a field with these properties, then using the Cauchy–Schwarz inequality

   $$\begin{gathered} \left|\mathfrak{c}(s,t)-\mathfrak{c}\left(s^{\prime },t^{\prime }\right)\right|\le \left|\mathbb{E}\left[\left(X_s-X_{s^{\prime }}\right)X_t+\left(X_t-X_{t^{\prime }}\right)X_{s^{\prime }}\right]\right| \\ \le \mathbb{E}\left[\left|X_s-X_{s^{\prime }}\right|\left|X_t\right|\right]+\mathbb{E}\left[\left|X_t-X_{t^{\prime }}\right|\left|X_{s^{\prime }}\right|\right] \\ \le \sqrt{\mathbb{E}\left[{\left(X_s-X_{s^{\prime }}\right)}^2\right]}\sqrt{\mathbb{E}\left[\underset{t\in S}{\text{max}}{X}_t^2\right]}+\sqrt{\mathbb{E}\left[{\left(X_t-X_{t^{\prime }}\right)}^2\right]}\sqrt{\mathbb{E}\left[\underset{s^{\prime }\in S}{\text{max}}{X}_{s^{\prime }}^2\right]} \\ \le C\left(\delta \left(s,s^{\prime }\right)+\delta \left(t,t^{\prime }\right)\right) \end{gathered}$$

   for some C < ∞ and therefore $\mathfrak{c}$ and the covariances of Z^I are continuous. We only show that $\partial \mathfrak{c}\left(s,s^{\prime }\right)/\partial s_d$ exists and is continuous. The argument is similar for the higher partial derivatives. From the definition we obtain for all s, s′

   $$\underset{h\to 0}{\text{lim}}{h}^{-1}\left(\mathfrak{c}\left(s,s^{\prime }\right)-\mathfrak{c}\left(s+h{e}_d,s^{\prime }\right)\right)=\underset{h\to 0}{\text{lim}}\mathbb{E}\left[h^{-1}\left(Z(s)-Z\left(s+h{e}_d\right)\right)Z\left(s^{\prime }\right)\right],$$

   where e_d denotes the dth element of the standard basis of ${ℝ}^D$. Thus, we only have to prove that we can interchange limits and integration. The latter is an immediate consequence of Lebesgue’s dominated convergence theorem, where we obtain the ${\mathcal{L}}^1$ majorant from the $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz property as AZ(s′), where $A\in {\mathcal{L}}^2$.

Proof of Theorem 3.

1. Since Z is $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz the main result in Jain and Marcus (1975) immediately implies (E1) with ${\tau }_N=\sqrt{N}$ and $\mathfrak{r}=\mathfrak{c}$. Condition (E2) is obtained from the second part of Lemma 11, since σ(s)Z(s) is $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz and has finite second $\mathcal{C}(S)$-moment.

2. We only need to show that the Gaussian limit field with the covariance $\mathfrak{c}$ fulfills (G1) and (G3). Note that condition (G3) is a consequence of (G1) and the ${\mathcal{C}}^3$-sample paths by Remark 1. But (G1) is already a consequence of Lemma 12.

Lemma 13.

Let Z fulfill the assumptions of Theorem 3(ii) except for (G2) and for all d, l ∈ {1, … , D} suppose that cov [(Z^(d)(s), Z^(d,l)(s))] has full rank for all s. Then $G=G(0,\mathfrak{c})$ fulfills (G2).

Proof.

Using the series expansions from Lemma 12 we have that for multi-indices I₁, … , I_K, $K\in \mathbb{N}$ and all $v\in {ℝ}^K$ it follows that

$$\left({\partial }^{\left|I_1\right|}G(s)/\partial s^{I_1},\dots ,{\partial }^{\left|I_K\right|}G(s)/\partial s^{I_K}\right)v^T=\sum _{i=1}^{\infty }\sqrt{{\lambda }_i}{A}_i\sum _{k=1}^K{v}_k{\phi }_i^{I_k}(s)$$

is convergent for all s (even uniformly). Note that we used here that the expansions are absolutely convergent such that we can change orders in the infinite sums. Thus, it is easy to deduce that (G^Ik, … , G^Ik) is a Gaussian field.

Therefore (G^(d)(s), G^(d,l)(s)) is a multivariate Gaussian random variable for all s ∈ S, which is non-degenerate if and only if its covariance matrix is non-singular. But this is the case by the assumption, since it is identical to the covariance matrix cov [(Z(d)(s), Z(d,l)(s))].

Proof of Theorem 4.

The proof is almost identical to the proof of Theorem 3 and therefore omitted.

B.6. Proof of Theorem 5

First note that using the definition of R_n from Eq. (13) we obtain

$$R_n^{(d)}={\left(\frac{\mu -\overline{Y}}{{\widehat{\sigma }}_N}\right)}^{(d)}+{\left(\frac{\sigma }{{\widehat{\sigma }}_N}\right)}^{(d)}{Z}_n+\frac{\sigma }{{\widehat{\sigma }}_N}{Z}_n^{(d)}.$$

Thus, the entries of the sample covariance matrix ${\widehat{\Lambda }}_N$ are given by

$$\begin{gathered} \widehat{\text{var}}[Z]{\left(\frac{\sigma }{{\widehat{\sigma }}_N}\right)}^{(d)}{\left(\frac{\sigma }{{\widehat{\sigma }}_N}\right)}^{(l)}+\widehat{\text{cov}}\left[Z,Z^{(d)}\right]\frac{\sigma }{{\widehat{\sigma }}_N}{\left(\frac{\sigma }{{\widehat{\sigma }}_N}\right)}^{(l)} \\ +\widehat{\text{cov}}\left[Z,Z^{(l)}\right]\frac{\sigma }{{\widehat{\sigma }}_N}{\left(\frac{\sigma }{{\widehat{\sigma }}_N}\right)}^{(d)}+\widehat{\text{cov}}\left[Z^{(d)},Z^{(l)}\right]\frac{{\sigma }^2}{{\widehat{\sigma }}_N^2} \end{gathered}$$ (20)

Now, the second part of Lemma 11 applied to Z, Z^(d) and Z^(l) and the fact that by

$${\widehat{\sigma }}_N^2(s)/{\sigma }^2(s)=\widehat{\text{var}}[\sigma (s)Z(s)]/{\sigma }^2(s)=\widehat{\text{var}}[Z(s)]$$ (21)

$${\left({\widehat{\sigma }}_N^2(s)/{\sigma }^2(s)\right)}^{(l)}=2\widehat{\text{cov}}\left[Z(s),Z^{(l)}(s)\right].$$ (22)

the terms involving σ’s convergence uniformly almost surely to one and zero by Lemma 11 implies

$${\widehat{\text{cov}}}_N\left[R^{(d)},R^{(l)}\right]\stackrel{N\to \infty }{\to }\text{cov}\left[Z^{(d)},Z^{(l)}\right]={\Lambda }_{dl}$$

uniformly almost surely. Thus, ${\widehat{\Lambda }}_N\to \Lambda$ uniformly almost surely.

Now let X, Y be $\left({\mathcal{L}}^4,\delta \right)$-Lipshitz, then

$$\left|X(s)Y(s)-X\left(s^{\prime }\right)Y\left(s^{\prime }\right)\right|\le \left(\Vert X{\Vert }_{\infty }A+\Vert Y{\Vert }_{\infty }B\right)\delta \left(s,s^{\prime }\right)$$

with A, B the random variables in the $\left({\mathcal{L}}^4,\delta \right)$-Lipshitz property of Y, X. Note that

$$\begin{gathered} \mathbb{E}\left[{\left(\Vert X{\Vert }_{\infty }A+\Vert Y{\Vert }_{\infty }B\right)}^2\right]\le 2\mathbb{E}\left[{\left(\Vert X{\Vert }_{\infty }A\right)}^2+{\left(\Vert Y{\Vert }_{\infty }B\right)}^2\right] \\ \le 2\sqrt{\mathbb{E}\left[\Vert X{\Vert }_{\infty }^4\right]\mathbb{E}\left[A^4\right]}+2\sqrt{\mathbb{E}\left[\Vert Y{\Vert }_{\infty }^4\right]\mathbb{E}\left[B^4\right]}<\infty . \end{gathered}$$

by (a + b)² ≤ 2a² + 2b² for all a, $b\in ℝ$ and the Cauchy–Schwarz inequality. Thus, a sample $X_1{Y}_1,\dots ,X_N{Y}_N\stackrel{i.i.d.}{~}XY$ fulfills the assumptions for the CLT in $\mathcal{C}(S)$ given in Jain and Marcus (1975). Therefore, the following sums converge to a Gaussian field in $\mathcal{C}(S)$:

$$\sqrt{N}(\widehat{\text{var}}[Z]), \sqrt{N}\widehat{\text{cov}}\left[Z,Z^{(l)}\right], \sqrt{N}\widehat{\text{cov}}\left[Z^{(d)},Z^{(l)}\right]\text{ for }d,l=1,\dots ,D.$$

Thus, using the latter together with Eq. (20) and the uniform almost sure convergence from (21) and (22), we obtain

$$\sqrt{N}\left(\widehat{\text{cov}}\left[R^{(d)},R^{(l)}\right]-{\Lambda }_{dl}\right)\stackrel{N\to \infty }{\Rightarrow }G\left(0,{\mathfrak{t}}_{dl}\right)$$

with $t_{dl}\left(s,s^{\prime }\right)=\text{cov}\left[Z^{(d)}(s)Z^{(l)}(s),Z^{(d)}\left(s^{\prime }\right)Z^{(l)}\left(s^{\prime }\right)\right]$. This combined with the standard multivariate CLT yields the claim.

B.7. Proof of Theorem 7

By Theorem 5 the claim follows from the functional delta method (Kosorok, 2008, Theorem 2.8), if we prove that the corresponding functions are Hadamard differentiable and can compute this derivative.

Case 1D:

We have to prove that the function

$$H:\left(\mathcal{C}(S),\Vert \cdot {\Vert }_{\infty }\right)\to ℝ, f\mapsto {\int }_S\sqrt{f(s)}ds$$

is Hadamard differentiable. Therefore, note that the integral is a bounded linear operator and hence it is Fréchet differentiable with derivative being the integral itself. Moreover, $f\mapsto \sqrt{f}$ is Hadamard differentiable by Kosorok (2008, Lemma 12.2) with Hadamard derivative $D{H}_f(\alpha )=1/\sqrt{4f}\alpha$ tangential even to the Skorohod space D(S). Combining this, we obtain the limit distribution $\sqrt{N}\left({\widehat{L}}_1^N-L_1\right)$ from the fCLT for ${\widehat{\Lambda }}_N$ given in Theorem 5 to be distributed as

$$D{H}_{\Lambda }(G)=\frac{1}{2}{\int }_S\frac{G(s)}{\sqrt{\Lambda (s)}}ds,$$

where G(s) is the asymptotic Gaussian field given in Theorem 5.

Case 2D:

The strategy of the proof is the same as in 1D, i.e. we need to calculate the Hadamard (Fréchet) derivative of

$$\begin{gathered} H:\left(\mathcal{C}(S)\times \mathcal{C}(S)\times \mathcal{C}(S),\Vert \cdot {\Vert }_{\infty }\right)\to {ℝ}^2, \\ \left(f_1,f_2,f_3\right)\mapsto \left(\frac{1}{2}{\int }_0^1\sqrt{{\frac{d\gamma }{dt}}^T(t)\iota \left(f_1(\gamma (t)),f_2(\gamma (t)),f_3(\gamma (t))\right)\frac{d\gamma }{dt}(t)}dt,{\int }_S\sqrt{\text{det}(\Lambda (s))}d{s}_{1}d{s}_2\right). \end{gathered}$$

The arguments are the same as before. Thus, using the chain rule and derivatives of matrices with respect to their components the Hadamard derivative evaluated at the field G is given by

$$\begin{gathered} d{H}_{\Lambda }(G)=(\frac{1}{2}{\int }_0^1\frac{1}{\sqrt{{\frac{d\gamma }{dt}}^T(t)\Lambda (\gamma (t))\frac{d\gamma }{dt}(t)}}\text{tr}(\Lambda (\gamma (t))\iota (G(\gamma (t))))dt, \\ {\int }_S\frac{1}{\sqrt{\text{det}(\Lambda (s))}}\text{tr}(\Lambda (s)\iota (\text{diag}(1,-1,1)G(s)))ds). \end{gathered}$$

B.8. Proof of Corollary 1

Note that it is well-known that the covariance function of the derivative of a differentiable field with covariance function $\mathfrak{c}$ is given by $\dot{\mathfrak{c}}\left(s,s^{\prime }\right)=D_s^1{D}_{s^{\prime }}^1\mathfrak{c}\left(s,s^{\prime }\right)$. Moreover, using the moment formula for multivariate Gaussian fields we have that

$$\begin{gathered} \text{cov}\left[{\left(Z^{\prime }(s)\right)}^2,{\left(Z^{\prime }\left(s^{\prime }\right)\right)}^2\right]=\mathbb{E}\left[\left({\left(Z^{\prime }(s)\right)}^2-\dot{\mathfrak{c}}(s,s)\right)\left({\left(Z^{\prime }\left(s^{\prime }\right)\right)}^2-\dot{\mathfrak{c}}\left(s^{\prime },s^{\prime }\right)\right)\right] \\ =\mathbb{E}\left[{\left(Z^{\prime }(s)\right)}^2{\left(Z^{\prime }\left(s^{\prime }\right)\right)}^2\right]-\dot{\mathfrak{c}}(s,s)\dot{\mathfrak{c}}\left(s^{\prime },s^{\prime }\right) \\ =\dot{\mathfrak{c}}(s,s)\dot{\mathfrak{c}}\left(s^{\prime },s^{\prime }\right)+2\dot{\mathfrak{c}}\left(s,s^{\prime }\right)-\dot{\mathfrak{c}}(s,s)\dot{\mathfrak{c}}\left(s^{\prime },s^{\prime }\right) \\ =2\dot{\mathfrak{c}}\left(s,s^{\prime }\right). \end{gathered}$$

Combining this with the observation that the variance of the zero mean Gaussian random variable $\frac{1}{2}{\int }_S\frac{G(s)}{\sqrt{\Lambda (s)}}ds$ is given by

$${\tau }^2=\frac{1}{4}{\int }_S{\int }_S\frac{\text{cov}\left[{\left(Z^{\prime }(s)\right)}^2,{\left(Z^{\prime }\left(s^{\prime }\right)\right)}^2\right]}{\sqrt{\Lambda (s)\Lambda \left(s^{\prime }\right)}}dsd{s}^{\prime }$$

yields the claim.

B.9. Proof of Theorem 8

We want to apply Pollard (1990, Theorem 10.6). Therefore, except for the indices we adapt the notations of that theorem and define the necessary variables. Recall that max_s∈S σ(s) ≤ B < ∞. We obtain

$$\begin{gathered} f_{Nn}(s,h)=\frac{1}{\sqrt{N}P}\sum _{p=1}^P\left(\sigma \left(s_p\right)Z_n\left(s_p\right)+{\epsilon }_{np}\right)K\left(s-s_p,h\right) \\ {F}_{Nn}=\sqrt{\frac{2}{N}}\left(B\underset{s\in S}{\text{max}}\left|Z_n(s)\right|+\underset{s\in S}{\text{max}}\left|{\epsilon }_n(s)\right|\right) \\ {X}_N(s,h)=\sum _{n=1}^N{f}_{Nn}(s,h). \end{gathered}$$

We have to establish the assumptions (i), (iii) and (iv) as (v) is trivially satisfied in our case and (ii) is Assumption (18). As discussed in Degras (2011, p.1759) the manageability (i) follows from the inequality

$$\begin{gathered} \left|f_{Nn}(s,h)-f_{Nn}\left(s^{\prime },h^{\prime }\right)\right|\le \frac{1}{\sqrt{N}}\sqrt{\frac{1}{P}\sum _{p=1}^P{\left(\sigma \left(s_p\right)Z_n\left(s_p\right)+{\epsilon }_n\left(s_p\right)\right)}^2}\sqrt{\frac{1}{P}\sum _{p=1}^P{\left(K\left(s-s_p,h\right)-K\left(s^{\prime }-s_p,h^{\prime }\right)\right)}^2} \\ \le \sqrt{\frac{2}{N}}\left(B\underset{s\in S}{\text{max}}\left|Z_n(s)\right|+\underset{s\in S}{\text{max}}\left|{\epsilon }_n(s)\right|\right)L{\Vert (s,h)-\left(s^{\prime },h^{\prime }\right)\Vert }^{\alpha } \\ =L{F}_{Nn}ϵ, \end{gathered}$$

if ‖(s, h) − (s′, h′)‖ < ϵ^1/α. Assumption (iii) follows since we can compute

$$\sum _{n=1}^N\mathbb{E}\left[F_{Nn}^2\right]=N\mathbb{E}\left[F_{N1}^2\right]\le 4B^2\mathbb{E}\left[\underset{s\in S}{\text{max}}{\left|Z_1(s)\right|}^2\right]+4\mathbb{E}\left[\underset{s\in S}{\text{max}}{\epsilon }_1^2(s)\right]<\infty$$

and (iv) is due to

$$\sum _{n=1}^N\mathbb{E}\left[F_{Nn}^{2}I\left(F_{Nn}>ϵ\right)\right]=N\mathbb{E}\left[F_{N1}^{2}I\left(\sqrt{N}{F}_{N1}>\sqrt{N}ϵ\right)\right]\stackrel{N\to \infty }{\to }0$$

for all ϵ > 0, which follows from the convergence theorem for integrals with monotonically increasing integrands and the fact that by Markov’s inequality

$$\mathbb{E}\left[I\left(\sqrt{N}{F}_{N1}>\sqrt{N}ϵ\right)\right]=\text{Pr}\left(\sqrt{N}{F}_{N1}>\sqrt{N}ϵ\right)\le \frac{\mathbb{E}\left[\sqrt{N}{F}_{N1}\right]}{\sqrt{N}ϵ}\stackrel{N\to \infty }{\to }0,$$ (23)

for fixed ϵ > 0.

The weak convergence to a Gaussian field now follows from Pollard (1990, Theorem 10.6).

B.10. Proof of Proposition 2

The first step is to establish that for each N the field with ${\mathcal{C}}^3$-sample paths

$$\tilde{Z}(s,h)=\frac{1}{P}\sum _{p=1}^P\left(\sigma \left(s_p\right)Z\left(s_p\right)+\epsilon \left(s_p\right)\right)K\left(s-s_p,h\right),$$

has finite second $\mathcal{C}(S)$-moment. Moreover, the constant is uniformly bounded over all N. Additionally, we require that the field itself and its first derivatives are $\left({\mathcal{L}}^2,\delta \right)$-Lipshitz again uniformly over all N, since then the same arguments as in Lemma 11 will yield the consistency of the estimators of the LKCs from Theorem 6. Therefore, note that

$$\begin{gathered} |\tilde{Z}(s,h)|\le \frac{1}{P}\sum _{p=1}^P\left|\sigma \left(s_p\right)Z\left(s_p\right)+\epsilon \left(s_p\right)\right|\cdot \left|K\left(s-s_p,h\right)\right| \\ \le \sqrt{\frac{1}{P}\sum _{p=1}^P{\left(\sigma \left(s_p\right)Z\left(s_p\right)+\epsilon \left(s_p\right)\right)}^2}\sqrt{\frac{1}{P}\sum _{p=1}^P{\left(K\left(s-s_p,h\right)\right)}^2} \\ \le \left(B\underset{s\in S}{\text{max}}|Z(s)|+\underset{s\in S}{\text{max}}|\epsilon (s)|\right)|K(s,h)|. \end{gathered}$$

This yields using (a + b)² ≤ 2(a² + b²) that

$$\mathbb{E}\left[\underset{(s,h)\in S\times \mathcal{H}}{\text{max}}|\tilde{Z}(s,h){|}^2\right]\le 2\left(B^2\mathbb{E}\left[\underset{s\in S}{\text{max}}|Z(s){|}^2\right]+C\right)\underset{(s,h)\in S\times \mathcal{H}}{\text{max}}K{(s,h)}^2<\infty ,$$

where the bound is independent of N. Basically, the same argument yields the $\left({\mathcal{L}}^2,\Vert \cdot \Vert \right)$-Lipshitz property for $\tilde{Z}(s,h)$ and all of its partial derivatives up to order 3 with a bounding ${\mathcal{L}}^2$ random variable independent of N. The differentiability of the sample paths of the limiting Gaussian field follows again from Lemma 12(i).