Statistical and Machine Learning Methods Applied to the Prediction of Different Tropical Rainfall Types

Abstract

Predicting rain from large-scale environmental variables remains a challenging problem for climate models and it is unclear how well numerical methods can predict the true characteristics of rainfall without smaller (storm) scale information. This study explores the ability of three statistical and machine learning methods to predict 3-hourly rain occurrence and intensity at 0.5° resolution over the tropical Pacific Ocean using rain observations the Global Precipitation Measurement (GPM) satellite radar and large-scale environmental profiles of temperature and moisture from the MERRA-2 reanalysis. We also separated the rain into different types (deep convective, stratiform, and shallow convective) because of their varying kinematic and thermodynamic structures that might respond to the large-scale environment in different ways. Our expectation was that the popular machine learning methods (i.e., the neural network and random forest) would outperform a standard statistical method (a generalized linear model) because of their more flexible structures, especially in predicting the highly skewed distribution of rain rates for each rain type. However, none of the methods obviously distinguish themselves from one another and each method still has issues with predicting rain too often and not fully capturing the high end of the rain rate distributions, both of which are common problems in climate models. One implication of this study is that machine learning tools must be carefully assessed and are not necessarily applicable to solving all big data problems. Another implication is that traditional climate model approaches are not sufficient to predict extreme rain events and that other avenues need to be pursued.

1. Introduction

Rainfall is fundamental to water resources, agriculture, and ecosystems and can cause massive damage in the form of too little or too much rain. However, rainfall can vary strongly in space and time making it hard to measure and even harder to predict. The rain rate distribution of most global climate models (GCMs) is far different than observed, with too much weak rain and not enough heavy rain (e.g., Stephens et al., 2010; Fiedler et al., 2020), which hinders predictions of extreme events. The goal of this study is to analyze the ability of advanced statistical and machine learning techniques to predict the occurrence and rain rate distribution of tropical rainfall using environmental temperature and humidity profiles as predictors. A salient question is if any of these techniques can improve upon existing GCM parameterizations in producing accurate rain characteristics from large-scale variables.

Rain is produced two main ways in GCMs. Convective rain is output from the convective parameterization, which typically involves a trigger function to activate the convection and a closure assumption to determine the intensity of the convection; convective parameterizations are used to represent the aggregate effect of many subgrid-scale convective clouds (Arakawa, 2004). Some convective parameterizations have shallow and deep schemes, while some models produce shallow convection in the boundary layer parameterization, although these clouds are often non-precipitating (e.g., Bretherton and Park, 2008). The rest of the rain in a GCM is produced explicitly at the grid scale as large-scale rain using a microphysical scheme (e.g., Dai, 2006). Recent studies have shown that the manner in which a GCM distributes rain between the convective and large-scale components strongly impacts the model’s climate projections (e.g., Kooperman et al., 2018; Stephens et al., 2019; Norris et al., 2021). Thus, it is important to analyze rain types separately when assessing a GCM’s efficacy in producing realistic total rain fields, especially when considering changes to precipitation extremes in a warming climate.

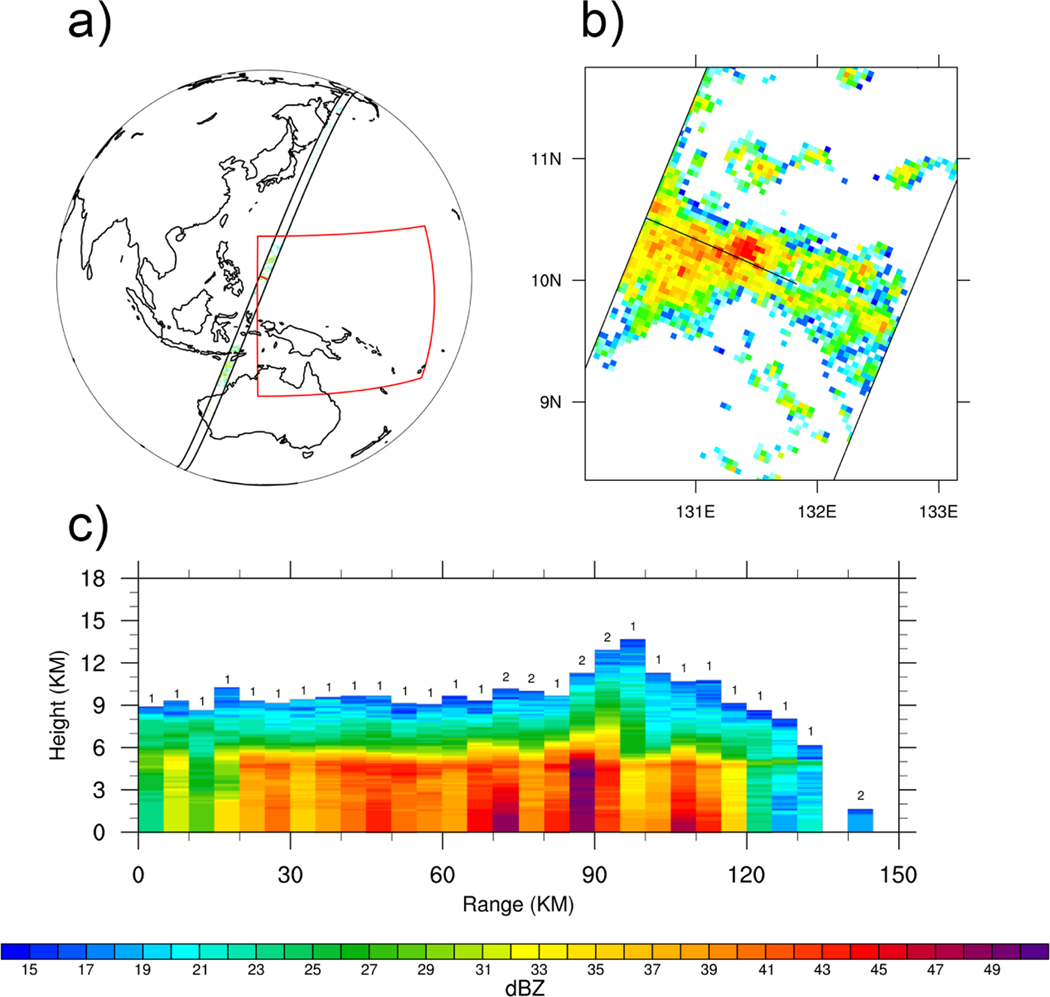
The real world does not produce rain the same way as GCMs, but it is possible to separate observed rainfall into types that have some analogies to GCM convective and large-scale rain. In particular, we focus on the separation of rain into deep convective, stratiform, and shallow convective components using radar measurements. Figure 1 shows an example convective system observed by the Global Precipitation Measurement (GPM; Hou et al., 2014) spaceborne radar over the tropical West Pacific. The most intense reflectivity in the horizontal and vertical indicates regions of active deep convection, while the more moderate and more horizontally homongeneous reflectivity indicates regions of less convectively-active stratiform rain (Houze, 1997; Schumacher and Houze, 2003a). Together, these rain types cover a region greater than 100 km that can span multiple GCM grid boxes. It has been shown that over half of the total rainfall in the tropics and warm season mid-latitudes comes from large, organized rain systems like this one (Nesbitt et al., 2006; Schumacher and Rasmussen, 2020). Shallow convection is ubiquitous over the tropical ocean and occurs regularly over some continental locations, but is much more isolated and does not produce nearly as much rain (Schumacher and Houze, 2003b; Funk et al., 2013).

Figure 1:

GPM radar reflectivity observations at 01 UTC on 4 February 2017. a) Black lines represent the GPM radar swath, red box is the bounds of the study area over the West Pacific. b) Horizontal cross section of reflectivity at 2 km AMSL near the red line in a). c) Vertical cross section of reflectivity taken along the black line in b). Stratiform profiles are labeled as 1, convective profiles are labeled as 2. The far right cell in the vertical cross section is considered shallow convection because its top is below the 0° C level (typically about 5 km in the tropics).

Radar-observed deep convection most closely aligns with rain produced by a model’s convective parameterization. A similar argument can be made for radar-observed shallow convection if a shallow convective scheme is included in the GCM formulation. GCM large-scale rain may also be equated to radar-observed stratiform rain that forms in the extratropics when large-scale lifting (like a warm front) is the main synoptic forcing and convection is minimal. In the tropics and warm-season midlatitudes, radar-observed stratiform rain forms as a result of the deep convection (Houze, 1997), so is not equivalent to GCM large-scale rain produced by a microphysics scheme that acts separately from the convective parameterization. Despite this physical disconnect over large swaths of the globe, radar-observed stratiform rain is often compared to GCM large-scale rain, but should only be done within the framework of comparing precipitation processes not produced by the strongest convection (either in the model or real world). As discussed by Mapes et al. (2006), these three rain types form the building blocks of larger convective systems ranging from mesoscale convective systems (with scales on the order of 100 km and 12 h) to the Madden-Julian Oscillation (with scales on the order of 1000 km and many weeks), so predicting each of these rain types is important to studies of weather and climate. However, the ability of GCMs to simulate these building blocks and their interactions remains a challenge, which was a main motivation of this work.

There are currently a number of efforts to use tools from data science to improve the representation of subgrid processes in climate models. Since there is often very limited amount of data available for unresolved processes, especially in situ measurements, many of these efforts apply machine learning techniques to conventional model parameterizations or a large ensemble of higher resolution simulations (Brenowitz and Bretherton, 2018; O’Gorman and Dwyer, 2018; Rasp et al., 2018). Training on conventional parameterizations can improve computational efficiency, but does not address the physical deficiencies. The higher resolution simulations also have their own built-in assumptions about a different set of smaller scale unresolved processes.

Yang et al. (2019) considered a data-centric approach, using a large satellite rainfall data set and reanalysis fields to show that a generalized linear model (GLM) can perform well at predicting the occurrence of different rain types in the tropics, but it fails at capturing the tail of the rain rate distributions. This is mainly due to the restriction of parametric probability distributions used for the rain rates. Although distributions such as Gamma, log-normal, or Weibull are commonly used for rain rates due to their shape of density curves with long tails, they are often not flexible enough to capture the heaviest rain rates. This study builds on Yang et al. (2019) by applying two machine learning techniques, i.e., a random forest (RF) and deep feedforward neural network (NN), to a similar data set to determine how well these methods compare to one another and the GLM in predicting rain occurrence and capturing the high rain rate end of the distribution for multiple rain types. RL and NN can potentially handle nonlinearities better, and are not constrained to follow a specific probability distribution like GLM. The purpose of the next section is to provide general background on each method so that readers can better understand the implications of the results shown in Section 4.

2. Statistical and Machine Learning Methods

2.1. Generalized Linear Model

GLMs (McCullagh and Nelder, 1989) are a popular class of statistical models used to predict a response variable whose mean is assumed to be some parametric function of covariates. It is a more general modeling framework than multiple linear regression in that response variables may not follow a Gaussian distribution. Furthermore, unlike multiple linear regression models, which often use the least squares method for model fitting, GLMs are fitted using a maximum likelihood estimation (MLE) method. The MLE method utilizes the distribution function of the response, thus giving generally better statistical properties of estimators than the least squares method. A GLM does not necessarily assume a direct linear relationship between the response and covariates, and often their nonlinear relationship is introduced by a link function. For instance, a common log-link function assumes that the log transformed mean of the response can be written as a linear combination of covariates. Widely used examples for distributions and link functions for GLMs include logistic regression (a Bernoulli distribution for the response and log link), loglinear regression (a Poisson distribution for the response and log link), and Poisson regression (a Poisson distribution for the response and log link).

In this work, we adopt the two-step modeling procedure used in Yang et al. (2019). Two separate GLMs, a logistic regression and a Gamma regression, are employed to deal with rain occurrence and rain amount, respectively. At a given time, let p(s) denote the probability of rain at a grid point s. Then the rain event is assumed to follow a Bernoulli distribution with

$$\log \left\{\frac{p(\mathbf{s})}{1-p(\mathbf{s})}\right\}={\beta }_0+{\beta }_1{z}_1(\mathbf{s})+\cdots +{\beta }_p{z}_p(\mathbf{s}),$$ (1)

where z_i(s) denotes predictors (i.e. covariates) at the grid point s. If y(s) denotes the rain amount at s, we assume that y follows a Gamma distribution with

$$\log [\text{E}\{y(\text{s})\}]={\eta }_0+{\eta }_1{z}_1(\text{s})+\cdots +{\eta }_p{z}_p(\text{s}).$$ (2)

For both models, parameters, including the coefficients β_i and η_i in (1) and (2), are estimated using the MLE method. We fit the GLM models using data aggregated over space and time altogether, similar to Yang et al. (2019). Although models (1) and (2) do not have explicit temporal structure in them, the temporal structure of the covariates effectively account for that of the responses, and it did not seem necessary to add more temporal terms in (1) or (2).

Statistical inference on the estimated parameters, including the significance of coefficients, is made possible by using GLMs, and the estimated coefficients are readily interpretable. On the other hand, a possible drawback of the approach outlined above is the linearity assumption given in (1) and (2), as well as the distribution assumption on rain amount. In particular, the Gamma distribution may be too restrictive to account for some heavy rain events (Yang et al., 2019). Other commonly used distributions such as log-normal and Weibull distributions have similar problems, due to their particular parametric forms and restrictions. In view of the potentially restrictive nature of GLMs, we explore two popular machine learning methods, RF and artificial NNs, which operate under much weaker (i.e., non-linear) assumptions compared to GLMs. RF and NNs offer the most competitive predictive performances in many applications, and are now standard tools for machine learning.

2.2. Random Forest

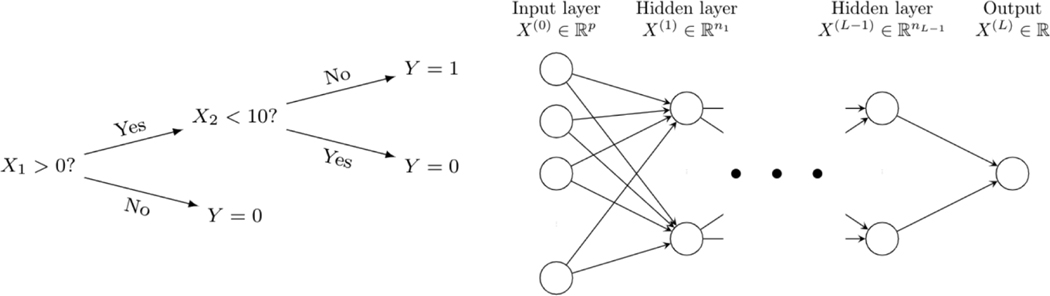
Random forest (Breiman, 2001) is an ensemble learning method that makes predictions based on multiple decision trees. A random forest is built upon these many decision trees. A decision tree is a simple model that predicts the label associated with a sample by a series of splitting rules. An example decision tree is shown in Figure 2, where a tree is used to determine if a binary response Y is 1 or 0. The root node has a splitting condition: “X₁ > 0?” If the observation fulfills this condition, it will be passed to the next condition: “X₂ < 10?” Otherwise, the tree predicts Y = 0. The procedure is applied recursively until the tree reaches a prediction of Y. For the construction of a decision tree, we refer the readers to Breiman (2001). In the above example, the underlying goal is classification, where the response is categorical. Decision trees can also be modified to handle a regression problem, where the response is quantitative.

Figure 2:

Illustrations for descision tree (left) and deep feedforward neural network (right).

The core idea of ensemble methods like RF is to combine weak predictive models to achieve strong predictive performance. A RF is usually trained with two “random” ideas. The first is bagging – for each tree, the training set is formed by resampling from the original data set with replacement. The second is feature randomness – each tree in a RF is trained with a random subset of features. Bagging lowers variance while feature randomization reduces the dependence across trees. They are beneficial to ensemble learning. The prediction of the RF is obtained by a majority vote over the predictions of the individual trees.

Similar to the GLM analysis, a two-step modeling procedure was implemented for RF in our work. Namely, we trained an RF model on rain occurrence and another RF model on rain amount. For both models, we used the default setting of the “randomForest” function from the R package“randomForest”, except that we restricted the number of decision trees to 100 when predicting rain amount in order to alleviate the computational burden. As opposed to GLM, RF is a nonparametric method and can produce a highly nonlinear regression function. On the other hand, it is significantly more difficult to interpret the results of the RF model, although RF provides a measure of variable importance. In practice, one might also examine individual classification trees within the random forest to understand the results.

2.3. Neural Network

In recent years, artificial NNs (especially those with deep architecture) have become one of the most prominent models for complicated functions. A NN is based on a collection of connected nodes. Different ways to connect the nodes result in different NN architectures, such as fully connected (Hsu et al., 1990), sparsely connected (Ardakani et al., 2016), convolutional (Lo et al., 1995), and recurrent (Mikolov et al., 2010). Nodes are typically organized into layers, which can be classified as input, hidden and output. Networks with multiple hidden layers are said to have deep architectures, and are referred to as deep NNs. Deep architectures are commonly used nowadays, due to their strong empirical performance in many areas.

In our analysis, we adopt a deep feedforward NN in which consecutive layers are fully connected (Svozil et al., 1997; Schmidhuber, 2015) because it is one of the most standard forms of deep NN. Figure 2 depicts an example. We use $X^{(l)}\in {ℝ}^{n_l}$ to represent the nodes at layer l, where n_l is the number of nodes at layer l. Take X⁽⁰⁾ as the input and X^(L) as the output. The hidden and output layers are generated as follows. Let $x_k^{(l)}$ be the node k of layer l, where l = 1, …, L and k = 1, …, n_l. Then

$$x_k^{(l)}={\sigma }_k^{(l)}\left(b_k^{(l)}+\sum _{i=1}^{n_{l-1}}{w}_{i,k}^{(l)}{x}_k^{(l-1)}\right),$$

Where ${\sigma }_k^{(l)}$ is the activation function, and $b_k^{(l)}$ and $w_{i,k}^{(l)}$ are parameters to be trained by the data. For simplicity, it is common to use the same activiations within the same layer: ${\sigma }^{(l)}:={\sigma }_k^{(l)}$, for k = 1, …, n_l.

Similar to the previous two models (GLM and RF), we adopted the two-step approach for the NN analysis. More specifically, we trained one NN to perform the binary classification on rain occurrence and another NN using training samples with positive rain values only to predict the rain amount. We considered different number of layers for NN. More specifically, we considered L = 2, 3, …, 10. Note that n₀ = 80 and n_L = 1 for all L since they are representing the input size and the output size. For any existing hidden layer, the number of nodes are set as follows: n₁ = 40, n₂ = 20, n₃ = ··· = n_L−2 = 6 and n_L−1 = 3. For instance, for L = 1, there is only one hidden layer and so only n₁ is relevant. For l = 1, …, L −1, the corresponding activation functions ${\sigma }_k^{(l)}$ were chosen as the rectified linear unit (ReLU) functions $(\sigma (x)=\max (0,x))$. The activation function for the output layer had to be chosen based on the response type, i.e., classification or regression. We used ${\sigma }^{(L)}(x)=1/(1+\exp (-x))$ for the classification, while we used the exponential function for the regression since the response is positive. For the loss functions, we adopted the binary cross entropy loss for the classification and the mean squared error for the regression. As for the estimation of the NN, we adopted mean square error as the loss function and trained the network via the popular algorithm Adam (Kingma and Ba, 2014).

To prevent over-fitting, we also adopted the dropout procedure, which is a common regularization method for training deep neural networks (Baldi and Sadowski, 2013; Gal et al., 2017). In the dropout procedure, neurons are stochastically dropped out during the training at each layer. In our implementation, the dropout rate was set to be the same at every layer and three possible values 0, 0.2, 0.5 were considered. Both the dropout rate and the number of layers, L, were regarded as the hyper-parameters and were chosen via a validation procedure — we randomly separated 20% of the training data as the validation set to select the best combination of dropout rate and number of layers.

3. Training and Test Data

We used two years of observations from the GPM dual-frequency precipitation radar (DPR) to calculate rain occurrence and rain rates, which were the predictands of the study. The full year of 2017 was used for training and the full year of 2018 was used for testing. The rain type classifications (i.e., deep convective, stratiform, and shallow convective; Funk et al., 2013) and associated rain rates were retrieved from 2ADPR V6 files. Figure 1 shows an example orbit from the GPM radar with all three rain types present. We regridded the DPR orbital rain observations, which are made at a 5-km footprint scale over a 245-km swath, to 0.5° horizontal resolution and 3-hourly temporal resolution. Note that the 3-hourly rain rate represents an instantaneous value and not a 3-hour average. The predictors for the study were temperature and humidity fields at 40 pressure levels from the MERRA-2 reanalysis (Rienecker et al., 2011) for 2017 and 2018. The MERRA-2 data was regridded to a similar horizontal and temporal resolution as the DPR data and points were only analyzed if a DPR orbit occurred in a grid during the 3-hour period. We limited our domain to the tropical West Pacific (130°E −180°E, 20°S −20°N; Figure 1a), but found similar results in the tropical East Pacific (not shown). Overall, we had 569,596 training samples and 572,968 test samples.

The training and test data are generally similar to the observational data sets used in Yang et al. (2019). However, we used rain observations from the GPM DPR instead of the Tropical Rainfall Measuring Mission (TRMM) precipitation radar (PR) because of the DPR’s higher sensitivity to weaker rain rates and thus better shallow convective rain retrievals (Hamada and Takayabu, 2016). We also used a slightly higher time resolution (3 hours vs 6 hours) to better isolate environment-rain relationships and we used all times of day instead of just 0–6 UTC to capture the full range of diurnal conditions (e.g., Hirose et al., 2008). We chose a warm ocean region with only small land amounts (i.e., New Guinea and the northwest coast of Australia) as a baseline test for our techniques, but a natural follow-on study would be over a tropical land region such as the Amazon or Congo. Finally, we only used temperature and humidity as predictors because they accounted for the majority of the predictive performance by the GLM in Yang et al. (2019), who also tested other environmental variables such as horizontal wind profiles and surface fluxes. We further utilized the full temperature and humidity profiles rather than just the first three empirical orthogonal functions so that the machine learning techniques had more flexibility in determining the vertical relationship of the predictors to the surface rain rate.

4. Prediction Results

4.1. Rain occurrence

When solving for occurrence, we treat grids with extremely small rain amounts as no-rain cases to avoid retrievals from the radar likely associated with clutter or noise. For each rain type, we selected a rain rate cutoff that accounts for less than 1% of the total rain amount in the training data. The cutoff values are 0.056, 0.0395, and 0.0087 mm/hr for deep convective, stratiform, and shallow convective rain, respectively. As will be illustrated in the next section, the three rain types produce different ranges of rain rate intensity, which is why separate cutoff values are needed for each rain type.

Rain does not very occur often at the time and space scales being considered in this study (i.e., 3 hourly and 0.5°), so there are significantly more no-rain cases than rain cases. To deal with this imbalanced classification problem, we created a “balanced” training data set by using a random under-sampling procedure. That is, we randomly sample the no-rain cases until we have the same number of no-rain and rain samples in our training data set. Note that we classify rain/no-rain cases for each rain type separately.

The top four rows of Table 1 show how well the three statistical and machine learning methods described in Section 2 predict no-rain and rain cases for each rain type. The actual time the GPM radar observed each rain type over the West Pacific is indicated by adding the false negative and true positive values (i.e., about 16%, 24%, and 35% for deep convective, stratiform, and shallow convective rain, respectively). All three methods do a reasonable job at distinguishing truly raining cases, with GLM slightly outperforming the other two methods. However, all methods suffer from a relatively high false positive rate (i.e., predicting rain too often), which is a persistent problem in most climate models as well (Fiedler et al., 2020). While GLM had the best true positive predictions, it had the worst true negative predictions (i.e., predicting no rain when no rain is observed). RF had the best true negative prediction and NN fell between the two other techniques. The results discussed above are obtained by taking the cutoff probability as 0.5 for the three methods. More specifically, when the predicted probability for a test case is larger or equal to 0.5, we treat it as “rain”; otherwise, it is considered as “not rain”. One may also choose different cutoffs. We provide the receiver operating characteristic (ROC) curves in Figure 4 in the Appendix, which illustrates the performance of the three methods with respect to different cutoffs.

Table 1:

The top four rows describe the performance of the occurrence predictions for each rain type by each method. The values in each column are the fraction of the total cases that fall into each prediction category and sum to one, while bold values are the highest correct predictions. The bottom two rows quanitify the accuracy of the the rain rate (mm/hr) prediction in terms of root mean square error (RMSE) and mean absolute error (MAE), with bold values representing the smallest errors among the three methods.

	Deep convective			Stratiform			Shallow convective
	GLM	RF	NN	GLM	RF	NN	GLM	RF	NN
True Negative	0.485	0.568	0.536	0.474	0.529	0.502	0.325	0.415	0.323
False Negative	0.036	0.054	0.054	0.052	0.069	0.076	0.084	0.137	0.106
True Positive	0.122	0.103	0.103	0.188	0.171	0.164	0.267	0.214	0.245
False Positive	0.357	0.275	0.387	0.286	0.231	0.306	0.324	0.234	0.325
RMSE	0.758	0.975	0.749	0.624	0.730	0.619	0.095	0.105	0.094
MAE	0.405	0.504	0.385	0.295	0.367	0.275	0.058	0.062	0.059

4.2. Rain rate distributions

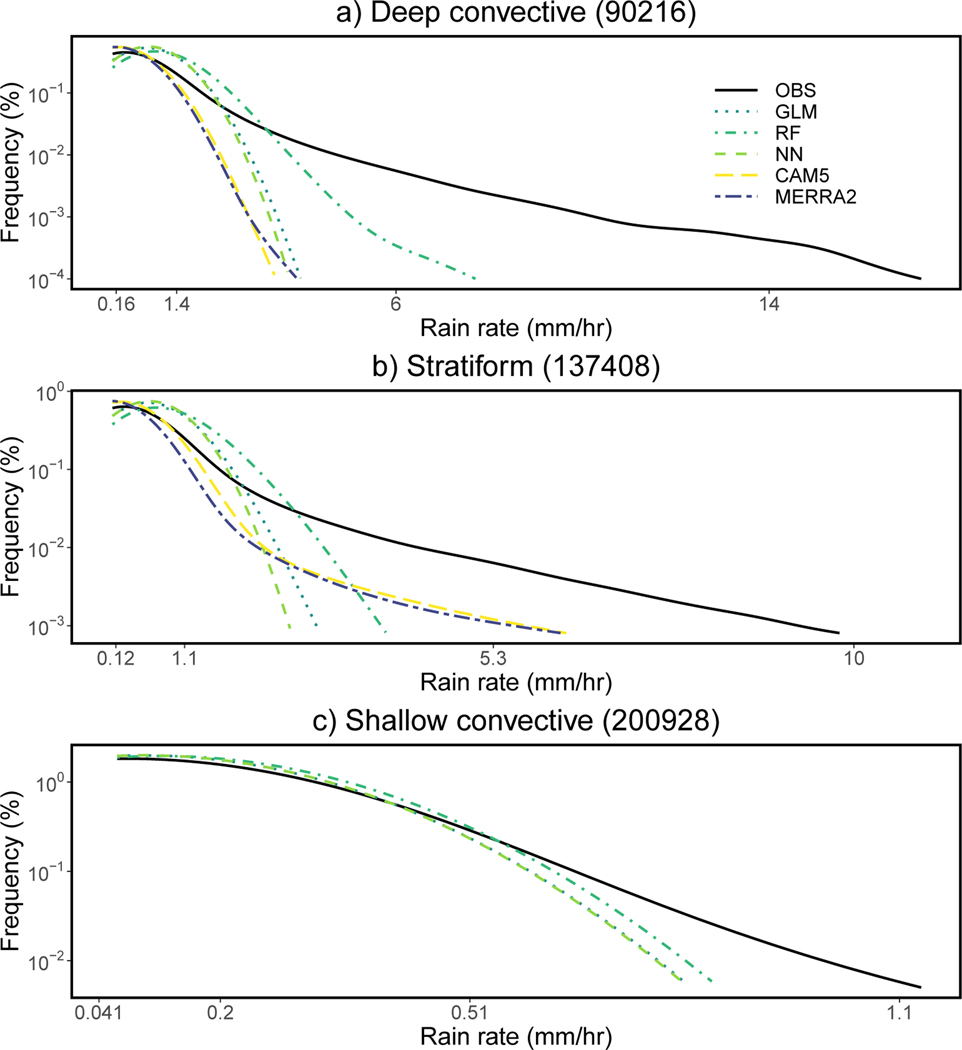
We next apply the statistical and machine learning methods to predict the rain rate distribution of the three rain types. Figure 3 compares the prediction of each method to the “True” distribution observed by the GPM DPR. Note that the GPM-observed 99.9% rain rate varies by rain type with values of 14, 10, and 1.1 mm/hr for deep convective, stratiform and shallow convective rain, respectively. Even though shallow convective rain has the highest occurrence, it has much smaller rain amounts over a 0.5° grid because shallow convection doesn’t cover much of a grid and is composed of more lightly raining cells. Stratiform rain is also normally less intense than deep convective rain on a pixel-by-pixel basis but because it tends to cover more area than deep convective cells, stratiform rain amounts approach deep convective values at 0.5° resolution.

Figure 3:

GPM-observed and model-predicted 3-hourly, 0.5° rain rate distributions over the tropical West Pacific for a) deep convective, b) stratiform, and c) shallow convective rain. Values in parentheses are the total cases in the testing data that rain. Values on the x-axis for the three plots are the 50, 90, 99, and 99.9% quantiles of the rain rate distribution, respectively.

Figures 3a and b show that all three methods (indicated by different green lines) tend to underestimate weaker rainrates (i.e., around the 50% quantile or first tick mark) in the deep convective and stratiform distributions, shifting to overestimations around the 90% quantile (or second tick mark). Between the 90 and 99% quantiles, there is a rapid drop off in prediction counts compared to the true distribution with NN and GLM showing the most rapid decrease. RF is the only technique to produce predictions past the 99% quantile for deep convective rain, the category associated with the most extreme rain amounts. All methods do better predicting the shallow convective rain rate distribution (Figure 3c) with the drop-off in counts not occurring until after the 99% quantile.

To provide context on how the observed and predicted rain rate distributions in Figure 3 compare to standard GCM output, we obtained a year of data from the NCAR Community Atmospheric Model, version 5 (CAM5; Neale et al., 2013). We use model output for 2003 instead of 2018 because it was readily available. While there may be small year-to-year variations in the rain rate distributions over the West Pacific, we do not expect them to be large, especially since neither 2003 or 2018 experienced strong El Niño or La Niña events. The original rain rate data had a 25 × 25km resolution so we aggregated rain rates to 0.5° grids to match our analysis. Hourly total precipitation (PRECT) and convective (PRECC) precipitation rates were also aggregated into 3-hourly rain rates. We use PRECC to represent deep convective rain and the difference between PRECT and PRECC (PRECT-PRECC) to represent the large-scale rain (i.e., rain that is produced from the grid-scale microphysics parameterization rather than via the subgrid-scale convective parameterization). GCMs do not typically calculate a separate shallow convective rain rate, but there are only small differences between the GPM convective deep rain rate distribution compared to when we combine the observed deep and shallow convective rain rate distributions (i.e., deep convective rain dominates the convective rain rate distribution in the tropical West Pacific). In addition, we included the MERRA-2 convective and large-scale + anvil rain rate distributions in Figure 3. Like CAM5, MERRA-2 does not provide a separate shallow convective rain rate.

As seen in Figure 3a, MERRA2 and CAM5 perform similarly and do not provide a good density estimation for deep convective rain (and are, in fact, close to the GLM and NN distributions). Recent work has shown that a stochastic version of the Zhang-McFarlane convective parameterization used in CAM5 can improve the deep convective rain rate distribution (Wang et al., 2021), but stochastic techniques are still not regularly implemented in standard GCM runs. CAM5 and MERRA2 large-scale rain appears to better characterize the GPM stratiform rain distribution (Figure 3b), although as discussed in the introduction, large-scale rain from GCMs and stratiform rain from radar are not considered to be be produced the same way in the tropics so caution must be taken in this comparison. Our CAM5 results are consistent with Kyselỳ et al. (2016) who showed that a suite of regional climate models highly underestimated extreme convective rain rates over central Europe, with a much better representation of extreme rain in the large-scale rain field.

To further assess predicted rain amounts using GLM, RF, and NN, we calculated the following metrics to measure the performance of the techniques:

1. Root mean squared error (RMSE) = $\sqrt{{\sum }_{i=1}^N{\left({\widehat{y}}_i-y_i\right)}^2/N}$ and

2. Mean absolute error (MAE) = ${\sum }_{i=1}^N\left|{\widehat{y}}_i-y_i\right|/N$,

where y_i is the observed rain amount for the i-th sample, and ŷ_i is the predicted rain amount for the i-th sample, for i = 1, …, N. Here samples are aggregated over space and time, and thus there are a total of N samples for each rain type. Note that MAE is in general less sensitive to large values compared to RMSE. Table 1 shows that RF has the highest (and thus worst) RMSE and MAE among the three techniques for each rain type. NN usually provides the smallest errors among the three methods, and GLM usually performs only slightly worse than NN.

5. Conclusions

Because of persistent GCM biases in rain occurrence and intensity, there is strong motivation to use empirical data to help understand and fix these biases. While training and testing data can come from higher resolution models, we chose to use a multi-year data set of rain observations from satellite radar along with temperature and humidity fields derived from a model constrained by observations (i.e., reanalysis). There are also a number of advanced statistical and machine learning techniques with which to analyze the available data. We chose a representative set that ranged in ease of implementation and interpretability: a generalized linear model, random forest, and deep feedforward neural network.

All three methods performed reasonably well in predicting the occurrence of each of the three tropical building block rain types: deep convective, stratiform, and shallow convective. Each method still predicted rain too often, although at moderate to strong rain rates instead of at the lightest rain rates more typically overpredicted by GCMs. Due to the high complexity of the model structure, regularization is usually needed for NN. With the dropout regularization, NN performed similarly to GLM in predicting the rain rate distributions of each rain type, while RF was somewhat more flexible in modeling the true response. However, RF produced the largest root mean square and mean absolute errors and the very highest rain rates were still underpredicted by all methods.

Our original goal was to determine the best overall method in order to implement it in a GCM to improve the representation of the full spectrum of tropical rain types. However, the results of each method were mixed and would require some sort of trade-off in more accurately characterizing the occurrence and intensity of each rain type. While there are other statistical and machine learning methods that could still be tested, we feel that this study highlights innate limitations in trying to deterministically predict rainfall probability distributions from standard grid-scale variables. That is, convection and its organization is simply not as parameterizable as we would like it to be, especially when attempting to predict extreme events. It has been argued that higher resolution climate models (on the order of a few km) may be necessary to solve this problem by voiding the need for the convective parameterization (e.g., Fiedler et al., 2020), but this path is computing intensive and doesn’t guarantee better solutions because of the remaining uncertainties in unresolved microphysics and turbulence. Thus, we advocate the continued exploration of creative, less resource-intensive solutions that include stochastic elements and unified schemes that don’t isolate rain types from one another (e.g., Cardoso-Bihlo et al., 2019; Hagos et al., 2020)

APPENDIX

A ROC curves

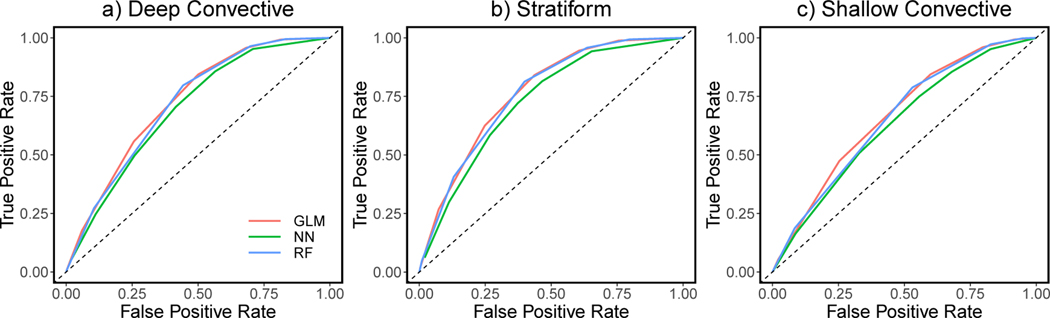
Figure 4 presents the ROC curves of the three methods for different rain types. ROC curves are created by plotting the true positive rate (TPR) against the false posifive rate (FPR) at various cutoff probabilities. The performance of the three methods are similar. GLM and RF have slightly larger TPRs than NN given the same FPRs.

Figure 4:

Receiver operating characteristic (ROC) curves obtained by GLM, RF and NN for a) deep convective, b) stratiform, and c) shallow convective rain.