Abstract
In the context of infectious disease transmission, high heterogeneity in individual infectiousness indicates that a few index cases can generate large numbers of secondary cases, a phenomenon commonly known as superspreading. The potential of disease superspreading can be characterized by describing the distribution of secondary cases (of each seed case) as a negative binomial (NB) distribution with the dispersion parameter, k. Based on the feature of NB distribution, there must be a proportion of individuals with individual reproduction number of almost 0, which appears restricted and unrealistic. To overcome this limitation, we generalized the compound structure of a Poisson rate and included an additional parameter, and divided the reproduction number into independent and additive fixed and variable components. Then, the secondary cases followed a Delaporte distribution. We demonstrated that the Delaporte distribution was important for understanding the characteristics of disease transmission, which generated new insights distinct from the NB model. By using real-world dataset, the Delaporte distribution provides improvements in describing the distributions of COVID-19 and SARS cases compared to the NB distribution. The model selection yielded increasing statistical power with larger sample sizes as well as conservative type I error in detecting the improvement in fitting with the likelihood ratio (LR) test. Numerical simulation revealed that the control strategy-making process may benefit from monitoring the transmission characteristics under the Delaporte framework. Our findings highlighted that for the COVID-19 pandemic, population-wide interventions may control disease transmission on a general scale before recommending the high-risk-specific control strategies.
Author summary
Superspreading is one of the key transmission features of many infectious diseases and is considered a consequence of the heterogeneity in infectiousness of individual cases. To characterize the superspreading potential, we divided individual infectiousness into two independent and additive components, including a fixed baseline and a variable part. Such decomposition produced an improvement in the fit of the model explaining the distribution of real-world datasets of COVID-19 and SARS that can be captured by the classic statistical tests. Disease control strategies may be developed by monitoring the characteristics of superspreading. For the COVID-19 pandemic, population-wide interventions are suggested first to limit the transmission at a scale of general population, and then high-risk-specific control strategies are recommended subsequently to lower the risk of superspreading.
This is a PLOS Computational Biology Methods paper.
1 Introduction
The response to infectious disease epidemics can be improved by understanding the characteristics defining the potential to transmit infections between individuals [1]. An intriguing aspect of infectious disease transmission is the circumstances under which the etiological agent is transmitted to a large number of secondary cases from merely a proportion of primary cases [2–6]. The number of secondary transmissions per index case shows levels of heterogeneity [7], while overdispersion refers to transmission with high heterogeneity [8]. Such situations are considered consequences of heterogeneity in individual infectiousness and stochasticity in disease transmission [9, 10] as documented by numerous superspreading events [3, 11–16]. For example, superspreading potentials and traceable events of COVID-19 transmission have frequently been reported in terms of a scale of k estimates [12, 17–19], which appear similar to those of previous epidemics of SARS and Middle East respiratory syndrome coronavirus (MERS-CoV) [5, 20–22]. The heterogeneity in transmission is determined by many factors including the characteristics of the host and the pathogen [23], the mode and setting of transmission [17, 24], the contact patterns [25], the viability of the pathogen, and the environmental components [8, 26–28]. Risk management and disease control strategies may vary and may be adjusted in response to different levels of individual heterogeneity in transmission [11, 29–31]. Thus, methods used to characterize heterogeneity in transmission are a public health priority to better understand patterns in infectious disease transmission [32] and in specifying informed control strategies [29, 33–36].
On one hand, the reproduction number R is commonly adopted to measure the average (or expected) number of secondary cases generated by a typical infectious individual [37]. The scales of R were sometimes given unwarranted priority in the assessment of pandemic potential [2, 38, 39], which means that R cannot reflect the scale of heterogeneity in individual infectiousness [40–43]. On the other hand, by acknowledging the heterogeneity in disease transmission patterns, a negative binomial (NB) distribution has been widely applied as a model for count data [44], particularly for offspring cases data that exhibit overdispersion [29], that is, with variance that is greater than the mean values. As such, the heterogeneity in transmission can be quantified by describing the distribution of secondary cases generated by each index case as the NB distribution with dispersion parameter, k [44]. The conceptualization of a NB distribution incorporates the stochastic effects of disease transmission [9] and the variability in individual infectiousness [29]. Mathematically, the framework for the NB distribution was formulated by compounding a Poisson distribution with a Gamma-distributed rate parameter, where the dispersion parameter k accounts for the variation in individual infectiousness reflected in the Gamma distribution [45]. This NB framework was widely adopted and yielded better fitting performance (against the Poisson distribution) in governing real-world observations of offspring cases or cluster sizes [17, 29, 40, 46]. A smaller k value suggests that transmission is more dispersive, and therefore outbreaks are likely to involve superspreading events [3]. When R is fixed, a smaller k corresponds to a lower effectiveness of non-pharmaceutical interventions in controlling epidemics [30, 47].
Regarding the description of heterogeneity in transmission from a theoretical standpoint, candidate models have been compared based on their fitting performances to real-world observations [29]. Inspired by the compounding relationship between Poisson and NB distributions, we considered that the composition of the Poisson rate can be modelled using a more generalized framework. In this study, to explain the heterogeneity in the distribution of offspring, we propose the application of the Delaporte distribution, which is a generalized version of the NB distribution and can also be derived by compounding the Poisson rate [48, 49]. By fitting several datasets of offspring (or secondary) cases, we illustrated that the Delaporte distribution led to an improved or equivalent fitting performance compared to the NB distribution, and this improvement becomes more evident as the sample size increases. For model selection using the likelihood ratio (LR) test, the Delaporte distribution demonstrated increasing statistical power but a conservative type I error rate for a wide range of sample sizes. We highlight the potential of the Delaporte distribution in quantifying the superspreading characteristics of infectious diseases and for recommending disease control strategies.
2 Methods
2.1 Decomposition of the variation in individual infectiousness
Following the classic theoretical framework of disease transmission [9], stochastic effects in transmission are considered to have a Poisson distribution [50], which is denoted X ~ Poisson(λ). Here, the random variable X denotes the number of secondary cases caused by a randomly-selected primary case, and the parameter λ is the Poisson rate. To account for the variation in individual infectiousness, the Poisson rate λ is a variable attribute among different hosts, and thus the distribution of X becomes a Poisson mixture, as proposed previously in [29].
We then decomposed the offspring number (X) of each index case into two components, including a fixed part (XF) and variable part (XV), such that XF + XV = X. Here, XF and XV were assumed to be independent variables and followed the compound Poisson distributions with rate parameters (λF and λV) that followed two Gamma distributions, so that λF ~ Gamma(mean = RF, dispersion = kF), and λV ~ Gamma(mean = RV, dispersion = kV). This was equivalent to the Poisson rate λ that was directly decomposed into two independent additive components denoted by λ = λF + λV [49], where both λF and λV are nonnegative values. As such, X is the sum of two independent negative-binomial distributed variables. Referring to the definition in [29], λ was conceptualized as the individual reproduction number [51], which is a random variable and represents the expected number of secondary cases caused by a (particularly) given primary case.
For the fixed component (XF), we modelled kF → ∞ assuming there was no variation in the fixed part (λF) of individual infectiousness. By denoting the probability mass function (PMF) of X as fD(X), the probability of generating function (PGF), gD(∙), was as follows:
Because the term kF vanishes, we denoted kV by k for convenience. The λF is the fixed component, which is a constant, and we defined RF = λF. The λV is the variable component, which follows a Gamma distribution with a mean RV and dispersion (or shape) parameter k. Mathematically, X ~ Poisson(λF + λV) on the condition that λV ~ Gamma(mean = RV, dispersion = k). Then, the PGF gD(∙) is defined as shown in Eq (1):
| (1) |
By identifying the PGF gD(∙), we find that the distribution of X was a Delaporte distribution, denoted by fD(∙), with parameters RF, RV, and k.
If we define R = RF + RV, R is the population reproduction number as the expected (or average) number of secondary cases caused by a (typical) primary case [52, 53], and thus we have R = E[X] = E[λ], where E[∙] is the expectation function. The RF and RV account for the fixed and variable components of the reproduction number (R), and thus we have R = E[X] = E[XF] + E[XV] = E[λ] = E[λF] + E[λV] = RF + RV, which is the mean of the Delaporte distribution fD(X). As such, XF and XV are components of the (observable) number of offspring cases X, λF and λV are components of the (latent) individual reproduction number λ, which is a variable, and RF and RV are components of the population reproduction number R, which is considered as a constant. In particular, the distribution function of λ has both a discrete part and a continuous part.
2.1.1 Delaporte distribution
Under the formulation of a Delaporte distribution [48], the probability mass function (PMF) fD(X) has three parameters, RF, RV, and k, and is given in Eq (2).
| (2) |
Here, Γ (∙) denotes the Gamma function, and the integer x denotes the number of secondary cases. Eq (2) can be considered as a ‘convolution’ between an NB distribution and a Poisson distribution.
Compared to the classic NB distribution proposed in [29], the Delaporte distribution can be restricted to an NB distribution if RF = 0, or equivalently RV = R. Similarly, if RV = 0 or k → ∞, the Delaporte distribution is restricted to a Poisson distribution [49]. Thus, either the NB or Poisson distribution is a special case of Delaporte distribution. Let the fraction of the fixed component ρ be defined as ρ = RF / R, and straightforwardly, we have 0 ≤ ρ ≤ 1. Equivalently, fD(X) in Eq (2) can also be formulated in an alternative version by replacing RF with ρR and RV with (1 – ρ)R, which is expressed in Eq (3),
| (3) |
Here, the three parameters for the Delaporte distribution change to R, ρ, and k. As such, the Delaporte distribution becomes a Poisson distribution when ρ = 1, or a NB distribution when ρ = 0, that is, .
The variance of X is derived as under the formula in Eq (3), or using the formula in Eq (2) in alternative. We derive for 0 ≤ ρ ≤ 1, and . Because Var[X] reflects the scale of variation in individual infectiousness, a smaller value for either ρ or k indicates a higher level of transmission heterogeneity or superspreading potential.
The implementation of Delaporte distribution is considered a generalization of the framework proposed in [29], and thus the interpretation of the dispersion parameter k generalizes its meaning in the NB distribution [45]. As the fixed part (RF) of R vanishes in the NB distribution, is the coefficient of variation (CV) of the Gamma distribution followed by the individual reproduction numbers (λ). In the context of the Delaporte distribution, the effect of k on shaping the variation of λ is restricted to the CV of its variable part (λV), which is also Gamma-distributed.
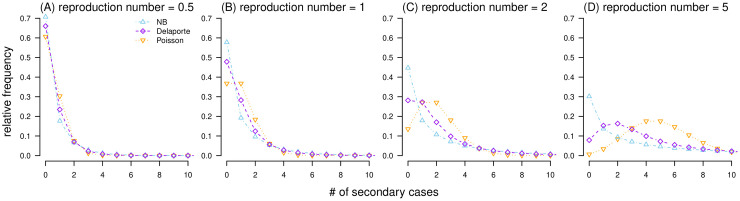
Differences in the PMF of Poisson, NB, and Delaporte distributions are shown in Fig 1.
Fig 1. Probability mass functions (PMF) of Poisson (in orange), negative binomial (in blue), and Delaporte (in purple) distributions.
In each panel, the dispersion parameter k is fixed at 0.5, and the fraction of fixed component ρ is fixed at 0.3.
2.1.2 Epidemiological measurements of heterogeneity in transmission
In epidemiological studies [3, 4, 17, 54], the heterogeneity in disease transmission is frequently reported as a general ‘20/80’ rule [21, 55], that is, according to the Pareto principle, whereby 20% of primary cases cause 80% of secondary cases [56]. With the three parameters of the Delaporte distribution, the transmission distribution profiles can be translated in the form of the ‘20/80’ rule. Following the framework proposed in [3, 57], the proportion (0 ≤ Q ≤ 1) of secondary cases can be determined by the transmission contributed by a proportion (0 ≤ P ≤ 1) of the most infectious primary cases [33], and vice versa, which was formulated in Eq (4).
, and the variable Z satisfies
| (4) |
Here, ⌊·⌋ denotes the floor function, which outputs the largest integer less than or equal to the given number. Note that the at the denominator is the mean of the Delaporte distribution, i.e., RF + RV or R. Conventionally, Q is fixed at 0.8, and the value of P is of interest. A smaller P indicates that a smaller but core proportion of high-risk cases may generate most offspring cases, indicating a higher level of heterogeneity in transmission.
Generally, Q is considered a function of P, which is bound between 0 and 1 for both Q and P. The concaveness of this ‘Q-P’ function is positively related to the level of transmission heterogeneity [29], which is constructed in the same manner as the Lorenz curve [58, 59]. For a perfectly homogeneous scenario, where X = R is a constant, we have Q = P.
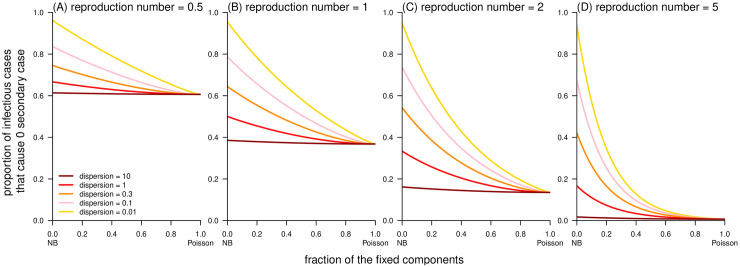
Another important measurement of transmission heterogeneity is the proportion of primary cases that generate 0 secondary cases, which is given as fD(0) = fD(X = 0) based on Eqs (2) or (3). With the reproduction number R fixed, a larger value of fD(0) implies a higher level of heterogeneity in transmission.
2.2 Datasets
We adopted six sets of contact tracing data and extracted the observations of offspring cases generated by each seed case for further exemplification. These included five COVID-19 datasets collected in mainland China (dataset #1), South Korea (datasets #2a and b), Hong Kong (dataset #3), and Tianjin, China (dataset #4), and one SARS dataset collected in Beijing, China (dataset #5). The transmission chains within each dataset were screened and then reconstructed with systematic and strict ‘inclusion-and-exclusion’ screening criteria based on plausible epidemiological evidence and rigorous consistency checks. All datasets were previously published and adopted for analysis in peer-reviewed studies.
2.2.1 Dataset #1: COVID-19 data in mainland China
For dataset #1, we used the COVID-19 contact tracing data published in [12], which was accessed freely via the public repository https://github.com/linwangidd/covid19_transmissionPairs_China/blob/master/transmission_pairs_covid_v2.csv. The same dataset was also adopted to estimate the dispersion parameter in [30].
Dataset #1 contains 1407 transmission pairs that were identified and reconstructed in previous studies, governmental news release, and official situation reports from 15 January to 29 February 2020 in mainland China. We identified 807 infectors with at least one secondary case and extracted the number of offspring infectees generated by each infector. A total of 1241 sporadic or terminal cases with 0 secondary cases were identified. Thus, dataset #1 includes observations of secondary case numbers with a sample size of 2048.
2.2.2 Datasets #2a and #2b: COVID-19 data in South Korea
For datasets #2a and #2b, we used the COVID-19 contact tracing data published in [33], which were shared by the authors. Both datasets shared the same source of information from the local public health authorities in South Korea, excluding the Daegu-Gyeongsangbuk region, where the data were not publicly reported.
Referring to [33], the original dataset was divided into different periods according to the onset dates of infectors. Dataset #2a contains 571 infectors with at least one secondary case and 830 sporadic or terminal cases during the epidemic period from 20 April to 16 October 2020. Dataset #2b contains 104 infectors and 240 sporadic or terminal cases occurring during the epidemic period from 19 January to 19 April 2020. As such, datasets #2a and #2b include observations of secondary case numbers with sample sizes of 1401 and 344, respectively.
2.2.3 Dataset #3: COVID-19 data in Hong Kong
For dataset #3, we used the COVID-19 contact tracing data published in [17], which was accessed freely via public repository, https://github.com/dcadam/covid-19-sse/blob/master/data/transmission_pairs.csv. Dataset #3 contains 169 transmission pairs that were identified and reconstructed according to governmental news releases and official situation reports published on 7 May 2020 in Hong Kong [60, 61]. There were 91 infectors, 153 terminal cases, and 46 local sporadic cases identified, and we extracted information on the number of offspring infectees generated by each infector. As such, dataset #3 included observations of secondary case numbers with a sample size of 290 cases.
2.2.4 Dataset #4: COVID-19 data in Tianjin, China
For dataset #4, we used the COVID-19 contact tracing data published in [19], which was freely obtained from the supplementary materials, accessed via https://www.mdpi.com/1660-4601/17/10/3705/s1. Dataset #4 contained 36 clusters of cases, including 47 cases of COVID-19, which were identified and reconstructed according to a governmental news releases and official situation reports between 21 January and 26 February 2020 in Tianjin, China [62], and each cluster was caused by a primary case. We identified seven infectors with 11 associated terminal cases and 29 local sporadic cases. Thus, dataset #4 contains observations of secondary case numbers with a sample size of 47.
2.2.5 Dataset #5: SARS data in Beijing, China
For dataset #5, we used the SARS contact tracing data of superspreading events from April to May 2003 previously published in [5], which was also attempted to estimate the dispersion parameter in [29]. The 34 cases in the first and second generation were considered the source cases, and we extracted the number of offspring infectees generated by each source case. Thus, dataset #5 contained observations of secondary case numbers with a sample size of 34.
2.3 Likelihood framework and statistical inference
We considered the number of secondary cases observed from each primary case with a sample size N. Considering the infector who generates j (≥ 0) secondary cases, or equivalently a cluster of cases with size (j + 1) in one transmission generation, we denoted the number of these infectors by nj. Then, similar to previous studies [3, 17], the likelihood of observing nj clusters with size (j + 1) was . Thus, we construct the overall log-likelihood function, ℓ, in Eq (5).
| (5) |
Hence, ∑j≥0 nj = N.
To match the real-world observations, we adopted a Bayesian fitting procedure with a Metropolis–Hastings Markov chain Monte Carlo (MCMC) algorithm with non-informative prior distributions for parameter estimation. Based on the likelihood in Eq (5), the MCMC was conducted with five chains and 100,000 iterations for each chain, including 40,000 iterations for the burn-in period, to obtain the posterior estimates. The convergence of each MCMC chain was visually checked using trace plots and the Gelman–Rubin–Brooks diagnostic quantitatively [63]. The median and 95% credible intervals (95%CrI) of the posterior distributions of RF, RV, and k were calculated and summarized for comparison with the previous estimates and across each dataset.
For comparisons with the classic Poisson or NB framework, we also repeated the estimation procedures by restricting RF = R (i.e., RV = 0) for the Poisson distribution, or RF = 0 (i.e., RV = R) for the NB distribution.
2.4 Evaluation of fitting and testing performance
In accordance with previous study [17], the Akaike information criterion (AIC) of MLE was used to measure the fitting performance of the Poisson, NB, and Delaporte distributions. Statistical evidence supporting the improvement in the fitting performance is claimed when the AIC units are reduced by 2 or more [40, 64].
The likelihood ratio (LR) test was adopted to assess the statistical significance of the improvement (in goodness-of-fit) of the Delaporte distribution versus the NB distribution. The test statistic (π*) of the LR test was given as follows.
where LNB denotes the likelihood of the NB distribution and L denotes the likelihood of the Delaporte distribution. Therefore, the p-value was calculated as the percentile of the Chi-squared distribution with degree of freedom df = 1 [11], which was expressed as follows:
Here, pChi (∙) denotes 1 minus the cumulative distribution function (i.e., survival function) of the Chi-squared distribution. Similar frameworks have also been adopted in previous studies [46, 64–66]. We considered p-value < 0.05 as a statistically significant improvement of the Delaporte distribution compared to the NB distribution, and thus the Delaporte distribution was selected as an optimization. Note that this appears statistically equivalent to having a significant estimate of 0 < ρ < 1, or both RF and RV > 0.
To test performance, the power and type I error of the LR test were evaluated. The testing power is calculated as the probability of p-value < 0.05 for fitting Delaporte distribution to the real-world observations compared to the NB distribution. We generated pseudo-datasets with different sample sizes by random sampling with replacement, a method similar to non-parametric bootstrapping, from the datasets described in Section 2.2. The type I error rate was calculated as the probability of p-value < 0.05 for fitting Delaporte distribution to the NB distributed datasets against the NB distribution. We generated the NB-distributed datasets with Monte Carlo random sampling from NB distributions. Note that statistically, the p-value < 0.05 from the LR test here was (roughly) equivalent to the AIC-based model selection with a cutoff of 2 units.
The parameter estimation of NB, and Delaporte distribution was obtained for each pseudo- or NB-distributed dataset using the approach described in Section 2.3. We summarized the test statistic (π*), power, and type I error rate based on the different sample sizes.
2.5 Extension of other types of real-world observations
Although helpful in estimating superspreading potentials, the number of offspring cases per index case in our dataset section was not always accurately reported [46]. In many situations, it is time or financially consuming for surveillance procedures to collect these datasets [67], and it is also difficult to maintain the consistency of reporting standards or secure sufficient samples [68]. Alternatively, the cluster size of next transmission generation, i.e., the one-generation cluster size, and the final outbreak size including a few seed cases are also commonly adopted to inform the characteristics of transmission. Thus, the theoretical frameworks in the following two sections were formulated to associate both types of real-world observations with the Delaporte distribution.
2.5.1 Next-generation cluster size
Cluster size data are frequently adopted to construct a statistical estimation [3, 40, 66]. Each one-generation cluster size observation is reported as the numbers of primary and secondary cases within a single transmission generation, which can also be simply translated into a number of primary cases and the cluster size of next-generation secondary cases. We discuss below the mathematical formulation of the distribution and likelihood function of a next-generation case cluster produced by a certain number of seed cases.
For a one-generation cluster of cases with size (i + j), that is, within a single transmission generation, where i (> 0) infectors generate j (≥ 0) infectees, we consider the summation of i independent and identically distributed (IID) random variables following the Delaporte distribution. Then, given the values of RF, RV, and k, the probability of observing an event in which i (≥ 0) infectors generate j (≥ 0) infectees can be formulated by employing the probability generating function (PGF) gD(∙) in Eq (1). Thus, the PGF of the PMF of infectees number (j) generated by i infectors, hD(∙), was as follows:
By identifying the PGF G(∙), we found that the distribution of the number infectees j generated by i infectors was also a Delaporte distribution, hD(j|i), with the parameters RFi, RVi, and ki, which was formulated as in Eq (6).
| (6) |
Alternatively, hD (∙) in Eq (6) could also be transformed by replacing RFi with ρRi and RV with (1 – ρ)R, which was expressed as follows,
It should be noted that for the new Delaporte distribution here, or in Eq (6), the fraction of fixed component (ρ) holds unchanged. As such, the likelihood function can be directly constructed by rearranging Eq (6) when one-generation cluster size observations were used to infer superspreading characteristics, that is, ρ and k.
When ρ approaches 0, the Delaporte distribution reduces to the NB distribution [49], and thus the ‘convolution’ in the equation above vanished, i.e., a = j. Then, the distribution of the number of infectees j generated by i infectors was from the NB distribution (hNB),
which was also derived or adopted in previous studies [3, 4, 11, 17, 19, 22, 40, 46, 69]. Likewise, by using the branching process approach to characterize the size distribution introduced in [40, 69, 70], the formulation of Eq (6) can also be derived by obtaining the j-th derivative of gD(∙) at 0 according to the property of PGF [71], which means the following relationship holds.
which can be shown algebraically or by mathematical induction (details omitted).
2.5.2 Final outbreak size with subcritical transmission
Many outbreaks occur in the form of isolated cases, short chains of transmission, or small clusters [3, 72], for example, diseases with weak human-to-human transmission [68] or vaccine-preventable infections in a vaccine-available setting [73]. Thus, offspring cases observations like those in our data section are limited and difficult to access because the transmission is unlikely to be sustained. These outbreaks are recognized as subcritical (or self-limited) outbreaks when the population reproduction number appears to be less than 1 [11, 69], that is, R < 1, namely a weakly transmitting disease. Although the final outbreak size is frequently linked to subcritical transmission, the final outbreak size may also be observable for supercritical transmission (R > 1), which we will introduce below more rigorously. Each self-limited outbreak includes a group of cases connected by an unbroken series of transmission events (or chains), which was named the ‘stuttering transmission chain’ in [11].
Except for the first i seed (or imported) cases, each case in a self-limited outbreak must be produced by one of the total cases with size denoted by c. According to [11], each secondary case must be linked to one of the other cases. Thus, the probability of observing a stuttering chain (or self-limited outbreak) size c (≥ i) including i (> 0) cases is (i/c) and multiplies the probability of c primary cases causing (c–i) secondary cases in one generation, i.e., . In other words, under the independent and identically distributed assumption of the branching process [71], the probability of having a stuttering chain of size c including i cases, denoted by ωD(c, i), is the (c − i)-th coefficient of , which is equivalent to . Hence, we have
The term is the normalization factor for the correction that i out of c cases are seed cases. This equation matches the relation derived in [40], which was also adopted in [57].
Rearranging the expression algebraically, we derive the exact formula of ωD(c, i) in Eq (7).
| (7) |
By replacing RFi with ρRi and RVi with (1 – ρ)Ri, an alternative version of ωD(c, i) was expressed as follows,
Therefore, the likelihood function can be constructed based on Eq (7) when stuttering chain size observations are available. When ρ approaches 0, the Delaporte distribution reduces to the NB distribution [49], and thus a = c − i. Thus, the probability of observing the final outbreak size c including i cases based on the NB distribution (ωNB),
Alternatively, the form below of ωNB(c, i) was previously adopted, which was mathematically equivalent.
Here, , and is the combination function calculating number of elements’ combinations with size (c − i) can be selected from a population of elements with size [kc + (c − i)]. This formula was also adopted previously in [57].
As reported in [11, 69], with adjustment, the formula in Eq (7) is also applicable for supercritical transmission. When R > 1, there is a chance of that the outbreak will never be extinct, which means the final outbreak size c becomes a defective random variable. Based on the property of the branching process, we may calculate the probability of outbreak extinction ε by solving ε = [gD(ε)i] [69]. Thus, the likelihood function can also be constructed by adjusting ε as the denominator for supercritical transmission.
Of particular interest is the final size of the outbreak generated by single seed case, i.e., i = 1, which is the probability of c (≥ 1) primary cases causing (c − 1) secondary cases, i.e., hD (j = c − 1|i = c) = hD (c − 1|c), as in Eq (8).
| (8) |
which was translated by rearranging Eq (6) and can alternatively be expressed as follows,
When ρ approaches 0, we have the NB version, ωNB(c, 1), as follows,
which is consistent with the formula derived or used in previous studies [3, 11, 33, 40, 69]. Note that c · Γ(c) = Γ(c + 1).
2.6 Theoretical framework of different control schemes
We formulated the following two control schemes (I) and (II) with same reduction amount in reproduction number and compared their respective control efficacies in reducing the risks of superspreading [outcome (I)] or outbreak [outcome (II)]. For both schemes, we considered the control effect (ξ) in terms of the fractional reduction in the reproduction number (R), where ξ = 0 reflects no control and ξ = 1 reflects complete blockage of transmission.
2.6.1 Scheme (I): Population-wide control
Population-wide control measures include intervention measures for all individuals, such as wearing a facemask [74], routine sterilization [75], social distancing [76], ‘work-from-home’ policy [77], and mass vaccination programs. Following [29], this control scheme (I) is expected to have the least efficacy in risk reduction and thus is treated as the baseline scenario.
In population-wide control measures, we consider that each individual reproduction number (λ) is reduced by a factor ξ (0 ≤ ξ < 1) for fixed and variable components (λF and λV), namely a relative reduction in the reproduction number. Then, on the population scale, the reproduction number (R) is also reduced by factor ξ, and thus the fixed and variable components become (1 − ξ)RF and (1 − ξ)RV, respectively. The controlled reproduction is (1 − ξ)R. Thus, the PMF of offspring cases (x) generated by one seed case is the following Delaporte distribution, .
The superscript ‘(1)’ is merely for labeling purposes rather than powering.
For the final outbreak size (c ≥ 1) generated by a single case under the control scheme (I), the PMF can be derived as follows,
which incorporated Eq (8) with .
2.6.2 Scheme (II): High-risk-specific control
High-risk-specific control measures target individuals with higher risk of superspreading potentials, e.g., individuals who frequently travel and contact others, and staff members sharing common facilities in the workplace. Thus, interventive measures such as city lockdowns and travel bans [78, 79], digital contact tracing at public places [80, 81], and gathering restrictions may interfere with the potential risks of spreading the disease by targeting high-risk individuals.
High-risk-specific control measures prioritize the variable component of the individual reproduction number (λV). Despite λF being unchanged, the value of λV is reduced so that individuals with higher risks of superspreading are less likely to achieve their potential for spreading diseases. To guarantee comparability with the population-wide control scheme, we maintain that controlled reproduction is (1 − ξ) R, and thus the value of RV reduces ξR units. Then, on the population scale, the reproduction number (R) is reduced by factor ξ. In the scenario that ξR > RV, equivalently ξ > RV / R = 1 – ρ or ξ + ρ > 1, the reduction will lead to RV = 0, the remaining amount (ξR − RV) for the reduction is then passed to the fixed component RF, and the Delaporte distribution reduces to the Poisson distribution with rate RF − (ξR − RV) = (1 − ξ)R. Thus, the PMF of offspring cases (x) generated by one seed case is formulated as follows, .
The superscript ‘(2)’ is merely for labeling purposes instead of powering.
For the final outbreak size (c ≥ 1) generated by a single case under the control scheme (II), the PMF can be derived as follows,
which incorporated Eq (8) with .
In particular, when the Delaporte distribution is restricted to the NB distribution, the distributions and become equivalent. When ξ = 0, , and .
2.6.3 Risk outcome (I): Superspreading event
The superspreading event is defined as the situation where an index case produces more secondary cases than the superspreading threshold (y). Following [29], when given R, the superspreading threshold y is calculated as the 99th percentile of the Poisson distribution with rate R [17]. Mathematically, y satisfies Pr(X ≤ y | X ~ Poisson(R)) = 0.99. For example, with the reproduction number in the range from 1.5 to 3 for COVID-19 [41, 82–85], the superspreading threshold (y) ranges from 5 to 8 secondary cases.
Because y can be determined for a given R, the risk of having a superspreading event is the probability that a seed case generates offspring cases equal to or greater than the superspreading threshold. When the control measures have no effect on reducing the reproduction number, i.e., ξ = 0, the risk of superspreading event rD is
Under control schemes (I) and (II), the risks of a superspreading event are as follows.
respectively. Therefore, the control efficacies can be compared within or between control schemes given the same values of R or ξ.
2.6.4 Risk outcome (II): Large-scale outbreak
A large-scale outbreak is defined as an outbreak with a final size (c) greater than 100, of which the threshold was adopted in [3, 29, 33]. Seeded by an index case, the final outbreak size c (≥ 1) is modelled in Eq (8) and is translated into and under control schemes (I) and (II), respectively.
When ξ = 0, the risk of large-scale outbreak rD is
Under control schemes (I) and (II), the risks of large-scale outbreak are
respectively.
2.6.5 Control efficacy
To compare different control strategies, the relative reduction in risk or relative efficacy approach was adopted [35]. For overdispersed transmission, most infected individuals do not contribute to the expansion of the epidemic, the final size of the outbreak could be drastically controlled by preventing relatively rare superspreading events [29]. Therefore, we measure the efficacy of control as the relative risk reduction (RRR) of having a superspreading event or leading to a large-scale outbreak in each seed case. As such, the following calculation applies to both risk outcomes (I) and (II).
Given R, the RRRs of control schemes (I) and (II) are
respectively. As such, both RRR(1)(ξ) and RRR(2)(ξ) should be interpreted as the control efficacy when there is a reduction in R by factor ξ against that there is no change in R.
For the comparison between two control schemes, the RRR of control scheme (II) against control scheme (I) is
Specially, when ρ = 0, that is, under the NB framework, RRR(1)(ξ) and RRR(2)(ξ) are equal or RRR(2,1)(ξ) = 0 for both risk outcomes (I) and (II).
We solved RRR(2,1)(ξ) as function of both ρ and ξ numerically for both outcomes with the dispersion k fixed at 0.2 for COVID-19.
3 Results and discussion
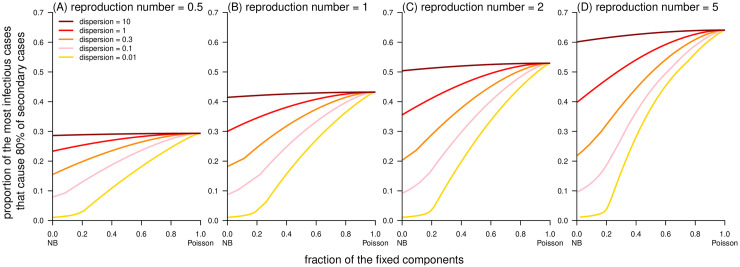
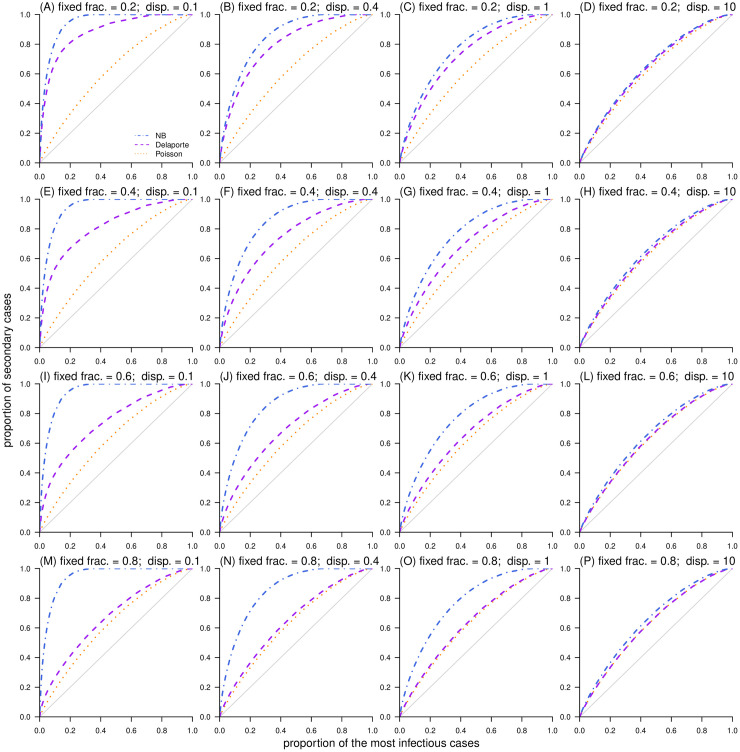
By definition, the Delaporte distribution allows the decomposition of the individual reproduction number (λ) into two independent and additive components (i.e., λF and λV). Although the offspring cases (XF) generated from the λF part are variable, the fixed component λF = RF is constant. In contrast, the variable component λV is a Gamma-distributed variable that accounts for the differences between individual cases and shares the same definition and interpretation as in the NB distribution [29, 45]. As a generalization of the NB distribution, the Delaporte distribution appears different from the Poisson and NB distributions given the same mean R and dispersion k (see Fig 1), which is due to the effect of the additional parameter ρ. The term ρ quantifies the fraction of the mean reproducibility that is fixed (or the same) across different cases. The classic NB model restricted the fixed (baseline) fraction λF to be 0, indicating that there must be a proportion of individuals with (almost) 0 transmissibility, which appears unrealistic. Conversely, the Delaporte distribution allowed λF to be a non-negative value, which is more flexible for complex situations. Theoretically, a lower value of either ρ or k indicates a higher scale of variability in individual infectiousness [29], that is, variance in the distribution of offspring. With other parameters fixed, a smaller ρ leads to a larger (smaller) proportion of the most infectious primary cases (P) that produce the most (zero) secondary cases (Figs 2 and 3). The consistent negative relationship between ρ and superspreading potential was demonstrated, and this relationship appears stronger as k decreases. The most heterogeneous transmission occurs when both k and ρ are small, and the Delaporte distribution approaches the NB distribution. With the same R and k, the Lorenz curve of the Delaporte distribution falls between those of the Poisson and NB distributions (Fig 4), where the position of the Delaporte distribution depends on ρ.
Fig 2. Simulation results of the proportion (P) of the most infectious cases that cause (Q =) 80% of secondary cases as a function of fraction of fixed component (ρ) generated from Delaporte distributions.
The ‘NB’ in the horizontal axis label stands for negative binomial (distribution).
Fig 3. Simulation results of the proportion of cases, i.e., fD(0), that cause 0 secondary case as a function of fraction of fixed component (ρ) generated from Delaporte distributions.
The ‘NB’ in the horizontal axis label stands for negative binomial (distribution).
Fig 4. Simulation results of the expected proportion of secondary cases (Q) due to the proportion of the most infectious cases (P), i.e., Lorenz curve, generated from Poisson (in orange), negative binomial (in blue), and Delaporte (in purple) distributions.
In each panel, the diagonal line shows the scenario of perfect homogeneity (i.e., uniform distribution). In each panel label, ‘fixed frac.’ is the fraction of fixed component (ρ), and ‘disp.’ is the dispersion parameter (k).
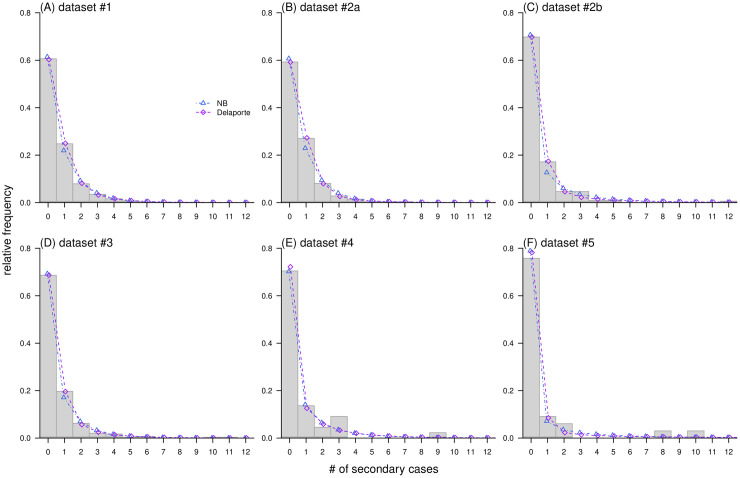
Fitting to several datasets of offspring (or secondary) cases, our estimates of NB parameters were consistent with previous studies (Table 1). When the RF estimate was greater than 0 for the Delaporte distribution, the dispersion k estimate became greater than the k estimate of the NB distribution. We found that the Delaporte distribution led to an improved or equivalent fitting performance compared to the NB distribution in terms of AIC values. The improvement in fitting performance was also reflected by the estimates of RF, or equivalently ρ (not shown as the main result). When the sample size is large, for example, datasets #1-#3, the Delaporte distribution has a higher goodness-of-fit in terms of likelihood values. The Delaporte distribution more accurately captures the observed offspring data than the NB distribution (Fig 5). In datasets #1-#3, the high-density regions of posterior distributions of ρ were roughly skewed from 0.1 to 0.5. However, the improvement in explaining the real-world dataset becomes weak, or even not evident as sample size decreases, for example, datasets #4 and #5, where the NB distribution also yields satisfactory fitting performance. For datasets #2b and #2a, collected from 19 January to 19 April 2020 and from 20 April to 16 October 2020, respectively. It is worth noting that the estimated medians of ρ increased from 0.21 to 0.56, while k only had minor changes. With the same scales of k and R, the increase in ρ would lead to a decrease in the overdispersiveness of disease transmission, as well as a reduction in the risk of superspreading. This finding was consistent with the conclusion in [33], which also discussed the impact of various local nonpharmaceutical interventions on the transmission characteristics of COVID-19 in South Korea.
Table 1. The summary of parameter estimates of offspring distribution in the existing literature and this study.
The ‘−2∙log(L)’ denotes twice of the negative log-likelihood. The highlighted estimates are considered as main results for Delaporte distribution (in red) and negative binomial (NB) distribution (in blue).
| disease | dataset | model distribution | reproduction number | components of Poisson rate | fitting performance | reference of estimation | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| label | source | fixed | variable | −2∙log(L) | AIC | |||||
| mean | dispersion | |||||||||
| COVID-19 | (#1) | Xu et al. [12] (n = 2214) | Poisson | equals the fixed component | 0.69 (0.65, 0.72) | none | 5137.46 | 5139.46 | this study | |
| negative binomial | equals the mean of variable component | none | 0.69 (0.62, 0.77) | 0.70 (0.59, 0.98) | not reported | He et al. [30] | ||||
| 0.69 (0.64, 0.74) | 0.74 (0.62, 0.89) | 4658.85 | 4662.85 | this study | ||||||
| Delaporte | 0.69 (0.64, 0.74) | 0.26 (0.16, 0.33) | 0.43 (0.35, 0.54) | 0.24 (0.15, 0.40) | 4635.37 | 4641.37 | this study | |||
| (#2a) | Lim et al. [33] (n = 1401) | Poisson | equals the fixed component | 0.68 (0.64, 0.72) | none | 3486.90 | 3488.90 | this study | ||
| negative binomial | equals the mean of variable component | none | not reported | 0.85 (0.70, 1.05) | not reported | Lim et al. [33] | ||||
| 0.68 (0.62, 0.74) | 0.85 (0.70, 1.06) | 3175.24 | 3179.24 | this study | ||||||
| Delaporte | 0.68 (0.62, 0.75) | 0.38 (0.30, 0.45) | 0.30 (0.22, 0.40) | 0.11 (0.06, 0.20) | 3134.44 | 3140.44 | this study | |||
| (#2b) | Lim et al. [33] (n = 344) | Poisson | equals the fixed component | 0.81 (0.71, 0.90) | none | 1234.96 | 1236.96 | this study | ||
| negative binomial | equals the mean of variable component | none | not reported | 0.23 (0.15, 0.28) | not reported | Lim et al. [33] | ||||
| 0.81 (0.64, 1.06) | 0.23 (0.17, 0.30) | 764.62 | 768.62 | this study | ||||||
| Delaporte | 0.81 (0.61, 1.18) | 0.17 (0.03, 0.27) | 0.65 (0.43, 1.00) | 0.09 (0.05, 0.19) | 751.66 | 757.66 | this study | |||
| (#3) | Adam et al. [17] (n = 290) | Poisson | equals the fixed component | 0.58 (0.50, 0.68) | none | 699.85 | 701.85 | this study | ||
| 0.58 (0.50, 0.69) | 699.85 | 701.85 | Adam et al. [17] | |||||||
| negative binomial | equals the mean of variable component | none | 0.58 (0.45, 0.72) | 0.43 (0.29, 0.67) | 589.93 | 593.93 | ||||
| 0.58 (0.45, 0.73) | 0.43 (0.29, 0.63) | 589.92 | 593.92 | this study | ||||||
| Delaporte | 0.59 (0.46, 0.78) | 0.17 (0.04, 0.30) | 0.42 (0.25, 0.63) | 0.16 (0.06, 0.40) | 585.80 | 591.80 | this study | |||
| (#4) | Zhang et al. [19] (n = 47) | Poisson | equals the fixed component | 0.71 (0.49, 1.01) | none | 126.42 | 128.42 | this study | ||
| negative binomial | equals the mean of variable component | none | 0.67 (0.54, 0.84) | 0.25 (0.13, 0.88) | not reported | Zhang et al. [19] | ||||
| 0.71 (0.39, 1.77) | 0.28 (0.10, 0.80) | 95.35 | 99.35 | this study | ||||||
| Delaporte | 0.72 (0.36, 1.70) | 0.00 (0.00, 0.08) | 0.72 (0.34, 1.69) | 0.23 (0.10, 0.54) | 95.21 | 101.21 | this study | |||
| SARS | (#5) | Shen et al. [5] (n = 34) | Poisson | equals the fixed component | 1.76 (1.37, 2.24) | none | 274.88 | 276.88 | this study | |
| negative binomial | equals the mean of variable component | none | 1.88 (0.41, 3.32) | 0.12 (0.08, 0.42) | not reported | Lloyd-Smith et al. [29] | ||||
| 1.96 (0.67, 4.37) | 0.10 (0.02, 0.19) | 78.78 | 82.78 | this study | ||||||
| Delaporte | 2.07 (0.52, 3.23) | 0.06 (0.00, 0.31) | 2.00 (0.51, 3.01) | 0.05 (0.01, 0.17) | 78.18 | 84.19 | this study | |||
Note: All parameter estimates were summarized in the ‘median (95% credible interval)’ of posterior distribution format.
Fig 5. Fitting results of offspring distributions using the medians of posterior distributions for model parameters.
In each panel, probability mass functions (PMF) of negative binomial (NB, in blue), and Delaporte (in purple) distributions are shown in dots and lines, and the observations of number of secondary cases per infector (in grey) are in histogram. Note: The PMFs of NB and Delaporte distributions were shifted horizontally in each panel with slight jitters at −0.05 and +0.05, respectively to aid visualization and comparison.
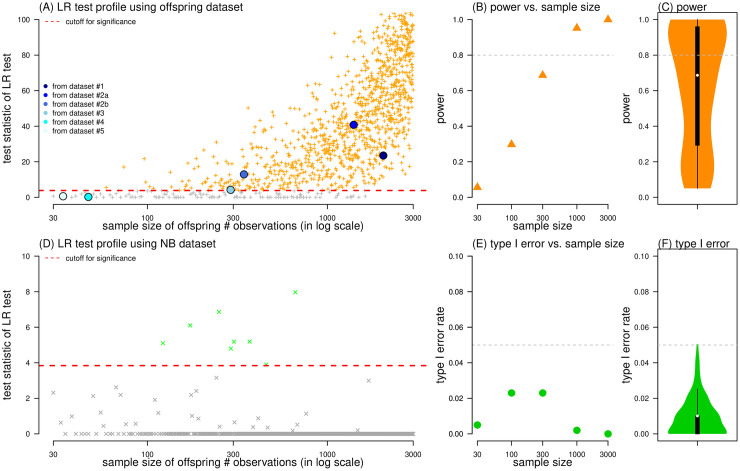
The likelihood ratio (LR) test has been proposed for model selection between the NB and the Delaporte distributions [11, 66], and yields satisfactory testing performance. We found an increasing statistical power of the LR test for identifying the improvement of Delaporte distribution as the sample size increased. The simulation results of the testing power show consistent trends as observed in datasets #1-#5 (Fig 6A). To secure a power larger than 0.80, surveillance may require a sample size above 400, see Fig 6B. Although the type I error rate appears slightly high around 0.03 when sample size ranges from 100 to 300 (Fig 6D–6E), while the type I error rate is generally conservative for a wide range of sample sizes from 30 to 3000 (Fig 6F). Similar non-monotone trends of the type I error rate have also been previously reported for other testing purposes [40]. The testing performance of increasing power and conservative type I error suggest that the LR test is informative in capture the true characteristics of over-dispersed offspring distribution with a low chance of false alarms.
Fig 6. The power and type I error rate of the likelihood ratio (LR) test for Delaporte distribution against negative binomial (NB) distribution.
Panels (A) and (D) show the test statistics (dots) from LR test, and the critical threshold (red horizontal dashed line) for p-value < 0.05. In panel (A), the ‘+’ dots are 10000 pseudo datasets generated by random sampling with replacement from the real-world datasets, and the circle dots represent datasets #1-#5. Panels (B) and (E) summarized the power and type I error rate of LR test for Delaporte distribution against NB distribution as a function of sample size. Panels (C) and (F) summarized the power and type I error rate of LR test with sample size reciprocal-distributed from 30 to 3000. In panel (D), the ‘×’ dots are generated by 10000 datasets generated by Monte Carlo sampling from NB distributions. In panels (B) and (C), the horizontal dashed line is the threshold of power at 0.80. In panels (E) and (F), the horizontal dashed line is the threshold of type I error rate at 0.05.
In practical analysis, one may also be interested in obtaining estimators for R and k given the parameter estimates of the Delaporte distribution. Because the closest theoretical formula may be complex to derive, a convenient approximation using moments of the Delaporte distribution could be considered. To distinguish the dispersion parameters, we denote kNB and kD for the NB and Delaporte distributions, respectively. For a given Delaporte distribution, the first moment (i.e., mean) is RF + RV, and the second central moment (i.e., variance) is . Thus, if let the NB distribution have the same value of mean and variance, for the approximated NB distribution, we have , and . Although this approximation can be directly calculated rapidly, by using the estimates of the example offspring datasets, we note that here appears slightly lower than the posterior estimates of kNB in Table 1.
The real-world datasets adopted in this study were offspring cases per seed case observations, but more generally, the Delaporte distribution can be extended to describing one-generation cluster or final outbreak size observations. For the one-generation cluster size j distribution, we derived that hD(j|i) also follows a Delaporte distribution with parameters not only determined on the original parameter set of fD(X) but also by the number of seed cases i. Specifically, fD(X) can be translated into hD(j|i) by multiplying parameters ρ and R by i, see Eq (6). A previous study determined that one-generation cluster size follows a NB distribution hNB(j|i) under the NB-distributed offspring assumption [40], which is similar to our extension of this finding to the situation of the Delaporte distribution. To assess the impact of ρ on disease outbreaks, the final outbreak size c distribution can be used to evaluate pandemic potentials seeded by i source (or imported) cases [2, 38, 73, 86]. Thus, ωD(c, i)was derived in Eq (7), and appeared to be an extension of the NB version ωNB(c, 1) in [3, 33], see the special case of Eq (8).
To illustrate the translation from the final outbreak size probability in Eq (7) to the likelihood-based estimation, we adopted the final outbreak size observations of the Middle East respiratory syndrome coronavirus (MERS-CoV infection in the Middle East region, which was reported in [87]. The dataset has a sample size of 55 outbreaks, including a total of 104 laboratory confirmed MERS cases, and all final outbreaks were seeded by single cases, as also summarized and studied in [3]. Hence, Eq (8) was used to construct the likelihood function for the Delaporte distribution. We estimated RF at 0.17 (95%CrI: 0.03, 0.45), RV at 0.32 (95%CrI: 0.01, 1.53), and k at 0.04 (95%CrI: 0.00, 0.19) with an AIC of 114.60. We also repeated the estimation using the NB distribution, which leads to R at 0.47 (95%CrI: 0.30, 0.78) and k at 0.27 (95%CrI: 0.10, 0.98) with an AIC of 115.68. For the previous estimates using NB in [3], it was estimated that R was 0.47 (95%CrI: 0.29, 0.80) and k was 0.26 (95%CrI: 0.09, 1.24), which was in line with our estimates. The k estimate appears lower in the Delaporte distribution, and the ρ estimate at 0.33 (95%CrI: 0.05, 0.98) was greater than 0, thus the fixed part of R was evident, which was also indicated by the difference in the AIC values.
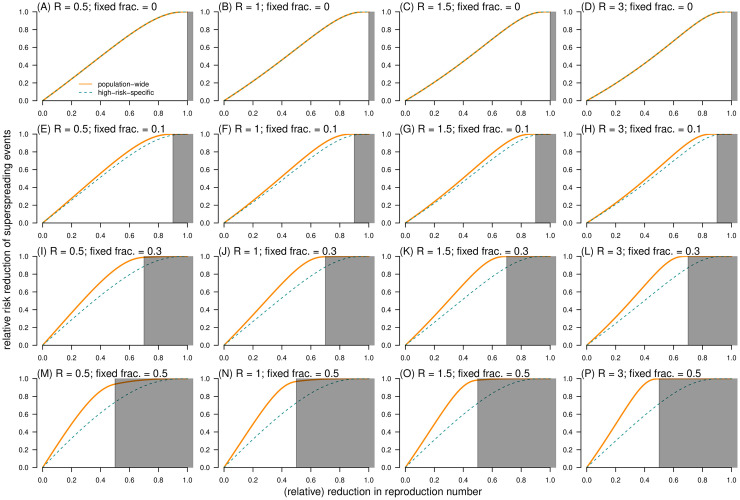
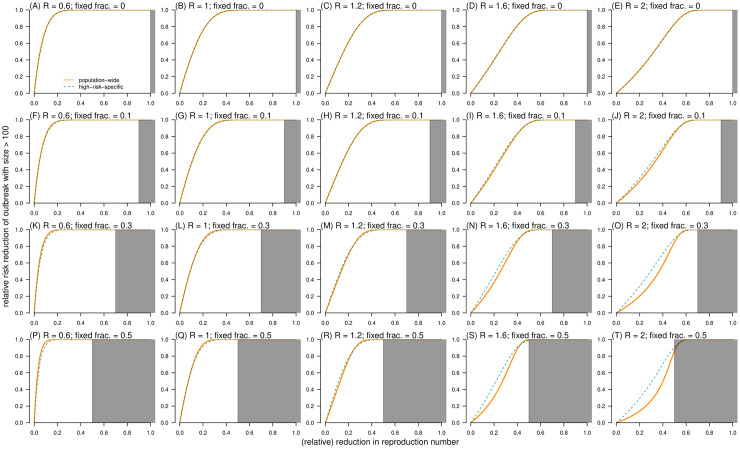
Aside from the impact of k in determining the probability of risk outcome (I): in superspreading events, as described in [3, 29], the parameter ρ also has an similar impact, and further influences the efficacy of different control strategies. With the same among (ξ) of reduction in R, the control efficacies (RRR) of both population-wide and high-risk-specific control schemes increased with ξ (Fig 7). To compare the two control schemes, we found that the control scheme (II) has a higher control efficacy than scheme (I) in terms of the RRR of superspreading event, i.e., RRR(2,1)(ξ). Effective control efforts may allow us to anticipate highly infectious source cases or the contexts in which a seed case may likely expose many susceptible individuals in advance. Then, the scale of the variable component of the reproduction number was reduced efficiently under the control scheme (II), such that a substantial proportion of superspreaders can be controlled. With ξ < 1 − ρ, the general (or linear) tendency of RRR(2,1)(ξ) increased rapidly as ξ or ρ increased (Fig 8). The largest value of RRR(2,1)(ξ) can be reached when ξ is close (but not necessarily approaching) to 1 − ρ. When ρ = 0, we illustrated that RRR(1)(ξ) = RRR(2)(ξ) (Fig 7A–7D), which indicated that RRR(2,1)(ξ) = 0. In other words, with the effects of ρ (> 0), the outperformance of high-risk-specific control scheme may become evident in terms of achieving RRR(2,1) > 0 for some values of ξ (Fig 8).
Fig 7. The relative risk reduction (RRR) of outcome (I): Having superspreading event as a function of the relative reduction in reproduction number (ξ).
The RRR of control scheme (I) RRR(1)(ξ) is dashed cyan curve, and the RRR of control scheme (II) RRR(2)(ξ) is bold orange curve. In each panel, the dispersion parameter k is fixed at 0.2, and the shading region indicates the situation that ξ ≥ 1 − ρ. In each panel label, ‘R’ is the reproduction number, and ‘fixed frac.’ is the fraction of fixed component (ρ).
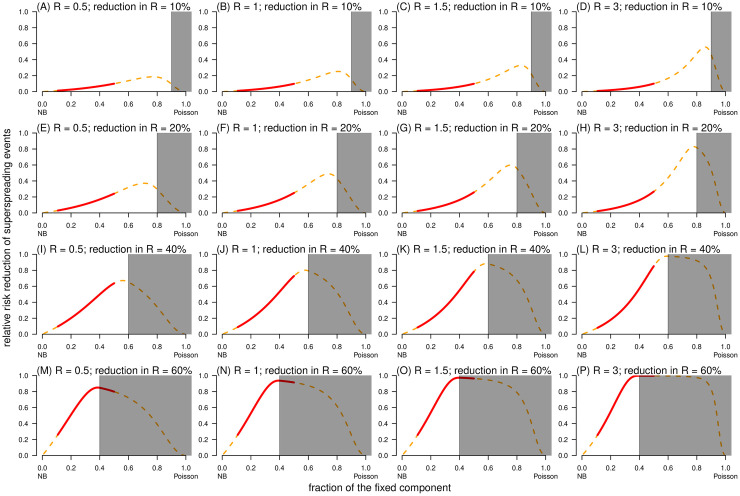
Fig 8. The relative risk reduction, RRR(2,1)(ξ), of outcome (I): Having superspreading event under control scheme (II) against scheme (I) as a function of the fraction of fixed component (ρ).
In each panel, the dispersion parameter k is fixed at 0.2, the shading region indicates the situation that ξ ≥ 1 − ρ, and the bold red segment highlights the range of ρ from 0.1 to 0.5, which characterizes the feature of COVID-19. In each panel label, ‘R’ is the reproduction number, and ‘reduction in R’ is the relative reduction in reproduction number (ξ). The ‘NB’ in the horizontal axis label stand = s for negative binomial (distribution).
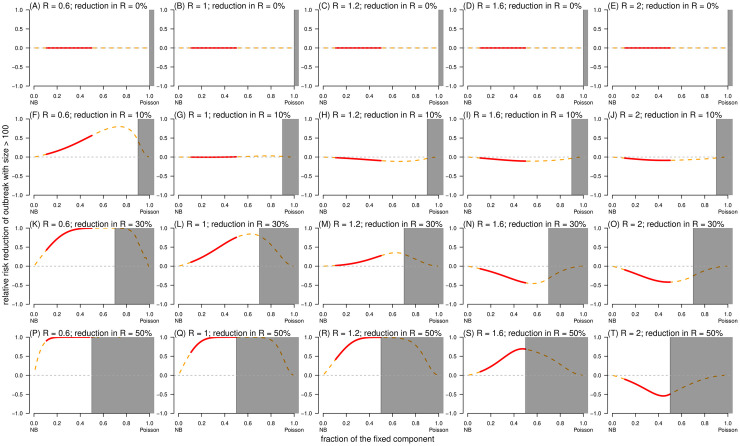
For effective control strategies aiming to reduce the risk of outcome (II): large-scale outbreak, the RRR was determined by ξ, ρ, and R. Consistent with the trends of risk outcome (I) in Fig 7, a large-scale outbreak was less likely to occur as ξ increased despite control schemes (Fig 9). When ρ = 0, we illustrated that RRR(1)(ξ) = RRR(2)(ξ), see Fig 9A–9E, which indicated RRR(2,1)(ξ) = 0. Unlike SSE, the population-wide control scheme outperformed the high-risk-specific control scheme with RRR(2,1) < 0 when R was large and ξ was small, but the direction (or sign) may change to RRR(2,1) > 0 for small R or large ξ (Fig 10). On one hand, the high-risk-specific control scheme was more effective in reducing the outbreak risks under subcritical transmission. In self-limited (or stuttering) outbreak, although SSEs rarely occur, they have a significant contribution to the expansion of transmission [57]; thus, the risk of outbreak can be drastically reduced by targeting high-risk individuals [36]. On the other hand, this implied that when the epidemic curve is growing in terms of reproduction numbers larger than 1, a substantial proportion of transmission is due to the fixed part (λF = RF) of individual infectiousness, that is, subspreading events [88]. Despite the variable part RV, a large RF results in stable reproducibility of infections, and RRR(2,1) < 0 with a moderate scale of ρ (from 0.1 to 0.5 for COVID-19) (Fig 10T). Therefore, population-wide interventions may successfully control disease transmission on a general scale before the implementation of high-risk-specific control strategies subsequently.
Fig 9. The relative risk reduction (RRR) of outcome (II): Having outbreak with final size c > 100 as a function of the relative reduction in reproduction number (ξ).
The RRR of control scheme (I) RRR(1)(ξ) is dashed cyan curve, and the RRR of control scheme (II) RRR(2)(ξ) is bold orange curve. In each panel, the dispersion parameter k is fixed at 0.2, and the shading region indicates the situation that ξ ≥ 1 − ρ. In each panel label, ‘R’ is the reproduction number, and ‘fixed frac.’ is the fraction of fixed component (ρ).
Fig 10. The relative risk reduction, RRR(2,1)(ξ), of outcome (II): Outbreak with final size c > 100 under control scheme (II) against scheme (I) as a function of the fraction of fixed component (ρ).
In each panel, the dispersion parameter k is fixed at 0.2, the shading region indicates the situation that ξ ≥ 1 − ρ, and the bold red segment highlights the range of ρ from 0.1 to 0.5, which characterizes the feature of COVID-19. In each panel label, ‘R’ is the reproduction number, and ‘reduction in R’ is the relative reduction in reproduction number (ξ). The horizontal dashed grey line marked the level of RRR = 0. The ‘NB’ in the horizontal axis label stand = s for negative binomial (distribution).
Conversely, under extremely intensive control measures in terms of ξ → 1, the chance of large-scale outbreak diminishes despite different control schemes. For example, mainland China has achieved satisfactory COVID-19 control outcomes [89]. Although Chinese authorities relaxed population-wide policies in recent months, high-risk-specific control measures secured intensive and compulsory digital contact tracing efforts to monitor the risks of infection at the level of an individual’s daily routine [90, 91]. In our theoretical framework, this indicates a high value of ξ for control scheme (II), which leads to a remarkably low risk of outbreaks (Fig 9).
This study has limitations. First, although the Delaporte distribution is a theoretical generalization of the NB distribution, our data analysis focused on determining whether there is statistical evidence supporting the improvement in fitting performance without investigating the mechanistic side of the decomposition of the reproduction number. For example, population-level factors such as contact size and frequency (e.g., household size) [25], and heterogeneity of population density, or individual-level factors such as biological determinants (e.g., evolutionary adaptation and in-host viral kinetics) [92, 93], behavioral or social factors [32], and lifestyle habits might contribute to establishing superspreading potentials [29, 40]. Second, with regard to the parameter estimation part, we assumed that all offspring observations were accurately reported without selection bias, which might not always be acceptable [85, 94–97]. In cases of considerable reporting or selection bias, adjustments on statistical inference can resolve such issues to some extent by modifying the likelihood framework, for example, by truncation and compounding [11, 46, 57]. Lastly, for the evaluation of control effects, although the final outbreak size (c) distribution was formulated under two schemes, we failed to find an analytical form for the condition with respect to R and ξ, such that RRR(2,1) > 0 or otherwise. Instead, we performed numerical simulations to check the sign of RRR(2,1) (shown visually in Fig 10), regarding the most feasible parameter ranges of COVID-19. Hence, the Delaporte distribution needs to be considered as a tool to monitor the three parameters to understand the transmission characteristics of infectious diseases and to provide information for strategic decision-making processes involving control measures.
In summary, as a generalization of the classic NB distribution, the Delaporte distribution can be adopted to decompose the reproduction number from the individual level to the population level and to characterize the transmission of infectious disease. The Delaporte distribution demonstrates statistical improvement in fitting the distributions of the real-world offspring cases’ distributions against the NB distribution, and it presents increasing power and conservative type I error rates in detecting such an improvement in the goodness-of-fit with the LR test. Numerical simulation illustrated that the three parameters of the Delaporte distribution are important in understanding disease transmission characteristics and for advising of appropriate control strategies and providing new insights distinct from the NB model.
Declarations
Ethics approval and consent to participate
The COVID-19 contact tracing data were obtained from literature, which were originally collected via the public domains, and thus neither ethical approval nor individual consent was applicable.
Data Availability
All data used in this work were publicly available in literature, which were originally collected via the public domains. The processed data and codes are shared via https://github.com/plxzpnxZBD/Superspreading_withDelaporteDist.
Funding Statement
DH was supported by Collaborative Research Fund [C7123-20G] of the Research Grants Council (RGC) of Hong Kong, China. MHW was supported by the National Natural Science Foundation of China [31871340, 71974165], Health and Medical Research Fund, the Food and Health Bureau, the Government of the Hong Kong Special Administrative Region [COVID190103, INF-CUHK-1], and the Chinese University of Hong Kong Grant [PIEF/Ph2/COVID/06, 4054600]. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Fraser C, Riley S, Anderson RM, Ferguson NM. Factors that make an infectious disease outbreak controllable. Proc Natl Acad Sci U S A. 2004;101(16):6146–51. Epub 2004/04/09. doi: 10.1073/pnas.0307506101 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Althaus CL. Ebola superspreading. Lancet Infect Dis. 2015;15(5):507–8. Epub 2015/05/02. doi: 10.1016/S1473-3099(15)70135-0 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kucharski AJ, Althaus CL. The role of superspreading in Middle East respiratory syndrome coronavirus (MERS-CoV) transmission. Euro surveillance: bulletin Europeen sur les maladies transmissibles = European communicable disease bulletin. 2015;20(25):14–8. Epub 2015/07/02. doi: 10.2807/1560-7917.es2015.20.25.21167 . [DOI] [PubMed] [Google Scholar]
- 4.Sun K, Wang W, Gao L, Wang Y, Luo K, Ren L, et al. Transmission heterogeneities, kinetics, and controllability of SARS-CoV-2. Science. 2021;371(6526). Epub 2020/11/26. doi: 10.1126/science.abe2424 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shen Z, Ning F, Zhou W, He X, Lin C, Chin DP, et al. Superspreading SARS events, Beijing, 2003. Emerg Infect Dis. 2004;10(2):256–60. Epub 2004/03/20. doi: 10.3201/eid1002.030732 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fasina FO, Shittu A, Lazarus D, Tomori O, Simonsen L, Viboud C, et al. Transmission dynamics and control of Ebola virus disease outbreak in Nigeria, July to September 2014. Eurosurveillance. 2014;19(40):20920. Epub 2014/10/18. doi: 10.2807/1560-7917.es2014.19.40.20920 . [DOI] [PubMed] [Google Scholar]
- 7.Fisman DN, Leung GM, Lipsitch MJTL. Nuanced risk assessment for emerging infectious diseases. 2014;383(9913):189–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Meyerowitz EA, Richterman A, Gandhi RT, Sax PE. Transmission of SARS-CoV-2: a review of viral, host, and environmental factors. Annals of internal medicine. 2021;174(1):69–79. Epub 2020/09/18. doi: 10.7326/M20-5008 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Diekmann O, Heesterbeek JAP. Mathematical epidemiology of infectious diseases: model building, analysis and interpretation: John Wiley & Sons; 2000. [Google Scholar]
- 10.Lipsitch M, Cohen T, Cooper B, Robins JM, Ma S, James L, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300(5627):1966–70. Epub 2003/05/27. doi: 10.1126/science.1086616 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blumberg S, Lloyd-Smith JO. Inference of R(0) and transmission heterogeneity from the size distribution of stuttering chains. PLoS Comput Biol. 2013;9(5):e1002993. Epub 2013/05/10. doi: 10.1371/journal.pcbi.1002993 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xu XK, Liu XF, Wu Y, Ali ST, Du Z, Bosetti P, et al. Reconstruction of Transmission Pairs for Novel Coronavirus Disease 2019 (COVID-19) in Mainland China: Estimation of Superspreading Events, Serial Interval, and Hazard of Infection. Clin Infect Dis. 2020;71(12):3163–7. Epub 2020/06/20. doi: 10.1093/cid/ciaa790 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liang W, Zhu Z, Guo J, Liu Z, He X, Zhou W, et al. Severe acute respiratory syndrome, Beijing, 2003. Emerging infectious diseases. 2004;10(1):25. Epub 2004/04/14. doi: 10.3201/eid1001.030553 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cowling BJ, Park M, Fang VJ, Wu P, Leung GM, Wu JT. Preliminary epidemiological assessment of MERS-CoV outbreak in South Korea, May to June 2015. Euro surveillance: bulletin Europeen sur les maladies transmissibles = European communicable disease bulletin. 2015;20(25):7–13. Epub 2015/07/02. doi: 10.2807/1560-7917.es2015.20.25.21163 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gire SK, Goba A, Andersen KG, Sealfon RSG, Park DJ, Kanneh L, et al. Genomic surveillance elucidates Ebola virus origin and transmission during the 2014 outbreak. Science. 2014;345(6202):1369–72. Epub 2014/09/13. doi: 10.1126/science.1259657 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liu Y, Eggo RM, Kucharski AJ. Secondary attack rate and superspreading events for SARS-CoV-2. The Lancet. 2020;395(10227):e47. Epub 2020/03/03. doi: 10.1016/S0140-6736(20)30462-1 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Adam DC, Wu P, Wong JY, Lau EHY, Tsang TK, Cauchemez S, et al. Clustering and superspreading potential of SARS-CoV-2 infections in Hong Kong. Nat Med. 2020;26(11):1714–9. Epub 2020/09/19. doi: 10.1038/s41591-020-1092-0 . [DOI] [PubMed] [Google Scholar]
- 18.Lau MSY, Grenfell B, Thomas M, Bryan M, Nelson K, Lopman B. Characterizing superspreading events and age-specific infectiousness of SARS-CoV-2 transmission in Georgia, USA. Proc Natl Acad Sci U S A. 2020;117(36):22430–5. Epub 2020/08/21. doi: 10.1073/pnas.2011802117 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhang Y, Li Y, Wang L, Li M, Zhou X. Evaluating Transmission Heterogeneity and Super-Spreading Event of COVID-19 in a Metropolis of China. Int J Environ Res Public Health. 2020;17(10):3705. Epub 2020/05/28. doi: 10.3390/ijerph17103705 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Riley S, Fraser C, Donnelly CA, Ghani AC, Abu-Raddad LJ, Hedley AJ, et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science. 2003;300(5627):1961–6. Epub 2003/05/27. doi: 10.1126/science.1086478 . [DOI] [PubMed] [Google Scholar]
- 21.Galvani AP, May RM. Epidemiology: dimensions of superspreading. Nature. 2005;438(7066):293–5. Epub 2005/11/18. doi: 10.1038/438293a . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chowell G, Abdirizak F, Lee S, Lee J, Jung E, Nishiura H, et al. Transmission characteristics of MERS and SARS in the healthcare setting: a comparative study. BMC Med. 2015;13(1):210. Epub 2015/09/04. doi: 10.1186/s12916-015-0450-0 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Arons MM, Hatfield KM, Reddy SC, Kimball A, James A, Jacobs JR, et al. Presymptomatic SARS-CoV-2 infections and transmission in a skilled nursing facility. N Engl J Med. 2020;382(22):2081–90. Epub 2020/04/25. doi: 10.1056/NEJMoa2008457 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cowling BJ, Ip DKM, Fang VJ, Suntarattiwong P, Olsen SJ, Levy J, et al. Aerosol transmission is an important mode of influenza A virus spread. Nature communications. 2013;4(1):1–6. doi: 10.1038/ncomms2922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fraser C, Cummings DA, Klinkenberg D, Burke DS, Ferguson NM. Influenza transmission in households during the 1918 pandemic. American journal of epidemiology. 2011;174(5):505–14. Epub 2011/07/14. doi: 10.1093/aje/kwr122 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wong G, Liu W, Liu Y, Zhou B, Bi Y, Gao GF. MERS, SARS, and Ebola: the role of super-spreaders in infectious disease. Cell Host Microbe. 2015;18(4):398–401. Epub 2015/10/16. doi: 10.1016/j.chom.2015.09.013 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lu J, Gu J, Li K, Xu C, Su W, Lai Z, et al. COVID-19 outbreak associated with air conditioning in restaurant, Guangzhou, China, 2020. Emerging infectious diseases. 2020;26(7):1628. doi: 10.3201/eid2607.200764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shim E, Tariq A, Choi W, Lee Y, Chowell G. Transmission potential and severity of COVID-19 in South Korea. International Journal of Infectious Diseases. 2020;93:339–44. Epub 2020/03/22. doi: 10.1016/j.ijid.2020.03.031 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438(7066):355–9. Epub 2005/11/18. doi: 10.1038/nature04153 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.He D, Zhao S, Xu X, Lin Q, Zhuang Z, Cao P, et al. Low dispersion in the infectiousness of COVID-19 cases implies difficulty in control. BMC Public Health. 2020;20(1):1558. Epub 2020/10/18. doi: 10.1186/s12889-020-09624-2 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sneppen K, Nielsen BF, Taylor RJ, Simonsen L. Overdispersion in COVID-19 increases the effectiveness of limiting nonrepetitive contacts for transmission control. Proceedings of the National Academy of Sciences. 2021;118(14). Epub 2021/03/21. doi: 10.1073/pnas.2016623118 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Althouse BM, Wenger EA, Miller JC, Scarpino SV, Allard A, Hébert-Dufresne L, et al. Superspreading events in the transmission dynamics of SARS-CoV-2: Opportunities for interventions and control. PLoS Biol. 2020;18(11):e3000897. Epub 2020/11/13. doi: 10.1371/journal.pbio.3000897 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lim J-S, Noh E, Shim E, Ryu S. Temporal Changes in the Risk of Superspreading Events of Coronavirus Disease 2019. Open Forum Infectious Diseases. 2021;8(7):ofab350. Epub 2021/07/30. doi: 10.1093/ofid/ofab350 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nielsen BF, Simonsen L, Sneppen K. COVID-19 superspreading suggests mitigation by social network modulation. Phys Rev Lett. 2021;126(11):118301. Epub 2021/04/03. doi: 10.1103/PhysRevLett.126.118301 . [DOI] [PubMed] [Google Scholar]
- 35.Endo A. Implication of backward contact tracing in the presence of overdispersed transmission in COVID-19 outbreaks. Wellcome open research. 2020;5:239. Epub 2021/04/10. doi: 10.12688/wellcomeopenres.16344.3 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kain MP, Childs ML, Becker AD, Mordecai EA. Chopping the tail: How preventing superspreading can help to maintain COVID-19 control. Epidemics. 2021;34:100430. doi: 10.1016/j.epidem.2020.100430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180:29–48. Epub 2002/10/22. doi: 10.1016/s0025-5564(02)00108-6 . [DOI] [PubMed] [Google Scholar]
- 38.Breban R, Riou J, Fontanet A. Interhuman transmissibility of Middle East respiratory syndrome coronavirus: estimation of pandemic risk. The Lancet. 2013;382(9893):694–9. Epub 2013/07/09. doi: 10.1016/S0140-6736(13)61492-0 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bauch CT. Estimating the COVID-19 R number: a bargain with the devil? The Lancet Infectious Diseases. 2021;21(2):151–3. Epub 2021/03/10. doi: 10.1016/S1473-3099(20)30840-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Blumberg S, Funk S, Pulliam JRC. Detecting differential transmissibilities that affect the size of self-limited outbreaks. PLoS Pathog. 2014;10(10):e1004452. doi: 10.1371/journal.ppat.1004452 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Riou J, Althaus CL. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Euro surveillance: bulletin Europeen sur les maladies transmissibles = European communicable disease bulletin. 2020;25(4):2000058. Epub 2020/02/06. doi: 10.2807/1560-7917.ES.2020.25.4.2000058 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fisman DN, Leung GM, Lipsitch M. Nuanced risk assessment for emerging infectious diseases. The Lancet. 2014;383(9913):189–90. Epub 2014/01/21. doi: 10.1016/S0140-6736(13)62123-6 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Delamater PL, Street EJ, Leslie TF, Yang YT, Jacobsen KH. Complexity of the basic reproduction number (R0). Emerging infectious diseases. 2019;25(1):1. Epub 2018/12/19. doi: 10.3201/eid2501.171901 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lloyd-Smith JO. Maximum likelihood estimation of the negative binomial dispersion parameter for highly overdispersed data, with applications to infectious diseases. PLoS One. 2007;2(2):e180. Epub 2007/02/15. doi: 10.1371/journal.pone.0000180 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Garske T, Rhodes CJ. The effect of superspreading on epidemic outbreak size distributions. J Theor Biol. 2008;253(2):228–37. Epub 2008/04/22. doi: 10.1016/j.jtbi.2008.02.038 . [DOI] [PubMed] [Google Scholar]
- 46.Zhao S, Shen M, Musa SS, Guo Z, Ran J, Peng Z, et al. Inferencing superspreading potential using zero-truncated negative binomial model: exemplification with COVID-19. BMC Med Res Methodol. 2021;21(1):1–8. doi: 10.1186/s12874-021-01225-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Leung K, Wu JT, Leung GM. Effects of adjusting public health, travel, and social measures during the roll-out of COVID-19 vaccination: a modelling study. The Lancet Public Health. 2021;6(9):e674–e82. Epub 2021/08/14. doi: 10.1016/S2468-2667(21)00167-5 Government and University Grant Council of The Government of Hong Kong Special Administrative Region, during the conduct of the study. JTW and GML declare no competing interests. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Delaporte PJ. Quelques problèmes de statistiques mathématiques poses par l’Assurance Automobile et le Bonus pour non sinistre. Bulletin Trimestriel de l’Institut des Actuaires Français. 1960;227:87–102. [Google Scholar]
- 49.Vose D. Risk analysis: a quantitative guide: John Wiley & Sons; 2008. [Google Scholar]
- 50.Farrington CP, Kanaan MN, Gay NJ. Branching process models for surveillance of infectious diseases controlled by mass vaccination. Biostatistics. 2003;4(2):279–95. Epub 2003/08/20. doi: 10.1093/biostatistics/4.2.279 . [DOI] [PubMed] [Google Scholar]
- 51.Fraser C. Estimating Individual and Household Reproduction Numbers in an Emerging Epidemic. PLoS One. 2007;2(8):e758. doi: 10.1371/journal.pone.0000758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Brauer F, Driessche PVd, Wu J. Lecture notes in mathematical epidemiology. Berlin, Germany: Springer. 2008;75(1):3–22. [Google Scholar]
- 53.Diekmann O, Heesterbeek JAP, Roberts MG. The construction of next-generation matrices for compartmental epidemic models. Journal of the Royal Society Interface. 2010;7(47):873–85. Epub 2009/11/07. doi: 10.1098/rsif.2009.0386 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Bi Q, Wu Y, Mei S, Ye C, Zou X, Zhang Z, et al. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. The Lancet Infectious Diseases. 2020;20(8):911–9. doi: 10.1016/S1473-3099(20)30287-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wang J, Chen X, Guo Z, Zhao S, Huang Z, Zhuang Z, et al. Superspreading and heterogeneity in transmission of SARS, MERS, and COVID-19: a systematic review. Computational and Structural Biotechnology Journal. 2021;19:5039–46. Epub 2021/09/07. doi: 10.1016/j.csbj.2021.08.045 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Woolhouse ME, Dye C, Etard J-F, Smith T, Charlwood J, Garnett G, et al. Heterogeneities in the transmission of infectious agents: implications for the design of control programs. Proceedings of the National Academy of Sciences. 1997;94(1):338–42. Epub 1997/01/07. doi: 10.1073/pnas.94.1.338 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Endo A, Abbott S, Kucharski AJ, Funk S. Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China. Wellcome Open Research. 2020;5(67):67. doi: 10.12688/wellcomeopenres.15842.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lorenz MO. Methods of measuring the concentration of wealth. Publications of the American statistical association. 1905;9(70):209–19. [Google Scholar]
- 59.Wittebolle L, Marzorati M, Clement L, Balloi A, Daffonchio D, Heylen K, et al. Initial community evenness favours functionality under selective stress. Nature. 2009;458(7238):623–6. Epub 2009/03/10. doi: 10.1038/nature07840 . [DOI] [PubMed] [Google Scholar]
- 60.Centre for Health Protection. Summary of data and outbreak situation of the Severe Respiratory Disease associated with a Novel Infectious Agent, Centre for Health Protection, the government of Hong Kong. 2020 [cited 2021]. https://www.chp.gov.hk/en/features/102465.html.
- 61.Centre for Health Protection. The collection of Press Releases by the Centre for Health Protection (CHP) of Hong Kong. 2020 [cited 2020]. https://www.chp.gov.hk/en/media/116/index.html.
- 62.The Government of Tianjin. Tianjin Municipal People’s Government, China. http://www.tj.gov.cn/xw/ztzl/tjsyqfk/yqtb/.
- 63.Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB. Bayesian data analysis: CRC press; 2013. [Google Scholar]
- 64.Bolker BM. Ecological models and data in R: Princeton University Press; 2008. [Google Scholar]
- 65.Lin Q, Chiu AP, Zhao S, He D. Modeling the spread of Middle East respiratory syndrome coronavirus in Saudi Arabia. Stat Methods Med Res. 2018;27(7):1968–78. Epub 2018/05/31. doi: 10.1177/0962280217746442 . [DOI] [PubMed] [Google Scholar]
- 66.Tariq A, Lee Y, Roosa K, Blumberg S, Yan P, Ma S, et al. Real-time monitoring the transmission potential of COVID-19 in Singapore, March 2020. BMC Med. 2020;18(1):166. Epub 2020/06/05. doi: 10.1186/s12916-020-01615-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Zhao S, Guo Z, Chong MKC, He D, Wang MH. Superspreading potential of SARS-CoV-2 Delta variants under intensive disease control measures in China. J Travel Med. 2022:taac025. doi: 10.1093/jtm/taac025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Cauchemez S, Fraser C, Van Kerkhove MD, Donnelly CA, Riley S, Rambaut A, et al. Middle East respiratory syndrome coronavirus: quantification of the extent of the epidemic, surveillance biases, and transmissibility. The Lancet infectious diseases. 2014;14(1):50–6. Epub 2013/11/19. doi: 10.1016/S1473-3099(13)70304-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Nishiura H, Yan P, Sleeman CK, Mode CJ. Estimating the transmission potential of supercritical processes based on the final size distribution of minor outbreaks. J Theor Biol. 2012;294:48–55. Epub 2011/11/15. doi: 10.1016/j.jtbi.2011.10.039 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Yan P. Distribution theory, stochastic processes and infectious disease modelling. Mathematical epidemiology: Springer; 2008. p. 229–93. [Google Scholar]
- 71.Dwass M. The total progeny in a branching process and a related random walk. J Appl Probab. 1969;6(3):682–6. [Google Scholar]
- 72.Lloyd-Smith JO, George D, Pepin KM, Pitzer VE, Pulliam JR, Dobson AP, et al. Epidemic dynamics at the human-animal interface. Science. 2009;326(5958):1362–7. doi: 10.1126/science.1177345 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Ferguson NM, Fraser C, Donnelly CA, Ghani AC, Anderson RM. Public health risk from the avian H5N1 influenza epidemic. Science. 2004;304(5673):968–9. Epub 2004/05/15. doi: 10.1126/science.1096898 . [DOI] [PubMed] [Google Scholar]
- 74.Rader B, White LF, Burns MR, Chen J, Brilliant J, Cohen J, et al. Mask-wearing and control of SARS-CoV-2 transmission in the USA: a cross-sectional study. The Lancet Digital Health. 2021;3(3):e148–e57. Epub 2021/01/24. doi: 10.1016/S2589-7500(20)30293-4 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Cowling BJ, Chan KH, Fang VJ, Cheng CK, Fung RO, Wai W, et al. Facemasks and hand hygiene to prevent influenza transmission in households: a cluster randomized trial. Annals of internal medicine. 2009;151(7):437–46. Epub 2009/08/05. doi: 10.7326/0003-4819-151-7-200910060-00142 . [DOI] [PubMed] [Google Scholar]
- 76.Du Z, Xu X, Wang L, Fox SJ, Cowling BJ, Galvani AP, et al. Effects of proactive social distancing on COVID-19 outbreaks in 58 cities, China. Emerging infectious diseases. 2020;26(9):2267. Epub 2020/06/10. doi: 10.3201/eid2609.201932 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Leung GM, Cowling BJ, Wu JT. From a Sprint to a Marathon in Hong Kong. N Engl J Med. 2020;382(18):e45. Epub 2020/04/16. doi: 10.1056/NEJMc2009790 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Kraemer MU, Yang C-H, Gutierrez B, Wu C-H, Klein B, Pigott DM, et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science. 2020;368(6490):493–7. doi: 10.1126/science.abb4218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Chinazzi M, Davis JT, Ajelli M, Gioannini C, Litvinova M, Merler S, et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368(6489):395–400. Epub 2020/03/08. doi: 10.1126/science.aba9757 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Anglemyer A, Moore TH, Parker L, Chambers T, Grady A, Chiu K, et al. Digital contact tracing technologies in epidemics: a rapid review. Cochrane Database Syst Rev. 2020;8(8):CD013699. Epub 2021/01/28. doi: 10.1002/14651858.CD013699 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Luo L, Liu D, Liao X, Wu X, Jing Q, Zheng J, et al. Contact Settings and Risk for Transmission in 3410 Close Contacts of Patients With COVID-19 in Guangzhou, China: A Prospective Cohort Study. Annals of internal medicine. 2020;173(11):879–87. Epub 2020/08/14. doi: 10.7326/M20-2671 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N Engl J Med. 2020;382(13):1199–207. Epub 2020/01/30. doi: 10.1056/NEJMoa2001316 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Read JM, Bridgen JRE, Cummings DAT, Ho A, Jewell CP. Novel coronavirus 2019-nCoV (COVID-19): early estimation of epidemiological parameters and epidemic size estimates. Philosophical Transactions of the Royal Society B. 2021;376(1829):20200265. Epub 2021/06/01. doi: 10.1098/rstb.2020.0265 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–97. Epub 2020/02/06. doi: 10.1016/S0140-6736(20)30260-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Zhao S, Musa SS, Lin Q, Ran J, Yang G, Wang W, et al. Estimating the Unreported Number of Novel Coronavirus (2019-nCoV) Cases in China in the First Half of January 2020: A Data-Driven Modelling Analysis of the Early Outbreak. Journal of Clinical Medicine. 2020;9(2):388. Epub 2020/02/07. doi: 10.3390/jcm9020388 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Jansen VA, Stollenwerk N, Jensen HJ, Ramsay M, Edmunds W, Rhodes C. Measles outbreaks in a population with declining vaccine uptake. Science. 2003;301(5634):804-. Epub 2003/08/09. doi: 10.1126/science.1086726 . [DOI] [PubMed] [Google Scholar]
- 87.Poletto C, Pelat C, Lévy-Bruhl D, Yazdanpanah Y, Boëlle PY, Colizza V. Assessment of the Middle East respiratory syndrome coronavirus (MERS-CoV) epidemic in the Middle East and risk of international spread using a novel maximum likelihood analysis approach. Euro surveillance: bulletin Europeen sur les maladies transmissibles = European communicable disease bulletin. 2014;19(23):20824. doi: 10.2807/1560-7917.es2014.19.23.20824 [DOI] [PubMed] [Google Scholar]
- 88.Parag KV. Sub-spreading events limit the reliable elimination of heterogeneous epidemics. Journal of The Royal Society Interface. 2021;18(181):20210444. Epub 2021/08/19. doi: 10.1098/rsif.2021.0444 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.World Health Organization, Coronavirus disease 2019 (COVID-19) situation reports. 2021 [cited 2021]. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports.
- 90.Ferretti L, Wymant C, Kendall M, Zhao L, Nurtay A, Abeler-Dorner L, et al. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science. 2020;368(6491):eabb6936. Epub 2020/04/03. doi: 10.1126/science.abb6936 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Mao Z, Yao H, Zou Q, Zhang W, Dong Y. Digital contact tracing based on a graph database algorithm for emergency management during the COVID-19 epidemic: Case study. JMIR mHealth and uHealth. 2021;9(1):e26836. Epub 2021/01/19. doi: 10.2196/26836 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.He X, Lau EHY, Wu P, Deng X, Wang J, Hao X, et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat Med. 2020:1–4. doi: 10.1038/s41591-020-0869-5 [DOI] [PubMed] [Google Scholar]
- 93.Néant N, Lingas G, Le Hingrat Q, Ghosn J, Engelmann I, Lepiller Q, et al. Modeling SARS-CoV-2 viral kinetics and association with mortality in hospitalized patients from the French COVID cohort. Proceedings of the National Academy of Sciences. 2021;118(8). doi: 10.1073/pnas.2017962118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Li R, Pei S, Chen B, Song Y, Zhang T, Yang W, et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science. 2020;368(6490):489–93. Epub 2020/03/18. doi: 10.1126/science.abb3221 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Tuite AR, Fisman DN. Reporting, Epidemic Growth, and Reproduction Numbers for the 2019 Novel Coronavirus (2019-nCoV) Epidemic. Annals of Internal Medicine. 2020;172(8):567–8. Epub 2020/02/06. doi: 10.7326/M20-0358 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Nishiura H, Kobayashi T, Yang Y, Hayashi K, Miyama T, Kinoshita R, et al. The Rate of Underascertainment of Novel Coronavirus (2019-nCoV) Infection: Estimation Using Japanese Passengers Data on Evacuation Flights. Journal of Clinical Medicine. 2020;9(2). Epub 2020/02/09. doi: 10.3390/jcm9020419 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Perkins TA, Cavany SM, Moore SM, Oidtman RJ, Lerch A, Poterek M. Estimating unobserved SARS-CoV-2 infections in the United States. Proceedings of the National Academy of Sciences. 2020;117(36):22597–602. Epub 2020/08/23. doi: 10.1073/pnas.2005476117 . [DOI] [PMC free article] [PubMed] [Google Scholar]