SEMIPARAMETRIC LATENT-CLASS MODELS FOR MULTIVARIATE LONGITUDINAL AND SURVIVAL DATA

Abstract

In long-term follow-up studies, data are often collected on repeated measures of multivariate response variables as well as on time to the occurrence of a certain event. To jointly analyze such longitudinal data and survival time, we propose a general class of semiparametric latent-class models that accommodates a heterogeneous study population with flexible dependence structures between the longitudinal and survival outcomes. We combine nonparametric maximum likelihood estimation with sieve estimation and devise an efficient EM algorithm to implement the proposed approach. We establish the asymptotic properties of the proposed estimators through novel use of modern empirical process theory, sieve estimation theory, and semiparametric efficiency theory. Finally, we demonstrate the advantages of the proposed methods through extensive simulation studies and provide an application to the Atherosclerosis Risk in Communities study.

1. Introduction.

Many clinical and epidemiological studies generate data on repeated measures of response variables at multiple time points as well as on time to the occurrence of a clinical event. In cardiovascular cohort studies, for example, data are often recorded for both repeated measures of risk factors (e.g., blood pressures, cholesterol levels) and time to a cardiovascular event (e.g., stroke, heart attack) or death [5]. Shared random-effect models and joint latent-class models have been proposed to investigate the dynamic relationships among such longitudinal and survival data.

In shared random-effect models, a linear mixed model with a set of unobserved random effects is assumed for the longitudinal outcomes, and a proportional hazards model or transformation model with the same random effects as covariates is assumed for the survival time [4, 23, 18, 24, 8]. The shared random effects account for the dependence between the longitudinal and survival outcomes. These models typically assume that, conditional on the random effects, the distribution of the survival time and the effects of covariates on the longitudinal and survival outcomes are the same across subjects.

Joint latent-class models assume that the population consists of subgroups and within each subgroup, subjects have the same distributions of longitudinal and survival outcomes [14, 7]. These models allow the baseline risk of event and the association pattern between the longitudinal and survival outcomes to vary flexibly across subgroups. However, the existing work is mostly confined to fully parametric models. Lin et al. [6] proposed a semiparametric latent-class model with a nonparametric baseline hazard function for the survival time in each latent class but did not investigate the theoretical properties of the proposed nonparametric maximum likelihood estimators (NPMLE). In fact, such NPMLEs are inconsistent [12, 20]; see Section S1 of the supplementary materials [21].

We propose a general model for the joint analysis of multivariate longitudinal data and survival time. We assume that the population consists of a mixture of latent subgroups such that within each subgroup, the joint distribution of the longitudinal and survival outcomes is described by a separate random-effect model, in which the survival time is characterized by a separate nonparametric baseline hazard function. This model naturally extends those of Henderson, Diggle and Dobson [4] and Tsiatis and Davidian [18] by allowing the existence of latent subgroups. The model can be used to address important scientific questions:

1. Identification of latent subgroups within a heterogeneous study population;

2. Estimation of the effects of baseline covariates, such as treatment, on longitudinal and survival outcomes within each subgroup;

3. Evaluation of the event risk given baseline covariates and trajectories of longitudinal outcomes; and

4. Estimation of the association between the trajectories of longitudinal outcomes and covariates with proper adjustment of informative dropout due to the occurrence of the event.

The proposed modeling framework also extends existing work by accommodating multivariate longitudinal outcomes measured at multiple time points. This framework is particularly useful in cardiovascular studies, where multiple risk factors, such as blood pressures and cholesterol levels, are repeatedly measured. Including multivariate longitudinal outcomes not only provides a comprehensive depiction of the dynamic relationships among the event of interest and relevant risk factors but also helps identify the latent subgroup structure.

Due to the presence of multiple nonparametric components in the model and the lack of a closed-form expression for the likelihood function, model estimation is highly challenging both theoretically and computationally. To overcome the non-identifiability of the fully nonparametric likelihood approach, we propose to combine nonparametric likelihood estimation with sieve estimation, such that the cumulative hazard function of a reference latent class is estimated by a step function with jumps at the observed event times, and the ratios of the baseline hazard functions across latent classes are estimated by spline functions. We develop a stable and efficient (accelerated) EM algorithm [3] to compute the proposed estimators.

We prove that the proposed estimators are consistent and the parametric components of the estimators are asymptotically efficient. The derivations involve novel applications of empirical process theory, sieve estimation theory, and semiparametric efficiency theory. One major challenge in our theoretical development is to show that the proposed model is identifiable with an invertible information operator. Due to the presence of latent classes, techniques for establishing model identifiability or invertibility of the information operator for semiparametric shared random-effect models are not directly applicable to the current setting. In addition, existing methods for latent-class models are not readily applicable to semiparametric models. To establish model identifiability and the invertibility of the information operator, we note that the likelihood and the score function are the sums of the terms arising from the likelihood of semiparametric shared random-effect models and show that the terms in the summation can be separated by properly varying the observed data values.

The rest of this article is structured as follows. In Section 2, we formulate the model and describe the proposed estimation approach. In Section 3, we discuss the computation of the proposed estimators, and in Section 4, we present the theoretical results. In Section 5, we report the results from our simulation studies. In Section 6, we provide an application to the Atherosclerosis Risk in Communities (ARIC) study [5]. In Section 7, we make some concluding remarks. We relegate technical proofs to the Appendix.

2. Model, likelihood, and sieve estimation.

Suppose that there are G latent classes. Let C denote the latent class membership, with C = g if a subject belongs to the gth latent class (g = 1,…,G). We relate C to a set of time-independent covariates W, which generally includes the constant 1, through a multinomial logistic regression model:

$$P\left(C=g|\mathit{W}\right)=\frac{e^{{\mathit{\alpha }}_g^{\text{T}}\mathit{W}}}{{\sum }_{l=1}^G{e}^{{\mathit{\alpha }}_l^{\text{T}}\mathit{W}}},$$ (1)

where α_g is the vector of class-specific regression parameters. For model identifiability, we set α_G = 0. Each latent class is characterized by class-specific trajectories of multivariate longitudinal outcomes and a class-specific risk of the event of interest. The longitudinal outcomes and the event time are assumed to be conditionally independent given the latent class membership and a multivariate random effect.

Suppose that there are J types of longitudinal outcomes and the jth type is measured at N_j time points. For j = 1,…,J and k = 1,…,N_j, let Y_jk denote the kth measurement of the jth longitudinal outcome and X_jk and ${\tilde{\mathit{X}}}_{jk}$ denote corresponding covariates, which include the constant 1. The covariates X_jk, ${\tilde{\mathit{X}}}_{jk}$ and W may partially or completely overlap. We relate Y_jk to X_jk and ${\tilde{\mathit{X}}}_{jk}$ through the multivariate linear mixed model:

$$Y_{jk}{|}_{C=g}={\beta }_g^{\text{T}}{\mathit{X}}_{jk}+{\mathit{b}}^{\text{T}}{\tilde{\mathit{X}}}_{jk}+{ϵ}_{jk}$$ (2)

for g = 1,…,G, where β_g is a vector of class-specific regression parameters, b is a vector of random effects assumed to follow the multivariate normal distribution with mean 0 and variance $\mathbf{\Sigma }\left({\mathit{\xi }}_g\right)$, $\left({ϵ}_{j1},\dots ,{ϵ}_{j{N}_j}\right)$ are independent zero-mean normal random variables with variance ${\sigma }_{gj}^2$, and Σ(ξ_g) is a covariance matrix indexed by a vector of class-specific variance parameters ξ_g.

Let T denote the event time of interest. We relate T to a set of potentially time-dependent covariates Z(·) through the proportional hazards model:

$$\text{λ}\left(t|\mathit{Z},\mathit{b},C=g\right)={\text{λ}}_g\left(t\right)e^{{\gamma }_g^{\text{T}}\mathit{Z}\left(t\right)+{\eta }_g^{\text{T}}\mathit{b}},$$ (3)

where λ_g(·) is an arbitrary class-specific baseline hazard function, and γ_g and η_g are class-specific regression parameters. In the presence of censoring, we observe $\tilde{T}=T\Lambda U$ and ∆ = I(T ≤ U), where U is the censoring time, and I(·) is the indicator function. Let Y = (Y₁₁,…,Y_1N1,…,Y_J1,…,Y_JNJ)^T, $\mathit{X}={\left({\mathit{X}}_{11},\dots ,{\mathit{X}}_{1N_1},\dots ,{\mathit{X}}_{J1},\dots ,{\mathit{X}}_{J{N}_J}\right)}^{\text{T}}$, and $\tilde{\mathit{X}}={\left({\tilde{\mathit{X}}}_{11},\dots ,{\tilde{\mathit{X}}}_{1N_1},\dots ,{\tilde{\mathit{X}}}_{J1},\dots ,{\tilde{\mathit{X}}}_{J{N}_J}\right)}^{\text{T}}$. The data consist of n independent observations ${\mathcal{O}}_i\equiv \left(N_{i1},\dots ,N_{iJ},{\mathit{Y}}_i,{\mathit{X}}_i,{\tilde{\mathit{X}}}_i,{\tilde{T}}_i,{\Delta }_i,{\mathit{W}}_i,{\left\{{\mathit{Z}}_i\left(t\right)\right\}}_{t\in \left[0,{\tilde{T}}_i\right]}\right)$, for i = 1, …, n, where $\tau$ is the end of study time.

Let $\mathit{\theta }\equiv \left({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_{G-1},{\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_G,{\sigma }_{11}^2,\dots ,{\sigma }_{1J}^2,\dots ,{\sigma }_{GJ}^2,{\mathit{\xi }}_1,\dots ,{\mathit{\xi }}_G,{\mathit{\gamma }}_1,\dots ,{\mathit{\gamma }}_G,{\mathit{\eta }}_1,\dots ,{\mathit{\eta }}_G\right)$ denote the set of all Euclidean parameters and ${\mathrm{\Lambda }}_g\left(t\right)={\int }_0^t{\lambda }_g\left(u\right)\text{d}u$ for $g=1,\dots ,G$. Under the assumption of noninformative censoring and longitudinal measurement times, rigorously formulated in Section S2 of the supplementary materials [21], the likelihood function concerning (θ,Λ₁,…,Λ_G) is proportional to

$$\begin{gathered} \prod _{i=1}^n\sum _{g=1}^G\frac{e^{{\mathit{\alpha }}_g^{\text{T}}{\mathit{W}}_i}}{{\sum }_{l=1}^G{e}^{{\mathit{\alpha }}_l^{\text{T}}{\mathit{W}}_i}}\int \prod _{j=1}^J\prod _{k=1}^{N_{ij}}{\sigma }_{gj}^{-1}{e}^{-\frac{1}{2{\sigma }_{gj}^2}{\left(Y_{ijk}-{\beta }_g^{\text{T}}{\mathit{X}}_{ijk}-{\mathit{b}}^{\text{T}}{\tilde{\mathit{X}}}_{ijk}\right)}^2}{\left\{{\lambda }_g\left(\widetilde{T_i}\right)e^{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left(\widetilde{T_i}\right)+{\eta }_g^{\text{T}}\mathit{b}}\right\}}^{{\Delta }_i} \\ \times \exp \{-{\int }_0^{\widetilde{T_i}}{e}^{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left(t\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}}\text{d}{\Lambda }_g\left(t\right)\}{\left|\mathbf{\Sigma }\left({\mathit{\xi }}_g\right)\right|}^{-1/2}{e}^{-\frac{1}{2}{\mathit{b}}^{\text{T}}\mathbf{\Sigma }{\left({\mathit{\xi }}_g\right)}^{-1}b}\text{d}\mathit{b}. \end{gathered}$$ (4)

We reparametrize the model by setting Λ = Λ₁ and ψ_g = log(λ_g/λ₁); we then estimate Λ nonparametrically and approximate ψ_g using a sieve of B-spline functions for g = 2,…, G. In particular, we treat Λ as a step function that jumps at the observed event times and replace ${\lambda }_1\left({\tilde{T}}_i\right)$ in the likelihood by $\Lambda \left({\tilde{T}}_i\right)$, where Λ{t} is the jump size of Λ at t. Let $B_1,\dots B_{m_n}$ be B-spline functions on a grid over $\left[0,\tau \right]$, where the number of spline functions m_n increases with the sample size. For g = 2,…, G, we approximate ${\psi }_g$ by ${\sum }_{s=1}^{m_n}{a}_{gs}{B}_s$, where $\mathit{a}\equiv {\left\{a_{gs}\right\}}_{g=2,\dots ,G;s=1,\dots ,m_n}$ is a set of regression parameters. Ideally, NPMLE would be adopted for every nonparametric function because it does not require tuning and is more flexible than splines. However, because the NPMLE for (Λ₁, …, Λ_G) is inconsistent, we estimate the cumulative baseline hazard function of a reference group using NPMLE and estimate the remaining nonparametric functions using splines, so as to achieve as much model flexibility as possible while ensuring estimation consistency.

Let $\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathit{a}}}_n\right)$ be the maximizer of

$$\begin{gathered} \prod _{i=1}^n\sum _{g=1}^G\frac{e^{{\mathit{\alpha }}_g^{\text{T}}{\mathit{W}}_i}}{{\sum }_{l=1}^G{e}^{{\mathit{\alpha }}_l^{\text{T}}{\mathit{W}}_i}}\int \prod _{j=1}^J\prod _{k=1}^{N_{ij}}{\sigma }_{gj}^{-1}{e}^{-\frac{1}{2{\sigma }_{gj}^2}{\left(Y_{ijk}-{\mathit{\beta }}_g^{\text{T}}{\mathit{X}}_{ijk}-{\mathit{b}}^{\text{T}}{\tilde{\mathit{X}}}_{ijk}\right)}^2} \\ \times {\left[\Lambda \left\{{\tilde{T}}_i\right\}{e}^{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left({\tilde{T}}_i\right)+{\sum }_{s=1}^{m_n}{a}_{gs}{B}_s\left({\tilde{T}}_i\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}}\right]}^{{\Delta }_i}\exp \left\{-{\int }_0^{{\tilde{T}}_i}{e}^{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left(t\right)+{\sum }_{s=1}^{m_n}{a}_{gs}{B}_s\left(t\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}}\text{d}\Lambda \left(t\right)\right\} \\ \times |\mathbf{\Sigma }\left({\mathit{\xi }}_g\right){|}^{-1/2}{e}^{-\frac{1}{2}{\mathit{b}}^{\text{T}}\mathbf{\Sigma }{\left({\mathit{\xi }}_g\right)}^{-1}\mathit{b}}\text{d}\mathit{b}, \end{gathered}$$

and let ${\widehat{\psi }}_{ng}={\sum }_{s=1}^{m_n}{\widehat{a}}_{ngs}{B}_s$, where ${\widehat{a}}_{ngs}$ is the corresponding element of ${\widehat{\mathit{a}}}_n$. Let $B=\left({\psi }_2,\dots ,{\psi }_G\right)$. The sieve NPMLE of $\left(\mathit{\theta },\Lambda ,B\right)$ is $\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)$, where ${\widehat{\mathcal{B}}}_n=\left({\widehat{\psi }}_{n2},\dots ,{\widehat{\psi }}_{nG}\right)$.

3. Computation of the sieve NPMLE.

In this section, we use Z(·) to denote the combination of the original set of time-dependent covariates and the B-spline functions (B₁, …, B_m), with γ_g being the corresponding vector of regression parameters for the gth latent class. We compute the sieve NPMLE using an accelerated version of the EM algorithm, with C and b treated as missing data. The proposed algorithm iteratively performs the EM steps. Unlike the standard EM algorithm, an E-step may not be performed under the current parameter estimates but under some function of the estimates at the previous steps.

We first introduce the standard EM algorithm. The complete-data log-likelihood function is

$$\begin{gathered} \sum _{i=1}^n\sum _{g=1}^{G}I\left(C_i=g\right)\left({\mathit{\alpha }}_g^{\text{T}}{\mathit{W}}_i-\log \left(\sum _{l=1}^G{e}^{{\mathit{\alpha }}_l^{\text{T}}{\mathit{W}}_i}\right)-\frac{1}{2}\log \left|\mathbf{\Sigma }\left({\mathit{\xi }}_g\right)\right|-\frac{1}{2}{\mathit{b}}_i^{\text{T}}\mathbf{\Sigma }{\left({\mathit{\xi }}_g\right)}^{-1}{\mathit{b}}_i\right. \\ -\sum _{j=1}^J\sum _{k=1}^{N_{ij}}\left\{\frac{1}{2}\log {\sigma }_{gj}^2+\frac{{\left(Y_{ijk}-{\mathit{\beta }}_g^{\text{T}}{\mathit{X}}_{ijk}-{\mathit{b}}_i^{\text{T}}{\tilde{\mathit{X}}}_{ijk}\right)}^2}{2{\sigma }_{gj}^2}\right\}+{\Delta }_i\left[{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left({\tilde{T}}_i\right)+{\mathit{\eta }}_g^{\text{T}}{\mathit{b}}_i+\log \mathrm{\Lambda }\left\{{\tilde{T}}_i\right\}\right] \\ \left.-\sum _{s\le {\tilde{T}}_i}\Lambda \left\{s\right\}{e}^{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left(s\right)+{\mathit{\eta }}_g^{\text{T}}{\mathit{b}}_i}\right). \end{gathered}$$

In the E-step, we compute the expectation of functions of (b,C) involved in the M-step. The conditional density of b_i given C_i = g and the observed data is proportional to

$$\begin{gathered} f_{ig}\left({\mathit{b}}_i\right)\equiv \left(\prod _{j=1}^J{\sigma }_{gj}^{-N_{ij}}\right)\prod _{j=1}^J\prod _{k=1}^{N_{ij}}\exp \left\{-\frac{{\left(Y_{ijk}-{\mathit{\beta }}_g^{\text{T}}{\mathit{X}}_{ijk}-{\mathit{b}}_i^{\text{T}}{\tilde{\mathit{X}}}_{ijk}\right)}^2}{2{\sigma }_{gj}^2}\right\}|\mathbf{\Sigma }\left({\mathit{\xi }}_g\right){|}^{-1/2} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times \exp \left\{-\frac{1}{2}{\mathit{b}}_i^{\text{T}}\mathbf{\Sigma }{\left({\mathit{\xi }}_g\right)}^{-1}{\mathit{b}}_i\right\}{e}^{{\Delta }_i\left\{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left({\tilde{T}}_i\right)+{\mathit{\eta }}_g^{\text{T}}{\mathit{b}}_i\right\}}\exp \left\{-{\int }_0^{{\tilde{T}}_i}{e}^{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left(t\right)+{\mathit{\eta }}_g^{\text{T}}{\mathit{b}}_i}\text{d}\Lambda \left(t\right)\right\}, \end{gathered}$$

and the conditional probability of C_i = g given the observed data is proportional to

$$q_{ig}\equiv e^{{\mathit{\alpha }}_g^{\text{T}}{\mathit{W}}_i}\int f_{ig}\left(\mathit{b}\right)\text{d}\mathit{b}.$$

The conditional expectation of any function h of (b_i,C_i) given the observed data is

$$E\left\{h\left({\mathit{b}}_i,C_i\right)|{\mathcal{O}}_i\right\}=\sum _{g=1}^G{\widehat{p}}_{ig}\frac{\int h\left(\mathit{b},g\right)f_{ig}\left(\mathit{b}\right)\text{d}\mathit{b}}{\int f_{ig}\left(\mathit{b}\right)\text{d}\mathit{b}},$$

where ${\widehat{p}}_{ig}=q_{ig}/{\sum }_{l=1}^G{q}_{il}$. The integrations in the above equation can be approximated with the adaptive Gauss–Hermite quadrature [9].

In the M-step, we update the parameters by maximizing the expected complete-data log-likelihood function given the observed data. In particular, we update α_g (g = 1,…,G − 1) by maximizing the weighted multinomial log-likelihood

$$\sum _{i=1}^n\left\{\sum _{g=1}^G{\widehat{p}}_{ig}{\mathit{\alpha }}_g^{\text{T}}{\mathit{W}}_i-\log \left(\sum _{g=1}^G{e}^{{\mathit{\alpha }}_g^{\text{T}}{\mathit{W}}_i}\right)\right\}$$

via the Newton-Raphson algorithm. Then, we update β_g and ${\sigma }_{gj}^2\left(j=1,\dots ,J;g=1,\dots ,G\right)$ by maximizing

$$-\frac{1}{2}\sum _{j=1}^J\sum _{i=1}^n{\widehat{p}}_{ig}\left[N_{ij}\log {\sigma }_{gj}^2+\sum _{k=1}^{N_{ij}}\frac{1}{{\sigma }_{gj}^2}{\widehat{\text{E}}}_g\left\{{\left(Y_{ijk}-{\mathit{\beta }}_g^{\text{T}}{\mathit{X}}_{ijk}-{\mathit{b}}_i^{\text{T}}{\tilde{\mathit{X}}}_{ijk}\right)}^2\right\}\right]$$

and update ξ_g (g = 1,…,G) by maximizing

$$-\frac{1}{2}\sum _{i=1}^n{\widehat{p}}_{ig}\left[\log \left|\mathbf{\Sigma }\left({\mathit{\xi }}_g\right)\right|+{\widehat{\text{E}}}_g\left\{{\mathit{b}}_i^{\text{T}}\mathbf{\Sigma }{\left({\mathit{\xi }}_g\right)}^{-1}{\mathit{b}}_i\right\}\right],$$

where ${\widehat{\text{E}}}_g$ denotes the conditional expectation with respect to b_i given C_i = g and the observed data. If closed-form solutions for the maximization problems are not available, then we employ the Newton-Raphson algorithm. In addition, we update (γ_g,η_g) (g = 1,…,G) by maximizing the (weighted) partial likelihood

$$\sum _{i=1}^n{\Delta }_i\left[\sum _{g=1}^G{\widehat{p}}_{ig}\left\{{\gamma }_g^{\text{T}}{\mathit{Z}}_i\left({\tilde{T}}_i\right)+{\mathit{\eta }}_g^{\text{T}}{\widehat{\text{E}}}_g\left({\mathit{b}}_i\right)\right\}-\log \left\{\sum _{g=1}^G\sum _{j=1}^{n}I\left({\tilde{T}}_j\ge {\tilde{T}}_i\right){\widehat{p}}_{jg}{e}^{{\gamma }_g^{\text{T}}{\mathit{Z}}_j\left({\tilde{T}}_i\right)}{\widehat{\text{E}}}_g\left(e^{{\mathit{\eta }}_g^{\text{T}}{\mathit{b}}_j}\right)\right\}\right]$$

via the Newton-Raphson algorithm. Finally, we update the cumulative baseline hazard function Λ by

$$\widehat{\Lambda }\left\{{\tilde{T}}_i\right\}=\frac{{\mathrm{\Delta }}_i}{{\sum }_{g=1}^G{\sum }_{j=1}^{n}I\left({\tilde{T}}_j\ge {\tilde{T}}_i\right){\widehat{p}}_{jg}{e}^{{\widehat{\gamma }}_g^{\text{T}}{\mathit{Z}}_j\left({\tilde{T}}_i\right)}{\widehat{\text{E}}}_g\left(e^{{\widehat{\mathit{\eta }}}_g^{\text{T}}{\mathit{b}}_j}\right)}$$

for i = 1,…,n, where (${\widehat{\mathit{\gamma }}}_g$, ${\widehat{\mathit{\eta }}}_g$) are the current estimates of the parameters.

The standard EM algorithm, which iteratively performs the E-step and M-step until convergence, may be slow, especially when the number of parameters is large. To accelerate the convergence, we adopt a modification of the EM algorithm proposed by Varadhan and Roland [19]. Let ϑ denote the set of all parameters and s(ϑ) be the set of updated parameters after a single EM step if the initial parameter value is ϑ. With ϑ^(k) being the set of current estimates, a step of the accelerated EM algorithm consists of

1. Calculate ϑ₁ = s(ϑ^(k)).

2. Calculate ϑ₂ = s(ϑ₁).

3. Calculate r = ϑ₁ −ϑ^(k), v = ϑ₂ −ϑ₁ −r, and a = −||r||₂/||v||₂.

4. Update the parameter estimates by ϑ^(k+1) = s(ϑ^(k) −2ar +a²v).

To improve stability, we update the parameters using the standard EM steps at early steps of the algorithm. Once the difference between consecutive parameter estimates becomes smaller than a certain threshold, we perform the accelerated EM steps until convergence. When the assumed number of latent classes is larger than the actual number, the model is nonidentifiable, and the parameter estimates may not converge; therefore, we terminate the algorithm when the difference between the log-likelihood values of consecutive iterations is smaller than a certain threshold.

The algorithm may converge to a local maximum of the log-likelihood. To improve the chance of obtaining the global maximum, we can run the algorithm with different initial values and set the estimates to the converged values that yield the largest log-likelihood. One strategy for setting the initial values is to classify subjects into G classes by some clustering method and set the parameter values for each class to be the estimates obtained from subjects assigned to the class.

Upon convergence, we use Louis’s formula [11] to compute the observed information matrix, essentially treating the model as parametric, with parameters θ, $\mathrm{\Lambda }{\left\{{\tilde{T}}_i\right\}}_{i:{\mathrm{\Delta }}_i=1}$ and ${\left\{a_{gs}\right\}}_{g=2,\dots ,G;s=1,\dots ,m_n}$. The submatrix of the inverse of the observed information matrix corresponding to θ can be used to estimate the standard errors of ${\widehat{\mathit{\theta }}}_n$. This submatrix is essentially an estimate of the inverse of the efficient information matrix $\tilde{\mathit{I}}$ defined in the proof of Theorem 4.2, where the least-favorable directions are estimated by solving the empirical counterparts of the integral equations they satisfy. The consistency of this standard error estimator is established in Theorem 4.3.

We propose to use the Bayesian information criterion (BIC) [16] to select the number of latent classes G. Specifically, for each G, we estimate the model using the sieve NPMLE and compute

$$\text{BIC}=-2\log L_n\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)+s\log n,$$

where L_n is the likelihood function, and s is the number of free parameters in the model, including the regression parameters for the B-spline functions. We select the G that yields the smallest BIC value.

4. Asymptotic properties of the sieve NPMLE.

Assume that the degree of the B-spline functions is fixed at some p ≥ 1 and that the distance between adjacent knots is within $\left(K^{-1}{m}_n^{-1},K{m}_n^{-1}\right)$ for some large constant K. Let d be the dimension of the Euclidean parameters and Θ be a known, compact parameter space of θ. Let $\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)$ denote the true parameter values, where ${\mathcal{B}}_0=\left({\psi }_{02},\dots ,{\psi }_{0G}\right)$. Let ${\mathrm{\Lambda }}_g\left(t\right)={\int }_0^t{\lambda }_g\left(u\right)\text{d}u$ and Λ_0g be its true value (g = 1,…,G).

We impose the following conditions.

(C1) The parameter θ₀ lies in the interior of Θ, and the function Λ_0g is continuously differentiable up to the third order on $\left[0,\tau \right]$ for g = 1, …, G.

(C2) With probability one, $P\left\{\tilde{T}=\tau |\mathit{W},\mathit{X},\tilde{\mathit{X}},\mathit{Z}\left(\cdot \right)\right\}>{\delta }_0$ for some fixed δ₀ > 0.

(C3) With probability one, Z(·) has left-continuous sample paths on $\left[0,\tau \right]$ with right derivatives. In addition, there exists a large constant K such that

$$P\left\{\underset{j=1,\dots ,J}{\max }{N}_j+{‖\mathit{W}‖}_2+{‖\mathit{X}‖}_2+{‖\tilde{\mathit{X}}‖}_2+\underset{t\in \left[0,\tau \right]}{\sup }{‖\mathit{Z}\left(t\right)‖}_2+\underset{t\in \left[0,\tau \right]}{\sup }{‖{\mathit{Z}}^{\prime }\left(t\right)‖}_2<K\right\}=1,$$

where Z′ is the (componentwise) left derivative of Z.

(C4) The number of knots m_n satisfies m_n = O(n^q) for some 1/12 < q < 1/8.

The next condition is more technical and ensures model identifiability and invertibility of the information operator. Essentially, it requires that the covariates take enough distinct values such that the class-specific distributions of the longitudinal outcomes can be distinguished and the effect of each covariate on each class-specific distribution can be identified. Let ${\mathbf{\Sigma }}_{0g}=\text{diag}\left({\sigma }_{0g1}^2{\mathbf{1}}_{N_1},\dots ,{\sigma }_{0gJ}^2{\mathbf{1}}_{N_J}\right)$, ${\mathbf{\Gamma }}_{0g}={\mathbf{\Psi }}_{0g}{\left(\mathit{I}+{\mathbf{\Psi }}_{0g}^{\text{T}}\tilde{\mathit{X}}{\mathbf{\Sigma }}_{0g}^{-1}{\tilde{\mathit{X}}}^{\text{T}}{\mathbf{\Psi }}_{0g}\right)}^{-1}{\mathbf{\Psi }}_{0g}^{\text{T}}$, and ${\mathbf{\Sigma }}_{0Y\hspace{0.17em}g}=\tilde{\mathit{X}}{\mathbf{\Psi }}_{0g}{\mathbf{\Psi }}_{0g}^{\text{T}}{\tilde{\mathit{X}}}^{\text{T}}+{\mathbf{\Sigma }}_{0\hspace{0.17em}g}$, where 1_k is a k-vector of ones, Ψ_0g is an orthogonal matrix such that $\mathbf{\Sigma }\left({\mathit{\xi }}_{0g}\right)={\mathbf{\Psi }}_{0g}{\mathbf{\Psi }}_{0g}^{\text{T}}$, and ${\sigma }_{0gj}^2$ and ξ_0g are the true values of the corresponding parameters. Note that Σ_{0Y g} is the covariance matrix of Y given C = g and (N₁,…,N_J).

(C5) There exist some positive integers (n₁,…,n_J) such that P(N₁ = n₁; …; N_J = n_J) > 0 and that the following holds. Let X be the set of possible values of $\left(\mathit{X},\tilde{\mathit{X}}\right)$ given (N₁ = n₁,…,N_J = n_J) such that ${\tilde{\mathit{X}}}^{\text{T}}\tilde{\mathit{X}}$ is invertible and

$$\tilde{\mathit{X}}\mathbf{\Sigma }\left({\mathit{\xi }}_{0g}\right){\tilde{\mathit{X}}}^{\text{T}}+{\mathbf{\Sigma }}_{0g}\ne \tilde{\mathit{X}}\mathbf{\Sigma }\left({\mathit{\xi }}_{0l}\right){\tilde{\mathit{X}}}^{\text{T}}+{\mathbf{\Sigma }}_{0l}$$

$$\text{or}\left(\mathit{X}\hspace{0.17em}{\mathit{\beta }}_{0g}\ne \mathit{X}\hspace{0.17em}{\mathit{\beta }}_{0l}\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbf{\Sigma }}_{0Y\hspace{0.17em}g}^{-1}\mathit{X}\hspace{0.17em}{\mathit{\beta }}_{0g}+{\mathbf{\Sigma }}_{0\hspace{0.17em}g}^{-1}\tilde{\mathit{X}}{\mathbf{\Gamma }}_{0g}^{\text{T}}{\mathit{\eta }}_{0g}\ne {\mathbf{\Sigma }}_{0Y\hspace{0.17em}l}^{-1}\mathit{X}\hspace{0.17em}{\mathit{\beta }}_{0l}+{\mathbf{\Sigma }}_{0\hspace{0.17em}l}^{-1}\tilde{\mathit{X}}{\mathbf{\Gamma }}_{0l}^{\text{T}}{\mathit{\eta }}_{0l}\right)$$

whenever g ≠ l. For k= 1, …, n_j and j = 1, …, J, if ${\mathit{W}}^{\text{T}}{\mathit{h}}_W=0$, ${\mathit{X}}_{jk}^{\text{T}}{\mathit{h}}_{X\hspace{0.17em}jk}=0$, ${\tilde{\mathit{X}}}_{jk}^{\text{T}}{\mathit{h}}_{\tilde{X}\hspace{0.17em}jk}=0$ and Z(t)^Th_Z = 0 almost surely for all $\left(\mathit{X},\tilde{\mathit{X}}\right)\in \mathit{\chi }$ and $t\in \left[0,\tau \right]$, then h_W = 0, h_Xjk = 0, ${\mathit{h}}_{X\hspace{0.17em}jk}=\text{0}$, ${\mathit{h}}_{\tilde{X}\hspace{0.17em}jk}=\text{0}$, and h_Z = 0, where h_W, ${\mathit{h}}_{X jk}$, ${\mathit{h}}_{\tilde{X} jk}$, and h_Z are fixed vectors of appropriate dimensions.

The final condition ensures that the least-favorable direction for the Euclidean parameters is sufficiently smooth.

(C6) The conditional density of the censoring variable U given the observed covariates is continuously differentiable on the support of U with respect to some dominating measure up to the third order.

Remark 1. Conditions (C1)–(C3) are common assumptions in the analysis of right-censored data under semiparametric survival models. Condition (C4) pertains to the rate at which the number of B-spline functions increases to infinity. Condition (C5) pertains to the class-specific distributions of the longitudinal outcomes and event time. Instead of directly assuming the identifiability and invertibility of the information operator of the proposed model, we derive these properties under assumptions on individual class-specific distributions. Condition (C5) requires that after removing specific covariate values that yield equality of certain quantities of the class-specific distributions of the observed variables, the set of possible covariate values are linearly independent. For latent-class models in general, linear independence of the covariates and distinctness of parameter values across latent classes are not sufficient for the invertibility of the information operator. To see this, consider a simple model with two latent classes, a known mixture probability of 0.5 for each class, a single binary covariate X, and a single outcome variable Y with Y | (X,C = g) ∼ N(α_g + β_gX,1) for g = 1,2, where C denotes the latent class membership. The score statistic along the direction α₁ = α₀₁ + ϵ, α₂ = α₀₂ ‒ ϵ, β₁ = β₀₁ ‒ ϵ, and β₂ = β₀₂ + ϵ, and is zero when α₀₁ = α₀₂, even if β₀₁ ≠ β₀₂, where (α₀₁,α₀₂,β₀₁,β₀₂) are the true parameter values. This model does not satisfy (a simplified version of) condition (C5) because the two latent classes are different only at X ≠ 0, but given X ≠ 0, (1,X) is no longer linearly independent. A simple sufficient condition for condition (C5) is that all covariates are linearly independent and the class-specific variances of Y are distinct almost surely.

Let || · ||_∞ be the supremum norm over $\left[0,\tau \right]$. We have the following results.

Theorem 4.1. Under conditions (C1)–(C5), there exists a local maximum of the nonparametric likelihood in the sieve space, denoted by $\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)$, such that

$${‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖}_2^2+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }^2+\sum _{g=2}^G{\int }_0^{\tau }{\left|{\widehat{\psi }}_{ng}\left(t\right)-{\psi }_{0g}\left(t\right)\right|}^2\text{d}t=o_p\left(n^{1/2}\right).$$

This theorem provides a preliminary, combined rate of convergence for the estimators of the Euclidean and infinite-dimensional parameters. Based on this convergence rate, the following theorem establishes that the Euclidean parameter estimators converge at the optimal n^1/2 rate and attain the semiparametric efficiency bound [1].

Theorem 4.2. Under conditions (C1)–(C6), $n^{1/2}\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0\right)$ converges weakly to the normal distribution with zero mean, and its asymptotic variance attains the semiparametric efficiency bound.

Let I_n be the negative Hessian matrix of the log-likelihood evaluated at the estimated parameters, with the jump sizes of ${\widehat{\mathrm{\Lambda }}}_n$ and the coefficients of the spline functions in ${\widehat{\psi }}_{n2},\dots ,{\widehat{\psi }}_{nG}$ treated as Euclidean parameters. Let ${\widehat{\mathit{V}}}_n$ be the submatrix of (n⁻¹I_n)⁻¹ that corresponds to θ.

Theorem 4.3. Under conditions (C1)–(C6), ${‖{\widehat{\mathit{V}}}_n-{\tilde{\mathit{I}}}^{-1}‖}_2=o_p\left(1\right)$, where $\tilde{\mathit{I}}$ is the efficient information matrix of θ defined in the proof of Theorem 4.2.

The proofs of Theorems 4.1 and 4.2 are given in Appendix A, whereas the proof of Theorem 4.3 is given in Section S3 of the supplementary materials [21].

5. Simulation studies.

We considered a longitudinal study where data were collected on repeated measures of longitudinal outcomes as well as on the time to the occurrence of an event of interest. Each subject was examined periodically until the event of interest occurred or the subject was lost to follow-up. At the initial examination, a set of baseline covariates, which may represent sex, age, and other information, were measured, and at each examination, two types of longitudinal outcomes were measured. The latent class for each subject was generated from model (1) with G = 3 and W = (1,X₁,X₂)^T, where X₁ and X₂ are independent Bernoulli(0,5) and N(0,1), respectively. We set the examination times at s_k = 0,15(k−1) for k = 1,…,10. For j = 1,2 and k = 1,…,10, we generated

$$Y_{jk}{|}_{C=g}={\mathit{\beta }}_{gj}^{\text{T}}{\mathit{X}}_k+b_j+b_3+{ϵ}_{jk},$$ (5)

where ${ϵ}_{jk}|\left(C=g\right)~\text{N}\left(0,{\sigma }_{gj}^2\right)$, X_k = (1,s_k,X₁,X₂)^T, $b_j|\left(C=g\right)~\text{N}\left(0,{\xi }_{gj}^2\right)$, and (b₁,b₂,b₃) are independent of each other and of (X₁,X₂). Note that the random effects b₁ and b₂ account for the dependence among repeated measures of a single type of longitudinal outcome, whereas b₃ accounts for the dependence between the two types of longitudinal outcomes. The event time T was generated from model (3) with a single random effect term b₃ and Z(t) = (X₁,X₂)^T for all t, and the censoring variable U was generated from Uniform $\left(0,\tau \right)$ with $\tau =5$. Note that the number of longitudinal outcome measurements is max{k : k ≤ 10,s_k ≤ T ∧U}.

The true values of the Euclidean parameters are given in Table S1 of the supplementary materials [21]. The class-specific baseline hazard functions are λ₁(t) = 0,5, λ₂(t) = exp(0,25t), and λ₃(t) = 1. The proportions of subjects belonging to latent classes 1, 2, and 3 are approximately 35%, 35%, and 30%, respectively. The average number of longitudinal outcome measurements per subject is about 5.4. The censoring proportion is about 25%.

We set the degree of the B-spline functions to be 1 and the number of interior knots to be 2; in our experience, the results are largely insensitive to the choice of the number of knots. The locations of the knots were set data-adaptively to be the 33% and 66% empirical quantiles of the observed event times. We considered G = 2, 3, and 4 latent classes and used BIC to select G. To set the initial values, we use k-mean clustering based on the event (or censoring) time, the censoring indicator, and the baseline longitudinal outcome values to classify subjects into subgroups with k = G. Then, we fit the generalized linear models and survival models (without random effects) on each subgroup and set the initial parameter values to be the corresponding estimated values. The initial values for the coefficients of the B-splines and the regression parameters of the random effects are set to 0, the initial values of Var(b_j)+Var(ϵ_jk) are set to be the estimated variances in the corresponding fitted linear models with Var(b_j) = Var(ϵ_jk) (j = 1,2; k = 1; …, 10), and the variance of b₃ is set to be 0.1. The initial cumulative baseline hazard function is set to be the Breslow estimator. We constrained all Euclidean parameter estimates (including the regression parameters for the B-spline functions and the logarithm of the variance parameters) to be smaller than or equal to 10 in absolute value. This constraint is imposed because in the early iterations of the EM algorithm, the unconstrained estimates may sometimes become too extreme and cause numerical problems. We set the sample size to be n = 1000 or 2000 and considered 1000 simulation replicates for each setting.

Under G = 3, in no replicates do any parameter estimates (in absolute value) equal the boundary value of 10. Some parameter estimates are equal to the boundary value in about 60% of the replicates for G = 4 and in less than 5% of the replicates for G = 2. The convergence to the boundary under G = 4 is expected, because the model is nonidentifiable. In all but ten replicates under n = 1000, BIC selected the correct number of latent classes, and thus we only present the estimation results under G = 3. Because the labels of the latent classes are arbitrary, after convergence of the EM algorithm, we redefined the latent classes such that the orders of the estimated values of certain parameters across latent classes match the orders of the corresponding true parameter values. The estimation results for n = 1000 and n = 2000 are summarized in Tables S1 and S2 in the supplementary materials [21], respectively. The estimators of all parameters, including the class-specific cumulative baseline hazard functions at particular time points, are virtually unbiased. The standard errors are estimated accurately, and the coverage probabilities of the confidence intervals are close to the nominal level, especially for n = 2000. Thus, the proposed estimation method effectively uncovers the latent structure of the population, produces consistent estimators, and yields valid statistical inference.

6. A real study.

The ARIC study is a prospective epidemiological cohort study conducted in the United States. In the study, a total of about 15,000 subjects received a baseline examination in 1987–1989 and potentially six subsequent examinations in 1990–1992, 1993–1995, 1996–1998, 2011–2013, 2016–2017, and 2018–2019. At each examination, medical data, such as body mass index (BMI), blood pressure, and cholesterol levels, were collected. The subjects were also followed through reviews of hospital records, and potentially right-censored observations on time to myocardial infarction (MI), stroke, and death were also obtained.

We aimed to study the risk of cardiovascular diseases or death among African American subjects and to detect the presence of latent subgroups. The event of interest is MI, stroke, or death. The African American subjects were recruited from two centers of study in Forsyth County, NC and Jackson, MS. We set study location, sex, and BMI, glucose level, smoking status, and age at the first examination as covariates; these are referred to as the baseline covariates in the sequel. We considered systolic blood pressure and total cholesterol level, which were measured at each examination, as longitudinal outcomes. After removing 347 subjects with prior (or unknown status of) stroke or coronary heart disease at baseline and 178 subjects with missing data, the sample size is 3284, and the censoring proportion is 49.2%.

We fit models (1)–(3), where T is the time from the first examination to MI, stroke, or death, whichever occurred first, (Y_1k,Y_2k) are respectively the systolic blood pressure and total cholesterol level at the kth examination, and N_j is the total number of examinations (k = 1,…,N_j;j = 1,2). The set of covariates W consists of the baseline covariates (and the constant 1 for the intercept). For the jth longitudinal outcome at the kth examination, we assumed model (5) with the set of covariates X_k consisting of the baseline covariates and the time of the kth examination. In the survival model, the set of covariates Z(t) is time-independent and consists of the baseline covariates, and the set of random effects consists of a single term b₃. We set the degree of the B-spline functions to be 1 and considered 2–4 interior knots. The locations of the knots were chosen to be empirical quantiles of the observed event times. We ranged the number of latent classes G from 1 to 6.

For any numbers of knots for the B-spline functions, the BIC picked G = 4 latent classes. The BIC values at G = 1,…,6 under 2 interior knots are plotted in Figure S1 of the supplementary materials [21]. Since the estimation results across different numbers of knots are similar, we reported the results under 2 interior knots. The point estimates, standard errors, and p-values of all Euclidean parameters in the survival model are given in Table 1, and the estimated class-specific cumulative hazard functions are plotted in Figure 1; the estimation results for the remaining Euclidean parameters are given in Tables S3 and S4 of the supplementary materials [21]. The estimated trajectories of the mean longitudinal outcomes for a typical subject from each latent class are plotted in Figure S2 of the supplementary materials [21]. We classified a subject to a latent class if the (estimated) posterior probability of the class is larger than 0.7; a subject is unclassified if none of the posterior probabilities is larger than 0.7. The Kaplan–Meier curves for the (predicted) latent classes are plotted in Figure S3 of the supplementary materials [21].

TABLE 1.

Estimation results for the Euclidean parameters in the survival model for the ARIC data

Parameter	Estimate	SE	p-value	Parameter	Estimate	SE	p-value
γ 1,Center	0.2431	0.3041	4.24E–01	γ 3,Glucose	0.2304	0.0450	3.15E–07
γ 1,BMI	−0.0775	0.0949	4.14E–01	γ 3,Smoke	0.8147	0.1487	4.26E–08
γ 1,Glucose	0.4086	0.1325	2.04E–03	γ 3,Sex	0.3840	0.1355	4.61E–03
γ 1,Smoke	0.7848	0.1505	1.84E–07	γ 3,Age	0.5433	0.0673	7.13E–16
γ 1,Sex	0.5965	0.1617	2.25E–04	γ 4,Center	0.0770	0.3369	8.19E–01
γ 1,Age	0.6440	0.1303	7.75E–07	γ 4,BMI	−0.1136	0.1082	2.94E–01
γ 2,Center	0.1269	0.1887	5.01E–01	γ 4,Glucose	0.2954	0.0411	7.05E–13
γ 2,BMI	0.1052	0.0552	5.65E–02	γ 4,Smoke	0.5983	0.2039	3.34E–03
γ 2,Glucose	0.0634	0.0403	1.16E–01	γ 4,Sex	0.4959	0.1986	1.25E–02
γ 2,Smoke	0.6472	0.1378	2.65E–06	γ 4,Age	0.2654	0.0980	6.78E–03
γ 2,Sex	0.3533	0.1298	6.49E–03	η 1	1.8929	2.5689	4.61E–01
γ 2,Age	0.3426	0.0721	2.00E–06	η 2	1.5561	0.6952	2.52E–02
γ 3,Center	−0.0954	0.1920	6.19E–01	η 3	0.9861	2.3893	6.80E–01
γ 3,BMI	0.1853	0.0641	3.86E–03	η 4	1.3614	1.0065	1.76E–01

NOTE: For the parameters labeled γ, the first subscript represents the latent class, and the second subscript represents the covariate that corresponds to the parameter. “Center” is the indicator for the Jackson center; “Sex” is the indicator for male; “Smoke” is the indicator for smoker; “Glucose” represents glucose level. All continuous covariates are standardized. The parameter η_g is the regression parameter of b₃ for the gth latent class.

FIG 1.

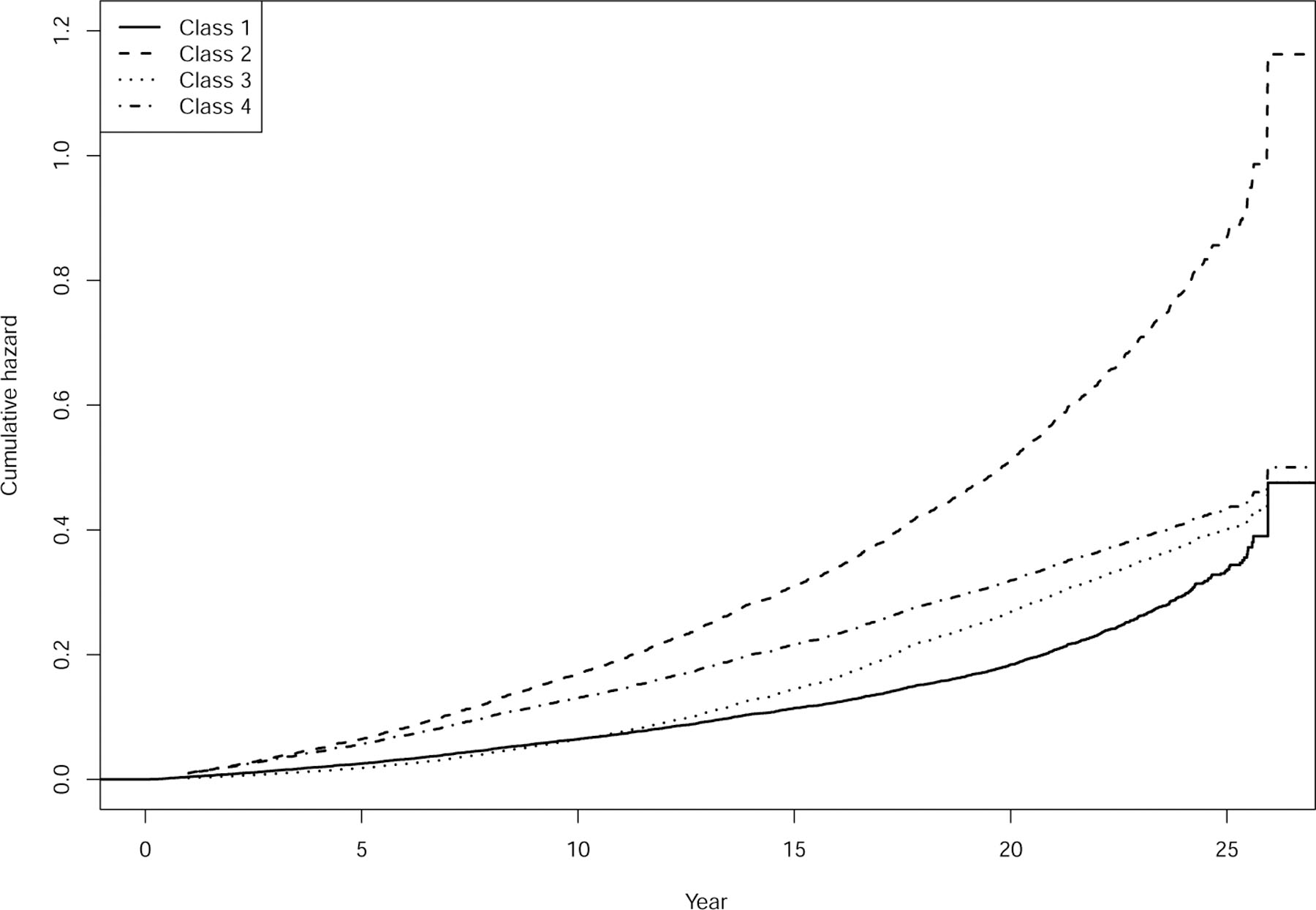
Estimated class-specific baseline hazard functions for the ARIC data.

Older subjects, males, and smokers have higher risk of MI, stroke, or death across all latent classes. Subjects with higher BMI tend to have higher risk of disease or death in the third latent class, but BMI has no significant association with the risk in other latent classes. Glucose level has highly significant positive effect on the risk of disease or death in all but the second latent class. The random effect b₃, which captures the dependence of the systolic blood pressure and the total cholesterol level, is significantly associated with the risk of disease or death only in the second latent class. This suggests that systolic blood pressure and total cholesterol level are associated with the risk of disease or death even conditional on the latent class membership. The estimated class-specific cumulative hazard of the second latent class is substantially higher than those of the other classes, and the empirical survival probabilities of the second latent class are smaller. The mean systolic blood pressure of subjects in the second latent class tends to be higher than those of the other classes. The results suggest that the second latent class is characterized by elevated risk of disease or death. The other groups also exhibit differences in the risk of disease or death, distributions of the longitudinal outcomes, and effects of covariates on the longitudinal and survival outcomes. In the latent-class membership model, the regression parameters for glucose level are significantly negative for the first three latent classes, suggesting that the fourth latent class is characterized by high glucose level. In addition, the second latent class is characterized by older subjects, and the third latent class is characterized by males and subjects with higher BMI.

Suppose that we are interested in the conditional survival function for a subject at risk at time s given the trajectories of the longitudinal outcome measurements up to s. For a subject with time-independent covariates in the survival model, this probability function can be estimated by h(t)/h(s) for t ≥ s, where

$$\begin{gathered} h\left(t\right)=\sum _{g=1}^G\frac{e^{{\mathit{\alpha }}_g^{\text{T}}\mathit{W}}}{{\sum }_{l=1}^G{e}^{{\mathit{\alpha }}_l^{\text{T}}\mathit{W}}}\int \exp \left\{-{\mathrm{\Lambda }}_g\left(t\right)e^{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}+{\mathit{\eta }}_g^{\text{T}}\mathit{b}}\right\}\prod _{j=1}^J\prod _{k=1}^{K_j}{\sigma }_{gj}^{-1}{e}^{-\frac{1}{2{\sigma }_{gj}^2}{\left(Y_{jk}-{\mathit{\beta }}_g^{\text{T}}{\mathit{X}}_{jk}-{\mathit{b}}^{\text{T}}{\tilde{\mathit{X}}}_{jk}\right)}^2} \\ \hspace{1em}\hspace{1em}\hspace{1em}\times {\left|\mathbf{\Sigma }\left({\mathit{\xi }}_g\right)\right|}^{-1/2}{e}^{-\frac{1}{2}{\mathit{b}}^{\text{T}}\mathbf{\Sigma }{\left({\mathit{\xi }}_g\right)}^{-1}\mathit{b}}\text{d}\mathit{b}, \end{gathered}$$

K_j is the number of observations on the jth longitudinal outcome by time s, and the parameters are evaluated at the sieve NPMLE. Figure S4 in the supplementary materials [21] shows the estimated curves for two hypothetical subjects at s = 10.

We use cross-validation to evaluate the robustness of the latent-class structure. We split the data into 20 pairs of training and validation datasets with a ratio of sample sizes of 3 : 2. On each training dataset, we fit the latent-class model with G = 4 and 2 interior knots for the B-spline functions, and for each subject in the corresponding validation dataset, we used the estimated model to compute the posterior probabilities of class membership given the subject’s covariates and longitudinal outcomes (but not the event time). A subject is predicted to belong to a latent class if the posterior probability of the class is larger than 0.7; a subject is unclassified if none of the posterior probabilities is larger than 0.7. Note that the prediction of latent class does not directly involve the event time of the subjects in the validation dataset.

To evaluate the explanatory power of the (predicted) latent classes, in each validation dataset, we fit the Cox model with covariates, including the baseline systolic blood pressure, the baseline total cholesterol level, and the predicted latent classes; unclassified subjects were discarded. We tested the significance of the latent classes in the model using the likelihood-ratio test. The combined p-value across data splits is 0.0248, where the combined p-value is defined as $\mathrm{\Phi }\left\{0.05{\sum }_{s=1}^{20}{\mathrm{\Phi }}^{-1}\left(p_s\right)\right\}$, p_s is the p-value for the sth split, and Φ is the standard normal distribution function. In addition, we fit a stratified Cox model, stratifying on the latent classes, with covariates including the baseline covariates, the baseline systolic blood pressure, the baseline total cholesterol level, and the interaction between the latent classes and the other covariates. The combined p-value for the likelihood-ratio tests for the interaction terms is 0.0250. These results suggest the existence of heterogeneity in the population that is not captured by the observed covariates. Subjects from different latent classes have not only different baseline hazards but also different association patterns between the covariates and the risk of disease or death.

7. Discussion.

In this article, we consider a semiparametric latent-class model for the joint analysis of longitudinal outcomes and a potentially right-censored event time. We develop a novel estimation approach that combines NPMLE and sieve estimation. We prove that the nonparametric components of the proposed estimators are consistent at a rate of o(n^1/4). Although sieve estimators generally converge at a rate slower than n^1/2, the Euclidean components of the estimators are nevertheless n^1/2-consistent and asymptotically normal.

Under the proposed model, covariates may be associated with the event time through the latent class membership or directly through the class-specific survival models. The regression parameters in the survival models are best interpreted conditional on the latent variables b and C, so that for a subject in a specific latent class, each covariate in the survival model contributes multiplicatively to the baseline hazard. To obtain an “overall” effect of the covariates, we may adopt a Monte-Carlo approach: repeatedly generate data from the estimated model and the observed covariates, and fit the Cox model on the generated event times and covariates. The estimated regression parameters could be interpreted as the overall effects of the covariates, combining the effects on the latent class membership and the class-specific event-time distributions.

We proposed to estimate the standard error of the estimators by the inverse of the observed information matrix. This approach yields satisfactory performance in our extensive numerical studies, but it may be numerically unstable in very large samples or models. If one is interested only in the inference of the Euclidean parameters, then alternative methods based on the profile likelihood can be adopted [22].

The constraints on the number of B-spline functions given by condition (C4) guarantee that ${\widehat{\psi }}_{ng}\left(g=2,\dots ,G\right)$ converges to the true value at a rate faster than n^1/4, so that the Euclidean parameters can attain the efficiency bound. Because ψ_0g’s are continuously differentiable up to the third order, the approximation error of the spline functions is of rate O(n^−3q), and q > 1/12 is necessary for ${‖{\widehat{\psi }}_{ng}-{\psi }_{0g}‖}_2=o_p\left(n^{-1/4}\right)$; this bound can be relaxed under stronger assumptions on the smoothness of Λ_0g’s. The upper limit q < 1/8 arises from the shrinking-neighborhood-based argument for consistency. In the proof, we show that a local maximum of the log-likelihood exists in an o(n^−1/4)-neighborhood of the true parameter values. The upper limit q < 1/8 is to guarantee that the second-order term in the linear expansion of the log-likelihood dominates other terms in the expansion.

An intuitively appealing nonparametric estimation approach is to set each class-specific cumulative baseline hazard function to be a step function that jumps at the observed event times. This approach, however, yields inconsistent estimators even in the simple settings considered by Ma and Wang [12] and Wang, Garcia and Ma [20] because the parameter space is overly complex. Each (uncensored) observation belongs to a specific latent class and should only contribute to the jump of the corresponding cumulative baseline hazard function at the observed event time. However, the latent class membership is unknown, and this nonparametric approach incorrectly allows all cumulative baseline hazard functions to jump at the event time. To overcome this difficulty, we only estimate the cumulative baseline hazard function of a reference class nonparametrically and approximate the relative magnitudes of the baseline hazard functions between the reference class and other classes using spline functions. With a properly-chosen number of grid points for the spline functions, the complexity of the parameter space is controlled to yield consistent estimators.

During the preparation of this article, independent work of Liu et al. [10] was brought to our attention. Our model is more general than that of Liu et al. [10], which allows only a single type of longitudinal outcome with a random intercept in the longitudinal outcome model, and Liu et al. [10] adopted spline approximation for all nonparametric functions. In addition, we establish the asymptotic properties of the proposed estimators under specific assumptions on the proposed models and the observed data, whereas the assumptions in Liu et al. [10] are expressed in very general terms and are difficult to verify for given models. To demonstrate the extra flexibility of the proposed model over that of Liu et al. [10], we conducted a simulation study, which showed that misspecification of the latent variable structure may yield substantial estimation bias; see Section S4 of the supplementary materials [21].

Our work can be extended in several directions. First, one may be interested in the joint analysis of multiple event times, such as the times to the occurrence of different diseases. The proposed modeling framework can be readily extended to allow for multivariate event times by assuming a separate regression model for each event time with a set of shared random effects b. The sieve NPMLE can be easily extended to the multivariate setting, and its theoretical properties can be established along the lines of the proofs of Theorems 4.1 and 4.2.

Second, one may consider interval-censored event time(s). In ARIC, the onset of asymptomatic diseases, such as diabetes and hypertension, was not directly observed but was known to fall within certain time intervals. To accommodate interval censoring, we can extend the proposed methods and use the NPMLE [28] to estimate the cumulative baseline hazard function of the reference class. However, interval censoring results in a different likelihood function, which poses great challenges to the derivation of the asymptotic properties of the sieve NPMLE.

Finally, it would be of interest to consider high-dimensional longitudinal outcomes or covariates. In current biomedical studies, different types of molecular data, such as DNA alteration and gene expression, are collected along with clinical data. Such molecular data are often high-dimensional, with the number of variables much larger than the sample size. These data contain rich genetic information that can be used to classify subjects into biologically distinct disease subtypes [17]. We can set variables for the molecular data as longitudinal outcomes or covariates in models (1)–(3) and adopt a penalized (sieve) likelihood approach for estimation.

APPENDIX A: PROOFS OF THEOREMS

In this appendix, we prove Theorems 4.1 and 4.2. The proofs make use of the lemmas given in Appendix B. To facilitate the presentation, we introduce the following notation. Let ${\mathcal{M}}_K=\left\{\Lambda \in {\ell }^{\infty }\left[0,\tau \right]:\Lambda \right.$ is monotone nondecreasing, $\Lambda \left(0\right)=0,\Lambda \left(\tau \right)<K$}. For some large enough positive constant K, let ${\Xi }_K=\Theta \times {\mathcal{M}}_K\times {\text{BV}}_K{\left[0,\tau \right]}^{G-1}$ be the parameter space of (θ,Λ,ψ₂,…,ψ_G), where ${\text{BV}}_K\left[0,\tau \right]=\left\{\psi \in {\ell }^{\infty }\left[0,\tau \right]:{‖\psi ‖}_{\text{V}}<K\right\}$, and || · ||_V is the total variation over $\left[0,\tau \right]$, such that

$${‖f‖}_{\text{V}}=\underset{0=t_0\le t_1<\cdots <t_m=\tau }{\sup }\sum _{j=1}^m\left|f\left(t_j\right)-f\left(t_{j-1}\right)\right|.$$

The subscript K for the parameter spaces may be suppressed in the sequel. Let $\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$ denote

$$\begin{gathered} \sum _{g=1}^G\frac{e^{{\mathit{\alpha }}_g^{\text{T}}\mathit{W}}}{{\sum }_{l=1}^G{e}^{{\mathit{\alpha }}_l^{\text{T}}\mathit{W}}}\int \prod _{j=1}^J\prod _{k=1}^{N_j}{\sigma }_{gj}^{-1}{e}^{-\frac{1}{2{\sigma }_{gj}^2}{\left(Y_{jk}-{\mathit{\beta }}_g^{\text{T}}{\mathit{X}}_{jk}-{\mathit{b}}^{\text{T}}{\tilde{\mathit{X}}}_{jk}\right)}^2}{\left\{e^{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}\left(\tilde{T}\right)+{\psi }_g\left(\tilde{T}\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}}\right\}}^{\mathrm{\Delta }} \\ \times \exp \left\{-{\int }_0^{\tilde{T}}{e}^{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}\left(t\right)+{\psi }_g\left(t\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}}\text{d}\Lambda \left(t\right)\right\}{\left|\mathbf{\Sigma }\left({\mathit{\xi }}_g\right)\right|}^{-1/2}{e}^{-\frac{1}{2}{\mathit{b}}^{\text{T}}\mathbf{\Sigma }{\left({\mathit{\xi }}_g\right)}^{-1}\mathit{b}}\text{d}\mathit{b}, \end{gathered}$$

so that the likelihood for a generic subject is proportional to $\Lambda {\left\{\tilde{T}\right\}}^{\Delta }\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$. Let ${\dot{\mathbf{\Psi }}}_{\theta }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$ denote the derivative of $\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$ with respect to θ, ${\dot{\mathbf{\Psi }}}_{\Lambda }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[H\right]$ denote the derivative of $\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$ with respect to Λ along the direction H, and ${\dot{\mathbf{\Psi }}}_{\psi g}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[h\right]$ denote the derivative of $\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$ with respect to ψ_g along the direction h.

In the sequel, we use || · || to denote the Euclidean norm for vectors and the L₂-norm with respect to the Lebesgue measure for functions over $\left[0,\tau \right]$. For a set of functions $\mathcal{B}\equiv \left({\psi }_2,\dots ,{\psi }_g\right)$, let ${‖\mathcal{B}‖}^2={\sum }_{g=2}^G{‖{\psi }_g‖}^2$. Let $\mathbb{P}$ and ${\mathbb{P}}_n$ denote the true and empirical measures, respectively.

Proof of Theorem 4.1. Following Schumaker [15], under condition (C1), there exist functions $\left({\tilde{\psi }}_{n2},\dots ,{\tilde{\psi }}_{nG}\right)$ such that ${‖{\tilde{\psi }}_{ng}-{\psi }_{0g}‖}_{\infty }=O\left(m_n^{-3}\right)$ for g = 2,…,G, where ${\tilde{\psi }}_{ng}={\sum }_{s=1}^{m_n}{\tilde{a}}_{gs}{B}_s$ for some regression parameters ${\tilde{a}}_{gs}\left(g=2,\dots ,G;s=1,\dots ,m_n\right)$. Let

$${\mathcal{N}}_{{ϵ}_n}=\left\{\left({\psi }_2,\dots ,{\psi }_G\right):{\psi }_g=\sum _{s=1}^{m_n}{a}_{gs}{B}_s:\sum _{s=1}^{m_n}{\left|a_{gs}-{\tilde{a}}_{gs}\right|}^2\le {ϵ}_n^2,g=2,\dots ,G\right\},$$

where ϵ_n is a positive sequence such that ${ϵ}_n=o\left(m_n^{-3/2}\right)$. For ${\mathcal{B}}_n\equiv \left({\psi }_{n2},\dots ,{\psi }_{nG}\right)\in {\mathcal{N}}_{{ϵ}_n}$,

$${‖{\psi }_{ng}-{\tilde{\psi }}_{0g}‖}_{\text{V}}\le \sum _{s=1}^{m_n}\left|a_{gs}-{\tilde{a}}_{gs}\right|{‖B_s^{\text{'}}‖}_{\infty }=O\left(m_n\right){\left({ϵ}_n^2{m}_n\right)}^{1/2}=o\left(1\right).$$

Therefore, each function ψ_ng of ${\mathcal{N}}_{{ϵ}_n}$ has bounded total variation and converges uniformly to ψ_0g.

The outline of the proof is as follows. For any sequence of ${\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}$, we define

$$\left({\widehat{\mathit{\theta }}}_n\left[{\mathcal{B}}_n\right],{\widehat{\mathrm{\Lambda }}}_n\left[{\mathcal{B}}_n\right]\right)=\underset{\left(\mathit{\theta },\Lambda \right)}{\arg \max }{\mathbb{P}}_n\ell \left(\mathit{\theta },\mathrm{\Lambda },{\mathcal{B}}_n\right).$$

First, we show that $\left({\widehat{\mathit{\theta }}}_n\left[{\mathcal{B}}_n\right],{\widehat{\mathrm{\Lambda }}}_n\left[{\mathcal{B}}_n\right]\right){\to }_p\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0\right)$ uniformly over ${\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}$. Then, we derive the rate of convergence of $\left({\widehat{\mathit{\theta }}}_n\left[{\mathcal{B}}_n\right],{\widehat{\mathrm{\Lambda }}}_n\left[{\mathcal{B}}_n\right]\right)$ in terms of ϵ_n. Finally, we show that the maximum of the profile log-likelihood ${\mathbb{P}}_n\ell \left({\widehat{\mathit{\theta }}}_n\left[{\mathcal{B}}_n\right],{\widehat{\mathrm{\Lambda }}}_n\left[{\mathcal{B}}_n\right],{\mathcal{B}}_n\right)$ over ${\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}$ lies in the interior of ${\mathcal{N}}_{{ϵ}_n}$ for some ${ϵ}_n=o\left(n^{-1/4}{m}_n^{1/2}\right)$ and for large enough n. For simplicity of presentation, we suppress the argument ${\mathcal{B}}_n$ in ${\widehat{\mathit{\theta }}}_n\left[{\mathcal{B}}_n\right]$ and ${\widehat{\mathrm{\Lambda }}}_n\left[{\mathcal{B}}_n\right]$ in the sequel.

Step 1. We prove the existence of the NPMLE, i.e., ${\widehat{\mathrm{\Lambda }}}_n\left(\tau \right)<\infty$. Let ${\pi }_g=e^{{\mathit{\alpha }}_g^{\text{T}}\mathit{W}}/{\sum }_{l=1}^G{e}^{{\mathit{\alpha }}_l^{\text{T}}\mathit{W}}$ and f_g(Y,b) denote the joint density of (Y, b) for the gth latent class (given N₁, …, N_J ); we suppress the parameter or covariate values in the expressions for simplicity of presentation. Note that

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{\Psi }\left(\mathcal{O};\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right) \\ \lesssim \sum _{g=1}^G{\pi }_g\int e^{\left\{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}\left(\tilde{T}\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}+{\psi }_g\left(\tilde{T}\right)\right\}\Delta }{\left\{1+{\int }_0^{\tilde{T}}{e}^{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}\left(s\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}+{\psi }_g\left(s\right)}\text{d}\Lambda \left(s\right)\right\}}^{-\kappa }{f}_g\left(\mathit{Y},\mathit{b}\right)\text{d}\mathit{b} \\ \le \sum _{g=1}^G{\pi }_g{e}^{{\psi }_g\left(\tilde{T}\right)\Delta }{\left\{1+{\int }_0^{\tilde{T}}{e}^{{\psi }_g\left(s\right)}\text{d}\Lambda \left(s\right)\right\}}^{-\kappa }\int e^{O\left(1+‖b‖\right)}{f}_g\left(\mathit{Y},\mathit{b}\right)\text{d}\mathit{b} \end{gathered}$$

for some constant κ > 1, where ≲ denotes “smaller than up to a scaling factor.” Therefore, if $\Lambda \left(\tau \right)=\infty$, then the right-hand side of the above inequality is zero. We conclude that ${\widehat{\mathrm{\Lambda }}}_n\left(\tau \right)<\infty$, so that the NPMLE exists.

Step 2. We show that the NPMLE is uniformly bounded. Note that

$$\begin{gathered} \frac{1}{n}\log L_n\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)\le \frac{1}{n}\sum _{i=1}^n{\mathrm{\Delta }}_i\log {\widehat{\mathrm{\Lambda }}}_n\left\{{\tilde{T}}_i\right\}+\frac{1}{n}\sum _{i=1}^n\log \left[\sum _{g=1}^G{\pi }_{gi}{e}^{{\psi }_{ng}\left({\tilde{T}}_i\right)\mathrm{\Delta }}\right. \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left.\times {\left\{1+{\int }_0^{{\tilde{T}}_i}{e}^{{\psi }_{ng}\left(s\right)}\text{d}{\widehat{\mathrm{\Lambda }}}_n\left(s\right)\right\}}^{-\kappa }\int e^{O\left(1+‖\mathit{b}‖\right)}{f}_g\left({\mathit{Y}}_i,\mathit{b}\right)\text{d}\mathit{b}\right]. \end{gathered}$$

Let ${\tilde{N}}_n=n^{-1}{\sum }_{i=1}^n{\mathrm{\Delta }}_{i}I\left({\tilde{T}}_i\le \cdot \right)$. We have

$$\frac{1}{n}\log L_n\left({\mathit{\theta }}_0,{\tilde{N}}_n,{\mathcal{B}}_n\right)\ge -\frac{1}{n}\sum _{i=1}^n{\mathrm{\Delta }}_i\log n+O_p\left(1\right),$$

where the second term on the right-hand side is asymptotically bounded uniformly over ${\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}$. Thus,

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \frac{1}{n}\log L_n\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-\frac{1}{n}\log L_n\left({\mathit{\theta }}_0,{\tilde{N}}_n,{\mathcal{B}}_n\right) \\ \le \frac{1}{n}\sum _{i=1}^n{\mathrm{\Delta }}_i\log \left[n{\widehat{\mathrm{\Lambda }}}_n\left\{{\tilde{T}}_i\right\}\right]-\frac{\kappa }{n}\sum _{i=1}^n\log \left\{1+{\widehat{\mathrm{\Lambda }}}_n\left(\tau \right)\right\}+O_p\left(1\right). \end{gathered}$$

Using a partitioning argument similar to that of Murphy [13], we can show that the right-hand side of the above inequality tends to ‒∞ if $\lim {\sup }_n{\widehat{\mathrm{\Lambda }}}_n\left(\tau \right)=\infty$. By the definition of $\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n\right)$, the left-hand side of the inequality is nonnegative, so that $\lim {\sup }_n{\sup }_{{\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}}{\widehat{\mathrm{\Lambda }}}_n\left(\tau \right)<\infty$.

Step 3. We show that $\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n\right)$ is consistent. Because ${\widehat{\mathrm{\Lambda }}}_n$ belongs to a function space with bounded total variation, by Helly’s selection theorem, for every subsequence of {n}_n=1,2,…, there exists a further subsequence such that ${\widehat{\mathit{\theta }}}_n\to {\mathit{\theta }}^{\ast }$ and ${\widehat{\mathrm{\Lambda }}}_n\to {\Lambda }^{\ast }$ for some (θ*,Λ*). We show that θ^∗ = θ₀ and Λ^∗ = Λ₀ for any subsequence. With an abuse of notation, let {n}_n=1,2,… be the subsequence. Let

$${\tilde{\Lambda }}_n\left(t\right)=-\sum _{i=1}^n{\mathrm{\Delta }}_{i}I\left({\tilde{T}}_i\le t\right){\left\{\sum _{j=1}^n\frac{{\dot{\mathbf{\Psi }}}_{\Lambda }\left({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[I\left({\tilde{T}}_i\le \cdot \right)\right]}{\mathrm{\Psi }\left({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)}\right\}}^{-1}.$$

Note that ${\dot{\mathrm{\Psi }}}_{\mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[I\left(\cdot \ge t\right)\right]=-I\left(\tilde{T}\ge t\right){\sum }_{g=1}^G{\pi }_g\int Q_g\left(\mathcal{O},\mathit{b}\right)e^{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}\left(t\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}+{\psi }_g\left(t\right)}\text{d}\mathit{b}$, where

$$Q_g\left(\mathcal{O},\mathit{b}\right)=e^{\left\{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}\left(\tilde{T}\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}+{\psi }_g\left(\tilde{T}\right)\right\}\mathrm{\Delta }}\exp \left\{-{\int }_0^{\tilde{T}}{e}^{{\mathit{\gamma }}_g^{\text{T}}\mathit{Z}\left(t\right)+{\mathit{\eta }}_g^{\text{T}}\mathit{b}+{\psi }_g\left(t\right)}\text{d}\mathrm{\Lambda }\left(t\right)\right\}{f}_g\left(\mathit{Y},\mathit{b}\right).$$

By the definition of the NPMLE, ${\mathbb{P}}_n\ell \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)\ge {\mathbb{P}}_n\ell \left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)$, so

$${\mathbb{P}}_n\mathrm{\Delta }\log \frac{{\widehat{\mathrm{\Lambda }}}_n\left\{\tilde{T}\right\}}{{\tilde{\mathrm{\Lambda }}}_n\left\{\tilde{T}\right\}}+{\mathbb{P}}_n\log \frac{\mathrm{\Psi }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)}{\mathrm{\Psi }\left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)}\ge 0.$$ (6)

Note that

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbb{P}}_n\log \mathrm{\Psi }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-\mathbb{P}\log \mathrm{\Psi }\left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0\right) \\ =\left({\mathbb{P}}_n-\mathbb{P}\right)\log \mathrm{\Psi }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)+\mathbb{P}\left\{\log \mathrm{\Psi }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-\log \mathrm{\Psi }\left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0\right)\right\}, \end{gathered}$$

where the first term on the right-hand side goes to zero almost surely because the class of $\log \mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$ is Gilvenko–Cantelli by Lemma B.1, and the second term is o(1) by the dominated convergence theorem; note that both terms converge uniformly over ${\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}$. By a similar argument on ${\mathbb{P}}_n\log \mathrm{\Psi }\left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)$, the second term on the left-hand side of (6) is

$${\mathbb{P}}_n\log \frac{\mathrm{\Psi }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)}{\mathrm{\Psi }\left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)}=\mathbb{P}\log \frac{\mathrm{\Psi }\left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0\right)}{\mathrm{\Psi }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)}+o_p\left(1\right),$$

where the o_p(1) term tends to 0 almost surely.

Consider the first term on the left-hand side of (6). Note that

$${\widehat{\mathrm{\Lambda }}}_n\left(t\right)={\int }_0^t\frac{{\mathbb{P}}_n\nu \left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0;s\right)}{{\mathbb{P}}_n\nu \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n;s\right)}\text{d}{\tilde{\mathrm{\Lambda }}}_n\left(s\right),$$ (7)

where $\nu \left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B};t\right)={\dot{\mathbf{\Psi }}}_{\mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[I\left(\cdot \ge t\right)\right]/\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)$. By Lemma B.1, $\left\{\nu \left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B};t\right):t\in \left[0,\tau \right],\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\in \Xi \right\}$ is Glivenko-Cantelli, so

$$\left|\underset{t\in \left[0,\tau \right]}{\sup }\left({\mathbb{P}}_n-\mathbb{P}\right)\nu \left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0;t\right)\right|+\left|\underset{{\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}}{\sup }\underset{t\in \left[0,\tau \right]}{\sup }\left({\mathbb{P}}_n-\mathbb{P}\right)\nu \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n;t\right)\right|{\to }_{\text{a}.\text{s}.}0.$$

By the dominated convergence theorem, $\mathbb{P}\nu \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n;t\right)$ converges to $\mathbb{P}\nu \left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0;t\right)$ for each t. In addition, it is easy to see that the derivative of $\mathbb{P}\nu \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n;t\right)$ with respect to t is uniformly bounded, so that $\mathbb{P}\nu \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n;t\right)$ is equicontinuous with respect to t. Thus, by the Arzela-Ascoli theorem, $\mathbb{P}\nu \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n;t\right)\to \mathbb{P}\nu \left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0;t\right)$ uniformly in $t\in \left[0,\tau \right]$. Furthermore, we can follow the argument in Zeng, Lin and Lin [26, p. 374] to show by contradiction that ${\min }_{t\in \left[0,\tau \right]}\left|\mathbb{P}\nu \left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0;t\right)\right|>0$. Taking limit on both sides of (7) yields

$${\mathrm{\Lambda }}^{\ast }\left(t\right)={\int }_0^t\frac{\mathbb{P}\nu \left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0;s\right)}{\mathbb{P}\nu \left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0;s\right)}\text{d}{\mathrm{\Lambda }}_0\left(s\right).$$

We conclude that Λ^∗ is absolutely continuous with respect to Λ₀ and thus is differentiable. Let λ^∗ be the derivative of Λ^∗. Combining the above results with (6), we have

$$\mathbb{P}\log \frac{{\lambda }^{\ast }{\left(\tilde{T}\right)}^{\mathrm{\Delta }}\mathrm{\Psi }\left({\mathit{\theta }}^{\ast },{\mathrm{\Lambda }}^{\ast },{\mathcal{B}}_0\right)}{{\lambda }_0{\left(\tilde{T}\right)}^{\mathrm{\Delta }}\mathrm{\Psi }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)}\ge 0.$$

By the nonnegativity of the Kullback-Leibler divergence and Lemma B.2, the left-hand side of the above inequality is nonpositive and is equal to zero if and only if (θ*,Λ^∗) = (θ*,Λ^∗). Therefore, $\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n\right)$ is consistent.

Step 4. We derive a bound on $‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }$ in terms of $‖{\mathcal{B}}_n-{\mathcal{B}}_0‖$. For any ${\mathit{h}}_{\theta }\in {ℝ}^d$ and $h_{\mathrm{\Lambda }}\in \text{BV}\left[0,\tau \right]$, let

$${\dot{\ell }}_{\theta \mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[{\mathit{h}}_{\theta },h_{\mathrm{\Lambda }}\right]={\left.\frac{\partial }{\partial ϵ}\ell \left(\mathit{\theta }+ϵ{\mathit{h}}_{\theta },\mathrm{\Lambda }+ϵ\int h_{\mathrm{\Lambda }}\text{d}\mathrm{\Lambda },\mathcal{B}\right)\right|}_{ϵ=0}.$$

Clearly, ${\mathbb{P}}_n{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)\left[{\mathit{h}}_{\theta },h_{\mathrm{\Lambda }}\right]=0$ and ${\mathbb{P}}_n{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\mathit{h}}_{\theta },h_{\mathrm{\Lambda }}\right]=0$ for any (h_θ,h_Λ). Suppressing the arguments (h_θ,h_Λ), we have

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)-\mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_n,{\mathcal{B}}_0\right) \\ =\mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)-{\mathbb{P}}_n{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right) \\ =-\left({\mathbb{P}}_n-\mathbb{P}\right){\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-\mathbb{P}\left\{{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_n,{\mathcal{B}}_0\right)-{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\right\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} -\mathbb{P}\left[\left\{{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_n\right)\right\}-\left\{{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\right\}\right]. \end{gathered}$$

By Lemma B.1, the class $\left\{{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[{\mathit{h}}_{\theta },h_{\mathrm{\Lambda }}\right]:\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\in \Xi ,‖{\mathit{h}}_{\theta }‖\le 1,{‖h_{\mathrm{\Lambda }}‖}_{\text{V}}\le 1\right\}$ is Donsker, so that the first term on the right-hand side above is O_p(n^−1/2) uniformly over ${\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}$. By repeated applications of the mean-value theorem, we can show that the second term is $O\left(‖{\mathcal{B}}_n-{\mathcal{B}}_0‖\right)$ and the third term is $o\left(‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }\right)$. To evaluate the left-hand side of the above display, note that ${\dot{\ell }}_{\theta \mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },{\mathcal{B}}_0\right)$ is the score statistic of a survival model with a single nonparametric component; the model falls under the framework of, for example, Zeng and Lin [25]. Using arguments analogous to the proof of Theorem 3.2 of Zeng and Cai [24] and the proof of Theorem 2 of Zeng and Lin [27], we can show that the map $\left(\mathit{\theta },\mathrm{\Lambda }\right)\mapsto \mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },{\mathcal{B}}_0\right)$ is Frechet-differentiable with a derivative $\nabla \mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}$ that takes the form of a Fredholm operator. By Lemma B.4, $\nabla \mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}$(evaluated at the true parameter values) is one-to-one, so it is continuously invertible. Therefore, there exists some positive constant c₁ such that $‖\nabla \mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0,{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0\right)‖\ge c_1\left(‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }\right)$, where the norm on the left-hand side of the inequality is the supremum norm over $\left\{\left({\mathit{h}}_{\theta },h_{\mathrm{\Lambda }}\right):‖{\mathit{h}}_{\theta }‖\le 1,{‖h_{\mathrm{\Lambda }}‖}_{\text{V}}\le 1\right\}$. By the consistency of $\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n\right)$ and the differentiability of $\mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}$,

$$‖\mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)-\mathbb{P}{\dot{\ell }}_{\theta \mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)‖\ge \left\{c_1+o\left(1\right)\right\}\left(‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }\right).$$

Combining the above results, we conclude that

$$‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }\le A_n\left(n^{-1/2}+‖{\mathcal{B}}_n-{\mathcal{B}}_0‖\right),$$

where A_n is some random variable that may depend on ${\mathcal{B}}_n$ and satisfies ${\sup }_{{\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}}\left|A_n\right|=O_p\left(1\right)$.

Step 5. We show that a local maximum of ${\mathbb{P}}_n\ell \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)$ with respect to ${\mathcal{B}}_n$ exists in the interior of ${\mathcal{N}}_{{ϵ}_n}$ for large enough n. It suffices to show that ${\sup }_{{\mathcal{B}}_n\in \partial {\mathcal{N}}_{{ϵ}_n}}{\mathbb{P}}_n\ell \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)<{\mathbb{P}}_n\ell \left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\tilde{\mathcal{B}}}_n\right)$ with probability going to 1 as n → ∞, where ${\tilde{\mathcal{B}}}_n=\left({\tilde{\psi }}_{n2},\dots ,{\tilde{\psi }}_{nG}\right)$. Let

$$\begin{gathered} B_n={\mathbb{P}}_n\ell \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-{\mathbb{P}}_n\ell \left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\tilde{\mathcal{B}}}_n\right) \\ \hspace{1em} =\left({\mathbb{P}}_n-\mathbb{P}\right)\left\{\ell \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-\ell \left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\tilde{\mathcal{B}}}_n\right)\right\}+\mathbb{P}\left\{\ell \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)-\ell \left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\tilde{\mathcal{B}}}_n\right)\right\} \\ \hspace{1em}\hspace{1em}\hspace{0.17em}-\mathbb{P}\left\{\ell \left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\tilde{\mathcal{B}}}_n\right)-\ell \left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)\right\}. \end{gathered}$$ (8)

By Lemma B.1, the first term on the right-hand side of (8) can be written as C_nn^−1/2 for some variable C_n such that ${\sup }_{{\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}}\left|C_n\right|=o_p\left(1\right)$. To evaluate the second term on the right-hand side above, let

$$\xi \left(ϵ;\mathrm{\Lambda }\right)=\mathbb{P}\ell \left\{{\mathit{\theta }}_0+ϵ\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0\right),\mathrm{\Lambda }+ϵ\int {\widehat{h}}_{\mathrm{\Lambda }}\text{d}\mathrm{\Lambda },{\mathcal{B}}_0+ϵ\left({\mathcal{B}}_n-{\mathcal{B}}_0\right)\right\},$$

where ${\widehat{h}}_{\mathrm{\Lambda }}$ is a step function that jumps at the observed event times, with ${\widehat{h}}_{\mathrm{\Lambda }}=\text{d}{\widehat{\mathrm{\Lambda }}}_n/\text{d}{\tilde{\mathrm{\Lambda }}}_n-1$ points. The second term of the right-hand side of (8) is equal to $\xi \left(1;{\tilde{\mathrm{\Lambda }}}_n\right)-\xi \left(0;{\tilde{\mathrm{\Lambda }}}_n\right)={\xi }^{\prime }\left(0;{\tilde{\mathrm{\Lambda }}}_n\right)+{\xi }^{″}\left(ϵ;{\tilde{\mathrm{\Lambda }}}_n\right)$ for some ϵ ∈[0, 1]. Note that ξʹ(0;Λ_en) is equal to

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \mathbb{P}\left\{\mathrm{\Delta }{\widehat{h}}_{\mathrm{\Lambda }}\left(\tilde{T}\right)+\dot{\mathrm{\Psi }}\left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)\left[{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0,\int {\widehat{h}}_{\mathrm{\Lambda }}\text{d}{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n-{\mathcal{B}}_0\right]/\mathrm{\Psi }\left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)\right\} \\ =\mathbb{P}\left\{\mathrm{\Delta }{\widehat{h}}_{\mathrm{\Lambda }}\left(\tilde{T}\right)+\dot{\mathrm{\Psi }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0,\int {\widehat{h}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0,{\mathcal{B}}_n-{\mathcal{B}}_0\right]/\mathrm{\Psi }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\right\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\mathbb{P}\left\{\dot{\mathrm{\Psi }}\left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)\left[{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0,\int {\widehat{h}}_{\mathrm{\Lambda }}\text{d}{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n-{\mathcal{B}}_0\right]/\mathrm{\Psi }\left({\mathit{\theta }}_0,{\tilde{\mathrm{\Lambda }}}_n,{\mathcal{B}}_0\right)\right. \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left.-\dot{\mathrm{\Psi }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0,\int {\widehat{h}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0,{\mathcal{B}}_n-{\mathcal{B}}_0\right]/\mathrm{\Psi }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\right\} \\ =O_p\left\{{‖{\tilde{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }\left(‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖+{‖{\widehat{h}}_{\mathrm{\Lambda }}‖}_{\text{V}}+{‖{\mathcal{B}}_n-{\mathcal{B}}_0‖}_{\text{V}}\right)\right\}, \end{gathered}$$

where $\dot{\mathrm{\Psi }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[{\mathit{h}}_{\theta },H_{\mathrm{\Lambda }},h_{\mathcal{B}}\right]={\dot{\mathbf{\Psi }}}_{\theta }{\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)}^{\text{T}}{\mathit{h}}_{\theta }+{\dot{\mathrm{\Psi }}}_{\mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[H_{\mathrm{\Lambda }}\right]+{\sum }_{g=2}^G{\dot{\mathrm{\Psi }}}_{\psi g}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[h_g\right]$ for $h_{\mathcal{B}}=\left(h_2,\dots ,h_G\right)$. The last equality above follows from the mean-value theorem and that the score statistic is mean zero. By standard arguments for the NPMLE, ${‖{\tilde{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }=O_p\left(n^{-1/2}\right)$. Also, ${‖{\tilde{h}}_{\mathrm{\Lambda }}‖}_{\text{V}}=o_p\left(1\right)$ and ${‖{\mathcal{B}}_n-{\mathcal{B}}_0‖}_{\text{V}}=o\left(1\right)$, so the right-hand side of the above equation is o_p(n^−1/2). To evaluate ${\xi }^{″}\left(ϵ;{\tilde{\mathrm{\Lambda }}}_n\right)$, we write

$${\xi }^{″}\left(ϵ;{\tilde{\mathrm{\Lambda }}}_n\right)=\left\{{\xi }^{″}\left(ϵ;{\tilde{\mathrm{\Lambda }}}_n\right)-{\xi }^{″}\left(0;{\tilde{\mathrm{\Lambda }}}_n\right)\right\}+\left\{{\xi }^{″}\left(0;{\tilde{\mathrm{\Lambda }}}_n\right)-{\xi }^{″}\left(0;{\tilde{\mathrm{\Lambda }}}_0\right)\right\}+{\xi }^{″}\left(0;{\tilde{\mathrm{\Lambda }}}_0\right).$$

Using the mean-value theorem, we can show that the first term on the right-hand side of the above equation is $O_p\left({‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖}^3+{‖{\widehat{h}}_{\mathrm{\Lambda }}‖}_{\infty }^3+{‖{\mathcal{B}}_n-{\mathcal{B}}_0‖}_3^3\right)+o_p\left({‖{\tilde{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }\right)$. Following the arguments for the evaluation of ${\xi }^{\prime }\left(0;{\tilde{\mathrm{\Lambda }}}_n\right)$, we can show that the second term is o_p(n^−1/2). Note that the third term is the negative information of the one-dimensional submodel θ = θ₀ + ϵh_θ, dΛ = (1 + ϵh_Λ)dΛ₀, and $\mathcal{B}={\mathcal{B}}_0+ϵ{\mathit{h}}_{\mathcal{B}}$, where ${\mathit{h}}_{\theta }={\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0$, $h_{\mathrm{\Lambda }}={\widehat{h}}_{\mathrm{\Lambda }}$, and ${\mathit{h}}_{\mathcal{B}}={\mathcal{B}}_n-{\mathcal{B}}_0$. Let $\mathcal{H}={ℝ}^d\times L_2{\left[0,\tau \right]}^G$. For any $h\equiv \left({\mathit{h}}_{\theta },h_{\mathrm{\Lambda }},h_{\psi 2},\dots ,h_{\psi G}\right)\in \mathcal{H}$, the score statistic of the submodel along direction h is

$$\begin{gathered} \dot{\ell }\left[h\right]=\sum _{g=1}^G{\pi }_g\int Q_g\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)\left[\left\{1-\frac{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\tilde{\mathit{b}}\right)\text{d}\tilde{\mathit{b}}}{\int Q_l\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\tilde{\mathit{b}}\right)\text{d}\tilde{\mathit{b}}}\right\}{\mathit{W}}^{\text{T}}{\mathit{h}}_{\alpha g}\right. \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\mathrm{\Delta }\left\{\mathit{Z}{\left(\tilde{T}\right)}^{\text{T}}{\mathit{h}}_{\gamma g}+{\mathit{b}}^{\text{T}}{\mathit{h}}_{\eta g}+h_{\mathrm{\Lambda }}\left(\tilde{T}\right)+h_{\psi g}\left(\tilde{T}\right)\right\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-{\int }_0^{\tilde{T}}{e}^{\mathit{Z}{\left(s\right)}^{\text{T}}{\mathit{\gamma }}_{0g}+{\mathit{\eta }}_{0g}^{\text{T}}\mathit{b}+{\psi }_{0g}\left(s\right)}\left\{\mathit{Z}{\left(s\right)}^{\text{T}}{\mathit{h}}_{\gamma g}+{\mathit{b}}^{\text{T}}{\mathit{h}}_{\eta g}+h_{\mathrm{\Lambda }}\left(s\right)+h_{\psi g}\left(s\right)\right\}\text{d}{\mathrm{\Lambda }}_0\left(s\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left.+\frac{{\mathit{f}}_g^{\left(1\right)}{\left(\mathit{Y},\mathit{b}\right)}^{\text{T}}{\mathit{h}}_{Y\hspace{0.17em}g}}{f_g\left(\mathit{Y},\mathit{b}\right)}\right]\text{d}\mathit{b}/\sum _{g=1}^G{\pi }_g\int Q_g\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)\text{d}\mathit{b} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\equiv \mathcal{K}\left(\tilde{T},\mathrm{\Delta },\mathit{Y};h\right), \end{gathered}$$

where $Q_g\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)=Q_g\left(\mathcal{O},\mathit{b}\right)$, ${\mathit{f}}_g^{\left(1\right)}\left(\mathit{Y},\mathit{b}\right)$ is the derivative of f_g(Y, b) with respect to $\left({\mathit{\beta }}_g,{\mathit{\sigma }}_g^2,{\mathit{\xi }}_g\right)$, ${\mathit{h}}_{Y\hspace{0.17em}g}={\left({\mathit{h}}_{\beta g}^{\text{T}},h_{\sigma g},{\mathit{h}}_{\xi g}^{\text{T}}\right)}^{\text{T}}$, $\left({\mathit{h}}_{\alpha g},{\mathit{h}}_{\beta g},{\mathit{h}}_{\sigma g},{\mathit{h}}_{\xi g},{\mathit{h}}_{\gamma g},{\mathit{h}}_{\eta g}\right)$ are the directions that correspond to the parameters $\left({\mathit{\alpha }}_g,{\mathit{\beta }}_g,{\mathit{\sigma }}_g^2,{\mathit{\xi }}_g,{\mathit{\gamma }}_g,{\mathit{\eta }}_g\right)$ for $g=1,\dots ,G$, ${\mathit{h}}_{\alpha G}=\text{0}$, and $h_{\psi 1}\left(\cdot \right)=0$. For h⁽¹⁾, $h^{\left(2\right)}\in \mathcal{H}$, we can write

$$\mathbb{P}\dot{\ell }\left[h^{\left(1\right)}\right]\dot{\ell }\left[h^{\left(2\right)}\right]={\mathit{h}}_{\theta }^{\left(1\right)\text{T}}{\mathit{G}}_1\left(h^{\left(2\right)}\right)+\sum _{g=1}^G{\int }_0^{\tau }\left\{h_{\mathrm{\Lambda }}^{\left(1\right)}\left(t\right)+h_{\psi g}^{\left(1\right)}\left(t\right)\right\}{G}_{2g}\left(t;h^{\left(2\right)}\right)\text{d}t,$$

where G₁(h) is some linear function of h, and G_2g(t;h) is equal to

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{E}\left\{\frac{{\pi }_g\int Q_g\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}}{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}}{f}_T\left(t|\mathit{Y}\right)S_U\left(t|\mathit{Y}\right)\mathcal{K}\left(t,1,\mathit{Y};h\right)\right\} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\text{E}\left\{I\left(t\le \tilde{T}\right)\frac{{\pi }_g\int Q_g\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)e^{\text{Z}{\left(t\right)}^{\text{T}}{\gamma }_{0g}+{\mathit{\eta }}_{0g}^{\text{T}}\mathit{b}+{\psi }_{0g}\left(t\right)}\hspace{0.17em}\text{d}\mathit{b}}{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}}\mathcal{K}\left(\tilde{T},\mathrm{\Delta },\mathit{Y};h\right)\right\}\lambda \left(t\right) \\ ={\mathit{a}}^{\text{T}}{\mathit{h}}_{\theta }+\text{E}\left\{\frac{{\pi }_g\int Q_g\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}}{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}}{f}_T\left(t|\mathit{Y}\right)S_U\left(t|\mathit{Y}\right)\right\}{h}_{\mathrm{\Lambda }}\left(t\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _{k=2}^G\text{E}\left[\frac{{\pi }_g{\pi }_k\int Q_g\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}\int Q_k\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}}{{\left\{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}\right\}}^2}{f}_T\left(t|\mathit{Y}\right)S_U\left(t|\mathit{Y}\right)\right]\hspace{0.17em}{h}_{\psi k}\left(t\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\sum _{k=1}^G{\int }_0^{\tau }\left\{h_{\mathrm{\Lambda }}\left(s\right)+h_{\psi k}\left(s\right)\right\}\left(I\left(s\le t\right)\text{E}\left[{\pi }_g{\pi }_k{f}_T\left(t|\mathit{Y}\right)S_U\left(t|\mathit{Y}\right)\right.\right. \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left.\times \frac{\int Q_g\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}\int Q_k\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}{e}^{\text{Z}{\left(s\right)}^{\text{T}}{\gamma }_{0k}+{\mathit{\eta }}_{0k}^{\text{T}}\mathit{b}+{\psi }_{0k}\left(s\right)}\hspace{0.17em}\text{d}\mathit{b}}{{\left\{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(t,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}\right\}}^2}\right]+I\left(t\le s\right)\text{E}\left[{\pi }_g{\pi }_k\right. \\ \left.\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \frac{\int Q_g\left(s,1,\mathit{Y},\mathit{b}\right)e^{\text{Z}{\left(t\right)}^{\text{T}}{\gamma }_{0g}+{\mathit{\eta }}_{0g}^{\text{T}}\mathit{b}+{\psi }_{0g}\left(t\right)}\hspace{0.17em}\text{d}\mathit{b}\int Q_k\left(s,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}}{{\left\{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(s,1,\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}\right\}}^2}{f}_T\left(s|\mathit{Y}\right)S_U\left(s|\mathit{Y}\right)\right] \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-\text{E}\left[I\left(s\le \tilde{T}\right)I\left(t\le \tilde{T}\right){\pi }_g{\pi }_k\right. \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \frac{\int Q_g\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)\hspace{0.17em}{e}^{\text{Z}{\left(t\right)}^{\text{T}}{\gamma }_{0g}+{\mathit{\eta }}_{0g}^{\text{T}}\mathit{b}+{\psi }_{0g}\left(t\right)}\text{d}\mathit{b}\int Q_k\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)\hspace{0.17em}{e}^{\text{Z}{\left(s\right)}^{\text{T}}{\gamma }_{0k}+{\mathit{\eta }}_{0k}^{\text{T}}\mathit{b}+{\psi }_{0g}\left(s\right)}\text{d}\mathit{b}}{{\left\{{\sum }_{l=1}^G{\pi }_l\int Q_l\left(\tilde{T},\mathrm{\Delta },\mathit{Y},\mathit{b}\right)\hspace{0.17em}\text{d}\mathit{b}\right\}}^2} \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \hspace{0.17em}{\mathit{\lambda }}_0\left(s\right)\text{d}s, \end{gathered}$$

where f_T (· | Y) is the conditional density of the survival time T given Y, S_U(· | Y) is the conditional survival function of the censoring time U given Y, and a is a d-dimensional vector. Define an inner product 〈.,.〉 on $\mathcal{H}$ such that

$$〈h^{\left(1\right)},h^{\left(2\right)}〉={\mathit{h}}_{\theta }^{\left(1\right)\text{T}}{\mathit{h}}_{\theta }^{\left(2\right)}+{\int }_0^{\tau }\left\{h_{\mathrm{\Lambda }}^{\left(1\right)}\left(t\right)h_{\mathrm{\Lambda }}^{\left(2\right)}\left(t\right)+\sum _{g=2}^G{h}_{\psi g}^{\left(1\right)}\left(t\right)h_{\psi g}^{\left(2\right)}\left(t\right)\right\}\text{d}t,$$

and let ${\dot{\ell }}^{\ast }$ be the adjoint operator of $\dot{\ell }$. By the definition of ${\dot{\ell }}^{\ast }$, $\mathbb{P}\dot{\ell }\left[h^{\left(1\right)}\right]\dot{\ell }\left[h^{\left(2\right)}\right]=〈h^{\left(1\right)},{\dot{\ell }}^{\ast }\dot{\ell }\left[h^{\left(2\right)}\right]〉$, such that

$${\dot{\ell }}^{\ast }\dot{\ell }\left[h\right]=\left({\mathit{G}}_1\left(h\right),\sum _{g=1}^G{G}_{2g}\left(\cdot ;h\right),G_{22}\left(\cdot ;h\right),\dots ,G_{2G}\left(\cdot ;h\right)\right).$$

On the space $\mathcal{H}$, we define a seminorm ${‖h‖}_I={〈h,{\dot{\ell }}^{\ast }\dot{\ell }\left[h\right]〉}^{1/2}$. By Lemma B.4, ||h||_I = 0 implies that h = 0, such that || · ||_I is a norm in $\mathcal{H}$. Clearly, ||h||_I ≤ c₂〈h,h〉^1/2 for some constant c₂. By the bounded inverse theorem in Banach spaces, we have 〈h,h〉^1/2 ≤ c₃||h||_I for some constant c₃. We conclude that

$${\xi }^{″}\left(0;{\mathrm{\Lambda }}_0\right)=-{‖\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0,{\widehat{h}}_{\mathrm{\Lambda }},{\mathcal{B}}_n-{\mathcal{B}}_0\right)‖}_I^2\le -c_3^{-2}\left({‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖}^2+{‖{\widehat{h}}_{\mathrm{\Lambda }}‖}^2+\sum _{g=2}^G{‖{\psi }_{ng}-{\psi }_{0g}‖}^2\right).$$

By Donsker properties of the class of $\nu \left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B};t\right)$ and the mean-value theorem,

$${‖{\widehat{h}}_{\mathrm{\Lambda }}‖}_{\infty }=O_p\left(‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }+{‖{\mathcal{B}}_n-{\mathcal{B}}_0‖}_2+n^{-1/2}\right).$$

In addition, a linear expansion argument shows that the third term of (8) is of order up to ${‖{\tilde{\mathcal{B}}}_n-{\mathcal{B}}_0‖}_{\infty }^2$. Combining the above results, we have

$$\begin{gathered} B_n\le D_n{n}^{-1/2}+E_n\left({‖{\mathcal{B}}_n-{\tilde{\mathcal{B}}}_n‖}_3^3+{‖{\tilde{\mathcal{B}}}_n-{\mathcal{B}}_0‖}_{\infty }^2\right)-c_3^{-2}\sum _{g=2}^G{‖{\psi }_{ng}-{\tilde{\psi }}_{0g}‖}^2 \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\le D_n{n}^{-1/2}+c_4{E}_n\left(m_n^{-1}{ϵ}_n^3+m_n^{-6}\right)-c_3^{-2}\sum _{g=2}^G{‖{\psi }_{ng}-{\tilde{\psi }}_{0g}‖}^2 \end{gathered}$$

for some sequences of positive variables D_n and E_n such that ${\sup }_{{\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}}{D}_n=o_p\left(1\right)$ and ${\sup }_{{\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}}{E}_n=O_p\left(1\right)$ and some positive constant c₄. The second inequality holds because by Theorem 5.2 of de Boor [2],

$${‖{\psi }_{ng}-{\tilde{\psi }}_{ng}‖}_3^3=O\left(m_n^{-1}\sum _{s=1}^{m_n}{\left|a_{gs}-{\tilde{a}}_{gs}\right|}^3\right)=O\left(m_n^{-1}{ϵ}_n^3\right).$$

Suppose that ${\mathcal{B}}_n\in \partial {\mathcal{N}}_{{ϵ}_n}$. By the same theorem of de Boor [2], ${‖{\psi }_{ng}-{\tilde{\psi }}_{ng}‖}^2\ge c_5{m}_n^{-1}{ϵ}_n^2$ for some g and c₅ > 0. Therefore, by choosing ϵ_n such that ${ϵ}_n=o\left(n^{-1/4}{m}_n^{1/2}\right)$ and

$${ϵ}_n^2\gg \underset{{\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}}{\sup }{D}_n{n}^{-1/2}{m}_n+m_n^{-5},$$

we have P(B_n < 0) → 1; the existence of such an ϵ_n with ${ϵ}_n=o\left(m_n^{-3/2}\right)$ is guaranteed under condition (C4). We conclude that there exists a local maximum of ${\mathbb{P}}_n\ell \left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\mathcal{B}}_n\right)$ with respect to ${\mathcal{B}}_n$ in the interior of ${\mathcal{N}}_{{ϵ}_n}$; let ${\widehat{\mathcal{B}}}_n$ be the maximizer. Note that by Theorem 5.2 of de Boor [2], ${‖{\psi }_{ng}-{\tilde{\psi }}_{ng}‖}^2=O\left(m_n^{-1}{\sum }_{s=1}^{m_n}{\left|a_{gs}-{\tilde{a}}_{gs}\right|}^2\right)=O\left(m_n^{-1}{ϵ}_n^2\right)$ for all ${\mathcal{B}}_n\in {\mathcal{N}}_{{ϵ}_n}$. We have

$${‖{\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0‖}^2+{‖{\widehat{\mathrm{\Lambda }}}_n-{\mathrm{\Lambda }}_0‖}_{\infty }^2+{‖{\widehat{\mathcal{B}}}_n-{\mathcal{B}}_0‖}^2=O_p\left(n^{-1}+{‖{\widehat{\mathcal{B}}}_n-{\mathcal{B}}_0‖}^2\right)=O_p\left(m_n^{-1}{ϵ}_n^2+m_n^{-6}\right)=o_p\left(n^{-1/2}\right).$$

□

Proof of Theorem 4.2. Let ${\dot{\ell }}_{\theta }$ be the score statistic for θ, ${\dot{\ell }}_{\mathrm{\Lambda }}\left[h_{\mathrm{\Lambda }}\right]$ be the score statistic for Λ along the submodel $\mathrm{\Lambda }+ϵ\int h_{\mathrm{\Lambda }}\text{d}\mathrm{\Lambda }$, and ${\dot{\ell }}_{\psi g}\left[h_{\psi g}\right]$ be the score statistic for ψ_g along the submodel ψ_g + ϵh_ψg (g = 2,…,G). For a set of functions h ≡ (h₁,…,h_d), let ${\dot{\ell }}_{\mathrm{\Lambda }}\left[\mathit{h}\right]={\left({\dot{\ell }}_{\mathrm{\Lambda }}\left[h_1\right],\dots ,{\dot{\ell }}_{\mathrm{\Lambda }}\left[h_d\right]\right)}^{\text{T}}$ and ${\dot{\ell }}_{\psi g}\left[\mathit{h}\right]={\left({\dot{\ell }}_{\psi g}\left[h_1\right],\dots ,{\dot{\ell }}_{\psi g}\left[h_d\right]\right)}^{\text{T}}$. Let ${\tilde{\mathit{h}}}_{\mathrm{\Lambda }}$ and ${\tilde{\mathit{h}}}_{\psi g}$ be the least favorable directions for the nonparametric functions, such that $\left({\tilde{\mathit{h}}}_{\mathrm{\Lambda }},{\tilde{\mathit{h}}}_{\psi 1},\dots ,{\tilde{\mathit{h}}}_{\psi G}\right)=\arg {\min }_{{\mathit{h}}_{\mathrm{\Lambda }},{\mathit{h}}_{\psi 2},\dots ,{\mathit{h}}_{\psi G}}\mathbb{P}{‖{\dot{\ell }}_{\theta }-{\dot{\ell }}_{\mathrm{\Lambda }}\left[\int {\mathit{h}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0\right]-{\sum }_{g=2}^G{\dot{\ell }}_{\psi g}\left[{\mathit{h}}_{\psi g}\right]‖}^2$, where the integration in the second term in the norm is carried out componentwise. The existence of ${\tilde{\mathit{h}}}_{\mathrm{\Lambda }}$ and ${\tilde{\mathit{h}}}_{\psi g}$ follows from the invertibility of the information operator, established in Step 5 of the proof of Theorem 4.1. In addition, from the expressions of ${\dot{\ell }}^{\ast }\dot{\ell }$ given in Step 5 of the proof of Theorem 4.1 and condition (C6), each component of ${\tilde{\mathit{h}}}_{\psi g}$ is continuously differentiable up to the third order. Let ${\tilde{\mathit{h}}}_{n,\psi g}$ be the (componentwise) projection of ${\tilde{\mathit{h}}}_{\psi g}$ onto the sieve space, such that ${‖{\tilde{\mathit{h}}}_{n,\psi g}-{\tilde{\mathit{h}}}_{\psi g}‖}_{\infty }=O\left(m_n^{-3}\right)$. By the definition of the sieve NPMLE, ${\mathbb{P}}_n{\dot{\ell }}_{\theta }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)=\text{0}$, ${\mathbb{P}}_n{\dot{\ell }}_{\mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\widehat{\mathrm{\Lambda }}}_n\right]=\text{0}$, and ${\mathbb{P}}_n{\dot{\ell }}_{\psi g}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[{\tilde{\mathit{h}}}_{n,\psi g}\right]=\text{0}$. Note that

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbb{P}}_n{\dot{\ell }}_{\psi g}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right] \\ ={\mathbb{P}}_n{\dot{\ell }}_{\psi g}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[{\tilde{\mathit{h}}}_{n,\psi g}\right]+\mathbb{P}{\dot{\ell }}_{\psi g}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\tilde{\mathit{h}}}_{\psi g}-{\tilde{\mathit{h}}}_{n,\psi g}\right] \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} +\left({\mathbb{P}}_n-\mathbb{P}\right){\dot{\ell }}_{\psi g}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[{\tilde{\mathit{h}}}_{\psi g}-{\tilde{\mathit{h}}}_{n,\psi g}\right] \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} +\mathbb{P}\left\{{\dot{\ell }}_{\psi g}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[{\tilde{\mathit{h}}}_{\psi g}-{\tilde{\mathit{h}}}_{n,\psi g}\right]-{\dot{\ell }}_{\psi g}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\tilde{\mathit{h}}}_{\psi g}-{\tilde{\mathit{h}}}_{n,\psi g}\right]\right\}. \end{gathered}$$

The first two terms of the right-hand side above are zero. By Lemma B.1, the class of ${\dot{\ell }}_{\psi g}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[h\right]$ is Donsker, so that the third term is o_p(n^−1/2). By the mean-value theorem, Theorem 4.1, and condition (C4), the fourth term is o_p(n^−1/2). Obviously, $\mathbb{P}{\dot{\ell }}_{\theta }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)=\text{0}$, $\mathbb{P}{\dot{\ell }}_{\mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0\right]=\text{0}$, and $\mathbb{P}{\dot{\ell }}_{\psi g}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right]=\text{0}$. We have

$$\begin{gathered} \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{n}^{1/2}\left({\mathbb{P}}_n-\mathbb{P}\right)\left\{{\dot{\ell }}_{\theta }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)-{\dot{\ell }}_{\mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\widehat{\mathrm{\Lambda }}}_n\right]-\sum _{g=2}^G{\dot{\ell }}_{\psi g}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right]\right\} \\ =-n^{1/2}\mathbb{P}\left\{{\dot{\ell }}_{\theta }\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)-\right.{\dot{\ell }}_{\mathrm{\Lambda }}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\widehat{\mathrm{\Lambda }}}_n\right]-\sum _{g=2}^G{\dot{\ell }}_{\psi g}\left({\widehat{\mathit{\theta }}}_n,{\widehat{\mathrm{\Lambda }}}_n,{\widehat{\mathcal{B}}}_n\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right] \\ \hspace{1em}\hspace{0.17em}\hspace{0.17em}-{\dot{\ell }}_{\theta }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)+{\dot{\ell }}_{\mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0\right]+\sum _{g=2}^G{\dot{\ell }}_{\psi g}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right]+o_p\left(1\right). \end{gathered}$$ (9)

By Lemma B.1, the class

$$\left\{{\dot{\ell }}_{\theta }{\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)}^{\text{T}}\mathit{v}-{\dot{\ell }}_{\mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[H_{\mathrm{\Lambda }}\right]-\sum _{g=2}^G{\dot{\ell }}_{\psi g}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right]:\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\in \Xi ,‖\mathit{v}‖\le 1,{‖H_{\mathrm{\Lambda }}‖}_{\text{V}}\le 1\right\}$$

is Donsker. Therefore, the left-hand side of (9) is equal to

$$n^{1/2}\left({\mathbb{P}}_n-\mathbb{P}\right)\left\{{\dot{\ell }}_{\theta }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)+{\dot{\ell }}_{\mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0\right]-\sum _{g=2}^G{\dot{\ell }}_{\psi g}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right]\right\}+o_p\left(1\right),$$

which converges in distribution to $\text{N}\left(\text{0},\tilde{\mathit{I}}\right)$, where

$$\tilde{\mathit{I}}\equiv \mathbb{P}{\left\{{\dot{\ell }}_{\theta }\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)-{\dot{\ell }}_{\mathrm{\Lambda }}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0\right]-\sum _{g=2}^G{\dot{\ell }}_{\psi g}\left({\mathit{\theta }}_0,{\mathrm{\Lambda }}_0,{\mathcal{B}}_0\right)\left[{\tilde{\mathit{h}}}_{\psi g}\right]\right\}}^{\otimes 2}$$

is the efficient information matrix for θ. By the Taylor series expansion, Theorem 4.1, and the definition of ${\tilde{\mathit{h}}}_{\mathrm{\Lambda }}$ and ${\tilde{\mathit{h}}}_{\psi g}\left(g=2,\dots ,G\right)$, the right-hand side of (9) is

$$-n^{1/2}{\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0\right)}^{\text{T}}\mathbb{P}\left\{{\ddot{\ell }}_{\theta \theta }-{\ddot{\ell }}_{\mathrm{\Lambda }\theta }\left[\int {\tilde{\mathit{h}}}_{\mathrm{\Lambda }}\text{d}{\mathrm{\Lambda }}_0\right]-\sum _{g=2}^G{\ddot{\ell }}_{\psi g\theta }\left[{\tilde{\mathit{h}}}_{\psi g}\right]\right\}+o_p\left(1\right)=n^{1/2}\tilde{\mathit{I}}\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0\right)+o_p\left(1\right),$$

where ${\ddot{\ell }}_{\theta \theta }$, ${\ddot{\ell }}_{\mathrm{\Lambda }\theta }$ are ${\ddot{\ell }}_{\psi g\theta }$ the derivatives of ${\dot{\ell }}_{\theta }$, ${\dot{\ell }}_{\mathrm{\Lambda }}$, and ${\dot{\ell }}_{\psi g}$ with respect to θ, respectively. As established in Step 5 in the proof of Theorem 4.1, the information operator is invertible, so the efficient information matrix is invertible. We conclude that $n^{1/2}\left({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0\right){\to }_d\text{N}\left(\text{0},{\tilde{\mathit{I}}}^{-1}\right)$. Because ${\widehat{\mathit{\theta }}}_n$ is an asymptotically linear estimator with the influence function lying in the space spanned by the score functions, ${\widehat{\mathit{\theta }}}_n$ is asymptotically efficient [1]. □

APPENDIX B: USEFUL LEMMAS

In this appendix, we present four lemmas that are useful for the proofs of Theorems 4.1 and 4.2. The proofs of the lemmas are given in Section S3 of the supplementary materials [21].

Lemma B.1. For any finite K, the classes of functions

$${\mathcal{G}}_1=\left\{\log \mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right):\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\in {\Xi }_K\right\}$$

$${\mathcal{G}}_2=\left\{\frac{{\dot{\mathrm{\Psi }}}_{\theta }{\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)}^{\text{T}}\mathit{v}}{\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)}:\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\in {\Xi }_K,\hspace{0.33em}‖\mathit{v}‖<K\right\}$$

$${\mathcal{G}}_3=\left\{\frac{{\dot{\mathrm{\Psi }}}_{\mathrm{\Lambda }}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[H_{\mathrm{\Lambda }}\right]}{\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)}:\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\in {\Xi }_K,\hspace{0.33em}{‖H_{\mathrm{\Lambda }}‖}_{\text{V}}<K\right\}$$

$${\mathcal{G}}_{4g}=\left\{\frac{{\dot{\mathrm{\Psi }}}_{\psi g}\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\left[h_{\psi g}\right]}{\mathrm{\Psi }\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)}:\left(\mathit{\theta },\mathrm{\Lambda },\mathcal{B}\right)\in {\Xi }_K,\hspace{0.33em}{‖h_{\psi g}‖}_{\text{V}}<K\right\}$$

are Donsker.

Lemma B.2. Under conditions (C1)–(C3) and (C5), the latent-class model given by (1)–(3) is locally identifiable.

Lemma B.3. Consider the following normal mixture model. Let W be a set of covariates and C be a latent class indicator with distribution specified by (1). For g = 1,…,G, let Y_g ∼ N(µ_g, Ω_g), where (µ₁, …,µ_G) are vectors of mean parameters, and (Ω₁,…,Ω_G) are covariance matrices. The observed outcome variable is $\mathit{Y}={\sum }_{g=1}^{G}I\left(C=g\right){\mathit{Y}}_g$. Let (µ_0g,Ω_0g) be the true values of (µ_g,Ω_g). If (µ₀₁,Ω₀₁),…,(µ_0G,Ω_0G) are distinct and the components of W are linearly independent, then the score statistic along any submodel is nonzero.

Lemma B.4. Under conditions (C1)–(C3) and (C5), the score statistic along any one-dimensional submodel for the latent-class model given by (1)–(3) is nonzero.