Abstract
The present study probed the creation of heat energy and concentrating into Newtonian liquids across vertical 3D-heated plates. The role of the Soret and Dufour theories in concentrating and energy formulas is discussed. The role of hybrid nanoparticles is introduced to illustrate particle efficiency in terms of solute and thermal energy. It is removed a viscous dissipation process and a changing magnetic field. The proposed approach is motivated by the need to maximize solute and thermal energy uses in biological and industrial domains. The constructed system of (partial differential equations) PDEs includes concentration, momentum, and thermal energy equations within various thermal characteristics. Transformations are used to formulate the system of (ordinary differential equations) ODEs for solution. To assess various features vs various variables, a Galerkin finite element approach is used. Motion into nanoscale components is shown to be smaller than motion into hybrid nanoparticles. Furthermore, fluctuations in heat energy and solute particle counts are seen in relation to changes in Soret, Eckert, magnetic, and Dufour numbers. The basic finding is that the generation of thermal energy for hybridized nanomaterials is much higher.
Subject terms: Applied mathematics, Computational science, Mechanical engineering, Engineering, Mathematics and computing, Nanoscience and technology
Introduction
Heat transfer is a thermal engineering subject that entails the manufacture, use, conversion, and alternate of warmth power among transportable structures. Heat transfer is split into diverse approaches, which include thermal conduction, thermal convection, thermal radiation, and energy transfer through section changes. Engineers additionally don't forget to shift an extensive variety of chemical compounds (advection mass switch), both bloodless or hot, to attain a heat switch. Although those techniques have unique characteristics, they generally arise concurrently withinside the identical system. Heat alternate happens while the waft of a huge quantity of liquid (fuel line or liquid) contains its warmth in a liquid. All convective approaches additionally transmit partial warmth to the circulation, as well1. Heat switch is one of the maximum vital commercial approaches. Throughout the economic field, warmth ought to be added, subtracted, or eliminated from the distribution of one technique to another. In theory, the heat dissipated through a hot liquid is in no way precisely similar to the heat received through a cold liquid because of the lack of herbal warmth2. Application for heat transfer in commercial manufacturing 99% of manufacturing makes use of a particular technique to transfer heat. Drying approaches are all types of heat transfer. The commercial makes use of heat transfer fluids vary, from simple, dry layouts to superior sized structures that carry out many features withinside the manufacturing technique. As there are numerous versions withinside the layout and alertness of approaches withinside the use of heat transfer fluids, the quantity of industries that use this technique is likewise huge3. Miniaturization has a large effect on the generation of heat exchangers and turns heat exchangers into an extra compact and extra green. The performance of the heat exchanger has an extremely good effect on the general performance and fitness of the thermal power system. The micro-channel heat sink is a brand new device in warmth alternate generation. The benefits of a huge heat transfer area and the excessive cohesiveness of a small channel heat sink make it a green warmth exchanger for the usage of electronic cooling4.
Zahra et al.5 investigated the effects of thermal radiation heat transfer with a solar system subjected to flow with nanoparticles. Sheikholeslami and Ganji6 discussed heat transfer in ferrofluids with nanoparticles exposed to a magnetic field. Zeeshan and Bhargav7 investigated the influence of dispersion of and in fluid on heat transfer in the fluid using the molecular dynamics approach. Sajjad et al.8 analyzed the influence of the Darcy-Forchheimer porous medium and nanoparticles on heat transfer in fluid over a moving surface.
A hybrid material is a substance that mixes bodily and chemical properties of various substances concurrently and affords those homes in a homogeneous segment. Synthetic hybrid nanomaterials show off first-rate physicochemical homes that don't exist withinside the character components. An enormous quantity of studies has been finished concerning the homes of those composites9 and hybrid substances which include carbon nanotubes (CNTs) had been utilized in electrochemical sensors, bio-sensors, nanocatalysts, etc.10 however the use of those hybrid nanomaterials in nanofluids has now no longer advanced as such. Work on hybrid nanofluids could be very restricted and a whole lot of experimental look continues to be being finished. According to Makishima11 while or greater substances are blended so that their aggregate has a specific chemical bond entitled “hybrid metals”. In fact, while or greater metals added the homogeneous segment with simultaneous blending named “hybrid nanofluid". This superior elegance of nanofluids confirmed promising enhancement in heat transfer traits and thermophysical and hydrodynamic homes as compared to unitary nanofluids. Hayat and Nadeem12 discovered that the hybrid nanofluid finished nicely with a better warmth switch charge as compared to unitary nanofluid even withinside the presence of heat generation, chemical reaction, and thermal radiation. They found this even as investigating the rotating three-d consistent waft of Ag–CuO/water hybrid nanofluid. Selimefendigil and Öztop13 compared the thermal overall performance of TiO2, Cu, and Al2O3 and located that Cu nanofluids furnished relatively higher results. Azmi et al.14 deliberated the hybrid nanofluids thermophysical homes, education methods, a current development, and execution outcomes on heat transfer, friction factor, and stress drop. Minea et al.15 mentioned the programs of hybrid nanofluids in solar power with the guidance of a few debates on thermophysical homes and mathematical modeling which include numerical details. Nazir et al.16 discussed the role of Williamson liquid in thermal energy and concentration involving hybrid nanoparticles toward melting surfaces via non-Fourier’s theory. Dogonchi et al.17 analyzed the role of hybrid nanoparticles on the thermal efficiency of fluid between two parallel plates subjected to thermal radiation. Chamkha et al.18 published on the simultaneous influence of hybrid nanoparticles, magnetic fields, and rotations of walls on the transfer of heat. Masayebidarched et al.19 performed theoretical analysis for the thermal enhancement in fluid with hybrid nanoparticles. Similar works published on the role of hybrid nanoparticles on thermal enhancement can be seen in references20–32.
To conclude, the latest development on the simultaneous transfer of heat and mass has revealed that compositional gradients are a favorable factor for the transfer heat. Similarly, a temperature gradient is supported to enhance mass transfer in fluids. The transfer of heat due to compositional differences of solute is termed the Dufour effect, whereas the transfer of mass due to temperature gradient is called the Soret effect. These effects have been studied theoretically in recent years. For instance, Hayat and Nawaz33 studied the combined effects of temperature and concentration gradients on mixed convection heat and mass transport in partially ion, second grade fluid subjected to a magnetic field. Nawaz et al.34 studied the Soret and Dufour effects on heat and mass transfer in an axisymmetric flow between two moving surfaces. Subrat et al.35 examined the Soret and Dufour effects on the transport phenomenon in thermochemical flow. Iskandar et al.36 analyzed the combined effects of Soret and Dufour due to the suspension of nanosized particles on heat and mass transfer in flow over a moving thin needle. Ambreen et al.37 also examined the impact of temperature and concentration gradients.
Recently extensive studies paintings have been completed on the fluid’s dynamics withinside the presence of a magnetic field. The effects of the magnetic discipline on fluids are well worth investigating because of its several packages in a huge variety of fields. The examination of the interplay of the magnetic discipline or the electromagnetic discipline on fluids has been documented, e.g., in nuclear fusion, chemical engineering, medication, and transformer cooling. A magnetic nanofluid (ferrofluid) is a magnetic colloidal suspension along with a base liquid and magnetic nanoparticles with a length variety of 5–15 nm in diameter coated with a surfactant layer Sheikholeslami and Rashidi38, Ganguly et al.39 studied the impact of a line dipole on warmth switch enhancement. They located that an enhancement withinside the general heat switch relies upon the internet magnetizing cutting-edge in addition to the relative placement of the dipoles. Parsa et al.40 investigated the magneto-hemodynamic laminar viscous glide of an accomplishing physiological fluid in a semi-porous channel beneath neath a transverse magnetic discipline. Sheikholeslami and Ellahi41 studied 3-dimensional mesoscopic simulation of magnetic discipline impact on herbal convection of nanofluid. They located that thermal boundary layer thickness growth with growth withinside the Lorentz force. The vortex dynamics in the back of diverse magnetic limitations and traits of warmth switches have been investigated by Zhang and Huang42. They located that the stress drop penalty isn't depending on the interplay parameter. Nanofluid glide and heat transfer traits among horizontal parallel plates in a rotating gadget have been investigated by Sheikholeslami et al.43. They located that the Nusselt range will increase with a growth in nanoparticle quantity fraction and the Reynolds range; however, it decreases with a growth withinside the Eckert range, the magnetic and the rotation parameters. Ghofrani et al.44 provided experimental research on pressured convection warmth switch of an aqueous ferrofluid glide passing thru a round copper tube withinside the presence of an alternating magnetic discipline. They located that the impact of the magnetic discipline in low Reynolds numbers is higher, and a most of 27.6% enhancement withinside the convection heat transfer is observed. Sheikholeslami et al.45 used lattice Boltzmann simulation (LBM) to simulate nanofluid glide and heat transfer outcomes in a horizontal cylindrical enclosure with an internal triangular cylinder. Rashidi et al.46 studied the results of magnetic interplay range, slip component, and relative temperature distinction on velocity and temperature profiles in addition to entropy technology in Magnetohydrodynamic (MHD) glide of a fluid over a rotating disk with variable properties47–57. include new additions that consider conventional and hybrid nanofluids with heat and mass transmission in a variety of physical circumstances.
The unique connections among thermophysical parameters, no previous study on thermal enhancement and mass transposition in three-dimensional Newtonian liquids flowing across vertical heated plates have been investigated. It is found that the basis liquids of the hybrid nanofluids tested include copper (Cu), silver (Ag), and water (H2O). Following the similarity approach, numerical solutions are obtained using the robust Galerkin finite element technique for the controlling PDEs system. Hybrid nanofluid passes through vertical heated plates and offers a wide range of industrial applications, including coating and suspensions, cooling of metallic plates, heat exchanger technology, and materials processing. Manufacturing of aerodynamically extruded plastic sheets, the production of paper, heat-treated materials were going between feed and winding-up rolls, and the cooling of an endless metallic plate in a cooling bath.
For this reason, this research comprises five sections, each of which presents a variety of alternative answers. Section "Flow analysis" lays out the specifics of the issue at hand. Meanwhile, an overview of the numerical approach is provided in section "Numerical method and code validation". Section "Results and discussion" discusses the results. Section "Core points and conclusions" wraps up this investigation.
Flow analysis
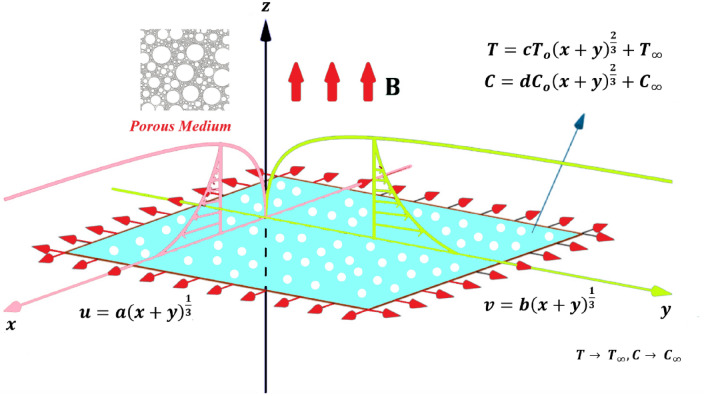
The features of thermal energy and solute particles in Newtonian liquid inserting hybrid nanostructures toward a heated vertical surface are considered under the impact of a variable magnetic field. A porous surface is taken to characterize the motion and thermal energy of particles along with the Dufour and Soret influences. The composite of and is called a hybrid nanostructure, while is known as a nanoparticle. The thermal properties of and are illustrated in Table 1.
Table 1.
Correlation among hybrid nanostructures and nanomaterials in polymers.
| Properties | Cu-Ag- polymer |
|---|---|
| Density | |
| Heat capacity | |
| Viscosity | |
| Thermal conductivity | |
| Thermal diffusivity () | |
| Electrical conductivity () |
Assumptions of the current problem
Following suppositions and requirements are observed for the mathematical model:
Hybrid nanofluid model
Copper (Cu) and silver (Ag) nanoparticles
Water (H2O)as base fluid
Magnetic field
Porous media
Heat source
Vertical 3D-heated plates
The schematic behavior of the current model is presented in Fig. 1.
Figure 1.
Geometry of hybrid nanostructures.
In Fig. 1, It noticed that x-axis is taken along vertical direction and y-axis is assumed along horizontal direction while magnetic field is inserted along y-direction. Magnetic field parameter reduces motion of particles. The flow region is exposed by taking a uniform transverse magnetic field and the maximum amount of thermal energy is achieved versus argument values of Eckert number, bouncy parameter and magnetic parameter.
PDEs, describing the problem58,59, can be stated as
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
For system Eqs. (1)–(5) the BCs are (see for details,58,59)
| 6 |
In the above equations, the velocity is , denotes the gravitational force, , is the kinematic viscosity, is the electrical conductivity, is called the specific heat, is the thermal conductivity, is the mass diffusion (coefficient), and is revealed by the hybrid nanostructures. It should be noted that a uniform magnetic field is taken along the z-direction of the surface while the flow runs due to stretching walls.
Table 1 demonstrates the composite relation between hybrid nanostructures and nanomaterials in polymers, which is called the base fluid.
In Table 1 the following denotes
| 7 |
Next, the similarity transformation is
| 8 |
Consequently, using similarity transformation in Eqs. 1–6, we have
| 9 |
| 10 |
where, the following denotes: (Dufour number) , (Eckert number) , Soret number (), (Schmidt number) , (Prandtl number) , (porous medium parameter) (), (volumetric thermal expansion number) , (heat generation) , (Grashof number) and (magnetic parameter) . The dimensionless numbers and defined here
The practical proposed model parameters used in this study are summarized in Table 2.
Table 2.
Thermal properties of water, copper and silver.
| Physical property | Water | Cu | Ag |
|---|---|---|---|
| 997.1 | 8933 | 10,500 | |
| 0.613 | 401 | 429 | |
| 4179 | 385 | 429 | |
| 0.05 | 5.96 × 107 | 6.3 × 107 |
The surface forces are captured as
| 11 |
| 12 |
Nusselt number is
| 13 |
the rate of mass diffusion is
| 14 |
where, , the Reynolds number.
Numerical method and code validation
The G-FEM (Galerkin finite element method)60–64 is used via COMSOL Multiphysics calculation software to obtain the solution of the presented problem. The working rules of G-FEM are given below:
The residual equations are constructed.
The residual is integrated over the typical element of the discretized domain.
The weighted residual integrals are approximated using the Galerkin approach, and stiffness matrices are derived.
The rules of assembly of elements are followed, and a nonlinear system of equations is linearized. The linearized system is solved under computational tolerances .
- The convergence is checked, and grid-independent results are obtained. The criterion of error analysis is used.
15 Table 3 reveals the investigation of mesh-free;
Convergence analysis is confirmed via 300 elements.
Table 3.
Mesh-free investigation of temperature and velocities within 300 elements.
| Division of elements | |||
|---|---|---|---|
| 30 | 0.49906667 | 0.443556676 | 0.055501654 |
| 60 | 0.88512223 | 0.872840112 | 0.345670987 |
| 90 | 0.62693678 | 0.621570046 | 0.058457122 |
| 120 | 0.59438123 | 0.509121334 | 0.057888099 |
| 150 | 0.59196567 | 0.497570987 | 0.057527446 |
| 180 | 0.60400213 | 0.592340987 | 0.057229098 |
| 210 | 0.61009098 | 0.509400003 | 0.056238099 |
| 240 | 0.60424098 | 0.499011223 | 0.056821432 |
| 270 | 0.50980001 | 0.507710098 | 0.058645667 |
| 300 | 0.59632222 | 0.506367767 | 0.056854098 |
In examples, a parametric study is elaborated to study heat energy and mass transfer in 3D flow of Newtonian fluid, showing the influences of heat generation, porous medium, viscous dissipation, temperature gradient, rate of mass diffusion and Joule heating.
It is remarked that the current study's findings are approximated using G-FEM. Table 4 shows a validation of results using the Nusselt number in the case of nanofluids (Table 5).
Table 4.
In the case of nanofluids, the temperature changes were compared to the reported data of Ref.65 and Ref.66.
Table 5.
Nanofluid properties and non-dimensional parameters as function of type and volume fraction of nanoparticles and hybrid nanoparticles.
| Ag | ||||||||
| 0.05 | 0.709 3 | 7.73 × 10−7 | 4.452 | 61 5.45 | 8.6 × 10−7 | 4.8 × 10−7 | ||
| 0.01 | 0.631 5 | 9.54 × 10−7 | 6.287 | 68 5.83 | 2.2 × 10−7 | 1.2 × 10−7 | ||
| Cu | ||||||||
| 0.03 | 0.669 6 | 8.75 × 10−7 | 5.418 | 66 1.57 | 7.3 × 10−7 | 3.7 × 10−7 | ||
| 0.05 | 0.709 3 | 8.17 × 10−7 | 4.758 | 65 0.81 | 1.2 × 10−6 | 6.3 × 10−7 | ||
| Nanofluids | Nanofluids | Hybrid nanofluids | Hybrid nanofluids | |||||
|---|---|---|---|---|---|---|---|---|
| Numeric | Analytic | Numeric | Analytic | Numeric | Analytic | Numeric | Analytic | |
| For different types of nanoparticles and hybrid particles | ||||||||
| 0.1 | 1.011 1 | 1.011 0 | 1.011 0 | 1.010 9 | 1.007 1 | 1.006 6 | 1.009 3 | 1.008 9 |
| 0.3 | 1.032 7 | 1.032 3 | 1.032 6 | 1.032 1 | 1.020 9 | 1.019 3 | 1.027 7 | 1.026 3 |
| 0.5 | 1.054 6 | 1.053 6 | 1.543 9 | 1.053 5 | 1.035 3 | 1.032 9 | 1.046 2 | 1.044 2 |
The Prandtl number decreases with the nano and hybrid particle volume fraction, whereas the Brownian motion parameter and the thermophoresis parameter increase with the nanoparticle volume fraction in Integral treatment for forced convection heat and mass transfer of nanofluids 300. It's interesting to note that the variation of the Lewis number has a varied pattern for different nanoparticles. In the case of Ag and Cu nano and hybrid nanoparticles, the Lewis number decreases as the nanoparticle volume percentage increases. As a result, for a fixed reference temperature (T) and a specified size of nano and hybrid particles. Furthermore, the density of the nanoparticles is usually substantially higher than that of the basic fluid. As a result, adding heavy nanoparticles will increase the density of the resulting hybrid nanofluid, and increasing the volume fraction of nanoparticles will simultaneously increase the dynamic viscosity and density.
Results and discussion
The aspect of heat energy and mass diffusion in Newtonian fluid flow over a surface with temperature (variable) and wall concentration (variable) is modeled, and a coupled mathematical model is solved numerically using the G-FEM. The parameter is called the flow fluid parameter; it determines the rheological behavior under yield stress. Yield stress is the characteristic by which fluid resists deformation until a certain amount of applied stress is reached. As the yield stress increases, the fluid’s ability to resist the applied stress attains its equilibrium state; therefore, a decrease in the velocity field (in both the and components) is observed (see Figs. 2 and 3).
Figure 2.
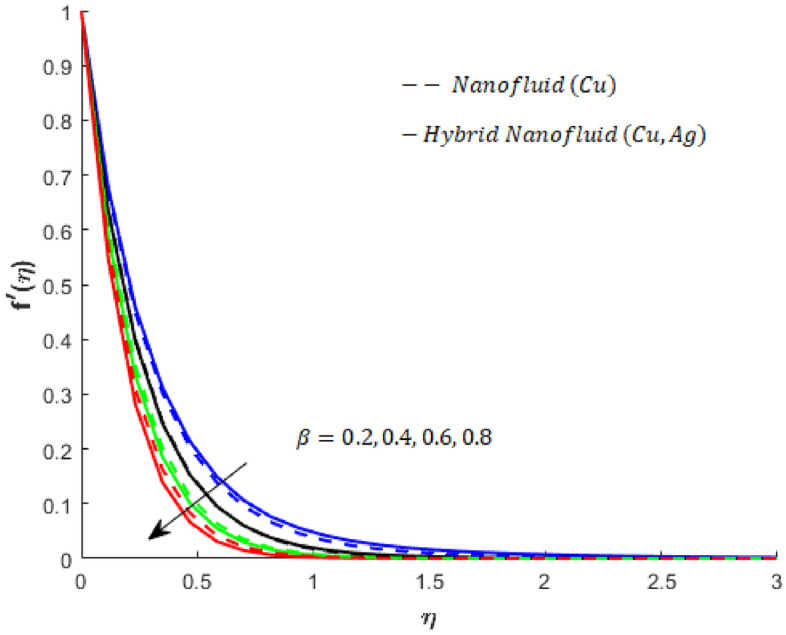
Influence of on when and .
Figure 3.
Influence of on when and .
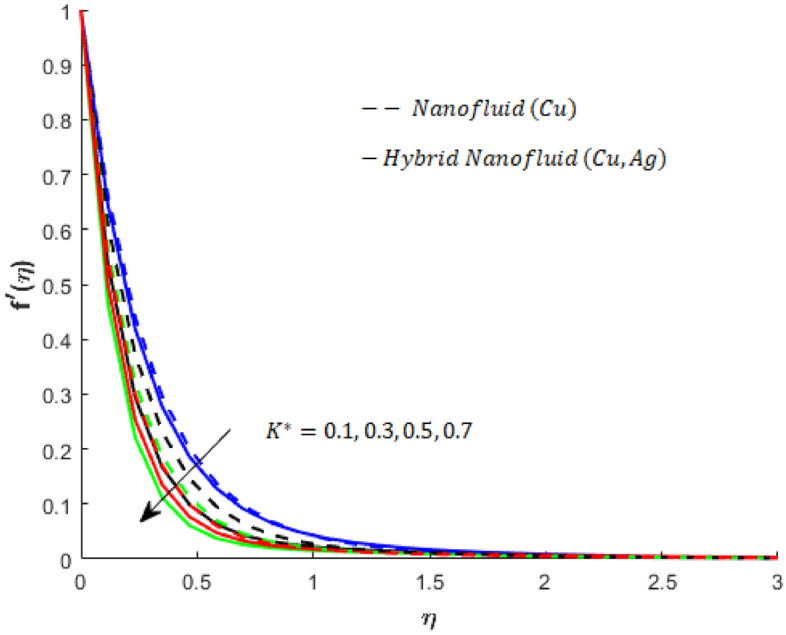
Various numerical experiments are performed with different samples of parametric values. Some crucial observations are obtained from the numerical experiments. It is important to note that dashed curves are associated with flow, heat transfer and mass diffusion in nanofluids (Cu-nanofluids), whereas solid curves are associated with flow, heat transfer and mass transport in hybrid nanofluids (Cu- Ag- nanofluids). The increase in the magnitude of the resistive force is captured first. Obviously, the flow in both the - and - directions decelerates; see Figs. 4 and 5). Moreover, the parameter associated with porous medium resistivity against the flow of fluid and its impact on the motion of fluid particles is shown in Figs. 6, and 7 decreasing velocity behavior can be seen in Figs. 6 and 7. These figures also show that the hybrid nanofluid experiences more resistance to the porous medium than the mono nanofluid. The viscous region for nanofluids is wider than that for hybrid nanofluids.
Figure 4.
Influence of on when and
Figure 5.
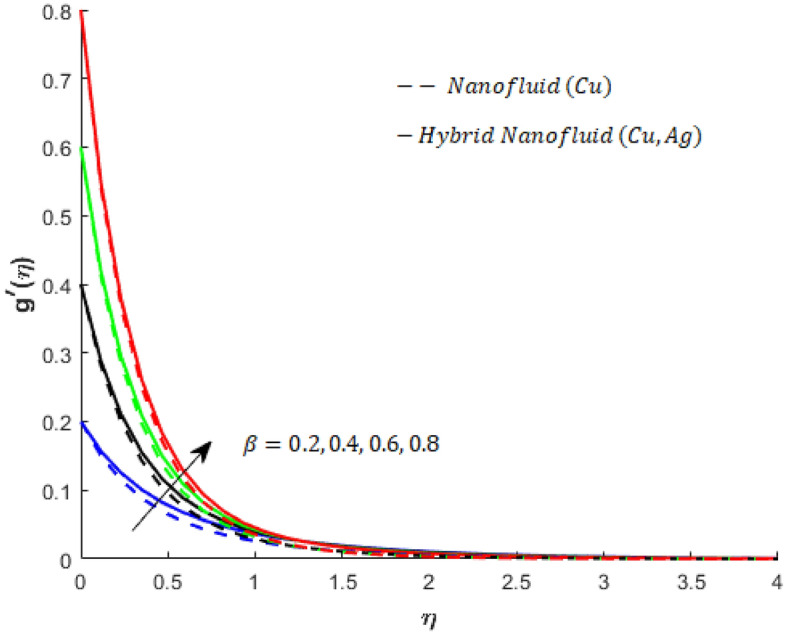
Influence of on when and .
Figure 6.
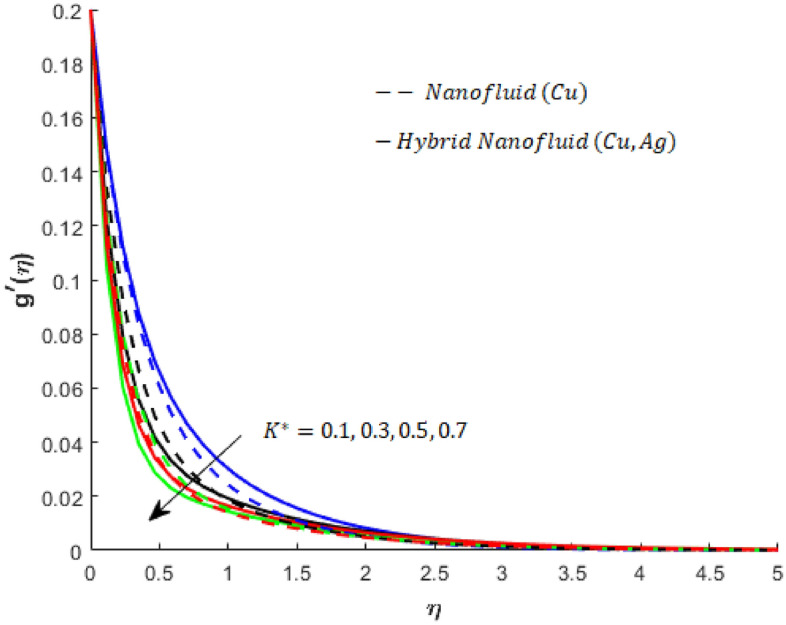
Influence of on when and
Figure 7.
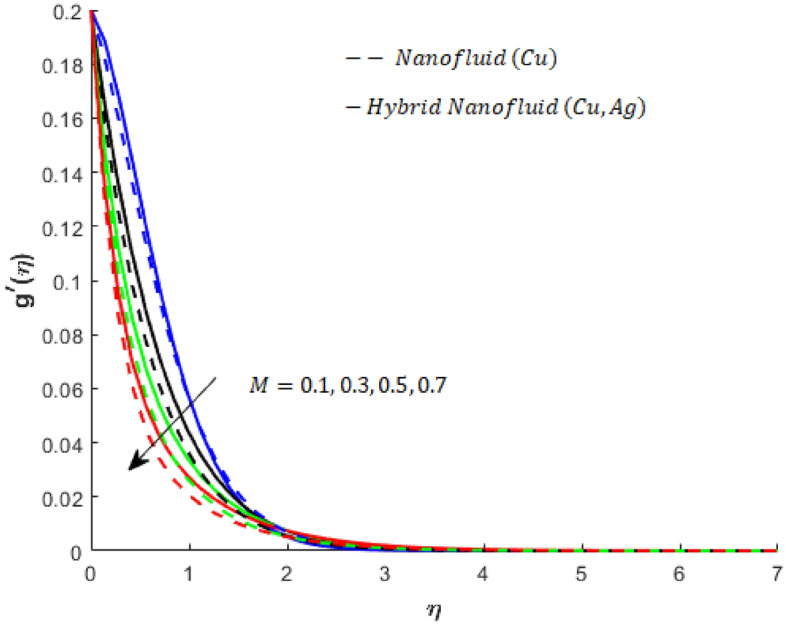
Influence of on when and .
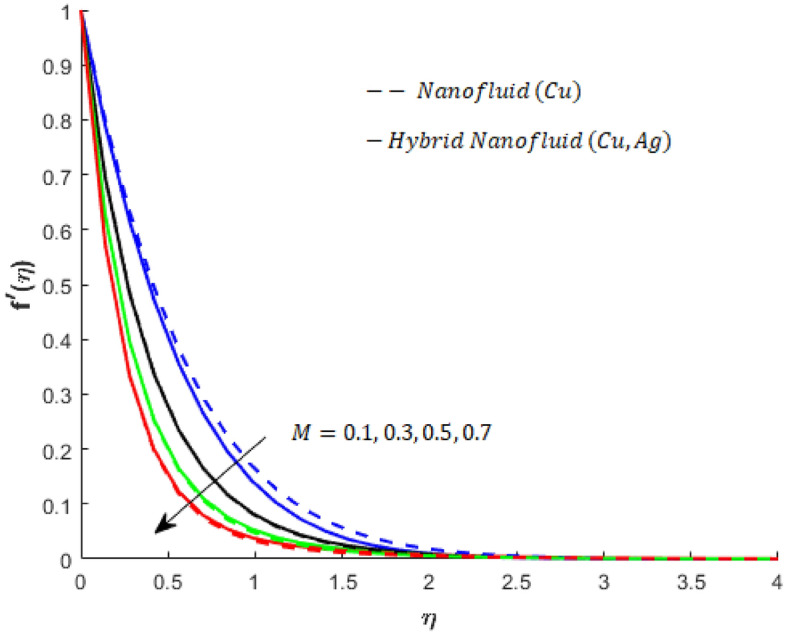
Role of magnetic field versus fluid flow
The direct relation is addressed to the magnetic field and Lorentz force. The influence of the Lorentz force on flow can be determined by the variation in . The large values of increase the opposing effect of the Lorentzian force. Therefore, flow experiences retardation due to the Lorentz force. (See Figs. 6 and 7). Thus, BLT is approached by varying the magnetic field (the intensity of applied). It is also noted that the Lorentz force for the case of flow of the Cu- Ag- nanofluids is greater than the Lorentz force in the case of flow of the Cu-nanofluid.
Temperature field versus variation of crucial model parameters
The effects of , , , and versus thermal energy for both nanofluids ( -nanofluids) and hybrid nanofluids (Cu- Ag- nanofluids) are examined. The observed influence of these parameters is shown in Figs. 8, 9. The parameter is called Dufour number. It appears in the dimensionless form of the energy equation when the transcript of thermal energy due to the concentration gradient is taken into account. It measures the transfer of heat energy due to compositional differences caused by nanoparticles and solute diffused in the fluid. The effects of on the temperature of the -nanofluid and Cu- Ag- hybrid nanofluid are shown in Fig. 8. The temperature of both types of fluids has an increasing tendency as a function of . The influence of on the temperature of the Cu- nanofluid is smaller than that on the temperature of the Cu- Ag- nanofluids. The effects of the buoyancy force on the temperature of the Cu-nanofluid and Cu- Ag- nanofluids are represented by Fig. 9. is the case when the buoyancy force is positive, and flow is assisted by this force. However, in the case when the buoyancy force is negative, the flow in this case is called opposing flow.
Figure 8.
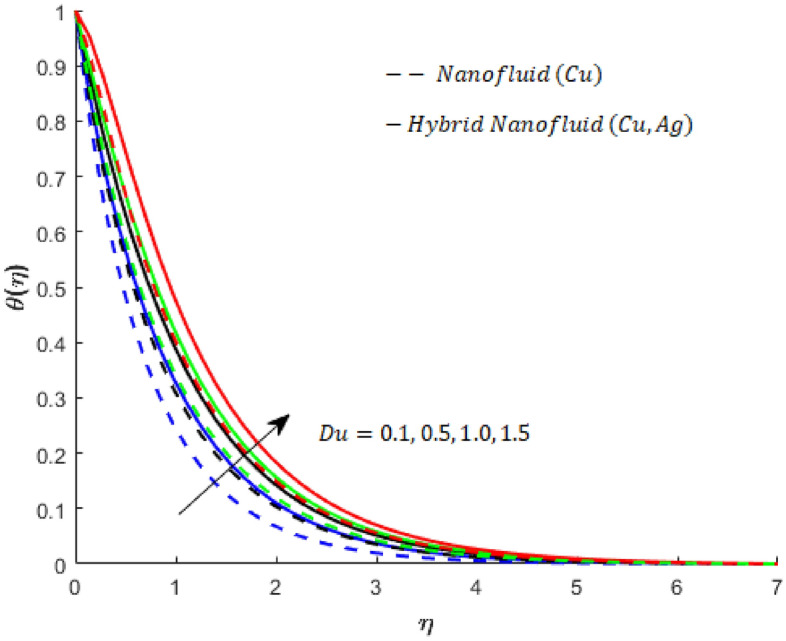
Influence of on when and .
Figure 9.
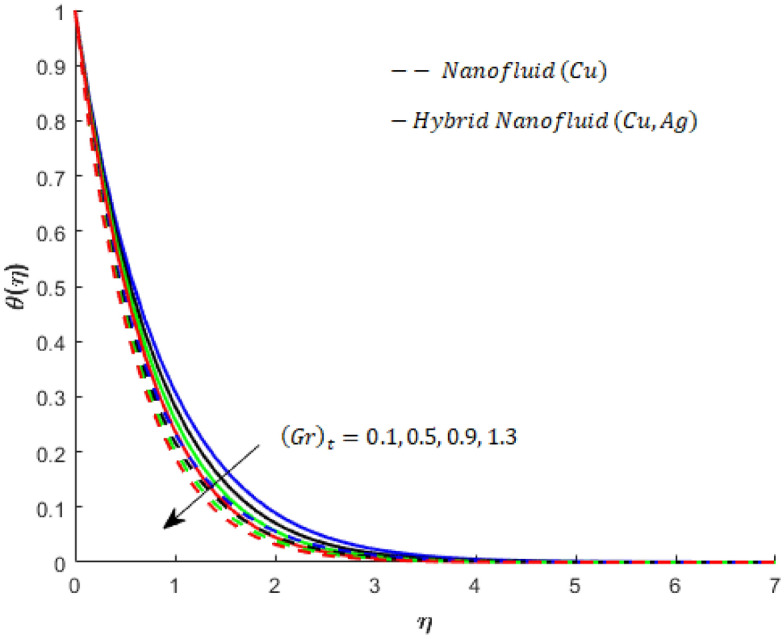
Influence of on when and
Wall shear stresses, heat transfer rate and mass flux
Numerical data related to wall shear stresses in the and -directions, wall heat transfer rate and wall mass flux for both types of fluids, -fluid (mono nanofluid) and - -fluid (hybrid nanofluid), are investigated versus the variation in key parameters, , , and (see Table 6). The numerical outcomes are summarized in Table 6. It appears that is inversely proportional to the voids present in the porous medium. Hence, the resistive force per unit area (stress) increases. Therefore, wall shear stresses in both the and -directions are increasing functions of . The temperature gradient and mass flux are both decreasing functions of . It is also observed that wall shear stress increases when is increased. On the other hand, a rise in wall mass flux against is noted. Finally, the temperature gradient on solute particles is determined by , and an increase in causes a decrease in wall shear stress. However, the opposite trend is noted for .
Table 6.
Simulations of physical quantities when and
| 0.0 | 1.224110 | 1.512023 | 2.910831 | 2.7091217 | |
| 0.31 | 1.313851 | 1.712213 | 2.710327 | 2.5291402 | |
| 0.43 | 0.511053 | 1.913205 | 2.411028 | 2.3045191 | |
| 0.0 | 1.701101 | 1.514165 | 2.450237 | 2.512043 | |
| 0.4 | 1.512553 | 1.321243 | 2.703033 | 2.710017 | |
| 0.8 | 1.312105 | 1.215345 | 2.910211 | 2.915321 | |
| 0.0 | 1.537013 | 1.7060183 | 2.346892 | 3.3012731 | |
| 0.3 | 1.303711 | 1.4139212 | 2.152565 | 3.1201361 | |
| 0.7 | 1.211321 | 1.3113031 | 2.511689 | 3.0231110 | |
| 0.0 | 1.211083 | 0.1280160 | 2.430243 | 2.3130353 | |
| 0.5 | 1.501333 | 0.2150133 | 2.511035 | 2.4131321 | |
| 1.3 | 1.710150 | 0.3352120 | 2.710115 | 0.8153113 |
Core points and conclusions
The features of heat energy and mass diffusion, which play essential roles in the behaviour of nanoparticles and hybrid nanostructures, are addressed over the vertical 3D melting surface. Newtonian fluid is considered under simultaneous influences of heat generation, porous medium, viscous dissipation, temperature gradient, rate of mass diffusion, and Joule heating. The mathematical modelling is solved using the famous FEM. The prime findings are listed below:
The convergence of the proposed problem is confirmed for finite element mesh density equal to 300.
The magnetic field reduces the motion of both nanoparticles and hybrid nanostructures, where the effect on hybrid nanofluid is more significant than on nanofluid.
The Dufour number amplified the temperature of both hybrid nanofluid and nanofluid while the temperature for hybrid nanofluid is higher than nanofluid.
The temperature for both fluids diminish as the buoyancy force acts onto the system.
The joule heating parameter intensified the temperature for both fluids, and hybrid nanofluid is stronger than nanofluid.
The Prandtl number decreases the temperature profile for both fluids, but the temperature for hybrid nanofluid is slightly higher than nanofluid.
The temperature profile for both fluids increases when the heat generation and viscous dissipation act onto the system.
The temperature gradient increased the concentration for both fluids, while the diffusion parameter decreased the concentration for both fluids.
Wall shear stress amplified with the porous medium parameter, Dufour number and diffusion parameter but the wall shear stress decrease for the temperature gradient parameter. The mass wall flux rises with the Dufour number and decreases the wall shear stress, while heat transfer rate and mass flux decrease as the porous medium parameter increases.
The Galerkin finite element method could be applied to a variety of physical and technical challenges in the future67–77.
Supplementary Information
List of symbols
- Du
Dufour number
- T
Temperature of nanofluid
- T∞
Ambient temperature
- g*
Gravitational force
- u, v
Velocity component in , direction
- D
Mass diffusion (coefficient)
- Ec
Eckert number
- k
Thermal conductivity
Dimensional space coordinates
- Pr
Prandtl number
- Sr
Soret number
- Sc
Schmidt number
- K*
Porous medium parameter
- Cfx
Surface force
- Re
Reynolds number
- M
Magnetic parameter
- G-FEM
Galerkin finite element method
- Nu
Nusselt number
- PDEs
Partial differential equations
- Ag
Silevr
- Cu
Copper
- Sh
Rate of mass diffusion
- H2O
Water
Thermal conductivity (W m-1 K-1)
- qw
Wall heat flux
Hybrid nanoparticles
Greek symbols
- ρ
Density
- β*
Heat source
- ρcp
Heat capacity
- ϕ
Volume fractions
Electrically conductivity (Ω m) −1
Thermal diffusivity of the hybrid nanofluid
Volumetric thermal expansion number
Author contributions
M.B.H. and M.K. formulated and solved the problem. M.B.H., M.K., H.S., A.A.P. and M.A., computed and scrutinized the results. All the authors equally contributed in writing and proof reading of the paper. All authors reviewed the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
This article has been retracted. Please see the retraction notice for more detail: https://doi.org/10.1038/s41598-024-59124-1
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
4/15/2024
This article has been retracted. Please see the Retraction Notice for more detail: 10.1038/s41598-024-59124-1
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-022-15560-5.
References
- 1.Bergman TL, Lavine AS, Incropera FP, DeWitt DP. Introduction to Heat Transfer. Hoboken: John Wiley & Sons; 2011. [Google Scholar]
- 2.Serrano J, Olmeda P, Arnau F, Reyes-Belmonte M, Lefebvre A. Importance of heat transfer phenomena in small turbochargers for passenger car applications. SAE Int. J. Engines. 2013;6(2):716–728. doi: 10.4271/2013-01-0576. [DOI] [Google Scholar]
- 3.Zhang H, Zhuang J. Research, development and industrial application of heat pipe technology in China. Appl. Therm. Eng. 2003;23(9):1067–1083. doi: 10.1016/S1359-4311(03)00037-1. [DOI] [Google Scholar]
- 4.Ramesh KN, Sharma TK, Rao GAP. Latest advancements in heat transfer enhancement in the micro-channel heat sinks: A review. Arch. Comput. Methods Eng. 2021;28(4):3135–3165. doi: 10.1007/s11831-020-09495-1. [DOI] [Google Scholar]
- 5.Zahra E, Sheikholeslami M, Farshad SA, Shafee A. Radiation heat transfer within a solar system considering nanofluid flow inside the absorber tube. Int. J. Numer. Methods Heat Fluid Flow. 2021;32(2):469–487. [Google Scholar]
- 6.Sheikholeslami M, Ganji DD. Ferrofluid convective heat transfer under the influence of external magnetic source. Alex. Eng. J. 2018;57(1):49–60. doi: 10.1016/j.aej.2016.11.007. [DOI] [Google Scholar]
- 7.Zeeshan, A. & Bhargav, A. Thermal interfacial resistance and nanolayer effect on the thermal conductivity of Al2O3-CO2 nanofluid: A molecular dynamics approach. arXiv preprint arXiv:2006.12805 (2020).
- 8.Sajjad SR, Hayat T, Ellahi R, Muhammad T, Alsaedi A. Darcy–Forchheimer flow of nanofluid due to a curved stretching surface. Int. J. Numer. Methods Heat Fluid Flow. 2019;29(1):2–20. doi: 10.1108/HFF-08-2017-0301. [DOI] [Google Scholar]
- 9.Li H, Ha CS, Kim I. Fabrication of carbon nanotube/SiO2 and carbon nanotube/SiO2/Ag nanoparticles hybrids by using plasma treatment. Nanoscale Res. Lett. 2009;4:1384–1388. doi: 10.1007/s11671-009-9409-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guo S, Dong S, Wang E. Gold/platinum hybrid nanoparticles supported on multiwalled carbon nanotube/silica coaxial nanocables: Preparation and application as electrocatalysts for oxygen reduction. J. Phys. Chem. C. 2008;112:2389–2393. doi: 10.1021/jp0772629. [DOI] [Google Scholar]
- 11.Makisima A. Possibility of hybrids materials. Ceram. Jpn. 2004;39:90–91. [Google Scholar]
- 12.Hayat T, Nadeem S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Res. Phys. 2017;7:2317–2324. [Google Scholar]
- 13.Selimefendigil F, Öztop HF. Mixed convection of nanofluids in a three-dimensional cavity with two adiabatic inner rotating cylinders. Int. J. Heat Mass Transf. 2018;117:331–343. doi: 10.1016/j.ijheatmasstransfer.2017.09.116. [DOI] [Google Scholar]
- 14.Nabil MF, Azmi WH, Hamid KA, Zawawi NNM, Priyandokoa G, Mamat R. Thermo-physical properties of hybrid nanofluids and hybrid nanolubricants: A comprehensive review on performance. Int. Commun. Heat Mass Transf. 2017;83:30–39. doi: 10.1016/j.icheatmasstransfer.2017.03.008. [DOI] [Google Scholar]
- 15.Minea AA, El-Maghlany WM. Influence of hybrid nanofluids on the performance of parabolic trough collectors in solar thermal systems: Recent findings and numerical comparison. Renew. Energy. 2018;120:350–364. doi: 10.1016/j.renene.2017.12.093. [DOI] [Google Scholar]
- 16.Nazir U, Sadiq MA, Nawaz M. Non-Fourier thermal and mass transport in hybridnano-Williamson fluid under chemical reaction in Forchheimer porous medium. Int. Commun. Heat Mass Transf. 2021;127:105536. doi: 10.1016/j.icheatmasstransfer.2021.105536. [DOI] [Google Scholar]
- 17.Dogonchi AS, Divsalar K, Ganji DD. Flow and heat transfer of MHD nanofluid between parallel plates in the presence of thermal radiation. Comput. Methods Appl. Mech. Eng. 2016;310:58–76. doi: 10.1016/j.cma.2016.07.003. [DOI] [Google Scholar]
- 18.Chamkha AJ, Dogonchi AS, Ganji DD. Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv. 2019;9(2):025103. doi: 10.1063/1.5086247. [DOI] [Google Scholar]
- 19.Mosayebidorcheh S, Sheikholeslami M, Hatami M, Ganji DD. Analysis of turbulent MHD Couette nanofluid flow and heat transfer using hybrid DTM–FDM. Particuology. 2016;26:95–101. doi: 10.1016/j.partic.2016.01.002. [DOI] [Google Scholar]
- 20.Sheikholeslami M, Kataria HR, Mittal AS. Effect of thermal diffusion and heat-generation on MHD nanofluid flow past an oscillating vertical plate through porous medium. J. Mol. Liq. 2018;257:12–25. doi: 10.1016/j.molliq.2018.02.079. [DOI] [Google Scholar]
- 21.Nazir U, Nawaz M, Alqarni MM, Saleem S. Finite element study of flow of partially ionized fluid containing nanoparticles. Arab. J. Sci. Eng. 2019;44(12):10257–10268. doi: 10.1007/s13369-019-04168-z. [DOI] [Google Scholar]
- 22.Sajjad SR, Muhammad T, Sadia H, Ellahi R. Hydromagnetic flow of Jeffrey nanofluid due to a curved stretching surface. Phys. A. 2020;551:124060. doi: 10.1016/j.physa.2019.124060. [DOI] [Google Scholar]
- 23.Bayones, F. S., Jamshed, W., Elhag, S. H. & Eid, M. R. Computational galerkin finite element method for thermal hydrogen energy utilization of first grade viscoelastic hybrid nanofluid flowing inside PTSC in solar powered ship applications. Energy Environ. 0958305X221081463 (2021).
- 24.Jamshed, W., Safdar, R., Brahmia, A., Alanazi, A. K., Abo-Dief, H. M. & Eid, M. R. Numerical simulations of environmental energy features in solar pump application by using hybrid nanofluid flow: Prandtl-eyring case. Energy Environ. 1–44 (2021).
- 25.Jamshed W, Alanazi AK, Mohamed Isa SSP, Banerjee R, Eid MR, Nisar KS, Alshahrei H, Goodarzi M. Thermal efficiency enhancement of solar aircraft by utilizing unsteady hybrid nanofluid: A single-phase optimized entropy analysis. Sustain. Energy Technol. Assess. 2021;52:101898. [Google Scholar]
- 26.Jamshed W, Prakash M, Devi SSU, Ibrahim RW, Shahzad F, Nisar KS, Eid MR, Abdel-Aty AH, Khashan MM, Yahia IS. A brief comparative examination of tangent hyperbolic hybrid nanofuid through a extending surface: Numerical Keller-Box scheme. Sci. Rep. 2021;11(1):1–32. doi: 10.1038/s41598-021-03392-8. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 27.Jamshed, W., Baleaznu, D., Mohd Nasir, N. A. A., Shahzad, F., Nisar, K. S., Shoaib, M., Ahmad, S. & Ismail, K. A. The improved thermal efficiency of Prandtl–Eyring hybrid nanofluid via classical Keller box technique. Sci. Rep. (2021). [DOI] [PMC free article] [PubMed]
- 28.Jamshed, W., Mohd Nasir, N. A. A., Qureshi, M. A., Shahzad, F., Banerjee, R., Eid, M. R., Nisar, K. S. & Ahmad, S. Dynamical irreversible processes analysis of Poiseuille magneto-hybrid nanofluid flow in microchannel: A novel case study. Waves Random Complex Media (2022).
- 29.Ouni M, Ladhar LM, Omri M, Jamshed W, Eid MR. Solar water-pump thermal analysis utilizing copper–gold/engine oil hybrid nanofluid flowing in parabolic trough solar collector: Thermal case study. Case Stud. Therm. Eng. 2022;30:101756. doi: 10.1016/j.csite.2022.101756. [DOI] [Google Scholar]
- 30.Jamshed W, Devi SU, Prakash SM, Hussain SM, Eid MR, Nisar KS, Muhammad T. Entropy amplified solitary phase relative probe on engine oil based hybrid nanofluid. Chin. J. Phys. 2022;77:1654–1681. doi: 10.1016/j.cjph.2021.11.009. [DOI] [Google Scholar]
- 31.Jamshed, W., Azeany Mohd Nasir, N. A., Brahmia, A., Nisar, K. S. & Eid, M. R. Entropy analysis of radiative [MgZn6Zr-Cu/ EO] Casson hybrid nanoliquid with variant thermal conductivity along a stretching surface: Implementing Keller box method. In Proceedings of the Institution of Mechanical Engineers, Part C 1–20 (2022).
- 32.Bouslimi J, Alkathiri AA, Alharbi AN, Jamshed W, Eid MR, Bouazizi ML. Dynamics of convective slippery constraints on hybrid radiative Sutterby nanofluid flow by Galerkin finite element simulation. Nanotechnol. Rev. 2022;11:1219–1236. doi: 10.1515/ntrev-2022-0070. [DOI] [Google Scholar]
- 33.Hayat T, Nawaz M. Soret and Dufour effects on the mixed convection flow of a second-grade fluid subject to Hall and ion-slip currents. Int. J. Numer. Meth. Fluids. 2011;67(9):1073–1099. doi: 10.1002/fld.2405. [DOI] [Google Scholar]
- 34.Nawaz M, Hayat T, Alsaedi A. Dufour and Soret effects on MHD flow of viscous fluid between radially stretching sheets in porous medium. Appl. Math. Mech. 2012;33(11):1403–1418. doi: 10.1007/s10483-012-1632-6. [DOI] [Google Scholar]
- 35.Subrata M, Shaw S, Shift GC. Fractional order model for thermochemical flow of blood with Dufour and Soret effects under magnetic and vibration environment. Colloids Surf. B. 2021;197:111395. doi: 10.1016/j.colsurfb.2020.111395. [DOI] [PubMed] [Google Scholar]
- 36.Iskandar, W., Ishak, A. & Pop, I. Dufour and Soret effects on Al2O3-water nanofluid flow over a moving thin needle: Tiwari and Das model. Int. J. Numer. Methods Heat Fluid Flow (2020).
- 37.Ambreen, K., Naeem, A. S., Ellahi, R., Sait, S. M. & Vafai, K. Dufour and Soret effects on Darcy-Forchheimer flow of second-grade fluid with the variable magnetic field and thermal conductivity. Int. J. Numer. Methods Heat Fluid Flow (2020).
- 38.Sheikholeslami M, Rashidi MM. Ferrofluid heat transfer treatment in the presence of variable magnetic field. Eur. Phys. J. Plus. 2015;130:115. doi: 10.1140/epjp/i2015-15115-4. [DOI] [Google Scholar]
- 39.Ganguly R, Sen S, Puri IK. Heat transfer augmentation using a magnetic fluid under the influence of a line dipole. J. Magn. Magn. Mater. 2004;271:63–73. doi: 10.1016/j.jmmm.2003.09.015. [DOI] [Google Scholar]
- 40.Parsa AB, Rashidi MM, Bégc OA, Sadri SM. Semi-computational simulation of magneto-hemodynamic flow in a semi-porous channel using optimal homotopy and differential transform methods. Comput. Biol. Med. 2013;43:1142–1153. doi: 10.1016/j.compbiomed.2013.05.019. [DOI] [PubMed] [Google Scholar]
- 41.Sheikholeslami M, Ellahi R. Three-dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015;89:799–808. doi: 10.1016/j.ijheatmasstransfer.2015.05.110. [DOI] [Google Scholar]
- 42.Zhang X, Huang H. Effect of magnetic obstacle on fluid flow and heat transfer in a rectangular duct. Int. J. Heat Mass Transf. 2014;51:31–38. doi: 10.1016/j.icheatmasstransfer.2014.01.011. [DOI] [Google Scholar]
- 43.Sheikholeslami M, Abelman S, Ganji DD. Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. Int. J. Heat Mass Transf. 2014;79:212–222. doi: 10.1016/j.ijheatmasstransfer.2014.08.004. [DOI] [Google Scholar]
- 44.Ghofrani A, Dibaei MH, Hakim Sima A, Shafii MB. Experimental investigation on laminar forced convection heat transfer of ferrofluids under an alternating magnetic field. Exp. Therm. Fluid Sci. 2013;49:193–200. doi: 10.1016/j.expthermflusci.2013.04.018. [DOI] [Google Scholar]
- 45.Sheikholeslami M, Bandpy MG, Vajravelu K. Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3–water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder. Int. J. Heat Mass Transf. 2015;80:16–25. doi: 10.1016/j.ijheatmasstransfer.2014.08.090. [DOI] [Google Scholar]
- 46.Rashidi MM, Kavyani N, Abelman S. Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties. Int. J. Heat Mass Transf. 2014;70:892–917. doi: 10.1016/j.ijheatmasstransfer.2013.11.058. [DOI] [Google Scholar]
- 47.Jamshed W, Aziz A. Entropy analysis of TiO2-Cu/EG casson hybrid nanofluid via cattaneo-christov heat flux model. Appl. Nanosci. 2018;08:01–14. [Google Scholar]
- 48.Hussain SM, Jamshed W. A comparative entropy based analysis of tangent hyperbolic hybrid nanofluid flow: Implementing finite difference method. Int. Commun. Heat Mass Transf. 2021;129:105671. doi: 10.1016/j.icheatmasstransfer.2021.105671. [DOI] [Google Scholar]
- 49.Jamshed W, Mohd Nasir NAA, Mohamed Isa SSP, Safdar R, Shahzad F, Nisar KS, Eid MR, Abdel-Aty AH, Yahia IS. Thermal growth in solar water pump using Prandtl-Eyring hybrid nanofluid: A solar energy application. Sci. Rep. 2021;11(1):1–21. doi: 10.1038/s41598-021-98103-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hiba B, Redouane F, Jamshed W, Saleel CA, Devi SU, Prakash SM, Nisar KS, Vijayakumar V, Eid MR. A novel case study of thermal and streamline analysis in a grooved enclosure filled with (Ag–MgO/Water) hybrid nanofluid: Galerkin FEM. Case Stud. Therm. Eng. 2021;27:101372. doi: 10.1016/j.csite.2021.101372. [DOI] [Google Scholar]
- 51.Jamshed, W. Thermal augmentation in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar energy application. Energy Environ. 1–44 (2021).
- 52.Shahzad F, Jamshed W, Sathyanarayanan SUD, Aissa A, Madheshwaran P, Mourad A. Thermal analysis on Darcy-Forchheimer swirling Casson hybrid nanofluid flow inside parallel plates in parabolic trough solar collector: An application to solar aircraft. Int. J. Energy Res. 2021;45(15):20812–20834. doi: 10.1002/er.7140. [DOI] [Google Scholar]
- 53.Jamshed W, Nisar KS, Mohamed Isa SSP, Batool S, Abdel-Aty AH, Zakarya M. Computational case study on tangent hyperbolic hybrid nanofluid flow: Single phase thermal investigation. Case Stud. Therm. Eng. 2021;27:101246. doi: 10.1016/j.csite.2021.101246. [DOI] [Google Scholar]
- 54.Jamshed W, Nisar KS, Ibrahim RW, Shahzad F, Eid MR. Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar thermal application. J. Mater. Res. Technol. 2021;14:985–1006. doi: 10.1016/j.jmrt.2021.06.031. [DOI] [Google Scholar]
- 55.Ali K, Faridi AA, Ahmad S, Jamshed W, Khan N, Alam MM. Quasi-linearization analysis for heat and mass transfer of magnetically driven 3rd-grade (Cu-TiO2/engine oil) nanofluid via a convectively heated surface. Int. Commun. Heat Mass Transf. 2022;135:106060. doi: 10.1016/j.icheatmasstransfer.2022.106060. [DOI] [Google Scholar]
- 56.Jamshed W, Eid MR, Hussain SM, Abderrahmane A, Safdar R, Younis O, Pasha AA. Physical specifications of MHD mixed convective of Ostwald-de Waele nanofluids in a vented-cavity with inner elliptic cylinder. Int. Commun. Heat Mass Transfer. 2022;134:106038. doi: 10.1016/j.icheatmasstransfer.2022.106038. [DOI] [Google Scholar]
- 57.Bejawada SG, Reddy YD, Jamshed W, Eid MR, Safdar R, Nisar KS, Mohamed Isa SSP, Alam MM, Parvin S. 2D mixed convection non-Darcy model with radiation effect in a nanofluid over an inclined wavy surface. Alex. Eng. J. 2022;61:9965–9976. doi: 10.1016/j.aej.2022.03.030. [DOI] [Google Scholar]
- 58.Hayat, T., Aziz, A., Muhammad, T. & Alsaedi, A. Darcy-Forchheimer flow of nanofluid in a rotating frame. Int. J. Numer. Methods Heat Fluid Flow (2018).
- 59.Hayat T, Aziz A, Muhammad T, Alsaedi A. Three-dimensional flow of Prandtl fluid with Cattaneo-Christov double diffusion. Res. Phys. 2018;9:290–296. [Google Scholar]
- 60.Ahmed SE. FEM-CBS algorithm for convective transport of nanofluids in inclined enclosures filled with anisotropic non-Darcy porous media using LTNEM. Int. J. Numer. Methods Heat Fluid Flow. 2020;31(1):570–594. doi: 10.1108/HFF-01-2020-0042. [DOI] [Google Scholar]
- 61.Ullah N, Nadeem S, Khan AU. Finite element simulations for natural convective flow of nanofluid in a rectangular cavity having corrugated heated rods. J. Therm. Anal. Calorim. 2021;143(6):4169–4181. doi: 10.1007/s10973-020-09378-4. [DOI] [Google Scholar]
- 62.Khan SA, Nie Y, Ali B. Multiple slip effects on MHD unsteady viscoelastic nanofluid flow over a permeable stretching sheet with radiation using the finite element method. SN Appl. Sci. 2020;2(1):1–14. doi: 10.1007/s42452-019-1831-3. [DOI] [Google Scholar]
- 63.Rehman KU, Qasem M, Qaiser AA, Malik MY, Ahmed MN. Finite element examination of hydrodynamic forces in grooved channel having two partially heated circular cylinders. Case Stud. Therm. Eng. 2020;18:100600. doi: 10.1016/j.csite.2020.100600. [DOI] [Google Scholar]
- 64.Bagh A, Rasool G, Hussain S, Baleanu D, Bano S. Finite element study of magnetohydrodynamics (MHD) and activation energy in Darcy-Forchheimer rotating flow of Casson Carreau nanofluid. Processes. 2020;8(9):1185. doi: 10.3390/pr8091185. [DOI] [Google Scholar]
- 65.Nazir U, Sohail M, Alrabaiah H, Selim MM, Thounthong P, Park C. Inclusion of hybrid nanoparticles in hyperbolic tangent material to explore thermal transportation via finite element approach engaging Cattaneo-Christov heat flux. PLoS ONE. 2021;16(8):0256302. doi: 10.1371/journal.pone.0256302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Qureshi IH, Nawaz M, Abdel-Sattar MA, Aly S, Awais M. Numerical study of heat and mass transfer in MHD flow of nanofluid in a porous medium with Soret and Dufour effects. Heat Transf. 2021;50:4501–4515. doi: 10.1002/htj.22085. [DOI] [Google Scholar]
- 67.Zhao, T. H., Khan, M. I. & Chu, Y. M. Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks. Math. Methods Appl. Sci. (2021).
- 68.Zhao TH, He ZY, Chu YM. On some refinements for inequalities involving zero-balanced hypergeometric function. AIMS Math. 2020;5(6):6479–6495. doi: 10.3934/math.2020418. [DOI] [Google Scholar]
- 69.Zhao TH, Wang MK, Chu YM. A sharp double inequality involving generalized complete elliptic integral of the first kind. AIMS Math. 2020;5(5):4512–4528. doi: 10.3934/math.2020290. [DOI] [Google Scholar]
- 70.Chu YM, Nazir U, Sohail M, Selim MM, Lee JR. Enhancement in thermal energy and solute particles using hybrid nanoparticles by engaging activation energy and chemical reaction over a parabolic surface via finite element approach. Fractal Fract. 2021;5(3):17. doi: 10.3390/fractalfract5030119. [DOI] [Google Scholar]
- 71.Chu, Y. M., Bashir, S., Ramzan, M. & Malik, M. Y. Model-based comparative study of magnetohydrodynamics unsteady hybrid nanofluid flow between two infinite parallel plates with particle shape effects. Math. Methods Appl. Sci. (2022).
- 72.Zhao TH, Chu HH, Chu YM. Optimal Lehmer mean bounds for the nth power-type Toader mean of n=-1, 1, 3. J. Math. Inequal. 2022;16(1):157–168. doi: 10.7153/jmi-2022-16-12. [DOI] [Google Scholar]
- 73.Zhao TH, Wang MK, Dai YQ, Chu YM. On the generalized power-type Toader mean. J. Math. Inequal. 2022;16(1):247–264. doi: 10.7153/jmi-2022-16-18. [DOI] [Google Scholar]
- 74.Iqbal SA, Hafez MG, Chu YM, Park C. Dynamical Analysis of nonautonomous RLC circuit with the absence and presence of Atangana-Baleanu fractional derivative. J. Appl. Anal. Comput. 2022;12(2):770–789. [Google Scholar]
- 75.Ashpazzadeh E, Chu Y-M, Hashemi MS, Moharrami M, Inc M. Hermite multiwavelets representation for the sparse solution of nonlinear Abel's integral equation. Appl. Math. Comput. 2022;427:127171. [Google Scholar]
- 76.Chu YM, Shankaralingappa BM, Gireesha BJ, Alzahrani F, Khan MI, Khan SU. Combined impact of Cattaneo-Christov double diffusion and radiative heat flux on bio-convective flow of Maxwell liquid configured by a stretched nano-material surface. Appl. Math. Comput. 2022;419:126883. [Google Scholar]
- 77.Nazeer M, Hussain F, Khan MI, Rehman AU, El-Zahar ER, Chu YM, Malik MY. Theoretical study of MHD electro-osmotically flow of third-grade fluid in micro channel. Appl. Math. Comput. 2022;420:126868. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.