Abstract
The brain regulates the body by anticipating its needs and attempting to meet them before they arise – a process called allostasis. Allostasis requires a model of the changing sensory conditions within the body, a process called interoception. In this paper, we examine how interoception may provide performance feedback for allostasis. We suggest studying allostasis in terms of control theory, reviewing control theory’s applications to related issues in physiology, motor control, and decision making. We synthesize these by relating them to the important properties of allostatic regulation as a control problem. We then sketch a novel formalism for how the brain might perform allostatic control of the viscera by analogy to skeletomotor control, including a mathematical view on how interoception acts as performance feedback for allostasis. Finally, we suggest ways to test implications of our hypotheses.
Keywords: Interoception, Allostasis, Predictive processing
1. Introduction: the functions of the brain in the body
Imagine that you are learning to play dodgeball as a beginner. You stand with the other players, divided into two teams, and when the game begins you need to pick up a large inflated ball from a pile in the middle and hit a member of the other team with it. As you run, throw, dodge, catch, and reach, your muscle cells require metabolic fuel in the form of molecules such as oxygen and glucose, which must be conveyed to those muscle cells via the blood. Your vascular system must deliver and distribute blood with speed, bringing nutrients and removing metabolites. Despite rapid muscle movements generating waste heat, your body temperature must remain within a narrow, viable range. As blood circulates more quickly throughout your body, your lungs must also increase the rate with which they breathe oxygen in and carbon dioxide out.
Playing a simple game of dodgeball, then, requires your brain to continually coordinate the systems of your body. At the same time, your body sends sensory information about internal events up the spinal cord and vagus nerve to the brain. It is standard practice in neuroscience to distinguish the brain’s “physiological sense of the condition of the body” (interoception (Craig, 2002, 2015; Quigley, Kanoski, Grill, Barrett, & Tsakiris, 2021)) from the collection of sensory modalities that inform the brain about the world outside the body (exteroception).
Interoception includes, but is not limited to, the brain’s modeling of the sensory signals from innervated visceral organs. Nociception, temperature, and C-tactile afferent-mediated (affective) touch on the skin are also considered interoceptive modalities, by virtue of their conveyance of sensory inputs to the brain via unmyelinated or lightly myelinated ascending fibers in the lamina 1 spinothalamic tract (Craig, 2002, 2009, 2015). A broad view of interoception also includes modeling chemosensation from within the body’s interior, such as changes in the endocrine system (Chen et al., 2021), changes in the immune system (Dantzer, 2018), and changes in the digestive system and gut (de Araujo, Schatzker, & Small, 2020; Muller et al., 2020). For simplicity’s sake, however, this paper will treat all these systems as “visceral”.
Viscerosensory signaling (i.e., the ascending signals from the sensory surfaces inside the body and the skin) informs the brain of the state of the body in an ever-changing and only partly predictable world. Since sensory signals themselves are ambiguous and noisy, this poses an inverse problem for the brain, one of inferring causes (the state of the body) from effects (the ascending viscerosensory signals). The brain solves this problem by means of an internal model (McNamee & Wolpert, 2019). Psychologists refer to the internal model, including interoception, by many terms, including memory (Buzsaki & Tingley, 2018), belief (Schwartenbeck, FitzGerald, & Dolan, 2016), perceptual inference (Aggelopoulos, 2015), unconscious inference (Von Helmholtz, 1867), embodied simulation (Barsalou, 2009), concepts and categories (Barrett, 2017), controlled hallucination (Grush, 2004), and prediction (Bar, 2009; Friston & Kiebel, 2009). Regardless of what it is called, the brain is hypothesized to construct a dynamic model of its body in the world (Barrett & Simmons, 2015; Hutchinson & Barrett, 2019). In this paper we will use the terms prediction, simulation, and concept.
The process of building and refining an internal model based on viscerosensory signals does not, in and of itself, accomplish the brain’s most basic task. This task is to maximize the energy efficiency of bodily functions, to “anticipate changing needs, evaluate priorities, and prepare the organism to satisfy them before they lead to errors” (page 4, Sterling, 2012), a process called allostasis (for further discussion on allostasis, see Sterling & Laughlin (2015); Schulkin & Sterling (2019)). Concurrent evolutionary (Cisek, 2019) and neuroanatomical (Barrett & Simmons, 2015; Chanes & Barrett, 2016; Barrett, 2017) evidence suggests that exteroceptive sensory signals, and the internal models anticipating them, contextualize and support motor control (McNamee & Wolpert, 2019). In a similar way, viscerosensory signals provide online feedback for allostasis, and interoceptive internal modeling subserves allostatic visceromotor control (Barrett & Simmons, 2015; Chanes & Barrett, 2016; Kleckner et al., 2017; Barrett, 2017). Many lines of evidence suggest the same conclusion: the brain is predictively regulating the body, which is a problem of motor control rather than of perceiving the world. It is a problem of regulating the body along a desired trajectory to achieve efficiency.
Existing formal models of interoception and body regulation (such as those reviewed by Hulme, Morville, & Gutkin (2019) and Petzschner, Garfinkel, Paulus, Koch, & Khalsa (2021), as well as recent works such as Unal et al. (2021)) have either formulated allostasis as a prospective decision-making problem (without considering how those decisions are enacted) or as a motor control problem (without considering where motor commands come from). Additionally, rather than treat metabolic efficiency as the objective, they discuss homeostasis, the regulation of bodily variables to fixed set points with fixed tolerances for error. While many interpretations allow for regulation to take place preemptively (see Carpenter (2004)), homeostasis is still assumed to correct deviations from a fixed set-point (Sterling, 2014). In addition, homeostasis is not well suited to deal with variation in demand on bodily systems across contexts and time, variation that has now been well-documented (e.g. (Mrosovsky, 1990; Cabanac, 2006; Woods & Ramsay, 2007; Kotas & Medzhitov, 2015)). This paper aims to fill this gap by proposing an initial formal model of allostatic regulation. In the process, it will connect existing accounts of motor control based on internal models (Kording & Wolpert, 2006; Gillespie, Ghasemi, & Freudenberg, 2016; McNamee & Wolpert, 2019) and accounts of brain function based on feedback control (Pezzulo & Cisek, 2016; Pezzulo, Donnarumma, Iodice, Maisto, & Stoianov, 2017; Maeda, Cluff, Gribble, & Pruszynski, 2018) to the brain’s regulation of the body’s internal environment.
This paper’s formal model of allostasis draws from control theory, a discipline widely employed in both systems biology and engineering. Control theory deals with driving dynamical systems to move (approximately) along a certain desired trajectory, despite physical disturbances to those systems that might drive it off that trajectory. Control theory also makes explicit the question of what the desired trajectory is, how the trajectory might be physically realized, and how one system can drive another to follow a more desired trajectory rather than a less desired one. This paper describes an approach to formally modeling regulation of the body that retains compatibility with previous empirical (e.g. Kleckner et al. (2017); Young, Gaylor, de Kerckhove, Watkins, & Benton (2019)) and theoretical (e.g. Pezzulo, Rigoli, & Friston (2015); Corcoran & Hohwy (2017); Petzschner et al. (2021)) investigations, while building upon control theory from first principles.
Four sections in this paper connect interoception to allostasis. Section 2 establishes how interoception enables the brain to estimate the physiological efficiency of the body in the present moment, which is precisely what it needs to know to evaluate and refine actions. Section 3 then introduces control theory and explains its applications in physiology, motor control, and decision making; these provide the conceptual tools for modeling how interoception informs allostasis. Section 4 applies the principles of control theory to derive a novel formal model of how the brain might estimate the desirability of physiological trajectories and make prospective regulatory decisions. Finally, Section 5 synthesizes the previous three sections to explore the direct implications of the proposed formalism. Appendix A provides a glossary of terms; Appendix B.1 provides mathematical details related to Section 3; and Appendix C.1 provides mathematical details related to Section 4.
2. Interoception: modeling the body, estimating its efficiency
This section takes up the question of how interoception offers performance metrics for visceromotor regulation. Many interoceptive modalities consist of viscerosensory signals whose values must remain within specific ranges conducive to efficient bodily function and survival (making these signals different from exteroceptive sensory signals in this regard). A core assumption is that the brain, as part of allostasis, estimates how efficiently physiological processes can enable or support needed changes in resource levels (Schulkin & Sterling, 2019). Towards that end, Section 2.1 differentiates two types of viscerosensory variables: those that represent quantities of resources (called regulated resources) and those that represent rates 1 at which processes act (called controlled processes) .2 Section 2.2 applies these concepts to the well-studied controlled process of the carotid baroreflex, which the brain must modulate by central command to meet oncoming demand for the oxygen, glucose, etc. in the blood. This subsection suggests that the brain predicts ongoing fluctuations in physiological efficiency. Section 2.3 considers a more complex regulatory setting, in which several physiological processes act on a common metabolic resource in different ways, and generalizes the proposed notion of physiological efficiency estimation to this more common case. Finally, Section 2.4 discusses how efficiency estimation in interoception could enable the brain to constructively evaluate a rich variety of predicted bodily conditions without requiring a modular, purpose-specific “reward” system.
The discussion of control theory in Section 3 then will use the concepts described here. In Section 4 these concepts will undergird a mathematical formalism for allostatic decision making.
2.1. Regulated resources and controlled processes in physiology
Regulated resources are kept relatively stable over time. Examples include blood glucose and core body temperature. By contrast, a non-regulated resource such as blood alcohol (ethanol) does not have its level stabilized by the body in most contexts. Insofar as a regulated resource like blood glucose represents a physical quantity3 or a substance (like glucose), its quantity cannot change instantaneously. Regulation of resources does not have to move levels towards a specific set point,4 and in fact, many can freely vary over a range of possible values without regulatory response. Such a range is called a settling range, since the level of a resource might settle anywhere in the range without provoking a regulatory response.
A regulated resource remains (relatively) stable over time thanks to the adaptive change of one or more controlled processes. Controlled process rates are the rates at which physiological processes operate. These regulatory processes contribute to the relative stability or change in regulated resources over time. Examples of controlled processes include sweating and shivering, while an example of a physiological change that is not a controlled process is when body temperature increases as a result of the body being in direct sunlight. The rates of controlled processes can speed up or slow down within a broad range by altering energy expenditure. Where a controlled process falls within its operating range will determine its effect upon the regulated resource to which it is coupled. Controlled processes do not have to affect the underlying regulated resource directly by a single causal mechanism; they can have their effect via other controlled processes (Box 1).
Box 1. Illustration by example.
Returning to the dodgeball example, the full range of physiological processes maintaining a person’s ability to play would include the metabolic necessities and byproducts carried in the blood itself: oxygen, glucose, and carbon dioxide chief among them. These can be viewed in terms of the functional categories delineated above. The levels of oxygen, glucose, and carbon dioxide in the blood, at any given moment, are called regulated resources. The demand for metabolic inputs by the muscles then can be considered a controlled process. In the specific case of the muscles, their metabolic uptake changes the circulating levels of oxygen, glucose, and carbon dioxide. In addition, blood pressure is a controlled process which subserves the maintenance or replenishment of the regulated resources. The heart rate and levels of autonomic activation (in both branches of the autonomic nervous system) then also function as controlled processes, modulated to indirectly keep the regulated resources in the desired range.
In evolutionary terms, controlled processes contribute to the fitness of the organism by responding to changes in the relevant underlying regulated resource to keep that variable within a viable range. In mathematical terms, changes in controlled process rates can be modeled as functions of regulated resource levels. However, those controlled processes also themselves have limited ranges of possible action. The limited ranges of both regulated resources and controlled processes can be predicted and modeled in terms of capacity curves, which are the topic of the next section.
2.2. Predicting and modeling the ranges of regulated and controlled processes
Both the heart rate and blood pressure must increase during aerobic exercise, as noted in the dodgeball example. If you were to try to play dodgeball at a resting level of blood flow, your muscles quickly would become fatigued and you would be unable to move (for a more detailed discussion, see Sterling & Laughlin (2015)). Your brain must therefore direct the sympathetic branch of your autonomic nervous system to increase its outflow, including increasing blood pressure via vasoconstriction .5 Under resting conditions, the baroreceptor-heart rate reflex would normally counter any rise in blood pressure by slowing the heartbeat. However, with exertion, your blood pressure and heart rate both must increase to support the needed increase in blood flow required by your exercising muscles. To accomplish this specific change, your brain modulates the response of your baroreceptor-heart rate reflex (Potts, Shi, & Raven, 1993, 1995), shifting the entire function relating a change in your blood pressure to a change in your heart rate (Ogoh et al., 2002). The alterations enable redistribution of blood to meet the new demand so that you can run to avoid the ball or throw the ball at someone else.
However, blood pressure is a controlled process, not a regulated resource. It must shift in order to stabilize the regulated resources of oxygen, glucose, and carbon dioxide concentrations in the blood. It therefore lacks a set point to which the brain will regulate the baroreceptor-heart rate reflex, the heartbeat, or other variables affecting the blood pressure. Although the controlled process regulating the blood pressure can and does shift its rate with time, that rate can only rise or fall so far before reaching physical limits, after which further modulation of the baroreceptor or the heartbeat will have no additional significant effect. The baroreflex’s responsive range can be defined as the range between where the controlled process (the blood pressure) effectively cannot decrease further (the threshold value point) and where it cannot increase further (the saturation value point .6
Threshold and saturation points partly define curves that are derived from functions which physiologists commonly use to model the connection between perturbations and regulatory responses, usually naming them response curves (e.g., Ogoh et al. (2005)) or transfer functions. The term capacity curves will be used to emphasize the fact that while such curves can shift over time, in any one instant they represent the current range of limited regulatory resources available to an organism. The terms threshold and saturation will also be used for the levels of the regulatory responses (plotted on the vertical axis) of a capacity curve, rather than the levels of the perturbing stimulus (plotted on the horizontal axis).
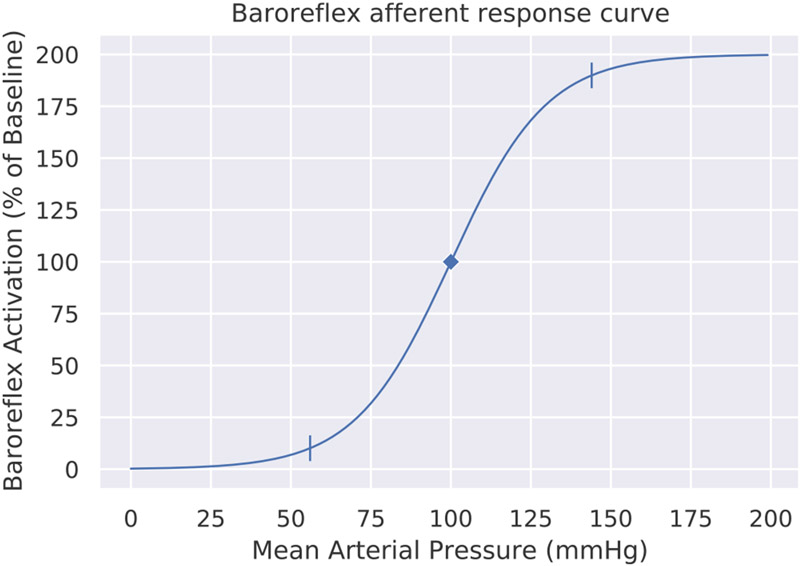
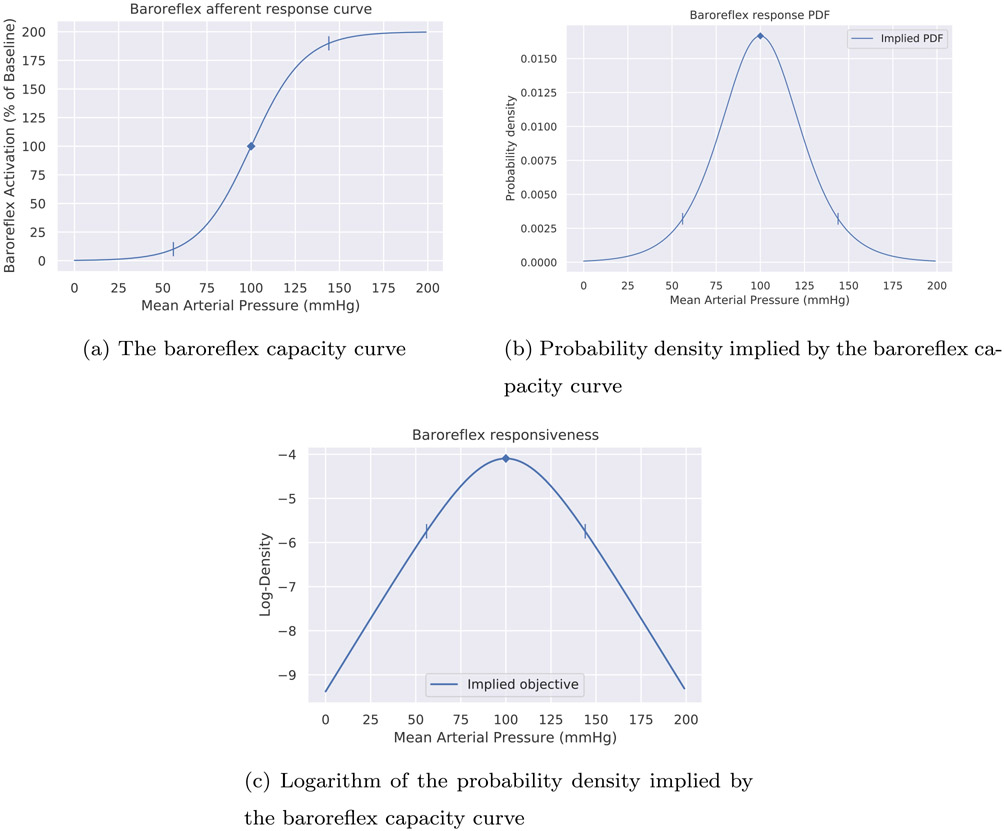
Fig. 1 shows an example capacity curve for afferent activity in human baroreceptors. The left tick marker shows the threshold value, and the right tick marker shows the safturation value. A parameter called the gain specifies the relative slope of the curve throughout its range, determining where the threshold and saturation values will fall. The mean arterial blood pressure (horizontal axis) is a controlled process, and so the baroreflex activation (vertical axis) is also a controlled process, one which only affects the underlying regulated resources (e.g., blood glucose, blood oxygen, etc.) indirectly.
Fig. 1.
Capacity curve for baroreceptor afferent firing, taken as a pedagogical example from Heesch (1999). As the curve flattens in either direction, the baroreflex can no longer respond proportionally to changes in blood pressure. The tick markers show the threshold value (the fifth percentile of response) and the saturation value (the 95th percentile of response) on the horizontal axis.
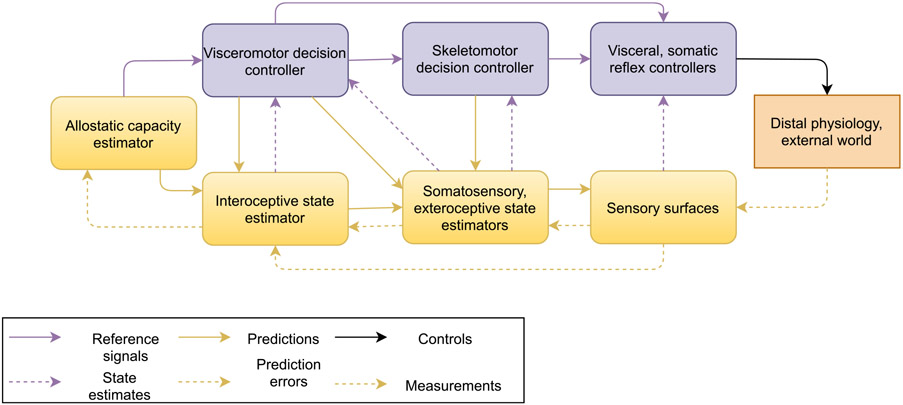
Mathematically, an ideal small change in the blood pressure will lead to a certain ideal small change in baroreflex activation .7 The operating point is where this potential response is greatest. For a symmetrical capacity curve such as that of the baroreceptor-heart rate reflex above, the operating point will lie in the center of the curve. Fig. 2 depicts the operating point with a diamond marker and the potential response around that point as a yellow dotted line. Physiologists often employ the sigmoidal form displayed here for a capacity curve because it provides a good empirical fit to data (see McDowall & Dampney (2006), Dampney (2016)).
Fig. 2.
Capacity curve from Fig. 1 above (blue), with the linearized response (orange) around the operating point (blue diamond marker). The diamond marker denotes the point of optimal responsiveness, or operating point. Responsiveness is optimal when the tangent line has maximal slope around the current blood pressure. Regulating to optimal responsiveness requires either keeping current blood pressure near the operating point, or relaxing the baroreflex’s gain to widen the curve. The latter sacrifices performance (slope) at the operating point but provides greater resilience against uncertainty and perturbations. Note that the operating point refers to the point on the horizontal axis.
The capacity curve in Fig. 1 has mathematical form
| (1) |
and its parameters will take values according to the figure. These values include the response range R (from lower to upper asymptote), the lower boundary B on the response, the operating point x = μ, and the gain k. The variable x on the figure’s horizontal axis represents the mean arterial blood pressure, while the variable y on the figure’s vertical axis represents the baroreflex activation as a percentage of the resting mean. For the figure, the parameters have the values
Eq. (1) defined y, the baroreflex activation, as a function of x, the mean arterial blood pressure. Elementary algebra allows the equation to be solved for x or y as a function of an intermediate quantity u ∈ (0, 1) called the quantile,
| (2) |
| (3) |
| (4) |
These equations outline the form of a generative model: a procedure for probabilistically predicting observed variables in terms of unobserved variables. μ, k, R, B, u serve as unobserved variables, which are sampled from a prior probability distribution not dependent on data. These variables are plugged into the equations to generate predictions for the observed variables: mean blood pressure x and baroreflex afferent activation y. Together, the prior and the likelihood can form a posterior probability distribution, which defines the probabilities of different values for the unobserved variables given the observed ones. In the brain, any internal generative model with similar structure to the above would likely obtain its probability densities for the unobserved variables from its general knowledge of the body in the world, rather than starting with an uninformed prior.
The proposal here has an unusual feature: the equations for x (the mean arterial blood pressure) and y (the baroreflex activation as a percent of baseline) are in terms of the quantile variable u. The quantile variable uniformly represents the relationship between the blood pressure and the baroreflex activation, irrespective of changes in the capacity curve’s operating point μ and gain k. The quantile depends only on the functional form of the capacity curve, not on the parameters. The distance u(x) − u(μ) (i.e., the relative distance between the current value of x and the operating point) therefore provides a time-independent performance metric for the regulatory task of the baroreceptor-heart reflex. Capacity curves change all the time due to variation in their underlying physiological systems (see plot of arterial pressure over time in Bevan, Honour, & Stott (1969), reprinted in Sterling (2012)), but quantiles will retain the same meaning no matter the current parameter values. This supports high regulatory flexibility, a concept often proposed by physiologists as an adjustable set point (Cabanac, 2006).
Any point on any capacity curve can be written in terms of quantiles, because capacity curves represent physical responses with finite ranges. Insofar as controlled process responses have the bounded form described above, they can potentially be described in terms of capacity curves, with mathematical description similar to that given above (although usually more complex in the details). Insofar as this remains empirically true, interoceptive internal modeling (Barrett & Simmons, 2015) could be described, mathematically, as estimating capacity curves over time. The brain could potentially model those capacity curves in terms of quantiles without loss of generality, and those quantiles would have a clear regulatory interpretation.
Overall, if the brain’s internal model were to infer capacity curves as a part of interoception, then a variety of sites in the brain would have to generate predictions, and integrate prediction errors, regarding both regulated resources and controlled processes. These sites would have to receive afferent viscerosensory signals to which to compare efferent predictions. The brain would have to generate efferent predictions for each capacity curve’s key parameters (e.g., operating point, gain, boundary, and range), and combine those parameters with an efferent prediction of the present state’s quantile representation. These would generate interoceptive predictions of viscerosensory stimuli: the regulated resources and controlled processes related by capacity curves. Afferent viscerosensory signals would confirm or correct these predictions, and thus correct or confirm the estimated performance metric u(x) − u(μ).
The process of correcting and/or confirming predictions will usually entail spending a sizable amount of energy just on neural firing to update the various predictions (Theriault, Young, & Barrett, 2021). On top of that, the brain also will have to spend energy to reconsider and re-plan current behavior. Imagine an internal chest pain during a game of dodgeball, when you know you haven’t been hit: it could be heartburn, or it could be a heart attack. Whatever the cause, the brain will have a metric of physiological efficiency with which to determine how to spend resources on updating predictions and behavior, so as to optimally keep regulated resources within the responsive ranges of their corresponding controlled processes.
2.3. Modeling the viable ranges of multiple controlled processes to support multi-system regulation and coordinated action
Unlike the simple regulatory relationship between blood pressure and heart rate, many regulated resources in the body cannot be tightly controlled by a small number of effectors. To return to the dodgeball example, the full range of physiological processes maintaining a person’s ability to play would include the metabolic necessities and byproducts carried in the blood itself: oxygen, glucose, and carbon dioxide are chief among them. In the specific case of the muscles, their metabolic uptake changes circulating levels of oxygen, glucose, and carbon dioxide, which are regulated resources that must remain within viable ranges. Heart rate, blood pressure, and the level of activation in both branches of the autonomic nervous are controlled processes that the brain modulates in service to the maintenance or replenishment of the regulated resources. Next, we focus on blood glucose as a regulated resource, with glucagon as the controlled process enabling secretion of glucose into the blood and insulin as the controlled process enabling removal of glucose from the blood.
Emerging theoretical (Saunders, Koeslag, & Wessels, 1998, 2000) and experimental (Sohn & Ho, 2020) evidence suggests that blood glucose levels are not actively defended at a biologically hard-coded set point any more than heart rate is. Instead, glucagon and insulin activity balance each other’s effects to bring the blood glucose to a point within its settling range (a settling point) with glucose entering the blood after the person ingests food and glucose then crossing from the blood into other bodily tissues to support their function. Recent evidence suggests that when glucagon stimulates insulin production in β-cells in the pancreas, it acts to suppress overshoot of the blood glucose level (Garzilli & Itzkovitz, 2018). This suggests that uptake of glucose into the blood from ingested food could plausibly act as the passive variable of a settling-point regulation model (Speakman et al., 2011). The rate of glucose uptake into tissues from the blood (which leads to insulin secretion) is plausibly a function of glucose availability in the blood.
Settling-point dynamics require either that a controlled process be regulated to decline proportionally to the current level of the regulated resource, or that outputs be regulated to increase proportionally to the current level of the regulated resource. Speakman et al. (2011) give the example of a water reservoir, with water as the resource and outflow from the reservoir as the controlled process. If the depth of the reservoir grows higher due to rain, so will the volume of outflow. The depth of the reservoir stabilizes when the incoming rain and the outgoing outflow over a period of time equal each-other.
In the body, both of these forms of regulation can and do happen: they are the job of the brain (Filippi, Abraham, Yue, & Lam, 2013). The brain may operate as an additional hierarchical level of control, actively balancing and minimizing the necessary metabolic control effort by preemptively regulating intake and uptake of glucose through behavior. Thus, uptake of glucose by the muscles during a game of dodgeball results in a fall in blood glucose and a corresponding increase in secretion of glucagon (Hall & Hall, 2020). Glucagon acts to cause the release of glucose into the blood (from liver cells). In the event of glucose overshoot (i.e., excess levels in blood), insulin will be secreted to restore blood glucose into its settling range. The brain also registers a “cost” of the glucagon release because it required energy expenditure (both in synthesis and secretion), an expenditure that could instead have been spent on the dodgeball game, had the glucose level been more actively maintained. The reverse can occur when the blood contains a surfeit of glucose stock, which then must be taken up into other tissues for storage or usage.
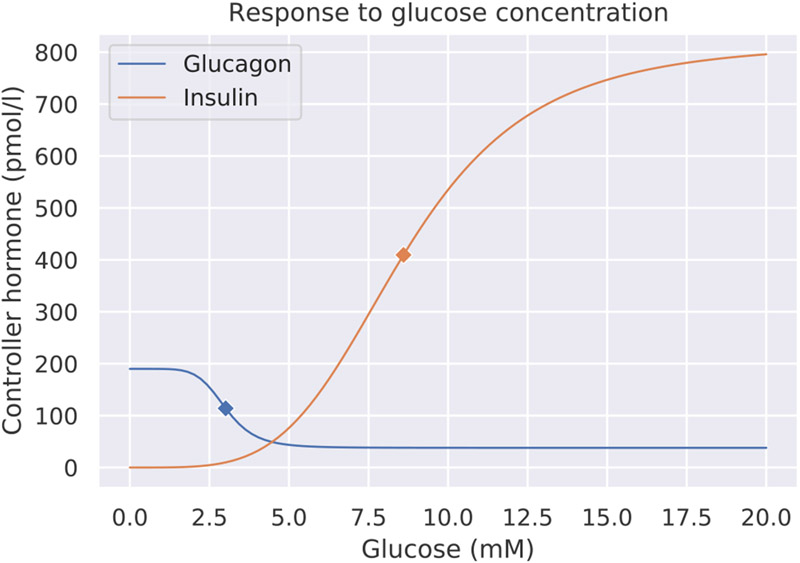
Mathematical modeling studies suggest that the inflection (operating) points on the generalized sigmoidal curves (generalized capacity curves) for glucagon and insulin can be found at 3.01 millimolar (mM) and 8.6 millimolar (mM) respectively, quite close to the lower and upper limits of normal human blood glucose (König, Bulik, & Holzhutter, 2012). Fig. 3 shows plots of the resulting functions, which can be interpreted as capacity curves. The inflection points are shown by the diamond markers, and by definition, each inflection point is a local optimum of regulatory responsiveness. If glucagon and insulin have their greatest responsiveness at the limits for hypoglycemia and hyperglycemia respectively, then regulation of glucose by behavior will aim to avoid straining either of the two hormones’ capacity curves, effectively keeping blood glucose in the normoglycemic range.
Fig. 3.
Capacity curves for glucagon (blue) and insulin (orange) responses to glucose levels in the blood, measured in millimolars. The diamond markers show the respective operating points (3.01 mM for glucagon, 8.6 mM for insulin) of the curves, and the space between those two markers denotes the potential settling range for blood glucose content.
Derived from König et al. (2012).
Evidence from existing studies (Filippi et al., 2013; Morville, Friston, Burdakov, Siebner, & Hulme, 2018; Zimmerman et al., 2016) suggests that chemo-sensory cells in the circumventricular organs and certain nuclei of the hypothalamus, which detect glucose, may be well-described as predictively modeling such generalized capacity curves. This kind of functionality may extend not only to insulin and glucagon, but to other paired (tandem) controlled processes in the endocrine system, such as leptin and ghrelin (Morville et al., 2018). Afferent hypothalamic firing can be interpreted as sending prediction errors to other parts of the forebrain (Chen & Knight, 2016; Morville et al., 2018) thereby signaling an unanticipated metabolic change, and potentially updating the brain’s internal model as described by these capacity curves. Each such capacity curve and the current point upon it could then motivate some mode of behavior: a predictable mixture of glucagon, ghrelin, and other similar signals could be well-described as motivating consumption behaviors (e.g., a shift in autonomic activity towards greater relative sympathetic nervous system activation, exploration of the environment, etc.), while a predictable mixture of insulin, leptin, etc. could be well-described as motivating satiety behaviors (e.g., a shift towards relatively greater parasympathetic activity, reduced motor activity, etc.).
Similar paired controlled processes seem to appear in a variety of regulatory “modalities” throughout the body, ranging from autonomic activity on the heart (Berntson, Cacioppo, & Quigley, 1991) to blood glucose (Filippi et al., 2013) (as above) to adiposity (Speakman et al., 2011) (in the form of leptin and ghrelin). Evidence also suggests that the brain can combine these signals when they operate in tandem to regulate common behaviors (Zimmerman & Knight, 2020). Allostasis may employ a generalized control motif of having paired peripheral controlled processes, which sometimes work together to drive regulatory behavior in one direction (e.g., a reciprocal mode of sympathetic increase and parasympathetic decrease which both drive the heart rate to increase), but can also “antagonize” each other’s effects (such as when both the sympathetic and parasympathetic branches coactivate, producing a heart rate that is the sum of these two countervailing forces, each driving the heart rate in a different direction). Interoceptive modeling in the brain also may employ these motifs. Such general motifs in interoceptive processing could provide a domain-general mechanism for quantifying regulatory imperatives in interoceptive internal models. This may provide greater flexibility in both physiological regulation and behavior than a centrally enforced set point can provide, as well as suffering less error against challenges in each direction (see (Saunders et al., 1998, 2000)).
2.4. Viable ranges and capacities could obviate a modular “reward system”
Standard accounts of allostatic regulation describe it chiefly on the physiological level of analysis, attributing allostatic control in the central nervous system to reinforcement learning. As Sterling (2012) writes,
The central representation of “reward” is a brief burst of spikes in neurons of the ventral midbrain that release a pulse of dopamine to the nucleus accumbens and prefrontal cortex. The precise correspondence between a “feeling” and a specific neuro-transmitter is difficult to establish and is probably oversimplified, since many chemicals change in concert. Yet, one imagines that the dopamine pulse evokes momentary relief from flagellating anxiety and a brief sense of satisfaction/pleasure – at last, the carrot.
The picture of “rewards” painted here suggests a modular “reward center” or “reward system” in the ventral midbrain, one whose specialized role is to perform apples-to-oranges comparisons in service to allostasis. However, insofar as the ventral midbrain would function as a “reward center”, the “reward” signals sent to the rest of the brain would not carry contextual information about the bodily needs to which they refer. More recent evidence shows that there is no unique, localized “reward center” or “reward system” in the brain: broad cortical and subcortical brain networks play various roles in reward as a construct (Berridge & Kringelbach, 2015) or an abstract concept in experiments.
Since there is no single brain site that specifically encodes appetitive or aversive reinforcement value, it is useful to reframe discrete “reward” and “decision” systems as a domain-general allostatic control system. Abundant empirical evidence supports such a reframing (Barrett & Satpute, 2013; Hackel et al., 2016), particularly analyses of the default-mode network and the salience network and their subcortical connections (Barrett & Simmons, 2015; Kleckner et al., 2017). Computationally, these networks could implement a formal model similar to what we introduce later in this paper, or they could translate interoceptive information into a teaching signal for a reinforcement learning system, as in Keramati & Gutkin (2014). The domain-generality of interoception provides further theoretical support for the idea that we do not need “mental modules” or “faculty psychology concepts” to understand how a brain works (Barrett, 2009; Lindquist & Barrett, 2012).
If interoceptive processes operate to estimate parameters analogous to operating points and tolerances, then those processes should be able to convey sufficient information to the brain for purposes of regulating the body. The ideas of Section 2.2 and Section 2.3 can be usefully combined here when considering controlled processes that regulate the same underlying resource. From this perspective, interoceptive prediction errors, in the context of decision-making experiments, can be interpreted as learning about “rewards” via “reward prediction errors”. Movement towards an operating point then can be considered a “reward”, and movement away from an operating point a “cost”. Each such movement can be weighted according to the same capacity curve’s gain or inverse-tolerance; this would convey the (momentary, estimated) relative “worth” of adapting to a load on one innervated organ system versus another. Conceived of in a high-dimensional space, such movements can be viewed as “towards” and “away from” trajectories of changing operating points.
Within a view of brain function not based on a modular reward system, the neurotransmitters produced by unmyelinated and lightly myelinated interoceptive nerve fibers (see Carvalho & Damasio (2021)) could play a role in signaling capacity curves. These neurotransmitters, which include dopamine and serotonin, are commonly thought to act as teaching signals for action (Boureau & Dayan, 2011). In support of this suggestion, dopaminergic neurons in the ventral tegmental area in mice (Dabney, Rowland, Bellemare, & Munos, 2018; Dabney et al., 2020; Lowet, Zheng, Matias, Drugowitsch, & Uchida, 2020) have been modeled using a class of mathematical functions that include our capacity curves.
A mathematically sound and biologically plausible account of allostatic control does not require a modular or separate “reward system” in the central nervous system. Rather, it simply requires a brain and a viscerosensory peripheral nervous system to behave as if parameters for capacity curves (describing how adaptable any given state would be to unexpected disturbances) were signaled alongside the location of current physiological states on the corresponding capacity curves. Different physiological needs (say, core body temperature versus blood glucose levels) could then be added, subtracted, compared, etc. by comparing the distance of the current state from the operating point in any given dimension, scaled by the capacity curve’s gain. Our formal model later will make this idea more precise, providing a way to put numbers to such “distances” and “movements”.
2.5. Summary
This section outlined a proposal for how the nervous system could potentially function to coordinate and control organ systems across timescales to provide allostatic regulation of the body. Section 2.2 considered the movement of physiological systems’ response curves (such as the example shown in Fig. 1) as signifying their capacity to adapt to challenge; the idea of matching actual system loads to operating points (along the lines of Fig. 2) provides a foundation for allostatic regulation. Section 2.3 extended the idea of capacity curves to systems based on more behavioral, settling-point regulation; in such systems the brain functions as the top level of a hierarchical control scheme, regulating the lower-level controllers. In Section 2.4 we then reasoned that movement toward or away from the responsive range of a capacity curve can be treated as “reward” or “cost”, respectively, and suggested that this could potentially obviate the need for a dedicated neural circuit or module that specifically calculates the behavioral constructs of “reward” and “cost”. Evidence from cognitive neuroscience supports the view that the brain lacks such modules, suggesting that we may gain empirical and theoretical traction by investigating decision-making constructs from an allostatic point of view. Section 3 will build on these ideas by introducing control theory, and consider the use of control theory in physiological regulation, motor control, and decision-making, as well as discuss the potential for control theory to unify previously disparate views on bodily regulation. Section 4 will build upon these foundations to propose a formalism for allostatic decision making. Embodied decision making includes all three of the forms of uncertainty to which allostatic regulation is subject: uncertainty about what is physiologically efficient, uncertainty about the consequences of movements, and uncertainty about the external world.
3. Control theory: A unifying lens for physiology, motor control, and decision making
Section 2 hypothesized that allostatic regulation can be understood in terms of controlled processes’ responsiveness to perturbation. It introduced capacity curves, responsive ranges, regulated resources, and controlled processes as ways to describe aspects of physiological regulation; it also sketched the functional form of a generative model that could infer capacity curves as latent properties of related interoceptive variables. It then suggested that moving actual physiological states towards the operating points of maximum adaptability, with each movement weighted by the relative gain (inverse-tolerance) of the response capacity, can formalize the functional dynamic of allostatic regulation. However, interoception is perception of the innervated body: it can include sensing allostatic responsiveness of present states of the body, as achieved by past actions, but it cannot produce present and future actions in and of itself. The latter is the role of visceromotor control processes. To investigate how the brain accomplishes visceromotor control, some additional theoretical tools are required.
This section introduces concepts from engineering control theory, and then reviews its applications in the life sciences. These include physiology (Section 3.1), skeletomotor movement (Section 3.2), and decision making (Section 3.3). Section 3.4 will connect future interoceptive states to present movements, illuminating what makes allostatic regulation more energy efficient than homeostatic regulation. The next section will build off the account of control used in physiology to suggest how interoception supports allostasis.
3.1. Control theory for physiology: A reliable body built from unreliable parts
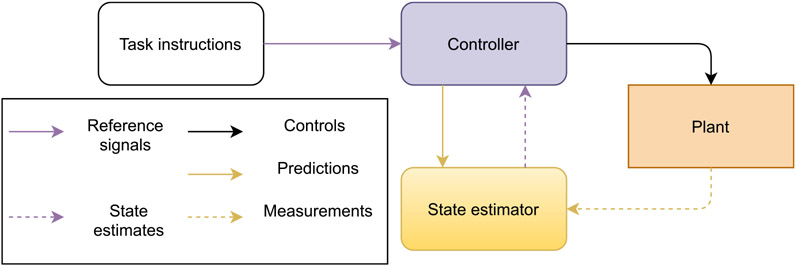
Broadly, control theory deals with driving a physical system towards a desired trajectory, even when the system is built from unreliable or unpredictable parts. Control theorists call the driven system the plant, and its desired trajectory the reference trajectory.8 Generally a plant must be made to conform to its reference trajectory by a driving system called the controller. In controls engineering, these systems are typically thought to be separate physical entities with connections between them, and along these connections the systems transmit signals to each other. The “reference signal” that specifies the reference trajectory goes into the controller, and signals that leave the controller and enter the plant are called controls. Controls affect the state of the plant over time. The reference signal is thought to derive from a source that is external to the system, such as an engineer or a machine operator. Fig. 4 shows an example “block diagram” for an engineered control system.
Fig. 4.
Functional block diagram of a model-based control system. The “plant” (orange) is the object or system whose motion or other behavior is controlled. The “controller” (purple) sends signals (“controls”, solid black arrows) that change how the plant moves, and signals the expected outcome (“predictions”, solid yellow arrow) to the “state estimator” (yellow). The task behavior of the plant is prescribed to the controller by an engineer or machine operator (transparent box), in the form of the reference signal (solid purple arrow). Measurements of the plant output (dashed yellow arrow) feed back to the state estimator to yield updated estimates (dashed purple arrow), which the controller compares to the reference signal to adjust the controls.
A controller functions to steer the plant along its reference trajectory, adapting to external disturbances that would push the plant away from the reference trajectory. From the standpoint of a brain controlling a body, “disturbances” might be thought of as uncontrolled changes in the workings of the body’s internal systems. There is an important distinction between an unpredictable event and a disturbance: unpredictable events can either push a system away from its reference trajectory or towards it, but a disturbance, which may or may not be surprising, is always an event that pushes the system away from its reference trajectory. Thus, a disturbance is always relative to the reference trajectory (Box 2).
Box 2. Illustration by example.
The dodgeball example illustrates the distinction between an unpredicted event and a disturbance. If a player looks across the field and sees a ball heading straight for her, her brain knows and predicts (by means of past experience) when and where the ball is likely to arrive. If she sees another player throw the ball, it will not be surprising (i.e., unpredicted) when the ball heads her way and hits her body. It will, nonetheless, be a disturbance; insofar as her brain estimated the movement of the ball and prepared her body to dodge, if she was unable to move fast enough, she deviated from her reference trajectory. By the same token, if a ball hits her from behind as she is standing still, her brain has made no estimate of its trajectory, nor has it prepared her body to dodge, but the hit remains a disturbance. For the same reason, if she positions herself in a way that enables her to catch, by luck or accident, a ball thrown at her, she has followed her reference trajectory, even though her brain will only register this after processing the ensuing prediction errors.
The whole point of a control system is to adapt to disturbances, and a system can attain much greater robustness and adaptability by using sensors to measure the plant’s actual behavior over time. Control theorists call these measurements the feedback for the controller, and the use of feedback to adjust control outputs is called feedback control. Physiologists recognize feedback control as a ubiquitous feature of bodily function (Carpenter, 2004; Cosentino & Bates, 2011), with endocrine control of blood glucose being a well-studied example (Saunders et al., 1998, 2000). Feedback control is essential because no controller is ever perfect: neither all forms of noise nor all external disturbances can ever be fully accounted for. If the feedback loop (seen in Fig. 4 as the arrows flowing from controller to plant, plant to state estimator, and state estimator to controller) is cut, the controller can no longer receive any information from the plant. The control signals calculated under such circumstances are called open-loop or feedforward controls, or even (somewhat idealistically) plans.
The concepts of control theory can illuminate the anatomy of the baroreflex, the example physiological system described above. For simplicity’s sake, the baroreflex and its components are considered the system in question. Its plant is the organs of the cardiovascular system as innervated by the autonomic nervous system (ANS). Its controller is a comparator circuit in the midbrain, specifically in the nucleus tractus solitarius (NTS) (Zanutto, Valentinuzzi, & Segura, 2010). Its reference signal comes from two sources: over the short term, top-down signaling from the cerebral cortex (which is outside the controller itself), and over the long term, midbrain structures rostral to the NTS, based upon (as yet not fully understood) endocrine signals (Osborn & Foss, 2017). These are compared to the actual blood pressure measured by the carotid and aortic baroreceptors (feedback state estimator). The baroreflex (the controller) adjusts cardiovascular variables to align the measured blood pressure (as sensed by the baroreceptors) with the reference trajectory of operating points (as specified by short-term signaling from the forebrain or longer-term endocrine signaling), by means of the sympathetic and parasympathetic branches of the autonomic nervous system (as control signals).
For a controller to perform well, it must contain some sort of copy or mirror of the plant’s expected behavior, which is referred to as an internal model (Conant & Ashby, 1970; Francis & Wonham, 1976). However, inaccuracies in the internal model limit controller performance (as does an absence of feedback in open-loop control). Internal models serve a dual purpose: to infer past trajectories 9 (including their control signals) on the basis of present or even counterfactual measurements (such as the reference signal) and to estimate future states and measurements10 in the plant on the basis of control signals. Fig. 4 divides these two functions into the components of a control system that they inform: the controller (purple) infers controls from state estimates to track the reference signal,11 and the state estimator (yellow) predicts future measurements on the basis of present control signals, refining those state estimates using measurements.12 Together, internal models predict the future and infer the past in the plant even when plant behavior is subject to process noise and measurements are subject to measurement noise.
Internal models play an important and specific role in control theory (Wolpert & Kawato, 1998; Kawato, 1999). State estimation of future measurements based on present control signals allows the difference between predicted and actual measurements, which is called the prediction error, to be used to measure the accuracy and precision of online control. The state estimator (yellow) can use prediction errors to send updated state estimates (dashed purple arrow) back to the controller. Comparing the updated state estimates to the reference signal then yields a quantity called the control error, on the basis of which the controller can refine the control signals. The process of calculating prediction errors and control errors online, and using them to improve control signals, is called feedback control. Model-based feedback control is widely used and well-known for driving control error to zero over time (a property called stability), particularly when prediction errors are also driven to zero by refining the internal model. This is a property that open-loop planning cannot enjoy, since an open-loop control system does not measure the control error, which amounts to (falsely) assuming it to be zero. An internal model alone only suffices for open-loop, feedforward planning, while control requires feedback.
Controllers also can couple to each other hierarchically: a higher-level controller can send a control signal to a lower-level controller, which functions as the reference signal for that lower-level controller. In turn, the lower-level controller may send a control error signal up to the higher-level controller. The higher-level and lower-level controller also each may have their own state estimators based on their own internal models. The next subsection will address hierarchical control in human motor control.
3.2. Moving the body: The referent control hypothesis
The referent control hypothesis (Feldman, 2015; Latash, 2021) describes the skeletomotor system in terms of a hierarchy of controllers, with higher-level controllers in the brain prescribing reference trajectories to the lower-level reflexes in the spinal cord. These reflexes then compare the actual length of the muscle, as signaled by afferent proprioceptor neurons, to the reference length sent down by the brain, and contracts the muscle to bring the two into agreement (Latash, 2010; Feldman, 2016). Effectively, higher level controllers tell lower ones what trajectory to visit, and the lower ones figure out how to track it successfully, a phenomenon beginning to be considered in engineered (i. e., non-biological) control systems (Merel, Botvinick, & Wayne, 2019).
Cortical regions involved in skeletomotor control (e.g., primary motor cortex, premotor cortices, etc.) also send a copy of the downward-flowing reference signals to somatosensory cortices (called an efferent copy), thereby providing prior predictions to somatosensory regions. These “prior” signals literally change the firing of neurons in somatosensory cortices, preparing them to receive incoming signals from the world based on upcoming skeletomotor movements. This dynamic takes place across all levels of the neural hierarchy, allowing the nervous system to use somatosensory prediction errors as feedback to confirm or correct movement performance; it also allows the nervous system to distinguish reafferent (self-caused) from exafferent (externally caused) sensory signals .13 Through this lens, the brain is considered to act as both a controller (in its visceromotor and skeletomotor functions) and a corresponding state estimator (in its perceptual and simulation functions). Since under the referent control hypothesis, skeletomotor “commands” take the form of descending signals specifying desired lengths and tensions for proprioceptive measurements, the brain’s state estimation machinery in sensory areas therefore can simulate the somatosensory consequences of those descending control signals.
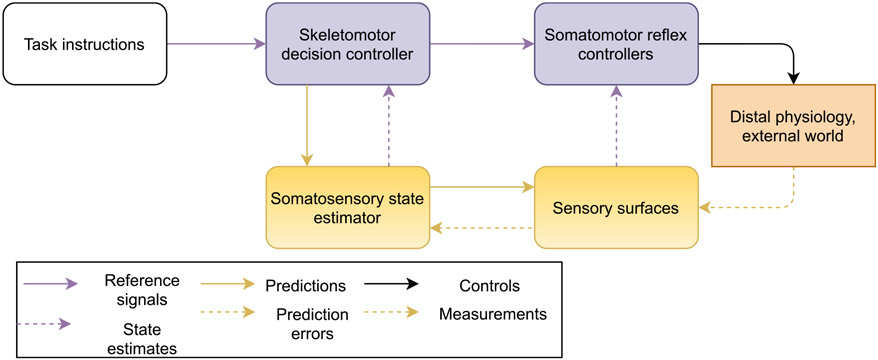
The brain is hypothesized to exploit its internal model of both the body and the local external environment to predictively construct populations of reference trajectories as embodied simulations (Barsalou, 2009). These simulated populations of referent trajectories can also be thought of as action concepts (Barrett & Finlay, 2018; Leshinskaya, Wurm, & Caramazza, 2020) (for similar ideas see also Wolpert, Pearson, & Ghez (2013) and Hickok (2014)). In the brain, motor areas are hypothesized to implement feedforward control with action concepts by decompressing low-dimensional referent trajectories from higher in the neural hierarchy into higher-dimensional referent trajectories lower in the neural hierarchy .14 Decompressive prediction by the brain eventually produces referent coordinates in the highest-dimensional, most redundant system of coordinates: references for individual peripheral stretch reflexes (Feldman, 2015). Each such stretch reflex circuit compares the ascending stimulus from its proprioceptor neuron to its centrally commanded reference, and activates its motoneuron to suppress the difference between the two. The motor system thus can be imagined as a hierarchy of controllers, with higher-level controllers specifying the reference signals for lower-level controllers as their output control signals. In addition to converting signals from the conceptual reference frame of the behavioral task to the concrete reference frames of individual limbs and muscles, this hierarchical structure finesses neural signaling delays to provide fast, accurate control (Nakahira, Liu, Bernat, Sejnowski, & Doyle, 2019). Fig. 5 shows an elegant “outside-in” view15 of the motor control problem, imagined along these lines. Here, an experimenter directs a participant to perform a task, who constructs an action concept from the instructions. This action concept seeds the construction of sensorimotor prediction populations in the skeletomotor decision controller. The skeletomotor controller further unpacks the action concept into an actual body posture and its attendant reference coordinates for muscles, as well as predictions for the somatosensory state estimator. The movements created by the reference coordinates are themselves are stabilized by fast proprioceptive feedback at the level of the individual stretch reflexes in the spinal cord. The hypothesis expressed by the figure assumes that all systems in the body, both somatomotor and visceromotor pathways, serve an externally driven behavioral task.
Fig. 5.
Functional block diagram for an experimental psychologist’s task-oriented view of motor control. The diagram shows a formal logical structure here, at a conceptual level; the boxes and arrows do not map onto the anatomy of the brain or nervous system. In contrast to Fig. 4, this diagram differentiates between skeletomotor (brain) and peripheral (stretch reflex) controllers and between sensory state estimators (brain) and peripheral sense organs (sensory surfaces). The diagram shows an engineering perspective on a psychology experiment, in which the experimenter prescribes a task or behavior to participants, and a participant’s brain then acts as control system to achieve the prescribed behavior. Systems that maintain the body therefore serve systems that move the body, which in turn serve a prescribed behavior.
However, the structure of a motor-control experiment has only limited overlap with the actual structure of motor control as it unfolds in the natural world. An experiment on reaching behaviors involves an experimenter prescribing the reaching task to their participants. A participant’s brain does not function specifically to follow instructions from an experimenter, but rather to regulate their own body. The actual organization of the central nervous system accords better with an “inside-out” view16 of motor function: movement of the body (the somatomotor pathways) serves regulation of the body. For example, in a game of dodgeball, if you unexpectedly step hard on a sharp rock, you (usually) do not purposely impale yourself to stabilize your posture. Rather, you recoil in pain, and the unplanned disturbance of any tissue damage requires you to make a decision about what to do next: excuse yourself to nurse your foot, or play through the pain.
This referent control hypothesis relies upon an important assumption: that once a higher-level controller specifies a reference for a lower-level controller, it can rely on that lower-level controller to successfully enact the desired movement. That lower-level controller stabilizes itself with measurements at a smaller spatial scale, and functions reactively rather than predictively. Neither do the lower-level control systems implemented by proprioceptors and motoneurons integrate information other than proprioception. The stretch reflex receives a signal specifying the referent length for the muscle, compares it to the proprioceptor’s signal of the muscle’s actual length, and fires the motoneurons to contract the muscle if the actual length exceeds the referent length (Box 3).
Box 3. Terminology.
The terms for directions of neural signaling, depending on the implied origin of the signal, are efferent, afferent, and reafferent. Motor neuroscientists refer to efferent signals (flowing from somatomotor cortex down to somatosensory areas, the midbrain, and the peripheral nervous system) as feedforward signals. They then refer to afferent signals, particularly reafferent somatosensory signals, as feedback signals. Since the usage from motor neuroscience agrees with that from control theory, this paper follows that usage.
3.3. Making decisions: constructing future reference trajectories
So far control theory has been presented as it applies to physiology and motor neuroscience. These control mechanisms have largely been local, in the sense that they only drive neural outputs to impact a small, narrow domain: blood vessels and baroreceptors modulating autonomic outflow to reduce the heart rate; proprioceptors in individual muscle spindles driving the stretch reflex. In the stretch reflex, the reference is set by top-down signaling from the brain as part of voluntary movement, and therefore varies widely. The baroreflex displays a similar structure, receiving parameters for its capacity curve via central command.
Reactive control requires reference signals before physiological needs are fully known. In contrast, the brain controls the body predictively, both viscerally and through overt somatomotor behavior. Predictive neural control of the viscera must take into account biological processes that change the body (such as those occurring with development) and cyclical routines such as the wake-sleep cycle. The brain also must coordinate across a variety of physiological demands in the moment, each with its own capacity curve that may change over time. At the same time, the brain is subject to uncertainty from both sensory/measurement noise and process noise in the innervated tissues. Decision making in the brain must therefore operate according to control principles that take into account competing demands over time.
A control theory formulation meeting these criteria is stochastic optimal control (SOC). Stochastic optimal control uses probability distributions over states x to model the effects of both process noise and measurement noise. The goal then is to optimize the probabilistic expectation of an objective function summed over the indefinite future. This expectation of a sum, accounting for both uncertainty and time, is called the value function, and is defined recursively by the Bellman equation. A control strategy is optimal when it maximizes the value function. Since objective functions include terms that quantify the relative tolerance for regulatory error, it supports a wide variety of approximate solution methods to find “good enough” controls, which drive the plant close to its reference trajectory even when noise and disturbances prevent exact reference tracking.
Objective functions generalize the simple comparators often used in classical control; they compare a reference state with an actual state to generate a real number as output. Generally the output value should be monotonically related to the degree of agreement or disagreement between the reference and the actual state. Objective functions with a fixed notional reference state and a fixed tolerance for deviation from that state can model fixed physiological set-points and tolerances, like those found in homeostatic theories of regulation (Box 4).
Box 4. Terminology.
Predictive homeostasis is the hypothesized mode of regulation in which anticipatory decision-making mechanisms maintain regulated resources at fixed set-points with fixed tolerances. Neurally, a homeostatic regulator would consist of a comparator circuit without an incoming signal modulating its reference. Since most existing computational models of visceromotor control and interoception (e.g., (Petzschner et al., 2021; Gu & FitzGerald, 2014)) fall into this camp, we consider them to model allostasis as predictive homeostasis, designed for settings in which long-run set-points and tolerances define the chief control mechanism. This family of models includes certain active inference approaches (Pezzulo et al., 2015, 2018; Corcoran, Pezzulo, & Hohwy, 2020) and homeostatic reinforcement learning (Keramati & Gutkin, 2014). Sometimes in stochastic optimal control, the objective function is not known a priori, and must be learned from samples. This special case is called reinforcement learning (abbreviated as RL). Neuroscientists have studied reinforcement learning (Sutton & Barto, 2018) as a model of how the brain might make decisions over time. Modeling midbrain phasic dopamine signaling with RL has led to a popular approach in computational neuroscience (the reward prediction error hypothesis (Niv, 2009; Colombo, 2014)), and continues to yield novel findings today (Lowet, Zheng, Matias, Drugowitsch, & Uchida, 2020). Notably, these successes rely on a specific way to approximate the value function for behavior over time by comparing predictions generated in the brain to the actual sensory effects of behavior.
Stochastic optimal control, at first glance, might seem unnecessarily complex. Taking an expectation of a sum over time seems almost repetitive: why should the brain not just wait until it arrives to a future bodily state, and then compare it to the corresponding reference using the objective function? This is, after all, precisely how reactive control mechanisms work. What problem is allostatic decision-making in the brain solving that a homeostatic reflex in the body cannot? Reflexive, reactive control under uncertainty carries a hidden assumption: that uncertainty in the moment is equivalent to uncertainty over time, and thus if control mechanisms can compensate for errors in the moment, they can compensate for all errors in the future. When that assumption holds, predictive and reactive control will be equivalent. When that assumption does not hold, stochastic optimal control can yield vastly better regulation than reactive control.
That assumption is called ergodicity, and it amounts (very roughly) to modeling time as having no effect on probability distributions. B.1.1 discusses ergodicity in detail, including its implications for experimental design. B.1.2 also discusses a paradigm for studying the brain as a whole that does assume ergodicity, allowing it to bridge perceptual processing with decision making and motor control. The following material places more emphasis on situations that are not ergodic, which include those with periodic structure, or with irreversible changes over time. Real life is filled with non-ergodic situations in which one must make decisions: the cycles of day and night (and circadian rhythms tracking them) are non-ergodic; processes of development (from childhood to adulthood) are non-ergodic; events like injury and death are non-ergodic. The brain accounts for these non-ergodic realities of life in decision-making processes (Mangalam & Kelty-Stephen, 2021).
One final alternative way to think of SOC is in terms of what a controller needs to model, and which signals into a controller may be subject to noise or disturbance. In a typical control problem, the control engineer “trusts” that she can provide an exact reference signal, while building the controller to be robust to noise and disturbances in the plant. In SOC and RL, the control engineer may not be able to specify the reference signal exactly, but she can provide the controller with encouragement (rewards) or discouragement (costs) for following observed trajectories. “Rewards” thus count as evidence in favor of the plant’s recent behavior following the reference trajectory, while “costs” count as evidence for behavior deviating from the reference trajectory (Friston, Adams, & Montague, 2012). This implies that an optimal controller, viewed from the perspective of Fig. 4 or Fig. 5, has two sources of uncertainty that require two separate state-estimation processes: one for the state of the plant, and another for the reference signal. The next subsection will describe how interoception works alongside somatosensory perception to reduce both of these uncertainties.
3.4. Allostatic control Motivating movements with an interoceptive model
The brain allostatically regulates the body. Accordingly, there ought to be a description of the brain in terms analogous to inferring capacity curves; these can be transformed into objective functions and projected into the future to construct a value function. This value function would allow the brain to take account of the future when deciding what to do now. When the value function successfully predicted instantaneous allostatic capacity curves, it would seem as if the future body prescribed a reference trajectory to the present brain. Since moving the body would predictably change allostatic capacities (i.e., operating points and tolerances) in the future, a “circular causation” of self-organization and autonomy would emerge. Fig. 6 diagrams allostatic regulation using the language of control theory. This figure employs the same visual vocabulary of plants (orange), controllers (purple), internal models (yellow), feedforward signals (solid arrows), and feedback signals (dashed arrows) as the earlier Figs. 4 and 5. Systems that move the body are hypothesized to be in the service of systems that maintain the body (i.e., movement is in service of allostasis).
Fig. 6.
Functional block diagram for a control-theoretic view of allostasis. In contrast to Fig. 5, this diagram shows a closed-loop control system design for autonomous regulation of the body. An experimenter’s desired “task behavior” is replaced by the allostatic capacity estimator, which sends predictions of capacity curves to the interoceptive state estimator and receives prediction errors with which to update its estimates. The updated estimates are issued as a reference signal to the visceromotor controller. This diagram shows a formal logical structure, at a conceptual level; the hypothesis depicted is constrained by the inferred anatomical structures in Barrett (2017) but the boxes and arrows do not map one-to-one onto the anatomy of the brain or nervous system (Lee, Ferreira-Santos, & Satpute, 2021).
Allostatic regulation contains homeostatic regulation as a special case. Allostasis consists of regulating a system’s state to track a reference trajectory, one which fully allows for system states to change over time. Homeostasis consists of regulating a system’s state towards reference points, independent of time. Thus, an allostatic controller can implement homeostatic control by prescribing a reference trajectory as a single, unchanging point, while a homeostatic controller cannot implement allostatic control. This is because homeostasis does not really deal with context. The allostatic trajectory approach allows for the possibility that past behaviors affect the present state and reference. It allows the effect of past perturbations or interoceptive conditions to influence what happens next (Box 5).
Box 5. Illustration by example.
A return to the dodgeball example will ground these ideas. During a game of dodgeball, muscles will demand greater amounts of oxygen and glucose than they had needed during rest. Successfully throwing the ball at an opposing player will require mobilizing both the skeletomotor musculature (“soma”, plant) as well as the internal bodily systems such as the cardiovascular system (“viscera”, plant) across a timescale of tens of seconds to minutes via the visceromotor and somatomotor controllers (purple). We hypothesize that a functional equivalent to an allostatic capacity estimator (yellow) anticipates the need, altering the reference trajectory conveyed as a prediction to the visceromotor controller (purple). The visceromotor controller must then mobilize the cardiovascular system to supply those metabolic necessities via the blood. In this instance, among other adjustments, the visceromotor controller shifts and flattens the baroreflex’s capacity curve (Dicarlo & Bishop, 1992), allowing both vasoconstriction and an increased heart rate to work in tandem to supply more blood flow to the muscles.
Translating the example into the language of Fig. 6, the allostatic capacity estimator (yellow) signals the anticipated demand as a reference trajectory (solid purple arrow) to the visceromotor decision controller. The visceromotor controller decompresses this low-dimensional reference trajectory into higher-dimensional reference trajectories (solid purple arrows) for the skeletomotor decision controller (purple) and peripheral reflex controllers (purple). Simultaneously, the visceromotor decision controller sends efferent copies (downward solid yellow arrows) to the viscerosensory (“interoceptive”) and somatosensory exteroceptive state estimators (yellow) to generate sensory predictions (e.g., predict that the heart rate will be close to the reference). The skeletomotor controller decompresses its own reference trajectory into even higher-dimensional reference trajectories (solid purple arrow) for peripheral reflex controllers (purple); these convey motor signals about where your hands and feet should be, how bent your knees should be, etc. The skeletomotor controller also emits efferent copies to the somatosensory model, which generates sensory predictions regarding the sense data coming from sensory surfaces: the strain of bending the knees, the thump of the heart against the chest, and so on. Finally, the local reflex controllers enact motor controls (solid black arrow) that move the body. Basing sensory predictions on the efference copies enables the resultant measurements at the sensory surfaces (dotted yellow arrow) to generate sensory prediction errors (dotted yellow arrows), which serve as feedback on the timescale of tens or hundreds of milliseconds. This feedback flows through the state estimators to update their state estimates, and these estimates are then signalled to controllers as control feedback. At the far end, updates to interoceptive state estimates generate prediction errors that update the estimated allostatic capacities, thus closing the loop.
3.5. Summary
This section discussed three applications of control theory to studying the body and brain. Section 3.1 described control theory as a whole and discussed its applications in physiology, providing an example of a control system in Fig. 4. Section 3.2 then discussed the study of voluntary motor control in the nervous system. The construct of reference trajectories in control theory finds a close analogue in the referent control hypothesis of somatomotor control, and its application in Fig. 5 shows an engineer’s view of motor control. Section 3.3 discussed the necessity for allostatic decision-making in the brain to take account of changing bodily conditions over time, constructing references based on physiological capacity curves. The next section will apply the concepts from this section to describe a formal model of allostatic regulation.
Before diving into formal modeling details below, it might be helpful to compare and contrast the approach here with a prominent modeling framework: active inference (Friston, Daunizeau, Kilner, & Kiebel, 2010; Friston, Samothrakis, & Montague, 2012). Like many active inference models, the formal model below takes the form of information-theoretic model-predictive control (similar to work such as Williams, Drews, Goldfain, Rehg, & Theodorou (2018) and Nasiriany et al. (2021) in engineering) with a hierarchically-defined objective (similar to Smith, Thayer, Khalsa, & Lane (2017), Pezzulo et al. (2018)). Insofar as such efforts can be considered “active inference”, the formal model outlined in the next section is also an active inference model. Unlike most active inference models in the literature, however (with the exception of Millidge (2020)), the material below considers an indefinite-time or “infinite horizon” control setting. Insofar as the research community prefers for the term “active inference” to refer specifically to formal models derived from the free energy principle (see B.1.2 and Kirchhoff, Parr, Palacios, Friston, & Kiverstein (2018)), with its ergodic assumptions and its unique expected free energy objective, the formal model below is distinct from these traditional active inference models.
4. Allostasis as trajectory-tracking stochastic optimal control
The previous section overviewed and applied control theory to study physiological reflexes, voluntary motor movements, and decision making in the brain. The previous section described stochastic optimal control (SOC) theory as a mathematical formalism capable of flexibly modeling decision making under uncertainty. This section will describe our formal model of allostatic decision making: the Allostatic Path-Integral Control (APIC) model. APIC has a simple idea at its core: just as perceptual concepts serve as internal models of the body’s sensory surfaces (Barrett, 2017; Barrett & Finlay, 2018; Barsalou, 2009), action concepts also serve as internal models of potential behaviors and their predicted outcomes. The brain refines and selects sensory predictions derived from a concept based on their fit to past and present sensory evidence; we suggest that it likewise refines and selects the motoric reference configurations derived from an action concept based on their present and future allostatic value. Section 4.1 derives an SOC objective function from the mathematical form by which Section 2.2 represented capacity curves. Section 4.2 marshals behavioral and ecological evidence of how animals balance and meet their needs over time into a long-run mathematical form. Section 4.3 then sketches a formal model of how action concepts fit into SOC. Section 4.4 describes how to exploit action concepts optimally in feedback control. These last two subsections include the motivations for particular modeling choices.
4.1. Transforming capacity curves into objective functions
Section 3 pointed out that allostatic control poses a decision-making problem: the brain must predict the body’s future needs in the form of a reference trajectory or value function, and move to satisfy those needs before they become acute. This subsection presents a mathematical treatment of capacity curves as objective functions. The resulting objective functions have maxima at the operating points, and have slopes away from the maxima corresponding to tolerances for error. Since this derivation of objective functions applies to arbitrary capacity curves, it can be applied to model a variety of interoceptive modalities.
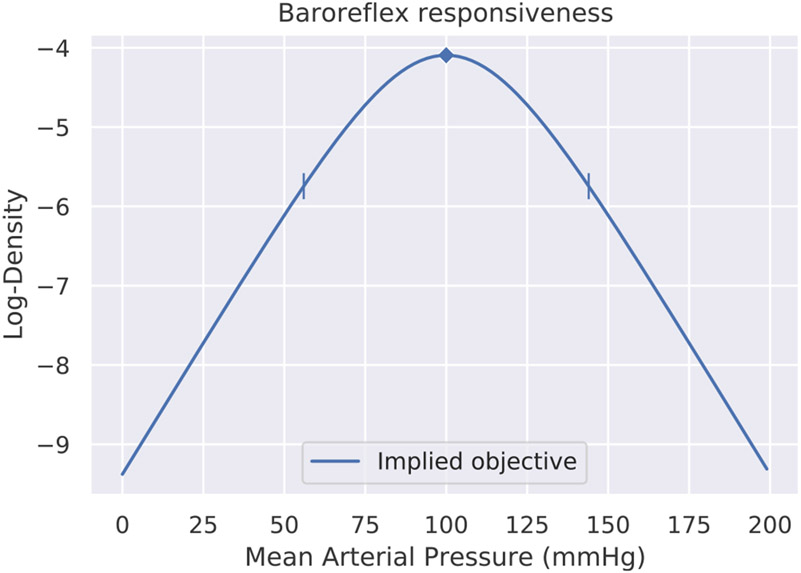
Since any given capacity curve (such as the one in Fig. 1 above) reaches a maximum value on the vertical axis, it can be divided by its maximum Y-value to “normalize” it to range between zero and one. Once normalized in this way, it can be interpreted as a cumulative distribution function (CDF) from probability theory. This is in fact precisely what Srinivasan, Laughlin, & Dubs (1982) did to interpret the firing of retinal neurons in flies as a form of predictive coding (for an excellent example, see their Fig. 1). The derivative (instantaneous slope) of a CDF yields a probability density function (PDF). This is the more familiar way of representing a probability distribution, where height on the vertical axis corresponds to likelihood, but for a PDF derived from a capacity curve, it represents relative responsiveness to perturbation. We will call such a distribution a reference distribution. Fig. 7 therefore shows the result of normalizing and differentiating the capacity curve in Fig. 2 to obtain its corresponding PDF. The density function’s graph clearly shows that the baroreflex’s capacity to adapt to changes in mean arterial pressure (MAP) degrades the further MAP moves from the peak at 100 mmHg. The rate at which it degrades, and the response elicited, is governed by the baroreflex gain. The gain of a capacity curve thereby defines the relative importance of deviations from the operating point, and thus corresponds neatly to precision in predictive coding. The greater the baroreflex gain, the more sharply curved the PDF around its operating point, and the greater the response mobilized by any deviation from the operating point. Section 2.3 described how the capacity curves in settling-point physiological controllers will often have inflection points that lie somewhere other than the center, thus being horizontally asymmetrical. This property translates neatly to probability densities: PDF’s need not be horizontally symmetrical either. Bodily responses such as inflammation or nociception could have highly asymmetrical capacity curves, with the operating point even potentially being located near a zero value of the PDF.
Fig. 7.
The probability density function (PDF) corresponding to the capacity curve shown in Fig. 1, with the tick-marks delineating threshold (left) and saturation (right) values. Probability density here corresponds to responsiveness to perturbation, not to an empirical frequency of events.
For analytical convenience, we take the practice from Todorov (2006) of using a log-density (the logarithm of a PDF) as an objective function, rather than the PDF itself. The operating point then continues to appear as a local maximum, while the gain determines the cost of movement away from the operating point, or the value of movement towards it. Fig. 8 shows the objective function (log-density) corresponding to the original baroreflex capacity curve, and the formal model below will use such log-densities as objective functions for optimal control. Fig. 9 further clarifies the relationship between the various forms of capacity curve by showing all three alongside each-other. Assuming that the brain’s internal model takes the form of a generative model (here with discrete time), the internal states of this generative model can be numbered as xt for natural numbers (that is, discrete counting numbers) , with some number L of levels of model hierarchy. We will later define a specific graphical model that suits these notations.
Fig. 8.
Logarithm of the probability density shown in Fig. 7, with the operating point shown as a diamond marker and tick-marks delineating threshold (left) and saturation (right) values. Probability density here corresponds to responsiveness to perturbation.
Fig. 9.
The complete set of functions employed to model the baroreflex response. The second comes from taking the derivative of the first and normalizing it, and the third comes from taking the logarithm of the second.
We define the PDF corresponding to a physiological capacity curve as the reference distribution for the value on the horizontal axis of the PDF. These reference distributions have parameters, which we name , and denotes their PDF’s. will denote the corresponding log-density objectives.
Our allostatic decision-making model focuses on optimizing a construct called the instantaneous capture rate (given informally in Eq. (5)), which we write as J(xt, xt−1). Since the model here works with discrete time steps, the instantaneous capture rate is defined as a function of the transition between one time-step and another. The instantaneous capture rate consists of a rate of resource intake minus a rate of effort expenditure. We suggest that we can identify the instantaneous capture rate with a rate of movement along capacity curves, which we will write mathematically below in Eq. (6).
| (5) |
The single-step capture rate is formalized as
| (6) |
Eq. (6) shows the difference between the log-density objective across two consecutive time steps. Since the reference distributions defining the log-density terms (at the lowest level, ) correspond to physiological capacity curves, movement towards an operating point will contribute positively to this equation, while movement away from an operating point will contribute negatively. Increases in responsiveness of controlled processes that handle metabolic inflow (such as glucagon) can be interpreted as “intake”, while decreases in responsiveness of controlled process that handle metabolic outflow (such as insulin) can be interpreted as “effort”. Section 4.2 below will present evidence for how the instantaneous capture rate is aggregated over time in foraging behaviors, particularly in feeding behaviors and the energetic efforts undertaken to enact them.
4.2. Optimal foraging theory suggests a functional form for allostatic control
Mathematically, combining momentary reference signals into a value function requires first writing those reference signals as objective functions, and then combining them into a long-run functional form. The subsection above derived a form of objective function that expresses movement towards and away from the operating point of a capacity curve. This subsection will identify a long-run functional form for allostatic decision-making that is based upon experimental findings.
Neural and ecological evidence supports the hypothesis that animals’ intake and outflow optimize a long-run functional form called the global capture rate (Stephens & Krebs, 2019; Shadmehr & Ahmed, 2020). Ecologists such as Stephens & Krebs (2019) define the global capture rate as the sum of all metabolic intake minus all effort expended, over the total time devoted to a behavior. Meanwhile, neuroscientists have used the global capture rate to help relate dopaminergic neuronal signaling (Kobayashi & Schultz, 2008) and animal behavior (Daw & Touretzky, 2000) to the discounting of rewards in decision-making tasks.
This formalism assumes a given behavior has a finite length in time of T, and that all intakes and efforts are zero at time t = 0. The global capture rate is then written
| (7) |
The global capture rate is thus the average over time of the individual “intake minus effort” instantaneous capture rates of Eq. (6) (Shadmehr, Huang, & Ahmed, 2016). Since the global capture rate is defined by dividing by time, it exists for any length of time, long or short. In the real world, intakes or rewards often only accrue at the conclusion of a behavioral episode, while efforts or costs necessarily accrue throughout the behavior as energy is spent. Averaging over time treats rewards and costs equally whenever they occur during a behavioral episode. The global capture rate helps make behaviors commensurable, even when they take different lengths of time or accumulate rewards at different points in time.
Defining the global capture rate with respect to an internal model p (x1:T∣T) entails generating trajectories of length T, conditioned upon an initial state x0 as context,
| (8) |
This is an indefinite-time form of the global capture rate that generalizes Eq. (7) from settings with a known beginning and end to arbitrarily long time scales.
4.3. Feedforward control with generative action concepts
This subsection will consider a formal model in discrete time, with arbitrary state-spaces and sensory observations. Specifically, we write sensory observations as indexed by discrete timesteps, t in ot, and do similarly for other variables. The formal model here incorporates the hypothesis that the brain’s internal model stretches across a hierarchy of time-scales (Kiebel, Daunizeau, & Friston, 2008). However, we restrict our description to L = 4 hierarchical “levels” (matching the sensory surfaces, somatosensory and exteroceptive state estimators, interoceptive state estimators, and allostatic capacity estimators in Fig. 6). We do not hypothesize a one-to-one mapping between functional structure and neuroanatomy, and so the structure we have given here may not match neuroanatomy – but, the graphical model is formulated with an eye to keeping it consistent with the biological details of allostasis. We consider it a first attempt to build a functionally coherent model that can then be critiqued and refined to match anatomical and empirical evidence.
The complete state of the generative model at a specific timestep t is written symbolically as
| (9) |
under the assumption that outcomes ot are observed, latent states track the unobservable state of the body, and parameterize reference distributions used below in Eq. (6). (as above) parameterizes a reference distribution for ot, and at models the closed-loop control action of motor reflexes; parameterize reference distributions for respectively. , as the highest level latent state, has no reference distribution. The factorization of control into hierarchical levels is based upon the referent-configuration control scheme from Section 3.2, so as to match as closely as possible what is known about somatomotor control.
A behavioral trajectory is written as contextualized by (conditioned upon) an initial state x0. This initial state corresponds to the beginning of a behavioral episode, within which interoceptive outcomes will be considered commensurable. The following states from time 1 until time T, sampled from a generative model pθ with parameters θ, are then written as
| (10) |
| (11) |
along with the corresponding approximate global capture rate. The internal model simulates a population of potential behavioral trajectories x1:T, and uses them to estimate the global capture rate for the simulated behavior. This quantity will play a role in the feedback control formalism described later. Fig. 10 summarizes the proposed model structure as a probabilistic graphical model,17 with L = 4 for purposes of exposition.
Fig. 10.

A hierarchical generative model capturing multiple timescales and reference distributions at each level. Without addressing empirical questions about neural hierarchies, here we employ a model with L = 4 levels to match Fig. 6. For l ∈ [1. . L − 1] each node denotes an unobserved latent state, and each represents parameters of a reference distribution for . ot represents observed sensory outcomes, and at represents the closed-loop control actions generated by motor reflexes. Arrows between random variables denote conditional dependencies. Arrows stretch further to the right when they denote change over longer time scales.
Table 1 summarizes the key notations, including the random-variable names and time indices. C.1.1 specifies the various distributions for our graphical model and control problem in detail.
Table 1.
Random variable names used in our APIC model.
| t | Discrete time-step index |
|---|---|
| ot | Sensory observations (external and visceral) |
| Unobserved states constructed by the internal model | |
| Parameters to a reference distribution | |
| a t | Control actions emitted by peripheral reflexes |
| x t | A complete model state for time t |
| p θ | Feedforward generative model with parameters θ |
| qϕ | Feedback generative model with parameters ϕ |
We do not claim that our graphical model accurately captures the anatomy of the brain (or the function of the entire brain). It captures reference-based sensorimotor control across a hierarchy of timescales, a single feature shared with the brain (Kiebel et al., 2008). There can be no one-to-one mapping between computational theories and neuroanatomical findings (Edelman & Gally, 2001; Friston & Price, 2003). We instead account here for what we already know about the brain that goes into our model, without assuming any one-to-one mapping of brain structure and function. In the actual brain, the hierarchy of timescales is also a hierarchy of dimensionalities: information is more concrete and higher-dimensional at the bottom of the hierarchy, more abstract and lower-dimensional at the top (Finlay & Uchiyama, 2015). Dimensionality reduction up the hierarchy entails compression up the hierarchy, so that state estimates in the higher-level variables have greater precision. Evidence from machine learning shows that learning to control a system in terms of a low-dimensional compressed representation (also called a “latent space”) provides greater performance with fewer episodes of experience compared to controlling the same system in terms of its raw measurements (Watter, Springenberg, Boedecker, & Riedmiller, 2015; Chua, Calandra, McAllister, & Levine, 2018; Becker-Ehmck, Karl, Peters, & van der Smagt, 2020). Since the visceromotor, premotor, and motor cortical areas that implement action concepts employ low-dimensional, compressed multimodal summaries rather than raw measurements (Satpute & Lindquist, 2019), we conjecture that they may benefit from the sample efficiency of latent-space control approaches. Finally, computational modeling has been directly applied in experiments that supported the presence of hierarchical Bayesian models in interoception Smith et al. (2020); Smith, Kuplicki, Teed, Upshaw, & Khalsa (2020); Harrison et al. (2021) (Box 6).
Box 6. Terminology.
The language of generative models in the brain is typically used in the context of predictive processing approaches to brain function. These approaches typically label as a “generative” model the processes producing efferent signals in sensory areas of the cortex, while suggesting that the processing of reafferent signaling in those same areas encodes a “recognition” model (Ramstead, Kirchhoff, & Friston, 2020). The efferent and reafferent signals themselves are typically then labeled “predictions” and “prediction errors”. We will continue to use “feedforward” for efferent signals (or computations) and “feedback” for reafferent signals (or computations).
Stochastic optimal control with a generative model requires (by definition) solving or approximating the recursive optimization problem called the Bellman equation. For a time-averaged problem, the Bellman equation will contain a term for the objective function J(xxt, xxt−1) at a particular state, a term for the (estimated) global capture rate of a behavior as a whole, and a recursive term. It is written as a definition of the optimal value function
| (12) |
However, this formalism only describes how to plan optimal behavior or learn an optimal policy (a mapping from states to actions) through forward simulation. This equation does not describe how to integrate afferent sensory information as control feedback; it also imposes the great computational difficulty of finding exact solutions to a recursive optimization problem. The following subsection will discuss a way to tackle both of these limitations, yielding a more neurally plausible form of stochastic optimal control.
4.4. Feedback control with generative action concepts
Standard theories of optimal decision-making ignore the variability of choice outcomes, while evidence shows that human behavior takes the level of risk into account (Braun, Nagengast, & Wolpert, 2011; Niv, Edlund, Dayan, & O’Doherty, 2012). This makes normative sense from the perspective of embodied action: the brain has to transform even seemingly clear and simple decisions (“reach to the left”) into noisy, high-dimensional motor movements (“change these and those muscle spindles’ referent lengths and sensitivities”). Risk and uncertainty remain part of a movement even once the body has actually enacted it, since the distal body and world remain only partially observable via the sensory surfaces. This subsection will consider what these facts imply for the combined problem of decision-making and motor control faced by the brain. After these considerations, this subsection will give a combined formulation of risk-sensitive decision making and feedback-stabilized motor control.
Neural firing contains stochastic noise (Faisal, Selen, & Wolpert, 2008), and so finding an exact maximum of a difficult recursive problem quickly seems implausible. Even if the brain could find the exact maximum quickly, noise in the motor system imposes its own cost factors into the decision value (Manohar et al., 2015). Experimentally, human and animal behavior show meaningful variability (Gallivan, Chapman, Wolpert, & Flanagan, 2018) across every level of task behavior, while Eq. (12) says that any given task ought to correspond to a unique optimal way to act. Behavior also displays meaningful variation attributable to predictive uncertainty in people’s internal models, both about the task goals themselves (McBeath, Shaffer, & Kaiser, 1995) and about appropriate sensorimotor strategies (Scholz & Schoner, 1999). A risk-neutral theory can explain neither of these effects, since the Bellman equation uses expectations to average away model-based uncertainty.
In fact, when sensory signals carry only partial and ambiguous information about the state of the body and environment (as they always do in the real world), Eq. (12) will have to be solved anew every time an xt is updated based upon sensory feedback. This is because the equation does not take into account the difference between planning ahead with a forward model and feedback control based on reafferent sensory signals.
Here we propose instead a feedback-control formalism which takes this difference into account. This formalism quantifies the deviation of the closed-loop, feedback-stabilized behavior from the open-loop, feedforward action concept. It balances this deviation with the present and future allostatic value of an online behavior to determine what to do. The formalism begins by updating the state estimate for each time-step t as the sensory signals ot become available. A probability model qϕ with parameters ϕ, conditioned upon the sensory observations and initial state, then acts as a feedback controller18 in updating state estimates and motor references
| (13) |
The updated state estimates, being based upon the observations ot, may significantly differ from the state estimates emitted by the feedforward action concept. This deviation imposes a penalty term in the objective function, called an information divergence (specifically, the Kullback-Leibler or KL divergence). The resulting function
| (14) |
trades off between the allostatic responsiveness objective of Eq. (6) and adherance to the “planned” population of predictions given by the feedforward action concept. The first term measures success at physiological regulation, while the second term penalizes the feedback controller qϕ for deviating from the action concept pθ or suffering sensory prediction errors. When movements result in sensory outcomes very close to those predicted under the feedforward action concept pθ, a low information divergence, that action concept can be considered robust in the face of sensory feedback.
Readers familiar with predictive processing (Friston & Kiebel, 2009; Clark, 2013; Bogacz, 2017) and active inference (Friston et al., 2010; Ramstead et al., 2020) will recognize the form of the above equation as a negative free-energy or a variational lower bound (see Millidge, Tschantz, & Buckley (2021) for discussion on the variety of such bounds). Such objectives can typically be written out and interpreted in several equivalent ways, each of which can come with its own intuitions. There are arguments for the computational (Chatterjee & Diaconis, 2018) and thermodynamic (Still, Sivak, Bell, & Crooks, 2012) efficiency of minimizing this specific divergence in the course of neural processing, but to date the available evidence does not rule out other, more complex information divergences for penalizing feedback correction of movements.
The long-run value function (Eq. (12)) for a control problem can be used to derive an equation for the optimal feedback controller. By treating the pre-planned action concept as a kind of probabilistic “prior belief” about the behavioral trajectory and the decision-value of the behavior as a “likelihood function” linking the action concept to the objective function in Eq. (14), Bayes’ rule (see Appendix C.1 for details) will yield the optimal feedback controller:
| (15) |
Eq. (15) links pre-planned action concepts (the “priors” pθ(xt+1∣xt)) to online feedback (the “likelihood” in a probabilistically optimal way (by treating them both as densities, multiplying, and normalizing the result). A system that can represent and simulate from this equation can (approximately) predict the way that an “optimal agent” (with the assumed objective function) ought to move.
Taking a generative modeling perspective, the controller defined in Eq. (15) treats the original action concept pθ as a prior, and conditions on the long-run value of the potential future state xt+1 as a selection criterion. It is therefore risk-sensitive and information-seeking. The term that would typically correspond to model evidence now corresponds to the expected exponentiated decision value of the present state xt.
Substituting the augmented objective (, Eq. (14)) and the analytical expression for the optimal feedback controller (above, Eq. (15)) into the Bellman equation (Eq. (12)) will yield
| (16) |
Now the intractable recursive term in the equation is . Finding a way to replace this term will yield a more (computationally) tractable problem. The information divergence term in provides just such a way, since it can be written as precisely the difference between the intractable “hard” maximum under q*ϕ and the more tractable “smooth maximum” under the preplanned action concept. In symbols
| (17) |
and so the penalty’s first term, when substituted into Eq. (16), will cancel the intractable recursion. Only the second term of the penalty will remain, yielding a smooth maximization problem across whole action trajectories. The equation can then be solved (once again, see Appendix C.1 for details) to write the value function without recursion as
| (18) |
| (19) |
This function contains an exponentiated sum over timesteps, where each timestep’s addend has the form of an advantage function,
| (20) |
This measures the relative decision value of transitioning into state xt relative to an estimated global capture rate for the initial context x0. Viewed another way, it measures how well the ongoing feedback-controlled behavior has performed, relative to the predicted average for the prior action concept (Box 7).
Box 7. Terminology.
A sum of a function across timesteps, under a probabilistic expectation, is often called a “path integral”. Since the value function in APIC can be expressed in terms of a path integral, APIC falls within the class of SOC methods known as path-integral control (Kappen, 2005).
Jensen’s inequality, commonly employed in predictive processing, allows moving the logarithm inside the expectation, at the cost of yielding a lower bound to the optimal value function rather than an expression for it. Doing so cancels the exponential function inside the expectation. The lower bound is written in terms of an arbitrary feedback controller qϕ and the sum of advantage values obtained over the course of the behavior,
| (21) |
It may seem obvious that any behavioral returns are less than or equal to the best possible returns. The implication of having a proper lower bound, however, is that any process for maximizing the value lower bound does in fact maximize the optimal value function by proxy. This includes the kind of computations19 which predictive processing theorists posit the brain can in fact perform (Bastos et al., 2012; Bogacz, 2017) to incrementally improve its action concept pθ and its feedback controllers qϕ.
This concludes the description of the Allostatic Path-Integral Control (APIC) model. Since APIC employs action concepts and context states x0, it only requires planning and adjusting behavior in context (e.g. from timesteps 1 to T), despite optimizing a “global” (indefinite) capture rate (Eq. (8)). Since it employs “smooth” maximization rather than a “hard” recursive maximization, it can accommodate the sensitivity of behavior to risk. APIC follows in the tradition of modelers such as Belousov, Neumann, Rothkopf, & Peters (2016), Mitchell et al. (2019), and Piray & Daw (2019), who consider the specific problem of making embodied decisions when sensory feedback contains noise and a ground-truth model of task dynamics is not available.
Summary
This subsection has detailed a formal model, called the Allostatic Path-Integral Control (APIC) model, for how the brain can realistically achieve allostatic regulation of the body in an online setting. APIC assumes that the brain starts with an action concept describing a potential behavior, and tries to maximize the allostatic returns on that behavior while keeping the online (feedback-stabilized) behavior close to the original plan. Incorporating an action concept, and penalizing deviation from it, provides an explicit expression for the optimal feedback controller. The infinite-horizon, average-objective setting for this stochastic optimal control model captures the time-averaging behind the global capture rate (i.e. Eq. (7)). This model can take advantage of neural stochasticity to optimize an objective function defined over a hierarchy of scales of space and time, allowing for both high-level and low-level behavioral control.
4.5. Summary
This section derived an objective function, formal problem setting, and formalism for allostatic control based upon the paradigm of path-integral control. Section 4.1 connected physiology’s ever-shifting capacity curves (such as Fig. 1) to probability density functions (shown in Fig. 7), and used that connection to define an objective function. Section 4.2 described a problem setting for decision making that accounts for much available evidence about how animals make allostatic decisions in ecological settings. Section 4.3 then sketched the formal definitions needed to apply path-integral control to a generative model; gave a generative model (Fig. 10) with the hierarchical structure that the literature suggests is found in the brain; and derived a stochastic optimal control formalism based on simulations of potential futures by an internal model. Section 4.4 then shifted the perspective to feedback control, obtaining a risk-sensitive and tractable formalism.
The next section will conclude the paper by discussing the implications of applying stochastic optimal control theory to allostatic physiological regulation in general, and the specific hypotheses for the brain implied by APIC.
5. Discussion: Interoception stabilizes action and constructs allostatic references
If the brain is an allostatic regulator, then its most basic task is to anticipate the body’s physiological needs and prepare to meet them before they arise. This paper provided a unified interpretation of allostasis in terms of brain-body interaction and neural computations. This unified interpretation is built around stable circular interactions between the brain and body, and control theory has provided language with which to describe the mechanisms stabilizing those interactions.
Each section of this paper addressed a particular circular interaction, and below we connect each with its implications for psychological investigation. Section 5.1 will discuss what the Allostatic Path-Integral Control (APIC) model in Section 4 implies about brain function. Section 5.2 will discuss what control theory brought to the study of physiology, motor control, and allostatic decision-making (with reference to Section 3). Section 5.3 will discuss interoception and capacity curves in light of Section 2’s overview of interoception. Each subsection will end with a paragraph giving specific predictions made by our view of allostasis in the brain and body.
5.1. Viewing the brain as an allostatic optimal controller
The Allostatic Path-Integral Control (APIC) model in Section 4 implies a number of specific hypotheses, beyond those generic to stochastic optimal control. This subsection will situate those commitments within the broader literature on formal modeling of motor and decision functions. We will first describe commitments shared with other modeling approaches, then describe less common commitments, and finally we will describe several commitments that are unique to the APIC model.
On the theoretical side, the APIC model shares a number of modeling choices with active inference models, perhaps enough for APIC to be considered an active inference model of sorts. APIC employs (normalized) probability densities as its objective function to provide a “common currency” for different “rewards” and “costs” (Friston et al., 2015; Morville et al., 2018; Allen, Levy, Parr, & Friston, 2019; Kobayashi & Hsu, 2019; Millidge et al., 2021; Tschantz et al., 2021). As in active inference models based on the free-energy principle (such as Stephan et al. (2016)), the objective in our APIC model is a function of (among other things) precision terms, which specify the relative worth of a change in one variable versus another. APIC and active inference both optimize motor behaviors via a variational lower bound on a long-run objective, and APIC is likely compatible with the neural process theories (Friston, Fitzgerald, Rigoli, Schwartenbeck, & Pezzulo, 2017) that have been forwarded to ground active inference in the brain. These commitments place APIC alongside active inference, in contrast to most reinforcement learning models of decision-making (e.g., Niv (2009)).
APIC also shares a number of features common to other predictive processing paradigms, beyond active inference. Most importantly, it uses a probabilistic, generative internal model. There is a broad family of predictive processing approaches to neural function, and a proposal for a neural implementation for APIC could depend on the neurocomputational details of any of them (e.g. Boerlin, Machens, & Deneve (2013), Spratling (2017), Kadmon, Timcheck, & Ganguli (2020)). These details are beyond the present scope, but, some important features can be highlighted. Predictive processing models must construct potential bodily movements from some distribution of possibilities, and neural evidence (Gallivan, Logan, Wolpert, & Flanagan, 2016; Barrett, Quigley, & Hamilton, 2016) suggests that neural representations may not summarize probability distributions in a small, fixed number of parameters. Therefore, to understand how movements are constructed, we must understand the entire distribution, and not just its summary statistics. APIC can accommodate this, and is therefore compatible with neural process theories of predictive processing not based on sufficient statistics.20
Unlike most work in predictive processing, APIC is designed from first principles to solve a combined problem of both decision making and motor control, rather than to address perceptual or cognitive problems.21 Unlike other predictive processing models, in APIC the objective is optimized by making capacity curve precisions small (implying greater resilience to challenge) rather than large (implying reduced resilience to challenge). The most elementary of the APIC model’s first principles are: the body, when considered as a set of coordinated systems, can only perform one action at a time, whereas the brain can imagine many possible actions. The study of embodied decision-making in neuroscience begins from these assumptions (Pezzulo & Cisek, 2016) and an emerging body of evidence suggests that the brain controls the body by keeping many possible actions “in the running” until sensory feedback forces an irreversible decision (Cisek, 2007; Cisek & Kalaska, 2010; Buzsaki, 2019; Cisek, 2019). The APIC model works this way by default, thanks to its roots in path-integral control (Kappen, 2005).
Finally, the APIC model implies some hypotheses that are (to our knowledge) unique. These derive largely from the APIC model’s combination of the neuroanatomy of Barrett (2017) and the feedback control formalism of Thijssen & Kappen (2015). Active inference modeling typically interprets qϕ as an approximate posterior belief. APIC re-conceptualizes qϕ as a feedback controller. This interpretation comes from the path-integral control (PIC) literature (Thijssen & Kappen, 2015; Kappen & Ruiz, 2016; Menchon & Kappen, 2019), whereby the same mechanism can both stabilize movements (keeping qϕ close to the original action concept pθ) and maximize decision value. APIC’s unification of inference with feedback control handles uncertainty about the consequences of movements (optimal feedback control); uncertainty about the state of the body and the world (predictive processing); and uncertainty about the reference or objective of action (reinforcement learning) in a single framework. The first term of APIC’s objective function is physiological: it represents the responsiveness of controlled processes in the body, as inferred through interoception. The second term of APIC’s objective function separately quantifies the difference between planned and actual movements (including visceromotor movements).
How would an implementation of APIC map onto the brain? We did not map functional descriptions in control theory terms to specific anatomic or functional assemblies in the brain, but nevertheless, research does suggest that brain systems can be described as enacting internal modeling, feedback control, and decision making. For example, the hippocampal-entorhinal complex is often considered to construct a predictive “cognitive map” (Stachenfeld, Botvinick, & Gershman, 2017) out of sequential episodes (Buzsaki & Tingley, 2018), which helps evaluate a value function for a control problem (Daw, Gershman, Momennejad, Russek, & Botvinick, 2017). The cerebellum may help exploit reafferent and ex00AFferent sensory prediction errors as online corrective feedback for movements (Wolpert, Miall, & Kawato, 1998; Hull, 2020), although the role of the cerebellum in visceromotor control requires more study to understand the mechanisms involved. Regions in the brain’s default mode network are thought to help construct state estimates (e.g., Buckner (2012), Barrett (2017)) and implement allostatic control (Kleckner et al., 2017). Evidence for common functional gradients across the cerebral cortex, cerebellum, and hippocampus suggests that future empirical studies should apply common computational paradigms to different brain regions (Katsumi et al., 2021).
Predictions
The APIC objective function proposes a theory of how behavioral reinforcement and allostatic control interact. This theory has implications for how a primary (unlearned) reinforcer would arise. According to APIC, a primary reinforcer arises when the dynamics of a controlled physiological process align with those of its capacity curve (as a function of an underlying regulated resource). If a primary reinforcer arose directly from a regulated resource, then the specific objective-function formulation we have suggested would be falsified; however, this would not necessarily falsify APIC as a computational unification of decision making and motor control for action concepts. Likewise, only the objective-function would be falsified if future work identified a modular“reward” or reinforcement systems in the brain-i.e. a reward system that operates separately from decision making and motor control. Alternatively, empirical tests for controlled variables (Marken et al., 2001; Yin, 2013) could determine which physiological parameters (if any) elicit global, behavioral responses to disturbance.
5.2. The body and brain through the lens of control theory
Section 3 introduced the concepts of control theory by describing their applications in peripheral physiology, motor control, and decision-making. This subsection first summarizes the theoretical “point of view” obtained from control theory, and then reviews several of the key ways in which control theory can be used to clarify brain-body interactions.
Control theory provides a way to conceptualize how physiological systems can function reliably as a whole, despite being built from unreliable parts. The dominant mechanism used by control theorists to ensure such stability is feedback, in which measurements flow from the underlying system being regulated (the plant) to the system doing the regulating (the controller). This constant flow of information from the plant to the controller helps the controller move the plant according to a desired trajectory, expressed physically as a reference signal. Fig. 6 shows the process of allostatic control in the body using the language of control theory.
Voluntary skeletomotor movements are controlled by central commands from the brain. The brain signals movements and bodily postures in terms of proprioceptive referent configurations, which then constrain the motor reflexes to minimize the difference between the reference and the actual prioceptive signal. This form of referent control extends all the way up through the brain, and in the form of posterior state estimates (see Fig. 6) provides an explanation for reafferent connections from sensory to motor areas of the cerebral cortex. We have hypothesized in this paper that referent control is shared between skeletomotor and visceromotor modalities .22 Visceromotor reflexes, such as the carotid baroreflex, are responsible for controlling blood pressure in response to central commands from the brain. These visceromotor reflexes may use feedback control mechanisms that are similar to those used by skeletomotor movements. This means that visceromotor reflex circuits, like the baroreflex, may only provide a single kind of feedback: the stabilization of movements, i.e., via the short loop between distal physiology, sensory surfaces, and peripheral reflex controllers (as in stretch reflex proprioceptors). Fig. 6 shows how visceral sense data ascend, in effect, to become ex00AFferent interoceptive prediction errors, which combine with efferent interoceptive predictions to generate posterior state estimates. From the posterior interoceptive state estimates, the brain can estimate the allostatic capacities of the many controlled processes in the body. Optimizing the responsiveness of these allostatic capacities then finally “closes the loop” and provides a reference signal, constraining the central command signals from the brain to the motor reflexes.
Predictions
Above we have hypothesized that the visceral nervous system (including visceromotor efferents, interoceptive afferents, and the autonomic nervous system) operates, in its motor operations, via referent control. This would imply that interoception can be anatomically segregated into motoneuron-interneuron-interoceptor reflexes that stabilize visceral “movements” (as in somatosensory modalities), and non-motor interoceptive endpoints, which serve another functional role. Rather than stabilizing a (visceral) “movement” that is constrained from the top down by central command, we suggest these visceral sense data may instead constrain the central commands themselves. Alternatively, empirical tests for controlled variables (Marken et al., 2001; Yin, 2013) could determine which physiological parameters elicit local, reflexive responses to disturbance.
5.3. Interoception and capacity curves
Section 2 introduced much of the physiology fundamental to this paper. It provided the distinction between regulated resources and controlled processes, and then described interoception as the predictive internal modeling of such variables. The section then described how capacity curves can quantify both the relations between variables and the objective of allostatic regulation. This subsection first clarifies the distinction between the actual state of the body and the interoceptive predictions constructed by the brain, and then elaborates on how that distinction affects the behavioral construct of “reward” in psychology.
This paper maintained a careful distinction between visceral sense data, interoceptive predictions, and (re)afferent viscerosensory signals. The distinction must be carefully navigated, because it is not yet known where, neurophysiologically, the distinction between raw viscerosensory data and prediction errors can be made. Most previous work on interoceptive predictive processing has assumed that peripheral interoceptive neurons fire in an entirely stimulus-driven way, without any modulation by descending predictions; this is because, to date, the large majority of research studying peripheral predictive coding has focused on the retina in certain model organisms (e.g., Srinivasan et al. (1982), Hosoya, Baccus, & Meister (2005), Liu, Hong, Rieke, & Manookin (2021)). However, some theories and at least one experiment take the other side of the issue. Theories of peripheral predictive coding (Sterling & Laughlin, 2015; Qian & Zhang, 2019) reason that a neuron’s most metabolically “cheap” responses should represent the predictable stimuli, while “expensive” responses are reserved for the most surprising stimuli. Barrett (2017) has suggested that descending visceromotor prediction signals modulate viscerosensory data as it ascends through the brainstem and midbrain. Dworkin (1993) demonstrated that certain peripheral interoceptors in humans reduced their afferent firing rate to zero under a constant stimulus; since the stimulus remained the same while neural firing changed, the interoceptors in that experiment could not be entirely stimulus driven. We hope that interoception researchers will invest future experimental effort in interoceptive modalities to differentiate the effect of repetition suppression from the function of predictive coding.
The question of where sense data are converted to prediction errors remains open, but it remains very likely that the brain issues interoceptive predictions, which are constrained and corrected by viscerosensory sense data. The predictive processes taking place in the brain form a model of the innervated viscera, but they can only directly affect the viscera through visceromotor signals. The basic relation between the brain and the world outside itself applies in the interoceptive realm as it does in exteroceptive modalities. The brain can constrain (or influence) the body using motor signals, and actual bodily sense data constrain (or influence) the interoceptive contents of the brain’s internal model.
Assuming that neither noise nor nervous dysfunction prevent the brain from accurately predicting the visceral sense data, we have hypothesized that the brain’s interoceptive representations contain both state estimates of the viscera and a functional analogue of allostatic capacity curves. The movement of estimated states along capacity curves, and the movement of the capacity curves themselves, then determines the brain’s estimate of allostatic responsiveness. We have hypothesized that increases in such responsiveness could function as “rewards”, positively reinforcing behavioral trajectories, while decreases in responsiveness could function as “costs”, negatively reinforcing behavioral trajectories. Such a hypothesis may account for alliesthesia (Cabanac, 1971) in decision making and behavior, in which the relation between an exogenous stimulus and the body’s internal state determines whether that stimulus positively or negatively reinforces skeletomotor and visceromotor action (Barrett & Bliss-Moreau, 2009; Barrett, 2017). This can include actions which alter the capacity curves themselves, such as relaxing the baroreflex gain during exercise to accommodate rising heart rate and blood pressure.
Note that rewards are not always experienced as pleasant (e.g., the removal of something unpleasant to strengthen a behavior, called negative reinforcement) and not all stressors are experienced as unpleasant (e.g., exercise), consistent with the suggestion that approach/avoid features of behavior and pleasant/unpleasant affective features of experience are not always aligned. The degree to which behavioral and experiential “valences” align with each other in a given situation, and even the choice of which specific variables within behavioral and experiential processes to compare, remain largely open questions.
Finally, this paper has taken a physiologist’s view of the innervated body, delineating regulated resources from controlled processes. The “ideal type” capacity curve treats the action of a controlled process as a function of an underlying regulated resource, and both variables receive peripheral interoceptive innervation. For example, glucose, glucagon, and insulin levels in the circulating blood are sensed separately. However, in many cases, the body employs hierarchies of regulatory mechanisms, making some controlled processes act as functions of other controlled processes. The baroreflex falls into this category. Thus, despite being a canonical interoceptive modality for experimentalists, the carotid baroreflex may actually be functionally atypical. The physiological differences between the baroreflex and chemosensing may provide some functional hints. The baroreflex forms an entire reflex circuit, whose visceromotor function under central command may resemble that of a somatomotor reflex (as suggested in Section 5.2 above).
Predictions
Physiological questions about regulated resources versus controlled processes may be amenable to anatomical investigation: where a reflexive control circuit is found, it may reflect the monitoring of a controlled process. Where peripheral interoceptors report “raw” visceral sensations, without an intervening motor reflex circuit, that may reflect the sensing of a regulated resource. The open question then would be how the central nervous system determines which controlled processes act as functions of which regulated resources. Speculating somewhat further, if an anatomical difference existed between viscerosensing of regulated resources and controlled processes, it would also enable inferences about the constraints provided for the brain by those respective viscerosensory endpoints. Interoception of regulated resources in relation to controlled processes would then constrain the brain’s representations of the allostatic responsiveness of behavior, its reference signal for movements. Interoception of controlled processes in relation to signaled top-down references would provide feedback to the brain that is analogous to what happens in somatosensory modalities: feedback stabilization of (visceral) movements.
5.4. Conclusions
Let’s return to our amateur dodgeball player. Under the hypothesis laid out in this paper, afferent sensory signaling (including viscerosensory afferents) conveys prediction errors, which update a predictive internal model in the brain of the body on the dodgeball field. Motor processes exploit the updated model contents to improve the player’s performance. Playing dodgeball, and improving one’s performance, requires anticipating the physiological and metabolic demands of the game (which capacity curves can capture) and mobilizing the body’s internal visceromotor systems to meet those demands before they arise. APIC offers a formal model of how allostatic decisions could potentially be made, given the referent-control hypothesis of motor control. Thanks to APIC’s posing a soft forward optimization problem instead of a recursive, hard backward optimization problem (see Section 4.4), APIC may afford a simpler and more computationally tractable potential neural implementations than previous computational decision-making formalisms.
Of course, within an allostatic view of the brain, the desire to play dodgeball does not arise ex nihilo, any more than a “desire” exists to maintain blood glucose within certain ranges. These desires (or “motivations”) are thought to begin as abstract conceptualizations (Barrett, 2017) that predict allostatic capacities and interoceptive states (and can be described with low dimensional features, such as reward, stress, threat, and so on), monitoring the controlled processes that constitute the body’s physiology. The APIC model’s regulatory targets consist of ever-moving capacity curves, and so the hypothetical dodgeball player’s brain can both predict the accuracy with which their skeletomotor movements aim at other players, and (paraphrasing Klein (2018)) be motivated to improve their aim. We posit that this integration of interoception and allostatic control, played out across nested temporal and spatial scales, enables the brain to make the decisions and enact the movements that enable us to score well in dodgeball.
Acknowledgements
The authors gratefully acknowledge the support of the Army Research Institute (grant W911NF-16-1-0191, principal investigator Quigley), the National Institutes of Health-National Institute of Mental Health (NIH-NIMH, grant R01MH113234, principal investigators Barrett and Isaacowitz), the National Institutes of Health-National Cancer Institute (NIH-NCI, grant 1U01CA193632-01A1, principal investigator Barrett), and the National Science Foundation (NSF-NCS, grant 1835309, principal investigator van de Meent). The authors would also like to thank Deniz Erdogmus for elucidating discussions on control theory.
Nomenclature
- advantage function
A function quantifying the relative decision value of visiting a given state, compared to the (estimated) time-average decision value across the course of a behavior
- allostasis
Brain-centered predictive regulation in which the brain anticipates the needs of the body and attempts to meet those needs before they arise
- control error
The difference between a measured or actual state and the reference state
- controller
A physical system whose behavior transforms signals encoding a reference trajectory into signals encoding controls to drive a plant
- controls
A signal or signals that drive the behavior of a plant by changing its state
- control theory
The engineering discipline of driving a physical system towards a desired trajectory
- disturbance
An outside factor that can disrupt the state of a physical system
- ergodicity
A condition of a stochastic system, or a probabilistic model of a system, in which averaging together a series of measurements taken over time is equivalent to averaging together the same number of measurements taken independently at the same time
- ex00AFferent
Afferent sensory signals arising from causes external to the body or outside the physiological control of the nervous system
- exteroception
The set of processes by which the nervous system takes in, integrates, and infers the causes of signals from outside the body
- feedback control
The adjustment of controls in real time based on measurements of plant state fed back into the controller
- flow
A variable in a (physiological) dynamical system that represents the rate of a process, counted in the ratio of physical units to temporal units
- controlled process
A particular ow variable that is manipulated by homeostatic or allostatic mechanisms to maintain the value of a regulated variable within a desired range
- generative model
A probability model of the joint distribution over unob served decision variables, and observed variables given the unobserved decision variables, from which novel instances can be sampled
- internal model
A physical system that partially and approximately encodes the dynamical structure of the plant to be controlled, or potentially a probability distribution over such structures
- forward model
An internal model that makes predictions forwards in time, on the basis of a present state
- inverse model
An internal model that makes predictions backwards in time, on the basis of an estimated or desired future state
- interoception
The set of processes by which the nervous system takes in, integrates, and makes meaning of sensory signals originating within the body
- measurement
A signal fed back from the plant to inform the controller of the plant state
- noise
Randomness or uncertainty intrinsic to physical systems which cannot be measured or controlled at an infinitely fine scale
- measurement noise
Randomness or uncertainty intrinsic to the instruments or sensors that take measurements and transmit them to the controller
- process noise
Randomness or uncertainty intrinsic to the plant as a physical system
- objective function
A function from actual or estimated plant states to real numbers, in which higher numbers denote better agreement with the reference trajectory
- operating point
The point on a response curve at which the response available to a local perturbation is greatest, often but not necessarily found at the center parent
- plant
A physical system to be controlled
- prediction error
The difference between a measurement or actual state, and the predictive estimate of that state
- probabilistic graphical model
A probability model in which the nodes and arrows of a graph express the conditional independence structure between random variables see
- reafferent
Afferent sensory signals arising from the consequences of movements or self-caused physiological changes
- reference distribution
A probability distribution whose probability mass or density at each point corresponds to the relative robustness of a physiological controller to perturbations from that point
- reference trajectory
The desired trajectory of evolution through a state space for plant behavior over time
- response curve
The plotted curve, usually S-shaped, showing a response to a stimulus as a function of the stimulus quantity or intensity
- capacity curve
The response curve of a centrally regulated physiological variable or reflex, which compels a central regulatory response when dysregulated
- generalized capacity curve
The capacity curve of a controlled physiological ow, with an inflection point not identical to its center
- gain
The parameter to a response curve determining its slope around the central point. Greater gain implies a smaller distance to an asymptote and a narrower adaptive range
- saturation value
The value of an input variable (such as a regulated variable) for which a process (such as a controlled variable’s underlying process) can yield no further increase in response
- set point
Fixed, specific points in the quantitative state-space of physiological variable to which regulatory systems work to return that variable
- settling point
The point at which a stock-and-flow system’s stock reservoir settles for any given level of the passively unregulated inflow or outflow variables
- settling range
A range throughout which a regulated variable can settle freely under physiologically unregulated (but perhaps behaviorally regulated) inflow and outflow, without triggering an active physiological response, see settling point
- stability
A property of the coupled dynamics of a controller and a plant, under which control error will eventually shrink arbitrarily close to zero after a disturbance
- state
A vector of real numbers that determine how plant behavior will evolve over time
- state estimate
Estimates of plant state based on measurements, including measurements accumulated over time
- stochastic optimal control
A variety of control theory in which we model all forms of noise and uncertainty using probability distributions, and write the reference trajectory in terms of finding the maximum of a function of the estimated plant state
- stock
A variable in a (physiological) dynamical system that represents a quantity, counted in physical units
- regulated resource
A particular stock variable that is maintained at or near a stable level by homeostatic or allostatic mechanisms in the body
- threshold value
The value of an input variable (such as a regulated variable) for which a process (such as a controlled variable’s underlying process) can yield no further reduction in response
- transfer function
The ratio of a system output to its input, written in the time-independent frequency domain via a mathematical transformation
- value function
The probabilistic average, over estimated plant states, of the sum of objective function values into the indefinite future
- Bellman equation
Equation that defines the optimal value function recursively over timesteps
- viscerosensory signaling
Afferent sensory signaling from the innervated viscera
Appendix
Appendix B. How ergodicity interacts with control
B.1.1. Ergodicity: whether uncertainty and noise make a difference over time
The concept of ergodicity formalizes the equivalence between present and future uncertainty or noise. In an ergodic system, averaging together a series of measurements taken over time is equivalent to averaging together the same number of measurements taken simultaneously with separate instruments. If we were to assume an objective function f(x) under an ergodic probability model p(xt), we would write that
| (B.1) |
This equation says that taking individual measurements f(xt) over any hypothetical period of time T and averaging them together (the left side of the equation) will yield the same result as just calculating the average measurement immediately (the right side of the equation).
Conceptually, if we would like to know the average speed at which a particular kind of car travels on a highway, we could either track a single such vehicle over an extended period of time, or measure the speed of multiple vehicles (of the same kind) at the same time. In either case, as long as we took sufficiently many measurements, we would obtain the same result, whether we calculate by dividing by time or by the number of vehicles. However, the very obscurity of this thought experiment should hint to us that many real-world measurements are not ergodic.
Situations that are not ergodic include those with periodic structure, or with irreversible changes. Our real lives are, therefore, filled with non-ergodic decisions to make: the cycles of day and night are non-ergodic; our development and aging processes are non-ergodic; injury and death are non-ergodic. Insofar as our internal environment has its own cycles (breathing, heartbeat, eating and drinking, etc.) it too is non-ergodic. The earliest brains contained body-clocks that synchronized bodily cycles to environmental cycles (Schulkin & Sterling, 2019); they were non-ergodic as well. This is why we invested the extra effort above of detailing a variety of control theory able to model non-ergodic decision-making.
In contrast, many typical behavioral experiments involve their participants in ergodic decision-making problems: we choose as experimenters to treat averaging within-participant measurements across time as equivalent to averaging between-participant measurements. In fact, an experimental participant can become fatigued, bored, excited, hungry, or thirsty through the course of the experiment. If given food and drink, they can cycle between hunger, satiation, and then hunger again. Assuming ergodicity in experimental design implies ignoring all the bodily and environmental factors that we do not design, and which do not conform to our assumption.
This has practical implications for decision-making processes in the brain, as well. Only in an ergodic problem can the brain rightfully equate averaging over the history of a real behavior with averaging over some population of mental simulations. This is why decision-making often involves mental simulations over the entire course of a possible behavior, allowing the brain to account for cyclical or irreversible events. In fact, when we give people non-ergodic decision making problems in experiments, the evidence suggests subjects may solve them “the right way”, imagining the temporal course of possible futures (Peters, 2019).
B.1.2. Formulating perception and control ergodically leads to the Free Energy Principle (FEP)
The brain’s internal model allows it to regulate its body in a world full of uncertainty by means of visceromotor commands, obtaining feedback by anticipating the commands’ viscerosensory consequences as interoceptive predictions. These interoceptive predictions implement “top-down” sensory simulations, fashioned from past experiences, that are continually compared against information received from the viscerosensory surfaces about the actual state of the body in the world.
These hypotheses can be integrated into an emerging theoretical consensus, dubbed predictive processing (Bar, 2009; Friston, 2010; Clark, 2013; Deneve & Machens, 2016; Hutchinson & Barrett, 2019). “Top down” sensory predictions continuously anticipate events within the body and outside it that are sensed via its sensory surfaces. Sensory prediction signals cascade across multiple gradients within the brain, including across the cerebral cortex (Huang & Rao, 2011; Zhang et al., 2019), cerebellum (Wolpert, Miall, & Kawato, 1998; Hull, 2020), and hippocampus (Buzsaki & Tingley, 2018), as well as across all levels of the neuraxis, involving hypothalamus, basal ganglia, superior colliculus and various midbrain and brainstem structures (Kleckner et al., 2017). In fact, it is possible that every sensory neuron, in effect, receives some form of prediction signalling from some of the neurons projecting to it, and sends prediction errors23 to other neurons via its own projections (Deneve and Machens, 2016). “Bottom-up” information coming from the sensory surfaces (such as the retina, the olfactory bulb, and the lamina I spinothalamic tract) acts as sensory prediction error signals and is visualized as the dashed arrows in Fig. 6. In this way, the brain continuously maintains a simulation of the sensory environment inside the body, as well as the relevant aspects of the sensory environment outside the body, and updates that running simulation according to computed error. The updated simulations constitute approximately optimal posterior inferences about the likely causes of sensory events.
Among predictive processing hypotheses of brain function, the free-energy principle (FEP) has enjoyed a particular popularity (Friston, 2010; Friston et al., 2010; Andrews, 2021). Under the ergodic assumptions of the Free-Energy Principle as formulated by Friston et al. (2010), organisms are hypothesized to minimize the entropy of their sensory outcomes
| (B.2) |
| (B.3) |
where p(o(t), s(t)) is interpreted as a generative model of sensory outcomes o(t) with hidden variables s(t), evolving in continuous time. Note that the first integral is a time average (denoted by dt) and the second an ensemble average (denoted by ds). The authors of Friston et al. (2010) propose that organisms carry out this task by minimizing an upper bound to the sensory entropy, called the variational free-energy, which also appears in related predictive-coding models of perception.
The equivalence of the time-average in Eq. (B.2) and the sample average in Eq. (B.3) is precisely the assumption of ergodicity discussed in B.1.1. This assumption renders the time-average equivalent to the instantaneous sample-average, making any one moment in time as good as any other for purposes of optimizing the free energy (or the entropy). Ergodicity also implies there exists a long-run stationary distribution, with no dependence on the start state or the particular sequencing of states s(t) across time.
Under such assumptions, we can formulate an extraordinarily elegant control formalism just by writing the sensory outcomes as functions of action a(t), yielding an objective function
and a variational bound in terms of approximate posterior beliefs q(s(t)) and their “free energy” ,
The variational bound can then be used as a proxy for the true objective, and implies that action should descend the gradient of free energy to minimize long-run sensory entropy. As a side-effect of giving action the same objective functional as sensory prediction, this active inference formulation under the free-energy principle implies a (partial, contextual) equivalence between precision and value. Accumulating evidence becomes the only true good, while losing it becomes the only true ill, and precision is the parameter whose optimization most easily affords increasing evidence. Precision here is mathematical equivalent (up to some constant factors) to the gain or inverse-tolerance we described as a parameter to capacity curves in Section 2.2. We employ the separate terminology to make sure it is understood that precision measures the confidence of a probabilistic estimate of some quantity, while the gain or tolerance measures the steepness or shallowness of a regulatory response.
Within this paradigm, active inference modeling has taken two general forms. Motor active inference (mActIf) tends to assume (local) ergodicity, so that local hill-climbing on the steady-state density becomes the best control strategy. In terms of classical control theory, when the reference signal is a set-point and disturbances are independently random across time, reactive behavior and homeostatic reflex arcs will suffice to maintain optimal regulation of physiology. In contrast, decision active inference (dActInf) maintains the appearance of ergodic homeostasis within the internal environment by writing a homeostatic distribution or “prior preferences” p(o∣m) (the notation of conditioning on m to write prior preferences comes from Friston et al. (2012)) and then using predictive decision-making to make internal states conform to that distribution.
Under decision active inference, mental simulations “try out” potential policies, considering their effects over a finite time horizon, and policies thereby compete to control action based on their expected free energy. dActInf thus implements what control engineers would call model-predictive control with an information-theoretic objective (Williams, Drews, Goldfain, Rehg, & Theodorou, 2018). Similarly, the “prior preferences” function as what we would call homeostatic set-points and tolerances, as addressed in Stephan et al. (2016), Corcoran & Hohwy (2017), Pezzulo, Rigoli, & Friston (2018), and many similar works. Under ergodic assumptions, time-averaging may be invoked to interpret all physiological changes as (survivable) deviations from fixed homeostatic set-points with fixed tolerances.
Ergodicity yields an especially elegant formulation of control because it collapses the distinction between information from the past and information from the future. The precise reason that stochastic optimal control problems are hard to solve is that computing the true optimal decision require knowledge of the future – not estimates, knowledge. Both mathematically and intuitively, you cannot really know you have chosen the best course of action without knowing the course of future events ahead of time. Without that knowledge, the best that any real controller, or brain, can do is to estimate the necessary quantities using all information available, make corrections as new information reveals itself, and wait until the notional end of a behavioral episode to evaluate performance retrospectively. Even small errors or misestimates compound, the further into the future you try to predict, because they cannot be corrected online by present sense-data. Unfortunately, a stochastic optimal control problem of the sort implied by the time-averaging we discussed in Section 4.2 requires prediction indefinitely far into the future.
Of course, this is what the brain’s internal model is for: refining information contained in past sensory signals into the optimal estimate of the future. The optimal estimate of the future will probably still be off by some amount, but it nonetheless represents the best possible estimate that can be made given the information available. The actual brain never makes a truly optimal estimate, of course: it approximates the optimal estimate, effectively approximating an approximation of the unavailable future information. Even so, this approximately optimal estimation enables feedforward, prospective control that performs drastically better than waiting to react until the body is actually challenged or harmed (Yeo, Franklin, & Wolpert, 2016). If you are walking on a dark road, and you see something that looks vaguely like a car careening towards you, you don’t wish for a more optimal estimate, you get out of the way. It is only in this sense of “prediction”, prediction without real-time correction, that predictive processing can be suitable for modeling sequential decision problems.
This has implications for the low-level motor control strategy employed in regulating the viscera. Previous motor active inference accounts of visceromotor action have noted that visceromotor cortical areas mostly lack integration of ascending prediction errors, and hypothesized that they “function more like deterministic models of actions that are to be executed” (Barrett & Simmons, 2015). They then extend the analysis of Adams, Shipp, & Friston (2013) to the visceromotor domain: they conceptualize visceromotor efferent signaling as specifying visceral reference coordinates rather than “predictions” to be revised in a Bayesian sense (Chanes & Barrett, 2016; Smith et al., 2017). Continuing the analogy, they suggest that the uncertainty of visceromotor predictions specifies physiological tolerances (Penny & Stephan, 2014; Stephan et al., 2016). However, this account of visceromotor active inference implicitly relied on the ergodicity assumption embedded in motor active inference as a theory. Our model will relax this ergodicity assumption, while providing an alternative explanation for the anatomical observations motor active inference can explain. In short, we could consider our model a probabilistic way of encoding hierarchical referent control (Feldman, 2016) and the ideomotor principle (James, 1890). We gratefully thank investigators such as Corcoran et al. (2020) who have considered allostasis explicitly for setting the stage for our work, and emphasize that the lens of control theory is what enables us to separate the idea of a reference coordinate from that of a prediction.
C.1. APIC model derivation details
C.1.1. A hierarchical generative model with reference distributions
The APIC model assumes a hierarchical generative model designed to explain sensory outcomes ot using hidden states across some number L ∈ [2, ∞) of levels. At each level of hierarchy l ∈ [1. . L], the variables parameterize a reference distribution, written
The parameters for reference distributions themselves come from multiple levels of policies, distributions π over lower-level goals or actions, conditioned upon higher-level states and goals:
At the bottom level, a joint likelihood predicts the exteroceptive, interoceptive, and somatosensory observations together, based upon the lowest-level hidden states and reference signals,
The prior densities for each hierarchical level l ∈ [1…L] are written
and transition densities for each hierarchical level l ∈ [1…L] are written
Fig. 10 displays the resulting complete graphical model for L = 4.
The above prior densities and likelihood imply that by Bayes’ rule there exists a posterior distribution
which APIC allows approximating by more-or-less any means. Since policies π also took the form of distributions above, Bayesian inference implies a posterior distribution over reference signals ρ and actions at as well.
The complete state of the generative model can be abbreviated as
The complete reference distribution, across all hierarchical levels, can be written
| (C.1) |
and the complete transition dynamics as
where
C.1.2. Full derivation of optimal value function and transition dynamics
The differential Bellman equation is the defining principle of stochastic optimal control, an equation for the long-run value function. In the infinite-time, average-reward setting, assuming a global capture rate of for a whole behavior, it can be written
with the maximization taking place with respect to achievable (by varying the actions) transition distributions. then denotes the best achievable value for any transition between individual states. Combining that expression with the transition dynamics as a Boltzmann or “softly maximizing” distribution will yield a generative model of the optimal transition dynamics, as seen in Eq. (15):
This transition distribution optimally trades off between probable transitions and valuable transitions. The optimal transition distribution’s mode, when it can be calculated or approximated, corresponds to the most likely trajectory for an optimal agent (with the assumed goals) to follow (Todorov, 2011). Writing it with a qϕ rather than a pθ denotes that it will be used as an observation-driven feedback controller, or more formally an importance sampling proposal. Just as the optimal transition distribution provides a generative model of an optimally controlled system, when used as an observation-driven proposal it also provides the optimal feedback controller.
Substituting the optimal feedback controller back into the differential Bellman equation will yield
which can be further expanded by substituting Eq. (14) for :
First, however, the information divergence penalty must be expanded in order to justify Eq. (17). First the divergence is written out in terms of its definition
and then the definition of q*ϕ is substituted into the expectation of the logarithm,
This substitutes into the equation for the divergence to imply that
The second and last terms of this equation are identical, and so cancel. This leaves a divergence of
and therefore a (subtractive) divergence penalty as seen in Eq. (17):
Substituting the above for the penalty in the differential Bellman equation will yield
| (C.2) |
the smooth differential Bellman equation. This equation is smoothly maximizing instead of exactly maximizing, and thus more likely to be compatible with neural stochasticity. Its recursive term makes the weak assumption about the future that the trajectory will continue as planned according to the generative action concept.
This equation can be shortened by applying the exponential function to both its sides, obtaining
and further shortened by defining the exponential of the value function as the desirability function,
to finally obtain
In this form, the differential Bellman equation is linear, allowing its terms to be expanded recursively. For example, at time step t = 1
and so on. When the expectations are regrouped together and moved to the outermost level, the equation as a whole can be written over a trajectory of length T as
| (C.3) |
This path-integral form for the value/desirability function gives its name to the technique of path-integral control. Eq. (C.3) also provides exactly the term required by Eq. (15) for computing the optimal feedback controller or transition distribution.
Footnotes
Declaration of Competing Interest
None of the authors report any potential or actual conflicts of interest. This manuscript meets the guidelines for ethical conduct and report of research, and all funding sources have been described in the manuscript.
Quantities of change per period of time
The terminology of regulated resources and controlled processes comes from Kotas & Medzhitov (2015) and Cabanac (2006).
which has physical units independent of time
A concept proposed by Cannon (1929)
Typically with a concomitant withdrawal of parasympathetic activity (Berntson, Cacioppo, & Quigley, 1991; Rowell, O’Leary, & Kellogg, 1996).
Terminology adapted from McDowall & Dampney (2006)
Mathematically educated readers will recognize this as a derivative.
Generally there is assumed to be a collection of possible desirable trajectories, so that a system can compensate for severe disturbances to its original trajectory by picking another acceptable trajectory from the collection. Theorists have labeled this quality “meta-stability”.
As an inverse model
As a forward model
Inverse modeling
Forward modeling
See Straka, Simmers, & Chagnaud (2018) for a thorough review.
A finding discussed commonly in the predictive processing (Clark, 2015) and neuro-robotics (Barter & Yin, 2021) literatures.
Language taken from Buzsáki (2019).
Language again taken from Buzsáki (2019).
For a primer on graphical models see Roller & Friedman (2009)).
Or equivalently within this context, an approximate posterior distribution over actions
Gradient updates, to be precise.
See Sanborn (2017) for a review of sampling and variational approaches to approximate inference in the brain.
See Ramstead et al. (2020) for a counterexample.
Note that this does not imply that people will have a sense of agency in controlling their autonomic nervous systems, as they do in skeletomotor control.
Formally, score functions, the gradients of a log-likelihood.
References
- Adams RA, Shipp S, & Friston KJ (2013). Predictions not commands: Active inference in the motor system. Brain Structure and Function, 218, 611–643. 10.1007/s00429-012-0475-5. arXiv:arXiv:1011.1669v3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggelopoulos NC (2015). Perceptual inference. Neuroscience and Biobehavioral Reviews, 55, 375–392. 10.1016/j.neubiorev.2015.05.001 [DOI] [PubMed] [Google Scholar]
- Allen M, Levy A, Parr T, & Friston KJ (2019). In the body’s eye: The computational anatomy of interoceptive inference. BioRxiv, Article 603928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews M (2021). The math is not the territory: Navigating the free energy principle. Biology & Philosophy, 36, 1–19. 10.1007/s10539-021-09807-0 [DOI] [Google Scholar]
- de Araujo IE, Schatzker M, & Small DM (2020). Rethinking food reward. Annual Review of Psychology, 71, 1–26. 10.1146/annurev-psych-122216-011643 [DOI] [PubMed] [Google Scholar]
- Bar M (2009). Predictions: A universal principle in the operation of the human brain. Philosophical Transactions of the Royal Society B: Biological Sciences, 364, 1181–1182. 10.1093/acprof:oso/9780195395518.001.0001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF (2009). The future of psychology: Connecting mind to brain. Perspectives on psychological science, 4, 326–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF (2017). The theory of constructed emotion: An active inference account of interoception and categorization. Social Cognitive and Affective Neuroscience, 12, 1–23. 10.1093/scan/nsw154 (arXiv:scan/nsw154). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, & Bliss-Moreau E (2009). Affect as a psychological primitive. Advances in Experimental Social Psychology, 41, 167–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, & Finlay BL (2018). Concepts, goals and the control of survival-related behaviors. Current Opinion in Behavioral Sciences, 24, 172–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, Quigley KS, & Hamilton P (2016). An active inference theory of allostasis and interoception in depression. Philosophical Transactions of the Royal Society B: Biological Sciences, 371. 10.1098/rstb.2016.0011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, & Satpute AB (2013). Large-scale brain networks in affective and social neuroscience: Towards an integrative functional architecture of the brain. Current opinion in neurobiology, 23, 361–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett LF, & Simmons WK (2015). Interoceptive predictions in the brain. Nature Reviews Neuroscience, 16, 419–429. 10.1038/nrn3950. ⟨papers3://publication/doi/10.1038/nrn3950⟩. arXiv:15334406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barsalou LW (2009). Simulation, situated conceptualization, and prediction. Philosophical Transactions of the Royal Society B: Biological Sciences, 364, 1281–1289. 10.1098/rstb.2008.0319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barter JW, & Yin HH (2021). Achieving natural behavior in a robot using neurally inspired hierarchical perceptual control. iScience, 24, Article 102948. 10.1016/j.isci.2021.102948. ⟨https://www.sciencedirect.com/science/article/pii/S2589004221009160⟩ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastos AM, Usrey WM, Adams RA, Mangun GR, Fries P, & Friston KJ (2012). Canonical microcircuits for predictive coding. Neuron, 76, 695–711. 10.1016/j.neuron.2012.10.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker-Ehmck P, Karl M, Peters J, & van der Smagt P (2020). Learning to fly via deep model-based reinforcement learning. Fourth Machine Learning in Planning and Control of Robot Motion Workshop at International Conference on Robotics and Automation, 1–14. arXiv:2003.08876. [Google Scholar]
- Belousov B, Neumann G, Rothkopf CA, & Peters J (2016). Catching heuristics are optimal control policies. Advances in Neural Information Processing Systems. [Google Scholar]
- Berntson GG, Cacioppo JT, & Quigley KS (1991). Autonomic determinism: The modes of autonomic control, the doctrine of autonomic space, and the laws of autonomic constraint. Psychological Review, 98, 459–487. 10.1037/0033-295X.98.4.459 [DOI] [PubMed] [Google Scholar]
- Berridge KC, & Kringelbach ML (2015). Pleasure systems in the brain. Neuron, 86, 646–664. 10.1016/j.neuron.2015.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevan A, Honour A, & Stott F (1969). Direct arterial pressure recording in unrestricted man. Clinical Science, 36, 329–344. [PubMed] [Google Scholar]
- Boerlin M, Machens CK, & Deneve S (2013). Predictive coding of dynamical variables in balanced spiking networks. PLoS Computational Biology, 9, 1–16. 10.1371/journal.pcbi.1003258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogacz R (2017). A tutorial on the free-energy framework for modelling perception and learning. Journal of Mathematical Psychology, 76, 198–211. 10.1016/j.jmp.2015.11.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boureau YL, & Dayan P (2011). Opponency revisited: Competition and cooperation between dopamine and serotonin. Neuropsychopharmacology, 36, 74–97. 10.1038/npp.2010.151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braun D, Nagengast A, & Wolpert D (2011). Risk-sensitivity in sensorimotor control. Frontiers in Human Neuroscience, 5(1). 10.3389/fnhum.2011.00001. ⟨https://www.frontiersin.org/article/10.3389/fnhum.2011.00001⟩ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL (2012). The serendipitous discovery of the brain’s default network. Neuroimage, 62, 1137–1145. 10.1016/j.neuroimage.2011.10.035. ⟨https://www.sciencedirect.com/science/article/pii/S1053811911011992⟩, 20 YEARS OF fMRI. [DOI] [PubMed] [Google Scholar]
- Buzsáki G (2019). The brain from inside out. Oxford University Press. [Google Scholar]
- Buzsáki G, & Tingley D (2018). Space and time: The Hippocampus as a sequence generator. Trends in Cognitive Sciences, 22, 853–869. 10.1016/j.tics.2018.07.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabanac M (1971). Physiological role of pleasure. Science, 1103–1107. [DOI] [PubMed] [Google Scholar]
- Cabanac M (2006). Adjustable set point: To honor Harold T. Hammel. Journal of Applied Physiology, 100, 1338–1346. 10.1152/japplphysiol.01021.2005 [DOI] [PubMed] [Google Scholar]
- Cannon WB (1929). Organization for physiological homeostasis. Physiological Reviews, 9, 399–431. [Google Scholar]
- Carpenter RHS (2004). Homeostasis: A plea for a unified approach. AJP: Advances in Physiology Education, 28, 180–187. 10.1152/advan.00012.2004. ⟨http://ajpadvan.physiology.org/cgi/doi/10.1152/advan.00012.2004⟩ [DOI] [PubMed] [Google Scholar]
- Carvalho GB, & Damasio A (2021). Interoception and the origin of feelings: A new synthesis. BioEssays, 43, 1–11. 10.1002/bies.202000261 [DOI] [PubMed] [Google Scholar]
- Chanes L, & Barrett LF (2016). Redefining the role of limbic areas in cortical processing. Trends in Cognitive Sciences, 20, 96–106. 10.1016/j.tics.2015.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee S, & Diaconis P (2018). The sample size required in importance sampling. Annals of Applied Probability, 28, 1099–1135. 10.1214/17-AAP1326. arXiv:1511.01437. [DOI] [Google Scholar]
- Chen WG, Schloesser D, Arensdorf AM, Simmons JM, Cui C, Valentino R, … Langevin HM (2021). The emerging science of interoception: Sensing, integrating, interpreting, and regulating signals within the self. Trends in Neurosciences, 44, 3–16. 10.1016/j.tins.2020.10.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, & Knight ZA (2016). Making sense of the sensory regulation of hunger neurons. BioEssays, 38, 316–324. 10.1002/bies.201500167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chua K, Calandra R, McAllister R, & Levine S (2018). Deep reinforcement learning in a handful of trials using probabilistic dynamics models. Advances in Neural Information Processing Systems, volume 2018-Decem, 4754–4765. arXiv:1805.12114. [Google Scholar]
- Cisek P (2007). Cortical mechanisms of action selection: The affordance competition hypothesis. Philosophical Transactions of the Royal Society B: Biological Sciences, 362, 1585–1599. 10.1098/rstb.2007.2054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P (2019). Resynthesizing behavior through phylogenetic refinement. Attention, Perception, and Psychophysics. 10.3758/s13414-019-01760-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, & Kalaska JF (2010). Neural mechanisms for interacting with a world full of action choices. Annual Review of Neuroscience, 33, 269–298. 10.1146/annurev.neuro.051508.135409 [DOI] [PubMed] [Google Scholar]
- Clark A (2013). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Sciences, 36, 181–204. 10.1017/S0140525X12000477. ⟨http://www.journals.cambridge.org/abstract_S0140525X12000477⟩. arXiv:0140-525X. [DOI] [PubMed] [Google Scholar]
- Clark A (2015). Surfing uncertainty: Prediction, action, and the embodied mind. Oxford University Press. [Google Scholar]
- Colombo M (2014). Deep and beautiful, the reward prediction error hypothesis of dopamine. Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences, 45, 57–67. [DOI] [PubMed] [Google Scholar]
- Conant RC, & Ashby WR (1970). Every good regulator of a system must be a model of that system. International Journal of Systems Science, 1, 89–97. 10.1080/00207727008920220 [DOI] [Google Scholar]
- Corcoran AW, & Hohwy J (2017). Allostasis, interoception, and the free energy principle: Feeling our way forward. Interoceptive Basis of the Mind, 1–16. 10.17605/OSF.IO/ZBQNX (psyarxiv.com/zbqnx). [DOI] [Google Scholar]
- Corcoran AW, Pezzulo G, & Hohwy J (2020). From allostatic agents to counterfactual cognisers: Active inference, biological regulation, and the origins of cognition. Biology & Philosophy, 35, 1–45. [Google Scholar]
- Cosentino C, & Bates D (2011). Feedback control in systems biology. CRC Press, ⟨https://books.google.com/books?id=wk_RBQAAQBAJ⟩. [Google Scholar]
- Craig AD (2002). How do you feel? Interoception: The sense of the physiological condition of the body. Nature Reviews Neuroscience, 3, 655–666. 10.1038/nrn894 [DOI] [PubMed] [Google Scholar]
- Craig AD (2009). How do you feel - now? The anterior insula and human awareness. Nature Reviews Neuroscience, 10, 59–70. 10.1038/nrn2555. arXiv:1511.04103. [DOI] [PubMed] [Google Scholar]
- Craig AD (2015). How do you feel?: An interoceptive moment with your neurobiological self. Princeton University Press. [Google Scholar]
- Dabney W, Kurth-Nelson Z, Uchida N, Starkweather CK, Hassabis D, Munos R, & Botvinick M (2020). A distributional code for value in dopamine-based reinforcement learning. Nature, 577, 671–675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dabney W, Rowland M, Bellemare MG, & Munos R (2018). Distributional reinforcement learning with quantile regression. Thirty-Second AAAI Conference on Artificial Intelligence. [Google Scholar]
- Dampney RA (2016). Central neural control of the cardiovascular system: Current perspectives. Advances in Physiology Education, 40, 283–296. 10.1152/advan.00027.2016 [DOI] [PubMed] [Google Scholar]
- Dantzer R (2018). Neuroimmune interactions: From the brain to the immune system and vice versa. Physiological Reviews, 98, 477–504. 10.1152/physrev.00039.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND, & Touretzky DS (2000). Behavioral considerations suggests an average reward TD model of the dopamine system. Neurocomputing, 32–33, 679–684. 10.1016/S0925-2312(00)00232-0 [DOI] [Google Scholar]
- Daw ND, Gershman SJ, Momennejad I, Russek EM, Botvinick MM (2017). Predictive representations can link model-based reinforcement learning to model-free mechanisms, volume 13. doi: 10.1371/journal.pcbi.1005768. arXiv:arXiv:1612.00429v2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denève S, & Machens CK (2016). Efficient codes and balanced networks. Nature Neuroscience, 19, 375–382. 10.1038/nn.4243 [DOI] [PubMed] [Google Scholar]
- Dicarlo SE, & Bishop VS (1992). Onset of exercise shifts operating point of arterial baroreflex to higher pressures. American Journal of Physiology - Heart and Circulatory Physiology, 262. 10.1152/ajpheart.1992.262.1.h303 [DOI] [PubMed] [Google Scholar]
- Dworkin BR (1993). Learning and physiological regulation. University of Chicago Press. [Google Scholar]
- Edelman GM, & Gally JA (2001). Degeneracy and complexity in biological systems. Proceedings of the National Academy of Sciences, 98, 13763–13768. 10.1073/pnas.231499798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faisal AA, Selen LP, & Wolpert DM (2008). Noise in the nervous system. Nature Reviews Neuroscience, 9, 292–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG (2016). Active sensing without efference copy: Referent control of perception. Journal of Neurophysiology, 116, 960–976. 10.1152/jn.00016.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG (2015). Referent control of action and perception. doi: 10.1007/978-1-4939-2736-4. [DOI] [Google Scholar]
- Filippi BM, Abraham MA, Yue JT, & Lam TK (2013). Insulin and glucagon signaling in the central nervous system. Reviews in Endocrine and Metabolic Disorders, 14, 365–375. 10.1007/s11154-013-9258-4 [DOI] [PubMed] [Google Scholar]
- Finlay BL, & Uchiyama R (2015). Developmental mechanisms channeling cortical evolution. Trends in Neurosciences, 38, 69–76. 10.1016/j.tins.2014.11.004. ⟨https://www.sciencedirect.com/science/article/pii/S0166223614002124⟩ [DOI] [PubMed] [Google Scholar]
- Francis BA, & Wonham WM (1976). The internal model principle of control theory. Automatica, 12, 457–465. 10.1016/0005-1098(76)90006-6 [DOI] [Google Scholar]
- Friston K (2010). The free-energy principle: a unified brain theory? Nature Reviews Neuroscience, 11, 127–138. 10.1038/nrn2787 [DOI] [PubMed] [Google Scholar]
- Friston K, Adams R, & Montague R (2012). What is value-accumulated reward or evidence? Frontiers in Neurorobotics, 6, 1–25. 10.3389/fnbot.2012.00011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, Fitzgerald T, Rigoli F, Schwartenbeck P, & Pezzulo G (2017). Active inference: A process theory. Neural Computation, 29, 1–49. 10.1162/NECO. arXiv:1206.1275. [DOI] [PubMed] [Google Scholar]
- Friston K, & Kiebel S (2009). Predictive coding under the free-energy principle. Philosophical Transactions of the Royal Society B: Biological Sciences, 364, 1211–1221. 10.1098/rstb.2008.0300. ⟨http://rstb.royalsocietypublishing.org/cgi/doi/10.1098/rstb.2008.0300⟩ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, Rigoli F, Ognibene D, Mathys C, Fitzgerald T, & Pezzulo G (2015). Active inference and epistemic value. Cognitive Neuroscience, 6, 187–224. 10.1080/17588928.2015.1020053 [DOI] [PubMed] [Google Scholar]
- Friston K, Samothrakis S, & Montague R (2012). Active inference and agency: Optimal control without cost functions. Biological Cybernetics, 106, 523–541. 10.1007/s00422-012-0512-8 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Daunizeau J, Kilner J, & Kiebel SJ (2010). Action and behavior: A free-energy formulation. Biological Cybernetics, 102, 227–260. 10.1007/s00422-010-0364-z [DOI] [PubMed] [Google Scholar]
- Friston KJ, & Price CJ (2003). Degeneracy and redundancy in cognitive anatomy. Trends in Cognitive Sciences, 7, 151–152. 10.1016/S1364-6613(03)00054-8. ⟨https://www.sciencedirect.com/science/article/pii/S1364661303000548⟩ [DOI] [PubMed] [Google Scholar]
- Gallivan JP, Chapman CS, Wolpert DM, & Flanagan JR (2018). Decision-making in sensorimotor control. Nature Reviews Neuroscience, 19, 519–534. 10.1038/s41583-018-0045-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallivan JP, Logan L, Wolpert DM, & Flanagan JR (2016). Parallel specification of competing sensorimotor control policies for alternative action options. Nature Neuroscience, 19, 320–326. 10.1038/nn.4214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garzilli I, & Itzkovitz S (2018). Design principles of the paradoxical feedback between pancreatic alpha and beta cells. Scientific Reports, 8, 1–12. 10.1038/s41598-018-29084-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie RB, Ghasemi AH, & Freudenberg J (2016). Human motor control and the internal model principle. IFAC-PapersOnLine, 49, 114–119. 10.1016/j.ifacol.2016.10.471 [DOI] [Google Scholar]
- Grush R (2004). The emulation theory of representation: Motor control, imagery, and perception. Behavioral and Brain Sciences, 27, 377. [DOI] [PubMed] [Google Scholar]
- Gu X, & FitzGerald T (2014). Interoceptive inference: Homeostasis and decision-making. Trends Cogn Sci, 18, 269–270. [DOI] [PubMed] [Google Scholar]
- Hackel LM, Larson GM, Bowen JD, Ehrlich GA, Mann TC, Middlewood B, Roberts ID, Eyink J, Fetterolf JC, Gonzalez F, et al. (2016). On the neural implausibility of the modular mind: Evidence for distributed construction dissolves boundaries between perception, cognition, and emotion. Behavioral and Brain Sciences, 39. [DOI] [PubMed] [Google Scholar]
- Hall J, & Hall M (2020). Guyton and Hall Textbook of Medical Physiology E-Book, Guyton Physiology. Elsevier Health Sciences. ⟨https://books.google.com/books?id=H1rrDwAAQBAJ⟩. [Google Scholar]
- Harrison OK, Nanz L, Marino S, Lüchinger R, Hennel F, Hess AJ, Fraessle SK, Iglesias S, Vinckier F, Petzschner FH, et al. (2021). Interoception of breathing and its relationship with anxiety. bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heesch CM (1999). Reflexes that control cardiovascular function. American Journal of Physiology - Advances in Physiology Education, 22, 234–244. [DOI] [PubMed] [Google Scholar]
- Hickok G (2014). The myth of mirror neurons: The real neuroscience of communication and cognition. WW Norton & Company. [Google Scholar]
- Hosoya T, Baccus SA, & Meister M (2005). Dynamic predictive coding by the retina. Nature, 436, 71–77. 10.1038/nature03689 [DOI] [PubMed] [Google Scholar]
- Huang Y, & Rao RP (2011). Predictive coding. Wiley Interdisciplinary Reviews: Cognitive Science, 2, 580–593. [DOI] [PubMed] [Google Scholar]
- Hull C (2020). Prediction signals in the cerebellum: Beyond supervised motor learning. Elife, 9, Article e54073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hulme OJ, Morville T, & Gutkin B (2019). Neurocomputational theories of homeostatic control. Physics of Life Reviews, 1, 1–19. 10.1016/j.plrev.2019.07.005 [DOI] [PubMed] [Google Scholar]
- Hutchinson JB, & Barrett LF (2019). The power of predictions: An emerging paradigm for psychological research. Current Directions in Psychological Science. 10.1177/0963721419831992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadmon J, Timcheck J, & Ganguli S (2020). Predictive coding in balanced neural networks with noise, chaos and delays. Advances in Neural Information Processing Systems, NeurIPS, 1–12. arXiv:2006.14178. [Google Scholar]
- Kappen HJ (2005). Path integrals and symmetry breaking for optimal control theory. Journal of Statistical Mechanics: Theory and Experiment 11011, 205–229. 10.1088/1742-5468/2005/11/P11011. arXiv:0505066. [DOI] [Google Scholar]
- Kappen HJ, & Ruiz HC (2016). Adaptive importance sampling for control and inference. Journal of Statistical Physics, 162, 1244–1266. 10.1007/S10955-016-1446-7. arXiv:1505.01874. [DOI] [Google Scholar]
- Katsumi Y, Kamona N, Zhang J, Bunce JG, Hutchinson JB, Yarossi M, & Barrett LF (2021). Functional connectivity gradients as a common neural architecture for predictive processing in the human brain. BioRxiv. [Google Scholar]
- Kawato M (1999). Internal models for motor control and trajectory planning. Current Opinion in Neurobiology, 9, 718–727. 10.1016/S0959-4388(99)00028-8 [DOI] [PubMed] [Google Scholar]
- Keramati M, & Gutkin B (2014). Homeostatic reinforcement learning for integrating reward collection and physiological stability. eLife, 3. 10.7554/eLife.04811.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiebel SJ, Daunizeau J, & Friston KJ (2008). A hierarchy of time-scales and the brain. PLoS Computational Biology, 4, Article e1000209. 10.1371/journal.pcbi.1000209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirchhoff M, Parr T, Palacios E, Friston K, & Kiverstein J (2018). The markov blankets of life: Autonomy, active inference and the free energy principle. Journal of the Royal Society Interface, 15. 10.1098/rsif.2017.0792 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleckner IR, Zhang J, Touroutoglou A, Chanes L, Xia C, Simmons WK, & FeldmanBarrett L (2017). Evidence for a large-scale brain system supporting allostasis and interoception in humans. Nature Human Behaviour, 1. 10.1038/s41562-017-0069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein C (2018). What do predictive coders want? Synthese, 195, 2541–2557. [Google Scholar]
- Kobayashi K, & Hsu M (2019). Common neural code for reward and information value. Proceedings of the National Academy of Sciences, 116, 13061–13066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi S, & Schultz W (2008). Influence of reward delays on responses of dopamine neurons. Journal of Neuroscience, 28, 7837–7846. 10.1523/JNEUROSCI.1600-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koller D, & Friedman N (2009). Probabilistic graphical models: Principles and techniques. MIT Press. [Google Scholar]
- König M, Bulik S, & Holzhütter HG (2012). Quantifying the contribution of the liver to glucose homeostasis: A detailed kinetic model of human hepatic glucose metabolism. PLoS Computational Biology, 8. 10.1371/journal.pcbi.1002577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Körding KP, & Wolpert DM (2006). Bayesian decision theory in sensorimotor control. Trends in Cognitive Sciences, 10, 319–326. 10.1016/j.tics.2006.05.003 [DOI] [PubMed] [Google Scholar]
- Kotas ME, & Medzhitov R (2015). Homeostasis, inflammation, and disease susceptibility. Cell, 160, 816–827. 10.1016/j.cell.2015.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML (2010). Motor synergies and the equilibrium-point hypothesis. Motor Control, 14, 294–322. 10.1123/mcj.14.3.294 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML (2021). Laws of nature that define biological action and perception. Physics of Life Reviews, 36, 47–67. 10.1016/j.plrev.2020.07.007 [DOI] [PubMed] [Google Scholar]
- Lee KM, Ferreira-Santos F, & Satpute AB (2021). Predictive processing models and affective neuroscience. Neuroscience and Biobehavioral Reviews, 131, 211–228. 10.1016/j.neubiorev.2021.09.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leshinskaya A, Wurm MF, & Caramazza A (2020). Concepts of actions and their objects. The Cognitive Neurosciences, 757–765. [Google Scholar]
- Lindquist KA, & Barrett LF (2012). A functional architecture of the human brain: Emerging insights from the science of emotion. Trends in Cognitive Sciences, 16, 533–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu B, Hong A, Rieke F, & Manookin MB (2021). Predictive encoding of motion begins in the primate retina. Nature Neuroscience, 24, 1280–1291. 10.1038/s41593-021-00899-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowet AS, Zheng Q, Matias S, Drugowitsch J, & Uchida N (2020). Distributional reinforcement learning in the brain. Trends in Neurosciences, 43, 980–997. 10.1016/j.tins.2020.09.004. ⟨https://www.sciencedirect.com/science/article/pii/S0166223620301983⟩ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowet AS, Zheng Q, Matias S, Drugowitsch J, & Uchida N (2020). Distributional reinforcement learning in the brain. Trends in Neurosciences. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maeda RS, Cluff T, Gribble PL, & Pruszynski JA (2018). Feedforward and feedback control share an internal model of the arm’s dynamics. Journal of Neuroscience, 38, 10505–10514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangalam M, & Kelty-Stephen DG (2021). Point estimates, Simpson’s paradox, and nonergodicity in biological sciences. Neuroscience and Biobehavioral Reviews, 125, 98–107. 10.1016/j.neubiorev.2021.02.017 [DOI] [PubMed] [Google Scholar]
- Manohar SG, Chong TT-J, Apps MA, Batla A, Stamelou M, Jarman PR, & Husain M (2015). Reward pays the cost of noise reduction in motor and cognitive control. Current Biology, 25, 1707–1716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marken RS, et al. (2001). Controlled variables: Psychology as the center fielder views it. American Journal of Psychology, 114, 259–282. [PubMed] [Google Scholar]
- McBeath MK, Shaffer DM, & Kaiser MK (1995). How baseball outfielders determine where to run to catch fly balls. Science, 268, 569–573. 10.1126/science.7725104. ⟨https://science.sciencemag.org/content/268/5210/569https://science.sciencemag.org/content/268/5210/569.abstract⟩ [DOI] [PubMed] [Google Scholar]
- McDowall LM, & Dampney RA (2006). Calculation of threshold and saturation points of sigmoidal baroreflex function curves. American Journal of Physiology - Heart and Circulatory Physiology, 291, 2003–2007. 10.1152/ajpheart.00219.2006 [DOI] [PubMed] [Google Scholar]
- McNamee D, & Wolpert DM (2019). Internal models in biological control, annual review of control. Robotics, and Autonomous Systems, 2, 339–364. 10.1146/annurev-control-060117-105206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menchón SA, & Kappen HJ (2019). Learning effective state-feedback controllers through efficient multilevel importance samplers. International Journal of Control, 92, 2776–2783. 10.1080/00207179.2018.1459857 [DOI] [Google Scholar]
- Merel J, Botvinick M, & Wayne G (2019). Hierarchical motor control in mammals and machines. Nature Communications, 10, 1–12. 10.1038/s41467-019-13239-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millidge B (2020). Deep active inference as variational policy gradients. Journal of Mathematical Psychology, 96, Article 102348. 10.1016/j.jmp.2020.102348. arXiv:1907.03876. [DOI] [Google Scholar]
- Millidge B, Tschantz A, & Buckley CL (2021). Whence the expected free energy? Neural Computation, 33, 447–482. arXiv:arXiv:2004.08128v3. [DOI] [PubMed] [Google Scholar]
- Mitchell BA, Lauharatanahirun N, Garcia JO, Wymbs N, Grafton S, Vettel JM, & Petzold LR (2019). A minimum free energy model of motor learning. Neural Computation, 31, 1945–1963. 10.1162/neco_a_01219 [DOI] [PubMed] [Google Scholar]
- Morville T, Friston K, Burdakov D, Siebner HR, & Hulme OJ (2018). The homeostatic logic of reward. bioRxiv, Article 242974. [Google Scholar]
- Mrosovsky N (1990). Rheostasis: The physiology of change. Oxford University Press. [Google Scholar]
- Muller PA, Matheis F, Schneeberger M, Kerner Z, Jové V, & Mucida D (2020). Microbiota-modulated CART+ enteric neurons autonomously regulate blood glucose. Science, 370, 314–321. 10.1126/science.abd6176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakahira Y, Liu Q, Bernat N, Sejnowski T, & Doyle J (2019). Theoretical foundations for layered architectures and speed-accuracy tradeoffs in sensorimotor control. Proceedings of the American Control Conference 2019-July, 809–814. 10.23919/acc.2019.8814897 [DOI] [Google Scholar]
- Nasiriany S, Pong VH, Nair A, Khazatsky A, Berseth G, & Levine S (2021). DisCo RL: Distribution-conditioned reinforcement learning for general-purpose policies. IEEE International Conference on Robotics and Automation. arXiv:2104.11707. [Google Scholar]
- Niv Y (2009). Reinforcement learning in the brain. Journal of Mathematical Psychology, 53, 139–154. [Google Scholar]
- Niv Y, Edlund JA, Dayan P, & O’Doherty JP (2012). Neural prediction errors reveal a risk-sensitive reinforcement-learning process in the human brain. Journal of Neuroscience, 32, 551–562. 10.1523/JNEUROSCI.5498-10.2012. ⟨https://www.jneurosci.org/content/32/2/551⟩. http://arxiv.org/abs/https://www.jneurosci.org/content/32/2/551.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogoh S, Fisher JP, Dawson EA, White MJ, Secher NH, & Raven PB (2005). Autonomic nervous system influence on arterial baroreflex control of heart rate during exercise in humans. Journal of Physiology, 566, 599–611. 10.1113/jphysiol.2005.084541 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogoh S, Wasmund WL, Keller DM, Yurvati AO, Gallagher KM, Mitchell JH, & Raven PB (2002). Role of central command in carotid baroreflex resetting in humans during static exercise. Journal of Physiology, 543, 349–364. 10.1113/jphysiol.2002.019943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osborn JW, & Foss JD (2017). Renal nerves and long-term control of arterial pressure. Comprehensive Physiology, 7, 263–320. 10.1002/cphy.c150047 [DOI] [PubMed] [Google Scholar]
- Penny W, & Stephan K (2014). A dynamic bayesian model of homeostatic control. Adaptive and Intelligent Systems, 60–69. [Google Scholar]
- Peters O (2019). The ergodicity problem in economics. Nature Physics, 15, 1216–1221. 10.1038/s41567-019-0732-0 [DOI] [Google Scholar]
- Petzschner FH, Garfinkel SN, Paulus MP, Koch C, & Khalsa SS (2021). Computational models of interoception and body regulation. Trends in Neurosciences, 44, 63–76. 10.1016/j.tins.2020.09.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezzulo G, & Cisek P (2016). Navigating the affordance landscape: Feedback control as a process model of behavior and cognition. Trends in Cognitive Sciences, 20, 414–424. 10.1016/j.tics.2016.03.013 [DOI] [PubMed] [Google Scholar]
- Pezzulo G, Donnarumma F, Iodice P, Maisto D, & Stoianov I (2017). Model-based approaches to active perception and control. Entropy, 19. 10.3390/e19060266 [DOI] [Google Scholar]
- Pezzulo G, Rigoli F, & Friston K (2015). Active Inference, homeostatic regulation and adaptive behavioural control. Progress in Neurobiology, 134, 17–35. 10.1016/j.pneurobio.2015.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezzulo G, Rigoli F, & Friston KJ (2018). Hierarchical active inference: A theory of motivated control. Trends in Cognitive Sciences, 22, 294–306. 10.1016/j.tics.2018.01.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piray P, & Daw N (2019). Linear reinforcement learning: Flexible reuse of computation in planning. grid fields, and cognitive control. 10.1101/856849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Potts JT, Shi X, & Raven PB (1995). Cardiopulmonary baroreceptors modulate carotid baroreflex control of heart rate during dynamic exercise in humans. American Journal of Physiology - Heart and Circulatory Physiology, 268. 10.1152/ajpheart.1995.268.4.h1567 [DOI] [PubMed] [Google Scholar]
- Potts JT, Shi XR, & Raven PB (1993). Carotid baroreflex responsiveness during dynamic exercise in humans. American Journal of Physiology - Heart and Circulatory Physiology, 265. 10.1152/ajpheart.1993.265.6.h1928 [DOI] [PubMed] [Google Scholar]
- Qian N, & Zhang J (2019). Neuronal firing rate as code length: A hypothesis. Computational Brain & Behavior, 34–53. 10.1007/s42113-019-00028-z [DOI] [Google Scholar]
- Quigley KS, Kanoski S, Grill WM, Barrett LF, & Tsakiris M (2021). Functions of interoception: From energy regulation to experience of the self. Trends in Neurosciences, 44, 29–38. 10.1016/j.tins.2020.09.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramstead MJ, Kirchhoff MD, & Friston KJ (2020). A tale of two densities: Active inference is enactive inference. Adaptive Behavior, 28, 225–239. 10.1177/1059712319862774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowell LB, O’Leary DS, & Kellogg DL (1996). Integration of cardiovascular control systems in dynamic exercise. Comprehensive Physiology, 770–838. 10.1002/cphy.cp120117 [DOI] [Google Scholar]
- Sanborn AN (2017). Types of approximation for probabilistic cognition: Sampling and variational. Brain and Cognition, 112, 98–101. 10.1016/j.bandc.2015.06.008. ⟨https://www.sciencedirect.com/science/article/pii/S0278262615300038⟩ (perspectives on Human Probabilistic Inferences and the ‘Bayesian Brain’). [DOI] [PubMed] [Google Scholar]
- Satpute AB, & Lindquist KA (2019). The default mode network’s role in discrete emotion. Trends in Cognitive Sciences, 23, 851–864. 10.1016/j.tics.2019.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saunders PT, Koeslag JH, & Wessels JA (1998). Integral rein control in physiology. Journal of Theoretical Biology, 194, 163–173. 10.1006/JTBI.1998.0746. ⟨https://www.sciencedirect.com/science/article/pii/S0022519398907469?via%3Dihub%0Ahttp://linkinghub.elsevier.com/retrieve/pii/S0022519398907469%5Cnpapers2://publication/doi/10.1006/jtbi.1998.0746⟩ [DOI] [PubMed] [Google Scholar]
- Saunders PT, Koeslag JH, & Wessels JA (2000). Integral rein control in physiology II: A general model. Journal of Theoretical Biology, 1–13. [DOI] [PubMed] [Google Scholar]
- Scholz JP, & Schöner G (1999). The uncontrolled manifold concept: Identifying control variables for a functional task. Experimental Brain Research, 126, 289–306. 10.1007/s002210050738 [DOI] [PubMed] [Google Scholar]
- Schulkin J, & Sterling P (2019). Allostasis: A brain-centered predictive mode of physiological regulation. Trends in Neurosciences, 42, 740–752. 10.1016/j.tins.2019.07.010 [DOI] [PubMed] [Google Scholar]
- Schwartenbeck P, FitzGerald TH, & Dolan R (2016). Neural signals encoding shifts in beliefs. Neuroimage, 125, 578–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, & Ahmed AA (2020). Vigor: Neuroeconomics of movement control. MIT Press. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Huang HJ, & Ahmed AA (2016). A representation of effort in decision-making and motor control. Current Biology, 26, 1929–1934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith R, Kuplicki R, Feinstein J, Forthman KL, Stewart JL, Paulus MP, & Khalsa SS (2020). A bayesian computational model reveals a failure to adapt interoceptive precision estimates across depression, anxiety, eating, and substance use disorders. PLoS computational biology, 16, Article e1008484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith R, Kuplicki R, Teed A, Upshaw V, & Khalsa SS (2020). Confirmatory evidence that healthy individuals can adaptively adjust prior expectations and interoceptive precision estimates. In International Workshop on Active Inference (pp. 156–164). Springer. [Google Scholar]
- Smith R, Thayer JF, Khalsa SS, & Lane RD (2017). The hierarchical basis of neurovisceral integration. Neuroscience and Biobehavioral Reviews, 75, 274–296. 10.1016/j.neubiorev.2017.02.003 [DOI] [PubMed] [Google Scholar]
- Sohn JW, & Ho WK (2020). Cellular and systemic mechanisms for glucose sensing and homeostasis. Pflugers Archiv European Journal of Physiology, 472, 1547–1561. 10.1007/s00424-020-02466-2 [DOI] [PubMed] [Google Scholar]
- Speakman JR, Levitsky DA, Allison DB, Bray MS, De Castro JM, Clegg DJ, & Westerterp-Plantenga MS (2011). Set points, settling points and some alternative models: Theoretical options to understand how genes and environments combine to regulate body adiposity. DMM Disease Models and Mechanisms, 4, 733–745. 10.1242/dmm.008698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spratling MW (2017). A review of predictive coding algorithms. Brain and Cognition, 112, 92–97. 10.1016/j.bandc.2015.11.003 [DOI] [PubMed] [Google Scholar]
- Srinivasan MV, Laughlin SB, & Dubs A (1982). Predictive coding: A fresh view of inhibition in the retina. Proceedings of the Royal Society of London - Biological Sciences, 216, 427–459. 10.1098/rspb.1982.0085 [DOI] [PubMed] [Google Scholar]
- Stachenfeld KL, Botvinick MM, & Gershman SJ (2017). Hippocampus as predictive map. Nature neuroscience, 28, 391–397. 10.1017/CBO9781107415324.004. arXiv:arXiv:1011.1669v3. [DOI] [PubMed] [Google Scholar]
- Stephan KE, Manjaly ZM, Mathys CD, Weber LA, Paliwal S, Gard T, … Seth AK (2016). Allostatic self-efficacy: a metacognitive theory of dyshomeostasis-induced fatigue and depression. Frontiers in human neuroscience, 10, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens DW, & Krebs JR (2019). Foraging theory. Princeton University Press. [Google Scholar]
- Sterling P (2012). Allostasis: A model of predictive regulation. Physiology and Behavior, 106, 5–15. 10.1016/j.physbeh.2011.06.004 [DOI] [PubMed] [Google Scholar]
- Sterling P (2014). Homeostasis vs allostasis: Implications for brain function and mental disorders. JAMA Psychiatry, 71, 1192–1193. [DOI] [PubMed] [Google Scholar]
- Sterling P, & Laughlin S (2015). Principles of neural design. MIT Press. [Google Scholar]
- Still S, Sivak DA, Bell AJ, & Crooks GE (2012). Thermodynamics of prediction. Physical Review Letters, 109, 1–5. 10.1103/PhysRevLett.109.120604. arXiv:1203.3271. [DOI] [PubMed] [Google Scholar]
- Straka H, Simmers J, & Chagnaud BP (2018). A new perspective on predictive motor signaling. Current Biology, 28, R232–R243. 10.1016/j.cub.2018.01.033 [DOI] [PubMed] [Google Scholar]
- Sutton Richard S., Barto Andrew G. (2018). Reinforcement learning, Second ed. [Google Scholar]
- Theriault JE, Young L, & Barrett LF (2021). The sense of should: A biologically-based framework for modeling social pressure. Physics of Life Reviews, 36, 100–136. 10.1016/j.plrev.2020.01.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thijssen S, & Kappen HJ (2015). Path integral control and state-dependent feedback. Physical Review E - Statistical, Nonlinear, and Soft Matter Physics, 91, 1–7. 10.1103/PhysRevE.91.032104. arXiv:1406.4026. [DOI] [PubMed] [Google Scholar]
- Todorov E (2006). Optimal control theory. Bayesian Brain: Probabilistic Approaches to Neural Coding, 268–298. [Google Scholar]
- Todorov E (2011). Finding the most likely trajectories of optimally-controlled stochastic systems. IFAC Proceedings Volumes (IFAC-PapersOnline), 44, 4728–4734. 10.3182/20110828-6-IT-1002.01704 [DOI] [Google Scholar]
- Tschantz A, Barca L, Maisto D, Buckley CL, Seth A, & Pezzulo G (2021). Simulating homeostatic, allostatic and goal-directed forms of interoceptive control using active inference. bioRxiv. [DOI] [PubMed] [Google Scholar]
- Unal O, Eren OC, Alkan G, Petzschner FH, Yao Y, & Stephan KE (2021). Inference on homeostatic belief precision. Biological Psychology, 165, Article 108190. 10.1016/j.biopsycho.2021.108190. ⟨https://www.sciencedirect.com/science/article/pii/S0301051121001836⟩ [DOI] [PubMed] [Google Scholar]
- Von Helmholtz H (1867). Treatise on physiological optics vol. iii. [Google Scholar]
- James W, The principles of psychology, se - 2vol ed., Henry Holt and Company, New York, NY, USA, 1890.⟨http://link.library.utoronto.ca/eir/EIRdetail.cfm?Resources_ID=1117305&T=F&,vol.=1⟩. [Google Scholar]
- Watter M, Springenberg JT, Boedecker J, & Riedmiller M (2015). Embed to Control: A locally linear latent dynamics model for control from raw images. Advances in Neural Information Processing Systems. [Google Scholar]
- Williams G, Drews P, Goldfain B, Rehg JM, & Theodorou EA (2018). Information theoretic model predictive control: Theory and applications to autonomous driving. IEEE Transactions on Robotics, 34, 1603–1622. [Google Scholar]
- Wolpert DM, & Kawato M (1998). Multiple paired forward and inverse models for motor control. Neural Networks, 11, 1317–1329. 10.1016/S0893-6080(98)00066-5 [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Miall RC, & Kawato M (1998). Internal models in the cerebellum. Trends in Cognitive Sciences, 2, 338–347. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Pearson KG, Ghez CP (2013). The organization and planning of movement, in: Principles of neuroscience, 5 ed., pp. 743–767. [Google Scholar]
- Woods SC, & Ramsay DS (2007). Homeostasis: Beyond Curt Richter. Appetite, 49, 388–398. 10.1016/j.appet.2006.09.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo SH, Franklin DW, & Wolpert DM (2016). When optimal feedback control is not enough: Feedforward strategies are required for optimal control with active sensing. PLoS Computational Biology, 12, 1–22. 10.1371/journal.pcbi.1005190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin HH (2013). Restoring purpose in behavior. In Computational and robotic models of the hierarchical organization of behavior (pp. 319–347). Springer. [Google Scholar]
- Young HA, Gaylor CM, de Kerckhove D, Watkins H, & Benton D (2019). Interoceptive accuracy moderates the response to a glucose load: A test of the predictive coding framework. Proceedings of the Royal Society B, 286, Article 20190244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanutto BS, Valentinuzzi ME, & Segura ET (2010). Neural set point for the control of arterial pressure: Role of the nucleus tractus solitarius. BioMedical Engineering Online, 9, 1–13. 10.1186/1475-925X-9-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Abiose O, Katsumi Y, Touroutoglou A, Dickerson BC, & Barrett LF (2019). Intrinsic functional connectivity is organized as three interdependent gradients. Scientific Reports, 9, 1–14. 10.1038/s41598-019-51793-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerman CA, & Knight ZA (2020). Layers of signals that regulate appetite. Current Opinion in Neurobiology, 64, 79–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmerman CA, Lin YC, Leib DE, Guo L, Huey EL, Daly GE, & Knight ZA (2016). Thirst neurons anticipate the homeostatic consequences of eating and drinking. Nature, 537, 680–684. 10.1038/nature18950 [DOI] [PMC free article] [PubMed] [Google Scholar]