Multi-outputs Gaussian process for predicting Burkina Faso COVID-19 spread using correlations from the weather parameters

Abstract

The novel coronavirus has affected all regions of the world, but each country has experienced different rates of infection. In West Africa, in particular, infection rates remain low as compared to other parts of the world. This heterogeneity in the spread of COVID-19 raises a lot of questions that are still unanswered. However, some studies point out that people's mobility, size of gatherings, rate of testing, and weather have a great impact on the COVID-19 spread. In this work, we first evaluate the correlation between meteorological parameters and COVID-19 cases using Spearman's rank correlation. Secondly, multi-output Gaussian processes (MOGP) are used to predict the daily confirmed COVID-19 cases by exploring its relationships with meteorological parameters. The number of daily reported COVID-19 cases, as well as, weather variables collected from March 9, 2020, to October 18, 2021, were used in the analysis. The weather variables considered in the analysis are the mean temperature, relative humidity, wind direction, insolation, precipitation, and wind speed. The predicting model was constructed exploiting the correlation between the data of the daily confirmed COVID-19 cases and data of the weather variables. The results show that a significant correlation between the daily confirmed COVID-19 cases was found with humidity, wind direction, wind speed, and insolation. These parameters are used to construct the predictive model using the Multi-Output Gaussian process (MOGP). Different combinations of the data of meteorological parameters together with the data of daily reported COVID-19 cases were used to derive different models. We found that the best predictor is obtained using the combination of Humidity and insolation. This model is then used to predict the daily confirmed COVID-19 cases knowing the humidity and Insolation.

1. Introduction

The first human cases of Coronavirus disease 2019 (COVID-19) were identified in Wuhan, China in December 2019 and it has been declared a global pandemic by World Health Organization (WHO) on March 11, 2020 (WHO2020). According to the WHO Coronavirus (COVID-19) report on January 31, 2022, there have been 373,229,380 confirmed cases of COVID-19, including 5,658,702 deaths. Burkina Faso reported its first two confirmed cases on March 9, 2020, since then, the number of cases has increased in both cities Ouagadougou and Bobo Dioulassao. As of January, 31, 2022 data from Corus Burkina Faso shows 20,624 confirmed cases and 368 deaths recorded.

At the beginning of the disease, different studies have been conducted to model the spread for the development and implementation of evidence-based public health and disease control policies. Mathematical models based on the susceptible-infectious-removed (SIR) class of models have been used to inform public policies (Calafiore, Novara, & Possieri, 2020; Chen, Lu, Chang, & Liu, 2020; Li & Muldowney, 1995; Yang et al., 2020). The difficulty of SIR class problems is to find the right epidemiological model according to the context and the relevant assumptions, which is not obvious due to a high level of uncertainty and lack of essential data, epidemiological models have shown low accuracy for long-term prediction. In the literature, recent studies have used various statistical and machine learning models for short-term forecasting of the COVID-19 pandemic (Kumar Mojjada, Yadav, Prabhu, & Natarajan, 2020; Liu et al., 2020; Niazkar Niazkar, 2020; PinterImre et al., 2020). Machine learning-based has been used to deal with many epidemic situation (Jiang, Hao, Ding, Fu, & Meng, 2018; Mamoona et al., 2021; Poostchi, Silamut, Maude, Jaeger, & George, 2018). This approach used the available data to construct a predictive model. Many machine learning techniques have been used to forecast COVID-19 spread, among these methods, we can cite Linear Regression, LASSO Regression, Support Vector Machine, Exponential Smoothing, artificial neural networks (Kumar Mojjada et al., 2020; Niazkar Niazkar, 2020).

Herein we focus on the use of the Multi-output Gaussian process(MOGP) to construct a low-cost and efficient COVID-19 predictive model in the context of Burkina Faso. Gaussian process (GP) is a Bayesian nonparametric model. GPs are designed through parametrizing a covariance kernel. The GP can be used to perform predictions under spatial, temporal, and spatiotemporal scenarios (Chiplunkar, Rachelson, Colombo, & Joseph, 2017, pp. 88–103; de Wolff, Cuevas, & MOGPTK, 2020; Parra & Tobar, 2017; Álvarez, Luengo, Titsias, Neil, & Lawrence, 2010, pp. 25–32). The approach has received much attention due to its flexibility to consider prior information in the construction of the predictive model. One advantage of using the Gaussian process as compared to other machine learning techniques is due to the natural prediction of uncertainty on prediction and the facility to consider the complex dependencies between input and outputs in the predictive model. In the field of health and infectious diseases, Gaussian processes have been extensively used to construct predictive models, for missing data, or for image reconstruction, (Cheng et al., 2018; David Futoma, 2018). In this work, we are exploring the flexibility of MOGP to consider the correlation between meteorological parameters and COVID-19 in the building of a prediction model. The idea is to first investigate the existence of a relationship between COVID-19 confirmed cases in Ouagadougou and meteorological parameters and secondly select the most correlated meteorological parameter to construct the MOGP. Which can be used to improve the prediction of future confirmed cases in Burkina Faso.

The influence of weather variability on the transmission of COVID-19 is a hot topic of research. Only in 2020 several articles have been published on this topic. In (McClymont & Hu, 2021) authors discuss the results of 23 studies published in 2020. According to the authors, there appears to be no consensus on the effect of certain climate variables on the spread of COVID-19. For example, Canada (To et al., 2021), Spain (Briz-Redón & Serrano-Aroca, 2020) and New South Wales (NSW) Australia (Ward, Xiao, & Zhang, 2020) shows no correlation between temperature on new daily cases. However studies from (sub)tropical cities of Brazil (Prata, Rodrigues, & Bermejo, 2020), Africa (Ayoade Adekunle, Adewale Tella, Oyesiku, & Olasunkanmi Oseni, 2020), New York City, USA (Bashir et al., 2020), Oslo(Norway) (Moges Menebo, 2020), Indonesia (Tosepu et al., 2020) show the existence of significant correlation between COVID19 spread and temperature. Concerning humidity, several studies have shown the existence of a correlation (McClymont & Hu, 2021). Nevertheless, authors are unanimous on the existence of very low or negligible correlation between COVID19 transmission and wind speed and precipitation (McClymont & Hu, 2021).

This article intends to first present the data used for modeling, Secondly, we show the existence of a correlation between COVID-19 spread and meteorological parameters using the Spearman rank correlation. In third, we present the modeling and prediction model using the MOGP, in last we present the conclusion and the Appendix.

2. Materials and methods

Herein, the datasets of daily confirmed cases of COVID-19 in Burkina Faso were obtained from the Health emergency response center named CORUS-BF. The meteorological data are obtained through the National Meteorological Agency (NAMA-BF). The mean temperature (°C), relative humidity (%), wind direction (°) , insolation(daily exposure), precipitation(mm), and wind speed (m/s) are obtained in Ouagadougou weather Station. The insolation or the duration of insolation is measured by a heliograph, is the time during which direct solar radiation is greater than a threshold of 120 W m⁻²; it is expressed in hour.

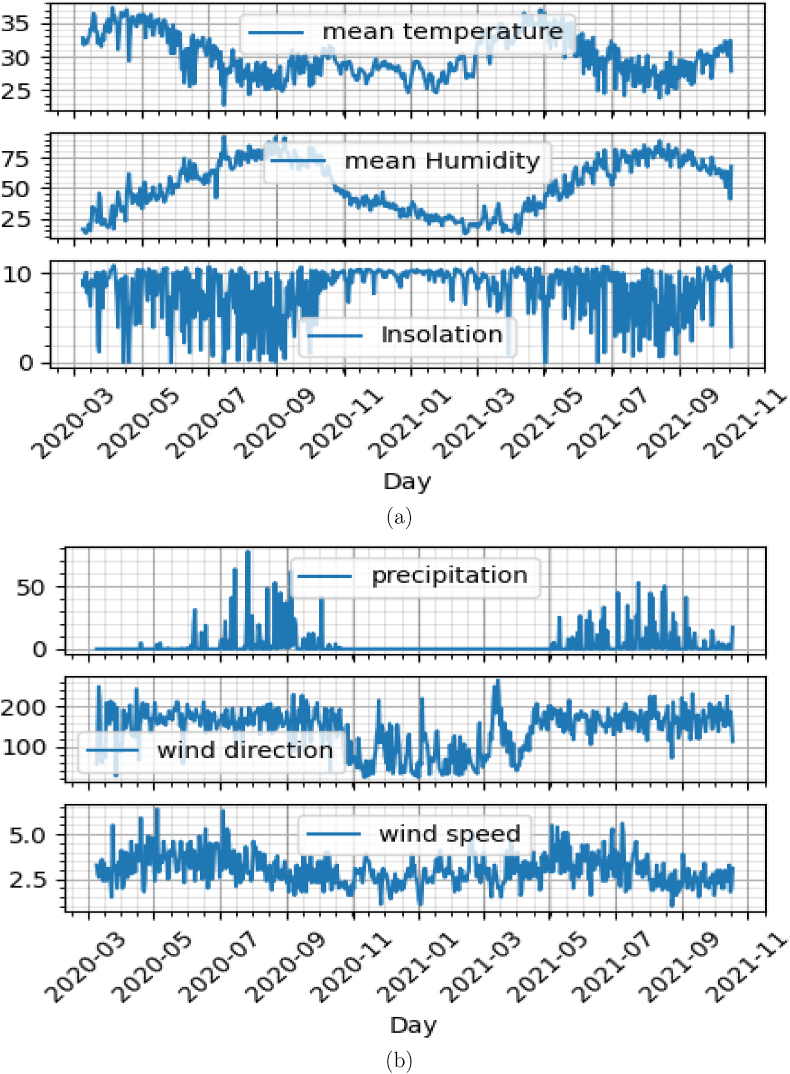
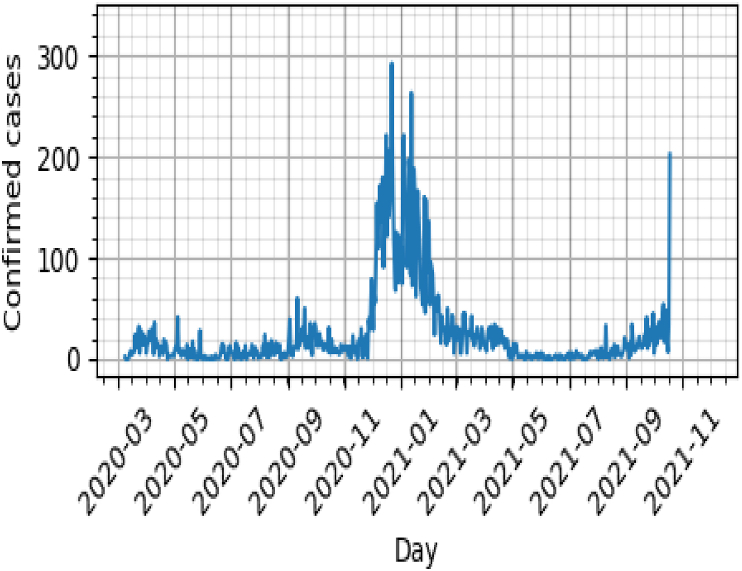
Fig. 1-(a,b) present the daily collected data of the aforementioned meteorological variables into the period of study while Fig. 2 shows the reported daily cases of COVID-19. The first look at these figures reveals that the number of COVID-19 cases presents the peak from November to January and the same period of time the humidity, wind direction, and insolation present some variation pattern. As can be seen from these figures, there is some reason to investigate possible correlation between the spread of the COVID-19 and the meteorological parameters. To quantify the degree of correlation that may exists between climate variables and the number of reported COVID-19 cases, we make use of the Spearman correlation coefficient as described next.

Fig. 1.

a) Above: daily mean temperature, mean humidity, mean insolation. b) below: precipitation, wind direction, wind speed.

Fig. 2.

COVID-19 confirmed cases.

3. Spearman's rank correlation

The correlation between weather variables and COVID-19 reported confirmed cases can be computed by using the well-known so-called Spearman's rank correlation (Glasser & Winter 1961; Spearman, 1904). The coefficient of Spearsman can be expressed as

$$\mathbf{\rho }=1-\frac{6\sum \underset{i}{\overset{2}{d}}}{N(N^2-1)}$$ (1)

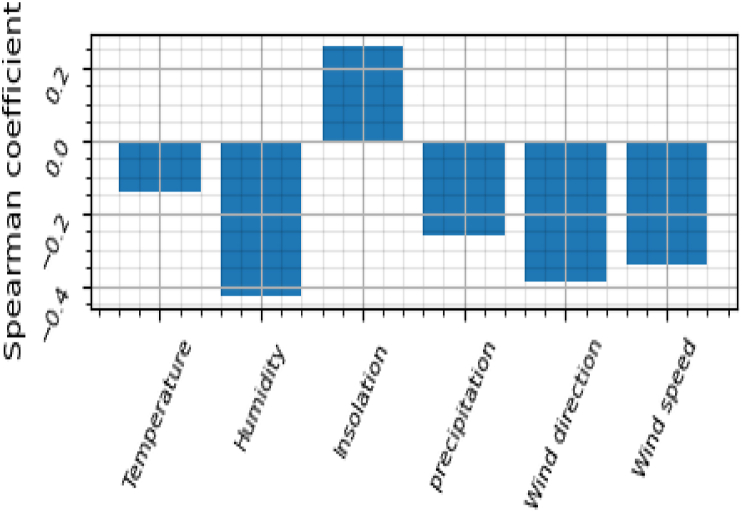
where d_i the pairwise distances of the ranks of the “ith” element, N the number of samples. This coefficient ranges between −1 and +1. |ρ| close to 0 means that there are no-correlation variables and when the coefficient is close to 1 there is a very strong correlation. We compute correlation coefficient ρ between the daily number of reported COVID-19 cases with the meteorological parameters. In Fig. 3, we show the histogram representing the Spearman correlation for each climatic variable associated with the daily number of reported COVID-19 cases. As it can be noticed in this figure humidity, wind direction, and wind speed are the climatic variables which are more correlated with the daily number of reported COVID-19 cases. The precipitation and insolation present a moderate correlation. Among the weather variables use in this study, the temperature is the less correlated variable. These results also reveal that the Humidity, temperature, wind direction, and wind speed present negative Spearman coefficient which means that when this variable increase, the number of confirmed cases decrease.

Fig. 3.

the Spearman correlation coefficient obtained by association between COVID19 cases and climatic variables.

4. Multi-output Gaussian process

A Gaussian process is an infinite-dimensional multi-variate Gaussian (Rasmussen & Williams, 2006). This process can be parametrized by mean and covariance functions. Considering that the output function is represented by y(t) obtained at time t. Assuming that y follow GP,

$$\mathbf{y}(t)\sim \mathcal{GP}(\mathbf{m}(\mathbf{t},\mathit{\theta }),K(\mathbf{t},{\mathbf{t}}^{\prime },\mathit{\theta })),$$ (2)

with mean m and a covariance K determined by the hyper-parameters θ. Given the datset inputs-outputs (t, y) the posterior mean m_∗ Eq (3) and variance C_∗ Eq (4) are expressed as:

$${\mathbf{m}}_{\ast }=K{(t_{\ast },t)}^{T}K{(t,t)}^{-1}y,$$ (3)

$${\mathbf{C}}_{\ast }=K(t_{\ast },t_{\ast })-K{(t_{\ast },t)}^{T}K{(t,t)}^{-1}K(t_{\ast },t).$$ (4)

Knowing the dataset, the hyper-parameters are obtained by the maximization of marginal likelihood (ML). Herein the GPy (GPy, 2012) and (de Wolff et al., 2020), a Gaussian Process (GP) framework in Python is used for GP simulation. The efficiency of GP model depends on the choice of the covariance function. However, there is not a standard method to choose the best covariance associated with the dataset. There are many types of GP covariance functions the most used are squared exponential function and the Matérn covariance family. These covariances can be organized to consider single or multi-outputs. The number of reported COVID-19 cases is represented as a time series, in which case the Gaussian processes use time as an input and can lead with one or several outputs. In the case of one output, the prediction models depend only on the past data-set. For various outputs, correlations between the outputs can be added to improve the model's prediction. The multi-outputs GP(MOGP) present the same assumption as single GP however the difference lies in covariance structure. The MOGP considers the auto and cross-covariance function between outputs. Suppose two outputs y₁(t) and y₂(t) using the MOGP it is possible to predict y₁ based on the relationship between both outputs. In MOGP this relationship is expressed on a covariance function which can be expressed as:

$$K(\mathbf{t}\mathbf{t})=\left[\begin{array}{cccc}{k}_{11}(\mathbf{t}\mathbf{t})& k_{12}(\mathbf{t}\mathbf{t})& \dots & k_{1m}(\mathbf{t}\mathbf{t})\\ k_{21}(\mathbf{t}\mathbf{t})& k_{22}(\mathbf{t}\mathbf{t})& \dots & k_{2m}(\mathbf{t}\mathbf{t})\\ \dots & \dots & \dots & \dots \\ k_{m1}(\mathbf{t}\mathbf{t})& k_{m2}(\mathbf{t}\mathbf{t})& \dots & k_{mm}(\mathbf{t}\mathbf{t})\end{array}\right],$$

where m is the number of outputs, k_ii are the auto-covariance function and k_ij(i ≠ j) are the cross-covariances outputs.

In this work, the outputs are represented by the weather variables and number of reported COVID-19 cases. However, we first present the prediction of the number of reported COVID-19 cases by considering the single GP model. This mean that only one output are used for predicting the future COVID-19 cases.

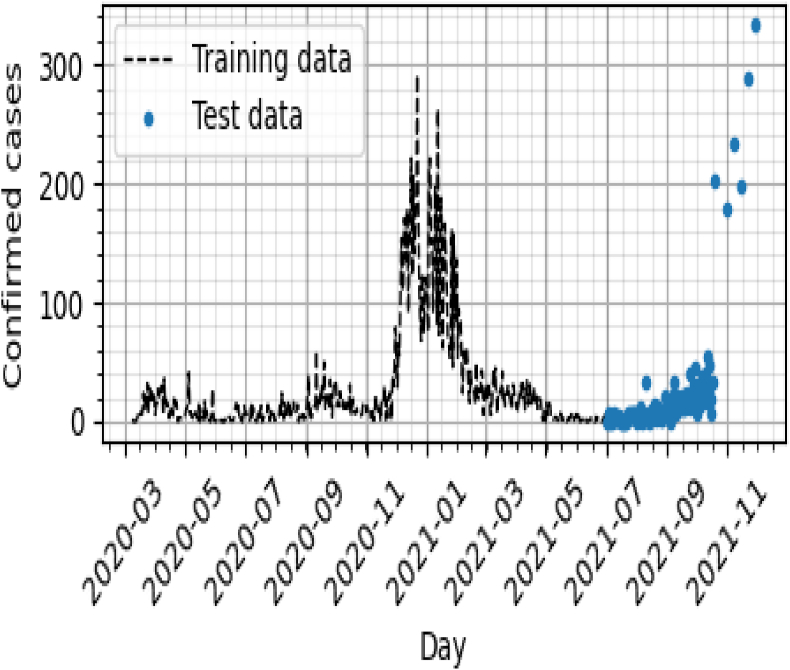
The Daily number of reported COVID-19 cases and the weather data are split into two sets named the training data (from March 9, 2020, to February 01, 2021) and the test data (From February 2, 2020, to April 16, 2021) see Fig. 4. Both, histories of the climatic variables (Humidity, wind direction, precipitation, and mean temperature and insolation.) and of the number of reported COVID-19 cases are used to build the prediction model are used to build the prediction model (see Fig. 5).

Fig. 4.

Train and test data.

Fig. 5.

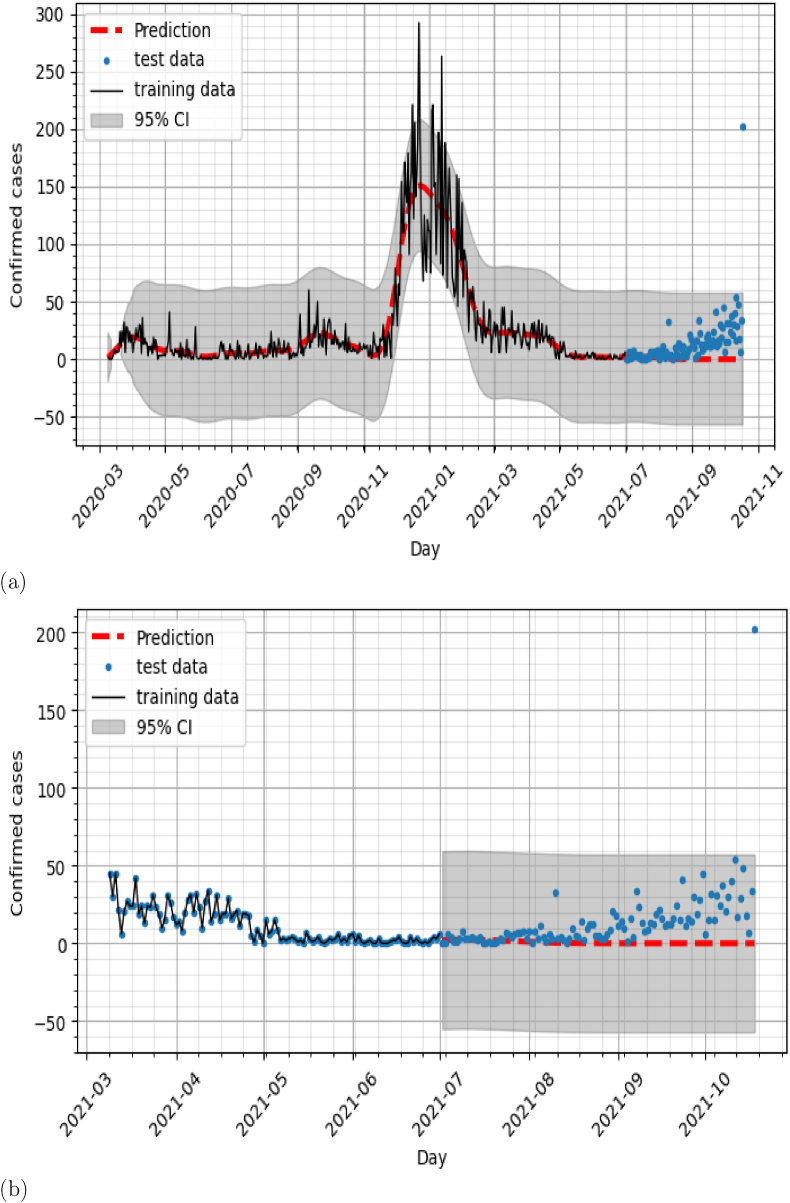
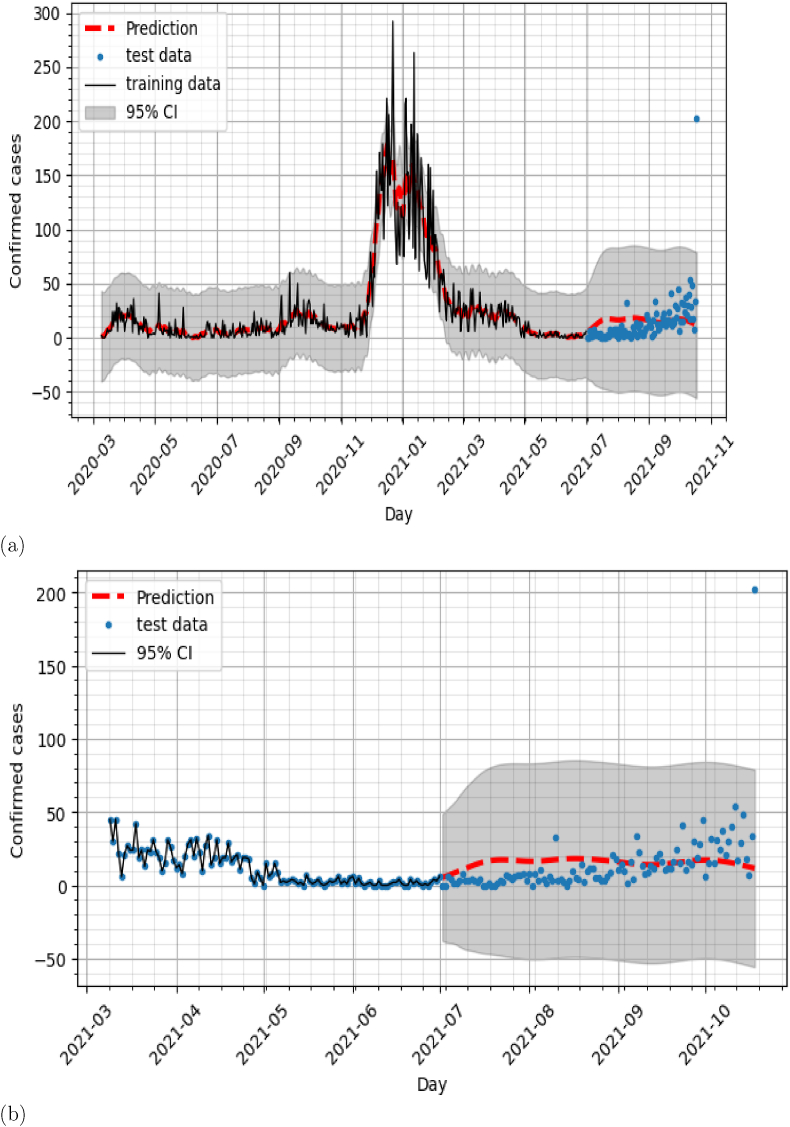
a)The square exponential: Comparison of the predicted number of reported COVID-19 cases with the reported data b) Zoom of a).

We asses the predictive accuracy of the models employing two different figures of merit: the normalised root mean square error (NRMSE) can be computed on NT testing points for each output:

$$NRMSE=\sqrt{\frac{1}{NT}\sum _{j=1}^{NT}{\left((y_{\mathit{true}}^j-y_{\mathit{pred}}^j)\right)}^2},$$ (5)

where NT is number of tested data, y_true and y_pred the true data and predict output.

4.1. Single output prediction model

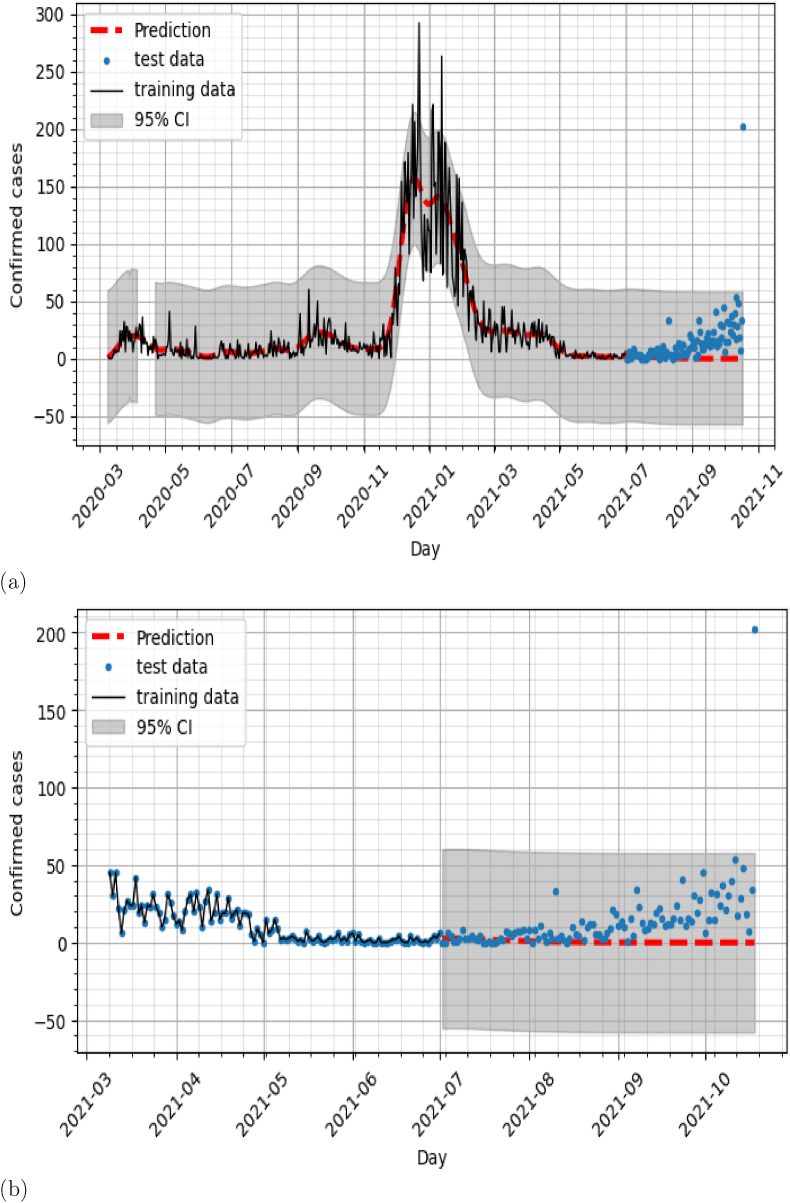
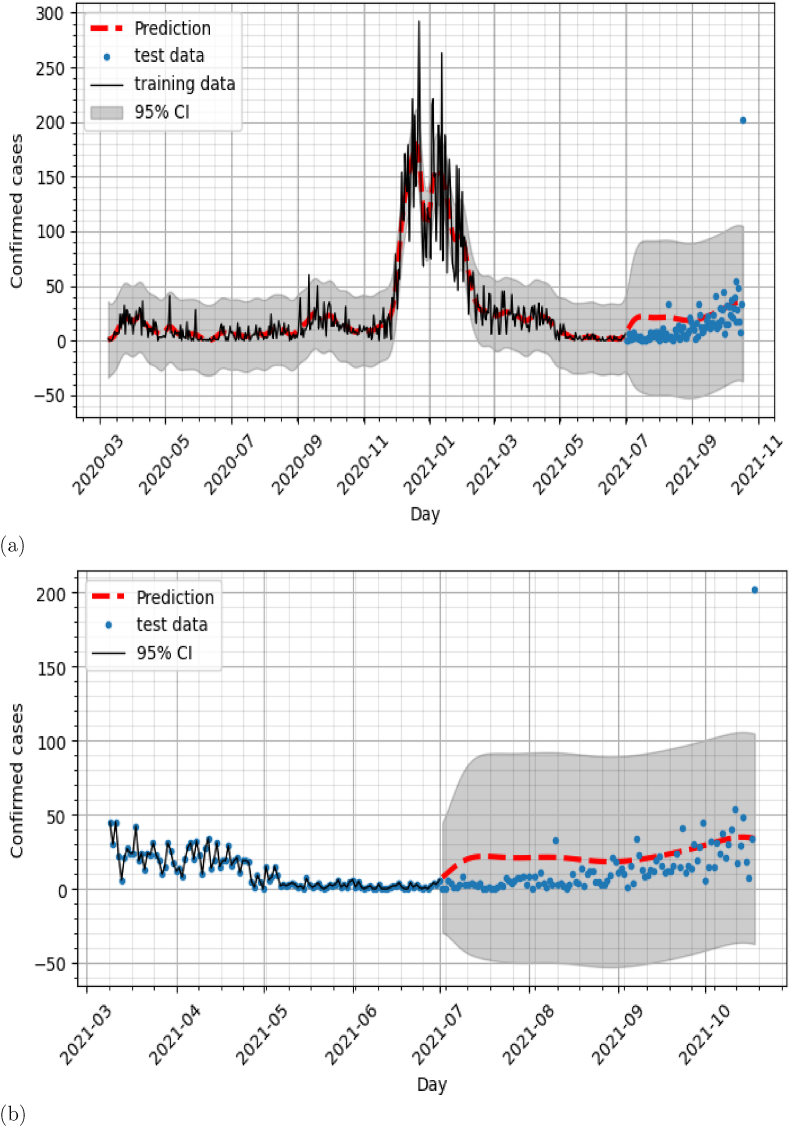
In this section, number of reported COVID-19 cases are predicted using the single GP model which consists of using only the historic data of number of reported COVID-19 cases to build the predictive model. The training data are used to estimate the hyperparameters and then we compared the prediction to the test data. The square exponential and Matern52 covariances are used as covariance functions. As can be seen in Fig. 4, Fig. 6, the predictions of both covariance models did not capture the new trend in the evolution of COVID-19 cases observed in months July, August, September. The NRSME for both predictions is 0.37. In the next section, we experiment with the association of COVID19 confirmed cases with the climatic variables in the construction of the prediction model.

Fig. 6.

a) The matern52: Comparison of the predicted number of reported COVID-19 cases with the reported data b)Zoom a).

In the rest of our investigation, we add information related to climates variables to the training data. This leads us to exploit the existence of a correlation between the cases of COVID-19 and the climatic variables. For that purpose, we use the Gaussian process with several outputs MOGP.

4.2. Multi-output prediction model

In this section, we present the predictive model of new cases of COVID-19 by considering the association between meteorological parameters and the daily number of reported COVID-19 cases. In this case, several associations can be considered as we have 6 climate variables.

The MOGP is used to build the predictive model, this method considers the correlation between two or more outputs in the construction of the model.

We consider 10 models presented in Table 1 to be tested, these models are defined based on the level of correlation with COVID-19 cases presented in section 4. Each model is a combination of COVID-19 cases with one or two meteorological parameters.

Table 1.

Performance of different association between COVID19 confirmed cases and weather variables.

models	Associations	NRMSE
1	Covid19 cases x Humidity	0.342
2	Covid19 cases x Wind direction	0.332
3	Covid19 cases x Wind speed	0.340
4	Covid19 cases x Insolation.	0.334
5	Covid19 cases x precipitation	0.360
6	Covid19 cases x Temperature	0.380
7	Covid19 cases x Humidity x Insolation.	0.315
8	Covid19 cases x Wind speed x Humidity	0.343
9	Covid19 cases x Wind direction x Humidity	0.328
10	Covid19 cases x Wind direction x Wind speed	0.380

The prediction efficiency of the models is assessed by calculating the normalize root mean square error (NRMSE). It can be seen in Table 1, that model 7 has the lowest value of NRMSE, therefore, it is chosen as the best model to predict new cases of COVID-19. This model is chosen as the best model to predict future cases of COVID-19 in Burkina Faso. The models associating the wind speed and direction are the worst, i.e. highest value of NRMSE.

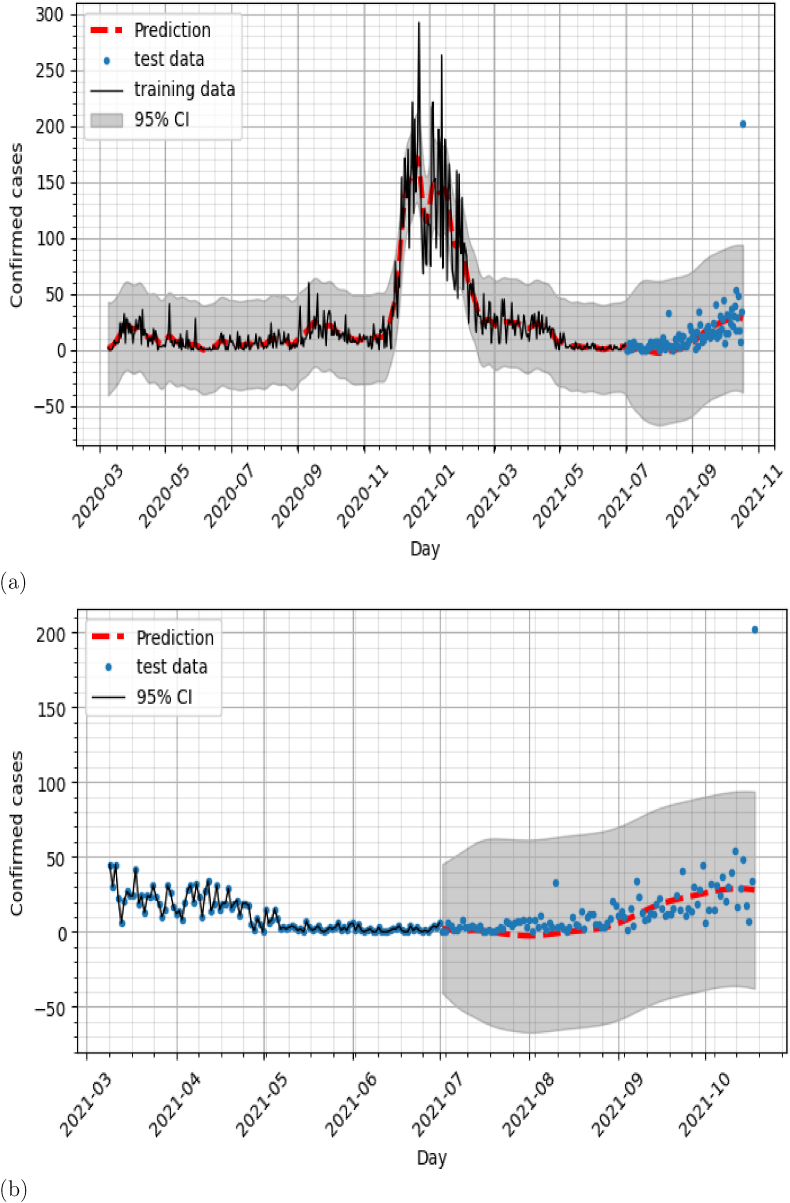
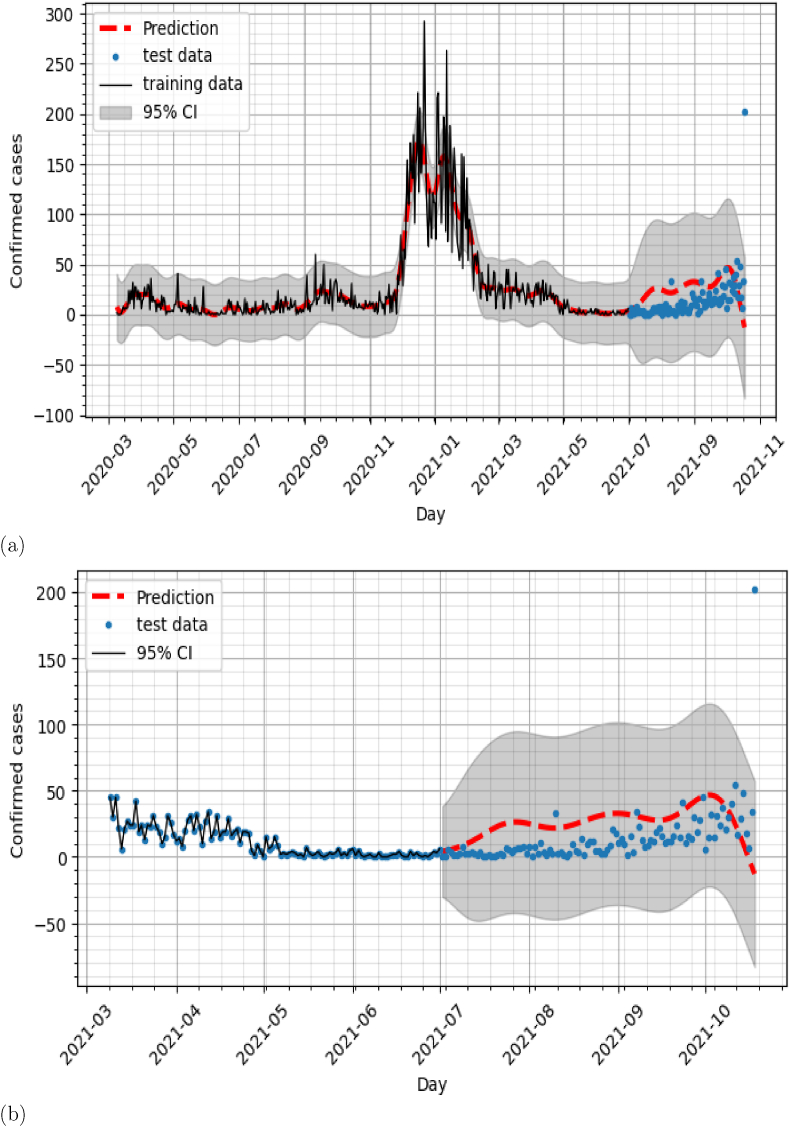
Fig. 7 presents the prediction obtained using model 7. It can be seen that compared to the single GP prediction presented in the section above, model 7 can follow the new evolution of the disease in July, August, September. The predictions of the remaining models defined in Table 1 are presented in the appendix.

Fig. 7.

a) model 7 (Covid19 cases x Humidity x Insolation) b) model 7: Zoom on test data prediction.

By examining Fig. 1.a, there seem to be a correlation between the collected mean humidity data and insolation data. Particularly, from March 2020 to September 2020, the mean humidity appears to increase while insolation exhibit large fluctuations. The same observations can be made from March 2021 to September 2021. On the other hand, in the period of time in between, that is October 2020 to February 2021, the fluctuations of the insolation are less significant and exhibit a steady behaviour around the highest magnitude, while, the mean humidity achieved lower values. Moreover, by comparing Figs. 2 and 1.a, one can notice that, the peak of COVID 19 confirmed cases, is located in the time frame October 2020–February 2021. These observations seem to corroborate with the better performance of model 7.

5. Conclusion

In this work, we investigated the impact of meteorological variables on COVID-19 spread in the context of Burkina Faso. We show that humidity, wind direction, wind speed, and insolation presented a great correlation with COVID-19 cases. Then we have developed the predictive model based on the spread of COVID-19 using the association between COVID-19 historical data and meteorological parameters. We use the Multi-Output Gaussian processes to construct the predictive model considering associations between meteorological variables. To validate the proposed model we have used available data on COVID-19 and weather data. In total, we have tested 10 models based on a combination between weather data and COVID-19 confirmed cases. The results show that the model built using Humidity and insolation presents better results. Therefore this model is used for predicting new cases of COVID-19 in Burkina Faso. The other models involving mean temperature, and wind speed are not elected for prediction. In our future work, we will look at the association between COVID-19 spread and other diseases such as malaria and will investigate the best model for predicting these diseases.

Handling Editor: Dr HE DAIHAI HE

Appendix.

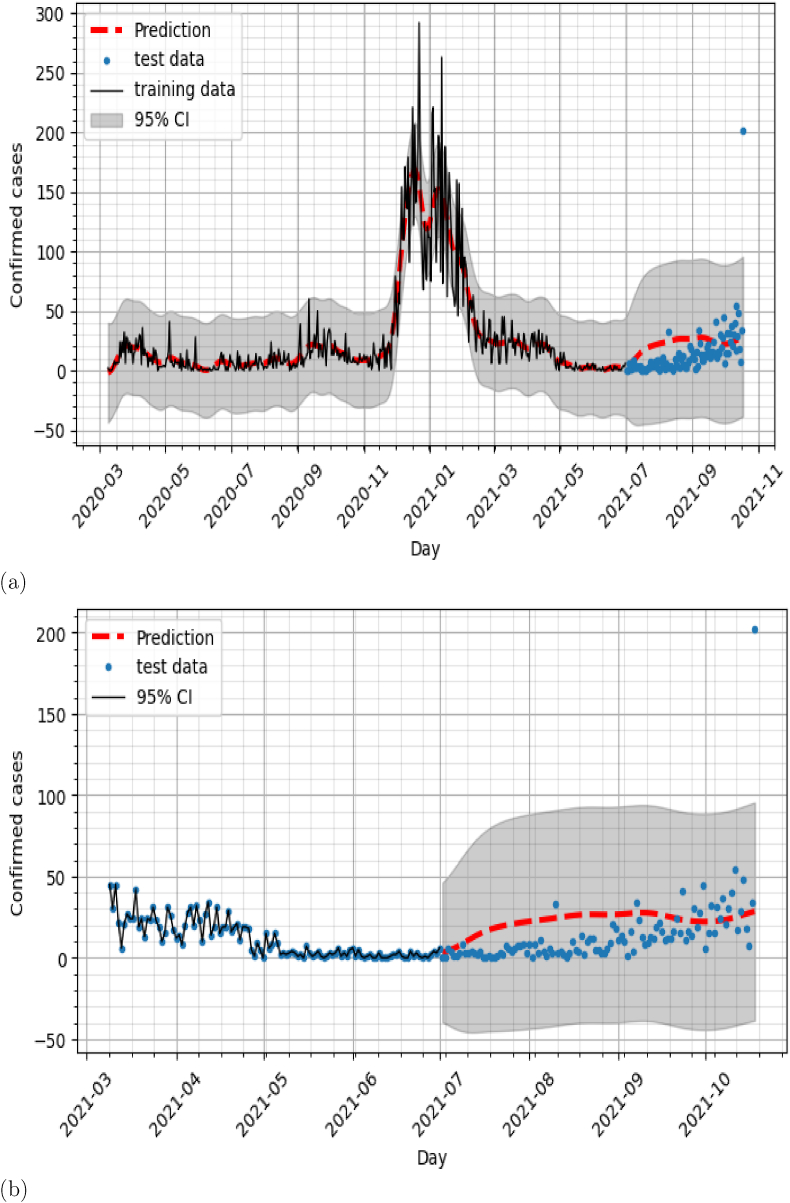
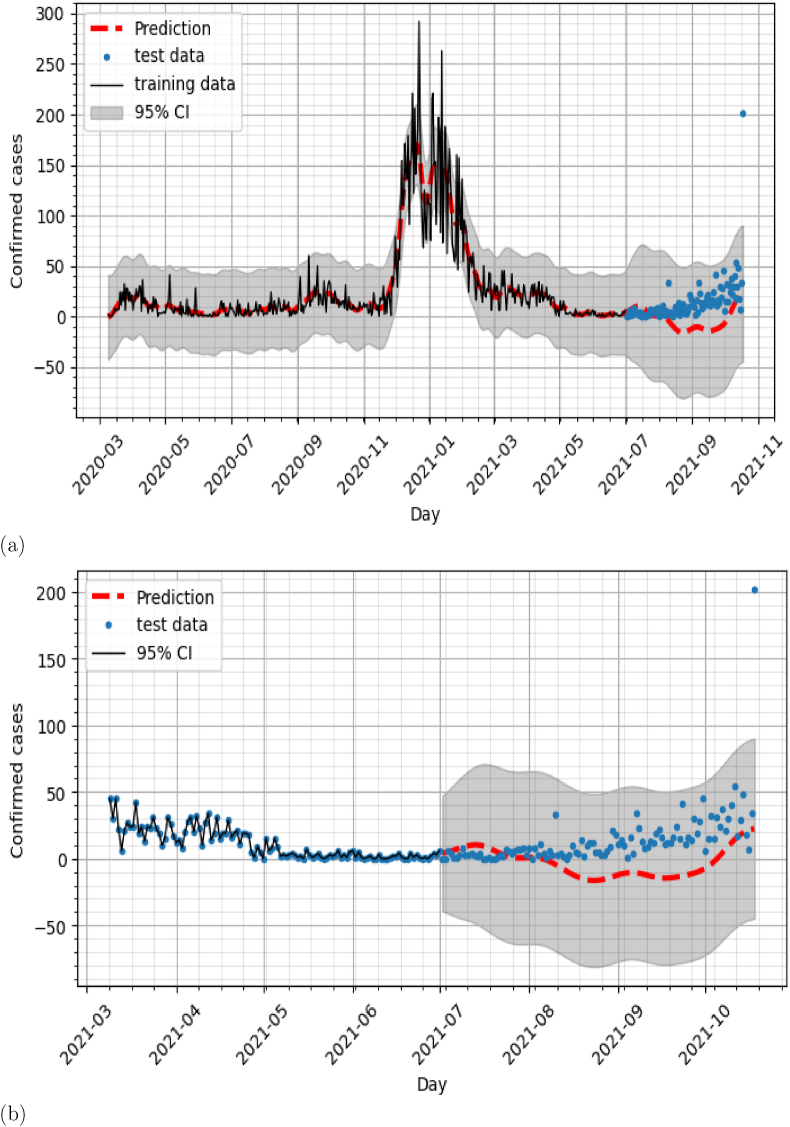
In this section, we present the figures representing the prediction of the models that have not been chosen for forecasting COVID-19 cases. As we observe that, climatic variables used in these models are not correlated to the COVID-19 cases Figs. 8–12.

Fig. 8.

a) model 1 (COVID-19 cases x Humidity) b) model 1: Zoom on test data prediction

Fig. 9.

a) model 3 (COVID-19 cases x Wind speed) b) model 3: Zoom on test data prediction

Fig. 10.

a) model 4 (COVID-19 cases x Insolation) b) model 4: Zoom on test data prediction

Fig. 11.

a) model 6 (COVID-19 cases x temperature) b) model 6: Zoom on test data prediction

Fig. 12.

a) model 10 (COVID-19 cases x wind speed x wind direction) b) model 10: Zoom on test data prediction