Coordinating tiny limbs and long bodies: Geometric mechanics of lizard terrestrial swimming

Significance

Lizards range in morphology from fully limbed with short bodies to elongate and limbless; little is known how diverse species “self-deform”—coordinate body and limb movements—for effective locomotion. We investigated the role of body movements for a spectrum of lizard morphologies in field and laboratory environments, discovering a heretofore unknown diversity of self-deformation patterns in which body dynamics were describable by a linear combination of standing wave body bending and traveling wave body undulation. Specifically, species with more elongate bodies and reduced limbs used a greater degree of traveling wave. Numerical, biological, and robophysical experiments reveal that the transition from lizard-like gaits to snake-like gaits is advantageous when thrust generation transitions from limbs to body.

Abstract

Although typically possessing four limbs and short bodies, lizards have evolved diverse morphologies, including elongate trunks with tiny limbs. Such forms are hypothesized to aid locomotion in cluttered/fossorial environments but propulsion mechanisms (e.g., the use of body and/or limbs to interact with substrates) and potential body/limb coordination remain unstudied. Here, we use biological experiments, a geometric theory of locomotion, and robophysical models to investigate body–limb coordination in diverse lizards. Locomotor field studies in short-limbed, elongate lizards (Brachymeles and Lerista) and laboratory studies of fully limbed lizards (Uma scoparia and Sceloporus olivaceus) and a snake (Chionactis occipitalis) reveal that body-wave dynamics can be described by a combination of standing and traveling waves; the ratio of the amplitudes of these components is inversely related to the degree of limb reduction and body elongation. The geometric theory (which replaces laborious calculation with diagrams) helps explain our observations, predicting that the advantage of traveling-wave body undulations (compared with a standing wave) emerges when the dominant thrust-generation mechanism arises from the body rather than the limbs and reveals that such soil-dwelling lizards propel via “terrestrial swimming” like sand-swimming lizards and snakes. We test our hypothesis by inducing the use of traveling waves in stereotyped lizards via modulating the ground-penetration resistance. Study of a limbed/undulatory robophysical model demonstrates that a traveling wave is beneficial when propulsion is generated by body–environment interaction. Our models could be valuable in understanding functional constraints on the evolutionary processes of elongation and limb reduction as well as advancing robot designs.

Recent studies have demonstrated that body elongation and limb reduction have convergently evolved in most major lineages, including, not but limited to, fishes (1), amphibians (2), reptiles (3), and even mammals (4). Of particular interest, in Squamate reptiles (lizards and snakes), snake-like body shapes have independently evolved at least 25 times (5, 6). While the exact selective pressures for this evolutionary transition remain a mystery, prior studies revealed possible advantages of certain body plans in navigating their corresponding environments (5, 7–9). One of the best-supported hypotheses is that limbless and/or short-limb forms have evolved as adaptations for fossoriality (underground environments) or cluttered environments (5, 10, 11).

Transitions in body morphology are just one of many aspects of evolutionary adaptations for cluttered or fossorial habitats. Another crucial, but less studied, aspect in such adaptation is how animals can use these diverse morphologies during locomotion. For example, stereotyped snakes and lizards have distinct body-movement patterns: Snakes primarily use traveling-wave body undulations to generate thrust (12–15). Lizards use a standing wave to assist limb retraction (16, 17) and employ traveling waves of axial body undulation at high speed (17–19), believed to help the limbs in transmitting forces along the axis of progression (17).

In lizards with short limbs and elongate bodies, because of the proximity to the substrate, both the body and limbs directly contribute to generate thrust and overcome drag (17). This regime, which because of its similarities to sand-swimming in lizards (20) and snakes (15, 21, 22) we refer to as “terrestrial swimming”, is less studied than inertial running in large-limbed lizards (17–19). Since the short limbs of elongate lizards typically cannot support the animal’s body weight, the two propulsive mechanisms (limb retraction and body undulation) can coexist, requiring proper coordination. Further, the support of body weight must be properly distributed between the ventral surface of the body and the limbs to facilitate effective thrust-generation mechanics. Thus, a challenge of studying terrestrial swimming lies in discerning the coordination between body undulation and limb retraction while generating effective body-weight distribution.

To address these questions, we take a comparative biological, robophysical, and theoretical modeling approach. We compile a collection of high-speed videos of a spectrum of lizard body forms collected in both field and laboratory settings. Through the use of neural network markerless tracking (23), we analyze the data and reveal a diversity in body-undulation dynamics. Specifically, we find that body undulation in lizards with short limbs is a linear combination of a standing wave and a traveling wave and that the ratio of the amplitudes of these two components is inversely related to the degree of limb reduction and body elongation. The fact that our animals move in highly damped environments, where frictional forces dominate over inertial forces, allows the use of a geometric mechanics framework (24, 25) to explain wave dynamics and body–limb coordination. This geometric mechanics theory, which replaces laborious calculation with diagrammatic analysis, rationalizes the advantage of using traveling waves in short-limbed elongate lizards and predicts that such advantages emerge when the primary thrust-generation source shifts from the limbs to the body. We test our hypothesis with biological experiments by manipulating the substrate on which fully limbed lizards move and with robophysical experiments by controlling the body and limb-thrust mechanism. Answering these questions will not only establish a relationship between what they have (the body morphology) and how they move (the body–limb coordination) (26–29), but also facilitate our understanding of the locomotor implications of the evolution of snake-like forms (9, 30).

Results

Diversity in Lizard Body Movements.

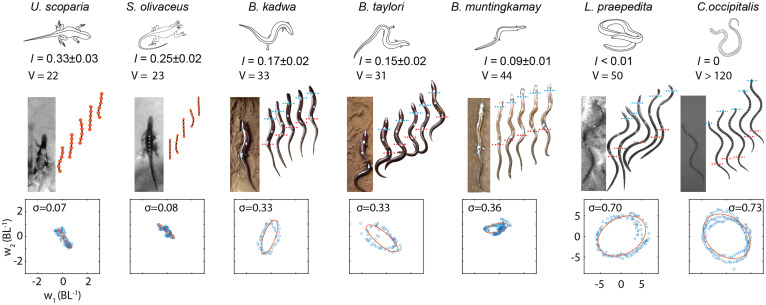
We investigated three short-limbed, elongate species with similarly developed fore and hind limbs (30, 31) (Brachymeles kadwa, Brachymeles taylori, and Brachymeles muntingkamay) and compared them with fully limbed lizards (Uma scoparia and Sceloporus olivaceus) and limbless species (the almost-limbless lizard Lerista praepedita and the shovel-nosed snake Chionactis occipitalis). These species were chosen because they form a spectrum of limb reduction and body elongation (Fig. 1). The relative limb size is defined as the hind limb length normalized by snout-vent length (SVL). The number of presacral vertebrae is a measure of elongation (30) (Fig. 2). We recorded field videos of these species moving on granular media (consisting of soil and poppy seeds) and compared the kinematics of their body movements. The snapshots of their body postures during locomotion are compared in Fig. 2, Middle. Qualitatively, we observed that the node* of body bending is almost stable in fully limbed lizards (at the shoulder and hip) and propagates from snout to cloaca in shovel-nosed snakes. Interestingly, in short-limbed, elongate species, one of the nodes is almost stable near the snout, and the other node propagates from the midbody to tail.

Fig. 1.

Target and model systems for understanding the role of body undulation in the lizard body-elongation and limb-reduction continuum. (Left, from top to bottom) Fully limbed lizards (U. scoparia and S. olivaceus) in comparison with extant short-limbed, elongate lizards (B. kadwa, B. taylori, and B. muntingkamay) and limbless/almost limbless species (L. praepedita and C. occipitalis). (Scale bars: 5 cm.) (Right) An illustrative diagram of force generation in short-limbed, elongate lizards: The force generated by limb retraction is labeled in red arrows; the forces generated by body undulation is labeled in yellow arrows.

Fig. 2.

The diversity of body waves in the body-elongation and limb-reduction continuum. (Top) Photos of species and the snapshots of their body motion during one period (at a scale of seconds) of locomotion. Seven species were studied (from left to right): U. scoparia, S. olivaceus, B. kadwa, B. taylori, B. muntingkamay, L. praepedita, and C. occipitalis. The relative limb size (l: the hind limb length normalized by SVL) and number of presacral vertebrae (V) for each species are labeled (30, 32). (Bottom) The projections of body curvature into the reduced shape space and the estimation of σ for each animal. Units of axes are identical to leftmost bottom panel.

We considered locomotion as a properly coordinated sequence of “self-deformations” (internal shape changes) that generate thrust to overcome drag forces (self-propulsion^†) via interactions with substrates. Prior work (33–37) suggested that despite possessing high dimensionality, the essence of self-deformation can be described by a linear combination of shape basis functions. Consider the body curvature^‡ $\kappa (s,t)$ at time t and location s ($s=0$ denotes the snout in snakes [or the shoulder in lizards], and s = 1 denotes the cloaca in snakes [or the hip in lizards]). Thus, the body-curvature profile can be approximated by:

$$\kappa (s,t)=w_1(t)\sin (2\pi \xi s)+w_2(t)\cos (2\pi \xi s),$$ [1]

where ξ is the spatial frequency of body undulation obtained from direct fitting ($1/\xi$ denotes the wavelength, λ, in the unit of SVL); $w_1(t)$ and $w_2(t)$ are the reduced shape variables describing the instantaneous shape of the locomotor at time t. In this way, we can map the original high-dimensional body-curvature profile $\kappa (s,t)$ into a space spanned by w₁ and w₂ (the shape space). In pure standing waves, the body-curvature trajectory in the reduced shape space can be described as a flattened ellipse (with eccentricity $e\to 1$). In pure traveling waves, the body-curvature trajectory in the reduced shape space can be described as a circle (with eccentricity $e\to 0$). In this way, an elliptical trajectory can be considered a linear combination of the flattened ellipse path and the circular path, the ratio of which can be quantified by the flatness ($\sigma =\sqrt{1-e^2}$), where $\sigma =0$ denotes a pure standing wave and $\sigma =1$ denotes a pure traveling wave. We compared the gait trajectories for species ranging from fully limbed to limbless animals in Fig. 2, Bottom, where we observed a transition from a flattened ellipse in stereotyped lizards to a circle in snakes.

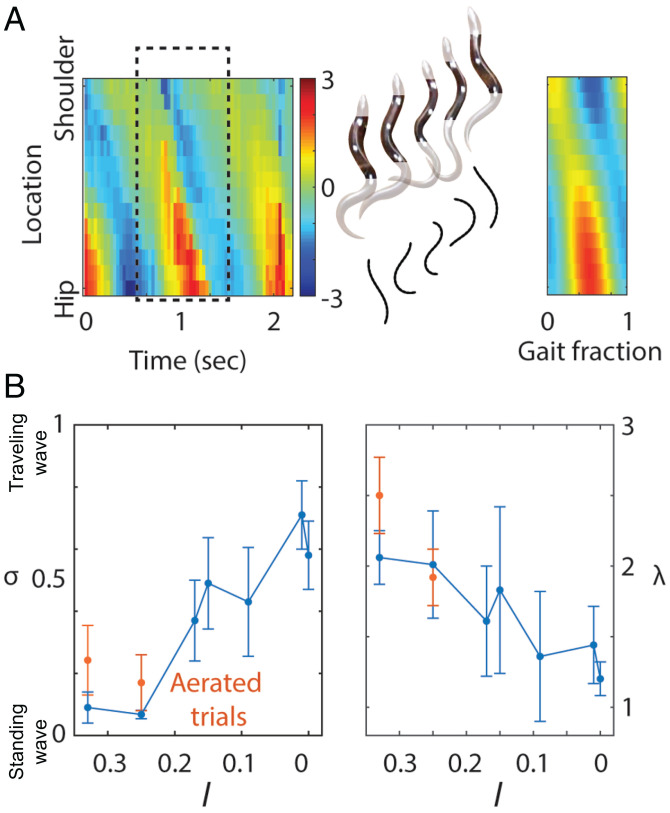
To quantitatively measure the flatness of the gait trajectories in the reduced shape space, we fit these trajectories with oriented ellipses. To test the accuracy of the fitting, we compared the original body-undulation profile (collected from tracking in field videos; Fig. 3 A, Left) and the fitted body-undulation profile (from a reconstruction of the ellipses in reduced shape spaces; Fig. 3 A, Right) in Fig. 3A. Interestingly, we observed that σ increased and λ decreased, indicating a transition from standing wave to traveling wave, as both limb size decreased (Fig. 3B) and number of presacral vertebrae increased (Fig. 2).

Fig. 3.

The role of limb length on wave type. (A) Comparison between the original body-curvature profile of B. taylori and the reconstructed body-curvature profile over a gait cycle from the estimated wavelength λ and flatness σ. The units of the colorbar are SVL⁻¹. (B) The relationship between the locomotion parameters (σ and λ) and morphology parameter (the relative hind limb length l). Red points with error bars correspond to the locomotion parameters of U. scoparia and S. olivaceus on an aerated granular medium to reduce the resistive force of the media. Note that we use l = 0.01 for L. praepedita on the plot and that the abscissa is reversed (descending left to right) to correspond to Fig. 2.

Wave Dynamics Are Important in Body–Limb Coordination.

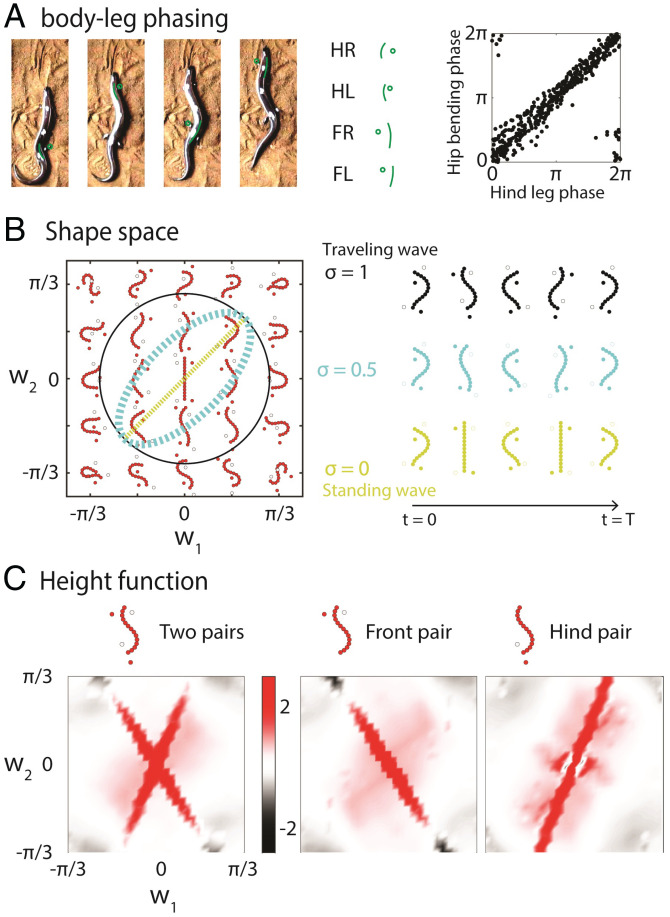
We further analyzed the limb movement in the short-limbed, elongate species (B. kadwa and B. taylori). Snapshots showing the body posture during the touchdown of each foot are illustrated in Fig. 4 A, Left. The limb movements in short-limbed, elongate species follow the sequence: FR–HL–FL–HR (where F, H, R, and L represent fore, hind, right, and left, respectively). Specifically, the hind limb leads the fore limb on the same side by 0.38 ±0.07 of a period, which is a lateral couplet sequence (38). Further, for each limb, the ground-contact (stance phase) duration is approximately the same as the off-ground (swing phase) duration, indicating that the duty factor (the fraction of a period that each limb is on the ground) is ∼0.5.

Fig. 4.

Geometric mechanics analysis of the body–limb coordination in short-limbed, elongate lizards. (A) The limb movement in short-limbed, elongate lizards follows the lateral couplet sequence (FR–HL–FL–HR). The phase relationship of hip bending and hind limb movements are plotted in Right. (B) The shape space for short-limbed, elongate lizards. The body movements are prescribed by the reduced shape variable w₁ and w₂, and the limb-contact states are inferred from the body movements. Gaits can be represented by closed-loop paths in the shape space. A standing-wave gait path, a traveling-wave gait path, and an intermediate-wave gait path are compared. (C) Height functions to investigate the body undulation in lizards with intermediate limbs. (Left) Two strips emerged in the height function for short-limbed, elongate lizards, such that a circular gait path can enclose significantly more surface than a flattened elliptic gait path. To further understand the two stripes, we calculated the height function for hypothetical lizards with one pair of limbs near the head (Center) and near the tail (Right). Each stripe is associated with a pair of limbs, in which case a flattened elliptic gait path can enclose sufficient surface in the height function. The units of the colorbar are ${10}^{-3}\times {\text{SVL}}^{-1}/{\text{rad}}^2$.

We also noticed that during a foot touchdown, the local body element develops maximal curvature (in the convex direction toward the limb) to increase its reach (Fig. 4 A, Center), which is consistent with observations of other quadrupedal locomotors (34, 39). This observation indicates that the fore (hind) limb movement should be in phase with shoulder (hip) bending. We quantify this observation by showing the phase relationship between the hind limb movement and hip bending in Fig. 4 A, Right. The relationship between the fore limb movement and shoulder bending is shown in SI Appendix, Fig. S1. We observed a stronger in-phase relationship between the hind limb and hip bending. We suspect that the relatively weak fore limb/shoulder phase relationship is a consequence of the low visibility of the fore limbs in the field-recorded videos and the low magnitude of the shoulder bending compared to hip bending.

The observations of the phase relationship between limb movements and body bending allow us to reduce the shape variables of short-limbed, elongate lizard locomotion into two dimensions. As discussed earlier, the body-undulation profile $\kappa (s,t)$ can be approximated by a linear combination of $\sin (2\pi \xi s)$ and $\cos (2\pi \xi s)$ (under coefficients w₁ and w₂). We took $\xi =0.65$ from our previous analysis ($\lambda \approx 1.5$ for B. taylori and B. kadwa; Fig. 3B). We could then infer the limb-contact states from the choice of reduced shape variables w₁ and w₂, such that the shoulder (hip) bending is in phase with the fore (hind) limb movement. The explicit shape space is shown in Fig. 4 B, Left.

Hypothesizing that terrestrial swimming is dissipation-dominated (ground-resistive forces dominate body or substrate inertial forces), we next used a geometric mechanics framework (24, 37, 40) to compare the effectiveness of standing and traveling waves in these short-limbed, elongate lizards. Geometric mechanics was originally developed to study locomotion via self-deformation at low Reynolds numbers (24, 41). Since the thrust is generated from properly coordinated self-deformation to counter drag forces, we refer to such thrust generation as self-propulsion. Recent work has shown that geometric mechanics replaces laborious calculation with a diagrammatic scheme and offers novel insights into the self-deformation patterns in various types of biological locomotion, such as slithering and sidewinding in snakes and body–limb coordination in salamanders (34, 37).

In the geometric mechanics framework, we seek to calculate performance (measured by body lengths moved per cycle) from the sequences of self-deformation. The space spanning the self-deformations (in our case, internal shapes of lizards) is then called shape space (Fig. 4B). For simplicity, we only analyze the overdamped regime^§ of lizard locomotion, where there is zero acceleration on the center of mass in lizards. In this way, the velocities in shape space (shape velocity) and body velocities are then connected by a matrix called the “connection-vector field” (e.g., SI Appendix, Fig. S3) (35). A gait, a periodic sequence of shape changes, can be represented as a closed-loop path in the shape space. In Fig. 4 B, Right, we compare the standing- and traveling-wave body movements and their corresponding limb-contact sequences. The net displacement of a gait can be approximated by a line integral of the vector field along the gait path (25). From Stokes’ theorem, the line integral of a closed-loop path over a vector field can be visualized by a surface integral over the curl of the vector field [the height function, or often referred to as a constraint curvature function (35, 37)]. The height function for the short-limbed, elongate lizards was computed in Fig. 4 C, Left. In summary, with the geometric mechanics framework, we can investigate the seemingly complicated and diverse lizard wave dynamics with the help of a precomputed diagram and analyze the locomotion performance by evaluating the surface integral.

The actual force model of environmental interactions generated by these lizards in the field is unknown. We chose to approximate them using a model granular medium (poppy seeds) to numerically calculate the connection-vector field (34, 42) (Fig. 4C). To bound the uncertainty in ground-reaction forces, we used different force models (rate-independent Coulomb friction and rate-dependent viscous fluid; SI Appendix, Fig. S2) and achieved similar conclusions as in Fig. 4C. Further, in the derivation of the local connection-vector field, we assumed that the magnitude of limb retraction is 0.17 of the total ground reaction force (body undulation and limb retraction), a value similar to the relative limb size.

Two stripes emerged in the height function with an oblique intersection, which we interpreted as corresponding to the coordination for limb movements. To better understand the meaning of the height function, we recomputed the height function for two hypothetical lizards: lizards with only fore limbs (Fig. 4 C, Center) and lizards with only hind limbs (Fig. 4 C, Right). One of these stripes emerged in each height function for the hypothetical lizards, supporting our hypothesis that each stripe corresponds with the coordination of one pair of limbs. From the structure of the height function, we inferred that an elliptical gait path with $\sigma \approx 0.5$ can lead to the greatest displacement, which was qualitatively the range of σ measured from animal experiments (Fig. 3B).

Body-Weight Distribution.

From the above analysis, we noticed that the presence of limbs significantly affects the dynamics of body movements. In fully limbed lizards, almost the entire body weight is supported by the limbs, whereas in limbless lizards, the ventral surface supports the entire body weight. But for short-limbed, elongate lizards, how should the body weight be distributed between the limbs and the ventral body surface for effective locomotion? We used the geometric mechanics modeling to predict the optimal body-weight distribution for short-limbed, elongate lizards.

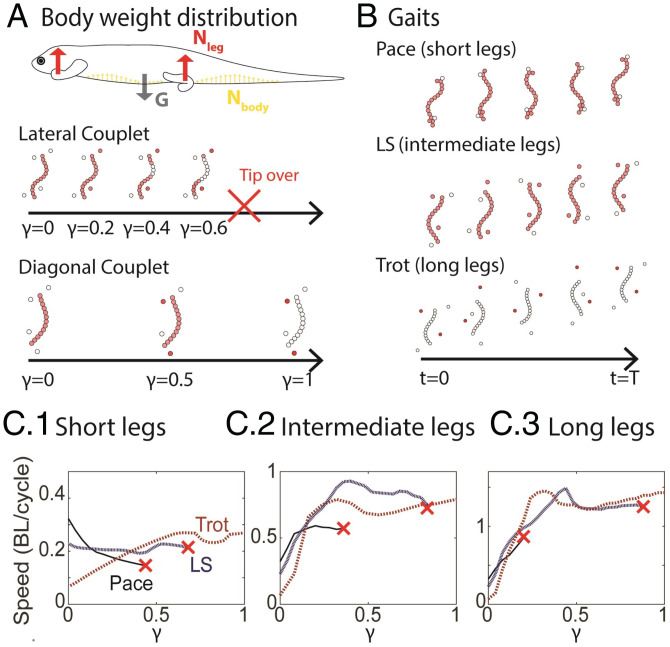
Quadrupedal locomotors typically utilize two types of limb-contact patterns: the diagonal couplet and the lateral couplet (38). In the diagonal couplet, the limbs in the ground-contact phase are distributed in pairs along the diagonal (FR/HL) or counterdiagonal (FL/HR), where the body weight can be stably supported by the limbs (Fig. 5A). In the lateral couplet, the limbs in the ground-contact phase are on the same side, which cannot stably support the entire body weight (Fig. 5A). Thus, some ventral surface support is essential for the lateral couplet. We quantified the fraction of body weight supported by the limbs as γ. There is a limit on the force that the limbs can support without the animals tipping over (the torque between lateral couplets is greater than the torque from gravity) in the lateral couplet (Fig. 5A). The detailed derivation to compute the body-weight distribution can be found in ref. 43.

Fig. 5.

The weight-distribution role of limbs in lizard locomotion. (A) The body weight can be supported by the limbs and the body; γ indicates the fraction of body weight supported by limbs. (B) Three typical gaits: the pace gait (duty factor $=$ 0.5, limb phase shift $=$ 0) implemented by lizards with short limbs, the LS (duty factor $=$ 0.5, limb phase shift $=$ 0.25) gait implemented by lizards with intermediate limbs, and the trot gait (duty factor $=$ 0.5, limb phase shift $=$ 0.5) implemented by lizards with long limbs. (C) The relationship between γ and speed for pace (solid black curves), LS (dashed blue curves), and trot (dashed red curves) gaits on lizards with short (1), intermediate (2), and long (3) limbs. Potential tip-overs are indicated by a red cross.

We compared three typical limb-contact patterns: the pace, the lateral sequence (LS), and the trot, where limb phase shifts (fraction of a period that the hind limb leads the ipsilateral fore limb) were 0, 0.25, and 0.5, respectively (Fig. 5B). In the pace, the contact patterns were entirely lateral couplets; in the trot, the contact patterns were entirely diagonal couplets; in the LS, there was a mix of lateral and diagonal couplets. Assuming the duty factor to be 0.5, the fraction of the lateral couplet in the pace, the LS, and the trot were 1, 0.5, and 0, respectively. Further, the body-bending spatial frequency ξ was 1, 0.75, and 0.5 for the pace, LS, and trot, respectively, to enforce the in-phase relationship between the fore (hind) limb movements and shoulder (hip) bending.

We conducted numerical simulations to predict the relationship between γ and the forward speed. We studied lizards with short limbs (a hypothetical locomotor with l = 0.05, shorter limbs than B. muntingkamay), lizards with intermediate limbs (a hypothetical locomotor with l = 0.17, similar to B. kadwa and B. taylori), and lizards with long limbs (a hypothetical locomotor with l = 0.30, similar to U. scoparia). We observed that for short-limbed lizards, it was optimal to use only body undulation to generate thrust (γ = 0, the pace; Fig. 5 C, 1), while intermediate-limbed lizards optimally used a hybrid thrust-generation mechanism using both body undulation and limb retraction ($\gamma =0.4$, the LS; Fig. 5 C, 2). Finally, one available optimum for long-limbed lizards is to solely use limbs to generate thrust (γ = 0, the trot; Fig. 5 C, 3).

Thus, we showed that limbs are crucial to locomotion by short-limbed, elongate lizards because they contribute to thrust as well as sharing some body weight with the ventral surface of the body, which can modulate lifting forces and, thus, the ground reaction force on the body. Depending on the limb size, our model suggests that lizards should properly distribute their body weight between the limbs and the ventral surface to generate effective locomotion. Therefore, we predict that a traveling wave enhances locomotor performance as the body-weight distribution (and, thus, thrust-generation mechanism) shifts from the limbs to the body.

Terrestrial Swimming.

In fully limbed lizards, nearly the entire body weight is supported by the limbs. It is thus commonly believed that at low speeds, lizards use standing-wave body bending to coordinate with their limb movements (34, 44, 45). Our geometric mechanics modeling predicts that the body-weight distribution will affect how much a traveling wave contributes to thrust. We tested this hypothesis by manipulating the substrate on which fully limbed lizards moved and investigated whether we could stimulate terrestrial swimming in fully limbed lizards.

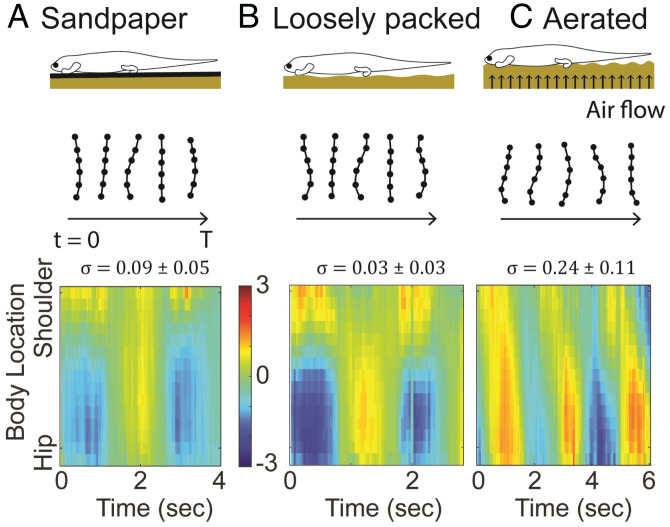
To modulate the body-weight distribution, we used an upward airflow through a granular medium to control the ground-penetration resistance^¶ (46), maintaining airflow below the onset of fluidization^ǁ as in ref. 47. This technique proved useful in previous biological and robotics studies to evaluate locomotors’ performance on flowable ground of various penetration resistance (47). In doing so, the lifting forces at the limbs no longer fully supported the body weight, and, therefore, some finite resistance-lifting force acted on the ventral surface. When the fully limbed lizards (U. scoparia and S. olivaceus) ran across the region with reduced ground-penetration force, they exhibited features of a traveling wave, indicated by the propagation of nodes (Fig. 6). We compared the wave flatness (σ) and wavelength λ of the body undulations (Fig. 3B) for lizards on the aerated granular medium, the loosely packed granular medium, and sandpaper. We found no difference in σ between sandpaper and loosely packed medium, but noted a significantly higher σ on the aerated medium than the loosely packed medium for both species (U. scoparia: t = 2.94, $\text{DoF}=11$, P = 0.013; S. olivaceus: t = 2.43, $\text{DoF}=9$, P = 0.038), indicating a higher degree of traveling wave.

Fig. 6.

Traveling wave in fully limbed lizards induced by substrate weakening. Comparison of the body-wave dynamics of U. scoparia on sandpaper (A), on a loosely packed granular medium (B), and on an aerated granular medium (C). An almost perfect standing wave is observed for U. scoparia on sandpaper and on the loosely packed granular medium, while features of a traveling wave emerge for U. scoparia on the aerated granular medium. Resulting σ and λ are shown in Fig. 3B. The units of the colorbar are SVL⁻¹ for all panels.

Robophysical Experiments.

In the previous sections, we showed that, although thrust generation in lizards results from a complex coordination of limb and body movements, we could modulate the degree to which traveling-wave undulations were used by modulating the ground-penetration resistance. We further explored the relative advantages of traveling waves and standing waves using a robophysical model, where we could precisely control the self-propulsion mechanism. Our robophysical model has four actuated limbs and two actuated body-bending joints. The body shape of the robot can be uniquely described by the body-joint angles: upper back α₁ and lower back α₂ (Fig. 7 A, Left). Two actuated body joints in our robot are the minimum degrees of freedom (DoF) needed to enable a traveling wave (48). We designed removable belly intrusion plates to control the belly thrust-generation mechanics. We compared the robot with belly thrust (Fig. 8 A, Upper) and the robot without belly thrust (Fig. 8 A, Lower) in Fig. 8A. The shoulder joints control the contact patterns of each limb. For simplicity, we only considered two combinations of contact patterns: diagonal contact and the counterdiagonal contact.

Fig. 7.

Geometric mechanics modeling for the robophysical experiments. (A) The definition of α₁ and α₂ and the body–limb coordination in the three-link swimmer and four limb contacts. ψ is the phase lag between the upper back and lower back actuators. Right demonstrates how limb contact patterns are coupled to the shape variables (α₁ and α₂). On the lower right half of the shape space, the contact patterns are counterdiagonal; on the upper left half of the shape space, the contact patterns are diagonal. Examples of the standing wave (ψ = 0) and the traveling wave ($\psi =\pi /2$) are compared in the shape space. (B) Vector-field and height functions for modeling the robophysical experiments on poppy seeds. The displacement can be approximated by the surface integral enclosed by the gait path over the height function (Right). The units of the colorbar are ${10}^{-3}\times {\text{SVL}}^{-1}/{\text{rad}}^2$. Units of axes in B are identical to the shape space in A.

Fig. 8.

Robophysical experiments to probe roles of body and limbs in locomotion. (A) Snapshots of robots (Upper: belly thrust; Lower: no belly thrust) implementing standing-wave ($\psi =0$) and traveling-wave ($\psi =\pi /2$) gaits over one gait cycle (T=12 sec). The snapshots are uniformly spaced in time. (B) The effect of ψ on locomotion performance for the robot with no belly thrust (blue curve) and the robot with belly thrust (orange curve).

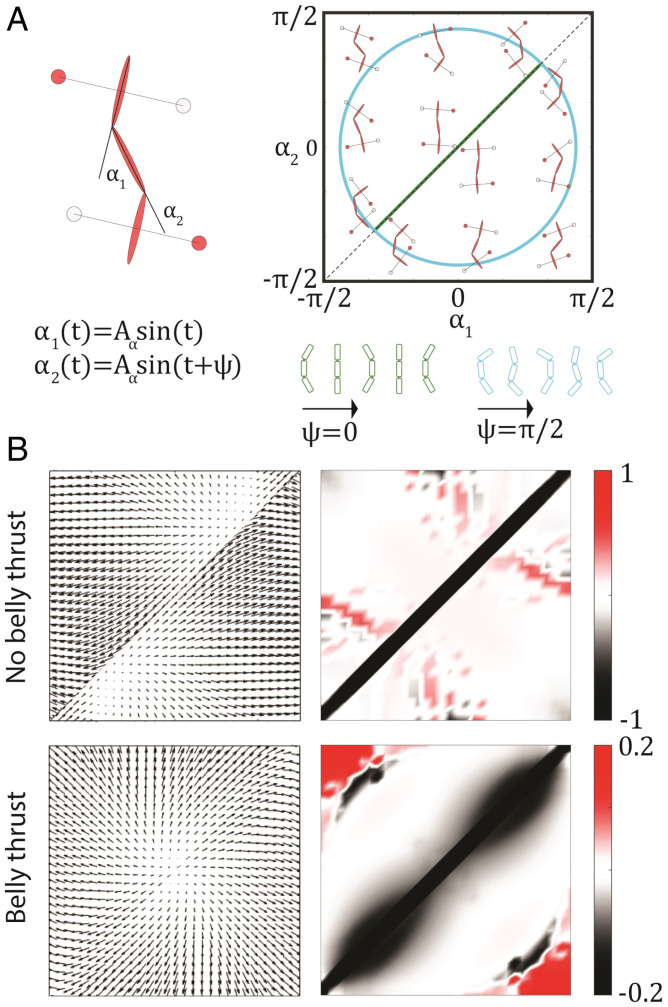
As with the geometric mechanics models presented earlier, the gait of the robot can also be represented by a closed path in its shape space (Fig. 7A). For simplicity, we considered the upper back and lower back as oscillating sinusoidal waves: ${\alpha }_1(t)=A_{\alpha }\sin (t)$ and ${\alpha }_2(t)=A_{\alpha }\sin (t+\psi )$, where $A_{\alpha }$ is the amplitude, and ψ is the phase lag between the upper back and the lower back. A typical traveling wave can be described such that the upper back and lower back are $\pi /2$ out of phase (35): $\psi =\pi /2$, which leads to a circular path in the shape space (blue curve in Fig. 7A). A typical standing wave can be described such that the upper back and lower back are in phase: ψ = 0, which leads to a flattened ellipse (with eccentricity $=$ 1) in the shape space (green curve in Fig. 7A).

We used contact-pattern-design algorithms to determine the coordination between the contact pattern and the body movements (49). The optimal coordination is shown in Fig. 7A, Right, in agreement with our data on body–limb coordination in the biological experiments. We then tested the effect of ψ on the robot.** Snapshots of the robot implementing standing and traveling waves are shown in Fig. 8A. All experiments were conducted with at least five trials. The experimental results are shown in Fig. 8B. We found that traveling waves only increase speed (measured by distance moved per cycle) in the robot with belly thrust (Pearson’s $\rho =0.883$, P = 0.001), whereas there are no significant differences between standing and traveling waves when the robot lacks belly thrust (Pearson’s $\rho =-0.147$, P = 0.438).

Geometric mechanics-derived height functions helped explain our observations (Fig. 7B, Right). As in the above analysis of lizard terrestrial swimming, the displacement can be approximated by the surface integral over the gait path in the shape space. Further, the magnitude of the height function for locomotors without belly thrust (Fig. 7 B, Upper) is much higher than that with belly thrust (Fig. 7 B, Lower), indicating that a robot without belly thrust should have higher speed than one with belly thrust. The trends in the theoretical predictions and experimental data agreed, but we posit that the discrepancy in magnitude (Fig. 8B) was due to the accumulation of granular media in front of the robot as it moves, impeding progress (29) as the robot implemented its gait.

From the structure of the height function, we observed that most of the negative regions (indicated by black color) are distributed along the narrow diagonal line, which can be sufficiently bounded by a flattened ellipse. It therefore predicts that the standing-wave body bending can be as good as those of traveling-wave body undulations. On the other hand, the traveling-wave body undulation can better coordinate the robot with belly thrust because the negative regions are distributed widely around the diagonal line. In the latter case, a higher surface integral can be achieved for ellipses with increasing ψ (and, thus, increasing σ). We interpreted our observations on traveling and standing waves by analyzing the connection-vector field in Fig. 7B, Left (50). The connection-vector field in locomotors with no belly thrust is almost curl-free (SI Appendix, Fig. S3), which indicates that the contribution of body-bending postures is almost path-independent. In other words, the trajectories of body-posture changes (e.g., traveling waves or standing waves) will not matter. On the other hand, the connection-vector field in locomotors with belly trust has nonnegligible curls (SI Appendix, Fig. S3), which indicates that the trajectory of body bending will affect locomotor performance.

Discussion and Conclusion

Lizards have evolved a diversity of body forms from fully limbed and short-bodied to limbless and elongate. We showed that this diversity in morphology coincides with a similar diversity in locomotion patterns, ranging from standing-wave to traveling-wave body undulation. We observed that the degree of body elongation and limb reduction were closely related to how the body and limb movements were coordinated, indicating an interconnected morphological and locomotor continuum. Using biological experiments, a geometric theory of locomotion, and robophysical experiments, we showed that the body-weight distribution between the limbs and the body (and, therefore, the primary propulsion-generation mechanism) plays a crucial role in the locomotor transition from fully limbed to limbless. Specifically, we found that fully limbed lizards adopted a traveling wave to undergo terrestrial swimming when the penetration resistance of the substrate was reduced and the belly contacted the medium. Further, our robophysical experiments revealed that a traveling wave enhanced locomotor performance only when some thrust was generated by the body.

One of the contributions presented in this paper was the use of geometric mechanics as a tool to analyze seemingly complicated lizard locomotion. Specifically, we formulated different body-wave dynamics as different paths in the shape space. The diagrammatic analysis by geometric mechanics then allowed us to visually and intuitively compare different wave dynamics. In this sense, our analysis simplified laborious calculations which would otherwise be required to study the diversity in lizard body-wave dynamics. In addition, geometric mechanics served as a bridge connecting biological experiments and robophysical experiments, allowing us to systematically test gaits and conditions that are less commonly seen in biological systems.

Limb reduction and body elongation result in a shift in body-weight distribution from the limbs to the body (51). We showed that a traveling wave of body undulation enhanced locomotor performance during this transition. However, traveling-wave body undulation requires larger local body curvatures, more complex neuromechanical control (to propagate the node in undulation) (45), and more DoF (at least two DoF) than standing-wave undulation (one DoF). That a fully limbed lizard adopted terrestrial swimming when crossing a medium with low penetration resistance suggests that the DoF and neuromechanical control necessary for traveling waves may be widespread among lizards. Our work shows that the coordination between body undulation and the limbs is a key feature of locomotion within the morphological transition between fully limbed, short-bodied, and limbless, elongate forms.

We used Brachymeles as morphologically intermediate species because they have similar levels of development of their fore and hind limbs (30, 31). However, the limbed species of this genus are secondarily limbed, having re-evolved their limbs from a limbless ancestor (8). Therefore, our results should not be interpreted as representing an evolutionary transition in locomotion. Despite this, the geometric mechanics and robophysical approaches we used are naïve to evolutionary history, and our observations on Brachymeles and the other, unrelated species that we used coincide closely with these approaches, suggesting that biomechanics may dictate locomotor patterns in many of these convergent evolutions of snake-like forms. The role of how the evolutionary history affects locomotion of these forms could be further tested in a clade like Lerista, which has evolved snake-like forms from limbed, short-bodied ancestors (9, 52). We also expect that our work on body and limb dynamics in these lizards will inform control of robots that must traverse complex terrain.

Materials and Methods

Tracking.

Positional data were extracted from videos with the animal-pose estimation software DeepLabCut (DLC) (23). Ten frames from each video were extracted and manually labeled. DLC would then provide positions for labeled points on all of the other frames. For each video, 21 points following the middle of the lizard body were labeled, including 5 head points, 13 body points, and 3 tail points. If the species possessed limbs, four additional points were labeled, marking each limb.

Data Analysis.

To quantify the time-varying body shape of lizards, we obtained the body curvature from the tracked body positions. We used the methods introduced in ref. 53 to estimate the curvature from a relatively noisy backbone curve.

Once we obtained the spatiotemporal information of the body curvatures, $\kappa (s,t)$, we reconstructed the body-curvature profile by fitting with the least error. The error is defined as $\left|\right|\kappa -B_{\xi }^T{(B_{\xi }{B}_{\xi }^T)}^{-1}{B}_{\xi }\kappa |{|}_2$, where $B_{\xi }=[\cos (\xi s)\sin (\xi s)]$ is the shape basis function, and ξ is the spatial frequency. The flatness of the trajectory in reduced shape space was approximated by using principal component analysis: $\sigma =e(2)/e(1)$, where e(i) is the percentage of the total variance explained by the i-th principal component. The phases of shoulder (and hip) body bending and fore (and hind) limb movements were estimated by using Hilbert Transforms.

Animal Experiments.

Experiments on stereotyped lizards, U. scoparia (N = 7) and S. olivaceus (N = 6), were performed in a 300-cm by 40-cm trackway filled with small glass spheres (mean ± SD, diameter $=$ 250 ± 30 µm) to a depth of 20 cm. Experiments on snakes, C. occipitalis (N = 11), were performed in the laboratory on 300-µm glass particles. Experiments on short-limbed, elongate lizards, B. kadwa (N = 14), B. taylori (N = 8), and B. muntingkamay ($N=7$), were performed in the field on soil. We used soil from the habitats in which they were found, giving us 0.5- to 2-mm-diameter (sieved and dry) particles (midpoint 1.25 mm), at 1-cm depth. L. praepedita experiments were conducted in Australia on sieved dry sand that was 0.25- to 0.50-mm in diameter, midpoint 0.375 mm, at 1-cm depth. We chose the low depth because otherwise the animals would bury themselves.

Robophysical Experiments.

The robophysical model (Fig. 8A) used in experiments is a 0.5-kg, quadrupedal robot with two body-bending joints and four limbs. Body-bending joints are capable of $\pm {90}^{°}$ of rotation, actuated by Dynamixel AX-12A servo motors. Each limb possesses one DoF: the shoulder joint to control the lifting and landing of the limb, actuated by a Dynamixel XL-320 servo motor. Limb paddles are 45 mm × 35 mm × 5 mm cuboids, and belly panels are 45 mm × 55 mm × 10 mm cuboids, all three-dimensional (3D)-printed with acrylonitrile butadiene styrene plastic. Two robot conditions were compared: a robot with belly thrust (robot with belly plate installed; Fig. 8 A, Upper) and a robot without belly thrust (robot with no belly plate; Fig. 8 A, Lower).

We emulated the trackways used in animal experiments for the robot using a 2.1-m-long, 0.5-m-wide granular media bed trackway. We filled the trackway with poppy seeds of ∼1-mm diameter to a depth of 12 cm. We had four leaf blowers (Toro 51599, 300 L/min) connected below the trackway that forced a continuous flow of air through a porous flow distributor to even the surface of the granular substrate every time before starting the experiment. To track the robot’s motion in its position space, six infrared reflective markers were attached to the body of the robot. For tracking the trajectories of the markers, an OptiTrack motion-capture system with four OptiTrack Flex 13 cameras were used to capture real-time 3D positions of the markers at 120 frames per second frame rate. Displacement of the robot was then calculated from the tracked marker trajectory using MATLAB.

Data Availability

Videos and code data have been deposited in Zenodo, https://doi.org/10.5281/zenodo.6614341 (54).