Influence of demographically-realistic mortality schedules on vaccination strategies in age-structured models

Abstract

Because demographic realism complicates analysis, mathematical modelers either ignore demography or make simplifying assumptions (e.g., births and deaths equal). But human populations differ demographically, perhaps most notably in their mortality schedules. We developed an age-stratified population model with births, deaths, aging and mixing between age groups. The model includes types I and II mortality as special cases. We used the gradient approach (Feng et al., 2015, 2017) to explore the impact of mortality patterns on optimal strategies for mitigating vaccine-preventable diseases such as measles and rubella, which the international community has targeted for eradication. Identification of optimal vaccine allocations to reduce the effective reproduction number ${\mathcal{R}}_v$ under various scenarios is presented. Numerical simulations of the model with various types of mortality are carried out to ascertain the long-term effects of vaccination on disease incidence. We conclude that both optimal vaccination strategies and long-term effects of vaccination may depend on demographic assumptions.

1. Introduction

Meta-population models of heterogeneous host populations, especially ones whose members mix non-randomly, have basic reproduction numbers, ${\mathcal{R}}_0$, that may be much larger than those from homogeneous host population models (Glasser et al., 2016). Similar discrepancies can also be present in effective reproduction numbers, ${\mathcal{R}}_v$, derived from these models. When a control measure such as vaccination is considered, ${\mathcal{R}}_v$ is a function of parameters representing effort levels in the several sub-populations. Feng et al. (2015) and Feng et al. (2017) showed that the optimal vaccine allocation among sub-populations can be identified by the gradient of ${\mathcal{R}}_v$ (its multivariate partial derivative) with respect to the vaccination rates.

The meta-population model of Feng et al. (2017) considers demographic heterogeneity, but does not distinguish births/immigration/aging and deaths/emigration/aging, in which respects age groups may differ. The model considered in this paper includes births, deaths and aging, but not immigration/emigration, which may be implicitly modeled via a mixing function. Moreover, we consider models with types I and II mortality (i.e., death occurs only in the last age group or at a constant rate in all groups), which may be more appropriate for developed and developing countries, respectively. This flexibility may be needed to evaluate vaccination programs to eliminate pathogens from countries with different mortality schedules en route to global eradication.

The effective reproduction number for the model with general mortality is derived using the next-generation matrix (NGM) approach. Because of complexities such as preferential mixing, aging, and heterogeneous vaccination coverage, the elements of the NGM involve long expressions. To ensure that they make biological sense, we provide intuitive interpretations of their constituent quantities that facilitate understanding how various complexities affect the magnitude of ${\mathcal{R}}_v$. We explore the influence of mortality schedules on optimal vaccination strategies and long-term impact of vaccination on incidence. Results suggest that, in some cases, mortality schedules may be influential.

This paper is organized as follows. In Section 2, we formulate a SEIR type age-structured meta-population model with age-dependent fertility and mortality rates, which include types I and II mortality as special cases. Derivation of the effective reproduction number is included in Section 3. Intuitive explanations for elements of the next-generation matrix, which are complicated by demographic processes, are also provided. In Section 4, we present optimal vaccination strategies derived via the gradient method for measles with various mortality schedules. This section also includes comparisons, in terms of optimal vaccine allocations, of models with types I and II mortality and the longterm effect of vaccination on incidence ascertained via numerical simulations. We discuss the findings in Section 5.

2. Formulation of the model

The meta-population model considered in this paper comprises n sub-populations (or groups) whose members are susceptible S_i, exposed (infected, but not yet infectious) E_i, infectious I_i, or removed R_i from the infection process (by virtue of immunization or naturally acquired immunity). The population size of group i is denoted by N_i = S_i + E_i + I_i + R_i and the total population size is

$$N=N_1+N_2+\cdots +N_n.$$

For demographic dynamics in the absence of disease and vaccination, we adopt the framework of Hethcote (2000), in which an ordinary differential equation model of an age-structured population with aging is derived from a partial differential equation system with continuous age (u). In his derivation, the n age groups are defined by the intervals [u_i−1, u_i), where 0 = u₀ < u₁ < u₂ < ⋯ < u_n−1 < u_n = ∞, and the per capita rates of fertility and mortality within age groups i are constants denoted by f_i and μ_i, respectively. Let θ_i denote the rates at which people exit age groups i due to aging (i.e., age from group i to i + 1) with θ_n = 0. Assume that the population has reached its stable age-distribution with constant growth rate ρ. Then N_i(t) = e^ρtP_i, where the P_i are constants satisfying

$$P_{i+1}=\frac{{\theta }_i{P}_i}{{\theta }_{i+1}+{\mu }_{i+1}+\rho },\text{for}1\le i\le n.$$ (1)

The constant P₁ is equal to N₁(0) under the assumption that

$$\sum _{i=1}^n{f}_i{N}_i=({\theta }_1+{\mu }_1+\rho )N_1,$$

as it leads to the equation $N_1^{\prime }=\rho N_1$. Because N₁(t) = e^ρtN₁(0), P₁ = N₁(0).

For the stable age distribution P_i to exist, the fertility (f_i), mortality (μ_i), aging (θ_i), and growth (ρ) rates must satisfy the following constraint (Hethcote, 2000):

$$\frac{f_1+f_2\frac{{\theta }_1}{{\theta }_2+{\mu }_2+\rho }+\cdots +f_n\frac{{\theta }_{n-1}\cdots {\theta }_1}{({\theta }_n+{\mu }_n+\rho )\cdots ({\theta }_2+{\mu }_2+\rho )}}{{\theta }_1+{\mu }_1+\rho }=1.$$ (2)

Thus, for given fertility, mortality, and aging rates, Eq. (2) can be used to determine the growth rate ρ. If ρ is negative, 0, or positive, the population is decreasing, constant, or increasing in size, respectively, with time. The exact formula for θ_i is θ_i = (μ_i + ρ)/(exp[(μ_i + ρ)(u_i − u_i−1)] − 1), but when μ_i and ρ are small, the approximation θ_i = 1/(u_i − u_i−1) for the aging rates can be used.

For the corresponding SEIR model, suppose that all newborn individuals are susceptible and that a proportion σ is immunized. Then the system of equations is

$$\begin{gathered} S_1^{\prime }=(1-\sigma )({\theta }_1+{\mu }_1+\rho )e^{\rho t}{P}_1-({\lambda }_1+{\theta }_1+{\mu }_1+{\chi }_1)S_1, \\ {S}_i^{\prime }={\theta }_{i-1}{S}_{i-1}-({\lambda }_i+{\theta }_i+{\mu }_i+{\chi }_i)S_i,1<i\le n, \\ {E}_1^{\prime }={\lambda }_1{S}_1-(\alpha +{\theta }_1+{\mu }_1)E_1, \\ {E}_i^{\prime }={\theta }_{i-1}{E}_{i-1}+{\lambda }_i{S}_i-(\alpha +{\theta }_i+{\mu }_i)E_i,1<i\le n, \\ {I}_1^{\prime }=\alpha E_1-(\gamma +{\theta }_1+{\mu }_1)I_1, \\ {I}_i^{\prime }={\theta }_{i-1}{I}_{i-1}+\alpha E_i-(\gamma +{\theta }_i+{\mu }_i)I_i,1<i\le n, \\ {R}_1^{\prime }=\sigma ({\theta }_1+{\mu }_1+\rho )e^{\rho t}{P}_1+\gamma I_1+{\chi }_1{S}_1-({\theta }_1+{\mu }_1)R_1, \\ {R}_i^{\prime }={\theta }_{i-1}{R}_{i-1}+\gamma I_i+{\chi }_i{S}_i-({\theta }_i+{\mu }_i)R_i,1<i\le n, \end{gathered}$$ (3)

where α is the reciprocal of the latent (pre-infectious) period, γ is the recovery rate, and χ_i is the vaccination rate for susceptible individuals in group i. The forces or hazard rates of infection among susceptible people are

$${\lambda }_i=a_i{\beta }_i\sum _{j=1}^n{c}_{ij}\frac{I_j}{N_j},1\le i\le n,$$ (4)

where a_i is the per capita contact rate, β_i is the probability of infection upon contacting an infectious person, c_ij is the proportion of the contacts of members of the ith sub-population that is with members of the jth, and I_j/N_j is the probability that a randomly encountered member of sub-population j is infectious. In this paper, we will consider the function of Jacquez et al. (1988), who modified that of Nold (Nold, 1980), defined as

$$c_{ij}={ϵ}_i{\delta }_{ij}+(1-{ϵ}_i)g_j,g_j=\frac{(1-{ϵ}_j)a_j{P}_j}{{\sum }_k(1-{ϵ}_k)a_k{P}_k},$$ (5)

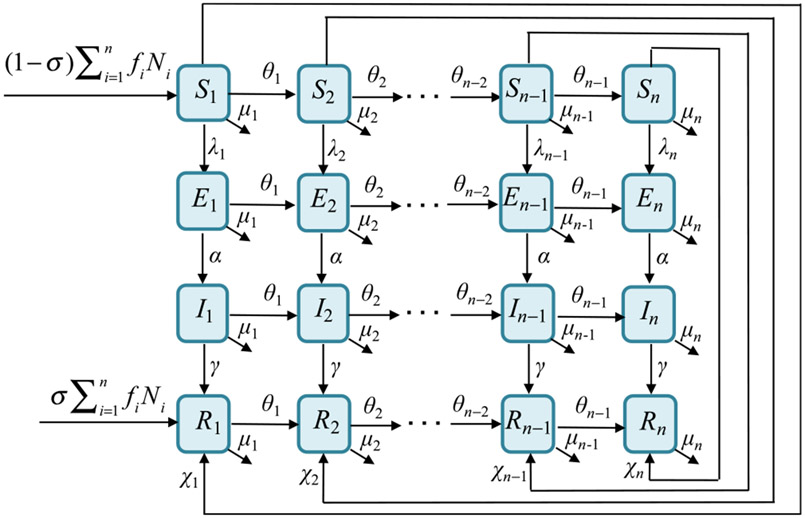
where the ϵ_i are fractions of contacts reserved for one’s own group (termed preferences), and δ_ij is the Kronecker delta (1 when i = j and 0 otherwise). The function g_j describes mixing that is random (i.e., proportional to unreserved contacts, [1 − ϵ_j]a_jP_j). A transition diagram corresponding to this model is depicted in Fig. 1.

Fig. 1.

Transition diagram for this demographically-realistic transmission model. Each epidemiological class has n sub-groups (horizontal flows) with transition rates θ_i due to aging.

The generality in choice of birth f_i and death rates μ_i allows the demographic model to cover age-dependent fertility and mortality rates, including types I and II mortality. For type I mortality, it is assumed that the lifespan is fixed at a maximum age u_max after which everyone dies; i.e., μ_i = 0 for all i < n and μ_n = ∞ (or a large value). For type II mortality, it is assumed that all age groups have the same constant per capita death rate μ_i = μ, where 1/μ corresponds to the mean lifespan.

The constraint (2) can be expressed using biologically relevant quantities. Let τ_i denote the mean sojourn in age group i and ϕ_i denote the probability of aging from group i to i + 1; i.e.,

$${\tau }_i(\rho )=\frac{1}{{\theta }_i+{\mu }_i+\rho },{\varphi }_i(\rho )=\frac{{\theta }_i}{{\theta }_i+{\mu }_i+\rho },1\le i\le n.$$

Note that ${\Phi }_j(\rho )={\prod }_{i=1}^{j-1}{\varphi }_i(\rho )$ (with Φ₁ = 1) represents the probability that a person ages from group 1 to group j. Thus, Eq. (2) can be rewritten as

$$\sum _{j=1}^n{f}_j{\Phi }_j(\rho ){\tau }_j(\rho )=1.$$ (6)

Expression (6) makes the condition more biologically transparent. When ρ = 0, the left-hand side is the population reproduction number

$${\mathcal{R}}_{pop}=\sum _{j=1}^n{f}_j{\Phi }_j(0){\tau }_j(0).$$

Clearly, ${\mathcal{R}}_{pop}$ is equal to 1 if and only if the population remains constant (i.e., growth rate ρ = 0), and ${\mathcal{R}}_{pop}>1(<1)$ if ρ > 0 (< 0).

Consider the fractions $x_i(t)=\frac{S_i(t)}{e^{\rho t}{P}_i}$, $y_i(t)=\frac{E_i(t)}{e^{\rho t}{P}_i}$, $z_i(t)=\frac{I_i(t)}{e^{\rho t}{P}_i}$, and let r_ij = P_i/P_j denote the ratio of the sub-populations i and j. Then the system of equations (3) becomes

$$\begin{gathered} x_1^{\prime }=(1-\sigma )({\theta }_1+{\mu }_1+\rho )-({\lambda }_1+{\theta }_1+{\mu }_1+\rho +{\chi }_1)x_1, \\ {x}_i^{\prime }=r_{(i-1)i}{\theta }_{i-1}{x}_{i-1}-({\lambda }_i+{\theta }_i+{\mu }_i+\rho +{\chi }_i)x_i,1<i\le n, \\ {y}_1^{\prime }={\lambda }_1{x}_1-(\alpha +{\theta }_1+{\mu }_1+\rho )y_1, \\ {y}_i^{\prime }=r_{(i-1)i}{\theta }_{i-1}{y}_{i-1}+{\lambda }_i{x}_i-(\alpha +{\theta }_i+{\mu }_i+\rho )y_i,1<i\le n, \\ {z}_1^{\prime }=\alpha y_1-(\gamma +{\theta }_1+{\mu }_1+\rho )z_1, \\ {z}_i^{\prime }=r_{(i-1)i}{\theta }_{i-1}{z}_{i-1}+\alpha y_i-(\gamma +{\theta }_i+{\mu }_i+\rho )z_i,1<i\le n. \end{gathered}$$ (7)

The fraction recovered is 1 − x_i − y_i − z_i for i = 1, 2, … , n.

3. Effective reproduction numbers

We derive the effective reproduction numbers using system (7), and provide a biological interpretation of the elements of the next-generation matrix (NGM). Let w_i denote the probabilities of susceptible people in group i being vaccinated before aging or dying; i.e., w_i = χ_i/(μ_i + θ_i + ρ + χ_i). The disease-free equilibrium is

$$\begin{gathered} x_1^{\ast }=(1-\sigma )(1-w_1), \\ {x}_i^{\ast }=r_{(i-1)i}\frac{{\theta }_{i-1}}{{\theta }_i+{\mu }_i+\rho +{\chi }_i}{x}_{i-1}^{\ast },2\le i\le n, \\ {y}_i^{\ast }=z_i^{\ast }=0,1\le i\le n, \end{gathered}$$

or equivalently,

$$\begin{gathered} x_i^{\ast }=(1-\sigma )\prod _{j=1}^i(1-w_j), \\ {y}_i^{\ast }=z_i^{\ast }=0,1\le i\le n. \end{gathered}$$ (8)

Proceeding via the NGM method (Diekmann and Heesterbeek, 2000; Van den Driessche and Watmough, 2002), the Jacobian (considering only the disease variables) is $J=\left(\begin{array}{cc}\hfill J_{11}\hfill & \hfill J_{12}\hfill \\ \hfill J_{21}\hfill & \hfill J_{22}\hfill \end{array}\right)$, where J₁₁, J₁₂, J₂₁ and J₂₂ are given in Box 1.

Box I. Simultation results.

$J_{11}=\left(\begin{array}{ccccc}\hfill -(\alpha +{\theta }_1+{\mu }_1+\rho )\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill r_{12}{\theta }_1\hfill & \hfill -(\alpha +{\theta }_2+{\mu }_2+\rho )\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill r_{(n-1)n}{\theta }_{n-1}\hfill & \hfill -(\alpha +{\theta }_n+{\mu }_n+\rho )\hfill \end{array}\right)$

$J_{12}=\left(\begin{array}{cccc}\hfill a_1{\beta }_1{x}_1^{\ast }{c}_{11}\hfill & \hfill a_1{\beta }_1{x}_1^{\ast }{c}_{12}\hfill & \hfill \cdots \hfill & \hfill a_1{\beta }_1{x}_1^{\ast }{c}_{1n}\hfill \\ \hfill a_2{\beta }_2{x}_2^{\ast }{c}_{21}\hfill & \hfill a_2{\beta }_2{x}_2^{\ast }{c}_{22}\hfill & \hfill \cdots \hfill & \hfill a_2{\beta }_2{x}_2^{\ast }{c}_{2n}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill a_n{\beta }_n{x}_n^{\ast }{c}_{n1}\hfill & \hfill a_n{\beta }_n{x}_n^{\ast }{c}_{n2}\hfill & \hfill \cdots \hfill & \hfill a_n{\beta }_n{x}_n^{\ast }{c}_{nn}\hfill \end{array}\right)$

$J_{21}=\alpha I_{n\times n},\text{and}$

$J_{22}=\left(\begin{array}{ccccc}\hfill -(\gamma +{\theta }_1+{\mu }_1+\rho )\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill r_{12}{\theta }_1\hfill & \hfill -(\gamma +{\theta }_2+{\mu }_2+\rho )\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill r_{(n-1)n}{\theta }_{n-1}\hfill & \hfill -(\gamma +{\theta }_n+{\mu }_n+\rho )\hfill \end{array}\right)$

For ease of presentation and interpretation, introduce the following biologically relevant quantities for group i (i = 1, 2, … , n):

$$\begin{gathered} {\xi }_i=\frac{\alpha }{\alpha +{\theta }_i+{\mu }_i+\rho }\text{Probabilities that latent people in} \\ \text{age-group}i\text{become infectious} \\ \text{before aging or dying}, \\ {p}_i=\frac{{\theta }_i}{\gamma +{\theta }_i+{\mu }_i+\rho }\text{Probabilities that infectious people} \\ \text{in age-group}i\text{age before} \\ \text{recovering or dying}, \\ {q}_i=\frac{{\theta }_i}{\alpha +{\theta }_i+{\mu }_i+\rho }\text{Probabilities that latent people in} \\ \text{age-group}i\text{age before becoming} \\ \text{infectious or dying}, \\ {\tau }_i^E=\frac{1}{\alpha +{\theta }_i+{\mu }_i+\rho }\text{Death- and aging-adjusted latent} \\ \text{periods in group}i, \\ {\tau }_i^I=\frac{1}{\gamma +{\theta }_i+{\mu }_i+\rho }\text{Death- and aging-adjusted} \\ \text{infectious periods in group}i. \end{gathered}$$ (9)

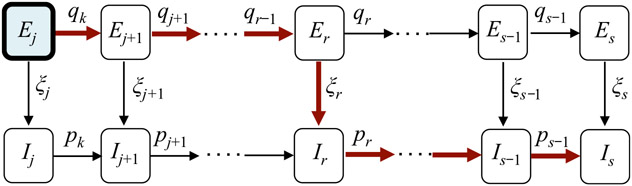
These symbols and definition are also listed in Table 1. Note that an infected person can take multiple routes, depending on the order of these events: aging, becoming infectious, and recovering. The diagram in Fig. 2 illustrates the scenario in which a person is infected while in group j and recovers while in group s.

Table 1.

Definition of the symbols used in the expression for ${\mathcal{R}}_v$ and in analyses.

Symbol	Description	Type I mortality	Type II mortality
ξi	Probability of becoming infectious while in age group i	α/(α + θi + ρ)	α/(α + θi + μi + ρ)
pi	Probability of aging while infectious from age group i to group i + 1	θi/(γ + θi + ρ)	θi/(γ + θi + μi + ρ)
qi	Probability of aging while incubating (in the latent or exposed class) from age group i to group i + 1	θi/(α + θi + ρ)	θi/(α + θi + μi + ρ)
${\tau }_i^E$	Aging and/or death adjusted mean latent period in age group i	1/(α + θi + ρ)	1/(α + θi + μi + ρ)
${\tau }_i^I$	Aging and/or death adjusted mean infectious period in age group i	1/(γ + θi + ρ)	1/(γ + θi + μi + ρ)
Pks	Probability of aging from group k to s while infectious (Pkk = 1)	${\prod }_{j=k}^{s-1}{p}_j$, s > k	Same
Qks	Probability of aging from group k to s while incubating (in the latent or exposed class) (Qkk = 1)	${\prod }_{j=k}^{s-1}{q}_j$, s > k	Same
Aij	Proportion of effective contacts with group i by an infectious person infected while in group j	See (10)	Same

Note: i, j, k, s = 1, 2, …, n.

Fig. 2.

A transition diagram showing the multiple paths that a person, who was infected while in group j, can take before recovering in group s (1 ≤ j ≤ s ≤ n). The probability of taking the path indicated by red (thick) arrows is ${\prod }_{m=j}^{r-1}{q}_m{\xi }_r{\prod }_{i=r}^{s-1}{p}_i$, where p_i, q_i, ξ_i, are defined in (9).

To facilitate description of the probabilities corresponding to various routes, which simplifies presentation of the elements of the NGM, we introduce the following quantities:

$Q_{jr}=\prod _{m=j}^{r-1}{q}_m$ Probabilities that a person who was infected while in age-group j aged to group r ≥ j before becoming infectious or dying (for ease of notation, define $Q_{jj}={\prod }_{m=j}^{j-1}{q}_m=1$).

$P_{rs}=\prod _{i=r}^{s-1}{p}_i$ Probabilities that a person who became infectious while in age-group r aged to group s ≥ r before recovering or dying (for ease of notation, define $P_{rr}={\prod }_{i=r}^{r-1}{p}_i=1$).

Using these notations, the probability that a person who was infected while in group j, became infectious while in group r ≥ j, and recovered while in group s ≥ r (i.e., the path illustrated in Fig. 2) is

$$\prod _{m=j}^{r-1}{q}_m{\xi }_r\prod _{i=r}^{s-1}{p}_i=Q_{jr}{\xi }_r{P}_{rs}.$$

Let J = F − V, where $F=\left(\begin{array}{cc}\hfill 0\hfill & \hfill J_{12}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$ and $V=\left(\begin{array}{cc}\hfill -J_{11}\hfill & \hfill 0\hfill \\ \hfill -J_{21}\hfill & \hfill -J_{22}\hfill \end{array}\right)$. It is easy to verify that $V^{-1}=\left(\begin{array}{cc}\hfill -J_{11}^{-1}\hfill & \hfill 0\hfill \\ \hfill -J_{22}^{-1}{J}_{21}{J}_{11}^{-1}\hfill & \hfill -J_{22}\hfill \end{array}\right)$, where

$$J_{11}^{-1}=\left(\begin{array}{ccccc}\hfill {\tau }_1^E\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill r_{12}{q}_1{\tau }_2^E\hfill & \hfill {\tau }_2^E\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill r_{1n}{Q}_{1n}{\tau }_n^E\hfill & \hfill r_{2n}{Q}_{2n}{\tau }_n^E\hfill & \hfill \cdots \hfill & \hfill r_{(n-1)n}{q}_{n-1}{\tau }_n^E\hfill & \hfill {\tau }_n^E\hfill \end{array}\right),$$

$$J_{22}^{-1}=\left(\begin{array}{ccccc}\hfill {\tau }_1^I\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill r_{12}{p}_1{\tau }_2^I\hfill & \hfill {\tau }_2^I\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill r_{1n}{P}_{1n}{\tau }_n^I\hfill & \hfill r_{2n}{P}_{2n}{\tau }_n^I\hfill & \hfill \cdots \hfill & \hfill r_{(n-1)n}{p}_{n-1}{\tau }_n^I\hfill & \hfill {\tau }_n^I\hfill \end{array}\right),$$

and the matrix $J_{22}^{-1}{J}_{21}{J}_{11}^{-1}$ is

$$\left(\begin{array}{ccccc}\hfill {\xi }_1{\tau }_1^I\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill r_{12}\sum _{j=1}^2{Q}_{1j}{\xi }_j{P}_{j1}{\tau }_2^I\hfill & \hfill {\xi }_2{\tau }_2^I\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill r_{1n}\sum _{j=1}^n{Q}_{1j}{\xi }_j{P}_{jn}{\tau }_n^I\hfill & \hfill r_{2n}\sum _{j=2}^n{Q}_{2j}{\xi }_j{P}_{jn}{\tau }_n^I\hfill & \hfill \cdots \hfill & \hfill r_{(n-1)n}\sum _{j=n-1}^n{Q}_{(n-1)j}{\xi }_j{P}_{jn}{\tau }_n^I\hfill & \hfill {\xi }_n{\tau }_n^I\hfill \end{array}\right).$$

The next-generation matrix is $K=F{V}^{-1}=\left(\begin{array}{cc}\hfill K_{11}\hfill & \hfill \ast \hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$, where $K_{11}=F_{12}{J}_{22}^{-1}{J}_{21}{J}_{11}^{-1}$. The ^‘*’ denotes a block matrix that does not affect the eigenvalues of K. The meta-population ${\mathcal{R}}_v$ is the dominant eigenvalue of K₁₁. Let

$$\begin{gathered} A_{ij}=c_{ij}{\tau }_n^I{\xi }_j+r_{j(j+1)}{c}_{i(j+1)}{\tau }_{j+1}^I({\xi }_j{p}_i+q_j{\xi }_{j+1})+\cdots \\ +r_{js}{c}_{is}{\tau }_s^I\sum _{r=j}^s{Q}_{jr}{\xi }_r{P}_{rs}+\cdots +r_{jn}{c}_{in}{\tau }_n^I\sum _{r=j}^n{Q}_{jr}{\xi }_r{P}_{rn} \\ =\sum _{s=j}^n{r}_{js}{c}_{is}{\tau }_s^I\sum _{r=j}^s{Q}_{jr}{\xi }_r{P}_{rs},1\le i,j\le n. \end{gathered}$$ (10)

Biological interpretations of the expressions A_ij are provided in the next section. The elements in the expression of A_ij for types I and II mortality are listed in Table 1. The matrix K₁₁ can be written as

$$K_{11}=(a_i{\beta }_i{x}_i^{\ast }{A}_{ij})=\text{diag}(a_1{\beta }_1{x}_1^{\ast },a_2{\beta }_2{x}_2^{\ast },\dots ,a_n{\beta }_n{x}_n^{\ast })(A_{ij}),$$ (11)

where the $x_i^{\ast }$ are steady-state numbers of susceptible people given in Eq. (8), (A_ij) is the matrix with elements A_ij, and the dominant eigenvalue of K₁₁ gives the effective reproduction number ${\mathcal{R}}_v$.

Notice that the influence of mixing on ${\mathcal{R}}_v$ is represented by A_ij. For the general mixing function described in Eq. (5) with n > 3, explicit formulae for the dominant eigenvalue of the matrix K₁₁ can be very difficult to derive, and ${\mathcal{R}}_v$ is usually computed numerically. However, in the case of proportionate mixing (i.e., ϵ_i = 0 for all i), K₁₁ has rank 1 and the ${\mathcal{R}}_v$ is given by the trace.

3.1. Interpretation of A_ij in K ₁₁

All entries in K₁₁ have the form $a_i{\beta }_i{x}_i^{\ast }{A}_{ij}$. The factor A_ij represents the proportion of effective contacts with people in group i of one person who was infected while in group j during his/her infectious period. As mentioned, this infected person can take various routes depending on the order of three events: aging, disease progression (becoming infectious), and recovery. For example, if the person became infectious while in group j, the total number of contacts with people in group i would be A_ij. Each path corresponds to one term in A_ij, as depicted in Fig. 2. More specifically, the first term corresponds to the path of disease progression (with probability ξ_i) and recovery before aging, in which case the infectious period is ${\tau }_j^I$ and proportion of contacts with group i is c_ij.

The second term in A_ij corresponds to the person recovering while in group j + 1, in which case s/he either became infectious in group j (with probability ξ_j) and then aged to group j + 1 before recovery (with probability p_j), or aged to group j +1 before becoming infectious (with probability q_j) and became infectious while in group j + 1 (with probability ξ_j). For both cases, the infectious period is ${\tau }_{j+1}^I$ and the proportion of contacts with group i is c_i(j+1). The ratio r_j(j+1) = P_j/P_j+1 represents the relative sizes of the sub-populations to which the infected and infectious people belong. This term is needed because of aging in the model.

The generic term in A_ij involving ${\tau }_s^I$, 1 < s < n, describes the case when recovery occurred while in group s. This includes several paths. The infected person can (i) become infectious while in group j (with probability ξ_j) and then age through all groups before recovering in group s (with probability $P_{js}={\prod }_{k=j}^{s-1}{p}_k$; (ii) age to group j + 1 (with probability q_j), become infectious within group j + 1 (with probability ξ_j), and then age through all groups before recovering in group s (with probability $P_{(j+1)s}={\prod }_{k=j+1}^{s-1}{p}_k$, etc.; and finally (iii) age to group s (with probability $Q_{js}={\prod }_{k=j}^{s-1}{q}_k$ and become infectious within group s (with probability ξ_s). For all such cases, the infectious period is ${\tau }_s^I$ and the proportion of contacts with group i is c_is.

It follows that $a_i{\beta }_i{x}_i^{\ast }{A}_{ij}$ represents the average number of new infections generated among susceptible people in group i by one person who was infected while in group j.

3.2. ${\mathcal{R}}_v$ In special cases

Consider first the case where mixing is proportionate (i.e., the c_ij are given by Eq. (5) with ϵ_i = 0). Note that c_1j = c_2j = ⋯ = c_nj for all j, which leads to A_1j = A_2j = ⋯ = A_nj for all j. In this case, K₁₁ has rank 1 and its dominant eigenvalue is the trace. Hence,

$${\mathcal{R}}_v=\sum _{i=1}^n{a}_i{\beta }_i{x}_i^{\ast }{A}_{ii},$$ (12)

where the A_ii are given in Eq. (10)

For general mixing, consider the case where n = 2 sub-populations. The matrix K₁₁ has the form $K_{11}=\left[\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill C\hfill & \hfill D\hfill \end{array}\right]$, where

$$A=a_1{\beta }_1{x}_1^{\ast }{A}_{11},B=a_1{\beta }_1{x}_1^{\ast }{A}_{12},C=a_2{\beta }_2{x}_2^{\ast }{A}_{21},D=a_2{\beta }_2{x}_2^{\ast }{A}_{22},$$

and

$$A_{i1}={\tau }_1^I{\xi }_1{c}_{i1}+{\tau }_2^I{c}_{12}\frac{N_1}{N_2}({\xi }_1{p}_1+q_1{\xi }_2),A_{i2}={\tau }_2^I{\xi }_2{c}_{i2},i=1,2.$$

In this case, for any mixing matrix (c_ij),

$${\mathcal{R}}_v=\frac{1}{2}\left[A+D+\sqrt{(A-D{)}^2+4BC}\right].$$

4. Optimal vaccination strategy

Assume that ${\mathcal{R}}_v>1$ and some number of additional vaccine doses is available. Let χ = (χ₁, χ₂, … , χ_n) ≥ 0 denote the vector of vaccination rates and let ${\mathcal{R}}_v(\chi )$ denote the effective reproduction number corresponding to χ. The optimal vaccine allocation can be obtained by solving the following Lagrange optimization problem:

$$\mathbf{Minimize}{\mathcal{R}}_v(\chi ),\mathbf{subject}\mathbf{to}\sum _{i=1}^n{\chi }_i{x}_i^{\ast }{P}_i=c.$$ (13)

The constant c represents the available vaccine doses and the $x_i^{\ast }{P}_i$ denote the number of susceptible people in group i, where $x_i^{\ast }$ is given by Eq. (8) with χ_i = 0

The solution to (13) can be determined by solving simultaneously the equations

$$\nabla {\mathcal{R}}_v+\lambda (x_1^{\ast }{P}_1,x_2^{\ast }{P}_2,\dots ,x_n^{\ast }{P}_n)=0\text{and}\sum _{i=1}^n{\chi }_i{x}_i^{\ast }{P}_i=c,$$ (14)

where λ is a Lagrange multiplier. Let $\widehat{X}=({\widehat{\chi }}_1,{\widehat{\chi }}_2,\dots ,{\widehat{\chi }}_n)$ denote the optimal solution to problem (13) and let ${\mathcal{R}}_{v\text{min}}={\mathcal{R}}_v(\widehat{X})$. It can be shown (Feng et al., 2015) that the gradient $\nabla {\mathcal{R}}_v(\widehat{X})$ is orthogonal to the hyperplane ${\sum }_{i=1}^n{\chi }_i{x}_i^{\ast }{P}_i=c$ at the point $\widehat{X}$, where the hypersurface ${\mathcal{R}}_v(\widehat{\chi })={\mathcal{R}}_{v\text{min}}$ intersects this hyperplane.

Another optimization problem aims at finding the minimum doses required to achieve a prescribed reduction in ${\mathcal{R}}_v$. Let δ be the reduction; i.e., $\delta ={\mathcal{R}}_v-{\mathcal{R}}_v(\chi )$. To find the vaccination strategy that requires the least doses, we solve the following optimization problem:

$$\mathbf{Minimize}\sum _{i=1}^n{\chi }_i{x}_i^{\ast }{P}_i,\mathbf{subject}\mathbf{to}{\mathcal{R}}_v(\chi )\le {\mathcal{R}}_v-\delta .$$ (15)

Using a similar approach, Feng et al. (2015) showed that the solution to problem (15) is given by the gradient $\nabla {\mathcal{R}}_v$.

4.1. Effect of mortality on the optimal strategy

Consider the case of n = 15 age groups: 0, 1–4, 5–9, …, 65+ years. Assume that the time unit is months. We adopt the parameters for measles in China (Hao et al., 2019): 1/α = 0.5 (month), 1/γ = 0.25 (month), and several vectors whose age-dependent values are listed in Table 2, including contact rates, (a_i), probabilities of infection per contact, (β_i), aging rates, (θ_i), 2014 fertility, (f_i) and mortality rates, (μ_i), and types I, (${\mu }_i^{\mathrm{I}}$), and II mortality with longer and shorter lifespans, ${\mu }_i^{\mathrm{II}}$ and ${\mu }_i^{\mathrm{II}}$, 1 ≤ i ≤ n. Using these parameter values, the population growth rate determined by condition (2) is ρ = 0.00067. For types I and II mortality, the f_i are scaled to satisfy equation (2) while preserving their age distribution.

Table 2.

Parameter values used in analyses of the optimal vaccine allocation for reducing ${\mathcal{R}}_v$ and numerical simulations of model (3).

Par	Values
(βi)	(1, 0.29, 0.093, 0.1, 0.13, 0.22, 0.24, 0.24, 0.23, 0.21, 0.18, 0.14, 0.11, 0.064, 0.2)
(ai)	(9.2, 11, 15.3, 18.7, 18.2, 14, 14.3, 14.4, 14.9, 14.8, 13.4, 13, 11.9, 10, 7.8)×30
(fi)	(0, 0, 0, 0, 0.98, 6.85, 7.61, 4.08, 1.44, 0.33, 0.09, 0, 0, 0, 0)×10−3
(μi)	(3.8, 0.4, 0.2, 0.2, 0.3, 0.3, 0.5, 0.7, 0.9, 1.5, 1.9, 3.6, 4.7, 8.4, 38.1)×10−4
(θi)	(1/12, 1/48, 1/60, 1/60, 1/60, 1/60, 1/60, 1/60, 1/60, 1/60, 1/60, 1/60, 1/60, 1/60, 0)
1/α	0.5
1/γ	0.25
	For other types of mortality
$({\mu }_i^{\mathrm{I}})$	0 for 1 ≤ i ≤ 14 and 1/(10 × 12) for i = 15 (Type I mortality)
$({\mu }_i^{\text{II}}{)}_a$	1/(70 × 12) for 1 ≤ i ≤ 15 (Type IIa mortality with a lifespan of 70 years)
$({\mu }_i^{\text{II}}{)}_b$	1/(40 × 12) for 1 ≤ i ≤ 15 (Type IIb mortality, a shorter lifespan than type IIa)

Note: i = 1, 2,…, 15 for 15 age groups. Time unit is months. The multiple 30 in the (a_i) vector converts daily rates to monthly ones.

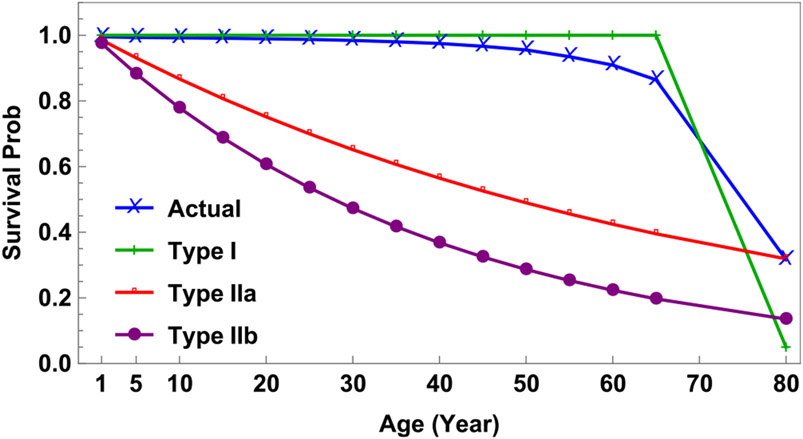
Fig. 3 illustrates the corresponding survivorship curves. One corresponds to the mortality schedule (μ_i) given in Table 2. The others represent two extremes, type I mortality with μ_i = 0 for 1 ≤ i ≤ 14 and 1/μ₁₅ = 5 × 12 (months) and type II mortality with different lifespans; i.e., a lifespan of 70 years (μ_i = 1/(70 × 12) for all i, labeled as Type IIa) or 40 years (μ_i = 1/(40 × 12) for all i, labeled as Type IIb).

Fig. 3.

Survivorship curves based on the 2014 Chinese death rates (μ_i) and three alternative scenarios labeled as type I, type IIa, and type IIb mortality as described in Table 2.

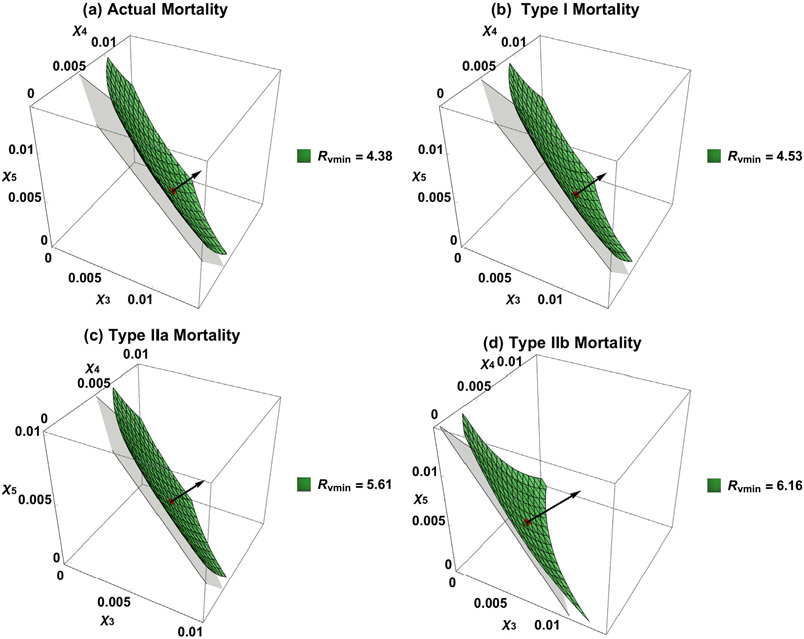
To demonstrate the influence of mortality, suppose that the existing vaccination program applies σ = 0.5 coverage to the infant group and consider the case when 5k additional doses per year are available for children aged 5–19 years (groups 3–5). We identify their optimal allocation from the model under four types of mortality. For comparability, we scale the β vector so that all four basic reproduction numbers are equal to 18. The scaling constants are 0.95 (type I), 1.05 (type IIa), and 0.97 (type IIb). We assume that mixing is proportionate for analyses in this section and simulations in the next. The results are illustrated in Fig. 4.

Fig. 4.

Comparison of results from model (3) with the four mortality schedules described in Fig. 3. Plots (a)–(d) show both the corresponding contour surfaces of the minimized value for ${\mathcal{R}}_{v\text{min}}$ and optimal vaccination rates (${\widehat{\chi }}_1$, ${\widehat{\chi }}_2$, ${\widehat{\chi }}_3$).

For the actual mortality schedule (Table 3(a)), the reproduction number, given routine vaccine coverage of σ = 0.5, is reduced from ${\mathcal{R}}_0=18$ to ${\mathcal{R}}_v=9$. With 5k additional vaccine doses per year, the optimal solution is $({\widehat{\chi }}_3,{\widehat{\chi }}_4,{\widehat{\chi }}_5)=(0.0082,0.0066,0.0045)$ and the corresponding reproduction number is ${\mathcal{R}}_{v\text{min}}=4.38$. Results for other three mortality types are also listed in Table 3.

Table 3.

Comparison of the minimized ${\mathcal{R}}_v$ under four mortality schedules and different vaccine doses.

Mortality	5k doses		10k doses
	${\mathcal{R}}_v$	Vaccination rates (× 10−3)	${\mathcal{R}}_v$	Vaccination rates (× 10−2)
(a) Actual	4.38	8.2, 6.6, 4.5	2.74	1.7, 1.3, 0.98
(b) Type I	4.53	7.8, 6.2, 4.2	2.86	1.6, 1.3, 0.92
(c) Type IIa	5.61	5.2, 4.9, 4.2	3.97	1.1, 0.96, 0.75
(d) Type IIb	6.16	4.2, 4.4, 3.5	4.64	0.94, 0.85, 0.68

The contour surface of ${\mathcal{R}}_v$ corresponding to the optimal solution is illustrated in Fig. 4(a). The light plane is the constraint corresponding to the additional 5k doses per year, which is tangent to the surface with their intersection corresponding to the optimal strategy. Notice that the gradient of the function ${\mathcal{R}}_v({\chi }_3,{\chi }_4,{\chi }_5)$ at the intersection point is normal to the constraint. Fig. 4(b)-(d) show the optimal solutions based on types I, IIa, and IIb mortality as shown in Table 3. In these cases, the reproduction numbers were all equal to 9 before additional vaccine doses were administered. With the additional 5k doses per year, the minimized values of ${\mathcal{R}}_{v\text{min}}$ in these three cases are 4.53, 5.61, and 6.16, respectively.

With 10k additional vaccine doses per year, the optimal solutions (${\widehat{\chi }}_3,{\widehat{\chi }}_4,{\widehat{\chi }}_5$) for the four mortality types are also listed in Table 3, and the corresponding minimized values of the reproduction numbers ${\mathcal{R}}_{v\text{min}}$ are 2.74, 2.86, 3.97, and 4.64, respectively.

4.2. Effect of mortality on the impact of control efforts

The comparisons in Section 4.1 are based on reductions in the effective reproduction number. Vaccination programs can also be evaluated by reductions in incidence. In this section, we present numerical simulations of model (3) with different mortality schedules.

To ensure that these models are comparable, we fix several parameter values. We choose the growth rate ρ and population size at the beginning of simulations. We consider the model with actual birth and death rates as the baseline. Using the values of β_i, θ_i, f_i, and μ_i in the top panel of Table 2, we determine the growth rate ρ using the formula (2), which is ρ = 0.00067. Choosing P₁ = 10 000, we compute P_i (2 ≤ i ≤ 15) using the formula (1) to get the stable age distribution:

$$\begin{gathered} (P_1,P_2,\dots ,P_{15})=(10000,38681,45429,44584,42787, \\ 41062,39362,37688,36045,34354,32669, \\ 30767,28797,26405,98234) \end{gathered}$$ (16)

with total population size $P_{total}={\sum }_{i=1}^{15}{P}_i=587864$. For initial conditions, we use disease surveillance and serological observations (Hao et al., 2019) to calculate the vectors of proportions p_S, p_I and p_R where

$$(p_S{)}_i=\frac{S_i}{P_i},(p_I{)}_i=\frac{I_i}{P_i},(p_R{)}_i=\frac{R_i}{P_i},i=1,2,\dots ,15,$$

from which we obtain the initial conditions for S, I and R. In the absence of information about the exposed class, we assume that E = 0 and determine new initial conditions after a burn-in period T. For example, choosing T = 117, the initial conditions are

$$\begin{gathered} S_{0i}=S_i(T),E_{0i}=E_i(T),I_{0i}=I_i(T),R_{0i}=R_i(T), \\ 1\le i\le 15. \end{gathered}$$ (17)

We remark that $e^{-\rho T}{\sum }_{i=1}^{15}(S_{0i}+E_{0i}+I_{0i}+R_{0i})=P_i$.

The solution of system (3) with initial condition (17) for the actual birth and death rates is shown in Fig. 5(a), which plots total incidence (new infections from all groups per 10⁶) scaled by e^−ρt. Scaling (i.e., multiplying by the factor e^−ρt) corrects for the solution increasing with positive growth rate ρ > 0.

Fig. 5.

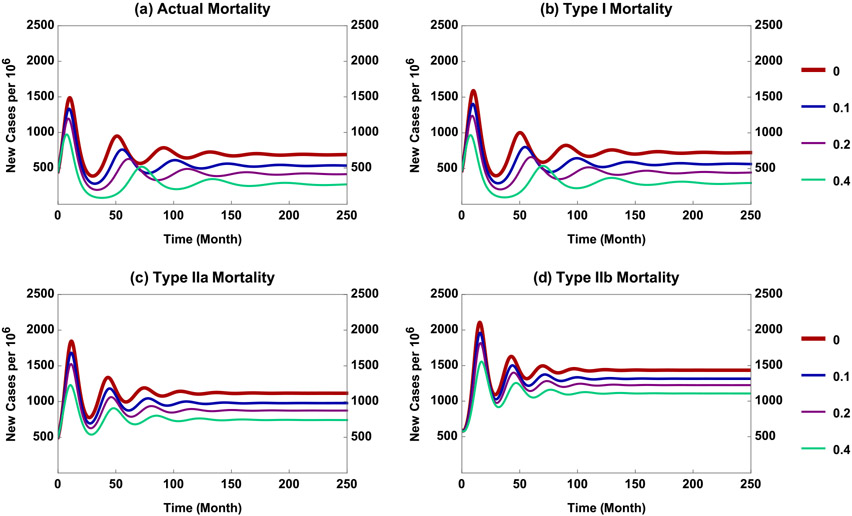
Results of simulating model (3) with four types of mortality when ages 5-19 years (age groups 3–5) are vaccinated at equal rates corresponding to coverage c = 0, 0.1, 0.2 and 0.4.

We scaled the actual fertility schedule by the factors 0.984, 1.457, and 1.923 for mortality types I, IIa, and IIb, respectively, to achieve the same ρ = 0.00067. And we chose P₁ = 10 520, 16 500, 21 200, respectively, so that the population sizes P_total were similar. Then we repeated the procedure described above for the actual birth and death rates. That is, using the same proportions for vectors p_S, p_I, and p_R together with P_total, we obtained the preliminary initial conditions. The burn-in periods T for mortality types I, IIa, and IIb are T = 117, 75, and 55, respectively. These T values were chosen to obtain similar total incidence values. Then we chose the solution values at T to be the new initial conditions (Table 4 in the Appendix A).

Table 4.

Initial conditions used for plots (a)–(d) in Fig. 5.

(a)	S(0) = (4509, 9821, 7384, 3910, 1820, 869, 503, 374, 320, 315, 363, 453, 508, 563, 2924) E(0) = (49, 40, 13, 9, 5, 3, 2, 2, 1, 1, 1, 1, 1, 1, 2) I(0) = (23, 20, 6, 4, 3, 2, 1, 1, 1, 1, 1, 0, 1, 0, 1) R(0) = (6234, 31955, 42812, 44296, 44448, 43537, 42065, 40386, 38662, 36839, 34968, 32822, 30636, 27994, 103317)
(b)	S(0) = (4737, 10231, 7709, 4082, 1881, 878, 495, 360, 306, 303, 357, 462, 539, 636, 1603) E(0) = (52, 42, 14, 10, 6, 3, 2, 2, 1, 1, 1, 1, 1, 1, 1) I(0) = (24, 20, 7, 5, 3, 2, 1, 1, 1, 1, 1, 1, 1, 0, 0) R(0) = (6565, 33799, 45257, 46842, 47080, 46194, 44760, 43146, 41519, 39906, 38298, 36699, 35186, 33708, 61975)
(c)	S(0) = (6143, 10272, 5960, 2430, 1105, 607, 394, 307, 260, 255, 302, 378, 396, 433, 535) E(0) = (69, 44, 11, 6, 3, 2, 2, 1, 1, 1, 1, 1, 1, 1, 0) I(0) = (33, 22, 6, 3, 2, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0) R(0) = (11105, 53373, 65665, 62009, 56865, 51543, 46520, 41896, 37705, 33898, 30421, 27260, 24467, 21933, 20966)
(d)	S(0) = (5950, 8756, 4412, 1722, 934, 558, 365, 287, 237, 228, 268, 319, 305, 317, 395) E(0) = (93, 54, 12, 6, 4, 3, 2, 2, 1, 1, 1, 1, 1, 1, 0) I(0) = (46, 28, 6, 3, 2, 2, 1, 1, 1, 1, 1, 1, 0, 0, 0) R(0) = (15907, 68875, 78938, 69818, 60464, 52135, 44859, 38526, 33073, 28359, 24266, 20736, 17765, 15191, 14514)

To facilitate comparison, equal vaccination rates were applied to children aged 5–19 years (groups 3–5). The simulation results with initial conditions described above, other parameter values the same as in Section 4.1, and vaccination coverage c = 0, 0.1, 0.2 and 0.4 are illustrated in Fig. 5. The corresponding immunization rates are $\chi =-\frac{1}{12}\text{ln}(1-0.95c)$ per month, where 0.95 is vaccine efficacy.

We observe from Fig. 5 that, under equal vaccination coverage c, the model with type IIb mortality has the highest long-term incidence and vaccination has the least effect (see (d)). The endemic levels corresponding to types I and IIa mortality are similar, while that with type IIb mortality is higher. The effect of increasing c is most apparent for type I and least for IIb (see (b) and (d)), with type IIa intermediate. For example, the endemic levels for c = 0.4 are decreased by about 60% and 20%, respectively, in comparison with that for c = 0. We also observe that, for the model with actual fertility and mortality rates, the endemic level and effects of increasing c are closer to those for type I than II mortality (see (a)–(c)).

5. Discussion

John (1990) compared age-specific transmission models with the same mortality, but different fertility schedules. She showed that time to equilibrium, age-specific incidence and proportions susceptible at equilibrium, and effectiveness of immunization all depended on fertility. Using actual and model mortality schedules, we investigated whether or not mortality affects optimal vaccination programs.

We developed a SEIR model with multiple age groups, aging and age-dependent fertility and mortality rates (system (3)). Using the method of Lagrange optimization with constraint, we identified the optimal allocation of supplemental vaccine doses to reduce the effective reproduction number ${\mathcal{R}}_v$ of the metapopulation. And we carried out numerical simulations to examine the effect of supplemental vaccination at equal age-specific rates on long-term incidence. Comparisons were made under various demographic schedules and vaccination scenarios, including actual fertility and mortality rates and mortality types I and II with fertility scaled to yield the same growth rate ρ. For ease of presentation, we refer to system (3) with mortality of types (a)–(d) in Table 3 as models (a)–(d).

Our main findings include the following regarding the influence of mortality schedules on the impact of supplemental immunization activities.

1. The impact of 5 or 10k supplementary vaccine doses is greatest in models with actual mortality and least in ones with type IIb mortality (see Fig. 4 and Table 3).

2. When models with mortality types I and II are compared, more dramatic differences are observed when type II mortality is combined with a shorter lifespan (model (d)), in terms of both ${\mathcal{R}}_{v\text{min}}$ and long-term incidence (see Table 3 and Fig. 5).

3. When models (a) and (b) are compared, outcomes are similar, presumably because their survival curves are similar (see Fig. 3).

These results are limited by our assumptions that mixing is proportionate and populations are at their stable age distributions, neither of which is true in nature. Insofar as many infectious disease modelers assume homogeneous mixing and either ignore demography or assume that births equal deaths, whereupon population sizes are constant, our analyses are more realistic even with these assumptions. And, while both could be relaxed in simulations, we retained them for consistency.

These limitations notwithstanding, our findings suggest that demographic details may affect the impact of measles vaccination. In our analyses and simulations, vaccination of children aged 5 to 19 years has more impact when mortality is type I (or actual in China during 2014) than type II simply because there are more people in those age groups (see Fig. 3). In turn, this suggests that vaccination may have less impact in countries where mortality from infectious diseases including measles is greatest. And, even if children survive, measles may compromise their immune systems such that they succumb to another pathogen (Mina et al., 2019).

A different approach to optimal vaccination strategies for age-structured models was taken by Hadeler and Müller (1996a,b) and by Castillo-Chavez and Feng (1998). Those authors studied a PDE model with an age-dependent vaccination function ψ(a). Their cost function C(ψ(a)) and effective reproduction number ${\mathcal{R}}_e(\psi (a))$ were functions of ψ(a) and the density of susceptible people at the steady-state under ψ(a). Thus, their optimal strategy informs “long-term” policymaking (e.g., vaccination schedules). Our optimal solutions are based on the “gradient.” That is, given a current state, find a vaccine allocation among different age groups that provides the largest reduction in ${\mathcal{R}}_v$. When the system has reached steady-state with these vaccination rates (after a short time), a new gradient direction can be computed. This answers the policy question, “On which age groups should supplementary immunization activities (SIAs) focus?”

A similar study, on optimal vaccination strategies for meta-populations with preferential mixing formulated as a Lagrange optimization problem, was presented by Poghotanyan et al. (2018), who provided a rigorous proof for the existence of the optimal solution. They showed also that the optimal solution matches that obtained using the gradient approach.

Appendix A. Initial conditions for simulations

The initial conditions used in Fig. 5 are shown in Table 4. They are based on measles in China at the beginning of 2014. See Section 4.2 for a description of the manner by which these initial conditions were chosen.

Appendix B. Stable age distribution

To confirm that system (3) indeed satisfies the assumption of stable age distribution, Fig. 6 illustrates simulations without infections; i.e., the following system for the demographics:

$$\begin{gathered} N_1^{\prime }=\left({\theta }_1+{\mu }_1+\rho \right)e^{\rho t}{P}_1-({\lambda }_1+{\theta }_1+{\mu }_1)N_1, \\ {N}_i^{\prime }={\theta }_{i-1}{N}_{i-1}-({\lambda }_i+{\theta }_i+{\mu }_i)N_i,2\le i\le 15. \end{gathered}$$ (18)

Fig. 6.

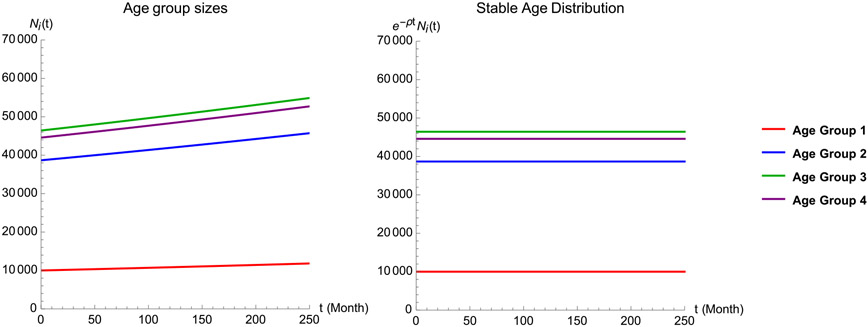
Simulation results of the model for demographics (population sizes of age groups in the absence of infections) for the case of actual birth and death rates. The left plot shows the population sizes for age groups 1–4 (N_i(t), 1 ≤ i ≤ 4). The right plot shows the age distribution: e^−ρtN_i(t), 1 ≤ i ≤ 4.

This figure is for the actual birth and death rates, with all other parameter values the same as in Fig. 5(a). The plot on the left shows solutions of (18) for the first four age groups, whereas that on the right shows e^−ρtNi(t), which are constant. This demonstrates that the population is at its stable age distribution.