Assessing the impact of SARS-CoV-2 infection on the dynamics of dengue and HIV via fractional derivatives

Abstract

A new non-integer order mathematical model for SARS-CoV-2, Dengue and HIV co-dynamics is designed and studied. The impact of SARS-CoV-2 infection on the dynamics of dengue and HIV is analyzed using the tools of fractional calculus. The existence and uniqueness of solution of the proposed model are established employing well known Banach contraction principle. The Ulam-Hyers and generalized Ulam-Hyers stability of the model is also presented. We have applied the Laplace Adomian decomposition method to investigate the model with the help of three different fractional derivatives, namely: Caputo, Caputo-Fabrizio and Atangana-Baleanu derivatives. Stability analyses of the iterative schemes are also performed. The model fitting using the three fractional derivatives was carried out using real data from Argentina. Simulations were performed with each non-integer derivative and the results thus obtained are compared. Furthermore, it was concluded that efforts to keep the spread of SARS-CoV-2 low will have a significant impact in reducing the co-infections of SARS-CoV-2 and dengue or SARS-COV-2 and HIV. We also highlighted the impact of three different fractional derivatives in analyzing complex models dealing with the co-dynamics of different diseases.

1. Introduction

The Severe Acute Respiratory Syndrome CoronaVirus 2 (SARS-CoV-2) has infected nearly 514,943,711 of the world's total population and caused more than 6,000,000 deaths [1]. Mutations of the original strain of the virus have emerged in recent times, and is creating more concerns in the world [2]. SARS-CoV-2 co-infections with other micro-organisms such as influenza virus, Legionella, Pneumocystis jirovecii, mycoplasma pneumoniae, cytomegalovirus and HIV have been investigated in the literature [3]. Qin et al. [4] reported that the function of the immune system is greatly reduced due to co-current infections with both HIV and SARS-COV-2. Suwanwongse and Shabarek [5], in a study, considered the co-infection of SARS-CoV-2 and Human immune deficiency virus (HIV) among some selected patients and observed that CD+ T-cell greatly suffers dysfunction in co-infected patients. The World Health Organization (WHO) has affirmed that individuals infected with both SARS-CoV-2 and HIV are prone to suffer severe illness leading to death [3]. In addition, a significant rise in cytokine production has been associated with patients co-infected with SARS-CoV-2 and HIV, thereby increasing viral load and suppression of the immune system [3].

Moreover, Cardiovascular diseases and hyperlipidemia are some of the co-morbidities linked with HIV and SARS-CoV-2 co-infected individuals [6]. HIV infected persons have been reported to have an increased risk of infection, severity of symptoms, reinfection and death from COVID-19 [7], [8]. It was reported in [9] that people infected with HIV were more likely to report a positive diagnosis and were at least twice as likely to die from COVID-19, and that they were more likely to be admitted to hospital and require mechanical ventilation, due to COVID-19 infection than those who were HIV-negative. Furthermore, the increased risk of COVID-19 complications in those infected and living with HIV, has mostly been observed among those with low CD4 cell count, advanced disease, those not taking antiretroviral treatment, and those with underlying health conditions [10], [11], [12].

On the other hand, dengue virus has been a major public health problem, especially in tropical countries in Asia and South America. [13]. Due to overlapping symptoms between SARS-CoV-2 and dengue virus, there is always a high possibility of mis-diagnosis of both infections [14]. Co-infections between SARS-CoV-2 and dengue have been established in many countries [15]. Dengue patients co-infected with SARS-CoV-2 can suffer worsening illness and hospitalization [15]. It is worth pointing out that persons co-infected with SARS-CoV-2 and dengue virus can have an enhanced glucose levels, which leads to proliferation of SARS-CoV-2 [16]. Increased mortality has also been linked with patients co-infected with dengue and SARS-CoV-2 infections [17]. Co-infection with HIV, SARS-CoV-2 and dengue has also been studied in [18]. Salvo et al. [18] reported the case of an untreated HIV patient who developed simultaneous infection with dengue and SARS-CoV-2.

In Argentina, the prevalence of HIV is estimated to be 0.4 % among the sexually active population. The prevalence is higher among men who have sex with men (MSM) and transgender women, where it is around 12–15 % and 34 %, respectively. In addition, it has been reported that about 37.5 % of men and 30 % of women receive a late HIV diagnosis [19]. In the last two decades, Argentina has experienced the re-emergence of epidemics of arboviral diseases caused by Aedes mosquitoes [20]. Cases of dengue fever, chikungunya, and Zika have been reported from northern and central provinces [21]. In 2009, there was the outbreak of dengue in central region of Argentina for the first time. Since then, dengue cases have been reported each year to date, with the largest number occurring in the year 2020 when more than 50 % of all cases in the nation occurred in this region [22].

Recently, fractional derivatives have largely been applied in modelling real life situations. Fractional differential operators which depend on a power-law kernel were first defined by Riemann-Liouville and Caputo [23]. However, these definitions involve singular kernels which have limitations to their usage in modelling biological and other physical phenomenon. To overcome these limitations, Caputo and Fabrizio (CF) [24] and Atangana and Baleanu (AB) [25] modified and improved the definitions of fractional-order derivatives, which are based on the exponential kernel and the generalized Mittag-Leffler function, respectively. A lot of models have been successfully studied using the Caputo and Caputo-Fabrizio derivatives. For instance, the authors [26] carried out a comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. The model was analyzed with the help of Caputo fractional derivative. The simulations of the model showed that, a particular case of the fractional-order model fits the real data more accurately than the other classical and fractional cases. Also, Baleanu et al. [27] investigated the asymptotic behavior of immunogenic tumor dynamics using the Caputo fractional derivative. Using a modified predictor-corrector scheme, numerical simulations were carried out on the model. Results obtained showed that, a general kernel in the fractional model provides high degree of flexibility to describe the real dynamics more precisely than the pre-existent classical integer-order models.

Baleanu et al. [28] analyzed a human liver model using the CF derivative. They established the existence and uniqueness of the solution of the model using the Picard-Lindelof approach and fixed-point theory. The model was solved using the homotopy analysis transform method. Numerical simulations to compare results with the real clinical data indicates higher efficacy of the new fractional model over the classical integer-order model. Mansal and Sene [29] studied a fractional order fishery model using the CF derivative. They analyzed the stability of the model and showed the effectiveness of fractional derivative on the study of the dynamics of the model. Gao et al. [30] studied a hepatitis B virus (HBV) model with time delay using the Caputo-Fabrizio derivative. They used Sumudu transform and Picard iteration to study the stability and approximate solution of the model. Rahman et al. [31] applied the Caputo-Fabrizio derivative to study a mathematical model for COVID-19. Comparing their results with the classical integer order derivatives, they observed that the simulations using the CF derivative shows better results for the model. Shaikh and Nisar [32] developed a typhoid Fever model using Caputo-Fabrizio derivative. However, there has been some concerns about the Caputo-Fabrizio derivative such as the kernel is not local; the associated integral is not a fractional operator but just an average of the function and its integral and merely acts as a filter. On the other hand, the AB derivative has found applications in several real life modelling problems. Hence, the usage of Atangana-Baleanu derivative in modelling complex real life phenomena is more preferable.

Jajarmi et al. [34] studied a model for the co-dynamics of diabetes and tuberculosis (TB) using the AB fractional derivative. They developed a new and efficient numerical scheme for the solution of the model. Simulations of the model revealed that increase in cases of diabetes mellitus could result in higher TB prevalence and incidence and could also escalate tuberculosis multi-drug resistance. Kolebaje et al. [33] modeled the dynamics of COVID-19 in some African countries using real data via the Atangana-Baleanu derivative and showed that the fractional derivative greatly influenced the dynamics of the disease. Bonyah textitet al. [35] modeled the dynamics of COVID-19 via the Atangana-Baleanu derivative. They proved the existence and uniqueness of the solution using the Banach contraction principle and Leray-Schauder alternative type theorem. Also, Omame et al. [36] considered a model for the co-interaction of tuberculosis and COVID-19, employing the Atangana-Baleanu derivative. They showed using numerical simulations, the effect of COVID-19 re-infection on the dynamics of the co-dynamics of both diseases. They established the conditions under which both diseases could co-exist or be eliminated. The authors in [37] studied a model for the co-dynamics of COVID-19 and diabetes using the AB derivative and showed that, mass COVID-19 vaccination was necessary to cut down COVID-19 and diabetes co-infections in Indonesia. Sene [38] considered a delayed SIR model and analyzed using the AB derivative. The model was solved using the Homotopy Analysis method. He equally showed how the fractional derivative could influence the disease dynamics. In a related research, the authors in [39] considered a model for the dynamics of COVID-19 using the AB derivative. They applied the q-homotopy analysis Sumudu transform method (q-HASTM) and the generalized Adams-Bashforth-Moulton method to solve the model.

Several methods have been laid down for solving fractional differential equations. Some of them are: Adomian decomposition method (ADM), homotopy analysis method (HAM), homotopy perturbation method (HPM), Laplace transformation, variational iteration method (VAM), corrected Fourier series, natural decomposition method [40], [41]. The Laplace-Adomian decomposition method (LADM) is one of the most effective techniques used in solving nonlinear FDEs. It possesses the combined behavior of the Laplace transformation and Adomian decomposition method (ADM). The method requires no predefined declaration size as in the Runge Kutta method. Also, LADM requires fewer number of parameters, no discretization and linearization as compared to other analytical techniques [42]. This is the motivation for the choice of the LADM for the solution of the proposed model, via different fractional derivatives in this study.

In this paper, we have contributed in the following ways:

• i.We have analyzed a non-integer order model for SARS-CoV-2, Dengue and HIV co-dynamics to assess the impact of SARS-CoV-2 infection on the dynamics of dengue and HIV through fractional derivatives, which, to the best of our knowledge, has not been done before.
• ii.We have considered three different fractional derivatives on this new complex model, and presented how SARS-CoV-2 could influence dengue and HIV infections.
• iii.The existence and uniqueness of solution of the proposed model has been studied using the Banach fixed point theorem.
• iv.We have established the stability of an iterative scheme for approximation of the solution of the developed model via some recent fixed point results.
• v.We used the Laplace Adomian decomposition method to solve the model via the Caputo, Caputo-Fabrizio and Atangana-Baleanu derivatives.
• vi.We have examined the impact of the three derivatives in analyzing complex disease models and we expect that our work will open some new avenues of research in this direction.

2. Preliminaries and model formulation

2.1. Preliminaries

Definition 1 ([43]). The Caputo fractional derivative of a function $f$ of order $\xi \in {\mathrm{ℝ}}^{+}$ is defined by

$${}^C{D}_t^{\xi }f\left(t\right)=J_t^{n-\xi }{\mathfrak{D}}^{n}f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(n-\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{n-\xi -1}{f}^{\left(n\right)}\left(\tau \right)\mathit{d\tau },$$

where $n$ is a positive integer and $n-1<\xi <n$, and the symbol $\mathrm{\Gamma }$ stands for the Gamma function defined by

$$\mathrm{\Gamma }\left(\xi \right)={\int }_0^{\infty }exp\left(-\tau \right){\tau }^{\xi -1}\mathit{d\tau },\mathrm{\Gamma }\left(\xi +1\right)=\xi \mathrm{\Gamma }\left(\xi \right),\mathit{Re}\left\{\xi \right\}>0.$$

If $0<\xi <1$, then the above Caputo fractional derivative of order $\xi >0$ reduces into

$${}^C{D}_t^{\xi }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(1-\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{-\xi }{f}^{\prime }\left(\tau \right)\mathit{d\tau }.$$

Definition 2 ([43]). The Caputo fractional integral of a function $f$ of order $\xi \in {\mathrm{ℝ}}^{+}$ is defined by

$${}^C{I}_t^{\xi }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}f\left(\tau \right)\mathit{d\tau },t>0,$$

If $f\left(t\right)=1$, the fractional integral of order $\xi >0$ is given by

$${}^C{I}_t^{\xi }\left(1\right)=\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\left(1\right)\mathit{d\tau }=\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}.$$

Definition 3 ([43]). The Laplace transform of Caputo fractional derivative is given by

$$\mathrm{ℒ}\left\{{}^C{D}_t^{\xi }f\left(t\right)\right\}=s^{\xi }\mathrm{ℒ}\left\{f\left(s\right)\right\}-s^{\xi -1}f\left(0\right),0<\xi <1,$$ (1)

where $\mathrm{ℒ}$ is the Laplace transform operator.

Definition 4 ([23]). The Sobolev space $H^1\left(a_1,a_2\right)$ of order 1 is defined as

$$H^1\left(a_1,a_2\right)=\left\{f\in L^2\left(a_1,a_2\right):\mathit{Df}\in L^2\left(a_1,a_2\right)\right\}$$

Definition 5 ([24]). Let $f\in H^1\left(a_1,a_2\right),a_2>a_1,\xi \in 0,1]$, then the Caputo-Fabrizio (CF) derivative of a function $f$ of order $\xi \in {\mathrm{ℝ}}^{+}$ is defined by

$${}^{\mathit{CF}}{D}_t^{\xi }f\left(t\right)=\frac{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{2\left(1-\xi \right)}{\int }_{a_1}^t{f}^{\text{'}}\left(\tau \right)\mathit{exp}\left[-\frac{\xi \left(t-\tau \right)}{1-\xi }\right]\mathit{d\tau },$$

where $\mathrm{ℱ}\left(\xi \right)=\left(1-\xi \right)+\frac{\xi }{\mathrm{\Gamma }\left(\xi \right)},$ denotes a normalization function satisfying $\mathrm{ℱ}\left(0\right)=\mathrm{ℱ}\left(1\right)=1$.However, if $f\notin H^1\left(a_1,a_2\right)$, then the derivative is defined as

$${}^{\mathit{CF}}{D}_t^{\xi }f\left(t\right)=\frac{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{2\left(1-\xi \right)}{\int }_{a_1}^t\left(f\left(t\right)-f\left(\tau \right)\right)\mathit{exp}\left[-\frac{\xi \left(t-\tau \right)}{1-\xi }\right]\mathit{d\tau },$$

Theorem 7 ([24]). The Caputo-Fabrizio fractional integral operator of order $\xi$ given by

$${}^{\mathit{CF}}{I}_t^{\xi }f\left(t\right)=\frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}f\left(t\right)+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^{t}f\left(\tau \right)\mathit{d\tau }.$$

Definition 6

([44]). The Laplace transform of the Caputo-Fabrizio derivative is given by

$$\mathrm{ℒ}\left\{{}^{\mathit{CF}}{D}_t^{\xi }f\left(t\right)\right\}\left(s\right)=\frac{s\mathrm{ℒ}\left\{f\left(t\right)\right\}-f\left(0\right)}{s+\xi \left(1-s\right)}.$$

Definition 7

([25]). The Atangana-Baleanu fractional derivative for a given function of order $\xi$ in Caputo sense is defined by

$${}_a^{\mathit{ABC}}{D}_t^{\xi }f\left(t\right)=\frac{\mathrm{ℱ}\left(\xi \right)}{\left(1-\xi \right)}{\int }_a^t\frac{\mathit{df}\left(\tau \right)}{\mathit{d\tau }}{E}_{\xi }\left[-\xi \frac{{\left(t-\tau \right)}^{\xi }}{1-\xi }\right]\mathit{d\tau },$$

where $\mathrm{ℱ}\left(\xi \right),$ satisfying $\mathrm{ℱ}\left(0\right)=\mathrm{ℱ}\left(1\right)=1$, is a normalization function and $E_{\xi }$ (.) is the Mittag-Leffler function, defined by,

$$E_{\xi }\left(t^{\xi }\right)=\sum _{k=0}^{\infty }\frac{t^{\xi }}{\mathrm{\Gamma }\left(\mathit{\xi k}+1\right)},\xi >0.$$

Definition 8

([25]). Atangana-Baleanu fractional integral of order $\xi$ is defined as

$${}_a^{\mathit{AB}}{I}_t^{\xi }f\left(t\right)=\frac{1-\xi }{\mathrm{ℱ}\left(\xi \right)}f\left(t\right)+\frac{\xi }{\mathrm{ℱ}\left(\xi \right)\mathrm{\Gamma }\left(\xi \right)}{\int }_a^{t}f\left(\tau \right){\left(t-\tau \right)}^{\xi -1}\mathit{d\tau }.$$

Definition 9

([25]). The Laplace transform for the Atangana-Baleanu fractional operator of order $\xi$, where $0<\xi <1$ is given as

$$\mathrm{ℒ}\left\{{}_a^{\mathit{ABC}}{D}^{\xi }f\left(t\right)\right\}\left(s\right)=\frac{\mathrm{ℱ}\left(\xi \right)}{1-\xi }\frac{s^{\xi }\mathrm{ℒ}\left\{f\left(t\right)\right\}\left(s\right)-s^{\xi -1}f\left(a\right)}{s^{\xi }+\frac{\xi }{1-\xi }}.$$

Theorem 2

([45]). “Let $\left(X,\parallel .\parallel \right)$ be a Banach space and $T:X\to X$ a contraction on $X$, that is, there exists a constant $a\in 0,1)$ such that $\parallel T\left(x\right)-T\left(y\right)\parallel \le a\parallel x-y\parallel ,\text{forall}x,y\in X$”. Then

• i.$T$ has fixed point $x^{\ast }\in X$, that is, ${\mathit{Tx}}^{\ast }=x^{\ast }$.
• ii.A sequence ${\left\{x_n\right\}}_{n=0}^{\infty }$ given by $x_{n+1}={\mathit{Tx}}_n$, for $n=\mathrm{0,1,2,3},\dots ,$ converges to $x^{\ast }.$

Theorem 3

([46]). “Let $\left(X,\parallel .\parallel \right)$ be a Banach space and $T:X\to X$ a weak contraction on $X$, that is, there exists a constant $a\in 0,1)$ and $L\ge 0$ such that $\parallel T\left(x\right)-T\left(y\right)\parallel \le a\parallel x-y\parallel +L\parallel x-\mathit{Tx}\parallel ,\text{for}\mathrm{all}x,y\in X$”. Then

• i.$T$ has fixed point $x^{\ast }\in X$.
• ii.A sequence ${\left\{x_n\right\}}_{n=0}^{\infty }$ given by $x_{n+1}={\mathit{Tx}}_n$, for $n=\mathrm{0,1,2,3},\dots ,$ converges to $x^{\ast }.$

2.2. Model formulation

At any time $t$, the total human population ${\mathcal{N}}^{\delta }\left(t\right)$ consists of the following states: Susceptible humans ${\mathcal{S}}^{\delta }\left(t\right)$, infectious humans with COVID-19 ${\mathrm{ℐ}}_V^{\delta }\left(t\right)$, infectious humans with dengue virus ${\mathrm{ℐ}}_D^{\delta }\left(t\right)$, infectious humans with HIV ${\mathrm{ℐ}}_V^{\delta }\left(t\right)$, humans co-infected with COVID-19 and dengue virus ${\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)$, humans co-infected with COVID-19 and HIV ${\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)$, where, ${\mathrm{ℛ}}_V^{\delta }\left(t\right),{\mathrm{ℛ}}_D^{\delta }\left(t\right)$ denotes humans who have recovered from COVID-19 and dengue fever, respectively. The total vector population, at any time $t$, ${\mathcal{N}}^{\theta }\left(t\right)$ consists of susceptible vectors: ${\mathcal{S}}^{\theta }\left(t\right)$ and infectious vectors with dengue virus, ${\mathrm{ℐ}}_D^{\theta }\left(t\right)$. It is to be stated here that, the superscript, $\delta$ denotes the human component, while the superscript $\theta$ represents the vector component of the model. The recruitment into the human population is denoted by ${\mathrm{\Delta }}^{\delta }$. Susceptible humans, ${\mathcal{S}}^{\delta }$ can get infected with SARS-CoV-2, dengue or HIV infection at the rates, ${\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }$, ${\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }$ and ${\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }$, respectively. Natural death rate is assumed same for all humans in each epidemiological state, at the rate ${\mu }^{\delta }$. Upon infection, individuals in SARS-CoV-2 infected, dengue-infected and HIV-infected compartments can suffer related disease induced death at the rates ${\varphi }_V,{\varphi }_D$ and ${\varphi }_H$, respectively. Individuals in SARS-CoV-2 infected class can also get co-infected with either dengue or HIV at the rates ${\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }$ and ${\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }$, respectively. Due to lack of sufficient clinical data and to avoid model complexity, we have assumed only co-infection with two diseases (one of which must be SARS-CoV-2). Future work with sufficient biological reports can consider co-infection with the three diseases, which is possible [18]. Recovery rates for SARS-CoV-2 and dengue infected individuals is given by ${\zeta }_V$ and ${\zeta }_D$, respectively. Upon recovery from dengue, an individual can loss immunity at the rate, ${\alpha }_D$. We have assumed infection acquired immunity for those who have recovered from COVID-19 due to current clinical reports. The other transitions in the model are given in the following equations, with parameters well defined in Table 1 .

$$\begin{array}{c}{}^{\mathit{cf}}{D}_t^{\xi }{\mathcal{S}}^{\delta }\left(t\right)={\mathrm{\Delta }}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\mu }^{\delta }\right){\mathcal{S}}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_D^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_V^{\delta }\left(t\right)={\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_V^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}}^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_D^{\delta }\left(t\right)={\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_D^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}}^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_H^{\delta }\left(t\right)={\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_H^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)={\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}}^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)={\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}}^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℛ}}_V^{\delta }\left(t\right)={\zeta }_V{\mathrm{ℐ}}_V^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_V^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℛ}}_D^{\delta }\left(t\right)={\zeta }_D{\mathrm{ℐ}}_D^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_D^{\delta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathcal{S}}^{\theta }\left(t\right)={\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right)+{\mu }^{\theta }\right]{\mathcal{S}}^{\theta },\\ {}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_D^{\theta }\left(t\right)={\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right){\mathcal{S}}^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_D^{\theta },\end{array}$$ (2)

subject to the initial conditions

$$\begin{array}{c}{\mathcal{S}}_0^{\delta }={\mathcal{S}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{V0}^{\delta }={\mathrm{ℐ}}_V^{\delta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\delta }={\mathrm{ℐ}}_D^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }={\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }={\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right),\\ {\mathrm{ℛ}}_{V0}^{\delta }={\mathrm{ℛ}}_V^{\delta }\left(0\right),{\mathrm{ℛ}}_{D0}^{\delta }={\mathrm{ℛ}}_D^{\delta }\left(0\right),{\mathcal{S}}_0^{\theta }={\mathcal{S}}^{\theta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\theta }={\mathrm{ℐ}}_D^{\theta }\left(0\right).\end{array}$$

Table 1.

Description of parameters in the model (2).

Parameter	Description	Value	Source
${\mathrm{\Pi }}^{\delta }$	Recruitment rate for humans	$\frac{\mathrm{29,289,357}}{78.07\times 365}$	[51]
${\mathrm{\Pi }}^{\theta }$	Recruitment rate for vectors	$1500$	Assumed
${\mu }^{\delta }$	Human natural death rate	$\frac{1}{78.07\times 365}$${\mathit{day}}^{-1}$	[51]
${\mu }^{\theta }$	Vector removal rate	$\frac{1}{21}$${\mathit{day}}^{-1}$	[52]
${\alpha }_1^{\delta }$	contact rate for transmission of COVID-19	$9.58558\times {10}^{-8}$${\mathit{day}}^{-1}$	Fitted
${\alpha }_2^{\delta }$	Effective contact rate for vector to human transmission of dengue virus	$4.3\times {10}^{-10}$	Estimated
${\alpha }_2^{\theta }$	Effective contact rate for human to vector transmission of dengue virus	$5.0\times {10}^{-5}$	Estimated
${\alpha }_3^{\delta }$	Contact rate for HIV transmission	$8.5890\times {10}^{-10}$	Estimated
${\zeta }_V$	COVID-19 recovery rate	$0.9826$${\mathit{day}}^{-1}$	Fitted
${\zeta }_D$	Dengue fever recovery rate	$0.15$${\mathit{day}}^{-1}$	[53]
${\varphi }_V$	COVID-19-induced death rate	$1.4948$${\mathit{day}}^{-1}$	Fitted
${\varphi }_D$	Dengue fever induced death rate	$0.09$${\mathit{day}}^{-1}$	Assumed
${\varphi }_H$	HIV induced death rates	$\frac{0.3425}{365}$${\mathit{day}}^{-1}$	[54]
${\alpha }_D$	rate of loss of infection acquired immunity for dengue virus	$0.026$${\mathit{day}}^{-1}$	[53]
${\mathrm{ℛ}}_{0V}^{\delta }$	COVID-19 related reproduction number	$1.0471$	Fitted
${\mathrm{ℛ}}_{0D}^{\delta }$	Dengue related reproduction number	$4.8103$	Fitted
${\mathrm{ℛ}}_{0H}^{\delta }$	HIV related reproduction number	$3.0592$	Fitted

2.3. Non-negativity of the solution

Theorem 4

The closed set$\mathcal{D}={\mathcal{D}}^{\delta }\times {\mathcal{D}}^{\theta }$, with

$${\mathcal{D}}^{\delta }=\left\{\left({\mathcal{S}}^{\delta },{\mathrm{ℐ}}_V^{\delta },{\mathrm{ℐ}}_D^{\delta },{\mathrm{ℐ}}_H^{\delta },{\mathrm{ℐ}}_{\mathit{VD}}^{\delta },{\mathrm{ℐ}}_{\mathit{VH}}^{\delta },{\mathrm{ℛ}}_V^{\delta },{\mathrm{ℛ}}_D^{\delta }\right)\in {\mathrm{\Re }}_{+}^8:{\mathcal{S}}^{\delta }+{\mathrm{ℐ}}_V^{\delta }+{\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_H^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }+{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }+{\mathrm{ℛ}}_D^{\delta }\le \frac{{\mathrm{\Delta }}^{\delta }}{{\mu }^{\delta }}\right\},$$

$${\mathcal{D}}^{\theta }=\left\{\left({\mathcal{S}}^{\theta },{\mathrm{ℐ}}_D^{\theta }\right)\in {\mathrm{\Re }}_{+}^2:{\mathcal{S}}^{\theta }+{\mathrm{ℐ}}_D^{\theta }\le \frac{{\mathrm{\Delta }}^{\theta }}{{\mu }^{\theta }}\right\}.$$

is positively invariant with respect to the model (2).

Proof:. Adding all the equations corresponding to the human components of the system (2) gives

$${}_0^{\mathit{cf}}{D}_t^{\xi }{\mathcal{N}}^{\delta }={\mathrm{\Delta }}^{\delta }-{\mu }^{\delta }{\mathcal{N}}^{\delta }\left(t\right)-\left[{\varphi }_V{\mathrm{ℐ}}_V^{\delta }+{\varphi }_D{\mathrm{ℐ}}_D^{\delta }+{\varphi }_H{\mathrm{ℐ}}_H^{\delta }+\left({\varphi }_V+{\varphi }_D\right){\mathrm{ℐ}}_{\mathit{VD}}^{\delta }+\left({\varphi }_V+{\varphi }_H\right){\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\right].$$ (3)

From (3), we have that

$${\mathrm{\Delta }}^{\delta }-\left({\mu }^{\delta }+7\varphi \right){\mathcal{N}}^{\delta }\le {}_0^{\mathit{cf}}{D}_t^{\zeta }{\mathcal{N}}^{\delta }\le {\mathrm{\Delta }}^{\delta }-{\mu }^{\delta }{\mathcal{N}}^{\delta },$$

where $\varphi =min\left\{{\varphi }_V,{\varphi }_H,{\varphi }_D\right\}$.which can be re-written as

$${}_0^{\mathit{cf}}{D}_t^{\xi }{\mathcal{N}}^{\delta }\le {\mathrm{\Delta }}^{\delta }-{\mu }^{\delta }{\mathcal{N}}^{\delta },$$ (4)

Without loss of generality, if we apply Laplace transform of the Caputo-Fabrizio derivative on the above inequality, and simplifying, we have that

$$N\left(t\right)\le \frac{{\mathrm{\Delta }}^{\delta }}{{\mu }^{\delta }}-\frac{{\mathrm{\Delta }}^{\delta }\left(2\xi -{\alpha }_1\right)}{\left[1+{\mu }^{\delta }\left(1-\xi \right)\right]{\alpha }_1}{e}^{-{\alpha }_{1}t}-\frac{{\mathcal{N}}^{\delta }\left(0\right)}{\left(1-\xi \right)\left[1+{\mu }^{\delta }\left(1-\xi \right)\right]\left({\alpha }_1-{\alpha }_2\right)}{e}^{-{\alpha }_{1}t}+\frac{{\mathcal{N}}^{\delta }\left(0\right)}{\left(1-\xi \right)\left[1+{\mu }^{\delta }\left(1-\xi \right)\right]\left({\alpha }_1-{\alpha }_2\right)}{e}^{-{\alpha }_{2}t},$$ (5)

where ${\alpha }_1=\frac{{\mu }^{\delta }\xi }{1+{\mu }^{\delta }\left(1-\xi \right)},{\alpha }_2=\frac{\xi }{\left(1-\xi \right)}$

Therefore, the total human population, ${\mathcal{N}}^{\delta }\left(t\right)\le \frac{{\mathrm{\Delta }}^{\delta }}{{\mu }^{\delta }}$ as $t\to \infty$. Following the same procedure, it can be shown that the total vector population, ${\mathcal{N}}^{\theta }\left(t\right)\le \frac{{\mathrm{\Delta }}^{\theta }}{{\mu }^{\theta }}$. Similar conclusions can be reached via the Caputo derivative and Atangana-Baleanu derivative. Hence, the system (2) has the solution in $\mathcal{D}$. Thus, the given system is positively invariant.

3. Existence and uniqueness of the solution

In this section, we shall apply some basic results from fixed point theory to the model (2), in order to establish existence and uniqueness of solution. The model (2) is re-written in the following form:

$$\left\{\begin{array}{ll}{}_0^{\mathit{CF}}{D}_t^{\xi }\mathrm{\Phi }\left(t\right)& =\mathrm{ℒ}\left(t,\mathrm{\Phi }\left(t\right)\right),\\ \mathrm{\Phi }\left(0\right)& ={\mathrm{\Phi }}_0,\end{array}\right)$$ (6)

where the vector $\mathrm{\Phi }\left(t\right)={\left({\mathcal{S}}^{\delta }\left(t\right){\mathrm{ℐ}}_V^{\delta }\left(t\right){\mathrm{ℐ}}_D^{\delta }\left(t\right){\mathrm{ℐ}}_H^{\delta }\left(t\right){\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right){\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right){\mathrm{ℛ}}_V^{\delta }\left(t\right){\mathrm{ℛ}}_D^{\delta }\left(t\right){\mathcal{S}}^{\theta }\left(t\right){\mathrm{ℐ}}_{\mathit{VD}}^{\theta }\left(t\right)\right)}^T\in {\mathrm{ℝ}}^{10}$ for $t\in \left[0,{\mathcal{T}}_{\mathit{max}}\right]$, denotes the states of the model and $\mathrm{ℒ}$ represents a continuous vector given below:

$$\mathrm{ℒ}=\left(\begin{array}{c}{\mathrm{ℒ}}_1\\ {\mathrm{ℒ}}_2\\ {\mathrm{ℒ}}_3\\ {\mathrm{ℒ}}_4\\ {\mathrm{ℒ}}_5\\ {\mathrm{ℒ}}_6\\ {\mathrm{ℒ}}_7\\ {\mathrm{ℒ}}_8\\ {\mathrm{ℒ}}_9\\ {\mathrm{ℒ}}_{10}\end{array}\right)=\left(\begin{array}{c}{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1{\mathrm{ℐ}}_V^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\mu }^{\delta }\right){\mathcal{S}}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_D^{\delta }\\ {\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_V^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\\ {\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_D^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\\ {\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_H^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }\\ {\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\\ {\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\\ {\zeta }_V{\mathrm{ℐ}}_V^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_V^{\delta }\\ {\zeta }_D{\mathrm{ℐ}}_D^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_D^{\delta }\\ {\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right)+{\mu }^{\theta }\right]{\mathcal{S}}^{\theta }\\ {\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right){\mathcal{S}}^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_D^{\theta }\end{array}\right).$$ (7)

The initial condition of the variables of the model is denoted by

$$\mathrm{\Phi }\left(0\right)={\left(\begin{array}{cccccccccc}{\mathcal{S}}^{\delta }\left(0\right)& {\mathrm{ℐ}}_V^{\delta }\left(0\right)& {\mathrm{ℐ}}_D^{\delta }\left(0\right)& {\mathrm{ℐ}}_H^{\delta }\left(0\right)& {\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)& {\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)& {\mathrm{ℛ}}_V^{\delta }\left(0\right)& {\mathrm{ℛ}}_D^{\delta }\left(0\right)& {\mathcal{S}}^{\theta }\left(0\right)& {\mathrm{ℐ}}_{\mathit{VD}}\left(0\right)\end{array}\right)}^T.$$

In addition, $\mathrm{ℒ}:\left[0,{\mathcal{T}}_{\mathit{max}}\right]\times {\mathrm{ℝ}}^{10}\to {\mathrm{ℝ}}^{10}$ is said to satisfy the Lipschitz condition in the second argument, if we have:

$$\begin{array}{l}‖\mathrm{ℒ}\left(t,{\mathrm{\Phi }}_1\right)-\mathrm{ℒ}(t,{\mathrm{\Phi }}_2)‖\le \mathrm{ℳ}‖{\mathrm{\Phi }}_1-{\mathrm{\Phi }}_2‖,\forall t\in \left[0,{\mathcal{T}}_{\mathit{max}}\right],\forall {\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2\in {\mathrm{ℝ}}^{10},\\ \text{where}\mathrm{ℳ}>0,{\mathcal{T}}_{\mathit{max}}\text{is\hspace{0.17em}the\hspace{0.17em}final\hspace{0.17em}time}.\end{array}$$ (8)

The existence of a unique solution to the model (2) is established in the following theorem:

Theorem 5

There exists a unique solution to the initial value problem(6)on$\mathcal{C}\left(\left[0,{\mathcal{T}}_{\mathit{max}}\right],{\mathrm{ℝ}}^{10}\right)$, provided that(8)and

$$\left(\frac{2\left(1-\xi \right)\mathrm{ℳ}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}+\frac{2\xi \mathrm{ℳ}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\mathcal{T}}_{\mathit{max}}\right)<1,$$ (9)

are satisfied.

Proof:

If we apply the Caputo-Fabrizio fractional integral on each sides of (6), then we have

$$\mathrm{\Phi }\left(t\right)={\mathrm{\Phi }}_0+\frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left(t,\mathrm{\Phi }\left(t\right)\right)+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^t\mathrm{ℒ}\left(\tau ,\mathrm{\Phi }\left(\tau \right)\right)\mathit{d\tau }.$$ (10)

Let $\mathcal{J}=\left[0,{\mathcal{T}}_{\mathit{max}}\right]$.

Let us define the operator $\mathcal{K}:\mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right)\to \mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right)$ by:

$$\mathcal{K}\left[\mathrm{\Phi }\right]\left(t\right)=V\left(t\right),\mathrm{\Phi },V\in \mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right)$$ (11)

where,

$$V\left(t\right)={\mathrm{\Phi }}_0+\frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left(t,\mathrm{\Phi }\left(t\right)\right)+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^t\mathrm{ℒ}\left(\tau ,\mathrm{\Phi }\left(\tau \right)\right)\mathit{d\tau },$$

The supremum norm on $\mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right)$ is given by:

$$\Vert V\Vert {=}_{t\in \mathcal{J}}^{\mathit{sup}}\Vert V\left(t\right)\Vert ,\forall V\in \mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right).$$

Clearly, $\mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right)$ equipped with $\Vert .\Vert$ is a Banach space.

Suppose, $W$ is the fixed point of the operator $\mathcal{K}:\mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right)\to \mathcal{C}\left(\mathcal{J},{\mathrm{ℝ}}^{10}\right)$, then $W$ becomes the solution of the initial value problem (6), and

$$\mathcal{K}\left[W\right]\left(t\right)=W\left(t\right),$$

where,

$$W\left(t\right)={\mathrm{\Phi }}_0+\frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left(t,W\left(t\right)\right)+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^t\mathrm{ℒ}\left(\tau ,W\left(\tau \right)\right)\mathit{d\tau }$$

Consider,

$$\begin{array}{l}‖\mathcal{K}\left[V\right]\left(t\right)-\mathcal{K}\left[W\right]\left(t\right)‖=\left.‖{\mathrm{\Phi }}_0+\frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}(t,V\left(t\right))+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^t\mathrm{ℒ}(\tau ,V\left(\tau \right))\mathit{d\tau }\right)\\ \left(-\left[{\mathrm{\Phi }}_0+\frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}(t,W\left(t\right))+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^t\mathrm{ℒ}(\tau ,W\left(\tau \right))\mathit{d\tau }\right]\right.‖\\ \le ‖\frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\left(\mathrm{ℒ}\right(t,V\left(t\right))-\mathrm{ℒ}(t,W\left(t\right)\left)\right)+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^t\left(\mathrm{ℒ}\right(\tau ,V\left(\tau \right))-\mathrm{ℒ}(\tau ,W\left(\tau \right)\left)\right)\mathit{d\tau }‖,\\ \le \frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}‖\left(\mathrm{ℒ}\right(t,V\left(t\right))-\mathrm{ℒ}(t,W\left(t\right)\left)\right)‖+\frac{2\xi }{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}‖{\int }_0^t\left(\mathrm{ℒ}\right(\tau ,V\left(\tau \right))-\mathrm{ℒ}(\tau ,W\left(\tau \right)\left)\right)\mathit{d\tau }‖,\end{array}$$ (12)

Since the operator $\mathrm{ℒ}$ satisfies the Lipschitz condition (eq. 8), we have that

$$\begin{array}{l}\le \frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\mathrm{ℳ}‖V\left(t\right)-W\left(t\right)‖+\frac{2\xi \mathrm{ℳ}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\int }_0^t‖V\left(t\right)-W\left(t\right)‖\mathit{d\tau },\\ \le \frac{2\left(1-\xi \right)}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{\mathrm{ℳ}}_{t\in \mathcal{J}}^{\mathit{sup}}‖V\left(t\right)-W\left(t\right)‖+\frac{2\xi \mathrm{ℳ}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}{{\int }_0^t}_{t\in \mathcal{J}}^{\mathit{sup}}‖V\left(\tau \right)-W\left(\tau \right)‖\mathit{d\tau },\\ =\left(\frac{\left(2\left(1-\xi \right)\right)\mathrm{ℳ}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}+\frac{2\xi \mathrm{ℳ}{\int }_0^t\mathit{d\tau }}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\right)‖V-W‖,\\ \le \left(\frac{\left(2\left(1-\xi \right)\right)\mathrm{ℳ}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}+\frac{2\xi {\mathrm{ℳ}\mathcal{T}}_{\mathit{max}}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\right)‖V-W‖.\end{array}$$ (13)

Thus if the condition (9) holds then,

$$‖\mathcal{K}\left[V\right]-\mathcal{K}\left[W\right]‖\le \left(\frac{\left(2\left(1-\xi \right)\right)\mathrm{ℳ}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}+\frac{2\xi {\mathrm{ℳ}\mathcal{T}}_{\mathit{max}}}{\left(2-\xi \right)\mathrm{ℱ}\left(\xi \right)}\right)‖V-W‖.$$

Hence, the operator $\mathcal{K}$ becomes a contraction. Therefore $\mathcal{K}$ has a unique fixed point which is a solution to the initial value problem (6) and hence a solution to the system (2).

3.1. The basic reproduction number of the model

By setting the right-hand sides of the equations in the model (2) to zero, DFE of the model (2) is given by

$$\begin{array}{c}{H}_0=\left({\mathcal{S}}^{\delta \ast },{\mathcal{I}}_V^{\delta \ast },{\mathcal{I}}_D^{\delta \ast },{\mathcal{I}}_H^{\delta \ast },{\mathcal{I}}_{\mathit{VD}}^{\delta \ast },{\mathcal{I}}_{\mathit{VH}}^{\delta \ast },{\mathcal{R}}_V^{\delta \ast },{\mathcal{R}}_D^{\delta \ast },{\mathcal{S}}^{\theta \ast },{\mathcal{I}}_{\mathit{VD}}^{\theta \ast }\right)\\ =\left({\mathcal{S}}^{\delta \ast },\mathrm{0,0,0,0,0,0,0},{\mathcal{S}}^{\theta \ast },0\right)\end{array}$$

with,

$${\mathcal{S}}^{\delta \ast }=\frac{{\mathrm{\Delta }}^{\delta }}{{\mu }^{\delta }},{\mathcal{S}}^{\theta \ast }=\frac{{\mathrm{\Delta }}^{\theta }}{{\mu }^{\theta }},$$

The stability of the DFE is established by applying the next generation operator principle [48] on the system (2). The transfer matrices are, respectively, given by

$$F=\left(\begin{array}{cccccc}{\alpha }_1^{\delta }{S}^{\delta \ast }& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& {\alpha }_2^{\delta }{S}^{\delta \ast }\\ 0& 0& {\alpha }_3^{\delta }{S}^{\delta \ast }& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& {\alpha }_2^{\theta }{S}^{\theta \ast }& 0& {\alpha }_2^{\theta }{S}^{\theta \ast }& 0& 0\end{array}\right),$$ (14)

$$V=\left(\begin{array}{cccccc}{K}_1^{\delta }& 0& 0& 0& 0& 0\\ 0& K_2^{\delta }& 0& 0& 0& 0\\ 0& 0& K_3^{\delta }& 0& 0& 0\\ 0& 0& 0& K_4^{\delta }& 0& 0\\ 0& 0& 0& 0& K_5^{\delta }& 0\\ 0& 0& 0& 0& 0& {\mu }^{\theta }\end{array}\right),$$ (15)

where,

$$K_1^{\delta }={\varphi }_V+{\zeta }_V+{\mu }^{\delta },K_2^{\delta }={\varphi }_D+{\zeta }_D+{\mu }^{\delta },K_3^{\delta }={\varphi }_H+{\mu }^{\delta },K_4^{\delta }={\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta },K_5={\varphi }_V+{\varphi }_H+{\zeta }_V+{\mu }^{\delta }.$$

The basic reproduction number of the model (2), is given by.

${\mathrm{ℛ}}_0=\rho \left({\mathit{FV}}^{-1}\right)=max\left\{{\mathrm{ℛ}}_{0V},{\mathrm{ℛ}}_{0D},{\mathrm{ℛ}}_{0H}\right\}$ where ${\mathrm{ℛ}}_{0V}$, ${\mathrm{ℛ}}_{0D}$ and ${\mathrm{ℛ}}_{0H}$ are the associated reproduction numbers for the COVID-19, Dengue and HIV, respectively, given by

$${\mathrm{ℛ}}_{0V}^{\delta }=\frac{{\alpha }_1^{\delta }{\mathrm{\Delta }}^{\delta }}{{\mu }^{\delta }\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right)},{\mathrm{ℛ}}_{0D}^{\delta }=\sqrt{\frac{{\alpha }_2^{\delta }{\alpha }_2^{\theta }{\mathrm{\Delta }}^{\delta }{\mathrm{\Delta }}^{\theta }}{{\mu }^{\delta }{\mu }^{\theta 2}\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right)}},{\mathrm{ℛ}}_{0H}^{\delta }=\frac{{\alpha }_3^{\delta }{\mathrm{\Delta }}^{\delta }}{{\mu }^{\delta }\left({\varphi }_H+{\mu }^{\delta }\right)}.$$

3.1.1. Assessing the impact of SARS-CoV-2 on dengue and HIV

Expressing the three reproduction numbers in terms of the human natural death rate, ${\mu }^{\delta }$, we have,

$${\mu }^{\delta }=\frac{{\alpha }_1^{\delta }{\mathrm{\Delta }}^{\delta }}{\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℛ}}_{0V}}=\frac{{\alpha }_2^{\delta }{\alpha }_2^{\theta }{\mathrm{\Delta }}^{\delta }{\mathrm{\Delta }}^{\theta }}{{\mu }^{\theta 2}\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℛ}}_{0D}^2}=\frac{{\alpha }_3^{\delta }{\mathrm{\Delta }}^{\delta }}{\left({\varphi }_H+{\mu }^{\delta }\right){\mathrm{ℛ}}_{0H}}$$ (16)

Differentiating the SARS-CoV-2 related reproduction number with respect to the dengue-related reproduction number, we obtain

$$\frac{\partial {\mathrm{ℛ}}_{0D}^{\delta }}{\partial {\mathrm{ℛ}}_{0V}^{\delta }}=\frac{1}{\sqrt{\left(\frac{{\alpha }_2^{\delta }{\alpha }_2^{\theta }{\mathrm{\Delta }}^{\theta }\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℛ}}_{0V}^{\delta }}{{\alpha }_1^{\delta }{\mu }^{\theta 2}\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right)}\right)}}\times \frac{{\alpha }_2^{\delta }{\alpha }_2^{\theta }{\mathrm{\Delta }}^{\theta }\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right)}{{\alpha }_1^{\delta }{\mu }^{\theta 2}\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right)}>0$$ (17)

$$\frac{\partial {\mathrm{ℛ}}_{0H}^{\delta }}{\partial {\mathrm{ℛ}}_{0V}^{\delta }}=\frac{{\alpha }_1^{\delta }\left({\varphi }_H+{\mu }^{\delta }\right)}{{\alpha }_3^{\delta }\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right)}>0$$ (18)

The two equations above, (17), (18) show that increase in SARS-CoV-2 cases will result in detrimental impact on dengue and HIV cases.

3.2. Local asymptotic stability of the disease free equilibrium (DFE) of the model

Theorem 6

The DFE, $\mathrm{\mathscr{H}}0$, of the model (2) is locally asymptotically stable (LAS) if ${\mathrm{ℛ}}_0<1$, and unstable if ${\mathrm{ℛ}}_0>1$.

Proof:

The local stability of the model (2) is analyzed by the Jacobian matrix of the system (2) evaluated at the disease-free equilibrium, $\mathrm{\mathscr{H}}0$, given by:

$$\left(\begin{array}{cccccccccc}-{\mu }^{\delta }& -{\alpha }_1^{\delta }{S}^{\delta \ast }& 0& -{\alpha }_3^{\delta }{S}^{\delta \ast }& 0& 0& 0& {\alpha }_D& 0& -{\alpha }_2^{\delta }{S}^{\delta \ast }\\ 0& {\alpha }_1^{\delta }{S}^{\delta \ast }-K_1^{\delta }& 0& 0& {\zeta }_D& 0& 0& 0& 0& 0\\ 0& 0& -K_2^{\delta }& 0& {\zeta }_V& 0& 0& 0& 0& {\alpha }_2^{\delta }{S}^{\delta \ast }\\ 0& 0& 0& {\alpha }_3^{\delta }{S}^{\delta \ast }-K_3^{\delta }& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -K_4^{\delta }& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -K_5^{\delta }& 0& 0& 0& 0\\ 0& {\zeta }_V& 0& 0& 0& 0& -{\mu }^{\delta }& 0& 0& 0\\ 0& 0& {\zeta }_D& 0& 0& 0& 0& -\left({\mu }^{\delta }+{\zeta }_D\right)& 0& 0\\ 0& 0& -{\alpha }_2^{\theta }{S}^{\theta \ast }& 0& -{\alpha }_2^{\theta }{S}^{\theta \ast }& 0& 0& 0& -{\mu }^{\theta }& 0\\ 0& 0& {\alpha }_2^{\theta }{S}^{\theta \ast }& 0& {\alpha }_2^{\theta }{S}^{\theta \ast }& 0& 0& 0& 0& -{\mu }^{\theta }\end{array}\right)$$

The eigenvalues are given by:

$$\begin{array}{l}{\rho }_1=-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right),{\rho }_2=-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\mu }^{\delta }\right),{\rho }_3=-{\mu }^{\delta }\left(\text{with\hspace{0.17em}multiplicity\hspace{0.17em}of}3\right),{\rho }_4=-\left(\zeta +{\mu }^{\delta }\right),\end{array}$$

and the solutions of the characteristic polynomial equations

$$\rho +K_1^{\delta }\left(1-{\mathrm{ℛ}}_{0V}^{\delta }\right)=0,$$ (19)

$$\rho +K_2^{\delta }\left(1-{\mathrm{ℛ}}_{0H}^{\delta }\right)=0,$$ (20)

$${\rho }^2+\left({\mu }^{\theta }+K_2^{\delta }\right)\rho +{\mu }^{\theta }{K}_2^{\delta }\left(1-{\mathrm{ℛ}}_{0D}^{\delta 2}\right)=0,$$ (21)

Following the Routh-Hurwitz criterion, all the three equations. (19), (20), (21) will have roots with negative real parts if and only if the associated reproduction numbers ${\mathrm{ℛ}}_{0V}^{\delta }<1$, ${\mathrm{ℛ}}_{0D}^{\delta }<1$ and ${\mathrm{ℛ}}_{0H}^{\delta }<1$. Hence, the DFE, $\mathrm{\mathscr{H}}0$ is locally asymptotically stable if ${\mathrm{ℛ}}_0=max\left\{{\mathrm{ℛ}}_{0V}^{\delta },{\mathrm{ℛ}}_{0D}^{\delta },{\mathrm{ℛ}}_{0H}^{\delta }\right\}<1$.

Note that Im $\left({\rho }_k\right)=0$, for $k=0,1,2,3,\dots ,10$, $\mid arg\left({\rho }_k\right)\mid =\pi >\frac{\mathit{\alpha \pi }}{2},\text{for}0<\alpha <1.$.

4. Ulam-Hyers stability

The Ulam-Hyers (UH) stability and generalized UH stability [49], [50] for the fractional system using the Caputo operator is discussed in this section. The same can also be studied using the Caputo-Fabrizio and Atangana-Baleanu operator.

Let $\mathbb{E}=C\left(\left[0,T_{\mathit{max}}\right];{\mathrm{ℝ}}^{10}\right)$ be the space of all continuous functions from $\left[0,T_{\mathit{max}}\right]$ to ${\mathrm{ℝ}}^{10}$, endowed with the norm:

$\parallel \mathrm{\Phi }\parallel {=}_{t\in \mathcal{J}}^{\mathit{sup}}\left|\mathrm{\Phi }\left(t\right)\right|$ where, $\mathcal{J}=\left[0,{\mathcal{T}}_{\mathit{max}}\right]$. Consider

$$\left\{\begin{array}{ll}{}_0^C{D}_t^{\xi }\mathrm{\Phi }\left(t\right)& =\mathrm{ℒ}\left(t,\mathrm{\Phi }\left(t\right)\right),\\ \mathrm{\Phi }\left(0\right)& ={\mathrm{\Phi }}_0,\end{array}\right)$$ (22)

Also, let $\epsilon >0$. Consider the following inequality:

$${\parallel }^C{D}^{\xi }\overline{\mathrm{\Phi }}\left(t\right)-\mathrm{ℒ}\left(t,\overline{\mathrm{\Phi }}\left(t\right)\right)\parallel \le \epsilon ,t\in \mathcal{J},\epsilon =max{\left({\epsilon }_i\right)}^T,i=\mathrm{1,2,3},\dots 10,\overline{\mathrm{\Phi }}\in E$$ (23)

Remark 4.1

“A function $\overline{\mathrm{\Phi }}\in \mathbb{E}$ satisfies the inequality (23) if and only if there exists a function $h\in \mathbb{E}$, having the following properties:”

$$\left|h\left(t\right)\right|\le \epsilon ,h=max{\left(h_j\right)}^T,t\in \mathcal{J}.$$

• i.${}^C{D}^{\xi }\overline{\mathrm{\Phi }}\left(t\right)=\mathrm{ℒ}\left(t,\overline{\mathrm{\Phi }}\left(t\right)\right)+h\left(t\right)$, $t\in \mathcal{J}$.

Definition 10

The fractional model (2) or the transformed system (22) is UH stable if for every $\epsilon >0$ there exists $k>0$, such that for any solution $\mathrm{\Psi }\in \mathbb{E}$ of the inequality (23), there exists a unique solution $\mathrm{\Phi }\in \mathbb{E}$, of the fractional system (22) such that the following inequality is satisfied:

$$\parallel \overline{\mathrm{\Phi }}\left(t\right)-\mathrm{\Phi }\left(t\right)\parallel \le \mathit{k\epsilon },t\in \mathcal{J},k=max{\left(k_j\right)}^T,j=\mathrm{1,2,3},\dots 10.$$

where,

$$\begin{array}{l}\overline{\mathrm{\Phi }}\left(t\right)={\left(\begin{array}{cccccccccc}{\overline{\mathcal{S}}}^{\delta }\left(t\right)& {{\overline{\mathrm{ℐ}}}_V}^{\delta }\left(t\right)& {\overline{\mathrm{ℐ}}}_D^{\delta }\left(t\right)& {\overline{\mathrm{ℐ}}}_H^{\delta }\left(t\right)& {\overline{\mathrm{ℐ}}}_{\mathit{VD}}^{\delta }\left(t\right)& {\overline{\mathrm{ℐ}}}_{\mathit{VH}}^{\delta }\left(t\right)& {\overline{\mathrm{ℛ}}}_V^{\delta }\left(t\right)& {\overline{\mathrm{ℛ}}}_D^{\delta }\left(t\right)& {\overline{\mathcal{S}}}^{\theta }\left(t\right)& {\overline{\mathrm{ℐ}}}_{\mathit{VD}}^{\theta }\left(t\right)\end{array}\right)}^T,\\ \mathrm{\Phi }\left(t\right)={\left(\begin{array}{cccccccccc}{\mathcal{S}}^{\delta }\left(t\right)& {\mathrm{ℐ}}_V^{\delta }\left(t\right)& {\mathrm{ℐ}}_D^{\delta }\left(t\right)& {\mathrm{ℐ}}_H^{\delta }\left(t\right)& {\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)& {\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)& {\mathrm{ℛ}}_V^{\delta }\left(t\right)& {\mathrm{ℛ}}_D^{\delta }\left(t\right)& {\mathcal{S}}^{\theta }\left(t\right)& {\mathrm{ℐ}}_{\mathit{VD}}^{\theta }\left(t\right)\end{array}\right)}^T,\\ \mathrm{\Phi }\left(0\right)={\left(\begin{array}{cccccccccc}{\mathcal{S}}^{\delta }\left(0\right)& {\mathrm{ℐ}}_V^{\delta }\left(0\right)& {\mathrm{ℐ}}_D^{\delta }\left(0\right)& {\mathrm{ℐ}}_H^{\delta }\left(0\right)& {\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)& {\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)& {\mathrm{ℛ}}_V^{\delta }\left(0\right)& {\mathrm{ℛ}}_D^{\delta }\left(0\right)& {\mathcal{S}}^{\theta }\left(0\right)& {\mathrm{ℐ}}_{\mathit{VD}}^{\theta }\left(0\right)\end{array}\right)}^T.\end{array}$$

Definition 11

The model system (22) is generalized UH stable if there exists a continuous function $\varphi :{\mathrm{ℝ}}^{+}\to {\mathrm{ℝ}}^{+}$ satisfying $\varphi \left(0\right)=0$, such that for any solution $\overline{\mathrm{\Phi }}\in \mathbb{E}$ of system (23), there exists a unique solution $\mathrm{\Phi }\in \mathbb{E}$ such that the following inequality is satisfied:

$$\parallel \overline{\mathrm{\Phi }}\left(t\right)-\mathrm{\Phi }\left(t\right)\parallel \le \varphi \left(\epsilon \right),t\in \mathcal{J},\varphi =max{\left({\varphi }_j\right)}^T,j=\mathrm{1,2,3},\dots 10.$$

Theorem 7

If$\overline{\mathrm{\Phi }}\in \mathbb{E}$satisfies the system(23), then we have the following:

$$\left|\overline{\mathrm{\Phi }}\left(t\right)-{\overline{\mathrm{\Phi }}}_0\left(t\right)-\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\mathrm{ℒ}(\tau ,\overline{\mathrm{\Phi }}\left(\tau \right))\mathit{d\tau }\right|\le \mathrm{\Omega }\epsilon ,\mathit{where},\mathrm{\Omega }=\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\mathit{d\tau }.$$ (24)

Proof:

Using (ii) of Remark 4.1, we have ${}^C{D}^{\xi }\overline{\mathrm{\Phi }}\left(t\right)=\mathrm{ℒ}\left(t,\overline{\mathrm{\Phi }}\left(t\right)\right)+h\left(t\right)$, $t\in \mathcal{J}$,which on applying the Caputo integral gives,

$$\overline{\mathrm{\Phi }}\left(t\right)={\overline{\mathrm{\Phi }}}_0+\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\mathrm{ℒ}\left(\tau ,\overline{\mathrm{\Phi }}\left(\tau \right)\right)\mathit{d\tau }+\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}h\left(\tau \right)\mathit{d\tau }$$

By re-arranging, applying norm on both sides and using (i) of Remark 4.1, it follows that

$$\left|\overline{\mathrm{\Phi }}\left(t\right)-{\overline{\mathrm{\Phi }}}_0-\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\mathrm{ℒ}(\tau ,\overline{\mathrm{\Phi }}\left(\tau \right))\mathit{d\tau }\right|\le \frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\left|h\left(\tau \right)\right|\mathit{d\tau }\le \mathrm{\Omega }\epsilon .$$

Theorem 8

Suppose $\mathrm{ℒ}:\mathcal{J}\times {\mathrm{ℝ}}^{10}\to {\mathrm{ℝ}}^{10}$ satisfies the Lipschitz condition, with Lipschitz constant $\mathrm{ℳ}>0$ and $1-\mathrm{\Omega ℳ}>0$, then the model (22) is generalized UH stable.

Proof:

Suppose that $\overline{\mathrm{\Phi }}\in \mathbb{E}$ satisfies the inequality in (23) and $\mathrm{\Phi }\in \mathbb{E}$ is a unique solution of (22). Then $\forall \epsilon >0,t\in \mathcal{J}$, using Lemma 1, we have

$$\begin{array}{l}\left|\overline{\mathrm{\Phi }}\left(t\right)-\mathrm{\Phi }\left(t\right)\right|{=}_{t\in \mathcal{J}}^{\max }\left|\overline{\mathrm{\Phi }}\left(t\right)-{\mathrm{\Phi }}_0-\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\mathrm{ℒ}(\tau ,\mathrm{\Phi }\left(\tau \right))\mathit{d\tau }\right|\\ \le {}_{t\in \mathcal{J}}^{\max }\left|\overline{\mathrm{\Phi }}\left(t\right)-{\mathrm{\Phi }}_0-\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\mathrm{ℒ}(\tau ,\mathrm{\Phi }\left(\tau \right))\mathit{d\tau }\right|+{}_{t\in \mathcal{J}}^{\max }\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\left|\mathrm{ℒ}(\tau ,\overline{\mathrm{\Phi }}\left(\tau \right))-\mathrm{ℒ}(\tau ,\mathrm{\Phi }\left(\tau \right))\right|\mathit{d\tau }\\ \le \left|\overline{\mathrm{\Phi }}\left(t\right)-{\mathrm{\Phi }}_0-\frac{1}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\mathrm{ℒ}(\tau ,\mathrm{\Phi }\left(\tau \right))\mathit{d\tau }\right|+\frac{\mathrm{ℳ}}{\mathrm{\Gamma }\left(\xi \right)}{\int }_0^t{\left(t-\tau \right)}^{\xi -1}\left|\overline{\mathrm{\Phi }}-\mathrm{\Phi }\right|\mathit{d\tau }\\ \le \mathrm{\Omega }\epsilon +\mathrm{\Omega ℳ}\left|\overline{\mathrm{\Phi }}-\mathrm{\Phi }\right|.\end{array}$$

Thus, we have

$$\parallel \overline{\mathrm{\Phi }}-\mathrm{\Phi }\parallel \le \mathit{k\epsilon },$$ (25)

where, $k=\frac{\mathrm{\Omega }}{1-\mathrm{\Omega ℳ}}$.

Hence, equating $\varphi \left(\epsilon \right)=\mathit{k\epsilon }$, so that $\varphi \left(0\right)=0$, we conclude that the model (22) is both UH and generalized UH stable.

5. Iterative schemes involving the three different fractional operators

This section is divided into three parts. We shall study an iterative scheme using the three different fractional derivatives, that is, Caputo-Fabrizio, Caputo and Atangana-Baleanu derivatives. We start with the following:

5.1. The Caputo-Fabrizio fractional operator

For the solution of the model, we shall adopt the Laplace Adomian Decomposition method. Applying the Laplace transform of the CF operator to both sides of the system (2), we have

$$\begin{array}{l}\mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathcal{S}}^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1{\mathrm{ℐ}}_V^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\mu }^{\delta }\right){\mathcal{S}}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_D^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_V^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_V^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_D^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_D^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_H^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_H+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_H^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℛ}}_V^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\zeta }_V{\mathrm{ℐ}}_V^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_V^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℛ}}_D^{\delta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\zeta }_D{\mathrm{ℐ}}_D^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_D^{\delta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathcal{S}}^{\theta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right)+{\mu }^{\theta }\right]{\mathcal{S}}^{\theta }\right\},\\ \mathrm{ℒ}\left\{{}^{\mathit{cf}}{D}_t^{\xi }{\mathrm{ℐ}}_D^{\theta }\left(t\right)\right\}=\mathrm{ℒ}\left\{{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right){\mathcal{S}}^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_D^{\theta }\right\}.\end{array}$$ (26)

Following the definition of Laplace transform for the Caputo-Fabrizio derivative, we have that

$$\begin{array}{l}\frac{s\mathrm{ℒ}\left\{{\mathcal{S}}^{\theta }\left(t\right)\right\}-{\mathcal{S}}^{\theta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1{\mathrm{ℐ}}_V^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\mu }^{\delta }\right){\mathcal{S}}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_D^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℐ}}_V^{\delta }\left(t\right)\right\}-{\mathrm{ℐ}}_V^{\delta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_V^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℐ}}_D^{\delta }\left(t\right)\right\}-{\mathrm{ℐ}}_D^{\delta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_D^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℐ}}_H^{\delta }\left(t\right)\right\}-{\mathrm{ℐ}}_H^{\delta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_H+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_H^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)\right\}-{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)\right\}-{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℐ}}_R^{\delta }\left(t\right)\right\}-{\mathrm{ℛ}}_V^{\delta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\zeta }_V{\mathrm{ℐ}}_V^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_V^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℛ}}_D^{\delta }\left(t\right)\right\}-{\mathrm{ℛ}}_D^{\delta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\zeta }_D{\mathrm{ℐ}}_D^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_D^{\delta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathcal{S}}^{\theta }\left(t\right)\right\}-{\mathcal{S}}^{\theta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right)+{\mu }^{\theta }\right]{\mathcal{S}}^{\theta }\right\},\\ \frac{s\mathrm{ℒ}\left\{{\mathrm{ℐ}}_D^{\theta }\left(t\right)\right\}-{\mathrm{ℐ}}_D^{\theta }\left(0\right)}{s+\xi \left(1-s\right)}=\mathrm{ℒ}\left\{{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right){\mathcal{S}}^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_D^{\theta }\right\},\end{array}$$ (27)

which can be written as

$$\begin{array}{l}\mathrm{ℒ}\left\{{\mathcal{S}}^{\delta }\left(t\right)\right\}=\frac{{\mathcal{S}}^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1{\mathrm{ℐ}}_V^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\mu }^{\delta }\right){\mathcal{S}}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_D^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℐ}}_V^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_V^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_V^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℐ}}_D^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_D^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_D^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℐ}}_H^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_H^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\left({\mathcal{S}}^{\delta }+{\mathrm{ℛ}}_V^{\delta }+{\mathrm{ℛ}}_D^{\delta }\right)-\left({\varphi }_H+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_H^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_D^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_H^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℛ}}_V^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℛ}}_V^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\zeta }_V{\mathrm{ℐ}}_V^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_D^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_V^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℛ}}_D^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℛ}}_D^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\zeta }_D{\mathrm{ℐ}}_D^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_H^{\delta }\right){\mathrm{ℛ}}_D^{\delta }\right\},\\ \mathrm{ℒ}\left\{{\mathcal{S}}^{\theta }\left(t\right)\right\}=\frac{{\mathcal{S}}^{\theta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right)+{\mu }^{\theta }\right]{\mathcal{S}}^{\theta }\right\},\\ \mathrm{ℒ}\left\{{\mathrm{ℐ}}_D^{\theta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_D^{\theta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_D^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right){\mathcal{S}}^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_D^{\theta }\right\}.\end{array}$$ (28)

According to the Adomian decomposition method, the solution will be in the following series type

$$\begin{array}{l}{\mathcal{S}}^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathcal{S}}_n^{\delta }\left(t\right),{\mathrm{ℐ}}_V^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\left(t\right),{\mathrm{ℐ}}_D^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }\left(t\right),{\mathrm{ℐ}}_H^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\left(t\right),\\ {\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\left(t\right),{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\left(t\right),{\mathrm{ℛ}}_V^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\left(t\right),{\mathrm{ℛ}}_D^{\delta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\left(t\right),\\ {\mathcal{S}}_n^{\theta }\left(t\right)=\sum _{n=0}^{\infty }{\mathcal{S}}_n^{\theta }\left(t\right),{\mathrm{ℐ}}_D^{\theta }\left(t\right)=\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\left(t\right).\end{array}$$ (29)

The thirteen nonlinear terms in the model (2) can be decomposed as

$$\begin{array}{l}\sum _{n=0}^{\infty }{\mathcal{A}}_{1n}\left({\mathrm{ℐ}}_V^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(t\right){\mathcal{S}}^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{2n}\left({\mathrm{ℐ}}_D^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_D^{\delta }\left(t\right){\mathcal{S}}^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{3n}\left({\mathrm{ℐ}}_H^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_H^{\delta }\left(t\right){\mathcal{S}}^{\delta }\left(t\right),\\ \sum _{n=0}^{\infty }{\mathcal{A}}_{4n}\left({\mathrm{ℐ}}_V^{\delta },{\mathrm{ℛ}}_D^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(t\right){\mathrm{ℛ}}_D^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{5n}\left({\mathrm{ℐ}}_D^{\delta },{\mathrm{ℐ}}_V^{\delta }\right)={\mathrm{ℐ}}_D^{\delta }\left(t\right){\mathrm{ℐ}}_V^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{6n}\left({\mathrm{ℐ}}_H^{\delta },{\mathrm{ℐ}}_V^{\delta }\right)={\mathrm{ℐ}}_H^{\delta }\left(t\right){\mathrm{ℐ}}_V^{\delta }\left(t\right),\\ \sum _{n=0}^{\infty }{\mathcal{A}}_{7n}\left({\mathrm{ℐ}}_D^{\theta },{\mathrm{ℛ}}_V^{\delta }\right)={\mathrm{ℐ}}_D^{\theta }\left(t\right){\mathrm{ℛ}}_V^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{8n}\left({\mathrm{ℐ}}_V^{\delta },{\mathrm{ℐ}}_D^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(t\right){\mathrm{ℐ}}_D^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{9n}\left({\mathrm{ℐ}}_H^{\delta },{\mathrm{ℛ}}_V^{\delta }\right)={\mathrm{ℐ}}_H^{\delta }\left(t\right){\mathrm{ℛ}}_V^{\delta }\left(t\right),\\ \sum _{n=0}^{\infty }{\mathcal{A}}_{10n}\left({\mathrm{ℐ}}_H^{\delta },{\mathrm{ℛ}}_D^{\delta }\right)={\mathrm{ℐ}}_H^{\delta }\left(t\right){\mathrm{ℛ}}_D^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{11n}\left({\mathrm{ℐ}}_V^{\delta },{\mathrm{ℐ}}_H^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(t\right){\mathrm{ℐ}}_H^{\delta }\left(t\right),\sum _{n=0}^{\infty }{\mathcal{A}}_{12n}\left({\mathrm{ℐ}}_D^{\delta },{\mathcal{S}}^{\theta }\right)={\mathrm{ℐ}}_D^{\delta }\left(t\right){\mathcal{S}}^{\theta }\left(t\right),\\ \sum _{n=0}^{\infty }{\mathcal{A}}_{13n}\left({\mathrm{ℐ}}_{\mathit{VD}}^{\delta },{\mathcal{S}}^{\theta }\right)={\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right){\mathcal{S}}^{\theta }\left(t\right).\end{array}$$

where the polynomial $A_n\left(x,y\right)$ is defined thus,

$$A_n\left(x,y\right)=\sum _{n=0}^{\infty }{A}_n\left(x,y\right)=\frac{1}{n}\frac{d^n}{d{\lambda }^n}{\left(\left[\sum _{i=0}^q{\lambda }^i{x}_i\left(t\right)\sum _{i=0}^q{\lambda }^i{y}_i\left(t\right)\right]\right|}_{\lambda =0}.$$ (30)

Particularly, we have that

$$\begin{array}{l}{\mathcal{A}}_{10}\left({\mathrm{ℐ}}_V^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(0\right){\mathcal{S}}^{\delta }\left(0\right),{\mathcal{A}}_{11}\left({\mathrm{ℐ}}_V^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(1\right){\mathcal{S}}^{\delta }\left(0\right)+{\mathrm{ℐ}}_V^{\delta }\left(0\right){\mathcal{S}}^{\delta }\left(1\right),\\ {\mathcal{A}}_{12}\left({\mathrm{ℐ}}_V^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(2\right){\mathcal{S}}^{\delta }\left(0\right)+{\mathrm{ℐ}}_V^{\delta }\left(1\right){\mathcal{S}}^{\delta }\left(1\right)+{\mathrm{ℐ}}_V^{\delta }\left(0\right){\mathcal{S}}^{\delta }\left(2\right),\\ {\mathcal{A}}_{13}\left({\mathrm{ℐ}}_V^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(3\right){\mathcal{S}}^{\delta }\left(0\right)+{\mathrm{ℐ}}_V^{\delta }\left(2\right){\mathcal{S}}^{\delta }\left(1\right)+{\mathrm{ℐ}}_V^{\delta }\left(1\right){\mathcal{S}}^{\delta }\left(2\right)+{\mathrm{ℐ}}_V^{\delta }\left(0\right){\mathcal{S}}^{\delta }\left(3\right),\\ {\mathcal{A}}_{14}\left({\mathrm{ℐ}}_V^{\delta },{\mathcal{S}}^{\delta }\right)={\mathrm{ℐ}}_V^{\delta }\left(4\right){\mathcal{S}}^{\delta }\left(0\right)+{\mathrm{ℐ}}_V^{\delta }\left(3\right){\mathcal{S}}^{\delta }\left(1\right)+{\mathrm{ℐ}}_V^{\delta }\left(2\right){\mathcal{S}}^{\delta }\left(2\right)+{\mathrm{ℐ}}_V^{\delta }\left(1\right){\mathcal{S}}^{\delta }\left(3\right)+{\mathrm{ℐ}}_V^{\delta }\left(0\right){\mathcal{S}}^{\delta }\left(4\right)\end{array}$$ (31)

Applying Eqs. (27), (28), (29), (30), (31) into the system (2), we have

$$\begin{array}{l}\mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathcal{S}}_n^{\delta }\left(t\right)\right\}=\frac{{\mathcal{S}}^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1\sum _{n=0}^{\infty }{\mathcal{A}}_{1n}\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathcal{S}}_n^{\delta }\right)+{\alpha }_2^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{2n}({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta },{\mathcal{S}}_n^{\delta })+{\alpha }_3^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{3n}({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathcal{S}}_n^{\delta })\right)\right)\\ \left(\left(+{\mu }^{\delta }\sum _{n=0}^{\infty }{\mathcal{S}}_n^{\delta }\right)+{\alpha }_D\sum _{n=0}^{\infty }{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_V^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_1^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{1n}\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathcal{S}}_n^{\delta }\right)+{\alpha }_1^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{4n}({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta })\right)\\ \left(-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right)\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }-{\alpha }_2^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{5n}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta },{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\right)-{\alpha }_3\sum _{n=0}^{\infty }{\mathcal{A}}_{6n}({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta })+{\zeta }_D\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_D^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_2^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{2n}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta },{\mathcal{S}}_n^{\delta }\right)+{\alpha }_2^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{7n}({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta },{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta })\right)\\ -\left(\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right)\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }-{\alpha }_1^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{8n}\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\theta },{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }\right)+{\zeta }_V\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_H^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_3^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{3n}\left({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathcal{S}}_n^{\delta }\right)+{\alpha }_3^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{9n}({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta })+{\alpha }_3^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{10n}({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta })\right)\\ \left(-\left({\varphi }_H+{\zeta }_H+{\mu }^{\delta }\right)\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }-{\alpha }_1^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{11n}\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\right)+{\zeta }_V\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_2^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{5n}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta },{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\right)+{\alpha }_1^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{8n}({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta })\right)\\ \left(-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right)\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_3^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{6n}\left({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\right)+{\alpha }_1^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{11n}({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta })\right)\\ \left(-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\zeta }_H+{\mu }^{\delta }\right)\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℛ}}_V^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\zeta }_V\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }-{\mu }^{\delta }\sum _{i=1}^{\infty }{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }-{\alpha }_2^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{7n}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta },{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\right)\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\left(t\right)\right\}=\frac{{\mathrm{ℛ}}_D^{\delta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\zeta }_D\sum _{i=1}^{\infty }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }-\left({\mu }^{\delta }+{\alpha }_D\right)\sum _{i=1}^{\infty }{\mathrm{ℛ}}_{\mathit{Dn}}-{\alpha }_1^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{4n}({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta })\right)\\ \left(-{\alpha }_3^{\delta }\sum _{n=0}^{\infty }{\mathcal{A}}_{10n}\left({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\right)\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathcal{S}}_n^{\theta }\left(t\right)\right\}=\frac{{\mathcal{S}}^{\theta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\theta }-{\alpha }_2^{\theta }\sum _{n=0}^{\infty }{\mathcal{A}}_{12n}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\delta },{\mathcal{S}}_n^{\theta }\right)-{\alpha }_2^{\theta }\sum _{n=0}^{\infty }{\mathcal{A}}_{13n}({\mathrm{ℐ}}_{\mathit{VDn}}^{\delta },{\mathcal{S}}_n^{\theta })-{\mu }^{\theta }\sum _{n=0}^{\infty }{\mathcal{S}}_n^{\theta }\right\},\\ \mathrm{ℒ}\left\{\sum _{n=0}^{\infty }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\left(t\right)\right\}=\frac{{\mathrm{ℐ}}_D^{\theta }\left(0\right)}{s}+\frac{s+\xi \left(1-s\right)}{s}\mathrm{ℒ}\left\{{\alpha }_2^{\theta }\sum _{n=0}^{\infty }{\mathcal{A}}_{12n}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\delta },{\mathcal{S}}_n^{\theta }\right)+{\alpha }_2^{\theta }\sum _{n=0}^{\infty }{\mathcal{A}}_{13n}({\mathrm{ℐ}}_{\mathit{VDn}}^{\delta },{\mathcal{S}}_n^{\theta })-{\mu }^{\theta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\right\}.\end{array}$$ (32)

Matching the terms on both sides of (32), and applying the inverse Laplace transform, we obtain

$$\begin{array}{l}{\mathcal{S}}_0^{\delta }\left(t\right)={\mathcal{S}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{V0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{V0}^{\delta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\delta }\left(t\right)={\mathrm{ℐ}}_D^{\delta }\left(0\right),{\mathrm{ℐ}}_{H0}^{\delta }\left(t\right)={\mathrm{ℐ}}_H^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right),\\ {\mathrm{ℛ}}_{V0}^{\delta }\left(t\right)={\mathrm{ℛ}}_V^{\delta }\left(0\right),{\mathrm{ℛ}}_{D0}^{\delta }\left(t\right)={\mathrm{ℛ}}_D^{\delta }\left(0\right),{\mathcal{S}}^{\theta }\left(t\right)={\mathcal{S}}^{\theta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\theta }\left(t\right)={\mathrm{ℐ}}_D^{\theta }\left(0\right),\\ {\mathcal{S}}_1^{\delta }\left(t\right)=\left[{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }+{\mu }^{\delta }\right){\mathcal{S}}_0^{\delta }+{\alpha }_D{\mathrm{ℛ}}_{D0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{V1}^{\delta }\left(t\right)=\left[{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_{V0}^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }-{\alpha }_3{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{D1}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{D0}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{H1}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_{H0}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VH}1}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℛ}}_{V1}^{\delta }\left(t\right)=\left[{\zeta }_V{\mathrm{ℐ}}_{V0}^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{V0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℛ}}_{D1}^{\delta }\left(t\right)=\left[{\zeta }_D{\mathrm{ℐ}}_{D0}^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{D0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathcal{S}}_1^{\theta }\left(t\right)=\left[{\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right)+{\mu }^{\theta }\right]{\mathcal{S}}_0^{\theta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{D1}^{\theta }\left(t\right)=\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_{D0}^{\theta }\right]\left[1+\xi \left(t-1\right)\right],\end{array}$$

$$\begin{array}{l}{\mathcal{S}}_2^{\delta }\left(t\right)=\left[{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }+{\mu }^{\delta }\right){\mathcal{S}}_1^{\delta }-{\alpha }_1^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }-{\alpha }_2^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_3^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_{D1}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{V2}^{\delta }\left(t\right)=\left[\left\{{\alpha }_1^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right)\right\}{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathcal{S}}_1^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℛ}}_{D1}-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }\right)\\ \left(-{\alpha }_3^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\left]\right[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{D2}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }\left({\mathcal{S}}_1^{\delta }+{\mathrm{ℛ}}_{V1}^{\delta }\right)+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{H2}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\left({\mathcal{S}}_1^{\delta }+{\mathrm{ℛ}}_{V1}^{\delta }+{\mathrm{ℛ}}_{D1}^{\delta }\right)+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_{H1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VD}2}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VH}2}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}1}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℛ}}_{V2}^{\delta }\left(t\right)=\left[{\zeta }_V{\mathrm{ℐ}}_{V1}^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{V1}^{\delta }-\left({\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\right){\mathrm{ℛ}}_{V0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℛ}}_{D2}^{\delta }\left(t\right)=\left[{\zeta }_D{\mathrm{ℐ}}_{D1}^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{D1}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\right){\mathrm{ℛ}}_{D0}^{\delta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathcal{S}}_2^{\theta }\left(t\right)=\left[{\mathrm{\Delta }}^{\theta }-{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_1^{\theta }-{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D1}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\mu }^{\theta }{\mathcal{S}}_1^{\theta }\right]\left[1+\xi \left(t-1\right)\right],\\ {\mathrm{ℐ}}_{D2}^{\theta }\left(t\right)=\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_1^{\theta }+{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D1}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_{D1}^{\theta }\right]\left[1+\xi \left(t-1\right)\right].\end{array}$$ (33)

5.2. The Caputo fractional operator

Applying the Laplace transform to system (2) and solving via the Caputo derivative, we have

$$\begin{array}{l}{\mathcal{S}}_0^{\delta }\left(t\right)={\mathcal{S}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{V0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{V0}^{\delta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\delta }\left(t\right)={\mathrm{ℐ}}_D^{\delta }\left(0\right),{\mathrm{ℐ}}_{H0}^{\delta }\left(t\right)={\mathrm{ℐ}}_H^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right),\\ {\mathrm{ℛ}}_{V0}^{\delta }\left(t\right)={\mathrm{ℛ}}_V^{\delta }\left(0\right),{\mathrm{ℛ}}_{D0}^{\delta }\left(t\right)={\mathrm{ℛ}}_D^{\delta }\left(0\right),{\mathcal{S}}^{\theta }\left(t\right)={\mathcal{S}}^{\theta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\theta }\left(t\right)={\mathrm{ℐ}}_D^{\theta }\left(0\right),\\ {\mathcal{S}}_1^{\delta }\left(t\right)=\left[{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }+{\xi }^{\delta }\right){\mathcal{S}}_0^{\delta }+{\alpha }_D{\mathrm{ℛ}}_{D0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{V1}^{\delta }\left(t\right)=\left[{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\xi }^{\delta }\right){\mathrm{ℐ}}_{V0}^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }-{\alpha }_3{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{D1}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{D0}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{H1}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_H+{\xi }^{\delta }\right){\mathrm{ℐ}}_{H0}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{\mathit{VH}1}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℛ}}_{V1}^{\delta }\left(t\right)=\left[{\zeta }_V{\mathrm{ℐ}}_{V0}^{\delta }-\left({\xi }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{V0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℛ}}_{D1}^{\delta }\left(t\right)=\left[{\zeta }_D{\mathrm{ℐ}}_{D0}^{\delta }-\left({\xi }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{D0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathcal{S}}_1^{\theta }\left(t\right)=\left[{\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right)+{\xi }^{\theta }\right]{\mathcal{S}}_0^{\theta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{D1}^{\theta }\left(t\right)=\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\xi }^{\theta }{\mathrm{ℐ}}_{D0}^{\theta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathcal{S}}_2^{\delta }\left(t\right)=\left[{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }+{\xi }^{\delta }\right){\mathcal{S}}_1^{\delta }-{\alpha }_1^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }-{\alpha }_2^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_3^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_{D1}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{V2}^{\delta }\left(t\right)=\left[\left\{{\alpha }_1^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\zeta }_V+{\xi }^{\delta }\right)\right\}{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathcal{S}}_1^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℛ}}_{D1}-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }\right)\\ \left(-{\alpha }_3^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{D2}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }\left({\mathcal{S}}_1^{\delta }+{\mathrm{ℛ}}_{V1}^{\delta }\right)+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right]\\ \times \left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{H2}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\left({\mathcal{S}}_1^{\delta }+{\mathrm{ℛ}}_{V1}^{\delta }+{\mathrm{ℛ}}_{D1}^{\delta }\right)+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_H+{\xi }^{\delta }\right){\mathrm{ℐ}}_{H1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right]\\ \times \left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{\mathit{VD}2}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{\mathit{VH}2}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}1}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℛ}}_{V2}^{\delta }\left(t\right)=\left[{\zeta }_V{\mathrm{ℐ}}_{V1}^{\delta }-\left({\xi }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{V1}^{\delta }-\left({\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\right){\mathrm{ℛ}}_{V0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℛ}}_{D2}^{\delta }\left(t\right)=\left[{\zeta }_D{\mathrm{ℐ}}_{D1}^{\delta }-\left({\xi }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{D1}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\right){\mathrm{ℛ}}_{D0}^{\delta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathcal{S}}_2^{\theta }\left(t\right)=\left[{\mathrm{\Delta }}^{\theta }-{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_1^{\theta }-{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D1}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\xi }^{\theta }{\mathcal{S}}_1^{\theta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right],\\ {\mathrm{ℐ}}_{D2}^{\theta }\left(t\right)=\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_1^{\theta }+{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D1}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\xi }^{\theta }{\mathrm{ℐ}}_{D1}^{\theta }\right]\left[\frac{t^{\xi }}{\mathrm{\Gamma }\left(\xi +1\right)}\right].\end{array}$$ (34)

5.3. The Atangana-Baleanu fractional operator

Applying the Laplace transform to system (2) and solving via the Atangana-Baleanu derivative, we have

$$\begin{array}{l}{\mathcal{S}}_0^{\delta }\left(t\right)={\mathcal{S}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{V0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{V0}^{\delta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\delta }\left(t\right)={\mathrm{ℐ}}_D^{\delta }\left(0\right),{\mathrm{ℐ}}_{H0}^{\delta }\left(t\right)={\mathrm{ℐ}}_H^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right),{\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right),\\ {\mathrm{ℛ}}_{V0}^{\delta }\left(t\right)={\mathrm{ℛ}}_V^{\delta }\left(0\right),{\mathrm{ℛ}}_{D0}^{\delta }\left(t\right)={\mathrm{ℛ}}_D^{\delta }\left(0\right),{\mathcal{S}}^{\theta }\left(t\right)={\mathcal{S}}^{\theta }\left(0\right),{\mathrm{ℐ}}_{D0}^{\theta }\left(t\right)={\mathrm{ℐ}}_D^{\theta }\left(0\right),\\ {\mathcal{S}}_1^{\delta }\left(t\right)=\left[{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }+{\xi }^{\delta }\right){\mathcal{S}}_0^{\delta }+{\alpha }_D{\mathrm{ℛ}}_{D0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{V1}^{\delta }\left(t\right)=\left[{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_V+{\zeta }_V+{\xi }^{\delta }\right){\mathrm{ℐ}}_{V0}^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }-{\alpha }_3{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{D1}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{D0}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{H1}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_H+{\xi }^{\delta }\right){\mathrm{ℐ}}_{H0}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VH}1}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℛ}}_{V1}^{\delta }\left(t\right)=\left[{\zeta }_V{\mathrm{ℐ}}_{V0}^{\delta }-\left({\xi }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{V0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℛ}}_{D1}^{\delta }\left(t\right)=\left[{\zeta }_D{\mathrm{ℐ}}_{D0}^{\delta }-\left({\xi }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{D0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathcal{S}}_1^{\theta }\left(t\right)=\left[{\mathrm{\Delta }}^{\theta }-\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right)+{\xi }^{\theta }\right]{\mathcal{S}}_0^{\theta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{D1}^{\theta }\left(t\right)=\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\xi }^{\theta }{\mathrm{ℐ}}_{D0}^{\theta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathcal{S}}_2^{\delta }\left(t\right)=\left[{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }+{\xi }^{\delta }\right){\mathcal{S}}_1^{\delta }-{\alpha }_1^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }-{\alpha }_2^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_3^{\delta }{\mathcal{S}}_0^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\alpha }_D{\mathrm{ℛ}}_{D1}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{V2}^{\delta }\left(t\right)=\left[\left\{{\alpha }_1^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }-{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\zeta }_V+{\xi }^{\delta }\right)\right\}{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathcal{S}}_1^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℛ}}_{D1}-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }\right)\\ \left(-{\alpha }_3^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\left]\right[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{D2}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }\left({\mathcal{S}}_1^{\delta }+{\mathrm{ℛ}}_{V1}^{\delta }\right)+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right]\\ \times \left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{H2}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\left({\mathcal{S}}_1^{\delta }+{\mathrm{ℛ}}_{V1}^{\delta }+{\mathrm{ℛ}}_{D1}^{\delta }\right)+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\left({\mathcal{S}}_0^{\delta }+{\mathrm{ℛ}}_{V0}^{\delta }+{\mathrm{ℛ}}_{D0}^{\delta }\right)-\left({\varphi }_H+{\xi }^{\delta }\right){\mathrm{ℐ}}_{H1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right]\\ \times \left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VD}2}^{\delta }\left(t\right)=\left[{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{D1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{D0}^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{\mathit{VH}2}^{\delta }\left(t\right)=\left[{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\xi }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VH}1}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℛ}}_{V2}^{\delta }\left(t\right)=\left[{\zeta }_V{\mathrm{ℐ}}_{V1}^{\delta }-\left({\xi }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{D0}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{V1}^{\delta }-\left({\alpha }_2^{\delta }{\mathrm{ℐ}}_{D1}^{\theta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\right){\mathrm{ℛ}}_{V0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℛ}}_{D2}^{\delta }\left(t\right)=\left[{\zeta }_D{\mathrm{ℐ}}_{D1}^{\delta }-\left({\xi }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{V0}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H0}^{\delta }\right){\mathrm{ℛ}}_{D1}^{\delta }-\left({\alpha }_1^{\delta }{\mathrm{ℐ}}_{V1}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{H1}^{\delta }\right){\mathrm{ℛ}}_{D0}^{\delta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathcal{S}}_2^{\theta }\left(t\right)=\left[{\mathrm{\Delta }}^{\theta }-{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_1^{\theta }-{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D1}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\xi }^{\theta }{\mathcal{S}}_1^{\theta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\\ {\mathrm{ℐ}}_{D2}^{\theta }\left(t\right)=\left[{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D0}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\right){\mathcal{S}}_1^{\theta }+{\alpha }_2^{\theta }\left({\mathrm{ℐ}}_{D1}^{\delta }+{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\right){\mathcal{S}}_0^{\theta }-{\xi }^{\theta }{\mathrm{ℐ}}_{D1}^{\theta }\right]\left[\frac{1}{\mathrm{ℱ}\left(\xi \right)}\left(1-\xi +\frac{\xi t^{\xi }}{\mathrm{\Gamma }\left(\xi \right)}\right)\right],\end{array}$$ (35)

and so on. Hence we obtain the required solution

$$\begin{array}{l}{\mathcal{S}}^{\delta }\left(t\right)={\mathcal{S}}_0^{\delta }\left(t\right)+{\mathcal{S}}_1^{\delta }\left(t\right)+{\mathcal{S}}_2^{\delta }\left(t\right)+\dots ,{\mathrm{ℐ}}_V^{\delta }\left(t\right)={\mathrm{ℐ}}_{V0}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{V1}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{V2}^{\delta }\left(t\right)+\dots ,{\mathrm{ℐ}}_D^{\delta }\left(t\right)={\mathrm{ℐ}}_{D0}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{D1}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{D2}^{\delta }\left(t\right)+\dots ,\\ {\mathrm{ℐ}}_H^{\delta }\left(t\right)={\mathrm{ℐ}}_{H0}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{H1}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{H2}^{\delta }\left(t\right)+\dots ,{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VD}0}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{\mathit{VD}1}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{\mathit{VD}2}^{\delta }\left(t\right)+\dots ,\\ {\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VH}0}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{\mathit{VH}1}^{\delta }\left(t\right)+{\mathrm{ℐ}}_{\mathit{VH}2}^{\delta }\left(t\right)+\dots ,{\mathrm{ℛ}}_V^{\delta }\left(t\right)={\mathrm{ℛ}}_{V0}^{\delta }\left(t\right)+{\mathrm{ℛ}}_{V1}^{\delta }\left(t\right)+{\mathrm{ℛ}}_{V2}^{\delta }\left(t\right)+\dots ,\\ {\mathrm{ℛ}}_D^{\delta }\left(t\right)={\mathrm{ℛ}}_{D0}^{\delta }\left(t\right)+{\mathcal{S}}_1^{\delta }\left(t\right)+{\mathcal{S}}_2^{\delta }\left(t\right)+\dots ,{\mathcal{S}}^{\theta }\left(t\right)={\mathcal{S}}_0^{\theta }\left(t\right)+{\mathcal{S}}_1^{\theta }\left(t\right)+{\mathcal{S}}_2^{\theta }\left(t\right)+\dots ,\\ {\mathrm{ℐ}}_D^{\theta }\left(t\right)={\mathrm{ℐ}}_{D0}^{\theta }\left(t\right)+{\mathrm{ℐ}}_{D1}^{\theta }\left(t\right)+{\mathrm{ℐ}}_{D2}^{\theta }\left(t\right)+\dots .\end{array}$$ (36)

5.4. Stability of the iterative scheme

In this subsection, the stability of the iterative scheme is established, in the framework of Ostrowski [47]. Let ${\mathrm{ℬ}}^{\delta }$ be a Banach space endowed with a norm defined by $\parallel x\parallel ={max}_{t\in \left[a,b\right]}\left\{|x\left(t\right)|:x\in {\mathrm{ℬ}}^{\delta }\right\}$. Assume that $F\left(\mathcal{G}\right)\ne \varnothing$ be the fixed point set of $\mathcal{G}$. Let $\mathcal{G}$ be a self-map on ${\mathrm{ℬ}}^{\delta }$. Let $\left\{y_n\right\}$ be a sequence in ${\mathrm{ℬ}}^{\delta }$, and $\left\{x_n\right\}$, denote an approximate sequence of $\left\{y_n\right\}$. An iterative technique of the type $y_{n+1}=g\left(\mathcal{G},y_n\right)$, for some function, say, $g$, where $y_n$ converges to a fixed point $y^{\ast }\in F\left(\mathcal{G}\right)$, is said to be $\mathcal{G}$-stable, provided that ${lim}_{n\to \infty }{k}_n=0$ if and only if ${lim}_{n\to \infty }{x}_n^{\ast }=y^{\ast }$, where $k_n=\Vert x_{n+1}-g\left(\mathcal{G},x_n\right)\Vert$. The following theorems are now established:

Theorem 9

Assume that$\mathcal{G}$be a self-map on${\mathrm{ℬ}}^{\delta }$such that

$$\Vert \mathcal{G}\left(x^{\delta }\right)-\mathcal{G}\left(y^{\delta }\right)\Vert \le C_1^{\delta }\Vert x^{\delta }-\mathcal{G}\left(x^{\delta }\right)\Vert +C_2^{\delta }\Vert x^{\delta }-y^{\delta }\Vert$$

for all $x^{\delta },y^{\delta }\in {\mathrm{ℬ}}^{\delta }$ with $C_1^{\delta }\ge 0,C_2^{\delta }\in \left[01\right)$. Then, the iterative scheme $\left\{y_n\right\}$ is $\mathcal{G}$-stable.

Theorem 10

Let$\mathcal{G}$be a self-map defined as

$$\begin{array}{l}\mathcal{G}\left({\mathcal{S}}_n^{\delta }\left(t\right)\right)={\mathcal{S}}_{n+1}^{\delta }\left(t\right),\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\left(t\right)\right)={\mathrm{ℐ}}_{\mathit{Vn}+1}^{\delta }\left(t\right),\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }\left(t\right)\right)={\mathrm{ℐ}}_{\mathit{Dn}+1}^{\delta }\left(t\right)\\ \mathcal{G}\left({\mathrm{ℐ}}_H^{\delta }\left(t\right)\right)={\mathrm{ℐ}}_{\mathit{Hn}+1}^{\delta }\left(t\right),\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\left(t\right)\right)={\mathrm{ℐ}}_{\mathit{Dn}+1}^{\delta }\left(t\right)\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\left(t\right)\right)={\mathrm{ℐ}}_{\mathit{VHn}+1}^{\delta }\left(t\right),\mathcal{G}\left({\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\left(t\right)\right)={\mathrm{ℛ}}_{\mathit{Vn}+1}^{\delta }\left(t\right)\\ \mathcal{G}\left({\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\left(t\right)\right)={\mathrm{ℛ}}_{\mathit{Dn}+1}^{\delta }\left(t\right),\mathcal{G}\left({\mathcal{S}}_n^{\theta }\left(t\right)\right)={\mathcal{S}}_{n+1}^{\delta }\left(t\right)\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\left(t\right)\right)={\mathrm{ℐ}}_{\mathit{Dn}+1}^{\theta }\left(t\right).\end{array}$$ (37)

It is $\mathcal{G}$-stable in $L^1\left(a,b\right)$ if

$$\left\{\begin{array}{l}\left({\mu }^{\delta }{f}_1\left(\xi \right)+{\alpha }_D{f}_2\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{f}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_1{f}_4\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_5{f}_5\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_1{f}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{f}_7\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_1{f}_8\left(\xi \right)\right)<1,\\ \left(K_1^{\delta }{g}_1\left(\xi \right)+{\zeta }_D{g}_2\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{g}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_1{g}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{g}_5\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_8{g}_6\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{g}_7\left(\xi \right)\right)\\ \left(+{\alpha }_2^{\delta }{\omega }_2{g}_8\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{g}_9\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_2{g}_{10}\left(\xi \right)\right)<1,\\ \left(K_2^{\delta }{h}_1\left(\xi \right)+{\zeta }_V{h}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_3{h}_3\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_1{g}_4\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_3{h}_5\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_7{h}_6\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{h}_7\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_3{h}_8\left(\xi \right)\right)<1,\\ \left(K_3^{\delta }{j}_1\left(\xi \right)+{\zeta }_V{j}_2\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_3\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_1{j}_4\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_5\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_7{j}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_7\left(\xi \right)\right)\\ \left(+{\alpha }_3^{\delta }{\omega }_8{j}_8\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{j}_9\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_4{g}_{10}\left(\xi \right)\right)<1,\\ \left(K_4^{\delta }{l}_1\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{l}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_2{l}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{l}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_3{l}_5\left(\xi \right)\right)<1,\\ \left(K_5^{\delta }{m}_1\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{m}_2\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_2{m}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{m}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_4{m}_5\left(\xi \right)\right)<1,\\ \left({\zeta }_V{n}_1\left(\xi \right)+{\mu }^{\delta }{n}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{n}_3\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_7{n}_4\left(\xi \right)\right)<1,\\ \left({\zeta }_D{p}_1\left(\xi \right)+{\mu }^{\delta }{p}_2\left(\xi \right)+{\alpha }_D{p}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{p}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_8{p}_5\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{p}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_8{p}_7\left(\xi \right)\right)<1,\\ \left({\mu }^{\theta }{q}_1\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_3{q}_2\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{q}_3\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_2{q}_4\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{q}_5\left(\xi \right)\right)<1,\\ \left({\mu }^{\theta }{r}_1\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_3{r}_2\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{r}_3\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_2{r}_4\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{r}_5\left(\xi \right)\right)<1,\end{array}\right)$$ (38)

Proof:

Consider the recursive formula below, associated with the system (2) (obtained via taking the inverse Laplace transform of the AB derivative).

$$\begin{array}{l}{\mathcal{S}}_{n+1}^{\delta }\left(t\right)={\mathcal{S}}^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathcal{S}}_n^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }{\mathcal{S}}_n^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }{\mathcal{S}}_n^{\delta }+{\mu }^{\delta }{\mathcal{S}}_n^{\delta }\right)+{\alpha }_D{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\right\}\right],\\ {\mathrm{ℐ}}_{\mathit{Vn}+1}^{\delta }\left(t\right)={\mathrm{ℐ}}_V^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\alpha }_1^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathcal{S}}_n^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }-\left({\varphi }_V+{\zeta }_V+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }-{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\right)\right)\\ \left(\left(-{\alpha }_3{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }+{\zeta }_D{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\right\}\right],\\ {\mathrm{ℐ}}_{\mathit{Dn}+1}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\left({\mathcal{S}}_n^{\delta }+{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\right)-\left({\varphi }_D+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_D^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_V^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\right\}\right],\\ {\mathrm{ℐ}}_{\mathit{Hn}+1}^{\delta }\left(t\right)={\mathrm{ℐ}}_H^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\left({\mathcal{S}}_n^{\delta }+{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }+{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\right)-\left({\varphi }_H+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }-{\alpha }_1^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }+{\zeta }_V{\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\right\}\right],\\ {\mathrm{ℐ}}_{\mathit{VDn}+1}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }-\left({\varphi }_V+{\varphi }_D+{\zeta }_V+{\zeta }_D+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\right\}\right],\\ {\mathrm{ℐ}}_{\mathit{VHn}+1}^{\delta }\left(t\right)={\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }-\left({\varphi }_V+{\varphi }_H+{\zeta }_V+{\zeta }_H+{\mu }^{\delta }\right){\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\right\}\right],\\ {\mathrm{ℛ}}_{\mathit{Vn}+1}^{\delta }\left(t\right)={\mathrm{ℛ}}_V^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\zeta }_V{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }-\left({\mu }^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\right){\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\right\}\right],\\ {\mathrm{ℛ}}_{\mathit{Dn}+1}^{\delta }\left(t\right)={\mathrm{ℛ}}_D^{\delta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\zeta }_D{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }-\left({\mu }^{\delta }+{\alpha }_D+{\alpha }_1^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\right){\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\right\}\right],\\ {\mathcal{S}}_{n+1}^{\theta }\left(t\right)={\mathcal{S}}^{\theta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\theta }-{\alpha }_2^{\theta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }{\mathcal{S}}_n^{\theta }-{\alpha }_2^{\theta }{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }{\mathcal{S}}_n^{\theta }-{\mu }^{\theta }{\mathcal{S}}_n^{\theta }\right\}\right],\\ {\mathrm{ℐ}}_{\mathit{Dn}+1}^{\theta }\left(t\right)={\mathrm{ℐ}}_D^{\theta }\left(0\right)+{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\alpha }_2^{\theta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }{\mathcal{S}}_n^{\theta }+{\alpha }_2^{\theta }{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }{\mathcal{S}}_n^{\theta }-{\mu }^{\theta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\right\}\right],\end{array}$$ (39)

where $\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}$ is a fractional Lagrange multiplier.

We will show that $\mathcal{G}$ has a fixed point. Thus, for all $\left(m,n\right)\in N\times N$, we evaluate the following:

$$\begin{array}{l}\mathcal{G}\left({\mathcal{S}}_n^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathcal{S}}_m^{\delta }\left(t\right)\right)\\ ={\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathcal{S}}_n^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }{\mathcal{S}}_n^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }{\mathcal{S}}_n^{\delta }+{\mu }^{\delta }{\mathcal{S}}_n^{\delta }\right)+{\alpha }_D{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\right\}\right]\\ -{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{{\mathrm{\Delta }}^{\delta }-\left({\alpha }_1{\mathrm{ℐ}}_{\mathit{Vm}}^{\delta }{\mathcal{S}}_m^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dm}}^{\theta }{\mathcal{S}}_m^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hm}}^{\delta }{\mathcal{S}}_m^{\delta }+{\mu }^{\delta }{\mathcal{S}}_m^{\delta }\right)+{\alpha }_D{\mathrm{ℛ}}_{\mathit{Dm}}^{\delta }\right\}\right]\\ ={\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{-\left({\alpha }_1{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }{\mathcal{S}}_n^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }{\mathcal{S}}_n^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }{\mathcal{S}}_n^{\delta }+{\mu }^{\delta }{\mathcal{S}}_n^{\delta }\right)+{\alpha }_D{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\right\}\right]\\ -{\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left\{-\left({\alpha }_1{\mathrm{ℐ}}_{\mathit{Vm}}^{\delta }{\mathcal{S}}_m^{\delta }+{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dm}}^{\theta }{\mathcal{S}}_m^{\delta }+{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hm}}^{\delta }{\mathcal{S}}_m^{\delta }+{\mu }^{\delta }{\mathcal{S}}_m^{\delta }\right)+{\alpha }_D{\mathrm{ℛ}}_{\mathit{Dm}}^{\delta }\right\}\right].\end{array}$$ (40)

Taking the norm on both sides and applying the triangular inequality, we have that

$$\begin{array}{l}\parallel \mathcal{G}\left({\mathcal{S}}_n^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathcal{S}}_m^{\delta }\left(t\right)\right)\parallel \\ ={\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\left[\parallel -{\mu }^{\delta }\left({\mathcal{S}}_n^{\delta }-{\mathcal{S}}_m^{\delta }\right)\parallel +\parallel {\alpha }_D\left({\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }-{\mathrm{ℛ}}_{\mathit{Dm}}^{\delta }\right)\parallel +\parallel -{\alpha }_1^{\delta }{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\left({\mathcal{S}}_n^{\delta }-{\mathcal{S}}_m^{\delta }\right)\parallel +\parallel -{\alpha }_1^{\delta }{\mathcal{S}}_m^{\delta }\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Vm}}^{\delta }\right)\parallel \right)\right)\\ \left(\left(+\parallel -{\alpha }_2^{\delta }{\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\left({\mathcal{S}}_n^{\delta }-{\mathcal{S}}_m^{\delta }\right)\parallel +\parallel -{\alpha }_2^{\delta }{\mathcal{S}}_m^{\delta }\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }-{\mathrm{ℐ}}_{\mathit{Dm}}^{\theta }\right)\parallel +\parallel -{\alpha }_3^{\delta }{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\left({\mathcal{S}}_n^{\delta }-{\mathcal{S}}_m^{\delta }\right)\parallel +\parallel -{\alpha }_3^{\delta }{\mathcal{S}}_m^{\delta }\left({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Hm}}^{\delta }\right)\parallel \right]\right].\end{array}$$ (41)

Now, noting that, ${\mathcal{S}}_m^{\delta },{\mathrm{ℐ}}_{\mathit{Vn}}^{\delta },{\mathrm{ℐ}}_{\mathit{Dn}}^{\delta },{\mathrm{ℐ}}_{\mathit{Hn}}^{\delta },{\mathrm{ℐ}}_{\mathit{VDn}}^{\delta },{\mathrm{ℐ}}_{\mathit{VHn}}^{\delta },{\mathrm{ℛ}}_{\mathit{Vn}}^{\delta },{\mathrm{ℛ}}_{\mathit{Dn}}^{\delta },{\mathcal{S}}_n^{\theta },{\mathrm{ℐ}}_n^{\theta }$ are convergent sequences, we bound them as follows:

$$\begin{array}{l}\parallel {\mathcal{S}}_m^{\delta }\parallel \le {\omega }_1,\parallel {\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\parallel \le {\omega }_2,\parallel {\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }\parallel \le {\omega }_3,\parallel {\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\parallel \le {\omega }_4,\parallel {\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\parallel \le {\omega }_5,\parallel {\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\parallel \le {\omega }_6,\parallel {\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\parallel \le {\omega }_7,\parallel {\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }\parallel \le {\omega }_8,\\ \parallel {\mathcal{S}}_n^{\theta }\parallel \le {\omega }_9,\parallel {\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }\parallel \le {\omega }_{10}.\end{array}$$

Also, as a result of similar pattern in the solutions, we assume that

$$\begin{array}{l}\parallel {\mathcal{S}}_m^{\delta }\left(t\right)-{\mathcal{S}}_n^{\delta }\left(t\right)\parallel \approxeq \parallel {\mathrm{ℛ}}_{\mathit{Dn}}^{\delta }-{\mathrm{ℛ}}_{\mathit{Dm}}^{\delta }\parallel ,\\ \parallel {\mathcal{S}}_m^{\delta }\left(t\right)-{\mathcal{S}}_n^{\delta }\left(t\right)\parallel \approxeq \parallel {\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Vm}}^{\delta }\parallel ,\\ \parallel {\mathcal{S}}_m^{\delta }\left(t\right)-{\mathcal{S}}_n^{\delta }\left(t\right)\parallel \approxeq \parallel {\mathrm{ℐ}}_{\mathit{Dn}}^{\theta }-{\mathrm{ℐ}}_{\mathit{Dm}}^{\theta }\parallel ,\\ \parallel {\mathcal{S}}_m^{\delta }\left(t\right)-{\mathcal{S}}_n^{\delta }\left(t\right)\parallel \approxeq \parallel {\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Hm}}^{\delta }\parallel .\end{array}$$ (42)

Thus, we have that

$$\begin{array}{l}\parallel \mathcal{G}\left({\mathcal{S}}_n^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathcal{S}}_m^{\delta }\left(t\right)\right)\parallel \le \left({\mu }^{\delta }{f}_1\left(\xi \right)+{\alpha }_D{f}_2\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{f}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_1{f}_4\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_5{f}_5\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_1{f}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{f}_7\left(\xi \right)\right)\\ \left(+{\alpha }_3^{\delta }{\omega }_1{f}_8\left(\xi \right)\right)\parallel {\mathcal{S}}_n^{\delta }-{\mathcal{S}}_m^{\delta }\parallel ,\end{array}$$ (43)

where, $f_i\left(\xi \right),i=1,\mathrm{...8}$ are functions resulting from ${\mathrm{ℒ}}^{-1}\left[\frac{s^{\xi }\left(1-\xi \right)+\xi }{s^{\xi }\mathrm{ℱ}\left(\xi \right)}\mathrm{ℒ}\right]$. In a similar manner, we have that,

$$\begin{array}{l}\parallel \mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Vm}}^{\delta }\left(t\right)\right)\parallel \le \left[K_1^{\delta }{g}_1\left(\xi \right)+{\zeta }_D{g}_2\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{g}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_1{g}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{g}_5\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_8{g}_6\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{g}_7\left(\xi \right)\right)\\ \left(+{\alpha }_2^{\delta }{\omega }_2{g}_8\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{g}_9\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_2{g}_{10}\left(\xi \right)\right]\parallel {\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Dm}}^{\delta }\parallel ,\\ \parallel \mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Dm}}^{\delta }\left(t\right)\right)\parallel \le \left[K_2^{\delta }{h}_1\left(\xi \right)+{\zeta }_V{h}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_3{h}_3\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_1{g}_4\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_3{h}_5\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_7{h}_6\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{h}_7\left(\xi \right)\right)\\ \left(+{\alpha }_1^{\delta }{\omega }_3{h}_8\left(\xi \right)\right]\parallel {\mathrm{ℐ}}_{\mathit{Dn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Dm}}^{\delta }\parallel ,\\ \parallel \mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Hm}}^{\delta }\left(t\right)\right)\parallel \le \left[K_3^{\delta }{j}_1\left(\xi \right)+{\zeta }_V{j}_2\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_3\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_1{j}_4\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_5\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_7{j}_6\left(\xi \right)\right)\\ \left(+{\alpha }_3^{\delta }{\omega }_4{j}_7\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_8{j}_8\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{j}_9\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_4{g}_{10}\left(\xi \right)\right]\parallel {\mathrm{ℐ}}_{\mathit{Hn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Hm}}^{\delta }\parallel ,\\ \parallel \mathcal{G}\left({\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{VDm}}^{\delta }\left(t\right)\right)\parallel \le \left[\left(K_4^{\delta }{l}_1\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{l}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_2{l}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{l}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_3{l}_5\left(\xi \right)\right)\right]\parallel {\mathrm{ℐ}}_{\mathit{VDn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{VDm}}^{\delta }\parallel ,\\ \parallel \mathcal{G}\left({\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{VHm}}^{\delta }\left(t\right)\right)\parallel \le \left[\left(K_5^{\delta }{m}_1\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{m}_2\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_2{m}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{m}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_4{m}_5\left(\xi \right)\right)\right]\parallel {\mathrm{ℐ}}_{\mathit{VHn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{VHm}}^{\delta }\parallel ,\\ \parallel \mathcal{G}\left({\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℛ}}_{\mathit{Vm}}^{\delta }\left(t\right)\right)\parallel \le \left[\left({\zeta }_V{n}_1\left(\xi \right)+{\mu }^{\delta }{n}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{n}_3\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_7{n}_4\left(\xi \right)\right)\right]\parallel {\mathrm{ℛ}}_{\mathit{Vn}}^{\delta }-{\mathrm{ℛ}}_{\mathit{Vm}}^{\delta }\parallel ,\\ \parallel \mathcal{G}\left({\mathrm{ℛ}}_{\mathit{Dn}}^{\theta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℛ}}_{\mathit{Dm}}^{\theta }\left(t\right)\right)\parallel \le \left[\left({\zeta }_D{p}_1\left(\xi \right)+{\mu }^{\delta }{p}_2\left(\xi \right)+{\alpha }_D{p}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{p}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_8{p}_5\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{p}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_8{p}_7\left(\xi \right)\right)\right]\\ \times \parallel {\mathrm{ℛ}}_{\mathit{Dn}}^{\theta }-{\mathrm{ℛ}}_{\mathit{Dm}}^{\theta }\parallel ,\\ \parallel \mathcal{G}\left({\mathcal{S}}_n^{\theta }\left(t\right)\right)-\mathcal{G}\left({\mathcal{S}}_m^{\theta }\left(t\right)\right)\parallel \le \left[\left({\mu }^{\theta }{q}_1\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_3{q}_2\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{q}_3\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_2{q}_4\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{q}_5\left(\xi \right)\right)\right]\parallel {\mathcal{S}}_n^{\theta }-{\mathcal{S}}_m^{\theta }\parallel ,\\ \parallel \mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Vn}}^{\theta }\left(t\right)\right)-\mathcal{G}\left({\mathrm{ℐ}}_{\mathit{Vm}}^{\theta }\left(t\right)\right)\parallel \le \left[\left({\mu }^{\theta }{r}_1\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_3{r}_2\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{r}_3\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_2{r}_4\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{r}_5\left(\xi \right)\right)\right]\parallel {\mathrm{ℐ}}_{\mathit{Vn}}^{\delta }-{\mathrm{ℐ}}_{\mathit{Vm}}^{\delta }\parallel .\end{array}$$ (44)

Thus, the mapping $\mathcal{G}$- has a fixed point. We now show that, $\mathcal{G}$ is valid for all the conditions in Theorem 9. Let (43), (44) hold. If we use $C_1^{\delta }=\left(\mathrm{0,0,0,0,0,0,0,0,0,0}\right)$, and

$$C_2^{\delta }=\left\{\begin{array}{l}\left({\mu }^{\delta }{f}_1\left(\xi \right)+{\alpha }_D{f}_2\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{f}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_1{f}_4\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_5{f}_5\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_1{f}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{f}_7\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_1{f}_8\left(\xi \right)\right)<1,\\ \left(K_1^{\delta }{g}_1\left(\xi \right)+{\zeta }_D{g}_2\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{g}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_1{g}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{g}_5\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_8{g}_6\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{g}_7\left(\xi \right)\right)\\ \left(+{\alpha }_2^{\delta }{\omega }_2{g}_8\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{g}_9\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_2{g}_{10}\left(\xi \right)\right)<1,\\ \left(K_2^{\delta }{h}_1\left(\xi \right)+{\zeta }_V{h}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_3{h}_3\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_1{g}_4\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_3{h}_5\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_7{h}_6\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{h}_7\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_3{h}_8\left(\xi \right)\right)<1,\\ \left(K_3^{\delta }{j}_1\left(\xi \right)+{\zeta }_V{j}_2\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_3\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_1{j}_4\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_5\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_7{j}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{j}_7\left(\xi \right)\right)\\ \left(+{\alpha }_3^{\delta }{\omega }_8{j}_8\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{j}_9\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_4{g}_{10}\left(\xi \right)\right)<1,\\ \left(K_4^{\delta }{l}_1\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{l}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_2{l}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{l}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_3{l}_5\left(\xi \right)\right)<1,\\ \left(K_5^{\delta }{m}_1\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{m}_2\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_2{m}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{m}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_4{m}_5\left(\xi \right)\right)<1,\\ \left({\zeta }_V{n}_1\left(\xi \right)+{\mu }^{\delta }{n}_2\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_{10}{n}_3\left(\xi \right)+{\alpha }_2^{\delta }{\omega }_7{n}_4\left(\xi \right)\right)<1,\\ \left({\zeta }_D{p}_1\left(\xi \right)+{\mu }^{\delta }{p}_2\left(\xi \right)+{\alpha }_D{p}_3\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_2{p}_4\left(\xi \right)+{\alpha }_1^{\delta }{\omega }_8{p}_5\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_4{p}_6\left(\xi \right)+{\alpha }_3^{\delta }{\omega }_8{p}_7\left(\xi \right)\right)<1,\\ \left({\mu }^{\theta }{q}_1\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_3{q}_2\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{q}_3\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_2{q}_4\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{q}_5\left(\xi \right)\right)<1,\\ \left({\mu }^{\theta }{r}_1\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_3{r}_2\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{r}_3\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_2{r}_4\left(\xi \right)+{\alpha }_2^{\theta }{\omega }_9{r}_5\left(\xi \right)\right)<1,\end{array}\right)$$ (45)

then all the conditions of Theorem 9 are fulfilled. Hence, the iterative scheme $\left\{y_n\right\}$ is $\mathcal{G}$-stable. Thus, completing the proof.

6. Numerical simulations

6.1. Initial conditions and data fitting

The sexually active population in Argentina (aged 15-64) is estimated to be $\mathrm{29,289,357}$ [51]. Also, the life expectancy is 78.07 years [51]. Thus, we set the human natural death rate, ${\mu }^{\delta }$ as $\frac{1}{\left(78.07\times 365\right)}$ per day. The human recruitment rate, ${\mathrm{\Delta }}^{\delta }$ is set to be $\frac{\mathrm{29,289,350}}{\left(78.07\times 365\right)}$. The initial total population, $N^{\delta }\left(0\right)=\mathrm{29,289,357}$. The initial conditions used for the fitting are: ${\mathcal{S}}^{\delta }\left(0\right)=N^{\delta }\left(0\right)=\mathrm{29,289,357},{\mathrm{ℐ}}_V^{\delta }\left(0\right)=1,{\mathrm{ℐ}}_D^{\delta }\left(0\right)=0,{\mathrm{ℐ}}_H^{\delta }\left(0\right)=0,{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)=0,{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)=0,{\mathrm{ℛ}}_V^{\delta }\left(0\right)=0,{\mathrm{ℛ}}_D^{\delta }\left(0\right)=0,{\mathcal{S}}^{\theta }\left(0\right)=0,{\mathrm{ℐ}}_{\mathit{VD}}^{\theta }\left(0\right)=0$.

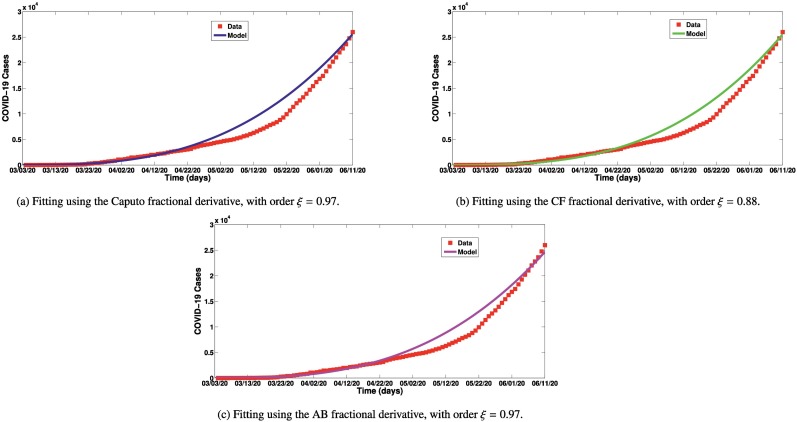
We performed the fitting using fmincon function in the Optimization Toolbox of MATLAB [56]. As depicted in Fig. 1 , we fit the COVID-19 data [57] for Argentina from March 3, 2020 to June 10, 2020. The parameters estimated from the fitting are presented in Table 1. With the Caputo operator, the model fits well to data when the fractional order $\xi =0.97$, as shown in Fig. 1a. With the Caputo-Fabrizio operator, the model fits well to data when the fractional order $\xi =0.88$, as shown in Fig. 1b. Using the Atangana-Baleanu operator, the model fits well to data when the fractional order $\xi =0.97$, as can be observed in Fig. 1c. Although using both Caputo and AB operators, the model fits well to data when the order is $\xi =0.97$, the Caputo operator gave a better fit as compared to the AB operator. It is also imperative to state that, these conclusions are based on the model proposed in this work. The series solutions for the best fits are also presented.

Fig. 1.

Model fittings using the three fractional derivatives. Series solution for best fit using the Caputo fractional derivative is: $I_V^{\delta }\left(t\right)=1.0+0.334438t^{0.97}+0.11195t^{1.94}+0.0374063t^{2.91}$, with order $\xi =0.97$. Series solution for best fit using the CF fractional derivative is: $I_V^{\delta }\left(t\right)=1.04127+0.315116t+0.0946194t^2+0.0245611t^3$, with order $\xi =0.88$. Series solution for best fit using the AB fractional derivative is: $I_V^{\delta }\left(t\right)=1.01019+0.336905t^{0.97}+0.112387t^{1.94}+0.0359822t^{2.91}$.

The following series solutions were obtained for the system (2), under an endemic scenario when all the three diseases are present in the population, using the initial conditions ${\mathcal{S}}^{\delta }\left(0\right)=N^{\delta }\left(0\right)=\mathrm{29,289,350},{\mathrm{ℐ}}_V^{\delta }\left(0\right)=1,{\mathrm{ℐ}}_D^{\delta }\left(0\right)=1,{\mathrm{ℐ}}_H^{\delta }\left(0\right)=1,{\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(0\right)=0,{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(0\right)=0,{\mathrm{ℛ}}_V^{\delta }\left(0\right)=0,{\mathrm{ℛ}}_D^{\delta }\left(0\right)=0,{\mathcal{S}}^{\theta }\left(0\right)=\mathrm{40,000},{\mathrm{ℐ}}_{\mathit{VD}}^{\theta }\left(0\right)=15$. The values of other parameters are exactly as given in Table 1. Series solutions via the Caputo-derivative is given by eq. (46). Here all the parameter values as given in Table 1 were used.

$$\begin{array}{l}{\mathcal{S}}^{\delta }\left(t\right)=29289350+2078.29t^{0.97}-0.716105t^{1.94}-0.157525t^{2.91},\\ {\mathrm{ℐ}}_V^{\delta }\left(t\right)=1.0+0.232988t^{0.97}+0.0543842t^{1.94}+0.0126472t^{2.91},\\ {\mathrm{ℐ}}_D^{\delta }\left(t\right)=1.0+0.168962t^{0.97}+0.0128365t^{1.94}+0.00301015t^{2.91},\\ {\mathrm{ℐ}}_H^{\delta }\left(t\right)=1.0+0.0253951t^{0.97}+0.000645793t^{1.94}+0.0000163699t^{2.91},\\ {\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)=0.0+9.748634592703136\times {10}^{-8}{t}^{0.97}-2.173844324613856\times {10}^{-7}{t}^{1.94}+5.825026712347771\times {10}^{-7}{t}^{2.91},\\ {\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)=0.0+9.792059369532225\times {10}^{-8}{t}^{0.97}-2.3023365866009796\times {10}^{-7}{t}^{1.94}+6.067783798771481\times {10}^{-7}{t}^{2.91},\\ {\mathrm{ℛ}}_V^{\delta }\left(t\right)=0.994816t^{0.97}-0.775467t^{1.94}+0.0540038t^{2.91},\\ {\mathrm{ℛ}}_D^{\delta }\left(t\right)=0.0+0.015187t^{0.97}+0.00256603t^{1.94}+0.000127204t^{2.91},\\ {\mathcal{S}}^{\theta }\left(t\right)=40000+697.061t^{0.97}+19.4575t^{1.94}-0.00694976t^{2.91},\\ {\mathrm{ℐ}}_V^{\theta }\left(t\right)=15.0+1.30175t^{0.97}+0.237782t^{1.94}+0.00997563t^{2.91}.\end{array}$$ (46)

Series solution via the Caputo-Fabrizio derivative is given by eq. (47). Here all the parameter values as given in Table 1 were used.

$$\begin{array}{l}{\mathcal{S}}^{\delta }\left(t\right)=2.92894\times {10}^7+1991.07t-0.670143t^2-0.138522t^3,\\ {\mathrm{ℐ}}_V^{\delta }\left(t\right)=1.00695+0.226335t+0.0509495t^2+0.0111216t^3,\\ {\mathrm{ℐ}}_D^{\delta }\left(t\right)=1.00502+0.162611t+0.0120278t^2+0.00264702t^3,\\ {\mathrm{ℐ}}_H^{\delta }\left(t\right)=1.00075+0.0243666t+0.000594089t^2+0.0000143951t^3,\\ {\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)=2.712870748778392\times {10}^{-9}+8.252505019668144\times {10}^{-8}t-1.5200340503322315\times {10}^{-7}{t}^2+5.122340890403097\times {10}^{-7}{t}^3,\\ {\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)=2.7150880462399953\times {10}^{-9}+8.227282176372782\times {10}^{-8}t-1.6181662730296436\times {10}^{-7}{t}^2+5.335813653985\times {10}^{-7}{t}^3,\\ {\mathrm{ℛ}}_V^{\delta }\left(t\right)=0.0287975+0.909197t-0.707371t^2+0.0474892t^3,\\ {\mathrm{ℛ}}_D^{\delta }\left(t\right)=0.000452256+0.014696t+0.00236565t^2+0.000111859t^3,\\ {\mathcal{S}}^{\theta }\left(t\right)=40020.7+668.927t+17.8588t^2-0.00611139t^3,\\ {\mathrm{ℐ}}_V^{\theta }\left(t\right)=15.0388+1.26067t+0.219067t^2+0.00877225t^3.\end{array}$$ (47)

Series solution via the Atangana-Baleanu derivative is given by (48). Here all the parameter values as given in Table 1 were used.

$$\begin{array}{l}{\mathcal{S}}^{\delta }\left(t\right)=2.92894\times {10}^7+2051.53t^{0.97}-0.711698t^{1.94}-0.151527t^{2.91},\\ {\mathrm{ℐ}}_V^{\delta }\left(t\right)=1.00708+0.233265t^{0.97}+0.0541099t^{1.94}+0.0121657t^{2.91},\\ {\mathrm{ℐ}}_D^{\delta }\left(t\right)=1.00511+0.167562t^{0.97}+0.0127739t^{1.94}+0.00289555t^{2.91},\\ {\mathrm{ℐ}}_H^{\delta }\left(t\right)=1.00077+0.0251072t^{0.97}+0.00063074t^{1.94}+0.0000157467t^{2.91},\\ {\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)=2.7579384914179242\times {10}^{-9}+8.486010185015\times {10}^{-8}{t}^{0.97}-1.604826527624194\times {10}^{-7}{t}^{1.94}+5.603260923141627\times {10}^{-7}{t}^{2.91},\\ {\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)=2.7600149768101183\times {10}^{-9}+8.458917964913127\times {10}^{-8}{t}^{0.97}-1.70863697964998\times {10}^{-7}{t}^{1.94}+5.836775954633293\times {10}^{-7}{t}^{2.91},\\ {\mathrm{ℛ}}_V^{\delta }\left(t\right)=0.0292943+0.936007t^{0.97}-0.750898t^{1.94}+0.0519478t^{2.91},\\ {\mathrm{ℛ}}_D^{\delta }\left(t\right)=0.000460291+0.0151449t^{0.97}+0.00251169t^{1.94}+0.000122362t^{2.91},\\ {\mathcal{S}}^{\theta }\left(t\right)=40021.+689.258t^{0.97}+18.9598t^{1.94}-0.00668517t^{2.91},\\ {\mathrm{ℐ}}_V^{\theta }\left(t\right)=15.0395+1.29919t^{0.97}+0.232588t^{1.94}+0.00959585t^{2.91}.\end{array}$$ (48)

6.2. Simulating the different classes using different fractional derivatives

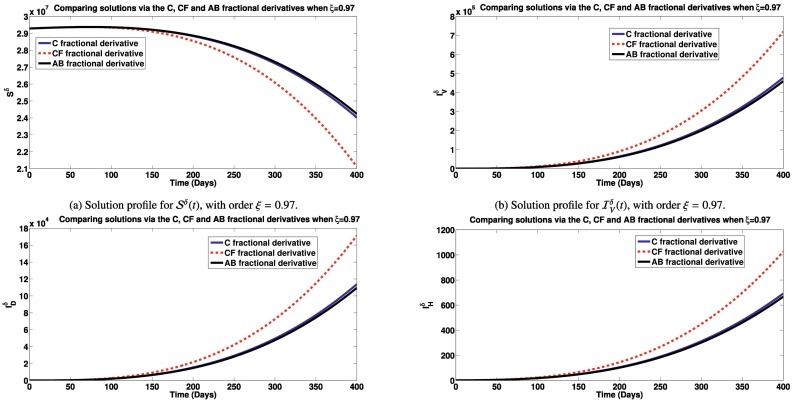
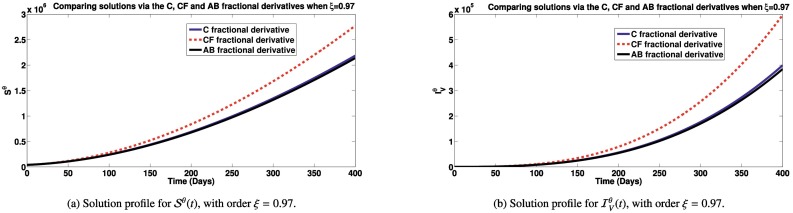
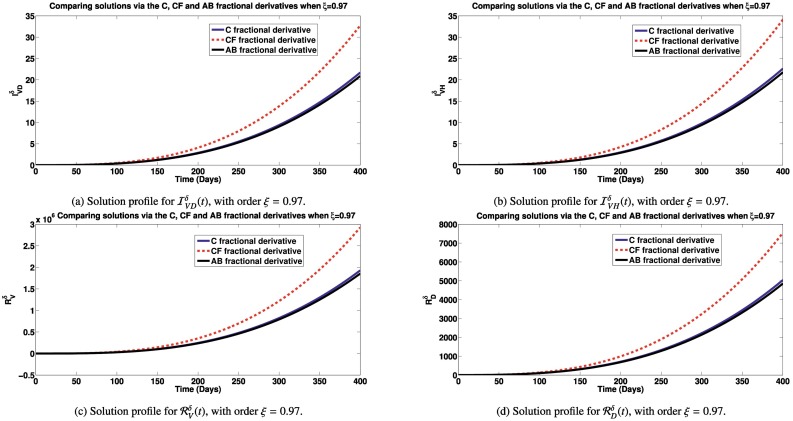
Here, we simulate the different classes in the model via Caputo, Caputo-Fabrizio and Atangana-Baleanu fractional derivatives to see how each derivative impact the dynamics of the model (2). Unless, otherwise stated in the plots description, the parameter values used are obtained from Table 1. In Figs. 2a – 4b, we present the various states of the model for different fractional operators. In Fig. 2a, the Simulations of the susceptible individuals for different fractional derivatives are presented. It is observed that, over time, the susceptible population decreases, under an endemic setting, with higher reduction recorded using the Caputo-Fabrizio derivative than with the Atangana-Baleanu and Caputo derivatives. Simulations of the individuals infected with SARS-CoV-2, dengue and HIV for different derivatives are presented in Fig. 2b, c and d, respectively. It is observed that, over time, lower number of infectious individuals are recorded using the Atangana-Baleanu derivative, followed by the Caputo-derivative derivative and then the Caputo-Fabrizio derivative. Our aim is to reduce the infection cases, using this model. Also, simulating the co-infected individuals with dual infections, for different fractional derivatives are shown by Fig. 3a and b. It is also observed that the Atangana-Baleanu derivative, records the lowest infections over time, in comparison with other fractional derivatives applied. The Atangana-Baleanu derivative gave us reduced number of infections over time, relative to Caputo and Caputo-Fabrizio derivative. Asamoah et al. [55] also recorded similar trend in the behavior of the AB derivative, when comparing simulations using the three fractional derivatives for a Q fever disease. Similar trend is observed for the classes of individuals who have recovered from SARS-CoV-2 and dengue as well as the population of susceptible vectors, as depicted by Figs. 3c, d and 4a. As for the total vector population with dengue (Fig. 4b), the Atangana-Baleanu derivative gave the least number as compared to simulations via Caputo and CF derivatives.

Fig. 2.

Solution profiles for ${\mathcal{S}}^{\delta }\left(t\right),{\mathrm{ℐ}}_V^{\delta }\left(t\right),{\mathrm{ℐ}}_D^{\delta }\left(t\right)$ and ${\mathrm{ℐ}}_H^{\delta }\left(t\right)$ via the different fractional derivatives. Parameters are exactly as given in Table 1.

Fig. 4.

Solution profiles for ${\mathcal{S}}^{\theta }\left(t\right)$ and ${\mathrm{ℐ}}_V^{\theta }\left(t\right)$via the different fractional derivatives. Parameters are exactly as given in Table 1.

Fig. 3.

Solution profiles for ${\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right),{\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right),{\mathrm{ℛ}}_V^{\delta }\left(t\right)$ and ${\mathrm{ℛ}}_D^{\delta }\left(t\right)$ via the different fractional derivatives. Parameters are exactly as given in Table 1.

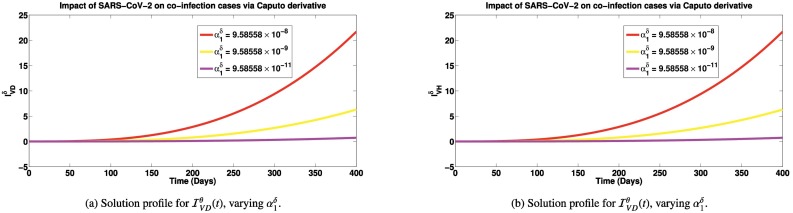
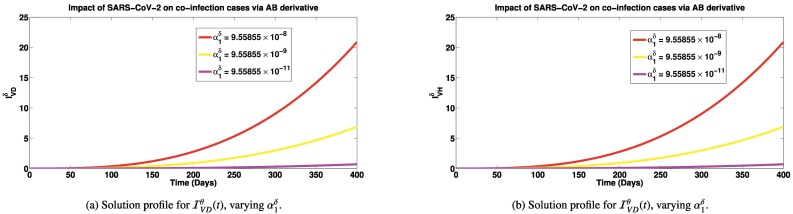
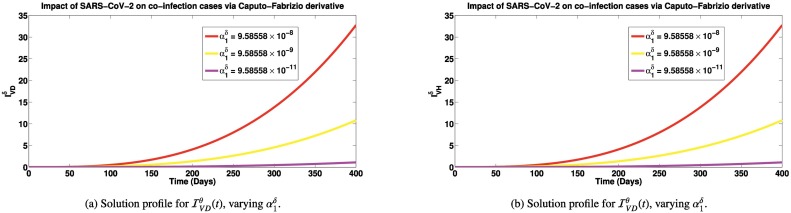
Simulations of the co-infected cases for different SARS-CoV-2 contact rates using the three fractional derivatives are presented in Figs. 5a-7b. It is observed in Fig. 5a, that as SARS-CoV-2 infection rate ${\alpha }_1^{\delta }$ decreases from $9.58558\times {10}^{-8}$ to $9.58558\times {10}^{-11}$, there is a significant reduction in the co-infected cases (number of persons having both SARS-CoV-2 and Dengue). Similar trend is also observed for individuals co-infected with SARS-CoV-2 and HIV (shown in Fig. 5b). In the introduction section, we have reported that patients co-infected with SARS-CoV-2 and dengue can suffer worsening illness, hospitalization and deaths [15], [17]. So reducing the co-infection of SARS-CoV-2 and dengue can cut down these worse cases in co-infected individuals. Also, we reported earlier, that individuals co-infected with SARS-CoV-2 and HIV are most likely to suffer severe illness and death [2]. Also, persons co-infected with HIV and SARS-CoV-2 infection can suffer great increase in cytokine production which could lead to increased viral load and subsequent immune suppression [2]. If co-infection cases are greatly reduced due to reduction in SARS-CoV-2 cases, then we shall equally have great reduction in cases of immune suppression and deaths which are direct consequences of the co-infection of both diseases. Similar reduction in co-infected cases are observed when the simulations are done via the Caputo-Fabrizio (presented in Fig. 6a and b) and Atangana-Baleanu derivatives (shown in Fig. 7a and b). The emphasis in these simulations is not to compare the results via the different derivatives, as done for the previous simulations, but to show that with any of the fractional derivatives, SARS-CoV-2 prevention can reduce worse co-infection cases with either Dengue or HIV.

Fig. 5.

Solution profiles for ${\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)$ and ${\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)$ via the Caputo fractional derivative. Here, $\xi =0.97$, while SARS-CoV-2 contact rate, ${\alpha }_1^{\delta }$ is varied. Other parameters are exactly as given in Table 1.

Fig. 7.

Solution profiles for ${\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)$ and ${\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)$ via the Atangana-Baleanu fractional derivative. Here, $\xi =0.97$, while SARS-CoV-2 contact rate, ${\alpha }_1^{\delta }$ is varied. Other parameters are exactly as given in Table 1.

Fig. 6.

Solution profiles for ${\mathrm{ℐ}}_{\mathit{VD}}^{\delta }\left(t\right)$ and ${\mathrm{ℐ}}_{\mathit{VH}}^{\delta }\left(t\right)$ via the Caputo Fabrizio fractional derivative. Here, $\xi =0.97$, while SARS-CoV-2 contact rate, ${\alpha }_1^{\delta }$ is varied. Other parameters are exactly as given in Table 1.

7. Conclusion

In this work, we have studied a new mathematical model for SARS-CoV-2, dengue and HIV co-dynamics, to assess the impact of SARS-CoV-2 infection on the dynamics of dengue and HIV via fractional derivatives. Some of the novelties of the current study are as follows: For the first time, we have considered a model for the co-dynamics of SARS-CoV-2, dengue and HIV. We have also considered three different fractional derivatives on this new complex model, and presented how SARS-CoV-2 could influence dengue and HIV. This has not been done before. The existence and uniqueness of solution is carried out using the Banach fixed point theorem. The stability analysis of the model is discussed in the context of Ulam-Hyers and generalized Ulam-Hyers criteria. We have applied the Laplace Adomian decomposition method, to investigate the model's approximate solutions, with the help of three different fractional derivatives, namely: Caputo, Caputo-Fabrizio and Atangana-Baleanu derivatives. We have equally established the stability of the iterative schemes for the solution of the developed model, applying some recent fixed point theorems. The model fittings, using the three fractional derivatives, were done using real data from Argentina. With the Caputo operator, the model fits well to data when the fractional order $\xi =0.97$. With the Caputo-Fabrizio operator, the model fits well to data when the fractional order $\xi =0.88$. Using the Atangana-Baleanu operator, the model fits well to data when the fractional order $\xi =0.97$. Although using both Caputo and AB operators, the model fits well to data when the order is $\xi =0.97$, the Caputo operator gave a better fit as compared to the AB operator. Simulations were also carried out with each non-integer derivative and the results thus obtained are compared. Furthermore, it was concluded that efforts to keep the spread of SARS-CoV-2 low, have a significant impact to reduce the co-infections of SARS-CoV-2 and dengue or SARS-COV-2 and HIV. We also highlighted the impact of the three fractional derivatives in analyzing complex models such as this novel co-infection model for the dynamics of three different diseases.

The current research has some limitations. In this study, so as to avoid model complexity, asymptomatic classes for SARS-CoV-2 and dengue were not considered. We also considered HIV infected compartment only without considering full blown AIDS class. These can be incorporated in a further study. In addition, Nothing is known about infection acquired or vaccine-derived cross-immunity between SARS-CoV-2, HIV and dengue. No detailed information yet, whether the current SARS-CoV-2 or dengue vaccines could have any impact on the dynamics of HIV. Thus, with more reliable data and detailed information about the interactions of the diseases, further study in this direction is much anticipated. Mutations of viral infections, including SARS-CoV-2 and dengue calls for further studies on their co-infections with other diseases. We could thus, consider a model for the co-dynamics of multi-strains of SARS-CoV-2 and dengue with HIV. Also, the proposed model in this current work did not consider triple co-infection. Future work with sufficient biological reports can also consider co-infection with the three diseases, which is possible [18]. For the data fitting, only SARS-CoV-2 daily reported data was used, as it was readily available. There was difficulty obtaining daily recorded cases for dengue and HIV. For a future study, we hope to fit the model to all the three data sets, as this will give better and more accurate estimates for the parameters, especially dengue and HIV associated parameters.

CRediT authorship contribution statement

Andrew Omame: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. Mujahid Abbas: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Supervision, Validation, Writing – original draft, Writing – review & editing. Abdel-Haleem Abdel-Aty: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – original draft, Writing – review & editing.

Declaration of competing interest

The authors show no conflict of interest to submit this paper.