Abstract
The origin of the peculiar amide spectral features of proteins in aqueous solution is investigated, by exploiting a combined theoretical and experimental approach to study UV Resonance Raman (RR) spectra of peptide molecular models, namely N-acetylglycine-N-methylamide (NAGMA) and N-acetylalanine-N-methylamide (NALMA). UVRR spectra are recorded by tuning Synchrotron Radiation at several excitation wavelengths and modeled by using a recently developed multiscale protocol based on a polarizable QM/MM approach. Thanks to the unparalleled agreement between theory and experiment, we demonstrate that specific hydrogen bond interactions, which dominate hydration dynamics around these solutes, play a crucial role in the selective enhancement of amide signals. These results further argue the capability of vibrational spectroscopy methods as valuable tools for refined structural analysis of peptides and proteins in aqueous solution.
Amide bands are considered sensitive probes of the secondary structures of proteins and peptides enabling prediction that provides a significant advance in the knowledge of protein activity and function. For this reason, vibrational spectroscopy experiments such as Infrared and Raman are well-established methods to identify and quantify distinct secondary structure motifs of proteins and polypeptides through exploration of the Amide fingerprint region.
The proper interpretation of ever more accurate experimental measurements makes the availability of reference studies analyzing the deep nature and physical origin of the spectroscopic response down to the atomistic detail highly desirable. N-Acetyl-glycine-methylamide (NAGMA) and N-acetyl-leucine-methylamide (NALMA) (see Figure 1) can be employed as minimal prototypes to model certain protein properties and behaviors.1−12 Compared to simple unmodified amino acids, both their C and N termini are modified to model the peptide bonding, while maintaining a small size and conformational flexibility; therefore, they are more suitable as “peptide models” than single amino acids, which do not exhibit the chemical heterogeneity and interactions that characterize a protein backbone. Being minimal models for larger molecular structures, they allow for extensive and highly detailed investigations into their physicochemical properties, both intrinsic and relating to their molecular environment, as well as the details of their spectroscopic properties,1,13−22 which is particularly crucial as advanced spectroscopic techniques are then applied to more complex biological polymers.
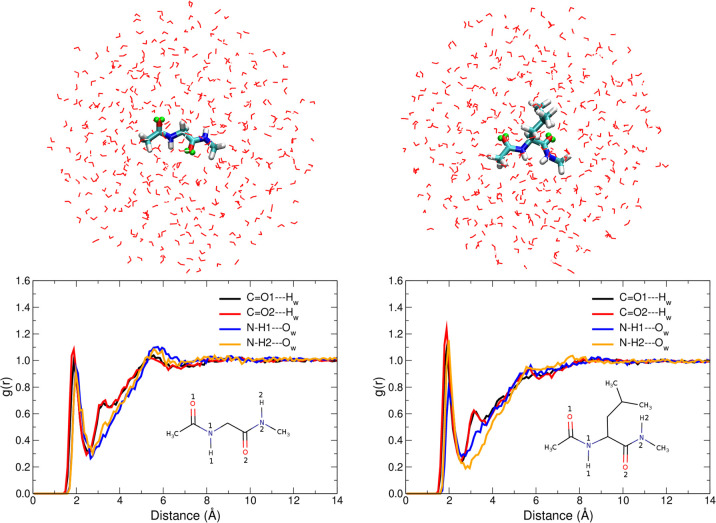
Figure 1.
Top: QM/FQ representation of NAGMA (left) and NALMA (right) in aqueous solution. Virtual sites (VS) in the C=O groups are depicted in green. VS are interaction sites constructed to improve the description of the hydrogen bonding. Bottom: Radial Distribution Functions (RDFs) for the intermolecular O···H interactions in solvated dipeptides.
The simplicity of the molecular models, however, hides the complexity that exists, as these systems are dissolved in aqueous solution, i.e. their physiological environment. Any attempt at modeling these peptides must therefore focus on the nature of solvation and its effects upon the properties of the systems. Indeed, the investigation of the hydration dynamics at hydrophilic and hydrophobic biomolecular sites of simple peptides has paved the way to appropriate models for understanding the dynamics of the first hydration shell of proteins.1,14,23
The unique combination of the capabilities of UV Resonance Raman (UVRR) spectroscopy (enhanced detection limit, high selectivity of specific chemical groups, no interfering signal of water solvent in the amide fingerprint spectral region)24−26 and the features of these small peptides result in local molecular probes for focusing on hydrogen bond (HB) rearrangements at specific sites of peptides, even under high diluted conditions. In this regard, it has already been shown22 that, due to the advantages of Synchrotron Radiation (SR)-based UVRR, the fine-tuning of the excitation wavelength allows the experimenter to select the best working conditions that ensure one can reliably detect the spectral changes of amide signals, as a function of peptide concentration and temperature.27,28 However, there are still some experimental features that are not fully understood. First, as also demonstrated in this work, a selective enhancement of the Amide II (AII) mode is experimentally observed at the shortest excitation wavelengths for both NAGMA and NALMA in aqueous solution and not for their microcrystalline form. Selectivity in this context means that excitation of π → π* transitions of the amide peptide bonds, lead to strong UVRR enhancement of Raman signals associated with the vibrations that have large components of C–N stretching, while smaller enhancement occurs for vibrations with strong C=O stretching. Second, Amide I (AI) and AII shapes and positions change going from microcrystalline/hydrated powders to solutions of both peptides. Third, in the measured spectra a dependence of wavenumbers of amide bands on concentration is reported. In this work, we explain the physical origin of the three aforementioned experimental findings, by interplaying experiments and simulations.
Often, simulations are unable to reproduce experimental findings of (Resonance) Raman spectra due to the intrinsic limitations in standard solvation models.29 Solvation affects molecular response properties both directly and indirectly by altering a molecule’s conformational landscape. The effects of solvation are commonly estimated either by implicit, continuum approaches or by simulation studies (MonteCarlo or Molecular Dynamics (MD)) in which the solvent molecules are explicitly considered in both the sampling and the calculation of the properties.30−34 Recently, some of the present authors have designed a multiscale computational protocol, combining MD and the Quantum Mechanics/Fluctuating Charges (QM/FQ) approach, a polarizable embedding model that keeps a fully atomistic representation of the solvent and provides accurate excitation energies and RR spectra of various systems, including small amides.35,36
Disentangling the role of each type of interaction in the generation of the UVRR spectra of these systems is a necessary first step if one hopes to fully rationalize and explain the spectroscopic behavior of peptides in aqueous solution, and due to the aforementioned complexities, this result can only be achieved by combining the highest possible level of techniques, both theoretical and experimental. To tackle these problems we therefore used the QM/FQ model in combination with SR-UVRR experiments at different excitation wavelengths and interpret, at the molecular level, the selective enhancement of the Amide II band experimentally detected at the shortest wavelengths. To this end, we performed extensive simulations using a hierarchy of solvation approaches on NAGMA and NALMA (see Computational Methods in the Supporting Information (SI)) and investigated the role of hydrogen bonding in the spectroscopic behavior of these systems, by comparing simulated results37,38 with the multiwavelengths experimental measurements made possible by the fine energy tunability of a SR source, which affords a much greater degree of flexibility compared to standard experimental setups, where the excitation radiation is provided by energy-fixed laser sources. Experimental procedure and terminology are part of the SI.
We began by examining the performance of QM/FQ, coupled to MD sampling, to describe UV–vis, Raman, and RR spectra of the two peptide systems (see Figure 1 for a picture of the representative systems used in the simulations). Furthermore, we evaluated gas phase, Polarizable Continuum Model (PCM), and cluster calculations as summarized in Table 1. All studied systems are depicted in Table S1 in the SI; their structural parameters are listed in Tables S2 and S3.
Table 1. Computed Vertical Excitation Wavelengths (in nm) for NAGMA and NALMA in Different Environments, Calculated at the B3LYP/6-311++G(d, p) Level of Theoryc.
| Absorption
maxima (nm) |
|||
|---|---|---|---|
| Motif | Environment | NAGMA | NALMA |
| Monomer C5 | Gas phase | 200.4, 180.5 | 190.1 |
| Monomer C7 | Gas phase | 196.6 | 196.0 |
| Monomer β2 | Gas phase | 194.6 | 200.2 |
| Monomer C5 | PCM | 178.9 | 184.1 |
| Monomer C7 | PCM | 182.6 | 187.9 |
| Monomer β2 | PCM | 184.5 | 189.0 |
| Monomer + 4W | PCM | 181.7 | 183.8 |
| Solution (366:1) | QM/MM NP | 174.0 | 177.3 |
| Solution (366:1) | QM/FQa | 175.2 | 178.5 |
| Solution (366:1) | QM/FQb | 175.3 | 177.5 |
| Solution (366:1) | QM/QMw/FQ | 178.3 | 181.5 |
| Dimer | Gas phase | 197.0 | 199.5 |
| Dimer solvated | Gas phase | 190.9 | 193.9 |
Due to their conformational flexibility, NAGMA and NALMA monomers may feature intramolecular HBs. Consistent with previous reports,8,10,12 we found that in the gas phase the stable conformers are located mainly in C5 (βL) and C7 (γ) regions, while solvent effects increase the prevalence of minima in the α and β2 (δL) regions. Ramachandran maps in Figure S2 in the SI indicate that β2 is the most representative conformer sampled by MD runs.
In dilute aqueous solution intramolecular hydrogen bonds compete with intermolecular interactions between solute and solvent, with the latter becoming dominant, as supported by the intra- and intermolecular radial distribution functions (RDFs) for the O···H contacts and by the HB strength estimated using Natural Bond Orbitals (NBO)44 (Figures S3 and S4 in the SI). Intermolecular RDFs are shown in Figure 1. For both molecules, the C=O and N–H groups of the backbone are involved in the same number of HBs (2, 1 each). Building upon this observation, we have saturated all potential HB sites using 4 water molecules to build what is generally called a “supermolecule” (see Table S1 in the SI).
Despite sharing some features, the maxima in the RDFs are always located at slightly shorter distances for NAGMA, confirming that the strength of the solute–solvent interactions is higher for NAGMA than for NALMA, due to the hydrophobic residue in the latter. This finding is consistent with the detected wavenumber shift between AI and AII signals in the UVRR spectra of NAGMA and NALMA that reflects a different strength of peptide–solvent interactions for the two peptides.22
Considering that strong UVRR intensities are to be expected when properly tuning excitation wavelengths, we calculated the UV–vis spectra of both molecules in the different environments considered in this study. Table 1 lists vertical excitation energies in each case. The bands in the electronic absorption spectra are very similar in appearance (Figure S5 in the SI), with the aqueous solution bands being blue-shifted by up to 20 nm relative to C7, the most stable conformer in the gas phase. In contrast, and regardless of the solvent representation, slight differences (5 nm at most) are noted in the case of the aqueous solution. We assign the strong electronic absorption band computed at ∼180 nm (190 nm is the experimental report) for both systems as the π → π* transition based on prior studies40 and the orbitals involved (Figure S6 in the SI). Thereupon, excitation within this absorption band will give rise to enhancements of the peptide bond vibrations.
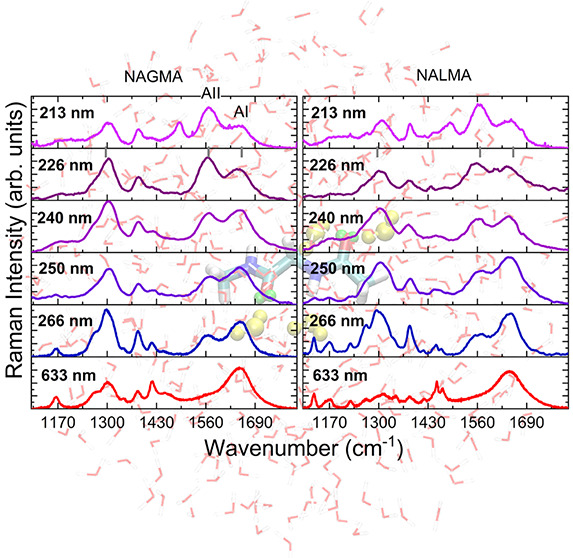
Raman (Far From Resonance, FFR) and UVRR spectra of solvated NAGMA and NALMA are displayed in Figure 2. At first glance, all the typical vibrational features can be recognized in both the measured and computed spectra, namely, (i) the presence of the Amide I (AI) band with a Raman signal around 1650 cm–1 which is mainly associated with the stretching vibration of the C=O of the amide linkage in the peptide backbone; (ii) the Raman signal at ∼1560 cm–1, assigned to the Amide II (AII) and resulting by the out-of-phase combination of N–H bending and C–N stretching movements of the groups in the amide linkage; and (iii) the Amide III (AIII) band, whose vibrational mode is mostly due to the in-phase combination of N–H bending and C–N stretching and which appears around 1260 cm–1. Notice that in the FFR visible spectra of peptides the Amide II mode is completely absent (as expected), while in the UVRR spectra this band clearly appears even in preresonance conditions (excitation wavelength at 266 nm). Normal modes are drawn in Figures S7 and S8 in the SI.
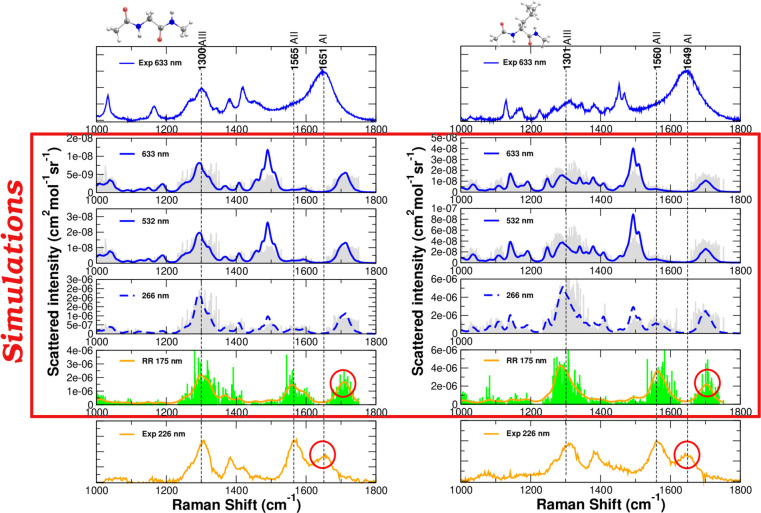
Figure 2.
Raman (blue) and Resonance Raman (orange) spectra of NAGMA and NALMA, left and right panels, respectively. Experimental spectra were measured at room temperature in aqueous solution at a concentration which corresponds to 366 molecules of water for each molecule of peptide. QM/FQ results for spontaneous (Far From Resonance) and Resonance Raman spectra were broadened using Lorentzian functions with an fwhm of 8 and 20 cm–1 respectively. RR intensities were calculated with a damping factor of 200 cm–1. Sticks in the simulated spectra are also included. The dashed blue curve indicates a preresonance condition.
The above results show that the mutually polarizable QM/FQ approach describes well Raman and RR spectra of the two systems, while fairly preserving positions and relative intensities, unlike results in PCM or using cluster/supermolecule approaches (see Figure S9 in the SI). However, it can be noted that when the FQ parameters taken from ref (42) are utilized, the accuracy in predicting AI band position is not entirely satisfactory (see red circles in Figure 2). One direction of improvement could be the usage of a different parametrization, where electrostatics and polarization effects are more accurately accounted for in the QM Hamiltonian.43 In fact, when FQb parameters are used, AI and AII bands approach each other, thus moving computed results toward experimental data (Figure S10 in the SI). Detailed analysis of the normal modes obtained with the parameters of ref (43) suggests that AI and AII modes are coupled.
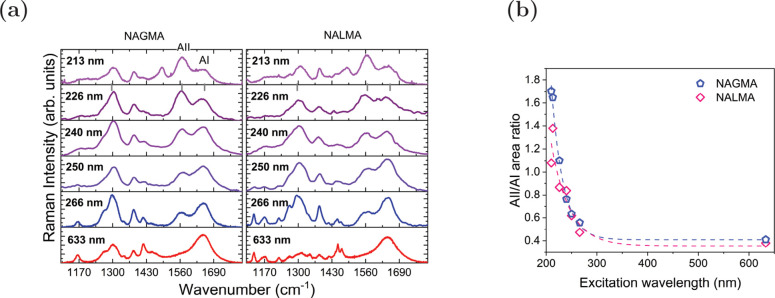
From the UVRR spectra in Figure 2, AI, AII, and AIII are the signals found to be particularly affected by the resonance enhancement, making their simultaneous measurement the ideal experimental target to be used to directly determine protein secondary structure.45 Nevertheless, the experimental scanning along the excitation wavelength reveals a selective enhancement of the AII mode at the shortest wavelengths, as shown in Figure 3a. This feature has been already pointed out in literature for peptides and proteins22,46,47 and is also relevant here, even though it is slightly more intense for NAGMA than for NALMA (compare for example spectra at 226 and 213 nm in Figure 3a) as can be seen in the ratio of the areas in Figure 3b. Interestingly, such an effect is observed only for solutions of peptides and not for the microcrystalline form of the molecules (see Figure S11 in the SI). This latter experimental evidence suggests a crucial role played by the hydration shell around the peptides in determining the spectral features of Amide Raman signals.
Figure 3.
Experimental results for NAGMA and NALMA dissolved in water at a concentration corresponding to 366 molecules of water for each molecule of peptide (a) FFR and UVRR spectra collected using different excitation wavelengths ranging from visible to deep UV energies. (b) Estimated ratio of the areas of amide modes AII/AI as a function of the excitation wavelength.
An explanation for the selective AII intensity increase has been proposed48 in terms of the stabilization of the ground state dipolar resonance structure −O–C=NH2+ that becomes more favored in aqueous solution with respect to the O=C–NH2 resonance form that lacks charge separation. Thus, the formation of HBs at the amide and carbonyl sites leads to a contraction of the C–N distance (see Table S2 in the SI) and the vibrations having significant contributions from the C–N stretching mode, namely, amide I, II, and III, will have appreciable intensity enhancements in the Raman lines. Our calculations of resonance structures using Natural Resonance Theory (NRT)49 indicate that 3 out of 4 main NAGMA resonance hybrids favor the dipolar form, namely, negative charges in the O atoms and positive charges on the N atoms (Figure S12 in the SI), and more importantly, the percentage values of all the hybrids bearing formal charges increase in solution. Indeed, when explicit water molecules are considered, dipolar structures become the leading resonance hybrids (Table S4 in the SI). The special preference for enhancing AII when excitation wavelengths approach the maxima in the absorption spectra might be further analyzed based on the orbitals involved in the in-plane π → π* transition. Computing 15 TD-DFT excited states on dipeptides structures revealed that the excited states with the highest oscillator strengths have an important charge transfer contribution, predominantly from HOMO and HOMO–1 to a wide assortment of virtual orbitals. For glycine and leucine dipeptides in solution, such states have larger contributions from the C–N regions of the molecules (Figure S6 in the SI). In addition, it is evident from inspection of Figure S6 (in the SI) that the orbitals involved not only belong to the solute but also involve the nearest water molecules, thus implying that charge transfer between peptides and solvent is an active component of molecular orbitals contributing to the 190 nm band. In view of the above findings, modeling the selective enhancement would require the inclusion of a few solvent molecules in the QM portion of the system.
Computed Resonance Raman Excitation Profiles (RREPs) are shown in the SI, Figures S13–S17 and S18–S22, for NAGMA and NALMA, respectively. The ratio between the areas of AI and AII in the simulated spectra using excitation wavelengths ranging from 633 to 166 nm is plotted in Figure S23 in the SI. Although QM/FQ with the two sets of parameters gives reasonable descriptions of the spectra, both parametrizations produce always an AI band with higher intensity and area than AII, leading to discrepancies when compared to the experiments. Conversely, it seems to be an important trend for the resonance enhancement of AII in the modeled RREPs of solvated NAGMA in the supermolecule case.
According to our molecular
dynamics simulations and those reported
by Boopathi and Kolandaive,6 an average
of two and three water molecules form persistent interactions with
NALMA and NAGMA dipeptides, respectively. Also, it is well-known that
the pattern of the relative intensities of the amide bands is determined
by the properties in the electronic excited states for the various
conformations.45,47 Hence, to gain a deeper insight
into the effect of these solvent molecules on the selective intensity
alteration, we have investigated the intensity dependence on the exciting
frequency of the AII by quantum-mechanically treating all water molecules
that fulfill at least one of the following geometric criteria: 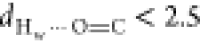 Å or
Å or 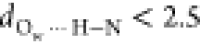 Å, hereafter noted as the
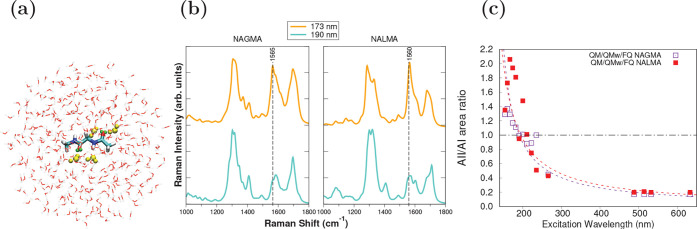
QM/QMw/FQ approach (details in Table S5 in the SI). This is graphically
depicted in Figure 4b for NAGMA. A better reproduction of the experimental trend shown
in Figure 3a was found
when explicit water molecules are part of the QM layer, as seen in Figure 4b for two selected
wavelengths. Furthermore, there is excellent agreement between the
ratio of the areas, dashed curves in Figure 4c, and its experimental counterpart, Figure 3b. This constitutes
an important piece of evidence of the role of hydrogen bonding and,
specifically, its quantum-mechanical covalent component, in the intensity
enhancement because just with solvent molecules linked to the C=O
and N–H groups, the distances within the peptide are properly
modified. Moreover, the orbitals of the transition are more concentrated
in the C–N regions of the molecules, which ultimately triggers
the enhancement. Regarding the NALMA case, the selective enhancement
is seen in the QM/QMw/FQ solvation model
only. So, we deduce that there is a similar solvation behavior for
the two peptides and that the hydrophilic part of the two molecules
dominates the spectral properties, in addition to the solvation dynamics
explained in ref (22).
Å, hereafter noted as the
QM/QMw/FQ approach (details in Table S5 in the SI). This is graphically
depicted in Figure 4b for NAGMA. A better reproduction of the experimental trend shown
in Figure 3a was found
when explicit water molecules are part of the QM layer, as seen in Figure 4b for two selected
wavelengths. Furthermore, there is excellent agreement between the
ratio of the areas, dashed curves in Figure 4c, and its experimental counterpart, Figure 3b. This constitutes
an important piece of evidence of the role of hydrogen bonding and,
specifically, its quantum-mechanical covalent component, in the intensity
enhancement because just with solvent molecules linked to the C=O
and N–H groups, the distances within the peptide are properly
modified. Moreover, the orbitals of the transition are more concentrated
in the C–N regions of the molecules, which ultimately triggers
the enhancement. Regarding the NALMA case, the selective enhancement
is seen in the QM/QMw/FQ solvation model
only. So, we deduce that there is a similar solvation behavior for
the two peptides and that the hydrophilic part of the two molecules
dominates the spectral properties, in addition to the solvation dynamics
explained in ref (22).
Figure 4.
Computational results obtained with the QM/QMw/FQ approach applied to NAGMA and NALMA in aqueous solution. (a) Representative structure, where selected water molecules (in yellow) are part of the QM portion. (b) Comparison between UVRR spectra simulated at 173 and 190 nm. (c) Computed ratio of the areas of the amide modes AII/AI as a function of excitation wavelength.
Next, the different shapes and positions for AI and AII are studied by focusing on the UVRR spectra of the microcrystalline forms (Figure S11 in the SI), hydrated powders (Figure S24 in the SI), and solvated (Figure 2) samples. Explicitly in the amides region, some clear distinctions are evident: on one hand, a significant difference in the shape of AI for the two peptides, with probably two subcomponents with slight changes in frequency and relative intensity. Such an experimental splitting of the AI band (NAGMA case) is also recovered by the calculated spectra and explained by having a look at the normal modes, where two sets of C=O oscillators (see modes 21 and 22) with slightly different strengths can be identified. In contrast, they are more compactly gathered in the NALMA case. This observation is in line with the two types of C=O···H interactions found in the hydration patterns (Figure S3 in the SI), due to the arrangements of the molecules’ backbone. On the other hand, it is also observed from Figure S24 in the SI that the position of Amide II (AII) has a red shift of about 5 cm–1 in the NALMA case. We recall here that the effect of the hydrophobic portion of NALMA is the lengthening of the N–H···Ow distances with respect to NAGMA, thus affecting the N–H bending associated with that band.
Finally, in order to rationalize the concentration-dependence of wavenumber positions, it is worth mentioning that at high dilution conditions, like those in our simulations, solute–solute interactions are weak (see NBO interaction energies, Figure S4 in the SI) and then the C=O is expected to be more involved in HBs with solvent molecules. In particular, it has been seen22 that for concentrations ≤50 mg/mL of both molecules in water (i.e., 144 molecules of water for each molecule of peptide), the position of the AI band becomes strongly dependent on concentration (severe red shift upon the increment of water content). Based upon the NRT results (Figure S12 and Table S4 in the SI), we argue that in aqueous solution, with the stabilization of the dipolar resonance structures, the double bond is more localized between C and N, leading to a shortening of the C–N bond and in turn to a lengthening of the C=O bond. Therefore, the force constant of a bond having a stronger single character compared to the resonance form that does not have a charge separation induces a decrease in the oscillation frequency for the C=O stretching and so a red shift of AI. The same explanation would apply for the concentration-dependent trend of AII in concentrations >50 mg/mL (144:1 water/peptide) where probably the solute–solute interactions become important. Aggregation propensities of these peptides in solution have been examined before in the literature.4 Here, we explore solute···solute interactions through an approximate treatment, namely, the dimeric and solvated dimeric forms of NAGMA and NALMA. Their modeled RR can be found in Figure S25 in the SI. While in the UVRR spectra of concentrated dipeptide solutions it is reported22 that there are no significant changes in the AI frequency position, AII, arising from the combination of C–N stretching and N–H bending motions, experiences a slightly monotonic blue shift, likely due to the strengthening of the C–N bond, which causes an increase in the force constant and, in turn, in the oscillation frequency. To verify the reliability of these arguments, we carefully checked the distances of the C=O and C–N in Tables S2 and S3 in the SI and concluded that, in all our representations of the solvent, the C=O and C–N bond lengths are actually longer and shorter, respectively, compared to the isolated cases. Consequently, it is again verified that the solvent does play a role in determining the positions, shapes, and intensities of the RR bands, as also pointed out by some authors.28,50−52
In summary, the interplay of computational and experimental data highlights two important observations: (i) The selective enhancement of the amides signals is hydrogen bonding-induced because it is intimately linked to the effect that water molecules exert on the C=O and N–H, C–N vibrations. We demonstrated that the inclusion of explicit water molecules concentrates the orbitals involved in the charge transfer in the C–N zones, which ultimately leads to the strong UVRR enhancement of vibrations that have large components of C–N stretching, particularly the AII signal. Thus, quantum effects must be present in any modeling of the solute–solvent interactions of RR spectroscopy for such systems. The unprecedented accordance found between the theoretical calculation and experimentally collected Raman and Resonance Raman spectra further testifies the reliability of our model. (ii) Due to the constant movement of the solute and its surrounding water molecules, a single snapshot (or cluster composed of the solute and some surrounding water molecules) is not representative of the dynamical nature of the system and can lead to heavily biased results if taken to be representative for the ensemble, which is more correctly modeled through an explicit average over a large set of structures. Through our investigation we put forward an explanation at the molecular level of the origin of the selective enhancements, emphasizing the crucial role of the backbone conformations and the dynamics of their surrounding waters. These results provide an important starting point to calibrate wavenumbers and intensities of the experimental Amide signals for the quantitative determination of structural parameters of protein and peptide in solutions. A key requirement of computational approaches to be truly useful and complementary for experimental measurements is the ability to properly describe and reproduce spectral features, and not just the energetics of a system. We have shown that the QM/QMw/FQ fulfills this by promisingly going beyond standard methodologies based on more crude approximations and is, therefore, expected to open up new possibilities for novel applications in a truly synergistic partnership with advanced experimental techniques applied to biologically relevant samples, as well as shed new light regarding the details of physicochemical phenomena that characterize the functioning of life. In this respect, our study could be also extended to Raman Optical Activity (ROA) spectroscopy, which, due to its sensitivity to chirality, constitutes an alternative to Raman/Resonance Raman when examining the structure and behavior of peptides, proteins, and biomolecules.53−56
Acknowledgments
We acknowledge Elettra Sincrotrone Trieste for providing access to its synchrotron radiation facilities and for financial support (Proposal Number 20200432). We thank A. Gessini and M. Tortora for assistance in using beamline IUVS. This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 818064). We gratefully acknowledge the Center for High Performance Computing (CHPC) at SNS for providing the computational infrastructure.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.2c01277.
Description of the experimental and computational methods, structural analysis, hydration patterns, measured and calculated spectra, Resonance Raman Excitation profiles, normal modes. (PDF)
Author Present Address
¶ Software for Chemistry & Materials BV, De Boelelaan 1083, 1081 HV Amsterdam, The Netherlands
The authors declare no competing financial interest.
Supplementary Material
References
- Qvist J.; Halle B. Thermal Signature of Hydrophobic Hydration Dynamics. J. Am. Chem. Soc. 2008, 130, 10345–10353. 10.1021/ja802668w. [DOI] [PubMed] [Google Scholar]
- Murarka R. K.; Head-Gordon T. Single Particle and Collective Hydration Dynamics for Hydrophobic and Hydrophilic Peptides. J. Chem. Phys. 2007, 126, 215101. 10.1063/1.2737050. [DOI] [PubMed] [Google Scholar]
- Johnson M. E.; Malardier-Jugroot C.; Murarka R. K.; Head-Gordon T. Hydration Water Dynamics Near Biological Interfaces. J. Phys. Chem. B 2009, 113, 4082–4092. 10.1021/jp806183v. [DOI] [PubMed] [Google Scholar]
- Nerenberg P. S.; Jo B.; So C.; Tripathy A.; Head-Gordon T. Optimizing Solute–Water van der Waals Interactions To Reproduce Solvation Free Energies. J. Phys. Chem. B 2012, 116, 4524–4534. 10.1021/jp2118373. [DOI] [PubMed] [Google Scholar]
- Panuszko A.; Pieloszczyk M.; Kuffel A.; Jacek K.; Biernacki K. A.; Demkowicz S.; Stangret J.; Bruździak P. Hydration of Simple Model Peptides in Aqueous Osmolyte Solutions. Int. J. Mol. Sci. 2021, 22, 9350. 10.3390/ijms22179350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boopathi S.; Kolandaivel P. Molecular Dynamics Simulations and Density Functional Theory Studies of NALMA and NAGMA Dipeptides. J. Biomol. Struct. Dyn. 2013, 31, 158–173. 10.1080/07391102.2012.698380. [DOI] [PubMed] [Google Scholar]
- Perczel A.; Angyan J. G.; Kajtar M.; Viviani W.; Rivail J. L.; Marcoccia J. F.; Csizmadia I. G. Peptide Models. 1. Topology of Selected Peptide Conformational Potential Energy Surfaces (Glycine and Alanine Derivatives). J. Am. Chem. Soc. 1991, 113, 6256–6265. 10.1021/ja00016a049. [DOI] [Google Scholar]
- Gould I. R.; Cornell W. D.; Hillier I. H. A Quantum Mechanical Investigation of the Conformational Energetics of the Alanine and Glycine Dipeptides in the Gas Phase and in Aqueous Solution. J. Am. Chem. Soc. 1994, 116, 9250–9256. 10.1021/ja00099a048. [DOI] [Google Scholar]
- Bisetty K.; Catalan J. G.; Kruger H. G.; Perez J. J. Conformational Analysis of Small Peptides of the Type Ac–X–NHMe, where X= Gly, Ala, Aib and Cage. J. Mol. Struct.: THEOCHEM 2005, 731, 127–137. 10.1016/j.theochem.2005.04.037. [DOI] [Google Scholar]
- Masman M. F.; Lovas S.; Murphy R. F.; Enriz R. D.; Rodríguez A. M. Conformational Preferences of N-Acetyl-l-leucine-N’-methylamide. Gas-Phase and Solution Calculations on the Model Dipeptide. J. Phys. Chem. A 2007, 111, 10682–10691. 10.1021/jp0716886. [DOI] [PubMed] [Google Scholar]
- Leavitt C. M.; Moore K. B. III; Raston P. L.; Agarwal J.; Moody G. H.; Shirley C. C.; Schaefer H. F. III; Douberly G. E. Liquid Hot NAGMA Cooled to 0.4 K: Benchmark Thermochemistry of a Gas-Phase Peptide. J. Phys. Chem. A 2014, 118, 9692–9700. 10.1021/jp5092653. [DOI] [PubMed] [Google Scholar]
- Cormanich R. A.; Rittner R.; Buehl M. Conformational Preferences of Ac-Gly-NHMe in Solution. RSC Adv. 2015, 5, 13052–13060. 10.1039/C4RA16472E. [DOI] [Google Scholar]
- Russo D.; Murarka R. K.; Copley J. R.; Head-Gordon T. Molecular View of Water Dynamics near Model Peptides. J. Phys. Chem. B 2005, 109, 12966–12975. 10.1021/jp051137k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russo D.; Ollivier J.; Teixeira J. Water Hydrogen Bond Analysis on Hydrophilic and Hydrophobic Biomolecule Sites. Phys. Chem. Chem. Phys. 2008, 10, 4968–4974. 10.1039/b807551b. [DOI] [PubMed] [Google Scholar]
- Born B.; Weingärtner H.; Bründermann E.; Havenith M. Solvation Dynamics of Model Peptides Probed by Terahertz Spectroscopy. Observation of the Onset of Collective Network Motions. J. Am. Chem. Soc. 2009, 131, 3752–3755. 10.1021/ja808997y. [DOI] [PubMed] [Google Scholar]
- Murarka R. K.; Head-Gordon T. Dielectric Relaxation of Aqueous Solutions of Hydrophilic versus Amphiphilic Peptides. J. Phys. Chem. B 2008, 112, 179–186. 10.1021/jp073440m. [DOI] [PubMed] [Google Scholar]
- Mazur K.; Heisler I. A.; Meech S. R. Ultrafast Dynamics and Hydrogen-Bond Structure in Aqueous Solutions of Model Peptides. J. Phys. Chem. B 2010, 114, 10684–10691. 10.1021/jp106423a. [DOI] [PubMed] [Google Scholar]
- Perticaroli S.; Comez L.; Paolantoni M.; Sassi P.; Morresi A.; Fioretto D. Extended Frequency Range Depolarized Light Scattering Study of N-Acetyl-leucine-methylamide–Water Solutions. J. Am. Chem. Soc. 2011, 133, 12063–12068. 10.1021/ja202272k. [DOI] [PubMed] [Google Scholar]
- Perticaroli S.; Nakanishi M.; Pashkovski E.; Sokolov A. P. Dynamics of Hydration Water in Sugars and Peptides Solutions. J. Phys. Chem. B 2013, 117, 7729–7736. 10.1021/jp403665w. [DOI] [PubMed] [Google Scholar]
- Comez L.; Lupi L.; Morresi A.; Paolantoni M.; Sassi P.; Fioretto D. More Is Different: Experimental Results on the Effect of Biomolecules on the Dynamics of Hydration Water. J. Phys. Chem. Lett. 2013, 4, 1188–1192. 10.1021/jz400360v. [DOI] [PubMed] [Google Scholar]
- Comez L.; Perticaroli S.; Paolantoni M.; Sassi P.; Corezzi S.; Morresi A.; Fioretto D. Concentration Dependence of Hydration Water in a Model Peptide. Phys. Chem. Chem. Phys. 2014, 16, 12433–12440. 10.1039/c4cp00840e. [DOI] [PubMed] [Google Scholar]
- Rossi B.; Catalini S.; Bottari C.; Gessini A.; Masciovecchio C. In UV and Higher Energy Photonics: From Materials to Applications 2019, Frontiers of UV Resonant Raman Spectroscopy by Using Synchrotron Radiation: The Case of Aqueous Solvation of Model Peptides; Lérondel G., Cho Y.-H., Taguchi A., Kawata S., Eds.; SPIE: 2019; Vol. 11086; pp 23–32. [Google Scholar]
- Russo D.; Teixeira J.; Kneller L.; Copley J. R. D.; Ollivier J.; Perticaroli S.; Pellegrini E.; Gonzalez M. A. Vibrational Density of States of Hydration Water at Biomolecular Sites: Hydrophobicity Promotes Low Density Amorphous Ice Behavior. J. Am. Chem. Soc. 2011, 133, 4882–4888. 10.1021/ja109610f. [DOI] [PubMed] [Google Scholar]
- Efremov E. V.; Ariese F.; Gooijer C. Achievements in Resonance Raman Spectroscopy: Review of a Technique with a Distinct Analytical Chemistry Potential. Anal. Chim. acta 2008, 606, 119–134. 10.1016/j.aca.2007.11.006. [DOI] [PubMed] [Google Scholar]
- Chowdhury J. In Molecular and Laser Spectroscopy, Chapter 7 - Resonance Raman Spectroscopy: Principles and Applications; Gupta V., Ed.; Elsevier: 2018; pp 147–164. [Google Scholar]
- Rossi B.; Bottari C.; Catalini S.; D’Amico F.; Gessini A.; Masciovecchio C. In Molecular and Laser Spectroscopy, Chapter 13 - Synchrotron-based Ultraviolet Resonance Raman Scattering for Material Science; Gupta V., Ozaki Y., Eds.; Elsevier: 2020; pp 447–482. [Google Scholar]
- Catalini S.; Rossi B.; Tortora M.; Foggi P.; Gessini A.; Masciovecchio C.; Bruni F. Hydrogen Bonding and Solvation of a Proline-Based Peptide Model in Salt Solutions. Life 2021, 11, 824. 10.3390/life11080824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catalini S.; Rossi B.; Foggi P.; Masciovecchio C.; Bruni F. Aqueous Solvation of Glutathione Probed by UV Resonance Raman Spectroscopy. J. Mol. Liq. 2019, 283, 537–547. 10.1016/j.molliq.2019.03.113. [DOI] [Google Scholar]
- Egidi F.; Bloino J.; Cappelli C.; Barone V. A Robust and Effective Time-Independent Route to the Calculation of Resonance Raman Spectra of Large Molecules in Condensed Phases with the Inclusion of Duschinsky, Herzberg–Teller, Anharmonic, and Environmental Effects. J. Chem. Theory Comput. 2014, 10, 346–363. 10.1021/ct400932e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giovannini T.; Egidi F.; Cappelli C. Molecular Spectroscopy of Aqueous Solutions: A Theoretical Perspective. Chem. Soc. Rev. 2020, 49, 5664–5677. 10.1039/C9CS00464E. [DOI] [PubMed] [Google Scholar]
- Giovannini T.; Lafiosca P.; Cappelli C. A General Route to Include Pauli Repulsion and Quantum Dispersion Effects in QM/MM Approaches. J. Chem. Theory Comput. 2017, 13, 4854–4870. 10.1021/acs.jctc.7b00776. [DOI] [PubMed] [Google Scholar]
- Giovannini T.; Riso R. R.; Ambrosetti M.; Puglisi A.; Cappelli C. Electronic Transitions for a Fully Polarizable QM/MM Approach Based on Fluctuating Charges and Fluctuating Dipoles: Linear and Corrected Linear Response Regimes. J. Chem. Phys. 2019, 151, 174104. 10.1063/1.5121396. [DOI] [PubMed] [Google Scholar]
- Egidi F.; Giovannini T.; Del Frate G.; Lemler P. M.; Vaccaro P. H.; Cappelli C. A Combined Experimental and Theoretical Study of Optical Rotatory Dispersion for (R)-glycidyl methyl ether in Aqueous Solution. Phys. Chem. Chem. Phys. 2019, 21, 3644–3655. 10.1039/C8CP04445G. [DOI] [PubMed] [Google Scholar]
- Gómez S.; Giovannini T.; Cappelli C. Absorption Spectra of Xanthines in Aqueous Solution: A Computational Study. Phys. Chem. Chem. Phys. 2020, 22, 5929–5941. 10.1039/C9CP05420K. [DOI] [PubMed] [Google Scholar]
- Gómez S.; Rojas-Valencia N.; Giovannini T.; Restrepo A.; Cappelli C. Ring Vibrations to Sense Anionic Ibuprofen in Aqueous Solution as Revealed by Resonance Raman. Molecules 2022, 27, 442. 10.3390/molecules27020442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gómez S.; Egidi F.; Puglisi A.; Giovannini T.; Rossi B.; Cappelli C. Unlocking the Power of Resonance Raman Spectroscopy: The Case of Amides in Aqueous Solution. J. Mol. Liq. 2021, 117841. [Google Scholar]
- Guthmuller J.; Champagne B. Resonance Raman Scattering of Rhodamine 6G as Calculated by Time-Dependent Density Functional Theory: Vibronic and Solvent Effects. J. Phys. Chem. A 2008, 112, 3215–3223. 10.1021/jp7112279. [DOI] [PubMed] [Google Scholar]
- Santoro F.; Cappelli C.; Barone V. Effective Time-Independent Calculations of Vibrational Resonance Raman Spectra of Isolated and Solvated Molecules Including Duschinsky and Herzberg–Teller Effects. J. Chem. Theory Comput. 2011, 7, 1824–1839. 10.1021/ct200054w. [DOI] [PubMed] [Google Scholar]
- Mark P.; Nilsson L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. B 2001, 105, 9954–9960. 10.1021/jp003020w. [DOI] [Google Scholar]
- Oladepo S. A.; Xiong K.; Hong Z.; Asher S. A. Elucidating Peptide and Protein Structure and Dynamics: UV Resonance Raman Spectroscopy. J. Phys. Chem. Lett. 2011, 2, 334–344. 10.1021/jz101619f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asher S. A.; Chi Z.; Li P. Resonance Raman Examination of the Two Lowest Amide ππ* Excited States. J. Raman Spectrosc. 1998, 29, 927–931. . [DOI] [Google Scholar]
- Rick S. W.; Stuart S. J.; Berne B. J. Dynamical Fluctuating Charge Force Fields: Application to Liquid Water. J. Chem. Phys. 1994, 101, 6141–6156. 10.1063/1.468398. [DOI] [Google Scholar]
- Giovannini T.; Lafiosca P.; Chandramouli B.; Barone V.; Cappelli C. Effective yet Reliable Computation of Hyperfine Coupling Constants in Solution by a QM/MM Approach: Interplay between Electrostatics and Non-Electrostatic Effects. J. Chem. Phys. 2019, 150, 124102. 10.1063/1.5080810. [DOI] [PubMed] [Google Scholar]
- Weinhold F.; Landis C.; Glendening E. What Is NBO Analysis and How Is It Useful?. Int. Rev. Phys. Chem. 2016, 35, 399–440. 10.1080/0144235X.2016.1192262. [DOI] [Google Scholar]
- Chi Z.; Chen X.; Holtz J. S.; Asher S. A. UV Resonance Raman-Selective Amide Vibrational Enhancement: Quantitative Methodology for Determining Protein Secondary Structure. Biochemistry 1998, 37, 2854–2864. 10.1021/bi971160z. [DOI] [PubMed] [Google Scholar]
- Harada I.; Sugawara Y.; Matsuura H.; Shimanouch T. Preresonance Raman Spectra of Simple Amides using Ultraviolet Lasers. J. Raman Spectrosc. 1975, 4, 91–98. 10.1002/jrs.1250040110. [DOI] [Google Scholar]
- Sugawara Y.; Harada I.; Matsuura H.; Shimanouchi T. Preresonance Raman Studies of poly(L-lysine), poly(L-glutamic acid), and Deuterated N-methylacetamides. Biopolymers 1978, 17, 1405–1421. 10.1002/bip.1978.360170603. [DOI] [Google Scholar]
- Punihaole D.; Jakubek R. S.; Dahlburg E. M.; Hong Z.; Myshakina N. S.; Geib S.; Asher S. A. UV Resonance Raman Investigation of the Aqueous Solvation Dependence of Primary Amide Vibrations. J. Phys. Chem. B 2015, 119, 3931–3939. 10.1021/jp511356u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glendening E. D.; Badenhoop J.; Weinhold F. Natural Resonance Theory: III. Chemical Applications. J. Comput. Chem. 1998, 19, 628–646. . [DOI] [Google Scholar]
- Manas E. S.; Getahun Z.; Wright W. W.; DeGrado W. F.; Vanderkooi J. M. Infrared Spectra of Amide Groups in α-Helical Proteins: Evidence for Hydrogen Bonding between Helices and Water. J. Am. Chem. Soc. 2000, 122, 9883–9890. 10.1021/ja001782z. [DOI] [Google Scholar]
- Mikhonin A. V.; Bykov S. V.; Myshakina N. S.; Asher S. A. Peptide Secondary Structure Folding Reaction Coordinate: Correlation between UV Raman Amide III Frequency, Ψ Ramachandran Angle, and Hydrogen Bonding. J. Phys. Chem. B 2006, 110, 1928–1943. 10.1021/jp054593h. [DOI] [PubMed] [Google Scholar]
- Myshakina N. S.; Ahmed Z.; Asher S. A. Dependence of Amide Vibrations on Hydrogen Bonding. J. Phys. Chem. B 2008, 112, 11873–11877. 10.1021/jp8057355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nafie L. A.Vibrational Optical Activity: Principles and Applications; John Wiley & Sons: 2011. [Google Scholar]
- Nafie L. A. Vibrational Optical Activity: From Discovery and Development to Future Challenges. Chirality 2020, 32, 667–692. 10.1002/chir.23191. [DOI] [PubMed] [Google Scholar]
- Barron L. D.Molecular Light Scattering and Optical Activity; Cambridge University Press: 2009. [Google Scholar]
- Berova N.; Polavarapu P. L.; Nakanishi K.; Woody R. W.. Comprehensive Chiroptical Spectroscopy: Applications in Stereochemical Analysis of Synthetic Compounds, Natural Products, and Biomolecules; John Wiley & Sons: 2012; Vol. 2. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.