HOMOTOPY CONTINUATION FOR THE SPECTRA OF PERSISTENT LAPLACIANS

Abstract

The p-persistent q-combinatorial Laplacian defined for a pair of simplicial complexes is a generalization of the q-combinatorial Laplacian. Given a filtration, the spectra of persistent combinatorial Laplacians not only recover the persistent Betti numbers of persistent homology but also provide extra multiscale geometrical information of the data. Paired with machine learning algorithms, the persistent Laplacian has many potential applications in data science. Seeking different ways to find the spectrum of an operator is an active research topic, becoming interesting when ideas are originated from multiple fields. In this work, we explore an alternative approach for the spectrum of persistent Laplacians. As the eigenvalues of a persistent Laplacian matrix are the roots of its characteristic polynomial, one may attempt to find the roots of the characteristic polynomial by homotopy continuation, and thus resolving the spectrum of the corresponding persistent Laplacian. We consider a set of simple polytopes and small molecules to prove the principle that algebraic topology, combinatorial graph, and algebraic geometry can be integrated to understand the shape of data.

1. Introduction.

Recent years witness the burst of advanced mathematical tools for data science [27, 22, 31, 12]. Persistent homology has been proved to be a powerful tool in analyzing the geometry shape and topological persistence of data [8, 10]. It has had much success in machine learning [7, 23, 26] ([7] is one of the first papers that combine persistent homology with machine learning), computational chemistry [31] and biology [29, 36, 25]. The methods of persistent homology start with constructing a filtration of simplicial complexes from the data so that multiscale geometrical information can be extracted thereafter from the computations of a family of topological invariants. Persistent homology is a quite informative method, since it can detect features that are persistent over a wide range of scales, rather than features that depend on a particular choice of parameters. Inspired by the theory of persistent homology, one recent generalization of a classical operator to its persistent version is the so-called persistent combinatorial Laplacian or persistent Laplacian for simplicity [34].

The applications of Laplace operators are ubiquitous in mathematics, physics, and data science. The graph Laplacian has been a fundamental concept in the study of graphs, partly because the spectrum of the graph Laplacian contains the topological information of the graph [11]. As one can think of a graph as a 1-dimensional simplicial complex and define the graph Laplacian as a sum of compositions of boundary operators, one can readily define a more general Laplacian called the combinatorial Laplacian for a high dimensional simplicial complex. The persistent combinatorial Laplacian, defined for a pair of simplicial complexes K ↪ L, is an extension of the aforementioned combinatorial Laplacian. When a filtration is given, it is natural to compute persistent Laplacians, and one may ask how persistent Laplacian and persistent homology are related. It turns out that the nullity of a persistent Laplacian is equal to the corresponding persistent Betti number (see Theorem 2.11). Moreover, nonzero eigenvalues and eigenvectors of a persistent Laplacian contain extra geometrical information of the filtration, and can be used to resolve a challenge about protein flexibility [34], therefore the theory of persistent Laplacian is a powerful tool for data analysis. Persistent Laplacians can be computed by software package HERMES [35].

Although the spectrum of an operator can be numerically computed in different ways, seeking new ways to calculate the spectrum of an operator is an active research topic [2]. In addition to the traditional methods of numerical linear algebra, one may alternatively resolve the spectrum by finding the roots of the characteristic polynomial associated with the operator. Homotopy continuation is an interesting method for solving a single polynomial or systems of polynomial equations. The essential idea is to build a homotopy between the system to be solved (called the target system) and an easier system with known roots (called the start system) and track down the known roots of the start system to the roots of the target system. As systems of polynomial equations arise in mathematics, science, and engineering, homotopy continuation methods have found applications in various areas, such as algebraic geometry [19, 20], robot kinematics [33], optimal control [3], differential equations [1, 17], and biology [14, 16, 28]. Several software packages implement homotopy continuation methods, such as Bertini [4], HomotopyContinuation.jl [6], Hom4PS-3 [9], and PHCpack [32].

In this work, we propose to solve the spectra of persistent Laplacians using homotopy continuation. In Section 2, we present the theory of persistent homology and persistent Laplacian. In section 3, we briefly explain how homotopy continuation works. In Section 4, we give a proof of principle application of our approach to some simple polytopes and small molecules. Our goal is to stimulate further research at the interface of algebraic geometry, algebraic topology, combinatorial graph, and data science. We use HERMES [35] to calculate the matrix representations of persistent Laplacians and then use Bertini [4] to find the roots of their associated characteristic polynomials. We hope this work can exposit the theory of persistent Laplacian and shed some light on the potential application of homotopy continuation methods in data science.

2. Persistent homology and persistent Laplacian.

In this section, we introduce basics of persistent homology and persistent Laplacian. Readers familiar with persistent homology can skip the subsection on simplicial homology and persistent homology. As to subsections on different versions of Laplacians, Proposition 1, Theorem 2.10, Theorem 2.11, and many examples can be skipped on a first read, as they are not directly related to the main contribution of this paper.

2.1. Simplicial homology and persistent homology.

We present here a very short introduction of persistent homology to establish concepts and notations [10].

Definition 2.1 (Simplex).

A q-simplex denoted as σ_q = [u₀,..., u_q] is the convex hull of q+1 affinely independent points {u₀,..., u_q} in ${ℝ}^n$. The orientation of σ_q is determined by the ordering of the vertices {u₀,..., u_q} and two orderings define the same orientation if and only if they differ by an even permutation. The dimension of σ_q = [u₀,..., u_q] is defined as q. For 0 ≤ i ≤ n, $\left[u_0,\dots ,{\widehat{u}}_i,\dots ,u_q\right]$ is said to be a face of σ_q, where the hat indicates the omission of the vertex.

Definition 2.2 (Simplicial complex).

A finite set of simplices, K, is a simplicial complex if the following conditions are satisfied: (1) all faces of any simplex in K are also in K; (2) the non-empty intersection of any two simplices in K is a common face of the two simplices. The dimension of a simplicial complex K is defined as the maximal dimension of its simplices.

Another important notion is the abstract simplicial complex.

Definition 2.3 (Abstract simplicial complex).

Suppose we have a finite collection of sets called K. For any set σ in K, if all subsets of σ are also in K, K is said to be an abstract simplicial complex. Subsets of σ are called faces of σ.

The notions of abstract simplicial complex and simplicial complex are closely related. One may build a simplicial complex from an abstract simplicial complex or vice versa [10]. They contain exactly the same combinatorial information. From now on we will not distinguish abstract simplicial complexes from simplicial complexes.

Definition 2.4 (Chain complex).

Suppose we have a simplicial complex K. For any q, the formal sums of all q-simplices with coefficients in a field, for instance ${\mathbb{Z}}_2$, form an abelian group denoted by C_q(K). Such a group is called a chain group and the elements of it are called q-chains. The boundary operator ∂_q : C_q(K) → C_q−1(K) is defined as

$${\partial }_q\left[u_0,\dots ,u_q\right]=\sum _{i=0}^q{(-1)}^i\left[u_0,\dots ,{\widehat{u}}_i,\dots ,u_q\right].$$

For simplicity we usually omit the subscript q and only write ∂. The collection of boundary operators and chain groups forms the so called chain complex of K

$$\cdots \stackrel{{\partial }_{q+2}}{\to }{C}_{q+1}(K)\stackrel{{\partial }_{q+1}}{\to }{C}_q(K)\stackrel{{\partial }_q}{\to }{C}_{q-1}(K)\stackrel{{\partial }_{q-1}}{\to }\cdots .$$

As ∂² = 0, the homology group H_q is defined as ker ∂_q/im∂_q−1. The rank of H_q is called the q^th Betti number and denoted by β_q.

Definition 2.5 (Cochain complex).

Given a chain complex

$$\cdots \stackrel{{\partial }_{q+2}}{\to }{C}_{q+1}(K)\stackrel{{\partial }_{q+1}}{\to }{C}_q(K)\stackrel{{\partial }_q}{\to }{C}_{q-1}(K)\stackrel{{\partial }_{q-1}}{\to }\cdots ,$$

the dual spaces C^q(K) of C_q(K) and dual maps d of ∂ form a cochain complex

$$\cdots \stackrel{{\partial }_{q+2}^{*}}{\leftarrow }{C}^{q+1}(K)\stackrel{{\partial }_{q+1}^{*}}{\leftarrow }{C}^q(K)\stackrel{{\partial }_q^{*}}{\leftarrow }{C}^{q-1}(K)\stackrel{{\partial }_{q-1}^{*}}{\leftarrow }\cdots$$

where ${\partial }_i^{*}$ is called a coboundary operator. The cohomology group H^q is defined as $\ker {\partial }_{q+1}^{*}/\mathrm{im}{\partial }_q^{*}$. As C_q(K) is formally generated by q-simplices, there is a canonical isomorphism between C_q(K) and C^q(K) such that any simplex σ is identified with σ^∗.

Definition 2.6 (Filtration).

A filtration $X=\left\{X_r\mid r\in ℝ\right\}$ is a series of finite simplicial complexes indexed over real numbers such that X_a ⊂ X_b if a ≤ b. When X is a finite set, we say that it is a finite filtration.

A filtration can be constructed in various ways from a set of points in ${ℝ}^d$.

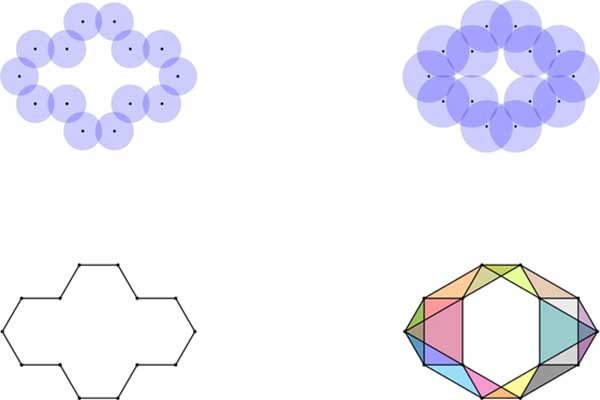
Example 2.1 (Rips complex).

The Rips complex is an abstract simplicial complex. Given a set $S\subset {ℝ}^d$ and a radius r, if a subset T of S has the property that the distance between any pair of points in T is at most 2r, then T is include in the Rips complex (see figure 2).

FIGURE 2.

Rips complexes corresponding to different r values.

Example 2.2 (Alpha complex).

Now we build an alpha complex from a finite set $S\subset {ℝ}^d$. First we define the Voronoi cell. The Voronoi cell of a point u in S is

$$V_u=\left\{x\in {ℝ}^d\mid \Vert x-u\Vert \le \Vert x-v\Vert ,v\in S\right\}.$$

Let B_u(r) be the closed ball with center u and radius r. Denote the intersection B_u(r) ∩ V_u by R_u(r). Then the alpha complex is defined as

$$\mathrm{Alpha}(r)=\left\{\sigma \subset S\mid \underset{u\in \sigma }{\cap }{R}_u(r)\ne \varnothing \right\}.$$

In other words, Alpha(r) is the nerve of cover {R_u(r), u ∈ S}. Let r go from 0 to the diameter of S, then we get a filtration of alpha complexes.

Definition 2.7 (Persistent Betti number).

Suppose a finite filtration X = {X_t | t ∈ T} is given. The inclusion X_t ↪ X_t+p induces a homomorphism

$$f_q^{t,p}:H_q\left(X_t\right)\to H_q\left(X_{t+p}\right)$$

on the simplicial homology groups for each dimension q. The q^th persistent homology groups are the images of such homomorphisms, and the q^th persistent Betti numbers ${\beta }_q^{t,p}$ are the ranks of persistent homology groups.

2.2. Graph Laplacian.

Let G(V, E) be a simple graph with V = {v_i} the vertex set and E the edge set.

Definition 2.8.

The Laplacian matrix $\mathcal{L}$ (also called the graph Laplacian) of G is defined as

$${\mathcal{L}}_{ij}=\{\begin{array}{ll}\mathrm{deg}{v}_i,\hfill & \text{if}i=j\hfill \\ -1,\hfill & \text{if}i\ne j\text{and}{v}_i\text{is}\text{adjacent}\text{to}{v}_j\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$

Example 2.3.

Take a 2-simplex [a, b, c]. Its graph Laplacian is

$$\begin{array}{c}a\\ b\\ c\end{array}\stackrel{\begin{array}{ccc}a& b& c\end{array}}{\left(\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right)}.$$

The Laplacian matrix is a symmetric positive semi-definite matrix. The topology of a graph can be inferred from the spectrum of the graph Laplacian. For instance, the number of connected components of a graph G is equal to the algebraic multiplicity of 0 in its graph Laplacian. The second smallest eigenvalue of a graph Laplacian is called the Fiedler value and can be regarded as a measure of topological connectivity. See [37] for more results concerning the graph Laplacian.

2.3. Combinatorial Laplacian.

Recall there is a canonical isomorphism between C^q(K) and C_q(K). The q-combinatorial Laplacian Δ_q : C_q(K) → C_q(K) is defined as

$${\mathrm{\Delta }}_q={\partial }_{q+1}{\partial }_{q+1}^{*}+{\partial }_q^{*}{\partial }_q,$$ (1)

and ${\mathrm{\Delta }}_0={\partial }_1{\partial }_1^{*}$. Alternatively, we may equip C_q(K) with an inner product ⟨·, ·⟩ such that for any two simplices σ_i and σ_j, ⟨σ_i, σ_j⟩ = δ_ij. Then one may regard ${\partial }_{q+1}^{*}$ as the adjoint map with respect to this inner product. Denote the matrix representation of the boundary operator ∂_q by ${\mathcal{B}}_q$, then the matrix representation ${\mathcal{L}}_q$ of Δ_q is

$${\mathcal{B}}_{q+1}{\mathcal{B}}_{q+1}^T+{\mathcal{B}}_q^T{\mathcal{B}}_q.$$ (2)

As the combinatorial Laplacian is symmetric and positive semi-definite, its spectrum consists of non-negative real eigenvalues.

Example 2.4.

_{${\mathcal{L}}_0$} coincides with Δ₀. Take a 2-simplex [a, b, c]. ${\mathcal{B}}_1$ is

$$\begin{array}{c}a\\ b\\ c\end{array}\stackrel{\begin{array}{ccc}ab& bc& ca\end{array}}{\left(\begin{array}{ccc}-1& 0& -1\\ 1& -1& 0\\ 0& 1& 1\end{array}\right)}\text{.}$$

Then

$$\left(\begin{array}{ccc}-1& 0& -1\\ 1& -1& 0\\ 0& 1& 1\end{array}\right)\left(\begin{array}{ccc}-1& 1& 0\\ 0& -1& 1\\ -1& 0& 1\end{array}\right)=\left(\begin{array}{ccc}2& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right),$$

i.e., ${\mathcal{B}}_1{\mathcal{B}}_1^T={\mathcal{L}}_0$.

Definition 2.9.

Two q-simplices σ_i, σ_j are said to be lower adjacent, denoted by ${\sigma }_i\stackrel{L}{~}{\sigma }_j$, if they share a common (q − 1)-face. They are said to be upper adjacent, denoted by ${\sigma }_i\stackrel{U}{~}{\sigma }_j$, if they both are faces of a (q + 1)-simplex. The lower degree deg_L(σ) of a q-simplex σ is q +1, the number of its (q −1)-faces. The upper degree deg_U(σ) of a q-simplex σ is defined as the number of (q+1)-simplices in K of which σ is a face. The degree of q-simplex σ is defined as

$${\mathrm{deg}}_U(\sigma )+{\mathrm{deg}}_L(\sigma )={\mathrm{deg}}_U(\sigma )+q+1.$$

Now suppose ${\sigma }_i\stackrel{U}{~}{\sigma }_j$ with common upper (q+1)-simplex τ. Let’s examine the signs of the coefficients of σ_i, σ_j in ∂_τ. We say that σ_i and σ_j are similarly oriented if the signs are the same; dissimilarly oriented if the signs are different. Next suppose ${\sigma }_i\stackrel{L}{~}{\sigma }_j$ with common lower (q − 1)-simplex η. Let’s examine the signs of the coefficients of η in ∂σ_i and ∂σ_j. We say that η is a similar common lower simplex of σ_i and σ_j if the signs are the same; a dissimilar common lower simplex if the signs are different.

The following proposition gives an explicit formula for ${\mathcal{L}}_q$.

Proposition 1.

[13, Thm. 3.3.4] Suppose we have a finite simplicial complex K and its set of q-simplices is {σ₁,..., σ_n}.

1. When q = 0,

$${\mathcal{L}}_{ij}=\{\begin{array}{ll}{\mathrm{deg}}_U{\sigma }_i,\hfill & \text{if}i=j\hfill \\ -1,\hfill & \text{if}i\ne j\text{and}{\sigma }_i\stackrel{U}{~}{\sigma }_j\hfill \\ 0,\hfill & \text{if}i\ne j\text{and}{\sigma }_i\stackrel{U}{\nsim }{\sigma }_j\hfill \end{array}$$

1. If q > 0, then

$${\mathcal{L}}_{ij}=\{\begin{array}{ll}{\mathrm{deg}}_U{\sigma }_i+q+1,\hfill & \text{if}i=j\hfill \\ 1,\hfill & \text{if}i\ne j,{\sigma }_i\stackrel{U}{\nsim }{\sigma }_j\text{and}\text{have}\text{a}\text{similar}\text{common}\hfill \\ \hfill & \text{lower}\text{simplex}\hfill \\ -1,\hfill & \text{if}i\ne j,{\sigma }_i\stackrel{U}{\nsim }{\sigma }_j\text{and}\text{have}\text{a}\text{dissimilar}\text{common}\hfill \\ \hfill & \text{lower}\text{simplex}\hfill \\ \hfill & \text{if}i\ne j\text{and}\text{either}{\sigma }_i\text{and}{\sigma }_j\text{are}\text{upper}\text{adjacent}\hfill \\ 0,\hfill & \text{or}\text{are}\text{not}\text{lower}\text{adjacent}\hfill \end{array}$$

The kernel of a combinatorial Laplacian contains topological information. We have

$${\beta }_q=\dim \ker {\partial }_q-\mathrm{dimim}{\partial }_{q+1}=\dim \ker {\mathrm{\Delta }}_q.$$ (3)

Later we will prove a generalized version of the above equality for persistent Laplacians.

2.4. Persistent Laplacian.

Suppose we have two simplicial complexes K_t ⊂ K_t+p from a filtration and boundary operators ${\partial }_q^t:C_q\left(K_t\right)\mapsto C_{q-1}\left(K_t\right)$ and ${\partial }_{q+1}^{t+p}:C_{q+1}\left(K_{t+p}\right)\mapsto C_q\left(K_{t+p}\right)$. From now on we use $C_q^t$ to denote C_q(K_t) for simplicity. Bearing in mind the inclusion map from $C_q^t$ to $C_q^{t+p}$, we define

$${ℂ}_{q+1}^{t,p}=\left\{e\in C_{q+1}^{t+p}\mid {\partial }_{q+1}^{t+p}(e)\in C_q^t\right\},$$

i.e., ${ℂ}_{q+1}^{t,p}$ consists of elements whose images under ${\partial }_{q+1}^{t+p}$ are in $C_q^t$. One can define an inner product ⟨·, ·⟩ on $C_q^t$ such that for any two simplices σ_i and σ_j, ⟨σ_i, σ_j⟩ = δ_ij. Denote ${{\partial }_{q+1}^{t+p}|}_{{ℂ}_{q+1}^{t,p}}$ as ${ð}_{q+1}^{t,p}$. As ${ℂ}_{q+1}^{t,p}$ inherits the inner product from $C_{q+1}^{t+p}$, the adjoint map ${\left({ð}_{q+1}^{t,p}\right)}^{*}$ of ${ð}_{q+1}^{t,p}$ is well defined. The p-persistent q-combinatorial Laplacian operator [34] is defined as

$${\mathrm{\Delta }}_q^{t,p}={ð}_{q+1}^{t,p}{\left({ð}_{q+1}^{t,p}\right)}^{*}+{\left({\partial }_q^t\right)}^{*}{\partial }_q^t.$$ (4)

Theorem 2.10.

[The matrix representation of ${\mathrm{\Delta }}_q^{t,p}$] [34, 24] Suppose we pick up a basis {v₁,··· ,v_m} of ${ℂ}_{q+1}^{t,p}$ and the associated inner product matrix is P. Let ${\mathcal{B}}_{q+1}^{t,p}$ be the matrix representation of ${ð}_{q+1}^{t,p}$ with respect to {v₁,··· , v_m} and the canonical basis of $C_q^t$, ${\mathcal{B}}_q^t$ the matrix representation of ${\partial }_q^t$ with respect to the canonical bases of $C_q^t$ and $C_{q-1}^t$. Then the matrix representation ${\mathcal{L}}_q^{t,p}$ of ${\mathrm{\Delta }}_q^{t,p}$ is

$${\mathcal{B}}_{q+1}^{t,p}{P}^{-1}{\left({\mathcal{B}}_{q+1}^{t,p}\right)}^T+{\left({\mathcal{B}}_q^t\right)}^T{\mathcal{B}}_q^t.$$ (5)

Proof.

Denote the matrix representation of the adjoint map ${\left({ð}_{q+1}^{t,p}\right)}^{*}$ by X. It suffices to determine X. Take two vectors $v\in {ℂ}_{q+1}^{t,p}$, $w\in C_q^t$. We abuse the notation a bit and use v, w to denote their coordinates in the form of column vector as well. We have

$${\langle {ð}_{q+1}^{t,p}v,w\rangle }_{C_q^t}={\langle v,{\left({ð}_{q+1}^{t,p}\right)}^{*}w\rangle }_{{ℂ}_{q+1}^{t,p}}$$

$${\left({\mathcal{B}}_{q+1}^{t,p}v\right)}^{T}w=v^{T}PXw$$

$$v^T{\left({\mathcal{B}}_{q+1}^{t,p}\right)}^{T}w=v^{T}PXw.$$

As v, w are arbitrarily taken, we conclude that $X=P^{-1}{\left({\mathcal{B}}_{q+1}^{t,p}\right)}^T$. □

Example 2.5.

Consider the ordered point set

$$\left\{\left(0,0,0.001\right),\left(3,-4,-0.001\right),\left(6,0,0.001\right),\left(3,4,-0.001\right),\left(11,0,0.001\right)\right\}.$$

From now on we denote these points as 0, 1, 2, 3, and 4 according to the order and we omit brackets and commas in the notation of any simplex. For example, the simplex [(0, 0, 0.001), (3, −4, −0.001)] will be denoted as 01. Using GUDHI [15] we can build the filtration K of alpha complexes up to 9.77:

$$\begin{array}{l}\{(0,1,2,3,4\to 0.00),(14,02,23,04,34\to 6.25),(24\to 9.00),\\ (024,234\to 9.77)\},\end{array}$$

where (0, 1, 2, 3, 4 → 0.00) means that K₀ = {0, 1, 2, 3, 4} and (14, 02, 23, 04, 34 → 6.25) means that K_6.25 = K₀ ∪ {14, 02, 23, 04, 34} and so on. Let’s first calculate ${\mathcal{L}}_1^{6.25,3.52}$. ${\mathcal{B}}_1^{6.25}$ is equal to

$$\begin{array}{c}0\\ 1\\ 2\\ 3\\ 4\end{array}\stackrel{\begin{array}{ccccc}14& 02& 23& 04& 34\end{array}}{\left(\begin{array}{lllll}0\hfill & -1\hfill & 0\hfill & -1\hfill & 0\hfill \\ -1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & -1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill & -1\hfill \\ 1\hfill & 0\hfill & 0\hfill & -1\hfill & 1\hfill \end{array}\right).}$$

${\mathcal{B}}_2^{9.77}$ is equal to

$$\begin{array}{c}14\\ 02\\ 23\\ 04\\ 34\\ 24\end{array}\stackrel{\begin{array}{cc}024& 234\end{array}}{\left(\begin{array}{cc}0& 0\\ 1& 0\\ 0& 1\\ -1& 0\\ 0& 1\\ 1& -1\end{array}\right)}\text{.}$$

Note that $24\notin C_1^{6.25}$. It is easy to see that $\mathrm{span}\{024+234\}={ℂ}_2^{6.25,3.52}$. So ${\mathcal{B}}_2^{6.25,3.52}$ is equal to

$$\begin{array}{c}14\\ 02\\ 23\\ 04\\ 34\end{array}\stackrel{\begin{array}{c}024+234\end{array}}{\left(\begin{array}{c}0\\ 1\\ 1\\ -1\\ 1\end{array}\right)}$$

and P is equal to ⟨024 + 234, 024 + 234⟩. So ${\mathcal{L}}_1^{6.25,3.52}$ is equal to

$$\left(\begin{array}{ccccc}2& 0& 0& 1& 1\\ 0& 2.5& -0.5& 0.5& 0.5\\ 0& -0.5& 2.5& -0.5& -0.5\\ 1& 0.5& -0.5& 2.5& 0.5\\ 1& 0.5& -0.5& 0.5& 2.5\end{array}\right).$$

Example 2.6.

Consider the graph

and the filtration {(1, 2 → 0), (3, 4, 13, 34, 42 → 1)}. Let’s compute ${\mathcal{L}}_0^{0,1}$. ${\mathcal{B}}_1^1$ is equal to

$$\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\stackrel{\begin{array}{ccc}13& 34& 42\end{array}}{\left(\begin{array}{ccc}-1& 0& 0\\ 0& 0& 1\\ 1& -1& 0\\ 0& 1& -1\end{array}\right)}.$$

After a few steps of Gauss elimination we get

$$\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\stackrel{\begin{array}{ccc}13& 13+34& 13+34+42\end{array}}{\left(\begin{array}{ccc}-1& -1& -1\\ 0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)}.$$

It is clear that ${ℂ}_1^{0,1}=\mathrm{span}\{13+34+42\}$, P = 3 and ${\mathcal{B}}_1^{0,1}$ is equal to

$$\begin{array}{c}1\\ 2\end{array}\stackrel{13+34+42}{\left(\begin{array}{c}-1\\ 1\end{array}\right)}.$$

Then ${\mathcal{L}}_0^{0,1}$ is

$$\left(\begin{array}{cc}1/3& -1/3\\ -1/3& 1/3\end{array}\right).$$

Its spectrum is {0, 2/3}.

As stated earlier, now we prove the theorem that connects the nullity of persistent Laplacian with persistent Betti number.

Theorem 2.11 (Persistent Betti numbers from persistent Laplacians).

[34, 24] Given a filtration K of simplicial complexes, for any positive integer q, we have

$${\beta }_q^{t,p}=nullity\left({\mathrm{\Delta }}_q^{t,p}\right).$$ (6)

To prove Theorem 2.11, we need the following lemma.

Lemma 2.12.

[21] Suppose A : U → V and B : V → W are two linear maps where U, V and W are inner product spaces. We have

1. ker(A^∗) = im(A)^⊥;

2. ker(A^∗A) = ker A;

3. If BA = 0, then

   $$\ker \left(A{A}^{*}+B^{*}B\right)=\ker \left(A^{*}\right)\cap \ker (B);$$
4. If BA = 0, then

   $$\ker (B)/\mathrm{im}(A)\cong \ker (B)\cap \ker \left(A^{*}\right);$$

5. If BA = 0, then from 4) and 5) we know

$$\ker (B)/\mathrm{im}(A)\cong \ker \left(A{A}^{*}+B^{*}B\right).$$

Proof.

1. If x ∈ im(A)^⊥, then for any y ∈ V,

   $$0=\langle x,Ay\rangle =\langle A^{*}x,y\rangle .$$
   So A^∗x = 0. If x ∈ ker(A^∗), then for any y ∈ V,

   $$0=\langle A^{*}x,y\rangle =\langle x,Ay\rangle .$$

   So x ∈ im(A)^⊥.

2. ⊃: obvious; ⊂: Let v ∈ ker(A^∗A), then

   $$0=\langle A^{*}Av,v\rangle =\langle Av,Av\rangle ,$$

   implying Av = 0.

3. ⊃: obvious; ⊂: Let v ∈ ker(AA^∗ + B^∗B). Then AA^∗v = −B^∗Bv. Apply B to both sides, we get −BB^∗Bv = 0. As B^∗Bv ∈ ker(B)∩im(B^∗) (recall that ker(B^∗B) = ker(B)), Bv must be 0. Applying A^∗ to both sides and reasoning similarly, one can show that A^∗v = 0.

4. Let π : V → im(A)^⊥ be the projection and π_B = π|_ker(B). ker(π_B) ⊂ ker(π) = im(A), and since ker(B) ⊃ im(A), we get ker(π_B) = im(A). Next we show that imπ_B = ker(B)∩im(A)^⊥. It suffices to show that im π_B ⊂ ker (B). This is true since for any v ∈ ker(B),

   $$B\left({\pi }_B(v)\right)=B(\pi v)=B(\pi v)+B((1-\pi )v)\stackrel{(1-\pi )v\in \mathrm{im}(A)}{=}B(v)=0.$$
   Now

   $$\ker (B)/\ker \left({\pi }_B\right)\cong \mathrm{im}\left({\pi }_B\right)$$

   $$\ker (B)/\mathrm{im}(A)\cong \ker (B)\cap \mathrm{im}{(A)}^{\perp }$$

   $$\ker (B)/\mathrm{im}(A)\cong \ker (B)\cap \ker \left(A^{*}\right).$$

   □

Proof of Theorem 2.11.

Since ${\partial }_q^t{ð}_{q+1}^{t,p}=0$, ker ${\mathrm{\Delta }}_q^{t,p}\cong \ker {\partial }_q^t/\mathrm{im}{ð}_{q+1}^{t,p}$. Also bear in mind that dim ${\partial }_q^t/\mathrm{im}{ð}_{q+1}^{t,p}={\beta }_q^{t,p}$. □

3. Method of homotopy continuation.

Our exposition of homotopy continuation follows [5]. A more theoretical treatment of this topic can be found elsewhere [30].

3.1. Path tracking.

Solving a system of polynomial equations f by homotopy continuation basically consists of three steps: 1) build a start system g such that g can be solved easily; 2) build a homotopy between two systems f and g; 3) track the roots of g to the roots of f.

We first look at a simple example. Let us say we wish to solve the following polynomial in one complex variable

$$f(z)=-2z^3-5z^2+4z+1.$$

We take a similar and simpler polynomial g(z) and deform the roots of g(z) to f(z). For instance we may take g(z) = z³ + 1 and construct a linear homotopy

$$h\left(z\text{,}s\right)=sg\left(z\right)\text{+}(\text{1}-s)f\left(z\right)$$

where s is a complex variable. Though the second parameter of h is a complex variable, we still call h a homotopy between f and g for convenience. Then we parametrize s by a curve

$$s(t)=\frac{\gamma t}{\gamma t+(1-t)},t\in [0,1],\gamma \in ℂ\backslash ℝ$$

(this is called the gamma trick [5, Section 6.1] and there are technical reasons behind such choice of parametrization). We substitute s(t) in h(z, s) and clear denominators, then obtain a usual homotopy

$$H(z,t)=\gamma tg(z)+(1-t)f(z),t\in [0,1].$$

For each t₀ ∈ [0, 1], H(z, t₀) is a polynomial. Once we know how to numerically solve H(z, t₀ − Δt) = 0 from the known roots of H(z, t₀), we can pick a grid of [0, 1] and track the known roots of g step by step all the way to the solutions of f. This process is called the path tracking. Now suppose H(z(t), t) = 0 for any t ∈ (0, 1] with z(1) a root of g. Differentiate H(z(t), t) with respect to t, we have the Davidenko differential equation

$$\frac{\partial H}{\partial t}(z(t),t)+\frac{\partial H}{\partial z}(z(t),t)\frac{dz(t)}{dt}=0.$$

If $\frac{\partial H}{\partial z}(z(t),t)$ is nonzero, the Davidenko differential equation can be rewritten as

$$\frac{dz(t)}{dt}=-{\left(\frac{\partial H}{\partial z}(z(t),t)\right)}^{-1}\frac{\partial H}{\partial t}(z(t),t)$$

As we know the value of z(t) at t₀, we have indeed transformed our original problem of tracking roots to the classical initial value problem of ordinary differential equation (ODE). One may use any ODE method to predict z(t₀ −Δt) (The default ODE solver employed by Bertini is RKF45). For instance we can apply the simplest Euler’s method and get

$$z\left(t_0-\mathrm{\Delta }t\right)=z\left(t_0\right)-{\left(\frac{\partial H}{\partial z}\left(z\left(t_0\right),t_0\right)\right)}^{-1}\frac{\partial H}{\partial t}\left(z\left(t_0\right),t_0\right)\mathrm{\Delta }t.$$

Since we also know that H(z(t₀ − Δt),t₀ − Δt) should be zero, we can apply several iterations of Newton’s method to update z(t₀ −Δt). Such a combination of an ODE predictor with Newton’s method is called a predictor-corrector method.

Now after the path tracking from t = 1 to t = 0, we get a sequence {z(t_i)}. If the limit $\underset{t_i\to 0}{\lim }z\left(t_i\right)$ exists and is finite, we think of $\underset{t_i\to 0}{\lim }z\left(t_i\right)$ as a solution of f.

Example 3.1.

The reader may wonder why we do not just use

$$H(z,t)=\mathrm{tg}(z)+(1-t)f(z),t\in [0,1].$$

Consider the example H(z, t) = t(z²−1)+(1−t)(5−z²). When t = 1/2, H(z, 1/2) = 2 has no roots. When t = 5/6, H(z, 5/6) = 2/3z² has a singular root 0, and the derivative of it at z = 0 is zero.

Example 3.2.

Though usually we are only interested in real roots of the target system, we should also track complex roots. Consider the homotopy

$$h(z,t)=z^4-e^{2\pi i(1-t)}+0.25=0,t\in [0,1].$$

At t = 1, h(z, 1) has two real roots $\pm \sqrt[4]{0.75}$ and two imaginary roots $\text{s}\pm \sqrt[4]{0.75}i$. As t goes from 1 to 0, e^2πi(1−t) travels around the unit circle in the complex plane counterclockwise. The two real roots will be deformed to the two imaginary ones and vice versa.

We have discussed how to apply homotopy continuation to solve a single polynomial. The procedure for a single polynomial can be generalized to solve a square system. We introduce some concepts first.

Definition 3.1 (Square system).

A system of polynomial equations

$$f(z)=\left[\begin{array}{c}{f}_1\left(z_1,\dots ,z_N\right)\\ ⋮\\ f_n\left(z_1,\dots ,z_N\right)\end{array}\right]=0$$

with n polynomials and N variables is said to be square if n = N.

Definition 3.2 (Isolated solution).

For any solution z^∗ of f, if there is r > 0 such that there is no other solutions but z^∗ contained in

$$B_r\left(z^{*}\right)=\left\{z\in {ℂ}^N\left|\right|z-z^{*}\mid <r\right\},$$

we say that z^∗ is isolated.

Definition 3.3.

We say that a solution z^∗ is nonsingular if

$$J\left(f,z^{*}\right)=\left[\begin{array}{ccc}\frac{\partial f_1}{\partial z_1}\left(z^{*}\right)& \dots & \frac{\partial f_1}{\partial z_N}\left(z^{*}\right)\\ ⋮& \ddots & ⋮\\ \frac{\partial f_N}{\partial z_1}\left(z^{*}\right)& \dots & \frac{\partial f_N}{\partial z_N}\left(z^{*}\right)\end{array}\right]$$

is non-singular. Otherwise z^∗ is said to be a singular solution.

Definition 3.4 (Good homotopy).

Suppose we have a square system of polynomial equations f, a start system g, a set of D distinct solutions ${\mathcal{S}}_1$ of g(z) = H(z, 1) = 0, and a system of infinitely differentiable functions

$$H(z,t)=\left[\begin{array}{c}{H}_1\left(z_1,\dots ,z_N,t\right)\\ ⋮\\ H_N\left(z_1,\dots ,z_N,t\right)\end{array}\right]$$

satisfying the following property:

1. For any t ∈ [0, 1], H(z, t) is a system of polynomial equations;

2. For any ${\omega }_j\in {\mathcal{S}}_1$, there exists a smooth map $p_j(t):(0,1]\mapsto {ℂ}^N$ such that p_j(1) = ω_j;

3. For any t^∗ ∈ (0, 1]:

   1. The associated paths of solutions ${\mathcal{S}}_1$ do not cross each other, i.e., there do not exist two integers j, k with 1 ≤ j < k ≤ D such that p_j(t^∗) = p_k(t^∗);
   2. All p_j(t^∗) are isolated solutions of H(z, t^∗) = 0.

4. If we denote the two-norm of a vector v by ‖v⃦₂, the set of finite limits

$${\mathcal{S}}_0=\left\{z\in {ℂ}^N\mid \Vert z{\Vert }_2<\infty \text{and}z=\underset{t\to 0}{\lim }{p}_j(t),1\le j\le D\right\}$$

contains every isolated solution of f(z) = 0.

Then we say that H is a good homotopy.

Now suppose we take a start system

$$g(z):=\left[\begin{array}{c}{g}_1\left(z_1,\dots ,z_N\right)\\ ⋮\\ g_N\left(z_1,\dots ,z_N\right)\end{array}\right]=0$$

with known roots and a good homotopy

$$H(z,t)=\left[\begin{array}{c}{H}_1\left(z_1,\dots ,z_N,t\right)\\ ⋮\\ H_N\left(z_1,\dots ,z_N,t\right)\end{array}\right]$$

such that for any solution p of g there is a map $z(t):[0,1]\mapsto {ℂ}^N$ satisfying

1. H(z(t),t) = 0 when t ∈ (0,1] and

2. The Jacobian ∂H/∂z of H with respect to z is non-singular for points (z(t), t) with t ∈ (0, 1].

In this multidimensional case, the Davidenko differential equation is

$$\frac{\partial H}{\partial t}(z(t),t)+\sum _{i=1}^N\frac{\partial H}{\partial z_i}(z(t),t)\frac{d{z}_i(t)}{dt}=0$$

where

$$\frac{\partial H}{\partial z_i}=\left[\begin{array}{c}\frac{\partial H_1}{\partial z_i}\\ ⋮\\ \frac{\partial H_N}{\partial z_i}\end{array}\right].$$

Let

$$\frac{dz}{dt}=\left[\begin{array}{c}\frac{d{z}_1}{dt}\\ ⋮\\ \frac{d{z}_N}{dt}\end{array}\right].$$

We rewrite the Davidenko equation as

$$\frac{\partial H}{\partial t}(z(t),t)+\frac{\partial H}{\partial z}(z(t),t)\frac{dz(t)}{dt}=0.$$

Since $\frac{\partial H}{\partial z}$ is invertible on the path (z(t), t), we get

$$\frac{dz(t)}{dt}=-{\left(\frac{\partial H}{\partial z}\right)}^{-1}\frac{\partial H}{\partial t}(z(t),t).$$

As in the one-dimensional case, we use predictor-corrector methods to track the roots of g to the roots of f.

Here we remind the reader that the predictor-corrector method may have trouble in dealing with singular solutions of f. If p^∗ is a singular solution of f = H(z, 0) and z(t) is its path, the Jacobian of H can be very small when (z(t), t) → (p*, 0). This would make the path tracking very slow and require high precision. A couple of methods called the endgames are invented to deal with singular solutions of f [4].

3.2. Bertini’s theorem.

We have described in previous sections how to solve a square system. How to tackle a non-square system? We need Bertini’s theorem. We introduce some basic definitions regarding algebraic sets first.

Definition 3.5 (Affine complex algebraic set).

Given a system f of n polynomials and N complex variables, an affine complex algebraic set V (f₁,..., f_n) is the locus of solutions on ${ℂ}^N$.

Definition 3.6 (Manifold point).

A point $p^{*}=\left(p_1^{*},\dots ,p_N^{*}\right)$ of $X=\mathbf{V}\left(f_1,\dots ,f_n\right)\subset {ℂ}^N$ is said to be a manifold point if there is a neighborhood U ⊂ X such that for some mapping Φ defined on ${ℂ}^N$, Φ|_U is a bijection from U to a neighborhood of 0 in ${ℂ}^k$. The set of regular points in X is refered to as X_reg. The dimension of p^∗ is defined as k. It can be shown that in the usual topology of ${ℂ}^N$ X_reg is dense in X.

Definition 3.7 (Zariski topology).

The Zariski topology is a weaker topology compared to the usual topology of Euclidean space. Given an affine algebraic set X, its open sets are taken to be intersections of X with sets of the form ${ℂ}^N\backslash Y$, where Y is an affine algebraic subset of ${ℂ}^N$.

Example 3.3.

The Zariski open sets of $ℂ$ are the complements of finite sets.

Definition 3.8 (Irreducible components of an algebraic set).

Given an affine algebraic set X, the irreducible components of X are closures of the connected components of X_reg.

Definition 3.9 (Pure dimension).

For any $p^{*}\in X,{\dim }_{p^{*}}X$, the dimension of X at p^∗, is defined to be the maximum dimension of the irreducible components that contains p^∗. The dimension of X is then defined as the maximum dimension of its points, i.e.,

$$\dim X=\max \left\{{\dim }_{p^{*}}X\mid p^{*}\in X\right\}.$$

If $\dim X={\dim }_{p^{*}}X$ for all p^∗ ∈ X, we say X is pure-dimensional.

Now we state the Bertini’s theorem.

Theorem 3.10.

[5, Thm. 1.15] Suppose we have n polynomials f₁(z),..., f_n(z) defined on a nonempty Zariski open subset U of $X\subset {ℂ}^N$ where X is an irreducible affine complex algebraic set. We further assume that for any point x ∈ U, not all f_j(x) are zero. Under such conditions, there is a nonempty Zariski open subset $\mathcal{U}$ of ${ℂ}^N$ such that for any λ = (λ₁,..., λ_n) in $\mathcal{U}$, $f_{\lambda }(z)={\sum }_{i=1}^n{\lambda }_i{f}_i(z)$ has the following property:

1. Z_λ = V (f_λ(z)) is either empty or of pure dimension N − 1; and

2. $\mathbf{V}\left(f_{\lambda }(z),\frac{\partial f_{\lambda }(z)}{\partial z_1},\dots ,\frac{\partial f_{\lambda }(z)}{\partial z_N}\right)=\varnothing$.

One variant of Bertini’s theorem is important to us.

Theorem 3.11 (Bertini’s theorem for systems).

[5, Thm. 9.3] Suppose we have a system of polynomial equations $f:{ℂ}^N\mapsto {ℂ}^n$, then there is a Zariski open dense subset $U\subset {ℂ}^{k\times n}$ such that for any matrix A ∈ U, the following is satisfied

1. V (A · f)\V (f) is either empty or smooth of pure-dimension N − k; and

2. The number of irreducible components of V (A · f)\V (f) has nothing to do with A and the irreducible components of V (A · f)\V (f) are disjoint.

Now suppose we are dealing with a system f with n polynomials and N variables and n > N. Such a system is called an overdetermined system. If we take a random matrix $A\in {ℂ}^{N\times n}$ and replace the system f with the system A·f. Bertini’s theorem tells us that the set V (A · f)\V (f) is either empty or N −N = 0 dimensional, i.e., Bertini’s theorem guarantees us that extra solutions introduced by A·f are isolated solutions. We can discard these extra solutions by simply verifying if they satisfy f = 0. A more detailed discussion of non-square system can be found in [5].

4. Experiments.

In this section, we study the geometry and topology of several small polytopes and molecules. For any polytope or molecule, a filtration of alpha complexes is generated (for a polytope or molecule lying in a plane we need to perturb its coordinates a bit beforehand). We use HERMES to calculate p-persistent 0-combinatorial Laplacians and use NumPy [18] to calculate the associated characteristic polynomials. Then we use Bertini to solve these polynomials and hence get the spectra of persistent Laplacians. As roots of a polynomial are unchanged under scalar multiplication, the maximal coefficient of any characteristic polynomial is scaled to 1. The configuration of Bertini is as follows: MPTYPE=2, FINALTOL=1e-8, COEFFBOUND=100, DEGREEBOUND=80, AMPSAFETYDIGITS1=1, AMPSAFETYDIGITS2=1, AMPMAXPREC=3328.

First let us look at 2-dimensional regular polygons, such as a pentagon, a heptagon, an octagon and a nonagon. In our experiments, the circumradius of any regular polygon is set to be 1.

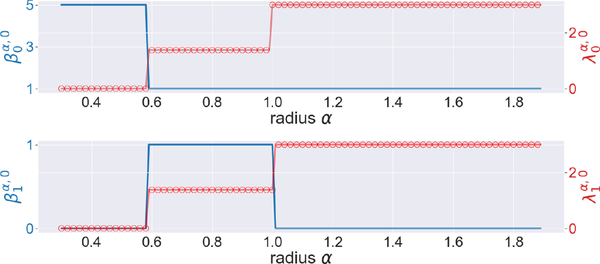
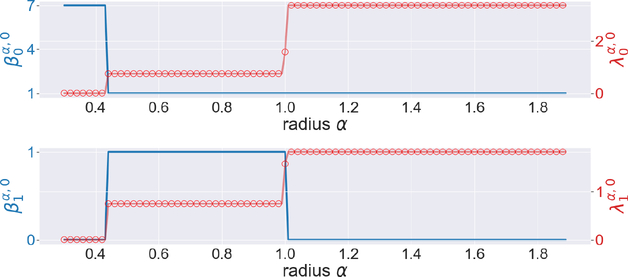
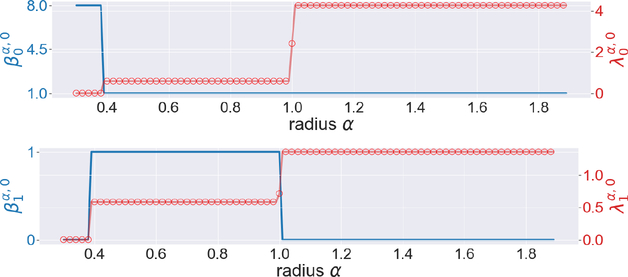
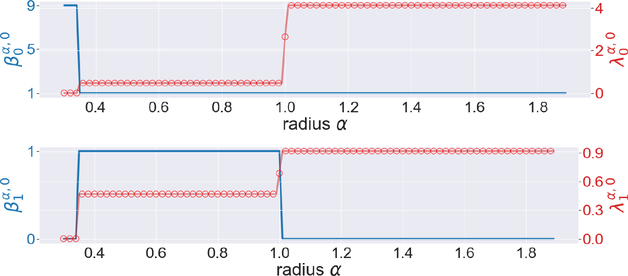
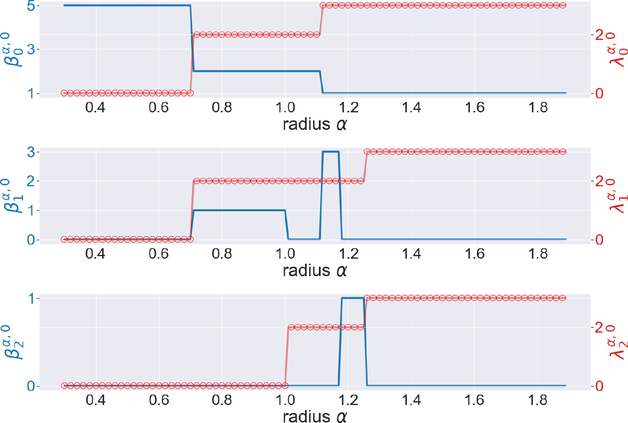
The persistent Betti numbers and the smallest nonzero eigenvalues of persistent Laplacians regarding the pentagon are shown in Figure 4. We see abrupt changes near 0.6 and 1. This coincides with the geometrical properties of our pentagon, for its edge length is sin(π/5) ≈ 0.58 and radius is 1. Results for Heptagon, Octagon, and Nonagon are presented in Figures 10, 11, and 12, respectively in the Appendix.

Figure 4.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ against the radius α for the pentagon. The persistent Betti numbers are shown by the blue line. The smallest nonzero eigenvalues calculated by HERMES and Bertini are shown by a red line and red circles, respectively and one can see that they almost coincide. The half edge length is approximately sin(π/5) ≈ 0.58.

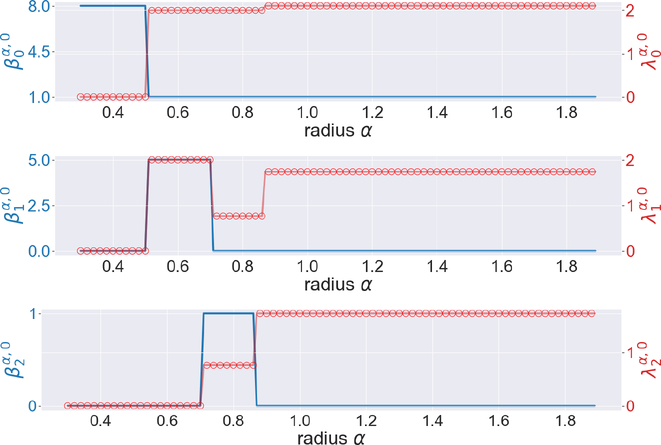
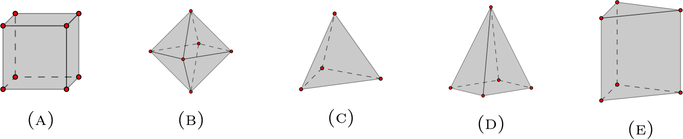
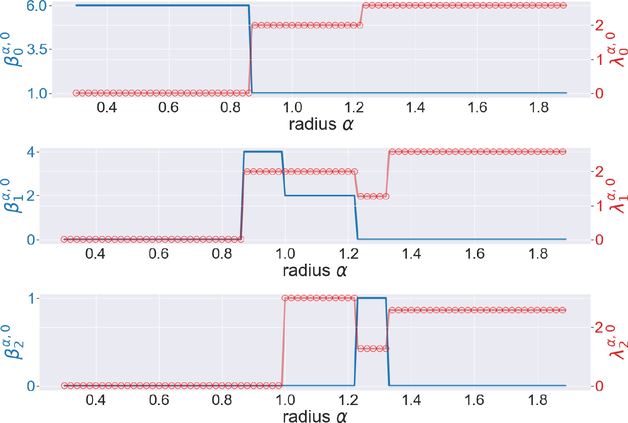
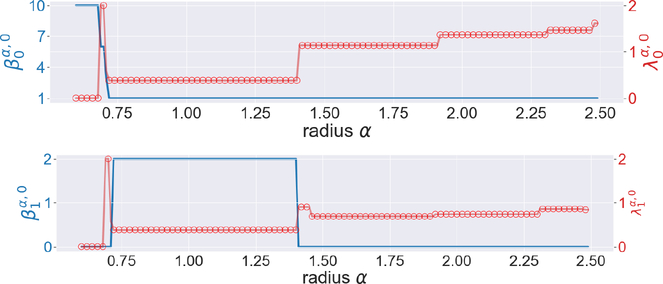
Next let us look at some 3-dimensional objects, such as a cube, and an octahedron. We first study the cube with edge length 1. As the length of its face diagonal is $\sqrt{2}\approx 1.4$ and the length of its main diagonal is $\sqrt{3}\approx 1.7$, one would expect some changes in the graphs near α = 0.5, α = 0.7 and α = 0.85. This is confirmed in Figure 6.

Figure 6.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the cube. The length of its face diagonal is $\sqrt{2}\approx 1.4$ and the length of its main diagonal is $\sqrt{3}\approx 1.7$.

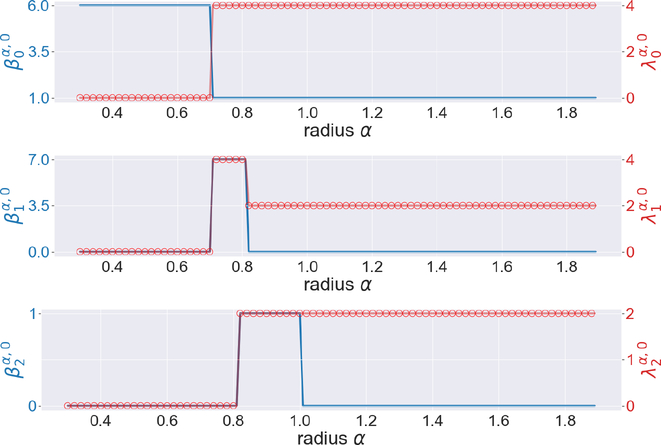
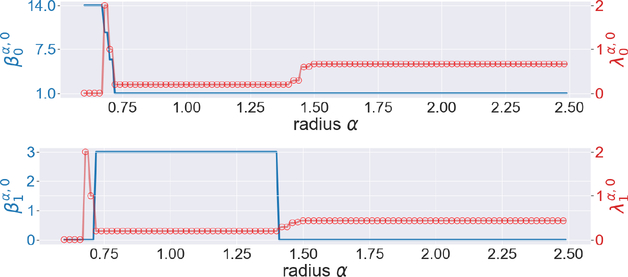
Another 3-dimensional example is the regular octahedron with edge length $\sqrt{2}$. The circumradius of any face is set to $\sqrt{2}/\sqrt{3}\approx 0.8$. The circumradius of the octahedron itself is set to 1. Such geometrical properties are reflected in Figure 7. Results for a tetrahedron, a triangular prism and a regular pyramid are illustrated in Figures 13, 14, and 15, respectively in the Appendix.

Figure 7.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the octahedron. Its edge length is $\sqrt{2}$. The circumradius of any face is equal to $\sqrt{2}/\sqrt{3}\approx 0.8$. The circumradius of the octahedron itself is equal to 1.

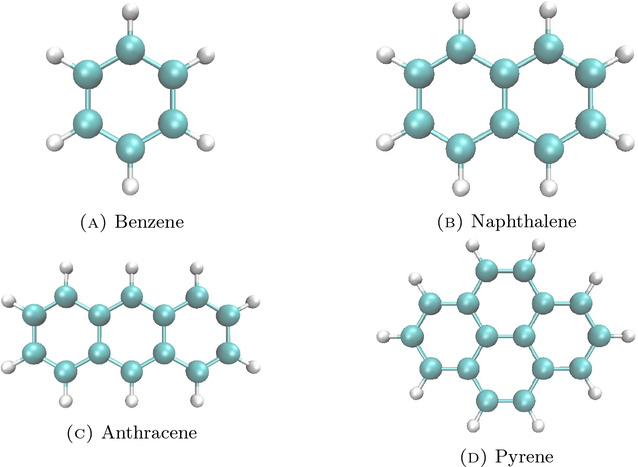
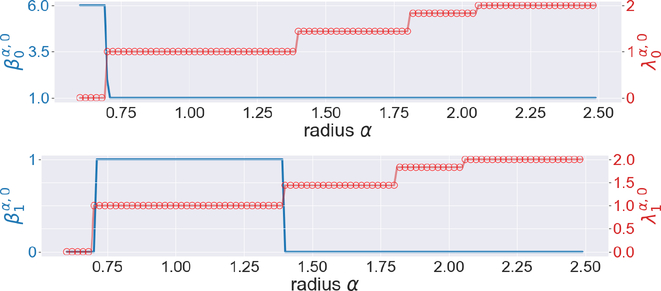
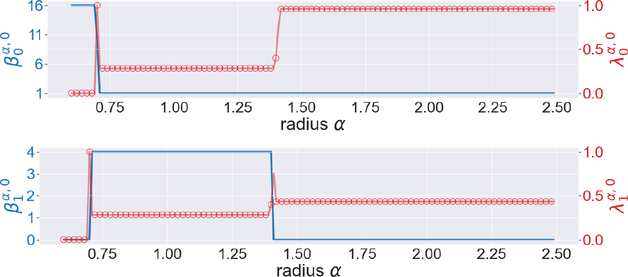
Next, we examine aromatic molecules, such as benzene, anthracene, naphthalene, and pyrene (see Figure 8). Here we only consider the C skeletons of them. First, consider the benzene molecule. The half-length of its edge is approximately 0.7Å, and its radius is approximately 1.4Å. One can see changes near 0.7 and 1.4 in Figure 9. Results for naphthalene, anthracene, and pyrene are presented in Figures 16, 17, and 18, respectively in the Appendix.

Figure 8.

Some aromatic molecules.

Figure 9.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the benzene. The half length of its edge is approximately 0.7Å, and its radius is approximately 1.4Å.

5. Conclusions.

Combinatorial Laplacian is a powerful tool for studying the shape of data. However, its performance is restricted partly because it is defined as a single graph or a simplicial complex and does not provide a multiscale analysis. Motivated by the theory of persistent homology, Wang et al. [34] introduced the persistent combinatorial Laplacian defined for a pair of complexes in a given filtration. Since the nullity of the spectrum of the persistent combinatorial Laplacian (aka persistent Laplacian) recovers the persistent Betti number, the persistent combinatorial Laplacian can be regarded as a unified tool to extract topological persistence and geometrical information out of high dimensional datasets.

Although the computation of the spectrum of the persistent Laplacian can be implemented in various ways, it is mathematically interesting to explore alternative ways, which might stimulate new mathematics in the long run. In this work, we explore the possibility of applying homotopy continuation methods. We have verified at least for some simple polytopes and small molecules in the three-dimensional space, the second smallest eigenvalues of persistent Laplacians calculated by homotopy continuation are very close to the result from HERMES. In other words, the geometrical properties of them can be inferred from the changes of the spectra obtained via homotopy continuation. The present work offers a unique example that combines algebraic topology, algebraic geometry, and combinatorial graph to solve problems in data science. For larger systems such as protein molecules, further research is needed to implement homotopy continuation.

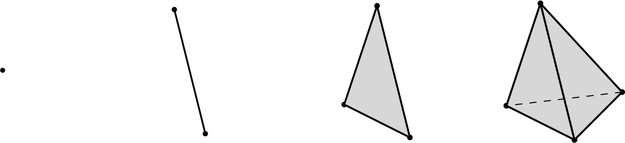
FIGURE 1.

0-simplex, 1-simplex, 2-simplex and 3-simplex.

Figure 3.

Pentagon, Heptagon, Octagon and Nonagon.

Figure 5.

(a) A cube with edge length 1. (b) A regular octahedron with edge length $\sqrt{2}$. (c) A regular tetrahedron with edge length $\sqrt{3}$. (d) A regular pyramid with square edge length $\sqrt{2}$ and height 2. (e) A triangular prism with edge length $\sqrt{3}$.

Appendix A. Supplementary figures.

Figure 10.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the heptagon.

Figure 11.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the octagon.

Figure 12.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the nonagon.

Figure 13.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the regular tetrahedron with edge length $\sqrt{3}$. The centroid to vertex distance is $3/\sqrt{8}\approx 1.06$.

Figure 14.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for a triangular prism. Its base is a regular triangle with edge length $\sqrt{3}$. Its side faces are squares. Important distances are $\sqrt{3}/2$, 1, $\sqrt{6}/2\approx 1.22$ and $\sqrt{7}/2\approx 1.32$.

Figure 15.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for a regular pyramid. Its base is a square with edge length $\sqrt{2}$ and its height is 2. Important distances are $\sqrt{2}/2$, 1, $\sqrt{5}/2\approx 1.12$, $5\sqrt{2}/6\approx 1.18$ and 5/4.

Figure 16.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the naphthalene.

Figure 17.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the anthracene.

Figure 18.

The illustration of the persistent Betti numbers ${\beta }_q^{\alpha ,0}$ and the smallest nonzero eigenvalues of persistent Laplacians ${\lambda }_q^{\alpha ,0}$ for the pyrene.

Appendix B. Coordinates of aromatic molecules. ¹

In this section the xyz coordinates of benzene, naphthalene, anthracene, and pyrene are listed. We omit hydrogen atoms since they are irrelevant for the computation.

benzene:	naphthalene:
1.400 0.000 0.000	2.404 0.756 0.000
0.700 1.212 0.000	2.433 −0.658 0.000
−0.700 1.212 0.000	1.267 −1.375 0.000
−1.400 0.000 0.000	0.014 −0.705 0.000
−0.700 −1.212 0.000	−0.014 0.705 0.000
0.700 −1.212 0.000	1.211 1.425 0.000
−1.267 1.375 0.000	−2.417 1.490 0.000
−2.433 0.659 0.000	pyrene:
−2.404 −0.756 0.000	0.000 1.214 −2.813
−1.211 −1.425 0.000	0.000 1.224 −1.410
anthracene:	0.000 −0.000 −0.705
3.661 0.585 0.000	0.000 −1.224 −1.410
3.611 −0.840 0.000	0.000 0.000 0.705
2.417 −1.490 0.000	0.000 −1.224 1.410
1.187 −0.753 0.000	0.000 −2.435 0.700
2.515 1.317 0.000	0.000 −2.435 −0.700
1.237 0.668 0.000	0.000 1.224 1.410
−0.049 −1.403 0.000	0.000 −1.214 −2.813
−1.237 −0.668 0.000	0.000 −0.000 −3.507
0.049 1.403 0.000	0.000 −1.214 2.813
−1.187 0.753 0.000	0.000 1.214 2.813
−2.515 −1.317 0.000	0.000 0.000 3.507
−3.661 −0.585 0.000	0.000 2.435 0.700
−3.611 0.840 0.000	0.000 2.435 −0.700