Skip to main content
PMC home page
BMJ - PMC COVID-19 Collection logoLink to BMJ - PMC COVID-19 Collection
. 2022 Jul 12;378:e069881. doi: 10.1136/bmj-2021-069881

Clinical prediction models for mortality in patients with covid-19: external validation and individual participant data meta-analysis

Valentijn M T de Jong 1 ,2 ,3,✉, Rebecca Z Rousset 1, Neftalí Eduardo Antonio-Villa 4,5, Arnoldus G Buenen 6 ,7, Ben Van Calster 8 ,9 ,10, Omar Yaxmehen Bello-Chavolla 4, Nigel J Brunskill 11 ,12, Vasa Curcin 13, Johanna A A Damen 1 ,2, Carlos A Fermín-Martínez 4 ,5, Luisa Fernández-Chirino 4 ,14, Davide Ferrari 13 ,15, Robert C Free 16 ,17, Rishi K Gupta 18, Pranabashis Haldar 16 ,17 ,19, Pontus Hedberg 20 ,21, Steven Kwasi Korang 22, Steef Kurstjens 23, Ron Kusters 23 ,24, Rupert W Major 11 ,25, Lauren Maxwell 26, Rajeshwari Nair 27 ,28, Pontus Naucler 20 ,21, Tri-Long Nguyen 1 ,29 ,30, Mahdad Noursadeghi 31, Rossana Rosa 32, Felipe Soares 33, Toshihiko Takada 1 ,34, Florien S van Royen 1, Maarten van Smeden 1, Laure Wynants 7 ,35, Martin Modrák 36; the CovidRetro collaboration, Folkert W Asselbergs 37 ,38 ,39, Marijke Linschoten 37; CAPACITY-COVID consortium, Karel G M Moons 1 ,2, Thomas P A Debray 1 ,2
PMCID: PMC9273913  PMID: 35820692

Abstract

Objective

To externally validate various prognostic models and scoring rules for predicting short term mortality in patients admitted to hospital for covid-19.

Design

Two stage individual participant data meta-analysis.

Setting

Secondary and tertiary care.

Participants

46 914 patients across 18 countries, admitted to a hospital with polymerase chain reaction confirmed covid-19 from November 2019 to April 2021.

Data sources

Multiple (clustered) cohorts in Brazil, Belgium, China, Czech Republic, Egypt, France, Iran, Israel, Italy, Mexico, Netherlands, Portugal, Russia, Saudi Arabia, Spain, Sweden, United Kingdom, and United States previously identified by a living systematic review of covid-19 prediction models published in The BMJ, and through PROSPERO, reference checking, and expert knowledge.

Model selection and eligibility criteria

Prognostic models identified by the living systematic review and through contacting experts. A priori models were excluded that had a high risk of bias in the participant domain of PROBAST (prediction model study risk of bias assessment tool) or for which the applicability was deemed poor.

Methods

Eight prognostic models with diverse predictors were identified and validated. A two stage individual participant data meta-analysis was performed of the estimated model concordance (C) statistic, calibration slope, calibration-in-the-large, and observed to expected ratio (O:E) across the included clusters.

Main outcome measures

30 day mortality or in-hospital mortality.

Results

Datasets included 27 clusters from 18 different countries and contained data on 46 914patients. The pooled estimates ranged from 0.67 to 0.80 (C statistic), 0.22 to 1.22 (calibration slope), and 0.18 to 2.59 (O:E ratio) and were prone to substantial between study heterogeneity. The 4C Mortality Score by Knight et al (pooled C statistic 0.80, 95% confidence interval 0.75 to 0.84, 95% prediction interval 0.72 to 0.86) and clinical model by Wang et al (0.77, 0.73 to 0.80, 0.63 to 0.87) had the highest discriminative ability. On average, 29% fewer deaths were observed than predicted by the 4C Mortality Score (pooled O:E 0.71, 95% confidence interval 0.45 to 1.11, 95% prediction interval 0.21 to 2.39), 35% fewer than predicted by the Wang clinical model (0.65, 0.52 to 0.82, 0.23 to 1.89), and 4% fewer than predicted by Xie et al’s model (0.96, 0.59 to 1.55, 0.21 to 4.28).

Conclusion

The prognostic value of the included models varied greatly between the data sources. Although the Knight 4C Mortality Score and Wang clinical model appeared most promising, recalibration (intercept and slope updates) is needed before implementation in routine care.

Introduction

Covid-19 has had a major impact on global health and continues to disrupt healthcare systems and social life. Millions of deaths have been reported worldwide since the start of the pandemic in 2019.1 Although vaccines are now widely deployed, the incidence of SARS-CoV-2 infection and the burden of covid-19 remain extremely high. Many countries do not have adequate resources to effectively implement vaccination strategies. Also, the timing and sequence of vaccination schedules are still debatable, and virus mutations could yet hamper the future effectiveness of vaccines.2

Covid-19 is a clinically heterogeneous disease of varying severity and prognosis.3 Risk stratification tools have been developed to target prevention and management or treatment strategies, or both, for people at highest risk of a poor outcome.4 Risk stratification can be improved by the estimation of the absolute risk of unfavourable outcomes in individual patients. This involves the implementation of prediction models that combine information from multiple variables (predictors). Predicting the risk of mortality with covid-19 could help to identify those patients who require the most urgent help or those who would benefit most from treatment. This would facilitate the efficient use of limited medical resources, and reduce the impact on the healthcare system—especially intensive care units. Furthermore, if a patient’s risk of a poor outcome is known at hospital admission, predicting the risk of mortality could help with planning the use of scarce resources. In a living systematic review (update 3, 12 January 2021; www.covprecise.org), 39 prognostic models for predicting short term (mostly in-hospital) mortality in patients with a diagnosis of covid-19 have been identified.5

Despite many ongoing efforts to develop covid-19 related prediction models, evidence on their performance when validated in external cohorts or countries is largely unknown. Prediction models often perform worse than anticipated and are prone to poor calibration when applied to new individuals.6 7 8 Clinical implementation of poorly performing models leads to incorrect predictions and could lead to unnecessary interventions, or to the withholding of important interventions. Both result in potential harm to patients and inappropriate use of medical resources. Therefore, prediction models should always be externally validated before clinical implementation.9 These validation studies are performed to quantify the performance of a prediction model across different settings and populations and can thus be used to identify the potential usefulness and effectiveness of these models for medical decision making.7 8 10 11 12 We performed a large scale international individual participant data meta-analysis to externally validate the most promising prognostic models for predicting short term mortality in patients admitted to hospital with covid-19.

Methods

Review to identify covid-19 related prediction models

We used the second update (21 July 2020) of an existing living systematic review of prediction models for covid-19 to identify multivariable prognostic models and scoring rules for assessing short term (at 30 days or in-hospital) mortality in patients admitted to hospital with covid-19.5 During the third update of the living review (12 January 2021),13 additional models were found that also met the study eligibility criteria of this individual participant data meta-analysis, which we also included for external validation.

We considered prediction models to be eligible for the current meta-analysis if they were developed using data from patients who were admitted to a hospital with laboratory confirmed SARS-CoV-2 infection. In papers that reported multiple prognostic models, we considered each model for eligibility. As all the prognostic models for covid-19 mortality in the second update (21 July 2020) of the living systematic review had a lower quality and high risk of bias in at least one domain of PROBAST (prediction model study risk of bias assessment tool),7 8 we only excluded models that had a high risk of bias for the participant domain and models for which applicability was deemed poor, as well as imaging based algorithms (see fig 1).

Fig 1.

Fig 1

Open in a new tab

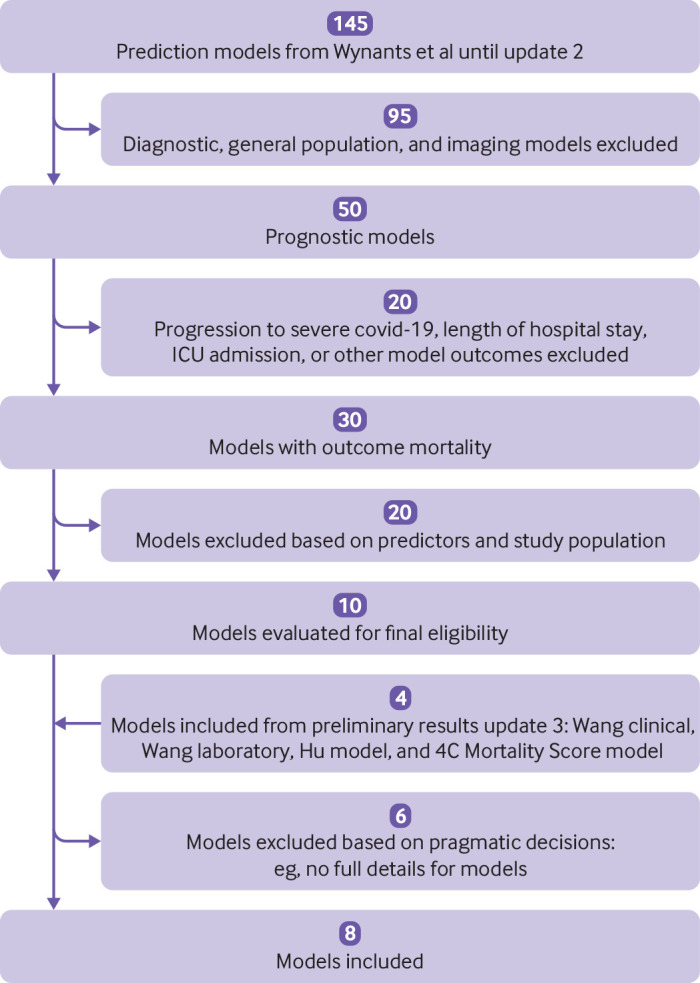
Flowchart of inclusion of prognostic models. The second update took place on 21 July 2020. ICU=intensive care unit

Review to identify patient level data for model validation

We searched for individual studies and registries containing data from routine clinical care (electronic healthcare records), and data sharing platforms with individual patient data of those admitted to hospital with covid-19. We further identified eligible data sources through the second update (21 July 2020) of the living systematic review.5 13 In addition, we consulted the PROSPERO database, references of published prediction models for covid-19, and experts in prognosis research and infectious diseases.

Data sources were eligible for model validation if they contained data on mortality endpoints for consecutive patients admitted to hospital with covid-19. We included only patients with a polymerase chain reaction confirmed SARS-CoV-2 infection. We excluded patients with no laboratory data recorded in the first 24 hours of admission. In each data source, we adopted the same eligibility criteria for all models that we selected for validation. We used 30 days for the scoring rule by Bello-Chavolla et al14 when available, otherwise in-hospital mortality was used (see table 1).

Statistical analyses

For external validation and meta-analysis we used a two stage process.15 16 The first stage consisted of imputing missing data and estimating performance metrics in individual clusters. For datasets that included only one hospital (or cohort) we defined the cluster level as the individual hospital (or cohort). In the CAPACITY-COVID dataset,17 which contains data from multiple countries, we considered each country as a cluster. For the data from UnityPoint Hospitals in Iowa, United States, we considered each hospital as a cluster. We use the term cluster throughout the paper. In the second stage we performed a meta-analysis of the performance metrics.18 19 We did not perform an a priori sample size calculation, as we included all data that we found through the review and that met the inclusion criteria.

Stage 1: Validation

We imputed sporadically missing data 50 times by applying multiple imputation (see supplementary material B). Using each of the eight models, we calculated the mortality risk or mortality score of all participants, in clusters where the respective models’ predictors were measured in at least some of the participants. Subsequently, we calculated the concordance (C) statistic, observed to expected ratio (O:E ratio), calibration slope, and calibration-in-the-large for each model in each imputed cluster.11 The C statistic is an estimator for the probability of correctly identifying the patient with the outcome in a pair of randomly selected patients of which one has developed the outcome and one has not.20 The O:E ratio is the ratio of the number of observed outcomes divided by the number of outcomes expected by the prediction model. The calibration slope is an estimator of the correction factor the prediction model coefficients need to be multiplied with, to obtain coefficients that are well calibrated to the validation sample.11 21 The calibration-in-the-large is an estimator for the (additive) correction to the prediction model’s intercept, while keeping the prediction model’s coefficients fixed.11 21 Supplementary material B provides details of the model equations.

Stage 2: Pooling performance

In the second stage of the meta-analysis, we pooled the cluster specific logit C statistic, calibration slope, and log O:E ratios from stage 1.22 We used restricted maximum likelihood estimation and the Hartung-Knapp-Sidik-Jonkman method to derive all confidence intervals.23 24 To quantify the presence of between study heterogeneity, we constructed approximate 95% prediction intervals, which indicated probable ranges of performance expected in new clusters.25 We performed the analysis in R (version 4.0.0 or later, using packages mice, pROC, and metamisc) and we repeated the main analyses in STATA.26 27 28 29 30 This study is reported following the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) checklist for prediction model validation (see supplementary material C).31 32

Sensitivity analysis

None of the datasets contained all predictors, meaning the models could not all be validated in a single dataset, which hampered the interpretation. As such, for each performance measure taken separately, we performed a meta-regression on all performance estimates where we included country (not cluster, to save degrees of freedom) and model as predictors (both as dummy variables), which we had not prespecified in our protocol. Then we used these meta-models to predict the performance (and 95% confidence intervals) of each prediction model in each included country, thereby allowing for a fairer comparison of the performance between models. All R code is available from github.com/VMTdeJong/COVID-19_Prognosis_IPDMA.

Patient and public involvement

Patients and members of the public were not directly involved in this research owing to lack of funding, staff, and infrastructure to facilitate their involvement. Several authors were directly involved in the treatment of patients with covid-19, have been in contact with hospital patients with covid-19, or have had covid-19.

Results

Review of covid-19 related prediction models

We identified six prognostic models and two scoring rules that met the inclusion criteria (fig 1). Table 1 summarises the details of the models and scores. The score developed by Bello-Chavolla et al predicted 30 day mortality,14 whereas the other score and the six models predicted in-hospital mortality.33 34 35 36 37

Table 1.

Overview of selected models for predicting short term mortality in patients admitted to hospital with SARS-CoV-2 infection

Model Country of development Development population Predicted outcome Predictors Model type Estimation method
Bello-Chavolla et al14 Mexico All reported confirmed cases of covid-19, including hospital admission, ICU admission, and outpatient treatment. 30 day mortality Age, diabetes (type 2), obesity (clinician- defined), pneumonia, chronic kidney disease, chronic obstructive pulmonary disease, immunosuppression Score Rounding of Cox regression coefficients (unpenalised)
Xie et al33 China Adults (≥18 years) with confirmed covid-19, admitted in officially designated covid-19 treatment centres In-hospital mortality Age, lactate dehydrogenase, lymphocyte count, oxygen saturation Prediction model Logistic regression (unpenalised)
Hu et al34 China Patients with severe covid-19 in Tongji Hospital, which specifically accommodated for people with covid-19. Patients directly admitted to intensive care unit were excluded. Patients with certain comorbidities (including cancer, uraemia, aplastic anaemia) were also excluded. Patients with a short hospital stay (<7 days) were excluded In-hospital mortality Age, high sensitivity C reactive protein, D-dimer, lymphocyte count Prediction model Logistic regression (unpenalised)
Zhang et al DCS and DCSL models35 China Adults (≥18 years) admitted to two hospitals In-hospital mortality DCS model: Age, sex, diabetes (unspecified), immunocompromised, malignancy, hypertension, heart disease, chronic kidney disease, cough, dyspnoea
DCSL model: Age, sex, chronic lung disease, diabetes (unspecified), malignancy, cough, dyspnoea, neutrophil count, lymphocyte count, platelet count, C reactive protein, creatinine		 Prediction model Logistic regression (lasso penalty)
Knight et al 4C Mortality Score36 UK Adults (≥18 years) admitted across 260 hospitals In-hospital mortality Age, sex, number of comorbidities (chronic cardiac disease, respiratory disease, renal disease, liver disease, neurological conditions; dementia; connective tissue disease; diabetes (type 1 and 2); AIDS/HIV; malignancy, obesity), respiratory rate, oxygen saturation (room air), Glasgow coma scale score, urea, C reactive protein Score Rounding of logistic regression coefficients (lasso penalty)
Wang et al clinical and laboratory models37 China Adults (≥18 years) admitted to hospital. Pregnant women were excluded In-hospital mortality Clinical model: Age, history of hypertension, history of heart disease
Laboratory model: Age, oxygen saturation, neutrophil count, lymphocyte count, high sensitivity C reactive protein, D-dimer, aspartate aminotransferase, glomerular filtration rate		 Prediction model Logistic regression (unpenalised). Intercept from nomogram
Open in a new tab

The six prognostic models were estimated by logistic regression. The Bello-Chavolla score and Knight et al 4C Mortality Score were (simplified) scoring rules that could be used to stratify patients into risk groups. The Bello-Chavolla score was developed with Cox regression, whereas the 4C Mortality Score was developed with lasso logistic regression and its weights were rescaled and rounded to integer values.

Although the 4C Mortality Score itself does not provide absolute risks, these were available through an online calculator. As the authors promoted the use of the online calculator, we have used these risks in our analysis. For two models by Wang et al (clinical and laboratory), no intercept was available and were approximated.38

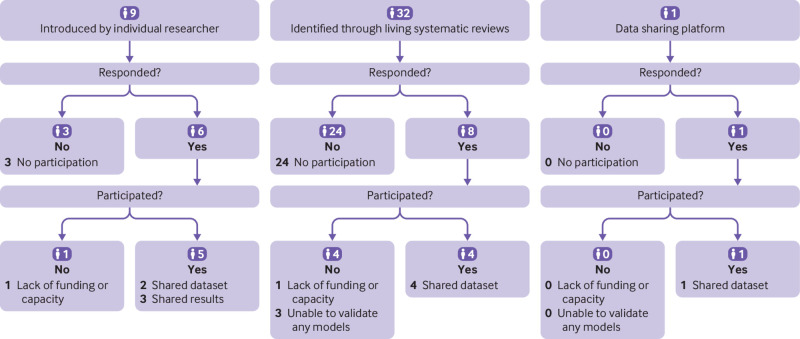
Review of patient level data for model validation

We identified 10 data sources, including four through living systematic reviews, one through a data sharing platform, and five by experts in the specialty (fig 2). The obtained datasets included 27 clusters from 18 different countries and contained data on 46 701 patients, 16 418 of whom died (table 2). Study recruitment was between November 2019 and April 2021. Most clusters included all patients with polymerase chain reaction confirmed covid-19, although in some clusters only patients admitted through a specific department were included (see supplementary material A, table S1). Mean age ranged from 45 to 71 years.

Fig 2.

Fig 2

Open in a new tab

Flowchart of data sources

Table 2.

Characteristics of the included external validation cohorts and clusters

Dataset, cluster No of patients Start recruitment date End recruitment date Total No (%) of deaths Mean (SD) age; (IQR) (years) No (%) male
Karolinska Institute, Sweden 1670 27 Feb 2020 1 Sep 2020 193 (11.56) 57.30 (18.70); (43-71) 983 (58.90)
Albert Einstein Hospital, Brazil 453 27 Feb 2020 25 Jun 2020 17 (3.75) 56.44 (14.92); (46-68.50) 295 (65.05)
Czech Republic Academy of Sciences, Czech Republic 213 3 Mar 2020 12 Oct 2020 42 (20)* 68.56 (16.56); (58-80) 105 (49)
University College London, UK 411 1 Feb 2020 30 Apr 2020 115 (28) 66 (53-79)† 252 (61.31)
General Directorate of Epidemiology, Mexico:
 All data, from this source 28 176 1 Mar 2020 16 Apr 2020 12 990 (46.10) 58.57 (15.93); (48-70) 17 019 (60.40)
 Development cohort excluded 25 056 11 556 (46.12) 59.08 (15.94); (49-70) 15 035 (60.01)
Tongji Hospital,39 China 332 10 Jan 2020 18 Feb 2020 155 (46.69) 58.98 (16.65); (46-70) 198 (59.64)
CAPACITY-COVID:
 Belgium 221 12 Feb 2020 14 Oct 2020 51 (23.08)* 68.14 (15.72); (57-81) 137 (61.99)
 Egypt 45 12 Apr 2020 12 Aug 2020 9 (20) 60.89 (14.37); (50-73) 21 (46.67)
 France 46 13 Feb 2020 18 Dec 2020 3 (6.52)* 67.96 (12.52); (62-77) 34 (73.91)
 Iran 90 10 Feb 2020 5 May 2020 13 (14.44)* 63.19 (15.39); (53.25-73) 59 (65.56)
 Israel 25 10 Apr 2020 9 Aug 2020 2 (8) 50.36 (20.15); (31-67) 14 (56)
 Italy 106 6 Feb 2020 4 May 2020 22 (20.75) 70.72 (11.63); (62.25-78.75) 72 (67.92)
 Netherlands 5100 22 Nov 2019 30 Jul 2020 1003 (19.67)* 66.37 (14.15); (57-76) 3172 (62.20)
 Portugal 44 25 Mar 2020 19 Aug 2020 10 (22.73)* 71.43 (13.32); (63.75-82) 30 (61.18)
 Russia 278 22 Apr 2020 4 Jun 2020 19 (6.83) 60.09 (15.49); (50.25-71) 137 (49.28)
 Saudi Arabia 389 29 Feb 2020 24 Sep 2020 57 (14.65)* 50.56 (16.79); (38-62) 270 (69.41)
 Spain 47 5 Mar 2020 20 Apr 2020 10 (21.28)* 70.98 (16.68); (55-83.75) 28 (59.57)
Jeroen Bosch Ziekenhuis, Netherlands 383 9 Mar 2020 29 Dec 2020 154 (40.21) 70.21 (14.79); (61-81) 226 (59.01)
Iowa (USA), UnityPoint Hospitals:
 Hospital 1 288 3 Mar 2020 31 Jul 2020 14 (4.86) 46.49 (19.29); (32-59) 147 (51.04)
 Hospital 2 929 3 Mar 2020 31 Jul 2020 67 (7.21) 50.12 (22.54); (33-68) 454 (48.87)
 Hospital 3 95 3 Mar 2020 31 Jul 2020 6 (6.32) 45.31 (20.54); (27-59) 45 (47.37)
 Hospital 4 66 3 Mar 2020 31 Jul 2020 6 (9.09) 48.77 (21.26); (31-65) 39 (59.09)
 Hospital 5 511 3 Mar 2020 31 Jul 2020 22 (4.31) 51.03 (20.63); (35-67) 240 (46.97)
 Hospital 6 393 3 Mar 2020 31 Jul 2020 22 (5.60) 45.35 (19.02); 30-60 176 (44.78)
 Hospital 7 295 3 Mar 2020 31 Jul 2020 18 (6.10) 47.60 (20.10); 32-63 162 (54.92)
Leicester covTrack, UK 3908 Jan 2020 Apr 2021 110 (28.22) 63.29 (19.19); (50-79) 2063 (52.79)
King’s College Hospital, UK 2400 28 Feb 2020 28 Mar 2021 295 (12.29) 59.76 (20.58); (47-76) 1314 (54.75)
Open in a new tab

SD=standard deviation; IQR=interquartile range.

*

Observed number of deaths before multiple imputation.

†

Median (IQR).

External validation and meta-analysis

All results are presented in supplementary material D. The Wang clinical model could be validated in 24 clusters (see supplementary table S2), followed by Hu et al’s model, which was validated in 16 clusters (see supplementary table S3). The remaining models were less often validated, as predictor measurements were available in fewer datasets: the Bello-Chavolla score was validated in seven clusters (see supplementary table S4), the model by Xie et al in nine clusters (see supplementary table S5), the DCS model by Zhang et al in six clusters (see supplementary table S6), the DCSL model by Zhang et al in six clusters (see supplementary table S7), the 4C Mortality Score in six clusters (see supplementary table S8), and the Wang laboratory model in three clusters (see supplementary table S9).

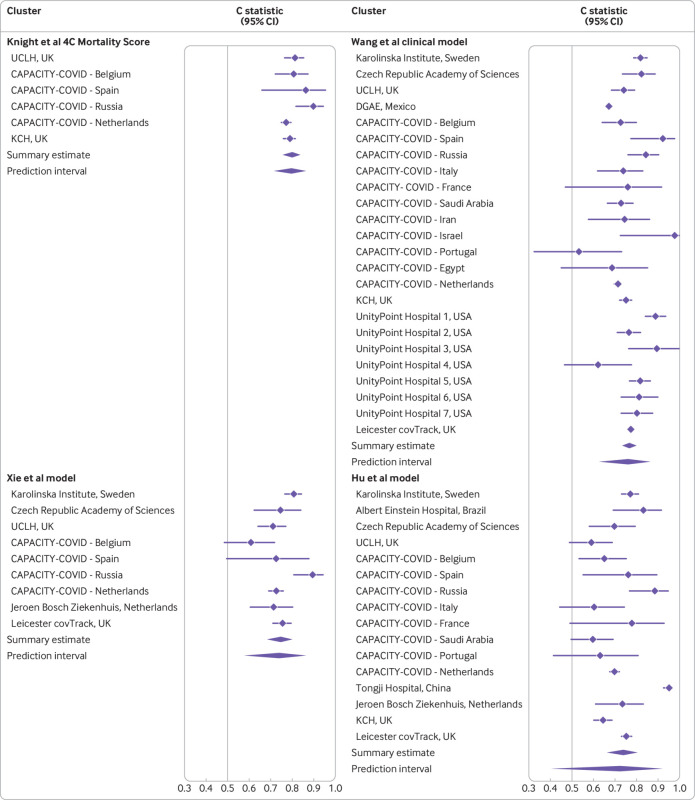
Discrimination

The 4C Mortality Score showed the highest discrimination, with a pooled C statistic of 0.80 (95% confidence interval 0.75 to 0.84, fig 3 and see supplementary fig S4). The heterogeneity of discrimination of this model across datasets (95% prediction interval 0.72 to 0.86) was low compared with that of the other models. The next best discriminating model was the Wang clinical model, with a pooled C statistic of 0.77 (0.73 to 0.80, fig 3), and a greater heterogeneity (95% prediction interval 0.63 to 0.87). Two other models attained a summary C statistic >0.70: the Xie model with a C statistic of 0.75 (0.68 to 0.80, 95% prediction interval 0.58 to 0.86, fig 3), and the Hu model with a C statistic of 0.74 (0.66 to 0.80, 95% prediction interval 0.41 to 0.92, fig 3). The summary C statistic estimates for the remaining models were <0.70 (see supplementary fig S1).

Fig 3.

Fig 3

Open in a new tab

Pooled C statistic estimates with corresponding 95% confidence interval and approximate 95% prediction intervals for four models (see supplementary file for full data). The Knight et al 4C Mortality Score had a C statistic of 0.786 (95% confidence interval 0.78 to 0.79) in the development data and 0.767 (0.76 to 0.77) in the validation data in the original publication. The Wang et al clinical model had a C statistic of 0.88 (0.80 to 0.95) in the development data and 0.83 (0.68 to 0.93) in the validation data in the original publication. The Xie et al model had a C statistic of 0.89 (0.86 to 0.93) in the development data, 0.88 after optimism correction, and 0.98 (0.96 to 1.00) in the validation data in the original publication. The Hu et al model had a C statistic of 0.90 in the development data and 0.88 in the validation data in the original publication. UCLH=University College London; DGAE=General Directorate of Epidemiology; KCH=King’s College Hospital

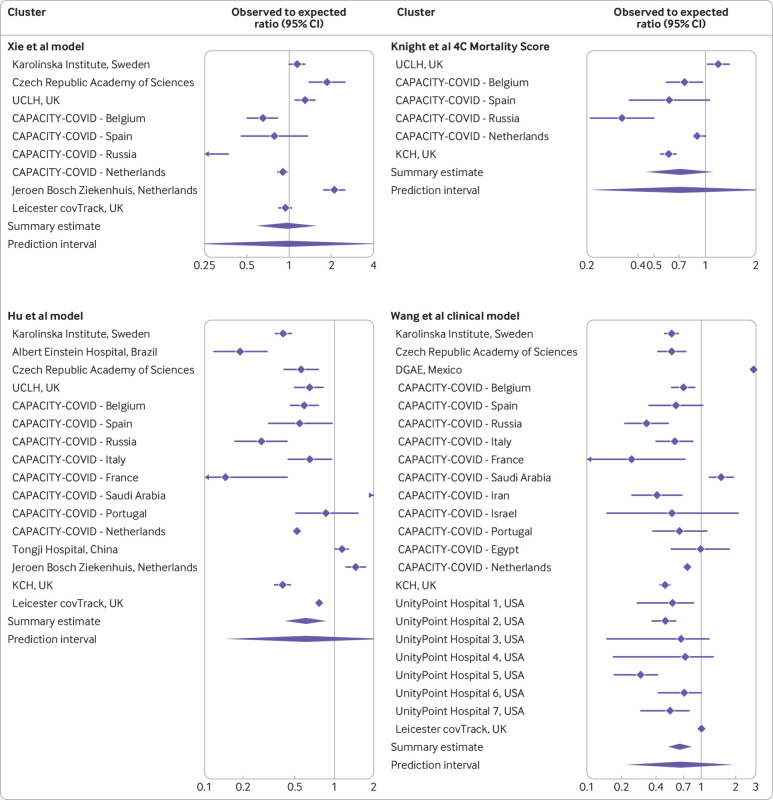
Calibration: observed to expected

The O:E ratio of the Xie model was the closest to 1, with a meta-analysis summary estimate of 0.96 (95% confidence interval 0.59 to 1.55, 95% prediction interval 0.21 to 4.28, fig 4), indicating on average the number of predicted deaths was in agreement with the number of observed deaths. However, the relatively wide 95% confidence interval and 95% prediction interval indicate some heterogeneity. The 4C Mortality Score attained an O:E ratio of 0.71 (0.45 to 1.11, 95% prediction interval 0.21 to 2.39, fig 4). The Hu model attained an O:E ratio of 0.61 (0.42 to 0.87, 95% prediction interval 0.15 to 2.48, fig 4). The Wang clinical model attained an O:E ratio of 0.65 (0.52 to 0.82, 95% prediction interval 0.23 to 1.89, fig 4). Supplementary figure S2 shows the O:E ratios of the other models and supplementary table S10 the calibration-in-the-large values.

Fig 4.

Fig 4

Open in a new tab

Pooled observed to expected ratio estimates with corresponding 95% confidence interval and approximate 95% prediction interval for four models. Estimates are presented on the log scale. See supplementary file for full data. UCLH=University College London; DGAE=General Directorate of Epidemiology; KCH=King’s College Hospital

Calibration: slope

Supplementary material D figures S3 and S4 show the forest plots for all calibration slopes. The estimate for the calibration slope was the closest to 1 for the 4C Mortality Score (1.22, 95% confidence interval 0.92 to 1.52, 95% prediction interval 0.63 to 1.80). The Wang clinical model had a calibration slope of 0.50 (0.44 to 0.56, 95% prediction interval 0.34 to 0.66). The calibration slope for the Xie model was 0.45 (0.27 to 0.63, 95% prediction interval −0.07 to 0.96) and for the Hu model was 0.32 (0.15 to 0.49, 95% prediction interval −0.34 to 0.98). Supplementary material D presents details of the remaining models that were estimated.

Sensitivity analyses—meta-regression

In the meta-regression, where all performance estimates were regressed on the country and the prediction model, the point estimate of the discrimination was the highest for the 4C Mortality Score (reference) and lowest for the Wang laboratory model. Country wise, the point estimate was highest in Israel and lowest in Mexico (see supplementary material D for point estimates and supplementary table S11 for predicted C statistics for each country).

The results for the predicted O:E ratio were less straightforward, as the predicted values for each model except the Wang laboratory model (see supplementary table S12) were greater than 1 in some countries and smaller than 1 in other countries. Similarly, this was the case for the predicted values of the calibration slopes for all models (see supplementary table S13). This implied that none of the included models were well calibrated to the data from all included countries. Supplementary table S14 shows the predicted calibration-in-the-large estimates.

Discussion

In our individual participant data meta-analysis we found that previously identified prediction models varied in their ability to discriminate between those patients admitted to hospital with covid-19 who will die and those who will survive. The 4C Mortality Score, the Wang clinical model, and the Xie model achieved the highest discrimination on average in our study and could therefore serve as starting points for implementation in clinical practice. The 4C Mortality Score could only be validated in six clusters, which might indicate limited usefulness in clinical practice. Whereas the discrimination of both Wang models and the Xie model was lower than in their respective development studies, the discrimination of the 4C Mortality Score was similar to the estimates in its development study.

Although the summary estimates of discrimination performance are rather precise owing to the large number of included patients, some are prone to substantial between cluster heterogeneity. Discrimination varied greatly across hospitals and countries for all models, but least for the 4C Mortality Score. For some models the 95% prediction interval of the C statistic included 0.5, which implies that in some countries these models might not be able to discriminate between patients with covid-19 who survive or die during hospital admission.

All models were prone to calibration issues. Most models tended to over-predict mortality on average, meaning that the actual death count was lower than predicted. The Xie model achieved O:E ratios closest to 1, but this model’s predicted risks were often too extreme: too high for high risk patients and too low for low risk patients, as quantified by the calibration slope, which was less than 1. The calibration slope was closest to 1 for the 4C Mortality Score, and this was the only model for which the 95% confidence interval included 1. All other summary calibration slopes were less than 1. This could be due to overfitting in the model development process. All the models were prone to substantial between cluster heterogeneity. This implies that local revisions (such as country specific or even centre specific intercepts) are likely necessary to ensure that risk predictions are sufficiently accurate.

Implementing existing covid-19 models in routine care is challenging because the evolution and management of SARS-CoV-2 and the consequences of changes to the virus over time and across geographical areas. In addition, the studied models were developed and validated using data collected during periods of the pandemic, and general practice might have subsequently changed. As a result, baseline risk estimates of existing prediction models (eg, the intercept term) might have less generalisability than anticipated and might require regular updating, as shown in this meta-analysis. As predictor effects might also change over time or geographical region, a subsequent step might be to update these as well.40 Since most data originate from electronic health record databases, hospital registries offer a promising source for dynamic updating of covid-19 related prediction models.41 42 43 As data from new individuals become available, the prognostic models should be updated, as well as their performance in external validation sets.41 42 43

Limitations of this meta-analysis

All the models we considered were developed and validated using data from the first waves of the covid-19 pandemic, up to April 2021, mostly before vaccination was implemented widely. Since the gathering of data, treatments for patients with covid-19 have improved and new options have been introduced. These changes are likely to reduce the overall risk of short term mortality in patients with covid-19. Prediction models for covid-19 for which adequate calibration has previously been established may therefore still yield inaccurate predictions in contemporary clinical practice. This further highlights the need for continual validation and updates.43

An additional concern is that prediction models are typically used to decide on treatment strategies but do not indicate to what extent patients benefit from individualised treatment decisions. Although patients at high risk of death could be prioritised for receiving intensive care, it would be more practical to identify those patients who are most likely to benefit from such care. This individualised approach towards patient management requires models to predict (counterfactual) patient outcomes for all relevant treatment strategies, which is not straightforward.44 45 These predictions of patients’ absolute risk reduction require estimation of the patients’ short term risk of mortality with and without treatment, which might require the estimation of treatment effects that differ by patient.45

As variants of the disease emerge, new treatments are developed, and the disease is better managed, predictor effects and the incidence of mortality due to covid-19 may vary, thereby potentially limiting the predictive performance of the models we investigated.

We only considered models for predicting mortality in patients with covid-19 admitted to hospital, as outcomes such as clinical deterioration might increase the risk of heterogeneity from variation in measurements and differences in definitions. Mortality, however, is commonly recorded in electronic healthcare systems, with limited risk for misclassification. Furthermore, it is an important outcome that is often considered in decision making.

We had to use the reported nomograms to recover the intercepts for two prediction models from one group.31 32 Ideally, authors would have adhered to the TRIPOD guidelines, which would have facilitated the evaluation of their models.

Conclusion

In this large international study, we found considerable heterogeneity in the performance of the prognostic models for predicting short term mortality in patients admitted to hospital with covid-19 across countries. Caution is therefore needed in applying these tools for clinical decision making in each of these countries. On average, the observed number of deaths was closest to the predicted number of deaths by the Xie model. The 4C Mortality Score and Wang clinical model showed the highest discriminative ability compared with the other validated models. Although they appear most promising, local and dynamic adjustments (intercept and slope updates) are needed before implementation in routine care. The usefulness of the 4C Mortality Score may be affected by the limited availability of the predictor variables.

What is already known on this topic

  • Numerous prognostic models for predicting short term mortality in patients admitted to hospital with covid-19 have been published

  • These models need to be compared head-to-head in external patient data

What this study adds

  • On average, the 4C Mortality Score by Knight et al and the clinical model by Wang et al showed the highest discriminative ability to predict short term mortality in patients admitted to hospital with covid-19

  • In terms of calibration, all models require local updating before implementation in new countries or centres

Acknowledgments

We thank the patients whose data support the findings in this study.

This study is supported by ReCoDiD (Reconciliation of Cohort data in Infectious Diseases; www.recodid.eu), COVID-PRECISE (Precise Risk Estimation to optimise COVID-19 Care for Infected or Suspected patients in diverse sEttings; www.covprecise.org), and CAPACITY-COVID (capacity-covid.eu). Together we form a large unique group of researchers and medical care providers who are actively involved in covid-19 related data gathering, management, sharing, and analysis.

We thank the participating sites and researchers, part of the COVID-PRECISE consortium and the CAPACITY-COVID collaborative consortium. CAPACITY-COVID acknowledges the following organisations for assistance in the development of the registry and/or coordination regarding the data registration in the collaborating centres: partners of the Dutch CardioVascular Alliance, the Dutch Association of Medical Specialists, and the British Heart Foundation Centres of Research Excellence. In addition, the consortium is grateful for the endorsement of the CAPACITY-COVID initiative by the European Society of Cardiology, the European Heart Network, and the Society for Cardiovascular Magnetic Resonance. The consortium also appreciates the endorsement of CAPACITY-COVID as a flagship research project within the National Institute for Health and Care Research/British Heart Foundation Partnership framework for covid-19 research. The views expressed in this paper are the personal views of the authors and may not be understood or quoted as being made on behalf of or reflecting the position of the regulatory agency/agencies or organisations with which the authors are employed or affiliated.

Web extra.

Extra material supplied by authors

Supplementary information: additional material, A-J

jonv069881.ww.pdf (1.3MB, pdf)

Contributors: FvR, JD, MvS, TT, KM, VdJ, TD, BVC, and LW were responsible for the systematic review and design of the study. VdJ and TD were responsible for the statistical analysis plan and R code. FWA, OB-C, VC, RZR, FS, YY, TT, PN, PH, SK, RK, ML, RKG, MN, LFCM, AB, CAPACITY-COVID consortium (see supplementary material E), and CovidRetro collaboration (see supplementary material F) were responsible for primary data collection. RZR, DF, MM, PH, RKG, RN, PN, MN, and ML were responsible for the primary data analysis. RZR and SKK were responsible for the meta-analysis. VdJ and RZR were responsible for the sensitivity analysis. VDJ and RZR were responsible for the initial draft of the manuscript. TD, TT, TLN, ML, FWA, LM, JD, BVC, LW, and KM revised the initial draft. RZR was responsible for the supplementary material on data and results (supplementary material A and D). VdJ and TT were responsible for the supplementary material on models (B). All authors contributed to the critical revision of the manuscript, approved the final version of the manuscript and agree to be accountable for the content. VdJ and RZR contributed equally. VdJ, TD, and KM are the guarantors of this manuscript.

Funding: This project received funding from the European Union’s Horizon 2020 research and innovation programme under ReCoDID grant agreement No 825746. This research was supported by the National Institute for Health and Care Research (NIHR) Leicester Biomedical Research Centre. RKG is supported by the NIHR. MN is supported by the Wellcome Trust (207511/Z/17/Z) and by NIHR Biomedical Research Funding to University College London and University College London Hospital. MM is supported by ELIXIR CZ research infrastructure project (MEYS grant No LM2018131), including access to computing and storage facilities. The CAPACITY-COVID registry is supported by the Dutch Heart Foundation (2020B006 CAPACITY), ZonMw (DEFENCE 10430102110006), the EuroQol Research Foundation, Novartis Global, Sanofi Genzyme Europe, Novo Nordisk Nederland, Servier Nederland, and Daiichi Sankyo Nederland. The Dutch Network for Cardiovascular Research, a partner within the CAPACITY-COVID consortium, received funding from the Dutch Heart Foundation (2020B006 CAPACITY) for site management and logistic support in the Netherlands. ML is supported by the Alexandre Suerman Stipend of the University Medical Centre Utrecht. FWA is supported by CardioVasculair Onderzoek Nederland 2015-12 eDETECT and by NIHR University College London Hospital Biomedical Research Centre. LW and BVC are supported by the COPREDICT grant from the University Hospitals KU Leuven, and by Internal Funds KU Leuven (C24M/20/064). The funders had no role in the study design; in the collection, analysis, and interpretation of data; in the writing of the report; and in the decision to submit the article for publication in the analysis and interpretation of data, in the writing of the report, and in the decision to submit the article for publication. We operated independently from the funders.

Competing interests: All authors have completed the ICMJE uniform disclosure form at https://www.icmje.org/disclosure-of-interest/ and declare: funding from the European Union’s Horizon 2020 research and innovation programme. ML and FWA have received grants from the Dutch Heart Foundation and ZonMw; FWA has received grants from Novartis Global, Sanofi Genzyme Europe, EuroQol Research Foundation, Novo Nordisk Nederland, Servier Nederland, and Daiichi Sankyo Nederland, and MM has received grants from Czech Ministry of Education, Youth and Sports for the submitted work; RKG has received grants from National Institute for Health and Care Research; FS has received an AWS DDI grant and grants from University of Sheffield and DBCLS; no financial relationships with any organisations that might have an interest in the submitted work in the previous three years; TD works with International Societiy for Pharmacoepidemiology Comparative Effectiveness Research Special Interest Group (ISPE CER SIG) on methodological topics related to covid-19 (non-financial); no other relationships or activities that could appear to have influenced the submitted work.

The manuscript’s guarantors (VdJ, TD, and KM) affirm that the manuscript is an honest, accurate, and transparent account of the study being reported; that no important aspects of the study have been omitted; and that any discrepancies from the study as originally planned (and, if relevant, registered) have been explained. All authors had access to statistical reports and tables. Authors did not have access to all data, for privacy, ethical and/or legal reasons. Authors listed under “Primary data collection” in the contributorship section had access to data and take responsibility for the integrity of the data. Authors listed under the analysis bullets in the contributorship section take responsibility for the accuracy of the respective data analyses. The corresponding author attests that all listed authors meet authorship criteria and that no others meeting the criteria have been omitted.

Dissemination to participants and related patient and public communities: We plan to share the results of this study on multiple social media platforms, including Twitter and LinkedIn. Copies of the manuscript will be sent to contributing centres, as well as being shared on the ReCoDID (www.recodid.eu ) and COVID-PRECISE (www.covprecise.org ) websites.

Ethics statements

Ethical approval

Medisch Ethische Toetsingscommissie (METC) Utrecht (protocol No 21-225) waived ethical approval.

Data availability statement

The data from Tongji Hospital, China that support the findings of this study are available from https://github.com/HAIRLAB/Pre_Surv_COVID_19. Data collected within CAPACITY-COVID is available on reasonable request (see https://capacity-covid.eu/for-professionals/). Data for the CovidRetro study are available on request from MM or the secretariat of the Institute of Microbiology of the Czech Academy of Sciences (contact via mbu@biomed.cas.cz) for researchers who meet the criteria for access to confidential data. The data are not publicly available owing to privacy restrictions imposed by the ethical committee of General University Hospital in Prague and the GDPR regulation of the European Union. We can arrange to run any analytical code locally and share the results, provided the code and the results do not reveal personal information. The remaining data that support the findings of this study are not publicly available.

References

  • 1. Dong E, Du H, Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis 2020;20:533-4. 10.1016/S1473-3099(20)30120-1  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2. Ong SWX, Young BE, Lye DC. Lack of detail in population-level data impedes analysis of SARS-CoV-2 variants of concern and clinical outcomes. Lancet Infect Dis 2021;21:1195-7. 10.1016/S1473-3099(21)00201-2  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3. Samadizadeh S, Masoudi M, Rastegar M, Salimi V, Shahbaz MB, Tahamtan A. COVID-19: Why does disease severity vary among individuals? Respir Med 2021;180:106356. https://www.resmedjournal.com/article/S0954-6111(21)00062-7/abstract. 10.1016/j.rmed.2021.106356  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4. Smith GD, Spiegelhalter D. Shielding from covid-19 should be stratified by risk. BMJ 2020;369:m2063. 10.1136/bmj.m2063  [DOI] [PubMed] [Google Scholar]
  • 5. Wynants L, Van Calster B, Collins GS, et al. Prediction models for diagnosis and prognosis of covid-19: systematic review and critical appraisal (update 2, 21 July 2020) . BMJ 2020;369:m1328. 10.1136/bmj.m1328  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6. Siontis GCM, Tzoulaki I, Castaldi PJ, Ioannidis JPA. External validation of new risk prediction models is infrequent and reveals worse prognostic discrimination. J Clin Epidemiol 2015;68:25-34. 10.1016/j.jclinepi.2014.09.007  [DOI] [PubMed] [Google Scholar]
  • 7. Altman DG, Vergouwe Y, Royston P, Moons KGM. Prognosis and prognostic research: validating a prognostic model. BMJ 2009;338:b605. 10.1136/bmj.b605  [DOI] [PubMed] [Google Scholar]
  • 8. Moons KGM, Kengne AP, Grobbee DE, et al. Risk prediction models: II. External validation, model updating, and impact assessment. Heart 2012;98:691-8. 10.1136/heartjnl-2011-301247  [DOI] [PubMed] [Google Scholar]
  • 9. Bleeker SE, Moll HA, Steyerberg EW, et al. External validation is necessary in prediction research: a clinical example. J Clin Epidemiol 2003;56:826-32. 10.1016/S0895-4356(03)00207-5  [DOI] [PubMed] [Google Scholar]
  • 10. Riley RD, van der Windt D, Croft P, Moons KGM. Prognosis Research in Healthcare: Concepts, Methods, and Impact. Oxford University Press, 2019. 10.1093/med/9780198796619.001.0001. [DOI] [Google Scholar]
  • 11. Steyerberg EW. Clinical Prediction Models: a Practical Approach to Development, Validation, and Updating. Springer Science & Business Media, 2009. 10.1007/978-0-387-77244-8. [DOI] [Google Scholar]
  • 12. Altman DG, Royston P. What do we mean by validating a prognostic model? Stat Med 2000;19:453-73.   [DOI] [PubMed] [Google Scholar]
  • 13. Wynants L, Van Calster B, Collins GS, et al. Prediction models for diagnosis and prognosis of covid-19: systematic review and critical appraisal (update 3, 12 January 2021) . BMJ 2020;369:m1328. 10.1136/bmj.m1328  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14. Bello-Chavolla OY, Bahena-López JP, Antonio-Villa NE, et al. Predicting Mortality Due to SARS-CoV-2: A Mechanistic Score Relating Obesity and Diabetes to COVID-19 Outcomes in Mexico. J Clin Endocrinol Metab 2020;105:2752-61. 10.1210/clinem/dgaa346  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15. Riley RD, Lambert PC, Abo-Zaid G. Meta-analysis of individual participant data: rationale, conduct, and reporting. BMJ 2010;340:c221. 10.1136/bmj.c221  [DOI] [PubMed] [Google Scholar]
  • 16. Debray TPA, Moons KGM, Abo-Zaid GMA, Koffijberg H, Riley RD. Individual participant data meta-analysis for a binary outcome: one-stage or two-stage? PLoS One 2013;8:e60650. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17. The CAPACITY-COVID Collaborative Consortium and LEOSS Study Group . Clinical presentation, disease course, and outcome of COVID-19 in hospitalized patients with and without pre-existing cardiac disease: a cohort study across 18 countries. Eur Heart J 2021;ehab656. [DOI] [PubMed] [Google Scholar]
  • 18. Debray TPA, Damen JAAG, Snell KIE, et al. A guide to systematic review and meta-analysis of prediction model performance. BMJ 2017;356:i6460. 10.1136/bmj.i6460  [DOI] [PubMed] [Google Scholar]
  • 19. Debray TPA, Damen JAAG, Riley RD, et al. A framework for meta-analysis of prediction model studies with binary and time-to-event outcomes. Stat Methods Med Res 2019;28:2768-86. 10.1177/0962280218785504  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20. Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982;143:29-36. 10.1148/radiology.143.1.7063747  [DOI] [PubMed] [Google Scholar]
  • 21. Cox DR. Two Further Applications of a Model for Binary Regression. Biometrika 1958;45:562-5 10.1093/biomet/45.3-4.562. [DOI] [Google Scholar]
  • 22. Snell KIE, Ensor J, Debray TPA, Moons KGM, Riley RD. Meta-analysis of prediction model performance across multiple studies: Which scale helps ensure between-study normality for the C-statistic and calibration measures? Stat Methods Med Res 2018;27:3505-22. 10.1177/0962280217705678  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23. Knapp G, Hartung J. Improved tests for a random effects meta-regression with a single covariate. Stat Med 2003;22:2693-710. 10.1002/sim.1482  [DOI] [PubMed] [Google Scholar]
  • 24. Sidik K, Jonkman JN. Robust variance estimation for random effects meta-analysis. Comput Stat Data Anal 2006;50:3681-701 10.1016/j.csda.2005.07.019. [DOI] [Google Scholar]
  • 25. Higgins JPT, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. J R Stat Soc Ser A Stat Soc 2009;172:137-59. 10.1111/j.1467-985X.2008.00552.x  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26. Buuren S, Groothuis-Oudshoorn K. mice: Multivariate imputation by chained equations in R. J Stat Softw 2011;45. https://doc.utwente.nl/78938/ 10.18637/jss.v045.i03. [DOI] [Google Scholar]
  • 27.R Core Team. R: A Language and Environment for Statistical Computing. 2021. https://www.R-project.org/. Accessed November, 9, 2021.
  • 28. StataCorp . Stata Statistical Software: Release 17. StataCorp, 2021. [Google Scholar]
  • 29.Debray TPA, de Jong VMT. metamisc: Meta-Analysis of Diagnosis and Prognosis Research Studies. 2021. https://cran.r-project.org/package=metamisc
  • 30. Robin X, Turck N, Hainard A, et al. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics 2011;12:77. 10.1186/1471-2105-12-77  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31. Collins GS, Reitsma JB, Altman DG, Moons KG. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD Statement. BMC Med 2015;13:1. 10.1186/s12916-014-0241-z  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32. Moons KGM, Altman DG, Reitsma JB, et al. Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD): explanation and elaboration. Ann Intern Med 2015;162:W1-73. 10.7326/M14-0698  [DOI] [PubMed] [Google Scholar]
  • 33. Xie J, Hungerford D, Chen H, et al. Development and external validation of a prognostic multivariable model on admission for hospitalized patients with COVID-19. medRxiv 2020;2020.03.28.20045997.
  • 34. Hu C, Liu Z, Jiang Y, et al. Early prediction of mortality risk among severe COVID-19 patients using machine learning. medRxiv 2020;2020.04.13.20064329 10.1101/2020.04.13.20064329. [DOI]
  • 35. Zhang H, Shi T, Wu X, et al. Risk prediction for poor outcome and death in hospital in-patients with COVID-19: derivation in Wuhan, China and external validation in London, UK. medRxiv 2020;2020.04.28.20082222.
  • 36. Knight SR, Ho A, Pius R, et al. ISARIC4C investigators . Risk stratification of patients admitted to hospital with covid-19 using the ISARIC WHO Clinical Characterisation Protocol: development and validation of the 4C Mortality Score. BMJ 2020;370:m3339. 10.1136/bmj.m3339  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37. Wang K, Zuo P, Liu Y, et al. Clinical and Laboratory Predictors of In-hospital Mortality in Patients With Coronavirus Disease-2019: A Cohort Study in Wuhan, China. Clin Infect Dis 2020;71:2079-88. 10.1093/cid/ciaa538  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38. Takada T, Hoogland J,, van Lieshout C, et al. Accuracy of approximations to recover incompletely reported logistic regression models depended on other available information. J Clin Epidemiol 2022;143:81-90. https://www.jclinepi.com/article/S0895-4356(21)00391-7/fulltext. [DOI] [PubMed] [Google Scholar]
  • 39. Yan L, Zhang HT, Goncalves J, et al. An interpretable mortality prediction model for COVID-19 patients. Nat Mach Intell 2020;2:283-8 10.1038/s42256-020-0180-7. [DOI] [Google Scholar]
  • 40. Toll DB, Janssen KJM, Vergouwe Y, Moons KGM. Validation, updating and impact of clinical prediction rules: a review. J Clin Epidemiol 2008;61:1085-94. 10.1016/j.jclinepi.2008.04.008  [DOI] [PubMed] [Google Scholar]
  • 41. Su TL, Jaki T, Hickey GL, Buchan I, Sperrin M. A review of statistical updating methods for clinical prediction models. Stat Methods Med Res 2018;27:185-97. 10.1177/0962280215626466  [DOI] [PubMed] [Google Scholar]
  • 42. Jenkins DA, Sperrin M, Martin GP, Peek N. Dynamic models to predict health outcomes: current status and methodological challenges. Diagn Progn Res 2018;2:23. 10.1186/s41512-018-0045-2  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43. Jenkins DA, Martin GP, Sperrin M, et al. Continual updating and monitoring of clinical prediction models: time for dynamic prediction systems? Diagn Progn Res 2021;5:1. 10.1186/s41512-020-00090-3  [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44. Nguyen TL, Collins GS, Landais P, Le Manach Y. Counterfactual clinical prediction models could help to infer individualized treatment effects in randomized controlled trials-An illustration with the International Stroke Trial. J Clin Epidemiol 2020;125:47-56. 10.1016/j.jclinepi.2020.05.022  [DOI] [PubMed] [Google Scholar]
  • 45. Hoogland J, IntHout J, Belias M, Rovers MM, Riley RD, Harrell FE. Jret al. A tutorial on individualized treatment effect prediction from randomized trials with a binary endpoint. Stat Med 2021;40:5961-81. https://onlinelibrary.wiley.com/doi/abs/10.1002/sim.9154 [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary information: additional material, A-J

jonv069881.ww.pdf (1.3MB, pdf)

Data Availability Statement

The data from Tongji Hospital, China that support the findings of this study are available from https://github.com/HAIRLAB/Pre_Surv_COVID_19. Data collected within CAPACITY-COVID is available on reasonable request (see https://capacity-covid.eu/for-professionals/). Data for the CovidRetro study are available on request from MM or the secretariat of the Institute of Microbiology of the Czech Academy of Sciences (contact via mbu@biomed.cas.cz) for researchers who meet the criteria for access to confidential data. The data are not publicly available owing to privacy restrictions imposed by the ethical committee of General University Hospital in Prague and the GDPR regulation of the European Union. We can arrange to run any analytical code locally and share the results, provided the code and the results do not reveal personal information. The remaining data that support the findings of this study are not publicly available.

Articles from The BMJ are provided here courtesy of BMJ Publishing Group

RESOURCES