Abstract
Optical imaging of calcium signals in the brain has enabled researchers to observe the activity of hundreds-to-thousands of individual neurons simultaneously. Current methods predominantly use morphological information, typically focusing on expected shapes of cell bodies, to better identify neurons in the field-of-view. The explicit shape constraints limit the applicability of automated cell identification to other important imaging scales with more complex morphologies, e.g., dendritic or widefield imaging. Specifically, fluorescing components may be broken up, incompletely found, or merged in ways that do not accurately describe the underlying neural activity. Here we present Graph Filtered Temporal Dictionary (GraFT), a new approach that frames the problem of isolating independent fluorescing components as a dictionary learning problem. Specifically, we focus on the time-traces—the main quantity used in scientific discovery—and learn a time trace dictionary with the spatial maps acting as the presence coefficients encoding which pixels the time-traces are active in. Furthermore, we present a novel graph filtering model which redefines connectivity between pixels in terms of their shared temporal activity, rather than spatial proximity. This model greatly eases the ability of our method to handle data with complex non-local spatial structure. We demonstrate important properties of our method, such as robustness to morphology, simultaneously detecting different neuronal types, and implicitly inferring number of neurons, on both synthetic data and real data examples. Specifically, we demonstrate applications of our method to calcium imaging both at the dendritic, somatic, and widefield scales.
Keywords: dictionary learning, sparse coding, calcium imaging, two-photon microscopy, re-weighted
I. Introduction
Functional optical imaging has become a vital technique for simultaneously recording large neural populations at single cell resolution hundreds of micrometers beneath the surface of the brain in awake behaving animals [1]–[3]. This class of techniques has become quite extensive, including one- two- and three- photon imaging [1], [4], [5], imaging at dendritic, somatic and widefield scales [1], [6]–[8], and imaging of various indicators of neural activity, including calcium, voltage etc. [9]–[11]. Of these methods, calcium imaging (CI) via two-photon microscopy has emerged as a dominant modality providing a practical method to optically record the calcium concentrations in neural tissue that is intrinsically representative of neural activity [1]–[3]. Novel extensions, such as volumetric imaging [12], [13] and widefield imaging [8], [14], [15], promise to even further increase the dimensionality of such data and the spatiotemporal statistics that must be leveraged for data processing and analysis.
Given the large, and ever-growing, size of CI datasets, recent advances in automated CI analysis have sought to remove the need for traditional manual annotation of such data. To date, automatic analysis of CI primarily focused on factoring the recorded video into two sets of variables: the spatial profiles1 representing the area that a neuron occupies, and the corresponding time-traces of fluorescence activity. As imaging of cell-bodies (somatic imaging) is the most prevalent, CI demixing algorithms have largely incorporated spatiotemporal regularization based on the statistics of cell-bodies, e.g., well localized spatially with sparse activity, to improve cell-finding [16].
Recent variants of optical imaging have aimed to expand the scope of accessible brain signals by imaging both larger and smaller neural structures (see Fig. 1A). At one end of this spectrum, imaging of finer-scale dendritic and spine structures captures how individual neurons communicate [17], [18]. Dendritic imaging, while also having sparse temporal statistics, can have long, thin spatial profiles that span the entire field-of-view (FOV). At the other end, cortex-wide (i.e., widefield) imaging can be achieved at resolutions too coarse to isolate activity signals of individual neurons, but instead can capture brain-wide activity patterns in head-fixed and freely moving animals [14]. At both scales, the spatial statistics of the sought-after components differ significantly from somatic imaging, and require new approaches that can be seamlessly applied across modalities.
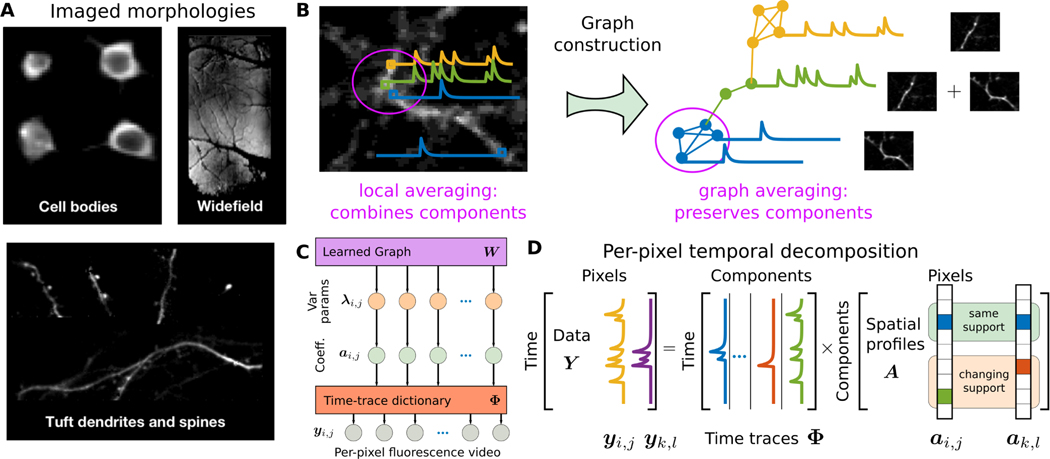
Fig. 1.
Graph-based dictionary learning for calcium image analysis. A: Optical imaging of different neural components at different scales. B: In calcium imaging, distant pixels might be highly correlated while neighboring pixels might be very different. For example, for two crossing dendrites any technique based on local averaging is prone to corruption by competing signals. By reorganizing the pixel relationships into a data-drive graph, local averaging defined by the graph can make more judicious use of temporal correlations between pixels and extract better signal estimates. C: The graphical model of GraFT organizes variables into three layers: a set of variance parameters interconnected by the data-driven graph W, a set of sparse coefficients conditioned on the parameters, and the observed fluorescence video which is linearly generated by the coefficients through the dictionary Φ. D: Matrix factorization model: GraFT emphasizes the role of time-traces and decomposes the data into a dictionary of component time-traces and correspoding spatial maps.
To fully realize the potential of functional imaging data and relate the observed neural activity to behavior and stimuli, the fundamental step for analysis is detecting neuronal components and inferring their corresponding time-traces. The majority of developed methods focus on calcium imaging, where the predominant form of automated analysis is regularized matrix factorization [19]–[22]. The matrix factorization model is formulated as
| (1) |
where , is the Nx × Ny pixel FOV sampled at T time-points, and are the M spatial profiles and corresponding time-traces for each component, and is i.i.d. Gaussian sensor noise2. Here we propose two major changes to improve the accuracy and scope of inferring fluorescing components from CI data. First, following our recent work [23], we refocus the goal of the problem onto finding the time-traces of each component. Mathematically, we reorient the matrix factorization model formulation in (1) to the model’s transpose
| (2) |
The goal for this step is not to change the model, as both formulations are trivially identical, however we aim to change the philosophy with which calcium imaging is viewed, putting the emphasis on the time-traces which are the critical component to studying how neural activity is linked to behavior, stimuli, learning, etc. This philosophical shift strongly recommends an algorithmic shift to a dictionary learning paradigm, where we treat the time-traces as the dictionary. Furthermore, the spatial regularization becomes a natural extension, correlating the dictionary decomposition between pixels [24].
The second contribution is generalizing the rigid spatial grid of the FOV to a more flexible graph model over the pixels. The additional graph modeling layer serves to remedy the fact that in many imaging scales the typical assumptions of co-localized spatial profiles (i.e., neighboring pixels are likely composed of similar components) no longer holds, e.g., in dendritic imaging (Fig. 1A-B). The graph essentially redefines what “neighborhood” means, either pulling together, or moving apart, pixels based on their temporal correlation structure and not their spatial adjacency. The graph-based regularization is used for deciding how the sparse coefficients (i.e., the spatial maps) are correlated as a function of the pixel-wise temporal correlations.
Taken together, these two complementary changes give us a flexible new tool for automated CI analysis: Graph Filtered Temporal (GraFT) dictionary learning. The graph creates a data-driven space where the correlation of dictionary coefficients over space during dictionary learning becomes a natural regularizer no matter what the scale of imaging. While we motivate and apply this method here to optical imaging data, the method itself is very broad and falls into the general class of graph-regularized dictionary learning (e.g., [25], [26]). We thus first present the algorithm in its most general form, followed by demonstrations both in simulated data, and in real recordings of somatic, dendritic and widefield data.
II. Related Work
Due to the importance of calcium imaging in neuroscientific inquiry, a number of methods have been developed to extract individual fluorescing components from calcium imaging. We summarize the main points here, and refer the interested reader to the recent review paper [16].
One class of methods focusing solely on identification of the spatial components have been mostly inspired by image segmentation. Each of these methods relies on a spatial model of the data, either preset or learned from the data. Some methods have addressed cell detection in calcium imaging as an image segmentation problem with solutions based on active contours [27] or clustering using graph cuts [28] or spectral embeddings [29], [30]. Dictionary learning has been applied to CI data where methods have focused on learning spatial dictionary elements [21], [31], [32], whose atoms represent neuronal shapes. The identified neuron shapes can then be used to estimate corresponding time-traces. Solutions are based on spatial generative models using convolutional sparse block coding [31], or learning spatial components via iterative merging and clustering [21]. Our approach, in contrast, simultaneously learns a temporal dictionary and sparse spatial coefficients.
The next class of methods take into account a spatiotemporal decomposition, identifying both the spatial footprint of the neuronal components as well as the time traces. For example, Diego and Hamprecht [32] propose a sparse space-time deconvolution which both learns a dictionary of cell shapes as well as recovers the sparse events of the corresponding time-traces. The majority of spatiotemporal approaches are based on regularized non-negative matrix factorization (NMF) [19], [20], [22], [33]–[35], and explicitly model the statistics of somatic components to improve cell-finding, specifically that somatic components are often well localized with sparse activity. Thus, these methods aim to solve the cost function
where here and represent appropriate regularizations that can vary between methods. Typical regularization terms include the component norms, the number of components, spatial and temporal sparsity, and spatial cohesion, and are necessary for interpretable results [19]–[22], [36], [37]. One of the state-of-the-art methods, Constrained NMF (CNMF) [20], [38] includes a linearized model of calcium dynamics to recover the time-traces and splits the decomposition into recovering localized cells and a background component [20]. As direct optimization is often difficult for problems of this size, alternating descent type algorithms are often employed, i.e., iteratively solving
In contrast to these approaches, GraFT while including non-negative constraints, flips the factorization model to define the critical features as temporal features (2). Furthermore, to still leverage the important spatial information in a flexible way, we incorporate a data-driven graph of the spatial domain to guide the inference of the spatial maps.
Finally, modern deep learning methods for image segmentation have also been adapted for CI analysis, and as opposed to the unsupervised approaches above, are supervised methods that require labeled training data. These methods either rely solely on spatial information [39], [40], or consider the spatiotemporal information via (2+1)D [41] convolutional networks, or 3D convolutional networks [42]. These methods solely extract spatial components and leave time-trace estimation for post-processing. So far these they have been solely applied to somatic imaging, and networks trained on somatic training data cannot extend to dendritic data (which is difficult to label) or widefield (for which ground truth segmentation does not even exist) due to the different morphology.
Previous work has suffered from several limitations. Methods focusing solely on identifying spatial components treat time-trace estimation as an afterthought, which reduces the utility of the estimated quantities in neuroscience. This also raises the need for additional post-processing steps such as neuropil (background) estimation and denoising. Matrix factorization methods can often be susceptible to noise and are, for example, particularly sensitive to initialization procedures and pre-processing (e.g., motion correction, baseline subtraction, variance normalization etc.). Finally, methods developed for specific imaging modalities and relying on calcium dynamics [20] do not generalize to new technologies and require developing extensions and adaptations for new modalities and scales [43], [44].
III. Background
A. Dictionary learning
Dictionary learning (DL) is an unsupervised method aimed at finding optimal, parsimonious representations given exemplar data [45], [46]. Consider the model in Equation (2) and the equivalent Gaussian likelihood model of the data given the coefficients A, i.e., , where σ2 is the noise variance, and assume a sparsity-inducing prior distribution p(A) over the coefficients A. The invoked sparsity encourages learned representations that parsimoniously represent the data, i.e. each data-point can be reconstructed using only a small number of dictionary elements. DL in its purest form seeks to infer only the dictionary Φ via maximum likelihood, marginalizing over the coefficients
This marginal maximum likelihood optimization involves an often intractable integral. In particular, the prior p(A) is often chosen to be an i.i.d. Laplacian distribution with parameter . To bypass this difficulty, variational methods are often employed to iteratively solve this optimization [47]–[49]. For DL, this often takes the form of alternatively solving for the sparse coefficients of a subset Γ of the data, i.e.,
| (3) |
followed by the equivalent of a stochastic gradient descent over Φ using this subset of estimated coefficients
| (4) |
for some step size μ. These steps are often termed the “inference” and “learning” steps, respectively, and stem from an interpretation as inference of the maximum marginal likelihood via an expectation-maximization procedure [47]–[49]. Traditional sparse coding assumes this model with Dirac-delta posterior approximations and an exponential (Laplacian) prior resulting in the commonly known inference/learning steps of
| (5) |
In general, more than one gradient step over Φ can be taken at once, resulting in a least-squares solution Φ = Y A#, where A# is the pseudo-inverse of A. This solution can be computed efficiently, e.g., using local updates based on sparsity [46].
The capabilities of DL to learn generic features that efficiently represent data have found use more generally in applications beyond the original image processing applications [45], [50]. For example, in hyperspectral imagery (HSI), DL has been used to identify material spectra directly from image cubes in an unsupervised manner [51], [52].
B. Sparsity-based Stochastic Filtering
The sub-selection of points Γ is often uniformly at random and thus DL does not inherently take into account relationships between exemplar data-points. More recent models, however, provide the tools to modify the sparse inference stage to take into account that some data-points may have similar decompositions [24], [53]–[55]. Specifically, a challenge in the past decade was to identify a filtering technique that enabled the correlation between the decomposition of similar data-points while maintaining the sparsity of the inferred coefficients. One such method, termed Re-weighted Spatial Filtering (RWL1-SF)—and the related work in dynamical filtering [54]—uses an auxiliary set of variables, λ, to correlate the probability of coefficients in neighboring vectors being active [24]. These approaches use the λ vector, which provide individual hyperparameters for each coefficient instead of a global λ parameter, to modify the probability of any such coefficient being active. The weights are shared between data-points, and have demonstrated marked improvements in both spatial data (HSI data [24]) and temporal data (video recovery [54]). Based on the reweighted- extension of basis pursuit denoising (BPDN) [56], [57], RWL1-SF alternates between updating the estimates λ and as
| (6) |
where is the 2D convolution between a kernel H and the coefficient image for the kth dictionary coefficient , is a vector of weights for the coefficients at point i, and β and ξ are model parameters that control the maximum value of and the rate of decay with increasing coefficient values. The convolution defines the local influence of the neighboring coefficients on the ith data-point’s decomposition. Prior work [24], [58] demonstrated that as opposed to directly constraining the coefficients via norms with their neighbors [59] (similar to filtering-via-local-averaging), filtering via a hierarchical model better maintains sparsity, and thus results in better estimates of the sparse underlying coefficient vectors. While previous work naturally fits into this deconvolution interpretation of a neighborhood [23], [24], in this work we expand on this idea and redefine what it means for two pixels to be “close”, using the formalism and tools of data-driven graph constructions and manifold learning.
C. Graph Sparse Coding
A prevalent assumption in high-dimensional data analysis is the manifold assumption, according to which in many real applications the data, while being observed in a high-dimensional feature space, actually lies on or near a low-dimensional manifold embedded in the high-dimensional ambient space [60]–[62]. Under this assumption, when learning a new representation for data, two datapoints should have a similar representation if they are intrinsically similar, i.e. close to one another on the manifold. The manifold assumption has played an increasing role in dictionary learning via graph regularized sparse coding (GRSC) [63]–[67], where the underlying manifold is represented in the discrete setting as a graph on the data-points. Formally the graph is denoted , where are the nodes in the graph, is the set of edges connecting the nodes, and W is the undirected weighted adjacency matrix for , with representing the similarity between nodes i and j. Let D be a diagonal matrix whose diagonal elements are the node degrees of the graph. The symmetric graph-Laplacian is defined as L = D − W, and is typically used in the sparse coding inference step to “encourage” datapoints who are close in the graph to employ similar representations with respect to the dictionary. For example, the coefficient inference objective in [65] is given by
| (7) |
where .
In image processing applications, GRSC enables incorporating non-local structure [68] by considering similarities in the high-dimensional feature domain as opposed to only relying on local spatial information. In this paper, we propose a new sparse coding solution, which adapts re-weighted spatial filtering [24] to a graph-based filter. Instead of the symmetric graph Laplacian, we use the normalized random-walk matrix K = D−1W. This matrix allows us to replace the spatial convolution kernel with diffusion along the data-driven graph constructed on the pixels. It can be interpreted as a non-local averaging filter [69]. Next we describe the mathematical model and derive the algorithm that accomplishes these tasks.
IV. GraFT Dictionary Learning for Functional Imaging
As DL was initially presented in the image processing literature, early applications to CI focused on learning spatial features indicative of fluorescing cells and processes [21], [31], [32]. The benefit to learning a set of temporal dictionary vectors instead is that we directly model the main objects of interest to science: the neural activity traces. To infer these traces we consider the hierarchical model in Figure 1C, which describes the statistical relationships between the time-traces Φ, data Y, presence coefficients A, weights λ, and data graph K. Mathematically we can define this model via the conditional probability distributions
| (8) |
| (9) |
| (10) |
| (11) |
Starting at the top, Equation (8) places an isotropic mean-zero, variance Gaussian likelihood on the fluorescence trace at each ith pixel given the temporal dictionary and coefficients. Next, in Equation (9), we place a mean-zero Matrix normal prior over the dictionary. The between-dictionary covariance matrix Σφ both penalizes unused time-traces (similar to [70]) and penalizes time-traces that are too similar. The prior over the coefficients (Eqn. (10)) takes the form of a sparsity-inducing Laplacian distribution where the parameter for the kth coefficient at pixel i is given by applying the i element of the filtered weights . The weights themselves, λ, follow a conjugate Gamma hyper-prior with parameters α and θ, comparable to previous work [23], [24]. Our model represents a Graph-filtered dictionary-based linear generative model where we can use a DL approach to learn the time-traces and graph-correlated sparse coefficients.
Inference under the above model can be complex and computationally intensive. We thus break down inference into three main stages: graph construction, coefficient inference and dictionary update. These stages are performed sequentially, as outlined in Algorithm 1 in an alternating minimization procedure. At a high level we are iterating over Equations (3) and (4). The main differences are a) we infer the coefficients for all data-points simultaneously, b) we replace the i.i.d. model with the graph-correlated model above, and c) we optimize the dictionaries completely at each iteration, rather than taking a single gradient step.
A. Re-weighted Graph Filtering
The first sub-step needed is to infer A under the model of Equations (8)-(11) given a fixed dictionary Φ. This involves expanding the idea of spatially filtered sparse inference (6) beyond the previous definition of neighborhood. Mathematically, we are moving from a convolutional kernel-based filtering to the more general graph filtering that defines the influence of the neighboring coefficients on the ith data vector’s decomposition weights for each dictionary index k. This optimization requires a definition of neighborhood, which previous convolution-based weights define using the spatial distance between pixel locations [23], [24]. In general applications, beyond imaging, it is difficult to define a universal pre-set sense of neighborhood, prompting the use of data-driven graph constructions. Thus can be interpreted as applying a single graph diffusion step to the coefficients. This generalizes the spatial averaging convolutional kernel to the graph setting.
There are multiple ways to construct a data-driven graph. Here we construct a graph on the pixels using k-nearest neighbors graph with the Euclidean distance between the time-traces yi. We calculate the weighted graph affinity matrix W using a Gaussian kernel for similarity, and set
| (12) |
if yi is among the k nearest-neighbors of or vice-versa. The bandwidth is set to be the self-tuning bandwidth [71], which is a local adaptive bandwidth. Then the diffusion graph filter is calculated by normalizing the rows of W as K = D−1W.
Given the filter, we can solve the maximum likelihood inverse problem defined by Equations (8), (10), (11) for A via minimizing the negative log-likelihood
The exact integration of the above integral (marginalizing over λ) is, in general intractable. The integral, however, can be very well approximated by the closed form
This prior results in a non-convex optimization negative log-likelihood cost function.
The sparse coding solution thus iteratively solves a weighted LASSO that can be interpreted as an approximation to a variational expectation-maximization (EM) optimization of the true ML problem [54], [57]. In this EM scheme, which we term Re-weighted Graph Filtering (RWL1-GF), the weights are updated at each algorithmic iteration based on smoothing with the graph-based kernel:
| (13) |
| (14) |
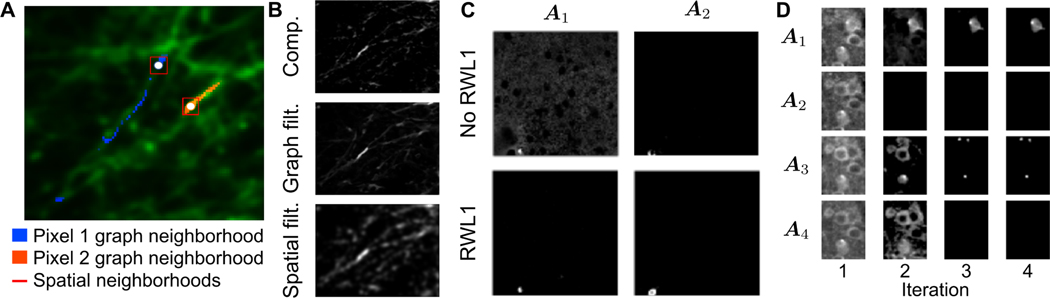
where β and θ are algorithmic parameters that depend only on the Gamma hyperparameters and can be tuned independently, and λ0 is included for numerical stability of the TFOCS [72] weighted BPDN solver. The weights λ in RWL1-GF incorporate spatial information into per-pixel solutions by sharing second-order statistics. Note that this spatial information is non-local, thus handling both components with compact spatial support such as cell-bodies, in addition to far ranging spatial components such as dendrites (Fig. 2A,B). Practically, the effect of RWL1-GF serves to better connect the entirety of neural components, as well as to suppress background activity (Fig. 2,C).
Fig. 2.
GraFT regularization effects. A. Mean projection of dense dendritic imaging. The graph neighborhood of two pixels (white points)—overlaid in blue and orange—respect the geometry of the underlying dendrites and extend far along them, compared to the extent of a spatial neighborhood of 7 × 7 (red squares). B. Graph filtering applied to estimated sparse components is limited to the pixels along dendritic structures, whereas spatial filtering blurs the pixels, incorporating information from the background into the inference. C. The RWL1 filtering becomes important for suppressing background activity (left) and finding all pixels within a component (right). D. Frobenius norm in the DL cost enables components “turning off”, thus leading to more accurate learning of the number of components in the data.
B. Updating the temporal dictionary
The second step in the dictionary learning procedure is to update the time-traces themselves with respect to a learning rule. We use the above probabilistic model to specify an appropriate cost function. In particular, the matrix normal prior induces two regularizing terms to the cost. The first penalty involves the Frobenious norm over Φ, essentially penalizing excess activity. This term serves to remove unneeded time-traces from the dictionary by setting them to zero [70] (Fig. 2D). Thus the exact number of components need not be known a prior and can be modified automatically. The second penalty, , is a function of the intra-dictionary correlations3. This penalty ensures that time-traces are not learned multiple times with minute differences stemming from subtle nonlinearities or noise. These terms come together in the cost function
| (15) |
where the parameters γ1 and γ2 trade-off these penalties. These parameters have a direct link to the covariance matrix Σφ in Equation (9) when Σφ is the sum of the identity plus a rank-one matrix.
We note that in our formulation we are optimizing the entire dictionary completely at each iteration. This is because we are inferring all pixels mixing coefficients at each iteration in order to maximally utilize the complex graph connectivity. We thus lose some of the robustness imbued by a stochastic gradient descent procedure, and therefore modify Equation (15) to ensure stable convergence. Specifically, we include a continuation term that penalizes the change in the estimate between updates. This term prevents too large a deviation in the dictionary between iterations, smoothing out the cost landscape and allowing for more robust solutions. Mathematically, the update for the estimate at the tth iteration is given by
| (16) |
where γ3 is the parameter determining the rate of change in the dictionary over iterations.
C. GraFT Dictionary Learning
The full algorithm incorporating all these elements—Data-driven graph correlations, re-weighted coefficient estimation, and robust, regularized time-trace learning—comes together in Algorithm 1. Specifically, we initialize with a graph constructed from the raw data4 temporal correlations and a randomly generated dictionary. The algorithm then iterates between using the new RWL1-GF algorithm to find approximate presence values, and the dictionary learning optimization of Equation (16). The final output is the learned dictionary .
D. Computational complexity and convergence
GraFT at its core relies on three main computationally intensive steps: the initial construction of the graph, the inference of the spatial maps via per-pixel re-weighted minimization, and the least squares optimization to update the dictionary. The graph construction only needs to be computed once, and operates over all N pixels. To construct the k-nearest neighbor graph we use Randomized approximate nearest neighbors algorithm [73]. Specifically, the algorithm iterates L times, and attempts to find k nearest neighbors for each pixel, where k is pre-specified by the user. Given k and L the total complexity of the algorithm is proportional
Algorithm 1.
GraFT DL
| Input: data Y, parameters ` |
| Initialize randomly |
| Learn the graph W via Equation (12) |
| Normalize K = D−1W |
| while not converged do |
| for all voxels do |
| Initialize |
| for l ≤ 3 do |
| Update via Equation (13) |
| Update λik via Equation (14) |
| end for |
| end for |
| Update via Equation (16) |
| end while |
to , where T is the number of time-points per pixel.
The second computational bottleneck is the weighted optimization that underlies the RWL1-GF inference procedure. Specifically, if the computational complexity of weighted is , then the computational complexity of RWL1-GF is , where N is the number of pixels, L is the number of iterations the RWL1 procedure is run and k is the number of nearest neighbors in the graph. itself can vary based on the algorithm and other considerations, such as warm-starts, and the end-distance to the optimal solution η. We found that the TFOCS package [72], which converges at an optimal rate of [72], was able to converge quickly in the RWL1 case when using past solutions as warm-starts for new iterations in the re-weighted procedure.
Finally, the least-squares optimization in Equation 16 uses the built in quadratic programming package in MATLAB, which uses an interior point method. The complexity of this algorithm is , where η bounds the solution distance from the global minima [74].
The total complexity of the algorithm can be reduced in a number of ways. First, the RWL1 optimizations per pixel are parallelizable across all pixels. Second, the full FOV can be broken down into smaller patches and later merged (as was done in, e.g., [38]). This reduces N dramatically and further reduces the number of dictionary elements M for each patch, speeding up all three of computational bottlenecks. The nearest neighbor search can be made faster by reducing the dimensionality of the data, e.g., by using PCA, thus reducing T by at least an order of magnitude.
While each stage of our algorithm is known to converge, the theoretical properties of the global convergence for GraFT are still as yet unknown. Future work will aim to fully analyze the performance, as well as seek further improvements both in the computational complexity and the convergence rate.
While the design of GraFT adds additional computational stages in performing repeated minimizations and constructing a graph, we note that our overall runtime is comparable to one of the more highly used methods in [38]. Other methods, such as Suite2p [35] and ABLE [27] are faster, however are less accurate.
V. Results
To test GraFT we assess its performance both on simulated benchmark data, as well as apply GraFT to multiple datasets across all scales of optical imaging. Specifically, we assess the utility of GraFT for somatic, dendritic and widefield data.
A. Implementation considerations
A number of practical considerations arise in our method, specifically initialization, selecting the number of neurons, setting the graph connectivity W, and parameter selection. First, we initialize Φ with random values, demonstrating a reduced sensitivity to initialization than other approaches [20]. Second, the number of dictionary components should be set to more than the expected number of neurons and background components. The sparsity and Frobenius norms serve to decay unused components (implicitly estimating the number of neurons), but cannot add new elements. We construct the weighted graph affinity matrix W using k-nearest neighbors [73], where each pixel is connected to k = 48 nearest neighbors and the affinity matrix is then symmetrized. For parameter selection, we manually adjusted parameters using intuition built from prior work in RWL1-based algorithms [23], [24], [54]. The full set of parameters to set are λ0, γ1, γ2, γ3, ξ, and β. We find that for appropriately normalized data (normalized by the the median pixel value across the entire dataset), γ2 = γ3 = 0.1 provide accurate results across all datasets. Similarly we find that γ1 = 0.2 appropriately penalizes extra components. For the RWL1 parameters, we set ξ = 2 and β = 0.01 for all experiments. This choice sets a maximum cap of 200 for the per-element sparsity parameter modulator, and enables the weights to meaningfully vary as ≈ a−1 for small values ≈ 1. The main parameter we find necessary to vary is λ0 and in our experiments we manually tune this parameter in the range 0.001 < λ0 < 0.1.
Operating on the entire dataset simultaneously can often be time-consuming. Thus, for somatic datasets we follow similar procedures in other pipelines whereby the full field-of-view is partitioned into smaller, overlapping spatial patches [20], of size ∼ 50×50 pixels with 5 pixels overlap between partitions on all sides. The number of dictionary atoms in each patch is set to be on the order of 5–10. Each partition can be analyzed in parallel, and the results are merged together to ensure that components present across patched are appropriately combined. Merging is accomplished by weighted averaging of highly correlated dictionary components (> 0.85), and then recalculating the spatial maps over all pixels.
A final consideration is the pre-processing that most algorithms use to denoise data before analysis. Optical imaging at micron scales and high framerates often incur significant additional noise. Essentially all methods use some pre-processing to reduce the noise levels, ranging from spatial and temporal low-pass filtering to deep neural networks [75]. GraFT in particular benefits from denoising in the preprocessing stage as the pixel connectivity graph is generated before the time-trace learning optimization has a chance to denoise via regularization. Specifically, the graph is based on time-trace correlations between pixels, which are sensitive to added noise. Thus, to maintain high-frequency temporal content, we denoise each pixel’s time-trace independent of all other pixels with a simple wavelet-based Block James-Stein (BJS) [76] denoising in a 2-level ‘sym4’ wavelet decomposition. With these aspects in mind, we implemented our code in MATLAB5.
B. NAOMi Simulated two-photon calcium imaging
To test our framework, we use recent advances in highly-detailed biophysical simulations that produce realistic two-photon imaging data based on computational models of anatomy and optics, i.e., the NAOMi simulator [37]. As the anatomy and time-traces are all simulated, the full spatiotemporal ground truth is known, including voxel/pixel occupancy of neurons (the spatial profiles of every fluorescing component), and the changes in fluorescence over time (each component’s time-trace). Rather than being “drawn from the generative model”, this data is generated by sampling 3D volumes of neural tissue and calcium activity, and then simulating the optical propagation and sampling to generate the CI data.
We applied GraFT to a 500 μm ×500 μm simulated field-of-view with 20,000 simulated frames. The simulation framerate was 30 Hz, and the spatial resolution was 1 μm/pixel. We compared our results to other methods from the literature: CNMF/CaImAn [20], [38]6, Suite2p [35], and PCA/ICA [19], ABLE [27], and STNeuroNet [42]. We note that of these CNMF/CaImAn, Suite2p, and PCA/ICA tend to be the most widely used, and in particular Suite2p and CNMF/CaImAn have active and ongoing code updates. Parameters for all methods were set via a combination of manual search, as well as the use of built-in parameter adjustments available in some methods, such as ABLE (see Appendix A for exact parameter settings).
As a further point of comparison, we compute the profile-assisted least-squares (PALS) time-traces based on oracle knowledge of the spatial maps. PALS uses the ground-truth spatial maps given by the NAOMi simulation, , where † indicates ground-truth, and computes the least-squares time traces as
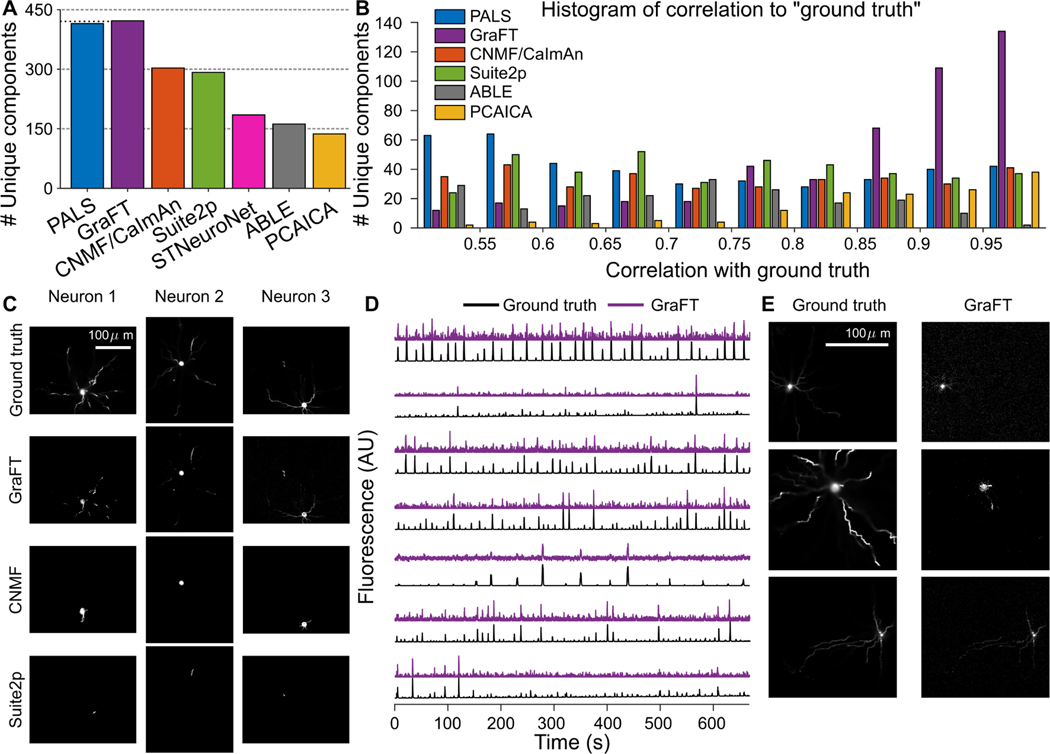
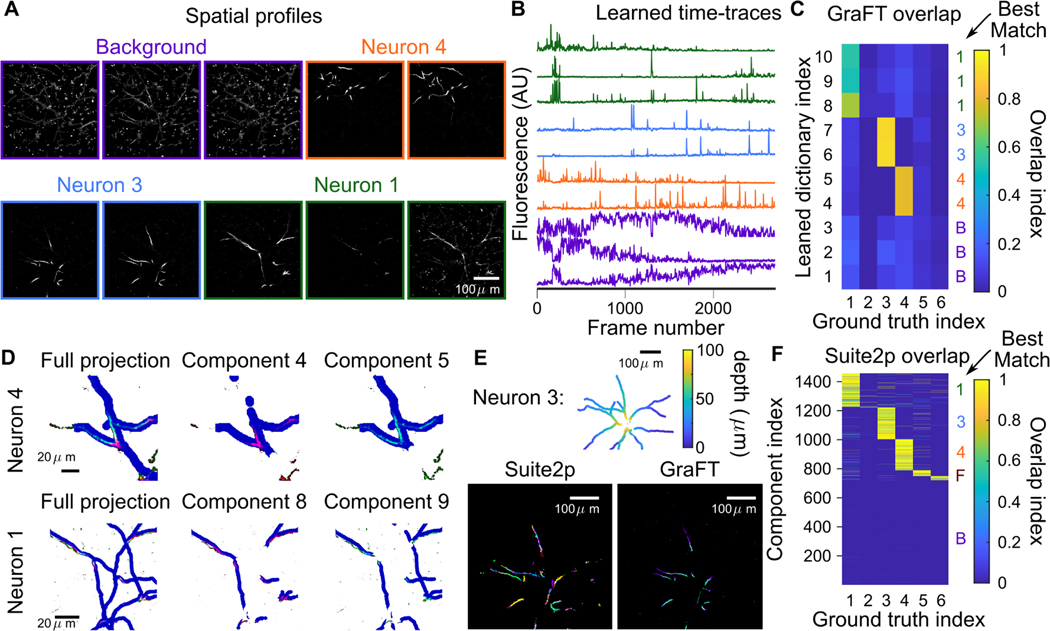
While PALS is not ground truth (the ground truth traces are independently provided by the NAOMi simulation), the traces PALS provides are an approximate baseline of per-neuron SNR and the general visibility of neurons in the dataset sans any regularization. We note, however, that they are not oracle traces, as PALS leverages no regularization or significant preprocessing (e.g., the denoising present in all other algorithms). When comparing the found components to the ground-truth traces, we find that GraFT identifies 434 unique neural components (i.e., including somatic and dendritic components), 37.76% more true positives than the next best performing algorithm, CNMF, that found 303 unique neurons, and even 19 (4.58%) more than the PALS time-traces (Fig. 3A,B,C). We note that the traces NAOMi identifies that other algorithms do not tend to have non-stereotyped shapes (Fig. 3D,E).
Fig. 3.
Assessment of GraFT and competing methods on anatomically-based calcium imaging simulations. A: The number of unique neurons found with each method. B: Histogram of temporal correlations between extracted time-traces and the ground truth traces. The GraFT dictionary better matches the ground-truth compared to other methods. C: GraFT finds more complete spatial profiles for neurons that are also identified by other methods, and dendrites are better identified. D: Time-traces for neurons not found via other methods correlate well with ground truth traces, but have low SNR. E: Neurons found only with GraFT tend to have less localized spatial profiles.
C. Two-photon population calcium imaging
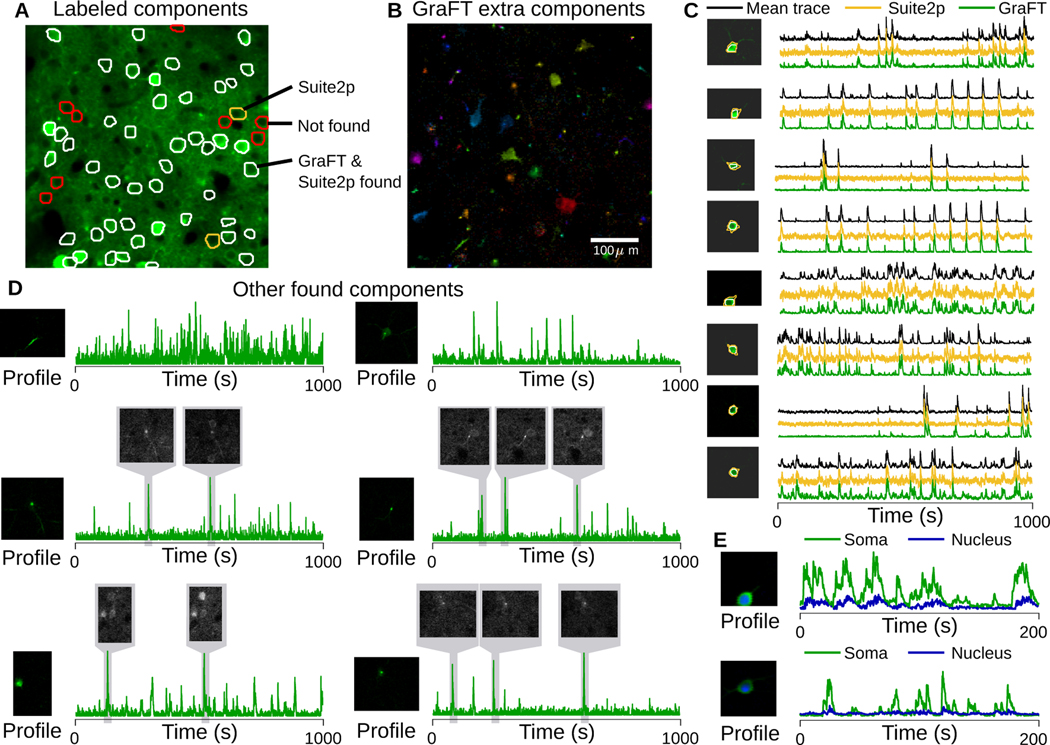
In addition to assessing GraFT on simulated data, we furthermore test GraFT on data from the NeuroFinder [77] dataset. NeuroFinder data includes two-photon calcium imaging at the somatic scale, along with manually annotated spatial maps for neurons. We note that while these labeled spatial maps are provided, they are limited in their use as ground truth. Some neurons are visible but do not fire and are thus functionally unidentifiable, while other active neurons are not labeled [42]. In addition, other clearly fluorescing components might not be labeled as they may represent dendritic (apical or otherwise) components. Note for example that there are obvious bright cells and dendritic components in Fig. 4A not labeled as ground-truth.
Fig. 4.
Somatic imaging from NeuroFinder. A: Mean projection of the field-of-view (green) with overlay of all manually identified cells. Most cells are identified by both GraFT and Suite2p (white), some (red) were not identified at all (i.e., due to inactivity), and a couple were identified only by Suite2p (yellow). B: All non-background (well-isolated) profiles found by GraFT that were not in the ground-truth, including many apical dendrites, several somatic components and other small components. C: Comparison of the average trace of the manually labeled spatial profile with GraFT and Suite2p time-traces. D: Additional identified components beyond the manual labels exhibited smaller, dendritic structure, even when these are in proximity to brighter somatic components (right column, middle). Local averages of frames from the movie demonstrate that these components do exist in the data and were simply not labeled manually. E: The sensitivity of GraFT enables for the cytoplasmic (green) and nuclear (blue) portions of individual neurons to be identified.
We ran GraFT on a 445 μm × 445 μm field of view in area vS1 of mouse visual cortex, recorded at 8 Hz. For comparison we ran Suite2p, optimizing parameters of both algorithms manually. Suite2p was run with ‘diameter’ set to 12, and 500 SVD components, and the remaining parameters were set to their default. In total, GraFT and Suite2p identified 150 and 103 components respectively. GraFT and Suite2p found 46 and 48 out of 56 labeled components respectively (Fig. 4A-C). Comparing the time-traces estimated by both approaches (Fig. 4C), the GraFT time-traces tend to have less noise, despite not explicitly regularizing for smoothness. Suite2p traces tend to exhibit negative “dips” indicating poor neuropil correction.
In addition, GraFT identifies a number of extra neuronal components, including somas, dendritic segments and apical dendrites. Further inspection revealed that movie frames during active bursts in the learned dictionary time-traces matched the spatial profiles, verifying that these components do represent real fluorescing components in the data (Fig. 4D). Identifying these additional components individually removes their localized activity from the soma-adjacent areas, improving neuropil estimation and subtraction.
Finally, we noted that some somatic components appeared to be found in duplicate. We explored these cases and discovered that GraFT was, in fact, separating the cytoplasmic and nuclear portions of these cells (Fig. 4E). When plotted together, the time-traces for each pair follow closely together, with a muted and delayed response for the nuclear component relative to the cytoplasmic. As expected, the nuclear signal is lower amplitude and has slower dynamics. Thus, GraFT is able to partition even very similar activity patterns, revealing potentially interesting differences within individual cells.
D. Sparsely labeled dendritic imaging
One of the principle benefits of GraFT is to enable the extraction of non-compact components in the data. While somatic-scale imaging contains some dendritic components, dendritic-specific imaging at high zoom levels drastically changes the spatial statistics of the data. We thus next apply GraFT to dendritic imaging of both sparsely and densely labeled tissue. First we use the sparsely labeled data to assess the accuracy of GraFT via comparisons to anatomical measurements.
We imaged dendritic calcium signals in an awake sparsely-labeled mouse using a Bruker 2P-Plus microscope with an dual-beam Insight X3 laser (Spectra Physics), equipped with an 8 kHz bidirectional resonant galvo scanner and a Nikon 16X CFI Plan Fluorite objective (NA 0.8). Fluorescence was split by a 565LP dichroic and filtered with 525/70 and 595/50 bandpass filters before collection on two GaAsP photomultiplier tubes (Hamamatsu H10770PB-40 and H11706–40, respectively). We imaged a square region 375 μm per side, 768 × 768 pixels. Frames were acquired at 20 Hz and 13-bit resolution. Illumination was centered at a wavelength of 940 nm, and laser power exiting the objective was in the range of 30–40 mW. PMT gains were set to minimize saturated pixels during calcium transients.
We supplemented the functional imaging with anatomical imaging to provide ground truth for assessing the GraFT decompositions. Immediately following calcium imaging experiments, we anaesthetized the mouse with 1–2% isoflurane and placed a heating pad underneath the mouse. We then recorded large field-of-view volumetric z-stacks (750 μm square, 1536×1536 pixels, 5 micron axial spacing) of mRuby2 fluorescence by illuminating at 1045nm using the galvo scanners at a 10 microsecond dwell time. This z-stack was manually traced, to recover a depth tracing of the dendrites of each of the individual neurons in the FOV, which serves as spatial ground-truth for assessment. The depth tracing reveals 6 neurons, 3 of which were active in the functional imaging data and identified by GraFT.
As a preprocessing step, we apply a structural mask to the imaging video which yields 91,737 pixels in the FOV. The mask was constructed by thresholding a mean projection of the mRuby2 fluorescence channel from the functional imaging session. For sparsely labeled data, GraFT identified 10 distinct components in the data (Fig. 5A,B). Seven of these components are well localized with distinct firing patterns, and three are baseline/background components. Comparisons to the anatomical image stack show that GraFT identifies both background components with approximately equal overlap across all dendrites and components with high overlap with only one anatomically traced dendrite structure (Fig. 5C).
Fig. 5.
Sparse dendrite data. A-B: 10 temporal dictionary elements and 10 corresponding spatial maps identified with GraFT. Dendritic components extend throughout the entire image. C: Correlations of GraFT components with anatomical labels. D: The two identified components found per ground truth structure (colored in red and green channels) overlap with slightly different portions of the dendritic structure (dilated in blue). The full ground truth projected onto one image on the right column, and the middle and right plots showing the ground truth at slices shifted by 2 μm. This reveals that each component corresponds to a slightly different axial portion of the neuron, indicating that the difference is due to axial motion. E: Suite2p run in “dendrite” mode identifies approximately 200 ROIs for Neuron 3 (different colors in the lower-left plot) comprise this single neuron. GraFT picks up the same neuron with two components: each corresponding to a different depth. F: Correlations of Suite2p ROIs with anatomical labels.
Interestingly, some components appeared to capture different spatial portions of the same dendritic branch. We further examined this effect and noted that these components are capturing the same anatomical object but at depth difference of approximately 10–15 μm (Fig. 5D). Thus GraFT is identifying the same anatomical component, but modulated due to the slow axial drift in the plane of imaging.
Since GraFT does not impose that the spatial maps need to be contiguous or spatially connected, we are able to extract disconnected segments of the same dendrite within a single spatial map. In comparison, we ran Suite2p—set to ‘dendrite’ mode with ‘diameter’ set to 5 and all other parameters set to their default values—which extracted 1,457 ROIs (note that we removed all ROIs Suite2p found that did not overlap with the structural mask used for GraFT). Of the extracted ROIs approximately 650 correspond to the 3 active neurons in the FOV, with about 200 ROIs matching each active neuron (Fig. 5E-F). GraFT thus easily enables studying the dynamics of the dendrite as a whole, whereas Suite2p requires post-processing by which ROIs need to be clustered together based on temporal correlations in order to study the dendrite as whole.
E. Dense dendritic imaging
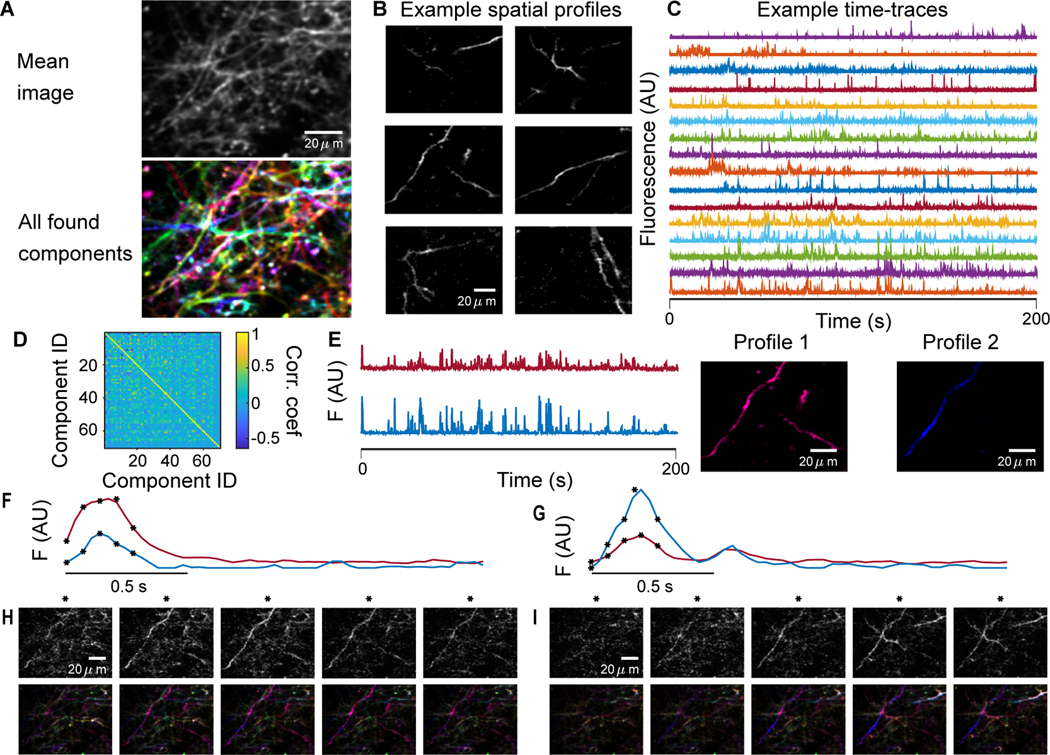
While sparse imagine provides the possibility of comparisons to anatomical imaging and tracing, we are also interested in the ability of GraFT to disentangle components in images of tissue with a higher density of labeled dendrites. We thus run GraFT on a dataset of densely labeled dendrites using the same imaging parameters as the sparse dataset. Overall GraFT extracted 60 individual components from the dataset, including many with spatial maps stretching across the entire field-of-view (Fig. 6A). In comparison, Suite2p extracted approximately 800 ROIs (results not shown). The time-traces for the GraFT components are more uniformly firing over the span of the imaging session, indicating a lack of axial drift that was noticed in the sparse imaging data (Fig. 6B). Furthermore, these components are significantly diverse in their time-traces (Fig. 6C), as can be seen in the correlation matrix between time traces (Fig. 6D). One interesting finding in this decomposition is the presence of multiple time-traces identified in the same dendritic branch (Fig. 6E). Specifically, for one pair of components we find that one of the components is much more localized around one small branch, specifically about one spine (Profile 2 in Fig. 6E). The time-traces for these two components, while correlated, do have different activity levels (Fig. 6F-G) as can be verified by tracking the components in the raw fluorescence video (Fig. 6H-I). In Fig. 6H Profile 1 appears brighter, as implied by Fig. 6F and in Fig. 6I Profile 2 appears brighter, as implied by Fig. 6G. Thus these profiles are truly independent components and not an artifact of the method.
Fig. 6.
Dense dendrite data. A: Many fluorescing components are highly overlapping as seen in the mean projection (top). GraFT identifies 60 components in this dataset (bottom; each component is plotted with a different color). B: Examples of spatial maps recovered by GraFT. C: Example time-traces demonstrate a diversity of activity patterns that overlap in time. D: Correlation matrix of the estimated time-traces indicates the decomposition is capturing sufficiently different time-traces. E: The two highest correlated time-traces, along with the corresponding spatial maps, indicate these two overlap significantly, perhaps both representing pieces of one true dendritic component. F-I: Closer inspection of the spatial profiles reveals that profile 2 actually represents a different process in the dendrite centered around a spine in the lower-left-hand corner of the image. Two example bursts of activity (F and G) demonstrate that these components have different activity at different times. Frames from the starred time-points in F and G are shown in H and I respectively, with the raw data frame in the top row and the reconstruction in the bottom row.
F. One-photon widefield imaging
Similar to dendritic imaging, widefield imaging captures activity patterns that can stretch across the entire field-of-view. Widefield imaging systems can be designed to capture dynamics across large areas of the surface of cortex at a resolution coarser than single neurons. Thus widefield captures global activity patterns across the brain’s surface, similar to very high density EEG, giving us a second imaging modality to test GraFT’s ability to capture complex neural activity patterns.
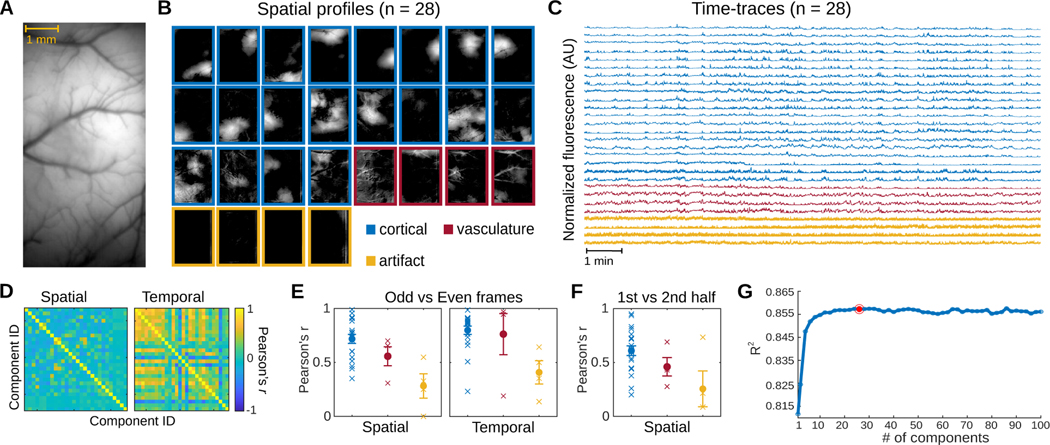
We applied GraFT to a 20-minute long video of calcium dynamics within an 8 mm × 4 mm FOV of the dorsal cortex of a GCaMP6f expressing transgenic rat. The recording was performed using a head-mounted widefield microscope [14] as the rat freely moved around its homecage (Fig. 7A). With 28 components, GraFT extracted a diverse set of dynamics from the widefield data (Fig. 7B-C). Most of the learned components featured spatial profiles that are either localized or widely distributed across the cortical surface (n = 20/28). Pixels belonging to observable vasculature were assigned low weights among these spatial profiles. In contrast, four other components showed spatial profiles with vasculature structures. The remaining components have spatial profiles with vertical stripes in the peripherals of the FOV suggesting they represent artifacts related to the imaging procedure. The 28 components exhibit unique spatial profiles but have time-traces that correlate to varying degrees (Fig. 7D).
Fig. 7.
Widefield data. A. The imaged cross-cortical field-of-view. B. GraFT spatial maps when run with n = 28 components. Three main classes of components can be identified: broad cortical activity (blue), vasculature-based fluorescence (red), and imaging artifacts (yellow). C. Time-traces for the n = 28 case, color coded by the class of the component. D. GraFT demonstrates inference consistency, as demonstrated by comparing the learned time-traces and spatial maps for GraFT run only on the odd and even frames separately. Pearson’s correlation between best-matched spatial and temporal maps are very high for all maps and dictionary elements for the case of n = 28. E. Breakdown of the diagonal elements of the correlation matrix in D by class (cortical, vascular, and artifactual). The learned spatial maps and time-traces for cortical maps was the most consistent, with the highest correlation values. F. A similar analysis of spatial maps learned separately across the first half and the second half of the imaging session for n = 28 demonstrates that consistent cortical areas are observed during the same behavior even over different epochs. G. Variance explained as a function of the number of dictionary elements shows a plateau at approximately 0.855 with ≈ 20 components.
To test the reliability of GraFT in extracting relevant dynamics in widefield calcium imaging data, we trained GraFT on odd and even frames of the widefield video separately (Fig. 7E). The learned components exhibit spatial profiles that overlapped between the odd and even frames (average Pearson’s r = 0.6324), indicating that GraFT can reliably recover dynamics in the data only from a portion of the total frames. We then trained GraFT on the first and second halves of the widefield video (Fig. 7F). The average coefficient along the diagonal of the spatial correlation matrix between the first and second half of the video is equal to 0.5376, suggesting that GraFT was able to extract sufficiently stable components in the video. We further assessed the performance of GraFT in extracting components in the widefield data, by measuring the R-squared between the original video and reconstructions based on the learned components. GraFT was able to capture a significant proportion of variance in the original data with only one component (R2 = 0.812) and achieved maximum performance with 44 components (R2 = 0.858). While the performance of GraFT increases with additional components, the change in performance seems to greatly decrease with ≈ 20 components (Fig. 7G). Together, these results indicated that GraFT reliably captures the spatial and temporal calcium dynamics recorded via widefield imaging in freely moving rodents.
VI. Discussion and future work
We propose a new algorithmic framework for dictionary learning based on data-driven graphs. These graphs permit the learning process to explicitly take advantage of correlated occurrences of features in the data. Specifically, we combined ideas from spatially correlated re-weighted- filtering with random walk diffusion on graphs to create a re-weighted- graph-filtering inference algorithm. Learning of the linear generative model under the RWL1-GF model was performed via a variationally-motivated dictionary learning algorithm and was able to uncover the fundamental time-traces in spatiotemporal data with complex spatial correlations.
A core component of GraFT is the graph-filtering algorithm leveraging graph-based analyses, such as graph signal processing; a class of approaches that is proving powerful across functional neuroimaging applications [78]–[80]. Our module is based on prior algorithmic development in both dynamic and spatial filtering that focused on the inference of correlated sparse vectors [24], [54]. These earlier works showed a clear improvement of using the hierarchical Laplacian prior over other filtering approaches that constrained the difference between coefficients of related data vectors via an norm (similar to the Kalman filter in the dynamic filtering case). It is an interesting question, however, if the filtering procedures or the graph constructions over which the filtering is implemented, can be improved, e.g., by changing the filtering approach or using alternative graph filters. We will explore such extensions in future work.
While this powerful framework could have many potential uses, we design and demonstrate this algorithm on the important and rapidly developing application of functional fluorescence microscopy. We applied GraFT to learn the time-traces from these complex and high dimensional data that are vital to understanding neural function. In particular we showed benefits both in standard somatic imaging, as well as in more complex dendritic and widefield imaging settings.
For somatic imaging we demonstrated via experiments on biophysical simulations the ability to identify many more true components in a given dataset than competing methods. These gains primarily come from components with highly non-somatic statistics. Despite the flexibility to capture such components, GraFT can still capture somatic signals, as demonstrated on both simulation and annotated Neurofinder data. In both cases the time-traces obtained by GraFT were less noisy despite having no temporal regularization or explicit modeling of the calcium dynamics (e.g., an autoregressive model as in [38]). The lack of explicit temporal modeling further endowed GraFT with a sensitivity to different signal time-scales. Specifically, in real data GraFT was able to identify and separate the cytoplasmic and nuclear signals within the same cell. These signals essentially have the same spike-train driving both signals, albeit with different temporal signal dynamics.
In dendritic imaging we validated the ability of GraFT to recover fluorescing dendrites via comparisons against manual anatomical tracing. In contrast to current methods, i.e., Suite2p in “dendritic mode”, GraFT does not force locality and compactness of components, which enabled GraFT to identify farreaching and segmented dendritic structures more accurately and more completely. Similarly, in widefield imaging GraFT was able to identify highly non-localized activity patterns in the data, including both hemodynamic and calcium related signals. Moreover, GraFT was able to isolate artifacts of the imaging procedure, effectively removing their effects from the true signal components. Finally, GraFT, as opposed to current widefield analysis [43], does not rely on anatomical atlases, which are not always available, and thus is a more generalizable approach.
One of the primary advantages GraFT has over previous algorithms is the reorganization of spatial distances onto a graph. Prior CI analysis methods all combat the variability in SNR, dynamic range, and other sources of error, e.g., residual motion, by using a signal model over the expected shapes of the components. This model can either be explicit, e.g. total variation normalization [22], implicit, e.g., by classifying correct/incorrect components via a trained classifier [38], or learned, e.g., via cell detection in trained convolutional neural networks [42]. GraFT avoids requiring any such spatial signal models by instead imposing the sparsity over time-traces: i.e., no more than a few neurons can overlap in a given pixel. For most calcium imaging settings, this assumption is reasonable due to the thin plane over which imaging is performed. The axial extent is not large enough for more than 2–3 components to overlap.
We note that for volumetric imaging using axially elongated beams, more components per pixel may be captured in the data [81]. This is especially true in dense labeling and in tissue with dense neuronal packing (e.g., hippocampus). Imaging of thick, dense volumes thus may not abide by the sparsity constraint as used in GraFT. What would need to be tested is if the total number of active coefficients is low enough per-pixel to justify the regularization. Similarly, completely overlapping components can occur in volumetric imaging if no axial encoding is accounted for (e.g., via spectroscopy [12]). In these cases the two components would be merged into a single component. Again, this situation is highly unlikely in standard single-plane imaging due to the thinness of the volume as compared to the sizes of neural processes.
GraFT is inherently based on identifying independent time-traces. Thus, if two neurons had exactly the same time-traces, the signals would be combined and the neurons would not be able to be distinguished from each other. While this is a potential issue in very short recordings, we note that in long recordings GraFT is able to separate very similar time-traces, e.g., somatic and nuclear signals from the same cell (Fig. 4E). Thus, GraFT is best suited to analyzing longer recordings where individual components are less likely to be completely synchronous. This does not impose large limitations, as many imaging sessions in neuroscience consist of thousands of frames.
A third current limitation, which is present in all algorithms, is the assumption of Gaussian noise. Low-light imaging, such as is being used for voltage imaging [82] can have more pronounced shot-noise reminiscent of Poisson statistics. In future work we will expand our noise model to better account for these statistics, such as the noise model used for denoising in [58], essentially creating extensions that will allow for low-light image analysis.
One aspect we note, that is not solved in any algorithm to date, is the effect of axial motion artifacts on the identified components. In the sparse imaging session we are able to identify manually when the resulting components represent the same neurons at different depths due to drift, however a full solution would require significant additional post-processing to the model that includes 3D spatial information.
GraFT, as with other segmentation algorithms, identifies multiple types of components. For example, in the Neurofinder data GraFT identified somas, nuclei, dendritic segments and rising apical dendrites. Currently, sub-selecting based on component type is a per-analysis choice, however future work (e.g., the post-processing classifier in CaImAn [38]) can provide additional methods that automatically classify the output of GraFT and other algorithms. As fluorescence microscopy continues to expand, for example in new volumetric imaging techniques across scales [12], [81], [83]–[87], we expect GraFT to become even more critical to the important fist step of extracting single component activities.
With regards to parameter setting we observed that the same basic parameters, with the exception of the sparsity parameter λ, produced good results across all imaging scales. This observation reinforces the ability for the graph learning step to incorporate the natural spatial correlations into the same algorithmic core. With one parameter left, manual adjustments or simple grid searches were sufficient to obtain good performance. Further improvements can be obtained by leveraging, for example, BayesOpt [88], in optimizing parameters.
Finally, our method is broader than fluorescence microscopy data and is applicable to other imaging modalities, e.g., hyper-spectral imaging, where spatial structure can be informative, but features can interact in complex ways. In such cases, the dictionary is in the feature space, and not necessarily temporal, e.g., spectral bands in hyper-spectral imaging. Our framework also falls under the general class of graph-based dictionary learning in graph signal processing, an emerging area focused on the analysis of high-dimensional signals that lie on a graph, or for which a graph can be learned based on correlated features. We leave the extension of our framework to additional domains for future work.
Acknowledgments
The authors thank Samuel Schickler for running the comparison experiment of Suite2p on sparse dendritic imaging.
Appendix
A. Algorithm parameter setting
For CNMF, CaImAn, Suite2p, and PCA/ICA parameters were manually adjusted to optimize the number of unique neurons identified. For ABLE, we use the built in visualization tool for parameter identification. For STNeuroNet we used the pre-trained model provided with the code.
For CNMF/CaImAn, CNMF provided better results than CaImAn, and the parameters used were fr = 30, tsub = 5, patch_size = [40,40], overlap = [8,8], K = 7, tau = 6, p = 0, and num_bg = 1. For Suite2P we used diameter = 12, DeleteBin = 1, sig = 0.5, nSVDforROI = 1000, NavgFramesSVD = 5000, signalExtraction = ‘surround’, innerNeuropil = 1, outerNeuropil = Inf, minNeuropilPixels = 400, ratioNeuropil = 5, imageRate = 30, sensorTau = 0.5, maxNeurop = 1, sensorTau = 0.5, and redmax = 1. For PCA/ICA we used fr = 30, ssub = 2, tsub = 10, nPCs = 1000, smwidth = 3, thresh = 2, arealims = 10, mu = 0.5, dt = tsub/fr, deconvtau = 0, spike_th = 2, norm = 1. While figures displayed typical outputs (i.e., denoised traces from CNMF), all quantitative comparisons were computed using the raw DF/F traces returned by each algorithm. For ABLE we used radius = 7, alpha = 0.45, lambda=10, mergeCorr = 0.95, and mergeDuring = 1.
Footnotes
We prefer to use the terminology “spatial profiles” over the alternate term “Regions of Interest” (ROIs), as we believe it more accurately captures the physical nature of these shapes as 2D projections of 3D anatomical shape.
While the noise in CI is actually not Gaussian, at higher photon counts the noise is more Gaussian-like, and we, as many others, have found that Gaussian noise assumptions a practical simplification.
In this definition we use the sav or sum-absolute-value which is the direct analog of the norm for vectors, i.e., . This is necessary as the has an alternate technical definition as the maximum norm of all the columns
We note that the graph normalization D−1 will never be singular since in our construction a vertex is always connected to itself and thus the minimal vertex degree of a node 1. Thus D is a diagonal matrix with diagonal elements for all i.
Code is available at https://github.com/adamshch/GraFT-analysis
We note that CNMF and CaImAn are based on the same approach, and so we present here the best performance across both code-bases in MATLAB and Python.
Contributor Information
Adam S. Charles, Department of Biomedical Engineering, Kavli Neuroscience Discovery Institute, Center for Imaging Science, and Mathematical Institute for Data Science, Johns Hopkins University, Baltimore, MD 21287 USA
Nathan Cermak, Technion - Israel Institute of Technology, Haifa, Israel, 31096. R. Affan and B. Scott are with the Department of Psychological and Brain Sciences, Boston University, MA 02215 USA.
Rifqi Affan, Department of Psychological and Brain Sciences, Boston University, MA 02215 USA.
Ben Scott, Department of Psychological and Brain Sciences, Boston University, MA 02215 USA.
Jackie Schiller, Technion - Israel Institute of Technology, Haifa, Israel, 31096. R. Affan and B. Scott are with the Department of Psychological and Brain Sciences, Boston University, MA 02215 USA.
Gal Mishne, Halıcıoğlu Data Science Institute and the Neurosciences Graduate Program, UC San Diego, CA 92093 USA.
References
- [1].Denk W, Strickler JH, and Webb WW, “Two-photon laser scanning fluorescence microscopy,” Science, vol. 248, no. 4951, pp. 73–6, 1990. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/2321027 [DOI] [PubMed] [Google Scholar]
- [2].Mank M. and Griesbeck O, “Genetically encoded calcium indicators,” Chem Rev, vol. 108, no. 5, pp. 1550–64, 2008. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/18447377 [DOI] [PubMed] [Google Scholar]
- [3].Tian L, Akerboom J, Schreiter ER, and Looger LL, “Neural activity imaging with genetically encoded calcium indicators,” Prog Brain Res, vol. 196, pp. 79–94, 2012. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/22341322 [DOI] [PubMed] [Google Scholar]
- [4].Jung JC, Mehta AD, Aksay E, Stepnoski R, and Schnitzer MJ, “In vivo mammalian brain imaging using one-and two-photon fluorescence microendoscopy,” Journal of neurophysiology, vol. 92, no. 5, pp. 3121–3133, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Rodriguez C, Liang Y, Lu R, and Ji N, “Three-photon fluorescence microscopy with an axially elongated bessel focus,” Optics letters, vol. 43, no. 8, pp. 1914–1917, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Sofroniew NJ, Flickinger D, King J, and Svoboda K, “A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging,” Elife, vol. 5, p. e14472, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Yasuda R, Harvey CD, Zhong H, Sobczyk A, Van Aelst L, and Svoboda K, “Supersensitive ras activation in dendrites and spines revealed by two-photon fluorescence lifetime imaging,” Nature neuroscience, vol. 9, no. 2, p. 283, 2006. [DOI] [PubMed] [Google Scholar]
- [8].Homma R, Baker BJ, Jin L, Garaschuk O, Konnerth A, Cohen LB, Bleau CX, Canepari M, Djurisic M, and Zecevic D, “Wide-field and two-photon imaging of brain activity with voltage and calcium-sensitive dyes,” in Dynamic Brain Imaging. Springer, 2009, pp. 43–79. [DOI] [PubMed] [Google Scholar]
- [9].Badura A, Sun XR, Giovannucci A, Lynch LA, and Wang SSH, “Fast calcium sensor proteins for monitoring neural activity,” Neurophotonics, vol. 1, no. 2, p. 025008, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Kannan M, Vasan G, Huang C, Haziza S, Li JZ, Inan H, Schnitzer MJ, and Pieribone VA, “Fast, in vivo voltage imaging using a red fluorescent indicator,” Nature methods, vol. 15, no. 12, p. 1108, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Shen Y, Wu S-Y, Rancic V, Aggarwal A, Qian Y, Miyashita S-I, Ballanyi K, Campbell RE, and Dong M, “Genetically encoded fluorescent indicators for imaging intracellular potassium ion concentration,” Communications biology, vol. 2, no. 1, p. 18, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Song A, Charles AS, Koay SA, Gauthier JL, Thiberge SY, Pillow JW, and Tank DW, “Volumetric two-photon imaging of neurons using stereoscopy (vtwins),” Nature methods, vol. 14, no. 4, p. 420, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Beaulieu DR, Davison IG, Bifano TG, and Mertz J, “Simultaneous multiplane imaging with reverberation multiphoton microscopy,” arXiv preprint arXiv:1812.05162, 2018. [DOI] [PMC free article] [PubMed]
- [14].Scott BB, Thiberge SY, Guo C, Tervo DGR, Brody CD, Karpova AY, and Tank DW, “Imaging cortical dynamics in gcamp transgenic rats with a head-mounted widefield macroscope,” Neuron, vol. 100, no. 5, pp. 1045–1058, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Barson D, Hamodi A, Shen X, Lur G, Constable R, Cardin J, Crair M, and Higley M, “Simultaneous mesoscopic and two-photon imaging of neuronal activity in cortical circuits,” bioRxiv, 2018. [Online]. Available: https://www.biorxiv.org/content/early/2018/11/11/468348 [DOI] [PMC free article] [PubMed]
- [16].Benisty H, Song A, Mishne G, and Charles AS, “Data processing of functional optical microscopy for neuroscience,” arXiv preprint arXiv:2201.03537, 2022. [DOI] [PMC free article] [PubMed]
- [17].Kerlin A, Mohar B, Flickinger D, MacLennan BJ, Dean MB, Davis C, Spruston N, and Svoboda K, “Functional clustering of dendritic activity during decision-making,” Elife, vol. 8, p. e46966, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Suratkal SS, Yen Y-H, and Nishiyama J, “Imaging dendritic spines: molecular organization and signaling for plasticity,” Current Opinion in Neurobiology, vol. 67, pp. 66–74, 2021. [DOI] [PubMed] [Google Scholar]
- [19].Mukamel EA, Nimmerjahn A, and Schnitzer MJ, “Automated analysis of cellular signals from large-scale calcium imaging data,” Neuron, vol. 63, no. 6, pp. 747–760, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Pnevmatikakis EA, Soudry D, Gao Y, Machado TA, Merel J, Pfau D, Reardon T, Mu Y, Lacefield C, Yang W. et al. , “Simultaneous denoising, deconvolution, and demixing of calcium imaging data,” Neuron, vol. 89, no. 2, pp. 285–299, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Petersen A, Simon N, and Witten D, “SCALPEL: Extracting Neurons from Calcium Imaging Data,” ArXiv e-prints, 2017. [DOI] [PMC free article] [PubMed]
- [22].Haeffele BD and Vidal R, “Structured low-rank matrix factorization: Global optimality, algorithms, and applications,” IEEE transactions on pattern analysis and machine intelligence, 2019. [DOI] [PubMed]
- [23].Mishne G. and Charles AS, “Learning spatially-correlated temporal dictionaries for calcium imaging,” in ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019, pp. 1065–1069. [Google Scholar]
- [24].Charles AS and Rozell CJ, “Spectral superresolution of hyperspectral imagery using reweighted spatial filtering,” IEEE Geosci. Remote Sens. Lett, vol. 11, no. 3, pp. 602–606, 2014. [Google Scholar]
- [25].Yankelevsky Y. and Elad M, “Dual graph regularized dictionary learning,” IEEE Transactions on Signal and Information Processing over Networks, vol. 2, no. 4, pp. 611–624, 2016. [Google Scholar]
- [26].Zhu X, Li X, Zhang S, Ju C, and Wu X, “Robust joint graph sparse coding for unsupervised spectral feature selection,” IEEE transactions on neural networks and learning systems, vol. 28, no. 6, pp. 1263–1275, 2016. [DOI] [PubMed] [Google Scholar]
- [27].Reynolds S, Abrahamsson T, Schuck R, Jesper Sjöstöm P, Schultz SR, and Dragotti PL, “ABLE: An activity-based level set segmentation algorithm for two-photon calcium imaging data,” eNeuro, 2017. [DOI] [PMC free article] [PubMed]
- [28].Spaen Q, Asín-Achá R, Chettih SN, Minderer M, Harvey C, and Hochbaum DS, “Hnccorr: A novel combinatorial approach for cell identification in calcium-imaging movies,” eNeuro, vol. 6, no. 2, 2019. [Online]. Available: https://www.eneuro.org/content/6/2/ENEURO.0304-18.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Mishne G, Coifman RR, Lavzin M, and Schiller J, “Automated cellular structure extraction in biological images with applications to calcium imaging data,” bioRxiv, 2018.
- [30].Cheng X. and Mishne G, “Spectral embedding norm: Looking deep into the spectrum of the graph laplacian,” SIAM Journal on Imaging Sciences, vol. 13, no. 2, pp. 1015–1048, 2020. [Online]. Available: 10.1137/18M1283160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Pachitariu M, Packer AM, Pettit N, Dalgleish H, Hausser M, and Sahani M, “Extracting regions of interest from biological images with convolutional sparse block coding,” in NIPS, 2013, pp. 1745–1753.
- [32].Diego F. and Hamprecht FA, “Sparse space-time deconvolution for calcium image analysis,” in NIPS, 2014, pp. 64–72.
- [33].Maruyama R, Maeda K, Moroda H, Kato I, Inoue M, Miyakawa H, and Aonishi T, “Detecting cells using non-negative matrix factorization on calcium imaging data,” Neural Networks, vol. 55, pp. 11–19, 2014. [DOI] [PubMed] [Google Scholar]
- [34].Pnevmatikakis E. and Paninski L, “Sparse nonnegative deconvolution for compressive calcium imaging: algorithms and phase transitions,” NIPS, 2013.
- [35].Pachitariu M, Packer AM, Pettit N, Dalgleish H, Hausser M, and Sahani M, “Suite2p: beyond 10,000 neurons with standard two-photon microscopy,” bioRxiv, 2016.
- [36].Gauthier JL, Koay SA, Nieh EH, Tank DW, Pillow JW, and Charles AS, “Detecting and correcting false transients in calcium imaging,” bioRxiv, p. 473470, 2018. [DOI] [PMC free article] [PubMed]
- [37].Song A, Gauthier JL, Pillow JW, Tank DW, and Charles AS, “Neural anatomy and optical microscopy (naomi) simulation for evaluating calcium imaging methods,” Journal of Neuroscience Methods, vol. 358, p. 109173, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Giovannucci A, Friedrich J, Gunn P, Kalfon J, Koay SA, Taxidis J, Najafi F, Gauthier JL, Zhou P, Tank DW et al. , “Caiman: An open source tool for scalable calcium imaging data analysis,” bioRxiv, p. 339564, 2018. [DOI] [PMC free article] [PubMed]
- [39].Klibisz A, Rose D, Eicholtz M, Blundon J, and Zakharenko S, “Fast, simple calcium imaging segmentation with fully convolutional networks,” in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Springer, 2017, pp. 285–293. [Google Scholar]
- [40].Kirschbaum E, Bailoni A, and Hamprecht FA, “Disco: Deep learning, instance segmentation, and correlations for cell segmentation in calcium imaging,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2020, pp. 151–162. [Google Scholar]
- [41].Apthorpe NJ, Riordan AJ, Aguilar RE, Homann J, Gu Y, Tank DW, and Seung HS, “Automatic neuron detection in calcium imaging data using convolutional networks,” in NIPS, 2016.
- [42].Soltanian-Zadeh S, Sahingur K, Blau S, Gong Y, and Farsiu S, “Fast and robust active neuron segmentation in two-photon calcium imaging using spatiotemporal deep learning,” Proceedings of the National Academy of Sciences, vol. 116, no. 17, pp. 8554–8563, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Saxena S, Kinsella I, Musall S, Kim SH, Meszaros J, Thibodeaux DN, Kim C, Cunningham J, Hillman EMC, Churchland A, and Paninski L, “Localized semi-nonnegative matrix factorization (locanmf) of widefield calcium imaging data,” PLOS Computational Biology, vol. 16, no. 4, pp. 1–28, 04 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Zhou P, Resendez SL, Rodriguez-Romaguera J, Jimenez JC, Neufeld SQ, Giovannucci A, Friedrich J, Pnevmatikakis EA, Stuber GD, Hen R, Kheirbek MA, Sabatini BL, Kass RE, and Paninski L, “Efficient and accurate extraction of in vivo calcium signals from microendoscopic video data,” eLife, vol. 7, p. e28728, Feb 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Olshausen BA and Field DJ, “Emergence of simple-cell receptive field properties by learning a sparse code for natural images,” Nature, vol. 381, no. 6583, p. 607, 1996. [DOI] [PubMed] [Google Scholar]
- [46].Aharon M, Elad M, and Bruckstein A, “k-svd: An algorithm for designing overcomplete dictionaries for sparse representation,” IEEE Trans. Signal Process, vol. 54, no. 11, pp. 4311–4322, 2006. [Google Scholar]
- [47].Dayan P, Abbott LF, and Abbott L, Theoretical neuroscience: computational and mathematical modeling of neural systems. MIT press Cambridge, MA, 2001. [Google Scholar]
- [48].Olshausen BA, “Learning linear, sparse, factorial codes,” MIT Tech Report, 1996.
- [49].Barello G, Charles A, and Pillow J, “Sparse-coding variational auto-encoders,” bioRxiv, p. 399246, 2018.
- [50].Elad M, Figueiredo MAT, and Ma Y, “On the role of sparse and redundant representations in image processing,” Proceedings of the IEEE, vol. 98, no. 6, pp. 972–982, 2010. [Google Scholar]
- [51].Charles AS, Olshausen BA, and Rozell CJ, “Learning sparse codes for hyperspectral imagery,” IEEE J. Sel. Topics Signal Process, vol. 5, no. 5, pp. 963–978, 2011. [Google Scholar]
- [52].Zhou M. et al. , “Nonparametric bayesian dictionary learning for analysis of noisy and incomplete images,” IEEE Trans. Image Process, vol. 21, no. 1, pp. 130–144, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Zhang Z. and Rao BD, “Sparse signal recovery with temporally correlated source vectors using sparse bayesian learning,” IEEE Journal of Selected Topics in Signal Processing, vol. 5, no. 5, pp. 912–926, 2011. [Google Scholar]
- [54].Charles AS, Balavoine A, and Rozell CJ, “Dynamic filtering of time-varying sparse signals via 1 minimization,” IEEE Trans. Signal Process, vol. 64, no. 21, pp. 5644–5656, 2016. [Google Scholar]
- [55].Qin J, Li S, Needell D, Ma A, Grotheer R, Huang C, and Durgin N, “Stochastic greedy algorithms for multiple measurement vectors,” arXiv preprint arXiv:1711.01521, 2017.
- [56].Candes EJ, Wakin MB, and Boyd SP, “Enhancing sparsity by reweighted ℓ1 minimization,” Journal of Fourier analysis and applications, vol. 14, no. 5–6, pp. 877–905, 2008. [Google Scholar]
- [57].Garrigues P. and Olshausen B, “Group sparse coding with a laplacian scale mixture prior,” NIPS, 2010.
- [58].Charles AS, Song A, Koay S, Tank DW, and Pillow JW, “Stochastic filtering of two-photon imaging using reweighted ℓ1,” in ICASSP, 2017, pp. 1038–1042.
- [59].Charles A, Asif MS, Romberg J, and Rozell C, “Sparsity penalties in dynamical system estimation,” in 2011 45th annual conference on information sciences and systems. IEEE, 2011, pp. 1–6. [Google Scholar]
- [60].Roweis ST and Saul LK, “Nonlinear dimensionality reduction by locally linear embedding,” Science, vol. 290, no. 5500, pp. 2323–2326, 2000. [DOI] [PubMed] [Google Scholar]
- [61].Belkin M. and Niyogi P, “Laplacian eigenmaps for dimensionality reduction and data representation,” Neural Computation, vol. 15, no. 6, pp. 1373–1396, 2003. [Google Scholar]
- [62].Coifman RR and Lafon S, “Diffusion Maps,” Applied and Computational Harmonic Analysis, vol. 21, no. 1, pp. 5–30, 2006. [Google Scholar]
- [63].Bengio S, Pereira F, Singer Y, and Strelow D, “Group sparse coding,” 2009.
- [64].Gao S, Tsang IW-H, Chia L-T, and Zhao P, “Local features are not lonely – laplacian sparse coding for image classification,” in 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2010, pp. 3555–3561. [Google Scholar]
- [65].Zheng M, Bu J, Chen C, Wang C, Zhang L, Qiu G, and Cai D, “Graph regularized sparse coding for image representation,” IEEE transactions on image processing, vol. 20, no. 5, pp. 1327–1336, 2010. [DOI] [PubMed] [Google Scholar]
- [66].Forero PA, Rajawat K, and Giannakis GB, “Prediction of partially observed dynamical processes over networks via dictionary learning,” IEEE transactions on signal processing, vol. 62, no. 13, pp. 3305–3320, 2014. [Google Scholar]
- [67].Yankelevsky Y. and Elad M, “Theoretical guarantees for graph sparse coding,” Applied and Computational Harmonic Analysis, 2019. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S106352031830232X
- [68].Buades A, Coll B, and Morel J-M, “A non-local algorithm for image denoising,” in 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), vol. 2. IEEE, 2005, pp. 60–65. [Google Scholar]
- [69].Singer A, Shkolnisky Y, and Nadler B, “Diffusion interpretation of nonlocal neighborhood filters for signal denoising,” SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 118–139, 2009. [Google Scholar]
- [70].Karklin Y. and Lewicki MS, “A hierarchical bayesian model for learning nonlinear statistical regularities in nonstationary natural signals,” Neural computation, vol. 17, no. 2, pp. 397–423, 2005. [DOI] [PubMed] [Google Scholar]
- [71].Zelnik-Manor L. and Perona P, “Self-tuning spectral clustering,” in Advances in neural information processing systems, 2005, pp. 1601–1608.
- [72].Becker SR, Candes EJ, and Grant MC, “Templates for convex conè problems with applications to sparse signal recovery,” Mathematical programming computation, vol. 3, no. 3, p. 165, 2011. [Google Scholar]
- [73].Jones PW, Osipov A, and Rokhlin V, “Randomized approximate nearest neighbors algorithm,” Proceedings of the National Academy of Sciences, vol. 108, no. 38, pp. 15679–15686, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Potra FA and Wright SJ, “Interior-point methods,” Journal of computational and applied mathematics, vol. 124, no. 1–2, pp. 281–302, 2000. [Google Scholar]
- [75].Lecoq J, Oliver M, Siegle JH, Orlova N, Ledochowitsch P, and Koch C, “Removing independent noise in systems neuroscience data using deepinterpolation,” Nature Methods, vol. 18, no. 11, pp. 1401–1408, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Cai TT, “On block thresholding in wavelet regression: Adaptivity, block size, and threshold level,” Statistica Sinica, pp. 1241–1273, 2002.
- [77].Berens P, Theis L, Stone JS, Sofroniew N, Tolias A, Bethge M, and Freeman J, “Standardizing and benchmarking data analysis for calcium imaging,” in COSYNE, 2017.
- [78].Huang W, Bolton TAW, Medaglia JD, Bassett DS, Ribeiro A, and Van De Ville D, “A graph signal processing perspective on functional brain imaging,” Proceedings of the IEEE, vol. 106, no. 5, pp. 868–885, 2018. [Google Scholar]
- [79].Li R, Yuan X, Radfar M, Marendy P, Ni W, O’Brien TJ, and Casillas-Espinosa PM, “Graph signal processing, graph neural network and graph learning on biological data: A systematic review,” IEEE Reviews in Biomedical Engineering, pp. 1–1, 2021. [DOI] [PubMed]
- [80].“Smooth graph learning for functional connectivity estimation,” NeuroImage, vol. 239, p. 118289, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Lu R, Sun W, Liang Y, Kerlin A, Bierfeld J, Seelig J, Wilson DE, Scholl B, Mohar B, Tanimoto M, Koyama M, Fitzpatrick D, Orger MB, and Ji N, “Video-rate volumetric functional imaging of the brain at synaptic resolution,” bioRxiv, 2016. [DOI] [PMC free article] [PubMed]
- [82].Platisa J, Ye X, Ahrens AM, Liu C, Chen IA, Davison IG, Tian L, Pieribone VA, and Chen JL, “High-speed low-light in vivo two-photon voltage imaging of large neuronal populations,” bioRxiv, 2021. [DOI] [PMC free article] [PubMed]
- [83].Botcherby EJ, Juskaitis R, and Wilson T, “Scanning two photon fluorescence microscopy with extended depth of field,” Optics Communications, vol. 268, no. 2, pp. 253–260, 2006. [Online]. Available: hGotoISIi://WOS:000242302100011 [Google Scholar]
- [84].Theriault G, Cottet M, Castonguay A, McCarthy N, and De Koninck Y, “Extended two-photon microscopy in live samples with bessel beams: steadier focus, faster volume scans, and simpler stereoscopic imaging,” Front Cell Neurosci, vol. 8, p. 139, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Gobel W, Kampa BM, and Helmchen F, “Imaging cellular network dynamics in three dimensions using fast 3d laser scanning,” Nat Methods, vol. 4, no. 1, pp. 73–9, 2007. [DOI] [PubMed] [Google Scholar]
- [86].Yang W, Miller JE, Carrillo-Reid L, Pnevmatikakis E, Paninski L, Yuste R, and Peterka DS, “Simultaneous multi-plane imaging of neural circuits,” Neuron, vol. 89, no. 2, pp. 269–84, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Grewe BF, Voigt FF, van ‘t Hoff M, and Helmchen F, “Fast two-layer two-photon imaging of neuronal cell populations using an electrically tunable lens,” Biomed Opt Express, vol. 2, no. 7, pp. 2035–46, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Martinez-Cantin R, “Bayesopt: a bayesian optimization library for nonlinear optimization, experimental design and bandits.” J. Mach. Learn. Res, vol. 15, no. 1, pp. 3735–3739, 2014. [Google Scholar]