Abstract
Here we seek to gain insight into changes in the plasma membrane of live cells upon the application of osmotic stress using Laurdan, a fluorescent probe that reports on membrane organization, hydration, and dynamics. It is known that the application of osmotic stress to lipid vesicles causes a decrease in Laurdan’s generalized polarization (GP), which has been interpreted as an indication of membrane stretching. In cells, we see the opposite effects, as GP increases when the osmolarity of the solution is decreased. This increase in GP is associated with the presence of caveolae, which are known to disassemble and flatten in response to osmotic stress.
Significance
Cells can experience multiple stresses in vivo. Furthermore, the application of osmotic stress is used as a biophysical tool to interrogate membrane processes in vitro. We sought to investigate the consequences of osmotic stress on the plasma membrane properties using the fluorescent probe Laurdan. Unexpectedly, we find that osmotic stress leads to an increase in generalized polarization in live cells. The opposite change in generalized polarization has been observed in model lipid bilayers, reminding us there are limitations to the utility of model systems in understanding cell membrane behavior. Despite years of research, the cell membrane still has ways to surprise us.
Introduction
The plasma membrane consists of a phospholipid bilayer with embedded proteins that mediate the communication with the external environment and control the transportation of molecules, such as nutrients and ions. The lipid bilayer is the structural backbone of the cellular membrane. For many years, it was believed to just provide a passive physical barrier to nonspecific, non-protein mediated passage of molecules (1). However, recent research has revealed that the lipid components can play an active role in cell physiology (2,3). It is now appreciated that the phospholipid bilayer is highly complex and dynamic, and it plays regulatory roles in many physiological processes such as cell signaling, synaptic neurotransmission, and metabolism.
Remarkably, cells possess two to three times the membrane needed to sustain their shape (4,5). The excess of membrane is primarily stored in the caveolae, 60- to 80-nm cup-shaped invaginations (6,7). The caveolae were first observed in electron microscopy experiments as pits with flask-shaped morphology and uniform curvature. These structures play an essential role in the cellular response to acute mechanical stress as they disassemble and flatten in a rapid process independent of ATP or actin (8). Thus, caveolae serve as a membrane reservoir to protect the cell (8). This role is of great physiological significance since cells can experience multiple stresses in vivo. For example, epithelial cells in our lungs are exposed to cycles of mechanical stress when we breathe, endothelial cells are constantly exposed to shear flow, and myocytes endure stress and strain regularly when muscles contract and relax (9, 10, 11, 12).
Here we investigate if the physical-chemical properties of the plasma membrane are altered upon the application of osmotic stress. We monitor changes in the membrane environment using Laurdan, a fluorescent probe that has been used for years to study lipid organization and dynamics in synthetic and biological membranes (13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29). Laurdan is an amphipathic fluorophore that incorporates into lipid bilayers and biological membranes. It is polarity sensitive and has been used previously to monitor changes in membrane bending, tension, and/or domain formation. When excited, Laurdan undergoes charge separation, creating a strong dipole. The coupling between the Laurdan dipole and the dipoles of nearby water molecules in the membrane results in a redshift in the Laurdan emission spectrum. This hydration-induced redshift can be assessed by quantifying a single parameter, the so-called generalized polarization (GP) (22,28,29). The value of GP decreases as Laurdan is exposed to an increasingly polar environment and increases as the environment becomes less polar. Thus, Laurdan has been used to study the hydration of membranes (30). However, recent work has expanded the understanding of the Laurdan fluorescence response (31, 32, 33, 34). It has been pointed out that free water molecules are sparse in lipid bilayers. Instead, the water molecules are tightly bound to lipid carbonyls, and thus the mobility of the lipids, along with the bound water, can also affect the fluorescence properties of Laurdan. Specifically, the GP of Laurdan has been shown to increase with decreased lipid mobility and to decrease as the lipid mobility is increased (31, 32, 33, 34).
Laurdan fluorescence has been used previously in the context of lipid vesicles that have been subjected to osmotic stress (35). In particular, a decrease in GP has been reported as a function of osmotic stress (35). These observations were interpreted as a proof for increased membrane tension and membrane stretching, which allows water molecules to enter the hydrophobic interior of the membrane. In this work, we sought to determine if similar effects are observed in the plasma membranes of live cells in response to osmotic stress.
Materials and methods
Cell culture
Experiments were performed in Chinese hamster ovary (CHO) and mouse embryonic fibroblast (MEF) cells. The MEFs included a (+/+) version that is homozygous for the caveolin-1 gene (or wild-type) and a (−/−) knockout.
The cells were cultured in Dulbecco’s modified Eagle medium (DMEM), supplemented with 10% fetal bovine serum (ThermoFisher, Waltham, MA), 1.8 g/L d-glucose, 1.5 g/L sodium bicarbonate, and 1 mM nonessential amino acids (NEEA). Cells were seeded in 35-mm glass-bottom collagen-coated dishes (MakTek, Ashland, MA) at a density of 2.0 × 104. Cells were kept in an incubator at 37°C with 5% carbon dioxide.
To apply the osmotic stress, cells were incubated with a hypotonic solution (swelling media) buffered with 25 mM HEPES, prepared with serum-free DMEM media (starvation media), and increasing amounts of diH2O. These different solutions contained 0, 10, 25, 40, 45, 50, 60, 65, 75, 90, 95, and 100% diH2O. Twenty-four hours after seeding, Laurdan from a methanol stock was premixed with 1 mL of starvation media to a concentration of 10 μM. The cells were incubated with the Laurdan solution for 15 min at 37°C and then washed with 1x PBS to remove the excess Laurdan. The swelling media was added to the cells at the preset imaging temperature at least 5 min before imaging. The temperature was adjusted using a Stable Z stage (Bioptechs, Butler, PA).
Vesicles
CHO cells were seeded into a six-well plate at a density of 5 × 104, as described in (36). Twenty-four hours after seeding, cells were vesiculated as previously described (37). Briefly, cells were first rinsed three times with 1x PBS supplemented with 750 μM calcium and 500 μM magnesium (CM-PBS). Then the cells were incubated with 10 μM Laurdan premixed with the vesiculation buffer for 1 h at 37°C. This buffer consisted of CM-PBS with 25 mM formaldehyde and 0.5 mM 1,4-dithiothreitol (DTT). The formaldehyde was quenched with 125 mM glycine. Vesicles were transferred to a four-well glass-bottom imaging slide (MakTek) and let to settle down for 1 h before imaging.
Laurdan spectra acquisition and analysis
Laurdan spectra were acquired with a two-photon microscope equipped with the OptiMis spectral imaging system (Aurora Spectral Technologies, Grafton, WI) (38). Laurdan was excited at 780 nm with a femtosecond Mai-Tai laser (Spectra-Physics, Milpitas, CA). The system allows the acquisition of full spectra for each pixel in the frame, and it records the emission in a stack of 200 images at different wavelengths, ∼1 nm apart. To extract the Laurdan spectra, the image stacks were analyzed using the ImageJ software to plot the emission spectra in the selected membrane region of interest, as shown in Fig. 1. The generalized fluorescence of Laurdan was calculated according to the equation:
| (1) |
where is the integrated spectral intensity in a 20-nm window centered at 430 nm, and is the integrated spectral intensity in a 20-nm window centered at 490 nm.
Figure 1.
(A) CHO cells at 90% media dilution with diH2O. A region of interest from a cell (yellow) is analyzed, and the average Laurdan spectrum is calculated and shown in Fig 3A. (B) Laurdan spectrum from a single pixel within the yellow region. To see this figure in color, go online.
Cells (or vesicles), under all conditions studied, were imaged in three or more independent experiments. Each data set was derived from at least 20 (typically 40 to 50) individual cells or vesicles. One or two regions of plasma membrane were analyzed per cell (as shown in Fig. 1 A). These regions were selected randomly, from membrane areas that were in focus, and not in contact with intracellular organelles or neighboring cells.
Statistical analysis
The statistical analysis was based on one-way ANOVA using GraphPad Prism 8.3.
Osmolarity measurements
Measurements were performed in the Johns Hopkins Hospital Core lab using an automated A2O osmometer (Advanced Instruments, Norwood, MA).
Results
Here we sought to understand how the application of osmotic stress changes the plasma membrane environment. Toward this goal, we used Laurdan as a membrane probe, as its emission spectrum depends on the environment. In the experiments, 10 μM Laurdan was added to CHO cells and incubated for 15 min. Cells were washed and subjected to reversible osmotic stress in serum-free media with increasing amounts of diH2O. After 5 min, the emission spectra of Laurdan in CHO plasma membranes were acquired as described in Methods. From these spectra, the GP of Laurdan was calculated using Eq. 1.
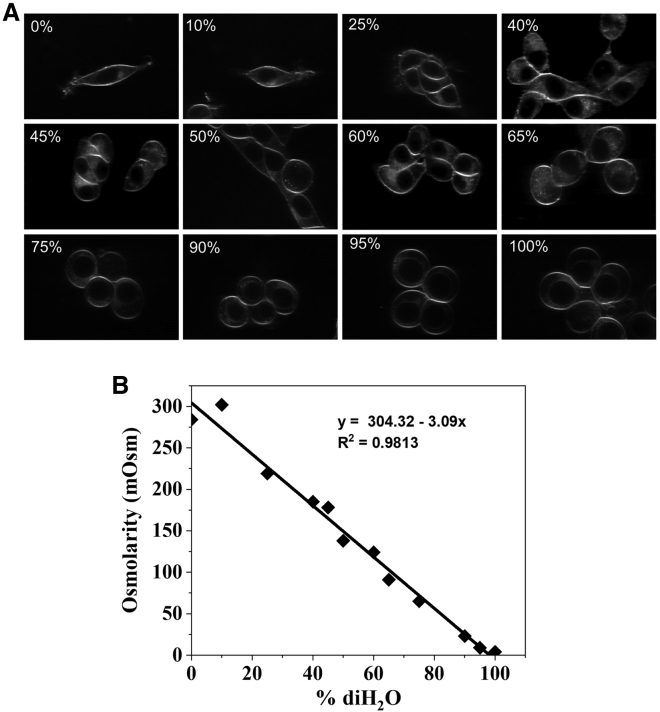
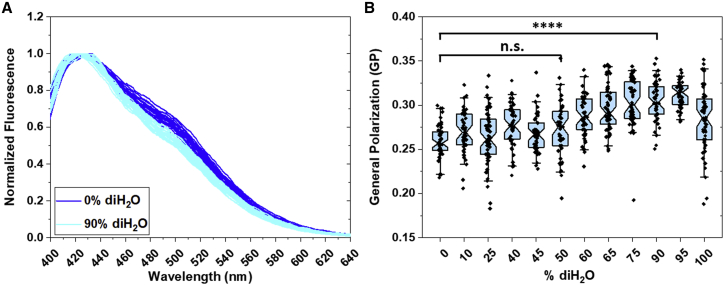
Integrated fluorescence images of cells at different media dilutions are shown in Fig. 2 A. The osmolarities of the media dilutions are shown in Fig. 2 B. Typical Laurdan spectra are shown in Fig. 3 A, for the cases of 0% and 90% media dilution with diH2O. In a standard medium (0% diH2O), we observe an emission maximum at ∼430 nm and a second less pronounced peak at ∼490 nm. The application of osmotic stress at 90% diH2O decreases the 490-nm peak. In Fig. 3 B, the Laurdan GP was calculated for all experimental conditions investigated. As diH2O in the swelling media increases, the GP stays constant up to 60% diH2O. GP increases afterward up to 95% diH2O. Imaging at 100% diH2O revealed a marked decrease in GP, likely indicating water penetration in the membrane. With time, many of the cells in 100% diH2O could not withstand the osmotic pressure, and their membranes ruptured.
Figure 2.
(A) Integrated fluorescence images of cells labeled with Laurdan, at different media dilutions with diH2O. (B) Osmolarity of the solutions as a function of diH2O content.
Figure 3.
(A) Emission spectra of Laurdan in CHO cells at 0% and 90% media dilution. (B) Laurdan GP in CHO cells as a function of diH2O media dilution. GP was calculated using Eq. 1. The notched box line represents the mean; the top and bottom represent the 75th and 25th percentiles, respectively, and the bars represent the standard deviations. To see this figure in color, go online.
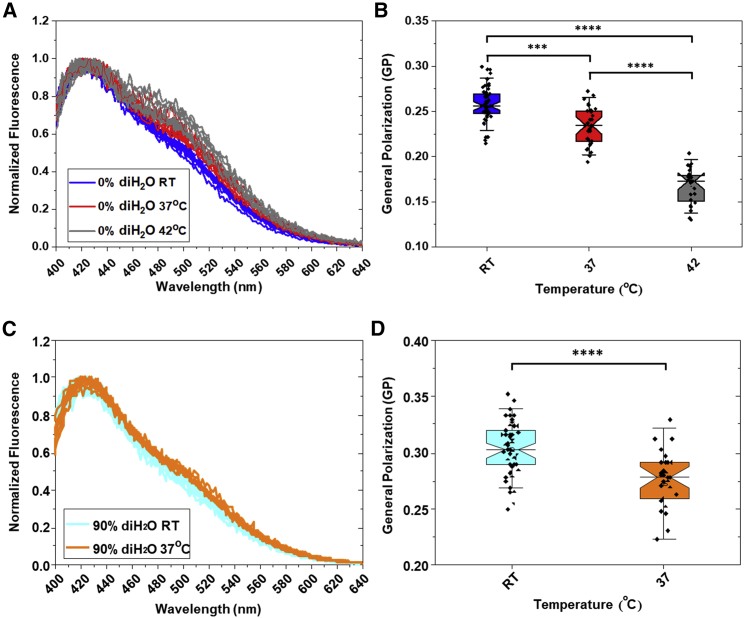
Our finding that the application of osmotic stress increases GP, whereas the opposite was observed in lipid bilayers, was surprising. To gain confidence in our results, we performed control experiments where we increased the temperature without swelling the cells. The Laurdan spectra at room temperature (RT), 37°C, and 42°C are shown in Fig. 4 A and reveal that the amplitude of the 490-nm peak increases with temperature. The calculated GP decreases when the temperature increases (Fig. 4 B). These results are consistent with the literature, as it is accepted that the increase in temperature increases water penetration into the membrane and disorders the membrane (39,40). Thus, we find that the temperature and the application of osmotic stress have opposite effects. Furthermore, a decrease in GP was observed when the temperature was increased even in cells under reversible osmotic stress (Fig. 4 C and D).
Figure 4.
(A) Emission spectra of Laurdan in CHO cells in normal media, as a function of temperature; RT in blue, 37°C in red, and 42°C in dark gray. (B) Laurdan GP as a function of temperature in CHO cells. (C) Emission spectra in CHO cells at 90% media dilution, as a function of temperature; RT in cyan, 37° in orange. (D) Laurdan GP as a function of temperature at 90% media dilution. The notched box line represents the mean; the top and bottom represent the 75th and 25th percentiles, respectively, and the bars represent the standard deviations. To see this figure in color, go online.
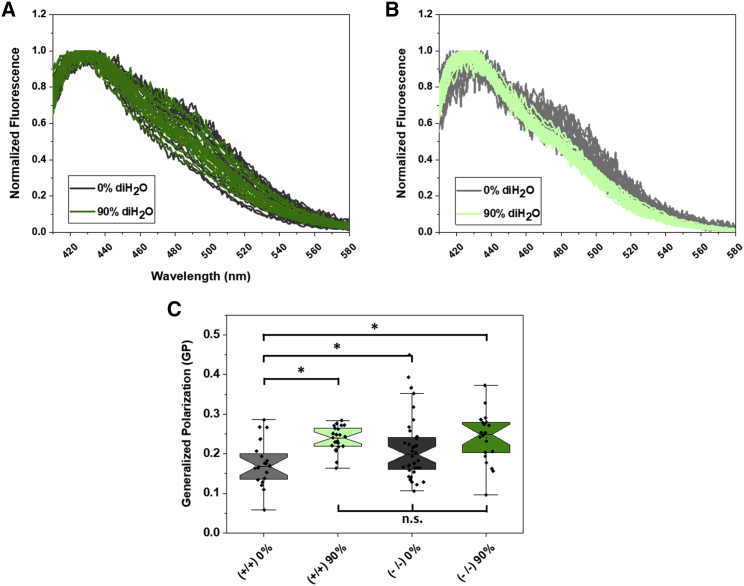
The application of osmotic stress has been linked to the flattening of the caveolae (8). We therefore hypothesized that our observations are intimately linked with caveolae, and thus GP would not increase if there were no caveolae. To test this hypothesis, we used mouse embryonic fibroblasts (3T3 MEFs) that do not express caveolin1 and thus do not have caveolae (3T3 MEFs (−/−)). As a control, we also used the normal 3T3 MEFs (+/+). Typical Laurdan spectra for the two cell lines are shown in Fig. 5 A and B, for the cases of 0% and 90% media dilution with diH2O. We found that the GP measured for 3T3 MEFs (+/+) is increased upon the application of reversible osmotic stress, similar to the results observed in CHO cells. On the other hand, the GP for 3T3 MEF (−/−) was the same in the presence and absence of osmotic stress. Furthermore, the GP value measured in 3T3 MEFs (−/−) lacking caveolae was different from the GP value for 3T3 MEFs (+/+) at 0% diH2O, but indistinguishable from the 3T3 MEF (+/+), 0% diH2O GP value. These results show that the cell membrane lacking caveolae is similar to normal cell membranes under reversible osmotic stress but has higher GP values when compared with normal cell membranes in regular cell media. These data are therefore consistent with our hypothesis that the GP increase is a consequence of the flattening of the caveolae or the “un-wrinkling” of the membrane.
Figure 5.
(A) Emission spectra of Laurdan in MEF (−/−) cells at 0% media dilution (dark gray) and 90% media dilution (dark green). (B) Emission spectra of Laurdan in MEF (+/+) cells at 0% media dilution (light gray) and 90% media dilution (mint green). (C) Comparison of Laurdan’s GP for MEFs (+/+) and MEFs (−/−) at 0% media dilution and 90% media dilution. The notched box line represents the mean; the top and bottom represent the 75th and 25th percentiles, respectively, and the bars represent the standard deviations. To see this figure in color, go online.
A cell under reversible osmotic stress has a topology that resembles a giant plasma membrane-derived vesicle (41). Such vesicles are produced by cells in response to the so-called vesiculation buffers and are increasingly being used in biophysical research (42, 43, 44). We used Laurdan as a probe to compare the membrane environment of cells under reversible osmotic stress and vesicles produced with the widely used formaldehyde method. The results are shown in Fig. 6. They demonstrate that there are no statistically significant differences between GP values of swollen cells and plasma membrane vesicles, suggesting that they have a similar membrane environment.
Figure 6.
(A) Emission spectra of Laurdan in CHO cells at 90% media dilution (cyan) and in plasma membrane-derived vesicles (light gray). (B) Comparison of Laurdan GP for CHO cells at 90% media dilution and membrane-derived vesicles. The notched box line represents the mean; the top and bottom represent the 75th and 25th percentiles, respectively, and the bars represent the standard deviations. To see this figure in color, go online.
Discussion
The main finding in this paper is that Laurdan’s GP, measured in the plasma membrane, increases upon the application of reversible osmotic stress. This increase in GP occurs only at high osmotic stress once the cell media is diluted by 50% or more with diH2O, likely after the disassembly of the caveolae. This finding is consistent with a report that the general structure of caveolae and the localization of their components are not significantly perturbed at ∼40% diH2O (45). The effect measured in response to osmotic stress is opposite to what is observed upon increase in temperature. Furthermore, the effect of osmotic stress is different in the plasma membranes of live cells and in lipid vesicles that are often used as models of the plasma membrane. The GP has been found to decrease in lipid vesicles in response to osmotic stress (35), and this decrease was interpreted as an indication of bilayer stretching, which leads to an increase in water penetration (35).
In the laboratory, researchers use reversible osmotic stress to flatten the caveolae and thus “un-wrinkle” the plasma membranes in a reversible manner, such that the membrane topology is known in biophysical experiments (46,47). Indeed, in fluorescence microscopy experiments, the application of osmotic stress results in spherical plasma membrane topology, where the membrane is perpendicular to the imaging plane. In this case, the two-dimensional concentration of fluorophores in the plasma membrane can be calculated from the effective 3D concentrations through a multiplication by the pixel length. The application of reversible osmotic stress to cells is nonlethal and is fully reversible (8,41,47,48). We have shown that once the swelling medium is replaced with starvation medium, and the cells are placed back in the incubator, they recover fully, consistent with other reports of complete reversibility (35). Furthermore, the FRET efficiencies measured for interacting membrane proteins are not affected by the application of reversible osmotic stress (48), suggesting that the interactions are very similar in unperturbed cells and in cells under reversible osmotic stress. However, a concern may arise that the lipid membrane is stretched due to the application of osmotic stress, which could have resulted in a decrease in GP. This concern motivated the current study. In our cellular study, a decrease in GP was observed only at the highest osmotic stress when the diH2O content was increased above 95%. Under these conditions, the plasma membranes often ruptured during the imaging session, indicating that pressures leading to membrane stretching were not well tolerated by cells. However, we found that cells could easily withstand media dilution up to 90% with no indications for membrane stretching, as judged by the measured GP values.
How can we explain the GP increase upon the application of osmotic stress? One possibility is that it is a direct consequence of hydration changes in the caveolae. In particular, the necks of the caveolae are sites of very high curvatures, imposed by the organizing proteins. It is possible that these regions are highly strained and hydrated, and the lipids are highly disordered. It could be speculated that the application of osmotic stress leads to highly localized changes in the necks of the caveolae that expel water molecules. Since these areas are much smaller than the diffraction limit of light, we likely observe an average increase in the GP in the membrane. Another possibility is that the GP in our experiments reports mainly on changes in lipid mobility in the membrane upon the application of osmotic stress, with an increase in GP indicating decreased mobility. It is known that the lipid composition of caveolae is enriched in cholesterol and sphingolipids, and thus caveolae are regions of low lipid mobility (49, 50, 51). Upon caveolae disassembly, the prevalence of cholesterol and sphingolipids in these regions should decrease. However, this effect cannot explain our observations as it would lead to an increase in GP, i.e., the opposite effect of what is observed. It is possible, however, that the dispersal of cholesterol and sphingolipids from the caveolae into the membrane has a marked effect on lipid mobility, which we measure here. In support of this view, the membranes of the caveolin-deficient MEFs (−/−) are known to be enriched in sphingomyelin and to exhibit decreased abundance of unsaturated phospholipids, compared with MEFs (+/+) (52).
GP is a phenomenological parameter that cannot fully reveal the mechanism behind the phenomenon we report. Caveolae play a role in signaling (49), and thus downstream signaling effects may contribute to the observations reported here. Indeed, Ca2+ signaling is reduced as a result of osmotic stress, due to perturbed association of caveolin with partners that play a role in signaling (53). Furthermore, the lack of caveolin in 3T3 MEF (−/−) cells likely affects the expression of cavin, which is known to be downregulated when caveolin expression is perturbed (54). Cavin carries out two distinct functions in cells: it participates in caveolae assembly, and it regulates ribosomal transcription (55, 56, 57). Thus, changes in cavin levels can affect cellular function through transcription alterations (58).
Future studies are needed to understand all cellular events that contribute to the observed increase in GP. Overall, although the interpretation of GP poses challenges, the fact remains that the change in GP upon the application of osmotic stress is exactly the opposite in lipid vesicles and in cells. Interestingly, the application of shear stress leads to a decrease in lipid order in cells, and a similar decrease in lipid order has been reported when lipid vesicles are exposed to shear stress (59). Thus, the behavior observed here in cells could not be predicted based on measurements in model systems. This has implications for the development of theoretical frameworks describing the swelling dynamics of vesicles, cells, and organelles (60).
Lipid bilayers as used as model systems to understand processes in cellular membranes. This study reminds us that measurements in this simplified system cannot be expected to always mirror the response of the plasma membrane. Likewise, plasma membrane-derived vesicles are increasingly being used in biophysical research (42,61). Our results suggest that these vesicles represent a membrane environment with similar physical-chemical properties as the plasma membrane in cells under reversible osmotic stress, as well as in cells with no caveolae. It is also interesting that cells can easily withstand very high media dilution with no indications for membrane stretching. This work contributes to our understanding of membrane models and the limitations they impose, as we seek to understand processes in native plasma membranes using biophysical tools.
Author contributions
E.Z.M.: designed research, performed research, analyzed data, co-wrote the paper; E.V.A.: performed research, K.H.: designed research, co-wrote the paper.
Acknowledgments
Supported by NSF MCB 1712740. We thank Dr. Anne K. Kenworthy for reading an early version of the manuscript, for insightful discussions, and for suggesting the 3T3 MEF (−/−) line as control. We thank Brandon Tenney, Maryann Ness, and Mark Marzinke from the Johns Hopkins Hospital Core Lab facility for the osmotic measurements.
Declaration of interests
The authors declare no competing interests.
Editor: Heiko Heerklotz.
References
- 1.Singer S.J., Nicolson G.L. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
- 2.Chan R.B., Oliveira T.G., et al. Di Paolo G. Comparative lipidomic analysis of Mouse and human brain with alzheimer disease. J. Biol. Chem. 2012;287:2678–2688. doi: 10.1074/jbc.m111.274142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Postila P.A., Rog T. A perspective: active role of lipids in neurotransmitter dynamics. Mol. Neurobiol. 2020;57:910–925. doi: 10.1007/s12035-019-01775-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Parmryd I., Onfelt B. Consequences of membrane topography. FEBS J. 2013;280:2775–2784. doi: 10.1111/febs.12209. [DOI] [PubMed] [Google Scholar]
- 5.Adler J., Shevchuk A.I., et al. Parmryd I. Plasma membrane topography and interpretation of single-particle tracks. Nat. Methods. 2010;7:170–171. doi: 10.1038/nmeth0310-170. [DOI] [PubMed] [Google Scholar]
- 6.Marx J. Caveolae: a once-elusive structure gets some respect. Science. 2001;294:1862–1865. doi: 10.1126/science.294.5548.1862. [DOI] [PubMed] [Google Scholar]
- 7.Anderson R.G.W. The caveolae membrane system. Annu. Rev. Biochem. 1998;67:199–225. doi: 10.1146/annurev.biochem.67.1.199. [DOI] [PubMed] [Google Scholar]
- 8.Sinha B., Koster D., et al. Nassoy P. Cells respond to mechanical stress by rapid disassembly of caveolae. Cell. 2011;144:402–413. doi: 10.1016/j.cell.2010.12.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Boyd N.L., Park H., et al. Jo H. Chronic shear induces caveolae formation and alters ERK and Akt responses in endothelial cells. Am. J. Physiol. Heart Circ. Physiol. 2003;285:H1113–H1122. doi: 10.1152/ajpheart.00302.2003. [DOI] [PubMed] [Google Scholar]
- 10.Rizzo V., Morton C., et al. Davies P.F. Recruitment of endothelial caveolae into mechanotransduction pathways by flow conditioning in vitro. Am. J. Physiol. Heart Circ. Physiol. 2003;285:H1720–H1729. doi: 10.1152/ajpheart.00344.2002. [DOI] [PubMed] [Google Scholar]
- 11.Park H., Go Y.M., et al. Jo H. Caveolin-1 regulates shear stress-dependent activation of extracellular signal-regulated kinase. Am. J. Physiol. Heart Circ. Physiol. 2000;278:H1285–H1293. doi: 10.1152/ajpheart.2000.278.4.h1285. [DOI] [PubMed] [Google Scholar]
- 12.Sedding D.G., Seay U., et al. Braun-Dullaeus R.C. Mechanosensitive p27Kip1 regulation and cell cycle entry in vascular smooth muscle cells. Circulation. 2003;108:616–622. doi: 10.1161/01.cir.0000079102.08464.e2. [DOI] [PubMed] [Google Scholar]
- 13.Gunther G., Malacrida L., et al. Sanchez S.A. LAURDAN since weber: the quest for visualizing membrane heterogeneity. Acc. Chem. Res. 2021;54:976–987. doi: 10.1021/acs.accounts.0c00687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Malacrida L., Gratton E. LAURDAN fluorescence and phasor plots reveal the effects of a H2O2 bolus in NIH-3T3 fibroblast membranes dynamics and hydration. Free Radic. Biol. Med. 2018;128:144–156. doi: 10.1016/j.freeradbiomed.2018.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Malacrida L., Astrada S., et al. Bagatolli L.A. Spectral phasor analysis of LAURDAN fluorescence in live A549 lung cells to study the hydration and time evolution of intracellular lamellar body-like structures. Biochim. Biophys. Acta. 2016;1858:2625–2635. doi: 10.1016/j.bbamem.2016.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Golfetto O., Hinde E., Gratton E. The Laurdan spectral phasor method to explore membrane micro-heterogeneity and lipid domains in live cells. Methods Mol. Biol. 2015;1232:273–290. doi: 10.1007/978-1-4939-1752-5_19. [DOI] [PubMed] [Google Scholar]
- 17.Bonaventura G., Barcellona M.L., et al. Gratton E. Laurdan monitors different lipids content in eukaryotic membrane during embryonic neural development. Cell Biochem. Biophys. 2014;70:785–794. doi: 10.1007/s12013-014-9982-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Golfetto O., Hinde E., Gratton E. Laurdan fluorescence lifetime discriminates cholesterol content from changes in fluidity in living cell membranes. Biophys. J. 2013;104:1238–1247. doi: 10.1016/j.bpj.2012.12.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bagatolli L.A., Sanchez S.A., et al. Gratton E. [20] Giant vesicles, laurdan, and two-photon fluorescence microscopy: evidence of lipid lateral separation in bilayers. Methods Enzymol. 2003;360:481–500. doi: 10.1016/s0076-6879(03)60124-2. [DOI] [PubMed] [Google Scholar]
- 20.Granjon T., Vacheron M.J., et al. Buchet R. Mitochondrial creatine kinase binding to phospholipids decreases fluidity of membranes and promotes new lipid-induced β structures as monitored by red edge excitation shift, laurdan fluorescence, and FTIR. Biochemistry. 2001;40:6016–6026. doi: 10.1021/bi002293e. [DOI] [PubMed] [Google Scholar]
- 21.Bagatolli L.A., Gratton E., Fidelio G.D. Water dynamics in glycosphingolipid aggregates studied by LAURDAN fluorescence. Biophys. J. 1998;75:331–341. doi: 10.1016/s0006-3495(98)77517-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Parasassi T., Gratton E., et al. Levi M. Two-photon fluorescence microscopy of laurdan generalized polarization domains in model and natural membranes. Biophys. J. 1997;72:2413–2429. doi: 10.1016/s0006-3495(97)78887-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Parasassi T., Gratton E. Membrane lipid domains and dynamics as detected by Laurdan fluorescence. J. Fluoresc. 1995;5:59–69. doi: 10.1007/bf00718783. [DOI] [PubMed] [Google Scholar]
- 24.Parasassi T., Di Stefano M., et al. Gratton E. Cholesterol modifies water concentration and dynamics in phospholipid bilayers: a fluorescence study using Laurdan probe. Biophys. J. 1994;66:763–768. doi: 10.1016/s0006-3495(94)80852-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kantar A., Giorgi P.L., et al. Fiorini R. Probing the interaction of PAF with human platelet membrane using the fluorescent probe laurdan. Platelets. 1994;5:145–148. doi: 10.3109/09537109409005527. [DOI] [PubMed] [Google Scholar]
- 26.Parasassi T., Di Stefano M., et al. Gratton E. Influence of cholesterol on phospholipid bilayers phase domains as detected by Laurdan fluorescence. Biophys. J. 1994;66:120–132. doi: 10.1016/s0006-3495(94)80763-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Parasassi T., Ravagnan G., et al. Gratton E. Modulation and dynamics of phase properties in phospholipid mixtures detected by Laurdan fluorescence. Photochem. Photobiol. 1993;57:403–410. doi: 10.1111/j.1751-1097.1993.tb02309.x. [DOI] [PubMed] [Google Scholar]
- 28.Parasassi T., Di Stefano M., et al. Gratton E. Membrane aging during cell growth ascertained by Laurdan generalized polarization. Exp. Cell Res. 1992;202:432–439. doi: 10.1016/0014-4827(92)90096-q. [DOI] [PubMed] [Google Scholar]
- 29.Parasassi T., De Stasio G., et al. Gratton E. Quantitation of lipid phases in phospholipid vesicles by the generalized polarization of Laurdan fluorescence. Biophys. J. 1991;60:179–189. doi: 10.1016/s0006-3495(91)82041-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ma Y., Benda A., et al. Gaus K. Time-resolved laurdan fluorescence reveals insights into membrane viscosity and hydration levels. Biophys. J. 2018;115:1498–1508. doi: 10.1016/j.bpj.2018.08.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Amaro M., Reina F., et al. Sezgin E. Laurdan and Di-4-ANEPPDHQ probe different properties of the membrane. J. Phys. D Appl. Phys. 2017;50:134004. doi: 10.1088/1361-6463/aa5dbc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pokorna S., Jurkiewicz P., et al. Hof M. Does fluoride disrupt hydrogen bond network in cationic lipid bilayer? Time-dependent fluorescence shift of Laurdan and molecular dynamics simulations. J. Chem. Phys. 2014;141:22D516. doi: 10.1063/1.4898798. [DOI] [PubMed] [Google Scholar]
- 33.Jurkiewicz P., Cwiklik L., et al. Hof M. Lipid hydration and mobility: an interplay between fluorescence solvent relaxation experiments and molecular dynamics simulations. Biochimie. 2012;94:26–32. doi: 10.1016/j.biochi.2011.06.027. [DOI] [PubMed] [Google Scholar]
- 34.Sachl R., Stepanek M., et al. Hof M. Fluorescence study of the solvation of fluorescent probes prodan and laurdan in poly(ε-caprolactone)-block-poly(ethylene oxide) vesicles in aqueous solutions with tetrahydrofurane. Langmuir. 2008;24:288–295. doi: 10.1021/la702277t. [DOI] [PubMed] [Google Scholar]
- 35.Boyd M.A., Kamat N.P. Visualizing tension and growth in model membranes using optical dyes. Biophys. J. 2018;115:1307–1315. doi: 10.1016/j.bpj.2018.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Del Piccolo N., Placone J., et al. Hristova K. Production of plasma membrane vesicles with chloride salts and their utility as a cell membrane mimetic for biophysical characterization of membrane protein interactions. Anal. Chem. 2012;84:8650–8655. doi: 10.1021/ac301776j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Scott R.E., Perkins R.G., et al. Maercklein P.B. Plasma membrane vesiculation in 3T3 and SV3T3 cells. I. Morphological and biochemical characterization. J. Cell Sci. 1979;35:229–243. doi: 10.1242/jcs.35.1.229. [DOI] [PubMed] [Google Scholar]
- 38.Biener G., Stoneman M.R., et al. Raicu V. Development and experimental testing of an optical micro-spectroscopic technique incorporating true line-scan excitation. Int. J. Mol. Sci. 2013;15:261–276. doi: 10.3390/ijms15010261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.White S.H., Wimley W.C., et al. Hristova K. Protein folding in membranes: pondering the nature of the bilayer milieu. Biol. Skr. Dan. Selsk. 1998;49:91–98. [Google Scholar]
- 40.Sun W.J., Tristram-Nagle S., et al. Nagle J.F. Structure of gel phase saturated lecithin bilayers: temperature and chain length dependence. Biophys. J. 1996;71:885–891. doi: 10.1016/s0006-3495(96)79290-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Singh D.R., Cao Q., et al. Hristova K. Unliganded EphA3 dimerization promoted by the SAM domain. Biochem. J. 2015;471:101–109. doi: 10.1042/bj20150433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Levental I., Grzybek M., Simons K. Raft domains of variable properties and compositions in plasma membrane vesicles. Proc. Natl. Acad. Sci. U S A. 2011;108:11411–11416. doi: 10.1073/pnas.1105996108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Levental I., Lingwood D., et al. Simons K. Palmitoylation regulates raft affinity for the majority of integral raft proteins. Proc. Natl. Acad. Sci. U S A. 2010;107:22050–22054. doi: 10.1073/pnas.1016184107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Veatch S.L., Cicuta P., et al. Baird B. Critical fluctuations in plasma membrane vesicles. ACS Chem. Biol. 2008;3:287–293. doi: 10.1021/cb800012x. [DOI] [PubMed] [Google Scholar]
- 45.Yang L., Scarlata S. Super-resolution visualization of caveola deformation in response to osmotic stress. J. Biol. Chem. 2017;292:3779–3788. doi: 10.1074/jbc.m116.768499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.King C., Stoneman M., et al. Hristova K. Fully quantified spectral imaging reveals in vivo membrane protein interactions. Integr. Biosci. 2016;8:216–229. doi: 10.1039/c5ib00202h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Singh D.R., Ahmed F., et al. Hristova K. EphA2 receptor unliganded dimers suppress EphA2 pro-tumorigenic signaling. J. Biol. Chem. 2015;290:27271–27279. doi: 10.1074/jbc.m115.676866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Singh D.R., Ahmed F., et al. Hristova K. Intracellular domain contacts contribute to ecadherin constitutive dimerization in the plasma membrane. J. Mol. Biol. 2017;429:2231–2245. doi: 10.1016/j.jmb.2017.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Parton R.G., Simons K. The multiple faces of caveolae. Nat. Rev. Mol. Cell Biol. 2007;8:185–194. doi: 10.1038/nrm2122. [DOI] [PubMed] [Google Scholar]
- 50.Pike L.J., Han X.L., Gross R.W. Epidermal growth factor receptors are localized to lipid rafts that contain a balance of inner and outer leaflet lipids. J. Biol. Chem. 2005;280:26796–26804. doi: 10.1074/jbc.m503805200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Pike L.J. Growth factor receptors, lipid rafts and caveolae: an evolving story. Biochim. Biophys. Acta Mol. Cell Res. 2005;1746:260–273. doi: 10.1016/j.bbamcr.2005.05.005. [DOI] [PubMed] [Google Scholar]
- 52.Le Lay S., Li Q., et al. Gaus K. Caveolin-1-dependent and -independent membrane domains. J. Lipid Res. 2009;50:1609–1620. doi: 10.1194/jlr.m800601-jlr200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Guo Y., Yang L., et al. Scarlata S. Osmotic stress reduces Ca2+ signals through deformation of caveolae. J. Biol. Chem. 2015;290:16698–16707. doi: 10.1074/jbc.m115.655126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Liu L., Pilch P.F. A critical role of cavin (polymerase I and transcript release factor) in caveolae formation and organization. J. Biol. Chem. 2008;283:4314–4322. doi: 10.1074/jbc.m707890200. [DOI] [PubMed] [Google Scholar]
- 55.Hayer A., Stoeber M., et al. Helenius A. Biogenesis of caveolae: stepwise assembly of large caveolin and cavin complexes. Traffic. 2010;11:361–382. doi: 10.1111/j.1600-0854.2009.01023.x. [DOI] [PubMed] [Google Scholar]
- 56.Hill M.M., Bastiani M., et al. Parton R.G. PTRF-Cavin, a conserved cytoplasmic protein required for caveola formation and function. Cell. 2008;132:113–124. doi: 10.1016/j.cell.2007.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Low J.Y., Nicholson H.D. Emerging role of polymerase-1 and transcript release factor (PTRF/Cavin-1) in health and disease. Cell Tissue Res. 2014;357:505–513. doi: 10.1007/s00441-014-1964-z. [DOI] [PubMed] [Google Scholar]
- 58.Liu L. Lessons from cavin-1 deficiency. Biochem. Soc. Trans. 2020;48:147–154. doi: 10.1042/bst20190380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yamamoto K., Ando J. Endothelial cell and model membranes respond to shear stress by rapidly decreasing the order of their lipid phases. J. Cell Sci. 2013;126:1227–1234. doi: 10.1242/jcs.119628. [DOI] [PubMed] [Google Scholar]
- 60.Khmelinskii I., Makarov V.I. On the effects of mechanical stress of membranes in modeling of swelling dynamics of biological systems. Sci. Rep. 2020;10:8395. doi: 10.1038/s41598-020-65217-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Baumgart T., Hammond A.T., et al. Webb W.W. Large-scale fluid/fluid phase separation of proteins and lipids in giant plasma membrane vesicles. Proc. Natl. Acad. Sci. U S A. 2007;104:3165–3170. doi: 10.1073/pnas.0611357104. [DOI] [PMC free article] [PubMed] [Google Scholar]