Abstract
The interactions between Na+ or Mg2+ ions with different parts of single-stranded RNA molecules, namely, the oxygen atoms from the phosphate groups or the guanine base, in water solution have been studied using first-principles molecular dynamics. Sodium ions were found to be much more mobile than Mg2+ ions and readily underwent transitions between a state directly bonded to RNA oxygen atoms and a completely solvated state. The inner solvation shell of Na+ ions fluctuated stochastically at a femtosecond timescale coordinating on average 5 oxygen atoms for bonded Na+ ions and 5.5 oxygen atoms for solvated Na+ ions. In contrast, the inner solvation shell of Mg2+ ions was stable in both RNA-bonded and completely solvated states. In both cases, Mg2+ ions coordinated 6 oxygen atoms from the inner solvation shell. Consistent with their stable solvation shells, Mg2+ ions were more effective than Na+ ions in stabilizing the RNA backbone conformation. The exclusion zones between the first and second solvation shells, solvation shell widths, and angles for binding to carbonyl oxygen of guanine for solvated Na+ or Mg2+ ions exhibited a number of quantitative differences when compared with RNA crystallographic data. The presented results support the distinct capacity of Mg2+ ions to support the RNA structure not only in the crystal phase but also in the dynamic water environment both on the side of the phosphate moiety and on the side of the nucleobase.
1. Introduction
Ribonucleic acid (RNA) molecules support essential physiological activities in living systems, including control of gene expression,1−3 encoding genetic information as a blueprint for protein synthesis,4,5 transferring amino acids into ribosomes,6 carrying out protein translation in ribosome complexes,7,8 catalysis of biochemical reactions,9,10 and regulation of cellular responses to environmental stimuli.11−13 This wide range of RNA functions is accomplished by the capacity of RNA to fold into specific three-dimensional conformations. Because the high negative charge of the sugar-phosphate backbone works against RNA folding into a compact structure, positively charged metal ions promote folding by reducing the electrostatic repulsion between RNA phosphate groups.14 The stabilizing effect of metal ions on the RNA structure, however, varies between different ion types. In particular, Mg2+ ions at millimolar concentrations enhance dramatically the stability of RNA tertiary structures that are otherwise only marginally stable in the presence of high monovalent cation concentrations.15,16 Magnesium ions also enhance catalytic activity of ribozymes17 and mediate catalytic processes in ribozyme active sites.18,19 The fact that RNA molecules possess specific Mg2+ binding motifs20 further implies that the role of Mg2+ ions in RNA folding is not limited to simple compensation of electrostatic repulsions, but it is driven by very specific contextual requirements.21,22
The interactions between metal ions and RNA have been previously studied employing a number of experimental techniques. The RNA binding sites of monovalent and divalent metal ions in solution and the crystal phase have been explored by nuclear magnetic resonance23−25 and vibrational spectroscopy methods including Fourier-transform infrared and Raman spectroscopy.26 The locations of the ions in the RNA crystal phase could be determined with improved spatial resolution by X-ray crystallography;27,28 however, the structure of RNA molecules in the crystalline phase may differ from that in solution.29 A serious problem is also the distinguishing of Na+ ions from the water molecules.30
Computer simulation of RNA dynamics is commonly performed with the use of classical molecular dynamics (MD)31−33 and Monte Carlo algorithms.34−36 The accuracy of these classical methods for MD simulations, however, depends critically on the appropriate choice of force field parameters.37 Other limitations in resolving ion dynamics in classical simulations is the difficulty of including explicit water molecules. The very slow exchange of water in the tight Mg2+ hexahydrate complex is a particular problem.38−41
To complement the available experimental and theoretical methods, first-principles quantum chemical simulations can be employed for detailed characterization of the dynamical interactions between metal ions and RNA. For example, the interactions of Na+ and Mg2+ ions with the phosphate groups have already been studied with Born–Oppenheimer MD, employing density functional theory (DFT) [at the generalized gradient approximation (GGA) level] to calculate the forces between atoms.29 The structural model that was used consisted of the sugar-phosphate backbone of single-stranded RNA (ssRNA), without taking into account the nucleobases.
In the present work, we complemented the model, studied earlier,29 with guanine and cytosine bases in order to make it much more realistic. In this way, we have the whole molecular structure of ssRNA. The ab initio molecular dynamic simulations are focused on the interaction of Na+ and Mg2+ ions with electronegative centers of ssRNA, namely, the oxygen centers from the sugar-phosphate backbone and the oxygen centers of the nucleobases. We explicitly model all interactions at the ab initio level and present real-time quantum dynamics using water as a liquid phase and solvent. This provides important insights into the possible function of X-ray crystallographic structures (such as those deposited in the Protein Data Bank), for which, as a rule, no water phase is presented.42
Noteworthily, the present study is primarily focused on the local interactions of the cations with ssRNA fragments, including phosphate groups and parts of the nucleobases. Because the dimensionality of the quantum wave function in ab initio methods grows exponentially with the total number of atoms, we are restricted to work with simple dinucleotide ssRNA fragments. This precludes direct simulation of secondary and tertiary RNA structure transitions, which occur at the microsecond to millisecond timescale.43 The employment of ab initio methods, however, grants us the ability to study the local interactions at the femtosecond to picosecond timescale with high fidelity,44 without the use of the predetermined force fields of the classical MD, and allows for direct extrapolation of our conclusions based on these precise simulations to physiological water-based solvents in living organisms.
2. Methods
Ab initio Born–Oppenheimer MD simulations of ssRNA with Na+ or Mg2+ countercations in water solution are performed using the freely available CP2K/Quickstep package.45 Kohn–Sham density functional theory46,47 with GGA is applied based on the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.48 The PBE was chosen as a tradeoff between the lower-precision LDA functional and the hybrid ones, which are too computationally expensive for the current task. Also, the studied interactions in the present article, between the charged Na+ and Mg2+ ions on one hand and the phosphate groups, H2O (O) atoms, and guanine on the other hand, are expected to be electrostatic in nature, which are properly described by the PBE functional. For all atoms, the basis set DZVP-MOLOPT-SR-Goedecker-Teter-Hutter (GTH) is employed, which is suitable for molecular studies in the condensed phase.49 For reducing the computational cost, Gaussian and plane-wave expansion sets are used for expanding the electronic wave functions.50,51 Only the valence electrons are explicitly considered. Their interaction with the remaining ions is described using the pseudopotentials of GTH.52,53 The charge density cutoff of the finest grid level is equal to 400 Ry. The number of used multigrids is 5.
All simulations are carried out in the NVT ensemble with a timestep of 1 fs. The temperature was set to 320 K using canonical sampling through a velocity rescaling thermostat.54,55 For each simulation, statistics is obtained after the initial 1 ps, which is required for thermal equilibration of the molecular system (Figure S11). The studied systems consist of a dinucleotide ssRNA fragments containing either two cytosine bases (CC) or one guanine and one cytosine (GC) and the metal countercations, two Na+ or one Mg2+, necessary to neutralize the negative charges of the phosphate groups. The dinucleotide abbreviations used throughout the article follow the standard FASTA format.56 The whole system is hydrated in a periodic box with dimensions of 12.645 Å × 17.3 Å × 17.3 Å. For simulations with CC 2Na+, GC 2Na+, CC Mg2+, or GC Mg2+, the box contains 106, 104, 110, or 107 water molecules, respectively, which assures that the density of the water phase is equal to 0.99 g/cm3. Periodic boundary conditions for all axes are used. The dinucleotide skeleton is oriented along the shortest axis (12.645 Å). The only spatial structure that the dinucleotide can form in this case is a straight ssRNA chain. It should be noted that such a periodic system has certain limitations concerning its conformational plasticity – the RNA chain cannot form secondary and tertiary structures, for example, loops, and it also cannot form double-stranded stems. Thus, we simulate an “infinite” straight chain of single-stranded RNA (ssRNA). Also, the simulation time of 100 ps is relatively short to capture all possible conformations of the dinucleotide. We emphasize that when the definition (ssRNA) is addressed in this work, concerning our DFT simulations, the dinucleotide model that we used should be considered. Despite the limitations, as can be seen further, the model is able to describe the primary modes of local interactions between the solvated counterions and RNA. After the initial placement of the metal ions, there are no structural constraints imposed on any of the atoms. Visualization and analysis of the MD are performed with visual MD version 1.9.3.57 Radial distribution functions (RDFs) between elements are computed with the default bin width of 0.1 Å. Coordination numbers in the inner solvation shells were computed using custom scripts with a cutoff at 3.2 Å or 2.8 Å for Na+ or Mg2+ ions, respectively. All simulations are started from geometry-optimized structures. After 1 ps, thermal equilibration of the systems is observed (a thermostat time constant of 50 fs or 50 steps). The temperature of the system remained stable (±30 K) during the whole simulations. After the 20th ps, the thermostat was practically switched off (a time constant of 1 ps or 1000). Also, after the 20th ps, no drift of the potential energy of the systems was observed.
Four major
conformations of the RNA backbone at the phosphate moiety
are distinguished:58
The absolute value of the angle between the adjacent C–O bond and the plane formed by the phosphodiester bond was considered >20° for g and ≤20° for t. Scattergrams were computed with the use of custom scripts in Microsoft Excel and Wolfram Mathematica.
Six ssRNA simulations with metal ions are performed. The initial location of cations and the duration time of the simulations are as follows:
CC 2Na+ simulation for 102.68 ps with two bound sodium ions, directly coordinated at phosphate group P1 or P2 in a CC ssRNA fragment.
CC 2Na+ simulation for 103.90 ps with two solvated sodium ions, coordinated through their inner water shells at phosphate group P1 or P2 in a CC ssRNA fragment.
GC 2Na+ simulation for 103.23 ps with two bound sodium ions, directly coordinated at the oxygen atom of guanine or the hydroxyl group attached to the pentose ring in the 2′ position of guanosine in a GC ssRNA fragment.
CC Mg2+ simulation for 101.68 ps with one bound magnesium ion, directly coordinated at phosphate group P2 in a CC ssRNA fragment.
CC Mg2+ simulation for 105.45 ps with one solvated magnesium ion, initially coordinated through its inner water shell at phosphate group P2 in a CC ssRNA fragment.
GC Mg2+ simulation for 101.68 ps with one bound magnesium ion, directly coordinated at the oxygen atom of guanine in a GC ssRNA fragment.
3. Results and Discussion
3.1. Mobility of Na+ Ions
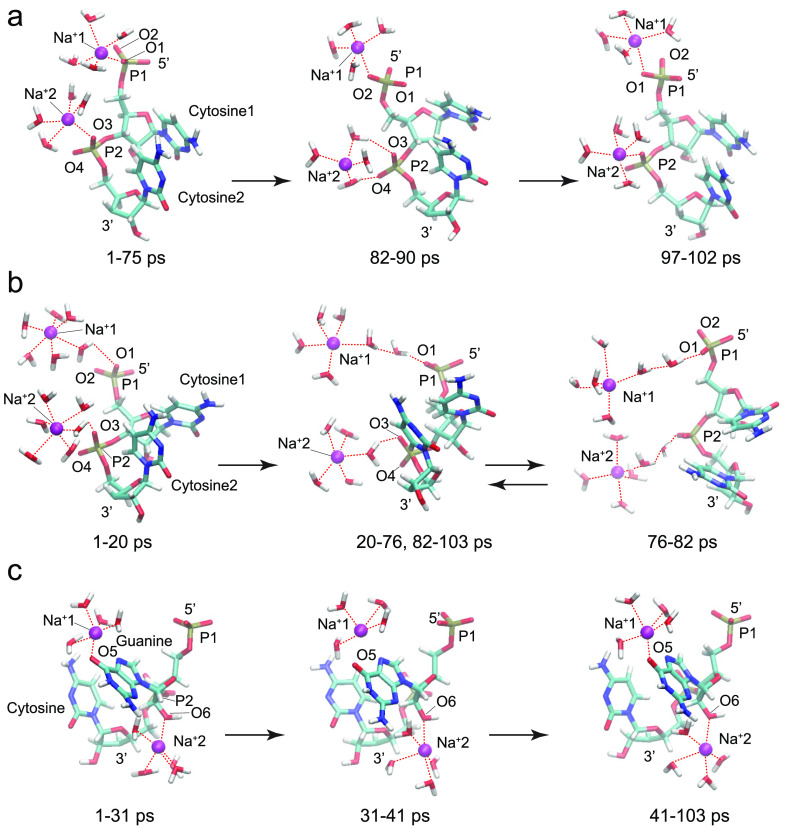
The interaction of sodium ions with RNA was studied in three simulations, each of which with a time duration of over 100 ps (see the selected snapshots in Figure 1). The interaction of sodium ions with the phosphate groups from the RNA backbone was studied in a model consisting of an ssRNA fragment containing two cytosine bases (CC) in water solution, whereas the interaction with the guanine base was studied in a model with an ssRNA fragment containing one guanine and one cytosine base (GC).
Figure 1.
Selected snapshots from the sodium-containing ssRNA simulations: (a) two bound Na+ ions directly coordinated at phosphate groups P1 and P2 in a CC ssRNA fragment; (b) two solvated Na+ ions interacting through their inner hydration shells with phosphate groups P1 and P2 in a CC ssRNA fragment; (c) two bound Na+ ions directly coordinated at O5 from the guanine base or O6 from the hydroxyl group attached to the pentose ring in the 2′ position of guanosine in a GC ssRNA fragment.
In the CC 2Na+ simulation with two bound sodium ions, directly coordinated at phosphate group P1 or P2 in a CC ssRNA fragment, both sodium ions stayed near their initial positions (Figure 1a). One of the sodium ions, denoted as Na+1, remained directly bonded to an oxygen atom, O1 or O2, from phosphate group P1 for the whole period of the simulation (1–102 ps). The other sodium ion, Na+2, interacted directly with oxygen atom O3 from phosphate group P2 for most of the simulation duration. However, for a short period of time (82–90 ps), it was solvated in water and interacted with both oxygen atoms O3 and O4 through water molecules from its inner hydration shell. The RDF for the Na+1-O1 distance during the time intervals 1–75 and 97–102 ps and for the Na+1-O2 distance during the interval 75–97 ps exhibited a maximum at 2.35 Å (Figure S1a–d), which indicates a direct contact between Na+1 and an oxygen atom from phosphate group P1. The sodium ion Na+2 was also directly bound to oxygen atom O3 from P2 during the intervals 1–82 and 90–102 ps, with the corresponding RDF peaks at 2.55 and 2.75 Å (Figure S1e,f,h). For a short time period 82–90 ps, however, Na+2 was solvated and interacted with oxygen atoms O3 and O4 through a water molecule as evidenced by the corresponding RDF peaks at 3.65 and 4.25 Å (Figures 1a and S1g). Distances between the phosphate groups (P atoms) and the sodium ions throughout the simulation are presented in Figure 3a. It should be noted that the distance to the P atom is roughly 1 Å longer than the distance to the nearest O atom of the PO4– group. Experimental results obtained with X-ray crystallography indicate Na+-O(P) distances in the interval 2.65–2.75 Å when the ion is directly bonded to the phosphate group.59,60 Comparison of the ab initio results is made with already performed classical MD simulations employing CHARMM27 and AMBER (ver. 2.0).29 Water molecules were described by TIP3P potential. The optimal distance Na+–O(P) in the classical MD simulation with AMBER is 2.35 Å, the same as the distance in the ab initio MD. The location of the cation in the case of classical MD (AMBER) differs from that obtained with the ab initio method. Calculations with AMBER suggest bidentate configuration (Na+ bonded to two oxygen atoms of a phosphate group), while DFT results suggest monodentate configuration. The simulation with CHARMM also suggests monodentate configuration. Both classical methods suggest Na+–O(P) shorter by 0.2 Å by the DFT method.
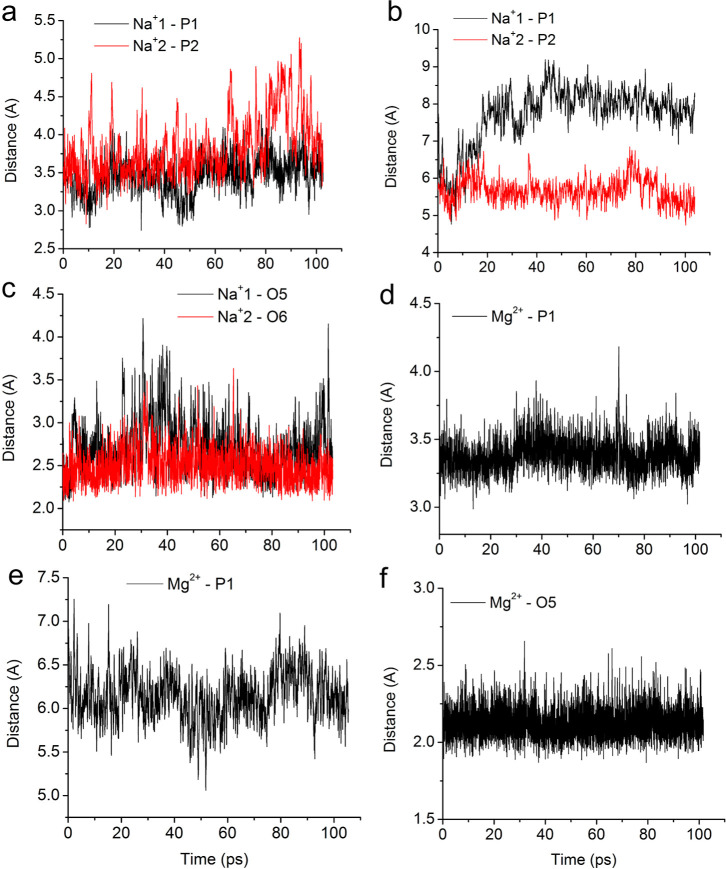
Figure 3.
Dynamics of the distances from the Na+ and Mg2+ ions to particular phosphorus and oxygen atoms of the systems: (a) Na+1-P1 and Na+2-P2 from the CC 2Na+ simulation with two bound sodium ions; (b) Na+1-P1 and Na+2-P2 from the CC 2Na+ simulation with two solvated sodium ions; distances to the closest phosphate groups are presented; (c) Na+1-O5 and Na+2-O6 from the GC 2Na+ simulation with two bound sodium ions; (d) Mg2+-P1 from the CC Mg2+ simulation with one bound magnesium ion; (e) Mg2+-P1 from the CC Mg2+ simulation with one solvated magnesium ion; (f) Mg2+-O5 from the GC Mg2+ simulation with one bound magnesium ion.
In the system containing CC and 2Na+, the two sodium ions remain completely solvated during the whole simulation, Figure 3b. The sodium ion Na+1 interacted with oxygen atom O1 from phosphate group P1 during the interval 1–20 ps (Figure 1b) through a water molecule as indicated by the RDF peak at 5.05 Å (Figure S2a,b). In the rest of the simulation, 20–103 ps, Na+1 remained fully solvated with RDF peaks at 6.95 and 8.05 Å from O1 and O2, respectively (Figure S2c). In the last time interval (20–103 ps), the distance between the Na+ ion and an oxygen atom of the phosphate group shorter than 6.5 Å indicates the interaction through two water molecules, and a higher distance indicates the interaction through three water molecules. The other sodium ion, Na+2, interacted with O3 from P2 through a water molecule for most of the simulation duration, with the corresponding RDF peaks at 4.75 or 4.65 Å, respectively, for the time intervals 1–76 and 82–103 ps (Figures 1b and S2d,e,g). Na+2 interacted with the phosphate group through two water molecules for a short time in the interval 76–82 ps (Figures 1b and S2f).
In the GC 2Na+ simulation with two bound sodium ions, one of the Na+ ions interacted directly with oxygen atom O5 from the guanine base, while the second Na+ ion was coordinated to O6 from the hydroxyl group attached to the pentose ring in the 2′ position of guanosine in a GC ssRNA fragment (Figures 1c and 3c). The sodium ion Na+1 was directly bound to O5 from guanine, with an RDF peak at 2.55 Å for the time intervals 1–31 and 41–103 ps, respectively (Figure S3a,b,d). Thermal fluctuations led to intermittent detachment of Na+1 from O5 in the interval 31–41 ps as evidenced by two RDF peaks at 3.15 and 2.75 Å (Figure S3c). The other sodium atom Na+2 was stably attached to oxygen atom O6 in the pentose ring of guanosine with an RDF peak at 2.45 Å for most of the simulation time, except for a short period, 31–33 ps, during which thermal noise created two RDF peaks at 2.85 and 3.15 Å (Figure S3e–h).
3.2. Mobility of Mg2+ Ions
We modeled the interaction of magnesium ions with phosphate groups from the RNA backbone or with the guanine base in the same molecular systems consisting of CC or GC ssRNA fragments in water (Figure 2). The simulations were performed for at least 100 ps.
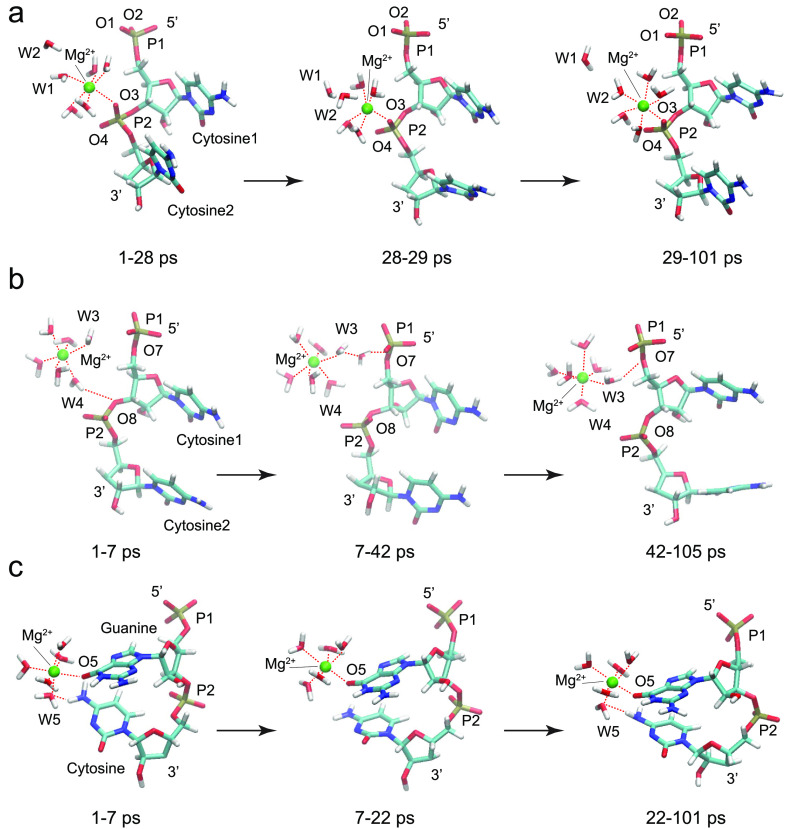
Figure 2.
Selected snapshots from the magnesium-containing ssRNA simulations: (a) one bound Mg2+ ion directly coordinated at phosphate group P2 in a CC ssRNA fragment; (b) one solvated Mg2+ ion interacting through its inner hydration shell with phosphate groups P1 and P2 in a CC ssRNA fragment; (c) one bound Mg2+ ion directly coordinated at O5 from the guanine base in a GC ssRNA fragment.
In the CC Mg2+ simulation with a bound magnesium ion, Mg2+, directly coordinated at phosphate group P2 in a CC ssRNA fragment, the magnesium ion stayed firmly attached to the phosphate group (oxygen atom O3) (Figures 2a and 3d) with an RDF peak at 2.15 Å for the whole period of the simulation 1–101 ps (Figure S4a,b). The inner hydration shell of Mg2+ invariably consisted of 5 water molecules in addition to the O3 center. One of the water molecules, denoted as W1, located on the opposite side of O3 along the Mg2+-O3 axis was exchanged with another water molecule W2 at the end of the time interval 28–29 ps (Figure 2a). The RDF for the Mg2+-W1O or Mg2+-W2O distance measured between Mg2+ and the water oxygen atoms during the time interval 1–28 ps exhibited a maximum at 2.15 or 4.35 Å, respectively (Figure S4c,d). In the rest of the simulation duration, 29–101 ps, the RDF peaks for Mg2+-W1O or Mg2+-W2O were reversed, 4.35 or 2.15 Å, which indicated the exchange of W1 with W2 (Figure S4e,f). The observed exchange of water molecules from the inner hydration shell of Mg2+ is consistent with dynamic instability of water molecules located opposite to the oxygen atom from the phosphate group.
In the CC Mg2+ simulation with a magnesium ion solvated by 6 water molecules, the Mg2+ ion interacted through a water molecule from its inner hydration shell with one of the bridging oxygen atoms from phosphate group P1 or P2 (Figures 2b, 3e, and S5). Initially, the Mg2+(H2O)6 complex interacted with 3′ bridging oxygen atom O8 from phosphate group P2 during the interval 1–7 ps (Figure 2b) through a water molecule, W4, that formed a hydrogen bond as indicated by the W4H1-O8 RDF peak at 2.55 Å (Figure S5e,f). Then, in the time interval 7–42 ps, the whole complex moved away from the phosphate groups (Figure 2b) with RDF peaks at 3.45, 3.25, 4.25, and 3.75 Å for W3H1-O7, W3H2-O7, W4H1-O8, and W4H2 O8 distances, respectively (Figure S5c,g), indicating the interaction of the Mg2+ with the phosphate group through two water molecules. For the rest of the simulation, 42–105 ps, the complex approached the RNA backbone again and interacted with the 5′ bridging O7 atom from the P1 moiety through a water molecule, W3, that formed a hydrogen bond as indicated by the W3H2-O7 RDF peak at 2.85 Å (Figure S5a,d).
In the GC Mg2+ simulation with a bound magnesium ion to the guanine base, Mg2+ remained directly attached to oxygen atom O5 of guanine for the whole simulation duration 1–101 ps with an RDF peak at 2.15 Å (Figures 2c, 3f, and S6a,b). The inner hydration shell of Mg2+ retained the same 5 water molecules in addition to the O5 atom and allowed for the intermittent formation of hydrogen bonds between the oxygen atom of water molecule W5 and the hydrogen atoms from the amine group of the cytosine base stacked below guanine during the time intervals 1–7 and 22–101 ps (Figures 2c and S6c,d,f). The observed Mg2+-mediated interaction between vertically stacked guanine and cytosine bases is consistent with the essential role of Mg2+ ions in facilitating high structural complexity and folding arrangements that allow RNA molecules to perform diverse life-supporting cellular functions.22
In one example, the experimentally determined distance between the directly bonded Mg2+ ion and the O6 oxygen atom of guanine has been experimentally determined by X-ray crystallography.61 The distance between (Mg2+-O6G) for the Mg2+ 201 ion from PDB 2A43 is 2.37 Å. Classical MD simulations with CHARMM27 and AMBER (ver. 2.0)29 for magnesium ions, interacting with RNA moieties, show similar positions of the cations with respect to the phosphate groups. For the directly bonded Mg2+ ion, monodentate coordination to one of the O atoms of the PO4– group is observed. The most commonly observed Mg2+-O distance is found to be 0.1–0.3 Å shorter than that for the DFT simulations (this work).
3.3. Solvation Shell Structures of Na+ and Mg2+ Ions
In their solvated complexes, sodium ions have a poorly defined radius of about 3.2 Å (Figure 4a) for their inner solvation shell due to frequent exchange of water molecules.29 This radius cutoff at 3.2 Å corresponds to a local minimum between the first and second solvation shells visualized through histograms of oxygen atoms surrounding the Na+ ion (Figure S7). The number of coordinated oxygen atoms in the inner solvation shell of Na+ ions varied from 3 to 8 (Figure S8), which on average was higher for solvated Na+ ions compared with Na+ ions coordinated to oxygen centers of RNA (Table S1). In the simulation with two Na+ ions bound to phosphate groups from the CC ssRNA backbone, the average coordination number was 5.0 ± 0.7, whereas for the simulation with two solvated Na+ ions, the average coordination number was somewhat higher, 5.5 ± 0.8. Interestingly, in the GC ssRNA simulation, the Na+1 ion bound to the guanine base exhibited an even lower average coordination number of 4.7 ± 0.5 (toward water oxygen atoms and the carbonyl group of guanine), whereas the Na+2 ion bound to the hydroxyl group of the sugar backbone had an average coordination number of 5.4 ± 0.6, which was closer to the coordination number of solvated ions. The histograms for these simulations are shown in Figure S7, and the variations of the coordination number with simulations time are presented in Figure S8.
Figure 4.
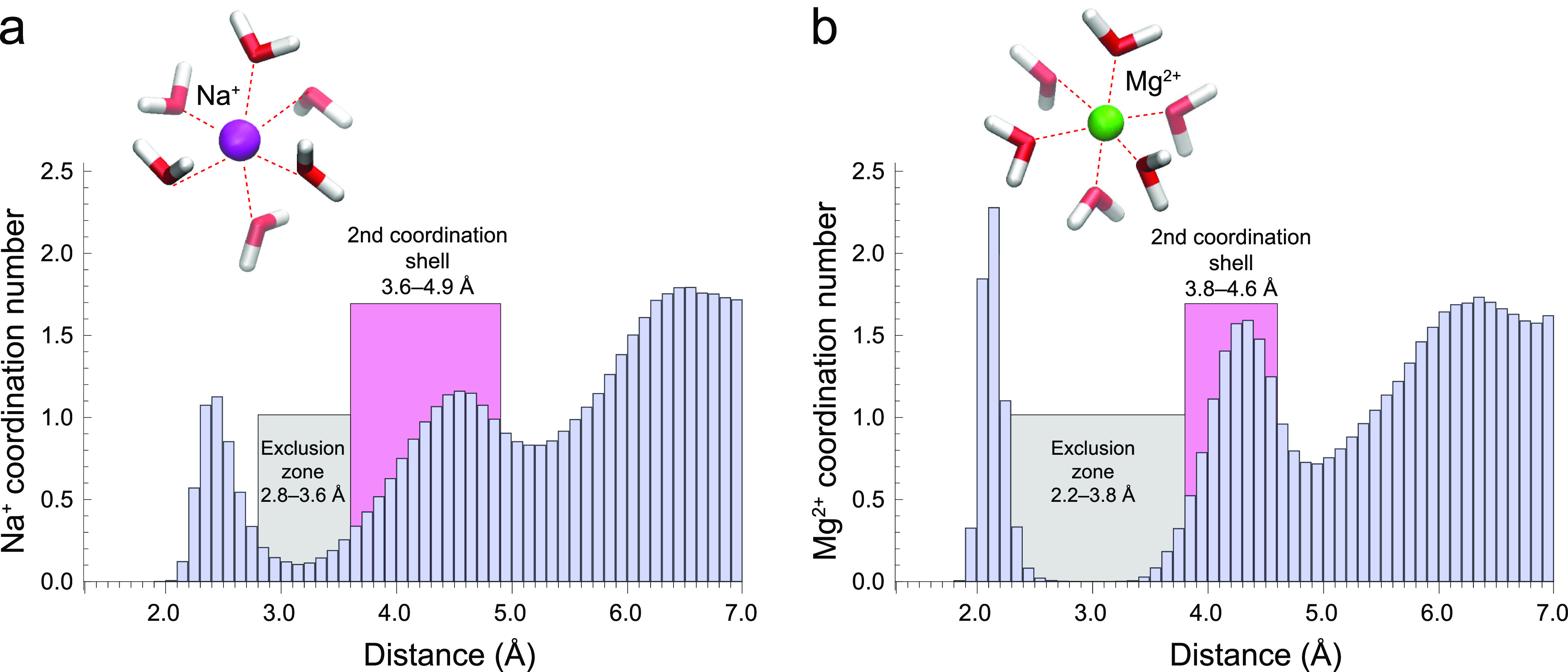
Histograms of the O atoms in the solvation shells of the Na+ ion (a) and Mg2+ ion (b) averaged over all performed CC and GC ssRNA simulations. The illustrated widths of the exclusion zones (gray) and the second coordination shells (pink) were determined in an extensive crystallographic PDB survey by Leonarski et al.(66) The exclusion zone in the crystal phase for Na+ is 2.8–3.6 Å, solvated: 3.1–3.3 Å (not depleted). The second coordination shell for Na+ in the crystal phase is 3.6–4.9 Å; solvated: 3.3–5.2 Å. The exclusion zone in the crystal phase for Mg2+ is 2.2–3.8 Å, solvated: 2.7–3.4 Å. The second coordination shell for Mg2+ in the crystal phase is 3.8–4.6 Å, solvated: 3.4–4.9 Å.
We can compare our theoretical results with experimental data from the literature. For example, fully hydrated Na+ ions in complexes with RNA motifs are studied with X-ray crystallography.62−64 It is observed that sodium ions coordinate 5 water molecules in the first solvation shell (Na+8—PDB 434D and Na+19—3ND4).62,63 A structure with 6 water molecules was also reported (Na+102—PDB 466D).64 Generally, for both bonded and completely solvated Na+ ions, the most frequently observed (via X-ray crystallography) solvation numbers are 4, 5, and 6.60 X-ray crystallographic results, however, may differ from the biological systems as they represent frozen in time system and ion solvation is altered. Classical molecular mechanics (MM) simulations give different coordination numbers for the sodium ion, dependent on the force field.65 For solvated Na+ ions, the coordination number can range from 7.1 (CHARMM27) to 5.3 (AMBER99). These variations are caused by the different parameters in the used force fields. With ab initio methods, however, such large variations are avoided as the properties of the different systems are calculated from the wave function. In this regard, for the solvated Na+ ion, we found a coordination number of 5.5 (this work), while an earlier study with the BLYP functional and the combined BLYP/MM method gave average values of 5 and 5.2, respectively,65 which is closer to the AMBER99 force field.
Solvated magnesium ions have a well-defined radius of 2.8 Å (Figure 4b) for their inner solvation shell.29 This radius cutoff at 2.8 Å includes a part of the completely depleted region of the exclusion zone between the first and second solvation shells of Mg2+ ions (Figure S9). In the solvated state, the Mg2+ ion exhibited an average coordination number of 6 oxygen atoms throughout the whole time period of the simulation (Figure S10). In the CC ssRNA simulation, the Mg2+ ion bound to a phosphate group was able to exchange a single water molecule from its inner solvation shell (Figure 2a). During the exchange, the Mg2+ ion transiently (less than 1% of the simulation time) exhibited a coordination number of 5 oxygen atoms. The exchange of the water molecule is obviously governed by local fluctuations of the water environment. Our simulation is relatively short (100 ps) for this result to be used to determine the lifetime of a water molecule in the Mg2+ solvation shell. Other studies indicate this time to be in the millisecond range.67 In the GC ssRNA simulation, the Mg2+ ion bound to the guanine carbonyl oxygen also transiently exhibited for a very short time a coordination number of 5 oxygen atoms but did not exchange any water molecules (Figure 2c). X-ray crystallographic data and MM simulations with either CHARMM or AMBER support a solvation number equal to 6 for Mg2+ in both bonded and hydrated states.60 The ab initio dynamics of Na+ and Mg2+ ions in solution supports qualitatively the results reported in an extensive crystallographic PDB survey by Leonarski et al.(66) but also reveals some quantitative differences. In the crystal phase, the reported exclusion zones between the first and second solvation shells were 2.8–3.6 Å for Na+ and 2.2–3.8 Å for Mg2+. Furthermore, the reported widths of the second solvation shells were 3.6–4.9 Å for Na+ and 3.8–4.6 Å for Mg2+ (Figure 4). In comparison, the histograms obtained from the quantum dynamics in solution revealed that the exclusion zones between the first and second solvation shells were narrower; for Na+, the exclusion zone extending in the region 3.1–3.3 Å is not depleted, while for Mg2+, the exclusion zone extending in the region 2.7–3.4 Å is depleted. Conversely, the widths of the second solvation shells were wider, 3.3–5.2 Å for Na+ and 3.4–4.9 Å for Mg2+. Thus, our results may assist in identification of Na+ for Mg2+ ions in crystallographic structures, particularly in the presence of solvating water molecules, and may help in avoiding misidentifications.
3.4. Na+ and Mg2+ Interaction with the Guanine Base
The carbonyl oxygen of guanine is a binding site with strong affinity for metal ions, which has been determined to exhibit an exclusion zone (i.e., in this range, the corresponding ion is not observed) at conical angles from 160 to 180° in crystallographic structures.66 In the crystal phase, the C=O···Na+/Mg2+ angle values were reported to be within the range from 100 to 160°.66 Remarkably, in solution, the average conical angles were manifestly different for each ion type, with the maximum probability at 108° for Na+ versus 144° for Mg2+, with only 4.4% overlap of the corresponding angle distribution histograms (Figure 5). This effectively makes Na+ and Mg2+ distinguishable in solution based on their binding angles to carbonyl oxygen of guanine. The exclusion zone for Na+ is <90° and 125–180° (Figure 5a), whereas for Mg2+, it is <120° and 170–180° (Figure 5b).
Figure 5.
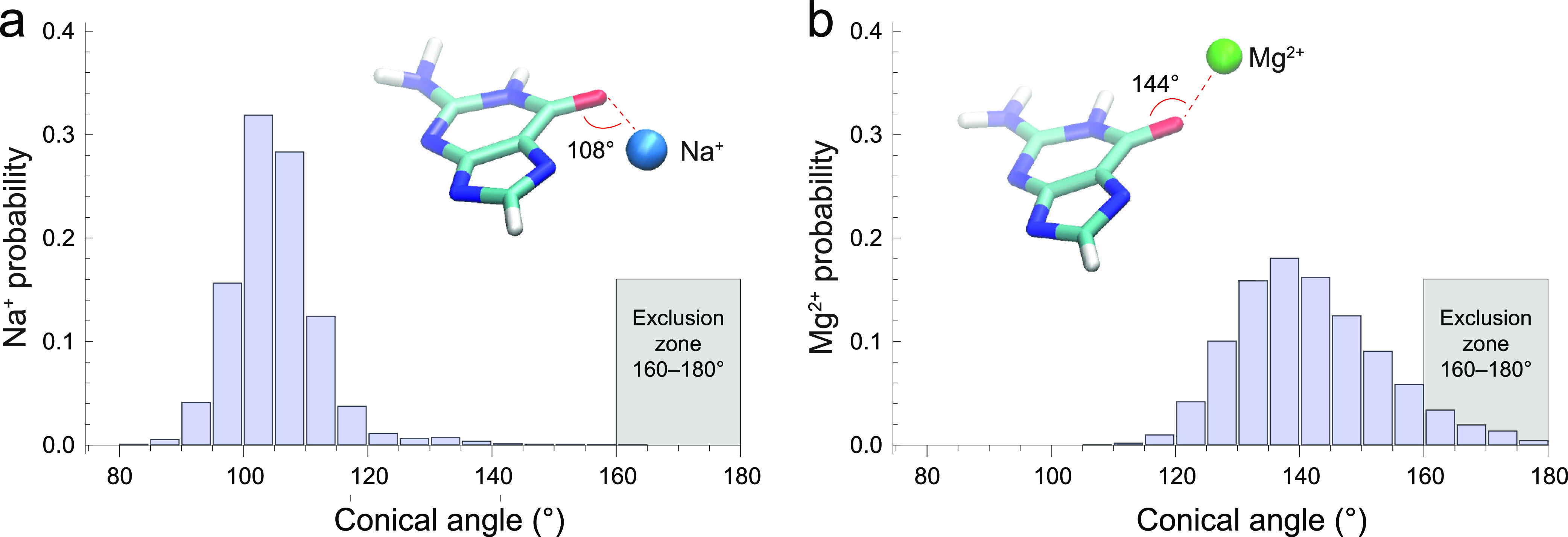
Histograms of the conical angles of the Na+ ion (a) and Mg2+ ion (b) relative to the C=O group in the guanine base in water solution. The illustrated exclusion zones were determined in an extensive crystallographic PDB survey by Leonarski et al.(66)
3.5. Conformational Effects on the Phosphoribose Backbone
Folding the phosphoribose backbone is important for both the structural stability and functional versatility of RNAs.68,69 To study the effects of metal ions on the RNA backbone conformation, we have computed two-dimensional scattergrams (Figure 6) of the angles between the adjacent C–O bonds and the plane formed by the phosphodiester bond and estimated the percentage of time spent by the RNA backbone in gg, gt, tg, or tt conformations (Table S2). Consistent with their dynamic solvation shells, Na+ ions were able to stabilize the RNA backbone in the gg conformation only when directly bound to the phosphate groups (Figure 6a) but allowed significant transition into the tg conformation when the Na+ ions were solvated or bound to the guanine base, respectively, for 2.3 or 7.1% of the simulated time period (Figures 5b,c and Table S2). In contrast, consistent with their stable solvation shells, Mg2+ ions were able to stabilize the RNA backbone in the gg conformation both when directly bound to the phosphate groups and when the interaction was mediated through a water molecule (Figures 5d,e and Table S2). Interestingly, the direct interaction of the Mg2+ ion with the carbonyl group of guanine was accompanied with the indirect interaction with the amino group of cytosine through the water molecule during most of the simulation, which may have caused rare transitions into tg or gt conformations (Table S2). These results support the proposed functional role of Mg2+ ions as potent stabilizers of the RNA secondary structure.22,70,71
Figure 6.
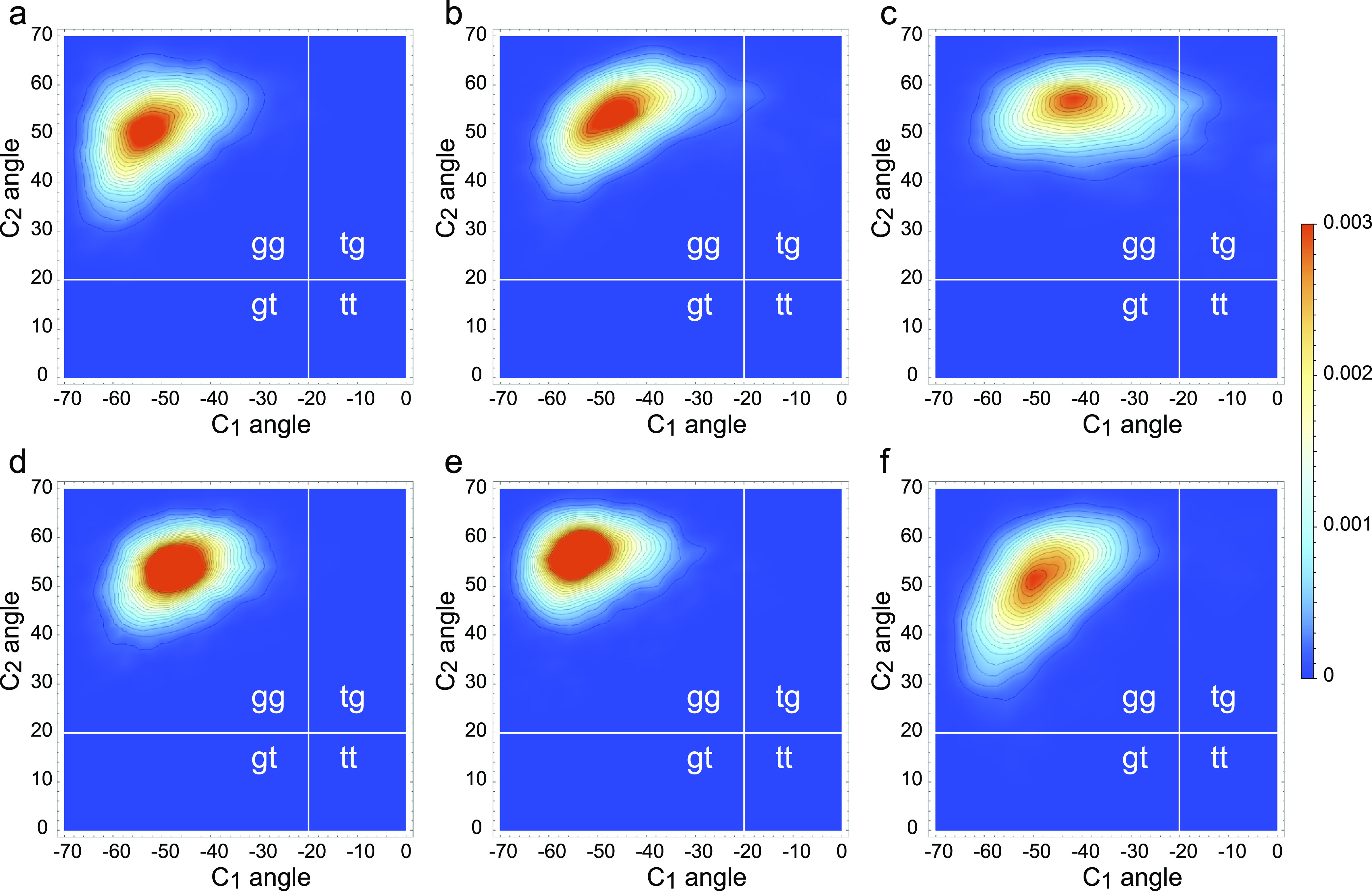
Scattergrams of the angles between the plane formed by the phosphodiester bond and each of the C1–O or C2–O bonds for (a) CC 2Na+ simulation with two bound sodium ions, (b) CC 2Na+ simulation with two solvated sodium ions, (c) GC 2Na+ simulation with two bound sodium ions, (d) CC Mg2+ simulation with one bound magnesium ion, (e) CC Mg2+ simulation with one solvated magnesium ion, and (f) GC Mg2+ simulation with one bound magnesium ion.
4. Conclusions
Density functional dynamic simulations of ssRNA interacting with Na+ or Mg2+ countercations in water solution have identified high-affinity binding sites, which coordinated the metal ions for extended periods of time of over 100 ps. While water molecules in the solvation shells of Na+ ions exchange easily, the Mg2+ ions demonstrated lower mobility, much more stable solvation shells, and therefore a stronger stabilization effect upon the phosphoribose backbone of RNA. Our simulations also suggested that magnesium may not only affect the folding of the ssRNA by interacting simultaneously with two distant phosphate groups as suggested earlier29,60 but also mediate the interaction between nucleobases in these molecules by coordinating simultaneously to both bases via the magnesium ion and one of the water molecules solvating it. This result is consistent with the observation that Mg2+ ions facilitate RNA folding and participate in hairpin formation.72 It also corroborates experimental evidence that regions with higher GC content are likely to have a more stable secondary RNA structure.73−75
The interactions of Na+ or Mg2+ ions with the guanine base in water solution exhibited differential distributions of the conical angle between the ionic bond and the carbonyl group, indicating distinct types of hybridization of the latter as a possible cause of the modified interaction of guanine in RNA secondary or tertiary structures for varying Na+ and Mg2+ electrolyte composition.76,77 In addition, the typical ranges of the angles C–O–Na/Mg obtained in our simulations in water media suggest somewhat different regions compared to the ranges reported for the crystal structures.66 These results support the interpretation that the differential effects of Na+ and Mg2+ ions upon the RNA structure may have dynamic origin and arise due to different abilities of the two types of ions to coordinate oxygen atoms, support their inner hydration shells, and move in the water solvent.31,71,78 The observed 100 ps-long periods of thermal stability of the inner hydration shell of Mg2+ ions, with brief subpicosecond exchange of water molecules, further suggest that the Mg2+-RNA interaction may also involve purely quantum phenomena such as tunneling through potential barriers, in addition to the classical over-the-barrier thermal transition.79,80 This means that quantum tunneling may speed up certain conformational transitions that would otherwise need higher classical driving potentials and extended periods of thermal agitation.81,82
The versatility of the RNA structure and function is intertwined with the chemical fragility of RNA.83−85 The ability of divalent cations such as Mg2+ to stabilize the RNA structure is pertinent to molecular biology research and synthesis of novel therapeutic agents, including RNA vaccines.86,87 Thus, the identification of the Mg2+-RNA binding sites and elucidation of the involvement of the solvent in structural stabilization/destabilization could be utilized for improvement of RNA-based medical treatment and prophylaxis of disease.
Classical MD force fields, unlike the ab initio methods, give results dependent on the used parameterization. Properties of the studied systems like coordination number and the mode of interaction with the phosphate groups appear to differ with the used classical force field, especially for the Na+ ions. In this respect, ab initio calculations using explicit water provide more reliable results and can be used for proper parameterization of the classical MD methods.
Data Availability
The data underlying this article will be shared on reasonable request to the corresponding author.
Acknowledgments
P.S.P. and G.N.V. acknowledge the support by the project EXTREME, funded by the Bulgarian Ministry of Education and Science, D01-76/30.03.2021, Program “European Scientific Networks”.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c01327.
Time each ion (Na+ or Mg2+) spends with different coordination numbers and also about the RNA backbone conformation; dynamics of the ions; ions’ solvation; and dynamics of the total energy of the simulated systems (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Serganov A.; Patel D. J. Ribozymes, riboswitches and beyond: regulation of gene expression without proteins. Nat. Rev. Genet. 2007, 8, 776–790. 10.1038/nrg2172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourgeois C. F.; Mortreux F.; Auboeuf D. The multiple functions of RNA helicases as drivers and regulators of gene expression. Nat. Rev. Mol. Cell Biol. 2016, 17, 426–438. 10.1038/nrm.2016.50. [DOI] [PubMed] [Google Scholar]
- Yao R.-W.; Wang Y.; Chen L.-L. Cellular functions of long noncoding RNAs. Nat. Cell Biol. 2019, 21, 542–551. 10.1038/s41556-019-0311-8. [DOI] [PubMed] [Google Scholar]
- Hoagland M. B.; Stephenson M. L.; Scott J. F.; Hecht L. I.; Zamecnik P. C. A soluble ribonucleic acid intermediate in protein synthesis. J. Biol. Chem. 1958, 231, 241–257. 10.1016/s0021-9258(19)77302-5. [DOI] [PubMed] [Google Scholar]
- Bentley D. L. Coupling mRNA processing with transcription in time and space. Nat. Rev. Genet. 2014, 15, 163–175. 10.1038/nrg3662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philipps G. R. Primary structure of transfer RNA. Nature 1969, 223, 374–377. 10.1038/223374a0. [DOI] [PubMed] [Google Scholar]
- Genuth N. R.; Barna M. Heterogeneity and specialized functions of translation machinery: from genes to organisms. Nat. Rev. Genet. 2018, 19, 431–452. 10.1038/s41576-018-0008-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klinge S.; Woolford J. L. Ribosome assembly coming into focus. Nat. Rev. Mol. Cell Biol. 2019, 20, 116–131. 10.1038/s41580-018-0078-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson T. J.; Liu Y.; Lilley D. M. J. Ribozymes and the mechanisms that underlie RNA catalysis. Front. Chem. Sci. Eng. 2016, 10, 178–185. 10.1007/s11705-016-1558-2. [DOI] [Google Scholar]
- Lilley D. M. J. The origins of RNA catalysis in ribozymes. Trends Biochem. Sci. 2003, 28, 495–501. 10.1016/S0968-0004(03)00191-9. [DOI] [PubMed] [Google Scholar]
- Ozata D. M.; Gainetdinov I.; Zoch A.; O’Carroll D.; Zamore P. D. PIWI-interacting RNAs: small RNAs with big functions. Nat. Rev. Genet. 2019, 20, 89–108. 10.1038/s41576-018-0073-3. [DOI] [PubMed] [Google Scholar]
- Li X.; Jin P. Roles of small regulatory RNAs in determining neuronal identity. Nat. Rev. Neurosci. 2010, 11, 329–338. 10.1038/nrn2739. [DOI] [PubMed] [Google Scholar]
- He L.; Hannon G. J. MicroRNAs: small RNAs with a big role in gene regulation. Nat. Rev. Genet. 2004, 5, 522–531. 10.1038/nrg1379. [DOI] [PubMed] [Google Scholar]
- Draper D. E. A guide to ions and RNA structure. RNA 2004, 10, 335–343. 10.1261/rna.5205404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein A.; Crothers D. M. Conformational changes of transfer RNA. The role of magnesium(II). Biochemistry 1976, 15, 160–168. 10.1021/bi00646a025. [DOI] [PubMed] [Google Scholar]
- Draper D. E. RNA folding: thermodynamic and molecular descriptions of the roles of ions. Biophys. J. 2008, 95, 5489–5495. 10.1529/biophysj.108.131813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inoue A.; Takagi Y.; Taira K. Importance in catalysis of a magnesium ion with very low affinity for a hammerhead ribozyme. Nucleic Acids Res. 2004, 32, 4217–4223. 10.1093/nar/gkh753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T.-S.; López C. S.; Giambaşu G. M.; Martick M.; Scott W. G.; York D. M. Role of Mg2+ in hammerhead ribozyme catalysis from molecular simulation. J. Am. Chem. Soc. 2008, 130, 3053–3064. 10.1021/ja076529e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S.; Stevens D. R.; Goyal P.; Bingaman J. L.; Bevilacqua P. C.; Hammes-Schiffer S. Assessing the potential effects of active site Mg2+ ions in the glmS ribozyme–cofactor complex. J. Phys. Chem. Lett. 2016, 7, 3984–3988. 10.1021/acs.jpclett.6b01854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng H.; Shabalin I. G.; Handing K. B.; Bujnicki J. M.; Minor W. Magnesium-binding architectures in RNA crystal structures: validation, binding preferences, classification and motif detection. Nucleic Acids Res. 2015, 43, 3789–3801. 10.1093/nar/gkv225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halder A.; Roy R.; Bhattacharyya D.; Mitra A. Consequences of Mg2+ binding on the geometry and stability of RNA base pairs. Phys. Chem. Chem. Phys. 2018, 20, 21934–21948. 10.1039/c8cp03602k. [DOI] [PubMed] [Google Scholar]
- Fischer N. M.; Polêto M. D.; Steuer J.; van der Spoel D. Influence of Na+ and Mg2+ ions on RNA structures studied with molecular dynamics simulations. Nucleic Acids Res. 2018, 46, 4872–4882. 10.1093/nar/gky221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez R. L.; Tinoco I. Identification characterization of metal ion binding sites in RNA. Methods Enzymol. 2002, 338, 421–443. 10.1016/S0076-6879(02)38231-4. [DOI] [PubMed] [Google Scholar]
- Bonneau E.; Legault P. NMR Localization of divalent cations at the active site of the neurospora vs ribozyme provides insights into RNA–metal-ion interactions. Biochemistry 2014, 53, 579–590. 10.1021/bi401484a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchanka A.; Carlomagno T. Solid-state NMR spectroscopy of RNA. Methods Enzymol. 2019, 615, 333–371. 10.1016/bs.mie.2018.08.029. [DOI] [PubMed] [Google Scholar]
- Erat M. C.; Sigel R. K. O.. Methods to detect and characterize metal ion binding sites in RNA. In Structural and Catalytic Roles of Metal Ions in RNA, Sigel A., Sigel H., Sigel R. K. O., Eds.; The Royal Society of Chemistry, 2011; Vol. 9, pp 37–100. [DOI] [PubMed] [Google Scholar]
- Bashan A.; Yonath A. The linkage between ribosomal crystallography, metal ions, heteropolytungstates and functional flexibility. J. Mol. Struct. 2008, 890, 289–294. 10.1016/j.molstruc.2008.03.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klostermeier D.; Hammann C.. RNA Structure and Folding: Biophysical Techniques and Prediction Methods; Walter de Gruyter, 2013. [Google Scholar]
- Kolev S.; Petkov P. S.; Rangelov M.; Vayssilov G. N. Ab initio molecular dynamics of Na+ and Mg2+ countercations at the backbone of RNA in water solution. ACS Chem. Biol. 2013, 8, 1576–1589. 10.1021/cb300463h. [DOI] [PubMed] [Google Scholar]
- Auffinger P.; Westhof E. Water and ion binding around RNA and DNA (C,G) oligomers. J. Mol. Biol. 2000, 300, 1113–1131. 10.1006/jmbi.2000.3894. [DOI] [PubMed] [Google Scholar]
- Šponer J.; Bussi G.; Krepl M.; Banáš P.; Bottaro S.; Cunha R. A.; Gil-Ley A.; Pinamonti G.; Poblete S.; Jurečka P.; et al. RNA structural dynamics as captured by molecular simulations: a comprehensive overview. Chem. Rev. 2018, 118, 4177–4338. 10.1021/acs.chemrev.7b00427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDowell S. E.; Špačková N. a.; Šponer J.; Walter N. G. Molecular dynamics simulations of RNA: an in silico single molecule approach. Biopolymers 2007, 85, 169–184. 10.1002/bip.20620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vangaveti S.; Ranganathan S. V.; Chen A. A. Advances in RNA molecular dynamics: a simulator’s guide to RNA force fields. Wiley Interdiscip. Rev.: RNA 2017, 8, e1396 10.1002/wrna.1396. [DOI] [PubMed] [Google Scholar]
- Liu F.; Ou-Yang Z.-C. Monte Carlo simulation for single RNA unfolding by force. Biophys. J. 2005, 88, 76–84. 10.1529/biophysj.104.049239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nivón L. G.; Shakhnovich E. I. All-atom Monte Carlo simulation of GCAA RNA folding. J. Mol. Biol. 2004, 344, 29–45. 10.1016/j.jmb.2004.09.041. [DOI] [PubMed] [Google Scholar]
- Faber M.; Klumpp S. Kinetic Monte Carlo approach to RNA folding dynamics using structure-based models. Phys. Rev. E 2013, 88, 052701. 10.1103/PhysRevE.88.052701. [DOI] [PubMed] [Google Scholar]
- Yoo J.; Aksimentiev A. Improved parametrization of Li+, Na+, K+, and Mg2+ ions for all-atom molecular dynamics simulations of nucleic acid systems. J. Phys. Chem. Lett. 2012, 3, 45–50. 10.1021/jz201501a. [DOI] [Google Scholar]
- Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Horn H. W.; Swope W. C.; Pitera J. W.; Madura J. D.; Dick T. J.; Hura G. L.; Head-Gordon T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- Mahoney M. W.; Jorgensen W. L. A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 2000, 112, 8910–8922. 10.1063/1.481505. [DOI] [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mustoe A. M.; Brooks C. L.; Al-Hashimi H. M. Hierarchy of RNA functional dynamics. Annu. Rev. Biochem. 2014, 83, 441–466. 10.1146/annurev-biochem-060713-035524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kühne T. D.; Iannuzzi M.; Del Ben M.; Rybkin V. V.; Seewald P.; Stein F.; Laino T.; Khaliullin R. Z.; Schütt O.; Schiffmann F.; et al. CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. 10.1063/5.0007045. [DOI] [PubMed] [Google Scholar]
- VandeVondele J.; Krack M.; Mohamed F.; Parrinello M.; Chassaing T.; Hutter J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. 10.1016/j.cpc.2004.12.014. [DOI] [Google Scholar]
- Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Lin L.; Lu J.; Ying L. Numerical methods for Kohn–Sham density functional theory. Acta Numer. 2019, 28, 405–539. 10.1017/S0962492919000047. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- VandeVondele J.; Hutter J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. 10.1063/1.2770708. [DOI] [PubMed] [Google Scholar]
- Lippert G.; Hutter J. x. r.; Parrinello M. The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations. Theor. Chem. Acc. 1999, 103, 124–140. 10.1007/s002140050523. [DOI] [Google Scholar]
- Lippert G.; Hutter J.; Parrinello M. A hybrid Gaussian and plane wave density functional scheme. Mol. Phys. 1997, 92, 477–487. 10.1080/002689797170220. [DOI] [Google Scholar]
- Goedecker S.; Teter M.; Hutter J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. 10.1103/PhysRevB.54.1703. [DOI] [PubMed] [Google Scholar]
- Hartwigsen C.; Goedecker S.; Hutter J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. 10.1103/PhysRevB.58.3641. [DOI] [PubMed] [Google Scholar]
- Braun E.; Moosavi S. M.; Smit B. Anomalous effects of velocity rescaling algorithms: the flying ice cube effect revisited. J. Chem. Theory Comput. 2018, 14, 5262–5272. 10.1021/acs.jctc.8b00446. [DOI] [PubMed] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Pearson W. R.; Lipman D. J. Improved tools for biological sequence comparison. Proc. Natl. Acad. Sci. U.S.A. 1988, 85, 2444–2448. 10.1073/pnas.85.8.2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Zhang C.; Lu C.; Wang Q.; Ponder J. W.; Ren P. Polarizable multipole-based force field for dimethyl and trimethyl phosphate. J. Chem. Theory Comput. 2015, 11, 5326–5339. 10.1021/acs.jctc.5b00562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Correll C. C.; Freeborn B.; Moore P. B.; Steitz T. A. Metals, Motifs, and Recognition in the Crystal Structure of a 5S rRNA Domain. Cell 1997, 91, 705–712. 10.1016/S0092-8674(00)80457-2. [DOI] [PubMed] [Google Scholar]
- Kolev S. K.; Petkov P. S.; Rangelov M. A.; Trifonov D. V.; Milenov T. I.; Vayssilov G. N. Interaction of Na+, K+, Mg2+ and Ca2+ counter cations with RNA. Metallomics 2018, 10, 659–678. 10.1039/c8mt00043c. [DOI] [PubMed] [Google Scholar]
- Pallan P. S.; Marshall W. S.; Harp J.; Jewett F. C.; Wawrzak Z.; Brown B. A.; Rich A.; Egli M. Crystal Structure of a Luteoviral RNA Pseudoknot and Model for a Minimal Ribosomal Frameshifting Motif. Biochemistry 2005, 44, 11315–11322. 10.1021/bi051061i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller U.; Schübel H.; Sprinzl M.; Heinemann U. Crystal structure of acceptor stem of tRNAAla from Escherichia coli shows unique G[bull ]U wobble base pair at 1.16 Å resolution. RNA 1999, 5, 670–677. 10.1017/S1355838299982304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mooers B. H. M.; Singh A. The crystal structure of an oligo(U):pre-mRNA duplex from a trypanosome RNA editing substrate. RNA 2011, 17, 1870–1883. 10.1261/rna.2880311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mueller U.; Muller Y. A.; Herbst-Irmer R.; Sprinzl M.; Heinemann U. Disorder and twin refinement of RNA heptamer double helices. Acta Crystallogr. D 1999, 55, 1405–1413. 10.1107/S0907444999007441. [DOI] [PubMed] [Google Scholar]
- Bucher D.; Guidoni L.; Carloni P.; Rothlisberger U. Coordination Numbers of K+ and Na+ Ions Inside the Selectivity Filter of the KcsA Potassium Channel: Insights from First Principles Molecular Dynamics. Biophys. J. 2010, 98, L47–L49. 10.1016/j.bpj.2010.01.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leonarski F.; D’Ascenzo L.; Auffinger P. Nucleobase carbonyl groups are poor Mg2+ inner-sphere binders but excellent monovalent ion binders—a critical PDB survey. RNA 2019, 25, 173–192. 10.1261/rna.068437.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwierz N. Kinetic pathways of water exchange in the first hydration shell of magnesium. J. Chem. Phys. 2020, 152, 224106. 10.1063/1.5144258. [DOI] [PubMed] [Google Scholar]
- Chamberlin S. I.; Merino E. J.; Weeks K. M. Catalysis of amide synthesis by RNA phosphodiester and hydroxyl groups. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 14688–14693. 10.1073/pnas.212527799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedekind J. E.; McKay D. B. Crystal structure of a lead-dependent ribozyme revealing metal binding sites relevant to catalysis. Nat. Struct. Biol. 1999, 6, 261–268. 10.1038/6700. [DOI] [PubMed] [Google Scholar]
- Serra M. J.; Baird J. D.; Dale T.; Fey B. L.; Retatagos K.; Westhof E. Effects of magnesium ions on the stabilization of RNA oligomers of defined structures. RNA 2002, 8, 307–323. 10.1017/S1355838202024226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemkul J. A.; Lakkaraju S. K.; MacKerell A. D. Characterization of Mg2+ distributions around RNA in solution. ACS Omega 2016, 1, 680–688. 10.1021/acsomega.6b00241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao C.; Zhang D.; Jiang Y.; Chen S.-J. Modeling loop composition and ion concentration effects in RNA hairpin folding stability. Biophys. J. 2020, 119, 1439–1455. 10.1016/j.bpj.2020.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan C. Y.; Carmack C. S.; Long D. D.; Maliyekkel A.; Shao Y.; Roninson I. B.; Ding Y. A structural interpretation of the effect of GC-content on efficiency of RNA interference. BMC Bioinf. 2009, 10, S33. 10.1186/1471-2105-10-S1-S33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gebert D.; Jehn J.; Rosenkranz D. Widespread selection for extremely high and low levels of secondary structure in coding sequences across all domains of life. Open Biol. 2019, 9, 190020. 10.1098/rsob.190020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez de Groot N.; Armaos A.; Graña-Montes R.; Alriquet M.; Calloni G.; Vabulas R. M.; Tartaglia G. G. RNA structure drives interaction with proteins. Nat. Commun. 2019, 10, 3246. 10.1038/s41467-019-10923-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grilley D.; Soto A. M.; Draper D. E. Mg2+–RNA interaction free energies and their relationship to the folding of RNA tertiary structures. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 14003. 10.1073/pnas.0606409103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xi K.; Wang F.-H.; Xiong G.; Zhang Z.-L.; Tan Z.-J. Competitive binding of Mg2+ and Na+ ions to nucleic acids: from helices to tertiary structures. Biophys. J. 2018, 114, 1776–1790. 10.1016/j.bpj.2018.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunha R. A.; Bussi G. Unraveling Mg2+–RNA binding with atomistic molecular dynamics. RNA 2017, 23, 628–638. 10.1261/rna.060079.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pusuluk O.; Farrow T.; Deliduman C.; Burnett K.; Vedral V. Proton tunnelling in hydrogen bonds and its implications in an induced-fit model of enzyme catalysis. Proc. Math. Phys. Eng. Sci. 2018, 474, 20180037. 10.1098/rspa.2018.0037. [DOI] [Google Scholar]
- Sutcliffe M. J.; Scrutton N. S. Enzyme catalysis: over-the-barrier or through-the-barrier?. Trends Biochem. Sci. 2000, 25, 405–408. 10.1016/S0968-0004(00)01642-X. [DOI] [PubMed] [Google Scholar]
- Kariev A. M.; Green M. E. Quantum calculations on ion channels: why are they more useful than classical calculations, and for which processes are they essential?. Symmetry 2021, 13, 655. 10.3390/sym13040655. [DOI] [Google Scholar]
- Georgiev D. D.; Kolev S. K.; Cohen E.; Glazebrook J. F. Computational capacity of pyramidal neurons in the cerebral cortex. Brain Res. 2020, 1748, 147069. 10.1016/j.brainres.2020.147069. [DOI] [PubMed] [Google Scholar]
- Chandler M.; Panigaj M.; Rolband L. A.; Afonin K. A. Challenges in optimizing RNA nanostructures for large-scale production and controlled therapeutic properties. Nanomedicine 2020, 15, 1331–1340. 10.2217/nnm-2020-0034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koonin E. V.; Senkevich T. G.; Dolja V. V. Compelling reasons why viruses are relevant for the origin of cells. Nat. Rev. Microbiol. 2009, 7, 615. 10.1038/nrmicro2108-c5. [DOI] [PubMed] [Google Scholar]
- Tosar J. P. Die hard: resilient RNAs in the blood. Nat. Rev. Mol. Cell Biol. 2021, 22, 373. 10.1038/s41580-021-00355-9. [DOI] [PubMed] [Google Scholar]
- Fuller D. H.; Berglund P. Amplifying RNA vaccine development. N. Engl. J. Med. 2020, 382, 2469–2471. 10.1056/NEJMcibr2009737. [DOI] [PubMed] [Google Scholar]
- Stuart L. M. In Gratitude for mRNA Vaccines. N. Engl. J. Med. 2021, 385, 1436–1438. 10.1056/NEJMcibr2111445. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data underlying this article will be shared on reasonable request to the corresponding author.