Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jul 1;7(27):24004–24011. doi: 10.1021/acsomega.2c02974

A Potent Antioxidant Sesquiterpene, Abelsaginol, from Abelmoschus sagittifolius: Experimental and Theoretical Insights

Thuc Dinh Ngoc †,*, Mai Vu Thi Ha †, Thanh Nguyen Le ‡, Hue Vu Thi ‡, Thi Van Anh Nguyen §, Adam Mechler ∥, Nguyen Thi Hoa ⊥, Quan V Vo ⊥,*
PMCID: PMC9280938  PMID: 35847298

Abstract

graphic file with name ao2c02974_0006.jpg

The sesquiterpenoid compound abelsaginol (AS) was successfully isolated from Abelmoschus sagittifolius for the first time. The compound was identified using NMR and MS data. The antioxidant activity of AS was also evaluated both theoretically and experimentally. AS was found to be a weak HOO• radical scavenger in organic solvents such as pentyl ethanoate and dimethyl sulfoxide (koverall = ∼ 102 M–1 s–1), in a good agreement with the results of the 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulfonic acid) assay. However, AS exhibited good HOO• antiradical activity in water at pH 7.40 (koverall = 9.00 × 106 M–1 s–1) through the single-electron transfer mechanism of the anion state. Further calculations also demonstrated that AS could exert good to moderate activity against CH3O•, CH3OO•, CCl3OO•, NO2, and SO4•– radicals, with kf values from 4.00 × 103 to 1.52 × 107 M–1 s–1. However, AS exerted much lower activity against HO•, CCl3O•, NO, O2•–, and N3• radicals under the studied conditions. In general, the activity of AS in water at pH 7.40 is higher than that of Trolox or butylated hydroxytoluene, which are common reference antioxidants. Thus, in an aqueous physiological milieu, AS is a promising natural antioxidant.

1. Introduction

Abelmoschus sagittifolius is a flowering plant that belongs to the Abelmoschus genus, which contains 15 species in the Malvaceae family. Abelmoschus was previously classified in the Hibiscus genus,1 but the current botanic database classifies it as a distinct genus. The A. sagittifolius plant is distributed in Australia and Africa as well as tropical and subtropical Asian regions such as China, India, and Southeast Asian countries.2,3 In Vietnamese and Chinese traditional medicine, the root tuber of A. sagittifolius is used for the treatment of cough, tuberculosis, constipation, neurasthenia, abscess, backache, headache, stomachache, phthisis, carbuncle sore, dizziness, and lumbosacral pain.4−7 However, formal studies of the chemical composition and biological activity of A. sagittifolius have been limited. Chinese scientists have reported the isolation of sesquiterpenes, lignans, phenolic, and amide constituents from A. sagittifolius.8−10 Several isolated compounds showed moderate cytotoxicities against HepG-2 and Hela cancer cell lines.9,10 These limited data suggest that this traditional medicine does indeed contain potent natural products that can be isolated and tested for their activity. Recently, we isolated several known sesquiterpenes from the roots of A. sagitifolis.11 Multiple chronic diseases are now know to be linked to oxidative stress.12,13 The ability of natural products to scavenge free radicals is an important part of their antibacterial, anti-inflammatory, and cancer-prevention activities and it is the driving force behind antioxidant research.14−17 In our continuing program of researching natural products, here we report the isolation and structural identification of a new sesquiterpenoid compound, abelsaginol (AS, Figure 1), that was tested for antioxidant activity both in vitro and in silico using quantum chemical calculations.

Figure 1.

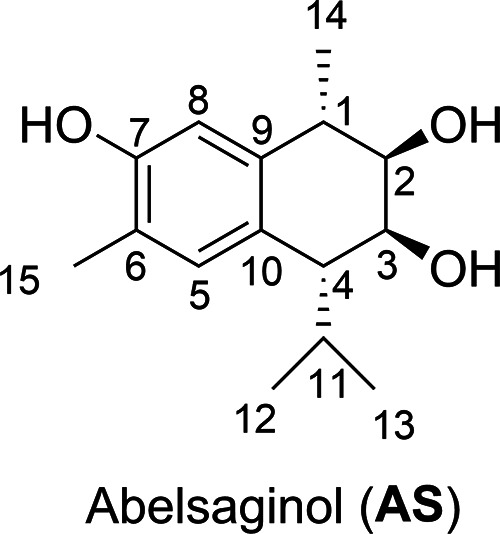
Figure 1

Open in a new tab

Molecular structure and atomic numbering of abelsaginol (AS).

2. Results and Discussion

2.1. Isolation and Identification of AS from A. sagittifolius

2.1.1. Isolation

The dried powder of the roots of A. sagittifolius (4.4 kg) was extracted with MeOH at room temperature for 24 h (20 L × 3 times). The extracts were combined and concentrated under reduced pressure at 50 °C to obtain the MeOH residue. The MeOH residue was dissolved in 1 L of distilled water, and the mixture was extracted again with n-hexane and ethyl acetate, respectively. After distillation and the removal of the organic solvent, the n-hexane extract (46 g) and the ethyl acetate extract (7 g) were obtained.

The ethyl acetate residue (7 g) was subjected to silica gel column chromatography (CC), which was eluted with a gradient solvent system of n-hexane/ethyl acetate (from 0% to 100% ethyl acetate), and the fractions were confirmed by thin layer chromatography (TLC). Nine corresponding fractions were obtained (E1–E9).

The E4 fraction (64 mg) was purified by RP-18 reverse-phase silica gel column chromatography (YMC) with an enluent of MeOH/water (1/2) to obtain compound 1 (8.4 mg), a white amorphous powder. [α]D25 −33.5 (c 0.2, MeOH). HR-ESI-MS m/z: 285.1253 [M + Cl]− (C15H22O3Cl calcd. 285.1257). 1H NMR (500 MHz, CDCl3) δH (ppm): 6.85 (1H, s, H-5), 6.60 (1H, s, H-8), 4.15 (1H, dd, J = 2.5 Hz, 4.0 Hz, H-3), 3.71 (1H, dd, J = 2.5, 7.0 Hz, H-2), 2.76 (1H, quin, J = 7.0 Hz, H-1), 2.61 (1H, dd, J = 4.0, 7.0 Hz, H-4), 2.18 (3H, s, H-15), 1.78 (1H, m, H-11), 1.38 (3H, d, J = 7.0 Hz, H-14), 0.99 (d, J = 7.0 Hz, H-13), 0.92 (d, J = 7.0 Hz, H-12). 13C NMR (125 MHz, CD3OD) δC (ppm): 152.7 (C-7), 137.9 (C-9), 132.8 (C-5), 127.2 (C-10), 121.8 (C-6), 113.9 (C-8), 73.7 (C-3), 70.4 (C-2), 51.7 (C-4), 38.2 (C-1), 32.7 (C-11), 21.9 (C-13), 20.2 (C-12), 19.7 (C-14), 15.5 (C-15).

2.1.2. Identification

Compound 1 was isolated from the ethyl acetate extract as a white amorphous powder with a molecular formula of C15H22O3, as determined by HR-ESI-MS at m/z 285.1253 ([M + Cl]− C15H22O3Cl calcd. 285.1257), indicating five degrees of unsaturation. The 1H NMR spectrum showed two aromatic proton signals at δH 6.85 (1H, s, H-5) and 6.60 (1H, s, H-8); two oxymethine groups at δH 4.15 (1H, dd, J = 2.5 Hz, 4.0 Hz, H-3) and 3.71 (1H, dd, J = 2.5, 7.0 Hz, H-2); three methine groups at δH 2.76 (1H, quin, J = 7.0 Hz, H-1), 2.61 (1H, dd, J = 4.0, 7.0 Hz, H-4), and 1.78 (1H, m, H-11); and four methyl groups at δH 2.18 (3H, s, H-15), 1.38 (3H, d, J = 7.0 Hz, H-14), 0.99 (d, J = 7.0 Hz, H-13), and 0.92 (d, J = 7.0 Hz, H-12). The 13C NMR and HSQC spectra revealed 15 carbon signals, including six aromatic carbon signals at δC 152.7 (C-7), 137.9 (C-9), 132.8 (C-5), 127.2 (C-10), 121.8 (C-6), and 113.9 (C-8); two oxymethine carbons at δC 73.7 (C-3) and 70.4 (C-2); three methine group signals at δC 51.7 (C-4), 38.2 (C-1), and 32.7 (C-11); and four methyl signal at 21.9 (C-13), 20.2 (C −12), 19.7 (C-14), and 15.5 (C-15). The NMR spectral data suggested 1 was a cardinane-type sesquiterpene. The assignments of all hydrogen and carbon signals were done using 1H–1H COSY, HSQC, and HMBC correlations. The 1H–1H COSY correlations of the H-14/H-1/H-2/H-3/H-4/H-11/H-12 (and H-13) system were observed. The HMBC spectrum showed the correlations from H-5 (δH 6.85) to C-4 (δC 51.7), C-7 (δC 152.7), C-9 (δC 137.9), and H-15 (δC 15.5) and the correlations from H-8 (δH 6.60) to C-1 (δC 38.2), C-6 (δC1 21.8), and C-10 (δC 127.2) (Figure S1). Thus, the planar structure of 1 was suggested as 2,3,7-trihydroxycalamenene, similar to the aglycone of compound 2β,7,3β-trihydroxycalamenene 3-O-β-d-glucoside, which was isolated from the Chinese A. sagittifolius stem tuber by Chen et al.8 The relative configurations of 1 were assigned using the NOESY spectrum and coupling constants. We found that compound 1 had the same relative configurations as 2β,7,3β-trihydroxycalamenene 3-O-β-d-glucoside at the C-1, C-2, and C-3 positions but a different relative configuration at the C-4 position. The NOESY correlation from H-2 (δH 3.71) to H-14 (δH 1.38) indicated that H-1 and H-2 were on opposite sides. The positions of H-1 and H-2 were further confirmed by the large coupling constant between H-1 and H-2 (J = 7.0 Hz). The small coupling constant between H-2 and H-3 (J = 2.5 Hz) suggested that H-2 and H-3 were on the same side. However, the isopropyl group at the C-4 position of 1 was assigned on the same side of the ring as H-2 and H-3 due to the NOESY correlations from H-2 (δH 3.71) to H-11 (δH 1.78) and H-12 (δH 0.92) and from H-3 (δH 4.15) to methyl groups H-12 (δH 0.92) and H-13 (δH 0.99), (Figure S2).18 We also observed that coupling constant between H-3 and H-4 of 1 was 4.0 Hz, while it was only 1.2 Hz in the case of 2β,7,3β-trihydroxycalamenene 3-O-β-d-glucoside.8 Thus, 1 was assigned as a new natural compound, as illustrated in Figure 1, and named abelsaginol (AS).

2.2. The Antioxidant Activity of AS

2.2.1. The ABTS Antioxidant Assay

To assess AS’s antioxidant activity, the 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulfonic acid (ABTS•+) test was used as recommended in the literature,19,20 with Trolox as a control antioxidant. Under the tested conditions, AS was shown to have an ABTS•+ scavenging activity two times lower (IC50 = 41.04 ± 6.07 mM) than that of Trolox (IC50 = 25.16 ± 1.64 mM). To properly evaluate this result, one has to keep in mind that the ABTS experiment is carried out in an organic solvent (dimethyl sulfoxide), hence the data can only show that AS has a lower radical scavenging activity than Trolox in organic solvents. Deprotonation of phenolic groups (i.e., O7–H) in aqueous solutions, on the other hand, can open routes to significantly improve the activity,21,22 especially at physiological pH. This must be studied further using computational chemistry.

2.2.2. The HOO• Radical Scavenging Activity

2.2.2.1. Evaluation of the Conformation

The molecular structure suggests that the OH and OMe groups in AS can rotate around the single bonds to yield a range of conformers.23 Thus, after the likely AS conformers were screened24 in the first step, the five lowest-electronic-energy conformers were evaluated utilizing the M06-2X/6-311++G(d,p) level of theory (Figure 2). AS has the lowest Gibbs free energy value among the conformers, whereas AS1–AS4 have free energies of formation 2.9–5.8 kcal mol–1 larger than AS. The relative numbers of the conformers were evaluated using the Maxwell–Boltzmann distribution,25,26 which confirmed that AS was the dominant conformer (>99%); hence, this conformer was investigated further.

Figure 2.

Figure 2

Open in a new tab

Typical conformers of AS and the relative free energies ΔG° (kcal mol–1) compared to the AS conformer.

2.2.2.2. Thermodynamic Evaluation

Antioxidant activity was assessed using thermodynamic computations that assumed one of the three main radical scavenging pathways,: (i) formal hydrogen transfer (FHT), (ii) single-electron transfer–proton transfer (SETPT), and (iii) sequential proton-loss electron transfer (SPLET).27 The thermodynamic parameters (ionization energy (IE), bond dissociation enthalpy (BDE), and proton affinity (PA)) of the first step of each pathway for all bonds were calculated for the HOO• antiradical activity of AS in pentyl ethanoate as a lipid medium and water at pH 7.4 as an aqueous physiological environment, as well as DMSO to obtain predictions directly comparable to the ABTS assay. The findings are summarized in Table 1.

Table 1. Calculated Thermodynamic Parameters (BDEs, PAs, and IEs; kcal mol–1) of AS in the Studied Environmentsa.
  BDE
 PA
 IE
positions G DMSO P W G DMSO P W G DMSO P W
C1–H 82.4 83.2 82.8 84.5         184.2 116.8 136.3 110.1
C2–H 92.6 92.6 92.5 93.3        
C3–H 96.0 95.7 95.7 96.7        
C4–H 86.9 87.1 86.8 88.1        
C11–H 93.3 93.9 93.5 94.7        
C12–H 99.9 100.4 100.2 101.2        
C14–H 99.9 101.0 100.5 101.8        
C15–H 89.7 90.3 90.2 91.1        
O2–H 106.0 104.7 105.0 107.7        
O3–H 105.0 104.4 104.6 106.8        
O7–H 86.1 84.9 85.0 86.3 339.6 33.4 86.1 48.4
Open in a new tab
a

Abbreviations are as follows: gas, G; pentyl ethanoate, P; dimethyl sulfoxide, DMSO; and water, W.

Tthe lowest BDE(C–H) values were found at C1–H (BDE(C1–H) = 82.4–84.5 kcal mol–1) and C4–H (BDE(C4–H) = 86.8–88.1 kcal mol–1), whereas those of the O–H bonds were found at O7–H, where BDE(O7–H) = 84.9–86.3 kcal mol–1 in all of the studied solvents. By contrast, bond dissociation is not favored at C12(C13)–H or, somewhat unexpectedly, at the O2(O3–-H bonds (BDE = 99.9–107.6 kcal mol–1). These site-specific actions can be explained by the assesment of the spin density distribution, as illustrated in Figure 3. The single electron is stabilized throughout a vast system by resonance, especially in the aromatic ring of the selected radicals. Nonfavored locations, such as C3 or C4, have a spin density distribution centered on the carbon atoms, making product formation difficult.

Figure 3.

Figure 3

Open in a new tab

Spin density distribution of the selected radicals

The presence of solvents could slightly affect the BDE values by about 0.8–2.1 kcal mol–1. The BDEs increased in the presence of water but varied in DMSO and the pentyl ethanoate solvents (compared with the gas phase). The IE values were larger than the lowest BDEs in all of the studied solvents (IE = 110.1–184.2 kcal mol–1). This suggests that the single-electron transfer (SET) pathway is not feasible for neutral AS in either of the environments. However, the deprotonation at the O7–H bond could preferentially occur in water and DMSO due to the lower PA values compared with the BDE and IE values (PA = 33.4–48.2 kcal mol–1).

Calculations of the Gibbs free energy change (ΔG°, Table 2) in the reaction of AS and HOO• indicated that the reaction was only spontaneous in the thermodynamic sense following the hydrogen transfer pathway, particularly at the C1(4)–H and O7–H bonds (ΔG° = −4.9 to 0.7 kcal mol–1). The FHT reactions at other C–H bonds were not spontaneous, with positive ΔG° values (ΔG° = 2.5–20.0 kcal mol–1). At the same time, the LP and SET reactions were not supported in any of the studied solvents. Thus, in the organic solvents, i.e., pentyl ethanoate and DMSO, and the gas phase, the HOO• radical scavenging activity is defined by the FHT pathway, whereas deprotonation and stable states of AS should be considered in polar environments such as water at pH 7.40.

Table 2. Calculated ΔG° (kcal mol–1) of the AS + HOO• Reactions Following the Studied Pathways (FHT, Lose Proton (LP), and SET Mechanisms) in the Studied Media.
  FHT
 LP
 SET
positions G D P W G D P W G D P W
C1–H –3.9 –2.8 –3.5 –4.9         160.6 52.1 73.4 29.0
C2–H 5.6 5.8 5.5 3.2        
C3–H 9.1 8.9 8.7 6.5        
C4–H 0.3 0.7 0.2 –1.7        
C11–H 5.7 6.4 5.9 3.9        
C12–H 13.0 13.7 13.3 11.1        
C14–H 13.7 14.9 14.2 12.3        
C15–H 4.3 5.0 4.7 2.5        
O2–H 20.0 18.9 19.1 18.5        
O3–H 19.0 18.5 18.5 17.6        
O7–H 0.0 –0.9 –1.1 –3.0 187.3 83.4 104.2 55.4
Open in a new tab
2.2.2.3. Kinetic Study

To examine the feasibility and kinetics of electron transfer reactions from the deprotonated species, the protonation state of AS at physiological pH must be determined. Protonation at the O7–H location is possible with the AS structure. The pKa values of AS were calculated according to the literature,28,29 and the results are shown in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Acid dissociation equilibrium of AS at pH 7.40.

The pKa value calculated for the O7–H group was 10.06. Thus, in a pH 7.4 aqueous solution, there is still a non-negligible amount of the monoanionic state (O7H, 0.2% (Figure 4). The kinetic evaluation of the HOO• antiradical activity of AS occurred in water at pH 7.4; therefore, has to take into account both the neutral and anionic species.

The kinetic calculations in the gas phase (Table S3 and Figure 5) showed that the H-abstraction of the O7–H bond defines the FHT reaction (k(O7–H) = 1.26 × 103 M–1 s–1, Γ = 99.4%). FHT reactions of the C1(C4)–H bonds played a minor role (Γ = 0.6%). Thus, the rate constants of the FHT reactions in the solvents, i.e. DMSO, pentyl ethanoate, and water, were computed on the basis of the H-abstraction of the hydroxyl group. Therefore, the total rate constant (koverall) of AS’s antiradical activity against the HOO• radical in the aqueous physiological environment can be calculated using eqs 1 and 2. Table 3 and Figure 5 show the final results.

Figure 5.

Figure 5

Open in a new tab

Optimized transition state (TS) structures and their imaginary frequencies (ν, cm–1) according to the FHT reaction of the AS + HOO• reaction (ν, cm–1. Abbreviations are as follows: dimethyl sulfoxide, DMSO; P, pentyl ethanoate; G, gas phase; and W, water).

Table 3. Calculated ΔG≠ (kcal mol–1), Tunneling Corrections (κ), Molar Fractions (f), Rate Constants (kapp, kf, and koverall; M–1 s–1), and Branching Ratios (Γ, %) in the AS + HOO• Reactiona.
solvents mechanisms ΔG≠ k kapp f kf Γ
P FHT 16.6 145.5 5.90 × 102     100.0
DMSO FHT 17.6 183.4 1.50 × 102     100.0
W SET 3.8 16.4b 4.50 × 109 0.002 9.00 × 106 100.0
FHT 16.7 605.3 2.20 × 103 0.998 2.20 × 103 0.0
koverall         9.00 × 106  
Open in a new tab
a

At 298.15 K in P, DMSO, and W solvents.

b

The nuclear reorganization energy (λ, kcal mol–1); kf = f·kapp and Γ = kf·100/koverall

In the organic solvents:
2.2.2.3. 1

In the aqueous solution:
2.2.2.3. 2

As shown in Table 3, AS exhibited a low HOO• radical scavenging activity in the organic solvents (pentyl ethanoate and DMSO) with kapp = 5.90 × 102 and 1.50 × 102 M–1 s–1, respectively. In the lipid medium, the HOO• trapping capability of AS was lower than those of typical antioxidants such as Trolox (koverall = 3.40 × 103 M–1 s–1),30 BHT (koverall = 1.70 × 104 M–1 s–1),31 resveratrol (koverall = 1.31 × 104 M–1 s–1),32 and ascorbic acid (koverall = 5.71 × 103 M–1 s–1).33 This activity was also lower than that of samwirin A (koverall = 6.70 × 103 M–1 s–1).20 However, AS exhibited significant hydroperoxyl antiradical activity (koverall = 9.00 × 106 M–1 s–1) in water at pH 7.40. The activity follows the SET reaction pathway of the anion state (Γ = 100%). The FHT reaction of the O7–H bond had no contribution to the overall rate constant. AS exhibited a higher HOO• radical scavenging activity than Trolox (k = 8.96 × 104 M–1 s–1)30 and BHT (koverall = 2.51 × 105 M–1 s–1)31 but a slightly lower activity than resveratrol (k = 5.62 × 107 M–1 s–1)32 and ascorbic acid (k = 9.97 × 107 M–1 s–1).33 Based on the computed data, AS is a promising radical scavenger in the aqueous physiological environment.

2.2.3. The Antiradical Activity of AS in an Aqueous Solution against Conventional Free Radicals

Due to its mild reactivity, the HOO• radical is regarded a model free radical for evaluating the antiradical activities of organic compounds.33,34 Studies on the radical scavenging ability of natural products against other common reactive oxygen and nitrogen species, such as HO•, CH3O•, CCl3O•, HOO•, CH3OO•, CCl3OO•, NO, NO2, O2•–, SO4•– and N3•, are critical to provide useful information regarding their antioxidant activities.35,36 Therefore, next the antiradical activity of AS was also modeled against these free radicals following the main mechanism (the SET reaction) in water at pH 7.40. The results are shown in Table 4

Table 4. Calculated ΔG≠, λ, (kcal mol–1), Diffusion-Limited Rate Constant (kD), kapp, and kf (M–1 s–1) of the Reaction Between AS– and Chosen Radicals in Aqueous Solution at pH 7.4a.
radicals ΔG≠ λ kD kapp kfb
HO• 18.7 4.4 8.50 × 109 1.20 × 10–1 2.40 × 10–4
CH3O• 0.0 5.6 8.10 × 109 8.10 × 109 1.62 × 107
CCl3O• 17.5 22.2 7.60 × 109 9.30 × 10–1 1.86 × 10–3
HOO• 3.8 16.4 8.20 × 109 4.50 × 109 9.00 × 106
CH3OO• 4.6 15.8 8.00 × 109 2.00 × 109 4.00 × 106
CCl3OO• 0.2 17.9 7.60 × 109 7.60 × 109 1.52 × 107
NO 79.4 15.3 8.30 × 109 3.90 × 10–46 7.80 × 10–49
NO2 0.5 28.8 8.10 × 109 8.10 × 109 1.62 × 107
O2•– 43.0 18.2 7.20 × 109 1.80 × 10–19 3.60 × 10–22
SO4•– 8.90 18.6 7.90 × 109 2.00 × 106 4.00 × 103
N3• 20.3 3.5 7.00 × 109 8.10 × 10–3 1.62 × 10–5
Open in a new tab
a

According to the SET reaction.

b

kf = f·kapp and f(AS–) = 0.002.

It was found that AS should have moderate activity against CH3O•, CH3OO•, CCl3OO•, NO2, and SO4•– radicals, with kf values ranging from 4.00 × 103 to 1.52 × 107 M–1 s–1, whereas HO•, CCl3O•, NO, O2•–, and N3• radicals could not be removed by AS under the examined conditions. Compared with fraxin35 and usnic acid,36AS exhibited lower HO•, CCl3O•, and N3· antiradical activity following the SET reaction but was more active against peroxyl radicals, i.e. HOO• and CH3OO•.

3. Conclusion

The novel sesquiterpenoid compound AS was successfully isolated and identified from A. sagittifolius. AS showed a low HOO• radical scavenging activity in the DMSO solvent (koverall = 1.50 × 102 M–1 s–1) both in silico and in the experimental ABTS•+ test. Similar results were also found for its activity in the lipid medium, i.e., the pentyl ethanoate solvent. Thus, AS is predicted to be a weak radical scavenger in lipid media. However, AS exhibited good HOO• antiradical activity in water at pH 7.40 (koverall = 9.00 × 106 M–1 s–1), primarily via the SET reaction of the anion state. AS is predicted to exhibit moderate activity against CH3O•, CH3OO•, CCl3OO•, NO2, and SO4•– radicals, with kf = 4.00 × 103 – 1.52 × 107 M–1 s–1, whereas it is expected to exhibit weak activity against HO•, CCl3O•, NO, O2•–, and N3• radicals. Compared with natural typical antioxidants, the activity of AS in water at pH 7.40 is generally higher than those of Trolox and BHT. Thus, AS is a promising natural antioxidant in the aqueous physiological environment.

4. Experimental and Computational Methods

4.1. Experimental Section

4.1.1. Plant Materials

The plant samples of A. sagittifolius were collected from Bao mountain (20°01′04.0″N 105°41′04.9″E), Vinh Loc district, Thanh Hóa province, Vietnam, in October 2020, which was the harvest season for A. sagittifolius growing in this area. The plant was identified by Prof. Dr. Tran The Bach of the Institute of Ecology and Biological Resources, Vietnam Academy of Science and Technology. The plant specimens (SB-2020) were deposited at the Botanical Museum (HN) Institute of Ecology and Biological Resources, 18 Hoang Quoc Viet, Cau Giay, Hanoi, Vietnam.

4.1.2. General Experimental Procedures

Solvents and chemicals used for extraction and isolation met experimental standards. Column chromatography was performed on 40–63 μm silica gel (Merck) and reverse-phase silica gel RP-18 (YMC). Thin layer chromatography (TLC) was performed on precoated plates (Merck 60 F254), which were visualized using a 254 nm ultraviolet lamp or a 10% sulfuric acid solution spray. Nuclear magnetic resonance (NMR) spectra were recorded on a 500 MHz Bruker Avance instrument. The HR-ESI-MS spectra were obtained using an Agilent 6530 Accurate Mass Q-TOF LC/MS system. The ABTS (2,2′-azino-di(3-ethylbenzthiazoline sulfonic acid) assay was performed following the literature procedure.19,20

4.2. Computational Details

All DFT calculations were carried out with the Gaussian 09 suite of programs.37 The M06-2X functional,38 one of the most dependable tools for studying the thermodynamics and kinetics of radical processes,21,30,33,38−41 and the 6-311++G(d,p) basis set were used for all calculations. The kinetics calculations were carried out using the quantum mechanics-based test for overall free radical scavenging activity (QM-ORSA) protocol,33 with the SMD solvation model42 for water, DMSO, and pentyl ethanoate solvents.21,41,43−48

Using the transition state theory (TST) at 298.15 K and 1 M standard state, the rate constant (k) was computed as follows:43−47

4.2. 3

where σ is the reaction symmetry number,49,50 ΔG‡ is the Gibbs free energy of activation, κ contains the tunneling corrections calculated using the Eckart barrier,51h is the Planck constant, and kB is the Boltzmann constant.

The reaction barriers of SET reactions in media were determined using the Marcus theory.52,53 The equations used to calculate the Gibbs free energy change of reaction (ΔG‡) for the SET pathway are

4.2. 4
4.2. 5

where ΔG0SET is the standard Gibbs free energy change of the reaction, while ΔESET is the nonadiabatic energy difference between reactants and vertical products for SET.54,55 A correction was applied to rate constants that were close to the diffusion limit.33 The apparent rate constants (kapp) for an irreversible bimolecular diffusion-controlled reaction were computed using the Collins–Kimball theory in solvents at 298.15 K;56 the steady-state Smoluchowski rate constant (kD) was estimated as follows using the literature:33,57

4.2. 6
4.2. 7

DAB = DA + DB (DAB is the mutual diffusion coefficient of the reactants A and B),56,58 where DA or DB is determined using the Stokes–Einstein formulation (8).59,60

4.2. 8

Here η is the viscosity of the solvents (i.e., η(pentyl ethanoate) = 8.62 × 10–4 Pa s and η(H2O) = 8.91 × 10–4 Pa s) and a is the radius of the solute.

To avoid overpenalizing entropy losses in solution, the solvent cage effects were added using Okuno’s adjustments,61 which were modified with the free-volume theory according to the Benson correction.33,62−64

For species with numerous conformers, all of them were energy minimized,23 and the lowest-electronic-energy conformer was included in the study. The existence of only a single imaginary frequency was the defining feature of all transition stages. To verify that each transition state was accurately related to the precomplex and postcomplex, intrinsic coordinate calculations (IRCs) were performed.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c02974.

  • NMR spectra, thermodynamic parameters, Cartesian coordinates, and frequencies and energies of all of the transition states in the studied environments (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c02974_si_001.pdf (15.1MB, pdf)

References

  1. Coombes A. J.The A to Z of Plant Names: A Quick Reference Guide to 4000 Garden Plants; Timber Press: Portland, OR, 2012. [Google Scholar]
  2. Abelmoschus sagittifolius (Kurz) Merr. Plants of the World Online. Royal Botanical Gardens, Kew: Richmond, England. http://powo.science.kew.org/taxon/urn:lsid:ipni.org:names:558042-1 (accessed on 2021-09-02).
  3. Patil P.; Sutar S.; Malik S. K.; John J.; Yadav S.; Bhat K. V. Numerical taxonomy of Abelmoschus Medik.(Malvaceae) in India. Bangladesh J. Plant Taxon. 2015, 22 (2), 87–98. 10.3329/bjpt.v22i2.26070. [DOI] [Google Scholar]
  4. Pham T.; Thi Q. N.; Cam L. N.; Minh D. T.; Van G. T. The effects of plant growth regulators on in-vitro culture of abelmoschus sagittifolius. Plant Cell Biotechnol. Mol. Biol. 2021, 32–40. [Google Scholar]
  5. Pham T. H.; Nguyen Q. N.; Pham T. N.; Lai V. H.; Phan V. T.; Nguyen V. H.; Dang M. T.; Nguyen T. H. L.; Duong T. P. T.; Pham T. H. N. Study on Morphological and Microscopic Characteristics of Abelmoschus sagittifolius (Kurz) Merr. in Vietnam. VNU J. Sci. Med. Pharm. Sci. 2021, 37 (2), 24–31. 10.25073/2588-1132/vnumps.4322. [DOI] [Google Scholar]
  6. State Administration of Traditional Chines Medicine “Chinese Materia Medica” Editorial Bord . Zhonghua ben cao, Vol. 15; Shanghai Scientific and Technology Press: Shanghai, 1999; p 643. [Google Scholar]
  7. Bich D.; Chung D.; Chuong B.; Dong N.; Dam D. T.; Hien P.; Lo V.; Mai P.; Man P.; Nhu D.. The Medicinal Plants and Animals in Vietnam; Science and Technology Publishing House: Hanoi, Vietnam, 2004. [Google Scholar]
  8. Li J.; Ye G.-y.; Liu H.-l.; Wang Z.-h. Complete chloroplast genomes of three important species, Abelmoschus moschatus, A. manihot and A. sagittifolius: Genome structures, mutational hotspots, comparative and phylogenetic analysis in Malvaceae. PloS one 2020, 15 (11), e0242591 10.1371/journal.pone.0242591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chen D.-L.; Li G.; Liu Y.-Y.; Ma G.-X.; Zheng W.; Sun X.-B.; Xu X.-D. A new cadinane sesquiterpenoid glucoside with cytotoxicity from Abelmoschus sagittifolius. Nat. Prod. Res. 2019, 33 (12), 1699–1704. 10.1080/14786419.2018.1431635. [DOI] [PubMed] [Google Scholar]
  10. Chen D.-L.; Zhang X.-P.; Ma G.-X.; Wu H.-F.; Yang J.-S.; Xu X.-D. A new sesquiterpenoid quinone with cytotoxicity from Abelmoschus sagittifolius. Nat. Prod. Res. 2016, 30 (5), 565–569. 10.1080/14786419.2015.1033624. [DOI] [PubMed] [Google Scholar]
  11. Thuc D. N.; Huong V. T.; Mai V. T. H.; Thanh L. N. Terpenoid Compounds from the Roots of Abelmoschus sagittifolius (Kurz) Merr. J. Med. Pharm. 2021, 17, 16–20. [Google Scholar]
  12. Loscalzo J. Oxidant stress: a key determinant of atherothrombosis. Biochem. Soc. Trans. 2003, 31 (5), 1059–1061. 10.1042/bst0311059. [DOI] [PubMed] [Google Scholar]
  13. Ferroni P.; Santilli F.; Cavaliere F.; Simeone P.; Costarelli L.; Liani R.; Tripaldi R.; Riondino S.; Roselli M.; Davi G.; et al. Oxidant stress as a major determinant of platelet activation in invasive breast cancer. Int. J. Cancer 2017, 140 (3), 696–704. 10.1002/ijc.30488. [DOI] [PubMed] [Google Scholar]
  14. Moore J. D.; Harned A. M.; Henle J.; Flynn D. L.; Hanson P. R. Scavenge– ROMP– Filter: A Facile Strategy for Soluble Scavenging via Norbornenyl Tagging of Electrophilic Reagents. Org. Lett. 2002, 4 (11), 1847–1849. 10.1021/ol0257880. [DOI] [PubMed] [Google Scholar]
  15. Tulipani S.; Mezzetti B.; Capocasa F.; Bompadre S.; Beekwilder J.; De Vos C. R.; Capanoglu E.; Bovy A.; Battino M. Antioxidants, phenolic compounds, and nutritional quality of different strawberry genotypes. J. Agric. Food Chem. 2008, 56 (3), 696–704. 10.1021/jf0719959. [DOI] [PubMed] [Google Scholar]
  16. Apak R. a.; Özyürek M.; Güçlü K.; Çapanoğlu E. Antioxidant activity/capacity measurement. 1. Classification, physicochemical principles, mechanisms, and electron transfer (ET)-based assays. J. Agric. Food Chem. 2016, 64 (5), 997–1027. 10.1021/acs.jafc.5b04739. [DOI] [PubMed] [Google Scholar]
  17. Ozkan G.; Franco P.; De Marco I.; Xiao J.; Capanoglu E. A review of microencapsulation methods for food antioxidants: Principles, advantages, drawbacks and applications. Food Chem. 2019, 272, 494–506. 10.1016/j.foodchem.2018.07.205. [DOI] [PubMed] [Google Scholar]
  18. Boonsri S.; Karalai C.; Ponglimanont C.; Chantrapromma S.; Kanjana-Opas A. Cytotoxic and antibacterial sesquiterpenes from Thespesia populnea. J. Nat. Prod. 2008, 71 (7), 1173–1177. 10.1021/np800055q. [DOI] [PubMed] [Google Scholar]
  19. Re R.; Pellegrini N.; Proteggente A.; Pannala A.; Yang M.; Rice-Evans C. Antioxidant activity applying an improved ABTS radical cation decolorization assay. Free Radic. Biol. Med. 1999, 26 (9–10), 1231–1237. 10.1016/S0891-5849(98)00315-3. [DOI] [PubMed] [Google Scholar]
  20. Dinh Ngoc T.; Ha M. V. T.; Nguyen Le T.; Nguyen T. V. A.; Mechler A.; Hoa N. T.; Vo Q. V. Antioxidant Activity of Natural Samwirin A: Theoretical and Experimental Insights. ACS omega 2021, 6 (41), 27546–27551. 10.1021/acsomega.1c04569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Vo Q. V.; Bay M. V.; Nam P. C.; Quang D. T.; Flavel M.; Hoa N. T.; Mechler A. Theoretical and Experimental Studies of the Antioxidant and Antinitrosant Activity of Syringic Acid. J. Org. Chem. 2020, 85 (23), 15514–15520. 10.1021/acs.joc.0c02258. [DOI] [PubMed] [Google Scholar]
  22. Vo Q. V.; Thong N. M.; Le Huyen T.; Nam P. C.; Tam N. M.; Hoa N. T.; Mechler A. A thermodynamic and kinetic study of the antioxidant activity of natural hydroanthraquinones. RSC Adv. 2020, 10 (34), 20089–20097. 10.1039/D0RA04013D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Dzib E.; Merino G. The hindered rotor theory: A review. WIREs Comput. Mol. Sci. 2022, 12, e1583 10.1002/wcms.1583. [DOI] [Google Scholar]
  24. Hehre W.; Yu J.; Klunzinger P.; Lou L.. Spartan Software.; Wavefunction. Inc.: Irvine, CA, 2000.
  25. Galano A.; Alvarez-Idaboy J. R. Glutathione: mechanism and kinetics of its non-enzymatic defense action against free radicals. RSC Adv. 2011, 1 (9), 1763–1771. 10.1039/c1ra00474c. [DOI] [Google Scholar]
  26. Vo Q. V.; Tam N. M.; Bay M. V.; Mechler A. The radical scavenging activity of natural ramalin: A mechanistic and kinetic study. Chem. Phys. Lett. 2020, 739, 137004. 10.1016/j.cplett.2019.137004. [DOI] [Google Scholar]
  27. Ingold K. U.; Pratt D. A. Advances in radical-trapping antioxidant chemistry in the 21st century: a kinetics and mechanisms perspective. Chem. Rev. 2014, 114 (18), 9022–9046. 10.1021/cr500226n. [DOI] [PubMed] [Google Scholar]
  28. Galano A.; Pérez-González A.; Castañeda-Arriaga R.; Muñoz-Rugeles L.; Mendoza-Sarmiento G.; Romero-Silva A.; Ibarra-Escutia A.; Rebollar-Zepeda A. M.; León-Carmona J. R.; Hernández-Olivares M. A.; Alvarez-Idaboy J. R. Empirically Fitted Parameters for Calculating p K a Values with Small Deviations from Experiments Using a Simple Computational Strategy. J. Chem. Inf. Model. 2016, 56 (9), 1714–1724. 10.1021/acs.jcim.6b00310. [DOI] [PubMed] [Google Scholar]
  29. Vo Q. V.; Hoa N. T.; Nam P. C.; Quang D. T.; Mechler A. In Silico Evaluation of the Radical Scavenging Mechanism of Mactanamide. ACS Omega 2020, 5 (37), 24106–24110. 10.1021/acsomega.0c03646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Alberto M. E.; Russo N.; Grand A.; Galano A. A physicochemical examination of the free radical scavenging activity of Trolox: mechanism, kinetics and influence of the environment. Phys. Chem. Chem. Phys. 2013, 15 (13), 4642–4650. 10.1039/c3cp43319f. [DOI] [PubMed] [Google Scholar]
  31. Boulebd H. Radical scavenging behavior of butylated hydroxytoluene against oxygenated free radicals in physiological environments: Insights from DFT calculations. Int. J. Chem. Kinet. 2022, 54, 50–57. 10.1002/kin.21540. [DOI] [Google Scholar]
  32. Iuga C.; Alvarez-Idaboy J. R. l.; Russo N. Antioxidant activity of trans-resveratrol toward hydroxyl and hydroperoxyl radicals: a quantum chemical and computational kinetics study. J. Org. Chem. 2012, 77 (8), 3868–3877. 10.1021/jo3002134. [DOI] [PubMed] [Google Scholar]
  33. Galano A.; Alvarez-Idaboy J. R. A computational methodology for accurate predictions of rate constants in solution: Application to the assessment of primary antioxidant activity. J. Comput. Chem. 2013, 34 (28), 2430–2445. 10.1002/jcc.23409. [DOI] [PubMed] [Google Scholar]
  34. Galano A.; Raúl Alvarez-Idaboy J. Computational strategies for predicting free radical scavengers’ protection against oxidative stress: Where are we and what might follow?. Int. J. Quantum Chem. 2019, 119 (2), e25665 10.1002/qua.25665. [DOI] [Google Scholar]
  35. Nam P. C.; Thong N. M.; Hoa N. T.; Quang D. T.; Hoang L. P.; Mechler A.; Vo Q. V. Is natural fraxin an overlooked radical scavenger?. RSC Adv. 2021, 11 (24), 14269–14275. 10.1039/D1RA01360B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hoa N. T.; Van Bay M.; Mechler A.; Vo Q. V. Is usnic acid a promising radical scavenger?. ACS omega 2020, 5 (28), 17715–17720. 10.1021/acsomega.0c02306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
  38. Zhao Y.; Truhlar D. G. How Well Can New-Generation Density Functionals Describe the Energetics of Bond-Dissociation Reactions Producing Radicals?. J. Phys. Chem. A 2008, 112 (6), 1095–1099. 10.1021/jp7109127. [DOI] [PubMed] [Google Scholar]
  39. Galano A.; Alvarez-Idaboy J. R. Kinetics of radical-molecule reactions in aqueous solution: A benchmark study of the performance of density functional methods. J. Comput. Chem. 2014, 35 (28), 2019–2026. 10.1002/jcc.23715. [DOI] [PubMed] [Google Scholar]
  40. Alvarez-Idaboy J. R. l.; Galano A. On the Chemical Repair of DNA Radicals by Glutathione: Hydrogen Vs Electron Transfer. J. Phys. Chem. B 2012, 116 (31), 9316–9325. 10.1021/jp303116n. [DOI] [PubMed] [Google Scholar]
  41. Dzib E.; Cabellos J. L.; Ortíz-Chi F.; Pan S.; Galano A.; Merino G. Eyringpy: A Program for Computing Rate Constants in the Gas Phase and in Solution. Int. J. Quantum Chem. 2019, 119 (2), e25686 10.1002/qua.25686. [DOI] [Google Scholar]
  42. Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113 (18), 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  43. Evans M. G.; Polanyi M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. 10.1039/tf9353100875. [DOI] [Google Scholar]
  44. Eyring H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3 (2), 107–115. 10.1063/1.1749604. [DOI] [Google Scholar]
  45. Truhlar D. G.; Hase W. L.; Hynes J. T. Current Status of Transition-State Theory. J. Phys. Chem. 1983, 87 (15), 2664–2682. 10.1021/j100238a003. [DOI] [Google Scholar]
  46. Furuncuoglu T.; Ugur I.; Degirmenci I.; Aviyente V. Role of chain transfer agents in free radical polymerization kinetics. Macromolecules 2010, 43 (4), 1823–1835. 10.1021/ma902803p. [DOI] [Google Scholar]
  47. Vélez E.; Quijano J.; Notario R.; Pabón E.; Murillo J.; Leal J.; Zapata E.; Alarcón G. A computational study of stereospecifity in the thermal elimination reaction of menthyl benzoate in the gas phase. J. Phys. Org. Chem. 2009, 22 (10), 971–977. 10.1002/poc.1547. [DOI] [Google Scholar]
  48. Dzib E.; Cabellos J. L.; Ortiz-Chi F.; Pan S.; Galano A.; Merino G. Eyringpy: A program for computing rate constants in the gas phase and in solution. Int. J. Quantum Chem. 2019, 119, e25686 10.1002/qua.25686. [DOI] [Google Scholar]
  49. Pollak E.; Pechukas P. Symmetry numbers, not statistical factors, should be used in absolute rate theory and in Broensted relations. J. Am. Chem. Soc. 1978, 100 (10), 2984–2991. 10.1021/ja00478a009. [DOI] [Google Scholar]
  50. Fernández-Ramos A.; Ellingson B. A.; Meana-Pañeda R.; Marques J. M.; Truhlar D. G. Symmetry numbers and chemical reaction rates. Theor. Chem. Acc. 2007, 118 (4), 813–826. 10.1007/s00214-007-0328-0. [DOI] [Google Scholar]
  51. Eckart C. The penetration of a potential barrier by electrons. Phys. Rev. 1930, 35 (11), 1303. 10.1103/PhysRev.35.1303. [DOI] [Google Scholar]
  52. Marcus R. A. Chemical and Electrochemical Electron-Transfer Theory. Annu. Rev. Phys. Chem. 1964, 15 (1), 155–196. 10.1146/annurev.pc.15.100164.001103. [DOI] [Google Scholar]
  53. Marcus R. A. Electron Transfer Reactions in Chemistry. Theory and Experiment. Rev. Mod. Phys. 1993, 65 (3), 599. 10.1103/RevModPhys.65.599. [DOI] [Google Scholar]
  54. Nelsen S. F.; Blackstock S. C.; Kim Y. Estimation of inner shell Marcus terms for amino nitrogen compounds by molecular orbital calculations. J. Am. Chem. Soc. 1987, 109 (3), 677–682. 10.1021/ja00237a007. [DOI] [Google Scholar]
  55. Nelsen S. F.; Weaver M. N.; Luo Y.; Pladziewicz J. R.; Ausman L. K.; Jentzsch T. L.; O’Konek J. J. Estimation of electronic coupling for intermolecular electron transfer from cross-reaction data. J. Phys. Chem. A 2006, 110 (41), 11665–11676. 10.1021/jp064406v. [DOI] [PubMed] [Google Scholar]
  56. Collins F. C.; Kimball G. E. Diffusion-Controlled Reaction Rates. J. Colloid Sci. 1949, 4 (4), 425–437. 10.1016/0095-8522(49)90023-9. [DOI] [Google Scholar]
  57. Von Smoluchowski M. Mathematical Theory of the Kinetics of the Coagulation of Colloidal Solutions. Z. Phys. Chem. 1917, 92, 129. [Google Scholar]
  58. Truhlar D. G. Nearly encounter-controlled reactions: The equivalence of the steady-state and diffusional viewpoints. J. Chem. Educ. 1985, 62 (2), 104. 10.1021/ed062p104. [DOI] [Google Scholar]
  59. Einstein A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. 10.1002/andp.19053220806. [DOI] [Google Scholar]
  60. Stokes G. G.Mathematical and Physical Papers. University Press: Cambridge, U.K., 2009. [Google Scholar]
  61. Okuno Y. Theoretical Investigation of the Mechanism of the Baeyer-Villiger Reaction in Nonpolar Solvents. Chem.: Eur. J. 1997, 3 (2), 212–218. 10.1002/chem.19970030208. [DOI] [PubMed] [Google Scholar]
  62. Benson S.The foundations of chemical kinetics. R.E. Krieger: Malabar, FL, 1982. [Google Scholar]
  63. Iuga C.; Alvarez-Idaboy J. R.; Vivier-Bunge A. ROS Initiated Oxidation of Dopamine under Oxidative Stress Conditions in Aqueous and Lipidic Environments. J. Phys. Chem. B 2011, 115 (42), 12234–12246. 10.1021/jp206347u. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Alvarez-Idaboy J. R.; Reyes L.; Mora-Diez N. The mechanism of the Baeyer–Villiger rearrangement: quantum chemistry and TST study supported by experimental kinetic data. Org. Biomol. Chem. 2007, 5 (22), 3682–3689. 10.1039/b712608e. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Citations

  1. Abelmoschus sagittifolius (Kurz) Merr. Plants of the World Online. Royal Botanical Gardens, Kew: Richmond, England. http://powo.science.kew.org/taxon/urn:lsid:ipni.org:names:558042-1 (accessed on 2021-09-02).

Supplementary Materials

ao2c02974_si_001.pdf (15.1MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES