Abstract
In this work, we have explored the interaction of three different polyphenols with the food protein β-lactoglobulin. Antioxidant activities of polyphenols are influenced by complexation with the protein. However, studies have shown that polyphenols after complexation with the protein can be more beneficial due to enhanced antioxidant activities. We have carried out molecular docking, molecular dynamics (MD) simulation, and quantum mechanics/molecular mechanics (QM/MM) studies on the three different protein–polyphenol complexes. We have found from molecular docking studies that apigenin binds in the internal cavity, luteolin binds at the mouth of the cavity, and eriodictyol binds outside the cavity of the protein. Docking studies have also provided binding free energy and inhibition constant values that showed that eriodictyol and apigenin exhibit better binding interactions with the protein than luteolin. For eriodictyol and luteolin, van der Waals, hydrophobic, and hydrogen bonding interactions are the main interacting forces, whereas for apigenin, hydrophobic and van der Waals interactions play major roles. We have calculated the root mean square deviation (RMSD), root mean square fluctuations (RMSF), solvent-accessible surface area (SASA), interaction energies, and hydrogen bonds of the protein–polyphenol complexes. Results show that the protein–eriodictyol complex is more stable than the other complexes. We have performed ONIOM calculations to study the antioxidant properties of the polyphenols. We have found that apigenin and luteolin act as better antioxidants than eriodictyol does on complexation with the protein, which is consistent with the results obtained from MD simulations.
1. Introduction
Antioxidants from natural sources for human use have gained much attention worldwide. Polyphenolic compounds are excellent sources of antioxidants. They enter the body via various sources such as vegetables, fruits, tea, flowers, wine, cereal grains, and coffee.1 The most important plant-based polyphenolic compounds known as “flavonoids” are in high demand due to their numerous health benefits including anticancer, antioxidant, and anti-inflammatory activities, among others.2−4 Flavonoids encompass a large number of structurally diverse subgroups, and the most common flavonoids are flavones, flavonols, flavanone, flavanonol, and anthocyanin.5 The basic chemical structure of flavonoids generally consists of two phenyl rings (A and B) and a heterocyclic pyran ring (C)6 (see Figure 1). Their main functions include their abilities to act as antioxidants to suppress the detrimental effect of free radicals on the macronutrients. The interactions of polyphenols with food components like proteins are of great interest to many food researchers and food analysts so as to modulate the functionalities and bioactivities of both the compounds.7−9 The protein–polyphenol interactions can take place prior to their intake during processing and preparation of food. Such interactions can show their effect on the biological aspects of protein by changing the thermal stability, digestibility, solubility, enzymatic activity, and nutritional value10,11 and are important from industrial, scientific, and economic viewpoints.
Figure 1.

General skeleton of flavonoids.
Incorporation of the polyphenols into the food enhances the antioxidant activity and nutritional value of the protein-based food product, which is considered to be an effective approach for functional foods. Polyphenols show strong antioxidant activity in both in vitro and in vivo environments.12,13 However, the antioxidant behavior of polyphenols is affected on complexation with protein, but the overall antioxidant activity of the polyphenols can be beneficial on complexation with protein due to the extended lifetime of the polyphenols in the complex. Most of the studies reveal that the polyphenols bind to the protein14,15 and their interactions are mainly governed by hydrophobic interactions and subsequently stabilized by hydrogen bonding.16,17 Hernandez et al. studied some low-molecular weight phenolic compounds with the protein bovine serum albumin and stated that their interaction could result in the reduction of the antioxidant activity of the phenolic compounds present in the food system.18 Nowadays, addition of polyphenols to milk as natural additives to increase the health benefit and nutritional value of dairy products has become an active area of research. Milk proteins can act as a natural vehicle for the delivery of many bioactive molecules19 and vital micronutrients. Some studies are reported to describe the underlying mechanism behind the influence of milk proteins on the polyphenols present in tea.14−16 There have been many controversies regarding the antioxidant behavior of tea polyphenols in the presence of milk proteins. Hasni et al. reported the effect of milk proteins α- and β-casein complexation with tea polyphenols. They suggested that the change in the casein structure can be a major factor in the antioxidant behavior of protein–polyphenol complexes.14 They showed that the protein–polyphenol interaction resulted in a major decrease of the α-helix and β-sheet content of the protein, and there was an increase of turn and random structure in the polyphenol–casein complexes. Meanwhile, Dubeau et al. reported the dual effect of milk on the antioxidant capacity of three types of tea using three different antioxidant assays.20 As the major constituent of milk, β-lactoglobulin (BLG) can unavoidably interact with the polyphenolic flavonoids. BLG is a globular protein that can not only act as an antioxidant nutrient but also carry other antioxidants to specific biological sites. BLG contains 162 amino acid residues and belongs to the family of lipocalins. Due to the presence of a hydrophobic calyx or core in its structure, BLG can accommodate many hydrophobic bioactive molecules and ensure the safe delivery of these molecules to their biological sites.21
There are a multitude of research studies that have been dedicated to explore the interaction of the protein BLG with dietary polyphenols. Most of the studies revealed that the main essence of binding of BLG and polyphenols is through noncovalent interactions. Jia et al. reported the interactions of polyphenols chlorogenic acid, ferulic acid, and epigallocatechin-3-gallate with the protein BLG with the aid of spectroscopy and molecular modeling studies. They found that hydrogen bonding and van der Waals (VDW) interactions are the main binding forces behind the binding of BLG with chlorogenic acid and ferulic acid, whereas hydrophobic interactions are the main driving forces in binding with epigallocatechin-3-gallate.8 Another study by Li et al. reported a combined spectroscopy and molecular docking study of BLG with some structurally different model polyphenols (apigenin, naringenin, kaempferol, and genistein) and observed that hydrogen bonding and hydrophobic interactions played a crucial role in their binding.22 The noncovalent interaction between the protein and polyphenol can influence the conformational change of the protein and the antioxidant activity of the polyphenols. From the literature, it is evident that the protein–polyphenol interaction is solely dependent on the structure of polyphenols and type of protein under investigation. Therefore, the present work deals with the interaction of BLG with three polyphenols (which differ in OH groups present in the B ring and hydrogenation of the double bond present between C2 and C3 of the C ring). These are systematically selected to study the influence of those structural parameters on the conformational stability of the protein BLG and on the antioxidant behavior of the polyphenols in the presence of BLG. Herein, we have analyzed the binding of three model polyphenols, i.e, apigenin (Figure 2a), luteolin (Figure 2b), and eriodictyol (Figure 2c), with the protein BLG with the aid of molecular docking study. The docking study reveals the kind of interaction present and the amino acids involved in the binding between polyphenols and BLG. The effects of protein–polyphenol binding on the stability of the complex and conformational changes of the protein are accessed through the molecular dynamics (MD) simulation technique. We have also included the probable mechanism of antioxidant activity with the considered polyphenols in the presence and absence of the protein with the help of a more accurate quantum mechanics/molecular mechanics (QM/MM) study. We envisage that this study will provide an in-depth molecular-level understanding regarding incorporation of novel polyphenols into food formulations, which will be valuable for food industries.
Figure 2.

(a–c) Chemical structure of the polyphenols.
2. Methodology
2.1. Docking Procedure
The molecular docking study is helpful in predicting the binding interaction of the protein and small molecules.23 The three-dimensional crystal structure of the protein BLG was taken from the Protein Data Bank (PDB ID: 3NPO) with an R value of 0.216, which is in the unliganded form. The structures of the polyphenols (apigenin, luteolin, and eriodictyol) were taken from PubChem. In this study, molecular docking calculations were done using AutoDock 4.2 software.24 All the nonstructural water molecules present in the PDB were removed. The polar hydrogens and kollman charges were added to the protein using AutoDock Tools (ADT). First, blind docking was performed to predict the binding sites of the protein for each of the polyphenols since the binding site information of the above-mentioned polyphenols with the BLG receptor was not known. During blind docking, the entire surface of the protein was considered as a potential binding site by creating grid maps using AutoGrid supplied with AutoDock 4.2. A grid box of dimension 100, 100, 100 points along the X, Y, and Z axes, respectively, was set for each of the systems so that the whole protein was covered. After determining the binding sites of each of the polyphenols in BLG, a grid box of dimensions 60, 60, 60 was centered around the active residues of the protein with a grid spacing of 0.375 Å for all the systems. Finally, the Lamarkian Genetic Algorithm25 was applied to all the systems considered for our study to find the best binding pose of the polyphenols with the protein with the lowest binding energy value. The independent docking runs were set to 50 with 2 500 000 maximum energy evaluations and 27 000 Genetic Algorithm operations for each run. The same parameters were used for all the systems.
2.2. Molecular Dynamics Simulation
The lowest-energy docked conformation for different complexes was taken for MD simulation to validate the stability of BLG–polyphenol complexes predicted by the docking study. The MD simulation studies of all the systems were performed using the AMBER 18 software package.26 The AMBERff14SB force field27 has been applied for the protein molecule and GAFF (general amber force field)28 for polyphenols. The restrained electrostatic potential (RESP)29 charges of the polyphenols were obtained using the Gaussian 16 package30 at the HF/6-31G* level. After assigning partial atomic charges of the polyphenols, the necessary parameter and topology files for all the systems were prepared using Antechamber31 and Leap programs32 supplied with AMBER 18 software. The protein–polyphenol complexes thus prepared were solvated using the TIP3P33 water model in a cubic box. The systems were solvated with 6808, 6804, and 6799 water molecules for BLG–apigenin, BLG–luteolin, and BLG–eriodictyol, respectively. Simulation of the protein without any polyphenol was also performed after solvating with 6808 water molecules and considered as a reference system. Each of the systems was added with eight Na+ ions so that the total charge of the systems became neutral. Initially, energy minimization was carried out followed by subsequent heating from 0 to 100, 100 to 200, and 200 to 300 K for 100 ps for each step. An additional equilibration step was done at a constant pressure of 1 bar and temperature of 300 K for 1 ns using a Berendsen barostat34 and Langevin dynamics35 to control the pressure and temperature, respectively. All bonds of hydrogen were fixed using the SHAKE algorithm.36 The particle mesh Ewald (PME) summation method37 was used for calculating the long-range electrostatic interactions. A cutoff distance of 9 Å was applied for all nonbonded interactions. Finally, we have performed a production run of 200 ns in an NVT ensemble for all the systems. The trajectories obtained from 200 ns production run were analyzed using the AMBER cpptraj module38 and visual molecular dynamics (VMD).39
2.3. QM/MM
The density functional theory (DFT) calculations of the considered systems were carried out using the Gaussian 16 suite of programs. We used the meta-GGA M06-2X density functional40,41 with the double zeta split valence and polarized 6-31+G* basis set42 in the gaseous phase. We prefer to use this functional for the present study since M06-2X is useful for main-group thermochemistry and noncovalent interactions.43 The complex structures were optimized using ONIOM,44,45 where the high layer was treated with the M06-2X level and the low layer was treated using molecular mechanics (MM) using the universal force field (UFF). After performing molecular dynamics simulation on each protein–polyphenol complex, the best interaction site was chosen. To decrease the computational demand of calculation, the system size was reduced, and we have considered protein residues located in the reactive site of the polyphenol without compromising the accuracy of the results. Our investigation mainly focused on the antioxidant properties of polyphenols in the presence and absence of the protein. Here, protein–polyphenol interactive sites are considered as the QM-layer, and other residual parts are considered under the MM-layer (see Figure 3). The selection of the reactive sites was done in accordance with the results obtained from Bader’s quantum theory of atoms in molecules (QTAIM)48,49 analysis (see Figure S1 in the Supporting Information). For apigenin and luteolin, the interacting residues were LEU46, LEU54, LEU56, VAL41, VAL92, ILE56, and PHE105 and LEU39, VAL41, ASN90, GLU108, and SER116, respectively. ASP130, ASP129, LYS101, GLU127, and THR125 were the interacting residues for eriodictyol. In two-layer ONIOM computation, the total energy (EONIOM) of the entire system was obtained from three independent energy calculations
| 1 |
Here, the real system contains full geometry of the molecules, and the model system comprises the chemically reactive part of the system. Following the above-mentioned procedure, the antioxidant activities of the polyphenols were calculated by computing the O–H bond dissociation of polyphenols.46,47
Figure 3.

General scheme for QM/MM calculations.
The antioxidant ability is mainly related to the position and number of hydroxyl groups and conjugated resonance effect. In previous studies, two main mechanisms were reported, namely hydrogen atom transfer (HAT) and single-electron transfer (SET).50 Also, it is evident that HAT and SET mechanisms are more efficient in the case of the polyphenols containing aromatic rings.50 To follow these mechanisms, two parameters were calculated, namely bond dissociation enthalpy (BDE) and ionization enthalpy (IE).51−53 In hydrogen atom transfer, a free radical Ṙ accepts a hydrogen atom from the antioxidant (ArOH)
| 2 |
The efficiency of the antioxidant depends upon the stability of the ArȮ radical, which is defined by the number of O–H bonds, conjugation, and resonance of the system. Here, the BDE of the O–H bond is evaluated by the following formula. The weaker the O–H bond, the more the stability of the antioxidant.
| 3 |
Here, enthalpies of the antioxidant radical, hydrogen radical, and antioxidant are represented as H(ArȮ), H(Ḣ), and H(ArOH), respectively. Again, according to the SET mechanism, the antioxidant (ArOH) gives one electron to the free radical along with the hydrogen atom
| 4 |
. Here, the stability of the radical cation decides the antioxidant action of the system where the ionization enthalpy is the significant factor, which can be evaluated by the following equation
| 5 |
Here, enthalpies of the antioxidant radical, hydrogen radical, and antioxidant are represented by H(ArO+.), H(e–), and H(ArOH), respectively.
3. Results and Discussions
3.1. Docking Results
Docking simulation was performed using AutoDock to determine the key interactions present between BLG and polyphenols. The AutoDock calculation results of the top-ranked cluster of the protein–polyphenol complexes are listed in Table 1. The table includes the values of binding energy, inhibition constant, number of hydrogen bonds, final intermolecular energy, and total internal energy of the complexes. Based on the docking results, the binding of apigenin was observed at the hydrophobic internal cavity of the protein, which is the common binding site for the hydrophobic molecules.54 The binding energy value for apigenin is found to be −5.34 kcal/mol. For luteolin, the binding energy value is −5.13 kcal/mol, and it binds into the internal cavity with slightly protruding outward. On the other hand, binding of eriodictyol is found in the region outside the internal cavity with a binding energy value of −5.70 kcal/mol. The binding of eriodictyol is in accordance with the predicted binding site for the naringenin molecule by Gholami and Bordbar, which belongs to the same flavanone subclass.55 The binding of apigenin, luteolin, and eriodictyol is found to be spontaneous, which can be observed from the negative binding energy values. The binding energy values indicate that apigenin and eriodictyol form more stable complexes than luteolin with the protein BLG (see Table 1). In addition to the binding free energies, the values of the inhibition constant dictate the efficacy of binding of the three polyphenols with the protein. Eriodictyol and apigenin with smaller values of inhibition constant (see Table 1), namely 66.91 and 122.34 μM, respectively, show more efficiency in binding than luteolin with an inhibition constant of 174.74 μM. The greater the intermolecular force between the receptor and the ligand molecule, the higher the binding affinity between the two. As evident from our docking calculation, the binding affinity of eriodictyol, which is a flavanone, is higher than that of apigenin and luteolin, which belong to the flavone subclass. This observation is consistent with the results obtained by other groups through spectroscopic techniques.56 The amino acid residues involved in binding between BLG and apigenin are ILE 56, ILE 71, and LEU 46 (through pi-sigma), PHE 105 (through pi-stacked), and VAL 41, VAL 43, VAL 92, LEU 54, and MET 107 (through pi-alkyl) (see Figure 4b). LEU 39 and VAL 41 (through pi-alkyl) are the amino acid residues that took part in the binding between BLG and luteolin (see Figure 4d). Furthermore, VAL 123 (through pi-alkyl), ASP 129, GLU 127 (through pi-anion), and LYS 101 (through pi-sigma) are the amino acids that participate in the binding interaction between BLG and eriodictyol (see Figure 4f). The docked complexes of luteolin and eriodictyol with BLG are also stabilized by hydrogen bonds. The amino acids of the protein involved in hydrogen bonding with luteolin and eriodictyol are PRO 38, ASN 109, and MET 107 and ASP 130, LYS 101, and THR 125, respectively. Surprisingly, no hydrogen bonds are found in the docked complex of apigenin with BLG. In addition, the conventional hydrogen bonds, luteolin and eriodictyol, also interact with protein residues LYS 60, ASN 88, ASN 90, SER 116, LEU 117, GLU 108, VAL 92, ILE 84, and ILE 71 and GLU 131 and ARG 124, respectively, through Van der Waals interactions (see Figure 4d,f). Therefore, it can be concluded that the binding of BLG and apigenin takes place mainly due to hydrophobic and van der Waals interactions, while van der Waals, hydrophobic, and hydrogen bonding interactions are the main driving forces behind the binding of luteolin and eriodictyol with BLG.
Table 1. Autodock Analysis of the Docked Protein–Polyphenol Complexes.
| protein | polyphenol | bindingenergy (kcal/mol) | inhibitionconstant (μM) | number of H-bonds(protein–polyphenol) | intermolecularenergy (kcal/mol) | internalenergy (kcal/mol) |
|---|---|---|---|---|---|---|
| BLG | apigenin | –5.34 | 122.34 | 0 | –6.53 | –0.87 |
| BLG | luteolin | –5.13 | 174.74 | 4 | –6.62 | –2.28 |
| BLG | eriodictyol | –5.70 | 66.91 | 4 | –7.19 | –2.05 |
Figure 4.
Best docked structures of BLG with (a) apigenin (blue structure), (c) luteolin (green structure), and (e) eriodictyol (pink structure) obtained from docking simulation. The protein secondary structures are represented in the cartoon ribbon, and the polyphenols are shown in the stick model. The 2D representations of the interactions of BLG and apigenin, luteolin, and eriodictyol are shown in (b), (d), and (f) respectively.
3.2. Molecular Dynamics Simulation Results
3.2.1. Root Mean Square Deviation (RMSD)
RMSD analysis is performed to extract information about the stability of the complex formed between the protein and ligand molecules. In this study, we have examined the RMSD of the protein backbone Cα- atoms to determine the stability of the unbound protein and protein–polyphenol complexes (see Figure 5). The RMSD of the unliganded native BLG is maintained within 1.01–1.82 Å up to 45 ns, and thereafter, the RMSD values increase to 2.05 Å till the end of the simulation. For the BLG–apigenin complex (see Figure 5a), RMSD is maintained between 1.01 and 1.75 Å, which is lower than the RMSD of the native BLG for the entire simulation run. Noticeably, the RMSD profile of the BLG–luteolin complex (see Figure 5b) shows maximum deviation of RMSD values that goes beyond 2.50 Å after 65 ns. This shows the alteration in the conformation of the protein in the BLG–luteolin complex. However, the BLG–eriodictyol system (see Figure 5c) shows much smaller fluctuations with RMSD values of 2.15 Å up to 50 ns, and after that, the value decreases to 2.05 Å, indicating a stable protein conformation for the rest of the simulation period. Clearly, we can infer that incorporation of apigenin enhances the stability of the protein BLG. Also, more stability has been gained by the protein–eriodictyol complex on incorporation of eriodictyol. We have also performed another set of independent simulations for each system using different random seeds. We have calculated RMSD for each system, and those are included in the Supporting Information (see Figure S3 in the Supporting Information). Plots of RMSD support similar behavior of the protein for different independent simulations. Therefore, results from first simulations are considered in the article.
Figure 5.
Root mean square deviations (RMSD) of Cα-atoms of the protein residues for (a) BLG–apigenin, (b) BLG–luteolin, and (c) BLG–eriodictyol complexes. Each figure is accompanied by RMSD of the unbound protein used as a reference.
3.2.2. Root Mean Square Fluctuations (RMSF)
We have calculated RMSF of Cα-atoms of different protein residues from their mean position. The RMSF values vs the number of residues are plotted (see Figure 6) to investigate the local fluctuations of the individual residues of the protein BLG on incorporation of the polyphenols. From Figure 6, it is clear that the residues involved in binding with the polyphenols are less fluctuating in nature compared to the other residues. This analysis suggests that the binding sites of all the complexes remain rigid throughout the simulation period. The RMSF profiles of the residues of BLG–apigenin and BLG–eriodictyol show lower fluctuations than those of the native protein BLG. However, the RMSF profile of the BLG–luteolin complex shows somewhat more residual fluctuations than the native protein BLG. The higher RMSF values of certain residues, namely LEU 32-ARG 40, PRO 50, GLU 62-GLU 65, THR 76-ALA 80, ASP 85-GLU 89, and SER 110-GLN 115, in the complex are associated with fluctuations in the coils and turns present in the protein. Interestingly, we have also noticed that similar regions of the protein exhibit more fluctuating RMSF values for all the three protein–polyphenol complexes.
Figure 6.
Root mean square fluctuations (RMSF) of Cα-atoms of the protein residues for all the systems.
3.2.3. Solvent-Accessible Surface Area (SASA)
SASA is an important parameter to examine the surface area of the protein accessible to solvent molecules, and as such, it helps in predicting the extent of the protein’s conformational changes upon binding with the polyphenols.57,58 The plot of the SASA value vs time of all systems considered in our study is included in Figure 7. Also, the average values of SASA for all the systems are listed in Table 2. The table shows that the SASA of the unliganded BLG is uniform throughout the simulation path, whereas on incorporation of apigenin, the SASA value decreases after 60 ns and is maintained after that. It is also evident from the average values of SASA calculated for all systems, which are shown in Table 2. The decrease in the average SASA value of unliganded BLG from 9223.95 to 9102.45 Å2 in the BLG–apigenin complex reinforces the idea that apigenin induces compactness to the native protein. Nonetheless, the increase in average SASA values of BLG–luteolin (9430.32 Å2) and BLG–eriodictyol (9253.91 Å2) complexes from that of the reference system indicates expansion in the protein conformation on incorporation of luteolin and eriodictyol to the protein. The results obtained above are further supported by hydrogen bond analysis (discussed in subsection 5) and secondary structure analysis of the protein (see Figure S2 and Table S1 in the Supporting Information). Figure S4 in the Supporting Information represents SASA for each system in repeated simulation and indicates the same behavior of the protein in both sets of simulation.
Figure 7.
Solvent-accessible surface area (SASA) during 200 ns of MD simulation of (a) BLG–apigenin, (b) BLG–luteolin, and (c) BLG–eriodictyol complexes.
Table 2. Average Values of SASA in Å2 Calculated from Converged Trajectoriesa.
| systems | SASA (Å2) |
|---|---|
| BLG (unliganded) | 9223.95 (±22.18) |
| BLG + API | 9102.45 (±36.78) |
| BLG + LUT | 9430.32 (±59.45) |
| BLG + ERI | 9253.91 (±40.02) |
Figures within parentheses indicate standard errors.
3.2.4. Interaction Energies
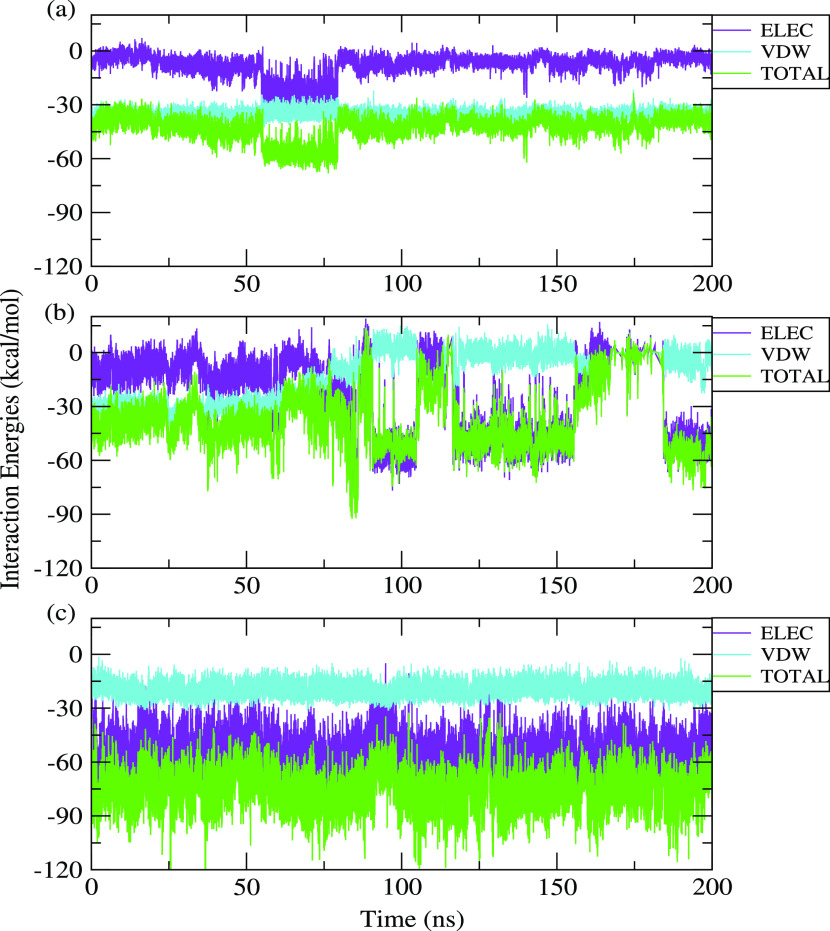
We have calculated interaction energies operating between the protein and different polyphenols using the NAMD259 suite provided with VMD. Calculation of interaction energy is important for the validation of binding energies obtained from docking calculations.60 Total interaction energies are calculated in terms of electrostatic and van der Waals energies. The plots of electrostatic, van der Waals, and total interaction energies of all systems are included in Figure 8 against simulation time. The average values are calculated for the converged simulation time shown in Table 3. The values reveal the stability and extent of binding of the different protein–polyphenol complexes. Table 3 shows that among all the complexes, the BLG–eriodictyol complex has the highest average total interaction energy of −76.94 kcal/mol followed by BLG–apigenin and BLG–luteolin with average total interaction energies of −41.57 kcal/mol and −41.81 kcal/mol, respectively. This observation is consistent with that obtained from docking studies. We have further noticed that the van der Waals interaction acts as a predominant factor in the case of the BLG–apigenin complex. However, for the BLG–luteolin and BLG–eriodictyol complexes, electrostatic interaction energy acts predominantly compared to van der Waals interaction energy. Thus, analysis of interaction energies reveals that both electrostatic and van der Waals energies play a crucial role in stabilization of the protein–polyphenol complexes. Among all the three complexes, the BLG–eriodictyol complex shows a better interaction strength as indicated by the more negative value of the total interaction energy. The reason behind the high value of electrostatic energy in the case of the eriodictyol–BLG complex may be attributed to the interactions of the more number of charged amino acid residues of the protein with eriodictyol, which is evident from docking results (see Figure 4).
Figure 8.
Interaction energies of (a) BLG–apigenin, (b) BLG–luteolin, and (c) BLG–eriodictyol complexes vs simulation time in ns.
Table 3. Electrostatic, VDW, and Total Energies of the Three Protein–Polyphenol Complexesa.
| systems | electrostatic energy(kcal/mol) | van der Waals energy(kcal/mol) | total energy(kcal/mol) |
|---|---|---|---|
| BLG + API | –6.13 (±0.61) | –35.44 (±0.50) | –41.57 (±0.52) |
| BLG + LUT | –38.58 (±0.69) | –3.24 (±0.62) | –41.81 (±0.60) |
| BLG + ERI | –56.82 (±0.27) | –20.11 (±0.23) | –76.94 (±0.29) |
Figures within parentheses indicate standard errors.
3.2.5. Hydrogen Bond Properties
Hydrogen bonds play an important role in determining the stability of the protein–ligand complex.61 In this study, we have analyzed intraprotein and protein–polyphenol hydrogen bonds for the entire 200 ns simulation period using VMD. The geometric criteria that we have considered are as follows: the distance cutoff is set as 3.5 Å and the angle cutoff is 120°.62 The average number of hydrogen bonds calculated for the intraprotein and protein–polyphenol complexes is included in Table 4. It is obvious that the average number of intraprotein hydrogen bonds slightly increases on incorporation of apigenin to BLG, while it decreases on incorporation of the ligands luteolin and eriodictyol. These results reveal that the increase in the number of intraprotein hydrogen bonds of the protein contributes to the more compact conformation of the protein on incorporation of apigenin into BLG. However, incorporation of luteolin significantly decreases the intraprotein hydrogen bonds. At the same time, we have noticed that there is a slight increase in the number of hydrogen bonds between BLG and luteolin, which contributes to the stability of the complex. However, eriodictyol forms the highest number of hydrogen bonds with BLG, namely 5.00. This indicates that eriodictyol forms a more stable complex with BLG among all the three polyphenols, which is also evident from the analysis of SASA and interaction energies. Furthermore, we have analyzed the lifetime of different hydrogen bonds formed during the simulation. From the fraction column in Table 5, it is quiet evident that apigenin forms a hydrogen bond between the N atom of residue ASP 85 and the O4 atom of the ligand for only 12.00% of the total simulation time. All other hydrogen bonds formed between apigenin and BLG are very short-lived and do not contribute much toward the stabilization of the BLG–apigenin complex. Meanwhile, for luteolin, there are two hydrogen bonds formed between the residues SER 116 and GLU 112 with the O5 atom of luteolin that exists for 12.00 and 11.00% of the total simulation time, respectively. The rest of the hydrogen bonds are formed with the same residue ASP 28 of the protein with different atoms of luteolin that act as different donor sites. Noticeably, eriodictyol forms more hydrogen bonds with the protein BLG, which exist for longer times. There is a hydrogen bond formed between eriodictyol and the residue GLU 127 of the protein existing for 76.00% of the total simulation period. In addition to this, other hydrogen bonds formed between eriodictyol and protein residues Asp 129, ASP 130, and THR 125 are also found to be populated for longer periods of time. The average numbers and life times of hydrogen bonds present in each system confirm the stability of each protein–polyphenol complex.
Table 4. Average Number of Hydrogen Bonds Calculated for the Converged Trajectories of All the Systemsa.
| system | nP–P | nP–L |
|---|---|---|
| BLG (unliganded) | 140.78 (±0.34) | |
| BLG + API | 140.15 (±0.95) | 0.65 (±0.30) |
| BLG + LUT | 135.24 (±1.31) | 1.52 (±0.18) |
| BLG + ERI | 138.19 (±0.46) | 5.00 (±0.30) |
Figures within parentheses indicate standard errors. Here, nP–P and nP–L refer to the average number of H-bonds formed in protein–protein and protein–ligand, respectively.
Table 5. Results Calculated by Hydrogen Bond Analysis of the Complexes during MD Simulationa.
| polyphenols | acceptor | donor H | donor | fraction | averagedistance |
|---|---|---|---|---|---|
| API 163@O4 | ASP 85@H | ASP 85@N | 0.12 | 2.91 | |
| apigenin | ASP 85@OD1 | API 163@H9 | API 163@O4 | 0.06 | 2.63 |
| ASP 85@OD2 | API 163@H9 | API 163@O4 | 0.05 | 2.63 | |
| SER 116@O | LUT 163@H9 | LUT 163@O5 | 0.12 | 2.75 | |
| GLU 112@OE1 | LUT 163@H9 | LUT 163@O5 | 0.11 | 2.57 | |
| GLU 112@OE1 | LUT 163@H10 | LUT 163@O6 | 0.11 | 2.57 | |
| luteolin | ASP 28@OD2 | LUT 163@H10 | LUT 163@O6 | 0.10 | 2.60 |
| ASP 28@OD2 | LUT 163@H9 | LUT 163@O5 | 0.10 | 2.60 | |
| ASP 28@OD1 | LUT 163@H9 | LUT 163@O5 | 0.10 | 2.60 | |
| ASP 28@OD1 | LUT 163@H10 | LUT 163@O6 | 0.08 | 2.61 | |
| GLU 127@O | ERI 163@H10 | ERI 163@O4 | 0.76 | 2.77 | |
| ASP 129@OD2 | ERI 163@H11 | ERI 163@O5 | 0.70 | 2.62 | |
| ASP 130@OD1 | ERI 163@H12 | ERI 163@O6 | 0.38 | 2.64 | |
| eriodictyol | ASP 130@OD2 | ERI 163@H12 | ERI 163@O6 | 0.30 | 2.64 |
| ERI 163@O4 | THR 125@HG1 | THR 125@OG1 | 0.24 | 2.87 | |
| ASP 129@OD1 | ERI 163@H11 | ERI 163@O5 | 0.23 | 2.62 | |
| ERI 163@O4 | THR 125@H | THR 125@N | 0.13 | 2.92 | |
| ERI 163@O5 | ASP 130@H | ASP 130@N | 0.13 | 2.91 |
Here API, LUT, and ERI stand for the polyphenols apigenin, luteolin, and eriodictyol, respectively.
3.3. QM/MM Study
In our studied systems, we have computed the bond dissociation enthalpy (BDE) and ionization enthalpy (IE) of O–H bonds of bound and free polyphenols using eqs 3 and 5. BDE and IE parameters are calculated to compare their antioxidant activities. ONIOM energies are calculated using eq 1
In the case of the polyphenols apigenin and luteolin, they have difference in the number of OH groups, as shown in Figure 2. There are two OH groups at C-3′ and C-4′ positions in luteolin, but apigenin has only one OH group at the C-3′ position. Again, eriodictyol has the same skeletal frame as luteolin but differs by the absence of a double bond between C-2 and C-3. ONIOM calculations (see Figure 9) show that the OH group at C-3′ of apigenin is not involved with any intra- or intersystem interactions and is free to scavenge radicals. Similarly, the OH groups at the C-7 position of luteolin and the C-4′ position of eriodictyol are not interacting with the protein residues, and their corresponding radicals are comparatively stable (see Table 6). These imply their antioxidant activity. Results obtained from ONIOM calculations of protein–ligand complexes and DFT calculation of free ligands are shown in Table 6. Table 6 also contains the BDE and IE values of polyphenols in bound and free states.
Figure 9.
Optimized geometry of protein residues involved in (a) BLG–apigenin, (b) BLG–luteolin, and (c) BLG–eriodictyol complexes calculated at the M06-2X/6-31+G*: UFF level.
Table 6. Results Calculated by the ONIOM Study of the Protein–Polyphenol Complexes.
| bond dissociation enthalpy (kcal/mol) | ionization enthalpy (kcal/mol) | |||
|---|---|---|---|---|
| polyphenols | free | bound | free | bound |
| apigenin | 200.8 | 115.2 | 94.1 | 62.2 |
| luteolin | 257.2 | 207.7 | 194.5 | 97.3 |
| eriodictyol | 414.2 | 463.5 | 202.3 | 232.4 |
QM/MM studies show that the BDE (free: 200.8 kcal/mol, bound: 115.2 kcal/mol) and IE (free: 94.1 kcal/mol bound: 62.2 kcal/mol) values of apigenin are the lowest in both free and bound states. BDE and IE values become maximum in the case of eriodictyol. The QM/MM values are consistent with the MD simulation results, which reveals that apigenin shows less interactions with protein residues in comparison to luteolin and eriodictyol. It is found that there is a good interaction between eriodictyol and protein, and more number of hydrogen bonds are observed, which is evident from Tables 6 and 5. The results indicate that eriodictyol forms a more stable complex with the protein. Thus, the OH group of eriodictyol will not readily form the respective radical. Therefore, it is expected to exhibit less antioxidant activity. Similarly, apigenin shows less binding toward the protein but has the highest antioxidant activity among the three polyphenols. Calculations of secondary structure contents of the protein (see Table 1 in the Supporting Information) reveal the fact that the protein–polyphenol interaction has changed the conformation of the protein. This in turn affects the antioxidant ability of the polyphenol. QM/MM calculations show that in comparison to the free polyphenol, radical stabilization in the protein–polyphenol complex is more due to the extensive interaction between the polyphenol radical (formed after removal of the H atom) and the protein moiety. This interaction leads to a significant change in the antioxidant ability of the polyphenol. Furthermore, Table 6 shows that the IE values of all polyphenols are less than the BDE values. This suggests that the considered polyphenols prefer to show antioxidant activities via the single-electron transfer (SET) mechanism rather than the hydrogen atom transfer (HAT) mechanism.
4. Summary and Conclusions
The present study demonstrates the binding interactions of apigenin, luteolin, and eriodictyol with BLG and their effect on the conformation of the protein through molecular docking and MD simulation studies. Also, the results of the QM/MM study give persuasive suggestions about the antioxidant activity of the above-mentioned polyphenols in the presence and absence of the protein. The molecular docking results reveal that apigenin binds in the internal cavity, luteolin binds at the mouth of the cavity, and eriodictyol binds outside the cavity. In addition to this, docking results also reveal that the hydrophobic and van der Waals interactions play a major role in the stability of the BLG–apigenin complex. Nonetheless, hydrophobic, van der Waals, and hydrogen bonding interactions are the main driving forces behind the stability of the BLG–luteolin and BLG–eriodictyol complexes. The RMSD profiles of both BLG–apigenin and BLG-eriodictyol complexes showed that equilibration is achieved after a 50 ns time period, indicating the stability of the complexes. However, deviation of RMSD values that goes beyond 2.50 Å after 65 ns indicates alteration in the conformation of the protein in the BLG–luteolin complex. It can be clearly seen from RMSD and SASA calculations that incorporation of apigenin into BLG induces more compactness to the protein. The RMSF profiles of all complexes suggest a rigid conformation of the interacting residues during the entire simulation period. Noticeably, eriodictyol forms a more stable complex with BLG than other complexes. This is quite evident from the analysis of total interaction energies, SASA values, and the number of intermolecular hydrogen bonds. Li et al.22 suggested that hydrogenation at the C2=C3 double bond resulted in a more weakened interaction of naringenin with β-lactoglobulin than apigenin. Since the same number of OH groups is present in both the molecules, their affinities were greatly affected by the presence/absence of the double bond at the C2–C3 position. In our study, the presence of one more number of OH group is expected to overshadow the effect of the absence of the double bond at the C2–C3 position of eriodictyol. As a consequence, the eriodictyol molecule displayed higher binding affinity toward the protein. Again, after MD, two-layer ONIOM calculations were performed, which revealed the antioxidant properties of these polyphenols in terms of properties such as BDE and IE. QM/MM studies indicate the mechanism of their action, which either follows HAT or SET mechanisms. A comparative study of the antioxidant properties of all these polyphenols considered in our study reveals that apigenin and luteolin are better antioxidants than eriodictyol in the protein environment. The probable reason behind such superior activity may be attributed to the presence of extensive conjugation in those polyphenols, which provides extra stability to the radicals formed by removal of one H atom from the polyphenols. It is also evident from MD study that the interaction of eriodictyol with BLG is highly favorable, which supports the decrease in the antioxidant activity of eriodictyol inside the protein environment. Overall, this study provides a state-of-the-art phenomenon of antioxidant activity of different polyphenols in the presence and absence of a protein environment, which we anticipate to be a step closer to the actual understanding of the radical trapping phenomenon taking place in vivo.
Acknowledgments
Financial support from the Department of Science and Technology (DST), Government of India, is gratefully acknowledged.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c00336.
Baders QTAIM analysis, dictionary of the secondary structure of protein plots, percentage of different secondary structure contents of the protein, and RMSD and SASA plots for repeated simulations (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Tsao R. Chemistry and biochemistry of dietary polyphenols. Nutrients 2010, 2, 1231–1246. 10.3390/nu2121231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Côté J.; Caillet S.; Doyon G.; Sylvain J. F.; Lacroix M. Bioactive compounds in cranberries and their biological properties. Crit. Rev. Food Sci. Nutr. 2010, 50, 666–679. 10.1080/10408390903044107. [DOI] [PubMed] [Google Scholar]
- Brand W.; Padilla B.; van Bladeren P. J.; Williamson G.; Rietjens I. M. C. M. The effect of co-administered flavonoids on the metabolism of hesperetin and the disposition of its metabolites in Caco-2 cell monolayers. Mol. Nutr. Food Res. 2010, 54, 851–860. 10.1002/mnfr.200900183. [DOI] [PubMed] [Google Scholar]
- Morabito G.; Trombetta D.; Brajendra K. S.; Ashok K. P.; Virinder S. P.; Naccari C.; Mancari F.; Saija A.; Cristani M.; Firuzi O.; Saso L. Antioxidant properties of 4-methylcoumarins in vitro cell-free systems. Biochimie 2010, 92, 1101–1107. 10.1016/j.biochi.2010.04.017. [DOI] [PubMed] [Google Scholar]
- Liu R. H. Potential synergy of phytochemicals in cancer prevention: mechanism of action. J. Nutr. 2004, 134, 3479S–3485S. 10.1093/jn/134.12.3479S. [DOI] [PubMed] [Google Scholar]
- de Souza Farias S. A.; da Costa K. S.; Martins J. B. Analysis of Conformational, Structural, Magnetic, and Electronic Properties Related to Antioxidant Activity: Revisiting Flavan, Anthocyanidin, Flavanone, Flavonol, Isoflavone, Flavone, and Flavan-3-ol. ACS Omega 2021, 6, 8908–8918. 10.1021/acsomega.0c06156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferraro V.; Madureira A. R.; Sarmento B.; Gomes A.; Pintado M. E. Study of the interactions between rosmarinic acid and bovine milk whey protein α-Lactalbumin, β-Lactoglobulin and Lactoferrin. Food Res. Int. 2015, 77, 450–459. 10.1016/j.foodres.2015.08.024. [DOI] [Google Scholar]
- Jia J.; Gao X.; Hao M.; Tang L. Comparison of binding interaction between β-lactoglobulin and three common polyphenols using multi-spectroscopy and modeling methods. Food Chem. 2017, 228, 143–151. 10.1016/j.foodchem.2017.01.131. [DOI] [PubMed] [Google Scholar]
- Cao Y.; Xiong Y. L. Interaction of whey proteins with phenolic derivatives under neutral and acidic pH conditions. J. Food Sci. 2017, 82, 409–419. 10.1111/1750-3841.13607. [DOI] [PubMed] [Google Scholar]
- Tomás-Barberán F. A.; Andres-Lacueva C. Polyphenols and health: current state and progress. J. Agric. Food Chem. 2012, 60, 8773–8775. 10.1021/jf300671j. [DOI] [PubMed] [Google Scholar]
- Ozdal T.; Capanoglu E.; Altay F. A. A review on protein-phenolic interactions and associated changes. Food Res. Int. 2013, 51, 954–970. 10.1016/j.foodres.2013.02.009. [DOI] [Google Scholar]
- Cook N. C.; Samman S. Flavonoids-chemistry, metabolism, cardioprotective effects, and dietary sources. J. Nutr. Biochem. 1996, 7, 66–76. 10.1016/0955-2863(95)00168-9. [DOI] [Google Scholar]
- Rice-evans C. A.; Miller N. J.; Bolwell P. G.; Bramley P. M.; Pridham J. B. The Relative Antioxidant Activities of Plant-Derived Polyphenolic Flavonoids. Free Radical Res. 1995, 22, 375–383. 10.3109/10715769509145649. [DOI] [PubMed] [Google Scholar]
- Hasni I.; Bourassa P.; Hamdani S.; Samson G.; Carpentier R.; Tajmir-Riahi H. A. Interaction of milk α and β-caseins with tea polyphenols. Food Chem. 2011, 126, 630–639. 10.1016/j.foodchem.2010.11.087. [DOI] [Google Scholar]
- Kanakis C. D.; Hasni I.; Bourassa P.; Tarantilis P. A.; Polissiou M. G.; Tajmir-Riahi H. A. Milk β-lactoglobulin complexes with tea polyphenols. Food Chem. 2011, 127, 1046–1055. 10.1016/j.foodchem.2011.01.079. [DOI] [PubMed] [Google Scholar]
- Yuksel Z.; Avci E.; Erdem Y. K. Characterization of binding interactions between green tea flavonoids and milk proteins. Food Chem. 2010, 121, 450–456. 10.1016/j.foodchem.2009.12.064. [DOI] [Google Scholar]
- Prigent S. V. E.; Gruppen H.; Visser A. J. W. G.; van Koningsveld G. A.; de Jong G. A. H.; Voragen A. G. J. Effect of non-covalent interactions with 5-O-coffeoylquinic acid (chlorogenic acid) on the heat denaturation and solubility of globular proteins. J. Agric. Food Chem. 2003, 51, 5088–5095. 10.1021/jf021229w. [DOI] [PubMed] [Google Scholar]
- Bartolome B.; Estrella I.; Hernandez M. T. Interaction of Low Molecular Weight Phenolics with Proteins (BSA). J. Food Sci. 2000, 65, 617–621. 10.1111/j.1365-2621.2000.tb16060.x. [DOI] [Google Scholar]
- Livney Y. D. Milk proteins as vehicles for bioactives. Curr. Opin. Colloid Interface Sci. 2010, 15, 73–83. 10.1016/j.cocis.2009.11.002. [DOI] [Google Scholar]
- Dubeau S.; Samson G.; Tajmir-Riahi H.-A. Dual effect of milk on the antioxidant capacity of green, Darjeeling, and English breakfast teas. Food Chem. 2010, 122, 539–545. 10.1016/j.foodchem.2010.03.005. [DOI] [Google Scholar]
- Baruah I.; Borgohain G. Binding interaction of a potential statin with β-lactoglobulin: An in silico approach. J. Mol. Graphics Modell. 2022, 111, 10807 10.1016/j.jmgm.2021.108077. [DOI] [PubMed] [Google Scholar]
- Li T.; Hu P.; Dai T.; Li P.; Ye X.; Chen J.; Liu C. Comparing the binding interaction between β-lactoglobulin and flavonoids with different structure by multi-spectroscopy analysis and molecular docking. Spectrochim. Acta, Part A 2018, 201, 197–206. 10.1016/j.saa.2018.05.011. [DOI] [PubMed] [Google Scholar]
- Skrt M.; Benedik E.; Podlipnik C.; Ulrih N. P. Interactions of different polyphenols with bovine serum albumin using fluorescence quenching and molecular docking. Food Chem. 2012, 135, 2418–2424. 10.1016/j.foodchem.2012.06.114. [DOI] [PubMed] [Google Scholar]
- Morris G. M.; Huey R.; Lindstrom W.; Sanner M. F.; Belew R. K.; Goodsell D. S.; Olson A. J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris G. M.; Goodsell D. S.; Halliday R. S.; Huey R.; Hart W. E.; Belew R. K.; Olson A. J. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 1998, 19, 1639–1662. . [DOI] [Google Scholar]
- Case D. A.; Ben-Shalon I. Y.; Brozell S. R.; Cerutti D. S.; Cheatham T. E. III; Cruzeiro V. M. D.. et al. AMBER 2018. University of California: San Francisco, 2018.
- Maier J. A.; Martinez C.; Kasavajhala K.; Wickstrom L.; Hauser K. E.; Simmerling C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J.Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Wang J.; Cieplak P.; Kollman P. A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules?. J. Comput. Chem. 2000, 21, 1049–1074. . [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.. et al. Gaussian 16, revision A.03; Gaussian, Inc.: Wallingford, CT, 2016.
- Wang J.; Wang W.; Kollman P. A.; Case D. A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graphics Modell. 2006, 25, 247–260. 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Case D. A.; Cheatham T. E. III; Darden T.; Gohlke H.; Luo R.; Merz K. M.; Onufriev A. Jr.; Simmerling C.; Wang B.; Woods R. J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar L. J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The missing term in effective pair potentials. J. Phys. Chem. A 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
- Hünenberger P. H. Thermostat algorithms for molecular dynamics simulations. Adv. Polym. Sci. 2005, 173, 105–149. 10.1007/b99427. [DOI] [Google Scholar]
- Ryckaert J. P.; Ciccotti G.; Berendsen H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. J. A smooth particleArial;sans-serif mesh ewald method. J. Chem. Phys. 1995, 103, 8577–8592. 10.1063/1.470117. [DOI] [Google Scholar]
- Roe D. R.; Cheatham T. E. III PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013, 9, 3084–3095. 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD-visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
- Zhao Y.; Schultz N. E.; Truhlar D. G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics and non-covalent interactions. J. Chem. Theory Comput. 2006, 2, 364–382. 10.1021/ct0502763. [DOI] [PubMed] [Google Scholar]
- McLean A. D.; Chandler G. S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11-18. J. Chem. Phys. 1980, 72, 5639–5648. 10.1063/1.438980. [DOI] [Google Scholar]
- Cervantes-Navarro F.; Glossman-Mitnik D. A. Brief performance test of the M06 family of density functionals for the prediction of the maximum absorption wavelength of thioindigo in several solvents. J. Mex. Chem. Soc. 2013, 57, 19–22. [Google Scholar]
- a Dapprich J. S.; Komaromi I.; Byun K. S.; Morokuma K.; Frisch M. J. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. 1999, 461–462, 1–21. 10.1016/S0166-1280(98)00475-8. [DOI] [Google Scholar]; b Chung L. W.; Sameera W. M. C.; Ramozzi R.; Page A. J.; Hatanaka M.; Petrova G. P.; Harris T. V.; Li X.; Ke Z.; Liu F.; et al. The ONIOM method and its applications. Chem. Rev. 2015, 115, 5678–5796. 10.1021/cr5004419. [DOI] [PubMed] [Google Scholar]
- Begum S. S.; Das D.; Gour N. K.; Deka R. C. Computational modelling of nanotube delivery of anti-cancer drug into glutathione reductase enzyme. Sci. Rep. 2021, 11, 4950 10.1038/s41598-021-84006-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Wright J. S.; Johnson E. R.; Di Labio G. A. Predicting the activity of phenolic antioxidants: theoretical method, analysis of substituent effects, and application to major families of antioxidants. J. Am. Chem. Soc. 2001, 123, 1173–1183. 10.1021/ja002455u. [DOI] [PubMed] [Google Scholar]; b Galano A.; Arriaga R. C.; González A. P.; Tan D. X.; Reiter R. J. Phenolic melatonin-related compounds: Their role as chemical protectors against oxidative stress. Molecules 2016, 21, 1442 10.3390/molecules21111442. [DOI] [PMC free article] [PubMed] [Google Scholar]; c Iuga C.; Idaboy J. R. A.; Russo N. Antioxidant activity of trans-resveratrol toward hydroxyl and hydroperoxyl radicals: a quantum chemical and computational kinetics study. J. Org. Chem. 2012, 77, 3868–3877. 10.1021/jo3002134. [DOI] [PubMed] [Google Scholar]; d Cordova-Gomez M.; Galano A.; Idaboy J. R. A. Piceatannol, a better peroxyl radical scavenger than resveratrol. RSC Adv. 2013, 3, 20209 10.1039/c3ra42923g. [DOI] [Google Scholar]; e Nogueira C. W.; Rocha J. B. Toxicology and pharmacology of selenium: emphasis on synthetic organoselenium compounds. Arch. Toxicol. 2011, 85, 1313–1359. 10.1007/s00204-011-0720-3. [DOI] [PubMed] [Google Scholar]
- Marković Z.; Milenković D.; Dorović J.; Marković J. M. D.; Stepanić V.; Luc̃ić B.; Amić D. PM6 and DFT study of free radical scavenging activity of morin. Food Chem. 2012, 134, 1754–1760. 10.1016/j.foodchem.2012.03.124. [DOI] [PubMed] [Google Scholar]
- a Bader R. F. W.Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, U.K., 1990. [Google Scholar]; b Bader R. F. W. A bond path: a universal indicator of bonded interactions. J. Phys. Chem. A 1998, 102, 7314 10.1021/jp981794v. [DOI] [Google Scholar]; c Bader R. F. W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893 10.1021/cr00005a013. [DOI] [Google Scholar]
- Tian L.A Multifunctional Wavefunction Analyzer (version 3.1) http://Multiwfn.codeplex.com (accessed May 22, 2015).
- Kashyap C.; Mazumder L. J.; Rohman S. S.; Ullah S. S.; Guha A. K. Re-visiting the Antioxidant Activity of Se- and Te-Carbohydrates: A Theoretical Study. ChemistrySelect 2019, 4, 1470–1475. 10.1002/slct.201803814. [DOI] [Google Scholar]
- Leopoldini M.; Pitarch I. P.; Russo N.; Toscano M. Structure, Conformation, and Electronic Properties of Apigenin, Luteolin, and Taxifolin Antioxidants. A First Principle Theoretical Study. J. Phys. Chem. A 2004, 108, 92–96. 10.1021/jp035901j. [DOI] [Google Scholar]
- Borpuzari M. P.; Rohman R.; Kar R. Antioxidant properties can be tuned in the presence of an external electric field: accurate computation of O-H BDE with range-separated density functionals. RSC Adv. 2015, 5, 78229–78237. 10.1039/C5RA13462E. [DOI] [Google Scholar]
- Borgohain R.; Handique J. G.; Guha A. K.; Pratihar S. A theoretical study on antioxidant activity of ferulic acid and its ester derivatives. J. Theor. Comput. Chem. 2016, 15, 1650028 10.1142/S0219633616500280. [DOI] [Google Scholar]
- Roufik S.; Gauthier S. F.; Leng X. J.; Turgeon S. L. Thermodynamics of binding interactions between bovine β-lactoglobulin A and the antihypertensive peptide β-Lg f142-148. Biomacromolecules 2006, 7, 419. 10.1021/bm050229c. [DOI] [PubMed] [Google Scholar]
- Gholami S.; Bordbar A. K. Exploring binding properties of naringenin with bovine β-lactoglobulin: A fluorescence, molecular docking and molecular dynamics simulation study. Biophys. Chem. 2014, 187–188, 33–42. 10.1016/j.bpc.2014.01.003. [DOI] [PubMed] [Google Scholar]
- Riihimäki L. H.; Vainio M. J.; Heikura J. M.; Valkonen K. H.; Virtanen V. T.; Vuorela P. M. Binding of phenolic compounds and their derivatives to bovine and reindeer β-lactoglobulin. J. Agric. Food Chem. 2008, 56, 7721–7729. 10.1021/jf801120a. [DOI] [PubMed] [Google Scholar]
- Durham E.; Dorr B.; Woetzel N.; Staritzbichler R.; Meiler J. Solvent accessible surface area approximations for rapid and accurate protein structure prediction. J. Mol. Modell. 2009, 15, 1093–1108. 10.1007/s00894-009-0454-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borgohain G.; Paul S. Model Dependency of TMAO’s Counteracting Effect Against Action of Urea: Kast Model versus Osmotic Model of TMAO. J. Phys. Chem. B 2016, 120, 2352–2361. 10.1021/acs.jpcb.5b10968. [DOI] [PubMed] [Google Scholar]
- Kalé L.; Skeel R.; Bhandarkar M.; Brunner R.; Gursoy A.; Krawetz N.; Phillips J.; Shinozaki A.; Varadarajan K.; Schulten K. NAMD2: greater scalability for parallel molecular dynamics. J. Comput. Phys. 1999, 151, 283–312. 10.1006/jcph.1999.6201. [DOI] [Google Scholar]
- Borgohain G.; Paul S. The opposing effect of urea and high pressure on the conformation of the protein β-hairpin: A molecular dynamics simulation study. J. Mol. Liq. 2018, 251, 378–384. 10.1016/j.molliq.2017.12.054. [DOI] [Google Scholar]
- Rao P.; Shukla A.; Parmar P.; Rawal R. M.; Patel B.; Saraf M.; Goswami D. Reckoning a fungal metabolite, Pyranonigrin A as a potential Main protease (Mpro) inhibitor of novel SARS-CoV-2 virusidentified using docking and molecular dynamics simulation. Biophys. Chem. 2020, 264, 106425 10.1016/j.bpc.2020.106425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cong Y.; Li M.; Feng G.; Li Y.; Wang X.; Duan L. Trypsin-Ligand binding affinities calculated using an effective interaction entropy method under polarized force field. Sci. Rep. 2017, 7, 17708 10.1038/s41598-017-17868-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.