Nonconventional NMR Spin-Coupling Constants in Oligosaccharide Conformational Modeling: Structural Dependencies Determined from Density Functional Theory Calculations

Abstract

Nonconventional NMR spin-coupling constants were investigated to determine their potential as conformational constraints in MA’AT modeling of the O-glycosidic linkages of oligosaccharides. Four (¹J_C1′,H1′, ¹J_C1′,C2′, ²J_C1′,H2′, and ²J_C2′,H1′) and eight (¹J_C4,H4, ¹J_C3,C4, ¹J_C4,C5, ²J_C3,H4, ²J_C4,H3, ²J_C5,H4, ²J_C4,H5, and ²J_C3,C5) spin-couplings in methyl β-d-galactopyranosyl-(1→4)-β-d-glucopyranoside (methyl β-lactoside) were calculated using density functional theory (DFT) to determine their dependencies on O-glycosidic linkage C–O torsion angles, ϕ and ψ, respectively. Long-range ⁴J_H1′,H4 was also examined as a potential conformational constraint of either ϕ or ψ. Secondary effects of exocyclic (hydroxyl) C–O bond rotation within or proximal to these coupling pathways were investigated. Based on the findings of methyl β-lactoside, analogous J-couplings were studied in five additional two-bond O-glycosidic linkages [βGlcNAc-(1→4)-βMan, 2-deoxy-βGlc-(1→4)-βGlc, αMan-(1→3)-βMan, αMan-(1→2)-αMan, and βGlcNAc(1→2)-αMan] to determine whether the coupling behaviors observed in methyl β-lactoside were more broadly observed. Of the 13 nonconventional J-couplings studied, 7 exhibit properties that may be useful in future MA’AT modeling of O-glycosidic linkages, none of which involve coupling pathways that include the linkage C–O bonds. The findings also provide new insights into the general effects of exocyclic C–O bond conformation on the magnitude of experimental spin-couplings in saccharides and other hydroxyl-containing molecules.

1. Introduction

Determinations of oligosaccharide structure in solution require, in part, assessments of the geometries of their constituent O-glycosidic linkages.¹⁻³ Theoretical methods such as aqueous molecular dynamics (MD) simulations⁴⁻⁸ can provide this information if their underlying force fields are parameterized to accurately and quantitatively recapitulate all of the covalent and non-covalent interactions that dictate geometry in solution. Conformational models obtained by MD simulations are only as reliable as the force field that underpins them. However, it has been difficult to obtain rigorous independent experimental validation of MD-derived models because current experimental methods do not provide continuous models of molecular torsion angles that can be superimposed on those obtained by MD. Recent developments using redundant experimental NMR spin-coupling constants and MA^’AT analysis⁹⁻¹² offer a solution to this problem. MA^’AT analysis allows the testing of uni- and multi-modal conformational models, but a significantly greater number of experimental observables is required to test the latter. For example, rotational models about the C5–C6 bond in methyl β-d-glucopyranoside (1) typically involve three states, each representing an idealized staggered rotamer of the C4–C5–C6–O6 torsion angle ω (Scheme 1). Testing this model of ω using MA^’AT analysis requires at least 7 redundant spin-coupling constants, and, in this case, >12 are available,¹³ rendering the treatment feasible mathematically.

Scheme 1. Conformational Model of the C4–C5–C6–O6 Torsion Angle in Methyl β-d-Glucopyranoside (1) in Solution, Comprising Three Idealized Staggered Rotamers gg, gt, and tg in Chemical Exchange.

Conventional modeling of O-glycosidic linkages using MA’AT analysis typically employs six trans-O-glycosidic J-couplings to characterize ϕ and ψ, which includes three redundant couplings to model ϕ and three to model ψ (Scheme 2).¹⁴ Recent work has shown that these six J-values associated with C–O–C–H, C–O–C–C, and C–O–C coupling pathways across O-glycosidic linkages are sufficient for unimodal modeling of each torsion angle.^10−12,15 These treatments yield mean torsion angles and circular standard deviations that are in good agreement with other techniques, the latter reporting on the degree of librational motion of each angle. Determinations of root mean squared deviations (RMSDs) of these models and inspections of parameter space plots yield information on how well unimodal models fit the available experimental J-couplings and whether the model is a unique fit of the experimental data, respectively. In the linkages studied to date, RMSDs are small (<0.3 Hz), and the majority produce unique fits, indicating that ϕ and ψ adopt highly preferred single states, although considerable averaging around the mean torsion angles is observed. MA’AT modeling of ϕ in different types of O-glycosidic linkages suggests that current MD models underestimate the librational motion about this glycosidic torsion angle.¹⁵ Despite these advances, however, it would be desirable to increase the number of redundant spin-coupling constants used in MA’AT analyses of linkage conformation (or include other types of NMR constraints) to test unimodal models more rigorously and/or to render feasible modeling beyond a single state.

Scheme 2. Conventional Trans-O-Glycosidic J-coupling Pathways in β-(1→4) Disaccharide 2, Showing Three J-Couplings Sensitive to φ (³J_H1′,C4, ²J_C1′,C4, and ³J_C2′,C4) and Three Sensitive to ψ (³J_C1′,H4, ³J_C1′,C3, and ³J_C1′,C5).

Atom numbering and glycosidic torsion angles φ and ψ are shown. Coupling pathways are highlighted in blue.

The results of the studies described herein address the structural dependences of several nonconventional NMR spin-coupling constants that may serve as potential constraints in MA’AT analyses of O-glycosidic linkages. The primary objective of the work was to determine which of these J-couplings have properties conducive to their use in MA^’AT analysis. The structural dependencies were determined by density functional theory (DFT) calculations in four different types of linkages (α-(1→2); β-(1→2); α-(1→3); and β-(1→4); Scheme 3) found in disaccharides 2–7 to determine the extent to which the results are generalizable. We show that several coupling pathways, some of which are peripheral to the linkages themselves and do not include linkage bonds explicitly, yield J-couplings that may prove useful in future MA’AT treatments of O-glycosidic linkages. This work also reveals the importance of understanding the conformational behaviors of exocyclic C–O bonds of saccharides in solution since they impact the values and structural interpretations of both conventional and nonconventional experimental J-couplings.

Scheme 3. Chemical Structures of Methyl β-d-Galactopyranosyl-(1→4)-β-d-glucopyranoside (2), Methyl 2-Acetamido-2-deoxy-β-d-glucopyranosyl-(1→4)-β-d-mannopyranoside (3), Methyl 2-Deoxy-β-d-arabino-hexopyranosyl-(1→4)-β-d-glucopyranoside(4), Methyl α-d-mannopyranosyl-(1→3)-β-d-mannopyranoside (5), Methyl α-d-mannopyranosyl-(1→2)-α-d-mannopyranoside (6), and Methyl 2-Acetamido-2-deoxy-β-d-glucopyranosyl-(1→2)-α-d-mannopyranoside (7), Showing Atom Numbering in the Pyranosyl Rings and Identification of the “a” and “b” Residues of Each Disaccharide.

The O-glycosidic torsion angles phi (φ) and psi (ψ) are shown in each structure.

2. Calculations

2.1. Geometry Optimizations

DFT calculations were conducted on fully substituted model structures 2–7 (Scheme 3) within Gaussian09¹⁶ using the B3LYP functional^17,18 and the 6-31G* basis set.¹⁹ In models 5 and 7, several sites of deoxygenation were introduced at carbons remote from the coupling pathways of interest (Schemes S6 and S8, Supporting Information; see explanation below). In all geometric optimizations, the effects of solvent water were treated using the self-consistent reaction field (SCRF)²⁰ and the integral equation formalism (polarizable continuum) model (IEFPCM).²¹ For calculations on 2, the phi (ϕ) and psi (ψ) O-glycosidic torsion angles, defined as O5′–C1′–O1′–C4 and C1′–O1′–C4–C3, respectively, were each rotated in 15° increments through 360°, giving a 24 × 24 matrix or 576 optimized structures (Scheme 4). Torsion angles C1′–C2′–O2′–H (θ₁), C3–C2–O2–H (θ₂), and C4–C3–O3–H (θ₃) were fixed at 180°. The remaining seven exocyclic torsion angles in 2 were held constant or were set at an initial value and optimized, as summarized in Scheme 4. Six additional datasets were generated for 2, in which θ₁, θ₂, or θ₃ was fixed at either 60 or 300°, while the other ring C−O torsion angles were fixed at 180°, each set containing 576 structures.

Scheme 4. Torsion Angle Constraints Used in DFT Calculations of Nonconventional Spin-Coupling Constants in 2.

Exocyclic torsion angles θ₁, θ₂, and θ₃ were sampled in three perfectly staggered geometries, yielding 27 datasets containing incremental rotations of φ and ψ through 360°. See text for details.

For structures 3–7, the ϕ and ψ torsion angles were each rotated in 15° increments through 360°, giving 24 × 24 matrices (576 structures). Only one set of exocyclic torsion angles was investigated in 3–7 as summarized in Schemes S4–S8 (Supporting Information). In DFT calculations of 5 and 7, deoxy analogs were used to simplify the structures and/or avoid unfavorable steric interactions when the ϕ and ψ torsion angles were rotated. The deoxy sites were kept to a minimum and judged based on prior work to be sufficiently distant from the coupling pathways of interest to not influence their calculated behaviors.

2.2. Calculations of NMR Spin-Coupling Constants

A group of J_HH, J_CH, and J_CCspin-coupling constants with potentially useful dependencies on ϕ or ψ was calculated in geometry optimized structures of 2–7 by DFT using the B3LYP functional^17,18 in Gaussian09.¹⁶ The Fermi contact,²²⁻²⁴ diamagnetic and paramagnetic spin–orbit, and spin-dipole terms²² were recovered using a tailored basis set, [5s2p1d|3s1p],^25,26 and raw (unscaled) calculated spin-couplings are reported and are similar to experimental values to within ±0.2–0.3 Hz based on prior work.^26,27 SCRF²⁰ and the IEFPCM²¹ were again used to treat the effects of solvent water during J-coupling calculations.

DFT calculations of ¹J_CH, ¹J_CC, ³J_CH, and ³J_CC values gave positive signs as expected, whereas those of ²J_CH and ²J_CC values gave either positive or negative signs. Experimental sign determinations of the latter geminal J-couplings have been reported in prior work,²⁸⁻³² and ample comparisons have been made between experimental and calculated signs to validate those obtained by DFT calculations.

2.3. Spin-Coupling Constant Equation Parameterization

Equations relating DFT-calculated J_HH, J_CH, and J_CC values to ϕ or ψ in 2–7 were parameterized to a trigonometric polynomial using R. Equations were parameterized using J-values calculated in a subpopulation of conformers that was selected using a 10 kcal/mol energy cut-off to remove a limited number of highly structurally strained conformers.^10,12 A secondary constraint was also applied when necessary to remove DFT-optimized structures containing distorted aldohexopyranosyl rings; Cremer-Pople puckering parameters were calculated from DFT-generated Cartesian coordinates, and a θ value of 35° was used as the cut-off.^10,12 The goodness-of-fit of each equation is reported as a root mean squared deviation (RMSD). Equation parameterization was further evaluated using the Akaike information criterion,³³ resulting in truncated forms of two equations.

3. Results and Discussion

3.1. Potential Nonconventional Spin-Coupling Constraints for ϕ

Criteria to determine whether a specific J-coupling may have value in MA’AT analyses of ϕ and ψ include: (1) dynamic range; (2) character of the torsion angle versus J-value plot (e.g., does the plot contain multiple maxima and minima?); (3) whether the J-value exhibits a significant secondary dependence on either ϕ or ψ; (4) whether the J-value exhibits other significant structural dependencies in addition to either ϕ or ψ (e.g., dependencies on proximal exocyclic C–O torsion angles); and (5) whether the experimental J-value can be conveniently and accurately measured and its sign determined if required, preferably without the need for stable isotopic labeling. Secondary dependencies or effects (criterion 3) refer to J-coupling behaviors where J-coupling depends primarily on one torsion angle but also shows dependencies on a second or third torsion angle. In the present work, a J-coupling might depend heavily on ϕ but also show some dependence on ψ or vice versa. Secondary dependencies can complicate the structural interpretations of J-couplings if they are not well understood and accounted for. In the following discussion, potential nonconventional J-couplings are identified that satisfy most, if not all, of these criteria.

Five nonconventional J-couplings to evaluate ϕ are shown in Scheme 5, illustrated in 2 although analogous J-couplings exist in disaccharides 3–7 (Scheme 3). These couplings include ¹J_C1′,H1′, ¹J_C1′,C2′, ²J_C1′,H2′, ²J_C2′,H1′, and ⁴J_H1′,H4. ¹J_C1′,H1′ and ¹J_C1′,C2′ are expected to depend on ϕ, based on anticipated vicinal lone-pair effects on C–H and C–C bond lengths caused by rotation of the C1′–O1′ bond (ϕ). The C1′–H1′ and C1′–C2′ bond lengths are affected by n→σ* donation when a lone-pair orbital on O1′ is anti to the bond, in general leading to bond elongation^34,35 (in the ensuing discussion, oxygen atoms are assumed to bear two sp³-hybridized lone-pair orbitals although other lone-pair arrangements may pertain³⁶⁻³⁸). Presumably the percent s-character of both bonds is greater (shorter bonds) for geometries in which both O1′ lone-pairs are gauche to them. For ¹J_C1′,C2′, overlapping vicinal lone-pair effects from C2′–O2′ bond rotation (θ₁) also pertain. Thus, at least two structural factors influence ¹J_C1′,C2′, namely, rotation about ϕ and θ₁. Superimposed on these stereoelectronic effects may be bond angle effects caused by the rotation of ϕ and θ₁.

Scheme 5. Nonconventional Spin-Coupling Constants That May Depend on φ, Illustrated for the Internal O-Glycosidic Linkage in 2.

Coupling pathways are highlighted in blue. Torsion angles θ₁, θ₂, and θ₃ denote rotations about the C2′–O2′, C3–O3, and C5–C6 bonds, respectively.

Geminal ²J_C1′,H2′ and ²J_C2′,H1′ values are expected to have strong configurational dependencies superimposed on conformational dependencies on ϕ and θ₁. Consider the generalized C_a–C_b–H_b coupling pathway shown in Scheme 6. Rotation of the C_a–C_b bond (γ₁) describes the configurational dependence of ²J_Ca,Hb, manifested in both coupling magnitude and sign. For ²J_C1′,H2′ and ²J_C2′,H1′ in 2, rotation about the analogous C1′–C2′ bond is constrained by the pyranosyl ring (i.e., the configuration is fixed) such that this constraint determines their baseline magnitudes and signs. C–O Bond rotations γ₂ and γ₃ are mainly responsible for the conformational dependencies of ²J_Ca,Hb. In general, for the C_a–C_b–H_b pathway, the effect of rotation of γ₃ is greater than that for rotation of γ₂; that is, rotation of the C–O bond involving the carbon bearing the coupled hydrogen exerts a greater effect on ²J_Ca,Hb than rotation of the C–O bond involving the coupled carbon. The difference in sensitivity is ∼2–3 fold.^39,40 Thus, while ²J_C1′,H2′ might be a potential constraint on ϕ (Scheme 5), rotation of ϕ exerts a smaller effect on the coupling than rotation of θ₁, reducing the dynamic range and consequently its usefulness as a ϕ constraint. Conversely, rotation of ϕ exerts a greater effect on ²J_C2′,H1′ than rotation of θ₁. Thus, all else being equal, ²J_C2′,H1′ is likely to be the better probe of ϕ than ²J_C1′,H2′. However, even in this case, contributions from θ₁ to ²J_C2′,H1′ cannot be ignored (i.e., independent information on θ₁ would be desirable to determine its contribution to the magnitude of experimental ²J_C2′,H1′ values in solution).

Scheme 6. Bond Torsions γ₁, γ₂, and γ₃ That Influence the Magnitude and Sign of ²J_Ca,Hb (Pathway Highlighted in Blue).

R₁ and R₂ are assumed to be sp³-hybridized carbons as found in typical saccharide carbon scaffolds.

⁴J_H1′,H4 is likely to exhibit sensitivities to both ϕ and ψ.⁴⁰⁻⁴² If this behavior is confirmed by DFT calculations, ⁴J_H1′,H4 values may serve only as independent tests of the conformational models of ϕ and ψ determined from more robust J-values (see discussion below). Even in this role, the very small dynamic range of ⁴J_H1′,H4 will limit its use in assignments of linkage conformation.

3.2. Potential Nonconventional Spin-Coupling Constraints for ψ

In 2, nine nonconventional J-couplings have the potential to serve as constraints on ψ (Scheme 7): ¹J_C4,H4, ¹J_C3,C4, ¹J_C4,C5, ²J_C3,H4, ²J_C4,H3, ²J_C5,H4, ²J_C4,H5, ²J_C3,C5, and ⁴J_H1′,H4. Analogous J-values exist in disaccharides 3–7. The structural dependencies of the ¹J_CH, ¹J_CC, and ²J_CCH values are expected to mimic those sensitive to ϕ (Scheme 5). For example, ¹J_C3,C4 will depend on the rotameric properties of the C3–C4, C3–O3 (θ₂), and C4–O1′ (ψ) bonds.⁴³ Since rotation about the C3–C4 bond is constrained by the pyranosyl ring, only the remaining C–O bonds will largely determine ¹J_C3,C4 in solution. Likewise, ²J_C3,H4 and ²J_C5,H4 are likely to be better constraints on ψ than ²J_C4,H3 and ²J_C4,H5 (see above discussion of Scheme 6). ⁴J_H1′,H4 is likely to serve as an independent test of the conformational models of ψ (and ϕ) determined from more robust J-values.

Scheme 7. Potential Nonconventional Spin-Coupling Constants That May Depend on ψ, Illustrated for the Internal O-Glycosidic Linkage in 2.

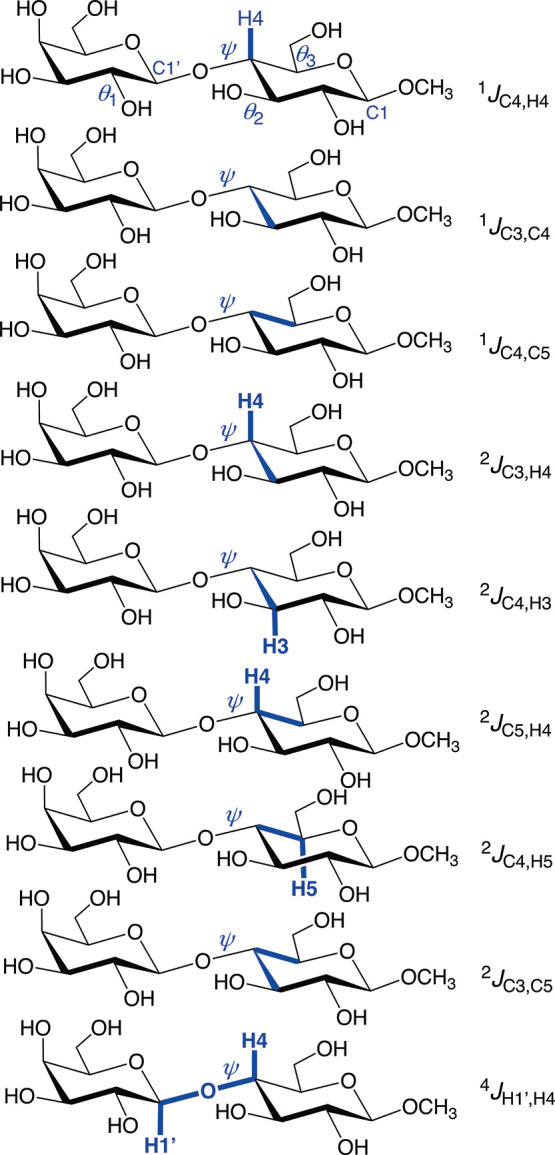
Coupling pathways are highlighted in blue. Torsion angles θ₁, θ₂, and θ₃ denote rotations about the C2′–O2′, C3–O3, and C5–C6 bonds, respectively.

The geminal ¹³C–¹³C spin-coupling, ²J_C3,C5, is expected to show configurational and conformational dependencies analogous to those of ²J_C1,C3 in aldopyranosyl rings.^40,44 Configuration at the terminal coupled carbons affects its magnitude and sign, especially O3 orientation (axial vs equatorial), while the effect of configuration at the intervening C4 carbon is expected to be small. Conformational effects derive from rotation of the C3–O3 (θ₂), C5–C6 (θ₃), and C4–O1′ (ψ) bonds, with ψ exerting a greater effect than θ₂ and θ₃. In 2, the configurational effects are fixed and determine the baseline value of ²J_C3,C5 in solution. This value will vary in response to the conformational effects. Consequently, the reliability of ²J_C3,C5 as a probe of ψ in solution will depend on the degree to which the contributions from θ₂ and θ₃ can be determined.

3.3. DFT Calculations of Nonconventional ϕ-Dependent Spin-Coupling Constants in 2

¹J_C1′,H1′,²J_C1′,H2′, ²J_C2′,H1′, and ¹J_C1′,C2′ were calculated as a function of ϕ in 2 (Figure 1). Scatter along the y-axis at discrete values of ϕ shows the secondary effect of ψ. The plots for ¹J_C1′,H1′ and ²J_C1′,H2′ contain significant scatter, indicating that neither J-value will be a reliable independent constraint for ϕ. The dynamic range for ²J_C1′,H2′ is also small (∼1 Hz), further reducing its usefulness. The shape of the curve can be understood by noting the calculated ²J_C1′,H2′ values in the three idealized staggered rotamers of ϕ (rotamers I–III, Scheme 8) and inspecting the corresponding Newman projections. Less negative values correlate with ϕ rotamers in which a lone-pair orbital on O1′ is anti to the C1′–C2′ bond (rotamers II and III). In contrast to ²J_C1′,H2′, ²J_C2′,H1′ displays a larger dynamic range (4–5 Hz) when its sign is taken into account, rendering it a better probe of ϕ than ²J_C1′,H2′ (Figure 1C). The ²J_C2′,H1′ plot also has considerably less y-axis scatter, especially at ϕ values of 0–180° (i.e., ²J_C2′,H1′ has less y-axis scatter overall than observed for ²J_C1′,H2′). In the three idealized staggered ϕ rotamers shown in Scheme 8, the calculated ²J_C2′,H1′ is more positive in III (∼3 Hz) than in I and II (∼0–1 Hz). In III, the C1′–H1′ and C1′–C2′ bonds are both anti to an O1′ lone-pair orbital, whereas in I and II, a lone-pair orbital is anti to only one of these bonds. These lone-pair orbital effects on ²J_CCH are consistent with those reported previously.^39,40

Figure 1.

Calculated dependencies of ¹J_C1′,H1′ (A), ²J_C1′,H2′ (B), ²J_C2′,H1′ (C) and ¹J_C1′,C2′ (D) on ϕ in 2. Black circles, full dataset; green circles, trimmed dataset. Solid green and black lines represent best fits to the green and black datasets, respectively. See Scheme 8 for the definitions of ϕ rotamers I–III identified in each plot. The scatter observed at discrete ϕ values in these plots reveals the secondary dependencies on ψ.

Scheme 8. Idealized Staggered Rotamers I–III of the C1′–O1′ Bond φ in 2.

The exo-anomeric effect favors rotamer I in the β-linkage of 2. One lone-pair orbital on O1′ is anti to the C1′–C2′ bond in II and III, whereas both orbitals are gauche to this bond in I.

Like ²J_C2′,H1′, the plot for ¹J_C1′,C2′ shows modest y-axis scatter and a relatively large dynamic range (∼6 Hz). Rotamers II and III (Scheme 8) contain an O1′ lone-pair orbital anti to the C1′–C2′ bond, and both give ¹J_C1′,C2′ values of ∼49 Hz. In contrast, both O1′ lone-pair orbitals are gauche to the C1′–C2′ bond in 1, yielding a ¹J_C1′,C2′ of ∼53 Hz. These observations are consistent qualitatively with the discussion above, namely, that rotamers II and III are likely to contain longer C1′–C2′ bonds than rotamer I, resulting in less s-character and a smaller ¹J_C1′,C2′.

3.4. DFT Calculations of Nonconventional ψ-Dependent Spin-Coupling Constants in 2

The dependencies of ¹J_C4,H4, ¹J_C3,C4, and ¹J_C4,C5 on ψ in 2 are shown in Figure 2. ¹J_C4,H4 behaves similarly to ¹J_C1′,H1′ (Figure 1A) with regard to y-axis scatter, indicating that, like ¹J_C1′,H1′, ¹J_C4,H4 is unlikely to be a useful constraint for ψ. ¹J_C3,C4 and ¹J_C4,C5 are more promising, with both showing moderate secondary dependencies on ϕ and adequate dynamic ranges (6–7 Hz). Newman projections of the O1′–C4 bond in 2 for the three idealized staggered rotamers IV–VI of ψ (Scheme 9) provide structural rationales for the behaviors of ¹J_C3,C4 and ¹J_C4,C5. ¹J_C3,C4 in rotamers V and VI (∼43 Hz) is smaller than that in rotamer IV (∼47 Hz), while ¹J_C4,C5 is smaller in rotamers IV and V (∼41 Hz) than in rotamer VI (∼46 Hz). Rotamers V and VI contain an O1′ lone-pair orbital anti to the C3–C4 bond, but rotamer IV does not, leading to a smaller r_C3,C4 in IV relative to V and VI and presumably to the larger ¹J_C3,C4 in IV. Similarly, rotamers IV and V contain an O1′ lone-pair orbital anti to the C4–C5 bond, whereas rotamer VI does not, resulting in a plot of ¹J_C4,C5 that mimics that observed for ¹J_C3,C4 (plots B and C in Figure 2 are essentially phase-shifted along the x-axis).

Figure 2.

Calculated dependencies of ¹J_C4,H4 (A), ¹J_C3,C4 (B), and ¹J_C4,C5 (C) on ψ in 2. See Figure 1 for the definitions of the green and black data points and lines. Scheme 9 contains the definitions of ψ rotamers IV–VI. The scatter observed at discrete ψ values in these plots reveals the secondary dependencies on ϕ.

Scheme 9. Idealized Staggered Rotamers IV–VI of the C4–O1′ Bond ψ in 2.

The dependences of the four ²J_CCH values in Scheme 7 on ψ in 2 are shown in Figure 3. The dynamic ranges for ²J_C4,H3 (∼1.5 Hz) and ²J_C4,H5 (∼1.5 Hz) are small, and neither J-coupling is likely to be a useful constraint for ψ. In contrast, the dynamic ranges of ²J_C3,H4 (∼2 Hz) and ²J_C5,H4 (∼5 Hz) are larger, especially the latter. The plot of ²J_C5,H4 indicates more negative values in rotamers V and VI relative to rotamer IV. In rotamer IV, O1′ lone-pair orbitals are anti to both the C4–H4 and C4–C5 bonds, whereas in rotamers V and VI, a lone-pair orbital is anti to only one of these bonds. This situation mimics that observed for ²J_C2′,H1′ where the less negative (more positive) J-coupling is associated with rotamer III (Figure 1C, Scheme 8). Applying the same analysis to ²J_C3,H4 (Figure 3A) leads to the prediction that rotamer VI should give a less negative (more positive) J-coupling than rotamers IV and V since it contains O1′ lone-pairs anti to both the C3–C4 and C4–H4 bonds (Scheme 9). The plot in Figure 3A supports this prediction, although rotamers IV and V yield different, albeit more negative values. Orienting an O1′ lone-pair anti to the C3–C4 bond (rotamer V) appears to reduce ²J_C3,H4 more significantly than orienting a lone-pair anti to the C4–H4 bond (rotamer IV).

Figure 3.

Calculated dependencies of ²J_C3,H4 (A), ²J_C4,H3 (B), ²J_C5,H4 (C), and ²J_C4,H5 (D) on ψ in 2. See Figure 1 for definitions of the green and black data points and lines, and Scheme 9 for the definitions of ψ rotamers IV–VI. The scatter observed at discrete ψ values in these plots reveals the secondary dependencies on ϕ.

Rotamer IV is associated with a more negative ²J_C4,H5 than rotamer V even though both contain an O1′ lone-pair orbital anti to the C4–C5 bond, but the most negative value, as expected, is associated with rotamer VI which lacks this interaction (Scheme 9). Likewise, rotamers V and VI are expected to be associated with more positive ²J_C4,H3 values than rotamer IV since the former contain an O1′ lone-pair orbital anti to the C3–C4 bond and the latter does not. In addition to vicinal lone-pair effects, longer-range 1,3 lone-pair effects⁴⁰ from O1′ on the C3–H3 or C5–H5 bond lengths may influence the behaviors of ²J_C4,H3 and ²J_C4,H5, but these effects cannot be visualized using the projections in Scheme 9.

Collectively, the nonconventional ²J_CCH values in 2 behave similarly with respect to the effects of oxygen vicinal lone-pair orbitals on coupling magnitude and sign. The presence of an oxygen lone-pair anti to either the C–C or C–H bond of the coupling pathway, or to both bonds, shifts the coupling to a more positive (less negative) value relative to the coupling observed in conformations lacking these anti arrangements. The lone-pair effects appear additive, although they are probably not equivalent, that is, the effect of a lone-pair anti to the C–C bond may be larger than when anti to the C–H bond. These conclusions are consistent with those drawn in an earlier study of the conformational dependencies of ²J_CCH values in saccharides.^39,40

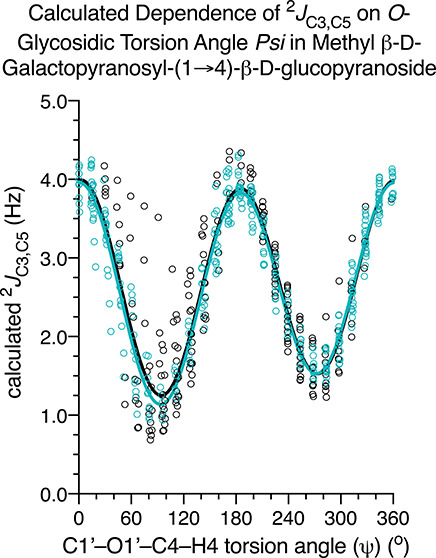
²J_C3,C5 shows a bimodal dependence on ψ and is positive in sign with a dynamic range of ∼3 Hz (Figure 4). Rotamers IV and VI correlate with smaller values (∼2 Hz) than rotamer V (∼4 Hz). In rotamer V, the two lone-pair orbitals on O1′ are anti to the C3–C4 and C4–C5 bonds (the two bonds comprising the coupling pathway), whereas in rotamers IV and VI only one of these lone-pair interactions exists (the remaining lone-pair orbital is anti to the C4–H4 bond). Prior studies have shown that the lone-pair arrangements in rotamer V shift ²J_CCC to more positive values in saccharides (i.e., this relationship pertains to ²J_C1,C3, ²J_C2,C4, and ²J_C4,C6 in aldohexopyranosyl rings).^39,40

Figure 4.

Calculated dependency of ²J_C3,C5 on ψ in 2. See Figure 1 for the definitions of the green and black data points and lines, and Scheme 9 for the definitions of ψ rotamers IV–VI. The scatter observed at discrete ψ values reveals the secondary dependence on ϕ.

Based on evaluations in Sections 3.3 and 3.4 above, the following seven nonconventional spin-coupling constants in Schemes 5 and 7 are good candidates for MA’AT modeling of ϕ and ψ in 2: for ϕ, ¹J_C1′,C2′ and ²J_C2′,H1′; for ψ, ¹J_C3,C4, ¹J_C4,C5, ²J_C3,H4 (marginal), ²J_C5,H4, and ²J_C3,C5. By extension, related J-couplings in other two-bond O-glycosidic linkages (e.g., those in 3–7, Scheme 3) should prove useful for MA^’AT modeling of their linkages, as discussed below.

3.5. Effects of Exocyclic C–O Bond Conformation on ϕ- and ψ-Dependent Nonconventional Spin-Couplings Constants in 2

Having identified seven potentially useful nonconventional ϕ- and ψ-dependent J-couplings, secondary conformational effects that influence them were evaluated. In the treatments discussed above, the effects of ϕ or ψ on these J-couplings were studied. All other exocyclic conformational features were fixed or highly constrained in geometries dictated by the ten torsion angles shown in Scheme 4. Superimposed on these ϕ and ψ dependencies are secondary conformational dependences whose magnitudes need to be understood and quantified in order to apply these nonconventional J-couplings to structural studies. These secondary dependencies arise largely from exocyclic C–O bond torsion angles θ₁–θ₃ (Scheme 5), and Scheme 10 shows which of these angles affect specific ϕ- and ψ-dependent non-conventional J-couplings. For example, for ¹J_C1′,C2′ and ²J_C2′,H1′, rotation about θ₁ affects their magnitudes and/or signs, in addition to rotation about ϕ. In a similar vein, ¹J_C3,C4 and ²J_C3,H4 are affected by θ₂ in addition to ψ. In the following discussion, the secondary effects of θ₁, θ₂, and θ₃ are discussed in more detail.

Scheme 10. Secondary Effects of Torsion Angles θ₁, θ₂, and θ₃ on Seven Nonconventional Spin-Coupling Constants Sensitive to φ and ψ in 2.

For each set of J-couplings shown on the right, the torsion angle(s) shown in blue affect their magnitudes and/or signs.

3.5.1. ¹J_C1′,C2′ and ²J_C2′,H1′ (ϕ-Dependent)

Plots of ¹J_C1′,C2′ as a function of ϕ adopt the same overall shape regardless of the values of θ₁, θ₂, and θ₃ (Figure 5A). However, a y-axis displacement of ∼5 Hz to smaller ¹J_C1′,C2′ is observed for θ₁ rotamers VII and IX relative to the remaining curves, including that for θ₁ rotamer VIII (reference state) (Scheme S1, Supporting Information). An inspection of θ₁ rotamers shows that an O2′ lone-pair orbital is anti to C1′ in rotamers VII and IX but not in VIII. The former geometry is expected to lengthen the C1′–C2′ bond (vicinal lone-pair interaction), leading to smaller ¹J_C1′,C2′ values.

Figure 5.

Effects of θ₁–θ₃ on the dependencies of ¹J_C1′,C2′ (A) and ²J_C2′,H1′ (B) on ϕ in 2. For each plot: black line, reference state; green dots, rotamer VII; green line, rotamer IX; blue dots, rotamer X; blue line, rotamer XII; red dots, rotamer XIII; red line, rotamer XV. For the definitions of rotamers and reference states, see Schemes S1–S3, Supporting Information.

The effects of θ₁–θ₃ on ²J_C2′,H1′ are modest (∼0.5 Hz) except for the curve for rotamer XV (Scheme S3, Supporting Information) near ϕ values of 300° (Figure 5B). ²J_C2′,H1′ values are most positive when the two lone-pair orbitals on O2′ are anti to the C1′–C2′ and C2′–C3′ bonds (θ₁ rotamer IX). The behavior in rotamer XV at ϕ near 300° probably results from greater data scatter from the secondary ψ dependence and its effect on parameterization since in these ϕ geometries, O2′ and O6 are in close proximity in some ψ rotamers. These findings show that rotation of the C–O bond involving the coupled carbon (in this case, θ₁) exerts a smaller effect on ²J_CCH than rotation of the C–O bond involving the carbon bearing the coupled hydrogen (in this case, ϕ) (Scheme 6).

3.5.2. ¹J_C3,C4 and ¹J_C4,C5 (ψ-Dependent)

The dependence of ¹J_C3,C4 on ψ (Figure 6A) mimics that of ¹J_C1′,C2′ on ϕ (Figure 5A) in that both curves are unimodal, although the former J-couplings are smaller by 6−7 Hz (the C3−C4 fragment bears only two oxygen substituents, whereas the C1′–C2′ fragment bears three). ¹J_CC decreases in magnitude as the number of oxygen substituents on the C–C fragment declines. Secondary effects may pertain when two oxygen substituents are involved in terms of whether both reside on the same carbon or different carbons. The effects of θ₁–θ₃ on curve shape are small, but the curves associated with θ₂ rotamers X and XII are shifted to smaller values by ∼5 Hz relative to θ₂ rotamer XI (reference state). An inspection of Scheme S2 (Supporting Information) shows an O3 vicinal lone-pair interaction with the C3–C4 bond in rotamers X and XII but not in rotamer XI. As found for ¹J_C1′,C2′, lengthening of the C3–C4 bond in the former two rotamers leads to smaller ¹J_CC values.

Figure 6.

Effects of θ₁–θ₃ on the dependencies of ¹J_C3,C4 (A) and ¹J_C4,C5 (B) on ψ in 2. For each plot: black line, reference state; green dots, rotamer VII; green line, rotamer IX; blue dots, rotamer X; blue line, rotamer XII; red dots, rotamer XIII; red line, rotamer XV. For the definitions of rotamers and reference states, see Schemes S1–S3, Supporting Information.

The curves for ¹J_C4,C5 are unimodal (Figure 6B) and are affected to a limited extent by θ₁–θ₃. The effect of θ₁ is small but not that of θ₂, especially for rotamer X. Exocyclic hydroxymethyl group conformation affects ¹J_C4,C5, with the curve for rotamer XV (tg) differing from those for rotamers XIII (gg) and XIV (gt). The hydroxymethyl group effects are probably caused by significant data scatter at ψ values of 60–180° where strong steric interactions between O5′ and the C6–O6 fragment occur, especially in the tg rotamer. This scatter may influence curve parameterization and render comparisons unreliable. For ψ values devoid of steric interactions (values of 0–60° and 180–360°), the curves are very similar (y-axis displacements of ≤1 Hz).

3.5.3. ²J_C3,H4, ²J_C5,H4, and ²J_C3,C5 (ψ-Dependent)

The effects of θ₁–θ₃ on the dependence of ²J_C3,H4 on ψ are modest (differences of ∼0.5 Hz) (Figure 7A). The single outlier is θ₃ rotamer XV (tg; Scheme S3, Supporting Information), and aberrant parameterization caused by significant data scatter at ψ values of 150–200° (steric clashes) is probably the cause. The effect of θ₁ is negligible (remote rotation), but a small θ₂ effect (rotation of the C3–O3 bond) is observed. ²J_C3,H4 values associated with rotamers X and XII are more positive (less negative) by ∼0.5 Hz than those associated with rotamer XI (reference state). C3–O3 Rotamers containing O3 lone-pair orbitals anti to the C2–C3 and C3–C4 bonds (θ₂ rotamer XII) or one O3 lone-pair orbital anti to the C3–C4 bond (θ₂ rotamer X) yield slightly more positive (less negative) ²J_C3,H4 values than rotamer XI that lacks either of these arrangements. Similar behavior was observed for ²J_C2′,H1 (Figure 5B).

Figure 7.

Effects of θ₁–θ₃ on the dependencies of ²J_C3,H4 (A), ²J_C5,H4 (B), and ²J_C3,C5 (C) on ψ in 2. For each plot: black line, reference state; green dots, rotamer VII; green line, rotamer IX; blue dots, rotamer X; blue line, rotamer XII; red dots, rotamer XIII; red line, rotamer XV. For the definitions of rotamers and reference states, see Schemes S1–S3, Supporting Information.

The effects of θ₁–θ₃ on the dependencies of ²J_C5,H4 and ²J_C3,C5 on ψ (Figure 7B,C) are small (<1 Hz); curve shapes are highly conserved. Rotation of θ₃ does not affect ²J_C5,H4 despite the proximity of the exocyclic hydroxymethyl group to the C5–C4–H4 coupling pathway. Rotation of θ₂ also does not much affect ²J_C5,H4 despite potential 1,3-lone-pair interactions between O3 lone-pair orbitals and the proximal C4–H4 bond.

Rotations of θ₂ and θ₃ exert small effects on ²J_C3,C5. The available data indicate that θ₂ rotamers that orient one of the O3 lone-pair orbitals anti to the C3–C4 bond (rotamers X and XII; Scheme S2, Supporting Information) shift ²J_C3,C5 to slightly less positive values relative to rotamer XI that lacks this interaction (Figure 7C). This result contrasts with the effect of ψ on ²J_C3,C5 (Figures 4 and 7C) where the most positive ²J_C3,C5 value correlates with rotamer V in which the lone-pair orbitals on O1′ are anti to the C3–C4 and C4–C5 bonds. The effects of oxygen lone-pair orbitals on ²J_C3,C5 depend on whether the lone-pair resides on an oxygen atom attached to C3 or to C4.

3.6. Summary of ²J_CCH Behavior in 2 and Saccharides in General

The results of studies on the effects of exocyclic C–O bond conformation on ²J_CCH values in 2 are summarized in Scheme 11. Two types of C–O bond rotations pertain to C–C–H coupling pathways, those associated with the coupled carbon and those associated with the carbon bearing the coupled hydrogen. The latter C–O rotations exert the greater effect on ²J_CCH values by a factor of 4–5. Thus, from the standpoint of conformational probes, the latter types of rotations, arising either from exocyclic C–O bonds of hydroxyl groups or C–O bonds involved in O-glycosidic linkages, are more likely to be interrogated successfully by ²J_CCH values than the former.

Scheme 11. Summary of Oxygen Lone-Pair Effects on ²J_CCH Values in Saccharides, Using ²J_C2′,H1′ and ²J_C3,H4 in 2 as Examples.

(A) Effect of the C–O bond rotation on the carbon bearing the coupled hydrogen. The φ (for ²J_C2′,H1′) or ψ (for ²J_C3,H4) rotamers that orient both oxygen lone-pair orbitals anti to both bonds in the C–C–H coupling pathway correlate with the most positive J-values (these interactions are expected to lengthen both bonds). (B) Effect of C–O bond rotation on the coupled carbon. The value of θ₁ (for ²J_C2′,H1′) and θ₂ (for ²J_C3,H4) rotamers in which the O–H bond is anti to the C–C bond in the coupling pathway, and one oxygen lone-pair orbital experiences a 1,3 interaction with the coupled hydrogen and correlates with the most negative J-values (both effects are expected to reduce the C–C and C–H bond lengths in the coupling pathway). See Schemes 8, 9, S1, and S2 for rotamers III, VI, VIII and XI, respectively.

In the preceding analysis, six ²J_CCH were treated: ²J_C1′,H2′, ²J_C2′,H1′, ²J_C3,H4, ²J_C4,H3, ²J_C5,H4, and ²J_C4,H5. DFT calculations show that all but ²J_C2′,H1′ have negative signs, regardless of C–O bond conformation at either carbon in the C–C–H coupling pathway. Application of the empirical projection rule of Pedersen and coworkers²⁸ gives signs that are generally consistent with the DFT calculations. The five DFT-calculated ²J_CCH that have negative signs give projection sums of either −0.5 or 0, whereas the single ²J_CCH having a positive sign (²J_C2′,H1′) gives a projection sum of +0.5. The former sums correlate with ²J_CCH values ranging from −3 to −5 Hz, whereas a +0.5 sum correlates with ²J_CCH values of ∼0 Hz (Figure S2, Supporting Information). Inspection of the ²J_C2′,H1′ curves in Figures 1C and 5B shows that both positive and negative signs are possible depending on ϕ and θ₁, giving an average value that is small in magnitude and positive in sign. The projection method only takes into account the configuration of the C–C–H coupling pathway and does not include contributions from C–O bond rotations at both carbons, which are significant.

3.7. Extensions to O-Glycosidic Linkages in Disaccharides 3–7

The preceding discussion of spin-coupling constants in 2 revealed several nonconventional ¹J and ²J values that may be useful in MA’AT analyses of the phi and psi torsion angles in O-glycosidic linkages. Do the conclusions drawn from studies of 2 apply to β-(1→4) linkages involving modified residues and to (1→2) and (1→3) O-glycosidic linkages? To address these questions, calculations were conducted on five model disaccharides: methyl 2-acetamido-2-deoxy-β-d-glucopyranosyl-(1→4)-β-d-mannopyranoside (3), methyl 2-deoxy-β-d-arabino-hexopyranosyl-(1→4)-β-d-glucopyranoside (4), methyl α-d-mannopyranosyl-(1→3)-β-d-mannopyranoside (5), methyl α-d-mannopyranosyl-(1→2)-α-d-mannopyranoside (6), and methyl 2-acetamido-2-deoxy-β-d-glucopyranosyl-(1→2)-α-d-mannopyranoside (7) (Scheme 3). The behaviors of seven non-conventional J-couplings in 3–7 were compared to those of analogous J-couplings in 2. The results are shown in Figures 8–10. For ¹J_C1′,C2′, the overall curve shape is conserved in 2–4 and 7, in which the C1′−O1′ bond is equatorial and the O1′–CX bond (CX is the aglycone carbon) is either axial (7) or equatorial (2–4) (Figure 8A). Absolute values of ¹J_C1′,C2′ decrease progressively in the order 2 > 3 ≈ 7 > 4. The introduction of an N-acetyl side-chain on C2′ shifts ¹J_C1′,C2′ to smaller values, and removal of an electronegative substituent at C2′ further reduces ¹J_C1′,C2′. These curves differ appreciably from those for 5 and 6 that contain α-linkages in which the O1′–CX bond is either axial (6) or equatorial (5). The curve for 5 is an approximate mirror image of that for 2, whereas that for 6 differs from that for 5 in the appearance of a local minimum near ϕ = 240°. The dynamic ranges of the curves for 3–7 are similar to that of the curve for 2, supporting the contention that ¹J_C1′,C2′ should be a useful probe of ϕ in 3–7. Separate equation parameterizations, however, will be required to treat ¹J_C1′,C2′ quantitatively in 2–7.

Figure 8.

Calculated dependencies of ¹J_C1′,C2′ (A) and ²J_C2′,H1′ (B) on the H1′–C1′–O1′–CX torsion angle (ϕ) in disaccharides 2–7, where CX represents the aglycone carbon. Bold black curve, 2. Purple curve, 3. Lime green curve, 4. Blue curve, 5. Teal curve, 6. Red curve, 7.

Figure 10.

Calculated dependencies of ²J_CX–1,HX (A), ²J_CX+1,HX (B), and ²J_CX–1,CX+1 (C) on the C1′–O1′–CX–HX torsion angle (ψ) in disaccharides 2–7, where CX represents the aglycone carbon. For example, in 5, ²J_CX–1,HX = ²J_C2,H3, ²J_CX+1,HX = ²J_C4,H3, and ²J_CX–1,CX+1 = ²J_C2,C4. Bold black curve, 2. Purple curve, 3. Lime green curve, 4. Blue curve, 5. Teal curve, 6. Red curve, 7.

The dependencies of ²J_C2′,H1′ on ϕ in 2–4 and 7 are very similar, differing only in shifts along the y-axis (Figure 8B). ²J_C2′,H1′ becomes increasingly more positive in the order 2 < 3 ≈ 7 < 4. Curves for the α-linked disaccharides 5 and 6 are similar and are approximate mirror images of those for 2–4 and 7. ²J_C2′,H1′ values are almost uniformly negative for the two α-linkages, whereas those for the β-linkages are almost uniformly positive, as observed for αMan and βGlc monosaccharides.⁴⁵ The dynamic ranges of all curves are similar, suggesting that ²J_C2′,H1′ may be uniformly applicable in MA’AT analyses of ϕ. However, separate equation parameterizations will be required to apply ²J_C2′,H1′ in MA’AT analyses.

One-bond ¹³C–¹³C spin-couplings sensitive to ψ are shown in Figure 9. The ¹J_CX,CX–1 curves (Figure 9A) adopt similar shapes for 5–7, whereas those for 2–4 overlap. The latter structures contain β-(1→4) linkages to aglycone residues bearing equatorial C–O bonds at C4 and C3. The side-chain structure at C2′ exerts little effect on this ¹J_CC nor does C–O bond orientation at the remote C2 (axial in 3 and equatorial in 2 and 4). ¹J_CX,CX–1 plots for 6 and 7 are similar and nearly overlap, and both are significantly shifted to larger ¹J_CC relative to the plot for 5. Inspection of 6 and 7 shows that both contain an axial O1′–C2 bond and an axial C1–O1 bond, whereas corresponding bonds in 5 are equatorial and axial, respectively. The relative disposition of oxygen substituents appended to the coupled carbons over one bond (i.e., the dihedral angle subtended by the vicinal oxygen substituents; ∼180° in 6 and 7 and ∼−60° in 5) is an important determinant of ¹J_CC values in saccharides.⁴³ The orientation of the C1′–O1′ bond, which is axial in 6 and equatorial in 7, does not appear to influence ¹J_CX,CX–1 values appreciably. The dynamic range of the curve for 5 is somewhat smaller than that for 2–4 and 6–7, which may render this ¹J_CC value less useful for MA’AT analyses of ψ in structures like 5.

Figure 9.

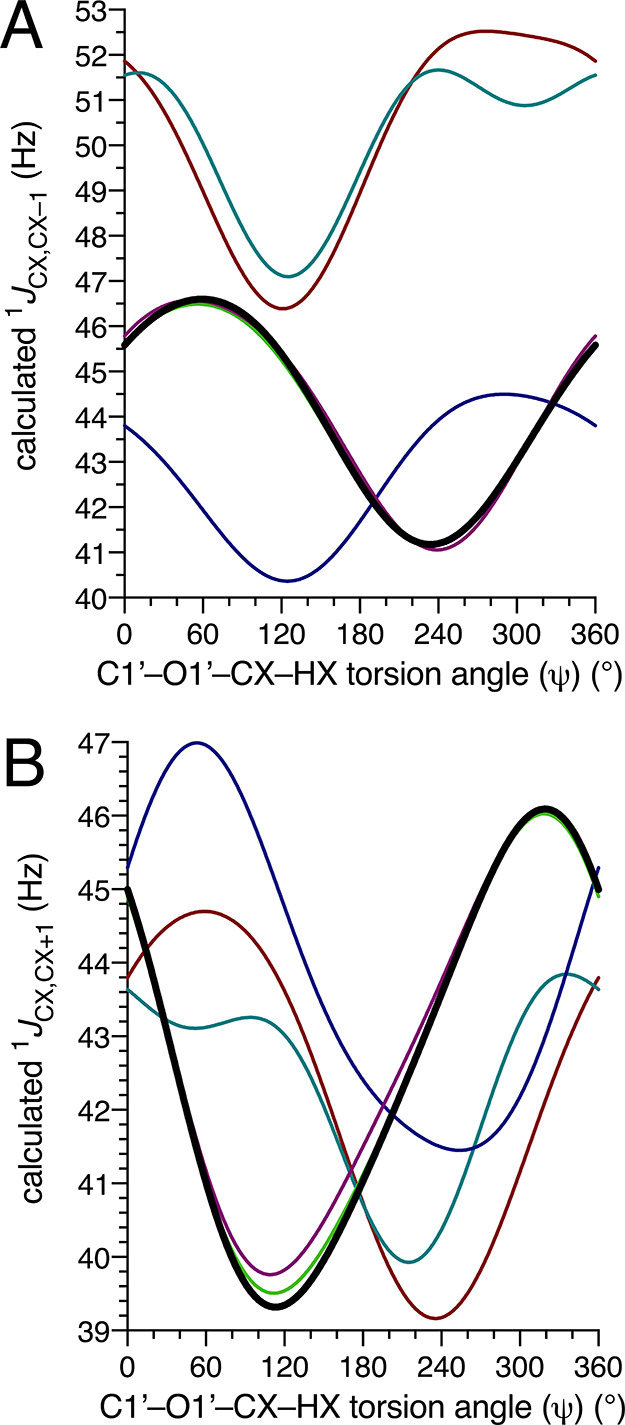
Calculated dependencies of ¹J_CX,CX–1 (A) and ¹J_CX,CX+1 (B) on the C1′–O1′–CX–HX torsion angle (ψ) in disaccharides 2–7, where CX represents the aglycone carbon. For example, in 5, ¹J_CX,CX–1 = ¹J_C3,C2 and ¹J_CX,CX+1 = ¹J_C3,C4. Bold black curve, 2. Purple curve, 3. Lime green curve, 4. Blue curve, 5. Teal curve, 6. Red curve, 7.

The dependencies of ¹J_CX,CX+1 on ψ in 2–4 are virtually identical, producing overlapping curves (Figure 9B). The latter structures contain β-(1→4) linkages to aglycone residues bearing equatorial bonds at C4 and C5. The side-chain structure at C2′ exerts little effect on this ¹J_CC nor does C–O bond orientation at the remote C2 (axial in 3 and equatorial in 2 and 4). The curves for 5–7, which contain α anomeric linkages, have roughly similar shapes that are distinct from those for 2–4. For 5, the C–O bonds at C3 and C4 are both equatorial. In contrast, the C–O bonds at C2 and C3 are axial and equatorial, respectively, in 6 and 7. These structural differences in the C_X–C_X+1 coupling pathway may explain why the curves for 6 and 7 are similar and distinct from that for 5.

Geminal ¹³C–¹H and ¹³C–¹³C spin-couplings in 2–7 are shown in Figure 10, all of which are sensitive to ψ. The curve shapes for ²J_CX–1,HX in 5–7 are conserved but are shifted along the y-axis, whereas the curves for 2–4 overlap and have shapes distinct from those found for 5–7 (Figure 10A). ²J_CX–1,HX is positive or negative in sign in 6–7 depending on ψ, whereas ²J_CX–1,HX is uniformly positive in 5. In contrast, ²J_CX–1,HX values in 2–4 are strongly negative. These observations are consistent with predictions based on the projection rule,²⁸ where a projection of 0 is associated with the C3–C4–H4 pathways in 2–4, and a projection of 1.5 is associated with the C2–C3–H3 pathway in 5, yielding predicted ²J_CCH values of ∼−3 and ∼+5 Hz, respectively (see Figure S2 in Supporting Information), in qualitative agreement with the DFT results. The dynamic ranges of ²J_CX–1,HX in 5–7 may render them more useful for MA’AT analysis of ψ than those of ²J_CX–1,HX in 2–4. Similar behavior is observed for ²J_CX+1,HX (Figure 10B) in that curves of similar shape are observed for 5–7 but are shifted along the y-axis, whereas the curves for 2–4 overlap and have shapes distinct from those for 5–7. ²J_CX+1,HX values in 2–7 are negative in sign and all exhibit a dynamic range suitable for MA’AT analysis of ψ.

The geminal ²J_CX–1,CX+1 shows a remarkable consistency in its dependency on ψ (Figure 10C), regardless of the location of the pathway in the pyranosyl ring. Two sets of curves are observed. One set includes ²J_CX–1,CX+1 values that have uniformly positive signs and is associated with pathways in which the oxygens on the terminal coupled carbons are both equatorial (structures 2–4). The second set includes ²J_CX–1,CX+1 values with signs near zero and is associated with pathways in which the oxygens on the terminal coupled carbons are axial and equatorial (structures 5–7). C–O Bond orientation (axial vs equatorial) at the intervening carbon in these C–C–C pathways appears to exert a minimal effect on ²J_CCC. The dynamic range of pathways having two equatorial terminal oxygens is larger than that of pathways having an axial-equatorial arrangement, leading to the expectation that ²J_CX–1,CX+1 values in the former will be more robust MA’AT constraints on ψ than ²J_CX–1,CX+1 values in the latter.

3.8. Behavior of ⁴J_H1′,H4 in Disaccharides 2, 5, and 6

Trans-O-Glycoside four-bond spin-coupling between H1′ and HX (HX is the hydrogen attached to the aglycone carbon) is not expected to be a useful probe in MA’AT analyses of O-glycosidic linkages. Nevertheless, it was investigated to gain a better understanding of its dependence on linkage conformation. Plots of calculated ⁴J_H1’,H4 in 2 as a function of ϕ and ψ are shown in Figure 11. ⁴J_H1′,H4 values are small in magnitude and have a dynamic range of ∼2 Hz. ⁴J_H1′,H4 is equally sensitive to ϕ and ψ, as indicated by the data scatter at discrete values of ϕ in Figure 11A and ψ in Figure 11B. This scatter reaches a minimum at a ϕ/ψ combination of 180/180°, that is, when the five atoms in the H1′–C1′–O1′–C4–H4 coupling pathway are coplanar and adopt a W-shaped arrangement.^40,46 Recent MA’AT analyses of 2(10) have yielded mean values of ϕ and ψ of 28° and −8°, respectively, where secondary effects on ⁴J_H1′,H4 are significant, thereby rendering ⁴J_H1′,H4 useless as an independent probe of either torsion angle. However, ⁴J_H1′,H4 could play a confirmatory role if ϕ and ψ in a given linkage were determined from MA’AT analyses of other J-couplings. In this case, complicating secondary effects are reduced, and ⁴J_H1′,H4 can be used as an ancillary test of the conformational assignment. This scenario is illustrated in Figure 12 for ⁴J_H1′,H4 in 2. Using MA’AT-determined mean values of ϕ and ψ, a ⁴J_H1′,H4 of ∼0.9 Hz should be observed, a value with a small uncertainty based on the imposed limited scatter from secondary effects. In practice, however, while coupling trends predicted by DFT are probably reliable, it remains to be established whether ⁴J_H1′,H4 values calculated by DFT are accurate; that is, the curves in Figures 11 and 12 may need to be shifted on the y-axes to bring calculated values in line with experiment.

Figure 11.

Calculated dependencies of ⁴J_H1′,H4 on (A) H1′–C1′–O1′–C4 (ϕ) and (B) C1′–O1′–C4–H4 (ψ) torsion angles in 2. In each plot, the black curve represents the best fit of the data. Point scatter at discrete values of ϕ in (A) and ψ in (B) indicate the extent to which ψ and ϕ, respectively, affect the calculated coupling.

Figure 12.

Calculated dependencies of ⁴J_H1′,H4 on (A) H1′–C1′–O1′–C4 (ϕ) and (B) C1′–O1′–C4–H4 (ψ) torsion angles in 2. In each plot, the black curve represents the best fit of the data. Point scatter at discrete values of ϕ in (A) and ψ in (B) indicate the extent to which ψ and ϕ, respectively, affect the calculated coupling, using restricted ranges of ψ (−30 to 15°) and ϕ (15–45°). The vertical dashed line in each plot identifies the mean value of ϕ (28°) and ψ (−8°) in 2 determined from prior MA’AT analysis.¹⁰

The behavior of ⁴J_H1′,H4 in 2 as a function of ϕ and ψ (Figure 11) appears to be independent of the type of O-glycosidic linkage. In 2, the C1′–O1′ and C4–O1′ bonds are both equatorial. In 5, the C1′–O1′ bond is axial and the C3–O1′ bond is equatorial, and in 6, the C1′–O1′ and C2–O1′ bonds are both axial. Plots similar to those shown in Figure 11 for 2 are shown in Figures S3 and S4 for 5 and 6, respectively (see Supporting Information). The latter plots are very similar to those found for 2 with respect to the location of the minimum, dynamic range, the absolute values of the calculated J-couplings, and the nature of the secondary dependencies. Thus, the conclusions drawn regarding the ancillary role of ⁴J_H1′,H4 in evaluating ϕ and ψ in 2 also apply to the corresponding trans-glycosidic ⁴J_HH values in 5 and 6 and probably to other types of O-glycosidic linkages.

3.9. DFT-Parameterized Spin-Coupling Equations for Structures 2–7

Plots of J-couplings in structures 2–7 as a function of either the phi (ϕ) or psi (ψ) O-glycosidic torsion angles (Figures 1–12) were parameterized and are found in the Supporting Information (eqs S1–S105). The curves were fit to the following modified Karplus-like equation (eq 1) using R.

1

This generalized form of the Karplus-like equation was first described by Pachler.⁴⁷ He proposed the use of this trigonometric function to account for asymmetry in the Karplus curve caused by substitution of a hydrogen atom in the coupling pathway. This trigonometric polynomial form was adopted because it provides the best parameterization to the DFT data with the smallest number of terms. This form of the equation is also amenable to simple integration, making it compatible with MA’AT analysis⁹⁻¹² for modeling torsional populations in solution.

4. Conclusions

MA’AT modeling of conformational equilibria and dynamics of saccharides depends in part on reliable equations that relate specific spin-coupling constants to molecular torsion angles.⁹⁻¹² It has been customary to use ³J values (e.g., ³J_HH, ³J_CH, and ³J_CC) in this modeling for three reasons: (1) these J-couplings typically exhibit strong dependencies on molecular torsion angles (i.e., have large dynamic ranges); (2) they are less prone to secondary structural effects, especially those associated with the rotation of proximal bonds bearing electronegative substituents (e.g., C–O bonds); and (3) the conformational dependencies of other types of spin-coupling constants (e.g., ¹J, ²J and ⁴J) are less well understood. Saccharides like other types of molecules are rich in ¹J, ²J, and ³J values involving carbon and hydrogen as coupled nuclei. However, restricting MA’AT analyses to ³J values eliminates nearly 60% of the available J-couplings in an aldohexopyranosyl ring, excluding those involving hydroxyl hydrogens.⁴⁰ For unimodal modeling, access to 3–4 redundant J-couplings (i.e., those sensitive to the same molecular torsion angle) is sufficient for successful MA’AT modeling.⁹⁻¹² For multimodal modeling, however, significantly more redundant J-couplings are needed, rendering the use of ¹J and/or ²J values important to wider applications of the method. In the absence of using ¹J and/or ²J values, additional types of NMR parameters (e.g., residual dipolar couplings or nuclear Overhauser effects) might also enable multimodal modeling.

This study investigated a group of nonconventional J-couplings (mainly ²J values) that are not commonly used in conformational analysis of the O-glycosidic linkages of oligosaccharides. Thirteen J-couplings in six different types of O-glycosidic linkages were investigated. The results show that seven of these J-couplings may prove useful in MA’AT modeling of either ϕ or ψ under certain conditions, regardless of the type of O-glycosidic linkage (e.g., 1→2 vs 1→3 linkages; α vs β linkages). The latter conditions are likely to include prior knowledge of the conformational behaviors of exocyclic C–O bonds proximal to the coupling pathway. This knowledge would reduce the negative impacts of secondary effects on MA’AT modeling of O-glycosidic linkage conformation when nonconventional J-couplings are used as conformational constraints. This knowledge would also improve, although more modestly, the reliability of MA’AT modeling of ϕ and ψ based on conventional ³J values. Experimental studies of the conformational properties of exocyclic C–O bonds in solution have been reported,⁴⁸⁻⁵³ and MD simulations provide additional information even though current force fields are not parameterized to provide this information quantitatively. MD simulations of exocyclic hydroxyl C–O bonds not participating in hydrogen bonding show three idealized staggered rotamers to be most stable, although often in different populations. Whether this behavior replicates that found in solution accurately awaits more rigorous experimental study.

While the present study investigated new nonconventional J-couplings of importance to MA’AT modeling of O-glycosidic linkage conformation and dynamics, nonconventional spin-couplings may also prove useful in MA’AT modeling of other conformational properties of saccharides in solution. Unlike O-glycosidic linkages that often adopt single-state conformations about ϕ and ψ, multi-state conformational equilibria may pertain to other conformational behaviors (e.g., exocyclic hydroxyl and hydroxymethyl group conformations). Multi-state modeling of hydroxyl group conformations by MA’AT analysis would be enabled by use of nonconventional J-couplings like those discussed in this report. This modeling not only would advance our current rudimentary understanding of exocyclic C–O bond conformational behavior in solution but would also improve MA’AT modeling in general by reducing or eliminating secondary effects displayed by some redundant J-couplings used in MA’AT analyses.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c02793.

• Three idealized staggered rotamers VII–IX about the C2′–O2′ bond (θ₁) in 2; three idealized staggered rotamers X–XII about the C3–O3 bond (θ₂) in 2; three idealized staggered rotamers XIII–XV about the C5–C6 bond (θ₃) in 2; plots of calculated ¹J_C1′,H1′, ²J_C1′,H2′, ¹J_C4,H4, ²J_C4,H3, and ²J_C4,H5 values as a function of either the H1′–C1′–O1′–C4 (ϕ) or the C1′–O1′–C4–H4 (ψ) torsion angle for different values of θ₁, θ₂, and θ₃ in 2; and a discussion of these plots; torsion angle constraints in DFT calculations of 3–7; plot of projection sums used to predict the magnitudes and signs of ²J_CCH values in saccharides; plots of calculated ⁴J_H1′,H3 in 5 as functions of ϕ and ψ; plots of calculated ⁴J_H1′,H2 in 6 as functions of ϕ and ψ; DFT-parameterized spin-coupling equations [S1]–[S105]; and representative Cartesian coordinates for 2–7 (PDF)

The authors declare no competing financial interest.