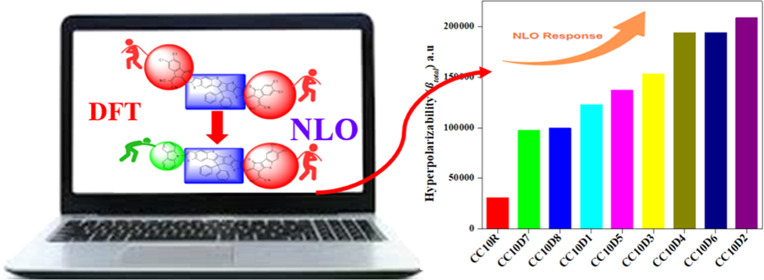
Abstract
Nonlinear optical (NLO) materials have several uses in many fields such as solid physics, biology, medicine, nuclear physics, and material research. Therefore, a series of nonfullerene-based derivatives (CC10D1–CC10D8) with a D−π–A configuration was planned for the NLO investigation using CC10R as the reference molecule with structural alternations at acceptor moieties. Natural bonding orbital (NBO), UV–vis spectra, frontier molecular orbitals (FMOs), global reactivity parameters (GRPs), transition density matrix (TDM), and density of states (DOS) were analyzed using the M06/6-311G(d,p) functional in chloroform solvent to understand the NLO responses of CC10R and CC10D1–CC10D8. The highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) band gaps of CC10D1–CC10D6 were illustrated to be lower than that of CC10R, with the larger bathochromic shift (726.408–782.674 nm) resulting in a significant NLO response. Along with the band gap, the FMO method also identified an efficient interfacial charge transfer from D to A moieties via a π-bridge, which was further supported by the DOS and TDM map. Moreover, NBO calculations demonstrated that extended hyperconjugation and strong internal molecular interactions were important in their stabilization. The dipole moment (μ), linear polarizability ⟨α⟩, hyperpolarizability (βtotal), and second-order hyperpolarizability (γtotal.) were studied for CC10R and CC10D1–CC10D8. Among all of the derivatives, CC10D2 was proven to be the most appropriate candidate because of its suitable NLO behavior such as being well-supported by a reduced band gap (2.093 eV) and having a suitable maximum absorption wavelength (782.674 nm). Therefore, CC10D2 was reported to have a greater value of first hyperpolarizability (208 659.330 a.u.) compared with other derivatives and CC10R. For the second hyperpolarizability, a greater value was obtained for CC10R (5.855 × 107 a.u.), and its derivatives showed results comparable to that of the parent chromophore for γtotal. This theoretical framework reveals that structural customization with different acceptor units plays a significant role in obtaining attractive NLO materials for optoelectronic applications.
Introduction
In the last few decades, nonlinear optic (NLO) materials have become significant in the field of photonic and optoelectronic materials.1 The field of nonlinear optics includes studies of the first-, second-, and third-order nonlinear optical properties, i.e., electro-optic and photorefractive effects, second-harmonic generation, etc. The development of NLO materials has become a region of advanced research in both experimental and theoretical areas.2 Enormous scientific attempts have been made in the past few decades to discover distinct NLO materials, including molecular dyes, synthetic resins, and inorganic and organic semiconductor diodes.3 Organic NLO materials are preferred for their tremendous benefits over inorganic ones such as their small dielectric constant value, high values of photoelectrical coefficients, low cost, schematics, ease of use, involvement of π-bond system electron delocalization, and elastic designing.4 To increase the charge-transfer capability, organic chromophores are combined with fullerene-based acceptor moieties. Nevertheless, fullerene chromophores are reported to have a few defects such as poor photostability and the least absorption in the visible region.5 Recently, the attention of scientists has shifted from fullerene to fullerene-free molecules because of their capability to adopt different chemical structures, tunable energy levels, wide range of electron affinities, and facile synthesis.6 NLO properties of organic compounds are assumed to emerge because of the powerful intramolecular charge transfer (ICT), which includes the transmission of the electron cloud from donor to acceptor segments via π-linkers. The ICT progression can be effected through a donor−π–acceptor organization of the nonlinear optical materials, establishing a “push–pull” mechanism. The non-centrosymmetric π-spacer chromophores enhance the density of CT between electron donors (D) and acceptors (A), thus accomplishing first-, second-, and third-order nonlinear polarizabilities.7,8
In the past several years, many metal-free organic D–A compounds have been recognized as NLO materials with π-linkers, which provide a route for the transfer of electrons under the influence of an electric field.9 Further, the π-conjugated system provides an efficient transfer of charges from the donor to the acceptor.10 It is also observed that π-conjugated linkers with a suitable length enhance the NLO properties.11 Many organic molecules are investigated using a simple D−π–A configuration that supports significant photoinduced ICT through chromophores.7 The NLO characteristics of these D−π–A species can be effectively adjusted by substituting suitable D and A segments and π-spacers at appropriate sites. The literature contains numerous reported designs, i.e., D–A, D−π–A, A−π–D−π–A, D−π–A−π–D, D−π–π–A, D–A−π–A, and D–D−π–A, where “D” stands for the donor moiety, “π” stands for the π-spacer, and “A” refers to the acceptor unit.12 These designs facilitate good communication between the D, π, and A units to build an appropriate push–pull architecture. Thus, appropriate push–pull arrangements cause a decrease in the molecular orbital band gap, boost asymmetric electrical density distribution, and cause a bathochromic shift of the absorption spectra, hence providing a well-known NLO response. However, extending the π-conjugation, by introducing various electron-deficient end-capped groups (nitro, cyano, and halogen groups) in the structure of the NFAs, boosts the NLO responses of fullerene-free chromophores. The introduction of a cyano group in the acceptor moiety makes the molecular surface electrostatic potential (SEP) positive, improves the vertical electron affinity (VEA), and lowers the energy of the lowest unoccupied molecular orbital (LUMO).13 Because of the higher electron-withdrawing ability of the −CN group, it is used in the manufacture of fused-ring electron acceptors (FREAs) expressing a high photovoltaic effect.14 The introduction of fluoro groups (fluorination) to the design of acceptor materials also enhanced ICT in the chromophore due to the higher electron-withdrawing ability of fluorine.15 NF molecules having a cyano group at the acceptor along with halogens (fluoro and chloro units) exhibited noteworthy NLO behavior but produced environmentally toxic products when used as a photonic material. Therefore, by replacing the −CN unit with a −NO2 unit, environmentally friendly photovoltaics can be synthesized.16 Therefore, considering the above features, here, we designed a novel series of strong push–pull chromophores with a D−π–A architecture (CC10D1–CC10D8) from A−π–A-configured CC10R.17 According to our literature review, NLO properties of the reference and designed compounds has not been investigated so far. Therefore, an NLO investigation of these D−π–A-type species is presented in this research paper. The density functional theory (DFT) and time-dependent density functional theory (TD–DFT) computations for the abovementioned chromophores were carried out to perform FMO, natural bonding orbital (NBO), global reactivity parameter (GRP), absorption spectra, density of states (DOS), transition density matrix (TDM), and NLO analyses in chloroform. It is anticipated that the modulated compounds CC10D1–CC10D8 would play a substantial role in the NLO field. We expect that this investigation might serve as the springboard for experimental physicists and chemists for the synthesis of chemical chromophores with outstanding NLO characteristics.
Results and Discussion
The current study is focused on computational analyses of NF-based chromophores for comprehensive NLO responses. The structural modeling of chromophores was performed by changing the configuration from A−π–A to D−π–A and then introducing various acceptor units (see Scheme 1). The IUPAC names and abbreviations of the used acceptors are given in the Supporting Information. The derivatives (CC10D1–CC10D8) contain three fragments, the donor (9H-carbazole), π-spacers, and acceptors, which enhanced their conjugation length and thereby boosted their NLO responses. The parent compound CC10 has a A−π–A architecture,17 where the hydrocarbon chain n-hexyl (−C6H13) group is used as the spacer. Nonetheless, in our investigation, the hydrocarbon chain n-hexyl (−C6H13) group was replaced with a methyl (−CH3) group at the spacer moieties in CC10 to overcome the computational cost. Therefore, the name of the reference chromophore is changed from CC10 to CC10R, as shown in Figure 1. A series of molecules, namely, CC10D1–CC10D8, were designed by amending the acceptor moieties in the fullerene-free parent compound (CC10R), as displayed in Figure 2. The π-linker of CC10R and the donor moiety of CC10D1 were preserved in all other designed molecules. The optimized geometries of the entitled chromophores with their atom numbers are shown in Figure S1, whereas their ChemDraw structures are displayed in Figure 2. The structures of the entitled molecules were optimized by investigating their vibrational frequencies at the M06/6-311G(d,p) level. The computed geometrical parameters, i.e., bond lengths (Å) and bond angles (°), are presented in Tables S1–S9. For CC10R and CC10D1–CC10D8, in the benzene ring, the C–C bond lengths of C28–C29, C28–C30, and C29–C31 were calculated to be 1.395, 1.392, and 1.386 Å, respectively. These simulated bond lengths of the benzene ring were found to be in excellent harmony with the literature values of C–C bond lengths.18 Furthermore, bond distances in the thiophene ring, such as C1–C2, C3–C4, and C3–S8, of the entitled molecules were found to be 1.379, 1.401, and 1.750 Å, respectively, which are in excellent agreement with experimental values.18 For CC10R, the bond lengths of C1–C2, C1–C39, C3–S8, C55–N56, and C64–O65 were found to be 1.378, 1.517, 1.749, 1.155, and 1.206 Å, respectively. Similarly, the bond angles of C33–C28–C59, C61–C27–C64, C22–C62–C63, and C23–C22–C62 were calculated to be 127.9, 117.5, 124.7, and 131.8°, respectively. Further, the bond angles of C56–C58–C59 and C57–C59–C58 were calculated to be 119.9 and 120.2°, accordingly, in CC10D1–CC10D8. The abovementioned simulated bond lengths and angles are found to be in excellent harmony with the literature data. The main objective of the current study was to design novel NF-based compounds that exhibited promising NLO properties. Comprehensive analyses have been performed to study the electronic properties, polarizability ⟨α⟩, first hyperpolarizability (βtotal), second hyperpolarizability (γtotal), spectral absorption, highest occupied molecular orbital (HOMO)/LUMO band gaps, and NBOs by DFT and TD–DFT computations to explore the NLO properties of CC10D1–CC10D8. It is anticipated that the compounds designed by us (CC10D1–CC10D8) with a D−π–A configuration show a strong push–pull mechanism that will result in stronger intramolecular charge-transfer (ICT) properties. Further, we also expect that this study will motivate future researchers to synthesize and analyze NLO materials with excellent properties.
Scheme 1. Sketch Map of the Designed Chromophores (CC10R and CC10D1–CC10D8) and Series of Acceptors Used for the Modulation of the CC10D1–CC10D8 Compounds.

Figure 1.
Modification of CC10 to CC10R by the substitution of a small alkyl group.
Figure 2.
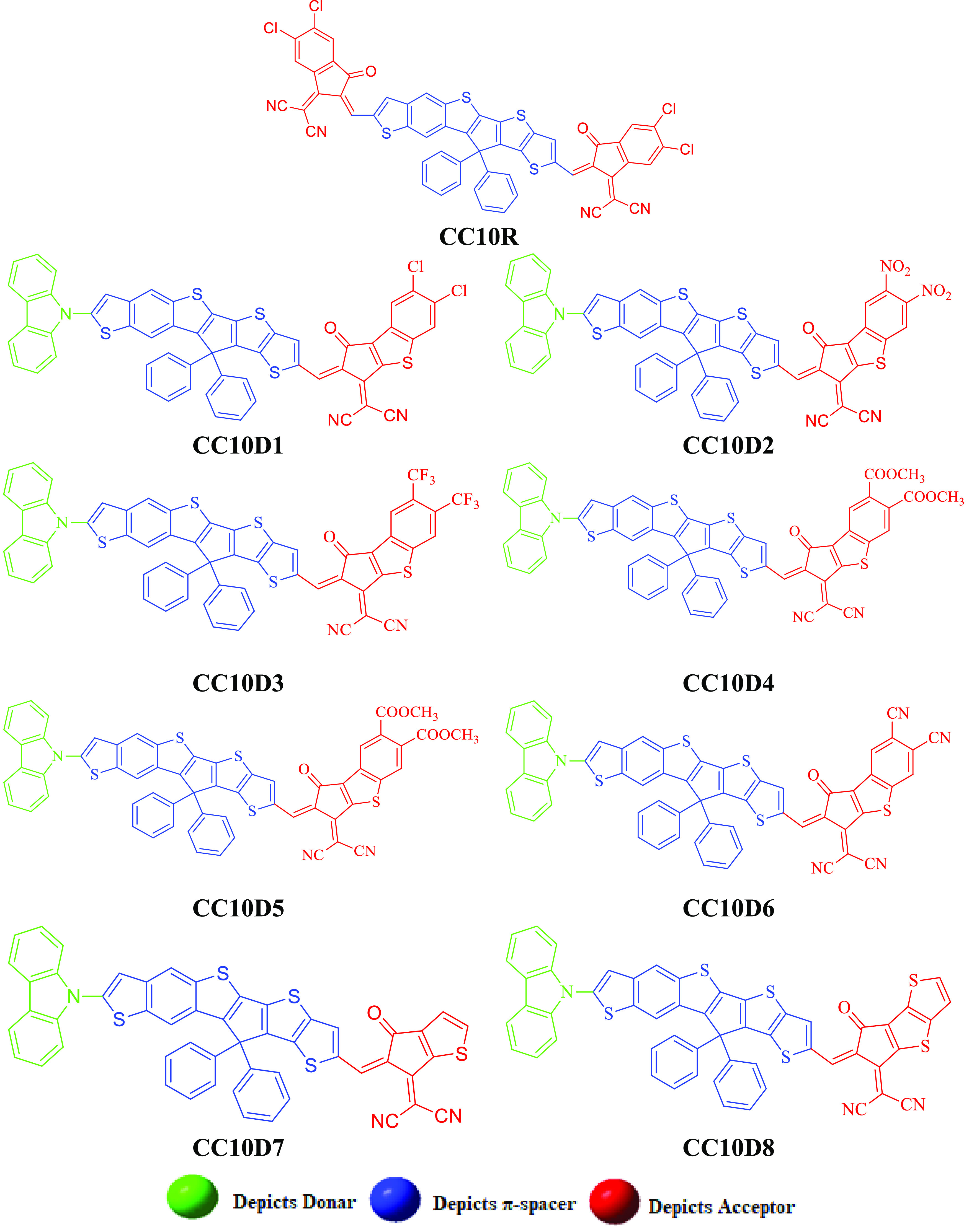
2D structures of the studied compounds (CC10R and CC10D1–CC10D8).
Electronic Structure
Frontier molecular orbital (FMO) analysis is a remarkable approach to study the various electronic transitions, molecular reactivities, chemical stabilities, and optical behaviors of organic systems.19 The energies of the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) play a key role in the optical and electronic characteristics of compounds.20 HOMOs exhibit the ability of nucleophiles to donate electrons, whereas LUMOs express the ability of electrophiles to accept electrons from nucleophiles.21 The FMO energy gap (Egap = ELUMO – EHOMO) of chromophores is considered to be a significant factor in determining the extent of softness, dynamic stability, hardness, and reactivity of molecules.22 A chromophore with a small Egap is generally regarded as a less stable, more reactive, softer molecule with a larger polarizability and an excellent NLO response.22b,23,24 In this study, we calculated the EHOMO and ELUMO, molecular orbital energy gaps (ΔE) of the aforementioned chromophores at the M06/6-311G(d,p) level, and the obtained results are provided in Table 1.
Table 1. EHomo, ELumo, and Energy Gap (ΔE) of the Entitled Compounds (Units in eV).
| compounds | ELUMO | EHOMO | ΔE |
|---|---|---|---|
| CC10R | –3.635(−4.016) | –5.954(−6.215) | 2.319(2.199) |
| CC10D1 | –3.472 | –5.775 | 2.303 |
| CC10D2 | –3.729 | –5.822 | 2.093 |
| CC10D3 | –3.572 | –5.787 | 2.215 |
| CC10D4 | –3.699 | 5.822 | 2.123 |
| CC10D5 | –3.502 | –5.762 | 2.261 |
| CC10D6 | –3.678 | –5.833 | 2.155 |
| CC10D7 | –3.302 | –5.748 | 2.446 |
| CC10D8 | –3.299 | –5.733 | 2.434 |
Table 1 shows that the computed HOMO/LUMO values of the reference compound are −5.954/–3.635 eV, which is extremely close to the experimentally determined values of −6.215/–4.016 eV.17 These results support the selection of the appropriate functional (M06) for the NLO study of CC10R and CC10D1–CC10D8 compounds. Interestingly, all of the derivatives expressed a reduction in the band gap (2.093–2.303 eV) compared to their parent molecules (2.319 eV), except CC10D7 and CC10D8 chromophores. This might be because the modulation of the D−π–A pattern in place of A−π–A promotes efficient internal charge transfer, which results in a decrease in the orbital energy gap.17 By replacing one terminal acceptor DMM with the 9H-carbazole donor unit and the other with a DBT acceptor moiety, the energy band gap in CC10D1 is reduced to 2.303 eV compared with that of CC10R (2.319 eV) because of the development of a strong push–pull architecture along with the enlargement of resonance. Further reduction in the energy gap is observed in CC10D2 (2.093 eV) when the DBT acceptor unit is replaced with (Z)-2-(2-ethylidene-6, 7-dinitro-1-oxo-1, 2-dihydro-3H-benzo[b] cyclopenta [d]thiophen-3-ylidene) malononitrile (MDC). The shuffling of the chloro (−Cl) with two nitro (−NO2) groups into MDC enhanced the electron-withdrawing effect of the acceptor, resulting in a powerful pull–push structure. A slight increase in ΔE (2.215 eV) was noticed when the MCT acceptor unit was introduced into CC10D3, where −NO2 groups are replaced with −CF3 units, as −CF3 has a lower electronegativity and electron-withdrawing effect compared with −NO2.1313 The band gap narrowed (2.123 eV) once again as the MCT acceptor was replaced again with the DCS moiety in CC10D4, where the −CF3 unit is shuffled with the −SO3H group. Similarly, a slight increase in the energy gap (2.26 eV) in CC10D5 was noticed when the −SO3H units were substituted with two acetate groups (−COOCH3) in ((Z)-2-(2-ethylidene-6,7-dimethyl-1-oxo-1,2-dihydro-3H-benzo[b]cyclopenta[d]thiophen-3-ylidene)malononitrile-carbon (IV) oxide (1/2)) (DMO). The introduction of the MOD acceptor group in CC10D6 was found to further narrow down the energy gap, as −COOCH3 is replaced by cyano (−CN) groups. This might be due to the fact that −CN groups are more electronegative than the −COOCH3 group;13 therefore, the enhanced electron-withdrawing behavior of MOD resulted in boosting the capability of the push–pull configuration. Therefore, it is concluded that a higher electronegativity of the moieties improved the movement of the electron cloud in the direction of A due to inductive electron withdrawal.7
Among all derivatives, CC10D7 and CC10D8, with MCM and MOC acceptor groups, expressed larger band gaps of 2.446 and 2.434 eV, respectively. This may be because of their different chemical frameworks, lower conjugation, and less efficient push–pull mechanism because of the absence of electronegative units as compared with other derivatives.25
Consequently, CC10D2 has the lowest band gap among all modulated structures because of the enhanced π-conjugation and resonance by two highly electron-withdrawing −NO2 groups substituted at its acceptor region. In short, the energy gap between HOMOs and LUMOs of the respective compounds decreases in the following order: CC10D7 > CC10D8 > CC10R > CC10D1 > CC10D5 > CC10D3 > CC10D6 > CC10D4 > CC10D2. This order demonstrates that structural tailoring by introducing various electronegative substituents at the acceptor moiety is an excellent way to reduce band gap values and hence enhance the NLO response.
The magnitude of the energy gap accounts for the shift of the electron cloud from D to A assisted by π-linkers, which is evidence of the NLO material’s functionality.26 The surfaces of FMOs are utilized to explore the transfer of charges, as shown in Figure 3. In CC10R, a slight change in the charge density over HOMO–LUMO is noted. The charge density is mainly concentrated across the π-linker and to a small extent across A units. In the designed compounds (CC10D1–CC10D8), the electron cloud for HOMO is mostly prevalent over the π-spacer and partially across the donor. However, in LUMOs, a minor part of the electron charge density is generally present on the acceptor portion and the major part is present on π-spacers. This implies that the electron donor species are linked to electron acceptor units with the help of π-spacers, which facilitate charge transfer between the D and A moieties. Because of this charge-transfer phenomenon, all of the studied compounds might be regarded as important NLO constituents.27
Figure 3.
HOMOs and LUMOs of the investigated compounds (units in eV).
Density of States (DOS)
The density of states analysis was used for the determination of electronic properties to support the FMO analysis28 of CC10R and modulated compounds (CC10D1–CC10D8), as revealed in Figure 4. The DOS results supported the results that are displayed in FMO diagrams. The patterns of electron charge distribution on molecular orbitals depend on the different acceptor moieties, which could be confirmed by calculating the DOS percentages on the HOMOs and LUMOs.29 The designed compounds (CC10D1–CC10D8) were divided into three moieties, i.e., the donor unit (donating group), the π-spacer (linker), and the acceptor moiety (end-capped acceptor unit), as shown by red, green, and blue lines, respectively, in the graphs. However, the reference compound (CC10R) is segmented into two parts (acceptor and π-spacer) because of the A−π–A configuration (See Figure 2). In this study, the acceptor showed an electron distribution pattern of 72.3, 81.9, 86.1, 84.6, 83.5, 85.5, 85.0, 80.4, and 83.4% to the LUMO and 16.9, 8.6, 8.9, 8.5, 8.7, 8.3, 9.1, 7.9, and 8.5% to the HOMO for CC10R and CC10D1–CC10D8, respectively. The donor contributed 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, and 0.1% to the LUMO and 9.8, 12.0, 11.3, 12.0, 10.3, 11.2, 8.8, and 9.3% to the HOMO in CC10D1–CC10D8, respectively. Similarly, the π-spacer contributed 27.7, 18.0, 13.8, 15.3, 16.4, 14.4, 14.9, 19.5, and 16.5% to the LUMO and 83.1, 81.7, 79.2, 80.2, 79.3, 81.4, 79.7, 83.3, and 82.2% to the HOMO for CC10R and CC10D1–CC10D8, respectively, as shown in Table S19. These contributions show that the electron-withdrawing influence of the end-capped A unit changes the distribution pattern around the HOMOs and LUMOs and also affects the band gap between them. The HOMO and LUMO electron density of CC10R is mainly situated on the π-linker and to a minor extent on the acceptor. In the case of CC10D1, the HOMOs are predominately located on the acceptor as well as the π-spacer, with a smaller involvement of the donor moiety, whereas the LUMOs are mainly distributed on the π-bridge group and equally on the donor and acceptor groups (see Figure 3). In the DOS graphs, the negatively charged values obtained represent HOMOs, whereas positively charged values demonstrate the LUMOs along the x-axis, and the distance between them represents the energy gap.30 In CC10R, the highest density on the HOMO and LUMO is present on the spacer and the acceptor. For CC10D1 and CC10D2, the highest peak of the density on the HOMO at −11 eV is confined by the π-spacer, whereas on the LUMO, most of the density is between 2 and 3 eV and is also trapped by the spacer, thus showing the transfer of electrons from the spacer to the acceptor. For CC10D3 and onward, the maximum charge density (−10 to −13 eV) on HOMOs is trapped by the acceptor and π-spacer, and the maximum density (2 to 4 eV) on LUMOs is trapped by the π-spacer, except for CC10D7. For CC10D7, on HOMOs, the maximum density of −10 to −14 eV is occupied by the spacer, and on LUMOs, the maximum density (1–5 eV) is located on the spacer, which indicates the movement of charge density from the D unit to the acceptor moiety through the π-linker. To sum up the whole discussion, the pictographs of density distribution in Figure 4 display the electron delocalization and a substantial amount of charge transfer occurring in all modulated compounds CC10D1–CC10D8 from the donating group (donor) to the acceptor unit through the π-bridge.
Figure 4.
Graphical representation of DOS for CC10R and CC10D1–CC10D8.
UV–Vis Spectral Analysis
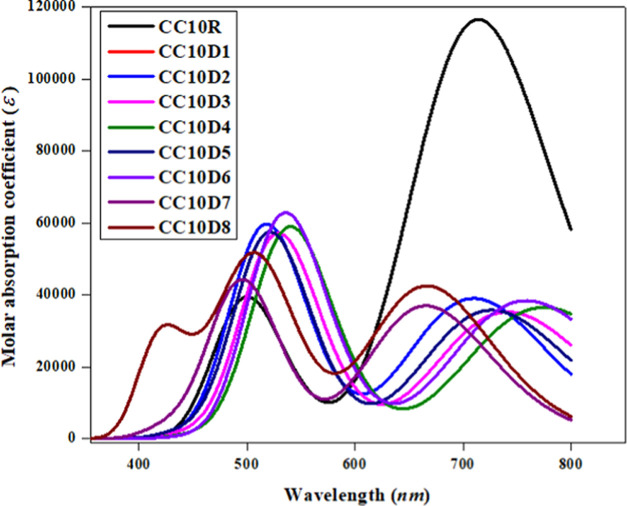
In an attempt to understand the absorption peaks of the entitled chromophores, UV–vis investigations were performed at the M06/6-311G(d,p) level in chloroform. The type of electron transition, maximum absorption (λmax), oscillator strength (fos), and excitation energy (E) of CC10R and CC10D1–CC10D8 compounds were determined, and are displayed in Table 2, whereas the six lowest singlet–singlet transitions are detailed in Tables S11–S19.
Table 2. Oscillator Strength (Fos), Wavelength (λ), and Excitation Energy (E) of CC10R and CC10D1–CC10D8a.
| compounds | λ (nm) | E (eV) | fos | MO contributions |
|---|---|---|---|---|
| CC10R | 714.354 | 1.736 | 1.602 | H → L (95%), H-1 → L+1 (2%) |
| CC10D1 | 709.896 | 1.747 | 0.538 | H → L (93%) H-2 → L (2%), H-1 → L (3%) |
| CC10D2 | 782.674 | 1.584 | 0.489 | H → L (93%), H-1 → L (3%) |
| CC10D3 | 741.305 | 1.673 | 0.486 | H → L (93%), H-2L (2%), H-1 → L (3%) |
| CC10D4 | 774.944 | 1.599 | 0.503 | H → L (94%), H-1 → L (3%) |
| CC10D5 | 726.408 | 1.706 | 0.493 | H → L (93%), H-2 → L (2%), H-1 → L (3%) |
| CC10D6 | 758.679 | 1.634 | 0.529 | H → L (94%), H-1 → L (3%) |
| CC10D7 | 665.539 | 1.863 | 0.509 | H → L (94%), H-2 → L (2%), H-1 → L (2%) |
| CC10D8 | 666.685 | 1.859 | 0.585 | H → L (93%), H-2 → L (2%), H-1 → L (3%) |
MO = molecular orbital; H = HOMO; L = LUMO; fos = oscillator strength.
It is estimated that a polar medium convoluted in the π–π* stabilization state connected with the n−π* state by the utilization of a suitable electron level.31 Generally, the energy of transition of a molecule in chloroform is influenced by polarity effects and van der Waal forces.32 This feature implies that hydrogen bonding and dipolar interactions play a key role in the stabilization of the first singlet electron level of the chromophore33 because the solvent polarity enhanced the absorbance toward a bathochromic shift. The excited state is considered to be highly polar compared with the ground state and consequently more stabilized in chloroform than the ground state.33 From the above table, we can find that all entitled chromophores exhibited absorbance spectra in the visible region. For the reference chromophore, the computed λmax is noted at 714.354 nm, which is comparable to its experimental absorption peak at 736 nm.19 It was observed that the effect of the acceptor moiety on λmax caused the absorption spectra to undergo a red shift.34 All derivatives expressed larger absorption peaks (726.408–782.674 nm), except CC10D1, CC10D7, and CC10D8. The absorption spectrum of CC10D1 was observed at 709.896 nm, with 1.747 eV transition energy and an oscillator strength of 0.538, which is comparable to that of the parent chromophore (λmax = 714.354 nm and excitation energy = 1.736 eV). The maximum absorption peak (λmax = 714.354) increased from 726.408 and 741.305 nm in CC10D5 and CC10D3 with lower excitation energies (E = 1.706 and 1.673 eV) as the electron-withdrawing moieties (−COOCH3 and −CF3) were introduced on the acceptor units, respectively. Further, a red shift was observed in CC10D6, CC10D4, and CC10D2 when more powerful electron-withdrawing units −CN, −SO3H, and −NO2, respectively, were incorporated into the A unit, which created a strong push–pull architecture that narrowed down the excitation energy. By removing the electron-withdrawing unit and changing the framework of the acceptor units in CC10D7 and CC10D8, a blue shift in the absorption spectra was observed (see Table 2 and Figure 5). The λmax of all entitled compounds in ascending order was as follows: CC10D7 < CC10D8 < CC10D1 < CC10R < CC10D5 < CC10D3 < CC10D6 < CC10D2. Similarly, the transition energies in the ascending order were as follows: CC10D2 < CC10D4 < CC10D6 < CC10D3 < CC10D5 < CC10R < CC10D1 < CC10D8 < CC10D7. The enhancement in λmax and the least excitation energy values show that the entitled chromophores possess a large charge-transfer ability, and consequently, facile excitation might occur over the HOMO–LUMO. The above-discussed HOMO/LUMO examination of entitled molecules supports the absorbance spectra with respect to higher λmax values and the least transition energy, which guide them to enrich their photoelectric response. Concisely, CC10D2 expressed the least excitation energy, the lowermost band gap, and the greatest λmax absorbance, which make it an ideal material with suitable optoelectronic properties for use in the NLO field.
Figure 5.
Absorption spectra of entitled compounds (CC10R and CC10D1–CC10D8).
Global Reactivity Parameters
The energy values of FMOs are undoubtedly important factors for the estimation of the global reactivity parameters (GRPs), i.e., global electrophilicity index (ω), electron affinity (EA), global softness (σ), chemical potential (μ), electronegativity (X), ionization potential (IP), and global hardness (η). Basically, the electron-donating and electron-accepting capacities are determined by the ionization potential as well as electron affinity, which is exactly equal to the energy required to pull electrons from the HOMO. In a chemical system, the reactivity and stability can be determined by the chemical hardness [η = −(ELUMO – EHOMO)/2], which is a measure of resistance to change in the electron density or charge in a chromophore.35 Similarly, electronegativity [χ = −(EHOMO + ELUMO)/2] is described as the power of an atom in a species to attract electrons toward itself.36 In the same way, the electrophilicity index (ω), the capacity or propensity of a compound to accept electrons, was introduced by Parr and is estimated using the electronic chemical potential and chemical hardness [ω = μ2/2η].37 The value of electronegativity of a molecule is defined as the chemical potential, which is determined using the expression μ = (EHOMO + ELUMO)/2.23b,38 There is a direct relation between hardness (η), energy gaps, stability of a compound, and chemical potential (μ), whereas in the case of reactivity, this relationship is inversed.34b The calculated results of GRPs are tabulated in Table 3.
Table 3. Computed Global Reactivity Parameters of CC10R and CC10D1–CC10D8 (Units are in eV).
| compounds | IP | EA | X | η | μ | ω | σ |
|---|---|---|---|---|---|---|---|
| CC10R | 5.954 | 3.635 | 4.7945 | 1.159 | –4.794 | 9.913 | 0.431 |
| CC10D1 | 5.775 | 3.472 | 4.624 | 1.152 | –4.624 | 9.282 | 0.434 |
| CC10D2 | 5.822 | 3.729 | 4.776 | 1.047 | –4.776 | 10.896 | 0.478 |
| CC10D3 | 5.787 | 3.572 | 4.680 | 1.108 | –4.680 | 9.886 | 0.451 |
| CC10D4 | 5.822 | 3.699 | 4.761 | 1.062 | –4.761 | 10.675 | 0.471 |
| CC10D5 | 5.762 | 3.502 | 4.632 | 1.132 | –4.632 | 9.494 | 0.442 |
| CC10D6 | 5.833 | 3.678 | 4.756 | 1.078 | –4.756 | 10.494 | 0.464 |
| CC10D7 | 5.748 | 3.302 | 4.525 | 1.223 | –4.525 | 8.371 | 0.408 |
| CC10D8 | 5.733 | 3.299 | 4.516 | 1.217 | –4.516 | 8.379 | 0.411 |
The data from the above table show higher values of IP = 5.733–5.954 eV and EA = 3.299–3.729 eV, with a larger electronegativity (X = 4.516–4.7945 eV), which characterize the ability of the entitled chromophores to pull electrons toward themselves. These results explain their greater tendency to accept electrons because of the existence of robust A moieties. All of the designed compounds had lower values of global hardness, with softness values higher than that of the parent molecule, indicating that the modulated chromophores have a higher reactivity along with a longer rate of polarizability, which boosted the NLO characteristics of these molecules. Further, high electrophilicity and chemical potential (μ = −4.516 to −4.794 eV) values indicate a high capability to withdraw electrons and hence to act as electrophiles. The influence of the A moiety on the accumulation of a highly negative chemical potential (μ) consequently makes the molecule highly polarizable, more reactive, and less stable, as demonstrated in the abovementioned molecules. Overall, this investigation found that the effective CT ability of molecules amid their LUMO and HOMO orbitals results in an improved polarizability and notable NLO behavior.
Natural Bonding Orbital Analysis
Natural bond orbital (NBO) analysis describes the charge distribution, types of intra- and intermolecular transitions, and types of bonding and interactions in organic systems.39 One of the most significant aspects of the NBO study is that it allows one to observe the delocalization of charge densities and their transfer from the D to A region of a system with the D−π–A configuration.40 Therefore, we executed an NBO analysis to evaluate the inter- and intramolecular transitions, such as hydrogen bonding, conjugative interactions, and delocalization of CC10R and CC10D1–CC10D8, which result in system stabilization, as tabulated in Tables S20–S28. The stabilization energy as well as the conjugative interactions were calculated using the second-order perturbation theory.41 The stabilization energy E(2) associated with the delocalization from i → j for each donor (i) and acceptor (j) is determined as follows:
| 1 |
where the donor orbital occupancy is represented by qi, the off-diagonal elements are shown by Fi,j, and the diagonal NBO Fock matrix elements are represented by Ei and Ej. Intensive interactions between the electron donor and acceptor moieties depend on higher stabilization energy E(2) values. The larger the value of E(2), the larger the intensive interaction between the electron-rich and electron-deficient counterparts of molecules.42 Normally, four different types of hyperconjugative events are found: i.e., π → π*, σ → σ*, LP → π*, and LP → σ* due to the overlapping of orbitals. Transitions from π → π* are the most dominant, LP → σ* and LP → π* are slightly dominant, whereas σ → σ* are the least dominant. In CC10R, for the π → π* transition, a strong intramolecular hyperconjugative interaction was observed as π(C22–C23) → π*(C24–C25), having the highest stabilization energy of 24.58 kcal/mol. However, the π(C1–C2) → π*(C1–C2) transition has the lowest stabilization energy of 0.5 kcal/mol. This low energy is associated with weak donor–acceptor push–pull interactions. Moreover, in σ → σ* transitions, σ(C1–C2) → σ*(C4–S7) has the highest energy value of 8.41 kcal/mol and σ(C1–C2) → σ*(C4–S7) has the lowest energy value of 1.21 kcal/mol. Among other LP → σ* transitions, LP(2) (S7) → π*(C3–C4) has the highest energy of 27.84 kcal/mol, whereas LP(2) (Cl39) → σ*(C21–C26) has an energy value of 0.53 kcal/mol. In CC10D1, for π → π* transitions, the highest interaction energy (23.81 kcal/mol) is observed in π(C21–C22) → π*(C70–C72), whereas the lowest interaction energy (13.24 kcal/mol) is observed for π(C82–C86) → π*(C15–C16). Further, among σ → σ* transitions of CC10D1, the highest interaction energy (9.15 kcal/mol) is observed in the σ(C83–H84) → σ*(C23–C54) transition, whereas the lowest interaction energy (0.51 kcal/mol) is observed in σ(C3–C4) → σ*(C2–C9) transition. Among LP → π* interactions, LP(1) (N67) → π*(C24–C50) has the highest energy of 33.53 kcal/mol, whereas LP(2) (Cl75) → σ*(C22–C70) exhibits the lowest energy value of 0.52 kcal/mol.
In CC10D2, for the π → π* transition, strong intramolecular hyperconjugative interactions are observed in the π(C21–C68) → π*(C71–C72) transition, with the highest stabilization energy of 27.82 kcal/mol, whereas the π(C54–C55) → π*(C23–C81) transition has the lowest stabilization energy of 8.37 kcal/mol. Moreover, among σ → σ* transitions, σ(C1–C2) → σ*(C4–S7) has the highest energy value (8.63 kcal/mol) and σ(C6–S7) → σ*(C3–C4) has the least energy (0.51 kcal/mol). Among LP → π* transitions, LP(1) (N67) → π*(C51–C89) has the highest energy (37.60 kcal/mol), whereas LP(2) (O96) → σ*(C71–C72) has the lowest energy of 0.51 kcal/mol. In CC10D3, π → π* transitions exhibit the highest stabilization energy (23.01 kcal/mol) in π(C15–C16) → π*(C11–C14) transition, whereas π(C1–C2) → π*(C9–C10) exhibits the lowest energy (14.84 kcal/mol). The σ → σ* transition σ(C1–C2) → σ*(C4–S7) exhibits 8.64 kcal/mol as the highest stabilization energy, whereas σ(C6–S7) → σ*(C5–C6) exhibits the lowest energy value (0.51 kcal/mol). The LP → π* transitions have the highest value of 33.40 kcal/mol for the LP(1) (N67) → π*(C24–C50) transition and the lowest value (0.51 kcal/mol) for the LP(2)(F97) → σ*(C21–C68) transition. In CC10D4, the important π → π* electron transition exhibits the highest stability value (24.66 kcal/mol) for π(C21–C22) → π*(C70–C72), whereas π(C54–C55) → π*(C23–C81) has the lowest stabilization energy (8.41 kcal/mol). Furthermore, for σ → σ* transitions, the highest energy in σ(C55–C58) → σ*(C58–N59) is observed to be 8.38 kcal/mol, whereas the lowest energy in σ(C3–C4) → σ*(C2–C9) is observed to be 0.52 kcal/mol. Among other LP → π* transitions, an even higher value of 33.30 kcal/mol is observed for LP(1)(N67) → π*(C24–C50) transition, whereas the least value of 5.76 kcal/mol is observed for LP(2) (O95) → σ*(S96–O99) transition. For CC10D5, the π → π* transition having the highest interaction energy (22.86 kcal/mol) is observed in the π(C15–C16) → π*(C11–C14) transition, whereas the π(C5–C6) → π*(C3–C4) transition is observed to have the lowest interaction energy of 14.52 kcal/mol. The σ(C81–H82) → σ*(C23–C54) transition has the highest energy of 9.05 kcal/mol, whereas the σ(C6–S7) → σ*(C3–C4) transition is of the lowest energy (0.50 kcal/mol). The LP → π* transition LP(2) (O93) → π*(C91–O92) has the highest interaction energy (47.07 kcal/mol) and LP(1) (N67) → σ*(S18–C34) is noted to have the lowest energy of 10.49 kcal/mol.
For CC10D6, the strongest hyperconjugative interaction within the molecule is observed between π → π*, with the highest energy contributions (24.97 kcal/mol) during the π(C2–S8) → π*(C2–C9) transition, whereas the lowest energy contribution (13.37 kcal/mol) is observed in the π(C80–C84) → π*(C15–C16) transition. However, among σ → σ* transitions, the highest energy is observed for σ(C72–C91) → σ*(C91–N92) (8.93 kcal/mol), whereas the lowest energy (0.51 kcal/mol) is observed for the σ(C6–S7) → σ*(C3–C4) transition. For LP → π* transitions, the highest energy found for LP(1) (N67) → π*(C24–C50) is 33.42 kcal/mol and the lowest energy observed for LP(1) (N67) → σ* (S18–C84) is 10.69 kcal/mol. In CC10D7, the important π → π* electron transition with the highest stabilization energy (23.65 kcal/mol) is observed in the π(C19–C20) → π*(C54–C55) transition and the lowest stabilization energy (13.13 kcal/mol) is observed in the π(C75–C78) → π*(C15–C16) transition. Meanwhile, among σ → σ* transitions, σ(C76–H77) → σ*(C23–C54) has the highest stabilization energy (9.02 kcal/mol) and σ(C3–C4) → σ*(C2–C9) has the lowest stabilization energy (0.50 kcal/mol). However, among LP → π* transitions, the highest stabilization energy is observed in LP1(N67) → π*(C24–C50) (33.57 kcal/mol), whereas the least value is observed in the LP1(N67) → σ*(S18–C78) transition (10.95 kcal/mol). For CC10D8, a strong intramolecular hyperconjugative π → π* interaction with the highest stabilization energy (24.15 kcal/mol) is observed in the π(C19–C20) → π*(C54–C55) transition. The π(C1–C2) → π*(C1–C2) transition is found to have the lowest stabilization energy of 0.51 kcal/mol, whereas the σ(C1–C2) → σ*(C4–S7) transition has the highest stabilization energy of 8.57 kcal/mol and σ(C1–C2) → σ*(C2–S8) has the lowest stabilization energy (0.60 kcal/mol). However, LP → π* has the highest value of 33.55 kcal/mol for the LP(1)(N67) → π*(C24–C50) transition, whereas the lowest value (10.64 kcal/mol) is calculated in the LP1(N67) → σ*(S18–C78) transition. Many other significant transitions are also noted in CC10R and CC10D1–CC10D8, which are presented in Tables S20–S28. Consequently, the NBO investigation of the aforementioned compounds showed that the enhancement in hyperconjugation and large intramolecular charge transfer play significant roles in stabilizing these investigated compounds. Moreover, it enhances CT characteristics that are vital for an NLO response.
Transition Density Matrix (TDMs) and Excitation Binding Energy (Eb)
The transition density matrix analysis is extensively used to understand the extent of transitions and their nature in the studied compounds. The electron excitation, extensive interactions between D and A species, and the electron–hole localization can be determined by TDM calculations.29 The TDM heat maps of CC10R and CC10D1–CC10D8 were determined by TDDFT computations at the M06 functional. In the present study, the influence of H atoms was neglected by default due to the very small contribution. The TDM diagrams of all investigated species demonstrate the nature of transitions in the aforementioned compounds, and the outcomes are shown in Figure 6. For the abovementioned analysis, we divided the reference CC10R into two parts, the donor and the acceptor, whereas the newly designed compounds (CC10D1–CC10D8) were divided into three parts, i.e., the donor, the π-bridge, and the acceptor.
Figure 6.
TDM graphs of the reference (CC10R) and the designed molecules (CC10D1–CC10D8).
The TDM maps demonstrated that in CC10R, charge is transferred diagonally, which is located mainly in the acceptor blocks. In the newly designed molecules, minor charge coherence was seen in the π-bridge and the majority in the acceptor unit. A remarkable diagonal transfer of electron charge was obtained in modulated CC10D1–CC10D8 molecules. The behavior and attributes of electron accumulation in the entitled compounds confirmed that the charge coherence shifts successfully from the donor via the π-bridge to the acceptor, as displayed by the green and red dots on the heat map. No charge was observed on the D unit, whereas a small amount of charge was observed on the π-bridge and a denser electron cloud was seen on A segments, which indicated significant transfer of density without any tapping. It also demonstrated that the coupling of electrons of all modulated species (CC10D1–CC10D8) may be lower than that of the reference molecule, but it could show very high and easy excitation dissociation in the excited state. Figure 6 illustrates the TDM functionality and charge distribution. Another significant and promising factor to estimate optoelectronic properties is the binding energy, which helps in finding the excitation dissociation potential.43 The binding energy (Eb) values of CC10R and CC10D1–CC10D8 compounds were calculated by eq 2:
| 2 |
Here, EH–L shows the energy gap between HOMO and LUMO. Eopt designates the least energy required for the first excitation, which is attained from S0 to S1, the first singlet excited state energy, by creating a pair of hole and electron.44 These computed results achieved for Eb values of CC10R and CC10D1–CC10D8 are tabulated in Table 4. The binding energy for CC10R was calculated to be 0.583 eV and the binding energies of CC10D1–CC10D8 were 0.556, 0.509, 0.542, 0.524, 0.554, 0.521, 0.583, and 0.575 eV, respectively.
Table 4. Computed HOMO–LUMO Band Gap (EH–L), Binding Energies (EB), and First Singlet Excited State Energies (EOpt) of the Investigated Compounds (CC10R and CC10D1–CC10D8).
| compounds | EH–L(eV) | Eopt (eV) | Eb (eV) |
|---|---|---|---|
| CC10R | 2.319 | 1.736 | 0.583 |
| CC10D1 | 2.303 | 1.747 | 0.556 |
| CC10D2 | 2.093 | 1.584 | 0.509 |
| CC10D3 | 2.215 | 1.673 | 0.542 |
| CC10D4 | 2.123 | 1.599 | 0.524 |
| CC10D5 | 2.26 | 1.706 | 0.554 |
| CC10D6 | 2.155 | 1.634 | 0.521 |
| CC10D7 | 2.446 | 1.863 | 0.583 |
| CC10D8 | 2.434 | 1.859 | 0.575 |
The obtained results of binding energy show that the CC10D2 compound can be easily dissociated into separate charges and has a higher flow rate of charges due to the lowest binding energy. All modulated compounds (CC10D1–CC10D8) show greater charge dissociation efficiencies and have lower excitation binding energies (Eb) than CC10R, except for the CC10D7 molecule. The increasing pattern of binding energies for all investigated compounds is as follows: CC10D2 (0.509) < CC10D6 (0.521) < CC10D4 (0.524) < CC10D3 (0.542) < CC10D5 (0.554) < CC10D1 (0.556) < CC10D8 (0.575) < CC10D7 (0.583) = CC10R (0.583). These results of Eb values for CC10D1–CC10D8 modulated compounds are in good agreement with the results of TDM. To sum up, these designed molecules have the least binding energies, which support the high polarizability of the molecules, making them appropriate materials for use in the NLO field.
Nonlinear Optical (NLO) Properties
The NLO study progressed rapidly after the discovery of lasers and is considered as the most promising technology toward the advancement of several fields such as photonics, optoelectronics, and biomedicine.45 The basis for establishing an NLO response in organic compounds is the asymmetric polarization due to the push–pull architecture of the chromophore. An NLO response actually depends on the nature of the donor and acceptor moieties that are connected through a π-conjugation framework.11,46 The M06 functional with a 6-311G(d,p) basis set was used to attain the NLO parameters (first- and second-order hyperpolarizabilities) of CC10R and CC10D1–CC10D8. The dipole moment (μtotal), polarizability ⟨α⟩, first-order hyperpolarizability (βtotal), and second-order hyperpolarizability (γtotal.) of the entitled molecules are listed in Table 5, whereas their contributing tensors are displayed in Tables S29–S31.
Table 5. Computed μtotal, ⟨α⟩, βtotal, and γtotal. of the Studied Compounds CC10R and CC10D1–CC10D8a.
| compounds | μtotal | ⟨α⟩ | βtotal | γtotal. × 107 |
|---|---|---|---|---|
| CC10R | 1.789 | 2065.256 | 30 743.497 | 5.855 |
| CC10D1 | 5.063 | 1199.509 | 122 887.144 | 2.219 |
| CC10D2 | 11.944 | 1384.652 | 208 659.330 | 3.557 |
| CC10D3 | 7.549 | 1332.867 | 153 379.300 | 2.457 |
| CC10D4 | 10.760 | 1409.837 | 194 229.039 | 3.151 |
| CC10D5 | 4.783 | 1382.124 | 137 266.966 | 2.327 |
| CC10D6 | 12.607 | 1391.293 | 194 229.039 | 3.116 |
| CC10D7 | 4.284 | 1168.865 | 97 661.614 | 1.414 |
| CC10D8 | 4.925 | 1279.240 | 99 438.835 | 1.764 |
μtotal in Debye (D); ⟨α⟩, βtotal, and γtotal. are in a.u.
The dipole moment of the reference compound CC10R is 1.789 D, and all of the derivatives exhibited larger dipole moment values (4.284–12.607 D). This enhancement in μ might be due to the alteration of the configuration from A−π–A to D−π–A along with the introduction of strong electron-withdrawing units. The highest value of dipole moment is observed in CC10D6 and CC10D2, which might be due to the presence of powerful electron-withdrawing units (−CN and NO2). The dipole moment data reveal that for CC10R, CC10D1, CC10D2, CC10D3, CC10D4, and CC10D6, the greater polarity lies along the x axis, as indicated by the dominant values of μx (0.266982, 1.334516, 4.422983, 2.625636, 3.955706, and 4.700863 D, respectively), represented in Table S38. In CC10D5, CC10D7, and CC10D8, the larger polarizability is noted along the z-axis (μz = 1.381098, 1.647804, and 1.846368 D, respectively). Further, we also compared results with standard urea chromophores (μurea = 1.771145 D), and our derivatives exhibited better polarity than urea. In the case of ⟨α⟩, all of the designed compounds CC10D1–CC10D8 contain higher values of polarizability ⟨α⟩ (1199.509, 1384.652, 1332.867, 1409.837, 1382.124, 1391.293, 1168.865, and 1279.240 a.u.) than urea (32.29690 a.u.). Conversely, all derivatives exhibited comparable results of linear polarizability with reference to the chromophore. Nevertheless, CC10D7 shows the lowest ⟨α⟩ value of 1168.865 a.u. among the newly designed compounds, and the order of ⟨α⟩ for all studied compounds is as follows: CC10R > CC10D4 > CC10D6 > CC10D2 > CC10D5 > CC10D3 > CC10D8 > CC10D1 > CC10D7.
Among organic chromophores, the NLO behavior can be determined by the efficacy of CT toward the acceptor from the donor through their respective π-bridges. In brief, an increase in hyperpolarizability responses of the entitled chromophores emerges in alliance with the delocalization of π-electrons. This delocalization narrows down the HOMO/LUMO band gap. As stated in the literature, the polarizability of molecules is considerably influenced by the HOMO–LUMO band gap, i.e., the smaller the band gap, the larger the polarizability values and vice versa.7 The same property has been examined for the chromophores in our study, where compound CC10D2 showed the largest βtotal value, i.e., 208 659.330 a.u. with the smallest band gap, i.e., 2.093 eV. The first hyperpolarizability value of compound CC10R is 30 743.497 a.u., and all derivatives exhibited excellent results (97 661.614–208 659.330 a.u.) compared with the parent molecule because of the strong push–pull configuration. In addition, a systematic relationship is observed among the molecular structures and βtotal values. The βtotal parameter was usually enhanced with the extension of the conjugated system, and the strength of the attached “A” substituents such as chloro, fluoro, nitro, and cyano groups contributes to the nonlinearity of the chromophore. Among all of the designed compounds, the largest value of βtotal was noticed in CC10D2 (208 659.330 a.u.) as it has powerful electron-withdrawing units (−NO2) compared with other chromophores. A decrease in the value of βtotal was observed in CC10D6 and CC10D4 (194 229.039 a.u.) when the nitro groups were replaced by −CN and −SO3H groups. Further decrease in βtotal was determined when the −CN and −SO3H groups on the acceptor were replaced with moderate electron-withdrawing −CF3 units (βtotal = 153 379.300 a.u.), and a decrease in values (βtotal = 122 887.144 and 137 266.966 a.u.) was observed when the −CF3 unit was replaced with −Cl and −COOCH3 groups in CC10D1 and CC10D5, respectively. This might be due to the fact that along with the inductive effect (−I), these units also possessed a mesomeric effect (+M). Interestingly, a larger reduction in hyperpolarizability values was observed when MCM and MOC acceptors were utilized in CC10D7 and CC10D8 (βtotal = 97 661.614 and 99 438.835 a.u.). This might be due to the removal of the electronegative group along with the reduction of resonance (see Figure 2). In all derivatives, the major contribution to hyperpolarizability values was seen along the x axis as larger values of β were obtained beside the βxxx tensor (see Table S39), whereas the parent chromophore showed higher hyperpolarizability values along the xz axis (βxxz= 6538.550 a.u.). The aforementioned parameters also affect γtotal amplitudes for CC10D1–CC10D8.47 Among the derivatives, a larger value of γtotal. was noticed in CC10D2, and for all studied chromophores, a large second-order hyperpolarizability response was observed along the x axis, as shown in Table S40. The second-order hyperpolarizability (γtotal.) values of the abovementioned compounds in descending order are as follows: CC10R > CC10D2 > CC10D4 > CC10D6 > CC10D3 > CC10D5 > CC10D1 > CC10D8 > CC10D7. For a comparative examination, we also analyzed the NLO behavior of urea molecules used as the standard chromophore at MO6/6-311G(d,p), and the results are presented in Tables S38–S40. The first-order hyperpolarizability responses of CC10R and CC10D1–CC10D8 were 401.5616, 1605.112, 2725.44, 2003.391, 2536.957, 1792.936, 2536.957, 1275.624, and 1298.838 times greater than that of the urea, respectively. Similarly, the second-order hyperpolarizability responses were 18610, 7053.401, 11306.420, 7809.917, 10015.893, 7396.694, 9904.640, 4494.596, and 5607.120 times larger than that of the urea molecule, accordingly. This comparative analysis with urea proves CC10R and CC10D1–CC10D8 to be potential NLO materials, with compound CC10D2 being the most efficient among them. In addition, a conclusion of the abovementioned discussion is that different types of acceptors with π-conjugations play extraordinary roles in yielding notable NLO amplitudes.
Conclusions
In this study, a series of fullerene-free chromophores (CC10D1–CC10D8) with a D−π–A configuration were designed via various acceptor moieties with suitable electron-withdrawing characteristics and fixed π-spacers as well as donor groups. The attained electronic assets showed that chromophores with a D−π–A-type configuration exhibit more variation in the intact behavior of derivatives than the synthetic compounds with a A−π–A framework and have an excellent NLO response. The frontier molecular orbital (FMO) investigations detected a reduction in the band gap (2.093–2.303 eV) compared with the reference chromophore (2.319 eV), with broader absorption spectra. Further, the FMO analysis showed that an effective transfer of charge takes place from the donor to the acceptor through the π-bridge in derivatives due to the strong push–pull architecture compared with that of CC10R. This excellent transfer of the electron cloud is further supported by DOS and TDM heat maps. Moreover, NBO and GRP studies reveal that conjugation in chromophores leads to a higher stability of organic structures. Remarkably, smaller Eb (0.509–0.583 eV) with huge μtotal (12.607–4.284 D) were observed for the chromophores, which indicate a larger excitation dissociation and higher polarity. Interestingly, the NLO findings were noteworthy: βtotal and γtotal. values are found to be 208 659.330 a.u. and 3.557 × 107 a.u., respectively, for CC10D2, which is significantly greater that those of all investigated chromophores. Moreover, the comparative analysis with urea showed that the entitled chromophores exhibited excellent NLO responses. Hence, we can use the suitable properties of our derivatives to derive better NLO responses. The CC10D1–CC10D8 derivatives may fascinate researchers in the field of synthetic chemistry. In addition, it is concluded from our above analyses that the aforementioned NF-based NLO molecules with a D−π–A configuration might show brilliant properties suitable for optoelectronics-associated hitech applications.
Computational Procedure
In the current investigation, DFT computations were employed to estimate the nonlinear optical properties of CC10R and CC10D1–CC10D8 having a D−π–A configuration. The computational studies of the abovementioned chromophores were executed at the M06/6-311G(d,p) level with the help of Gaussian 09 program package.48 To perform the natural bond orbital (NBO) analysis, NBO 3.1 program package was utilized by applying the aforementioned functional of DFT.7 The NLO analysis was also performed at the same level. The FMO analysis, transition density matrix (TDM), and UV–vis spectral analysis were calculated by TD–DFT at the same level. Further, with the help of HOMO and LUMO energies, global reactivity parameters (GRPs) were determined to understand the reactivity of the entitled chromophores. Moreover, GaussView 5.0 package,49 Avogadro,50 and Chemcraft51 were used to interpret the results from output files. The dipole moment was calculated using eq 3:52
| 3 |
The polarizability ⟨α⟩ and first hyperpolarizability (βtotal) were calculated using eqs 4 and 5, respectively. We obtained six linear polarizability tensors (αxx + αyy + αzz + αxy + αxz + αyz) and ten hyperpolarizability tensors (βxxx, βxyy, βxzz, βyyy, βxxy, βyzz, βzzz, βxxz, βyyz, βxyz) from Gaussian output files along the x, y, and z coordinates.53
| 4 |
| 5 |
The second hyperpolarizability was calculated using eq 6.53
| 6 |
Acknowledgments
The authors are thankful for the cooperation and collaboration of A.A.C.B from IQ-USP, Brazile, especially for his continuous support and for providing computational lab facilities. M.I appreciates the Deanship of scientific research at King Khalid University is greatly appreciated for funding this work under grant no: R.G.P-2/ 62/43.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c02052.
Geometrical parameters (bond lengths and bond angles), UV–vis data (wavelengths, excitation energies, and oscillator strengths), NBO analysis, optimized geometries with IUPAC names, dipole moments, linear polarizabilities with major contributing tensors, first (βtot) and second (γtot) hyperpolarizabilities with their contributing tensors of the reported compounds, calculated using M06/6-311G(d,p) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Karakaş A.; Elmali A.; Ünver H.; Svoboda I. Nonlinear optical properties, synthesis, structures and spectroscopic studies of N-(4-nitrobenzylidene)-o-fluoroamine and N-(3-nitrobenzylidene)-p-fluoroamine. Spectrochim. Acta, Part A 2005, 61, 2979–2987. 10.1016/j.saa.2004.11.011. [DOI] [PubMed] [Google Scholar]
- a Ghiasuddin; Akram M.; Adeel M.; Khalid M.; Tahir M. N.; Khan M. U.; Asghar M. A.; Ullah M. A.; Iqbal M. A combined experimental and computational study of 3-bromo-5-(2, 5-difluorophenyl) pyridine and 3, 5-bis (naphthalen-1-yl) pyridine: Insight into the synthesis, spectroscopic, single crystal XRD, electronic, nonlinear optical and biological properties. J. Mol. Struct. 2018, 1160, 129–141. 10.1016/j.molstruc.2018.01.100. [DOI] [Google Scholar]; b Ahmad M. S.; Khalid M.; Shaheen M. A.; Tahir M. N.; Khan M. U.; Braga A. A. C.; Shad H. A. Synthesis and XRD, FT-IR vibrational, UV–vis, and nonlinear optical exploration of novel tetra substituted imidazole derivatives: A synergistic experimental-computational analysis. J. Phys. Chem. Solids 2018, 115, 265–276. 10.1016/j.jpcs.2017.12.054. [DOI] [Google Scholar]
- a Datta A. Role of metal ions (M= Li+, Na+, and K+) and pore sizes (Crown-4, Crown-5, and Crown-6) on linear and nonlinear optical properties: New materials for optical birefringence. J. Phys. Chem. C 2009, 113, 3339–3344. 10.1021/jp810198n. [DOI] [Google Scholar]; b Datta A.; Pati S. K. Dipolar interactions and hydrogen bonding in supramolecular aggregates: understanding cooperative phenomena for 1st hyperpolarizability. Chem. Soc. Rev. 2006, 35, 1305–1323. 10.1039/b605478a. [DOI] [PubMed] [Google Scholar]
- Ivanova B. B.; Spiteller M. Possible application of the organic barbiturates as NLO materials. Cryst. Growth Des. 2010, 10, 2470–2474. 10.1021/cg100284r. [DOI] [Google Scholar]
- a Wadsworth A.; Moser M.; Marks A.; Little M. S.; Gasparini N.; Brabec C. J.; Baran D.; McCulloch I. Critical review of the molecular design progress in non-fullerene electron acceptors towards commercially viable organic solar cells. Chem. Soc. Rev. 2019, 48, 1596–1625. 10.1039/C7CS00892A. [DOI] [PubMed] [Google Scholar]; b Guldi D. M. Fullerenes: three dimensional electron acceptor materials. Chem. Commun. 2000, 5, 321–327. 10.1039/a907807j. [DOI] [Google Scholar]
- a Arshad M. N.; Shafiq I.; Khalid M.; Asiri A. M.. Exploration of the Intriguing Photovoltaic Behavior for Fused Indacenodithiophene-Based A–D–A Conjugated Systems: A DFT Model Study. ACS Omega. 20227 10.1021/acsomega.1c06219. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Lin Y.; Zhan X. Non-fullerene acceptors for organic photovoltaics: an emerging horizon. Mater. Horiz. 2014, 1, 470–488. 10.1039/C4MH00042K. [DOI] [Google Scholar]
- Khalid M.; Lodhi H. M.; Khan M. U.; Imran M. Structural parameter-modulated nonlinear optical amplitude of acceptor−π–D−π–donor-configured pyrene derivatives: A DFT approach. RSC Adv. 2021, 11, 14237–14250. 10.1039/D1RA00876E. [DOI] [Google Scholar]
- a Prasad P. N.; Williams D. J.. Introduction to Nonlinear Optical Effects in Molecules and Polymers; Wiley: New York, 1991; Vol. 1. [Google Scholar]; b Zyss J.; Chemla D. S.. Nonlinear optical properties of organic molecules and crystals, chapter II-1. In Quantum Electronics—Principles and Applications; Academic Press, Inc.: New York, 1987; pp 222–223. [Google Scholar]
- a Janjua M. R. S. A.; Jamil S.; Ahmad T.; Yang Z.; Mahmood A.; Pan S. Quantum chemical perspective of efficient NLO materials based on dipolar trans-tetraammineruthenium (II) complexes with pyridinium and thiocyanate ligands: First theoretical framework. Comput. Theor. Chem. 2014, 1033, 6–13. 10.1016/j.comptc.2014.01.031. [DOI] [Google Scholar]; b Janjua M. R. S. A.; Jamil S.; Mahmood A.; Zafar A.; Haroon M.; Bhatti H. N. Solvent-Dependent Non-Linear Optical Properties of 5, 5′-Disubstituted-2, 2′-bipyridine Complexes of Ruthenium (ii): A Quantum Chemical Perspective. Aust. J. Chem. 2015, 68, 1502–1507. 10.1071/CH14736. [DOI] [Google Scholar]; c Janjua M. R. S. A. Quantum mechanical design of efficient second-order nonlinear optical materials based on heteroaromatic imido-substituted hexamolybdates: First theoretical framework of POM-based heterocyclic aromatic rings. Inorg. Chem. 2012, 51, 11306–11314. 10.1021/ic3002652. [DOI] [PubMed] [Google Scholar]; d Janjua M. R. S. A.; Yamani Z. H.; Jamil S.; Mahmood A.; Ahmad I.; Haroon M.; Tahir M. H.; Yang Z.; Pan S. First principle study of electronic and non-linear optical (NLO) properties of triphenylamine dyes: Interactive design computation of new NLO compounds. Aust. J. Chem. 2016, 69, 467–472. 10.1071/CH15402. [DOI] [Google Scholar]; e Janjua M. R. S. A.; Mahmood A.; Nazar M. F.; Yang Z.; Pan S. Electronic absorption spectra and nonlinear optical properties of ruthenium acetylide complexes: a DFT study toward the designing of new high NLO response compounds. Acta Chim. Slov. 2014, 61, 382–390. [PubMed] [Google Scholar]; f Yang P.; Zhu Z.; Chen M.; Zhou X.; Chen W. Microwave-assisted synthesis of polyamine-functionalized carbon dots from xylan and their use for the detection of tannic acid. Spectrochim. Acta, Part A 2019, 213, 301–308. 10.1016/j.saa.2019.01.043. [DOI] [PubMed] [Google Scholar]; g Wielopolski M.; Kim J.-H.; Jung Y.-S.; Yu Y.-J.; Kay K.-Y.; Holcombe T. W.; Zakeeruddin S. M.; Grätzel M.; Moser J.-E. Position-dependent extension of π-conjugation in D−π–A dye sensitizers and the impact on the charge-transfer properties. J. Phys. Chem. C 2013, 117, 13805–13815. 10.1021/jp402411h. [DOI] [Google Scholar]; h Katono M.; Wielopolski M.; Marszalek M.; Bessho T.; Moser J.-E.; Humphry-Baker R.; Zakeeruddin S. M.; Grätzel M. Effect of extended π-conjugation of the donor structure of organic D–a– π–A dyes on the photovoltaic performance of dye-sensitized solar cells. J. Phys. Chem. C 2014, 118, 16486–16493. 10.1021/jp411504p. [DOI] [Google Scholar]
- Mahmood A.; Khan S. U. D.; Rana U. A.; Janjua M. R. S. A.; Tahir M. H.; Nazar M. F.; Song Y. Effect of thiophene rings on UV/visible spectra and non-linear optical (NLO) properties of triphenylamine based dyes: a quantum chemical perspective. J. Phys. Org. Chem. 2015, 28, 418–422. 10.1002/poc.3427. [DOI] [Google Scholar]
- Janjua M. R. S. A.; Khan M. U.; Bashir B.; Iqbal M. A.; Song Y.; Naqvi S. A. R.; Khan Z. A. Effect of π-conjugation spacer (CC) on the first hyperpolarizabilities of polymeric chain containing polyoxometalate cluster as a side-chain pendant: A DFT study. Comput. Theor. Chem. 2012, 994, 34–40. 10.1016/j.comptc.2012.06.011. [DOI] [Google Scholar]
- Panneerselvam M.; Kathiravan A.; Solomon R. V.; Jaccob M. The role of π-linkers in tuning the optoelectronic properties of triphenylamine derivatives for solar cell applications–A DFT/TDDFT study. Phys. Chem. Chem. Phys. 2017, 19, 6153–6163. 10.1039/C6CP07768D. [DOI] [PubMed] [Google Scholar]
- Yao C.; Yang Y.; Li L.; Bo M.; Zhang J.; Peng C.; Huang Z.; Wang J. Elucidating the key role of the cyano (−C≡N) group to construct environmentally friendly fused-ring electron acceptors. J. Phys. Chem. C 2020, 124, 23059–23068. 10.1021/acs.jpcc.0c08022. [DOI] [Google Scholar]
- Yao C.; Yang Y.; Li L.; Bo M.; Peng C.; Huang Z.; Wang J. Replacing the cyano (−C≡N) group to design environmentally friendly fused-ring electron acceptors. Phys. Chem. Chem. Phys. 2021, 23, 18085–18092. 10.1039/D1CP02566J. [DOI] [PubMed] [Google Scholar]
- Yao C.; Peng C.; Yang Y.; Li L.; Bo M.; Wang J. Elucidating the key role of fluorine in improving the charge mobility of electron acceptors for non-fullerene organic solar cells by multiscale simulations. J. Mater. Chem. C 2018, 6, 4912–4918. 10.1039/C8TC01315B. [DOI] [Google Scholar]
- Yao C.; Yang Y.; Li L.; Bo M.; Peng C.; Wang J. Quad-rotor-shaped non-fullerene electron acceptor materials with potential to enhance the photoelectric performance of organic solar cells. J. Mater. Chem. A 2019, 7, 18150–18157. 10.1039/C9TA04084F. [DOI] [Google Scholar]
- Jiao C.; Guo Z.; Sun B.; Yi Y.-q.-q.; Meng L.; Wan X.; Zhang M.; Zhang H.; Li C.; Chen Y. An acceptor–donor–acceptor type non-fullerene acceptor with an asymmetric backbone for high performance organic solar cells. J. Mater. Chem. C 2020, 8, 6293–6298. 10.1039/D0TC00981D. [DOI] [Google Scholar]
- Khalid M.; Ali A.; Rehman M. F. U.; Mustaqeem M.; Ali S.; Khan M. U.; Asim S.; Ahmad N.; Saleem M. Exploration of noncovalent interactions, chemical reactivity, and nonlinear optical properties of piperidone derivatives: a concise theoretical approach. ACS Omega 2020, 5, 13236–13249. 10.1021/acsomega.0c01273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uzun S.; Esen Z.; Koç E.; Usta N. C.; Ceylan M. Experimental and density functional theory (MEP, FMO, NLO, Fukui functions) and antibacterial activity studies on 2-amino-4-(4-nitrophenyl)-5, 6-dihydrobenzo [h] quinoline-3-carbonitrile. J. Mol. Struct. 2019, 1178, 450–457. 10.1016/j.molstruc.2018.10.001. [DOI] [Google Scholar]
- Pearson R. G. Absolute electronegativity and hardness correlated with molecular orbital theory. Proc. Natl. Acad. Sci. U.S.A. 1986, 83, 8440–8441. 10.1073/pnas.83.22.8440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Khalid M.; Ali M.; Aslam M.; Sumrra S. H.; Khan M. U.; Raza N.; Kumar N.; Imran M. Frontier molecular, Natural bond orbital, UV-Vis spectral stduy, Solvent influence on geometric parameters, Vibrational frequencies and solvation energies of 8-Hydroxyquinoline. Int. J. Pharm. Sci. Res. 2017, 8, 13040. 10.13040/IJPSR.0975-8232.8(2).457-69. [DOI] [Google Scholar]; b Prashanth J.; Ramesh G.; Naik J. L.; Ojha J. K.; Reddy B. V. Molecular geometry, NBO analysis, Hyperpolarizability and HOMO-LUMO energies of 2-azido-1-phenylethanone using Quantum chemical calculations. Mater. Today: Proc. 2016, 3, 3761–3769. 10.1016/j.matpr.2016.11.025. [DOI] [Google Scholar]
- a Janjua M. R. S. A. Prediction and Understanding: Quantum Chemical Framework of Transition Metals Enclosed in a B12N12 Inorganic Nanocluster for Adsorption and Removal of DDT from the Environment. Inorg. Chem. 2021, 60, 10837–10847. 10.1021/acs.inorgchem.1c01760. [DOI] [PubMed] [Google Scholar]; b Janjua M. R. S. A. How does bridging core modification alter the photovoltaic characteristics of triphenylamine-based hole transport materials? Theoretical understanding and prediction. Chem. – Eur. J. 2021, 27, 4197–4210. 10.1002/chem.202004299. [DOI] [PubMed] [Google Scholar]
- a Streitwieser A.; Salzberg H. Molecular orbital theory for organic chemists. J. Electrochem. Soc. 1962, 109, 116C. 10.1149/1.2425396. [DOI] [Google Scholar]; b Fukui K. Role of frontier orbitals in chemical reactions. Science 1982, 218, 747–754. 10.1126/science.218.4574.747. [DOI] [PubMed] [Google Scholar]
- Koparir M.; Orek C.; Koparir P.; Sarac K. Synthesis, experimental, theoretical characterization and biological activities of 4-ethyl-5-(2-hydroxyphenyl)-2H-1, 2, 4-triazole-3 (4H)-thione. Spectrochim. Acta, Part A 2013, 105, 522–531. 10.1016/j.saa.2012.12.052. [DOI] [PubMed] [Google Scholar]
- Haroon M.; Janjua M. R. S. A. Prediction of NLO response of substituted organoimido hexamolybedate: First theoretical framework based on p-anisidine adduct [Mo6O18 (p-MeOC6H4N)] 2. Mater. Today Commun. 2021, 26, 101880. 10.1016/j.mtcomm.2020.101880. [DOI] [Google Scholar]
- Katariya S.; Rhyman L.; Alswaidan I. A.; Ramasami P.; Sekar N. Triphenylamine-based fluorescent styryl dyes: DFT, TD–DFT and non-linear optical property study. J. Fluoresc. 2017, 27, 993–1007. 10.1007/s10895-017-2034-1. [DOI] [PubMed] [Google Scholar]
- Khalid M.; Khan M. U.; Azhar N.; Arshad M. N.; Asiri A. M.; Braga A. A. C.; Akhtar M. N. Exploration of nonlinear optical enhancement and interesting optical behavior with pyrene moiety as the conjugated donor and efficient modification in acceptor moieties. Opt. Quantum Electron. 2022, 54 (7), 1–21. 10.1007/s11082-022-03782-w. [DOI] [Google Scholar]
- a Khalid M.; Shafiq I.; Zhu M.; Khan M. U.; Shafiq Z.; Iqbal J.; Alam M. M.; Braga A. A. C.; Imran M. Efficient tuning of small acceptor chromophores with A1-π–A2-π–A1 configuration for high efficacy of organic solar cells via end group manipulation. J. Saudi Chem. Soc. 2021, 25, 101305. 10.1016/j.jscs.2021.101305. [DOI] [Google Scholar]; b Ans M.; Iqbal J.; Eliasson B.; saif M. J.; Ayub K. Opto-electronic properties of non-fullerene fused-undecacyclic electron acceptors for organic solar cells. Comput. Mater. Sci. 2019, 159, 150–159. 10.1016/j.commatsci.2018.12.009. [DOI] [Google Scholar]
- Ans M.; Iqbal J.; Ahmad Z.; Muhammad S.; Hussain R.; Eliasson B.; Ayub K. Designing Three-dimensional (3D) Non-Fullerene Small Molecule Acceptors with Efficient Photovoltaic Parameters. ChemistrySelect 2018, 3, 12797–12804. 10.1002/slct.201802732. [DOI] [Google Scholar]
- Lu T.; Chen F. Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Rahmalia W.; Fabre J.-F.; Usman T.; Mouloungui Z. Aprotic solvents effect on the UV–visible absorption spectra of bixin. Spectrochim. Acta, Part A 2014, 131, 455–460. 10.1016/j.saa.2014.03.119. [DOI] [PubMed] [Google Scholar]
- Kamlet M. J.; Abboud J. L.; Taft R. The solvatochromic comparison method. 6. The. pi.* scale of solvent polarities. J. Am. Chem. Soc. 1977, 99, 6027–6038. 10.1021/ja00460a031. [DOI] [Google Scholar]
- Adeoye M. D.; Adeogun A. I.; Adewuyi S.; Ahmed S. A.; Odozi N. W.; Obi-Egbeedi N. O. Effect of solvents on the electronic absorption spectra of 9, 14 dibenzo (a, c) phenazine and tribenzo (a, c, i) phenazine. Sci. Res. Essays 2009, 4, 107–111. 10.5897/SRE.9000408. [DOI] [Google Scholar]
- a Ans M.; Ayub K.; Muhammad S.; Iqbal J. Development of fullerene free acceptors molecules for organic solar cells: A step way forward toward efficient organic solar cells. Comput. Theor. Chem. 2019, 1161, 26–38. 10.1016/j.comptc.2019.06.003. [DOI] [Google Scholar]; b Khalid M.; Ali A.; Jawaria R.; Asghar M. A.; Asim S.; Khan M. U.; Hussain R.; ur Rehman M. F.; Ennis C. J.; Akram M. S. First principles study of electronic and nonlinear optical properties of A–D−π–A and D–A–D−π–A configured compounds containing novel quinoline–carbazole derivatives. RSC Adv. 2020, 10, 22273–22283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parr R. G.; Pearson R. G. Absolute hardness: companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. 10.1021/ja00364a005. [DOI] [Google Scholar]
- Parr R. G.; Donnelly R. A.; Levy M.; Palke W. E. Electronegativity: the density functional viewpoint. J. Chem. Phys. 1978, 68, 3801–3807. 10.1063/1.436185. [DOI] [Google Scholar]
- Chattaraj P. K.; Roy D. R. Update 1 of: electrophilicity index. Chem. Rev. 2007, 107, PR46–PR74. 10.1021/cr078014b. [DOI] [Google Scholar]
- Khalid M.; Khan M. U.; Shafiq I.; Hussain R.; Mahmood K.; Hussain A.; Jawaria R.; Hussain A.; Imran M.; Assiri M. A.; et al. NLO potential exploration for D−π–A heterocyclic organic compounds by incorporation of various π-linkers and acceptor units. Arab. J. Chem. 2021, 14, 103295. 10.1016/j.arabjc.2021.103295. [DOI] [Google Scholar]
- Weinhold F.; Landis C. R. Natural bond orbitals and extensions of localized bonding concepts. Chem. Educ. Res. Pract. 2001, 2, 91–104. 10.1039/B1RP90011K. [DOI] [Google Scholar]
- a Khalid M.; Ali A.; Khan M. U.; Tahir M. N.; Ahmad A.; Ashfaq M.; Hussain R.; de Alcântara Morais S. F.; Braga A. A. C. Non-covalent interactions abetted supramolecular arrangements of N-Substituted benzylidene acetohydrazide to direct its solid-state network. J. Mol. Struct. 2021, 1230, 129827. 10.1016/j.molstruc.2020.129827. [DOI] [Google Scholar]; b Pasha A. R.; Khalid M.; Shafiq Z.; Khan M. U.; Naseer M. M.; Tahir M. N.; Hussain R.; Braga A. A. C.; Jawaria R. A comprehensive study of structural, non-covalent interactions and electronic insights into N-aryl substituted thiosemicarbazones via SC-XRD and first-principles DFT approach. J. Mol. Struct. 2021, 1230, 129852. 10.1016/j.molstruc.2020.129852. [DOI] [Google Scholar]
- Gokula Krishnan K.; Krishnan K. G.; Sivakumar R.; Thanikachalam V.; Saleem H. Synthesis, spectroscopic investigation and computational study of 3-(1-(((methoxycarbonyl) oxy) imino) ethyl)-2H-chromen-2-one. Spectrochim. Acta, Part A 2015, 144, 29–42. 10.1016/j.saa.2015.02.021. [DOI] [PubMed] [Google Scholar]
- Glendening E. D.; Landis C. R.; Weinhold F. Natural bond orbital methods. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 1–42. 10.1002/wcms.51. [DOI] [Google Scholar]
- Köse M. E. Evaluation of acceptor strength in thiophene coupled donor–acceptor chromophores for optimal design of organic photovoltaic materials. J. Phys. Chem. A 2012, 116, 12503–12509. 10.1021/jp309950f. [DOI] [PubMed] [Google Scholar]
- a Naeem M.; Jabeen S.; Khera R. A.; Mubashar U.; Iqbal J. Tuning of optoelectronic properties of triphenylamines-based donor materials for organic solar cells. J. Theor. Comput. Chem. 2019, 18, 1950036. 10.1142/S0219633619500366. [DOI] [Google Scholar]; b Dkhissi A. Excitons in organic semiconductors. Synth. Met. 2011, 161, 1441–1443. 10.1016/j.synthmet.2011.04.003. [DOI] [Google Scholar]
- a Hakim N. Z.; Saleh B. E.; Teich M. C. Signal-to-noise ratio for lightwave systems using avalanche photodiodes. J. Lightwave Technol. 1991, 9, 318–320. 10.1109/50.70006. [DOI] [Google Scholar]; b Raju T. S.; Panigrahi P. K.; Porsezian K. Nonlinear compression of solitary waves in asymmetric twin-core fibers. Phys. Rev. E 2005, 71, 026608 10.1103/PhysRevE.71.026608. [DOI] [PubMed] [Google Scholar]
- a Khan M. U.; Khalid M.; Ibrahim M.; Braga A. A. C.; Safdar M.; Al-Saadi A. A.; Janjua M. R. S. A. First theoretical framework of triphenylamine–dicyanovinylene-based nonlinear optical dyes: structural modification of π-linkers. J. Phys. Chem. C 2018, 122, 4009–4018. 10.1021/acs.jpcc.7b12293. [DOI] [Google Scholar]; b Khan M. U.; Ibrahim M.; Khalid M.; Jamil S.; Al-Saadi A. A.; Janjua M. R. S. A. Quantum chemical designing of indolo [3, 2, 1-jk] carbazole-based dyes for highly efficient nonlinear optical properties. Chem. Phys. Lett. 2019, 719, 59–66. 10.1016/j.cplett.2019.01.043. [DOI] [Google Scholar]; c Khan M. U.; Ibrahim M.; Khalid M.; Braga A. A. C.; Ahmed S.; Sultan A. Prediction of second-order nonlinear optical properties of D−π–A compounds containing novel fluorene derivatives: a promising route to giant hyperpolarizabilities. J. Cluster Sci. 2019, 30, 415–430. 10.1007/s10876-018-01489-1. [DOI] [Google Scholar]; d Janjua M. R. S. A.; Amin M.; Ali M.; Bashir B.; Khan M. U.; Iqbal M. A.; Guan W.; Yan L.; Su Z. M. A DFT Study on The Two-Dimensional Second-Order Nonlinear Optical (NLO) Response of Terpyridine-Substituted Hexamolybdates: Physical Insight on 2D Inorganic–Organic Hybrid Functional Materials. Eur. J. Inorg. Chem. 2012, 2012, 705–711. 10.1002/ejic.201101092. [DOI] [Google Scholar]
- Saeed A.; Muhammad S.; Rehman S.-u.; Bibi S.; Al-Sehemi A. G.; Khalid M. Exploring the impact of central core modifications among several push-pull configurations to enhance nonlinear optical response. J. Mol. Graphics Modell. 2020, 100, 107665. 10.1016/j.jmgm.2020.107665. [DOI] [PubMed] [Google Scholar]
- Frisch M.; Trucks G.; Schlegel H.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Petersson G.; Nakatsuji H.. Gaussian 16; Gaussian, Inc.: Wallingford, CT, 2016.
- Dennington R.; Keith T.; Millam J.. GaussView 5.0; Gaussian. Inc.: Wallingford, 2008.
- Hanwell M. D.; Curtis D. E.; Lonie D. C.; Vandermeersch T.; Zurek E.; Hutchison G. R. Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. J. Cheminf. 2012, 4, 17 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhurko G.Chemcraft. http://www.chemcraftprog.com rec. 22 October, 2014.
- Ullah F.; Ayub K.; Mahmood T. Remarkable second and third order nonlinear optical properties of organometallic C 6 Li 6–M 3 O electrides. New J. Chem. 2020, 44, 9822–9829. 10.1039/D0NJ01670E. [DOI] [Google Scholar]
- Kromann J. C.; Steinmann C.; Jensen J. H. Improving solvation energy predictions using the SMD solvation method and semiempirical electronic structure methods. J. Chem. Phys. 2018, 149, 104102. 10.1063/1.5047273. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.