Abstract
The world has faced the COVID-19 pandemic for over two years now, and it is time to revisit the lessons learned from lockdown measures for theoretical and practical epidemiological improvements. The interlink between these measures and the resulting change in mobility (a predictor of the disease transmission contact rate) is uncertain. We thus propose a new method for assessing the efficacy of various non-pharmaceutical interventions (NPI) and examine the aptness of incorporating mobility data for epidemiological modelling. Facebook mobility maps for the United Arab Emirates are used as input datasets from the first infection in the country to mid-Oct 2020. Dataset was limited to the pre-vaccination period as this paper focuses on assessing the different NPIs at an early epidemic stage when no vaccines are available and NPIs are the only way to reduce the reproduction number (). We developed a travel network density parameter to provide an estimate of NPI impact on mobility patterns. Given the infection-fatality ratio and time lag (onset-to-death), a Bayesian probabilistic model is adapted to calculate the change in epidemic development with . Results showed that the change in clearly impacted . The three lockdowns strongly affected the growth of transmission rate and collectively reduced by 78% before the restrictions were eased. The model forecasted daily infections and deaths by 2% and 3% fractional errors. It also projected what-if scenarios for different implementation protocols of each NPI. The developed model can be applied to identify the most efficient NPIs for confronting new COVID-19 waves and the spread of variants, as well as for future pandemics.
Keywords: Non-pharmaceutical interventions, COVID-19, Epidemiological modelling, Mobility maps
1. Introduction
The rapid global spread of COVID-19 has resulted in a wide range of strategic non-pharmaceutical interventions (NPI) by various governments to suppress the transmission rate (Flaxman et al., 2020). These target social distancing towards limiting mobility (work-at-home initiatives, banning or limiting public events, travel restrictions, closure of schools and universities, limiting internal traffic, quarantine of symptomatic/contact individuals, etc.). The nature and extent of these measures are substantially varied between countries depending upon the intervention readiness (i.e., how quick was it applied), nature of the application, adoption rate and enforcement level (Bryant & Elofsson, 2020). Before the rollout of vaccines, NPIs are the primary strategy to control disease spread by achieving behavioural changes in the mobility patterns of the local populace. In this context, analysing pre-vaccination epidemic data is critical to assess the efficacy of different NPIs at an early stage of a pandemic when these are the only way to reduce epidemic spread. The performance analysis of NPIs implementation provides an opportunity to make decisions for the continuous battle against COVID-19 and its variants as well as the future pandemics.
The present literature analysing NPIs effect on COVID-19 spread largely varies by the type of epidemiological model from the classic compartmental to agent-based, statistical and metapopulation models––using different types of data (Perra, 2021). All these models (Huang et al., 2020; Jia et al., 2020) have attempted to assess the efficacy of NPIs by combining policy data with robust real-time disease progression trajectory data (Xu et al., 2020) of COVID-19. For instance, Li, Pei, et al. (2020) used a flow-SEIR (Susceptible, Exposed, Infection, and Recovered) model to recommend locking down high transmissibility zones. Lau et al. (2020) correlated COVID-19 growth curves with the controlled lockdown of air traffic in China. Yuan (2020) applied regression modelling to exhibit that mobility between highly infected zones and others is a predictor of the infection growth rate. Ali et al. (2021) applied a non-integer Caputo derivative technique to capture the impact of NPIs in absence of vaccines. Pepe et al. (2020) used mobile phone geolocation data in Italy to model the changes in mobility with NPIs over time. As one of the more popular statistical models, the Bayesian model by Flaxman et al. (2020) at Imperial College London (ICL), and its variants (Brauner et al., 2021; Bryant & Elofsson, 2020; Candido Darlan et al., 2020) used a discrete renewal approach for estimating the infection spread and growth in reproduction number () with each NPI.
In addition to these studies (explored more in Section 2), one of the most focused topics on NPIs is the resulting change in mobility. Despite this focus, the impact of changes in mobility patterns specifically beyond partial interlinking of regression models with compartmental or metapopulation models is uncertain. The compounding effect on the epidemic spread rate from population densities within zones in a city and the mobility through these zones is also not modelled. Even the earlier mentioned Bayesian model from ICL and its variants lacked parameterisation of the actual changes in mobility due to each modelled NPI. These mobility changes were not included in the equation for calculating the value or the number of cases, as only a dichotomous value was assigned to each variable. One exception is the study by Lau, Grenfell, et al. (2020) which used Facebook's mobility data1 to estimate the infectiousness of different population groups. However, this study did not include any calculation methods for the interrelation between spread parameters (daily cases, reproduction number, fatalities) and mobility parameters. It lacked modelling reduction in cases and deaths as a direct consequence of mobility, and a potential data-driven exit strategy towards normalcy through controlled and well-aimed NPIs.
This paper contributes by proposing an elaboration to the Bayesian model for COVID-19 spread to identify the impact of NPIs, due to changes in mobility, on value. The spatiotemporal fluctuations in mobility due to NPI implementation are modelled using big social media data from Facebook mobility maps1 (Maas et al., 2019). A travel network density parameter is developed for representing mobility, as input in the modified Cox's hazard model to estimate the effective time-variant reproduction number , and other parameters to project the daily number of infections and fatalities. The proportional effect of each NPI is assumed to be correlated with the change in value, and the paper examines the validity of this assumption by comparing projected pandemic data with actual observations. In contrast to earlier approaches to the Bayesian epidemiological model, the impact in terms of changes in population contact rate during the pandemic has been modelled to project . These changes in contact rate are a key factor for determining the epidemic spread and are crucial for controlling epidemic spread among the local population of a country.
The paper is organised as follows. Section 2 presents a brief literature review on different epidemiological models for COVID-19. In Section 3, the empirical context of our study as the COVID-19 spread trajectory in the United Arab Emirates (UAE), data collection methodology and the proposed epidemiological model are presented. Section 4 then presents our results and a discussion on the fitness of epidemic data calculated by the developed model to actual observations. We also elaborate model convergence and forecasting accuracy. Additionally, hypothetical epidemic progression in multiple what-if scenarios for different NPIs is presented.
2. Literature review
Since its initial identification in Wuhan, China, researchers and world governments have aimed to track and control the COVID-19 spread (Chinazzi et al., 2020). A flurry of mathematical models have come out to track the disease spread rate in terms of , estimate the transmissibility impacts of lockdowns and devise an exit strategy towards normalcy (Fang et al., 2020; Verity et al., 2020) due to the severity of COVID-19 epidemic. This section introduces the key results of these studies discretised by their primary modelling approach.
2.1. Compartmental models
Majority of the epidemiological models currently available for modelling COVID-19 spread rate are some variations on the classic compartmental susceptible-infected-recovered (SIR) model. The value is a ratio of transmission and recovery rates which affects the spread rate (Awais et al., 2020). These types of epidemiological models split the population into different compartments based on the patients’ health phases in the disease progression. Multiple variations use a different range of compartments and use some form of metapopulation, statistical or agent-based models as add-ons to calculate the impact of NPIs. For example, Fang et al. (2020) evaluated the interlink between outbreak trajectory and NPIs by performing simulations of the COVID-19 spread dynamics through a parameterised susceptible-exposed-infected-recovered (SEIR) model. Results exhibited the effectiveness of NPIs such as isolation in reducing transmissibility. Lin et al. (2020) fitted epidemiological data over another SEIR model for projecting the infection spread in China by integrating zoonotic introduction, public reactions and NPIs under multiple scenarios. Results showed a strong interrelation between the public behavioural response and lockdown policy measures.
Li, Pei, et al. (2020) proposed a flow-SEIR model incorporating a traffic blockage factor to simulate the impact of NPIs. Simulation results showed a high correlation between traffic blockage and infection spread rate. Jia et al. (2020) proposed a linear variation to the SIR model by assuming a time-variant change in transmission rate due to NPIs. Cotta et al. (2020) modified it by assuming an exponential time-variant growth similar to the Cox's proportional-hazard statistical model (Cox, 1972). In both studies, the input transmission spread parameters are obtained from Bayesian Markov-Chain models. In more detailed compartmental models, population stratification based on infection fatality ratio due to the age distribution of the population is also performed (Lei et al., 2020). Others (Di Domenico et al., 2020; Goscé et al., 2020) focused on multiple NPI scenarios for optimal control and the return to normalcy. Each found the contact matrices to be affected by the compounding effect of multiple NPIs, recommending stricter complete lockdowns and complete school closures, among others, for optimal spread control. However, these forecasting models rely on the mechanistic cycle of disease progression from susceptible populations to infected and recovered cases and lack detailed infection-spread dynamics.
2.2. Agent-based and metapopulation models
Focusing more on simulating the contact rate between different population groups, agent-based models serve to provide an assessment of the performance of different isolation measures and the nation or city-wide effect of implementing NPIs. Typically, these models track the changes in mobility of different population groups within a region using a wide range of input parameters. For instance, Aleta et al. (2020) used mobile phone data from selected users in Seattle and New York to show that infection risk is dependent upon the characteristics of the visited location and found grocery stores, restaurants and offices as the primary spreading locations. Hoertel et al. (2020) used around 200 parameters (socio-demographics, age, comorbidities, etc.) to project the spread rate.
Metapopulation models link compartmental models with geospatial spread dynamics of different population groups to assess the changes in mobility patterns with different NPIs (Perra, 2021). The metapopulation SEIR study by Chang et al. (2021) for metropolitan residents in the USA is a good example. They extended hourly mobile phone data from users to simulate their interaction at different nodes (contact points) within regions and found that reducing contact rate in potential high-risk areas is the most effective NPI. As this study and similar models contain less detailed mobility data, the aggregated mobility matrices from Google were used by Ruktanonchai et al. (2020) to observe that strategized lockdown NPIs are highly effective in reducing spread.
2.3. Statistical models
These epidemiological models are an alternative to the modelling approaches discussed in the earlier studies. According to an in-depth comparison of these models with the more popular compartmental-type models by Perra (2021) covering 348 studies, statistical models have been applied for COVID-19 to directly quantify the impact of NPIs on the observed number of infections and fatalities compared to the expected spread data. As an early example, the correlation between human mobility and epidemic progression was noted by Yuan (2020) utilising regression modelling of pandemic data for Wuhan. Results exhibited that interzonal mobility between Wuhan and other regions is a significant indicator of the reported infection growth rate. Chu et al. (2021) proposed a fractional-order transmission model to assess the spread dynamics in Saudi Arabia. Results highlighted the capability of mathematical models in predicting spread dynamics and the effect of environmental parameters on the epidemic.
The earlier mentioned Bayesian model by the ICL team (Flaxman et al., 2020) is probably the most popular epidemiological model in the statistical model category. The model calculates the number of infections at any given time to be a function of the susceptible population, effective time-variant reproduction number () due to NPIs, and infected individuals in the preceding day regulated by the generation time. COVID-19 epidemic spread was modelled for eleven European countries that implemented similar NPIs for similar population distributions. It accurately accounted for the probabilistic progression trajectory of disease spread with NPIs by inferring changes in the value, number of cases and deaths due to changes in mobility. Subsequent adoptions of this model improved upon the study by incorporating slightly larger disease spread data of an additional month (Fernández-Recio, 2020), or partially substituting the uninformative prior distribution of NPI impact by Google mobility data that aggregates trends of Google Map users’ visits to grocery stores, recreational and residential facilities, workplaces and transit stations (Bryant & Elofsson, 2020).
A major assumption of both the ICL model and the extended study (Fernández-Recio, 2020) was that the NPI impact was generalised to be the same across all countries, which is rarely the case. The size of the data sample was also considerably small even after the extension as the peak of the COVID-19 cases trajectory was not yet realised and the impact of a complete lockdown was not explicitly modelled on the longer timeseries. The extended model included only part of the Google mobility data by substituting the variables for each NPI with those that represented relative changes in mobility to parks, residential and recreational facilities, etc. In addition to using only a dichotomous value for change in mobility, the same normal distribution prior was used to calculate the mobility change as used by the ICL model. Thus, transmission dynamics in these studies disregarded changes in contact between various zones within a territory collected on an individual scale and aggregated territory-wide, which might be indicative of the efficacy of any actual lockdown implementation in the studied regions.
2.4. Contributions of this study
In this study, a unification of mobility data and network theory is introduced to identify the risk of contact and transmissibility between different areas (modelled as nodes) in a country, in a weighted structured mobility network. Here, a denser network is associated with a high risk. Similarly, a high concentration of people at a particular node is assumed to produce the same effect to represent the actual nature of disease spread. The ICL Bayesian model is modified and adapted to model the mobility data against epidemiological data timeseries, identified by changes on . The resulting model can describe the actual effectiveness of each NPI measurably and visually comparable to the spread dynamics graph in terms of reduction in new cases and deaths.
3. Methodology
3.1. Location and NPIs
The study is conducted in the UAE. Adequate testing of the local population severely hampers the validity of any predictive model for describing the COVID-19 spread in any territory (Bryant & Elofsson, 2020). Adjusting for the country's total population, the UAE is among the most tested countries in the world accounting for 6781.06 tests per 1000 population by December 2020, before large-scale vaccine rollouts (Hasell et al., 2020) and this large verified case spread dataset is used in this study as the epidemiological data. The UAE had its first confirmed case on January 29, 2020 and early travel restrictions were announced on February 29, 2020 followed by the closure of schools and universities, national sterilization programs/night curfews, and work-at-home initiatives. It was followed by different lockdown strategies: 24-hrs and 10-hrs lockdown, and interstate movement restrictions between Abu Dhabi and Dubai that considerably reduced the mobility of the local populace.
Interestingly, the NPIs evaluated in datasets considered by the earlier models lacked the breadth of changes in the extent of lockdown strategies (work-at-home, night curfew, different lockdown hours, etc.) that can help decision-makers for more strategized NPIs. Big social media data of people travelling between different areas collected by Facebook for the UAE is used to model spatiotemporal mobility trend sensitivity to lockdown policies in the country. This way, realistic human mobility patterns can be collected and the relationship between government actions and public response can be accurately characterised by different data, timeseries, and lockdown intensities.
3.2. Data collection
The data on the government intervention measures, including the nature, date and intensity of application, and rescindment dates were sourced from the local governmental websites, newspapers, and media resources. The analysis criteria for plotting the government measures on the spatiotemporal mobility datasets were based on the distinctiveness of each measure and a total of seven NPIs were aggregated (Table 1).
Table 1.
Description of the non-pharmaceutical initiatives (NPIs) evaluated in the Bayesian model.
| NPI | Description | Implementation Date |
|---|---|---|
| Multiple minor preventative measures | Closure of educational institutes. Travel restrictions and flight suspension. Limited occupancy at recreational facilities. | February 29, 2020 |
| Multiple work-at-home measures | 70% private and 100% public sector workforce mandated to work remotely. Minor restrictions on public mobility. Suspension of public transport services. | March 25, 2020 |
| Twenty-four-hour Dubai lockdown | All outdoor movements are restricted in Dubai. Limited mobility in other regions. Remote working and occupancy restrictions are further extended. | April 05, 2020 |
| Ten-hour nationwide night-time lockdown | Outdoor movement after 10 p.m. is restricted in the entire UAE. Mosques and recreational facilities closed. Malls operating at 25% capacity. | April 24, 2020 |
| Nationwide relaxed night curfew | Reopening of recreational facilities with limited occupancy. Remote work for 50% of workers in the public sector. Only night-time mobility is partially restricted and daytime curfews are lifted. Private sector returning to office work. | May 25, 2020 |
| Abu Dhabi–Dubai border closure | Only closure of border between the most populated northern emirates (Dubai, Sharjah etc.) and the largest Emirate of Abu Dhabi. Business activity resumed in Dubai. Malls and private businesses operations at full capacity. | June 05, 2020 |
| Abu Dhabi controlled entry/exit | Movement of only vaccinated or negatively tested individuals is allowed between northern emirates and Emirate of Abu Dhabi. Travel restrictions significantly eased throughout the country. Resumption of flights to limited countries. On-site workforce resumed in private and public sectors. | July 01, 2020 |
Real-time epidemiological data consisting of the proportion of infected, recovered, and death cases from the tested population were gathered from publicly available databases (such as HDX datasets from the United Nations Office for the Coordination of Humanitarian Affairs) to maintain transparency and verifiability of the analysis. The time horizon of the data extended from the first verified case in the UAE (Jan 29, 2020) to Oct 18, 2020. This allowed an adequate time window for both the application and lifting of any NPI, including the last evaluated NPI of “Abu Dhabi controlled entry/exit”. The parameterisation of mobility flow patterns was performed using social media data from Facebook disaster maps. They are used here as a measure of daily mobility across all significant decisions up to the last day of the analysis to model the outbreak as a continuous chain that may be stochastically impacted by the various control measures.
3.3. Mobility model
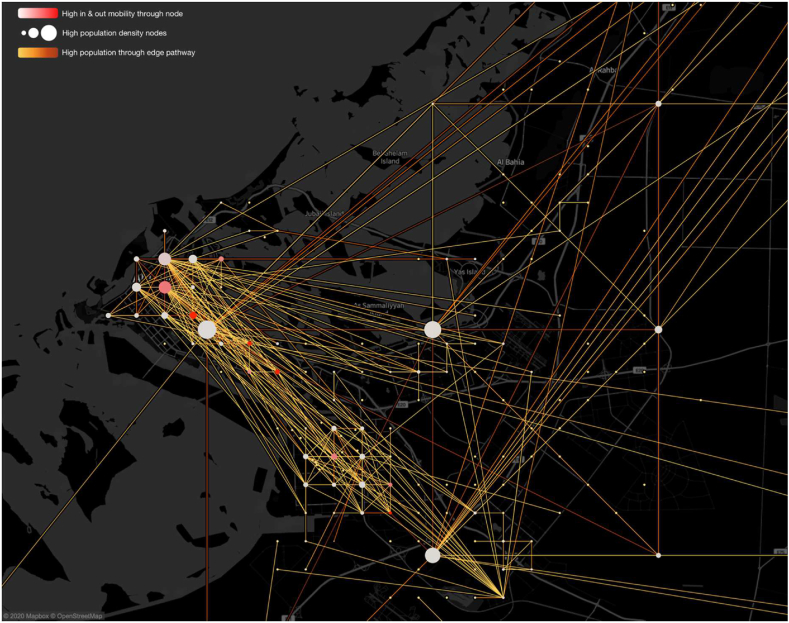
The purpose of the mobility model is to augment the epidemiological data with extensive mobility data to discover traffic flow patterns between different geographical zones, represented by nodes in weighted structured networks. An example of the modelled data for Abu Dhabi city is shown in Fig. 2 for illustrative purposes for a representative day, whereas the mobility data for the entire country is used in the actual analysis. Mobility patterns were reported by Facebook for three timeseries: 12 a.m.–8 a.m., 4 p.m.–12 a.m., and 8 a.m.–4 p.m. for each day, capturing regular traffic, peak, and off-peak hours for maximum dataset variability. Maps were created for each timeseries for the whole country for the entire duration of the analysis. The Facebook dataset contained information about country-wide changes compared to a pre-pandemic baseline level in the population density at each geographical zone, mobility in-out of each zone at an individual scale and geospatial information about the different zones. Aggregated anonymised data from Facebook clearly shows the variations in people's adherence to NPI-mandated lockdowns and these mobility changes are proxies for public exposure to disease spread risk (Chin et al., 2021) as it shows the closeness of contact between individuals and the number of individuals.
Fig. 2.
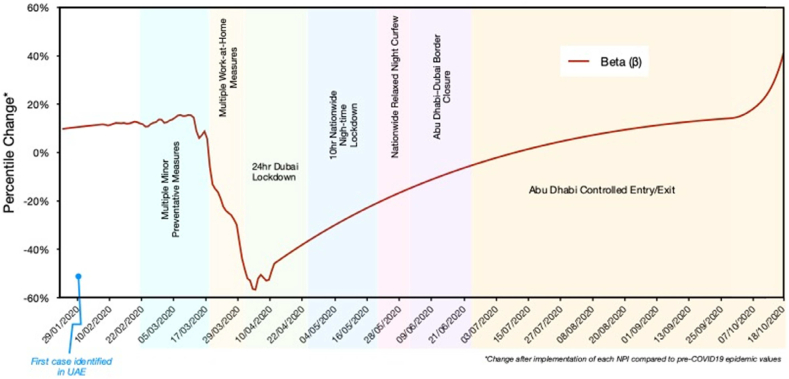
Trend analysis results of changes in population mobility and travel network density metric () due to NPIs.
The pseudo-code, description of the variables and the model used for determining the changes in mobility for all nodes in the network shown in Fig. 1 above are as follows:
Fig. 1.
A section of the mobility directional map for Abu Dhabi City on Apr 26, 2020
Mobility model input:Travel origin-destination (OD)-matrix of people from Facebook.
Mobility model parameters:Number of nodes, number of trip pathways between nodes (i.e., edges), in/out mobility for each node, trip loop distribution, geospatial network geometry, and population density at each node.
Mobility model outputs:Travel network density distribution weighted by mobility-in/out and density at each node.
Step 1:Matrix transformation: Rearranging trips into nodes (geographical zone) and edges (travel path between zones) for the entire network, containing m edges between i nodes at time :
| (1) |
| (2) |
The OD distribution matrices for the nodes and edge pathways are then pruned based on the trip distance to remove insignificant loops (i.e., trips where the travel distance is approximately zero kilometres). This is done to prevent double-counting of contact between individual clusters at the same location since this value is already included as part of the population density data for each node.
- Step 2:Graph analysis: Trip frequency between o origin and d destination at time is taken as input.
-
a.Calculating the total number of nodes and edges in the network as:
-
a.
| (3) |
-
b.
Calculating weight of edges at time . Weight is based on a theoretical understanding of the significance of each edge pathway between nodes in terms of spreading the disease. As a higher contact rate between individuals is expected to increase the spread of disease, is assigned here as the number of people taking the trip between i origin nodes and n destination nodes at a given time :
| (4) |
Implementation of an NPI is aimed at reducing both the number of edges in the travel network as fewer people travel between nodes and the number of people travelling through each edge.
-
c.
Calculating weight of nodes that exist in the city-wide travel network at time . The population density of individuals at each node (based on the number of people residing within the area of coverage of each node) is taken as its weight:
| (5) |
Contrarily to the edge pathway, lockdowns resulting from the implementation of NPIs shall increase the number of people at a particular node, represented by the density of the analysed node.
-
d.
We based our mobility-change parameter on quantifiable graph-theoretic connectivity metric from the network topology. The beta index is a basic measure of graph connectivity and is calculated as the ratio between the number of edges and nodes. A complex network, such as a mobility network for a region, generally has a higher beta index due to more connections (Rodrigue, 2020). Ecological differences between the different nodes and edges in a network are typically recognised using weight parameters such as the magnitude of movement through edges, distances, position, or sizes of nodes, etc. (Theobald, 2006). To represent the NPI-based interaction of transmission contact rate between individuals in a city and their movement between nodes through edge pathways, the spatial interaction parameter of the beta index for time is modified as:
| (6) |
The weight of nodes has an inverse sign as it is assumed that it shows the density of people at the node and a higher concentration within any zone is proportional to higher contact between not only the individuals at that location but also with the people passing through that node. This also implies that a larger value is associated with a higher risk of disease spread since it implies more contact between the population of a country represented by the mobility network graph. To calculate the impact of NPI:
| (7) |
Where the subscripts “base” and “crisis” represent the pre-pandemic and pandemic datasets, respectively at time . The difference metric is required to estimate the change in mobility due to each NPI. The generated values were then modelled in the epidemiological models to calculate the effective reproduction number (). Before creating Bayesian models that use the NPI-based mobility difference metric , statistical trend and Pearson correlation analyses were performed. Dependence of the daily rate of fatalities in the country on changes in the parameter was checked, as it is assumed that the reported death toll due to epidemic is a more reliable indicator than the reported number of infections due to under-reporting and asymptomatic cases. The correlations were performed using a lag of up to 40 days (almost twice the adapted infection-to-death time) to make sure an optimum range is analysed. The set of equations from Eqs. (1)–(7) represent the mobility model while the set of equations from Eq. (8) to Eq. (15) constitute the epidemiological model.
3.4. Model for time-variant reproduction number
Forecasting models rely on the mechanistic cycle of disease progression from infected individuals to the susceptible population to determine new infections, after scaling it by the reproduction number. This reproduction number is not only time-variant but also depends upon the country-related factors that influence the contact transmission between infector and infected. Additionally, the number of new cases is also weighted by a discretised distribution of serial intervals (Flaxman et al., 2020). The ICL model (Flaxman et al., 2020) and its variation models (Bryant & Elofsson, 2020; Fernández-Recio, 2020) rely on a modified version of the Cox's proportional hazard model as a constant function containing two components to generate time-variant reproduction number , given as following for a country m:
| (8) |
is the time-variant baseline prior corresponding to the hazard situation without any external factors, represents the number of NPIs that were in effect at time . The variable when the NPI has been implemented and the negative sign shows the reduction effect of each NPI, while shows the NPI effect. The benefit of using the ICL Bayesian model as the theoretical basis for our epidemiological model is that it can formulate key features of the pandemic spread and uses actual data to estimate the model parameters, thereby using fixed parameters and fewer assumptions (Manevski et al., 2020).
The primary difference between our model and the ICL model is the calculation method for the time-variant value. These models relied on a gamma distribution prior to represent the effect of all NPIs, multiplied with a dichotomous variable where a value of “1” is assigned in case the NPI is implemented and zero otherwise. On the other hand, we introduce a data-driven term (defined earlier) that provides an accurate approximation effect of mobility change due to governmental decisions associated with each NPI, unlike the parameter by the ICL model which assumes similar value distribution for all countries. The proportional effect of NPIs on is assumed to be correlated with the change in value, and this paper will examine the validity of this assumption. The UAE government implemented seven NPIs shown in Table 1 earlier. The following equation presents the evolution of in the UAE as per our model:
| (9) |
Where and represent the same as Eq. (8). As all NPIs have already been implemented by the UAE government, a time-variant distribution effect of each NPI can be determined following statistical distribution-fitting techniques, which can be useful to forecast mobility change in future, provided the status of the implemented NPI. This has been used in our supplementary forecasting model and the generated values are compared with actual pandemic data in the country. The above model only allows for a stepwise change in as each NPI is implemented, accounting for a reduction in contact rate between population clusters with change in mobility. Other factors, such as the effect of pre-existing immunity, vaccinations, etc., are not modelled as such data relations remain unavailable. The prior for baseline is calculated as per Flaxman et al. (2020):
| (10) |
3.5. Models for time-variant infections and death toll
A discrete renewal process is used to model the number of infections over time and this process is strongly based on epidemiological models such as SIR models and Bellman-Harris and Hawkes processes (Flaxman et al., 2020). Following the approach explained in earlier research (Flaxman et al., 2020), the time duration when an infected individual infects susceptible individuals (i.e., serial interval distribution) is plotted as a gamma distribution with 0.62 days as the standard deviation and 6.5 days as the mean value, discretised as per day level steps (to simulate the actual disease spread reporting intervals) and weighted by the time-variant value for the country. This relation is given by:
| (11) |
In this relation, is the number of infections at time , is the effective reproduction number influenced by the mobility changes in the country after implementing NPI. is the number of infected individuals on the previous day and is the serial interval distribution (i.e., the average time from infection onset of primary and secondary infections) as described earlier (Flaxman et al., 2020). Previous research (Flaxman et al., 2020) recommends that the seeding of new infections starts 30 days prior to a cumulative observation of 10 fatalities in the country. An exponential distribution of 0.03 is used to seed new cases for six days (Li, Pei, et al., 2020) and the model is then initialised for calculating the further infection spread dynamics.
Due to discrepancies in reporting of the daily case data, Bryant and Elofsson (2020) recommend using the reported number of fatalities as a more accurate measure for modelling the infection spread and our study uses this approach following the death model described by Flaxman et al. (2020) as the posterior for Bayesian modelling which models (daily deaths in the country) as:
| (12) |
here is modelled as a half-normal distribution as per the source ICL model (Flaxman et al., 2020):
| (13) |
To model the actual number of daily deaths , initially the infection-to-death distribution () needs to be estimated which depends upon three factors. Firstly, the probability of fatality for an infected individual is given by the case fatality ratio (CFR). There are many estimates available for age-distributed CFR for many European countries that can be used if the model is applied to these regions. Following the approach by Flaxman et al. (2020) and Verity et al. (2020), we calculated it as the percentile ratio of deaths from COVID-19 and the confirmed cases in the UAE on Apr 03, 2020, when a total of 10 deaths had been observed in the country, calculated to be 0.66%. Secondly, the incubation period is taken as a gamma probability distribution with a variance of 0.86 days and 5.1 days as the mean value (Flaxman et al., 2020). Thirdly, the time duration in days from onset to death is modelled as a gamma distribution (mean = 18.8, variance = 0.45) (Flaxman et al., 2020). The value at time is given by:
| (14) |
This distribution is discretised in per day steps. For calculating the daily number of expected fatalities at time in the country when the number of infections is , the relation is given by the following:
| (15) |
3.6. Baseline model fitting and convergence of Markov-chain Monte-Carlo simulations
The above death model in Eq. (15) assumes that the number of fatalities on any given day is influenced by the cumulative sum of previous infections, which itself is dependent upon the reproduction number as affected by the implementation of NPI, the probabilities of infection and death and the basic assumption that entire population is considered susceptible as the effects of vaccination and other external factors are not considered due to comprehensive and reliable data unavailability. The parameter estimation model was written in R, while the Bayesian inference model was developed in the accompanying RStan package and model fitting was done based on the adaptive Hamiltonian Monte-Carlo Sampler. After parameter estimation, the model was run using a thinning-factor of 4, 2000 warmup samples and 4000 iterations with 8 chains. Divergent transition chains were avoided by setting the adapt delta value as per the original model description (Flaxman et al., 2020). R-hat statistics histogram was plotted to analyse the convergence of the Markov-Chain Monte-Carlo simulations. The simulations converge when the R-hat comparison metric of within- and between-chain estimates a value of 1 for R-hat (Bryant & Elofsson, 2020).
3.7. Forecast modelling
Another objective of the modelling process was to create reliable forecasting estimates. The parameters and fitted model estimates from the baseline model were used to create a forecasting model to evaluate the predictive validity of the model assumptions on a dataset that was not utilised for fitting the baseline model. The period used for forecasting estimates was 6 weeks from the end of our original dataset (Oct 19, 2020–Nov 30, 2020) to allow for adequate visual and analytical comparison of the forecasted data well beyond the modelled effect lag of 22.9 days from infection to death. As the epidemiological data for this time is already available, we compared our forecasted number of cases and deaths against actual data. The average fractional error was analysed to evaluate the prediction model.
4. Results and discussion
4.1. Impact of NPIs on mobility ( value)
Plotting the trend of changes in the developed network density metric shows a considerable impact of implementing each NPI (see Fig. 2). Initially, the results display an increase in the network density (increasing by 8–17%) compared to the pre-epidemic condition. This trend is understandable as no NPI was yet implemented and traffic is reasonably expected to grow each year in the country by at least 5% (Hasan et al., 2021). As minor preventative measures of flight restrictions and closure of educational institutions were instigated, a sudden drop of 4% in value was observed on the day of NPI implementation compared to the pre-epidemic conditions. However, the value continued to increase generally at an average increase of 12–13% until 25 Mar compared to the pre-epidemic baseline data as the dates for baseline data for this time period coincided with the school vacation period where educational institutes were already closed.
After this, most NPIs showed almost an instantaneous reduction trend, with the 24-hr lockdown in Dubai NPI showing the maximum change. The easing of lockdowns from 24 Apr with 10-hr night-time and later complete lifting on 05 June when only the border between the most populated northern emirates and Abu Dhabi was controlled, displayed a gradual increase in . In this situation, the travel within each city particularly the northern six emirates returned to normal (i.e., pre-epidemic levels) which resulted in a steady increase in mobility. On 17 Jul, the mobility patterns first hit the baseline levels with value marginally (0.2%) higher than pre-epidemic values. Consequently, it surpassed baseline levels by 5% on Aug 04, 2020. The trend continued with a sharper increase noticed after 10 Oct, increasing by approximately 40% on 18 Oct. Several reasons produced this cumulative effect for increasing the value apart from the expected yearly traffic growth. Initially, the lockdowns within the country were considerably eased (TDRA, 2021). Secondly, the movement in the tourist-centric high mobility Emirate of Dubai significantly increased compared to the pre-pandemic levels in 2019 as the curfews were completely lifted (Reuters Staff, 2020). Finally, this period observed a surge in domestic tourism as it doubled, increasing by over 107% (Report, 2020). These upsurges in mobility were thus accompanied by a high increase in the daily number of reported infections (Crisis24, 2020).
4.2. Dependency of epidemic spread (deaths) on NPI-based value
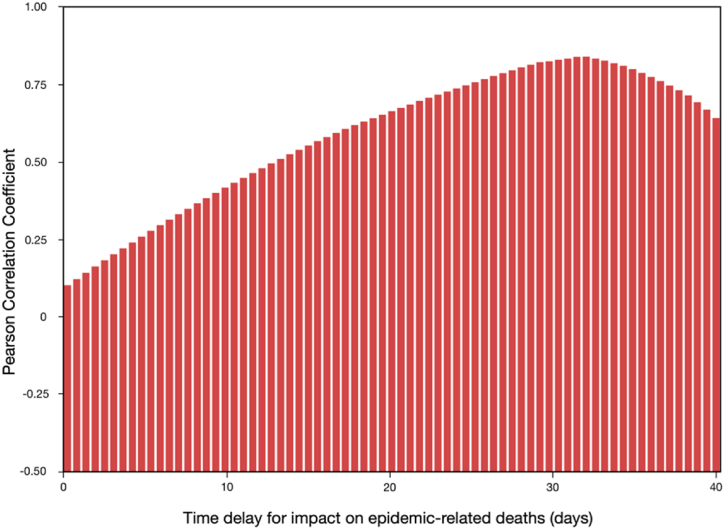
Analysis of the interrelation between changes in the travel behaviour of the country's residents due to the implementation of NPIs is performed by plotting Pearson correlation coefficients (PCC) with varying time lags. After trying different values for the time delay, an optimum range for the correlation was found that can visually show a simplistic relation between NPI and death toll in the country. Results shown in Fig. 3 indicate a strong correlation between daily deaths reported in the country and , with time delay. The relationship for changes in compared to the pre-pandemic conditions shows that the PCC value was maximised at 0.85 corresponding to a time delay of 32.5 days. Our model assumed a lag of 22.9 days between infection and death, this is roughly consistent with the observed delay between changes in our mobility-related parameter and the reported number of daily deaths in the country. The time-delay range correlation is also closer to the adapted infection-to-death than other studies using similar models (e.g., Bryant and Elofsson (2020)).
Fig. 3.
Correlation between daily deaths and NPI-induced changes in travel network density “”
4.3. Model validation and impact of NPIs on time-variant effective reproduction number
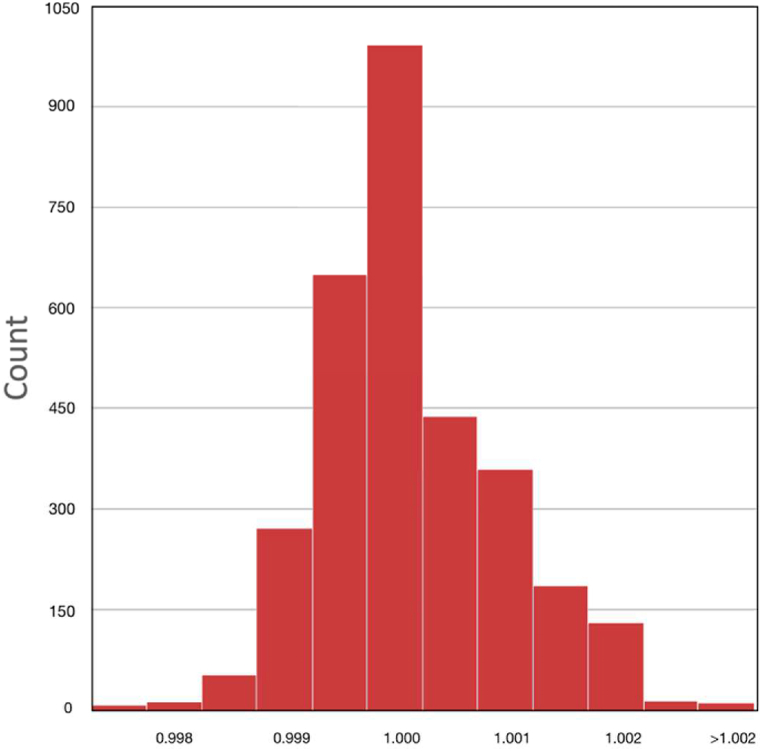
The correlation between the parameter for population travel patterns and the reported daily deaths attributed to the COVID-19 epidemic provided an interesting observation about the underlying assumption for our model that used it to predict the values of over time. For validating the estimated Markov-chains and the modelling assumptions, a histogram of R-hat statistics for the parameters of our model in the simulations is illustrated in Fig. 4.
Fig. 4.
R-hat statistics for the modelling parameters in the simulation. Simulation convergence = values of 1.
Since most of the values are equal to 1, it confirms model validation of our simulation assumptions and parameters according to the literature (Bryant & Elofsson, 2020; Flaxman et al., 2020). The focus of this study was to identify the impact of the NPIs implemented by the government of the case study region in terms of reducing the epidemic spread. For UAE, a total of seven NPIs were enforced on managing public mobility and transmission contact among the population. It was observed that the change in the travel habits of the regional population was almost immediate, following the implementation of each NPI.
Across all NPI measures, significant reductions in both direct mobility and travel network density parameters were calculated compared to the pre-epidemic values, as tabulated in Table 2. It can be noted that the changes in mobility were more drastic compared to the values. We propose that including the population density within the metric acted as a normalising factor that may have contributed to a better estimation of the effects of NPIs on the epidemic spread rate, calculated through time-variant values. Additionally, the reduction in population mobility and the metric due to the various lockdown-centric NPIs was accompanied by a reduction in values. Similarly, an increase in both travel pattern related variables after the curfews were lifted and lockdowns were considerably eased with only the Abu Dhabi–Dubai border being controlled, resulted in a hike noticed for the values. After model fitting on case study mobility and epidemiological data, the results of the changes in effective reproduction number are shown in Fig. 5.
Table 2.
Model estimated changes in mobility, and values during the epidemic due to different NPIs.
| NPI | Population Mobilitya | Travel Network Density a | Median b |
|---|---|---|---|
| Multiple minor preventative measures | 36.29% | 11.73% | – |
| Multiple work-at-home measures | −21.94% | −23.43% | −21% |
| Twenty-four-hour Dubai lockdown | −35.53% | −49.89% | −54% |
| Ten-hour nationwide night-time lockdown | −26.01% | −30.65% | −41% |
| Nationwide relaxed night curfew | −19.05% | −18.69% | −25% |
| Abu Dhabi–Dubai border closure | −13.31% | −10.16% | −29% |
| Abu Dhabi controlled entry/exit | 5.32% | 9.12% | 63% |
Median change in value after implementation of NPI compared to pre-epidemic levels.
Relative change after NPI implementation compared to pre-NPI implementation levels for each NPI.
Fig. 5.
Model results for changes in due to the implementation of NPIs based on travel network density.
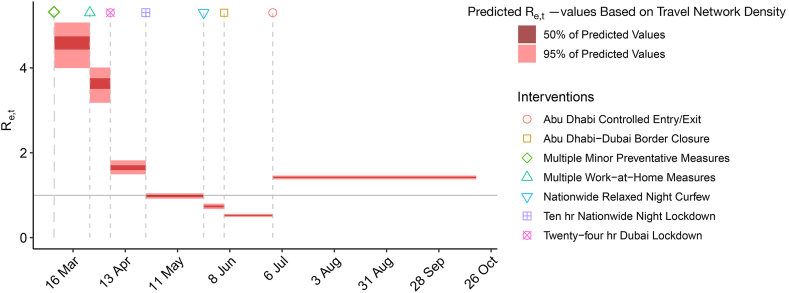
It should be noted here that this figure does not represent the individual impact of each lockdown measure on curtailing the reproduction number but shows the values after implementing each subsequent NPI due to its cumulative effect with all of its predecessor NPIs. This is why the minimum values were noted when the nationwide relaxed curfew and Abu Dhabi-Dubai border closure were implemented, despite these two NPIs being a relaxation of the lockdowns, as they succeeded the two most mobility-restricting NPIs of 24-hr Dubai and 10-hr nationwide lockdown. The reason for this is that the value in each subsequent day is dependent upon the number of infected and susceptible population weighted by a discretised distribution of serial intervals. This explains as to why the value further dropped to levels <1 after the 24-hr and 10-hr (where ) were succeeded by the easement of lockdowns as the value and numbers of susceptible and infected individuals in the preceding days were lower. However, as the per day increase in contact rates and the resulting number of infected individuals continued to increase with the lifting of curfews, the value also started to increase. These trends of changes in values due to a cumulative effect follow a similar trajectory as the ICL model results (Flaxman et al., 2020). The individual effect of each NPI is explored in the what-if scenarios presented in Section 4.7.
The model results estimated a value ranging from a posterior mean of 0.53 (95% prediction interval of 0.49–0.56) to 4.58 (95% values in the 4.0–5.07 range) based on . Our results suggest that the NPIs produced a sizeable effect in terms of reducing the transmission rate as quantified by the relative change in . As suggested earlier, the most significant impact was due to a combination of a 24-h Dubai-based lockdown and a 10-hr nationwide night-time curfew that considerably affected travel habits. We found that the values continued a downward trajectory for the first six NPIs with an average posterior mean of 0.98, accounting for a 78% reduction compared to the pre-implementation of these NPIs as they considerably affected the travel habits of the regional population in the country.
However, as the lockdown and other travel restrictions eased in the country, a sudden increase in mobility and density of the travel network (in comparison to the weeks when the earlier NPIs were still in place) was observed. Following the earlier discussion, this might have caused a jump in the transmission rate between the infected and susceptible population clusters within the country, as indicative through an increase in the value. It should be noted here that despite showing a considerable impact of the on the epidemic spread, the results cannot yet be conclusive to enlist mobility as the winner among prevention measures since vaccination, herd immunity and other epidemiological parameters are not accounted for here. Furthermore, these results do not infer that the exact NPIs that were successful in bringing below 1 (i.e., the target value) for the case of UAE would produce the same impact in other countries.
Nonetheless, a combination of these NPIs can serve as a guideline for measuring the influence of the herein proposed parameter on the epidemic and the probable success rate of similar NPIs that are common to most nations (travel restrictions, night curfews, closing high mobility locations, etc.), if implemented in other countries. Interestingly, the values measured here for the first quarter of 2020 for UAE are somewhat similar to the values for some European countries in the study using the ICL Bayesian model (Fernández-Recio, 2020), where it dropped from 3.14 to 4.82 range to 0.58–0.71 post lockdown. Our results showed a re-rise in values upon relaxing of the lockdown measures which were not observed in their study or similar studies as their studied datasets were unable to capture the increase in public mobility due to the epidemic being still in its early stages. Similarly, many NPIs were still in their implementation stages and uncertainties existed that significantly affected the models presented in these studies to link mobility with the epidemic transmission.
4.4. Impact of NPIs on number of infections
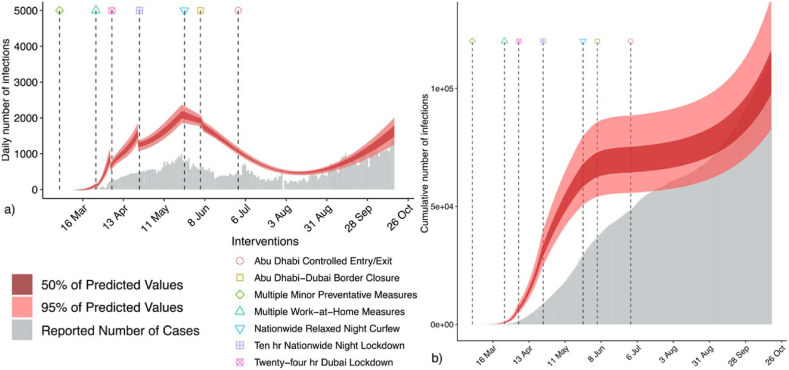
Utilising the time-variant effective reproduction number generated by the fitted model, Bayesian estimation of the infections from the start of the epidemic in the case study country to Oct 18, 2020 was obtained. Fig. 5 shows the evolution of daily infections in UAE compared to the reported number of cases for each day. From visual inspections, the model seemed to provide a good fit for the infections spread in the modelled country. In UAE, the detection rate for COVID-19 cases was second (currently fourth) in the world at 1280.19 tests per thousand inhabitants as of Oct 26, 2020 (Al-Hosani et al., 2021) as well as top ten detection rates (tests per confirmed cases) (Our World in Data, 2021), i.e., much higher than any other country modelled in the studies predicting COVID-19 spread rates. This high level of infection ascertainment greatly increases the validation accuracy of the model results.
Reported data shows that the daily number of infections in the UAE initially peaked on May 23, 2020 with 994 infections as shown by the grey bars in Fig. 6 after which a downward trend was noticed, dipping to 179 cases on 11 Aug. Considering our model estimates that are displayed in Fig. 6, the daily cases for 23 May were 2097 with 95% credible interval (CI) in 1846 (11% lower-bound) to 2354 (12% upper-bound) range. These model calculated results implied an overestimation of 52% compared to the observed values. On 07 June, the observed daily infections were 626 while estimated results were 1727 cases with 95% CI in the range of 1580 (9% lower-bound) to 1895 (10% upper-bound). Similarly, for 01 July the model estimated 1053 cases with 95% CI in the 963 (9% lower) to 1160 (10% upper) range. For the 11 Aug plunge, our model estimated 440 cases (95% CI: 387–495 at ±12% bound limit) which is one-and-a-half times higher than the actual cases. This CI width is representative of the variability in the population-level aggregates. A slight variation of ±2% in the interval throughout the analysis period, irrespective of the distance from the starting point, is common in epidemiological models using probabilistic serial interval and relations where the analysis from outbreak to post-peak period was conducted (Camacho et al., 2018; Leung et al., 2021; Price et al., 2020). Generally, it can be proposed that the implementation of an NPI that limited the mobility of people might have also resulted in reducing the infections. However, this drop is not immediate and follows a certain degree of lag after each intervention as the cumulative effect generated a significant reduction of active cases.
Fig. 6.
Model results for NPIs–implementation impact on a) daily, and b) cumulative infections based on travel network density.
On 01 July, most lockdown measures were relaxed and only the border between the two highly populated emirates was controlled. Following some lag, this resulted in an increase in mobility accompanied by a new wave of infections peaking on Oct 18, 2020 with 1583 active infections. Our daily infection estimates for the same were 1716 cases (95% CI: 1496–1945 at ±13% bound limit), which is only 8% higher than the reported number of cases. The cumulative number of infections predicted by the model exhibited a similar trend. The model was not only capable of predicting the general trend of infection spread as well as the peaks of the epidemic outbreak with a small degree of uncertainty. These estimates suggest a good estimation rate of daily infections for our model. Additionally, both lower and upper bounds of the predicted values are well above the confirmed daily infections. Due to the shorter prediction interval, these estimates provide useful information on the prediction accuracy. It can be noted here that the difference between reported and predicted values is not several times higher compared to the other studies utilising a similar ICL Bayesian modelling approach. This indicates that a mobility parameter, particularly a time-variant travel network density, should be factored in to improve the prediction probabilities of epidemic models for COVID-19.
4.5. Impact of NPIs on deaths
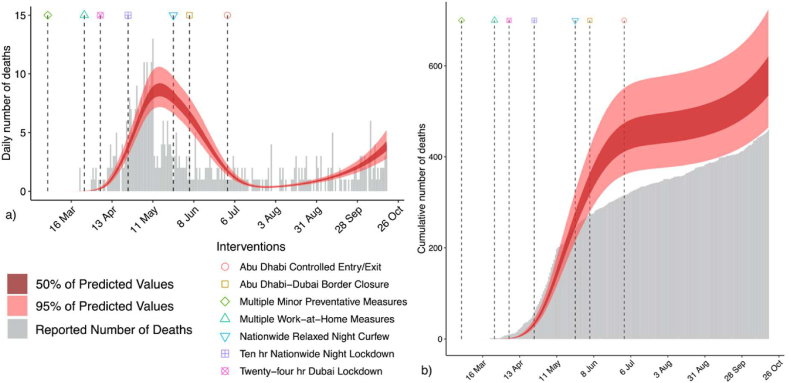
Fig. 6 shows the reported number of deaths in the UAE from the first reported case to Oct 18, 2020, along with predicted time-variant fatalities according to our fitted model. On 04 Apr, our model estimated 1 death against an observed value of 1 with 95% credible interval (CI) in 0.872 (10% lower-bound) to 1.07 (10% upper-bound) range. For 22 Apr, with 3 observed deaths the model estimated 4 deaths (95% CI: 3.28–4.72 at ±18% bound limit) which further increased on 23 Apr to 5 estimated deaths (95% CI: 3.32–4.87 at ±19% bound limit) against 6 observed. Similar trends were observed for 23 May (8 estimated, 95% CI: 6.94–9.89 at ±18% bound limit), 05 June (7 estimated, 95% CI: 5.51–8.10 at ±19% bound limit), 01 July (2 estimated, 95% CI: 1.93–2.76 at ±18% bound limit), 11 Aug (1 estimated, 95% CI: 0.96–1.35 at ±17% bound limit), and 18 Oct (4 estimated, 95% CI: 3.01–4.25 at ±17% bound limit). Although there is a slight variation of ±2% between the upper- and lower-bound values from 22 Apr to the last analysis period at 18 Oct, it can be attributed to population-level aggregation and an inherent result of epidemiological prediction models as has been discussed in previous section. In general, the NPIs, particularly the two lockdowns (24-hr followed by 10-hr) were more effective in reducing the daily death toll due to the epidemic spread. This effect followed a lag period of more than 30 days, further conforming to our model assumption of 22.9 days between infection and death of individuals. The graphical representation of the daily deaths predicted by the model in Fig. 7 does not dramatically deviate from the reported daily fatalities for the studied country of the UAE.
Fig. 7.
Model results for NPIs–implementation impact on a) daily, and b) cumulative deaths based on travel network density.
We assessed our estimates against reported per day deaths and found an average under-prediction error of 2 death for the first nine weeks ending on May 08, 2020 (95% CI of 3–1 deaths). After this, an average overestimation error of approximately 5 deaths or less was observed. The upper-bound overestimates included values as high as 7 deaths and the lower-bound values fell to an underestimation of 1 death. The prediction intervals for the predicted number of cumulative deaths were considerably wide. The median value for the first nine weeks since the start of the epidemic was an underestimation of 39 deaths or less (95% CI: 1–58 deaths) whereas subsequent weeks had an overestimation value as high as 129 deaths (95% CI: 3–251 deaths). Although the prediction interval is significantly wide which shows a higher uncertainty level, it is still considerably lower than those estimated by other studies (Bryant & Elofsson, 2020; Fernández-Recio, 2020; Flaxman et al., 2020) where even unrealistically high numbers were reported. Nonetheless, the time-variant death trend predicted by the Bayesian model presented here using travel network density provides a strong case for representativeness of mobility-related parameters to factor in the implementation impact of countermeasures on epidemic spread among the local population of a country.
4.6. Forecasting distribution of infections and deaths
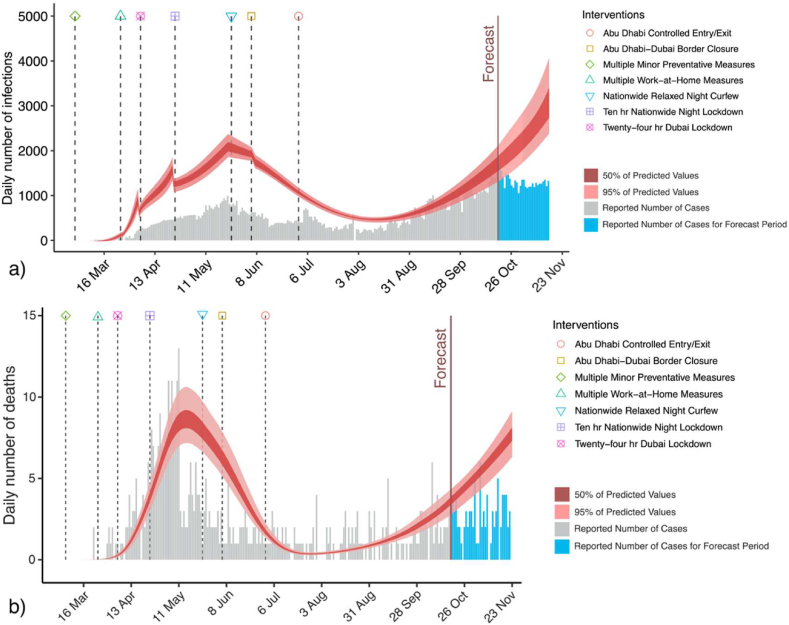
Additional to predicting the epidemic spread rate from the beginning of the epidemic in the UAE on Jan 29, 2020 to Oct 18, 2020 by modelling the transmission contact rate among the population through detailed travel networks, the forecasting reliance of the created model was evaluated by estimating daily infections and deaths from the end of this period to Nov 30, 2020. These forecasting distribution results are shown in Fig. 8 along with the reported data for the forecasted period, while the results for the predicted period from the previous section are also reproduced for visual comparison. Results show that the prevalence of COVID-19 had slightly increased in the forecasted period over time as recorded through daily infections and deaths among the susceptible population in the country, partially explainable by the increased mobility that came with the relaxation of NPI measures.
Fig. 8.
Forecasting results for NPIs–implementation impact on daily a) infections, and b) deaths based on travel network density.
The predicted values, as illustrated in the figure, follow a smooth daily transition trend. This is because the model follows a Bayesian probabilistic approach, where the predicted values for t are based on a prior of the prediction values at t-1. This is unlike the reported data which is more scattered. However, the predicted values have a similar profile and follow the trend of the reported cases. For epidemiological modelling, what matters is to identify the general trend where the peaks of the outbreak are probably arising.
Across these six weeks, our forecasted infections had an average per-day over-predictive fractional error of 2%. After comparing daily deaths for this period, a slightly higher error of 3% was observed. The model estimated a total of 170 deaths (95% CI: 136–197) during the six weeks. This suggests that the forecast reliability of the model proposed here is relatively higher than the comparative models in studies using the ICL model as the theoretical basis. It appears to confirm the link between mobility and transmission contact rate, while also explaining the usability of the proposed value in modelling the time-variant impact of NPI implementation and epidemic spread.
4.7. Predicting epidemic progression in alternate NPI implementation scenarios
The actual relation between the fluctuations in effective reproduction number and NPI measures is among the key unknowns of any strategy for curtailing the epidemic spread and is attempted in several studies through empirical models. None of the studies have presented a viable parameter to identify the changes in mobility caused by these preventive actions that directly result in changing the transmission contact rate. The model presented in this study can be a useful tool for not only calculating the infections and death toll evolution due to the COVID-19 pandemic but also for predicting the potential changes in epidemiological data considering the possibility of non-implementation or extension of the different NPI measures. Some benefits of this include, painting an empirical picture of the reduction in patients and fatalities as a direct consequence of these NPIs, and a potential exit strategy directed by well-aimed and timed NPIs. The key factor for determining the NPI effect is the impact in terms of change in population contacts during this hypothetical epidemic evolution. The Bayesian model presented in this study estimates the time-variant values by considering changes in travel network density as an input in a modified Cox's hazard model.
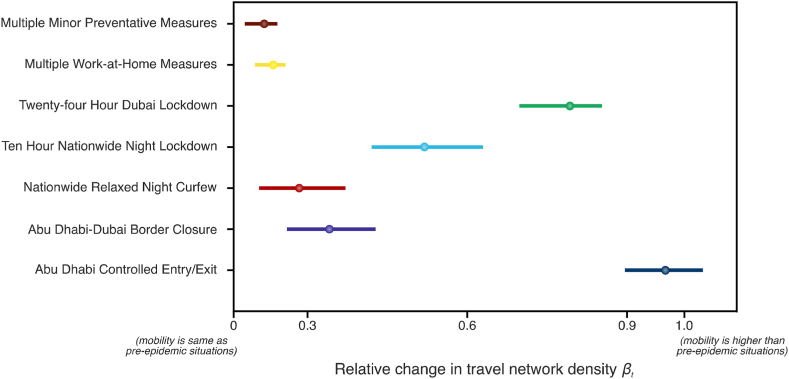
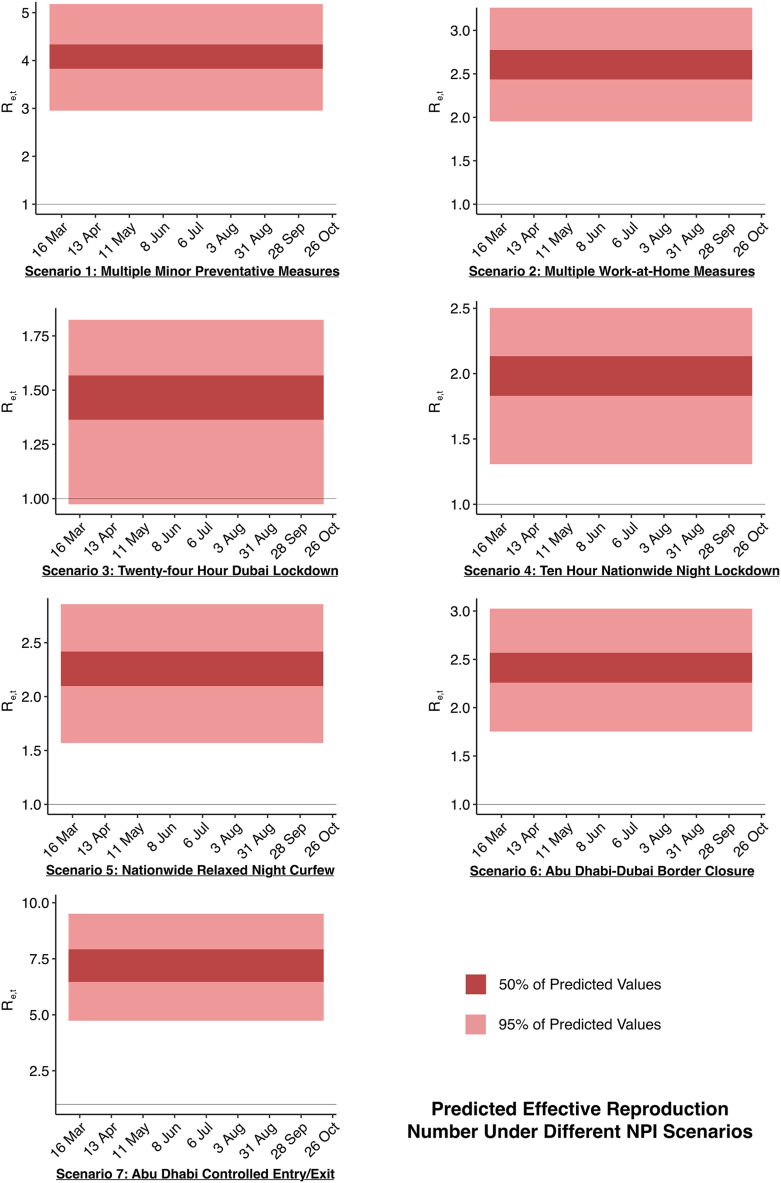
Considering the need for an amalgamation of several deterrent NPI measures to keep the COVID-19 pandemic under control, the individual impact of each action against values needs to be estimated that can reflect upon the success of keeping over the long-term at the country level as we progress towards normalcy in the post-epidemic era. For this, we analysed scenarios for each NPI measure, allowing for the application of only one NPI in each scenario and estimating the change in that could be representative of the corresponding infections and deaths attributable to COVID-19. To achieve this, the temporal distribution of associated with the implementation of each NPI is projected over the entire analysis time horizon using their statistical distribution plots. In Fig. 9, we have presented our estimates for these values under the seven hypothetical intervention scenarios. If then it implies an increase in population mobility during the epidemic. If means that the implementation of NPI measures failed in producing any change in mobility, while the values in the middle range describe the relative change in due to NPIs. The associated projected results for these projected values are shown in Fig. 10.
Fig. 9.
Mean relative change in travel network density with 95% CIs for each NPI compared to the pre-epidemic condition.
Fig. 10.
Comparison of the Re,t values and 50% and 95% CIs between different NPI implementation scenarios for the analysed country of UAE at the baseline time horizon (Jan 29, 2020 to Oct 18, 2020) predicted by changes in network travel density.
Analysing the temporal plots, the first observation is that the scale of is noticeably influenced by the change in value as it is significantly varied between all scenarios. The highest values were calculated for the scenario similar to the seventh NPI where only the border between the highly populated southern and northern emirates is controlled, allowing for the movement of only negatively tested individuals through the borders. Results show that if this NPI was in place from the first case to the present, would have been on average 406% higher at 7.2 (95% CI: 4.74–9.68). The second highest value range of 186% was in scenario 1 at (95% CI: 2.78–5.18) where an extension of the first governmental response was presumed throughout the epidemic and ending on Oct 18, 2020. Only minor measures such as cancelling flights, dissuading mass gatherings, postponement of large public events, and closure of educational institutes were devised here.
On the other hand, a complete border closure from scenario 6 shows considerably lower values which were 75% more than the current situation at 2.4 (95% CI: 1.58–3.07). Similar values of (95% CI: 1.75–3.31) were computed in the 2nd scenario where it was assumed that no restrictions apart from mandating remote work and suspension of public transport is implemented. In contrast, if we assume the 3rd scenario of a 24-hr lockdown in Dubai and limited mobility in the rest of the country, we can foresee a significantly lowered (95% CI: 0.95–1.86). Even though this range exhibits a possible scenario where the transmission rate is kept under control well before the pandemic reaches critical levels, a 24-hr long-term lockdown to limit mobility is not realistic due to substantial economic impacts. When we considered more realistic lockdown options, the two scenarios of 10-hr night-time (scenario 4) and partially restricting night-time mobility and public gatherings (scenario 5) also had low values at (95% CI: 1.25–2.53) and (95% CI: 1.47–2.86), respectively. This shows that although the was falling before the lockdown through multiple small actions, potentially staying at , an extension or early implementation of the lockdown, realistically either of the two night-time lockdowns, may have resulted in a hypothetical decrement of the outbreak. These impacts are assumed considering that no alternate prevention measures have been applied, additionally, the reduction in the epidemic spread is dependent upon the early implementation date of the individual NPIs. Nonetheless, the model provided different inferences for each NPI scenario. It can be beneficial for assessing the efficacy of control measures and a controlled exit strategy may also be deducible by analysing this data under several developed scenarios with varying degrees of lockdown measures.
5. Conclusion
Estimating the number of infections and deaths due to COVID-19 is the key to understanding the infection dynamics of the pandemic. Although many studies have scaled between the infection and fatality rates from statistical models and actual epidemic data for a target country, such strategies often depend upon several assumptions about transmission contact rates and population mobility trends that often cannot fully reflect the real situation. Many of the studies were performed over a year ago and rely on limited data ending at the start of the epidemic when the wide ranges of NPI measures were in early implementation stages and any definite associated trends or peaks were not realised. Some of the studies used realistic infection-to-death probability distributions and serial intervals based on detailed analysis of the actual epidemic spread data, yet the infections and deaths were underreported in the studied countries due to lack of testing, while the predicted values were exceptionally overestimated.
This generates a high degree of unreliability over these results and models due to poor data quality. To address these gaps, we have developed a new algorithm for control of COVID-19 spread by merging mobility data, Bayesian epidemiological models initially proposed by the team at ICL which allows for pandemic time-series modelling through reported death toll, and network theory for geo-temporal mobility matrices. Due to the central role played by transmission contact rate in spreading the disease, a network density parameter is introduced as a ratio between the number of individuals staying and passing through any given area. This model is expected to not only help decision-makers in establishing disease control but also help in assessing the efficacy of different control measures for an optimum NPI scenario that balances economical and epidemiological gains. It can thus also provide a solid data-driven exit strategy towards normalcy.
The model accounts for the time-delay between infection onset and death based on reported intervals, which is also supported by the correlation analyses of and epidemic data as an integral part of the modelling approach together with country-specific case fatality ratio (CFR) that can be readily changeable based on the analysed country. Considering the rapid change in mobility patterns due to the implementation of NPI measures, a modified hazard model is used to predict . The model assumes the entire population as susceptible without regard for immunisation or the effect of vaccination as pre-vaccination period data was used, because this paper focuses on assessing different NPIs at an early pandemic stage when no vaccines are available, and the only way to reduce the spread is through NPIs. The time-variant effective reproduction numbers are then used to calculate Bayesian probabilistic estimates of infections and deaths due to COVID-19. Owing to the high reporting accuracy of pandemic data in the UAE compared to other countries, as exhibited by it being the fourth most tested country in the world, it is used as a case study country. High data resolution daily mobility maps from Facebook are used to estimate the population density and the number of people travelling through any area at a given time is used as input for travel networks.
This paper makes a theoretical contribution by examining the suitability of including a mobility input parameter in epidemiological modelling. Generally, NPIs were effective in changing the mobility patterns of the local population as the changes in were highly correlated with those in . Our model estimates exhibited a strong correspondence with the observed infections and fatalities and compared to other similar models that lacked a mobility input parameter, the lower- and upper-bound values had fewer uncertainties with infections and deaths overestimation which suggests a strong case for using mobility-based for accurate estimates of infections and deaths. This provides a detailed data-driven technique to track the current progression of the disease as well as project the results of the existing lockdown measures, supported by visual interlink between the observed and calculated infections and mobility fluctuations for predicting epidemic outbreak. The model created using baseline nine months data from Jan 29, 2020 to Oct 18, 2020 was used to predict a further six weeks of infections and death toll between 18 Oct and end-November 2020. The model indicated an overprediction error of and for daily infections and deaths, respectively. Long-term identification of effective NPI strategies is an incrementally significant policy objective. To that end, scenario modelling for each NPI implemented in the case study country is performed to provide the consequent estimates in terms of value. The results show the applicability of our model as a useful tool for governments to dynamically adjust their counter-measures using anonymised real-time mobility data and influence the outbreak trajectory of the epidemic. In a further study, we will re-evaluate our modelling approach against data from the post-vaccination period and propose adjustment factors that consider population immunity.
Declaration of competing interest
None.
Handling editor: Dr Lou Yijun
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Facebook has collected extensive social media data of people travelling between different geographical zones. Data collection methodology is described in Maas et al. (2019). Dataset contains aggregated anonymised spatiotemporal data as movement vectors of Facebook services (Facebook, Instagram, and WhatsApp messaging application) users between geographical zones that are represented by standardised map tiles.
References
- Al-Hosani F., Al-Mazrouei S., Al-Memari S., Koornneef E. A review of COVID-19 mass testing in the United Arab Emirates [policy and practice reviews] Frontiers in Public Health. 2021;9(528) doi: 10.3389/fpubh.2021.661134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aleta A., Martín-Corral D., Bakker M.A., Longini I.M. Quantifying the importance and location of SARS-CoV-2 transmission events in large metropolitan areas. Proceedings of the National Academy of Sciences. 2020;119(26):1–8. doi: 10.1073/pnas.2112182119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ali A., Alshammari F.S., Islam S., Ullah S. Modeling and analysis of the dynamics of novel coronavirus (COVID-19) with Caputo fractional derivative. Results in Physics. 2021;20 doi: 10.1016/j.rinp.2020.103669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Awais M., Alshammari F.S., Ullah S., Islam S. Modeling and simulation of the novel coronavirus in Caputo derivative. Results in Physics. 2020;19 doi: 10.1016/j.rinp.2020.103588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brauner J.M., Mindermann S., Sharma M., Mikulik V. Inferring the effectiveness of government interventions against COVID-19. Science. 2021;371(6531) doi: 10.1126/science.abd9338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryant P., Elofsson A. Estimating the impact of mobility patterns on COVID-19 infection rates in 11 European countries. PeerJ. 2020;8 doi: 10.7717/peerj.9879. e9879-e9879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camacho A., Bouhenia M., Alyusfi R., Sagrado M.J. Cholera epidemic in Yemen, 2016–18: An analysis of surveillance data. Lancet Global Health. 2018;6(6):e680–e690. doi: 10.1016/S2214-109X(18)30230-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Candido Darlan S., Claro Ingra M., de Jesus Jaqueline G., Faria Nuno R. Evolution and epidemic spread of SARS-CoV-2 in Brazil. Science. 2020;369(6508):1255–1260. doi: 10.1126/science.abd2161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang S., Pierson E., Koh P.W., Leskovec J. Mobility network models of COVID-19 explain inequities and inform reopening. Nature. 2021;589(7840):82–87. doi: 10.1038/s41586-020-2923-3. [DOI] [PubMed] [Google Scholar]
- Chinazzi M., Davis J.T., Ajelli M., Vespignani A. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368(6489):395. doi: 10.1126/science.aba9757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chin V., Ioannidis J.P.A., Tanner M.A., Cripps S. Effect estimates of COVID-19 non-pharmaceutical interventions are non-robust and highly model-dependent. Journal of Clinical Epidemiology. 2021;136:96–132. doi: 10.1016/j.jclinepi.2021.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chu Y.-M., Ali A., Khan M.A., Ullah S. Dynamics of fractional order COVID-19 model with a case study of Saudi Arabia. Results in Physics. 2021;21 doi: 10.1016/j.rinp.2020.103787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotta R.M., Naveira-Cotta C.P., Magal P. Mathematical parameters of the COVID-19 epidemic in Brazil and evaluation of the impact of different public health measures. Biology. 2020;9(8) doi: 10.3390/biology9080220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D.R. Regression models and life tables (with discussion) Journal of the Royal Statistical Society. 1972;34(2):187–220. [Google Scholar]
- Crisis24 . 2020. UAE: Highest daily increase of COVID-19 cases reported October 13/update 56.https://crisis24.garda.com/alerts/2020/10/uae-highest-daily-increase-of-covid-19-cases-reported-october-13-update-56 GardaWorld. [Google Scholar]
- Di Domenico L., Pullano G., Sabbatini C.E., Colizza V. Impact of lockdown on COVID-19 epidemic in Île-de-France and possible exit strategies. BMC Medicine. 2020;18(1):1–13. doi: 10.1186/s12916-020-01698-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Y., Nie Y., Penny M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions: A data-driven analysis. Journal of Medical Virology. 2020;92(6):645–659. doi: 10.1002/jmv.25750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández-Recio J. Modelling the evolution of COVID-19 in high-incidence European countries and regions: Estimated number of infections and impact of past and future intervention measures. Journal of Clinical Medicine. 2020;9(6):1825. doi: 10.3390/jcm9061825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flaxman S., Mishra S., Gandy A., Imperial College C.-R.T. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. 2020;584(7820):257–261. doi: 10.1038/s41586-020-2405-7. [DOI] [PubMed] [Google Scholar]
- Goscé L., Phillips P.A., Spinola P., Abubakar P.I. Modelling SARS-COV2 spread in London: Approaches to lift the lockdown. Journal of Infection. 2020;81(2):260–265. doi: 10.1016/j.jinf.2020.05.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasan U., Whyte A., Al Jassmi H. Assessing lifecycle environmental footprint of autonomous mass-mobility for urban highways by microsimulation-modelling. SSRN Electronic Journal. 2021 doi: 10.2139/ssrn.3991829. [DOI] [Google Scholar]
- Hasell J., Mathieu E., Beltekian D., Ritchie H. A cross-country database of COVID-19 testing. Scientific Data. 2020;7(1):345. doi: 10.1038/s41597-020-00688-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoertel N., Blachier M., Blanco C., Leleu H. A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nature Medicine. 2020;26(9):1417–1421. doi: 10.1038/s41591-020-1001-6. [DOI] [PubMed] [Google Scholar]
- Huang Y., Yang L., Dai H., Chen K. Epidemic situation and forecasting of COVID-19 in and outside China. Bulletin of the World Health Organization. 2020 doi: 10.2471/BLT.20.255158. [DOI] [Google Scholar]
- Jia W., Han K., Song Y., Li J. Extended SIR prediction of the epidemics trend of COVID-19 in Italy and compared with Hunan, China. medRxiv. 2020 doi: 10.1101/2020.03.18.20038570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau M.S.Y., Grenfell B., Thomas M., Lopman B. Characterizing superspreading events and age-specific infectiousness of SARS-CoV-2 transmission in Georgia, USA. Proceedings of the National Academy of Sciences. 2020;117(36) doi: 10.1073/pnas.2011802117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau H., Khosrawipour V., Kocbach P., Khosrawipour T. The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. Journal of Travel Medicine. 2020 doi: 10.1093/jtm/taaa037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei H., Wu X., Wang X., Shu Y. Different transmission dynamics of COVID-19 and influenza suggest the relative efficiency of isolation/quarantine and social distancing against COVID-19 in China. Clinical Infectious Diseases: An Official Publication of the Infectious Diseases Society of America. 2020 doi: 10.1093/cid/ciaa1584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung K., Wu J.T., Leung G.M. Real-time tracking and prediction of COVID-19 infection using digital proxies of population mobility and mixing. Nature Communications. 2021;12(1):1–8. doi: 10.1038/s41467-021-21776-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li D., Liu Z., Liu Q., Wang Q. Estimating the efficacy of quarantine and traffic blockage for the epidemic caused by 2019-nCoV (COVID-19): A simulation analysis. medRxiv. 2020 doi: 10.1101/2020.02.14.20022913. [DOI] [Google Scholar]
- Lin Q., Zhao S., Gao D., He D. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. International Journal of Infectious Diseases. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R., Pei S., Chen B.…Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368(6490):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maas P., Iyer S., Gros A., Dow P.A. Proceedings of the 16th International Conference on Information Systems for Crisis Response and Management (ISCRAM); Valencia, Spain: 2019. Facebook disaster maps: Aggregate insights for crisis response and recovery. [Google Scholar]
- Manevski D., Ružić Gorenjec N., Kejžar N., Blagus R. Modeling COVID-19 pandemic using Bayesian analysis with application to Slovene data. Mathematical Biosciences. 2020;329 doi: 10.1016/j.mbs.2020.108466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Our World in Data . 2021. Total COVID-19 tests per 1,000 people. Aug 6, 2021 ourworldindata.org/coronavirus-testing#source-information-country-by-country. [Google Scholar]
- Pepe E., Bajardi P., Gauvin L., Tizzoni M. COVID-19 outbreak response, a dataset to assess mobility changes in Italy following national lockdown. Scientific Data. 2020;7(1):1–7. doi: 10.1038/s41597-020-00575-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perra N. Non-pharmaceutical interventions during the COVID-19 pandemic: A review. Physics Reports. 2021;913:1–52. doi: 10.1016/j.physrep.2021.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price D.J., Shearer F.M., Meehan M.T., Wood J. Early analysis of the Australian COVID-19 epidemic. Elife. 2020;9 doi: 10.7554/eLife.58785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Report S. How domestic tourism in the UAE has surged 107% during coronavirus crisis. Arabian Business. 2020 https://www.arabianbusiness.com/industries/travel-hospitality/456228-how-domestic-tourism-in-the-uae-has-surged-107-during-coronavirus-crisis?fbclid=IwAR1JOqNFUQrP8d9gZLNu-x-hwIpKw3R-4Yaa33CiHFDELj4MGcQGwQ5g6zs [Google Scholar]
- Rodrigue J.-P. The geography of transport systems. 5th ed. Routledge; 2020. Appendix A.6 – graph theory: Measures and indices; p. 480. [Google Scholar]
- Ruktanonchai N.W., Floyd J.R., Lai S., Tatem A.J. Assessing the impact of coordinated COVID-19 exit strategies across Europe. Science. 2020;369(6510):1465–1470. doi: 10.1126/science.abc5096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staff R. Reuters; 2020. UAE lifts coronavirus-related curfew: Tweet.https://www.reuters.com/article/us-health-coronavirus-uae-idUSKBN23V2ZE [Google Scholar]
- TDRA . 2021. Gradual return to normal life after the outbreak of COVID-19.https://u.ae/en/information-and-services/justice-safety-and-the-law/handling-the-covid-19-outbreak/gradual-return-to-normal-life-after-the-outbreak-of-covid-19 [Google Scholar]
- Theobald D.M. In: Crooks K.R., Sanjayan M., editors. Vol. 14. Cambridge University Press; 2006. Exploring the functional connectivity of landscapes using landscape networks; p. 732. (Connectivity conservation). [Google Scholar]
- Verity R., Okell L.C., Dorigatti I., Ferguson N.M. Estimates of the severity of coronavirus disease 2019: A model-based analysis. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu B., Gutierrez B., Mekaru S., Kraemer M.U.G. Epidemiological data from the COVID-19 outbreak, real-time case information. Scientific Data. 2020;7(1):106. doi: 10.1038/s41597-020-0448-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan C. A simple model to assess Wuhan lock-down effect and region efforts during COVID-19 epidemic in China Mainland. medRxiv. 2020 doi: 10.1101/2020.02.29.20029561. [DOI] [Google Scholar]