Abstract

Time-dependent density functional theory has become state-of-the-art for describing photophysical and photochemical processes in extended materials because of its affordable cost. The inclusion of exact exchange was shown to be essential for the correct description of the long-range asymptotics of electronic interactions and thus a well-balanced description of valence, Rydberg, and charge-transfer excitations. Several approaches for an efficient treatment of exact exchange have been established for the ground state, while implementations for excited-state properties are rare. Furthermore, the high computational costs required for excited-state properties in comparison to ground-state computations often hinder large-scale applications on periodic systems with hybrid functional accuracy. We therefore propose two approximate schemes for improving computational efficiency for the treatment of exact exchange. Within the auxiliary density matrix method (ADMM), exact exchange is estimated using a relatively small auxiliary basis and the introduced basis set incompleteness error is compensated by an exchange density functional correction term. Benchmark results for a test set of 35 molecules demonstrate that the mean absolute error introduced by ADMM is smaller than 0.3 pm for excited-state bond lengths and in the range of 0.02–0.04 eV for vertical excitation, adiabatic excitation, and fluorescence energies. Computational timings for a series of covalent-organic frameworks demonstrate that a speed-up of at least 1 order of magnitude can be achieved for excited-state geometry optimizations in comparison to conventional hybrid functionals. The second method is to use a semiempirical tight binding approximation for both Coulomb and exchange contributions to the excited-state kernel. This simplified Tamm–Dancoff approximation (sTDA) achieves an accuracy comparable to approximated hybrid density functional theory when referring to highly accurate coupled-cluster reference data. We find that excited-state bond lengths deviate by 1.1 pm on average and mean absolute errors in vertical excitation, adiabatic excitation, and fluorescence energies are in the range of 0.2–0.5 eV. In comparison to ADMM-approximated hybrid functional theory, sTDA accelerates the computation of broad-band excitation spectra by 1 order of magnitude, suggesting its potential use for large-scale screening purposes.
1. Introduction
The description of excited states in large extended systems using quantum-mechanical approaches is still a challenge for theoretical spectroscopy.1 In contrast to the electronic ground state, the quest of finding an appropriate model with a well-balanced accuracy–cost ratio for the excited state is complicated by various electronic states of different natures having to be described simultaneously. For instance, this renders the parametrization of transferable classical force fields for excited states an almost impractical task. The cost of highly accurate wave function methods scales prohibitively with system size, making routine large-scale applications impossible. When a robust and efficient tool set for the treatment of extended periodic systems is the aim, density functional theory and semiempirical tight binding approaches therefore represent a suitable compromise. While time-dependent density functional theory (TDDFT) has been established as efficient and broadly applicable for the treatment of excited states,2,3 there has also been a recent revival of semiempirical approaches to extend treatable system sizes from hundreds to thousands of atoms.4 Both the re-emergence of semiempirical methods as well as the continuing improvement of density functional approximations are among the most important future developments in computational chemistry.5
The correct description of exact exchange has proven to be crucial for an adequate treatment of excited states in TDDFT. It has a much greater influence on the geometrical displacement upon excitation, and thus on transition energies and spectra, than the exchange-correlation functional.6 Benchmarks on molecular systems, including radicals and ions, suggest including 30–40% exact exchange to obtain reliable spectroscopic data.6 Straight-forward evaluation of the two-electron exact exchange integrals leads to a formal scaling of N4 with system size N for localized basis sets, emphasizing the need for more cost-efficient approximation schemes. An overview of recent developments and the various existing algorithms can, e.g., be found in ref (7). One approach is the auxiliary density matrix method (ADMM),8 where the gain in efficiency is achieved by evaluating a model exact exchange energy within a relatively small auxiliary basis augmented by a correction term based on a local exchange functional. The assumption that the basis set incompleteness error can be corrected in terms of a cost-efficient density functional correction term was shown to be well-founded,7 and benchmarks including liquids, solids as well as proteins in solution with up to 3000 atoms revealed that memory requirements and computational efficiency are improved by at least 1 order of magnitude.8 Kumar et al. showed that ADMM achieves good accuracy for ground- and excited-state energies, even though rather large errors were found for polarizabilities and hyperpolarizabilities.9 The least complex variant of ADMM is based on a simple least-squares fitting projection of molecular orbitals onto the smaller auxiliary basis. More sophisticated ADMM variants have been proposed including density matrix purification and projections enforcing orthogonality or charge constraints.7 In a comparison among the developed ADMM variants, additional constraints as well as an adequate choice of the exchange functional for the correction term were shown to further improve accuracy for total energies while retaining a comparable efficiency. With respect to other sophisticated exact exchange algorithms10 including the pair-atomic resolution-of-the-identity method (PARI-K)11,12 and the chain-of-spheres algorithm (COSX),13−16 total as well as orbital, reaction, and atomization energies were found to be 1 to 3 orders of magnitude less accurate. However, ADMM achieves a computational efficiency comparable to the cost required for density fitting Coulomb algorithms. ADMM was thus classified as a promising model with an “impressive speedup”, encouraging further development to improve accuracy and calling for careful optimization of the required auxiliary basis sets.10
For even larger system sizes of several thousands of atoms, it is necessary to go from ab initio excited-state calculations toward semiempirical tight binding approximations. In recent years, a class of tight binding approaches was suggested by Grimme et al.,4 on the basis of the idea of reducing the computational effort of electron repulsion integrals while retaining an adequate description of the physics of electronic interactions. More specifically, Coulomb and exchange contributions are approximated using an electron repulsion operator that captures the correct long-range 1/R asymptotics by construction17−19 but allows for a short-range empirical parametrization. It was shown that this choice provides a balanced description of valence, charge-transfer as well as Rydberg states. The developed methods were dubbed simplified TDDFT (sTDDFT)20 or simplified Tamm–Dancoff approximation (sTDA)21,22 corresponding to the related ab initio electronic structure method and were extended to treat, e.g., spin-flip excitations23−26 or to be combined with the idea of range separation.27 In contrast to other common tight binding approaches like density functional-based tight binding (DFTB),28 sTDA and sTDDFT involve only a limited number of global parameters, which enables their straightforward application over the whole periodic table.29 Benchmark results demonstrated that the simplified approaches achieve computational savings of at least 2 orders of magnitude while the loss in accuracy is minor with an average deviation of 0.2–0.3 eV for excitation energies when compared to conventional TDDFT or experiments. Using a semiempirical ground-state reference, sTDA errors were found to be slightly larger with mean absolute deviations in the range of 0.3–0.5 eV. Most importantly, accuracy was found to be consistent for both the low-energy valence as well as the high-energy Rydberg transitions.21,22 Simplified approaches were also suggested for the Bethe–Salpeter equation (BSE) and the GW approximation.30 These methods provided sGW ionization potentials within the GW100 test set differing only by 0.2 eV while improving the cubic scaling with system size. Deviations in sBSE excitation energies amount up to 0.5 eV and are thus in an error range comparable to those of sTDA and sTDDFT.30 A closely related TDDFT+TB approach has been suggested by Visscher et al. that relies on the same monopole approximation for the electron repulsion integrals but is, in contrast to sTDA and sTDDFT, not designed for hybrid but rather pure density functionals.31,32
The mentioned advantages of ADMM and sTDA regarding their physically correct description of exact exchange qualify both approaches as promising for an efficient calculation of excited-state properties. Excited-state gradients within the framework of linear response TDDFT were pioneered for molecular systems by Van Caillie and Amos33,34 as well as Furche and Ahlrichs.35,36 This work was extended to periodic systems and plane wave basis sets.37 Furthermore, TDDFT excited-state properties for exact exchange have been extended to global and local hybrid functionals38,39 as well as range separation.40 Implementations are also available for tight binding approaches including long-range corrections.41 However, algorithms are most often restricted to molecular systems. We implemented sTDA- and ADMM-approximated hybrid density functional excited-state gradients based on the Gaussian and plane wave (GPW) framework within the CP2K program package.42−44 The GPW methods allow for a natural extension of algorithms to periodic boundary conditions and thus enable the treatment of extended systems. The implementation is based on earlier works of Iannuzzi et al.45 and Strand et al.46 already featuring the calculation of ADMM excitation energies for model systems of up to 1000 atoms.47 As outlined in section 2.1, the CP2K implementation is based on the Sternheimer equations,48−50 thus depending solely on the occupied molecular and atomic orbital space. Such a formulation requires, e.g., adjustments in the formulation of the ADMM equations and the sTDA eigenvalue problem (see sections 2.2 and 2.3). Going from molecular to periodic systems also requires Coulomb interactions to be treated using Ewald summation techniques and the minimum image approximation to capture exact exchange (see section 2.4). We tested our excited-state gradient implementations using a molecular benchmark set of Jacquemin et al.,51 which is one of the state-of-the-art test sets for excited-state properties. ADMM-approximated hybrid functional and semiempirical sTDA kernels are compared to conventional hybrid functional TDDFT exploiting the therein provided EOM-CCSD geometries and excited-state (ES) data. Finally, in section 3.2, the computational efficiency of the proposed algorithms is demonstrated by applications on porous covalent-organic framework (COF) materials taken from the CURATED COFs database.52,53
2. Theoretical Background
2.1. The Tamm–Dancoff Approximation
Within the Tamm–Dancoff approximation,54 the excitation energy Ω and corresponding excited-state eigenvectors X for each excited state are defined in terms of the variational Lagrangian G
| 1a |
| 1b |
| 1c |
implying the stationary conditions
| 2 |
| 3 |
| 4 |
Equation 2 represents
a hermitian eigenvalue problem that is
for molecular orbital (MO)-based formulations solved under the constraint
that the excited-state eigenvectors remain orthonormalized (eq 3).55 The Lagrange multiplier introducing the normalization constraint
of eq 3 is thereby chosen
to be equal to the excitation energy Ω according to the canonical
gauge (eq 1b). In an
atomic orbital (AO)-based formalism relying solely on occupied MOs,
{i, j, k, l, ... }, and AOs, {μ, ν, κ, λ,
... }, it furthermore has to be ensured that the excited-state eigenvector X is orthogonal to the ground-state (GS) MO coefficients C (eq 4), a constraint
introduced in the Lagrangian G via the Lagrange multiplier  (eq 1c)
(eq 1c)
| 5 |
By taking the derivative of G with respect to the excited-state eigenvectors X and projecting onto the occupied MO coefficients C, it can be shown that this second normalization constraint represents a projection of the kernel contributions onto the virtual space, already inserted in the eigenvalue problem of eq 2 in terms of the projection operator Q
| 6 |
| 7 |
Thus, the contribution of the  constraint to eq 2 is
taken into account by inserting Q, a reformulation that
is given in detail in section 1 of
the Supporting Information. Both Ω
and
constraint to eq 2 is
taken into account by inserting Q, a reformulation that
is given in detail in section 1 of
the Supporting Information. Both Ω
and 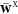 constraints are ensured in the
TDDFT module
of CP2K by explicitly orthonormalizing the ES eigenvectors as well
as by orthogonalizing the ES eigenvectors with respect to the MO coefficients
at each step of the Davidson algorithm. Equation 5 implies the transformation rules from AO
to MO basis and vice versa, which are given for vectors V and matrices M in general as
constraints are ensured in the
TDDFT module
of CP2K by explicitly orthonormalizing the ES eigenvectors as well
as by orthogonalizing the ES eigenvectors with respect to the MO coefficients
at each step of the Davidson algorithm. Equation 5 implies the transformation rules from AO
to MO basis and vice versa, which are given for vectors V and matrices M in general as
| 8 |
| 9 |
| 10 |
| 11 |
with the overlap matrix S being defined in terms of the AOs φμ(r)
| 12 |
Depending on the applied density functional, the eigenvalue
problem
of eq 2 comprises one-electron h, Coulomb J, and exact exchange KEX contributions as well as contributions because of the
exchange-correlation (XC) potential 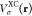 or kernel
or kernel  , with the Kohn–Sham matrix F and the kernel matrix K being defined as
, with the Kohn–Sham matrix F and the kernel matrix K being defined as
 |
13 |
 |
14 |
where aEX is a global parameter to scale the amount of exact exchange and the two-electron repulsion integrals are defined as
| 15 |
The corresponding density matrices D and DX are defined based on the MO coefficients C implying symmetrization
| 16 |
| 17 |
Symmetrization is necessary to ensure that the linear response density is real. Furthermore, within the implementation for periodic systems using a Γ-point only description, we can assume real wave functions. The basis functions and MOs are periodically replicated, integrals are over the computational unit cell, and all Coulomb terms evaluated using Ewald sums.
2.2. Exact Exchange Using the Auxiliary Density Matrix Method (ADMM)
The basic idea of ADMM7,56 is to introduce a small and rapidly decaying auxiliary density matrix  to speed up the calculation of the exact
Hartree–Fock exchange matrix, KEX,
with the latter being evaluated within a smaller auxiliary basis,
to speed up the calculation of the exact
Hartree–Fock exchange matrix, KEX,
with the latter being evaluated within a smaller auxiliary basis,  . The
total exchange energy contribution
to the ES energy is thus approximated by a model term,
. The
total exchange energy contribution
to the ES energy is thus approximated by a model term,  , and to compensate the
so-introduced basis
set incompleteness error, a correction term based on a local density
functional EGGA is added
, and to compensate the
so-introduced basis
set incompleteness error, a correction term based on a local density
functional EGGA is added
| 18 |
Different approaches have been developed
to obtain the auxiliary density matrix  and corresponding MO coefficients
and corresponding MO coefficients  , e.g., by minimizing solely the square
difference between the occupied orbital and auxiliary basis functions
or by adding an orthonormality constraint to the fitting procedure.
We will restrict the discussion to the ADMM2 variant, which is often
also dubbed nonpurified wave function fitting and which can be expressed
in terms of the projection matrix
, e.g., by minimizing solely the square
difference between the occupied orbital and auxiliary basis functions
or by adding an orthonormality constraint to the fitting procedure.
We will restrict the discussion to the ADMM2 variant, which is often
also dubbed nonpurified wave function fitting and which can be expressed
in terms of the projection matrix 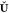 . For the sake of convenience, we will nevertheless
refer to ADMM2-approximated results in the following by the general
acronym ADMM. Auxiliary basis functions and corresponding auxiliary
matrices are indicated as
. For the sake of convenience, we will nevertheless
refer to ADMM2-approximated results in the following by the general
acronym ADMM. Auxiliary basis functions and corresponding auxiliary
matrices are indicated as  and
and  . The projection matrix
. The projection matrix 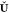 is obtained according to
is obtained according to
| 19 |
| 20 |
| 21 |
based on the overlap matrices 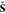 and
and  of the auxiliary and mixed auxiliary-primary
basis
of the auxiliary and mixed auxiliary-primary
basis
| 22 |
| 23 |
The exact exchange matrix KEX (eq 14) is thus approximated within ADMM as
| 24 |
with the local GGA exchange density functional correction term
| 25 |
If relying also on an ADMM-approximated GS reference, exchange contributions to the KS matrix F of eq 13 imply an analogous correction with the second term of eq 24 now depending on the XC potential
| 26 |
2.3. Semiempirical Coulomb and Exchange Contributions within the Simplified Tamm–Dancoff Approximation (sTDA)
In contrast to conventional TDA, sTDA21 neglects all contributions because of the exchange-correlation kernel and approximates the remaining two-electron repulsion integrals based on the semiempirical Mataga–Nishimoto–Ohno–Klopman operator γ(A, B).17−19 The simplified kernel contribution to eq 2 is given as
| 27 |
with γ(A, B) describing either Coulomb (J) or exchange (EX) interactions depending on the interatomic distance RAB of atoms A and B
| 28 |
| 29 |
Note that the nomenclature classifying eqs 28 and 29 as exchange- or Coulomb-like interaction operators differs from the original paper21 to match with the definitions for ADMM. The parameter s is equal to −1 for singlet closed-shell wave functions. For triplet closed-shell, it is set to s = 1 and for open-shell wave functions to s = 0. Four different global parameters are included. The chemical hardness η, which is specified for each element according to ref (57), powers of α and β allowing to modify the distance dependence of γ independently for either Coulomb or exchange interactions, and, analogously to conventional TDA, a Fock-exchange mixing parameter aEX. The latter can be chosen freely, it was adjusted for molecular systems and global hybrids21 and in this case shows the best performance for aEX = 0.5.22 Furthermore, we chose to set γEX(A, B) to zero if aEX = 0. The transition density charge qA is defined as
| 30 |
with the sum over κA running over
all atomic orbitals located at atom A.  or
or  are Löwdin transformed MO coefficients
or excitation vectors and
are Löwdin transformed MO coefficients
or excitation vectors and  and
and  related doubly contracted
intermediates
related doubly contracted
intermediates
| 31 |
| 32 |
2.4. Periodic Boundary Conditions
When the methods are generalized to account for periodic boundary conditions (PBC), an adequate description of the long-range Coulomb forces using Ewald summation techniques is required to ensure convergence of the slowly decaying potential at large distances.58 In the case of sTDA, the Coulomb operator is therefore split into a semiempirical short-range and an exact long-range contribution
| 33 |
implying that the semiempirical electron repulsion
operator  for the short-range
contribution is cut
off at an atom-specific radius Rcut
for the short-range
contribution is cut
off at an atom-specific radius Rcut
 |
34 |
Rcut is defined
according to the cutoff radius of the atomic basis functions and the
function  smoothes the potential around Rcut and
is chosen such that both the first and second
derivative of γJ vanish at the cutoff
borders
smoothes the potential around Rcut and
is chosen such that both the first and second
derivative of γJ vanish at the cutoff
borders
| 35 |
| 36 |
Thus, the polynomial  is constructed to include those terms of
the Taylor expansion of 1/R, which ensure that
is constructed to include those terms of
the Taylor expansion of 1/R, which ensure that 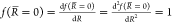 and
and  with integer
expansion coefficients chosen
accordingly, so that
with integer
expansion coefficients chosen
accordingly, so that  for the limit of RAB → Rcut – Rsmooth and
for the limit of RAB → Rcut – Rsmooth and  for RAB → Rcut. Rsmooth defines the width of the smoothing function and
is set to Rsmooth = 1 a.u. The long-range
contribution 1/RAB is calculated using
the smooth particle mesh Ewald method as implemented for tight binding
approaches in CP2K,59 scaling as N logN with system size N. Exchange interactions based on γEX are treated by implying the minimum image convention, thus
restricting the sum over AB to neighbors within the
unit cell.
for RAB → Rcut. Rsmooth defines the width of the smoothing function and
is set to Rsmooth = 1 a.u. The long-range
contribution 1/RAB is calculated using
the smooth particle mesh Ewald method as implemented for tight binding
approaches in CP2K,59 scaling as N logN with system size N. Exchange interactions based on γEX are treated by implying the minimum image convention, thus
restricting the sum over AB to neighbors within the
unit cell.
2.5. The Excited-State Lagrangian in the Tamm–Dancoff Approximation
Nuclear gradients for the excited state are state-of-the-art in many program codes, so that the general procedure will only be outlined in short to discuss modifications that are necessary for ADMM and sTDA kernels. To avoid the computational cost of calculating the first-order response of the MO coefficients and to take into account the geometry dependence of the AOs, the Lagrangian of eqs 1a, 1b, and 1c needs to be extended by means of two additional constraints and thus is given as
| 37a |
| 37b |
| 37c |
The first additional constraint (eq 37b) ensures the stationarity of the GS Kohn–Sham (KS) equations, the Brillouin condition, which can be rearranged using the definition of Q to emphasize the equivalence with MO-based formulations
| 38 |
Note that only the virtual-occupied part of
the Z vector 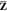 is taken into account and that the occupied–occupied
part is implied to be zero
is taken into account and that the occupied–occupied
part is implied to be zero
| 39 |
The second additional constraint (eq 37c) ensures the orthogonality of the occupied
MOs and, in analogy to  and
and  , the hereby introduced Lagrange multiplier
, the hereby introduced Lagrange multiplier 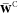 is assumed to be symmetric.
is assumed to be symmetric.  and
and  are determined by taking the derivative
of L with respect to the MO coefficients C and projecting onto either the virtual or occupied orbital space
are determined by taking the derivative
of L with respect to the MO coefficients C and projecting onto either the virtual or occupied orbital space
| 40 |
The final equations for the 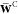 multiplier are given as
multiplier are given as
| 41 |
with the relaxed and unrelaxed difference density matrices P and T being defined as
| 42 |
| 43 |
| 44 |
Note that the unrelaxed difference density matrix T in
the AO basis as defined in eq 44 corresponds to the sum of the virtual–virtual
and occupied–occupied blocks of the corresponding MO matrix TMO with the mixed virtual–occupied blocks
being equal to zero. Regarding the comparison to MO formulations,35,36 the matrix  as defined in eqs 37c, and 41 only comprises
occupied–occupied contributions while analogous MO formulations
treat the combined occupied–virtual space. Contributions referring
to the virtual space of refs (35 and 36) are included in our formalism via Q projections, explicitly
taken into account because of the reformulated Brillouin condition
(eq 38) and the
as defined in eqs 37c, and 41 only comprises
occupied–occupied contributions while analogous MO formulations
treat the combined occupied–virtual space. Contributions referring
to the virtual space of refs (35 and 36) are included in our formalism via Q projections, explicitly
taken into account because of the reformulated Brillouin condition
(eq 38) and the 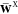 constraint. Furthermore, the intermediate H stems from
the KS matrix contributions of eq 14 and thus the explicit formula
depends on the chosen GS reference, given here for hybrid functionals
with or without ADMM
constraint. Furthermore, the intermediate H stems from
the KS matrix contributions of eq 14 and thus the explicit formula
depends on the chosen GS reference, given here for hybrid functionals
with or without ADMM
| 45 |
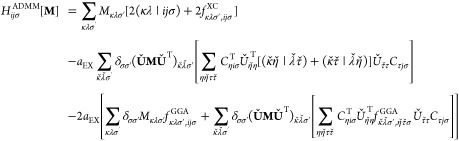 |
46 |
The linear  vector equation
vector equation
| 47 |
| 48 |
contains contributions on the left-hand side, which stem from the KS matrix (eq 13) and are independent of the chosen excited-state kernel K (eq 14). Such a dependence is solely included on the right-hand side R, summarizing a first term stemming from the KS matrix as well as kernel contributions that have to be adjusted for ADMM and sTDA
| 49 |
Finally, the gradient Lζ with respect to the nuclear coordinate ζ can be written in terms of the effective difference density matrix Γ analogously to the formulations of refs (35 and 36)
| 50 |
with the intermediates
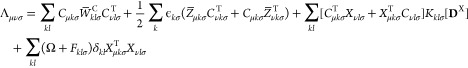 |
51 |
| 52 |
Note that the total nuclear forces sum contributions
because of
the ES energy functional and the additional constraints, as listed
in eq 50, as well as
the GS energy contributions  .
.
Regarding the discussed kernel options, additional terms for the gradient have to be considered for the transformed ADMM matrix of eq 24, with all contributions implying the chain rule
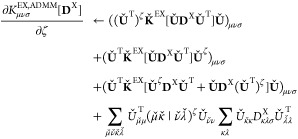 |
53 |
encompassing the gradient
for the ADMM projection
matrix 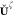 ,
,
| 54 |
Analogous contributions have to be considered for the correction term of eq 25. sTDA kernels bear the advantage that they do not require third-order derivatives of the XC kernel, but additional derivatives of the overlap matrix S1/2(60)
| 55 |
with the eigenvalues s and eigenvectors US of the overlap matrix. On the basis of the outlined Lagrange formalism, nuclear gradients were implemented for both ADMM-approximated hybrid functional theory and semiempirical sTDA in the CP2K program package, relying for the Z vector equation on already available linear response solvers.45,46 Details on the applied Block–Davidson algorithm61 and the preconditioners can, e.g., be found in refs (46 and 62). The current implementation of ES nuclear gradients paves the way for adiabatic and nonadiabatic nuclear dynamics, enabling, e.g., the combination with trajectory surface hopping methods assuming time derivative or empirical coupling vectors.63
3. Results and Discussion
3.1. Tests for Accuracy: Benchmark Results for 35 Main-Group Molecules
To assess the accuracy of ADMM and sTDA excited-state properties, we performed a benchmark on a molecular test set by Budzak et al. containing 35 small molecules. The test set contains main-group atoms of the first and second row as well as sulfur, selenium, chlorine, and bromine. Reported EOM-CCSD geometries were obtained using Gaussian16,64 correlating all electrons (including core electrons) and choosing a def2-TZVPP basis.65 The nature of the GS and ES reference structures was furthermore checked by performing frequency calculations and computing T1 diagnostics. We selected these structures as the highest-accuracy level reference and performed, for comparison, all-electron PBE0 calculations with the Turbomole program package,66 first using the def2-TZVPP basis to unravel the effect of the underlying electronic structure method and then increasing the basis set to def2-QZVPP67 quality to get an estimate for the basis set error. Deviations of PBE0 computations with CP2K to the mentioned EOM-CCSD and PBE0 reference data originate then mainly from core–shells being described in terms of pseudopotentials and correspondingly adapted basis sets. More specifically, we used pseudopotentials and basis sets that were optimized for the PBE0 functional with the numerical atom code of CP2K and that are available within the database and distribution of CP2K.42,68 To check consistency of the chosen CP2K basis sets and pseudopotentials, we investigated a hierarchy of MOLOPT as well as correlation consistent ccGRB-X basis sets. Benchmark data on vertical singlet excitation energies, geometries of the first excited state, adiabatic excitation and fluorescence energies (for PBE0, ADMM-PBE0, and sTDA kernels based on PBE0 and ADMM-PBE0 references) are given for the two basis set families in comparison to EOM-CCSD/def2-TZVPP/Gaussian, PBE0/def2-TZVPP/Turbomole, and PBE0/def2-QZVPP/Turbomole references in the Supporting Information, demonstrating that MOLOPT and ccGRB-X basis sets yield comparable accuracy and that converged results are in general obtained for triple-ζ basis sets. For the sake of convenience, we therefore restrict the following discussion to subsets of MOLOPT type basis sets, concentrating on the assessment of the mentioned excited-state properties regarding (a) the accuracy of ADMM in comparison to conventional hybrid functional TDDFT as well as (b) the comparison of semiempirical sTDA and ADMM-approximated hybrid functional kernels in comparison to highly accurate EOM-CCSD reference data.
Regarding the performed benchmark, a coupling parameter with a default value of aEX = 0.2 was chosen for the exchange contribution for sTDA computations throughout the following discussion. As noted in the Supporting Information, adjustments only had to be made in the case of formyl chloride to avoid dissociation upon ES geometry optimization. A default value for aEX might not correspond to an optimal choice, but a thorough and careful optimization of aEX for the investigated benchmark sets and the assessed extended materials is beyond the scope of this work. The general idea of ADMM is to reduce computational costs of the exact exchange contribution by trading in basis set incompleteness with a GGA correction term. The introduced error is then, however, dependent on both the auxiliary basis set size as well as the chosen exchange density functional. To discriminate between the two error sources, the discussed ADMM calculations for the molecular benchmark set are performed without correction. An optimally chosen GGA exchange functional contribution could improve the discussed results, with the latter representing the lowest limit for the ADMM accuracy. It was, e.g., shown in ref (7) that exchange functionals like KT3X and OPTX improve over PBEX for ground-state properties, but analogous investigations for the excited state are left for future work. For the subsequently discussed assessment of computational timings for periodic systems, we, however, included a PBEX exchange functional correction to account for the additionally required resources.
3.1.1. Excited-State Geometries: Impact of the Auxiliary Basis Set Size for ADMM Kernels
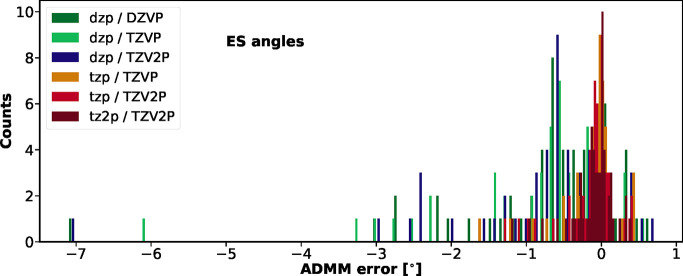
Relaxed excited-state geometries for PBE0 and ADMM-PBE0 kernels using MOLOPT and ccGRB-X basis sets as well as sTDA kernels based on PBE0 and ADMM-PBE0 references are reported in Tables S3 and S4. The data includes a corresponding statistical analysis on the error in the geometrical data with respect to EOM-CCSD/def2-TZVPP, PBE0/def2-TZVPP, and PBE0/def2-QZVPP references (Tables S6–S10). In contrast to the study of ref (51), we excluded first excited states of the eclipsed structures of nitrosomethane and trifluoronitrosomethane as these singlet states represent transition-state structures with an imaginary frequency. Because of the large number of geometries that had to be optimized considering different kernels and basis sets, we calculated vibrational frequencies only for those structures that differed significantly from the reference geometries, ensuring that they represent local minima. In the earlier benchmarks of ref (69), MAEs for bond lengths of GS structures are predicted to be in the range from 0.5 to 1.0 pm for hybrid functionals, with the largest errors found for CO, CN, CS, and CSe bonds. In general, it is concluded that deviations are largest for polarized bonds. Furthermore, increased errors were found when going from the GS to the ES rising up to a MAE range from 0.9 to 2.8 pm for bond lengths. In Figure 1, the error introduced by ADMM in bond lengths of GS or first singlet ES geometries is depicted for selected bonds of the 35 molecules of the benchmark set, with “ADMM error” being defined as the deviation that results from comparing the conventional PBE0 computations with approximated ADMM-PBE0 ones choosing the same primary basis set. The assessment is thus reflecting the accuracy of the auxiliary basis set size. Corresponding statistical data can be found in Tables S11, S12, and S13. The statistics are based only on the selected geometrical data listed explicitly in the Supporting Information following the selection of ref (51), omitting less polarized C–H bonds for larger molecules, but including all bonds that undergo significant changes to ensure meaningful MEs and MAEs. For both GS and ES, results relying on the smallest dzp basis, colored in green or blue depending on the chosen primary basis, deviate significantly from computations using larger auxiliary basis sets, depicted in orange and red. Predicted bond lengths are too long, with dzp errors amounting up to 3.8/3.5 pm for GS/ES geometries and being thus much larger than the corresponding error range for the tzp and tz2p auxiliary basis sets; both tzp and tz2p bonds combined with a TZVP or TZV2P primary basis deviate by at most 1.0 pm. Comparing GS and ES distributions, the error spread for the ES is as broad as for the GS. Both tzp distributions suggest a classification in two or more groups depending on the type of atoms involved and resulting in two maxima in the histograms. Bonds including H, S, Se, and C–C bonds can be associated with relatively small errors corresponding to the first maximum and Gaussian distribution around 0.0 pm. Larger deviations in the range from 0.3 to 0.6 pm can be found for oxygen or halogen bonds contributing to the second maximum in both GS and ES histograms. Outliers corresponding to the maximum errors of 1.0 pm can be traced back to nitrogen bonds. An analogous classification and assignment for the dzp auxiliary basis is less conclusive because of the broader distributions, but it still holds true with the exception that C–C bonds fall into the error range of the second maximum around 1.5 pm. For comparison, the ADMM error in selected angles of the optimized ES geometries is depicted in Figure 2, demonstrating that the impact of the chosen auxiliary basis on the angles is less dependent on the basis set size than it is for the bond lengths, even though the width of the Gaussian distribution is reduced when going from double- to triple-ζ basis sets. An analogous plot for the GS, given in Figure S1, looks nearly identical.
Figure 1.
Error (in pm) for selected bond lengths for (a) optimized ground- and (b) first singlet excited-state geometries comparing conventional PBE0 and ADMM-PBE0 computations for different auxiliary (ABS) and primary basis sets (PBS) indicated as ABS/PBS.
Figure 2.
Error (in deg) for selected angles for optimized first singlet excited-state geometries comparing conventional PBE0 and ADMM-PBE0 computations.
A similar and transferable result is found for dihedral angles investigated for a subset of 13 molecules for which excitation leads to a significantly bent excited-state structure. While dihedral angles of corresponding GS geometries are consistently predicted to describe a planar geometry for all auxiliary and primary basis set sizes, the bending angle of the excited state is more accurately described when increasing the cardinal number of the auxiliary basis from double- to triple-ζ size. Again, the effect of additional polarization functions as included within the largest tz2p basis is negligible. A plot for the ADMM error in dihedral angles analogous to Figure 2 is given in Figure S2.
A summarized look at the corresponding statistical data of Table 1, listing mean errors (MEs), mean absolute errors (MAEs), and standard deviations (STDs) for bond lengths, angles, and dihedral angles of ES geometries optimized within the various primary and auxiliary basis set combinations, emphasizes again the impact of the chosen auxiliary basis: while MAEs of the dzp basis amount up to 1.4 pm for bond lengths and up to 0.8° or 2.1° for bond and dihedral angles, tzp results are converged with remaining deviations of 0.3 pm/0.2°/0.3°. The ADMM error is negligibly small in comparison to the error of PBE0 or hybrid functionals in general, which was found to be for MAEs in the range from 0.9 to 2.8 pm for bond lengths in comparison to highly accurate coupled-cluster results.69 ADMM error distributions are relatively broad for the dzp auxiliary basis and nearly equally narrow for tzp and tz2p basis sets. MEs and MAEs are of the same magnitude, indicating that the dzp auxiliary basis predicts bonds that are consistently too long and angles too narrow. This trend is in agreement with the finding that increasing the amount of exact exchange in hybrid functionals results in shorter bond lengths and larger bond angles.39,70,71 Going to larger ADMM auxiliary basis set sizes achieves a more accurate description of the fraction of exact exchange that is included in the underlying hybrid functional. It thus increases the Hartree–Fock nature of the bond with the one-determinant Hartree–Fock wave function representing the maximum amount of bonding character and corresponding to the shortest bonds. ADMM ES bond lengths are therefore shortened, and bond angles broadened when going from double- to triple-ζ auxiliary basis sets. Studies on the effect of exact exchange on dihedral angles furthermore reveal that hybrid functionals improve on the overestimation of GGA functionals, a result that is thus in line with our findings following the same rationale.72,73
Table 1. Statistics Including Mean Errors (MEs), Mean Absolute Errors (MAEs), and Standard Deviations (STDs) for Different Auxiliary and Primary Basis Sets (ABS/PBS) Visualizing that the ADMM Error in ES Bond Lengths (pm), Angles (deg), and Dihedral Angles (deg) as well as in the First Adiabatic Excitation (Ead), the First 10 Vertical Excitation (Evert), and the First Fluorescence (Efl) Energy (eV) Is Converged for Auxiliary Basis Sets of Triple-ζ Size.
| Bonds
(pm) |
Angles
(deg) |
Dihedrals
(deg) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| ABS/PBS | ME | MAE | STD | ME | MAE | STD | ME | MAE | STD |
| dzp/DZVP | 1.31 | 1.31 | 0.55 | –0.74 | 0.85 | 1.19 | 2.07 | 2.07 | 1.20 |
| dzp/TZVP | 1.37 | 1.37 | 0.57 | –0.75 | 0.85 | 1.13 | 1.94 | 1.94 | 1.11 |
| dzp/TZV2P | 1.38 | 1.38 | 0.56 | –0.73 | 0.83 | 1.18 | 2.05 | 2.05 | 1.23 |
| tzp/TZVP | 0.21 | 0.23 | 0.25 | –0.11 | 0.21 | 0.35 | 0.07 | 0.34 | 0.54 |
| tzp/TZV2P | 0.25 | 0.26 | 0.24 | –0.13 | 0.20 | 0.32 | 0.30 | 0.36 | 0.49 |
| tz2p/TZV2P | 0.21 | 0.22 | 0.26 | –0.10 | 0.18 | 0.28 | 0.02 | 0.13 | 0.16 |
|
Evert (eV) |
Ead (eV) |
Efl (eV) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| ABS/PBS | ME | MAE | STD | ME | MAE | STD | ME | MAE | STD |
| dzp/DZVP | –0.064 | 0.095 | 0.117 | –0.023 | 0.048 | 0.054 | –0.055 | 0.080 | 0.074 |
| dzp/TZVP | –0.058 | 0.091 | 0.109 | –0.025 | 0.055 | 0.061 | –0.057 | 0.083 | 0.075 |
| dzp/TZV2P | –0.062 | 0.093 | 0.109 | –0.028 | 0.054 | 0.058 | –0.058 | 0.081 | 0.073 |
| tzp/TZVP | –0.012 | 0.036 | 0.057 | 0.004 | 0.022 | 0.031 | –0.002 | 0.022 | 0.030 |
| tzp/TZV2P | –0.015 | 0.035 | 0.048 | 0.004 | 0.022 | 0.032 | 0.003 | 0.022 | 0.029 |
| tz2p/TZV2P | –0.021 | 0.033 | 0.044 | –0.004 | 0.016 | 0.022 | –0.005 | 0.019 | 0.025 |
3.1.2. Excited-State Geometries: ADMM and sTDA Kernels in Comparison to EOM-CCSD References
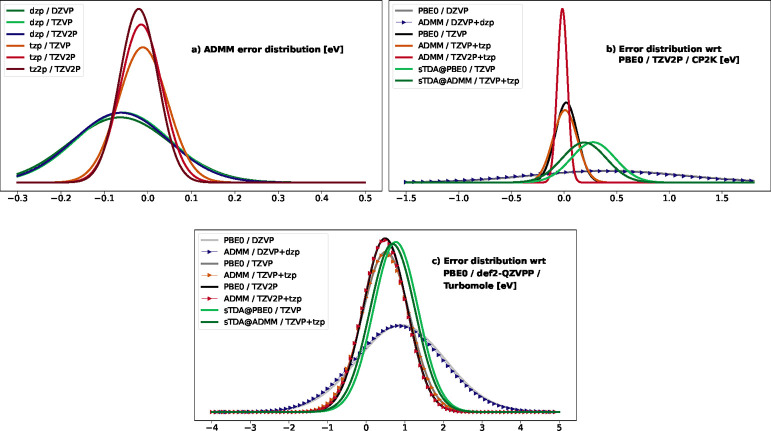
To analyze the performance of ADMM-PBE0 and sTDA kernels in comparison to highly accurate EOM-CCSD reference data, we restricted investigations to basis sets of triple-ζ size. In Figure 3 the error in the geometrical data is given as normal distributions based on the corresponding MEs and STDs; more detailed statistical analysis and explicit errors listed for each molecule can be found in sections 3.4 and 3.5 of the Supporting Information. To give not only an upper limit for a desired high-accuracy reference but also a lower reference point of reachable performance, conventional hybrid functional PBE0 results are depicted in black, deviating by MEs of −0.15 pm/0.32°/0.80° from the EOM-CCSD reference. As for the preceding assessment on the ADMM auxiliary basis size, PBE0 results represent the basis set limit for ADMM computations, a fact that is reflected in the similarity of the PBE0 error distributions with the ones obtained for analogous ADMM computations, colored in orange and red for a tzp auxiliary and a TZVP or TZV2P primary basis, respectively. PBE0 and ADMM-PBE0 results are thus in agreement with the conclusions of ref (69), with the latter stating that global hybrids yield slightly too short bonds and that functionals with a rather small amount of exact exchange show negative signed MEs. MAEs are also in agreement, with our result of 0.9 pm for the triple-ζ computations being at the lower boundary of the reported MAE range from 0.9 to 2.8 pm for CC3 or CCSDR(3) references. The relatively good performance can probably be argued with our chosen EOM-CCSD reference, which was shown to yield underestimated TDDFT errors for strongly polarized bonds.69 All in all, we thus confirm the tendency of PBE0 to provide too compact distances and that errors are most pronounced for polarized carbonyl bonds. In comparison, error distributions for sTDA kernels are increasingly broadened when going from PBE0/TZVP to ADMM-PBE0/TZVP+tzp references. The deviation of the semiempirical results is most pronounced for dihedral angles, with maximum errors amounting up to −13.29° and −14.1° for PBE0/TZVP and ADMM-PBE0/TZVP+tzp references. However, it should be noted that the error distribution for the dihedrals is still nearly equally broad as the corresponding PBE0 one with STDs of 3.2–3.4° for PBE0 and 4.0–4.1° for sTDA. The apparently large mean error of sTDA in dihedral angles is biased because of the fact that sTDA consistently overestimates the dihedral angle while PBE0 gives an equally broad distribution of both negative and positive signed errors. Because the computations were performed using, e.g., a default value of aEX = 0.2 for the exact exchange scaling parameter, it remains to be investigated if the overestimation represents the general difficulty of recovering a weak stabilizing force or if it could be cured by optimizing the amount of exact exchange in line with refs (72 and 73).
Figure 3.
Normal distributions based on the mean errors (ME) and standard deviations (STD) wrt EOM-CCSD reference geometries in (pm)/(deg)/(deg) for selected (a) bond lengths/(b) angles/(c) dihedral angles for optimized first singlet excited-state geometries comparing conventional PBE0, ADMM-PBE0, and sTDA computations using triple-ζ basis sets.
3.1.3. Vertical Excitation Energies
Benchmarking excited-state methods with the focus on vertical excitation energies has been established as a common assessment tool (see, e.g., ref (74) and references therein). Here one assumes that excitations occur without a change in geometry. Corresponding studies showed that TDDFT excitation energies, which are classified as Rydberg states or associated with a significant amount of charge transfer, are underestimated leading to errors on the order of several eV.75 A common remedy is to include exact exchange, suggesting that the investigated ADMM-approximated hybrid kernel as well as the sTDA kernel with its motivation to capture the correct physics and asymptotics of electronic interactions could be well-suited compromises to retain sufficient accuracy while reaching high efficiency for a broad range of applications. Analyzing the nature of a transition is beyond the scope of the current work and, for the sake of convenience, we restricted the analysis of vertical excitation energies to a direct comparison of the first 10 excitation energies with states being assigned solely by the corresponding ES energy. Such a simplified comparison might not be justified and lead to wrong assignments when comparing different basis set sizes but also should give a valid assessment of the accuracy of the different kernels for basis sets of the same type. Figure 4 displays normal distributions based on the MEs and STDs for the first 10 vertical excitation energies for optimized geometries, comparing ADMM-PBE0 computations with conventional PBE0 results as well as assessing the performance of PBE0, ADMM-PBE0, and sTDA kernels with respect to a PBE0/TZV2P/CP2K and a PBE0/def2-QZVPP/TURBOMOLE reference. Corresponding statistical data is furthermore summarized in Tables 1 and 2 as well as in section 4 of the Supporting Information. As shown by the upper plot on the left, the auxiliary basis set size reduces, in analogy to our findings for the geometrical data, the ADMM error in the vertical excitation energies when increasing from double- to triple-ζ size and brings only a little further improvement when polarization functions are added. Taking the PBE0 computations within the largest TZV2P basis as a reference exposes the impact of the increasingly large primary basis set as visualized in the upper plot on the right: PBE0/DZVP as well as ADMM-PBE0/DZVP+dzp computations show an equally broad error distribution with MEs and STDs rising up to 0.42 and 0.72 eV, respectively. The broad distribution emphasizes the insufficiency of double-ζ basis sets and that discrepancies between DZVP and TZV2P basis sets are, as already commented on at the beginning of the section, presumably too large to allow for a straightforward comparison of excitation energies. On the other end of the accuracy spectrum, ADMM-PBE0/TZV2P+tz2p results have a relatively sharp distribution with a ME and STD of −0.02 and 0.04 eV. TZVP errors for the PBE0, ADMM-PBE0, and sTDA kernels lie between those extreme values, highlighting that ADMM has only a negligible impact on excitation energies and that the MEs of sTDA are below 0.28 or 0.19 eV depending on the chosen GS reference. This result is in agreement with the error range of 0.2–0.5 eV of the original molecular benchmark studies.21,22
Figure 4.
Normal distributions based on the MEs and STDs for vertical excitation energies (in eV) depicting (a) the error introduced by ADMM-PBE0 in comparison to conventional PBE0 computations (upper left plot), (b) the performance of PBE0, ADMM-PBE0, and sTDA kernel computations using double- and triple-ζ basis sets in comparison to a PBE0/TZV2P/CP2K reference (upper right plot) as well as (c) an analogous assessment of the kernels with respect to a PBE0/def2-QZVPP/Turbomole reference (lower plot).
Table 2. Statistics Including Mean Errors (MEs), Mean Absolute Errors (MAEs) and Standard Deviations (STDs) Visualizing the Error for Both ADMM-PBE0 and sTDA Kernels for Excited-State Geometries Comprising ES Bond Lengths (pm), Angles (deg), and Dihedral Angles (deg) as well as First Adiabatic Excitation (Ead), Vertical Excitation (Evert), and Fluorescence Energies (Efl) (eV)a.
| Bonds
(pm) |
Angles
(deg) |
Dihedrals
(deg) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kernel | PBS+ABS | ME | MAE | STD | ME | MAE | STD | ME | MAE | STD |
| PBE0 | TZVP | –0.15 | 0.93 | 1.18 | 0.32 | 1.24 | 2.20 | 0.80 | 2.34 | 3.21 |
| ADMM-PBE0 | TZVP+tzp | 0.06 | 0.92 | 1.18 | 0.20 | 1.18 | 2.09 | 0.86 | 2.31 | 3.46 |
| sTDA@PBE0 | TZVP | 0.10 | 1.06 | 1.50 | –0.03 | 1.60 | 2.57 | 3.98 | 4.06 | 3.95 |
| sTDA@ADMM-PBE0 | TZVP+tzp | 0.28 | 1.03 | 1.35 | –0.05 | 1.51 | 2.34 | 4.03 | 4.14 | 4.06 |
|
Evert (eV) |
Ead (eV) |
Efl (eV) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ME | MAE | STD | ME | MAE | STD | ME | MAE | STD | ||
| PBE0 | DZVP | –0.02 | 0.05 | 0.06 | –0.16 | 0.30 | 0.42 | –0.05 | 0.06 | 0.05 |
| PBE0 | TZVP | –0.01 | 0.03 | 0.03 | –0.15 | 0.29 | 0.41 | –0.04 | 0.05 | 0.04 |
| PBE0 | TZV2P | 0.00 | 0.02 | 0.03 | –0.13 | 0.28 | 0.40 | –0.02 | 0.02 | 0.02 |
| ADMM-PBE0 | TZVP+tzp | –0.01 | 0.03 | 0.04 | –0.14 | 0.29 | 0.41 | –0.05 | 0.07 | 0.06 |
| sTDA@PBE0 | TZVP | 0.45 | 0.45 | 0.18 | 0.23 | 0.34 | 0.39 | 0.27 | 0.30 | 0.21 |
| sTDA@ADMM-PBE0 | TZVP+tzp | 0.34 | 0.34 | 0.17 | 0.10 | 0.33 | 0.44 | 0.14 | 0.18 | 0.16 |
Errors in the geometrical data and Ead are calculated with respect to the EOM-CCSD reference data of ref (51); errors in Evert and Efl are referring to PBE0/def2-QZVPP/TURBOMOLE reference computations.
3.1.4. Adiabatic Excitation Energies and Fluorescence
Adiabatic excitation energies, defined as the energy difference between lowest vibrational levels of the relaxed ground- and excited-state energies, are often benchmarked to assess ES methods. In contrast to vertical excitation energies, adiabatic excitations have the advantage of being experimentally observable and less structure sensitive. They show not a linear but rather a quadratic dependence on nuclear displacements.76 The difference between calculated vertical and adiabatic excitation energies is the ES relaxation energy, and fluorescence energies are defined as vertical de-excitation energies. The errors in adiabatic excitation and fluorescence energies for the investigated 35 molecules are depicted in Figures 5 and 6, the former comparing the ADMM errors for different auxiliary basis set sizes with respect to conventional PBE0 and the latter assessing the performance of ADMM and sTDA kernels for adiabatic excitation energies with respect to EOM-CCSD reference data and for fluorescence energies with respect to the performed PBE0/def2-QZVPP/Turbomole computations, respectively.
Figure 5.
ADMM error distribution in (a) adiabatic excitation and (b) fluorescence energies comparing approximated ADMM-PBE0 and conventional PBE0 results for different auxiliary basis set sizes (in eV).
Figure 6.
Comparison of (a) adiabatic excitation energies with respect to EOM-CCSD reference data and (b) fluorescence energies with respect to PBE0/def2-QZVPP/Turbomole reference data for PBE0, ADMM-PBE0, and sTDA kernels (in eV).
Explicit data and a corresponding statistical analysis is given in sections 5 and 6 of the Supporting Information. Despite the varying references, ADMM errors are comparable for both the excitation and de-excitation processes, ranging from −0.3 to −0.1 eV for the smallest dzp auxiliary basis. The tzp and tz2p auxiliary basis sets reduce the maximum error to +0.1 or −0.06 eV, respectively. Corresponding MEs are of meV magnitude and MAEs smaller than 0.02 eV. Analyzing the total error of the different kernels in the scatter plots of Figure 6 highlights that sTDA errors are consistently shifted to larger and more positive errors. The correlation between the relative shift of sTDA errors with respect to both PBE0 and EOM-CCSD results and the considered amount of exact exchange was not investigated any further, but will be part of future work. However, even when a nonoptimized fraction of 0.2 is chosen for the coupling parameter aEX of eq 29, sTDA curves are close to the hybrid functional results when compared to EOM-CCSD reference data achieving statistical measures of the same order of magnitude, with MEs of 0.2/–0.1/–0.1 eV, MAEs of 0.3/0.3/0.3 eV, and maximum errors of −1.3/1.0/1.0 eV for sTDA/ADMM-PBE0/PBE0 adiabatic excitation energies. Switching to a PBE0/TURBOMOLE reference for fluorescence energies favors PBE0 and ADMM-PBE0 results over the semiempirical ones, with the former now only accounting for deviations in the basis sets and the ADMM error with MEs of −0.05/–0.05 eV, MAEs of 0.07/0.05 eV, and maximum errors of −0.2/0.1 eV for ADMM-PBE0/PBE0. The sTDA errors are, however, consistent, yielding an equivalent ME, MAE, and maximum error of 0.3 eV.
3.2. Increasing Computational Efficiency: Treating Extended Systems Using ADMM-PBE0 and sTDA Kernels
To analyze computational timings of ADMM-PBE0 and sTDA excited-state properties and to demonstrate the suitability of the two approaches for large-scale periodic systems, we investigated a series of porous COF materials taken from the CURATED COFs database.52,53 The chosen subset includes the prototypes of the first ever synthesized COFs77 as well as pairs of COFs that were demonstrated to show more or less bright fluorescence depending on either accordingly tuned linker molecules or the surrounding solvent.78,79 The CURATED COFs database provides cleaned-up DFT-optimized GS structures at a GGA level of accuracy, obtained with the PBE functional, D3(BJ) correction, and DZVP-MOLOPT-SR basis sets. We reoptimized these geometries using a corresponding ADMM-PBE0 GS reference and triple-ζ ccGRB-T primary and tzp auxiliary basis sets to ensure a consistent accuracy of both structural and electronic GS and ES properties. Structural details are provided in the Supporting Information. In all calculations a truncated Coulomb operator with a radius of 4 Å has been used. In Table 3, detailed timings for the first 3 ES geometry optimization steps are given for COF 05000N2 for ADMM-approximated and sTDA kernels in comparison to conventional PBE0 results, with the latter relying on an exact analytical evaluation of the two-electron-four-center exchange integrals. The formal scaling of both excited-state energy and gradient implementations is cubic with respect to the number of atomic orbital basis functions and increases linearly with the number of computed excited states. Memory requirements and execution times for the main computational steps of the algorithm are analogous to corresponding density functional ground-state implementations, as analyzed in detail in refs (56) and (43). As outlined in ref (46), the computation of electron repulsion integrals (ERIs) represents the main bottleneck for hybrid functional computations, with the number of integrals and thus the required memory scaling quadratically with the number of atomic and occupied molecular orbitals, N × Nocc, when considering sparsity and applying Cauchy–Schwarz screening. At best linear scaling with a still significant prefactor can be achieved when relying on additional density matrix screening and when using truncated exchange operators.
Table 3. Explicit Computational Timings (s) for COF 05000N2 Comprising 84 Atoms/276 Electrons in the Unit Cell for PBE0, ADMM-PBE0, and sTDA@ADMM-PBE0 Kernelsa.
| PBE0 | ADMM-PBE0 | sTDA@ADMM-PBE0 | |
|---|---|---|---|
| GS SCF | 301 | 137 | 134 |
| ES energy and gradient | 1919 | 403 | 148 |
| ERI for ES energy | 687 | 86 | 33 |
| DERI for ES gradient | 1265 | 11 | 7 |
| Total computation time | 2220 | 540 | 282 |
Computations were performed using a ccGRB-T primary basis (2076 basis functions) and a tzp auxiliary basis (1164 basis functions). Timings are reported for a Intel Xeon E5-2670 processor using in total 4608 cores, analysing the cost for converging the GS SCF computation, for calculating the ES energy and gradient as well as for the computation of the ERIs needed for the ES energy calculation and the DERIs needed for the ES gradient.
The measured total computation time
of 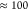 hours for a ccGRB-T basis with 2076 basis
functions reflects that an analytical computation of exchange integrals
within a large primary orbital basis cannot provide optimal efficiency
for large periodic systems. The fact that 31% and 57% of the PBE0
computation times are solely attributed to the computation of ERIs
and derivative electron repulsion integrals (DERIs) emphasizes the
need for approximations. Applying ADMM with a triple-ζ auxiliary
basis and thus reducing the basis set size by a factor of 2 to 1164
functions accelerates the computation by a factor of
hours for a ccGRB-T basis with 2076 basis
functions reflects that an analytical computation of exchange integrals
within a large primary orbital basis cannot provide optimal efficiency
for large periodic systems. The fact that 31% and 57% of the PBE0
computation times are solely attributed to the computation of ERIs
and derivative electron repulsion integrals (DERIs) emphasizes the
need for approximations. Applying ADMM with a triple-ζ auxiliary
basis and thus reducing the basis set size by a factor of 2 to 1164
functions accelerates the computation by a factor of  with a remaining
total time of 9.0 min.
The small auxiliary basis reduces the number of ERIs and, in combination
with increased sparsity and thus more efficient Schwarz screening,
the reduction of the basis size results in timings for the integral
evaluation that are reduced by a factor of
with a remaining
total time of 9.0 min.
The small auxiliary basis reduces the number of ERIs and, in combination
with increased sparsity and thus more efficient Schwarz screening,
the reduction of the basis size results in timings for the integral
evaluation that are reduced by a factor of 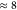 . More drastic is
even the speed-up for
the computation of DERIs because of the here applied density-matrix
screening. In comparison to PBE0, the computation of DERIs is 115
times faster for ADMM-PBE0 and thus represents not 57% but solely
2% of the total costs. Timings comparable to ADMM-PBE0 can also be
achieved with the semiempirical tight binding setup: sTDA reduces
the total costs to 4.7 min, thus by a factor of
. More drastic is
even the speed-up for
the computation of DERIs because of the here applied density-matrix
screening. In comparison to PBE0, the computation of DERIs is 115
times faster for ADMM-PBE0 and thus represents not 57% but solely
2% of the total costs. Timings comparable to ADMM-PBE0 can also be
achieved with the semiempirical tight binding setup: sTDA reduces
the total costs to 4.7 min, thus by a factor of  in comparison to
conventional PBE0 and
by a factor of
in comparison to
conventional PBE0 and
by a factor of 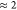 in comparison to
ADMM. The speed-up with
respect to ADMM is because of the faster ERI evaluation relying on
the semiempirical description of both Coulomb and exchange contributions
when solving the ES eigenvalue problem. sTDA and ADMM timings are
on the same order of magnitude, but further acceleration could be
expected when switching to a complete semiempirical setup for both
GS and ES. We are also aware that absolute timings for the sTDA ES
gradient computations could still be improved by further code optimization.
in comparison to
ADMM. The speed-up with
respect to ADMM is because of the faster ERI evaluation relying on
the semiempirical description of both Coulomb and exchange contributions
when solving the ES eigenvalue problem. sTDA and ADMM timings are
on the same order of magnitude, but further acceleration could be
expected when switching to a complete semiempirical setup for both
GS and ES. We are also aware that absolute timings for the sTDA ES
gradient computations could still be improved by further code optimization.
To give an estimate on the required relative costs of ADMM and sTDA for the computation of broad-band absorption spectra and for the geometry optimization of low-lying excited states, we report timings for all six COFs in Table 4. Computations were performed for the lowest 500 excited states and the geometry optimization of the first ES when a manifold of 8 singlet states was selected. The investigated system sizes range from unit cells of 84 to 300 atoms and include basis set sizes of 2076 to 7440 basis functions, respectively. Comparing the computational timings for the calculation of the lowest 500 excitation energies clearly shows the advantage of the semiempirical setup. While computations using the ADMM kernel take ≈4 to 10 h, sTDA is 1 order of magnitude faster with a maximum computation time of less than 44 min. With the current setup, the tight binding approach is, however, less favorable for ES geometry optimization. First, the number of required optimization cycles is increased for five out of six COFs. Second, the average computation time per optimization cycle is accelerated only by a factor of 1.4 to 5, so that ADMM-PBE0 and sTDA computation times are of the same order of magnitude. For both ADMM-PBE0 and sTDA computations, timings of 4–30 min per optimization cycle and total timings of 2.5–40 h for an ES geometry optimization can thus be expected for periodic systems in the size range of hundreds of atoms and using the indicated computational resources.
Table 4. Computational Timings (s) for ADMM-PBE0 and sTDA@ADMM-PBE0 Kernels for a Series of Fluorescent COFs as Required for the Computation of Broad-Band Absorption Spectra over the Lowest 500 Excited States as well as for the ES Geometry Optimization of the First Excited State when Selecting a Manifold of the Lowest 8 Singlet Statesa.
| Absorption
spectra |
ES optimization |
|||||||
|---|---|---|---|---|---|---|---|---|
| ADMM | sTDA | ADMM |
sTDA |
|||||
| # Atoms | # Basis | Time | Time | Time | Time/Step | Time | Time/Step | |
| 05000N2 | 84 | 2076 | 15758 | 2157 | 9590 | 461 | 8937 | 329 |
| 05001N2 | 192 | 4848 | 33678 | 2472 | 77332 | 1556 | 33837 | 637 |
| 15100N2 | 300 | 7440 | 36907 | 2623 | 155696 | 1729 | 37804 | 433 |
| 15101N2 | 192 | 5028 | 30931 | 1932 | 67962 | 1680 | 29258 | 417 |
| 20610N2 | 240 | 5700 | 30014 | 2119 | 59603 | 1086 | 16627 | 266 |
| 20611N2 | 262 | 6188 | 27965 | 1993 | 136122 | 1818 | 35955 | 362 |
Timings are reported for a Intel Xeon E5-2670 processor using in total 2304 cores.
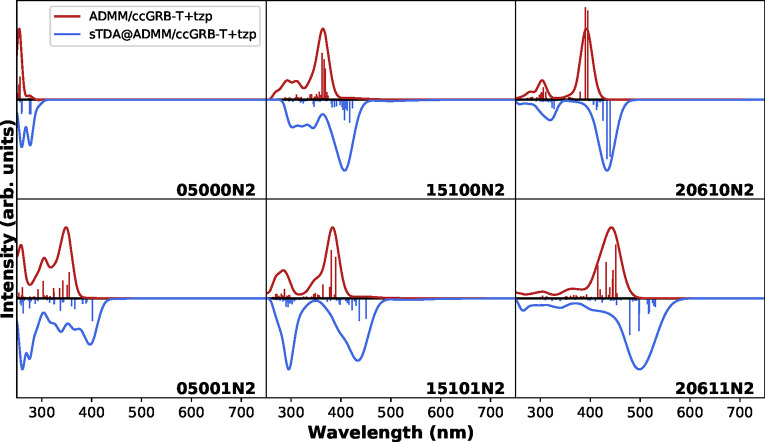
To compare the relative accuracy of ADMM-PBE0 and sTDA for periodic systems, the computed broad-band spectra are depicted in Figure 7. Corresponding vertical excitation, adiabatic excitation, and fluorescence energies, as well as Stokes’ shifts are listed in Table 5. As highlighted by the six plots of Figure 7, sTDA and ADMM provide absorption spectra with qualitatively matching oscillator strengths. sTDA excitations are, however, in all cases shifted to smaller energies, with MAEs for the first and the first ten vertical excitation energies amounting both up to 0.31 eV. Because the exchange mixing parameter aEX was set to the same value as for the molecular systems (aEX = 0.2), it remains to be investigated if this apparently systematic shift could be improved by adjusting the amount of exchange. However, even with this default setting, the MAE in adiabatic excitation and fluorescence energies is within the error range found for molecular systems. ADMM-PBE0 and sTDA energies differ by 0.42 or 0.40 eV, respectively. Corresponding Stokes’ shifts are thus also predicted with a relatively small error of 0.17 eV.
Figure 7.
Comparison of ADMM-PBE0 and sTDA absorption spectra for a series of fluorescent COFs.
Table 5. Vertical Excitation (Evert), Adiabatic Excitation (Ead), and Fluorescence Energies (Efl) as well as Corresponding Stokes’ Shifts (λ) (eV) for ADMM-PBE0 and sTDA Kernels for the First Excited Singlet State for a Series of Fluorescent COFs.
|
Evert |
Ead |
Efl |
λ |
|||||
|---|---|---|---|---|---|---|---|---|
| ADMM | sTDA | ADMM | sTDA | ADMM | sTDA | ADMM | sTDA | |
| 05000N2 | 4.71 | 4.95 | 4.40 | 3.87 | 4.49 | 4.16 | 0.22 | 0.79 |
| 05001N2 | 3.77 | 3.44 | 2.60 | 2.14 | 2.97 | 2.56 | 0.80 | 0.88 |
| 15100N2 | 3.54 | 3.08 | 2.27 | 1.85 | 2.43 | 1.98 | 1.11 | 1.10 |
| 15101N2 | 3.10 | 2.67 | 2.04 | 1.46 | 2.18 | 1.68 | 0.92 | 0.98 |
| 20610N2 | 3.97 | 3.67 | 2.82 | 2.45 | 3.08 | 2.74 | 0.89 | 0.93 |
| 20611N2 | 3.21 | 3.10 | 2.47 | 1.96 | 2.65 | 2.25 | 0.56 | 0.85 |
| MAE | 0.31 | 0.42 | 0.40 | 0.17 | ||||
4. Conclusions
Approaches based on TDDFT are well established to calculate excited-state properties. However, when dealing with periodic systems, the routine usage of hybrid functionals is often hindered because of the increased computational costs in comparison to GGA functionals. We presented two approximate schemes based on the ADMM and sTDA approaches with the goal to reach hybrid functional accuracy at a reduced cost. Benchmark results for molecular and periodic systems show that the two methods can indeed reach the required accuracy for excited-state properties and allow for an efficient calculation of many excited states. First, the implemented ADMM-approximated hybrid functional kernel leads to a speed-up of at least 1 order of magnitude in comparison to conventional hybrid functional TDDFT and thus enables practical calculations on large systems of hundreds of atoms at a moderate cost. Timings could be further improved by accelerating the evaluation of the exact exchange integrals using either standard resolution-of-the-identity approaches or seminumerical integration. In comparison to inherent methodological errors of TDDFT because of the chosen density functional, the loss in accuracy for ADMM-approximated kernels is minor when auxiliary basis sets of at least triple-ζ size are selected. ADMM/TZVP+tzp MAEs in excited-state bond lengths are in the range of 0.3 pm and corresponding vertical and adiabatic excitation and fluorescence energies are off by 0.02–0.04 eV. In contrast, conventional PBE0/TZVP bond lengths and adiabatic excitation energies show MAEs of 0.9 pm and 0.3 eV with respect to EOM-CCSD/def2-TZVPP reference data. The given ADMM accuracy estimate represents a lower limit that was found to be reliable when the simplest ADMM variant was chosen based on basis projection in combination with a triple-ζ auxiliary basis. It could be further improved by either adding an exchange density functional correction to compensate the incompleteness error or, regarding the perpendicular methodological error, by switching to more sophisticated ADMM schemes with the latter, however, increasing the complexity of implementation. The semiempirical sTDA method is particularly useful when aiming for broad-band absorption or emission spectra and efficient prescreening of large-scale test sets. An order of magnitude speedup was achieved with sTDA in comparison to ADMM when spectra over the lowest 500 excitation energies were computed, with resulting timings being in the range of minutes rather than hours. Because of the reduced amount of ERIs, the sTDA kernel also accelerates timings by a factor of 2 for each ES geometry optimization cycle. However, an increased number of optimization steps can lead to total timings comparable to ADMM. We expect that further savings could be achieved when optimizing the current sTDA ES gradient implementation as well as when choosing a semiempirical GS reference. In comparison to hybrid functional kernels, sTDA MAEs in excited-state bond lengths with respect to EOM-CCSD reference results are only slightly increased to 1.1 pm. According to the molecular benchmarks, the error estimate for vertical and adiabatic excitation and fluorescence energies can be assumed to be below 0.5 eV, a deviation that is slightly increased but still comparable to the MAE of 0.3 eV of conventional PBE0 with respect to EOM-CCSD references. Similar relative error ranges are found for the investigated COFs, and a comparison of ADMM and sTDA oscillator strengths suggests qualitative accuracy of the tight binding method. The most critical parameter in the sTDA method is the exact exchange scaling. This parameter should be adjusted with respect to the selected hybrid functional ground-state reference and a suboptimal value can lead to large geometrical errors and even negative excitation energies. In the case of formyl chloride, the scaling parameter had to be adjusted to avoid dissociation when the first excited singlet state was optimized. Further studies are required to investigate the optimal fraction of exact exchange for periodic systems because the choice might differ from the values that were originally suggested for molecular systems. Further empirical shifts might also be required when the sTDA excited-state method is combined with corresponding semiempirical ground-state calculations. A consistent setup remains to be investigated, but we expect it to pave the way to treat even larger systems. It also remains to be investigated in future work if efficiency and accuracy of ADMM-approximated hybrid functional TDDFT and sTDA are beneficial for excited-state molecular dynamic simulations.
Acknowledgments
We thank Dr. Augustin Bussy (University of Zurich) for his kind support and the valuable discussions. This work was supported in parts by the MARVEL National Centre for Competence in Research funded by the Swiss National Science Foundation (grant agreement ID 51NF40-182892). We thank the Swiss National Supercomputing Center (CSCS) for providing computational resources (Grant No. S1109). Furthermore, this work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 798196. M.W. and S.C. were assisted by membership of the UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c00144.
Treatment of the virtual space, structural information for molecular benchmark set, geometrical data on optimized molecular geometries, statistical analysis for ADMM and sTDA vertical excitation energies, adiabatic excitation energies and statistical analysis, fluorescence energies and statistical analysis, and structural information for covalent organic frameworks (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- González L.; Escudero D.; Serrano-Andrés L. Progress and Challenges in the Calculation of Electronic Excited States. ChemPhysChem 2012, 13, 28–51. 10.1002/cphc.201100200. [DOI] [PubMed] [Google Scholar]
- Dreuw A.; Head-Gordon M. Single-Reference ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009–4037. 10.1021/cr0505627. [DOI] [PubMed] [Google Scholar]
- Laurent A. D.; Jacquemin D. TD-DFT benchmarks: A review. Int. J. Quantum Chem. 2013, 113, 2019–2039. 10.1002/qua.24438. [DOI] [Google Scholar]
- de Wergifosse M.; Grimme S. Perspective on Simplified Quantum Chemistry Methods for Excited States and Response Properties. J. Phys. Chem. A 2021, 125, 3841–3851. 10.1021/acs.jpca.1c02362. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Schreiner P. R. Computational Chemistry: The Fate of Current Methods and Future Challenges. Angew. Chem., Int. Ed. 2018, 57, 4170–4176. 10.1002/anie.201709943. [DOI] [PubMed] [Google Scholar]
- Dierksen M.; Grimme S. The Vibronic Structure of Electronic Absorption Spectra of Large Molecules: A Time-Dependent Density Functional Study on the Influence of Exact Hartree-Fock Exchange. J. Phys. Chem. A 2004, 108, 10225–10237. 10.1021/jp047289h. [DOI] [Google Scholar]
- Merlot P.; Izsák R.; Borgoo A.; Kjærgaard T.; Helgaker T.; Reine S. Charge-constrained auxiliary-density-matrix methods for the Hartree-Fock exchange contribution. J. Chem. Phys. 2014, 141, 094104. 10.1063/1.4894267. [DOI] [PubMed] [Google Scholar]
- Guidon M.; Hutter J.; VandeVondele J. Auxiliary Density Matrix Methods for Hartree-Fock Exchange Calculations. J. Chem. Theory Comput. 2010, 6, 2348–2364. 10.1021/ct1002225. [DOI] [PubMed] [Google Scholar]
- Kumar C.; Fliegl H.; Jensen F.; Teale A. M.; Reine S.; Kjærgaard T. Accelerating Kohn-Sham response theory using density fitting and the auxiliary-density-matrix method. Int. J. Quantum Chem. 2018, 118, e25639 10.1002/qua.25639. [DOI] [Google Scholar]
- Rebolini E.; Izsák R.; Reine S. S.; Helgaker T.; Pedersen T. B. Comparison of Three Efficient Approximate Exact-Exchange Algorithms: The Chain-of-Spheres Algorithm, Pair-Atomic Resolution-of-the-Identity Method, and Auxiliary Density Matrix Method. J. Chem. Theory Comput. 2016, 12, 3514–3522. 10.1021/acs.jctc.6b00074. [DOI] [PubMed] [Google Scholar]
- Merlot P.; Kjærgaard T.; Helgaker T.; Lindh R.; Aquilante F.; Reine S.; Pedersen T. B. Attractive electron–electron interactions within robust local fitting approximations. J. Comput. Chem. 2013, 34, 1486–1496. 10.1002/jcc.23284. [DOI] [PubMed] [Google Scholar]
- Manzer S. F.; Epifanovsky E.; Head-Gordon M. Efficient Implementation of the Pair Atomic Resolution of the Identity Approximation for Exact Exchange for Hybrid and Range-Separated Density Functionals. J. Chem. Theory Comput. 2015, 11, 518–527. 10.1021/ct5008586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neese F.; Wennmohs F.; Hansen A.; Becker U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. 10.1016/j.chemphys.2008.10.036. [DOI] [Google Scholar]
- Izsák R.; Neese F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. 10.1063/1.3646921. [DOI] [PubMed] [Google Scholar]
- Laqua H.; Thompson T. H.; Kussmann J.; Ochsenfeld C. Highly Efficient, Linear-Scaling Seminumerical Exact-Exchange Method for Graphic Processing Units. J. Chem. Theory Comput. 2020, 16, 1456–1468. 10.1021/acs.jctc.9b00860. [DOI] [PubMed] [Google Scholar]
- Holzer C. An improved seminumerical Coulomb and exchange algorithm for properties and excited states in modern density functional theory. J. Chem. Phys. 2020, 153, 184115. 10.1063/5.0022755. [DOI] [PubMed] [Google Scholar]
- Ohno K. Some remarks on the Pariser-Parr-Pople method. Theor. Chim. Acta 1964, 2, 219–227. 10.1007/BF00528281. [DOI] [Google Scholar]
- Klopman G. A Semiempirical Treatment of molecular Structures. II. Molecular Terms and Application to diatomic Molecules. J. Am. Chem. Soc. 1964, 86, 4550–4557. 10.1021/ja01075a008. [DOI] [Google Scholar]
- Nishimoto K.; Mataga N. Z. Electronic Structure and Spectra of Some Nitrogen Heterocycles. Z. Phys. Chem. 1957, 12, 335. 10.1524/zpch.1957.12.5_6.335. [DOI] [Google Scholar]
- Bannwarth C.; Grimme S. A simplified time-dependent density functional theory approach for electronic ultraviolet and circular dichroism spectra of very large molecules. Comput. Theor. Chem. 2014, 1040–1041, 45–53. 10.1016/j.comptc.2014.02.023. [DOI] [Google Scholar]
- Grimme S. A simplified Tamm-Dancoff density functional approach for the electronic excitation spectra of very large molecules. J. Chem. Phys. 2013, 138, 244104. 10.1063/1.4811331. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Bannwarth C. Ultra-fast computation of electronic spectra for large systems by tight-binding based simplified Tamm-Dancoff approximation (sTDA-xTB). J. Chem. Phys. 2016, 145, 054103. 10.1063/1.4959605. [DOI] [PubMed] [Google Scholar]
- de Wergifosse M.; Bannwarth C.; Grimme S. A Simplified Spin-Flip Time-Dependent Density Functional Theory Approach for the Electronic Excitation Spectra of Very Large Diradicals. J. Phys. Chem. A 2019, 123, 5815–5825. 10.1021/acs.jpca.9b03176. [DOI] [PubMed] [Google Scholar]
- De Wergifosse M.; Grimme S. Nonlinear-response properties in a simplified time-dependent density functional theory (sTD-DFT) framework: Evaluation of excited-state absorption spectra. J. Chem. Phys. 2019, 150, 094112. 10.1063/1.5080199. [DOI] [PubMed] [Google Scholar]
- De Wergifosse M.; Grimme S. Nonlinear-response properties in a simplified time-dependent density functional theory (sTD-DFT) framework: Evaluation of the first hyperpolarizability. J. Chem. Phys. 2018, 149, 024108. 10.1063/1.5037665. [DOI] [PubMed] [Google Scholar]
- Bannwarth C.; Seibert J.; Grimme S. Electronic Circular Dichroism of [16]Helicene With Simplified TD-DFT: Beyond the Single Structure Approach. Chirality 2016, 28, 365–369. 10.1002/chir.22594. [DOI] [PubMed] [Google Scholar]
- Risthaus T.; Hansen A.; Grimme S. Excited states using the simplified Tamm-Dancoff-Approach for range-separated hybrid density functionals: development and application. Phys. Chem. Chem. Phys. 2014, 16, 14408–14419. 10.1039/C3CP54517B. [DOI] [PubMed] [Google Scholar]
- Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. 10.1103/PhysRevB.58.7260. [DOI] [Google Scholar]
- Seibert J.; Pisarek J.; Schmitz S.; Bannwarth C.; Grimme S. Extension of the element parameter set for ultra-fast excitation spectra calculation (sTDA-xTB). Mol. Phys. 2019, 117, 1104–1116. 10.1080/00268976.2018.1510141. [DOI] [Google Scholar]
- Cho Y.; Bintrim S. J.; Berkelbach T. C.. A simplified GW/BSE approach for charged and neutral excitation energies of large molecules and nanomaterials; 2021, arXiv:2109.04421. 10.48550/arXiv.2109.04421. [DOI] [PubMed] [Google Scholar]
- Rüger R.; van Lenthe E.; Heine T.; Visscher L. Tight-binding approximations to time-dependent density functional theory — A fast approach for the calculation of electronically excited states. J. Chem. Phys. 2016, 144, 184103. 10.1063/1.4948647. [DOI] [PubMed] [Google Scholar]
- Asadi-Aghbolaghi N.; Pototschnig J.; Jamshidi Z.; Visscher L. Effects of ligands on (de-)enhancement of plasmonic excitations of silver, gold and bimetallic nanoclusters: TD-DFT+TB calculations. Phys. Chem. Chem. Phys. 2021, 23, 17929–17938. 10.1039/D1CP03220H. [DOI] [PubMed] [Google Scholar]
- Van Caillie C.; Amos R. D. Geometric derivatives of excitation energies using SCF and DFT. Chem. Phys. Lett. 1999, 308, 249–255. 10.1016/S0009-2614(99)00646-6. [DOI] [Google Scholar]
- Van Caillie C.; Amos R. D. Geometric derivatives of density functional theory excitation energies using gradient-corrected functionals. Chem. Phys. Lett. 2000, 317, 159–164. 10.1016/S0009-2614(99)01346-9. [DOI] [Google Scholar]
- Furche F.; Ahlrichs R. Adiabatic time-dependent density functional methods for excited state properties. J. Chem. Phys. 2002, 117, 7433–7447. 10.1063/1.1508368. [DOI] [Google Scholar]
- Furche F.; Ahlrichs R. Erratum: ”Time-dependent density functional methods for excited state properties” [J. Chem. Phys. 117, 7433 (2002)]. J. Chem. Phys. 2004, 121, 12772–12773. 10.1063/1.1824903. [DOI] [Google Scholar]
- Hutter J. Excited state nuclear forces from the Tamm-Dancoff approximation to time-dependent density functional theory within the plane wave basis set framework. J. Chem. Phys. 2003, 118, 3928–3934. 10.1063/1.1540109. [DOI] [Google Scholar]
- Petrenko T.; Kossmann S.; Neese F. Efficient time-dependent density functional theory approximations for hybrid density functionals: Analytical gradients and parallelization. J. Chem. Phys. 2011, 134, 054116. 10.1063/1.3533441. [DOI] [PubMed] [Google Scholar]
- Grotjahn R.; Furche F.; Kaupp M. Development and Implementation of Excited-State Gradients for Local Hybrid Functionals. J. Chem. Theory Comput. 2019, 15, 5508–5522. 10.1021/acs.jctc.9b00659. [DOI] [PubMed] [Google Scholar]
- Kretz B.; Egger D. A. Accurate Molecular Geometries in Complex Excited-State Potential Energy Surfaces from Time-Dependent Density Functional Theory. J. Chem. Theory Comput. 2021, 17, 357–366. 10.1021/acs.jctc.0c00858. [DOI] [PubMed] [Google Scholar]
- Sokolov M.; Bold B. M.; Kranz J. J.; Höfener S.; Niehaus T. A.; Elstner M. Analytical Time-Dependent Long-Range Corrected Density Functional Tight Binding (TD-LC-DFTB) Gradients in DFTB+: Implementation and Benchmark for Excited-State Geometries and Transition Energies. J. Chem. Theory Comput. 2021, 17, 2266–2282. 10.1021/acs.jctc.1c00095. [DOI] [PubMed] [Google Scholar]
- Kühne T. D.; Iannuzzi M.; Del Ben M.; Rybkin V. V.; Seewald P.; Stein F.; Laino T.; Khaliullin R. Z.; Schütt O.; Schiffmann F.; Golze D.; Wilhelm J.; Chulkov S.; Bani-Hashemian M. H.; Weber V.; Borštnik U.; Taillefumier M.; Jakobovits A. S.; Lazzaro A.; Pabst H.; Müller T.; Schade R.; Guidon M.; Andermatt S.; Holmberg N.; Schenter G. K.; Hehn A.; Bussy A.; Belleflamme F.; Tabacchi G.; Glöß A.; Lass M.; Bethune I.; Mundy C. J.; Plessl C.; Watkins M.; VandeVondele J.; Krack M.; Hutter J. CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. 10.1063/5.0007045. [DOI] [PubMed] [Google Scholar]
- VandeVondele J.; Krack M.; Mohamed F.; Parrinello M.; Chassaing T.; Hutter J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. 10.1016/j.cpc.2004.12.014. [DOI] [Google Scholar]
- Lippert G.; Hutter J.; Parrinello M. A hybrid Gaussian and plane wave density functional scheme. Mol. Phys. 1997, 92, 477–488. 10.1080/00268979709482119. [DOI] [Google Scholar]
- Iannuzzi M.; Chassaing T.; Wallman T.; Hutter J. Ground and Excited State Density Functional Calculations with the Gaussian and Augmented-Plane-Wave Method. CHIMIA Int. J. Chem. 2005, 59, 499–503. 10.2533/000942905777676164. [DOI] [Google Scholar]
- Strand J.; Chulkov S. K.; Watkins M. B.; Shluger A. L. First principles calculations of optical properties for oxygen vacancies in binary metal oxides. J. Chem. Phys. 2019, 150, 044702. 10.1063/1.5078682. [DOI] [PubMed] [Google Scholar]
- Poli E.; Elliott J. D.; Chulkov S. K.; Watkins M. B.; Teobaldi G. The Role of Cation-Vacancies for the Electronic and Optical Properties of Aluminosilicate Imogolite Nanotubes: A Non-local, Linear-Response TDDFT Study. Front. Chem. 2019, 7, 210. 10.3389/fchem.2019.00210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sternheimer R. On Nuclear Quadrupole Moments. Phys. Rev. 1951, 84, 244–253. 10.1103/PhysRev.84.244. [DOI] [Google Scholar]
- Baroni S.; de Gironcoli S.; Dal Corso A.; Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. 10.1103/RevModPhys.73.515. [DOI] [Google Scholar]
- Sternheimer R. M. Electronic Polarizabilities of Ions from the Hartree-Fock Wave Functions. Phys. Rev. 1954, 96, 951–968. 10.1103/PhysRev.96.951. [DOI] [Google Scholar]
- Budzak S.; Scalmani G.; Jacquemin D. Accurate Excited-State Geometries: A CASPT2 and Coupled-Cluster Reference Database for Small Molecules. J. Chem. Theory Comput. 2017, 13, 6237–6252. 10.1021/acs.jctc.7b00921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ongari D.; Yakutovich A. V.; Talirz L.; Smit B. Building a Consistent and Reproducible Database for Adsorption Evaluation in Covalent–Organic Frameworks. ACS Cent. Sci. 2019, 5, 1663–1675. 10.1021/acscentsci.9b00619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ongari D.; Talirz L.; Smit B. Too Many Materials and Too Many Applications: An Experimental Problem Waiting for a Computational Solution. ACS Cent. Sci. 2020, 6, 1890–1900. 10.1021/acscentsci.0c00988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirata S.; Head-Gordon M. Time-dependent density functional theory within the Tamm-Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291–299. 10.1016/S0009-2614(99)01149-5. [DOI] [Google Scholar]
- Casida M. E. In Recent Advances in Density Functional Methods, Part I; Chong D. P., Ed.; World Scientific: Singapore, 1995; p 155. [Google Scholar]
- Guidon M.; Hutter J.; VandeVondele J. Auxiliary Density Matrix Methods for Hartree-Fock Exchange Calculations. J. Chem. Theory Comput. 2010, 6, 2348–2364. 10.1021/ct1002225. [DOI] [PubMed] [Google Scholar]
- Ghosh D. C.; Islam N. Whether electronegativity and hardness are manifest two different descriptors of the one and the same fundamental property of atoms? @ TA quest. Int. J. Quantum Chem. 2011, 111, 40–51. 10.1002/qua.22415. [DOI] [Google Scholar]
- Marx D.; Hutter J. In Modern Methods and Algorithms of Quantum Chemistry; Grotendorst J., Ed.; John von Neumann Institute for Computing, Forschungszentrum Jülich: Jülich, Germany, 2000; pp 301–449 (first edition, paperback, ISBN 3-00-005618-1) or pp 329–477 (second edition, hardcover, ISBN 3-00-005834-6), see http://www.theochem.rub.de/go/cprev.html.
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Mayhall N. J.; Raghavachari K.; Hratchian H. P. ONIOM-based QM:QM electronic embedding method using Löwdin atomic charges: Energies and analytic gradients. J. Chem. Phys. 2010, 132, 114107. 10.1063/1.3315417. [DOI] [PubMed] [Google Scholar]
- Davidson E. R. The iterative calculation of a few of the lowest eigenvalues and corresponding eigenvectors of large real-symmetric matrices. J. Comput. Phys. 1975, 17, 87–94. 10.1016/0021-9991(75)90065-0. [DOI] [Google Scholar]
- Chassaing T.Excitation Energy Calculations with TD-DFT. PhD thesis, University of Zurich, Zurich, Switzerland, 2005. [Google Scholar]
- Ryabinkin I. G.; Nagesh J.; Izmaylov A. F. Fast Numerical Evaluation of Time-Derivative Nonadiabatic Couplings for Mixed Quantum–Classical Methods. J. Phys. Chem. Lett. 2015, 6, 4200–4203. 10.1021/acs.jpclett.5b02062. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16, Revision C.01; Gaussian Inc.: Wallingford, CT, 2016.
- Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Balasubramani S. G.; Chen G. P.; Coriani S.; Diedenhofen M.; Frank M. S.; Franzke Y. J.; Furche F.; Grotjahn R.; Harding M. E.; Hättig C.; Hellweg A.; Helmich-Paris B.; Holzer C.; Huniar U.; Kaupp M.; Marefat Khah A.; Karbalaei Khani S.; Müller h.; Mack F.; Nguyen B. D.; Parker S. M.; Perlt E.; Rappoport D.; Reiter K.; Roy S.; Rückert M.; Schmitz G.; Sierka M.; Tapavicza E.; Tew D. P.; van Wüllen C.; Voora V. K.; Weigend F.; Wodyński A.; Yu J. M. TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations. J. Chem. Phys. 2020, 152, 184107. 10.1063/5.0004635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigend F.; Furche F.; Ahlrichs R. Gaussian basis sets of quadruple zeta valence quality for atoms H-Kr. J. Chem. Phys. 2003, 119, 12753–12762. 10.1063/1.1627293. [DOI] [Google Scholar]
- VandeVondele J.; Hutter J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 2007, 127, 114105. 10.1063/1.2770708. [DOI] [PubMed] [Google Scholar]
- Brémond E.; Savarese M.; Adamo C.; Jacquemin D. Accuracy of TD-DFT Geometries: A Fresh Look. J. Chem. Theory Comput. 2018, 14, 3715–3727. 10.1021/acs.jctc.8b00311. [DOI] [PubMed] [Google Scholar]
- Chan G. K.-L.; Handy N. C. C8H8: a density functional theory study of molecular geometries introducing the localised bond density. J. Chem. Soc., Faraday Trans. 1996, 92, 3015–3021. 10.1039/ft9969203015. [DOI] [Google Scholar]
- Neumann R.; Nobes R. H.; Handy N. C. Exchange functionals and potentials. Mol. Phys. 1996, 87, 1–36. 10.1080/00268979600100011. [DOI] [Google Scholar]
- Sancho-García J. C.; Cornil J. Assessment of recently developed exchange-correlation functionals for the description of torsion potentials in π-conjugated molecules. J. Chem. Phys. 2004, 121, 3096–3101. 10.1063/1.1774976. [DOI] [PubMed] [Google Scholar]
- Vikramaditya T.; Lin S.-T. Limitations of Global Hybrids in Predicting the Geometries and Torsional Energy Barriers of Dimeric Systems and the Role of Hartree Fock and DFT Exchange. J. Comput. Chem. 2019, 40, 2810–2818. 10.1002/jcc.26056. [DOI] [PubMed] [Google Scholar]
- Fang C.; Oruganti B.; Durbeej B. How Method-Dependent Are Calculated Differences between Vertical, Adiabatic, and 0—0 Excitation Energies?. J. Phys. Chem. A 2014, 118, 4157–4171. 10.1021/jp501974p. [DOI] [PubMed] [Google Scholar]
- Peach M. J. G.; Benfield P.; Helgaker T.; Tozer D. J. Excitation energies in density functional theory: An evaluation and a diagnostic test. J. Chem. Phys. 2008, 128, 044118. 10.1063/1.2831900. [DOI] [PubMed] [Google Scholar]
- Send R.; Kühn M.; Furche F. Assessing Excited State Methods by Adiabatic Excitation Energies. J. Chem. Theory Comput. 2011, 7, 2376–2386. 10.1021/ct200272b. [DOI] [PubMed] [Google Scholar]
- Côté A. P.; Benin A. I.; Ockwig N. W.; O’Keeffe M.; Matzger A. J.; Yaghi O. M. Porous, Crystalline, Covalent Organic Frameworks. Science 2005, 310, 1166–1170. 10.1126/science.1120411. [DOI] [PubMed] [Google Scholar]
- Das G.; Biswal B. P.; Kandambeth S.; Venkatesh V.; Kaur G.; Addicoat M.; Heine T.; Verma S.; Banerjee R. Chemical sensing in two dimensional porous covalent organic nanosheets. Chem. Sci. 2015, 6, 3931–3939. 10.1039/C5SC00512D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das P.; Chakraborty G.; Tyagi S.; Mandal S. K. Design of Fluorescent and Robust Covalent Organic Framework Host Matrices for Illuminating Mechanistic Insight into Solvatochromic Decoding. ACS Appl. Mater. Interfaces 2020, 12, 52527–52537. 10.1021/acsami.0c12785. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.