Tough, aorta-inspired soft composites

Significance

Biological composites have excellent fracture and fatigue properties that can be partially attributed to spatial variations of fiber alignment. We three-dimensionally print fiber-reinforced silicone composites with aorta-inspired fiber orientations and with a strengthened fiber–matrix bond to produce a composite with mechanical properties similar to those of skin. The materials are resistant to mechanical failure, even in the presence of large defects, including under cyclic loading.

Abstract

Spatial variations in fiber alignment (and, therefore, in mechanical anisotropy) play a central role in the excellent toughness and fatigue characteristics of many biological materials. In this work, we examine the effect of fiber alignment in soft composites, including both “in-plane” and “out-of-plane” fiber arrangements. We take inspiration from the spatial variations of fiber alignment found in the aorta to three-dimensionally (3D) print soft, tough silicone composites with an excellent combination of stiffness, toughness, and fatigue threshold, regardless of the direction of loading. These aorta-inspired composites exhibit mechanical properties comparable to skin, with excellent combinations of stiffness and toughness not previously observed in synthetic soft materials.

Soft materials play a crucial role in applications as diverse as tissue engineering (1), stretchable electronics (2–4), bio-adhesives (5), hydrogel optical fibers (6), stretchable ionic conductors (7), and soft robotics (8–11). In order to meet these engineering demands, soft materials with a wide variety of chemical functionalities and mechanical properties have been developed. However, engineered soft materials still typically suffer from low toughness, which causes poor reliability and premature failure under both static and cyclic loading (12, 13). New soft materials with higher toughness and fatigue thresholds are critical for these applications.

Nature provides many examples of both structural and soft materials that are resistant to failure, even when cracks or other flaws are present in the material. This is typically achieved via some form of heterogeneity, such as tiling of soft and stiff materials (14) or spatial variations in fiber orientation (15). For example, nacre is extremely resistant to failure due to its “brick and mortar” geometry, comprising hard mineral “bricks” and soft proteinaceous “mortar” that can deflect and slow crack propagation (16–18). Helical arrangements of collagen fibers contribute to toughening by inhibiting crack propagation in biological materials such as arterial walls (19) and osteons (14, 20). Similarly, the dactyl club of the mantis shrimp contains helical (Bouligand) arrangements of chitin fibers that provide toughening by forcing cracks to twist as they propagate (21). Toughening mechanisms that rely on such spatial variations of fiber orientation have also been realized in synthetic materials to improve both toughness and fatigue properties (22).

In all of the above examples of natural microstructures, the geometric arrangement of internal interfaces is crucial for achieving crack deflection, a key mechanism for higher toughness (14). However, the geometric arrangement of material phases is not sufficient in itself for achieving the failure properties necessary to an organism’s function, including strength, toughness, and fatigue resistance; the interfacial properties between different material phases in the microstructure are equally important for achieving these and must exist within relatively narrow bounds. In order for cracks to dissipate a meaningful amount of energy as they deflect, the interfacial toughness needs to be high. However, if it is too high, cracks penetrate through interfaces instead of deflecting (23, 24). In nacre, the outermost layer is the most resistant to failure, with the highest interfacial toughness between the minerals and protein (25). This arrangement best shields the shell from rapid crack propagation through the protein layers. In fibrous composites, the role of adhesion between fiber and matrix is also important to the toughness of the composites. In general, higher interfacial toughness and critical shear strength between the matrix and fibers can lead to higher toughness (26). However, the toughness cannot be improved without bound. Other failure mechanisms, such as fiber fracture and matrix fracture (which are even more relevant for soft composites), will eventually initiate. Nevertheless, the importance of these interfacial properties are often neglected in research on bioinspired composites. In many cases, this is due to the use of commercial multimaterial three-dimensional (3D) printers with limited materials and little, if any, control over interfacial properties between these materials.

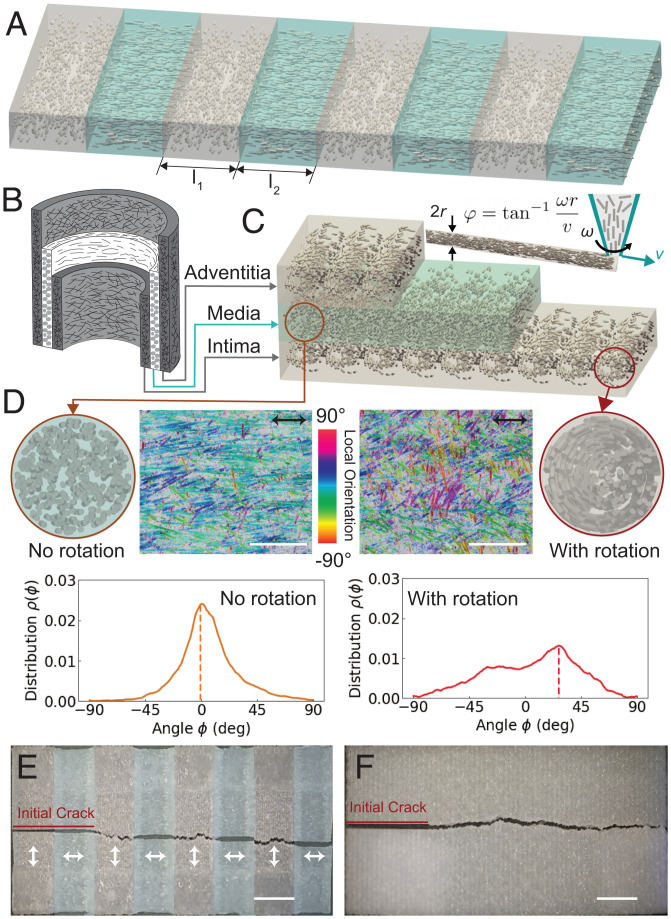
We employ direct ink writing (DIW) (27, 28) to 3D-print composites that consist of polydimethylsiloxane (PDMS) reinforced with short glass fibers (GFs). The shear between the material and the nozzle as it is extruded causes alignment of elongated fillers along the print path (29, 30). This can impart significant mechanical anisotropy to the composite, including both elastic properties (31–33) and failure properties (34). By controlling the print path, we can therefore control the spatial distribution of the fiber orientation and, hence, the spatial distribution of the mechanical anisotropy. With the ultimate goal of understanding the failure properties of complex, aorta-inspired fiber composites, we first consider the failure characteristics of the simpler case of composites with in-plane spatial heterogeneity, illustrated in Fig. 1A. During failure of such specimens, a crack must propagate through alternating regions, in which fibers are oriented parallel with or perpendicular to the direction of crack growth. In past work, similar specimens with alternating “soft” and “stiff” domains have been shown to have excellent failure characteristics (35). However, in this work, the mechanical contrast is obtained with a single material, instead of relying on two distinct materials, simply by printing a sequence of regions with unidirectional, perpendicularly oriented fiber orientations (Fig. 1A). As shown later, the toughness can be tuned to exceed that of unidirectional composites by changing the size of each region. After this, we consider the more complex case of aorta-inspired spatial variations in fiber orientation. These latter specimens are printed by using the same GF-reinforced PDMS material, but now with a rotating nozzle (Fig. 1 B and C). The rotating nozzle imparts a rotational shear during extrusion of the composite, causing the fibers to be oriented helically (Fig. 1 C and D) (34). The fibers at the surface of the filament, where they are near the rotating inner wall of the nozzle, experience a shear field with nominal angle $\phi ={\tan }^{-1}\frac{\omega r}{v}$ (Fig. 1C), as determined by the rotational speed ω, the translational speed v, and the radius of the nozzle r (34). We designate the actual distribution of fiber orientations at the surface of the filament as $\rho (\varphi )$ (distinct from $\phi$, defined above, which is the predicted angle corresponding to the idealized shear field). $\rho (\varphi )$ is measured by analysis of microscope images (Fig. 1D, with Left and Right showing the fiber-orientation distribution for the cases of no rotation and rotation, respectively). With no nozzle rotation, the fibers are predominantly aligned in the printing direction (0°). With nozzle rotation, the fibers at the surface of the filaments have an orientation distribution with a peak at a nonzero angle with respect to the printing direction, as shown in Fig. 1D. In general, a larger value for $\phi$ shifts the peak value of the distribution to a larger angle and widens the fiber-orientation distribution at the surface of the filament (see discussion in SI Appendix, Figs. S1–S3). Note, however, that the fibers at the center of the filament remain nominally aligned in the printing direction, leading to a quasi-isotropic mechanical response in regions of the specimen printed with nozzle rotation (34). The aorta-inspired soft composite is printed in three layers, as shown in Fig. 1C. The first and third layers are designed to mimic the intima and adventitia, respectively, requiring a wide distribution of fiber orientations and approximately isotropic mechanical properties (Fig. 1A). This is achieved by printing these layers with the nozzle rotating. The middle layer is designed to mimic the media layer, which has a narrow distribution of fiber orientations and significant mechanical anisotropy. This is achieved by printing without rotation. The aorta-inspired composites are significantly less anisotropic than unidirectional composites, making them much more suitable for combined loading conditions. Moreover, the aorta-inspired materials have a combination of stiffness, toughness, and fatigue threshold that places them in previously unoccupied property space for synthetic soft materials, with similar stiffness and higher toughness than skin. This combination of properties could allow the composites developed in this work to have wide application in soft robotics, stretchable electronics, and medical devices.

Fig. 1.

(A) Schematic of composites with in-plane heterogeneity through spatial variations in fiber orientation leading to elastic contrast. (B) Schematic of the aorta, with three concentric layers; the outermost and innermost layers show a wide distribution of fiber orientations, associated with relatively isotropic mechanical properties; the middle layer has circumferentially oriented, nominally unidirectional fiber orientation, causing mechanical anisotropy. (C) Schematic of an aorta-inspired composite printed via DIW using a rotational nozzle. (D) Cross-sectional schematic, artificially colored microscope image, and fiber-orientation distribution for layers printed without (Left) and with (Right) nozzle rotation. Printing direction is indicated by black arrows. For the microscope images, the focal plane is near the top surface of the filaments, showing the fiber alignment where the rotational shear field was large; the false color indicates the local fiber alignment (Materials and Methods). (Scale bar: 1 mm.) (E) Image of cracked composites with in-plane heterogeneity. (Scale bar: 10 mm.) (F) Image of cracked composites with aorta-inspired heterogeneity. (Scale bar: 10 mm.).

In Fig. 1E and F, we show the postfracture images of the entire specimens with in-plane heterogeneity and aorta-inspired heterogeneity, respectively. The toughness (or critical energy-release rate) of soft materials is characterized by loading both notched and unnotched specimens under tension at a constant displacement rate until failure, as illustrated in Fig. 2A (36, 37). First, the strain energy density is obtained for unnotched specimens from their stress–stretch curves (Fig. 2 A, Upper). The toughness is then computed as the energy per crack area stored in the material ahead of the crack at a critical stretch λ_c when the crack starts to propagate. We first investigate the fracture properties of the unidirectional composites. The fiber volume fraction is a key factor influencing the toughness of the unidirectional composites, as indicated in SI Appendix, Fig. S4. Toughness increases linearly with fiber volume fraction up to 10 vol.%, after which there is no further improvement. This is a result of the drop in critical stretch (SI Appendix, Fig. S4F) that occurs above volume fractions of 10 vol.%. Such a drop could occur due to the decrease in the mean distance between fibers at higher volume fractions (38). Fiber length is also a key factor that was investigated, though the range of fiber lengths is limited due to fiber breakage during mixing of the ink (see SI Appendix for details, including SI Appendix, Figs. S9 and S10). In addition to volume fraction, the strength of the interfacial bond between the fibers and matrix also plays a critical role in determining the toughness. Recent work on glass–polymethylmethacrylate composites illustrates this point clearly (39). This shows that the geometric arrangement of materials in a composite (e.g., arrangements inspired by nacre or other natural composites) is not sufficient by itself to obtain good failure characteristics. Following this line of reasoning, we treated the glass fibers with sulfuric acid prior to mixing our printable inks to increase the strength of the fiber–matrix bond, increasing the toughness of the heterogeneous composites. This process increases the ultimate strength, regardless of volume fraction (though softening still occurs prior to fracture, which is indicative of fiber–matrix debonding). The toughness of the unidirectional composites improves significantly (most notably for specimens with 5 vol.% fibers), as shown in SI Appendix, Fig. S5H. Importantly, for both high- and low-volume fractions, the stiffness of the unidirectional composite remains unaffected (shown in SI Appendix, Fig. S5D), suggesting that the acid treatment of the fibers does not physically alter the fiber morphology.

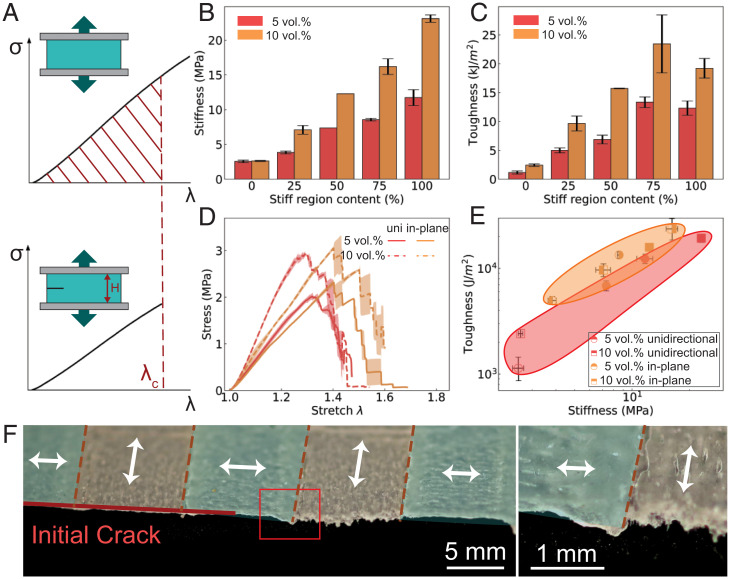
Fig. 2.

(A) Schematic illustrating the approach used to measure toughness. (B and C) Effect of the fraction of stiff region in the composite with in-plane heterogeneity $l_1/(l_1+l_2)$ on stiffness and toughness, respectively. (D) Fracture behavior of the composites with in-plane heterogeneity with stiff fraction $l_1/(l_1+l_2)=0.75$ compared with unidirectional (uni) composites (both with acid-treated fibers). (E) Toughness vs. stiffness for the four specimens shown in B. (F) Optical images of the crack path with alternating regions of fiber alignment (indicated by the direction of the white arrows).

Next, we consider the simpler case of in-plane heterogeneity (Fig. 1A), in which fibers are oriented differently in each domain, but always unidirectionally within a given domain (i.e., no nozzle rotation is used). Elastic contrast under this in-plane configuration is controlled via the fiber orientation and the volume fraction of the fibers, as shown in SI Appendix, Figs. S6 and S7. A larger volume fraction of fibers results in a higher degree of mechanical anisotropy, leading to increased elastic contrast between two regions. However, there is a practical limit to the maximum volume fraction, deriving, for example, from nozzle clogging and nonuniform extrusion, as explored in previous works (30–32, 34). In addition, we control the width of each region (l₁ and l₂, which are stiff and soft, respectively, due to the orientation of fibers in these regions with respect to the loading direction), as indicated in Fig. 1A. The total width ($l_1+l_2$) for each period is kept constant, while l₁ is varied, leading to different fractions of the stiff region (fibers oriented parallel to the loading direction) calculated as $l_1/(l_1+l_2)$. If this fraction is zero, loading is fully perpendicular to the fiber orientation (0% stiff region). If the fraction is one, loading is fully parallel with the fiber direction (100% stiff region). All samples shown are printed with acid-treated fibers, resulting in better fiber–matrix bonding. In Fig. 2 B and C, we show the stiffness and toughness of composites with in-plane heterogeneity and with unidirectional alignment for two volume fractions. The stiffness increases linearly with the fraction of the sample occupied by stiff regions. In contrast, toughness is maximized with composites composed of 75% stiff regions. Fig. 2D compares the stress–stretch responses of the composites with in-plane heterogeneity (consisting of 75% stiff regions) to that of the unidirectional composites for both 5 vol.% and 10 vol.%. The fiber heterogeneity leads to a larger critical stretch than that of the unidirectional composites. However, this comes at the cost of a reduction in stiffness due to the presence of the soft regions. The delay of fracture is a result of the soft–stiff interface rather than the size of the soft and stiff regions. The critical stretch is almost constant at ${\lambda }_c=1.40$ for all three values of l₁ tested, leading to higher toughness that exceeds that of the unidirectional composites when $l_1=0.75$. To better compare all composites with in-plane heterogeneity and unidirectional alignment, we plot toughness vs. stiffness in Fig. 2E. Composites with in-plane heterogeneity generally show lower stiffness and comparable or higher toughness, moving to the left on the toughness vs. stiffness plot. Fig. 2F shows the specimen after fracture, with distinct crack morphology observed in the two types of domains of fiber alignment. As the crack reaches the interface from the softer region (fibers aligned perpendicular to loading) to the stiffer region (fibers aligned parallel with loading), it stops before it propagates again through the next stiff and soft region, stopping at the next soft-to-stiff interface until it reaches the end of the notched specimen (Movie S1). The interfaces between the soft and stiff regions inhibit the crack as it propagates. Each large drop in stress in the stress–stretch data for the notched composites shown in Fig. 2D corresponds to growth of the crack through an interface between the soft and stiff regions. As the crack reaches the next interface, it stabilizes with additional loading before going through the interface again. This behavior leads to the jagged loading curve observed in Fig. 2D, similar to that observed in other PDMS systems (35, 40).

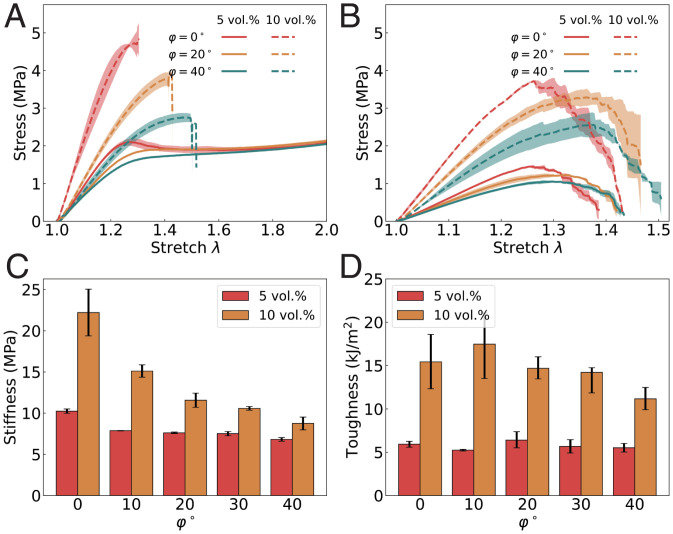
To understand the behavior of aorta-inspired composites, we first consider the effect of the idealized fiber rotation ($\phi$) on the stress–stretch responses of composites printed with nozzle rotation. The stress–stretch responses are shown as a function of $\phi$ with volume fractions of 5 vol.% and 10 vol.% in Fig. 3 A and B for unnotched and notched specimens, respectively. For both volume fractions, the stiffness decreases as a function of rotation speed, since increased rotation speeds cause fewer fibers to be oriented along the loading axis (Fig. 3C). This trend is consistent with prior observations in carbon–fiber epoxy composites (34). In addition to this trend in stiffness, the softening instability that results from fiber–matrix debonding (41) for 5 vol.% composites is less pronounced as $\phi$ is increased, similar to the effect of off-axis loading. At 10 vol.%, as $\phi$ is increased, the increased helicity of the fiber distribution results in higher ductility. The stretch of rupture for composites printed with $\phi ={40}^{°}$ is ${\lambda }_R=1.5$, whereas composites printed with $\phi =0^{°}$ (no rotation) have a stretch of rupture of ${\lambda }_R=1.3$ (see SI Appendix, Fig. S8B for stretch to rupture for all specimens).

Fig. 3.

(A) Response of unnotched specimens with various helical fiber orientations for 5 vol.% and 10 vol.%. (B) Response of notched specimens with various idealized fiber orientations ($\phi$) for 5 vol.% and 10 vol.%. (C and D) Stiffness (C) and toughness (D) as a function of volume fraction and idealized fiber orientation ($\phi$).

For both volume fractions, an increase in $\phi$ is associated with an increase in the critical stretch λ_c, at which crack propagation initiates (SI Appendix, Fig. S8C). Particularly, for composites with 10 vol.% fibers, the critical stretch increases from ${\lambda }_c=1.28$ ($\phi =0^{°}$) to ${\lambda }_c=1.39$ ($\phi ={40}^{°}$). However, this increase in critical stretch does not result in higher toughness (Fig. 3D). For $\phi =0^{°}$, the toughness is low due to a low critical stretch. For $\phi ={40}^{°}$, the toughness is low due to the low stiffness. The nonmonotonic dependence of toughness on $\phi$ is the result of this competition between critical stretch and stiffness. The composites with the highest toughness have intermediate fiber orientations, $\phi ={20}^{°}$ for 5 vol.% and $\phi ={10}^{°}$ for 10 vol.%. Most interestingly, the composites with any fiber rotation at 10 vol.% break at a stretch that is very close to the stretch of rupture for unnotched composites. This suggests that these composites are insensitive to flaws as large as the initial crack length (a = 20 mm).

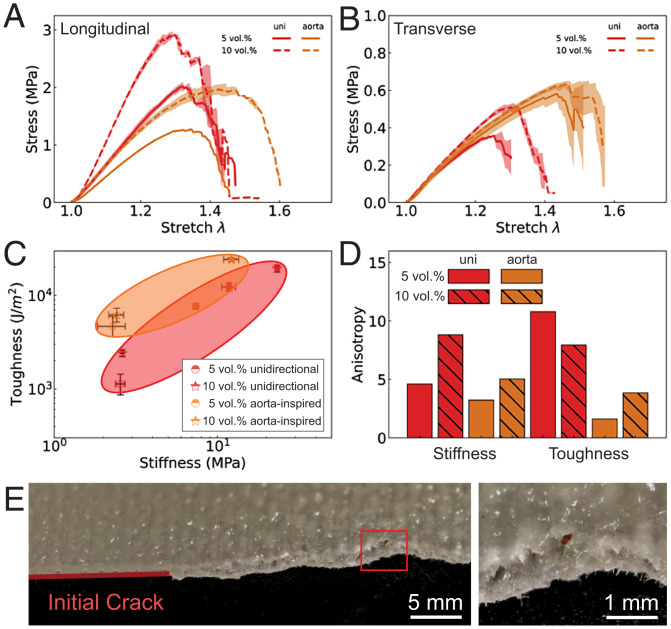
Now that we have characterized the effects of fiber angle and volume fraction for single-layer specimens, we next considered three-layer composites with aorta-inspired, out-of-plane heterogeneity, as illustrated in Fig. 1C. We printed the top and bottom layers with $\phi ={20}^{°}$, which was chosen because this case has the highest toughness (Fig. 3D) at 5 vol.%. We kept the same angle for 10 vol.% aorta-inspired composites (though it was not quite optimal) in order to see the effect of volume fraction. We tested these aorta-inspired composites both parallel with the print path (“longitudinal”) and perpendicular to the print path (“transverse”). We compare the stress–stretch relationship for notched specimens for both unidirectional and aorta-inspired composites in Fig. 4 A and B. When loaded longitudinally, the aorta-inspired composites performed well at 10 vol.%, with a very large critical stretch (${\lambda }_c=1.45$). The stress–stretch relationships for transverse loading are provided in Fig. 4B, showing significant improvement in critical stretch (from 1.30 to 1.50). The aorta-inspired composites have comparable toughness to the unidirectional composites when both are loaded longitudinally, as shown in Fig. 4C. When loaded transversely, the aorta-inspired composites have a toughness of 7,000 J/m² compared to 1,000 J/m² for unidirectional composites. This effect can be quantified by defining an anisotropy ratio, i.e., the ratio of the value of a property measured longitudinally to the value of that property measured transversely. The anisotropy ratios for both stiffness and toughness are shown in Fig. 4D. It is not surprising that the anisotropy in stiffness is larger with increasing volume fraction for both types of composites (34, 41). Unidirectional composites have an anisotropy ratio for toughness up to 10. This is not desired when the composites are subjected to unknown or complex loading, often leading to premature failure. The composites with aorta-inspired heterogeneity have a much lower anisotropy ratio for toughness (below 3.5). Moreover, the aorta-inspired composites exhibit much smoother stress–stretch curves during failure. This observation is supported by the crack morphology after fracture, as shown in Fig. 4E. The aorta-inspired composites exhibit out-of-plane variations in the crack surface, corresponding to the out-of-plane fiber arrangements inspired by the three-layer aorta structure (Fig. 1B). It is not favorable for the crack to propagate straight through the layers with rotated fibers. The arrangement of fibers within the layers of the composites is associated with this crack morphology, which has been previously shown to be associated with high toughness (due to the additional energy required to twist the crack as it propagates) (21).

Fig. 4.

Fracture behavior of the composites with aorta-inspired heterogeneity as a function of volume fraction and loading direction. (A and B) Stress–stretch response of notched unidirectional (uni) and aorta-inspired composites, loaded longitudinally or transversely, respectively, with the print direction. (C) Toughness vs. stiffness of the composites. Points with solid infill are loaded longitudinally; points without infill are loaded transversely. (D) Anisotropy ratio (i.e., the ratio between a property measured longitudinally and that property measured transversely) for both stiffness and toughness for unidirectional and aorta-inspired composites. (E) Optical microscope images of the crack path.

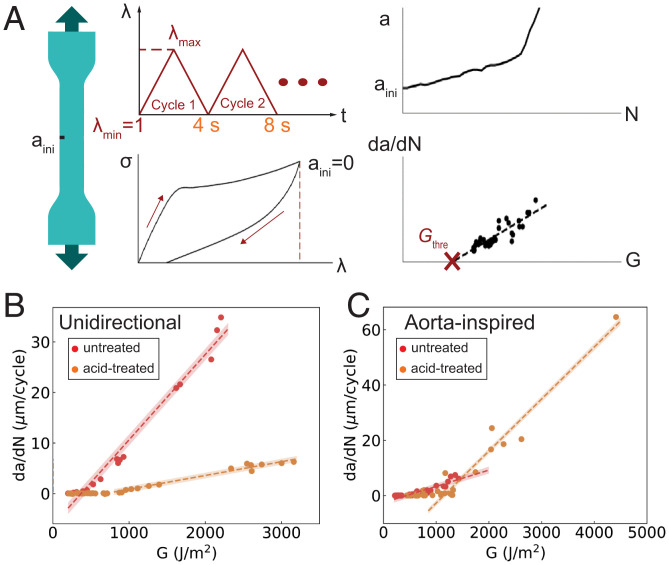
Lastly, we investigated the response of the composites under cyclic loading. Cyclic loading can lead to failure via sequential growth of cracks. The fatigue threshold quantifies the maximum loading amplitude during cyclic loading below which a crack will not grow. To obtain the fatigue threshold experimentally, both notched and unnotched tensile specimens were loaded cyclically at maximum applied stretches λ_max ranging from 1.10 to 1.30 (Fig. 5A). During cyclic loading of the unnotched specimens, the first cycle dissipates a large amount of energy (i.e., there is a large area enclosed between the loading and unloading portions of the stress–stretch curve; see details in SI Appendix, Figs. S12–S15), while subsequent cycles dissipate much less energy. Unidirectional composites with 5 vol.% untreated fibers exhibit poor fatigue properties when cyclically loaded with initial cracks (SI Appendix, Fig. S13). Cracks grow rapidly at a low stretch amplitude of 1.20. Specimens with acid-treated fibers perform better under cyclic loading, surviving more than 5,000 cycles at a stretch of 1.25 (SI Appendix, Fig. S13B). Whether or not the fibers are treated with acid, fatigue specimens with initial crack loaded to a large stretch of ${\lambda }_{\mathit{max}}=1.25$ exhibit an initial phase of rapid crack growth, but can eventually reach a stable crack-growth phase (see SI Appendix, Figs. S12 and S13 for details). The extracted crack-growth rate da/dN vs. applied energy-release rate for unidirectional composites is shown in Fig. 5B. The applied energy-release rate is related to the maximum applied stretch, as quantified with measured strain-energy density and crack length (see Materials and Methods for details). We tested all composites at low stretch amplitude (where no crack growth is observed) for at least 15,000 cycles to ensure that the fatigue threshold exists. When fitting the experimental data to quantify the fatigue threshold, we applied Bayesian linear regression, which estimates a range of possible linear fittings (shaded area in Fig. 5 B and C). The uncertainty in fitting also quantifies the uncertainty in the fatigue threshold. The measured fatigue limits of unidirectional specimens with 5 vol.% fibers are 499 ± 66 J/m² and 689 ± 224 J/m² for composites with fibers not treated with acid and those treated with acid, respectively, when loaded optimally (i.e., loaded with the direction of the fibers), as shown in Fig. 5B. However, the unidirectional composites have drastically different responses in different loading directions. When loaded in the transverse direction (perpendicular to the fibers), the failure is dominated by fracture of the matrix (PDMS), with the fibers not providing reinforcement. Both the toughness and fatigue response of transversely loaded unidirectional composites are therefore approximately the same as the toughness and fatigue response of the PDMS matrix [i.e., around 1,000 J/m² and 50 J/m², respectively (35, 42)]. We also characterized the fatigue threshold of composites printed with nozzle rotation only, resulting in composites with helical arrangements of GFs. These have a higher fatigue threshold than that of the unidirectional composites (G_c = 854 J/m² for 10 vol.% acid-treated fibers, as shown in SI Appendix, Figs. S15–S18). Finally, the aorta-inspired composites have the highest fatigue thresholds of all tested composites (Fig. 5C), with thresholds of 554 ± 183 J/m² and 1,145 ± 62 J/m² for untreated and acid-treated fibers, respectively. In addition to a higher fatigue threshold when loaded in the longitudinal direction, composites with aorta-inspired heterogeneity would also withstand combined fatigue loading better than unidirectional composites.

Fig. 5.

(A) Illustration of fatigue-threshold measurement: unnotched tensile specimens are first cyclically loaded to measure the strain-energy density associated with each cycle. Notched specimens are loaded to measure crack length a vs. cycle number N. Combining both tests, the crack-growth rate da/dN vs. applied energy-release rate is plotted. The fatigue threshold is taken as the location at which the linear fit intercepts the horizontal axis of the plot. (B) Fatigue-threshold determination for unidirectional composites with 5 vol.% untreated and acid-treated fibers (498.7 ± 66.27 J/m² and 688.97 ± 223.5 J/m², respectively). (C) Fatigue threshold for aorta-inspired composites with 10 vol.% untreated and acid-treated fibers (554.2 ± 183.4 J/m² and 1,145.47 ± 61.67 J/m², respectively). These two composites have comparable stiffness; hence, they are compared here.

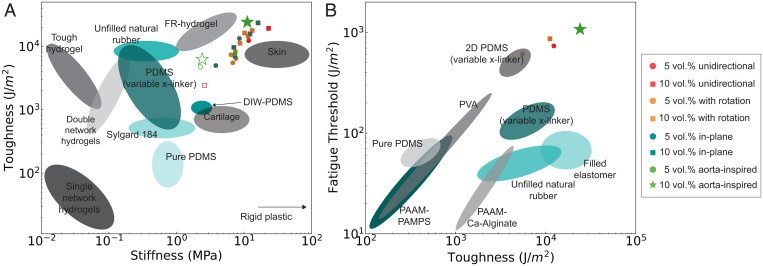
In summary, we present the toughness and fatigue threshold of all composites tested in this work in two plots: toughness vs. stiffness and fatigue threshold vs. toughness (Fig. 6). The PDMS-GF composites studied in this work occupy areas in these plots that were previously unoccupied. Spatial variations in fiber orientation, programmed merely by choosing the print path and the nozzle-rotation rates, can lead to significant improvements in the fracture and fatigue properties of soft composites. Composites with in-plane heterogeneity exhibit delayed initiation of crack propagation, leading to higher toughness compared to unidirectional composites (moving to the upper left of the toughness vs. stiffness plot, as shown in Fig. 6A). Furthermore, aorta-inspired composites are less anisotropic than unidirectional composites, enabling better failure properties when subjected to a variety of loading directions. When loaded parallel with the print direction, these composites have comparable toughness to unidirectional composites. However, when loaded in the transverse direction, aorta-inspired composites have seven times the toughness of unidirectional composites. In summary, these fiber-reinforced soft composites have similar stiffness to that of skin, but with superior toughness. Moreover, by making use of heterogeneities and strengthened fiber–matrix interactions, the fatigue threshold can be increased from 500 J/m² for unidirectional composites to 1,150 J/m² for aorta-inspired composites. We summarize our results in Fig. 6B, plotting the fatigue threshold vs. toughness of our composites with data from several previous studies, including other elastomers (13), rubbers (48), and hydrogels (49–51). This work demonstrates the importance of spatial variations in fiber alignment and provides insight into the arrangement of the reinforcing phase in biological composites. These principles can also be transferred to other composite systems for which the main failure mechanism is fiber–matrix debonding and pullout. Moreover, the materials developed in this work could find use in emerging applications, such as stretchable electronics, structural components in soft robotics, and lightweight protection.

Fig. 6.

(A) Toughness vs. stiffness for soft elastomers characterized in previous work (unfilled points are loaded in the transverse direction). DIW-PDMS refers to rheologically modified PDMS for DIW 3D printing (shown in SI Appendix, Fig. S11). Tough hydrogels (37, 43), fiber-reinforced (FR) hydrogels (3), PDMS (44), rubber (45), double-network elastomers (46), and PDMS with variable cross-linker (35). (B) Fatigue threshold vs. toughness; data were gathered from refs 40 and 47. PAAM, polyacrylamide; PAMPS, poly(2-acrylamido-2-methyl-1-propanesulfonic acid); PVA, poly(vinyl alcohol).

Materials and Methods

Fiber Treatment.

Prior to mixing, the GFs were ultrasonically cleaned in isopropanol for 30 min and dried at 60 °C overnight. Then, the washed GFs were treated by 0.5 mol/L H₂ SO₄ solutions for 30 min with active stirring. The acid was removed by rinsing with deionized water, followed by drying at 60 °C overnight.

DIW Printing.

Specimens were printed with a modified commercial fused deposition modeling 3D printer. We mixed a 3D-printable PDMS by combining 85 wt.% SE 1700 (Dow Corning) and 15 wt.% Sylgard 184 (Dow Corning), using a 1:10 cross-linker ratio. Milled GFs (Fiber Glast 29, 1/16”) were subsequently mixed with PDMS using a vacuum mixer (FlackTek). The material was then transferred to a syringe and centrifuged to remove air. We extruded the material pneumatically through a 610-µm nozzle at a pressure of 30 psi, with the fibers nominally aligned along the print path, as in previous studies (29, 30). Unidirectional specimens were produced by using a raster pattern of parallel extruded filaments. Specimens with in-plane heterogeneity (as in Fig. 1A) were printed with eight unidirectional regions of equal width (10 mm). The print path was chosen such that each unidirectional region would have a fiber orientation that was either perpendicular to or parallel with the loading direction. For aorta-inspired composites, three total layers were printed. The first layer was printed with parameters corresponding to $\phi ={20}^{°}$. The second layer was printed without rotation. The third layer was again printed with parameters corresponding to $\phi ={20}^{°}$. Helical fiber orientations were obtained by mounting a motor (maximum rotational speed of 500 rpm) on the custom DIW printer. The rotational speed was determined by the applied voltage, which was controlled directly through the printer’s communication channel. For each maximum fiber rotation $\phi$, the rotation speed ω was maximized, while the translational speed v was varied to match the corresponding parameter $\tan \phi =\omega r/v$. A syringe adapter was used to allow free rotation of the nozzle during printing. After printing and thermal cross-linking, the local orientation of the fibers was measured from optical microscope images, taken with transmitted light, using OrientationJ (52).

Mechanical Testing.

Tensile tests and fracture tests were both conducted at strain rates of 0.02/s, using an Instron 68SC-5 mechanical test system. Testing of thin strip-like specimens was performed by using a 150-mm by 75-mm jaw face, allowing the grip to hold the entire specimen. Fatigue tests were conducted with a conventional tensile specimen with gauge length of 35 mm, width of 7 mm, and thickness of 1 mm. Cyclic loading was applied to the sample with a triangular loading profile in displacement control at a frequency of 0.25 Hz. For each cycle, the specimen was stretched to a maximum stretch of ${\lambda }_{\text{max}}$ and then unloaded to the initial length λ = 1. The fatigue response of the unnotched specimens was measured by using a tensile specimen. The strain energy for each loading cycle was calculated as $W({\lambda }_{\text{max},N})={\displaystyle {\int }_1^{{\lambda }_{\text{max}}}\sigma d\lambda }$. Fatigue tests of the notched specimens were conducted by using a precracked tensile specimen (Fig. 5A), with a camera used to record the crack length a(N) every 20 cycles. The applied energy-release rate was calculated as $G({\lambda }_{\text{max}},N)=6a(N)W({\lambda }_{\text{max},N})/\sqrt{{\lambda }_{\text{max}}}$. The fatigue threshold was extracted from all such plots as the location at which the linear fit intercepts the horizontal axis.

Toughness Calculation.

Toughness can be calculated by performing two types of tests on specimens of the same material. First, we calculated strain-energy density W as the area under the stress–stretch curve during stretching of unnotched specimens. Second, the critical stretch λ_c can be calculated from tensile loading of specimens with a precut crack designed to initiate crack propagation. Under this configuration, the toughness is calculated as the strain-energy density W of the remaining material at the critical stretch λ_c (the stretch at which the crack propagates) multiplied by the height of the specimen H. Specifically, the toughness was computed as $G=W({\lambda }_c)H$. For specimens with homogeneous fiber orientation, we tested a long, thin strip of length L = 80 mm, with a distance between the grips of $H_0=20$ mm and a thickness of t = 0.9 mm, with a precut crack of 20 mm. We tested the precracked specimens until failure to measure the critical stretch λ_c.

Data Availability

All study data are included in the article and/or supporting information.