Significance
In a supersaturated vapor, the phase transition is initiated by the formation of clusters. While classical nucleation theory assumes clusters to be in thermal equilibrium with the surroundings, the inevitable release of latent heat and its limited dissipation during cluster formation drive the system out of thermal equilibrium. Using atomistic simulations considering both nonequilibrium and equilibrium dynamics, we present a detailed analysis of homogeneous gas-phase nucleation and cluster growth processes. Our findings show that despite the substantial amount of excess energy carried by the entire cluster population, those clusters relevant for nucleation evolve from cold to hot while the critical cluster is in thermal equilibrium with the surroundings, a mechanism proposed but also disputed in literature.
Keywords: nonisothermal nucleation, cluster formation, out-of-equilibrium dynamics, molecular simulation
Abstract
Nucleation of clusters from the gas phase is a widely encountered phenomenon, yet rather little is understood about the underlying out-of-equilibrium dynamics of this process. The classical view of nucleation assumes isothermal conditions where the nucleating clusters are in thermal equilibrium with their surroundings. However, in all first-order phase transitions, latent heat is released, potentially heating the clusters and suppressing the nucleation. The question of how the released energy affects cluster temperatures during nucleation as well as the growth rate remains controversial. To investigate the nonisothermal dynamics and energetics of homogeneous nucleation, we have performed molecular dynamics simulations of a supersaturated vapor in the presence of thermalizing carrier gas. The results obtained from these simulations are compared against kinetic modeling of isothermal nucleation and classical nonisothermal theory. For the studied systems, we find that nucleation rates are suppressed by two orders of magnitude at most, despite substantial release of latent heat. Our analyses further reveal that while the temperatures of the entire cluster size populations are elevated, the temperatures of the specific clusters driving the nucleation flux evolve from cold to hot when growing from subcritical to supercritical sizes and resolve the apparent contradictions regarding cluster temperatures. Our findings provide unprecedented insight into realistic nucleation events and allow us to directly assess earlier theoretical considerations of nonisothermal nucleation.
Gas-phase nucleation, where nanoscale clusters emerge from a supersaturated vapor, is ubiquitous and important (e.g., particle formation from atmospheric trace gases directly impacts on regional aerosol concentrations as well as the global climate) (1–3). Despite the long history of nucleation studies, dating back to Lord Kelvin (4), our understanding of some of the most basic mechanisms of cluster formation remains incomplete. One key issue is related to the latent heat release and its dissipation from the clusters into the surroundings during the phase transition. Latent heat is inevitably present in any first-order phase transition, yet the amount of latent heat involved in gas-to-cluster nucleation is much higher than, for example, in liquid-to-solid transitions. Classical nucleation theory, as many other models, assumes perfectly isothermal conditions (i.e., that the dissipation and thermal equilibration of clusters occur instantaneously). However, in reality, the heat transfer with the thermalizing medium, here carrier gas, occurs at a finite rate, leading to potential temperature differences between the clusters and their surroundings. As nucleation is highly sensitive to temperature, elevated cluster temperatures would cause a significant suppression of the nucleation rate.
While in the isothermal models of nucleation, only the clusters and condensable monomers are explicitly considered, the different treatments—whether thermodynamic, statistical, or simulation based—of nonisothermality necessarily consider the presence of a carrier gas with a given density. This is illustrated in Fig. 1 with a couple of snapshots of nucleating clusters at different carrier gas densities taken from large-scale molecular dynamics (MD) simulations carried out for this study. As the description of the process is restricted to unary homogeneous nucleation, the carrier gas is chemically inert and unable to condense at the temperatures and pressures considered. Thus, the carrier gas only exchanges energy with the vapor and the clusters but does not directly influence the nucleation free energy barrier separating the two phases as in binary or heterogeneous nucleation.
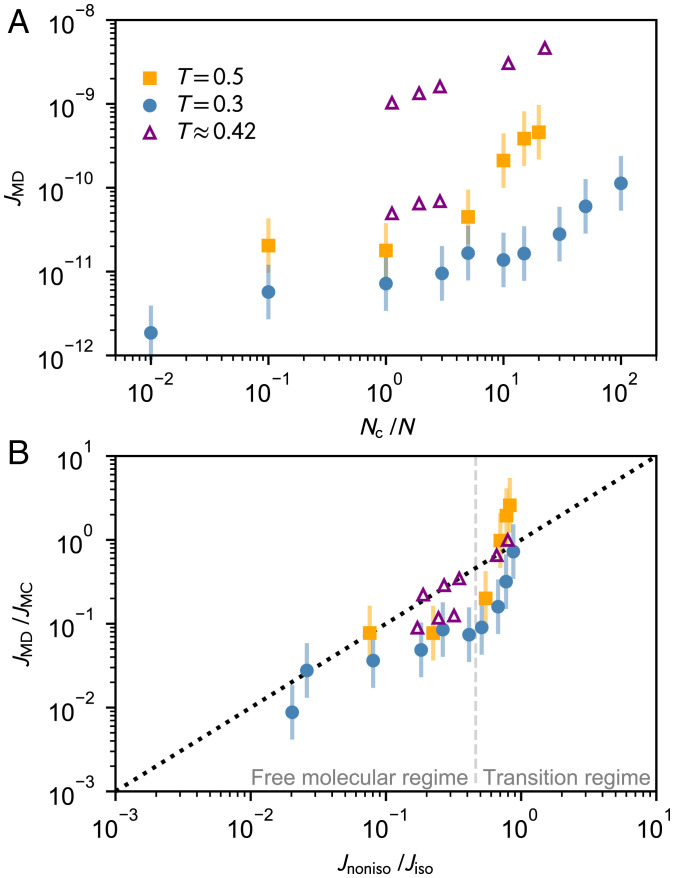
Fig. 1.
Illustration of cluster formation in an atmosphere of carrier gas. (A) A simulation box containing nucleating vapor and clusters (red) and CGAs (blue). Atomistic details of a cluster and the surrounding CGAs at low (B) or high (C) density. Snapshots were taken from large-scale MD simulations of an LJ system at a reduced temperature of 0.3 and carrier gas to nucleating vapor density ratios of (B) 15 and (C) 100, respectively. The dashed line indicates a sphere with a radius of 10 LJ distance units.
One of the first theoretical attempts to understand the influence of latent heat during nucleation was by Feder et al. (5) already in 1966. In their model, they considered both the clusters’ size and energy instead of just their size as in isothermal nucleation theories. Based on the principle of detailed balance for stationary cluster distributions, they derived a simple factor for the isothermal nucleation rate suppression due to insufficient thermalization:
| [1] |
where and are the nonisothermal and isothermal nucleation rates, respectively. The mean squared energy transfer between a monatomic cluster and monatomic carrier gas between two subsequent condensation/evaporation events is described by the parameter b2 (5, 6),
| [2] |
where is the Boltzmann constant and T is the bath temperature. N1 and as well as m and denote the number and masses of condensable monomers and carrier gas, respectively. The energy, q, released upon the addition of a monomer to a cluster at the critical size is crudely modeled in the original work by Feder et al. (5); however, this parameter can be refined using thermodynamic arguments (7) or atomistic simulations, as done here (SI Appendix, section A). The level of nucleation rate suppression based on Eq. 1 is typically quite modest, , even in the absence of carrier gas as the heat of vaporization (and thus, q) is of the order of for many liquids. While several studies of nonisothermal nucleation (7–13) have observed or estimated suppression to be in good agreement with Eq. 1, this prediction has also been challenged (14).
By definition, the distinction between cluster temperatures and bath temperature is at the heart of nonisothermal nucleation. According to the nonisothermal theory (5), the difference between the average kinetic temperature of an n-cluster, , and the well-defined carrier gas temperature, T, is given as
| [3] |
This was originally formulated in terms of cluster excess energy (5) but has been translated to temperature difference in subsequent literature. Due to the classical functional form of the cluster formation free energy barrier, , Eq. 3 implies that subcritical clusters have average temperatures below , supercritical clusters have temperatures higher than , and critical clusters have the temperature of the heat bath . While the nucleation rate suppression predicted by the nonisothermal theory is rather well accepted, the implications for the cluster temperatures are still strongly debated; in particular, the question of whether nucleating clusters evolve from “cold to hot,” as implied by Eq. 3, or if they are above the bath temperature throughout their size range is still open.
Some authors have supported the possibility of finding cool subcritical clusters (6, 10, 15, 16), while a significant body of studies (8, 9, 11, 17–20) disagrees with Eq. 3 and expects all clusters to be warmer than the surroundings. Considering the amount of released energy upon condensation, one could in fact anticipate a more drastic deviation from the isothermal nucleation rates than just a few orders of magnitude (14, 21). The uncertainty regarding cluster temperatures is further complicated by the issue of temperature definition for finite-size systems. Especially in the case of atomistic simulations (6, 15, 19), the conclusions drawn from the data depend crucially on the way the temperature is calculated, as will be discussed in more detail later.
Despite recent experimental advances, atomistic simulations are still the only route to fundamental understanding of the details of nucleation processes at the nanoscale. A vast majority of modern gas-phase nucleation (or new particle formation) studies focuses on estimating stabilities of clusters based on their free energies obtained from high-level quantum chemistry calculations and implementing this information to appropriate kinetic models to compute the cluster size distributions and nucleation rates (2, 13, 22, 23). While this approach often yields very accurate free energies, it is, however, constrained to thermal equilibrium and unable to explicitly explore out-of-equilibrium processes, such as nonisothermality. The only available method to study the dynamic details of actual cluster formation remains direct MD simulations of a supersaturated vapor, described by classical force fields (6, 15, 16, 20, 24–27). However, to observe nucleation on the timescale accessible to atomistic MD, simulations are typically restricted to rather extreme densities. The computational effort is even greater when the thermalization is treated properly, through explicit carrier gas, instead of applying global thermostatting schemes directly to the nucleating vapor (6, 12).
Thus, in order to address the open questions related to nonisothermal nucleation, we perform both direct MD simulations of supersaturated vapor as well as free energy calculations using Monte Carlo (MC) methods for Lennard–Jones (LJ) systems. As the nucleating system is studied independently with both nonequilibrium (nonisothermal) and equilibrium (isothermal) approaches, the previous theories and considerations related to nonisothermal nucleation and cluster formation can be tested quantitatively. The key findings are further supported by additional simulations of carbon dioxide nucleation in argon carrier gas using atomistic interaction potentials. We hope that the presented results and insights are helpful in clarifying fundamental aspects of homogeneous nucleation and resolving the apparent controversies related to cluster temperatures during the phase transition in a supersaturated vapor.
Results
The Level of Thermalization Has a Moderate Effect on Nucleation Rates.
To ensure a sufficient amount of nucleating clusters for a statistically representative analysis, a large number of monomers has to be included in the simulations. In the large-scale MD simulations of LJ systems reported here, the systems contain from N = 32,000 to over 400,000 nucleating atoms (NAs) and varying amounts of carrier gas atoms (CGAs; ranging from 0.01 up to 100). In total, 16 different simulations were carried out at bath temperatures T = 0.3 and 0.5 and densities and . Detailed descriptions of the simulation setup and data analysis are provided in Materials and Methods and SI Appendix, Table S1. For the sake of simplicity, we adopt dimensionless units for LJ systems (i.e., the unit mass, distance, energy, time, and are all set to one). To complement and validate our simulations, we have included in our analysis previous MD results of rather similar LJ systems at by Wedekind et al. (6, 26) (differences in simulation methodology and pair interactions are specified in SI Appendix, section B). The formation of the smallest clusters (mainly dimers) is rather rapid, and monomer depletion is noticeable at the beginning of the simulations. Thus, to ensure the accuracy of our results, the corresponding free energies from MC simulations are estimated for converged monomer densities at the nucleation stage (SI Appendix, Fig. S1 and Table S1).
For our large-scale MD simulations, the nucleation rates, , were calculated based on the time evolution of cluster distributions (SI Appendix, section C). As shown in Fig. 2A, from our simulations and the simulations of Wedekind et al. (6, 26) increases with carrier gas density but only by one or two orders of magnitude in the studied range of . This is in agreement with the theoretical estimate given by Eq. 1. Due to the difference in simulation setups and underlying methodology, the simulation data by Wedekind et al. (6, 26) have better statistics. However, we argue that the large-scale MD simulations carried out in this work provide a more realistic setup for the time evolution of cluster populations.
Fig. 2.
Nonisothermal nucleation rates of simulated LJ systems. (A) Simulated nucleation rates as a function of carrier gas ratio and (B) the ratios of and ratios predicted from nonisothermal nucleation theory using Eq. 1 at different temperatures and carrier gas densities used in the MD simulations of this work (circles and squares) and by Wedekind et al. (6, 26) (triangles). The error bars represent the arbitrary uncertainty of a factor of two, and the dotted line in B indicates perfect agreement. The estimated boundary between free molecular and transition regimes (Kn ) is indicated by the vertical dashed line in B (SI Appendix, section E).
Using the standard kinetic scheme of nucleation (Materials and Methods and SI Appendix, section D) with the cluster free energies from MC simulations, the nucleation rates, , at thermal equilibrium and in the free molecular regime can be readily calculated. At the simulated monomer densities, the critical cluster sizes of 6 and 14 at T = 0.3 and 0.5, respectively, obtained from the free energy curves are consistent with the ones estimated from the MD data as shown in SI Appendix, Table S1. For such cluster sizes and temperatures, the nonisothermal parameter q is about 3 energy units (SI Appendix, section A). For very high carrier gas densities, near-perfect thermalization is expected according to Eqs. 1 and 2. Indeed, as shown in Fig. 2B, the simulated and theoretically predicted values for the nucleation rate suppression (i.e., and ) are in good agreement at all temperatures and over a wide range of carrier gas densities. While we fail to obtain a perfect linear relation between simulation and nonisothermal nucleation theory, the “sub-order-of-magnitude” agreement observed here is quite remarkable in the context of theoretical nucleation studies.
The possible sources of inaccuracies are manifold and include the simulation methods, the high vapor density conditions, and the general stochastic nature of nucleation. The statistical errors are, however, minor with respect to the general uncertainties in both MD simulations and MC-based kinetic modeling. Here, we assign an overall uncertainty of a factor two for , which is roughly equivalent to the effect of an error of in the formation free energies, and a factor of two in the threshold method (27) or in the collision rate coefficients (28). The agreement with the results of Wedekind et al. (6, 26) implies that the details of the interactions between NAs and CGAs do not significantly affect the general trend observed in Fig. 2B. In the MC simulations, both the pressure–volume work effect (26) and the atom–cluster interactions (29) are neglected, as their contribution is very minor at the studied conditions (12). The data only start to diverge significantly for the highest carrier gas densities considered, which are quite extreme, as illustrated in Fig. 1C. According to the estimated Knudsen numbers, Kn, the most dense systems already correspond to the transition regime (Kn < 10), where fundamental assumptions of kinetic modeling most likely do not apply.
Despite the small nonlinearities in Fig. 2B, considering the complexity of nucleation processes and the very high sensitivity of nucleation rates to system parameters, such good agreement between both MD and MC simulations and the classical nonisothermal theory is very encouraging. Moreover, the results in Fig. 2B not only reflect the adequacy of the nonisothermal theory but also, validate the standard kinetic scheme of steady-state nucleation incorporated in the majority of nucleation theories.
The Smallest Clusters Have Skewed Temperature Distributions.
The relatively minor effect of carrier gas densities on the nucleation rates observed here [and elsewhere (6, 7, 9, 26)] seems rather surprising at first, as many studies have shown that the temperature of the critical cluster can be significantly above the bath temperature during nonisothermal nucleation. Such elevated cluster temperatures should result in much larger suppressions of the nucleation rate than just a few orders of magnitude. Despite some debate about the temperature definition in finite-size or nonequilibrium systems (e.g., refs. 30–32), here it is consistent with respect to both Eq. 3 and previous studies to use the kinetic definition to calculate the temperature of an n-cluster from its kinetic energy Kn:
| [4] |
For the temperature distribution in finite-size systems, Boltachev and Schmelzer (17) proposed a non-Gaussian expression based on the principles of statistical mechanics:
| [5] |
where is the gamma function.
According to Boltachev and Schmelzer (17), the average kinetic temperature is the appropriate thermodynamic measure of the temperature of an n-cluster, , whereas Wedekind et al. (6) and Angélil et al. (15) considered the maximum (i.e., the most probable value of the distribution) in their studies. As shown in Fig. 3, where thousands of LJ cluster configurations per size are analyzed, the temperature distributions of different-sized clusters observed in the MD simulation follow Eq. 5 very closely. As the kinetic energies are bound to be nonnegative and the temperature fluctuations are inversely proportional to cluster size (33), the distributions for the smallest clusters are skewed toward higher temperatures, and thus, they clearly deviate from the Gaussian distribution expected in classical (continuum) thermodynamics. Nearly Gaussian behavior is observed for larger clusters (). For all cluster sizes, the temperature fluctuations closely follow the expected statistics, as shown in SI Appendix, Fig. S2. Although the maxima of the temperature distributions are below the bath temperature for the subcritical clusters, their average temperatures are very close to the bath temperature. At the same time, the average temperatures of the entire cluster populations are above the bath temperature without exceptions, and their temperature systematically increases with size, as reported earlier (6, 15, 20).
Fig. 3.
Temperature distributions of the entire cluster populations at bath temperatures (A) T = 0.3 and (B) T = 0.5. The thick lines show the distributions in the MD simulation with , with the average temperatures marked by circles. The dashed black lines represent the theoretical distribution function given by Eq. 5. The bath temperature is indicated by the vertical gray lines. Due to the longer duration of the nucleation stage and notably larger number of clusters formed, better statistics are obtained for T = 0.3 compared with T = 0.5.
Nucleation Is Driven by Cool Subcritical Clusters.
As the average temperatures of the entire cluster populations are above the bath temperature, they are also more prone to evaporation compared with similar-sized clusters in thermal equilibrium. Hence, it is worth considering that a substantial part of the supercritical clusters rapidly decays into subcritical clusters, which would imply that the entire population of clusters does not correspond to the actual population of nucleating clusters. To verify that this is the case, we have further analyzed the individual clusters and their trajectories in the MD simulations carried out at both temperatures, T = 0.3 and 0.5, and . We have also included data from all-atom MD nucleation simulations of carbon dioxide in argon carrier gas at T = 90 K (Materials and Methods). The largest supercritical clusters, well above the critical size, present at the end of the nucleation stage were individually followed back in time, and their size and kinetic energy were recorded in short intervals of 500 time steps. This retrospective approach allows us to distinguish the nucleating clusters from the background population of clusters. The difference between the clusters’ average temperature and the bath temperature, , is shown in Fig. 4A for both LJ and CO2 systems. As expected, for the largest clusters, the distributions and average temperatures of the entire population and the nucleating clusters are very similar (SI Appendix, Fig. S3). However, as shown clearly in Fig. 4A, the average temperature of nucleating clusters below and near the critical size is significantly lower than the average temperature of the entire populations.
Fig. 4.
(A) Temperature deviation from the bath temperature as a function of cluster size n for the entire population of clusters (circles) and nucleating clusters (crosses) in MD simulations. The blue and orange symbols correspond to LJ clusters at T = 0.3 and 0.5 (in LJ units), respectively, whereas the red symbols show the temperature deviations for CO2 clusters at T = 90 K (scaled by a factor of 1/200 K). The predictions based on the theory of Feder et al. (5) using the MC data are shown with solid lines. (B) Theoretical formation free energy surface as a function of Z and n for the LJ system simulated at T = 0.5 (SI Appendix, section D). As indicated by the black solid line, the nonisothermal cluster growth path deviates from the isothermal minimum free energy path shown as a white solid line. These two paths, however, cross at the saddle point at the critical size (marked by a white cross and a dashed line, respectively).
For all systems considered, the nucleating cluster data points closest to the intersect coincide with the estimated critical cluster sizes [about 6 and 14 for LJ systems and about 5 for CO2 (20)]. Hence, the critical clusters driving the nucleation are indeed near thermal equilibrium with the surroundings, as predicted by Eq. 3. To further demonstrate the general adequacy of Eq. 3, for the LJ clusters we used the free energy values from MC to calculate the theoretical temperature differences represented as solid lines in Fig. 4A. Again, as for the nucleation rates, the temperature differences seen in the MD simulations agree with the nonisothermal theory by Feder et al. (5) remarkably well when using the adequate values of q and from atomistic simulations.
Discussion
Recent MD studies of nucleation (6, 15, 20) have found average temperatures of clusters uniformly above the bath temperature, and without making the distinction between the entire cluster populations and nucleating clusters, this has led to the conclusion that cluster temperatures are elevated during nucleation. In addition to these atomistic simulations, a number of theoretical studies have supported the idea that the critical clusters are significantly above the bath temperature (8, 11, 14, 18, 19). On the other hand, the notion of cold nucleating clusters has appeared in some studies (6, 15) but only as a consequence of the ambiguity of the temperature definition (average vs. most probable temperature) (17). Toxvaerd (16) was the first to provide some evidence of cold clusters acting as drivers of nucleation using MD simulations but with limited statistics and without reporting the cluster size–dependent temperature distributions.
In the presence of a well-defined free energy barrier to nucleation, the nucleation rate mostly depends on the thermodynamic properties of the critical cluster (5, 34). Therefore, the rather minor suppression of the nucleation rates due to insufficient thermalization, reported in Fig. 2 and SI Appendix, Table S2, is understandable as the critical clusters are found to be in near-thermal equilibrium with the surroundings. According to the nonisothermal theory (5), the nucleating clusters are not exactly constrained to the bottom of the valley in the free energy surface of cluster size and energy but will travel along the slopes. This nonisothermal growth pathway along the free energy surface is illustrated in Fig. 4B. Consequently, the nonisothermal correction to the theoretical nucleation rate originates from out-of-equilibrium clusters near the equilibrated critical cluster. With the nonisothermal correction, the nucleation rates from MD simulations are well captured by the standard kinetic scheme of nucleation incorporating accurate free energy data.
Analyzing energetics of individual clusters obtained from MD simulations of nucleation in a supersaturated vapor of LJ particles or fully atomistic CO2 molecules, we have demonstrated the clear difference between the temperatures of the entire cluster populations (elevated at all sizes) and the specific clusters carrying the nucleation flux, with nucleating subcritical clusters below, critical clusters at, and supercritical clusters above the bath temperature. Our findings explain the often reported apparent contradiction between the elevated critical cluster temperature and the relatively small nucleation rate suppression observed in many nonisothermal nucleation studies. Furthermore, our results rigorously support the theoretical reflections by Feder et al. (5), and the nucleation rate suppression due to insufficient thermalization/lack of carrier gas predicted using Eq. 1 adequately describes the observations in our simulations. Whether it is due to notable latent heat release in gas-phase cluster formation or for example, rapid depletion around the nucleation sites in precipitation from solution (35, 36), unraveling the dynamical effects caused by the inevitable breakdown of equilibrium during nucleation is highly important for understanding phase transitions.
Materials and Methods
Simulation Setup for LJ Systems.
We performed MD simulations of homogeneous nucleation of an LJ vapor (NAs) in an atmosphere of CGAs. The pairwise interactions between two atoms, separated by a distance r, are described by the LJ interaction as
| [6] |
where the parameters ϵ and σ are the same for NA–NA and NA–CGA (here, we have used dimensionless units; i.e., ). CGA–CGA interactions are neglected to speed up the simulations. The NA–NA and NA–CGA interactions were cut off and shifted at 5 and LJ distance units, respectively, leading to a purely repulsive interaction between the nucleating substance and the carrier gas. The mass ratio between NAs and CGAs, , is 0.1. All simulations were performed with the LAMMPS MD code (37) using a Velocity–Verlet integrator and a time step of 0.002. The standard approach of using a global thermostatting algorithm is not suitable for directly simulating a nucleating vapor, as it leads to an unphysical removal of latent heat from the nucleating clusters. It has been shown that the best way to avoid this artifact is to introduce explicit carrier gas molecules in the simulation and apply a thermostat only to the latter, even though this increases the computational cost significantly (6, 12). Here, we have applied a Nosé–Hoover thermostat with time constant 1 to the CGAs. Clusters are distinguished from the vapor using a Stillinger criterion (38) with an NA–NA distance cutoff of 1.5. Details of the simulated systems and an example LAMMPS input are provided in SI Appendix, Table S1 and section F, respectively. The nucleation rates (and the critical cluster sizes) for these systems are determined from the simulated time evolution of the number of clusters using the Yasuoka–Matsumoto threshold method (24) (SI Appendix, section C).
Simulation Setup for CO2 Systems.
Similarly, an MD simulation was performed to study homogeneous nucleation of carbon dioxide in argon carrier gas at T = 90 K and Å−3. The details of CO2 simulations and the obtained results are discussed in ref. 20. In essence, the simulated CO2 molecules are rigid bodies described by the transferable potentials for phase equilibria (TraPPE) force field (39), consisting of intermolecular LJ and Coulomb interactions between carbon and oxygen atoms. The thermalizing carrier gas is modeled as LJ argon coupled to a Nosé–Hoover thermostat with time constant 0.1 ps. The interactions between carbon and oxygen atoms in CO2 and the argon atoms were obtained from Lorentz–Berthelot mixing rules. We used a Velocity–Verlet integrator with a time step of 5 fs. The particular system simulated here contained 32,000 CO molecules and Ar atoms, and eventually, 129 supercritical clusters () were produced.
Cluster Tracking and Temperature Distributions.
By carefully following the trajectories of the collected supercritical clusters back in simulation time in short intervals of 500 time steps, we were able to distinguish nucleating clusters from the background based on their size and spatial coordinates. As the path of a growing cluster in size space involves significant fluctuations, the captured nucleating cluster populations consisted of at least 1,000 samples for each studied cluster size. In comparison, the entire set of n-clusters, not just the nucleating ones, easily contained millions of samples. These very good statistics enabled the calculation of relatively smooth temperature distributions for each cluster size, especially for the LJ systems shown in SI Appendix, Fig. S3. Note that due to extra degrees of freedom, the kinetic temperature of an n cluster consisting of rigid CO2 molecules is defined as .
Standard Kinetic Scheme of Steady-State Nucleation and Semigrand Canonical MC Simulations.
While considering systems of rather weak intermolecular interactions and low vapor densities, the cluster growth pathways can be assumed to be predominantly monomeric (i.e., only collisions with and evaporations into monomers are considered). Furthermore, the growth is assumed to take place at a constant monomer density. Using these assumptions as a basis, the steady-state nucleation rate can be expressed as
| [7] |
where βn is the collision rate between a monomer and an n-cluster. The upper limit of the summation, , should be about twice as large as the size of the critical cluster. The equilibrium cluster distribution is given by
| [8] |
Here, the formation free energies for the LJ clusters are calculated using the semigrand canonical metropolis MC simulations (40–42) at T = 0.3, 0.42, and 0.5. The obtained free energies can be trivially scaled to any monomer density N1, and thus, can be easily calculated using Eq. 7. In addition, based on these MC calculations, we have estimated the derivative of to determine the theoretical using Eq. 3.
A more detailed description of the kinetic model, the MC method, and the results can be found in SI Appendix, section D.
Supplementary Material
Acknowledgments
This work was supported by European Research Council Project 692891 DAMOCLES, Academy of Finland Grant 337549, and the University of Helsinki Faculty of Science ATMATH Project. Computational resources were provided by CSC–IT Center for Science, Ltd., Finland.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. D.K. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2201955119/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Kulmala M., et al., Direct observations of atmospheric aerosol nucleation. Science 339, 943–946 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Almeida J., et al., Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere. Nature 502, 359–363 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gordon H., et al., Causes and importance of new particle formation in the present-day and preindustrial atmospheres. J. Geophys. Res. Atmos. 122, 8739–8760 (2017). [Google Scholar]
- 4.Thomson W. T., LX. On the equilibrium of vapour at a curved surface of liquid. Philos. Mag. 42, 448 (1871). [Google Scholar]
- 5.Feder J., Russell K. C., Lothe J., Pound G. M., Homogeneous nucleation and growth of droplets in vapours. Adv. Phys. 15, 111–178 (1966). [Google Scholar]
- 6.Wedekind J., Reguera D., Strey R., Influence of thermostats and carrier gas on simulations of nucleation. J. Chem. Phys. 127, 064501 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Barrett J. C., A stochastic simulation of nonisothermal nucleation. J. Chem. Phys. 128, 164519 (2008). [DOI] [PubMed] [Google Scholar]
- 8.Wyslouzil B. E., Seinfeld J. H., Nonisothermal homogeneous nucleation. J. Chem. Phys. 97, 2661–2670 (1992). [Google Scholar]
- 9.Barrett J. C., Clement C. F., Ford I. J., Energy fluctuations in homogeneous nucleation theory for aerosols. J. Phys. A 26, 529 (1993). [Google Scholar]
- 10.ter Horst J. H., Bedeaux D., Kjelstrup S., The role of temperature in nucleation processes. J. Chem. Phys. 134, 054703 (2011). [DOI] [PubMed] [Google Scholar]
- 11.Schweizer M., Sagis L. M. C., Nonequilibrium thermodynamics of nucleation. J. Chem. Phys. 141, 224102 (2014). [DOI] [PubMed] [Google Scholar]
- 12.Halonen R., Zapadinsky E., Vehkamäki H., Deviation from equilibrium conditions in molecular dynamic simulations of homogeneous nucleation. J. Chem. Phys. 148, 164508 (2018). [DOI] [PubMed] [Google Scholar]
- 13.Dingilian K. K., et al., New particle formation from the vapor phase: From barrier-controlled nucleation to the collisional limit. J. Phys. Chem. Lett. 12, 4593–4599 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ford I. J., Clement C. F., The effects of temperature fluctuations in homogeneous nucleation theory. J. Phys. A 22, 4007 (1989). [Google Scholar]
- 15.Angélil R., Diemand J., Tanaka K. K., Tanaka H., Properties of liquid clusters in large-scale molecular dynamics nucleation simulations. J. Chem. Phys. 140, 074303 (2014). [DOI] [PubMed] [Google Scholar]
- 16.Toxvaerd S., Dynamics of homogeneous nucleation. J. Chem. Phys. 143, 154705 (2015). [DOI] [PubMed] [Google Scholar]
- 17.Boltachev G. S., Schmelzer J. W. P., On the definition of temperature and its fluctuations in small systems. J. Chem. Phys. 133, 134509 (2010). [DOI] [PubMed] [Google Scholar]
- 18.Barrett J. C., Note: Cluster temperatures in non-isothermal nucleation. J. Chem. Phys. 135, 096101 (2011). [DOI] [PubMed] [Google Scholar]
- 19.Schmelzer J. W., Sh. Boltachev G., Abyzov A. S., Temperature of critical clusters in nucleation theory: Generalized Gibbs’ approach. J. Chem. Phys. 139, 034702 (2013). [DOI] [PubMed] [Google Scholar]
- 20.Halonen R., et al., Homogeneous nucleation of carbon dioxide in supersonic nozzles. II. Molecular dynamics simulations and properties of nucleating clusters. Phys. Chem. Chem. Phys. 23, 4517–4529 (2021). [DOI] [PubMed] [Google Scholar]
- 21.Yang H., Drossinos Y., Hogan C. J. Jr., Excess thermal energy and latent heat in nanocluster collisional growth. J. Chem. Phys. 151, 224304 (2019). [DOI] [PubMed] [Google Scholar]
- 22.Elm J., et al., Modeling the formation and growth of atmospheric molecular clusters: A review. J. Aerosol Sci. 149, 105621 (2020). [Google Scholar]
- 23.Halonen R., A consistent formation free energy definition for multicomponent clusters in quantum thermochemistry. J. Aerosol Sci. 162, 105974 (2022). [Google Scholar]
- 24.Yasuoka K., Matsumoto M., Molecular dynamics of homogeneous nucleation in the vapor phase. I. Lennard-Jones fluid. J. Chem. Phys. 109, 8451–8462 (1998). [DOI] [PubMed] [Google Scholar]
- 25.Yasuoka K., Zeng X. C., Molecular dynamics of homogeneous nucleation in the vapor phase of Lennard-Jones. III. Effect of carrier gas pressure. J. Chem. Phys. 126, 124320 (2007). [DOI] [PubMed] [Google Scholar]
- 26.Wedekind J., Hyvärinen A. P., Brus D., Reguera D., Unraveling the “pressure effect” in nucleation. Phys. Rev. Lett. 101, 125703 (2008). [DOI] [PubMed] [Google Scholar]
- 27.Tanaka K. K., Tanaka H., Yamamoto T., Kawamura K., Molecular dynamics simulations of nucleation from vapor to solid composed of Lennard-Jones molecules. J. Chem. Phys. 134, 204313 (2011). [DOI] [PubMed] [Google Scholar]
- 28.Halonen R., Zapadinsky E., Kurtén T., Vehkamäki H., Reischl B., Rate enhancement in collisions of sulfuric acid molecules due to long-range intermolecular forces. Atmos. Chem. Phys. 19, 13355–13366 (2019). [Google Scholar]
- 29.Oh K., Zeng X. C., Formation free energy of clusters in vapor-liquid nucleation: A Monte Carlo simulation study. J. Chem. Phys. 110, 4471–4476 (1999). [Google Scholar]
- 30.Mandelbrot B. B., Temperature fluctuation: A well-defined and unavoidable notion. Phys. Today 42, 71 (1989). [Google Scholar]
- 31.Hoover W. G., Holian B. L., Posch H. A., Comment I on “Possible experiment to check the reality of a nonequilibrium temperature.” Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 48, 3196–3198 (1993). [DOI] [PubMed] [Google Scholar]
- 32.Jellinek J., Goldberg A., On the temperature, equipartition, degrees of freedom, and finite size effects: Application to aluminum clusters. J. Chem. Phys. 113, 2570–2582 (2000). [Google Scholar]
- 33.Landau L. D., Lifshitz E. M., Statistical Physics (Butterworth-Heinemann, ed. 3, 1980). [Google Scholar]
- 34.Vehkamäki H., Classical Nucleation Theory in Multicomponent Systems (Springer Science & Business Media, 2006). [Google Scholar]
- 35.Russell K. C., Linked flux analysis of nucleation in condensed phases. Acta Metall. 16, 761–769 (1968). [Google Scholar]
- 36.Peters B., On the coupling between slow diffusion transport and barrier crossing in nucleation. J. Chem. Phys. 135, 044107 (2011). [DOI] [PubMed] [Google Scholar]
- 37.Plimpton S., Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995). [Google Scholar]
- 38.Stillinger F. H. Jr., Rigorous basis of the Frenkel-Band theory of association equilibrium. J. Chem. Phys. 38, 1486–1494 (1963). [Google Scholar]
- 39.Potoff J. J., Siepmann J. I., Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE J. 47, 1676–1682 (2001). [Google Scholar]
- 40.Vehkamäki H., Ford I. J., Critical cluster size and droplet nucleation rate from growth and decay simulations of Lennard-Jones clusters. J. Chem. Phys. 112, 4193–4202 (2000). [Google Scholar]
- 41.Merikanto J., Vehkamäki H., Zapadinsky E., Monte Carlo simulations of critical cluster sizes and nucleation rates of water. J. Chem. Phys. 121, 914–924 (2004). [DOI] [PubMed] [Google Scholar]
- 42.Lauri A., Merikanto J., Zapadinsky E., Vehkamäki H., Comparison of Monte Carlo simulation methods for the calculation of the nucleation barrier of argon. Atmos. Res. 82, 489–502 (2006). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.