Neuronal population dynamics during motor plan cancellation in nonhuman primates

Significance

A core question in neuroscience is how the brain generates arm movements. Most studies have approached this issue by investigating the neuronal dynamics that accompany movement production, leaving unanswered the question of which aspects of this dynamics are logically necessary to make the movement. Here, we explored this topic by characterizing the neuronal correlates of movement decisions between active inhibition and release of movements. We found that active inhibition and stillness require neuronal signals to be confined in a functional subspace, while actions depend on the transit of activities in an orthogonal space. This dynamics is characterized by a threshold mechanism finally allowing the translation of the motor plan into overt action.

Abstract

To understand the cortical neuronal dynamics behind movement generation and control, most studies have focused on tasks where actions were planned and then executed using different instances of visuomotor transformations. However, to fully understand the dynamics related to movement control, one must also study how movements are actively inhibited. Inhibition, indeed, represents the first level of control both when different alternatives are available and only one solution could be adopted and when it is necessary to maintain the current position. We recorded neuronal activity from a multielectrode array in the dorsal premotor cortex (PMd) of monkeys performing a countermanding reaching task that requires, in a subset of trials, them to cancel a planned movement before its onset. In the analysis of the neuronal state space of PMd, we found a subspace in which activities conveying temporal information were confined during active inhibition and position holding. Movement execution required activities to escape from this subspace toward an orthogonal subspace and, furthermore, surpass a threshold associated with the maturation of the motor plan. These results revealed further details in the neuronal dynamics underlying movement control, extending the hypothesis that neuronal computation confined in an “output-null” subspace does not produce movements.

Our brain controls voluntary movements. However, the cortical computation behind this control capability is still under investigation.

To uncover how neurons in motor areas participate in arm movement control, most of the studies focused on different versions of the delayed reaching task. Here, a cue signal providing information about movement parameters is given ahead of the Go signal finally instructing the move. The delay epoch allows to easily separate visual-related activities from those more related to movement execution (1, 2). Using the delayed reaching task and different approaches, in the last 15 y the dorsal premotor cortex (PMd) has been suggested to be a key area in which during motor preparation, a cascade of neuronal events brings the collective activity into a preferred and stereotyped (attractor-like) state (3–5). Such a preparatory state (1) allows neuronal population activity to vary after sensory instructions without eliciting any movement onset, thus defining an “output-null” state well separated by the inner representation of the successive movement execution (6, 7). Within this framework, movement generation is the consequence of a further change in the neuronal state, corresponding to the transition from the output-null space toward the “output-potent” space (6, 7). All these studies exploited the delayed reaching task, which always requires the generation of the planned movement. However, what happens when the planned movement is cancelled? How is the neuronal ensemble dynamics of motor cortices reshaped in this case? Only comparing conditions in which a movement is performed vs. those in which the same prepared movement is cancelled can reveal whether the unfolding of the specific neuronal dynamics is required for the movement to be made.

To tackle this issue, we recorded single neuronal activity from PMd of rhesus monkeys while performing the countermanding task (8–12). In this task, a Stop signal presented in some trials during the reaction time (RT) asks for the cancellation of a movement during the motor plan development. In the population of neurons simultaneously recorded, we applied a state-space approach to reveal whether a specific neuronal dynamics is necessary to generate a movement. Put simply, if a neuronal dynamics underlies movement generation, it must occur when the movement is executed, while it must be absent when the movement is actively withheld. Here, we propose and test a generalization of the hypothesis that motor-related neuronal activity must be confined within an output-null state region to successfully suppress the translation of motor plans into overt movements and that only the pullout from this region can lead to the movement. Such confinement is an active process determined by a possible “attractive” capability of this state region, and the “escape” from it in the network dynamics is found to be due to a specific contribution of a heterogeneous set of single units.

Results

Two monkeys (P and C), after completing their training period, performed a countermanding reaching task composed of 66% no-stop trials and 34% stop trials (Fig. 1A), with targets located either to the right or to the left of the work space. Among the 21 recorded sessions, we focused our neuronal analyses on those sessions (9 total; 5 from monkey P and 4 from monkey C) having the highest number of engaged trials (at least about 300 no-stop and at least about 90 stop trials) and well-isolated units and in which the animal behavior was compatible with the race model hypotheses (independence assumption) (SI Appendix, SI Materials and Methods, Fig. S1 A and B, and Table S1) such that a reliable estimate of the stop signal reaction time (SSRT) (SI Appendix, Table S1) could be computed. This is because the SSRT is an estimate of the time necessary to suppress the movement in the task, needed information to further identify the dynamical organization of PMd units participating in movement inhibition.

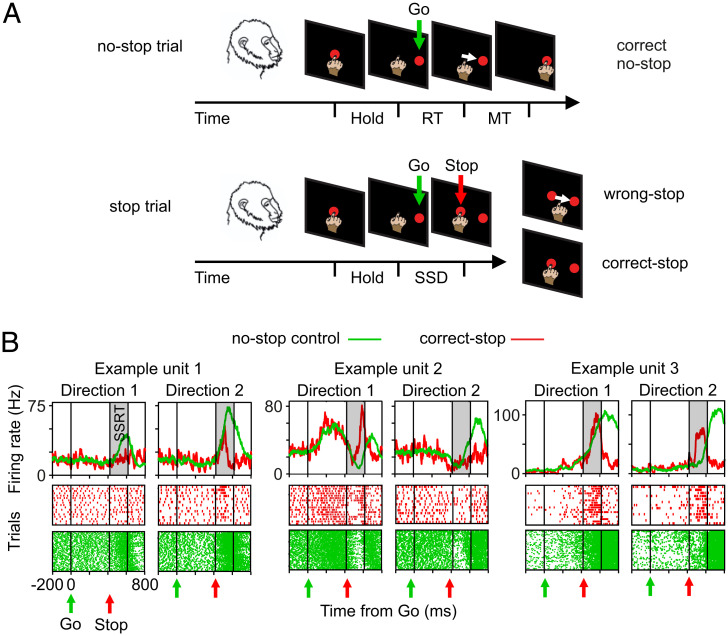
Fig. 1.

Behavioral task and heterogeneity of single-unit modulation during executed and cancelled movements. (A) No-stop trials and stop trials were randomly intermingled on each block. Monkeys were required to touch the central target, hold the position (Hold), and wait until the Go signal (Go) instructed them to reach the peripheral target (red circles; presented either to the right or to the left; here, only one position is shown). In stop trials, after the Go signal, the Stop signal (Stop; central target reappearance) instructed them to stay still (correct-stop). Wrong stop indicates trials with failed inhibition. (B) Examples of units recorded. Spike density functions (SDFs) and raster plots for correct-stop trials (red) and latency-matched (control) no-stop trials (green) are shown for a specific SSD separately for each movement direction. RT and MT schematically represent the reaction time and the movement time, respectively.

Premotor Units, Associated with Both Movement Execution and Inhibition, Are Heterogeneous.

We selected for each session those units whose activity was modulated before movement onset and/or after the Stop signal presentation in at least one movement direction compared with a control period preceding the Go signal presentation. We then considered for further analysis only those units with a Stop-related modulation for at least one movement direction. Specifically, we searched for units differently modulated in the SSRT interval (Fig. 1B and SI Appendix, SI Materials and Methods).

For the sake of simplicity, we decided to report the main results for two exemplificative sessions (one for each animal) in the text; other data and details are provided in SI Appendix. For the two example sessions, 139 units were selected (i.e., about two-thirds of the dataset [93 of 113 for monkey P and 46 of 91 for monkey C]). The other sessions are shown in SI Appendix, Table S2. A common observation was that the selected units are heterogeneous because they showed a variety of activity profiles in the two directions of movement during the task (for no-stop trials) and in relation to movement inhibition (either increasing or decreasing—after the Stop signal—their activity in correct-stop trials when compared with latency-matched trials) (Fig. 1B and SI Appendix, SI Materials and Methods) as previously described in other experiments in PMd (8, 13). As expected, neuronal modulation was not different in latency-matched no-stop trials and wrong-stop trials (SI Appendix, SI Materials and Methods, SI Results, and Figs. S2 and S3). Overall, these results confirm previous evidence (i.e., that single units in the PMd signal in heterogeneous and complex ways the action generation and suppression) (13, 14).

Population Neuronal Dynamics during Movement Execution and Inhibition.

The heterogeneity of the neuronal patterns observed is a confounding element in determining which aspect of the neuronal dynamics underlies movement inhibition and generation. To solve this issue, we analyzed data at the population level and reduced the dimensionality of the state space resorting to the principal components analysis (PCA) (Materials and Methods).

Fig. 2A shows, aligned to the Go signal, the average neuronal trajectories both in correct-stop (red) and latency-matched no-stop (control trials; green) trials in the low-dimensional subspace determined by the first three principal components (PCs; explaining more than 60% of the variance in all conditions; embedding dimensions ≤ 3) (SI Appendix, SI Materials and Methods and Fig. S4) for one direction separately for each monkey and for the two example sessions. As expected, the two neuronal trajectories develop similarly until the appearance of the Stop signal (empty red dots). In control no-stop trials (green lines), population activity continues, describing a volley until the movement occurs (green diamonds; movement onset). Conversely, after the Stop signal, the trajectory in correct-stop trials (red lines) diverges from the green one moving backward to approach the initial state. Importantly, the divergence between the two trajectories occurs well before the end of the behavioral estimate of SSRT (filled red dots).

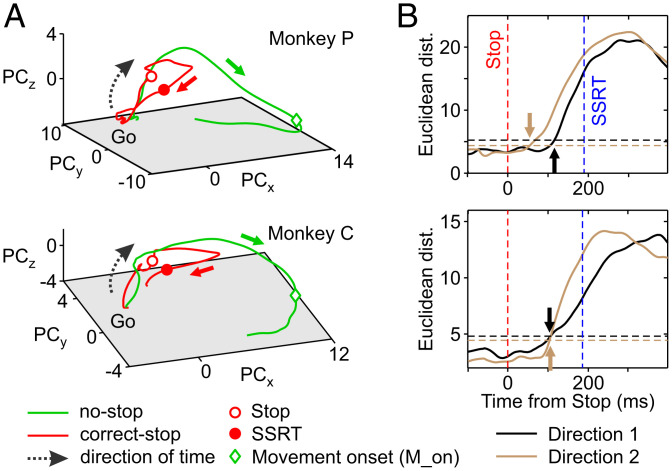
Fig. 2.

Neuronal dynamics and population estimate of the time when movements are inhibited. (A) Neuronal trajectories of latency-matched no-stop and correct-stop trials for a single movement direction (direction 1) in the state space defined by the first three PCs. (B) For each monkey, the average Euclidean distances between trajectories corresponding to correct-stop and latency-matched no-stop trials, aligned to the Stop signal, are represented. Arrows point out the time of significant divergence between trajectories. Horizontal dotted lines represent the reference thresholds for each movement direction (Materials and Methods).

At a first glance, the trajectories dynamics suggests that in no-stop trials, the neuronal population activity moves toward a functional state corresponding to movement generation and that movement inhibition is the active avoidance of such a process. We obtained a population estimate of the time of divergence (Fig. 2B) by calculating the Euclidean distances between the corresponding neuronal trajectories within a time window aligned to the Stop signal (from 100 ms before to 200 ms after; i.e., up to the SSRT duration) (Materials and Methods and SI Appendix, Table S1). In the example sessions, we found that such divergence occurred between 70 and 116 ms following the Stop signal presentation for the two directions (Fig. 2B), anticipating in time both the equivalent neuronal correlate derived from the single-unit analysis (SI Appendix, SI Results and Fig. S5) and the differences detected at the electromyographic level when evident (SI Appendix, SI Results and Fig. S6). Combining the data from the two monkeys (across all the sessions), the latency was of 93 (23) ms (mean [SD]) from the Stop signal (monkey P = 89 [21]; monkey C = 96 [27]). Interestingly, the average SSRT across sessions was 188 (12) ms (SI Appendix, Table S1). Thus, the divergence anticipates the behavioral estimate of movement inhibition of about 90 ms.

Movement Inhibition and Stillness Require Neuronal Activities to Be Limited into a Functional Subspace.

We wanted to investigate whether the dynamics we observed for no-stop and correct-stop trials could be better accounted for by the existence of distinct functional subspaces. Fig. 3A shows, for one animal (with data referring to the same session as in Fig. 2A, Upper), the average neuronal trajectories in correct-stop (red), control latency-matched no-stop (green), and wrong-stop (black) trials obtained from the first three PCs.

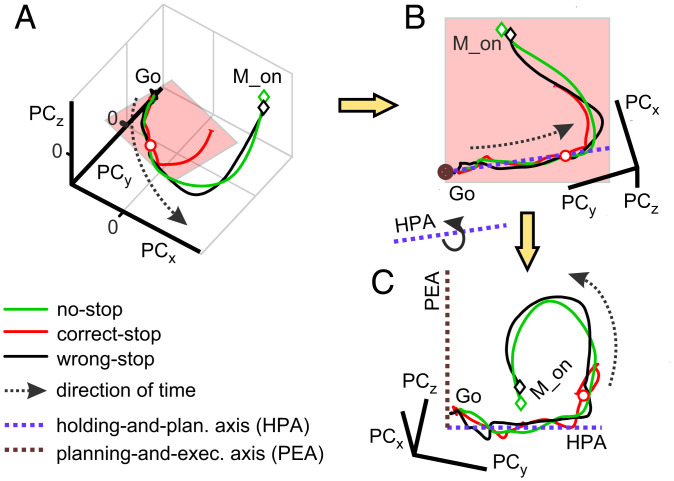
Fig. 3.

Schematic of the neuronal trajectories unfolding within the holding plane and a plane orthogonal to it. (A) Average neuronal trajectories for all trial types aligned to Go onset. (B) The holding plane, where correct-stop trajectories mostly reside, highlighted by a rotation of the trajectories in A. The blue dotted line represents the axis that best fit the trajectories of all groups of trials projected on the holding plane in the first 300 ms following the Go signal (HPA). (C) A further rotation around the blue axis allows for finding the PEA (brown dotted line). M_on, movement onset time.

After the Go signal, the population activity in correct-stop trials initially follows a trajectory almost indistinguishable from the ones measured in no-stop and wrong-stop trials. The late divergence of the correct-stop trajectory (as in Fig. 2) could indicate the existence of a subspace in the neuronal state space where activities are confined before movement generation and during movement suppression. Such a hypothesis would support the generalization of the computational strategy relying on the output-null subspace described for PMd neurons in animals tested in a delayed reaching task (6, 7).

To verify the existence of such subspaces, we focused on the collective states visited by the correct-stop trials averaged and grouped by stop signal delays (SSDs) for each animal and direction of (potential) movement. Relying on the singular value decomposition (SVD) analysis (Materials and Methods has details), we found all trajectories of the correct-stop trials to fluctuate around a reference planar section. Fig. 3B shows the view on this planar section of the average trajectories in Fig. 3A here obtained, for illustrative purposes, after a suited rotation of the original three-dimensional space. In this holding plane, the similarity among no-stop, wrong-stop, and correct-stop trajectories is remarkable. Thus, the dimensionally reduced population dynamics highlighted from this perspective does not contain any information about whether or not the movement will be generated.

However, as premotor cortices are known to also represent the motor output in reaching tasks (2), a related activity subspace must exist to allow for independently and robustly reading out these motor commands from the activity evolution of the network (7), thus allowing us to distinguish between trials where movement is executed or inhibited. To this end, we extracted from the same plane an axis by further fitting data from the trajectories of all grouped trials in the 300 ms following the Go signal (Fig. 3B). This linear subspace together with the axis orthogonal to the holding plane identified a second orthogonal plane. Fig. 3C shows (again for illustrative purposes only) this latter plane together with the corresponding dynamics of all average neuronal trajectories. Fig. 3C shows (again for illustrative purposes only) this orthogonal plane together with the corresponding dynamics of all average neuronal trajectories. From this last perspective, it is rather apparent that movement-related activities (no-stop and wrong-stop trajectories) depart from a reference holding plane where correct-stop activities are instead confined for most of the time.

We called the first axis the holding-and-planning axis (HPA) and the second subspace the planning-and-execution axis (PEA). The reason for these definitions will be apparent in the following.

Movement Generation as an Escape from Movement Inhibition Subspace.

Our first step of analysis suggested the presence of two subspaces, where the decision-related neuronal dynamics unfolds differently. Thus, some questions arise. How can these segregated dynamics explain movement generations and suppression? What makes a stop trial correct or wrong? To address these issues, we inspect in more detail how the projections of the neuronal trajectories onto the described axes change in time.

Fig. 4A shows (for the same example sessions; grouping trials by either RT or SSD for wrong/no-stop trials and correct-stop trials, respectively) (SI Appendix, Fig. S7) that neuronal activities, observed as projections in the PEA, immediately after the Go signal are roughly stable, slightly fluctuating around the reference zero baseline. During the same period, neuronal activities observed as projections in the HPA (Fig. 4B) show a peaking ramp-like dynamics, similar for all trials and conditions (SI Appendix, Fig. S7). For some sessions (SI Appendix, Fig. S8), activities in the PEA evolve toward more negative values, drawing a trough.

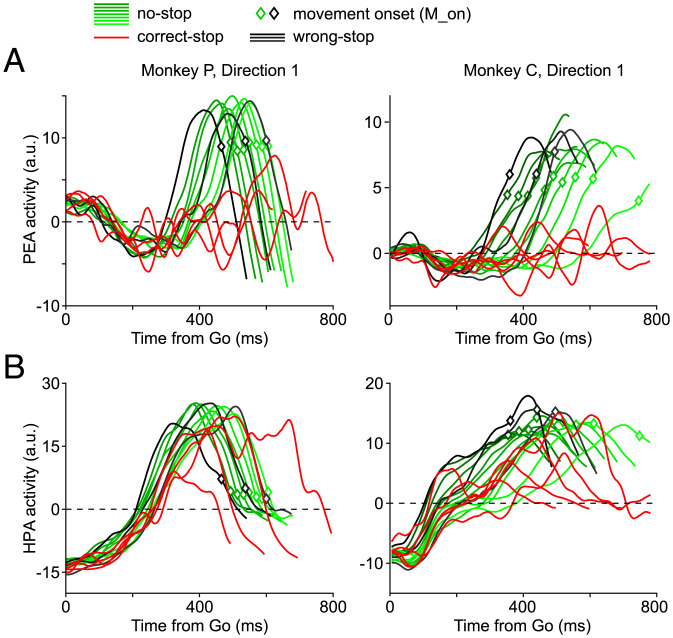
Fig. 4.

Components of the neuronal dynamics determining RTs and correct-stop trials. (A) Projections on the PEA of the neuronal trajectories (direction 1)—namely, PEA activity—grouped by RTs (no-stop trials in deciles and wrong-stop trials in tertiles) or SSDs (correct-stop trials). After an initial period around the Go signal in which trajectories are overlapped, no-stop and wrong-stop trial projections diverge from correct-stop trials projections. (B) Projections on the HPA of the same neuronal trajectories—namely, HPA activity—as above; in this case, the projections display an initial ramp-like dynamics and similar features for all trials and conditions.

M_on, movement onset time. a.u., arbitrary units.

In a successive phase, Fig. 4A shows that PEA activities, in particular those related to wrong-stop (black lines) and no-stop trials (green lines), escape from the plane, signaling an important change in the overall state. In the HPA, as described above, it is instead very difficult to differentiate among the opposed behavioral outcomes.

In all sessions, projections on both the HPA and the PEA show a strong correlation with RTs. The relationship was slightly stronger when considering projections on the PEA. Indeed, across sessions and monkeys, the mean beta coefficient was overall (mean [SD]) higher for PEA conditions (0.98 [0.05]) compared with HPA conditions (0.83 [0.09]; Wilcoxon rank-sum test, P = 8 10⁻⁶; monkey P: PEA = 0.99 [0.04]; HPA = 0.82 [0.4]; monkey C: PEA = 0.98 [0.05]; HPA = 0.84 [0.12]).

The different patterns in the two planes are also confirmed by comparing the Interquartile ranges of the beta coefficients (PEA = 0.07 [0.07]; HPA = 0.33 [0.16]; Wilcoxon rank-sum test, P = 3 10⁻⁶). The higher Interquartile ranges suggest a more variable relationship of projections onto the HPA with RTs.

The example sessions were well representative of these findings (monkey P: direction 1: PEA = 0.99 [0.03]; HPA = 0.83 [0.38]; direction 2: PEA = 0.97 [0.057]; HPA = 0.82 [0.44]; monkey C: direction 1: PEA = 0.97 [0.04]; HPA = 0.65 [0.44]; direction 2: PEA = 0.85 [0.07]; HPA = 0.89 [0.4162]; all P values < 0.02) (SI Appendix, Fig. S9 has details).

We further asked in which of the two projections the relationship with RTs first emerged. Interestingly, we found no evidence of correlation with RT during the post-Go initial phase of neuronal modulation in the PEA (i.e., during the stable and sometimes descending phase, toward more negative values). In fact, we found that in the HPA, the significant relationship between neuronal activities and RTs emerged earlier than in the PEA. Overall, there was a lag (mean [SD]) of about 170 ms (PEA [437 (135)]; HPA [267 (154)]; Wilcoxon rank-sum test, P = 8.3 10⁻⁴; monkey P: HPA = 235 [78] ms; PEA = 460 [151] ms; monkey C: HPA = 304 [202] ms; PEA = 410 [109] ms).

The same holds for the example sessions (monkey P: direction 1: HPA = 218 [41] ms; PEA = 314 [86] ms; direction 2: HPA = 138 [43] ms; PEA = 329 [84] ms; monkey C: direction 1: HPA = 148 [29] ms; PEA = 323 [19] ms; direction 2: HPA = 219 [18] ms; PEA = 267 [24] ms; P < 0.05 in all cases, Wilcoxon rank-sum test). Thus, although in both projections, a significant relationship with RTs emerged, this relationship developed as a chain first involving the HPA projections and only afterward involving the PEA projections.

Ramps in HPA Contribute to Motor Planning without Relying on a Threshold Mechanism.

The ramp-like dynamics after the Go signal in the HPA (Fig. 4B) is typically observed in decision processes or when an internal generated timing signal is employed to elaborate an input signal (15, 16) and is associated with a threshold mechanism. In such threshold mechanisms, the amount of activity, per se, is sufficient to determine the transition toward a different state once a certain level is reached. Concurrently, a premovement reduction in neuronal variability is usually observed, deemed to correspond to the termination of a decision-related process (2, 3).

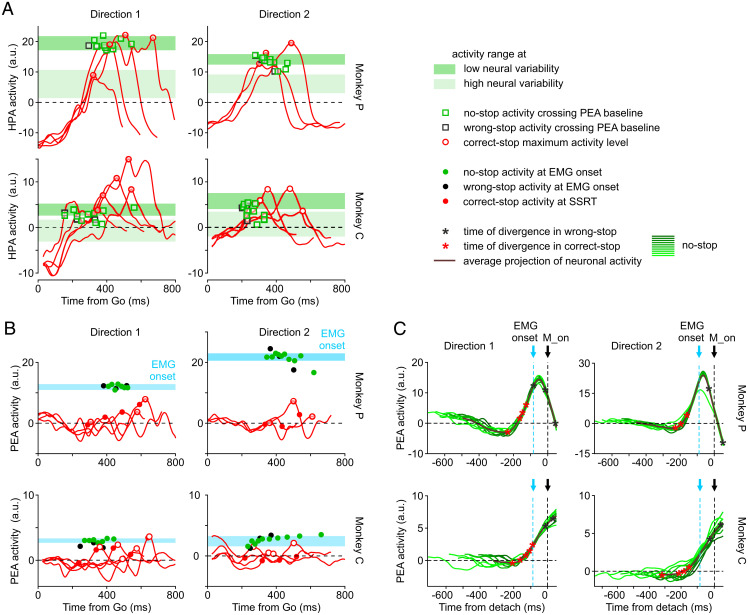
Fig. 5A shows, on one hand, that when activities escape from the reference plane in PEA and a movement is generated (wrong-stop trials and no-stop trials) (empty black and green squares, respectively, in Fig. 5A), the activity in the HPA tends to stay close to a subspace where neuronal variability shrinks (SI Appendix, Fig. S10). On the other hand, it is evident that one cannot predict movement onset relying only on this level of activity in the HPA. In fact, activity of correct-stop trials (red traces and empty red circles in Fig. 5A) can be even higher than the activity observed in no-stop trials in the HPA. Conversely, Fig. 5B shows the presence of a threshold when activities are observed in the PEA. Indeed, when movements are inhibited, the projection of activity in the PEA (red traces in Fig. 5B) tends to remain under the level necessary for muscle activation. This level is instead reached by both no-stop and wrong-stop trials activities (green and black dots, respectively, in Fig. 5B).

Fig. 5.

Dynamics for movement generation exploits a threshold-based mechanism in the PEA only. (A) Projections of correct-stop activities in the HPA as in Fig. 4 (red traces); the maximum activity level is indicated by the empty red circles. Green and black squares indicate the HPA activities for no-stop and wrong-stop, respectively, measured at the times when projections on the PEA of the same activities crossed the zero baseline (B). The shadow bars represent the levels of no-stop activity (mean ± SD) measured in the HPA when the neural variability across trials (Fano factor) was high (light green) or low (dark green) before movement onset (M_on; see SI Appendix, Fig. S10). (B) Projections of correct-stop activities in the PEA as in Fig. 4 (red traces); the maximum activity level is indicated by the empty red circles. Filled red circles correspond to the PEA activity of correct-stop trials at SSRT. Green (black) filled circles display the PEA activity during no-stop (wrong-stop) trials at the time of electromyographic (EMG) muscle onset. Cyan bars represent the range of activities projected in the PEA when muscles are activated before movement generation (mean ± SD; calculated on the muscle’s latency CI). (C) Each panel represents the PEA activity for the no-stop trials (thick lines, average; green lines, deciles) aligned to the movement onset. In the average activity, asterisks highlight the activity at the time of neuronal divergence for correct-stop (red) and wrong-stop (black) trials. The timing of the neuronal divergence is computed as in Fig. 2B relying on single values of SSD for correct-stop trials and on the average SSD for wrong-stop trials. a.u., arbitrary units.

To describe the results for all recording sessions, we compared two contrast indices, one for PEA and the other for HPA, in the form $(a-b)/(a+b)$. The first contrast index was used to compare the average level of no-stop PEA activity (as for the green dots in Fig. 5B) measured in a 10-ms window centered at the average electromyographic (EMG) activation vs. the maximum level of correct-stop PEA activity obtained across SSDs for the same session. The second contrast index was used to compare the peak level of no-stop HPA vs. the peak level of correct-stop HPA. Positive values indicate that the activity (either the PEA or HPA) is higher in no-stop compared with correct-stop trials. Note that to be conservative, we did not use the higher values of PEA, typically detected later in time. We found that contrast indices in the PEA (0.21 [0.28]) are higher compared with those in the HPA (−0.04 [0.21]; Wilcoxon rank-sum test, P = 0.001) (SI Appendix, Fig. S11). This confirms, at the population level, that the PEA can clearly distinguish between movement generation and inhibition.

Why does the ramp-like increase of activity in the HPA resulted highly correlated to the RT although the movement onset is not determined by the crossing of a threshold activity? We suggest that this ramping activity is needed to bring the system into a state necessary (but not sufficient) to elicit the motor-related activity in the PEA, thus encoding an essential part of the movement plan. To corroborate such a hypothesis, we used a different paradigm in monkey P (SI Appendix, SI Results and Fig. S12). The animal was informed whether the movement was possible, certain, or not required by presenting a cue well before the presentation of a Go or No-Go signal. We found that activity in the HPA only ramps when movements are possible or certain. Indeed, when the movement is not required, even the presentation of the Go signal does not induce any significant change in the HPA. Thus, the dynamics we described in the HPA cannot be considered a mere lack of movement-related activity but instead, is an active process involved in both initial position holding and planning of the incoming movement.

Movements Are Generated When PEA Activities Cross the Boundary of the Holding Subspace.

As can be expected from Fig. 4, PEA activities for no-stop and wrong-stop trials are also highly stereotyped in time when aligned to the movement onset (Fig. 5C). It is important to remark here that this dynamics occurs while specification of movement direction is already determined (SI Appendix, Fig. S13). Conversely, the PEA activity during correct-stop trials (Fig. 4A) does not deviate too much from the baseline. This is compatible with the hypothesis that correct-stop activity trajectories are trapped into a specific subspace as in these trials, movement planning is not yet mature at all or it is cancelled well before its complete maturation, compatible with what was preliminary observed in refs. 4 and 9.

In this framework, a successful stop trial could be obtained by temporarily suppressing the translation of the motor plan into an overt movement (i.e., avoiding the escape from the reference level in the PEA). Thereafter, movement onset is possible only if activities also cross a point of no return represented by the muscle activation. This picture is confirmed in our experiments as the Stop signal can be effectively processed only if occurring before muscle contraction (Fig. 5C). This is, once again, clearly reminiscent of a threshold-like mechanism. Indeed, the PEA activity is higher when a movement is performed (Fig. 5C, black asterisks before movement onset) compared with the activity at the time of neuronal divergence in correct-stop trials (Fig. 5C, red asterisks). Conversely, the HPA activity does not show a clear differentiation between movement generation and inhibition; indeed, in correct-stop trials, peaks of HPA activity can be as high as the ones observed in no-stop trials or very close to them (SI Appendix, Fig. S14).

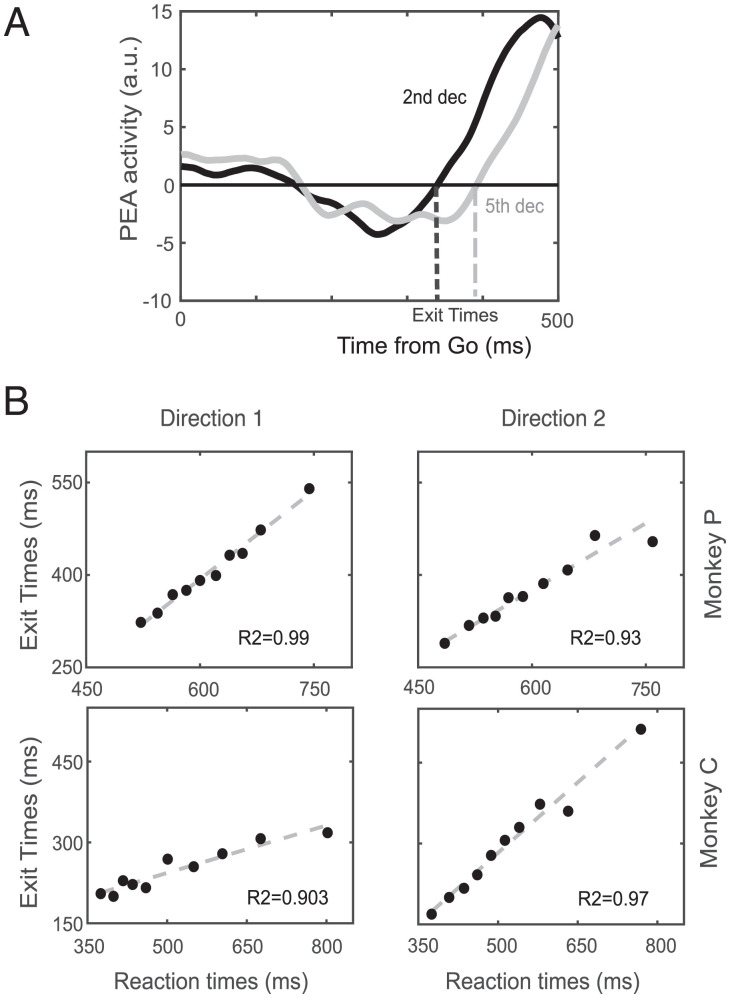
Note that PEA activity in Fig. 5C was confined for variable durations before the movement onset. In Fig. 6, we quantified the relationship between such time intervals and the RT finding that the exit times (Fig. 6A) are highly predictive of the movement onset (Fig. 6B and SI Appendix, Fig. S12B). Movement generation is then kept at bay for so long as neuronal activity is confined to the reference subspace (negative values observed: mean ± SD; monkey C: direction 1 = −0.5 ± 0.3; direction 2 = −0.59 ± 0.36; monkey P: direction 1 = −2.0 ± 1.0; direction 2 = −1.6 ± 1.1; t test P < 0.01 for all cases).

Fig. 6.

Exit time estimate and relationship with RT. (A) Schematic of the exit time computation for two deciles in the dataset. (B) Correlation between exit time occurrences and RTs for each movement direction separately for each monkey. a.u., arbitrary units.

The overall strong relationship between RTs and exit times was confirmed in all sessions (average R² = 0.92 [0.06], robust fit) (SI Appendix, Fig. S15). The exit from the PEA was followed by a stereotyped activity volley unfolding along an almost constant time interval before the movement onset (188 [59] ms). Noteworthy, this value is very close to the behavioral estimate of SSRT. Thus to avoid the generation of the movement, the unfolding of neuronal activity must be blocked within few tens of milliseconds from its exit from the PEA.

Overall, the emerging picture is that after target onset, the neuronal dynamics visits different states better differentiated when observed as distances from different subspaces. The movement is generated when this activity grows, reaching a threshold (Fig. 5B). Importantly, this growth of activity in the PEA starts only when the activity reaches a certain level in the HPA, purportedly corresponding to the end of a decision process. However, the reach of this level in the HPA is not sufficient to determine the movement onset. Indeed, it is also reached in correct-stop trials when there is no movement production.

Discussion

In the present study, we investigated the premotor neuronal dynamics underlying the control of arm movements by combining two complementary lines of research: 1) neuronal population analysis by exploiting a state-space approach (for example, refs. 6, 17, and 18) and 2) the countermanding task, an experimental design ideally suited to investigate and model volitional control of movement (19, 20).

First, we confirmed that PMd units modulate their activity before the end of the SSRT, thus having temporal characteristics that allow for predicting whether a movement will be halted (8). Second, we further extended this finding by showing that neuronal modulation precedes muscle modulation in successfully inhibited trials, strongly supporting a causal role for this area in movement generation. Third and most importantly, by applying dimensionality reduction techniques, we uncovered the existence at the population level of a holding subspace, which we suggest generalizes the previously introduced output-null subspace (6). In our view, this subspace is where the premotor neuronal activity must actively be confined to avoid the transition of the motor plan into execution. Such dynamics behind the control strategy extends the concept of the output-null subspace, and it is complementary to the one adopted in previous works on delayed reaching tasks.

Movement Control in a State-Space Framework.

The main goal of this study was to uncover the premotor neuronal dynamics that characterizes movement generation by contrasting neuronal activity during movement production with neuronal activity during active movement inhibition. We found that following the Go signal, the neuronal activity is confined to a (holding) subspace, where it is initially similar between correct-stop, wrong-stop, and no-stop trials. In this initial stage, the neuronal activity is “trapped” into a specific state, sometimes appearing as a trough, from a specific perspective, possibly reflecting the specific task context that is required to block movement execution (also, the control task results) (SI Appendix, Fig. S12). As the neuronal dynamics evolves, a clear differentiation emerges; in no-stop and wrong-stop trials, the neuronal activity moves away from the reference subspace toward a state-space region, which almost deterministically anticipates the movement generation. Differently, in correct-stop trials (where no movement is produced), the neuronal activity remains confined in the initial subspace, separate from the trajectory observed in no-stop trials. Importantly, the temporal evolution in no-stop trials (and wrong-stop trials) is strongly related to RTs, and it shows a clear stereotyped nature when aligned to the movement onset. These pieces of evidence demonstrate the existence of neuronal dynamics that anticipates motor behavior, clearly distinguishing the active inhibition vs. the movement generation. Thus, we conclude that PMd expresses specific neuronal dynamics, underpinning either movement generation or inhibition. This conclusion is further strengthened by the fact that the divergence between no-stop and correct-stop trials occurs before the end of the SSRT (21).

Our data are in line with a series of findings obtained from studies investigating the preparation and execution of reaching movements by using state-space approaches (6, 22–24). In most of these experiments, monkeys are provided with prior information about movement direction by a cue followed by a Go (move) signal after a delay. During the preparation phase (delay period), a cascade of neural events brings the collective activity into a prepare and hold (attractor) state (2, 4, 17). As proposed, the goal of this state is to set the motor plan (i.e., a neuronal state that functions as the initial condition determining the upcoming movement) (2, 24, 25). The neuronal trajectories will then evolve toward a complementary subspace, but linked, to the previous one (7). In this last subspace, the neuronal dynamics unfolds while reaching movements are executed (18). Within this framework, the preparatory activity does not generate the movement per se, but it always occurs before the movement onset, even when very brief times to prepare the movement (zero delay) are available (6, 23, 26). The transition from preparation to execution is characterized by some degree of overlapping between preparation and movement phases (23) and by a strong condition-invariant signal that precedes the movement onset (27).

In summary, an important aspect of the previous studies is that the generation of the movement was always required; thus, it is not clear which aspect of the dynamics can be deemed necessary for movement generation. We employed the countermanding task to address this issue. To this purpose, we exploited the concept of neural manifolds (28), finding a holding subspace where neuronal trajectories of the correct-stop trials as well in the initial part of no-stop and wrong-stop trials are confined. The escape of neuronal trajectories from this subspace determines the transition from the prepare and hold state to the movement generation. This dynamics is highly stereotyped and precedes the movement onset by a fixed time lag, similar to what is observed in other studies (27). This dynamics could correspond to the information to start the movement, an internal Go signal, that PMd can provide to other cortical and subcortical structures, as previously suggested (6, 7).

This allows us to avoid searching for specific inhibitory circuits that, so far, have been impossible to define in the premotor and motor cortices of primates due to the difficulties in accounting for the connections of cortical neurons to subcortical, brain stem, and spinal cord neurons (29), although recent attempts have been promising (30).

Nonlinear Network Dynamics Underpinning the Holding Subspace.

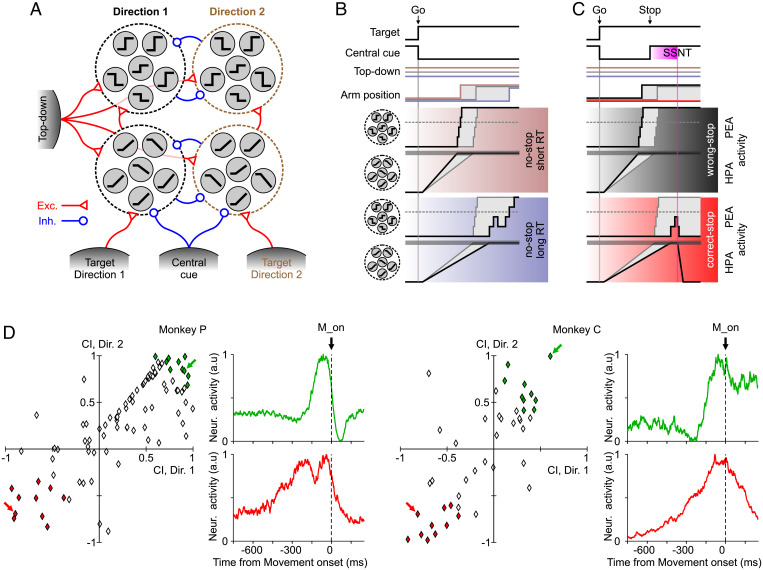
The HPA and the PEA are orthogonal axes, meaning that activity projection on such axes is mainly due to different subsets of units (Fig. 1B). In other words, ramping activity along the HPA is probably due to a subset of units displaying a post-Go quasilinear increase/decrease of the firing rate (sketched in Fig. 7A, Lower). Instead, the sudden increase of PEA activity tightly locked to the movement onset is determined by a pool of units displaying sharp transitions from low to high activity levels and vice versa (Fig. 7A, Upper).

Fig. 7.

Schematic proposal of PMd organization underlying movement execution and inhibition. (A) Pools of ramp-like and switch-like units (gray circles) respond differently depending on the target to be reached signaled by a selective excitatory input coming from other brain areas (gray shaded units at the bottom). Target-related representations are mutually exclusive due to cross-inhibition. Ramp-like units contributing to the rising of HPA activity elicit sharp transitions in switch-like units. The latter contributes to the changes of PEA activity that indirectly react to the target-related input. An unspecific top-down input (Left) making differently excites all the PMd units from trial to trial. Onset and offset of the central cue signaling to stop and start, respectively, have an inhibitory effect on the PMd units. Red and blue arrows represent excitatory and inhibitory connections, respectively. (B) Behavioral, environmental (Top), and neuronal changes in no-stop trials with long (Bottom) and short (Middle) RTs, which are determined by relatively weak (bluish) and strong (reddish) top-down excitation, respectively. Gray traces represent a reference trial with average RT. Black traces show pooled activity of switch-like and ramp-like units plotted in black side by side with the respective unit icons. These traces are those resulting from projecting the high-dimensional population activity on the PEA and the HPA, respectively. Horizontal dashed gray lines show the activity level when movement onset is irreversibly elicited when crossed in the PEA. Simultaneously, when in the HPA, the pooled ramp-like units reach the horizontal gray strip, and the switch units are facilitated to change state. (C) The same as in B but for those trials in which the Stop signal is presented. Black and red shaded subpanels correspond to example wrong- and correct-stop trials, respectively. SSNT corresponds to the time of significant divergence between trajectories after the Stop signal, as in Fig. 2B). (D) Scatterplot of contrast indices for each movement direction in both monkeys. Contrast index = (HPA_weight − PEA_weight)/(HPA_weight + PEA_weight), where the weight is the element associated with a single unit in the corresponding axis (Materials and Methods). Green and red diamonds represent units with extreme values in PEA and HPA contributions, respectively. Example units of the extreme groups, highlighted by colored arrows, are shown using the same color code of the scatterplots. The stop signal neuronal time (SSNT) here is considered equivalent, at the single-neuron level, to the divergence time of Fig. 2. CI, contrast index. M_on, movement onset. Exc and Inh indicate excitatory and inhibitory connections/inputs, respectively.

In the specific framework investigated here, the relatively slow and linear drifting along the HPA determines a post-Go “refractory phase,” where presumably target-related information accumulates and no movement occurs (Fig. 7B and C). The passage across a region (Fig. 5A, low neuronal variability) after a variable time elicits the rise of the PEA activity. In those trials with short RTs (Fig. 7B and C, Middle), the related sharp transitions of that activity are strongly stereotyped even in the Go-centered profiles (Fig. 5C), meaning that units displaying a fast switching of activity are rather synchronized in time (4).

In correct-stop trials (Fig. 7C, Bottom) and in no-stop trials with long RTs (Fig. 7B, Bottom), more gradual HPA ramps and less stereotyped PEA activations of the switching units are visible. Intriguingly, the latter appears to fluctuate up and down (Fig. 4A), and under this condition, motor program maturation can then be interrupted if it is not fully developed (i.e., the activity is confined below a trigger threshold) (Fig. 7C, Bottom). Indeed, only when planning has reached a sufficient degree of maturation, it can be translated into an overt movement.

To test the existence of two segregated sets of neurons (Fig. 7A), we compared the contribution to the PEA and to the HPA of each single unit, finding a continuum of neuronal types (Fig. 7D), which is preserved across movement directions. However, a subset of these neurons displayed a rather polarized role, showing either highly positive or negative contrast indexes. In our model, they represent the units having sharp (green units in Fig. 7D) or ramping-like activity (red units), respectively. These two neuronal types appear to be universal components in cortical areas involved in arm movement planning and motor decision (4, 15, 16, 31).

RTs are both determined by the time needed to reach an accumulation threshold (dashed lines in Fig. 7B) and by a variable time in which switching units complete the transformation of the cortical state into the one encoding the motor plan. The latter phase has a more prominent role only for relatively long RTs, and the Stop signal can be successfully processed if SSRT falls after the end of the first accumulation stage. In possible short-RT trials, the onset of the Stop signal must be early in correct-stop trials such that the SSRT could precede the beginning of the activity rise along the PEA. If one of these two conditions is not fulfilled, a wrong-stop trial is performed (Fig. 7C, Middle).

A mechanistic implementation of the discussed interplay between ramping and switching units on one hand requires that the former provide input to the latter, such that once the input received by the switching units crosses a trigger threshold, a cascade of activity switches occurs (4, 32). On the other hand, one should also explain the trial by trial variability of such a chain of reactions, which underlies both the capability to inhibit an instructed movement and the variability of the RTs. To this aim, an additional unspecific input has to be taken into account. Indeed, a tonic input modulating the excitability of both unit types would allow for changing from trial to trial the switching rate and the ramp slope (33, 34). This input could be provided by a proactive tonic top-down control, which varies across trials (the top-down signal in Fig. 7A). Finally, we remark that ramping activity in principle can be obtained by pooling time-shifted switch units, just to mention the possibility to have the latter kind of neurons contributing to both pools sketched in Fig. 7A (35, 36).

The existence of such a proactive control mechanism in models of saccadic countermanding tasks is not new (37, 38). For instance, in ref. 37, a top-down control of frontal origin implemented a post-Go phasic reduction of the excitatory input to a specific subset of neurons. This sudden change in the input resembled the effects of a homunculus intervening at specific random times, aiming at recovering the RT statistics and inhibition function (19). To work around such limitations, it has been suggested that another proactive mechanism is at work, leading to a modulation of the “response caution” governed by the baseline activity of the inferior frontal gyrus (IFG) (38). This, in turn, slows down or accelerates the movement production via the IFG–subthalamic nucleus hyperdirect pathway. Our results are compatible with this second scenario, as each trial has its own degree of excitability/stability of the ramping and switching units that we suggest being associated with a different top-down tonic input (i.e., the IFG baseline activity). Differential stability of the no-movement condition can be interpreted as a different speed of the go process in the race model (39, 40), and we predict that it is related to the high-beta state found in ref. 41 associated with the capability of the cortical–basal ganglia circuits to stabilize selected motor plans.

Under this hypothesis, the permanence in the found holding subspace (i.e., represented by the trough often found in the PEA activity) appears to be effectively separated from the boundaries delimiting the previously introduced output-null space (6). This in our view is obtained by making the holding subspace a more “attracting” region. In the framework we propose, the attracting force is modulated by an unspecific top-down control (input from other areas; Fig. 7A), while the premotor network can autonomously implement the machinery needed to produce and inhibit an instructed movement. In turn, the stability of this holding state allows for having complex and computationally relevant population dynamics, such as the accumulation process preceding the full maturation of the motor plan, without the danger to cross the boundary of the output-null subspace, triggering the movement onset.

Materials and Methods

Subjects and Behavioral Task.

Two adult male rhesus macaque monkeys (Macaca mulatta; P and C) weighing 7 to 9.5 kg performed a countermanding task (Fig. 1A and SI Appendix, SI Materials and Methods). They had to touch the stimulus with their fingers, hold, and fixate it (holding time range: 400 to 900 ms). Thereafter, the central stimulus disappeared, and simultaneously, a target appeared (Go signal) randomly at one of two opposite peripheral positions (left and right) instructing for a movement in the corresponding direction (indicated as direction 1 and direction 2). In no-stop trials to get a juice reward, monkeys had to start the arm movement within a maximum time (1,000 ms) to discourage them from adopting a procrastination strategy due to the presence of stop trials and to maintain their fingers on it for a random time (400 to 800 ms; 100-ms step). In stop trials at a variable delay (SSD) after the Go signal was presented, the central stimulus reappeared (Stop signal), instructing the monkey to keep the hand on the starting position (additional holding time; 400- to 1,000-ms interval; 100-ms step) to perform a correct-stop trial and earn the juice. If the monkey moved the hand during stop trials, the trial was considered a wrong-stop trial, and no reward was given. No-stop and stop trials were randomly intermingled in such a way that the no-stop trials were more frequent (66%).

Data were collected using a staircase tracking procedure to change the SSD from one stop trial to the next according to the behavioral performance. If the monkey succeeded in withholding the response (correct-stop trial), the SSD increased by a fixed amount (100 ms); if it failed (wrong-stop trial), the SSD decreased by the same amount of time. The goal of the tracking procedure is to determine an SSD for which the probability of response (i.e., the probability to have a wrong-stop trial) is 0.5 or very close to this value. This allows for estimating a reliable SSRT (40, 42, 43); further details are given below.

All experimental procedures, animal care, housing, and surgical procedures conformed with European (Directive 86/609/ECC and 2010/63/UE) and Italian (D.L. 116/92 and D.L. 26/2014) laws on the use of nonhuman primates in scientific research and were approved by the Italian Ministry of Health.

Behavioral Analysis.

The countermanding task permits estimating the SSRT by extracting three main variables: the RT distributions of no-stop trials and wrong-stop trials and the probability to respond [p(R)] by error to the Stop signal. Error trials here are those where the central position was released after the Stop signal presentation. These data are modeled according to the race model (39) to establish first if the assumptions of the model are respected and in this instance, to estimate the SSRT (SI Appendix, SI Materials and Methods).

We calculated the SSRT by using the integration method because it is the most reliable (44). This method requires subtracting a given SSD from the finishing time of the stop process. The finishing time of the stop process is calculated by integrating the no-stop trial RT distribution from the onset of the Go signal until the integral equals the corresponding observed proportion of wrong-stop trials for the given SSD (45). We obtained the estimate first by calculating the mean SSD presented in each session and then, subtracting it from the finishing time obtained by considering the overall p(R) (44, 46, 47).

Neural Recordings.

In both monkeys, 96-channel Utah arrays (BlackRock Microsystems) were implanted using anatomical landmarks (arcuate sulcus and precentral dimple) after dura aperture on the PMd contralateral to the arm employed during the experiments (SI Appendix, Fig. S1E).

Extracellular signal from each electrode was amplified and digitized employing a Tucker Davies Technologies RZ2 system equipped with a PZ2 preamplifier (unfiltered raw signal; sampling rate of 24.4 kHz). Single-unit activity was isolated offline by using KiloSort3 (48), an automated spike sorter based on the template-matching approach (SI Appendix, SI Materials and Methods).

In this work, we included both single-unit as well as multiunit activity (the median inter-spike-interval violation statistic was 0.27, with 68.5% < 0.5 and 20% > 1; signal-to-noise-ratio of the units selected mean [SD] = 7.1 [16]; median = 5). This was because the main analyses we performed are based on population activity and dimensionality reduction techniques and typically produce very similar results regardless of the employment of single units or multiunits (27, 49). The final numbers of units included are described in SI Appendix, Table S2 for all recording sessions. The temporal distance between the first and the last selected recording session was 11 mo in monkey P and 1 mo in monkey C.

Neuronal Analysis at the Single-Unit Level.

To perform some of the neuronal analyses, we represented the neuronal activity by a spike density function (SDF) obtained by convolving the spike train with an exponential function mimicking a postsynaptic potential; we used the same equation described in ref. 50, where the convolution kernel K(t) of the neuronal activity is

$$K\left(t\right)=[1-\text{exp}(-t/{\tau }_g)]\cdot \text{exp}(-t/{\tau }_d),$$

where τ_g = 1 ms corresponds to the growth phase of the synaptic potential and τ_d = 20 ms is the decay phase (51). Other details are in SI Appendix, SI Materials and Methods.

Neuronal Population Analysis in a Low-Dimensional State Space.

To study the neuronal dynamics at the population level, we resorted to a standard PCA to reduce the dimensionality of the recorded state space. The approach we developed consists of two main steps. First, we characterized the neuronal dynamics of the movement suppression process and the latency of its neuronal correlate at the population level. Then, we evaluated the planning and movement generation process across different trial types and RTs.

In the first step, we calculated average SDFs in 1-ms time bins by aligning the trials to the Go and to the Stop signals separately. For no-stop trials where the Stop signal was absent, we considered the hypothetical SSD corresponding to the average SSD obtained for correct-stop trials. As results, for each trial type and movement direction the spike densities from all the different units composed a matrix of samples. We then concatenated these three matrices preserving the number of rows (n = number of units). The activity of each unit was then normalized by subtracting mean activity and dividing the activity SD computed across all conditions. The obtained neuronal activities (matrix rows) were eventually smoothed with a Gaussian kernel of 50-ms width. In this framework, the population state of the probed cortex at any time was represented by an N-dimensional vector (a column of the aforementioned activity matrix).

At this stage, we computed the distance between average no-stop and correct-stop trials trajectories to estimate the time of divergence at the population level. More specifically, in the above N-dimensional state space, we carried out the Euclidean distance between no-stop and correct-stop trials at each 1-ms time bin in (−100, 200 ms) aligned to the Stop signal. We set a threshold level corresponding to the mean + 3 SD of the distances between no-stop and correct-stop trials around the Go signal. We then evaluated when starting from the Stop signal onset, the distance between the trajectories calculated in the Stop signal epoch exceeded the threshold level.

To capture the intertrial variability associated with different behaviors and at the same time, to reduce the unavoidable fluctuations of the estimated spike densities, we further divided the no-stop trials into 10 groups (deciles) and the less numerous wrong-stop trials into 3 groups (tertiles) based on the ordered RTs (the neuronal activity spanned from 50 ms before the Go signal up to 50 ms after movement onset) (Figs. 4–6). The correct-stop trials were grouped based on the length of the SSDs, and the neuronal activity was shown from 50 ms before the Go signal. The group number of correct-stop trials varied from three to five depending on the condition. Three-dimensional trajectories were then obtained from grouped trials by averaging in each group the population activity, eventually smoothing it with a Gaussian kernel (50 ms).

Starting from these grouped spike densities, in the second stage of the analysis we performed the PCA on the concatenated matrix of such average population activities with dimensions N (neurons) × Ctg (conditions × time bins per trial group × number of groups). In each monkey, we estimated the embedding dimensions from fraction of variance $p_k={\lambda }_k/{\displaystyle {\sum }_j{\lambda }_j}$ explained by each PC (${\lambda }_k$ are the eigenvalues of the covariance matrix) of the neuronal activity. The effective dimension $D=e^{H-1}$, where $H=-{\displaystyle {\sum }_k{p}_k}\log p_k$ is the Shannon entropy. Under the hypothesis of an exponential distribution of the variance, $p_k\propto e^{-k/D}$ provided that $D\ll N$, where N is the number of single units we considered (52). In all cases, the embedding dimensions were below three.

As illustrated in the text (Figs. 4–6), we further singled out some relevant subspaces. First, we looked for a plane where correct-stop trajectories for a given condition resided. This was defined as the holding plane (Fig. 3B) best fitting (SVD) the cloud of points composing all the three-dimensional trajectories associated with the average population activity for each group of correct-stop trials. We then looked for the axis that best fitted the trajectories of all groups of trials projected on the holding plane in the time window between 0 and 300 ms from the Go signal. This HPA is represented by a dashed blue dotted line in Fig. 3B, and we found it to be the ideal subspace to represent the first phase of motor plan maturation (always occurring after 200 ms from the Go signal for all conditions and animals), as shown in Fig. 4A. Finally, we defined the PEA (brown dotted line in Fig. 3C) as the one orthogonal to the holding plane. The trajectory projections onto this direction optimally highlighted the maturation process of the motor plan and the neuronal correlate of the movement execution. The time course of such projections for each trial group is shown in Fig. 4A. The three-dimensional average trajectories for the no-stop, correct-stop, and wrong-stop trials in Fig. 3C are shown on a plane after a suited rotation around the HPA.

We evaluated the contribution of each unit to the activity in the HPA and in the PEA by calculating a contrast index = (HPA_weight − PEA_weight)/(HPA_weight + PEA_weight) based on the “weight” of the contribution of each unit to the corresponding axis. We performed this calculation separately for each direction. We then averaged across directions the contrast indices and ordered the units based on this value.

Data Availability

Data and codes for reproducing manuscript’s results are publicly available in Zenodo (53).