Deep-learning-based image registration and automatic segmentation of organs-at-risk in cone-beam CT scans from high-dose radiation treatment of pancreatic cancer

Abstract

Purpose:

Accurate deformable registration between computed tomography (CT) and cone-beam CT (CBCT) images of pancreatic cancer patients treated with high biologically effective radiation doses is essential to assess changes in organ-at-risk (OAR) locations and shapes and to compute delivered dose. This study describes the development and evaluation of a deep-learning (DL) registration model to predict OAR segmentations on the CBCT derived from segmentations on the planning CT.

Methods:

The DL model is trained with CT-CBCT image pairs of the same patient, on which OAR segmentations of the small bowel, stomach and duodenum have been manually drawn. A transformation map is obtained, which serves to warp the CT image and segmentations. In addition to a regularity loss and an image similarity loss, an OAR segmentation similarity loss is also used during training, which penalizes the mismatch between warped CT segmentations and manually drawn CBCT segmentations. At test time, CBCT segmentations are not required as they are instead obtained from the warped CT segmentations. In an IRB-approved retrospective study, a dataset consisting of 40 patients, each with 1 planning CT and 2 CBCT scans, was used in a 5-fold cross-validation to train and evaluate the model, using physician-drawn segmentations as reference. Images were preprocessed to remove gas pockets. Network performance was compared to two intensity-based deformable registration algorithms (large deformation diffeomorphic metric mapping [LDDMM] and multi-modality free-form [MMFF]) as baseline. Evaluated metrics were Dice similarity coefficient (DSC), change in OAR volume within a volume of interest (enclosing the low-dose PTV plus 1 cm margin) from planning CT to CBCT, and maximum dose to 5 cm³ of the OAR [D(5cc)].

Results:

Processing time for one CT-CBCT registration with the DL model at test time was less than 5 s on a GPU-based system, compared to an average of 30 min for LDDMM optimization. For both small bowel and stomach/duodenum, the DL model yielded larger median DSC and smaller interquartile variation than either MMFF (paired t-test p< 10⁻⁴ for both type of OARs) or LDDMM (p< 10⁻³ and p=0.03, respectively). Root-mean-square deviation (RMSD) of DL-predicted change in small bowel volume relative to reference was 22% less than for MMFF (p = 0.007). RMSD of DL-predicted stomach/duodenum volume change was 28% less than for LDDMM (p = 0.0001). RMSD of DL-predicted D(5cc) in small bowel was 39% less than for MMFF (p = 0.001); in stomach/duodenum, RMSD of DL-predicted D(5cc) was 18% less than for LDDMM (p < 10⁻³).

Conclusions:

The proposed deep network CT-to-CBCT deformable registration model shows improved segmentation accuracy compared to intensity-based algorithms and achieves an order-of-magnitude reduction in processing time.

1. Introduction

Pancreatic cancer is one of the deadliest cancers in the U.S., with a 5-year survival rate of 9%¹. Several clinical trials have shown encouraging improvement in survival of patients with locally advanced unresectable pancreatic cancer when treated with high biologically effective radiation dose (≥ 100Gy BED)^2,3. Because of the proximity of organs at risk (OARs) to the high-dose region, advanced organ motion management, image guidance and adaptive treatment planning techniques are required to ensure safe delivery of dose. The principal OARs for this disease site include highly mobile luminal gastrointestinal organs such the small bowel, stomach and duodenum. Each clinical plan must respect departmental OAR constraints (based on clinical experience and peer-reviewed publications). But in the presence of OAR motion and deformation, it is hard to determine the delivered dose and to know, in a timely way, whether there is a need for treatment plan adaptation. Hence, localization of the OARs in the planning computed tomography (CT) and daily cone-beam CT (CBCT) scans is required to evaluate the displacement and deformation of the OARs. Additionally, it is desirable to compute dose delivered to OARs at each treatment fraction for purposes of assessing the need for plan adaptation. Because of a lack of reliable CT-to-CBCT deformable image registration tools for soft tissues, visual inspection of CBCT images is used in current practice to estimate changes in the OAR volumes that are receiving above-tolerance doses. This requires considerable clinical experience since the evaluation of the dose is only qualitative. Therefore, a fast and reliable registration method is desired to help evaluate OAR movement, especially for organs that move into the high-dose region.

Registrations between CT and CBCT are challenging due to image artifacts presented in the images, which include scattering, streaking and cupping artifacts. Gas pockets within the stomach, small and large bowels also complicate the registration. These gas pockets usually do not have the same locations and shapes between the planning CT image and the daily CBCT image. Since most registration methods are based on image intensity, these artifacts and gas pockets can adversely affect registration accuracy. One way to alleviate this is to compare OAR contour mismatch in the registration, which would allow the registration to focus on more relevant parts of the image, such as OARs. However, this approach would require manual segmentation of both moving and target images. While segmentations are always available for planning CT, it is not the case for daily CBCT images. Drawing such contours for CBCT is time and labor intensive. It also requires experience as CBCT images usually have low contrast and strong artifacts.

In this paper, we propose a deep-learning-based registration model for CT and CBCT images. It uses the vector momentum parametrization⁴ for large deformation diffeomorphic metric mapping (LDDMM)⁵. The transformation is then obtained via smoothing the momentum followed by integration. Using the momentum parametrization, we can explicitly control the smoothness of the velocity field even at test time, and thus can obtain diffeomorphic transformations. The network learns to match the manually segmented OAR segmentations between the warped planning CT and the CBCT during the training phase, but does not require segmentations for CBCT images during the prediction phase (i.e. when processing test cases). These concepts are further explained below.

2. Material and Methods

2.A. Datasets

Patient images were collected under an IRB-approved retrospective research protocol. Data were collected from 40 patients who received ablative hypofractionated radiation treatment³. Patients were simulated in the supine position with customized immobilization and arms extended above head. The planning CT was obtained with the patient in a deep inspiration breath hold (DIBH) state using an external respiratory monitor (Real-time Position Management RPM, Varian Medical Systems) and diagnostic quality scanner (Brilliance Big Bore, Philips Health Systems; or Discovery ST, GE Healthcare). Image acquisition started 45 s after the start of contrast administration (150 mL iodinated contrast at 5 mL/s). For the patient’s treatment plan, two or three planning target volumes were defined: (1) microscopic dose (referred to hereafter as the low-dose PTV), (2) simultaneous integrated boost (SIB) to the gross tumor volume (high-dose PTV), and (3) in some cases, a second SIB to a higher dose to the hypoxic center (ultra-high-dose PTV). Treatment in breath hold was delivered in 15 or 25 fractions (Varian TrueBeam v. 2.5) with daily DIBH cone-beam CT image guidance. Prescription dose follows the regimen described by Reyngold et al³: dose to low-dose PTV is 37.5 Gy or 45 Gy for 15 or 25-fraction scheme, respectively; 67.5Gy or 75Gy to the high-dose PTV; and 90 Gy or 100Gy to the ultra-high-dose PTV. A volume of interest (VOI) was defined on the planning CT. Its purpose was to define a volume fully contained within both the planning CT and CBCT reconstruction volumes. It included the portions of the OARs receiving moderate to high dose, and excluded the periphery of the CBCT volume which was subject to cupping artifacts. The VOI was obtained from the low-dose PTV defined on the planning CT plus a 1 cm margin (3-dimensional expansion) and included the high-dose PTV, and ultra-high-dose PTV in those cases where it was defined.

For the purposes of this study, two CBCT scans, acquired on different days, were selected from each patient’s treatment course. The kilovoltage CBCT scans were acquired with a 200-degree gantry rotation, which yielded faster acquisition (relative to a 360-degree rotation), reduced the likelihood of patient motion during the scan, and increased likelihood that the scan was acquired in a single breath hold. The resultant CBCT reconstruction diameter was 25 cm and length 17.8 cm (the CBCT reconstruction volume is cylindrical).

Initial image registration and segmentation were carried out on a commercial software system designed for this purpose (MIM v. 6.9.7, MIM Software Inc.). Each CBCT image was rigidly registered to its corresponding planning CT by aligning to one of the physician-selected fiducial markers implanted near the tumor, or to a stent implanted during resection surgery. The CBCT was resampled to match the voxel dimensions and volume of the planning CT. On the planning CT and each of the CBCT scans, two OAR volumes were delineated by a radiation oncologist: (1) stomach with the first two segments of the duodenum, and (2) the remainder of the small bowel. On the CBCT scans, only the portions of the OARs within the VOI were delineated, whereas on the planning CT scans, the OAR delineations extended up to 2 cm outside of the VOI. The latter ensured that the deformed delineations from the planning CT onto the CBCT during the deformable registration adequately covered the OARs within the VOI.

Planning CT and CBCT images were distributed among six radiation oncologists for manual delineation, such that all images of a given patient were done by the same physician. Two trained medical physicists subsequently reviewed the segmentations (each physicist was assigned the images drawn by three of the physicians) and edited them as needed to maintain consistency with delineation guidelines. The resultant manual segmentations were used as the reference segmentations for training and evaluation of the auto-segmentation methods examined in this study. To quantify inter-observer variation of the manual segmentations on the CBCT, one of the trained physicists independently delineated the OARs on a subsample of ten CBCT images, each from a different patient and previously reviewed by the other physicist, and of sufficient image quality such that OAR boundaries were deemed to be discernable within the VOI. The planning CT and associated OAR segmentations were available as a guide, but the independent observer was blinded to any prior segmentations on the CBCT. The inter-observer variation was analyzed by calculating the Dice similarity coefficient between the reference and independent-observer segmentations.

Data augmentation was carried out by artificially deforming the planning CT and CBCT images to mimic variations in breath-hold level. Commercial software was used (ImSimQA v. 4.1, Oncology Systems Limited, Shrewsbury, Shropshire, UK) to simulate the expansion and shrinkage of delineated lung volumes by displacing the diaphragm approximately 1 cm inferiorly and superiorly, respectively, yielding deformations of the abdominal organs in the image sets. Hence the number of registrations for each patient was increased nine-fold, to 18 registration pairs between three planning CT and six CBCT images. In order to accommodate GPU memory limitations, CT and CBCT images were cropped to a volume of 20.5 × 20.0 × 17.0 cm (0.1 × 0.1 × 0.1 cm voxel size) and with the center of volume aligned to that of the CBCT. In all cases the VOI with at least 2 cm surrounding margin was fully enclosed. In order to improve deformable registration performance, any gas pockets detected in the cropped images were filled, i.e. voxel intensities replaced with values derived from surrounding voxels (algorithm described below). Finally, for each image, predefined range-based CT numbers (Hounsfield units) were used to map the intensities to [−1, 1] via an affine transformation (y=ax+b). The upper bound of the intensity range is mapped to 1 and the lower bound is mapped to −1. Intensities that were outside the range were clamped, such that values greater than 1 are set to 1 and values less than −1 are set to −1. The effect of the normalization was to remove outlier voxels and increase image contrast of the VOI.

2.B. Gas Pocket Filling

Gas pockets occurred frequently inside the patient stomach, small and large bowels due to physiological processes. These gas pockets appeared as dark regions that usually changed location and shape between CT and CBCT images. First a threshold was applied to the image, based on a predefined CT number to obtain dark regions S_dark. The region outside the patient was regarded as the background and hence was excluded from S_dark. In addition, we obtained segmentations for both lungs S_lung which also appeared dark in the image. The lungs were automatically segmented in the planning CT, using a region-growing algorithm in MIM, followed by manual transfer and alignment to the lungs in the CBCT. Gas pockets S_gas1 were initially identified as the complement of S_lung from S_dark, such that S_gas1 = S_dark \ S_lung (i.e. S_dark not S_lung). Then a region-growing⁶ method was applied to expand the initial region and obtain final gas pockets S_gas. Next, an inpainting algorithm⁷ was applied to fill the gas pockets. The algorithm was based on fluid dynamics, which preserved the edges from surrounding regions that intersected the gas regions by matching the gradient vectors. Since the algorithm was designed for 2D images, the in-painting process was applied slice by slice. As a final step, images were smoothed by a 3D Gaussian kernel with a standard deviation of [2 mm, 2 mm, 2 mm].

2.C. Overview of Image Registration

Given a moving image I₀ and a target image I₁, the goal of image registration is to find a 3-dimensional spatial transform Φ⁻¹ to transform the moving images, such that images are aligned after the transformation. Typically, registration is formulated as an optimization problem,

$${\Phi }^{*}=\underset{\Phi }{\text{argmin}}\text{\hspace{0.17em}Reg}[\Phi ]+\frac{1}{{\sigma }^2}\text{Sim}\left[I_0\circ {\Phi }^{-1},I_1\right],$$ (1)

where σ is a weight balancing the two terms, Reg[·] penalizes the irregularity of the transformation, and Sim[·] penalizes the dissimilarity between the warped moving image and the target image.

Registration models which directly regularize the displacement field typically cannot express large deformations as these are heavily penalized. However, fluid-based registration models parametrize the transformation via a velocity field⁸. In such a model the velocity field is regularized. Therefore, large deformations can be captured. Our LDDMM (large deformation diffeomorphic metric mapping) model is a type of fluid-registration model. In consequence, it can also capture large deformations. In particular, LDDMM estimates a spatio-temporal velocity field. The deformation map is then obtained via numerical integration. Intuitively, the resulting solution amounts to chaining together multiple small deformations (one for each time discretization step), which then allows capturing large deformations. Examples of such models include the stationary velocity field (SVF) model⁹ where the velocity field v(x) is constant over time, and large deformation diffeomorphic metric mapping (LDDMM) approaches⁵ where the velocity field is spatially and temporally dependent, i.e., v(x, t). A diffeomorphic transformation is guaranteed for sufficiently smooth velocity fields¹⁰. The corresponding optimization problem is

$$v^{*}=\underset{\Phi }{\text{argmin}}{\int }_0^1\Vert v{\Vert }_L^2+\frac{1}{{\sigma }^2}\text{Sim}\left[I_0\circ {\Phi }^{-1},I_1\right],\text{\hspace{1em} s.t.}$$

$${\Phi }_t^{-1}+D{\Phi }^{-1}v=0,\text{\hspace{1em} and \hspace{1em}}{\Phi }^{-1}(0)=id.$$ (2)

Here D denotes the Jacobian, $\Vert v{\Vert }_L^2=\langle L^{†}Lv,v\rangle$, where L is a self-adjoint differential operator and L^† is the adjoint. The first constraint is the advection equation that transports the transformation map Φ⁻¹ via the velocity field v and the second one indicates that at t = 0 the transformation map is the identity map. Although equation (2) is optimized over the velocity field, it can also be parametrized by a vector momentum m, i.e.,

$$m^{*}=\underset{m_0}{\text{argmin}}\langle m_0,v_0\rangle +\frac{1}{{\sigma }^2}\text{Sim}\left[I_0\circ {\Phi }^{-1},I_1\right],\text{ s.t.}$$

$${\Phi }_t^{-1}+D{\Phi }^{-1}v=0,{\Phi }^{-1}(0)=id,v={\left(L^{†}L\right)}^{-1}m,\text{\hspace{1em} and }{m}_t+\mathit{\text{mdiv}}(v)+{(Dv)}^{T}m+(Dm)v=0,$$ (3)

where m₀ and v₀ are the initial momentum (at t = 0) and initial velocity, respectively. The last constraint for the vector momentum parametrization is also known as the EPDiff equation¹¹. This is a shooting formulation of LDDMM registration, which is entirely parameterized via initial conditions.

Non-parametric image registration models such as SVF and LDDMM require optimizing over millions of parameters in 3D, which can be slow. Hence, deep learning (DL) approaches have been proposed^4,12,13 to speed up the registration process. By shifting the computational cost to the training phase, DL approaches are orders of magnitudes faster at test time than numerical optimizations, while retaining registration accuracy.

Quicksilver¹² was the first deep learning model for fluid-based medical image registration. Its goal was to replace the costly numerical optimization for LDDMM⁵ by a deep learning model. While the velocity field is smooth for an optimization method, the smoothness is not guaranteed when a deep network directly outputs this velocity field. Hence Quicksilver predicts a vector momentum parametrization for LDDMM. This parametrization allows for the explicit control of the smoothness of the velocity as the velocity field is obtained by smoothing the predicted momentum. A related deep learning-based registration network is vSVF⁴.

Different from Quicksilver, this network does not require precomputed momentum fields, but instead provides an end-to-end formulation for image registration, as for spatial transformers¹⁴ or in VoxelMorph¹³. The loss function of the network is the combination of a regularization loss and an image similarity loss. The network learns a vector momentum-parametrized stationary velocity field (vSVF) model from the training data, and the deformation field is calculated by smoothing the momentum followed by time integration based on the velocity field.

2.D. LDDMM-based Registration Network

Inspired by the previous two deep learning-based fluid registration networks, we propose an LDDMM-based deep network to register CT and CBCT images. Fig. 1 shows a flow chart of the proposed network. Specifically, the network takes a pair of CT and CBCT images as its input. Additionally, as the segmentations for the CT images are available, the network also uses the small bowel and the stomach duodenum segmentations of the CT image as inputs. Further, the volume of interest (VOI) is also provided as an input to the network. The output of the deep network is a vector momentum field for LDDMM. The transformation map Φ is then obtained by smoothing the momentum field to obtain the corresponding velocity field followed by time integration. We choose to use the momentum parametrization^4,12 for the same reason: it allows explicit control of the smoothness of the velocity field and, hence, results in a diffeomorphic transformation.

Figure 1:

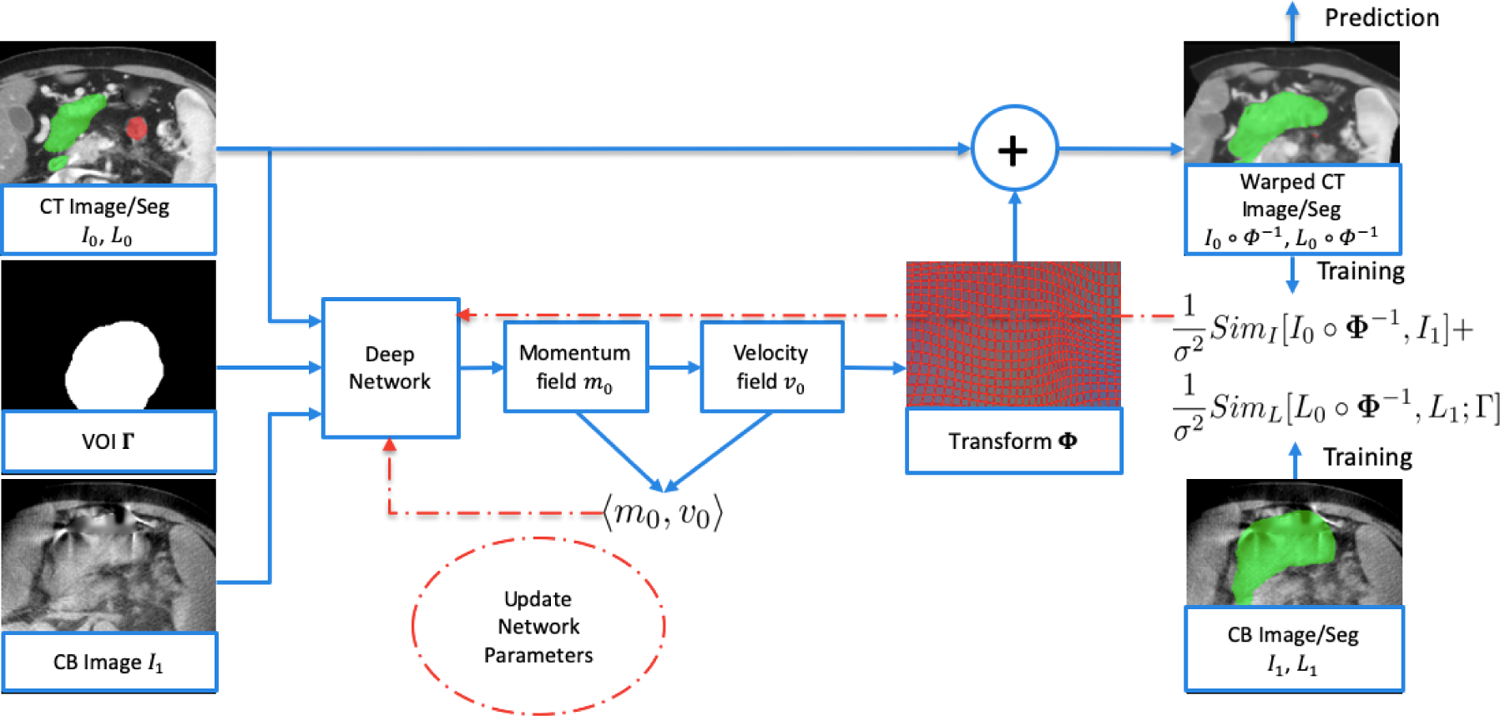
Flowchart of the proposed deep network. The input to the network is CT images I₀ with OAR segmentations L_0, CBCT images I₁ and volume of interest (VOI) Γ. The transformation map Φ is obtained from the deep network which includes smoothing of the momentum field followed by integration of the velocity field over time. During training, CT images and segmentations are warped and the resultant image similarity loss (Sim_I), segmentation similarity loss (Sim_L) and regularization loss (Reg) are computed. Computation of segmentation similarity loss requires the physician-drawn OAR segmentations on the CBCT (L₁) as input (lower right). Loss functions are backpropagated to update the network parameters (red arrows). At prediction time, network parameters are fixed, and only one forward pass is required (i.e. no backpropagation) to obtain the transformation and to calculate the warped CT images and warped CT segmentations (upper right), which results in much shorter processing time.

The relatively large component of x-ray scatter in CBCT images, motion-induced blurring and streaking, plus cupping artifacts resulting from the limited field-of-view reconstruction, can adversely affect the accuracy of CT-to-CBCT deformable registration, particularly for registration algorithms that are driven by image similarity as in Eq (2). Our approach makes use of the segmentations of both CT and CBCT images during training, by incorporating a segmentation similarity loss in the network. Since our focus is on the VOI, the segmentation similarity loss is only evaluated inside the VOI. The overall loss function for the network is as follows:

$$m^{*}=\underset{m_0}{\text{argmin}}\langle m_0,v_0\rangle +\frac{1}{{\sigma }^2}{\text{Sim}}_I\left[I_0\circ {\Phi }^{-1},I_1\right]+\frac{1}{{\sigma }^2}{\text{Sim}}_L\left[L_0\circ {\Phi }^{-1},L_1;\Gamma \right],\text{ s.t.}$$

$$\begin{gathered} {\Phi }_t^{-1}+D{\Phi }^{-1}v=0,\text{\hspace{1em} and \hspace{1em}}{\Phi }^{-1}(0)=id,v={\left(L^{†}L\right)}^{-1}m,\text{\hspace{1em} and } \\ {m}_t+\mathit{\text{mdiv}}(v)+{(Dv)}^{T}m+(Dm)v=0,m(0)=m_0, \end{gathered}$$ (4)

where I₀ and I₁ are CT and CBCT images, L₀ and L₁ are CT segmentations (i.e. binary images of the small bowel and stomach duodenum) and CBCT segmentations. The segmentation similarity loss Sim_L is only evaluated inside the VOI Γ. We use localized normalized cross correlation (LNCC)⁴ as the image similarity loss and sum of squared differences as the segmentation similarity loss. Note that during the prediction phase, although both planning CT and CBCT images are input to the network, only CT segmentations are used as additional input, since the warped CT segmentations serve to predict the segmentations on the CBCT. Therefore, CBCT segmentations are only required during the training phase, and not during prediction. We also note that the regularization, image similarity and segmentation similarity terms are balanced by a constant σ in Eq [4]. In our implementation, σ is set to 0.5. Because of this balance between terms, during training the network in general does not warp the CT segmentations to exactly match the CBCT segmentations. The same weighting was chosen for simplicity in the hyperparameter tuning.

Our network adopts a U-Net-like¹⁵ structure, which learns the image features at three different scales. Our network is implemented in pyTorch¹⁶. It is trained end-to-end. AdamW is used as the optimizer with a cosine annealing learning rate scheduler. The initial learning rate is 5×10⁻⁴. The network is trained with a batch size of 4 for 800 epochs. To smooth the momentum field, we use a multi-Gaussian kernel with standard deviations {0.05, 0.1, 0.15, 0.2, 0.25} and weights {0.067, 0.133, 0.2, 0.267, 0.333}. Image space is scaled to [0,1]³ when interpreting the standard deviations. The implementation of our deep network is based on the end-to-end deep-learning framework for 3D image registration described by Shen et al⁴, which is available at https://github.com/uncbiag/mermaid.

2.E. Evaluation

Predicted results from the deep network were accomplished using five-fold cross-validation. The datasets from 40 patients were randomly separated into five groups, with each group consisting of eight patients. Each group was used once as a testing set for prediction, and the remaining four groups were used to train the deep network (three for training and one for validation). The validation group served to tune the deep network and find the best training model that fitted the validation group. The validation loss included the Dice similarity coefficients of the OAR segmentations inside the VOI, in addition to the training loss functions. The artificially deformed images and segmentations were used only in the training phase, whereas only the original images and segmentations were used for evaluation. The transformation maps served to deform the OAR segmentations from the planning CT to the CBCT for comparison to the physician-drawn segmentations on the CBCT. Performance comparison was made to two intensity-based DIR algorithms as benchmarks: LDDMM; and multi-modality free-form (MMFF, MIM v. 6.9.7) deformation. Neither benchmark DIR algorithm made use of segmentations during optimization, which is consistent with current DIR methods used in clinical practice. MMFF settings were: CBCT-to-CT DIR profile; smoothness factor 0.5; and “use normalization” option, which scaled the CBCT intensity values to be similar to those of the CT. Following MMFF registration, the contours from the CT were deformably transferred to the CBCT for comparison to the physician-drawn contours. The following metrics were evaluated: Dice similarity coefficient (DSC), change in OAR volume within the VOI between planning CT and CBCT, and maximum dose to 5 cm³ of the OAR [D(5cc)]. The latter two quantities were representative measures of dosimetric interest for the stomach and the bowel, for which high dose constraints must be respected by the treatment plan.

3. Results

Processing time for one training group of 32 patients (576 CT-CBCT registration pairs) was about 3.5 days on an NVIDIA GeForce GTX1080 Ti GPU with 11GB memory. Although the training time is long, once the network is trained, it is fast at test time (i.e. prediction of test cases). Processing time for one CT-CBCT registration at test time was less than 5 seconds on the same GPU, including writing the warped image, warped segmentations, and transformation map to disk. Computations for the optimization-based LDDMM method were performed on a 5-node GPU cluster, each node consisting of eight GeForce GTX1080 GPUs (Pascal architecture) with 8 GB memory. Processing time for optimization-based registration varied across cases from 20 to 50 minutes, but on average required about 30 minutes for one registration pair.

Inter-observer variation of manual OAR segmentations within the VOI, quantified as the mean ± one-standard-deviation DSC between reference and independent-observer segmentations from a subsample of ten CBCT images (section 2.A), was found to be 0.820±0.068 (range 0.687–0.899) for small bowel and 0.858±0.059 (range 0.714–0.933) for stomach/duodenum.

Figure 2 shows an example of gas filling results for one CT image and one CBCT image. For CT images, which exhibited consistent CT numbers with tissue density, gas pocket in-painting performed reliably using the same tissue- to-gas threshold for all CT images. CT numbers were more variable between CBCT images, however, owing to more pronounced artifacts such as x-ray scatter, cupping and streaking, which required adjustment of the threshold prior to applying the in-painting algorithm.

Figure 2:

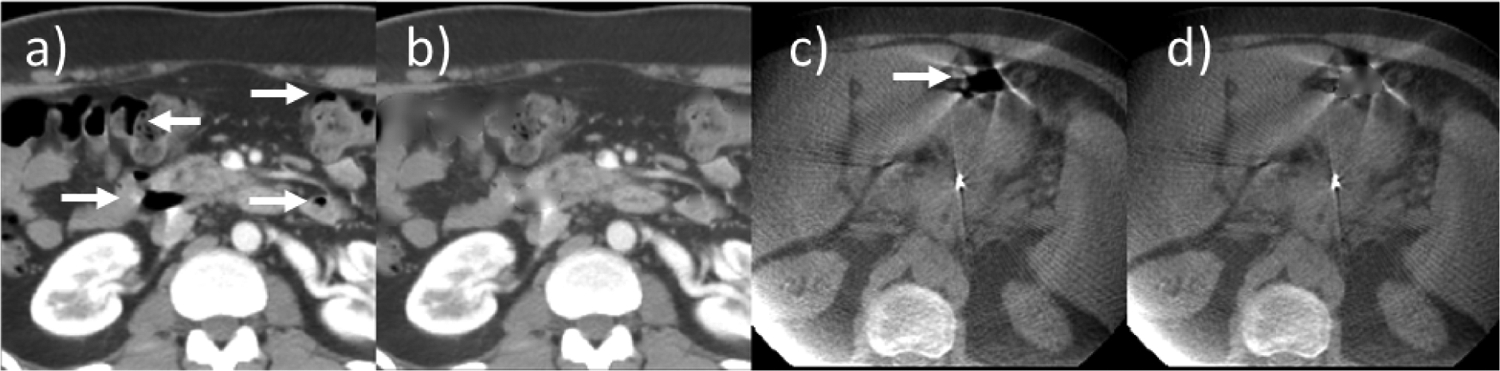
Example of gas filling: planning CT, a) before and b) after gas filling; cone-beam CT, c) before and d) after. Arrows indicate gas pockets.

Figure 3 shows the box plots of DSC from the 40 patients (80 registration pairs). The calculations were done on those portions of the OAR volumes that were within the VOI. For both small bowel and stomach/duodenum, the deep learning model yielded larger median DSC and smaller 25-to-75% quartile variation than either MMFF or LDDMM. Paired 2-tailed t-tests of DSC between DL vs. MMFF (DL vs. LDDMM) yielded p < 10⁻⁴ (p < 10⁻³) for small bowel, and p < 10⁻⁴ (p = 0.03) for stomach/duodenum.

Figure 3:

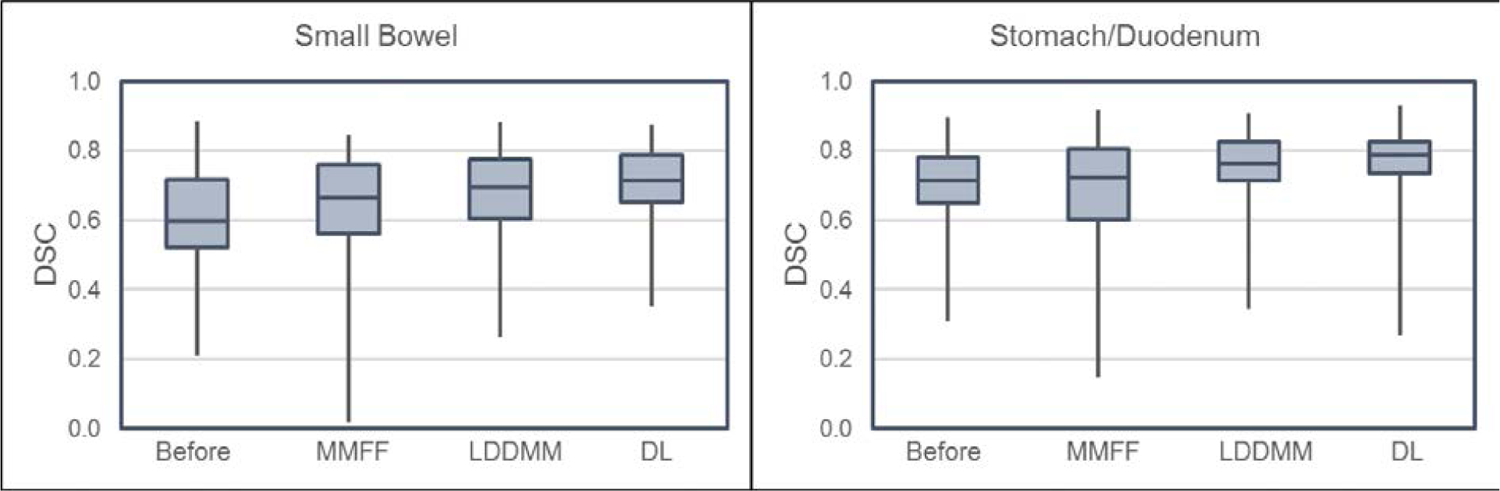
Box plots of Dice similarity coefficient (DSC) for the portions of small bowel (left) and stomach/duodenum (right) planning CT segmentations enclosed within the VOI and using physician-drawn segmentations on the CBCT as reference. In each graph, box plots from left to right are: planning CT segmentations before deformable registration (i.e. only rigid registration fiducial alignment between planning CT and CBCT); multi-modality free-form (MMFF); large deformation diffeomorphic metric mapping (LDDMM); and proposed deep learning (DL) model. In the latter three, planning CT segmentations were deformed by the stated method.

Figure 4 shows an example of stomach/duodenum contour alignment that compares the performance between the deep learning model, MMFF and LDDMM registrations. In this example, the volume of stomach/duodenum within the VOI exhibited a large increase between the planning CT and the CBCT at treatment (from 111 cm³ to 193 cm³, an increase of 82 cm³). The MMFF and LDDMM predictions severely underestimated the volume change (they predicted a decrease of 32 cm³ and an increase of 5.7 cm³ respectively). As can be seen in the figure, LDDMM contours appear very similar to the plan-CT contours, consistent with the small increase in predicted volume. In contrast, the DL prediction was more accurate (an increase of 46 cm³). This was likely due, at least in part, to the segmentation similarity term during the training process [Sim_L in Eq (4)] which helped to increase the alignment of segmentations within the VOI.

Figure 4:

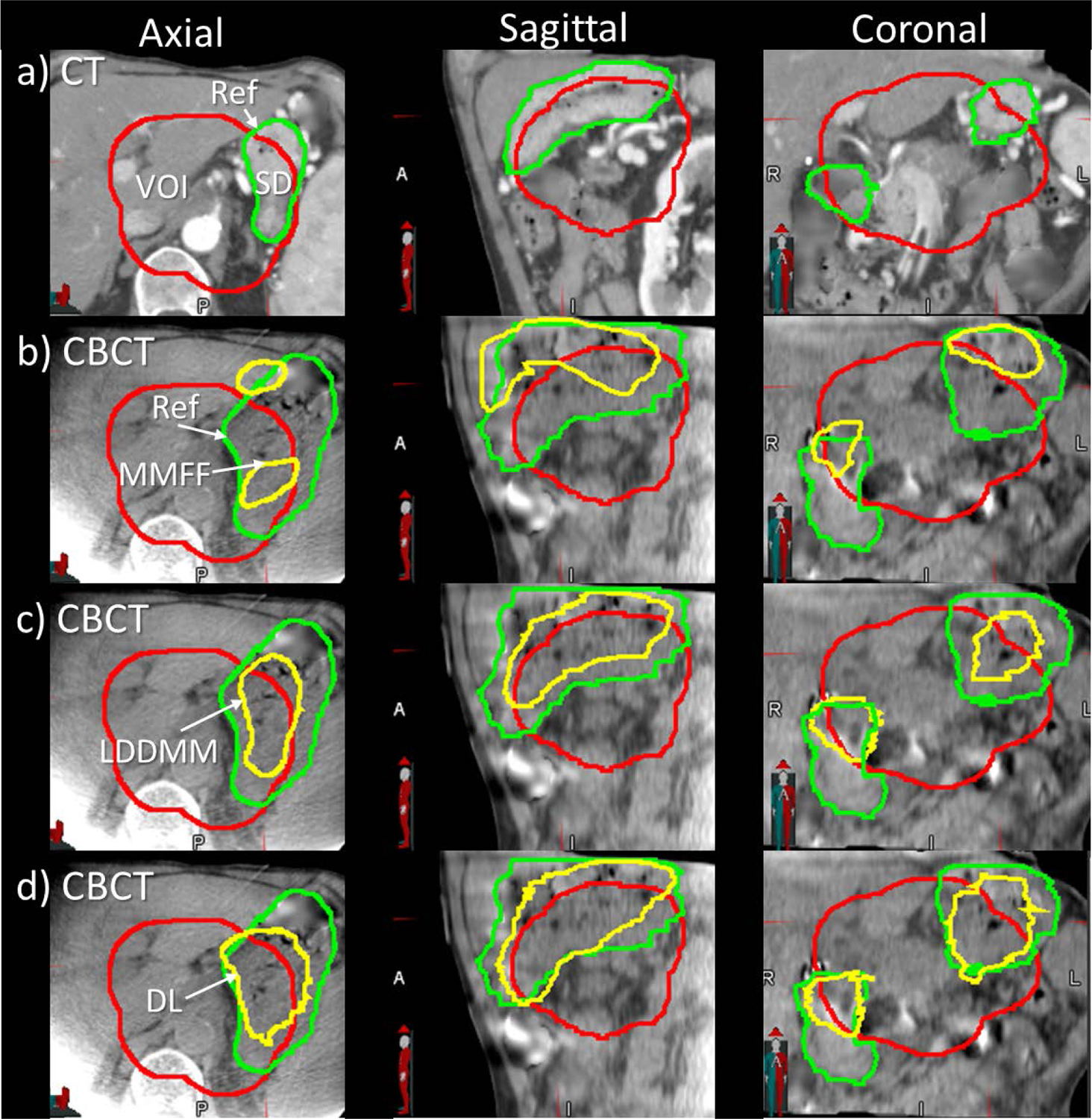
Example of stomach/duodenum (SD) contour alignment from a case in which there was a large increase in stomach volume in the CBCT. Axial, sagittal and coronal views of a) plan CT with physician-drawn reference contours (green); b) CBCT with physician-drawn reference (green) and multi-modality free-form contours (MMFF, yellow); c) CBCT with large deformation diffeomorphic metric mapping contours (LDDMM, yellow); d) CBCT with deep-learning-predicted contours (DL, yellow). Red contour indicates the volume-of-interest (VOI) enclosing low-dose planning target volume with 1 cm margin expansion.

Figure 5 compares DSC of DL-, MMFF- and LDDMM-predicted OAR segmentations vs. DSC of planning CT segmentations, using the physician-drawn segmentations on the CBCT as reference. Data points above (below) the diagonal lines indicate cases where DSC of predicted contours is larger (smaller) than DSC of plan-CT contours. For DL-model prediction, DSC was larger relative to that for plan-CT contours in 91% of small bowel and 78% of stomach/duodenum cases; for LDDMM, in 89% and 82% of cases; and for MMFF, in 71% and 46% of cases, respectively.

Figure 5:

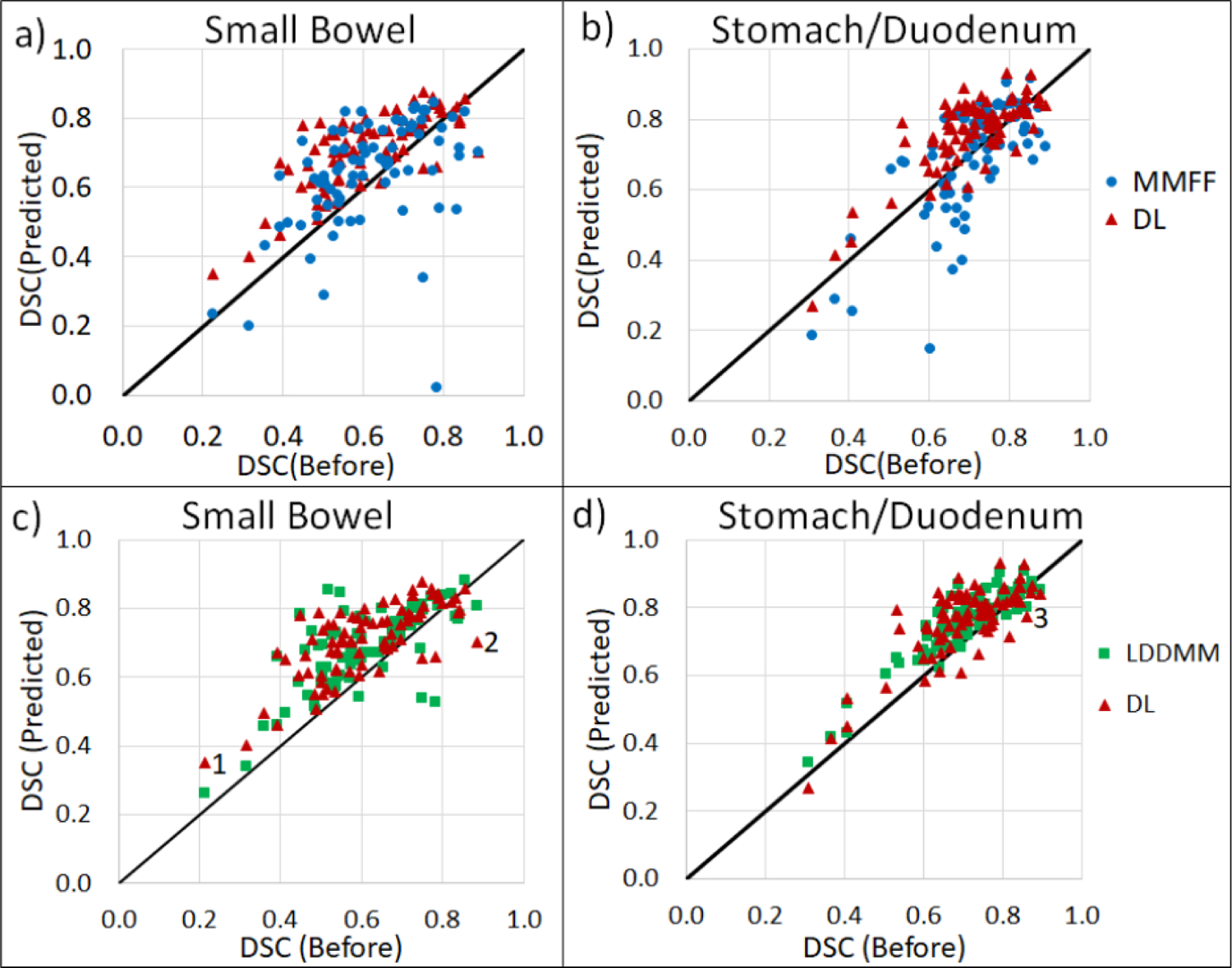
Scatterplots of Dice similarity coefficient (DSC) from predicted CBCT contours following deformable registration, vs DSC from plan-CT contours, for portions of small bowel (left) and stomach/duodenum (right) enclosed within the VOI. DSC is computed using physician-drawn segmentations on the CBCT as reference. Plots a) and b) are comparisons between DL and MMFF; c) and d) are comparisons between DL and LDDMM. Data points labeled 1, 2 in c) and 3 in d) correspond to specific cases discussed in the text.

We examined cases in which DL-based registration performed less well. Fig 6 shows an example of increased but low DSC(DL) in small bowel (data point labeled “1” in Fig 5). This result was caused by large changes in the shapes of the physician-drawn segmentations between planning CT and CBCT, specifically changes in the number of disconnected segments of small bowel, which was difficult for the segmentation similarity term [Eq (4)] to resolve during training. Data points labeled “2” and “3” in Fig 5 were cases in which DSC decreased following DL-based registration and are shown in Fig 7. Both cases involved low-quality CBCT scans which adversely affected the image registration, i.e., image noise in Case 2 and motion-induced image blurring and streaking in Case 3.

Figure 6:

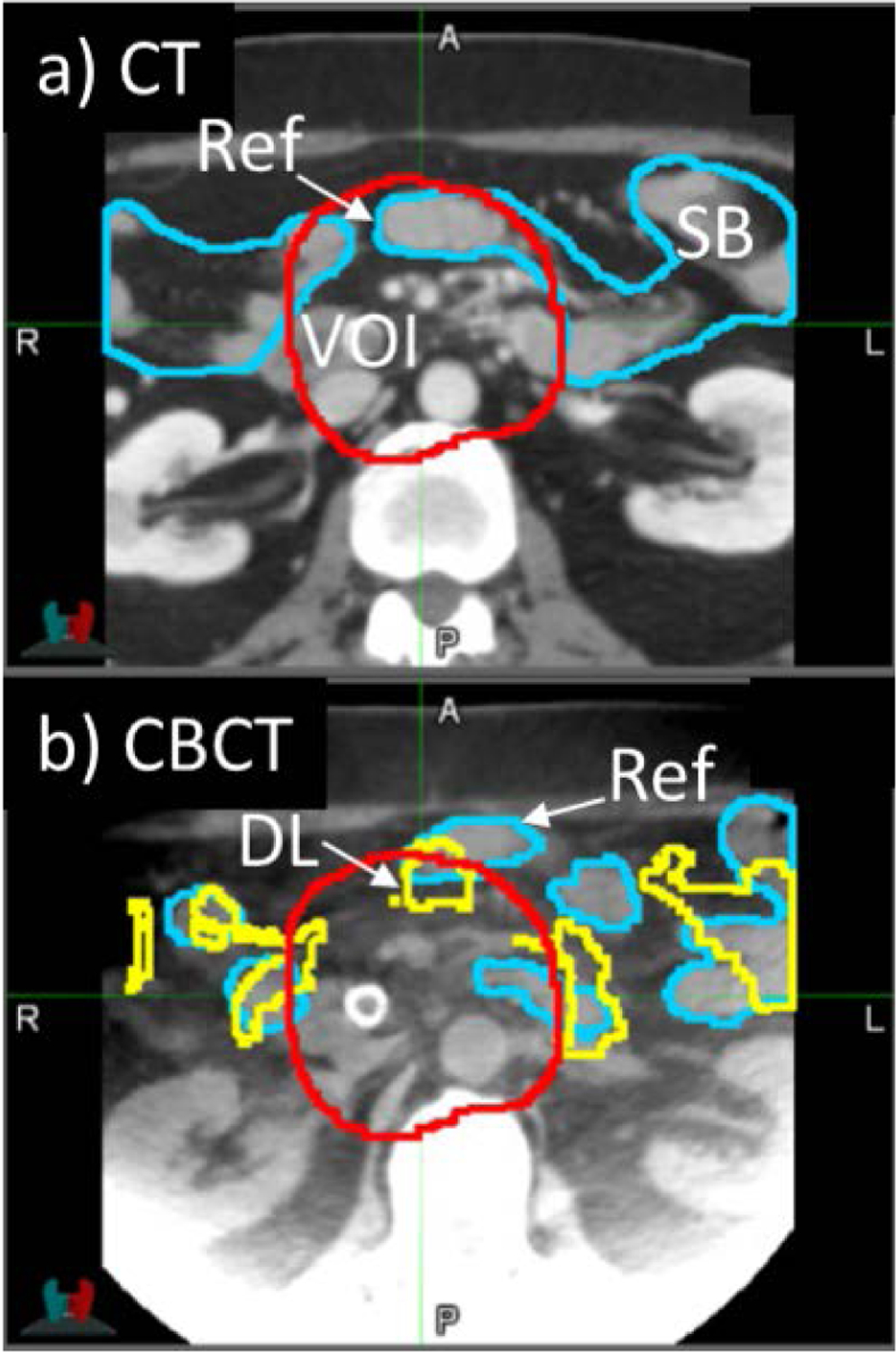
Example Case 1 from Fig 5. Axial view of a) planning CT with physician-drawn reference contours of small bowel (SB, blue); b) cone-beam CT with reference contours drawn on CBCT (blue) and deep-learning-predicted contours (DL, yellow). Note the topological differences between the two images: in the CT there are two separate small bowel segments, whereas in the CBCT there are additional segments

Figure 7:

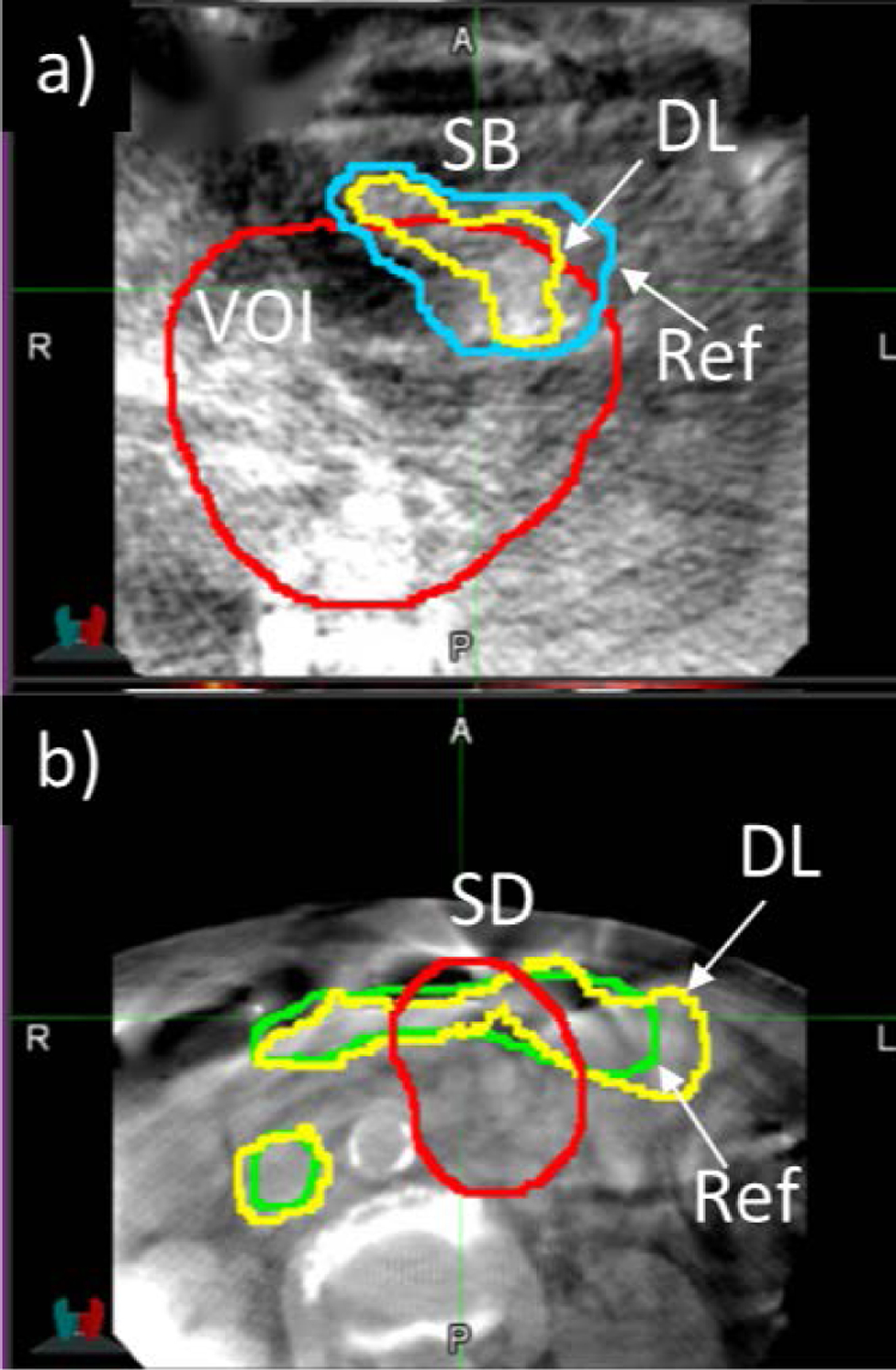
Two example cases from Fig 5. Axial view of a) Case 2 CBCT with reference (blue) and deep learning-predicted (yellow) contours of small bowel (SB); b) Case 3 CBCT with reference (green) and deep-learning-predicted contours of stomach/duodenum (SD). Case 2 CBCT exhibits noisy image quality, whereas Case 3 CBCT exhibits motion-induced blurring and streaking artifacts.

Figure 8 compares the performance of the three methods in predicting changes in OAR volume within the VOI between planning CT and CBCT. An accurate evaluation of the changes in OAR volume is clinically important, since treatment plan adaptation may be needed in cases when a substantial portion of OAR moves into the PTV region and accumulated dose exceeds the planned values. For small bowel, root-mean-square deviation (RMSD) of DL-predicted volume change was 22% less than MMFF (10.2 vs. 13.0 cm³, p = 0.007) and 6% less than LDDMM (10.2 vs. 10.9 cm³, p = 0.08). For stomach/duodenum, RMSD of DL-predicted volume change, relative to reference, was 41% less than that of MMFF-predicted change (14.9 vs. 25.1 cm³ respectively, p = 0.09) and 28% less than LDDMM (14.9 vs. 20.6 cm³, p = 0.0001). In the three cases (data points within dashed ellipse in Fig 8) with the largest increases in stomach/duodenum reference volume (81.9, 83.0 and 101.4 cm³), deep-learning yielded predicted increases of 46.3, 74.4 and 70.9 cm³, whereas MMFF and LDDMM predictions showed little or no increase (−32.2, 37.1 and −4.6 cm³ for MMFF; 5.7, 17.0 and 10.6 cm³ for LDDMM).

Figure 8:

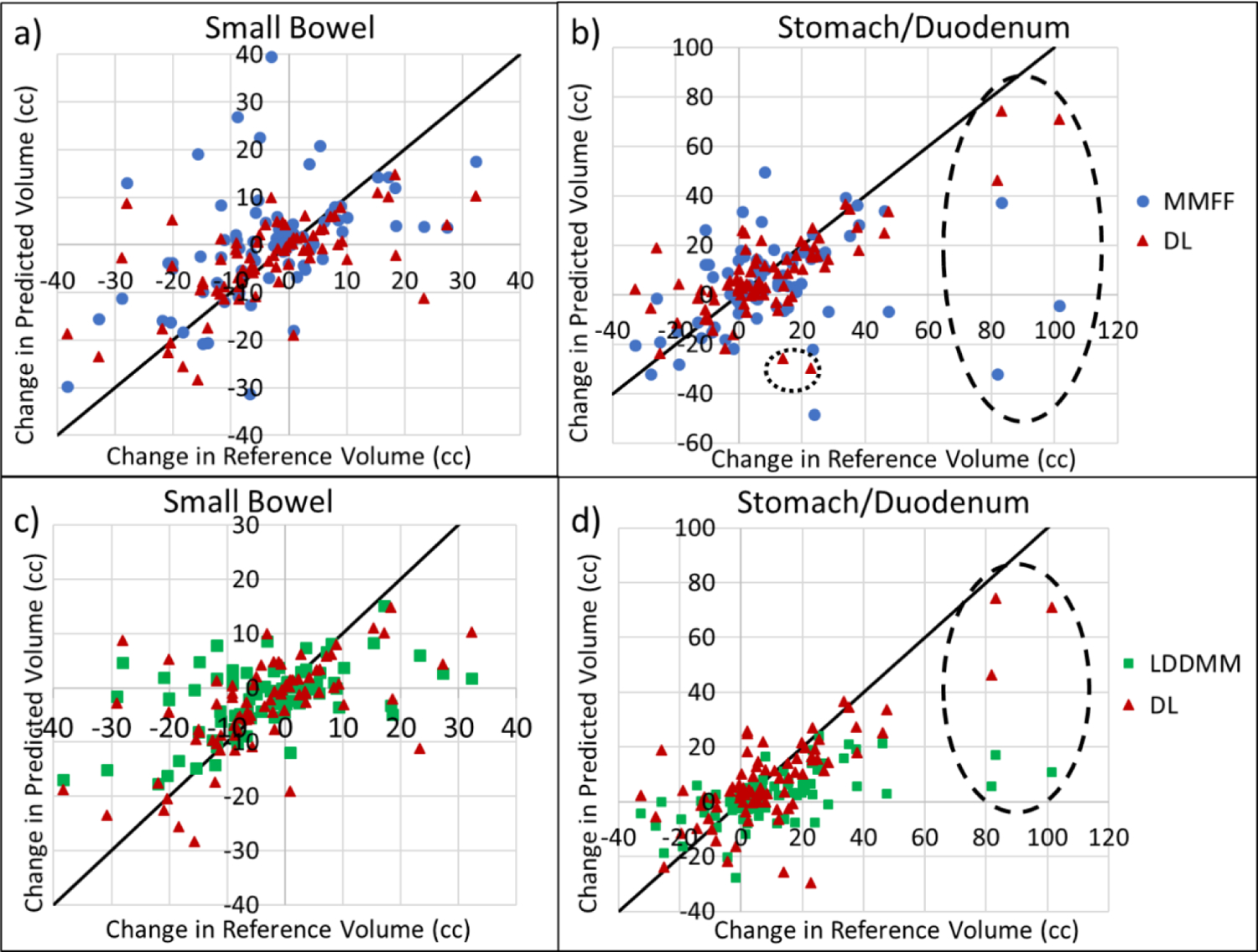
Scatterplots of the change in predicted volume, from plan CT to CBCT, enclosed within the volume of interest vs. change in physician-drawn reference volume, for small bowel (left) and stomach/duodenum (right). Plots a) and b) are comparisons between DL and MMFF, c) and d) are comparisons between DL and LDDMM. Dashed ellipses indicate cases where there was a large increase in the volume of stomach/duodenum within the VOI. Dotted circle in b) indicates cases with low CBCT image quality.

Finally, we investigated the possible dosimetric impact of OAR movement for this type of radiation treatment. Specifically, we examined the predicted maximum dose to 5 cm³ OAR volume [D(5cc)], compared to reference D(5cc) of physician-drawn segmentations on the CBCT (Fig 9). RMSD of DL-predicted D(5cc), relative to reference, in small bowel was 39% less than that for MMFF (3.61 vs. 5.96 Gy, p = 0.001); there was no statistically significant difference in RMSD between DL and LDDMM. In stomach/duodenum, RMSD for the DL prediction was 18% less than that for LDDMM (3.51 vs 4.30 Gy, p < 10⁻³); there was no statistically significant difference in RMSD between DL and MMFF. Deviations of predicted values from reference increased noticeably for reference values above 45 Gy (discussed further in the Discussion section).

Figure 9:

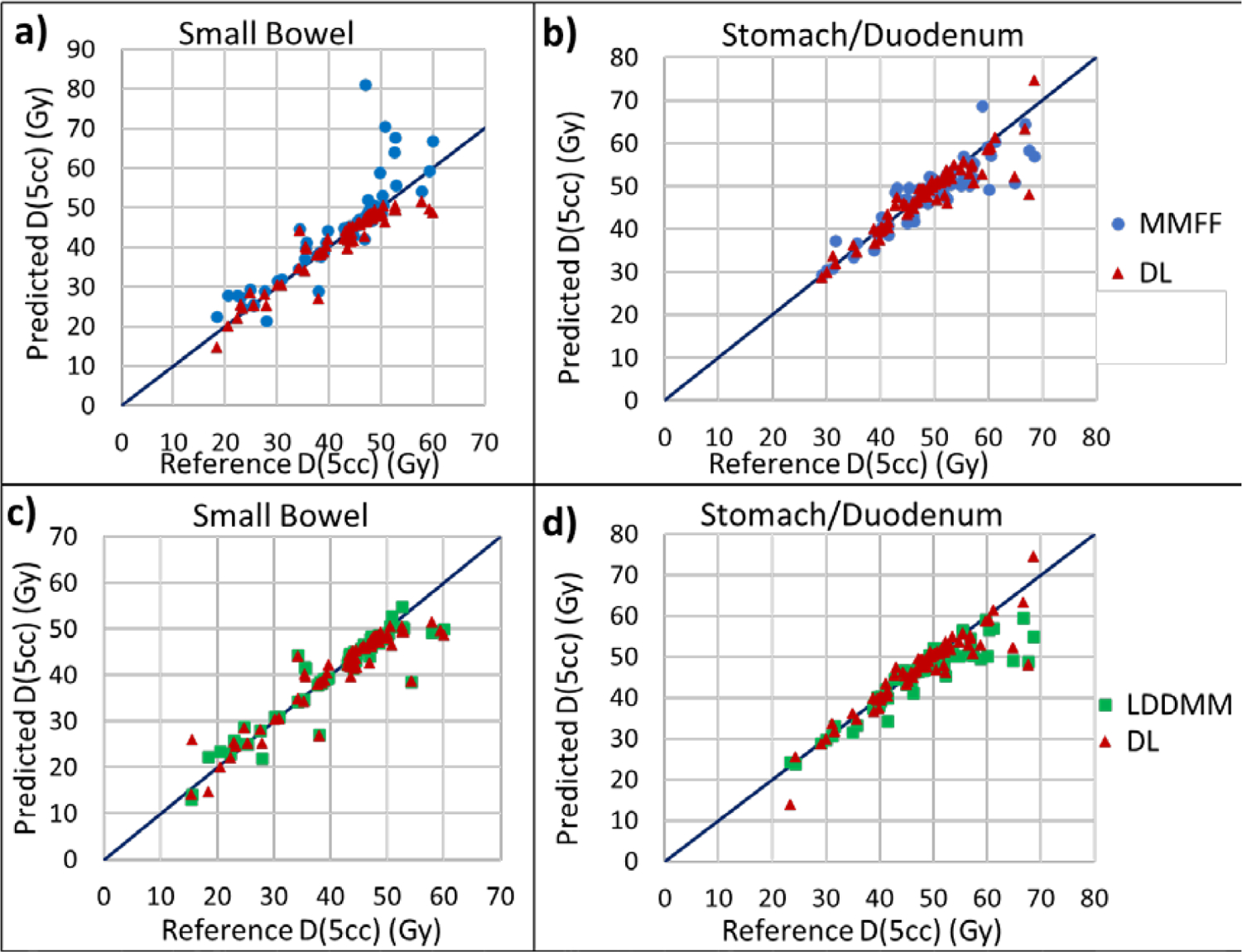
Scatterplots of maximum dose to 5 cm3 of predicted OAR segmentations [Predicted D(5cc)] vs physician-drawn OAR volumes on the CBCT [Reference D(5cc)], for small bowel (left) and stomach/duodenum (right). Plots a) and b) are comparisons between DL and MMFF, c) and d) are comparisons between DL and LDDMM. D(5cc) was computed by transferring OAR segmentations from the CBCT to the planning CT following rigid registration to fiducial marker and using the treatment plan dose distribution.

4. Discussion

Our findings indicate that the proposed deep-learning registration model yields more accurate OAR segmentations on breath-hold CBCT scans of pancreatic cancer patients than LDDMM and MMFF methods, relative to expert-drawn segmentations as a reference. Further, the deformable registration and automatic segmentation process of a new test case completes in seconds rather than minutes with current methods. This is because in the prediction phase, only one forward pass is required through the deep-learning network (Fig 1) which results in a much shorter processing time.

The deep-learning model is dependent on the size of the dataset used in training, which in turn is limited by the labor-intensive segmentation of organs in the cone-beam CT images. In this study, the dataset consisted of 120 image sets from 40 patients (one planning CT and two CBCT per patient). Augmentation of the training data increased the number of image sets three-fold by artificially deforming via expansion and contraction of lung segmentations. We found that augmentation yielded only an incremental improvement in DL performance: mean DSC in the small bowel increased by 3% and in the stomach/duodenum by 2% (data not shown). The modest improvement was likely due to the limited amount of deformation: 1 cm displacement of the diaphragm corresponded to approximately 3–5 mm tissue displacement at the VOI center. In addition, the simulation did not alter image quality, patient geometry, or imaging artifacts, which varied considerably in the actual image sets and hence influenced the training and prediction capabilities of the model.

The accuracy of the deep-learning model is also dependent on the quality of both the images and manual segmentations. Since the training process uses both image similarity and segmentation similarity in the loss function, inconsistency between segmentation and visible image features could adversely affect registration performance. As seen in the examples, noisy images or gas pockets with streaking artifacts could obscure the visibility of OAR boundaries, thus increasing the uncertainty in the manual segmentations (Fig 7). The small bowel posed additional challenges owing to its folding luminal structure: in some cases, the visibility of individual bowel segments varied considerably between CT and CBCT, resulting in inconsistencies in the segmentations (Fig 6). A possible way to address this in future is to use the segmentation drawn on the planning CT as a template to overlay, align and edit on the CBCT, in such a way as to maintain consistency in topology, i.e., in the number of bowel segments.

Our findings suggest that the accuracy of the DL-based model increased with the number of instances of similar cases in the training data. Conversely, the model was less accurate in cases where there were few similar cases in the training data, such as those exhibiting large increases in stomach/duodenum volume within the VOI (dashed ellipse in Fig 8). In an earlier analysis with only 20 patients (data not shown), there was only one such case with an increase in reference volume of 81.9 cm³, whereas the predicted increase was only 17.6 cm³. Since there was only one such case in the 20-patient data set, in the cross validation there was no such case in the training data. In the more recent 40-patient analysis, there were 3 such cases, and the predicted increase improved to 46.2 cm³. Increasing the training set with more patient statistics (e.g. another doubling of the number of cases) is expected to further improve prediction accuracy.

We assessed the generalization gap in our deep learning model, that is, the difference in DSC between training and test cases. In our cross-validation strategy a particular image was used for training in some folds and for testing in other folds. We recorded the performance differences between training and testing for a given image and averaged over all images. For 31 patients that were selected at least once in a training fold, average training DSC for small bowel was 0.867 compared to the testing result of 0.694, whereas average training DSC for stomach/duodenum was 0.896 compared to the testing result of 0.768. Note that not all the patients were selected for training; some patients were selected only for validation or testing. A generalization gap between training and testing is to be expected in deep learning, since the training error is explicitly minimized. Furthermore, since the number of images in our study was limited, overfitting was more likely; thus, a separate validation set was used as a stopping condition during training. Increasing the training data in future is expected to reduce the generalization gap.

As mentioned in the Results section, deviations of predicted D(5cc) from reference in both the DL model and MMFF increased for reference values above 45 Gy (Fig 9). Cases in which reference D(5cc) on the CBCT exceeded 45 Gy indicated that the OAR had moved closer to the high-dose (or ultra-high-dose) PTV and thus a portion of the OAR volume was within a higher dose-gradient region. Hence uncertainties in the predicted segmentation may have resulted in larger uncertainty in D(5cc) than for cases with reference D(5cc) below 45 Gy.

To our knowledge there has been only one publication reporting on CT-to-CBCT deformable registration and automatic segmentation of OARs for radiation treatment in pancreas¹⁷. Ziegler et al. used deformable image registration and contour propagation between planning CT and limited field-of-view CBCT acquired at each fraction to determine accumulated dose from radiation treatment of pancreatic cancer patients¹⁷. Images and treatment were performed with breath hold. A B-spline DIR algorithm, developed prior to the advent of deep-learning-based methods, was used in the study. DIR accuracy was evaluated by measuring the alignment of a fiducial marker in the warped CT and CBCT images, and visually inspecting the alignment of liver, kidneys, bones, air pockets and outer patient surface. No quantitative results were presented on the accuracy of propagated contours to those organs, however. Liu et al. developed a deep-learning-based method for automatic segmentation of OARs from diagnostic-quality CT scans for pancreatic radiotherapy¹⁸. The method consisted of a three-dimensional U-Net to differentiate multiple organs including small bowel, duodenum and stomach. The study focused on registration of single-modality CT scans and did not address automatic segmentation with CBCT, which is used by most radiotherapy clinics for CT-based guidance at treatment.

5. Conclusion

We have developed and evaluated a deep learning-based model for deformable CT-CBCT registration in radiation treatment of pancreatic cancer. It uses a segmentation similarity loss, in addition to the image similarity loss, to train the network to predict the transformation between the CT and CBCT images. Processing of new test cases requires only the CT segmentations as input, which are propagated according to the transformation to predict OAR segmentations in the CBCT images. Our findings indicate that it is more accurate than image-intensity-based LDDMM and MMFF methods while substantially speeding up the registration process at prediction time.