The geometry of domain-general performance monitoring in the human medial frontal cortex

Abstract

Controlling behavior to flexibly achieve desired goals depends on the ability to monitor one’s own performance. It is unknown how performance monitoring can be both flexible to support different tasks and specialized to perform well on each. We recorded single neurons in the human medial frontal cortex while subjects performed two tasks that involve three types of cognitive conflict. Neurons encoding conflict probability, conflict, and error in one or both tasks were intermixed, forming a representational geometry that simultaneously allowed task specialization and generalization. Neurons encoding conflict retrospectively served to update internal estimates of conflict probability. Population representations of conflict were compositional. These findings reveal how representations of evaluative signals can be both abstract and task-specific and suggest a neuronal mechanism for estimating control demand.

One sentence summary:

Representations of evaluative signals in human frontal cortex are both abstract and task-specific

Humans can rapidly learn to perform novel tasks given abstract rules, even if task requirements differ drastically. To achieve this, cognitive control must coordinate processes across a diverse array of perceptual, motor and memory domains and at different levels of abstraction over sensorimotor representations (1–3). A key component of cognitive control is performance monitoring, which enables us to evaluate whether we have made an error, experienced conflict, and responded fast or slow (4, 5). It provides task-specific information about which processes cause an error or a slow response so that they can be selectively guided (6–16). At the same time, performance monitoring needs to be flexible and domain-general to enable cognitive control for novel tasks (17), to inform abstract strategies (e.g., “win-stay, lose-switch”, exploration versus exploitation (18, 19)), and to initiate global adaptations (20–28). As an example, errors and conflicts can have different causes in different tasks (task-specific) but all signify failure or difficulty to fulfill an intended abstract goal (task-general); performance monitoring should satisfy both requirements. Enabled by its broad connectivity (29, 30), the medial frontal cortex (MFC) serves a central role in evaluating one’s own performance and decisions (4, 10, 13, 16, 19, 24, 31–43). However, little is known about how neural representation in the MFC can support both domain-specific and domain-general adaptations.

Specialization and generalization place different constraints on neural representations (44, 45). Specialization demands separation of encoded task parameters, which can be fulfilled by increasing the dimensionality of neural representations (46, 47). By contrast, generalization involves abstracting away details specific to performing a single task, which can be achieved by reducing the representational dimensionality (3, 46). Theoretical work shows that the geometry of population activity can be configured to accommodate both of these seemingly conflicting demands (44), provided that the constituent single neurons multiplex task parameters non-linearly (48, 49). While recent experimental work has shown that neuronal population activity is indeed organized this way in the frontal cortex and hippocampus in macaques (44) and humans (50) during decision making tasks, it remains unknown whether this framework is applicable to the important topic of cognitive control.

A key aspect of behavioral control is learning about the identity and intensity of control needed to correctly perform a task and deploy control proactively based on such estimates (13, 51). This requires integrating internally-generated performance outcomes over multiple trials. BOLD-fMRI studies localize signals related to control demand estimation to the insular-frontostriatal network (52). However, the neuronal mechanisms of how these estimates are updated trial-by-trial and whether the underlying substrate is domain-general or task-specific remain unknown.

Results

Task and behavior

Subjects (see Table S1) performed the Multi Source Interference Task (MSIT) and the color word Stroop task (Fig. 1A and Methods). Conflict and errors arose from different sources in these two tasks: competition between prepotency of reading and color naming in the Stroop task, and competition between the target response and either the spatial location of target (“Simon effect”, denoted by “fl”) or flanking stimuli (“Flanker effect”, denoted by “si”), or both (“sf”) in MSIT. In the MSIT, we refer to trials with or without a Simon conflict as “Simon” and “non-Simon” trials, respectively (and similarly for Flanker trials). Stimulus sequences were randomized, and each type of trial occurred with a fixed probability (see Methods for details).

Fig. 1. Tasks, Bayesian conflict learning model, reaction time analyses.

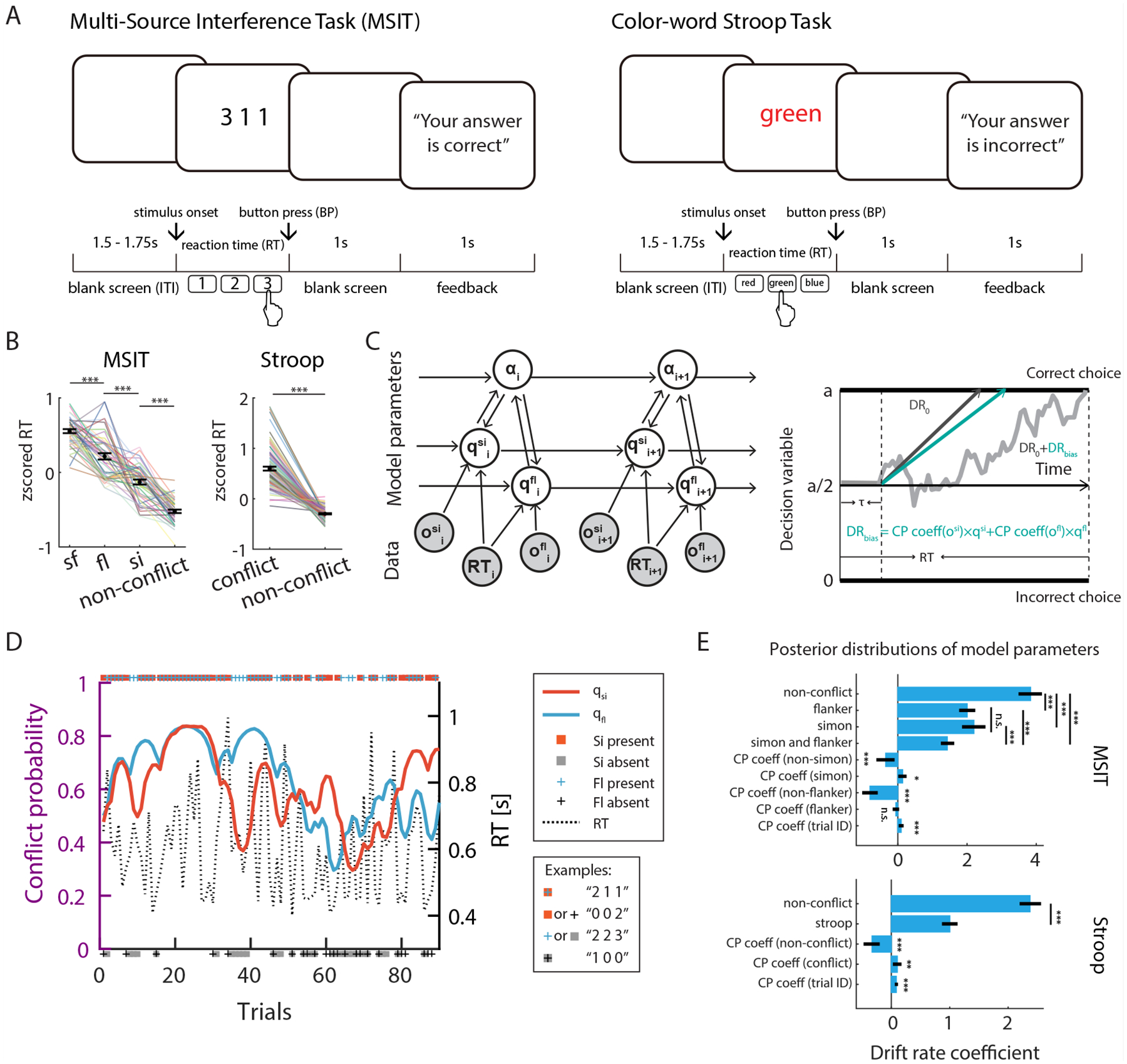
(A) Task structure. (B) RTs were significantly prolonged by conflict in MSIT (left, N=41 sessions) and Stroop task (right, N=82 sessions). (C) The conflict probability estimation process (left) and the decision process modelled as a drift diffusion (right). Shown is the MSIT model, which has the six variables learning rate (α), Simon probability (q_si), Flanker probability (q_fl), observed Simon conflict (o_si), observed Flanker conflict (o_fl), and RT. Observables (trial congruency, RT, and outcome) are shown in gray, model parameters are in white. Arrows indicate information flow.

(D) Estimated Simon probability (red) and Flanker probability (blue) from an example MSIT session. Markers placed on the top indicated the type of conflict present. (E) Posterior distributions of model parameters after fitting to the behavior of all subjects. Black bars show high density intervals. Conflict probability (CP) had a significant effect on RT. Vertical bars with asterisks showed comparisons between posterior distribution, and singled asterisks marked comparisons with zero. *p < 0.05, ** p < 0.01, *** p < 0.001, n.s., not significant (p > 0.05).

Subjects performed well (Stroop error rate: 6.3±5%; MSIT error rate: 6.0±5%). Reaction times (RT) on correct trials were significantly prolonged in the presence of conflicts (Fig. 1B; Fig. S1D–E shows raw RTs). Participants’ performance (RT and accuracy) were modeled with a hierarchical Bayesian model (52–54). The model (Fig. 1C) assumes that participants iteratively updated internal estimates of how likely they were to encounter a certain type of conflict trial (“conflict probability”) based on their previous estimates and new evidence (experienced conflict and RT) on the current trial using Bayes’ law. Given that trial sequences were randomized by the experimenter, subjects could not predict with certainty whether an upcoming trial has conflict or not; but could instead estimate the probability of a conflict trial, which is fixed a priori but unbeknownst to the subject. The decision process was modeled as a drift-diffusion process (DDM), with drift rates as a function of conflict and subject’s estimated conflict probability (“CP coeff” in Fig. 1E). Model parameters (DDM parameters and trial-wise CP estimation) were inferred from subjects’ behavioral data (RT and trial outcomes) and conflict sequences using data from all sessions and full Bayesian inference (see Methods for details). Significance of model parameters were determined from the posterior distributions directly (see Methods). The posterior predictive distributions captured the true RT distribution well (Fig. S2A–B). The Bayesian models were identifiable (Fig. S2C–D). Fig. 1D shows RT and estimated conflict probability of an example MSIT session. Unless specified otherwise, we use the term “conflict probability” or “CP” to refer to the posterior means of the estimated conflict probability.

Conflicts reduced drift rates and thus prolonged RT (P(dr_{Stroop non–conflict} < dr_{Stroop conflict}) < 0.001, P(dr_{MSIT non–conflict} < dr_simon) < 0.001, P(dr_{MSIT non–conflict} < dr_flanker) < 0.001, P(dr_{MSIT non–conflict} < dr_{simon and flanker}) < 0.001). High estimated CP prolonged RT on non-conflict trials (negative CP coeff decreases drift rate: P(CP coeff_{Stroop non-conflict} > 0) < 0.001, P(CP coeff_non-Simon > 0) < 0.001, P(CP coeff_non-Flanker > 0) < 0.001) but hastened RT on conflict trials (positive CP coeff increases drift rate: P(CP coeff_Stroop < 0) < 0.01, P(CP coeff_Simon < 0) < 0.05, Fig. 1E). Our model yielded qualitatively similar results when applied to data from a separate group of healthy control subjects (Fig. S1C). In a separate control model where only trial outcomes and conflict sequences were used (but not RT), high CP correlated with reduced likelihood of making an error on conflict trials (Bayesian logistic regression; negative CP coeff reduces error likelihood: P(CP coeff_Stroop > 0) < 0.01, P(CP coeff_Simon > 0) < 0.05, Fig. S1B), suggesting that higher CP predicted higher level of control. See (98) for more about model comparisons.

Neuronal correlates of performance monitoring signals

We collected single-neuron recordings from two regions within the MFC (Fig. 2A): the dorsal anterior cingulate cortex (dACC) and the pre-supplementary motor area (pre-SMA). We isolated in total 1431 putative single neurons (Stroop: 584 in the dACC and 607 in the pre-SMA across 34 participants (10 females); MSIT: 326 in the dACC and 412 in the pre-SMA in 12 participants (6 females)). Neurons in the dACC and the pre-SMA were pooled unless specified otherwise, because neurons responded similarly (but see section “Comparison between the dACC and the pre-SMA” for notable differences).

Fig. 2. Recording locations and example neurons.

(A) Recording locations shown on top of the CIT168 Atlas brain. Each dot indicates the location of a microwire bundle. (B-D) Activity of three example neurons that show similar response dynamics in both tasks. Shown is a neuron signaling action error (B), conflict by firing rate increase (C), and conflict by firing rate decrease (D). The black triangles mark stimulus onset. Trials are resorted by type and subsampled to equalize trial numbers for visualization only.

We identified neurons selective for the mean and variance of the posterior distribution of CP, error and conflict surprise (unsigned prediction error of CP: 1 − |conflict − CP|; conflict is an indicator variable) in the ex-post epoch, and conflict in the ex-ante and ex-post period (see example neurons in Fig. 2; schematic of analysis epochs in Fig. 3A; and a summary of overall cell counts in Fig. 3B).

Fig. 3. Single neuron tuning properties.

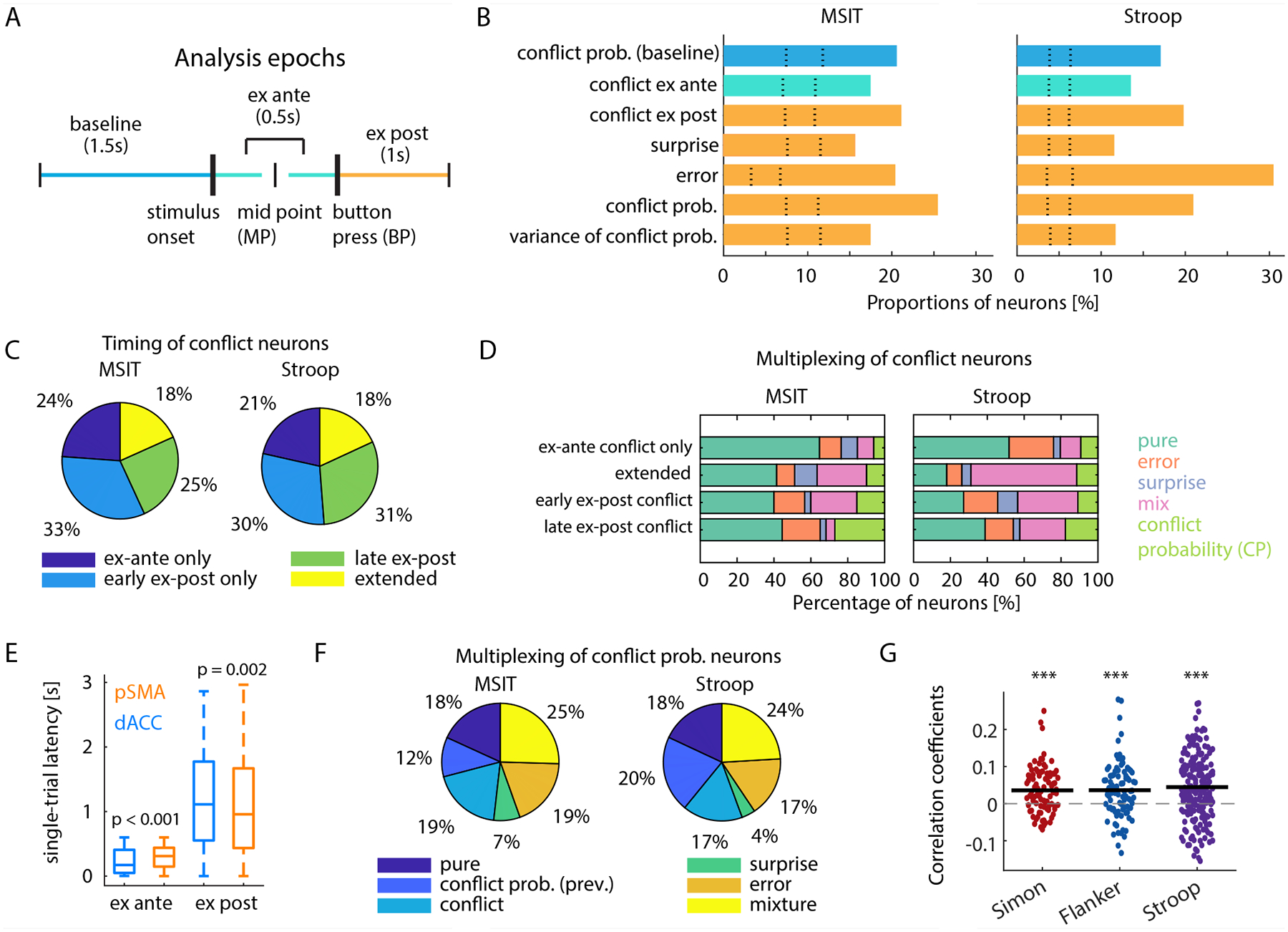
(A) Illustration of epochs used for analysis. Thick vertical bars represent physical events, the slim vertical bars demarcate epochs. (B) Percentage of neurons encoding the variable indicated in the two tasks. The color code is as indicated in (A). Dotted lines represent 2.5^th and 97.5^th percentiles of the null distribution obtained from permutation. For all groups shown, p < 0.001. (C) Percentage of conflict neurons that are selective in each time period. Early and late ex-post epochs denote 0–1s and 1–2s after button press. (D) Percentage of conflict neurons that were also selective for error, surprise, conflict probability (CP), or any combination of these factors (“mix”). (E) Comparison of single-trial neuronal response latency of conflict neurons in dACC and pre-SMA (correct trials only, t=0 is stimulus onset for ex-ante and button press for ex-post conflict neurons). (F) Percentage of conflict probability neurons that were also selective for conflict probability on the last trial, conflict, surprise, error, or all combinations of these variables (“mix”). (G) Neuronal signature of updating conflict probability estimation. Correlation is computed between the difference between current estimation and conflict probability on the last trial (behavioral update) and the difference between demeaned FR_ex-post and FR_baseline (neural update) for all conflict probability neurons. *** p < 0.001.

A significant proportion of neurons encoded the mean and variance of CP posterior distribution in the ex-post epoch (Fig. 3B, 25% and 17% of neurons in MSIT; 21% and 12% in Stroop). CP is maintained up to the baseline of the next trial (Fig. 3B “conflict prob. (baseline)”), blue; 21% in MSIT; 17% in Stroop). Neurons encoded conflict in the ex-ante epoch (17% and 14% of neurons in MSIT and Stroop, respectively; Fig. 3B, green), consistent with previous reports (33, 38), but intriguingly, also in the ex-post epoch (21% in MSIT; 20% in Stroop). Neurons encoded conflict surprise (16% in MSIT; 12% in Stroop), errors (20% in MSIT; 30% in Stroop; see Fig. 2B for an example) in the ex-post epoch. The distributions of selective units were similar between the two tasks (Fig. 3B).

Approximately 30% of conflict neurons were selective exclusively in either the ex-ante, early (0–1s after button presses) or late (1–2s after button presses) ex-post epochs (Fig. 3C), with some (18%) selective in the ex-ante, early and late ex-post epochs (“extended”). Distributions of conflict signal across time were similar between the MSIT and Stroop tasks (Fig. 3C). We were intrigued by neurons signaling conflict ex post (20% of neurons in both tasks; Fig. 2C–D shows examples), which have not been reported before. This conflict signal, which arises too late to be useful for within-trial cognitive control, was more prominent compared to the one found in the ex-ante epoch in both tasks (15% vs. 20%; χ²(1) = 18.34, p < 0.001, chi-squared test).

Many conflict neurons also signaled errors, surprise, CP, or a conjunction of these variables (Fig. 3D). This multiplexing depended on the timing of conflict signals. The proportion of conflict neurons that multiplexed CP (light green bars) increased significantly towards the end of the trial, when updating would be mostly complete (proportion in the late ex-post epoch vs. that in all other epochs; χ²(1) = 6.86, p = 0.008 for MSIT; χ²(1) = 3.6, p = 0.04 for Stroop, chi-squared test). Consistent with this idea, the group of neurons signaling conflict exclusively in the ex-ante epoch showed the least multiplexing, consistent with a primary role in monitoring conflict during action production (proportion of “pure” conflict neurons active only during the ex-ante epoch vs. those that are active in other epochs; χ²(1) = 4.93, p = 0.03 for MSIT; χ²(1) = 9.36, p = 0.002 for Stroop, chi-squared test).

We next investigated the temporal stability of the multivariate coding patterns for the performance monitoring variables in each task. We trained a decoder with data from all recorded neurons in one epoch and tested it on data from a different epoch. RT were equalized across conditions for this analysis. Error decoders trained on early ex-post data generalized poorly to later epochs, but the ones trained on late ex-post data generalized well into earlier epochs (Fig. S6A–B), suggesting that some neurons represented errors only late in the trial with a possible role in post-error adjustments (33). The multivariate coding patterns for conflict changed substantially to prevent generalization between the ex-post and ex-ante epochs (Fig. S6C–E; green horizontal lines overlapped with orange and blue only minimally), demonstrating that the MFC encoded these two types of conflict information with different populations of neurons. The magnitude of CP (quantized to allow construction of pseudo-populations) could also be decoded from population activity trial-by-trial. Decoders trained to decode CP before updating before updating (constructed with baseline spike counts) generalized well to decode CP after updating (using ex-post spike counts), and vice versa, suggesting that CP representation was stably maintained (Fig. S7A–F). Representation of previous trial conflict (indicator; “1” denotes previous trial had conflict) was relatively weak (Fig. S8A–C; < 60% decoding accuracy), consistent with the model comparison results where previous conflict alone was a poor predictor of RT compared to estimated CP (Table S2 and S3). CP neurons demonstrated the greatest degree of multiplexing (Fig. 3F). Only 18% of these neurons signaled CP exclusively, with the remainder multiplexing information about estimated CP on the last trial, conflict, conflict surprise, or conjunction of these variables. CP neurons changed their firing rates ex post by an amount commensurate with the numerical change of conflict probability between adjacent trials (Fig. 3G, p < 0.001, t test against zero. Mean correlations in Simon, Flanker and Stroop are 0.036, 0.036, 0.045, respectively), reflecting a neural “updating” process. Although for some neurons the updating process started in the ex-ante epoch, the majority started in the ex-post epoch and continued well into the ex-post period (Fig. S3C–E shows time courses).

CP neurons differed qualitatively from those of other recorded neurons. First, their trial-by-trial baseline spike rates (treated as a time series) had higher self-similarity than all other types of neurons studied (Fig. S4A–B; self-similarity quantified by α values from the Detrended Fluctuation Analysis. Fig.S4C–F show DFA analysis of two example neurons). Second, the extracellular spikes generated by these neurons had significantly narrower width compared to other neurons (Fig. S4G–H right panels; more broadly, DFA alpha is negatively correlated with spike width, shown in Fig. S4G–H left panels).

Representational geometry of conflict within a single task

We next investigated the representational geometry of conflict in the high dimensional neural state space formed by all recorded neurons. This is possible because different types of cognitive conflict coexist within MSIT. We first tested whether the four MSIT conflict conditions (si, fl, sf, non-conflict) are separable in the neural state space. A “coding dimension” was defined as the high dimensional vector flanked by the means of the “sf” and “none” trials (Fig. 4A, broken lines; see Methods). Held-out single-trial data projected onto this coding dimension allowed a decoder to differentiate with high accuracy between all pairs of conflict conditions in the ex-ante epoch (Fig. 4B, left), and all but one pair (si vs. sf, p = 0.16) in the ex-post epoch (Fig. 4B, right). Notably, si and fl conflict could be differentiated above chance by this coding dimension. Conflict conditions were still separable after equalizing for RT across conditions (Fig. S9C; See Methods for RT equalization), suggesting that the separation was independent of trial difficulty for which RT is a proxy (55). We next investigated whether representations generalized between Simon and Flanker conflict. For each time bin, a coding dimension was constructed by connecting, in the neural state space, the mean of Simon (si+sf) with the mean of non-Simon (fl+none), and a separate one by connecting the Flanker (fl+sf) vs non-Flanker (si+none) means. Held-out single-trial data from either conflict type projected onto the coding dimension constructed using data from another conflict type allowed decoding with high accuracy (Fig. 4C; grey trace, Flanker coding dimension decoding Simon vs. non-Simon; black trace, Simon coding dimension decoding Flanker vs. non-Flanker).

Fig. 4. State-space representation of conflict and conflict probability.

(A) State-space representation of conflict (left, ex-ante; right, ex-post) in MSIT task visualized in PCA space. Dotted line is the vector used to classify pairs of conflict conditions in (B). (B) Decoding accuracy from classification of pairs of conflict conditions in MSIT. (C) Coding dimensions invariant between Simon and Flanker conflict. At each time point, a decoder is trained on Simon vs. non-Simon and tested on held out Flanker vs. non-Flanker trials (black), and vice-versa (grey). (D) Conflict representations are compositional. Decoders trained on one edge of the parallelogram were able to differentiate between conditions along the opposite parallel edge (orange and blue edges shown in A, respectively, shown on left and right). Dotted lines show 97.5^th percentile of the null distribution. (E-G) State-space representation of conflict probability in MSIT and Stroop, visualized in PCA space. Green dots mark baseline start, the two cyan squares delineate the range of stimulus onsets, blue dots mark button press and red dots mark end of trial. Trials are aligned to button press. Color fades as the trial progresses. Numbers signify percentage of variance explained by each principal component (PC). *p < 0.05, ** p < 0.01, *** p < 0.001, n.s., not significant (p > 0.05). MP=mid point. BP=button press. Stim=Stim onset.

We next tested whether the representation of conflict was compositional. If true, relative to the mean of “none” trials, the “sf” representation should be located where the linear vector sum of Simon (“si”) and Flanker (“fl”) trials lands, forming a parallelogram with the none-sf axis at its diagonal (Fig. 4A). Testing this with a decoding approach, a decoder trained to differentiate between the two classes connected by one edge of this parallelogram should be able to decode the two classes connected by the opposite edge (and vice-versa). Indeed, a decoder trained to differentiate “sf” from “fl” trials, which is simply the vector connecting “sf” and “fl” (blue edge in Fig. 4A), was able to decode “si” from non-conflict trials projected to this axis with above chance performance, and vice versa (Fig. 4D, p < 0.001 for both the ex-ante and ex-post data, permutation test). The same was true for the other pair of edges (Fig. 4D, testing blue edges in Fig. 4A; p < 0.001 for both the ex-ante and ex-post data, permutation test). The parallelism was imperfect because the decoding accuracy, while well above chance, was relatively low (< 70%) compared to within-condition decoding performance (Fig. 4C). Neurons that demonstrated non-linear mixed selectivity for Simon and Flanker conflicts (as measured by the F statistic of the interaction term between Simon and Flanker derived from an ANOVA model) contributed the most to this deviation from parallelism at the population level (Fig. S9F, r = 0.74, p < 0.001, for ex-post data; Fig. S9E, r = 0.75, p < 0.001, for ex-ante data; Spearman’s rank correlation). This representation structure was disrupted on error trials: generalization performance dropped in the ex-ante (Fig. S9D; for both edges, 68% and 61% on correct trials vs. 56% and 47% on error trials) as well as the ex-post epoch (Fig. S9D; for both edges, 55% and 68% on correct trials vs. 51% and 59% on error trials) on error trials.

Representational geometry of conflict probability

Conflict probability representation can be viewed as a state (an initial condition) that is present before stimulus onset and to which the population returns after completing a trial. To test this idea, we binned trials by CP quartiles (4 “levels” were generated as trial labels) for each session and aggregated neuronal data across different sessions to generate pseudo-populations. PCA analysis, performed separately for each type of conflict, revealed that the variability across different CP levels (8–11% of explained variance) was captured mostly by a single axis (PC3s in Fig. 4E–G; green dots mark trial start, red dot trial end), which was orthogonal to time-dependent but condition-independent firing rate changes (captured by PC1s and PC2s, 57–63% of explained variance). We quantified this impression in the full neural state space (not in PCA space). Before stimulus onset (demarcated by green and cyan filled circles in Fig. 4E–G), the neural state evolved with low speed (blue points in Fig. S9G–I). The neural state then changed more quickly after stimulus onset (orange points in Fig. S9G–I; p < 0.001, paired t-test), before eventually returning to a low-speed state that hovered near the starting position (red filled circles in Fig. 4E–G; yellow points in Fig. S9G–I). The distance between the four trajectories was also kept stable across time. A coding dimension in the full neural space (which corresponds to PC3 in Fig. 4E–F), were constructed by connecting the means of neural representations of the first and fourth CP levels. The held-out single-trial data, when projected onto this coding dimension, separated into four levels with their ordering (in projection values) being strongly correlated with the ordering of CP levels (Fig. S9J–L). This ordering is maintained into the baseline period of the next trial (Fig. S9J–L). For single sessions, CP predicted using spike counts from all MFC neurons in the session as regressors were correlated with the true values of CP trial-by-trial (Fig. S15M–N). These analyses in the full neural space confirmed the insights gained from PCA visualization in Fig. 4E–G.

Domain-general performance monitoring signals at the population level

We next investigated whether the geometry of performance monitoring representations supported readout invariant across MSIT and Stroop, while simultaneously allowing robust separation of conditions specific to MSIT. Within MSIT, a geometry can be extracted that supports invariance across types of conflicts while keeping the four conflict conditions separate (Fig. 4A–C). However, it is unclear whether such representation is unique to a single task that required construction of a task set. We thus studied the activity of the same neurons in two behavioral tasks separately performed (Table S1 shows session information). We used demixed PCA (dPCA) (56) to factorize population activity into coding dimensions for performance monitoring variables (error, conflict and conflict probability) and for the task identity. The dPCA provided a principled way to optimize for cross-task decoding and could serve as an existence proof for domain generality. The statistical significance of the dPCA coding dimensions was similarly assessed by out-of-sample decoding. Successful “demixing” should correspond to (near) orthogonality between the performance monitoring and task identity coding dimension.

The dPCA coding dimensions extracted using error and conflict contrasts (Stroop-Simon and Stroop-Flanker separately) each explained 10–21% of variance, supported task-invariant decoding across time and were orthogonal to the task identity dimension (Fig. 5A for error, Fig. 5B for Stroop-Simon, Fig. S10A for Stroop-Flanker conflict decoding over time, and Fig. 5C for conflict decoding restricted in the ex-ante and ex-post epochs separately. For all clusters, p < 0.01, cluster-based permutation tests; clusters with significant decoding performance demarcated by horizontal bars; For error, angle = 92.1°, p=0.92, tau=0.005; for Stoop-Simon conflict, angle = 81.9°, p=0.31, tau=0.04; for Stroop-Flanker conflict, angle = 80.8°, p=0.09, tau=0.06; Kendall’s rank correlation).

Fig. 5. Domain-general representation of performance monitoring signals.

(A) Task-invariant decoding of errors. Bar on the right shows the variance explained by the different dPCA components. Data from the whole trial were used. (B) Task-invariant decoding of conflict. The bar on the right represents variance explained by the different dPCA components (color code see figure legend). Data from the whole trial were used. (C) Separability of conflict conditions along the domain-general conflict axis in both the ex-ante (left) and ex-post epochs (right). The dPCA coding dimension was constructed (separately for each epoch) using Stroop, SF conflict and no conflict trials and supported decoding of Stroop, Simon and Flanker conflicts (“task-invariant”) as well as separation of Simon and Flanker conditions. (D) Task-invariant decoding of conflict probability. The dPCA coding axis was constructed using Stroop and Simon conflict probability (binned by quartiles into four levels) and supported pairwise decoding of conflict probability levels in both tasks. Bar at the bottom shows variance explained of dPCA components. Data from single ROIs were used. (E-F) Relationship between task-invariant single neuron tuning strength of error (E), conflict ex post (F) and the corresponding dPCA weights. Pie charts show the percentages of “task-invariant” neurons (red slice) that had a significant main effect for performance monitoring variable and those that had significant effect only in either MSIT or Stroop (“task-dependent”, blue slice). Scatter plots (left) shows significant correlation between task-invariant coding strength and the corresponding dPCA weights. Y-axis shows correlation of firing rate of a neuron with the given variable, after removing task information by partial correlation (see Methods). *p < 0.05, ** p < 0.01, *** p <= 0.001, n.s., not significant (p > 0.05). MP = mid point. BP=button press. Stim=Stim onset.

The task-invariant conflict coding dimension (extracted by removing the task difference between MSIT sf and Stroop conflict trials and between non-conflict trials in both tasks) was also able to differentiate 5 out of 6 pairs of conflict conditions with high accuracy (60% - 90%) within MSIT in both the ex-ante and ex-post epochs (Fig. 5C; statistics see figure, permutation tests). Similar task-invariant decoding performance were obtained when restricting to only trials with similar RTs across conditions, suggesting again that task-invariant representations of error and conflict was not due to subjective difficulty (Fig. S10B–E), for which RT is a proxy (55).

Similarly, the coding dimensions for Stroop-Simon conflict probability (Fig. 5D and Fig. S10G) and Stroop-Flanker conflict probability (Fig. S10F, H) each explained 27–35% of variance, supported task-invariant decoding and were orthogonal to the task identity dimension (p > 0.05, Kendall’s rank correlation). Importantly, this task generalizability did not compromise the capacity of this coding dimension to separate different levels of CP within Stroop or MSIT (Fig. 5D, Fig. S10F–H).

As a control analysis, we also examined whether a decoder trained on a single task would generalize to the other task. These “within-task” coding dimensions supported decoding of data from the other task with high accuracy, albeit with slightly lower performance than the dPCA coding dimensions that were optimized for cross-task decoding (Fig. S12A–F for decoding performance, weight correlation between tasks). This is expected given the robust correlation between the weights of these within-task coding dimensions (scatters in Fig. S12G–M). This correlation was confirmed by the fact that the angles between the two within-task coding dimensions were significantly smaller than the null distribution (which approximately equaled 90°; inset histograms in Fig. S12G–M). The angle between the task-invariant coding dimensions optimized by dPCA and the within-task dimensions trained with either Stroop or MSIT data alone were similar (angular “equidistant”; angles reported in insets, Fig. S12G–M). The optimization performed by dPCA can thus be understood geometrically: it sought a coding dimension that is angularly “centered” between each of the within-task dimensions trained using data from one task only. Task-invariant representations for all performance monitoring variables can be found using simultaneously recorded data at the single-session level in subjects with enough neurons (Fig. S15), highlighting that it is the same population of neurons that subserve such a geometry.

Subjects responded more slowly on the trials that followed error trials in both tasks, demonstrating robust post-error slowing (PES: 40±1ms and 44±1ms in Stroop and MSIT, respectively; Fig. S8D). However, this trial-by-trial measure of PES was not significantly correlated with spike rates (on the error trials) of error neurons in either task individually, or for error neurons that signaled errors in both tasks (definition of “task-invariant” see methods. Fig. S8E).

Domain-general performance monitoring signals at the single-neuron level

We sought to understand how tuning profiles of single neurons contributed to the population geometry that simultaneously allowed task-invariant and task-specific readouts. While some neurons encoded error, conflict, and CP in a task-invariant manner (Fig. 2, Fig. 3), others encoded these variables in only one task. The extent to which single-neuron tuning depended on the task was assessed using partial correlations (“task-invariant turning strength”; higher correlation with variable of interest after controlling for task variable means higher task invariance). According to this test, neurons that had significant correlation were labelled “task-invariant” (65–83%), and those with insignificant cross-task correlation but significant correlation within either task were labelled “task-dependent” (17–35%, Fig. 5E–F, Fig. S13A–C, red and cyan slices, respectively). Across all neurons, the dPCA weight assigned to each neuron was strongly correlated with the neuron’s task-invariant tuning strength (scatter plots in Fig. 5E–F, Fig. S13A–C; p < 0.001 for all panels, Spearman rank correlation). Both the task-invariant and the task-dependent neurons were assigned significant larger weights compared with non-selective (“other”) neurons (Fig. 5E–F, Fig. S13A–C, dot density plots). Similar conclusions hold when using a permutation-based feature importance measure instead of the dPCA weights (Fig. S14; see Methods for details). Importantly, the distributions of dPCA weights or feature importance (probability density shown insets in Fig. 5E–F, Fig. S13A–C, Fig. S14A–E) across neurons, with many showing non-zero weights, suggested that the task-invariance coding was not driven by few neurons but instead reflected population activity.

Neurons with higher self-similarity for baseline spike counts contributed more to the task-invariant coding dimension of conflict probability, after controlling for single-neuron coding strength (partial correlation between absolute values of dPCA weights and DFA α values; r = 0.16, p = 0.003 for Stroop-Simon conflict probability; r = 0.20, p < 0.001 for Stroop-Flanker conflict probability).

Comparison between the dACC and the pre-SMA

The distributions of neuronal selectivity were similar in dACC and pre-SMA (Fig. S3A–B). Both areas contained similar proportions of task-invariant and task-dependent neurons. Both areas independently supported compositional conflict coding and domain-general readouts for error (Fig. S11A–B), conflict (Fig. S11C–F), and conflict probability (Fig. S10G–J). However, there were three notable differences between the two areas. First, the temporal profiles of decoding performance for error, conflict and conflict probability were similar between the areas but decoding accuracy in pre-SMA was consistently higher (Fig. S5A–E). Second, the task-invariant error response appeared earlier in pre-SMA than in dACC (Δ_latency = 0.55s for Stroop and 0.5s for MSIT), consistent with our previous report in the Stroop task (33). Third, ex-ante conflict information was first available in dACC, followed by pre-SMA (Fig. 3E; median difference = 138ms; p < 0.001, Wilcoxon rank sum test; single-trial spike train latency). Third, by contrast, ex-post conflict information was available first in pre-SMA, followed by dACC (Fig. 3E; median difference = 161ms; p = 0.002, Wilcoxon rank sum test).

Discussion

Within the MFC, some neurons encoded error, conflict and conflict probability in a task-invariant way, some encoded these variables exclusively in one task, and yet some more multiplexed domain/task information to varying degrees. They were intermixed at similar anatomical locations and demonstrated non-linear “mixed selectivity” (47, 48) for task identity and performance monitoring variables. Such complexity at the single-neuron level precludes a simplistic interpretation of domain generality. By contrast, population activity can be factorized into a task dimension and a task-invariant dimension that were, in most cases, orthogonal to each other. The geometry of MFC population representation allows simple linear decoders to read out performance monitoring variables with high accuracy (>80%) in both tasks, and simultaneously to differentiate different types of conflict or different levels of estimated conflict probability within a task. Importantly, it is the same group of neurons that gave rise to this geometry. This finding contrasts with neuroimaging studies that either report domain-specific and domain-general conflict signals encoded by distinct groups of voxels (57, 58), or an absence of domain-general conflict signals (59) within the MFC.

Several studies have proposed that the lateral PFC is topographically organized to subserve cognitive control, with more abstract processing engaging the anterior regions (1–3, 60, 61). Unlike in the LFPC, domain-general and domain-specific neurons were intermixed within the MFC. The representational geometry we report here is well suited to provide performance monitoring signals to these subregions: downstream neurons within these LPFC regions can select performance monitoring information at different degrees of abstraction by adjusting connection weights, similar to input selection mechanisms described in the PFC (62). Curiously, we did not observe a prominent difference between the pre-SMA and the dACC in the degree of domain generality of performance monitoring, which may be related to the fact these two areas are highly interconnected.

Domain-general error signals

A key component of performance monitoring and metacognitive judgement is the ability to self-monitor errors without relying on external feedback (4, 37, 40, 41, 63, 64). A subset of neurons not only signaled error in the Stroop task (as previously reported in (33)) but also in MSIT. The error signal is thus domain-general, that is, abstracted away from the sensory and motor details as well as the types of response conflicts encountered across the two tasks (Fig. 2B). At the population level, these domain-general error neurons enabled trial-by-trial readout of self-monitored errors with > 90% accuracy equally across tasks (Fig. 5A, E). Compatible with earlier results (33), the activity of neither task-specific nor task-general error neurons directly predicted the extent of PES. This result is consistent with the evaluative roles of MFC error signals and suggests that the control process may lie outside of the MFC. Given the fMRI-BOLD finding that the MFC is a domain-general substrate for metacognition (65), an interesting open question is whether the same neural mechanisms we describe here support metacognitive judgement across different domains, such as perceptual or memory confidence.

Domain-specific performance monitoring

The causes of conflict and errors in the two tasks differs: distraction by the prepotent tendency to read in the Stroop task, and distraction by location of target number (Simon) or by numbers flanking the target (Flanker) in the MSIT. Such performance perturbations call for specific compensatory mechanisms, such as suppressing attention to task-irrelevant stimulus dimensions. Consistent with this requirement, a subset of neurons signaled errors, conflict and conflict probability exclusively in one task, giving rise to a task identity dimension that supported robust decoding of which task the performance disturbance occurred in (>90% accuracy). This provides the domain-specific information about the sources of performance disturbances for cognitive control, consistent with the reported role of MFC neurons in credit assignment (16). The existence of task-specific neurons also suggests that the performance monitoring circuitry can be rapidly and flexibly reconfigured in different tasks to subserve different task sets (66, 67), consistent with the rapid reconfiguration of functional connectivity among cognitive control networks to enable novel task performance (68).

Compositionality of conflict representation

Compositionality of conflict representation can be formulated as a problem of generalization: if Simon and Flanker conflict are linearly additive, decoders trained to identify the presence of only Simon or Flanker conflict should continue to do so when both types of conflict are present. We found that this was the case, with the neural state approximately equal to the vector sum of the two neural states when the two types of conflict are present individually. The (approximate) factorization of conflict representation is important for both domain-specific and domain-general adaptation: when different types of conflict occur simultaneously and the representation can be factorized, downstream processes responsible for resolving each type of conflict can all be initiated. On the other hand, domain-general processes can also read out the representation as a sum and initiate domain-general adaptations.

Estimating control demand enabled by ex-post conflict neurons

Our model for conflict probability estimation predicts that conflict should be signaled twice: once during response competition (ex ante), and again after the action has been committed (ex post). While the former, predicted by conflict monitoring theory (13, 69), provides transitory metacognitive evidence of conflict and is important for recruiting within-trial cognitive control (69), the latter provides a stable “indicator” of whether conflict occurs or not. Both signals arise independent of external feedback, thus qualifying as correlates of metacognitive self-monitoring (63, 64). One interpretation for the ex-post signals (conflict or error), as proposed by connectionist models of conflict monitoring, is that they reflect conflict between the committed response and continuing stimulus processing (69, 70), which should also activate the ex-ante conflict neurons. However, our data demonstrated that these two types of conflict signals were encoded by separate neurons and their multivariate coding patterns differed substantially enough to prevent generalization (Fig. S6C–E).

There is significant overlap between error neurons and ex-post conflict neurons. Common coding dimensions that simultaneously decode both error and conflict do exist, though the decoding accuracy for conflict is significantly lower than for error (Fig. S9A–B). In macaque SEF, ex-post activation is found after non-cancelled and successfully cancelled saccades (41). These ex-post evaluative signals may reflect a common process that compares a corollary discharge signal (conveying the actual state of action selection/cognitive control) with cognitive control state predicted by “forward models” (71–73) and may underlie sense of agency (74). Future work is needed to test this new hypothesis.

The neurons that reported conflict probability changed their firing rates trial-by-trial, and this “updating” in firing rates occurred primarily upon commitment of an action. The distinct functional properties of conflict probability neurons, i.e. significantly narrower extracellular spike waveforms and higher self-similarity of baseline spike counts (Fig. S4C–H), suggest that they may be interneurons with strong recurrent connectivity, consistent with a prior report where dACC neurons that encode past outcomes have narrower extracellular waveforms (75). At the population level, these single-neuron properties contribute to the formation of a task-invariant line attractor dynamics. Computational modelling demonstrates the importance of inhibitory interneurons in maintaining information in working memory, which occurs on the scale of several seconds (76). Similar circuit-level mechanisms could provide a basis for retaining the history of performance monitoring and reward, which is on the scale of several minutes. These conflict probability neurons might thus provide a neural substrate for proactive control and learning the value of control, both of which requires stable maintenance of learned information (13, 51). The trade-off between flexible updating and stable maintenance of performance monitoring information remains an open question.

Data and materials availability:

Data needed to reproduce results have been deposited at OSF (77).