Forecasting daily Covid-19 cases in the world with a hybrid ARIMA and neural network model

Abstract

The use of models to predict disease cases is common in epidemiology and related areas, in the context of Covid-19, both ARIMA and Neural Network models can be applied for purposes of optimized resource management, so the aim of this study is to capture the linear and non-linear structures of daily Covid-19 cases in the world by using a hybrid forecasting model. In summary, the proposed hybrid system methodology consists of two steps. In the first step, an ARIMA model is used to analyze the linear part of the problem. In the second step, a neural network model is developed to model the residuals of the ARIMA model, which would be the non-linear part of it. The neural network model was superior to the ARIMA when considering the capture of weekly seasonality and in two weeks, the combination of models with the capture of seasonality in two weeks provided a mixed model with good error metrics, that allows actions to be premeditated with greater certainty, such as increasing the number of nurses in a location, or the acceleration of vaccination campaigns to diminish a possible increase in the number of cases.

1. Introduction

Covid-19 (Sars-CoV-2), was already previously present in nature, however, until now due to a mutation in its Spike protein, the virus has exponentially increased its transmissibility [1], being spread all over the world. In general, the incubation period for the virus is 1 to 14 days. In addition to personal protective measures, such as social distancing and the use of masks and hand sanitizers, it is also recommended that the infected, or people that could possibly be infected, avoid contact with pets, due to the possibility of human–animal transmission, given as a suggestion that some animals such as cats may act like intermediaries for the virus [2].

Despite the symptomatic cases of Covid-19, there are also asymptomatic cases, which can also contaminate their surroundings, even though there are no symptoms, they also pose risks for those who come into contact with these individuals [3]. In studies to understand the historical behavior of the pandemic such as in [4] the historical process in which the World Health Organization (WHO) initially identified a cluster of pneumonia cases in China from December 31 in the city of Wuhan is minutiously detailed and it gets to the point from November 2020 to January 2021 when there was growth concerning the new variants of Sars-CoV-2.

The use of models to predict disease cases is very common in epidemiology and related areas, in the context of Covid-19, some works chose to investigate risk prediction deciding to work with Neural Network models and X-ray images in the field of computer vision like the works of [5], [6], the main contribution of this paper is to discuss and present the use of hybrid modeling to predict the number of cases in order to help planning and resource optimization. [7] classified the scenarios of main application of AI in the Covid-19 pandemic in three main fields, where works that deal with computer vision and image classification are classified in the field of early detection and diagnosis of infection, the field of potential treatment, containing studies and applications that deal with the use of AI for predicting effective and safe drugs, and the field of outbreak and prediction of virus spread, with studies and applications of forecasting models, which is also the subject of this work.

In the context of Covid-19 both ARIMA and Neural Network models can be applied for purposes of optimized resource management, such as purchasing masks, ICU beds or to guide the adoption of public policies, however there may be limitations in applying only one of these models separately [8], while reviews on Covid-19 forecasting literature such as [9] suggests that studies addressing the development of hybrid approaches to forecast the pandemic should be proposed, the literature review of [10] revealed that studies based on the conventional machine learning models such as Support Vector Machine, Random Forest and Multilayer Perceptron Neural Networks showed poor performance while implemented standalone, even though the authors identify these models as the mostly used in the pandemic, pointing that the performance appeared to be better for hybrid models coupled with optimization techniques.

Works about hybrid AI modeling in the context of the Sars-CoV-2 pandemic were also traced by reviews such as [11], that showed that this method was also used in studies of the field of computer vision with X-ray images, but also traces one study that used a hybrid machine learning model for time series forecasting with data from China, apart from that the authors also identify CNN, RF, ResNet and SVM approaches as the most used against Covid-19, and found that from 264 studies 84% used either computational tomography or X-ray images. In this context the aim of this study is to capture the linear and non-linear structures of daily Covid-19 cases in the world, using a classical approach proposed by [8], to evaluate the construction of a hybrid model for forecasting daily Covid-19 cases around the world and discussing its use to help the management of resources and action-taking in the healthcare sector.

2. Methodology

The database is publicly available and it is owned by the organization Our World In Data (OWID) [12], containing information on the number of daily cases in several countries around the world, the database is real-time updated and the information is collected from various government and press agencies and it was used to build the time series of daily Covid-19 cases in the world until April 25th 2021, the R software (Version 4.0.3) was used to build forecast models and database processing.

2.1. Forecasting models

A hybrid model based on [8], using a multilayer perceptron neural network (MLP) and an ARIMA model was constructed in order to make predictions for the daily number of Covid-19 infections in the world. ARIMA models and MLP Neural Network structures were initially adjusted, then the models with the best error metrics were used to build the hybrid model, the error metrics used to evaluate the models are the MASE (Mean Absolute Scaled Error), the SMAPE (Symmetric Mean Absolute Percentage Error) and the R2 (Coefficient Of Determination).

The MASE is considered by some authors the best error measure available for predictions [13], since it is less sensitive to outliers, when MASE ¡ 1, on average, the errors are smaller than a simple naïve model. The SMAPE was used as an alternative to the MAPE (Mean Absolute Percentage Error), since problems that could arise from small values are less severe for the SMAPE. The coefficient of determination R2 close to 1 indicates an almost perfect relationship between the fitted model and the data, while an R2 close to 0 implies that just fitting the mean is similar to the fitted model [14].

2.2. ARIMA model

There is great utility in using the Arima model to guide disease management so that the effects of the intervention on the disease studied can be predicted. It is stated by [15] that “Clinical studies have benefited from the use of these techniques, given the great applicability of the ARIMA model”. In this work, we chose the Arima model to predict the number of daily cases of Covid-19 in the world in the year 2021, for such, since we dealt with real-time updated data, a model was fitted in 4 time windows of 7 days, the model that presented the best average MASE was considered as the best model for later prediction of cases. The study by [15] briefly describes the ARIMA model and also suggests that “since the periodic structures of infectious disease epidemics change over time. In this case, it is suggested to use short periods of time segment to analyze the effects of each segment”. In [16] this technique is used, the paper also mentions a few studies that used time intervals between epidemics in Japan.

Although [8] summarizes the ARIMA model, the model is also detailed in other studies such as [17], where the forecasting process is mathematically described, however the Box–Jenkins methodology used to adjust the Arima(p,d,q) model and the autoregressive models ARMA, ARIMA, SARIMA and ARMAX, may be found with a more developed definition in studies like the one developed by [18], which also defines the autoregressive model of order p AR(P), the process of moving averages MA(q) of order q, the order d in which the process is stationary and SARIMA models (p,d,q)x(P,D,Q)[m] where m is the seasonal period of the model, the model parameters and the Box–Jenkins methodology can also be found briefly in [19].

$y_t^{\prime }$ is the differenced series in the full ARIMA(p,d,q) model, which may be written as:

$$y_t^{\prime }=c+{\varphi }_1{y}_{t-1}^{\prime }+\cdots +{\varphi }_p{y}_{t-p}^{\prime }+{\theta }_1{\varepsilon }_{t-1}+\cdots +{\theta }_q{\varepsilon }_{t-q}+{\varepsilon }_t$$ (1)

For the analysis we used the auto.arima() function of R, its entire methodology, in addition to being available on R’s CRAN, is well explained in chapter 8 in [20], for the seasonal part, for example, the work in chapter 2.1 demonstrates that for daily cases “If the frequency of observations is greater than once a week, there is usually more than one way to deal with the frequency. For example, data with daily observations can have a weekly seasonality (frequency = 7) or an annual seasonality (frequency = 365.25)”. In addition the include.drift argument, which was used in our practical part is also explained in chapter 8.7, the drift method is defined in chapter 3.1 and is a variation of the naïve method allowing forecasts to grow or decrease over time, the amount of change over time (drift) is defined as the average of the changes seen in historical data.

2.3. MLP neural networks

Neural networks are flexible computing structures to model a wide range of nonlinear problems, a significant advantage of neural network models over other nonlinear models is that neural networks are universal approximators that can approximate a large class of functions with a high degree of accuracy. It is further stated by [8] that the single hidden layer feedforward network is the most widely used form of modeling for forecasting time series, this affirmative is one of the reasons we used our neural network models with only one layer. In addition, the author of the mlp() function that we use in the R software to adjust the model, mentions in his work [21] that the most commonly used form of neural networks for prediction is the MLP neural network and that the one step ahead prediction is calculated using inputs that are lagged observations of the time series or other explanatory variables.

Mathematically the form of our ${\hat{y}}_{t+1}$ forecasts are represented in Eq. (2), where $I$ is the number of inputs $p_i$ of the $NN$, $H$ is the number of hidden nodes in the network, $g(.)$ is a non-linear transfer function, ${\beta }_0$ and ${\gamma }_{0i}$ are the biases of each neuron, $w=(\beta ,\gamma )$ are the network weights with $\beta$ for the output and $\gamma$ for the hidden layers:

$${\hat{y}}_{t+1}={\beta }_0+\sum _{h=1}^H{\beta }_{h}g\left({\gamma }_{0i}+\sum _{i=1}^I{\gamma }_{hi}{p}_i\right)$$ (2)

One of the concerns with the definition of neural network models was the structure of the model, as they would later be compared with Arima models and used to generate a mixed model, the inputs were built based on the statements given by [22] that the number of neurons in the input layer indicates the maximum cycle size or seasonality that the model can detect, a model of six neurons in the input layer could therefore capture a period seasonality equal to or less than six, in this case the models with similar seasonality will be compared in ARIMA and MLP, in addition the order of differences of the MLP models that capture seasonality were built based on the D parameter of the SARIMA models, the best MLP will be used to build the mixed model.

2.4. Hybrid MLP–ARIMA model

Proposed by [8] as a solution to the possibility that the approximation of ARIMA models to complex nonlinear problems does not get to be adequate enough and the use of neural networks when used to model linear problems can produce mixed results. In general, it is difficult to fully know the characteristics of the data in a real problem, the hybrid methodology proposed by Zhang has linear and non-linear modeling capabilities, it can be a good strategy for practical use, when combining different models, different aspects can be captured. In summary, the proposed hybrid system methodology consists of two steps. In the first step, an ARIMA model is used to analyze the linear part of the problem. In the second step, a neural network model is developed to model the residuals of the ARIMA model, which would be the non-linear part of it.

Since the ARIMA model cannot capture the nonlinear structure of the data, the residuals from the linear model will contain information about nonlinearity. The Neural network’s results can be used as residual predictions for the ARIMA model. The hybrid model uses the unique capability and strength of the ARIMA Model and the neural network model in determining different patterns. Therefore, according to Zhang, it may be advantageous to model linear and non-linear patterns separately using different models and then combine the predictions to improve overall modeling and prediction performance.

Basically the predictions can be summarized with the following equation, where ${\hat{L}}_t$ is the linear part and ${\hat{N}}_t$ is the non-linear part of the forecast:

$${\hat{y}}_t={\hat{L}}_t+{\hat{N}}_t$$ (3)

The ARIMA and MLP models chosen were those with the lowest MASE, with predictions for the short, medium and long time lengths (respectively 7, 14 and 28 days) made considering the daily cases until April 25, 2021. The prediction of the linear part was made using the ARIMA model, the MLP neural network was trained on the residuals of the ARIMA model to predict the non-linear part of our time-series, finally our predicted variable would then be the linear part of the model plus the non-linear part, just like in Eq. (3).

3. Results

For the prediction models adjusted to the daily number of Covid-19 cases in the world (Table 1), the lesser computationally intensive model in all considered time periods was the ARIMA model both without and with seasonality being considered. Although the MLP(1,5.1) model without capturing the seasonal effect also required a higher level of computational power in comparison to the adjusted ARIMA, the MLP(7,5,1), MLP (14,5, 1) and hybrid MLP(14,5,1)-Arima(2,0,4)(0,1,2)[14] were the most computationally intensive models.

Table 1.

Error measures of the adjusted forecasting models.

Forecast horizon	Short term(7 days)			Medium term(14 days)			Long term(28 days)
Models	MASE	SMAPE	R2	MASE	SMAPE	R2	MASE	SMAPE	R2
Arima(2,1,2)a	0.8147	0.0666	0.3655	0.7893	0.0663	0.5368	1.3533	0.1553	−0.1938
Arima(2,0,3)(0,1,2)[7]a	0.6033	0.0508	0.7426	0.6122	0.0506	0.7061	1.4004	0.1640	−0.2233
Arima(2,0,4)(0,1,2)[14]a	0.5441	0.0453	0.7113	0.5179	0.0439	0.7593	1.2644	0.1467	0.0401
MLP(1,5,1)	1.2615	0.1073	−0.1680	1.4714	0.1114	−1.0805	1.6767	0.1609	−1.0199
MLP(7,5,1)	0.4250	0.0355	0.8442	0.8180	0.0655	0.5554	1.5633	0.1887	−0.3784
MLP(14,5,1)	0.3584	0.0302	0.8851	0.3181	0.0267	0.9098	1.0262	0.1182	0.2815
MLP(14,5,1)Arima(2,0,4)(0,1,2)[14]a	0.2904	0.0236	0.9192	1.4191	0.1101	−0.3109	0.5865	0.0710	0.7596

^aWith the drift technique.

When considering a short term forecast horizon (7 days) the best models were the ones which considered a seasonal effect of 14 days, the Arima(2,0,4)(0,1,2)[14] and the MLP(14,5,1) neural network had the best MASE and SMAPE error measures. In prediction horizon of medium (14 days) and long (28 days) term the behavior was similar, the best models were the ARIMA and the MLP neural network with a seasonality of 14 days, even though in long time forecast horizons the error measure MASE was higher than 1 in both models by using the hybrid MLP-ARIMA model in these 28 days prediction horizon the error measures improved, and the MASE was way lower in short time term forecasts with the mixed model.

For medium term forecasts, despite the good performance of the Arima(2,0,4)(0,1,2)[14] and MLP(14,5,1) models in the error metrics, the combination of the models generated mixed results, there was not a good capture of the linear and non-linear part of the models resulting in a high value for the MASE statistic in the hybrid MLP(14,5,1)-Arima(2,0,4) (0,1,2)[14] model, the R2 measure had a negative value, while the SMAPE was one of the highest recorded in comparison to the other ARIMA and MLP fitted models, only inferior to the MLP(1,5,1) model without capturing seasonality.

4. Discussion

It is important to point out that database corrections can generate changes in error measures, there are corrections made to information prior to April 25th for example, this changed some error measures, some for less and some for more, which may reveal a limitation of the work, even though there is a slight degree of instability in all models because we are dealing with real-time updated data and already started with a great amount of data in the midst of the pandemic, which differs our work from some that also used from hybrid methodologies such as [23] that proposed a hybrid methodology using a polynomial neural network (PNN) with corrective feedback to forecast in early stage epidemic, but did not deal with constant updates in the data. In the database corrections throughout our work the ARIMA and MLP models calculated with the functions in R kept their structures, revealing that the changes in the database were not enough to change the structure of the models.

The SMAPE measure proved to be more resilient to forecast errors, hence the importance of using it with the support of MASE and the R2 coefficient, for the mixed model MLP(14,5,1)-Arima(2,0,4)(0,1,2)[14] in short-term forecasts the use of the three error metrics demonstrate that the MASE was adequate for being close to 0 and much below 1, being the model therefore better than a simple naïve, the R2 coefficient was close to 1, so the model fit was quite good, then we can go on to analyze the SMAPE, because despite being more resistant to errors, its value was low, even after analyzing the support error metrics.

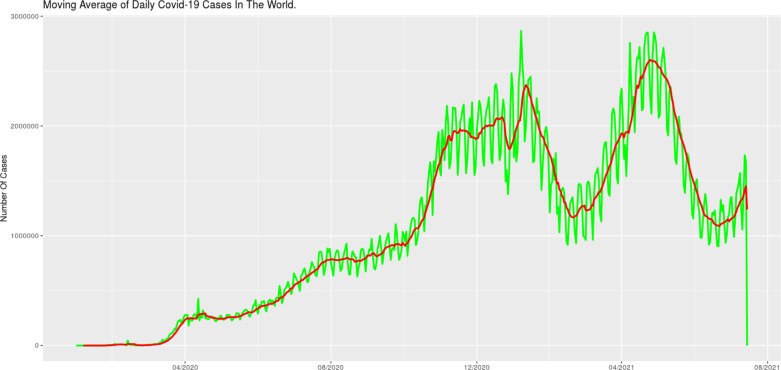
The role of prediction models in the management of Covid-19 would be to create a preparation to deal with the behavior of daily cases of the disease in a specific location, and to forecast the consequence of adopted measures, considering the world in (Fig. 1), with the use of models considering the use of each with its specificity or need, ARIMA could be used in cases where a low amount of computational power is needed, but even if its error metrics are inferior to neural network or mixed models, ARIMA allows for planning for small health units in the short and/or medium term.

Fig. 1.

Moving average of daily cases of Covid-19 in the world.

Among the most computationally intensive models, the MLP(14,5,1) should be considered for planning actions that should be taken for the medium term planning, and the mixed for short and long term planning, in which the level of preparation to deal with an atypical situation in the health sector is higher, by capturing the two natures (linear and nonlinear) the mixed model allows actions to be premeditated with greater certainty, such as increasing the number of nurses in a location, or the acceleration of vaccination campaigns to diminish a possible increase in cases.

5. Conclusion

The ARIMA models proved to be less computationally intensive compared to neural networks and the hybrid model, when there is no capture of the seasonal effect, the ARIMA model was better than the MLP, both in terms of computational performance and error metrics, however, as expected, the neural network model was superior to the ARIMA when considering the capture of weekly seasonality and in two weeks, the combination of models with the capture of seasonality in two weeks provided a mixed model with good error metrics.

The use of models should therefore be considered to assist in decision-making and in short, medium and long-term planning, representing a greater use for the preparation than an objective forecast, mainly due to the dynamic update character of the data and its corrections like [24] that also cited the lack of accurate information in the beginning of the pandemic as a problem, the important thing is to know whether the trend in the coming days will be a growth or a decrease in the daily number of cases, to then guide decision making, in fact the models that obtained a MASE ¡ 1 can be considered for this, being the MLP(14,5,1)-Arima(2,0.4)(0,1,2)[14] model a good option for short and long-term planning and the MLP(14,5,1) for medium-term planning.

It is also important to point out that there are a few limitations in this work, such as the heterogeneity which is characteristic of the data, since we dealt with data from all over the world, the paper also does not consider the impact caused by the great number of variants of Covid-19, therefore not capturing its effect, so the usability of the model built in this work may not be ideal, but when used in certain controlled conditions this technique may bring up good results for longer forecast horizons.

While some state of art works conducted in the Sars-CoV-2 pandemic have not focused mainly in predicting the random component of Covid-19 data, but also dealt with real-time updated data like [25] that proposed a model that showed accuracy even after 3 weeks working with data, there are still plenty of possibilities to be explored in this field and future research should be conducted with the use of hybrid methodologies and support of previous studies that proposed deep learning or classical statistical models, to evaluate the impact of forecasting in controlled conditions.

CRediT authorship contribution statement

Lucas Rabelo de Araújo Morais: Methodology, Writing – original draft, Visualization, Investigation, Writing – review & editing. Gecynalda Soares da Silva Gomes: Supervision, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.