Abstract
Outbreaks of an endemic infectious disease can occur when the disease is introduced into a highly susceptible subpopulation or when the disease enters a network of connected individuals. For example, significant HIV outbreaks among people who inject drugs have occurred in at least half a dozen U.S. states in recent years. This motivates the current study: how can limited testing resources be allocated across geographic regions to rapidly detect outbreaks of an endemic infectious disease? We develop an adaptive sampling algorithm that uses profile likelihood to estimate the distribution of the number of positive tests that would occur for each location in a future time period if that location were sampled. Sampling is performed in the location with the highest estimated probability of triggering an outbreak alarm in the next time period. The alarm function is determined by a semiparametric likelihood ratio test. We compare the profile likelihood sampling (PLS) method numerically to uniform random sampling (URS) and Thompson sampling (TS). TS was worse than URS when the outbreak occurred in a location with lower initial prevalence than other locations. PLS had lower time to outbreak detection than TS in some but not all scenarios, but was always better than URS even when the outbreak occurred in a location with a lower initial prevalence than other locations. PLS provides an effective and reliable method for rapidly detecting endemic disease outbreaks that is robust to this uncertainty.
Keywords: HIV, Endemic disease, Surveillance, Adaptive sampling, Quickest change detection, Profile likelihood
1 |. INTRODUCTION
For many endemic infectious diseases that are present at a low level in a population, outbreaks with much higher incidence can occur when the disease is introduced into a highly susceptible subpopulation or when the disease enters a network of individuals who have close contact. This has occurred, for example, with HIV among people who inject drugs (PWID) in the United States (U.S.). Since an outbreak of HIV among PWID in Scott County, Indiana1 in 2014–2015, at least a half a dozen similar outbreaks have occurred across the U.S. in Cincinnati, Ohio and Northern Kentucky2; Lawrence and Lowell, Massachusetts3; several counties in West Virginia4; North Seattle, Washington5; and the Overtown neighborhood of Miami, Florida.6 Many of these outbreaks have been driven by risky behaviors among PWID. Earlier detection of these outbreaks could greatly reduce their impact.7
In the wake of the initial HIV outbreak in Indiana, the Centers for Disease Control and Prevention (CDC) developed a list of 220 counties in the U.S. deemed at high risk of outbreaks of HIV (and other diseases such as hepatitis C).8 However, some of the subsequent outbreaks (in Washington, Massachusetts, and Florida) occurred outside of the counties considered at high risk by the CDC. This suggests that the ability to quickly detect and stop these outbreaks has not been sufficient. Although the U.S. has a system of both passive and active surveillance for HIV, resource constraints do not allow for regular, widespread HIV testing in all communities at risk. Furthermore, given the low prevalence of HIV in the general U.S. population, it is not clear that comprehensive testing efforts such as those in heavily affected sub-Saharan African countries are warranted here.
Mobile HIV testing services such as those provided by the AIDS Healthcare Foundation9, Project UJIMA10, and numerous health organizations provide the opportunity to quickly re-allocate testing capacity across different geographic locations in response to new data. Such clinics typically visit a relatively small number of locations in a city or county (e.g., a street corner, neighborhood, or zip code, selected for accessibility by at-risk individuals) on a recurring basis. An estimated 2,000 mobile clinics in the U.S. provide up to 6.5 million visits annually, with services that include testing for HIV and a range of endemic diseases.11 Here we focus on adaptively locating a single mobile HIV testing unit that serves a city, county, or state. The CDC risk model prioritizes counties but it is a static model that does not adaptively re-distribute testing resources as new data is collected in real time.
Surveillance for endemic diseases (e.g., HIV, hepatitis B, hepatitis C, and various sexually transmitted infections) is fundamentally different from detecting a disease for which we expect no cases (e.g., anthrax, smallpox) because we expect to see some endemic cases, and thus we must model how the disease incidence changes over time; in contrast, for diseases such as smallpox, the detection of a single case would trigger an alarm.
Previous work has suggested using Thompson sampling to choose between testing locations to maximize yield of previously undiagnosed cases of HIV infection in a local community.12 Thompson sampling is a Bayesian method that dynamically creates a belief distribution about the probability of finding new cases in each location, then randomly selects a value from the belief distribution for each location, and then samples in the location for which the selected probability of finding new cases is highest.13 The idea is that there are multiple locations with existing cases of a disease, yet undetected, in which a Bayesian search tool will use regular disease testing data to hone in on the most likely places to find undiagnosed cases over the course of daily or weekly testing in these locations. The goal is to maximize the cumulative number of undiagnosed cases that are detected.
Such an approach will not necessarily work for the early detection of new incident cases; that is, an outbreak. The Thompson sampling algorithm uses new data to update probabilities of finding new cases in each location and thereby maximize the yield of testing. An emerging cluster may start in a region with low prevalence and thus yield no positive tests initially. When this happens, the Thompson sampling algorithm will not frequently visit this location until its prevalence begins to approach that of other locations, by which time the outbreak may be out of control. Earlier, more frequent surveillance of the location could detect the growth in prevalence earlier.
Thus, for early detection of new incident cases of an endemic infectious disease we face the following situation: limited resources for testing are available to deploy over time and space, and locations sampled might result in no incident diagnoses that could indicate a new cluster. However, if and when an outbreak emerges, delays in detection will allow the outbreak to spread, with attendant human and economic costs. This motivates the subject of the present study: How can limited testing resources be allocated to rapidly detect outbreaks of an endemic infectious disease?
The problem of detecting an endemic disease outbreak as early as possible is a quickest change detection, or sequential surveillance, problem. In this canonical problem, a system changes state at some unknown point in time (the change point or outbreak start time) while an algorithm observes a sequence of observations over time. The algorithm uses the observations to decide whether the change point has occurred, and sounds an alarm if it believes that a change point has occurred. A false alarm cost is incurred for declaring a change too early and a delay cost is incurred that grows in the time difference between the alarm and the change point. The classical quickest change detection problem is an optimal stopping partially observed Markov decision process with a known optimal solution that sounds an alarm if the belief that the system’s state has changed crosses a threshold.14 A number of variants of the classical problem have been considered: for example, risk averse utility functions or delay costs that grow exponentially.14,15 Frisén16 provides additional evaluation methods and optimality criteria for sequential surveillance methods and presents several other methods, including the Shiryaev-Roberts method, Shewhart method, CUSUM method and exponentially weighted moving average models. These methods have been applied to detecting outbreaks of diseases such as tularemia and influenza.17,18
In the problem setup considered by most of the literature, there is only one system (location), so there is no decision about which system (location) to sample from. In our work, we have an additional decision about which location to sample in each time step. We think of this as a multi-arm quickest change detection problem.
Our problem is similar to a multi-armed bandit problem19 in that we have a set of arms (locations) to choose from in each time step and we do not know the underlying state of the arms, but we can learn from the data we observe. The study using Thompson sampling to allocate HIV testing resources treated the problem of allocating testing resources as a multi-armed bandit problem.12 Multi-armed bandits have been extended to deal with non-stationary reward distributions (e.g.,20,21,22), such as when the prevalence of a disease in different geographic areas changes over time. Non-stationary multi-armed bandits have been applied to disease surveillance: for example, in allocating limited COVID-19 testing resources.23,24
While multi-armed bandits have useful applications for allocating testing resources for controlling infectious disease, the problem we consider here is fundamentally different. Multi-armed bandit problems are concerned with maximizing observed cumulative reward over some fixed time horizon, whereas in sequential surveillance we are concerned with an unobserved, terminal reward (false alarm cost and delay) at the time an alarm is declared. In the multi-arm quickest change detection problem, we are not only concerned with a sampling rule, but also an outbreak alarm decision that would trigger a larger response. We aim to balance the need to detect an outbreak early (thereby minimizing outbreak spread) with the cost of false alarms (which waste response resources).
While most of the quickest change detection literature does not consider multiple sampling locations, some recent literature has dealt with this problem, using the term multi-stream data. One study develops a second-order asymptotically optimal algorithm when only one location (or stream) is assumed to change.25 The algorithm samples from a single location until determining there is no change, moves to another location and continues until becoming confident there is no change, eventually cycling through all locations until an alarm is raised. Another study uses Thompson sampling to sample statistics for each location based on the Shiraev-Roberts procedure.26 These statistics, which are treated like the rewards in a multi-armed bandit framework, contain information about how likely a change has occurred. Finally, Banerjee and Veeravalli27 consider the quickest change detection problem when there is a cost for sampling; in contrast, in our problem we have a constraint on the number of locations we can sample in each time step.
Here we propose an adaptive sampling method for solving the multi-arm quickest change detection problem. In each period the algorithm samples from the location with the highest likelihood of triggering an alarm. We show how to calculate the probability of triggering an alarm by fitting a predictive distribution using profile likelihood estimation28 that requires very little prior information. We demonstrate the effectiveness of our method by a simulation study, and compare it to uniform random sampling, Thompson sampling, a clairvoyant method with perfect information about where the outbreak will occur, and a sampling method that has perfect information about the future alarm probability in each location.
2 |. METHODS
We model a set of independent locations, l ∈ [L], in which a decision maker conducts tests for the disease using a mobile testing unit that can visit only one location in each discrete time step, t = 1, 2, 3, … We let xt ∈ [L] denote the decision variable that indicates which location is tested at time t. The unknown, endemic prevalence of the disease in each location is before an outbreak has started. At some time step, Γl > 0, an outbreak begins in location l, and the prevalence monotonically increases following an unknown sequence where and . The decision maker does not know the outbreak times a priori. The first outbreak start time is denoted Γ = minl Γl, which is the first time the whole system changes from an “in-control” to an “out-of-control” state.
The mobile testing unit conducts n tests in each time step. If the unit tests in location l at time step t, then the number of positive tests, Zt+1, follows a binomial distribution
| (1) |
We let denote the data collected from location l up to time t where denotes the times at which we sampled location l and denotes the positive test counts that we observed at those times. For example, means that location 1 was sampled at time steps 2 and 5 with positive test counts of 5 and 4 observed, respectively, and we have this information available at time step 5. We let denote the data for all locations available at time t.
At any time step t > 0, an alarm can be triggered in a location according to a predefined alarm indicator function, , and an outbreak investigation is launched. We let τ denote the first time the alarm function sounds an alarm:
As with the classical change point detection problem, we want to minimize the worst case delay in detecting the first change in the system
subject to a false alarm constraint
where is referred to as the average run length when there is no outbreak. In our problem, we need to select both a sampling policy and an alarm statistic; thus, at each time step we decide which location to sample, and whether to sound an alarm.
2.1 |. Alarm Statistic
We use the following semiparametric likelihood ratio test for our alarm function for a location l at time t, suggested by Frisén:17
| (2) |
We trigger an alarm if the sum of the largest r values of Rlt(·) exceeds a threshold, as suggested by Zhang and Mei.26 Assume that the values of Rlt(·) have been sorted in non-increasing order, and define R(k)t(·) as the kth largest value of Rlt(·). Then,
| (3) |
where α is a constant parameter that controls the false alarm probability, and R(1)t ≥ … ≥ R(k)t … ≥ R(L)t. Higher values of α reduce the false alarm probability but increase the expected delay. The appropriate value of α depends on the relative cost of delay in detecting the outbreak versus the cost of a false alarm. The function L(·) is the likelihood of the data. We do not know the pre-outbreak prevalence nor the post-outbreak prevalence sequence, so we do not know the parameters of the likelihood functions. We maximize the likelihood function in our likelihood ratio test to set the parameters of the likelihood functions, which is why this method is a semiparametic method.
The denominator in the likelihood ratio (3) is the likelihood function under a static system. In our case, for the binomial distribution, we have
where
The quantity is just the number of positive test results for location l divided by the number of tests conducted in that location so far.
To calculate , we fit a maximum likelihood model under an assumed growth model. In our work, we assume a logistic growth model, described in section 2.2.1, and solve the maximum likelihood estimation problem by solving a sequence of convex optimization problems (MLE1, described in section 2.2.3). Alternatively, Frisén et al.17 proposed using isotonic regression to enforce the monotonicity constraint for prevalence without assuming a parameteric growth model. The authors showed how to calculate the alarm function for Poisson data.
2.2 |. Sampling Policy
The sampling policy takes the datasets, , for each location at the end of time step t − 1, and decides which location to sample in time step t. We propose a heuristic that selects the location with the highest probability of triggering an alarm following data collection in the next time step. We refer to this probability as the future alarm probability in location l:
The future alarm probability is equal to the expectation that the new data, (t, Zt), combined with the existing data, , will trigger the alarm function in the next time step. Note that the future alarm probability depends on values observed at all locations up to time t − 1 (that is, ) because our alarm function considers the top r likelihood ratio values. Zt is an unknown random variable at time step t − 1 that can take on values 0, …, n, so we can express the expectation of the alarm indicator function as the sum of the probabilities of Zt taking on values i = 0, …, n multiplied by the alarm function given a specific value of i.
We select the location to sample in the next time step, xt, as the one that maximizes the future alarm probability:
In our expression for the future alarm probability, we must calculate the probability of observing a specific count i, , given the data collected so far. To do so, we must assume a model for how the prevalence of the disease in a location changes over time. In the following sections, we describe a model for prevalence and then describe Bayesian and frequentist approaches to calculating the future alarm probability.
2.2.1 |. Logistic growth model
We propose a simple model of an epidemic where the prevalence increases, starting at the unknown change point, according to a logistic growth curve. A logistic function for prevalence is the solution to the fraction of infected individuals in a susceptible-infected (SI) model with no flow from the infected state back to the susceptible state, and is a good approximation for the early stage of an epidemic when exponential growth occurs. In any realistic scenario, the epidemic will be detected during the exponential phase; for our purposes, we are not concerned with what happens after detection.
In this model, the prevalence remains at before the outbreak starts and then increases according to a logistic function with transmission rate parameter βl:
| (4) |
| (5) |
| (6) |
where and (·)+ = max(0, ·).
2.2.2 |. Bayesian approach
In the Bayesian approach to calculating the future alarm probability, we integrate over the unknown prevalence, θt, to calculate the probability of observing a specific count:
We then determine the posterior probability of a specific prevalence level given the data, , by considering two cases: the prevalence given that the outbreak has not started yet and the prevalence given that the outbreak has started:
The Bayesian approach requires a prior for the initial prevalence, the growth rate, and the change point. While we could readily specify a prior for the initial prevalence and growth rate, specifying a prior for the change point is more difficult. If we have no knowledge about whether and when an outbreak will occur, we would want a prior distribution that assigns equal probability to an outbreak occurring in any future time period (from the initial time period to ∞). Such a prior does not exist, as it is not possible to have a sum of a constant probability over infinite possible values that equals 1, as required by a probability distribution. If we specify that outbreaks occur frequently then our model will not use the data to learn when the outbreak has started because, as time passes, our model will develop near certainty that the outbreak has already occurred. Conversely, if we specify that outbreaks are extremely rare then our model will initially ignore the growth model to determine prevalence, and treat the system as static. For these reasons, we instead consider a frequentist approach that learns from the data rather than relying on a prior distribution for the change point.
2.2.3 |. Frequentist approach
We require a predictive distribution for the number of positive tests in the next time step. In a frequentist framework, we could determine maximum likelihood estimates for , βl, and Γl and then plug these into the binomial probability mass function (pmf) to calculate the probability of a specific count. However, this approach does not take into account the uncertainty in estimating the true values of , βl, and Γl; it only takes into account the uncertainty due to sampling from a known binomial distribution. This approach will lead to overly narrow distributions for the positive counts: for example, if our model observes 0 positive counts in the first time step and sets , then our model will assign a probability of 1.0 to a count of 0. Clearly, this is overly confident because it does not take into account that was estimated from a finite sample, and thus may not be the true value, . To resolve this issue, we instead use the concept of profile likelihood to develop a predictive distribution28:
We set the probability of observing a specific count, i, proportional to the likelihood function maximized with the specific count appended to the data. So, for each possible value of i, we maximize the likelihood function and obtain different parameter values.
The likelihood function under a logistic growth model is
which is a concave function for a fixed value of Γl. We can restrict Γl ∈ {0, 1, …, t} because for all Γl ≥ t, the values of βl and that maximize the likelihood function are the same. Therefore, we can find the globally optimal values of Γl, βl, and υl that maximize the likelihood function by solving a sequence of convex optimization problems for each Γl ∈ {0, 1, …, t} and selecting the value of Γl with the maximum likelihood. Furthermore, we can add linear constraints on the values of βl and υl given what we know about the problem. For example, we know that the transmission rate of any given disease is limited, and the initial prevalence is very small. In summary, we obtain the following optimization problem for each value of i:
| (MLE1) |
where and are optional upper bounds on the transmission rate and initial prevalence, respectively. These bounds can be set based on prior knowledge of the disease, and should be set to values well above the expected true values.
Algorithm 1 summarizes our method for selecting the next location to sample. In practice, Algorithm 1 should be implemented using log probabilities to prevent floating point errors. We visit each location at least twice in a warm-up period before using Algorithm 1.

3 |. SIMULATION STUDY
We performed a simulation study to evaluate the performance of the profile likelihood method. We programmed Algorithm 1 using the Julia programming language. We enumerate the active sets of constraints in (MLE1). We use Newton’s method to solve the problem for an active set, then check to see whether the solution satisfies the Karush-Kuhn-Tucker (KKT) conditions; we stop when a solution satisfies the KKT conditions. The algorithm is relatively straightforward to implement and runs quickly. For example, for a single location with 50 weeks of data, Algorithm 1 requires an average of 40 milliseconds on a 3.8 GHz 8-core Intel Core I7 machine using multi-threading. The code is available at https://github.com/MFairley/AdaptiveSurveillance.jl.
3.1 |. Predictive Distributions
We first examine properties of the predictive distribution as a function of the number of samples and the prediction time horizon for a given location l. Figure 1 shows an example of the number of positive tests over time for a given location, generated by sampling according to equation (1). In this example, the sample size is n = 200, initial prevalence is , and the outbreak starts at time Γl = 100 with transmission rate βl = 0.015 (similar to the transmission rate in a model for the HIV outbreak in Scott County, Indiana7), growing according to a logistic epidemic curve (equation (6)). We assume a weekly time step.
FIGURE 1.
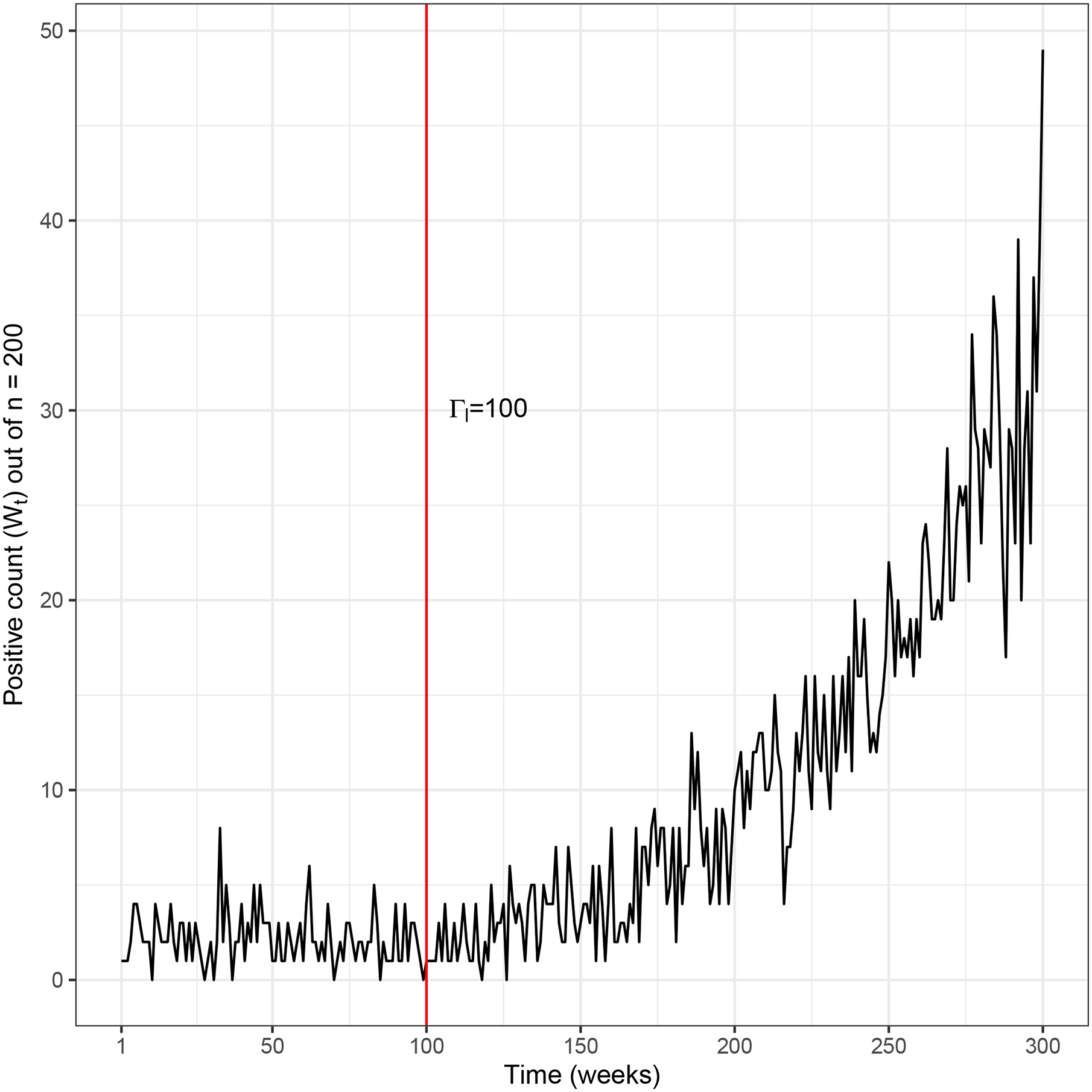
Example sample data with initial prevalence , and outbreak start time Γl = 100 with transmission rate βl = 0.015.
Figure 2 shows the predictive distributions for the new number of positive test results, generated according to Algorithm 1 and using the data in Figure 1, for a prediction horizon of 1 and 10 weeks, and for predictions made at the end of week 2, 50, or 150. Note that when there are multiple locations (L > 1), we make predictions more than one time step ahead for all locations except the location visited most recently. While we always make a prediction for time step t at time step t − 1, we have old data for other locations (the set when x(t−1) ≠ l), so a prediction for time step t at time step t − 1 is equivalent to making a prediction for time step t at an earlier time step. Hence, in this example, we consider a prediction horizon of 10, not just 1.
FIGURE 2.
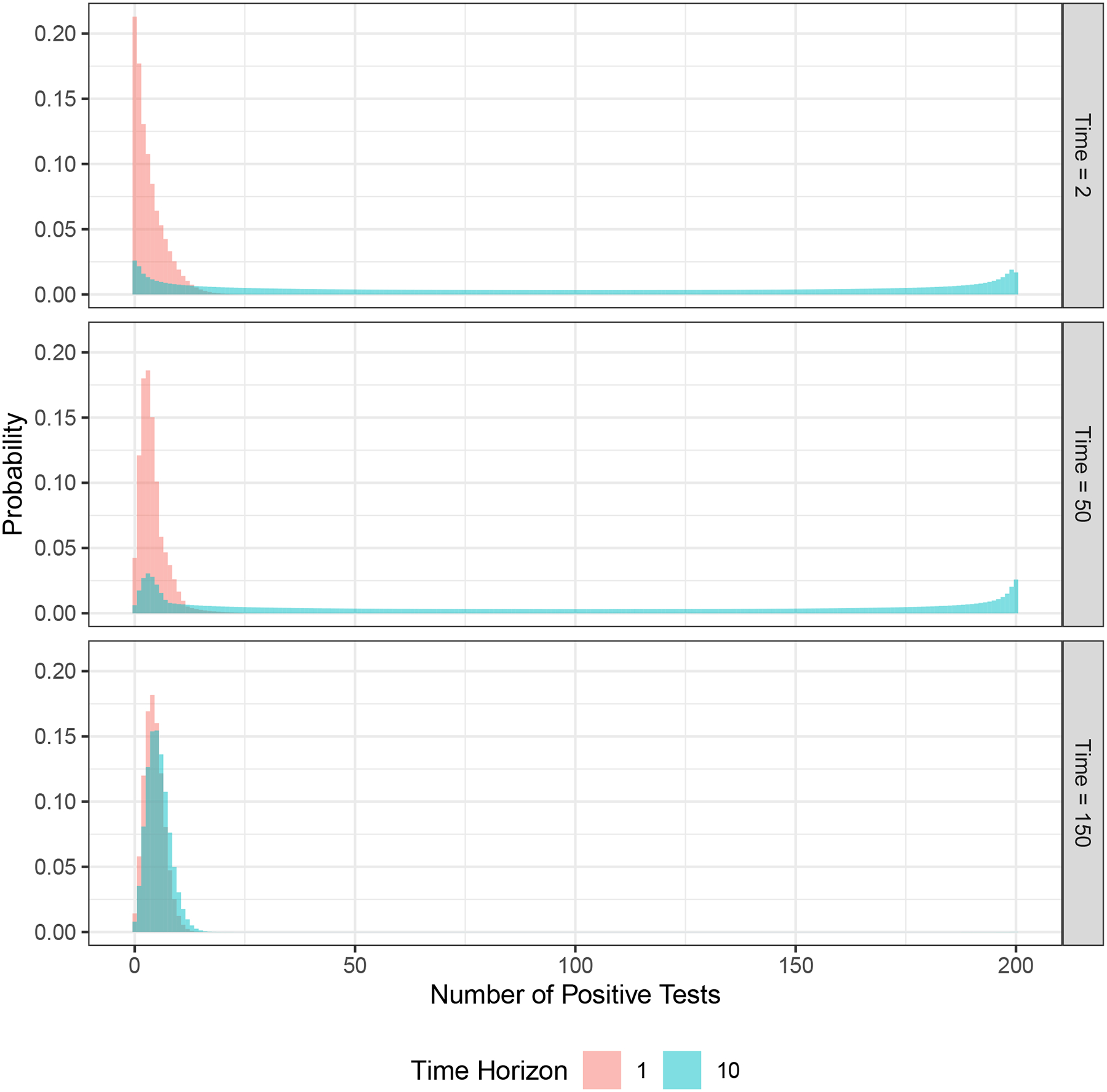
Example predictive distributions at different time steps (week 2, 50, 150) and for different time horizons (1 and 10 weeks) using the sample data shown in Figure 1.
At the end of week 2, we have only two samples, for weeks 1 and 2. In each of those weeks, 1 positive result was found (Figure 1). As shown in the figure, the prediction for the next week ranges from 0 to approximately 15 positive tests (with very small probabilities for values higher than 15), with a mean of approximately 3.4. In contrast, the prediction for week 12 (10 weeks in the future) is a nearly uniform distribution between 0 and 200, reflecting the fact that an outbreak could start in those weeks. The prediction for week 51 made at the end of week 50 has a narrower probability mass function than the prediction for week 3 made in week 2 and a slightly higher mean (4.0), reflecting the additional 49 weeks of data. However, the prediction for week 60 is similar to the prediction for week 12 that was made in week 2, again reflecting the fact that an outbreak could occur. When we make a prediction at the end of week 150, the outbreak has already occurred (at week 100) and we have 50 weeks of data after the outbreak. In this case, the model predicts a much narrower range of future values, both for weeks 151 and 160, as it has learned the transmission rate from the sample data. The predicted mean and range for week 160 are higher than for week 151 (mean 5.8 versus 4.5), reflecting potential epidemic growth over those future 10 weeks.
3.2 |. Outbreak Detection
We next examine the performance of the profile likelihood method in detecting an outbreak. We perform 1000 replications of each problem instance. We simulate weekly until the first alarm occurs for each replication. We consider five locations. For locations 3, 4 and 5 we assume 1% initial prevalence, and for locations 1 and 2 we consider three cases for initial prevalence: . We assume that an outbreak will occur in location 1 in either week 1 or week 50 (Γ1 = 1 or 50), with transmission rate β = 0.015. No outbreak occurs in locations 2, 3, 4, and 5, so prevalence in those locations is constant over the time horizon. Testing can be done in any one of the locations each week, with a sample size of n = 200. For the maximum likelihood estimation problem (MLE1) we set the upper bounds on the transmission rate and initial prevalence to and , respectively, for all locations.
We compare our method to four other sampling methods: a clairvoyant method where we always sample in location 1; a true future alarm probability method where we always sample in the location that has the true highest probability of a future alarm (calculated using true values of initial prevalence, growth rate, and outbreak start time); a uniform random sampling method where any location is equally likely to be sampled in each period; and Thompson sampling. In contrast to the true future alarm probability method, our profile likelihood method must account for uncertainty in initial prevalence, growth rate, and outbreak start time. We note that the location with the true highest probability of a future alarm is not always location 1 because the alarm function depends on the specific, random sample counts that have been observed thus far. Thompson sampling uses the number of positive tests as its reward function and focuses on locations with the highest prevalence.12 For the Thompson sampling algorithm we assumed a Beta(1, 1) prior distribution for the prevalence in each location.12 This is an uninformative prior that assumes that all prevalence levels are equally likely and thus encourages exploration of alternative locations at early time steps.
In order to have a fair comparison, we calibrate all five sampling methods such that they have the same false alarm constraint. Specifically, we set the alarm threshold parameter α from equation (3) for each sampling method to have an average run length, when there is no outbreak, of 56 for each scenario, and we set r = 2 (see equation (3)). We visit each location twice before we begin adaptive sampling, first visiting location 1 twice, and then location 2 twice, and so forth.
For each of the six problem instances (which vary by initial prevalence and time of outbreak) and each of the five surveillance methods, we calculate the mean delay (and 95% confidence intervals) in triggering an alarm given that an outbreak has happened (Table 1). For each problem instance and surveillance method we also plot the cumulative probability of an alarm over time (Figure 3).
TABLE 1.
Comparison of surveillance methods for example problem: mean conditional delay (mean delay in triggering an alarm given that the alarm is triggered after the outbreak starts). 95% confidence intervals are shown in brackets.
| Mean Conditional Delay | ||||
|---|---|---|---|---|
| * | † | Algorithm | Γ1 = 1‡ | Γ1 = 50‡ |
| 0.01 | 0.01 | Clairvoyant | 31 [29, 31] | 19 [18, 20] |
| True Future Alarm Probability | 44 [43, 46] | 33 [31, 35] | ||
| Profile Likelihood | 47 [45, 49] | 36 [32, 39] | ||
| Thompson Sampling | 43 [42, 45] | 40 [35, 39] | ||
| Uniform Random | 52 [51, 56] | 42 [40, 47] | ||
| 0.01 | 0.02 | Clairvoyant | 30 [28, 30] | 18 [16, 19] |
| True Future Alarm Probability | 44 [42, 47] | 35 [32, 36] | ||
| Profile Likelihood | 47 [45, 50] | 37 [35, 42] | ||
| Thompson Sampling | 73 [59, 65] | 117 [97, 123] | ||
| Uniform Random | 52 [50, 55] | 42 [38, 47] | ||
| 0.02 | 0.01 | Clairvoyant | 28 [26, 28] | 16 [15, 17] |
| True Future Alarm Probability | 38 [36, 39] | 28 [26, 29] | ||
| Profile Likelihood | 40 [39, 42] | 29 [26, 31] | ||
| Thompson Sampling | 31 [29, 32] | 18 [16, 18] | ||
| Uniform Random | 47 [45, 50] | 35 [32, 38] | ||
Initial prevalence in location 1, where the outbreak occurs
Initial prevalence in location 2
Outbreak start time in location 1
FIGURE 3.
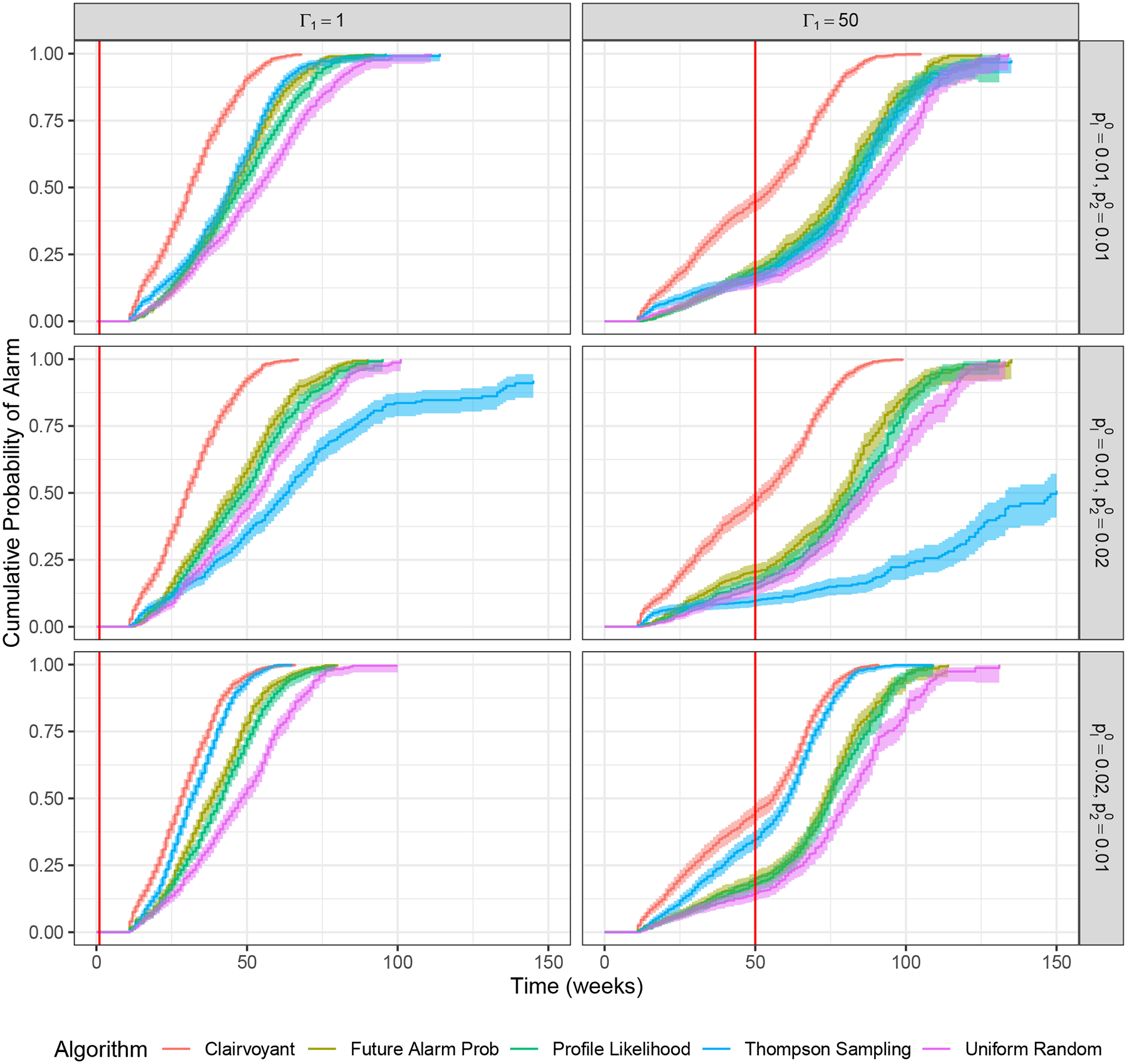
Comparison of surveillance methods for example problem: Cumulative probability of alarm over time. Shaded regions represent 95% confidence intervals. The vertical red line denotes outbreak occurrence.
Time to outbreak detection
As expected, the clairvoyant method has the shortest mean time to detect the outbreak because this method samples location 1 every time period. Similarly, as expected, uniform random sampling always performs worse than the profile likelihood method because uniform random sampling does not learn from the sampling data. The true future alarm probability method was only slightly better than the profile likelihood method, indicating that the estimate of the future alarm probability using profile likelihood is accurate.
The mean time to detect the outbreak for the profile likelihood method compared to Thompson sampling depends on the initial prevalence in location 1 compared to location 2. When locations 1 and 2 have similar initial prevalence (in this case, 1%), the profile likelihood method and Thompson sampling have similar performance. When location 1 has lower initial prevalence than location 2 (1% in location 1 vs. 2% in location 2), the profile likelihood method significantly outperforms Thompson sampling. This is because Thompson sampling first focuses on the location with higher prevalence (location 2) and does not take many samples from location 1 until the estimated prevalence for location 1 exceeds that of location 2. When location 1 has higher initial prevalence than location 2 (2% in location 1 vs. 1% in location 2), then Thompson sampling performs better than the profile likelihood method. This is because Thompson sampling focuses on the location with the highest expected prevalence, which is always location 1. These differences are illustrated graphically in Figure 3.
4 |. DISCUSSION
The profile likelihood method we have introduced estimates the distribution of the number of positive tests in each location that would occur if that location were sampled, and takes into account the uncertainty due to sample size and time horizon. In numerical experiments, Thompson sampling either performed well or very poorly: Thompson sampling was worse than uniform random sampling when the outbreak occurred in a location with lower initial prevalence than other locations. The profile likelihood method had lower time to outbreak detection than Thompson sampling in some but not all scenarios we considered, but was always better than uniform random sampling even when the outbreak occurred in a location with a lower initial prevalence than other locations. In practice, outbreaks of endemic disease can occur in any location, regardless of initial disease prevalence. Profile likelihood sampling provides an effective and reliable method for rapidly detecting endemic disease outbreaks that is robust to this uncertainty.
Similar to existing studies in the literature (e.g.,26) we minimize the time to outbreak detection, as indicated by an alarm being triggered. It is possible that the alarm is triggered after an outbreak has occurred, but in the wrong location, potentially leading to a costly delay in detecting the true outbreak. In this case, after a false alarm has occurred, we would update information and continue sampling in each time period. One could potentially create an objective function that incorporates location-specific outbreak times and false alarm definitions that depend on where the alarm was triggered. However, such a model would be difficult to analyze as a stopping time formulation because an alarm does not necessarily stop the process; after a false alarm, the process would continue with additional information from investigation in the location where the false alarm occurred. This is an area for future exploration.
A number of possible extensions could be made to this work. We assumed that the locations are independent; in reality, contact networks can span multiple locations so an outbreak in one location may make an outbreak in a nearby location more likely. Future work could take into account these network effects to make more efficient use of the data. We assumed that we can visit exactly one location in each time period. Future work could consider a fleet of mobile testing units that can sample multiple locations in any time period. We also assumed a fixed sample size but the sample size could be less than this fixed value due to randomness in the number of individuals who come to the unit for testing (presumably a combination of baseline demand plus outreach efforts). Future work could model the sample size as a random variable. We assumed a fixed value for the alarm threshold α. It is possible that the performance of the profile likelihood method could be improved using a dynamic value of α that is specific to each location, possibly as a function of the number of times a location has been visited. Finally, we compared the profile likelihood method to the standard Thompson sampling method. It is possible that the Thompson sampling method could be improved for the disease surveillance problem, for example by using only recent data to parameterize belief distributions.
Undetected outbreaks of endemic infectious disease can lead to significant morbidity, mortality, and health care expenditure (e.g.,1,29,30,31,32). Improved methods for endemic infectious disease detection are needed. Because limited public health budgets preclude testing in all locations all the time, effective and efficient methods are needed to determine where and when to test. The profile likelihood sampling method we present here is one such method.
ACKNOWLEDGEMENTS
This research was funded by grant R37-DA15612 and DP2-DA049282 from the National Institute on Drug Abuse. Michael Fairley was additionally supported by the Shaper Family Graduate Fellowship from Stanford University.
DATA AVAILABILITY STATEMENT
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
- 1.Peters PJ, Pontones P, Hoover KW, et al. HIV infection linked to injection use of oxymorphone in Indiana, 2014–2015. New Engl J Med 2016; 375(3): 229–239. [DOI] [PubMed] [Google Scholar]
- 2.Furukawa NW, Blau EF, Reau Z, et al. Missed opportunities for human immunodeficiency virus (HIV) testing during injection drug use–related healthcare encounters among a cohort of persons who inject drugs with HIV diagnosed during an outbreak — Cincinnati/Northern Kentucky, 2017–2018. Clin Infect Dis 2021; 72(11): 1961–1967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alpren C, Dawson EL, John B, et al. Opioid use fueling HIV transmission in an urban setting: An outbreak of HIV infection among people who inject drugs — Massachusetts, 2015–2018. Am J Public Health 2020; 110(1): 37–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Atkins A, McClung RP, Kilkenny M, et al. Notes from the field: Outbreak of Human Immunodeficiency Virus infection among persons who inject drugs — Cabell County, West Virginia, 2018–2019. Morb Mortal Wkly Rep 2020; 69(16): 499–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Golden MR, Lechtenberg R, Glick SN, et al. Outbreak of human immunodeficiency virus infection among heterosexual persons who are living homeless and inject drugs — Seattle, Washington, 2018. Morb Mortal Wkly Rep 2019; 68(15): 344–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mack S New HIV Cases and an investigation on a closed street: Doctor explains situation under 836 overpass. WLRN; Miami; Oct. 2018. [Google Scholar]
- 7.Gonsalves GS, Crawford FW. Dynamics of the HIV outbreak and response in Scott county, IN, USA, 2011–15: A modelling study. Lancet HIV 2018; 5(10): e569–e577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Van Handel MM, Rose CE, Hallisey EJ, et al. County-level vulnerability assessment for rapid dissemination of HIV or HCV infections among persons who inject drugs, United States. J Acquir Immune Defic Syndr 2016; 73(3): 323–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McDonald PR. Righteous Rebels: AIDS Healthcare Foundation’s Crusade to Change the World. Altadena, CA: Raymond Press. 2016. [Google Scholar]
- 10.Liang TS, Erbelding E, Jacob CA, et al. Rapid HIV testing of clients of a mobile STD/HIV clinic. AIDS Patient Care STDs 2005; 19(4): 253–257. [DOI] [PubMed] [Google Scholar]
- 11.Yu SWY, Hill C, Ricks ML, Bennet J, Oriol NE. The scope and impact of mobile health clinics in the United States: A literature review. Int J Equity Health 2017; 16(1): 178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gonsalves GS, Crawford FW, Cleary PD, Kaplan EH, Paltiel AD. An adaptive approach to locating mobile HIV testing services. Med Decis Making 2018; 38(2): 262–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thompson WR. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika 1933; 25(3/4): 285–294. [Google Scholar]
- 14.Krishnamurthy V Stopping time POMDPs for quickest change detection. In: Partially observed Markov decision processes: From filtering to controlled sensing Cambridge, UK: Cambridge University Press. 2016. [Google Scholar]
- 15.Poor HV. Quickest detection with exponential penalty for delay. Ann Stat 1998; 26(6): 2179–2205. [Google Scholar]
- 16.Frisén M Optimal sequential surveillance for finance, public health, and other areas. Seq Anal 2009; 28(3): 310–337. [Google Scholar]
- 17.Frisén M, Andersson E, Schioler L. Robust outbreak surveillance of epidemics in Sweden. Stat Med 2009; 28(3): 476–493. [DOI] [PubMed] [Google Scholar]
- 18.Frisén M, Sonesson C. Optimal surveillance. In: Spatial and Syndromic Surveillance for Public Health New York, NY: John Wiley & Sons. 2005. [Google Scholar]
- 19.Lattimore T, Szepesvári C. Bandit Algorithms. Cambridge, UK: Cambridge University Press. 2020. [Google Scholar]
- 20.Liu F, Lee J, Shroff N. A change-detection based framework for piecewise-stationary multi-armed bandit problem. arXiv 2017. [Google Scholar]
- 21.Mintz Y, Aswani A, Kaminsky P, Flowers E, Fukuoka Y. Nonstationary bandits with habituation and recovery dynamics. Oper Res 2020; 68(5): 1493–1516. [Google Scholar]
- 22.Cheung WC, Simchi-Levi D, Zhu R. Hedging the drift: Learning to optimize under non-stationarity. arXiv 2021. [Google Scholar]
- 23.Bastani H, Drakopoulos K, Gupta V, et al. Efficient and targeted COVID-19 border testing via reinforcement learning. Nature 2021; 599: 108–113. [DOI] [PubMed] [Google Scholar]
- 24.Kasy M, Teytelboym A. Adaptive targeted infectious disease testing. Oxford Rev Econ Policy 2020; 36(1): S77–S93. [Google Scholar]
- 25.Xu Q, Mei Y, Moustakides GV. Second-order asymptotically optimal change-point detection algorithm with sampling control. In: 2020 IEEE International Symposium on Information Theory (ISIT). 2020: 1136–1140. [Google Scholar]
- 26.Zhang W, Mei Y. Bandit change-point detection for real-time monitoring high-dimensional data under sampling control. arXiv 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Banerjee T, Veeravalli VV. Data-efficient quickest change detection with on-off observation control. Seq Anal 2012; 31(1): 40–77. [Google Scholar]
- 28.Yudi P In All Likelihood: Statistical Modelling and Inference Using Likelihood. Oxford, UK: Oxford University Press. 2013. [Google Scholar]
- 29.Gountas I, Sypsa V, Papatheodoridis G, et al. A hepatitis C outbreak preceded the HIV outbreak among persons who inject drugs in Athens, Greece: Insights from a mathematical modelling study. J Viral Hepat 2019; 26(11): 1311–1317. [DOI] [PubMed] [Google Scholar]
- 30.Centers for Disease Control and Prevention. Managing HIV and hepatitis C outbreaks among people who inject drugs: A guide for state and local health departments. https://www.cdc.gov/hiv/pdf/programresources/guidance/cluster-outbreak/cdc-hiv-hcv-pwid-guide.pdf; 2018.
- 31.Mindra G, Wortham JM, Haddad MB, Powell KM. Tuberculosis outbreaks in the United States, 2009–2015. Public Health Rep 2017; 132(2): 157–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zibbell JE, Asher AK, Patel RC, et al. Increases in acute hepatitis C virus infection related to a growing opioid epidemic and associated injection drug use, United States, 2004 to 2014. Am J Public Health 2018; 108(2): 175–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.


