Combined QM/MM, machine learning path integral approach to compute free energy profiles and kinetic isotope effects in RNA cleavage reactions

Abstract

We present a fast, accurate and robust approach for determination of free energy profiles and kinetic isotope effects for RNA 2’-O-transphosphorylation reactions with inclusion of nuclear quantum effects. We apply a deep potential range correction (DPRc) for combined quantum mechanical/molecular mechanical (QM/MM) simulations of reactions in the condensed phase. The method uses 2nd-order density-functional tight-binding method (DFTB2) as a fast, approximate base QM model. The DPRc model enables the DFTB2 base model to be corrected to reproduce ab initio DFT (PBE0/6-31G*) QM/MM energies and forces by modifying the QM and QM/MM interactions without altering the MM atom interactions with other MM atoms. The DPRc thus enables both internal QM and QM/MM interactions to be tuned to high accuracy, and it is designed to smoothly vanish at a specified cutoff boundary (6 Å in the present work). The computational speed-up afforded by the QM/MM+DPRc model enables free energy profiles to be calculated that include rigorous long-ranged QM/MM interactions under periodic boundary conditions and nuclear quantum effects through a path integral approach using a new interface between the AMBER and i-PI packages. The approach is demonstrated in the calculation of free energy profiles for native RNA cleavage model reaction along with reactions that involve thio substitutions which are important as experimental mechanistic probes. Simulations illustrate the influence of nuclear quantum effects on the reaction profiles, and are used to aid in the interpretation of primary and secondary experimental ¹⁸O kinetic isotope effects.

Graphical Abstract

1. Introduction

RNA strand cleavage by 2′-O-transphosphorylation is ubiquitous in biology^1–3 and has far-reaching implications for medicine.⁴ There is thus great interest in obtaining a predictive understanding of the mechanisms of these reactions and the nature of the transition states that control their rates. The most sensitive experimental probes that report on changes in the structure and bonding in the transition state are the measurement of kinetic isotope effects (KIEs).^5–7 These experiments are challenging, often requiring painstaking synthetic efforts and careful, highly sensitive measurements to realize.⁵ Further, for complex systems, the interpretation of these measurements in terms of structure and bonding requires recourse into computational simulations.^8–10

Ab initio combined quantum mechanical/molecular mechanical (QM/MM) simulations with rigorous treatment of long-ranged electrostatic interactions under periodic boundary conditions^11,12 affords a powerful tool to gain insight into the pathways of these reactions, their transition states and intermediates, and environmental factors that modulate reactivity.^13,14 However, ab initio QM/MM methods are extremely computationally intensive, and hence the elucidation of the free energy surfaces (FES) for complex reactions that require extensive sampling is often not practical. Methods that enable the treatment of nuclear quantum effects, despite great advances in new methods and software for their computation, nonetheless considerably exacerbate the computational cost making all but the most modest calculations prohibitive.

Machine learning potentials offer a potential mechanism to improve the accuracy and efficiency of QM/MM simulations, and have had considerable impact in the development of methods to study chemical reactions.^15–21 Herein we develop an approach whereby we employ a recently developed deep-potential range correction (DPRc) model²² to enhance the accuracy of a fast, approximate base QM/MM model to that of a much more computationally costly target QM/MM model. We develop the QM/MM+DPRc potential using a recently reported active learning neural network training procedure,²² employing 2nd-order density-functional tight-binding (DFTB2)^23–25 and PBE0/6-31G* as the base and target QM/MM models. We then develop a framework for introducing nuclear quantum effects into the calculations using path integral molecular dynamics (PIMD) through an interface between AMBER20²⁶ and i-PI²⁷ software packages. Together, this enables the calculation of QM/MM+DPRc free energy profiles^28–30 with and without nuclear quantum effects, and the prediction of primary and secondary KIE values. The methods are demonstrated and tested using a well-characterized native non-enzymatic RNA transphosphorylation reaction model for which KIE values are available experimentally, as well as a series of chemically modified (thio substituted) reactions that are often used experimentally in mechanistic studies.^31,32

2. Methods

2.1. Reaction models and initial system setup

The ML network parameters within the DFTB2 QM/MM+DPRc method were parametrized to reproduce PBE0/6-31G* QM/MM total energies and forces for a series of RNA-like non-enzymatic model systems, shown in Fig. 1. The initial solute structures were generated from SMILES using Openbabel.³⁴ The QM region was defined as the entire RNA-like solute molecule. The solute was solvated by 1510 TIP4P/Ew waters.³⁵ Simulations were performed with the SANDER program within AMBER20²⁶ using a 1 fs time step. The systems were equilibrated by performing DFTB2 (“mio” parameter set) QM/MM simulations that gradually heated the system from 0 K to 298 K over the course of 100 ps using the Langevin thermostat.³⁶ This was followed by 100 ps of density equilibration in the isothermal-isobaric ensemble at 1 atm and 298 K using the Berendsen barostat with a 5 ps collision frequency.³⁷ The Lennard-Jones potential was truncated at 8 Å, and a long-range tail correction was used to model the interactions beyond the cutoff. The long-range electrostatics were evaluated with the particle mesh Ewald method using a 1 ų grid spacing.³⁸

Figure 1:

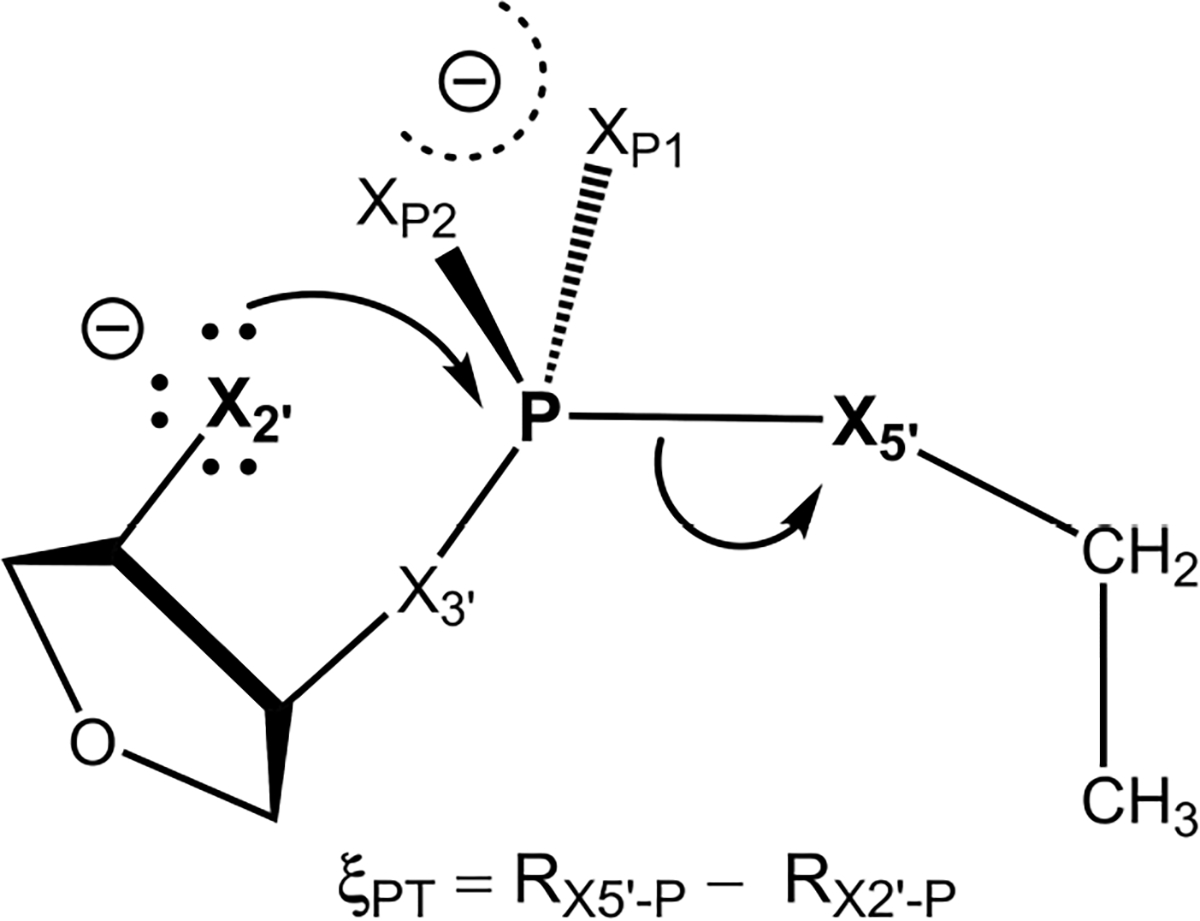
Model non-enzymatic phosphoryl transfer reaction in solution. In a native RNA system, the positions labeled “X” correspond to oxygen positions (canonical RNA numbering scheme is used to identify atomic positions). However, chemically modified variants involving thio substitution at one or more of these positions are commonly used in experimental mechanistic studies of RNA-cleaving enzymes.³³ In addition to the native model system, we will consider single thio substitutions at the 2′, 3′, 5′ and OP1 positions, as well as a double thio substitution at the OP1 and OP2 positions. We designate these reactions as S2′, S3′, S5′, S1P and S12, respectively. The phosphoryl transfer reaction coordinate, ξ_PT = R_X5’-P − R_X2’-P, is a difference between bond-breaking and bond-forming bond lengths R_X5’-P and R_X2’-P, respectively.

2.2. Ab initio quantum mechanical/molecular mechanical simulations

Umbrella window PBE0/6-31G* QM/MM simulations were performed to generate reference free energy surfaces and provide structures, energies, and forces to initiate the DFTB2 QM/MM+DPRc network parameter optimization. The RNA cleavage reaction³⁹ is described by the the collective variable (progress variable) for phosphoryl transfer (PT), ξ_PT, defined as the difference between the 5′-P and 2′-P bond distances.

$${\xi }_{\text{PT}}=R_{\text{X}5’-\text{P}}-R_{\text{X}2’-\text{P}}$$ (1)

R_X5’-P and R_X2’-P are the bond-breaking and bond-forming bond lengths in Fig. 1, respectively, and X is either O or S, depending on the thio-substitution. The FESs were reconstructed from a series of umbrella window simulations that vary the location of the restraining potential from −3.5 to 5 Å is steps of 0.1 Å. The umbrella window force constants were all 100 kcal mol⁻¹ Å⁻². The simulations were performed with TIP4P/Ew rigid water in the canonical ensemble for 25 ps at 298 K. The ambient potential composite Ewald method was used to compute the ab initio QM/MM electrostatic interactions using a 1 ų regular grid spacing and a 8 Å real-space cutoff.¹¹ The value of ξ_PT was written to file during the simulation, and the FESs were generated by analyzing the ξ_PT time series using the variational free energy profile (vFEP) method^28,29 implemented in the FE-ToolKit software.³⁰

2.3. Range-Corrected Deep Potential (DPRc)

The DFTB2 QM/MM+DPRc method modifies the DFTB2 QM/MM total energy by the inclusion of a machine learning potential which provides a non-electrostatic correction (that is, it does not directly alter the QM wavefunction) to the QM-QM and nearby QM-MM interactions.

$$E(\mathbf{R};\mathbf{P})=E_{\text{QM}}(\mathbf{R};\mathbf{P})+E_{\text{QM}/\text{MM}}(\mathbf{R};\mathbf{P})+E_{\text{MM}}(\mathbf{R})+E_{\text{ML}}(\mathbf{R})$$ (2)

R is a N × 3 array of atomic coordinates and P is the QM Hamiltonian’s single particle density matrix. E_QM(R;P) and E_MM(R) are the QM and MM energies, respectively. E_QM/MM(R;P) contains the electrostatic and Lennard-Jones (or other non-electrostatic-nonbonded model) interactions between the QM and MM regions. E_ML(R) is the DPRc potential. The DPRc correction is fully described in Ref. 22. In brief, the DPRc potential is an extension of the DeepPot-SE model⁴⁰ that includes corrections for the interactions between the QM and MM atoms. The key features of the correction are that it does not modify the interactions between MM atoms, the MM atoms do not contribute a constant to the total energy, and the correction between the QM and MM atoms smoothly approaches zero as the distance between the QM and MM atoms nears the correction cutoff (a parameter that can be adjusted). By constructing the correction potential to have these properties, the system total energy is conserved as the MM atoms approach or diffuse from the vicinity of the QM region during the course of simulation. In the present work, the correction cutoff between the QM and MM atoms is 6 Å. There is no correction cutoff between the QM and other QM atoms. The DPRc (and DeepPot-SE) machine learning correction consists of 2 neural networks: a “filtering network” composed of 3 hidden layers with 13, 26, 52 neurons, and a “fitting network” consisting of 3 hidden layers with 240 neurons per layer. Both networks are activated by the tanh function. The role of the filtering network is to provide a description of an atom and its surroundings, whereas the fitting network outputs an energy correction for an atom, given the atom’s description. The underlying DeepPot-SE model, on which the DPRc potential is based, uses “atom type” assignments to describe the environment around each atom. For the QM atoms, we use the atomic number. For MM atoms, we prepend the atomic number by the letter “m”, so that the MM atoms can be corrected differently than the QM atoms. We have implemented the DPRc method into the DeePMD-kit software package⁴¹ and created an interface with a development version of AMBER’s SANDER program.²⁶

The network parameters are optimized using an active learning approach described in detail elsewhere.²² The parameter optimizations were performed with the DP-GEN software,⁴² and the DP Compress algorithm⁴³ was applied to the trained models to improve computational performance and reduce the memory requirements. In brief, the active learning procedure involves the collection of initial reference data used to parametrize multiple sets of trial network parameters. Additional simulations are performed and agreement between the corrections produced by the sets of trial network parameters are tested. If the sets of trial network parameters produce significantly different corrections, then the trajectory frame is saved for use as additional training data in the next round of parametrization. Specifically, an initial set of reference PBE0/6-31G*⁴⁴ energies and forces were obtained from the ab initio QM/MM umbrella window simulations. The DFTB2 QM/MM^45–47 energies and forces are evaluated from the saved trajectory frames, and the DPRc network parameters are optimized to reproduce the difference between the DFTB2 and PBE0/6-31G* energies and forces. The stochastic optimization procedure produces different network parameters for different initial random number seeds. Performing the optimization with 4 seeds produces 4 sets of network parameters. The DeePMD-kit interface to SANDER was used to perform 25 ps of umbrella window simulations of the reactions with DFTB2 QM/MM+DPRc for one set of trial network parameters. At regular intervals, the energies and forces of all 4 parametrizations are calculated, the standard deviation (between DPRc corrections) is obtained for each atom, and if the maximal standard deviation is in the range 0.1 – 0.25 eV/Å, then the trajectory frame is saved. The PBE0/6-31G* and DFTB2 QM/MM energies and forces are evaluated for the newly saved frames and included as additional training data in the next round of network parameter optimizations. The active learning procedure is terminated when the 4 parameter sets agree for 99.8% of the frames in the final simulations (see Supporting Information). For clarity, the umbrella window simulations of the native non-enzymatic reaction and the 5 thio-substituted systems were included in the training procedure.

2.4. Path Integral Molecular Dynamics (PIMD) Simulations

After training the DFTB2 QM/MM+DPRc network parameters to the Born-Oppenheimer umbrella window simulations, we applied the final 4 parameter sets to the calculation of FESs that consider nuclear quantum effects by performing umbrella window simulations with PIMD. The PIMD simulations were performed by interfacing the i-PI software²⁷ to a development version of AMBER’s SANDER program.²⁶ The i-PI software is responsible for dynamically evolving the system through time, and it sends requests (either via Linux sockets or internet protocol) for energy and force evaluations. In this respect, SANDER is merely used as a calculator of the QM/MM total energy and force of the system, which is returned to i-PI via the internet protocol interface. When launching SANDER, new command line options were introduced that supply the internet protocol address of the computer running i-PI and the network port number to communicate messages. Rather than performing classical MD, SANDER enters an infinite loop in which it listens for messages on the specified port until a message is received to stop execution. A PIMD simulation requires multiple energy and force evaluations at each time step, which can be easily parallelized by launching multiple instances of SANDER, each of which may further parallelize the energy and force evaluation.

The PIMD dynamical motion was propagated with 6 beads (replicas) at a 0.25 fs timestep at 298 K using the PIGLET quantum thermostat;^48,49 therefore, up to 6 SANDER instances can be launched. The parameters for the PIGLET thermostat were taken from the GLE4MD website,^50,51 and chosen to reproduce the quantum fluctuations at 298 K and which span a range of frequencies up to 4142 cm⁻¹. The DFTB2 QM/MM+DPRc PIMD umbrella window simulations were performed with the q-SPC/Fw flexible water model.^52,53 The systems were prepared by replacing the TIP4P/Ew solvent with q-SPC/Fw, and each umbrella window simulation system density was re-equilibrated at 298 K and 1 atm pressure for 100 ps using classical MD. The final structure of the classical QM/MM density equilibration was used as the initial structure in the PIMD umbrella window simulation. The PIMD umbrella potentials were applied to the centroid positions, rather than the positions within each bead, to avoid an artificial perturbation of the nuclear wavepackets. The umbrella potentials were therefore applied via i-PI, as opposed to SANDER, by making use of the i-PI interface to PLUMED.^54,55 Each umbrella window simulation was performed 16 times for 20 ps (0.25 fs timestep) using a 200 kcal mol⁻¹ Å⁻² force constant. The 16 runs correspond to 4 simulations initiated from different thermostat random seeds for each of the 4 network parameter sets. During the course of simulation, the value of ξ_PT (as calculated from the centroid positions) was written to file, and the vFEP method was used to produce 16 FESs for each non-enzymatic system. At each point along ξ_PT we report the average and standard deviation of the 16 FESs. An alternative approach for calculating FESs from PIMD simulations⁵⁶ is to use a semiempirical reference potential and apply the weighted thermodynamic perturbation method.^56–58

For comparison, we performed classical MD DFTB2 QM/MM+DPRc umbrella window simulations with SPC/Fw solvent. Four sets of classical MD umbrella window simulations were performed with SANDER, corresponding to the 4 sets optimized network parameters. Each simulation was run for 100 ps using a 1 fs timestep, and each set of simulations was independently analyzed with vFEP to produce 4 FESs. At each point along ξ_PT we report the average and standard deviation of the 4 FESs. Note that the FES obtained from classical MD were performed with the SPC/Fw water model, whereas the PIMD simulations were performed with the q-SPC/Fw water model. The SPC/Fw water model was designed for use in classical MD simulations,⁵² whereas the q-SPC/Fw water model has slightly modified parameters tuned to improve the properties of bulk water in PIMD simulations.⁵³ We compare the FESs obtained from classical MD simulations using both water models in the Supporting Information. In brief, the minor differences between the two water models does not significantly impact the calculated FESs; the FESs agree to within the uncertainties of the calculations. The Supporting Information also provides a comparison between FESs calculated from classical MD simulations performed with SANDER and classical MD simulations performed through i-PI (in which case SANDER is used to evaluate the energies and forces). The resulting FESs obtained from both programs agree to within the uncertainties of the calculations.

2.5. Kinetic isotope effects

We applied the parametrized DFTB2 QM/MM+DPRc models to the calculation of O5′ and O2′ heavy atom kinetic isotope effects (KIE). KIE values are the ratios of reaction rate constants upon isotopic substitution, which can be calculated from eq. 3.

$$\frac{k_L}{k_H}=e^{\beta \left(\text{Δ}{A}_{\text{TS}}-\text{Δ}{A}_{\text{Min}}\right)}$$ (3)

k_L/k_H is the light-to-heavy ratio of reaction rate constants, and ΔA_TS and ΔA_Min are the free energies associated with changing the light isotope mass to a heavy isotope mass in the transition state and reactant minimum, respectively. In this work, there are two approaches for calculating KIE values: the TD-FEP method⁵⁹ and the local minimum harmonic approximation.

PIMD TD-FEP approach. The TD-FEP method, described in Ref. 59 and implemented within the i-PI software, calculates the KIE from eq. 3 by estimating the values of ΔA_TS and ΔA_Min from free energy perturbation of the atomic masses. In brief, the TD-FEP free energy estimation of transforming a mass from m to m′ is given by eq. 4,

$$\text{Δ}A=\frac{d}{2\beta }\log \frac{m^{\prime }}{m}-{\int }_m^{m^{\prime }}\frac{\langle T(\mu )\rangle }{\mu }\text{d}\mu$$ (4)

where d is the dimensionality of the problem and 〈T(μ)〉 is the ensemble average quantum kinetic energy of the atom with mass μ. In principle, one could evaluate the integral by performing a series of PIMD simulations that differ only by the chosen atomic mass μ and writing the atom’s quantum kinetic energy to file during the course of simulation. From the series of PIMD simulations, the 〈T(μ)〉 averages can be computed, and the integral could be performed either by numerical quadrature or by integrating a spline. This would be analogous to performing multiple thermodynamic integration simulations at intermediate states that connect two physical states. An advantage of the TD-FEP method is its ability to provide estimates of T(μ) for many values of μ from a single PIMD simulation performed using the light atomic masses. We instruct i-PI to calculate T(μ) of the selected atoms at 11 uniformly spaced mass values that range from the most abundant isotopic mass to the second most abundant isotopic mass. In this work, we calculate KIE values that transform ¹⁶O to ¹⁸O at the 2’, 5’, and nonbridge positions. The thiosubstituted model systems transform ³²S to ³⁴S when the selected positions have been replaced with sulfur atoms. The integral appearing in eq. 4 is calculated by representing the 〈T(μ)〉 values as an Akima spline and interpolating its values at 1000 uniformly spaced masses for trapezoidal-rule numerical integration.

Because ΔA_TS and ΔA_Min are both required, one must perform PIMD simulations of both the reactant and transition state. To perform simulations of these states, we restrain ξ_PT to the appropriate value, based on the location of the minimum and transition state identified on the FES by applying a 200 kcal mol⁻¹ Å⁻² harmonic restraint to the centroid positions. The simulations were performed with the SPC/Fw water model for 10 ps (0.25 fs timestep) at 298 K using a 6-bead PIGLET quantum thermostat.^48,49 Each DFTB2 QM/MM+DPRc simulation was repeated 4 times, corresponding to the use of the 4 active learning parameter sets, yielding 4 independent estimates of the KIE. We also performed an analogous set of DFTB2 QM/MM PIMD simulations (without the DPRc correction) with different random seeds to provide 4 estimates of the KIE for comparison. Furthermore, we performed PBE0/6-31G* QM/MM PIMD simulations to estimate the KIE; however, due to the much higher cost of the ab initio QM/MM PIMD simulations, only 1 estimate of the KIE was made.

Local minimum harmonic approximation: Bigeleisen-Mayer equation. An alternative approach to estimating KIE values is their calculation from vibrational analysis at geometrical stationary points using the Bigeleisen-Mayer equation.^60,61 The application of this approach to condensed phase systems with explicit waters is complicated by the myriad possible stationary points. To make a comparison with this approach, we attempted to find many minima and transition state structures starting from structures encountered during classical QM/MM simulations. The stationary point geometry optimizations were performed by interfacing SANDER to the DL-Find geometry optimization software.⁶²

A set of reaction minimum structures were found by performing classical QM/MM simulations near the minimum of the FES, extracting configurations from the trajectory file, removing the harmonic restraints, and optimizing the geometry for a minimum using the limited memory Broyden–Fletcher–Goldfarb–Shanno algorithm (LBFGS). Only the solute and the nearby 6 Å of SPC/Fw solvent molecules were allowed to change their atomic positions. The atomic positions of the remaining system were fixed; however, the energy and forces are computed for the entire unit cell. After the stationary point was found, the Hessian was calculated from finite differentiation of the atomic gradients. The dimensions of the Hessian is proportional to the number of optimizable atoms; however, the forces are obtained from the full periodic system. The vibrational frequencies were obtained from diagonalization of the mass weighted Hessian upon removal of the translational and rotational degrees of freedom.

The vibrational frequencies of the transition state structures was performed analogously; however, the optimization of the transition state structures used the following procedure: (1) A structure near the transition state was taken from a stored trajectory file. (2) The solute and nearby 6 Å of solvent molecules were selected for optimization. (3) A series of restrained geometry minimizations were performed, each differing by the position of a ξ_PT umbrella window restraint. (4) The unrestrained potential energy of each structure was monitored, and the structure with the maximum potential energy was selected for further optimization. (5) The solute and nearby 3 Å of solvent molecules were allowed to move during transition state search using the partitioned rational function algorithm.

3. Results and Discussion

3.1. ab initio QM/MM and QM/MM+DPRc free energy profiles

Figure 2 compares FESs produced by DFTB2 QM/MM, PBE0/6-31G* QM/MM, and DFTB2 QM/MM+DPRc umbrella window classical MD simulations in TIP4P/Ew solvent. The DFTB2 QM/MM simulations were run 4 times initiated from different random number seeds, yielding 4 estimates of the FES. The figure plots the mean, and the vertical bars are the standard error of the mean. The DFTB2 QM/MM+DPRc simulations were similarly run 4 times, once for each set of optimized network parameters. The PBE0/6-31G* simulations were run once, except for the native non-enzymatic model, which was run 4 times. The relevant collective variable coordinates and free energies describing the free energy surfaces are summarized in Table 1.

Figure 2:

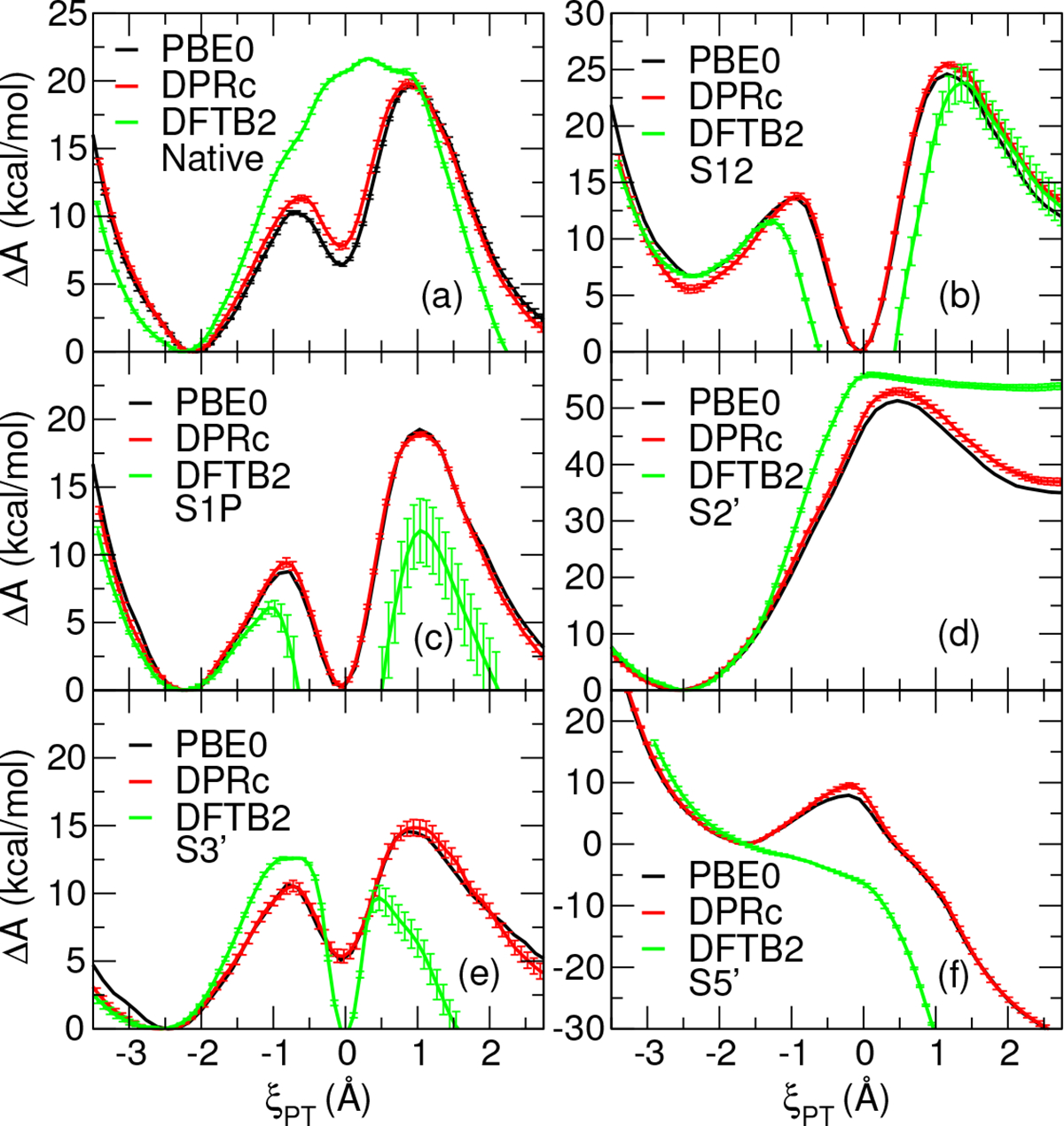
Comparison of DFTB2 QM/MM, PBE0/6-31G* QM/MM, and DFTB2 QM/MM+DPRc FESs generated from classical QM/MM umbrella window simulations. The DFTB2+DPrc model provides more than 200-fold speed-up in wallclock time relative to PBE0/6-31G* calculations on a 2.10 GHz Intel Xeon Gold 6230 CPU with 28MB of cache and an NVIDIA V100 GPU,approximately 1,400 ps/day (1.4×10⁶ time steps/day).

Table 1:

Summary of the free energy surfaces shown in Fig. 2.^a

System	Method	${\xi }_{\text{PT}}^{\text{Min}}$	${\xi }_{\text{PT}}^{\text{TS}}$	ΔA‡	ΔA
		Å	Å	kcal mol−1	kcal mol−1
Native	DFTB2	−2.27	0.32	21.65 ± 0.04	−6.3 ± 0.6
	PBE0/6-31G*	−2.11	0.94	19.68 ± 0.13	1.5 ± 0.4
	DPRc	−2.13	0.88	19.82 ± 0.28	1.1 ± 0.1
S12	DFTB2	−2.39	1.40	17.15 ± 1.65	2.5 ± 1.7
	PBE0/6-31G*	−2.38	1.15	17.94	5.0
	DPRc	−2.40	1.16	19.92 ± 0.20	6.0 ± 0.5
S1P	DFTB2	−2.25	1.05	11.79 ± 2.36	5.2 ± 2.4
	PBE0/6-31G*	−2.20	1.03	19.25	2.6
	DPRc	−2.21	1.05	18.92 ± 0.17	1.7 ± 0.5
S2′	DFTB2	−2.47	0.11	55.93 ± 0.43	55.2 ± 0.6
	PBE0/6-31G*	−2.58	0.47	51.33	35.6
	DPRc	−2.57	0.47	52.98 ± 0.60	37.5 ± 0.4
S3′	DFTB2	−2.54	−0.68	12.58 ± 0.05	−9.2 ± 0.7
	PBE0/6-31G*	−2.47	0.86	14.59	5.2
	DPRc	−2.53	0.95	14.85 ± 0.60	3.6 ± 0.6
S5′	DFTB2	...	...	...	...
	PBE0/6-31G*	−1.62	−0.21	7.87	−33.2
	DPRc	−1.64	−0.18	9.55 ± 0.40	−33.4 ± 0.3
MAE	DFTB2	0.08	0.56	3.37	9.4
MAE	DPRc	0.02	0.03	1.01	1.0

^aListed are the location of the minimum ${\xi }_{\text{PT}}^{\text{Min}}$ and rate-controlling transition state ${\xi }_{\text{PT}}^{\text{TS}}$ (where ξ_PT = R_X5’-P − R_X2’-P), the activation free energy ΔA^‡, and reaction free energy ΔA. Mean absolute errors (MAE) for DFTB2 and DFTB2 QM/MM+DPRc models with respect to PBE0/6-31G* reference curves are shown at the bottom.

The uncorrected DFTB2 model differs significantly from PBE0/6-31G*. When one (S1P) or both (S12) non-bridge oxygens are replaced with sulfurs, the DFTB2 model is likely to result in a nonphysical bond-breakage of the non-bridge P-S bond, resulting in a S²⁻ ion drifting into solution. This can occur in the range −0.90 ≤ ζ_PT ≤ 0.80 Å for S12 and −1.30 ≤ ζ_PT ≤ 0.90 Å for S1P. Regardless, we show these DFTB2 FESs to emphasize the significant degree of correction the DPRc model must undertake to achieve agreement with PBE0/6-31G*. The DFTB2 S5′ stationary points are not included in Table 1 because it does not display any local minima or transition states. In comparison, the DFTB2 QM/MM+DPRc free energy surfaces agree much more closely to the PBE0/6-31G* results. Whereas the mean absolute error (MAE) for activation and reaction free energies for DFTB2 with respect to PBE0/6-31G* reference values are 3.4 and 9.4 kcal/mol, respectively, the corresponding MAE values for the DFTB2+DPrc are 1.0 kcal/mol. For DFTB2, the MAE of the reaction coordinate at the minimum is fairly small (0.08 Å) whereas for the transition state is significantly larger (0.56 Å). The DFTB2+DPRc model, on the other hand, has corresponding MAE values of 0.02 and 0.03 kcal/mol, respectively. Thus, overall the DFTB2+DPRc model is able to very closely reproduce the PBE0/6-31G* results, whereas DFTB2 exhibits significant differences. The DFTB2+DPrc model provides more than 100-fold speed-up relative to PBE0/6-31G* calculations on a 2.10 GHz Intel Xeon Gold 6230 CPU with 28MB of cache and an NVIDIA V100 GPU.

3.2. QM/MM+DPRc free energy profiles with and without nuclear quantum effects

In order to gain insight into the effect of nuclear quantum effects on the FES, we compared simulations using two closely related flexible water models, SPC/Fw⁵² and q-SPC/Fw,⁵³ that were designed for classical MD and PIMD simulations, respectively (see Methods for details). The classical MD simulations using SPC/Fw were overall very similar to those using the rigid TIP4P/Ew model (Figure S3 of the Supporting Information).

Figure 3 compares DFTB QM/MM+DPRc FESs produced by classical MD and PIMD simulations. The classical MD and PIMD curves are the average of 4 and 16 FESs, respectively, and the vertical bars are the standard error of the mean. The classical MD simulations were performed using SANDER module of AMBER20, whereas the PIMD simulations were performed with i-PI interfaced with SANDER to calculate energies and forces. In our approach for calculating the FESs, we must choose an arbitrary zero of free energy, we choose as the lowest local free energy minimum. That is, we do not directly obtain a nuclear quantum correction to the free energy as an absolute quantity. Nevertheless, the practical consequences of including nuclear quantum corrections on the FESs can be seen in Figure 3. In all cases, the PIMD FES activation energies are smaller than those calculated from classical MD by 1.48 kcal/mol on average. Specifically, the PIMD activation energies are lowered by 2.10 (Native), 1.48 (S12), 1.32 (S1P), 1.65 (S2′), 1.14 (S3′), and 1.20 (S5′) kcal/mol. This reflects, among other things, differences in the vibrational environments of the reactant minimum and transition state. The latter being overall more “loose”,⁵ thus leading to smaller zero point energies in the transition state relative to the reactant state and results in lower barriers when nuclear quantum effects are included. As will be seen in the next section, these differences are important in the calculation of KIE values to aid in the interpretation of experimental measurements and provide insight into the structure of the transition state and the mechanism of the chemical reaction.^8,63–65

Figure 3:

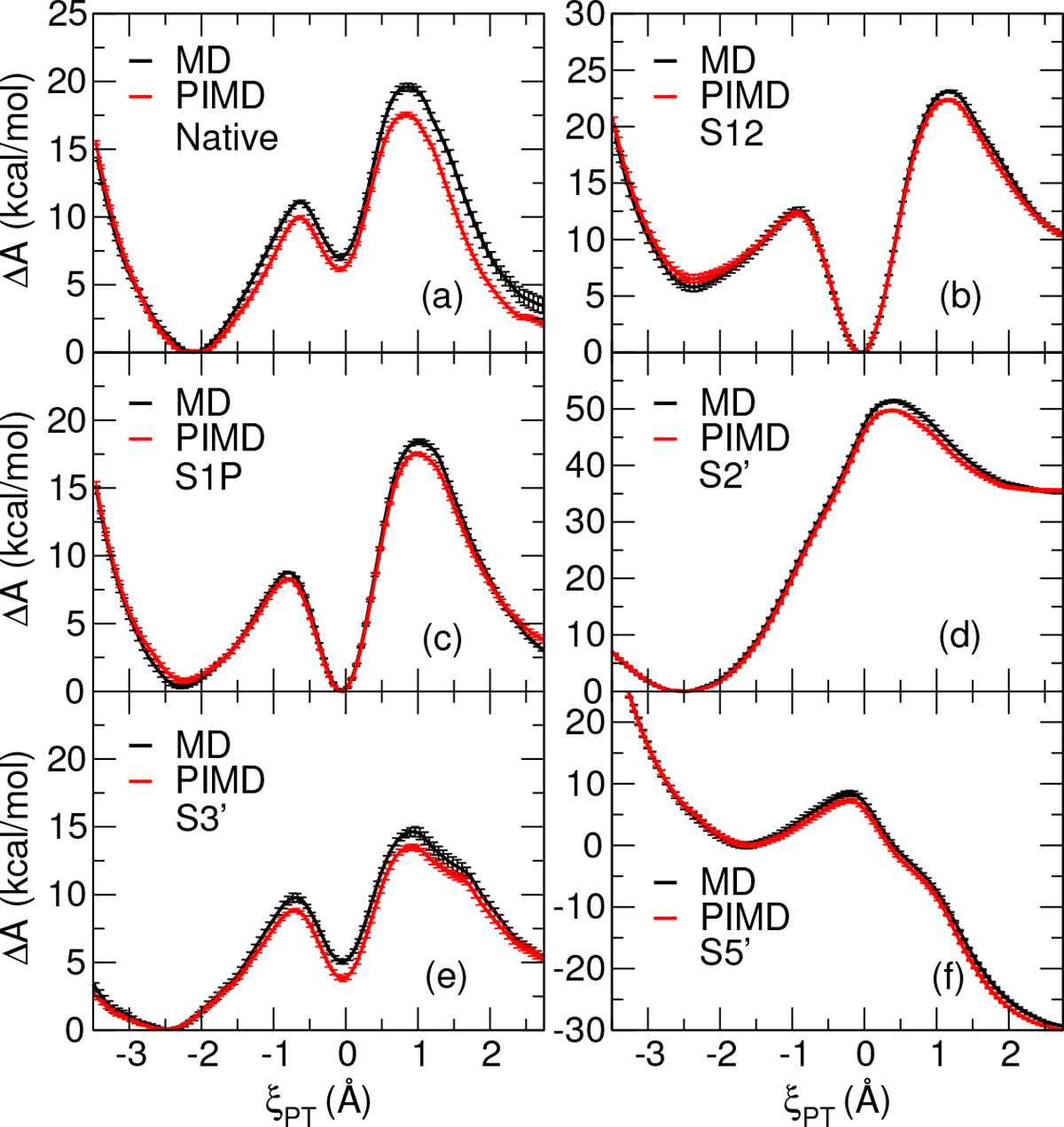
Comparison of DFTB2 QM/MM+DPRc FESs generated from classical MD with SPC/Fw and PIMD with q-SPC/Fw umbrella window simulations.

3.3. KIE values calculated with TD-FEP and Bigeleisen-Mayer equation

Table 2 compares KIE estimates of the native non-enzymatic model using the TD-FEP method to experimental values. The DFTB2 QM/MM and DFTB2 QM/MM+DPRc simulations were performed 4 times, and the results shown in the table are the average of the 4 KIE values and the standard error of the mean. The PBE0/6-31G* QM/MM simulations were performed only one time. The experimental values are for UpG in alkaline conditions.⁸ Although the DFTB2 QM/MM KIE values agree more closely with experiment than DFTB2 QM/MM+DPRc, the DFTB2 QM/MM+DPRc method does a much better job of reproducing PBE0/6-31G* results, to which it was parametrized. Considering the poor quality of the uncorrected DFTB2 FESs, one should be skeptical to rely on it for calculating KIE values.

Table 2:

Comparison of the native model reaction KIE values computed from PIMD simulations to experiment (Ref. 8).

Atom	DFTB2	DPRc	PBE0	Expt.
O2′	0.986 ± 0.000	0.989 ± 0.001	0.989	0.984
O5′	1.030 ± 0.001	1.024 ± 0.000	1.022	1.034
OP1	1.003 ± 0.002	1.003 ± 0.000	1.004	...
OP2	1.002 ± 0.001	1.002 ± 0.000	1.002	...

Table 3 compares DFTB2 QM/MM+DPRc KIE values computed from Bigeleisen’s equation applied to an ensemble of stationary structures and the TD-FEP KIE value calculated from PIMD simulations. As we’ve described, the Bigeleisen equation is applied many times corresponding to a collection of stationary structures obtained by geometry optimizing trajectory frames either for a minimum or a transition state. The table lists the mean KIE value, the standard error of the mean, the number of KIE values (the number transition state structures that we found), the standard deviation of the KIE values, and the minimum and maximum value in the observed KIE distribution.

Table 3:

Comparison of DFTB2+ML KIE values computed from path integral simulations to those computed from Bigeleisen’s equation. The columns N, σ, “Min.”, and “Max.” are the number of KIE values, the standard deviation of the KIE distribution, and minimum and maximum KIE values, respectively.

System	Atom	TD-FEP	Bigeleisen
		KIE	KIE	N	σ	Min.	Max.
Native	O2′	0.989 ± 0.001	0.991 ± 0.001	26	0.005	0.980	0.998
	O5′	1.024 ± 0.000	1.038 ± 0.002	26	0.008	1.023	1.051
	OP1	1.003 ± 0.000	1.004 ± 0.001	26	0.003	1.000	1.016
	OP2	1.002 ± 0.001	1.003 ± 0.000	26	0.002	0.999	1.007
S12	O2′	0.993 ± 0.001	0.996 ± 0.001	19	0.005	0.989	1.010
	O5′	1.013 ± 0.000	1.024 ± 0.002	19	0.009	1.004	1.035
	SP1	1.000 ± 0.000	1.001 ± 0.000	19	0.001	1.000	1.003
	SP2	1.000 ± 0.000	1.001 ± 0.000	19	0.001	0.998	1.003
S1P	O2′	0.990 ± 0.000	0.993 ± 0.001	62	0.005	0.983	1.005
	O5′	1.018 ± 0.000	1.032 ± 0.001	62	0.009	1.010	1.051
	SP1	1.000 ± 0.000	1.002 ± 0.000	62	0.002	0.994	1.007
	OP2	1.003 ± 0.000	1.003 ± 0.000	62	0.003	0.996	1.012
S2′	S2′	0.997 ± 0.000	1.001 ± 0.001	30	0.007	0.996	1.028
	O5′	1.021 ± 0.000	1.032 ± 0.002	30	0.014	0.993	1.054
	OP1	1.003 ± 0.000	1.008 ± 0.001	30	0.007	0.992	1.032
	OP2	1.002 ± 0.001	1.008 ± 0.002	30	0.010	0.995	1.051
S3′	O2′	0.988 ± 0.001	0.994 ± 0.001	19	0.005	0.986	1.005
	O5′	1.021 ± 0.001	1.037 ± 0.002	19	0.010	1.016	1.050
	OP1	1.002 ± 0.001	1.003 ± 0.001	19	0.004	0.997	1.010
	OP2	0.998 ± 0.000	1.001 ± 0.001	19	0.004	0.994	1.013
S5′	O2′	1.008 ± 0.001	1.026 ± 0.001	111	0.012	0.988	1.051
	S5′	1.000 ± 0.000	1.003 ± 0.000	111	0.002	0.998	1.024
	OP1	1.002 ± 0.001	1.004 ± 0.000	111	0.004	0.995	1.015
	OP2	1.002 ± 0.000	1.002 ± 0.000	111	0.003	0.993	1.009

The average O5′ (or S5′) KIE values obtained from Bigeleisen’s equation is often 0.01 units larger than those obtained from the TD-FEP method, which is a significant difference when it comes to KIEs; however, the distribution of KIE values that one obtains from the local harmonic approximation can vary by 0.03 units. Therefore, caution should be exercised when using the harmonic approximation in explicit solvent if only 1 structure was used. The average of many structures may be necessary to assign any confidence to the calculated value. The two methods agree much more closely for the non-bridge oxygen (or sulfur) secondary KIE values, which are close to unity.

3.4. QM/MM+DPRc KIE values computed along the reaction coordinate

One can use PIMD TD-FEP simulations to estimate KIE values as a function of collective variable. Figure 4 illustrates the ¹⁸O primary (O2′ and O5′) KIE values of the native non-enzymatic reaction as a function of ξ_PT. The KIE values were generated by restraining the centroid collective variable position with a harmonic restraint and treating the sampled state as the effective transition state ensemble when computing eq. 3, whereas the reactant state ensemble was simulated at the FES minimum. Each of the 4 ML parameter sets was simulated twice with different random number seeds, yielding 8 KIE estimates per ξ_PT value. The dots in Figure 4 are the raw KIE value estimates, and the black line is a Gaussian process regression fit through the scattered data. The red line is the ensemble average of the centroid ξ_PT value. The dashed green line is an overlay of the FES to aid the reader orient the relationship of the ξ_PT values to the location of the reaction minimum and transition state. The reaction mechanism is associative and proceeds through two distinct transition states separated by a shallow minimum. The first transition state is “early” (ξ_PT < 0) and characterized by partial formation of the O2′-P bond, whereas the second rate-controlling transition state is “late” (ξ_PT > 0) and characterized by partial cleavage of the O5′-P bond. It is noteworthy that the maximum O2′ and O5′ KIE values are normal (KIE >1) and occur at the corresponding early and late transition states, respectively, where the bonding environments are the most “loose” (lower frequency local vibrational modes), as expected for associative phosphoryl transfer mechanisms.^5,66

Figure 4:

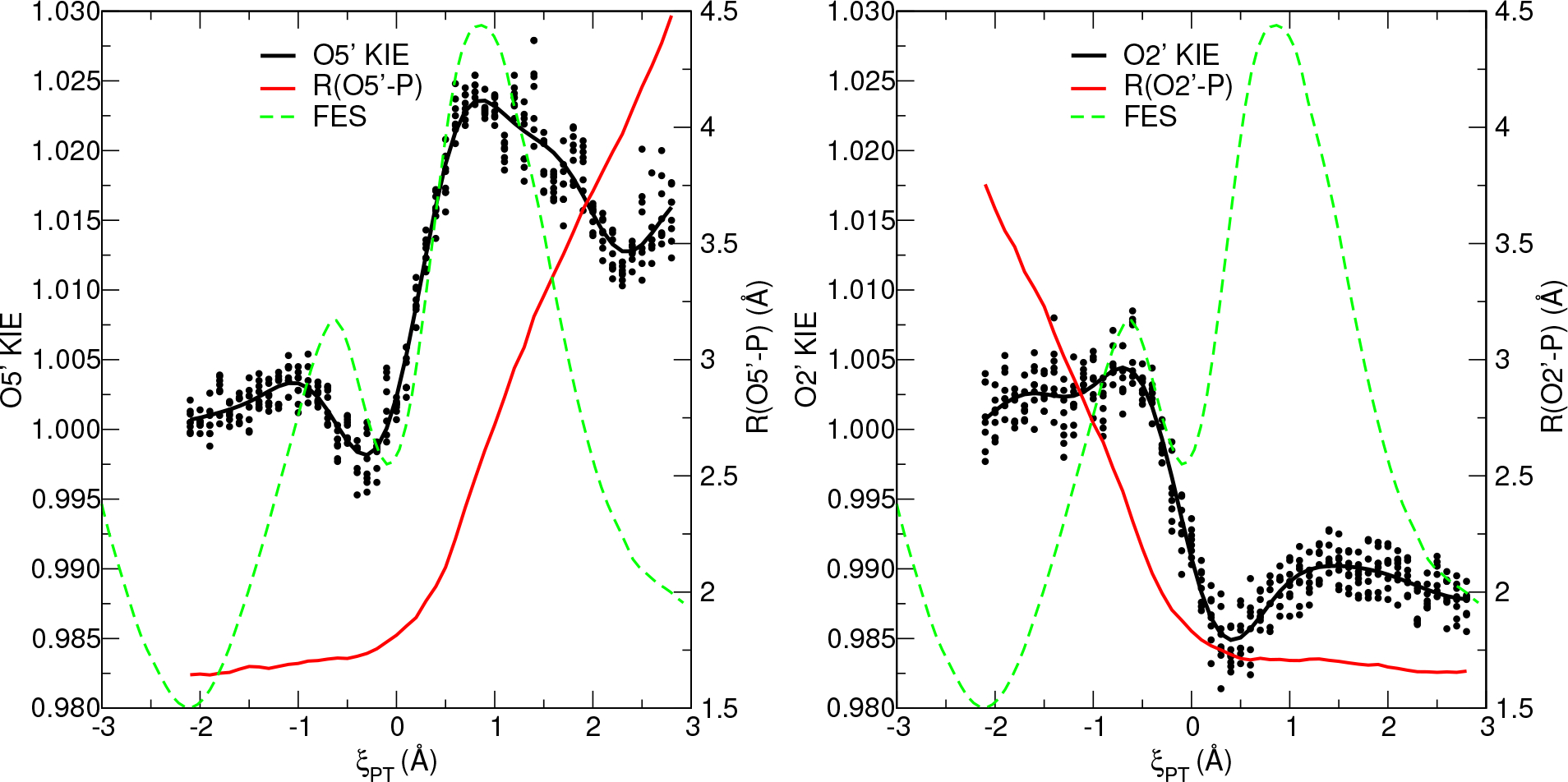
The O5′ and O2′ TD-FEP KIE values of the native reaction as a function of collective variable defining the position of the effective transition state. The solid black line is a fit through the KIE values. The red line is the average value of covalent bond length. The green line is an overlay of the FES.

3.5. Conclusion

We developed a new DFTB2+DPRc model (DFTB2 with a DPRc machine learning potential correction) and parametrized it to reproduce the PBE0/6-31G* QM/MM energies and forces of native and thio-substituted non-enzymatic models of RNA 2′-O-transphosphorylation. The DPRc potential applies corrections to the QM interactions and the QM/MM interactions out to 6Å without altering the MM atom interactions with other MM atoms. The parametrized model was found to significantly improve the prediction of free energy surfaces, computed from umbrella window simulations in explicit solvent with more than 2 orders of magnitude speed-up relative to the ab initio QM/MM simulations.

We interfaced the SANDER program within AMBER20 with the i-PI software package to perform path integral molecular dynamics simulations with the DFTB2 QM/MM+DPRc model. A series of umbrella window restraints were applied to the centroid positions, and the resulting path integral free energy surfaces were compared to those obtained from classical QM/MM molecular dynamics. It was found that nuclear quantum effects lower the activation free energy by an average of about 1.5 kcal/mol for these reactions.

The new interface between i-PI and SANDER module of AMBER allowed us to compute primary ¹⁸O kinetic isotope effects of the native model reactions from path integral molecular dynamics. We found that the DFTB2 QM/MM+DPRc does a much better job than uncorrected DFTB2 at reproducing the PBE0/6-31G* 2′ and 5′ primary kinetic isotope effects. We compared the kinetic isotope effect predictions made by TD-FEP and the local harmonic approximation, which involves finding geometry stationary points, diagonalizing a mass weighted Hessian, and evaluating the kinetic isotope value from the Bigeleisen equation. The comparison was made for the native and thio-substituted model reactions. The two methods predict 5′ kinetic isotope values that differ by approximately 0.01 units; however, the spread of computed values calculated from the local harmonic approximation vary by approximately 0.03 units. The DFTB2 QM/MM+DPRc method was used to map the TD-FEP kinetic isotope effect values as a function of collective variable by using umbrella window restraints to the centroid positions and treating the simulation as an effective transition state. Taken together, the QM/MM+DPrc model and i-PI PIMD simulations provide a powerful new tool to study mechanisms and pathways of phosphoryl transfer reactions and verify the structure and bonding of the transition states by prediction of kinetic isotope effects.