Evaluating statistical significance in a meta-analysis by using numerical integration

Graphical abstract

Abstract

Meta-analysis is a method for enhancing statistical power through the integration of information from multiple studies. Various methods for integrating p-values (i.e., statistical significance), including Fisher’s method under an independence assumption, the permutation method, and the decorrelation method, have been broadly used in bioinformatics and computational biotechnology studies. However, these methods have limitations related to statistical assumption, computing efficiency, and accuracy of statistical significance estimation. In this study, we proposed a numerical integration method and examined its theoretical properties. Simulation studies were conducted to evaluate its Type I error, statistical power, computational efficiency, and estimation accuracy, and the results were compared with those of other methods. The results demonstrate that our proposed method performs well in terms of Type I error, statistical power, computing efficiency (regardless of sample size), and statistical significance estimation accuracy. P-value data from multiple large-scale genome-wide association studies (GWASs) and transcriptome-wise association studies (TWASs) were analyzed. The results demonstrate that our proposed method can be used to identify critical genomic regions associated with rheumatoid arthritis and asthma, increase statistical significance in individual GWASs and TWASs, and control for false-positives more effectively than can Fisher’s method under an independence assumption. We created the software package Pbine, available at GitHub (https://github.com/Yinchun-Lin/Pbine).

1. Introduction

Fisher’s p-value combination method [1], which integrates statistical significance (i.e., p-value $p_i$) from many statistical hypothesis tests was originally proposed to examine a joint null hypothesis (i.e., an intersection of the individual null hypotheses) in a meta-analysis [2]. Test statistic of Fisher’s method is defined as negative two times the summation of log-transformed p-values (i.e., $F=-2{\sum }_i\mathrm{l}\mathrm{n}(p_i)$) [1]. This method has been broadly applied in bioinformatics and computational biotechnology studies, such as the meta-analysis of genome-wide association study (GWAS) [3], [4], [5] and that of transcriptome-wide association study (TWAS) [6], [7], [8].

If all the p-values $\left\{p_i,i=1,\cdots ,K\right\}$ follow Uniform (0,1) distribution under a null hypothesis independently, test statistic $F$ follows a chi-squared distribution with $2K$ degrees of freedom. As such, the exact p-value ($p_{\mathrm{F}}$) of F can be derived. However, when the p-values are correlated, the mathematical derivation for the sampling distribution of $F$ becomes intractable. Remarkably, ignorance of the correlation of p-values will inflate false-positives in the subsequent statistical inference [9].

The permutation procedure [10], which involves non-parametric resampling without replacement based on a set of observed data, has been applied to generate a null distribution and calculate an empirical p-value ($p_{\mathrm{P}}$) of $F$ when the independence assumption of p-values is violated. The permutation procedure is simple in concept and robust to various correlation structures of p-values. However, this method has some limitations. For instance, in a GWAS with a large sample size, which is used to evaluate the phenotype–genotype relationship, permutations over the phenotype status of study samples require intensive computation. Permutations over single nucleotide polymorphisms (SNPs) may distort the inherent structure of SNPs (i.e., linkage disequilibrium). In addition, numerous permutations and intensive computation are required for a correction for multiple testing in GWASs and TWASs [11], [12].

The permutation procedure requires raw data (only p-value data itself cannot perform permutations), which are not always available. For instance, in a meta-analysis of GWAS, the p-values of single-locus association tests from public genomic databases (e.g., GWAS Catalog [13] and GWAS Central [14]) are available and can be combined to infer the genetic association between SNPs and a phenotype of interest. However, no raw genotype and phenotype data are provided in GWAS Catalog and GWAS Central.

Without the need for raw data, a decorrelation procedure [15] transforms dependent p-values into independent p-values only on the basis of p-value data and the correlation structure of the p-values. The distribution F can thus be derived and computed rapidly. However, in this study, we demonstrated that the order of the combination of p-values influences the results (the order-noninterchangeable property). For example, if $p_1=0.9970$ and $p_2=0.1903$ are combined and their correlation coefficient $r$ = 0.5, then the decorrelation procedure provides a p-value of F ($p_{\mathrm{D}})=0.0297$; however, if the order of the combination of p-values is reversed, then $p_{\mathrm{D}}=0.5060$.

Considering the permutation and decorrelation methods’ limitations, we suggested a numerical integration method ($p_{\mathrm{N}}$) to evaluate the statistical significance of F. Herein, the theoretical properties of a p-value combination are examined. Type I error, statistical power, computational efficiency, and estimation accuracy were evaluated through simulation studies and compared with those of Fisher’s method under an independence assumption ($p_{\mathrm{F}}$), permutation ($p_{\mathrm{P}}$), and decorrelation ($p_{\mathrm{D}}$). Real-world examples of meta-analyses of GWASs and meta-analyses of TWASs are given. R codes Pbine are provided in GitHub at https://github.com/Yinchun-Lin/Pbine.

2. Methods

2.1. Proposed method

Let $\mathbf{R}=\left\{p_i,i=1,\cdots ,K\right\}$ denote a list of dependent p-values from K hypothesis tests with a correlation $corr\left(\mathbf{R}\right)=\mathrm{\Sigma }$. Because the correlation is approximately invariant under monotone transformations [15], $\mathbf{R}$ satisfies the following transformation T: $\mathbf{R}=1-\mathrm{\Phi }\{\mathbf{C}{\mathrm{\Phi }}^{-1}(1-{\mathbf{R}}^{\#})\}$, where $\mathbf{C}$ is the Cholesky factor of $\mathrm{\Sigma }$ (i.e. $\mathrm{\Sigma }={\mathbf{C}\mathbf{C}}^{\mathrm{T}}$), ${\mathbf{R}}^{\#}$ is a list of independent p-values, and $\mathrm{\Phi }$ denotes the cumulative distribution function of a standard normal random variable. Let $\left\{p_i^{\ast },i=1,\cdots ,K\right\}$ be the p-values calculated from the raw data observations for testing K null hypotheses. In our method, the p-value of F is calculated as follows:

$$p_{\text{N}}={\int }_D{J}_{T^{-1}},$$

where $J_{T^{-1}}$ is the joint probability density function of $\mathbf{R}$ (Text S1), $D$ is the region enclosed by $0<p_i<1,\forall i$ and $\prod p_i<\prod p_i^{\ast }$. Noted that $p_{\mathrm{N}}$ is fixed for any permutation on $\left\{p_i^{\ast },i=1,\cdots ,K\right\}.$

For reduced case $K=2$ with correlation $0<r<1$, then $\mathbf{C}=\left(\begin{array}{cc}1& 0\\ r& \sqrt{1-r^2}\end{array}\right)$. The p-value of $F$ is derived (Text S1) as follows:

$$p_N=\underset{D}{\iint }\frac{1}{\sqrt{1-r^2}}\mathrm{\Phi }\prime \left(\frac{{\mathrm{\Phi }}^{-1}\left(1-v\right)-r{\mathrm{\Phi }}^{-1}\left(1-u\right)}{\sqrt{1-r^2}}\right){\left({\mathrm{\Phi }}^{-1}\right)}^{\prime }\left(1-v\right)d\left(u,v\right),$$ (1)

where $D=\left\{\left(u,v\right)|0<u,v<1,uv<p_1^{\ast }{p}_2^{\ast }\right\}$ and ${\mathrm{\Phi }}^{\prime }$ is the derivative of a cumulative distribution function of a standard normal variate.

A logarithm transformation of $p_i$’s was considered to prevent integration on curvilinear region $D$. $p_{\mathrm{N}}$ in Eq. (1) can be rewritten as follows:

$$p_N=1-\underset{D^{\prime }}{\iint }\frac{1}{\sqrt{1-r^2}}\mathrm{\Phi }\prime \left(\frac{{\mathrm{\Phi }}^{-1}\left(1-e^{v\prime }\right)-r{\mathrm{\Phi }}^{-1}\left(1-e^{u^{\prime }}\right)}{\sqrt{1-r^2}}\right){\left({\mathrm{\Phi }}^{-1}\right)}^{\prime }\left(1-e^{v\prime }\right)e^{u\prime }{e}^{v\prime }d\left(u\prime ,v\prime \right)$$

where $\left(u^{\prime },v^{\prime }\right)=\left(\ln \left(u\right),\ln \left(v\right)\right)$ and $D^{\prime }=\left\{\left(u^{\prime },v^{\prime }\right)|u^{\prime },v^{\prime }<0,u^{\prime }+v^{\prime }>\ln \left(p_1^{\ast }\right)+\ln \left(p_2^{\ast }\right)\right\}$.

If correlation of two p-values is $r=0$, $p_{\mathrm{N}}$ in Eq. (1) can be reduced to Fisher’s method as follows:

$$p_{\mathrm{N}}=p_{\mathrm{F}}=p_1^{\ast }{p}_2^{\ast }-p_1^{\ast }{p}_2^{\ast }\mathrm{l}\mathrm{n}(p_1^{\ast }{p}_2^{\ast })$$ (2)

For $K=2$, the detailed derivation of $J_{T^{-1}}$ (Text S1), the symmetric behavior and limiting behavior of $J_{T^{-1}}$ (Text S2), and a comparison of the p-value of our proposed method ($p_{\mathrm{N}}$) with the individual p-values (Text S3 and Fig. S1) are provided.

2.2. Simulation studies

To evaluate the Type I error, power, and computation time of the p-value combination methods, bivariate linear regression models were applied to generate data in the simulation studies. Model parameters were assigned or estimated following the purposes of the simulation study. The p-values of our numerical integration method ($p_{\mathrm{N}}$), the Fisher’s method under an independence assumption ($p_{\mathrm{F}}$), and the decorrelation method ($p_{\mathrm{D}}$) were calculated and compared with the benchmark method – the permutation method ($p_{\mathrm{P}}$).

2.2.1. Evaluation of Type I error

A bivariate linear regression model was applied to generate two phenotypes ($y_{\mathit{ng}}$, $z_{\mathit{ng}}$) and gene expression ($x_{\mathit{ng}}$) data in the simulation study as follows:

$$\left(\genfrac{}{}{0.0pt}{}{y_{\mathit{ng}}}{z_{\mathit{ng}}}\right)=\left(\genfrac{}{}{0.0pt}{}{{{\beta }_{j}x}_{\mathit{ng}}}{{{\gamma }_{j}x}_{\mathit{ng}}}\right)+\left(\genfrac{}{}{0.0pt}{}{{\epsilon }_{\mathit{ng}}}{{\phi }_{\mathit{ng}}}\right),n=1,\cdots ,N,g=1,\cdots ,G$$ (3)

where N denotes the total number of samples and G indicates the total number of genes. Random error terms ${\epsilon }_{\mathit{ng}}$ and ${\phi }_{\mathit{ng}}=w{\epsilon }_{\mathit{ng}}+(1-w){∊}_{\mathit{ng}}$ have correlation coefficient $corr\left({\epsilon }_{\mathit{ng}},{\phi }_{\mathit{ng}}\right)=w$. We assumed that ${\epsilon }_{\mathit{ng}}$ and ${∊}_{\mathit{ng}}$ would be independent white noises following a standard normal distribution. Gene expression $x_{\mathit{ng}}$ was independently generated from $\mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\left(0,1\right)$.

Here, we considered the regression coefficient under the null hypothesis: ${\beta }_j={\gamma }_j=0$; sample size $N=500$; gene number $G=2,000$; simulation replications $K=2,000$. Given a specified $w$, we generated the phenotypes and gene expression data. In each of the simulated datasets, p-values ${\mathit{p}}_{\mathrm{y}}$ and ${\mathit{p}}_{\mathrm{z}}$ were obtained by testing null hypotheses ${\mathrm{H}}_{0g}^{\beta }:{\beta }_g=0$ and ${\mathrm{H}}_{0g}^{\gamma }:{\gamma }_g=0$, respectively, through Student’s t test.

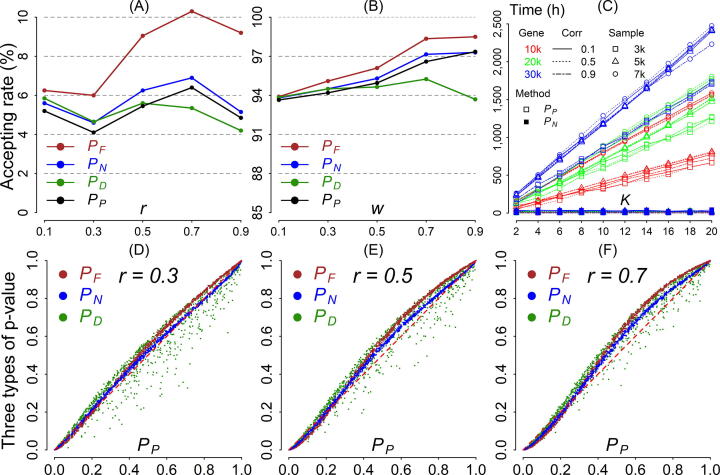
The results demonstrate that the methods control Type I error well for uncorrelated p-values, i.e., $corr\left({\mathit{p}}_{\mathrm{y}},{\mathit{p}}_{\mathrm{z}}\right)=0$ (Fig. 1A). For the positively correlated p-values $\left({\mathit{p}}_{\mathrm{y}},{\mathit{p}}_{\mathrm{z}}\right)$, Fisher’s method (red line) under an independence assumption ($p_{\mathrm{F}}$) exhibited an inflated Type I error particularly for an increased correlation of p-values. Our method $p_{\mathrm{N}}$ and the decorrelation procedure $p_{\mathrm{D}}$ exhibited a Type I error similar to that of the benchmark method $p_{\mathrm{P}}$; the false-positive was 0.05–0.06. This indicates that p-value dependency must be considered when the sampling distribution of a p-value combination is derived. Therefore, our proposed method controls Type I errors well.

Fig. 1.

(A) Type I error for the p-value combination methods. The x-axis represents correlation $corr\left({\mathit{p}}_{\mathrm{y}},{\mathit{p}}_{\mathrm{z}}\right)=r$. The y-axis represents Type I error. (B) Statistical power for the p-value combination methods. The x-axis represents correlation $corr\left({\epsilon }_{\mathit{ng}},{\phi }_{\mathit{ng}}\right)=w$. The y-axis represents statistical power. (C) Computation time of the proposed method (${\mathit{p}}_{\mathbf{N}}$) and the permutation method (${\mathit{p}}_{\mathbf{P}}$). The x-axis indicates number of thousand permutations (K). The y-axis indicates computation time. Red, green, and blue lines denote gene sizes G of 10,000, 20,000, and 30,000, respectively. The squares, triangles, and circles denote sample sizes N of 3,000, 5,000, and 7,000, respectively. Solid, dotted, and dot-dashed lines represent correlation coefficients $r$ of 0.1, 0.5, and 0.9, respectively. (D)–(F) Estimation accuracy of p-value. The x-axis represents the p-values of the benchmark method ($p_{\mathrm{P}}$). The y-axis indicates the p-values of the other p-value combination methods: $p_{\mathrm{F}}$, brown; $p_{\mathrm{N}}$, blue; $p_{\mathrm{D}}$, green). The results based on correlation coefficients $r=$ 0.3, 0.5, and 0.7 are arranged from left to right.

2.2.2. Evaluation of statistical power

A bivariate linear regression model was applied to generate two phenotypes ($y_{\mathit{ng}}$, $z_{\mathit{ng}}$) and gene expression ($x_{\mathit{ng}}$) data in the simulation study as follows:

$$\left(\genfrac{}{}{0.0pt}{}{y_{\mathit{ng}}}{z_{\mathit{ng}}}\right)=\left(\genfrac{}{}{0.0pt}{}{{{\beta }_{j}x}_{\mathit{ng}}}{w{{\beta }_{j}x}_{\mathit{ng}}}\right)+\left(\genfrac{}{}{0.0pt}{}{{\epsilon }_{\mathit{ng}}}{{\phi }_{\mathit{ng}}}\right),n=1,\cdots ,N,g=1,\cdots ,G$$ (4)

where N indicates the total number of samples and G indicates the total number of genes. That is, $z_{\mathit{ng}}=w{y}_{\mathit{ng}}+\left(1-w\right){∊}_{\mathit{ng}}$ and ${\phi }_{\mathit{ng}}=w{\epsilon }_{\mathit{ng}}+(1-w){∊}_{\mathit{ng}}$, and $corr\left(y_{\mathit{ng}},z_{\mathit{ng}}\right)=corr\left({\epsilon }_{\mathit{ng}},{\phi }_{\mathit{ng}}\right)=w$. We assumed that random error terms ${\epsilon }_{\mathit{ng}}$ and ${∊}_{\mathit{ng}}$ would follow an independent standard normal random distribution individually. Gene expression $x_{\mathit{ng}}$ was generated from $\mathrm{U}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\left(0,1\right)$ independently. Here, we considered ${\beta }_j=0.6$; $w=0.1,0.3,0.5,0.7,0.9$; sample size $N=500$; number of genes $G=2,000$; simulation replications $K=2,000$. P-values ${\mathit{p}}_{\mathrm{y}}$ and ${\mathit{p}}_{\mathrm{z}}$ were obtained by testing null hypotheses ${\mathrm{H}}_{0g}^{\beta }:{\beta }_g=0$ and ${\mathrm{H}}_{0g}^{\gamma }:{\gamma }_g=0,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{\gamma }_g=w{\beta }_g$. The relationship between $corr\left({\epsilon }_{\mathit{ng}},{\phi }_{\mathit{ng}}\right)=w$ and $corr\left({\mathit{p}}_{\mathrm{y}},{\mathit{p}}_{\mathrm{z}}\right)=r$ is discussed (Text S4 and Fig. S2).

The results demonstrated that the four methods have similar power and that the power increases with $r$ (Fig. 1B). $p_{\mathrm{F}}$ has the highest power, particularly for a higher $r$; however, the high power is accompanied by an inflated Type I error as mentioned in the previous section (Fig. 1A). $p_{\mathrm{D}}$ has the lowest power and deviates from the benchmark $p_{\mathrm{P}}$, particularly for a high $r$. The proposed method $p_{\mathrm{N}}$ has high power similar to that of the benchmark $p_{\mathrm{P}}$.

2.2.3. Evaluation of computation time

The simulation model for an evaluation of Type I error was then applied. We compared the computation time between the proposed method ($p_{\mathrm{N}}$) and the benchmark method ($p_{\mathrm{P}}$) with various sample sizes ($N=$ 3,000, 5,000, and 7,000), gene numbers ($G=$ 10,000, 20,000, and 30,000), correlation coefficients ($w=0.1,0.5,\mathrm{a}\mathrm{n}\mathrm{d}0.9$), and permutation times ($K=$ 2,000–20,000, with increments of 2,000). The results show that the computation time of the proposed method ($p_{\mathrm{N}}$) is unchanged with the sample size, number of genes, and correlation coefficient (Fig. 1C). The computation time for the permutation method ($p_{\mathrm{P}}$) increases with sample size, number of genes, and permutation time, but it did not change as the correlation coefficient increased; it required approximately 2,500 h to compute 30,000 pairs of p-value combinations. Our proposed method was more computationally efficient, requiring < 10 h for computation. Because Fisher’s method under an independence assumption ($p_{\mathrm{F}}$) and the decorrelation method ($p_{\mathrm{D}}$) do not involve complex re-sampling or integration procedures, they are computationally efficient.

2.2.4. Evaluation of estimation accuracy

We applied the model for an evaluation of Type I error with $G=1,000$, $N=500,$ and $K=5,000$, and compared the estimation accuracy of the three p-value combination methods $p_{\mathrm{N}}$, $p_{\mathrm{F}}$, and $p_{\mathrm{D}}$ with that of the benchmark permutation $p_{\mathrm{P}}$. Correlation coefficients $corr\left({\mathit{p}}_{\mathrm{y}},{\mathit{p}}_{\mathrm{z}}\right)=r=0.1,0.5,0.9$ were considered. The results demonstrate that $p_{\mathrm{N}}$, $p_{\mathrm{F}}$, and $p_{\mathrm{D}}$ deviate from the benchmark $p_{\mathrm{P}}$ as $corr\left({\mathit{p}}_{\mathrm{y}},{\mathit{p}}_{\mathrm{z}}\right)=r$ increases (Fig. 1D–1F). In addition, $p_{\mathrm{D}}$ exhibits a certain proportion of outliers (Fig. 1D–1F). The biased estimation can be explained by the order-noninterchangeable property (Text S5) and non-uniformity property (Fig. S3) of $p_{\mathrm{D}}$. Compared with $p_{\mathrm{F}}$ and $p_{\mathrm{D}}$, the proposed method ($p_{\mathrm{N}}$) is closest to the benchmark $p_{\mathrm{P}}$. Thus, the proposed method provides a more accurate estimate than do $p_{\mathrm{F}}$ and $p_{\mathrm{D}}$.

3. Real data applications

3.1. Meta-GWAS for rheumatoid arthritis

This meta-analysis identified SNPs associated with rheumatoid arthritis on the basis of two large-scale population-based GWASs – The North American Rheumatoid Arthritis Consortium (NARAC) data $\left(N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=868,N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=1,194\right)$[16] and Wellcome Trust Case Control Consortium (WTCCC) data $\left(N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=1,999,N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=3,002\right)$ [17]. In each of the two GWASs, a logistic regression analysis with covariate adjustment for sex and SNP coding based on an additive genetic model was performed to examine the genetic associations between rheumatoid arthritis disease status and individual SNP markers. At each SNP, p-values based on NARAC and WTCCC data were obtained separately.

We applied Fisher’s ($p_{\mathrm{F}}$) and our ($p_{\mathrm{N}}$) methods to combine the two p-values at each SNP locus in the NARAC and WTCCC data. There were 4,963 statistical tests (because of 4,963 SNPs on chromosome 6) in this meta-GWAS. Bonferroni’s correction [18] for multiple testing was performed to obtain adjusted p-values for $p_{\mathrm{F}}$ and $p_{\mathrm{N}}$ separately. The result demonstrate that both the methods could be used to identify the major histocompatibility complex (MHC) region on chromosome 6p21.3 (Fig. 2), which is strongly associated with rheumatoid arthritis [19], [20]. Our method ennabled us to identify the SNP rs9391858 (p = $3.495\times {10}^{-6}$) truly associated with rheumatoid arthritis [21] (Fig. 2); however, the individual GWASs could not detect this SNP $\mathrm{p}=1.020\times {10}^{-5}$ in NARAC and $\mathrm{p}=1.291\times {10}^{-4}$ in WTCCC; Fig. S4). Fisher’s method but not ours identified six false-positive SNPs: rs2394102, rs11752073, rs12697946, rs9394169, rs3818528, and rs3130014 (Fig. 2).

Fig. 2.

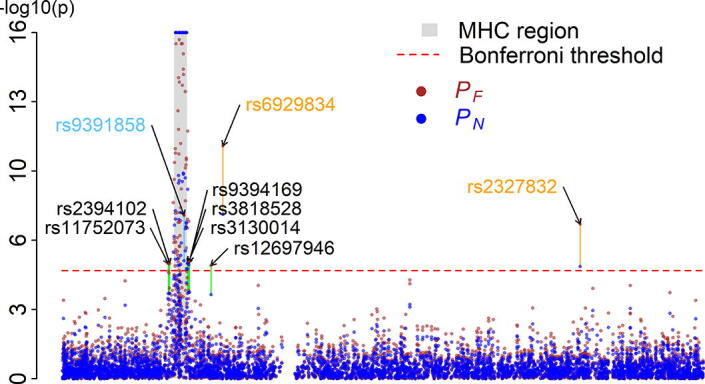
Manhattan plots for chromosome 6 in the meta-GWAS. This meta-GWAS contained 4,963 SNPs on chromosome 6. The Fisher’s method ($p_{\mathrm{F}}$) and our method ($p_{\mathrm{N}}$) were employed. Each point indicates a SNP. The x-axis indicates physical position of a SNP. The y-axis indicates p-value in a scale of –log₁₀. The green lines indicate false-positive events identified by the Fisher’s method ($p_{\mathrm{F}}$) but not by our method ($p_{\mathrm{N}}$); they involved six SNPs: rs11752073, rs2394102, rs3130014, rs3818528, rs9394169, and rs12697946 (green line). The orange lines indicate false-positive events identified by both of the Fisher’s method ($p_{\mathrm{F}}$) and our method ($p_{\mathrm{N}}$). The light blue line indicates the SNP known to be associated with rheumatoid arthritis and identified by the Fisher’s method ($p_{\mathrm{F}}$) and our method ($p_{\mathrm{N}}$), but not by either of the two studies (Fig. S4). The red dashed line indicates the significance level after Bonferroni correction for multiple testing.

The real data analysis demonstrated that our method can be used to identify crucial genomic regions strongly associated with rheumatoid arthritis, detect some of rheumatoid arthritis-associated loci not detected by individual GWASs, and control for false-positive more efficiently than can Fisher’s method.

3.2. Meta-TWAS for rheumatoid arthritis

This meta-analysis was performed to identify genes differentially expressed in patients with rheumatoid arthritis and normal controls of European descent based on the two large-scale TWASs: Eyre et al. $\left(N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=13,838,N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=33,742\right)$ [22] and Stahl et al. $\left(N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=5,539,N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=20,169\right)$ [23]. In each TWAS, the gene-level p-values used to examine the association of rheumatoid arthritis disease status with gene expression were downloaded from webTWAS [24]. However, raw gene expression data were unavailable on the website. When the p-value data were downloaded, Elastic-net was used as a model for transcriptome data prediction in the MetaXcan framework [25].

We applied Fisher’s ($p_{\mathrm{F}}$) and our ($p_{\mathrm{N}}$) methods to combine the two p-values from the two TWASs. There were 3,175 statistical tests (because of 3,175 genes overlapping between the two studied TWAS datasets) in this meta-TWAS. Bonferroni’s correction [18] for multiple testing was performed to obtain adjusted p-values for $p_{\mathrm{F}}$ and $p_{\mathrm{N}}$ separately. The results indicate that both methods identified the MHC region as a key genomic region for rheumatoid arthritis (Fig. 3). Fisher’s method identified 11 genes outside the MHC region. Except ANKRD55 was a true-positive, all other 10 genes were false-positively identified. Our method did not have false-positives but failed to detect ANKRD55 ($p_{\mathrm{N}}=4.410\times {10}^{-5}$). Our and Fisher’s methods did not identify additional genes associated with rheumatoid arthritis detected by individual TWASs; nevertheless, our method demonstrated a more significant signal for several rheumatoid arthritis genes. For instance, in the TWAS of Eyre et al [22], the TWAS of Stahl et al [23], and this meta-TWAS, the p-values were $\mathrm{p}=1.93\times {10}^{-6}$, $\mathrm{p}=6.33\times {10}^{-7}$, and $\mathrm{p}=1.39\times {10}^{-7}$, respectively, for AFF3 on chromosome 2, and $\mathrm{p}=3.07\times {10}^{-5}$, $\mathrm{p}=1.30\times {10}^{-5}$, and $\mathrm{p}=4.09\times {10}^{-6}$, respectively, for IRF5 on chromosome 7 (Fig. S5). Thus, this real data analysis demonstrated the inference of our meta-TWAS.

Fig. 3.

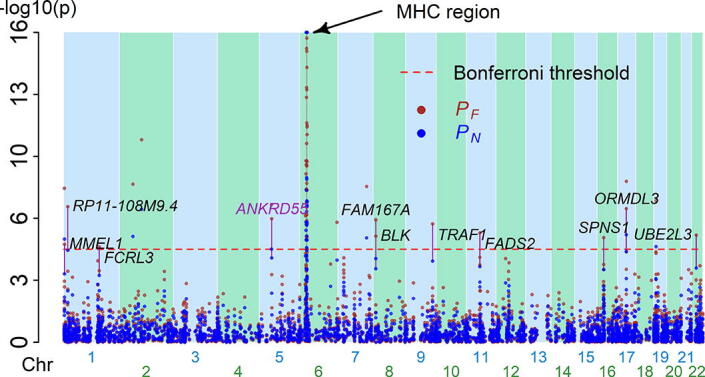
Manhattan plots for 22 autosomes in the meta-TWAS. This meta-TWAS contained 3,175 genes overlapping between the two studied TWAS datasets. The Fisher’s method ($p_{\mathrm{F}}$) and our method ($p_{\mathrm{N}}$) were employed. Each point indicates a gene. The x-axis indicates the physical position of a gene in an autosome. The y-axis indicates p-value in a scale of –log₁₀. The 11 purple lines indicate the genes for which Fisher’s method ($p_{\mathrm{F}}$) reported genetic association but our method ($p_{\mathrm{N}}$) did not. All genes, ANKRD55, were false-positively detected. The red dashed line indicates the significance level after Bonferroni correction for multiple testing.

3.3. Meta-TWAS for asthma

We evaluated the performance of the proposed method in combining p-values from more than two studies. We downloaded the gene-level p-values data in four large-scale studies for asthma from webTWAS [24] – Canela-Xandri et al. [26] with $N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=52,269$ and $N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=399,995$; Zhu et al. [27] with $N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=14,085$ and $N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=76,768$; Zhu et al. [28] with $N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=46,802$ and $N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=347,481$; and Demenais et al. [29] with $N_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}=19,954$ and $N_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{l}}=107,715$. We analyzed 15 genes, including 10 asthma-associated genes (HLA-G, ATP6V1G2, TAP1, TRIM10, HLA-DRB1, LST1, HLA-DRB5, DDX39B, MSH5, and HLA-A) in the MHC region and five genes that they are located outside the MHC region and no studies have reported association of asthma with the genes (PHIP, EED, PYGB, SMARCD2, and BORCS8) (Table S1).

We applied Fisher’s ($p_{\mathrm{F}}$) and our ($p_{\mathrm{N}}$) methods to identify differentially expressed genes in this meta-TWAS. After applying Bonferroni’s adjustment for multiple testing correction, the adjusted p-values are provided (Table 1). Fisher’s method ($p_{\mathrm{F}}$) identified all the ten asthma-associated genes, but also identified a high proportion of false-positive genes. Our method ($p_{\mathrm{N}}$) identified most of the asthma-associated genes, except for HLA-DRB5 (adjusted p-value = 0.069) and controlled false positive well. The results suggest that our method performs well and better than Fisher’s method in combining more than two p-values.

Table 1.

Our method performs better than Fisher’s method when combining more than two p-values. Ten asthma related genes and five asthma unrelated gene were analyzed in this meta-TWAS. Adjusted p-values of Fisher’s method ($p_{\mathrm{F}}$), our method with equal weights ($p_{\mathrm{N}}$), and our method with unequal weights ($p_{\mathrm{N}}^w$) are provided. All the p-values were adjusted using Bonferroni’s correction for multiple testing. The numbers marked in bold indicate they are statistically significant.

	Gene name	Chromosome	$p_{\mathrm{F}}$	$p_{\mathrm{N}}^w$	$p_{\mathrm{N}}$
Asthma	HLA-G	Chr. 6	0.0000127	0.0244885	0.0012742
Related	ATP6V1G2	Chr. 6	0.0005959	0.0030811	0.0168662
Genes	HLA-DRB5	Chr. 6	0.0059697	0.0386449	0.0689027
	TAP1	Chr. 6	0.0003276	0.0025073	0.0118823
	TRIM10	Chr. 6	0.0000009	0.0002722	0.0000589
	HLA-DRB1	Chr. 6	0.0000018	0.0004108	0.0003191
	LST1	Chr. 6	0.0000009	0.0002963	0.0000931
	DDX39B	Chr. 6	0.0000008	0.0001398	0.0000000
	MSH5	Chr. 6	0.0005163	0.0009750	0.0154954
	HLA-A	Chr. 6	0.0016827	0.0046854	0.0318339
Asthma	PHIP	Chr. 6	0.0418319	0.0986147	0.2299088
Unrelated	EED	Chr. 11	0.0094608	0.0100037	0.0915084
Genes	PYGB	Chr. 20	0.0124950	0.0805022	0.1086624
	SMARCD2	Chr. 17	0.0131833	0.0153122	0.1123372
	BORCS8	Chr. 19	0.0233820	0.1422346	0.1601654

Furthermore, our method can assign different weights to p-values in different TWASs. Here, the sample size of a study relative to the total sample size in the four TWASs was calculated as a weight; that is, a higher weight was assigned to a study with a higher sample size. Our weighted method ($p_{\mathrm{N}}^w$) can identify all the ten asthma-associated genes, including HLA-DRB5 that cannot be detected by the equal-weighted method ($p_{\mathrm{N}}$). However, $p_{\mathrm{N}}^w$ obtained some false-positive findings, such as EED and SMARCD2 in this analysis.

4. Conclusion and discussion

In this study, we proposed a novel numerical integration method ($p_{\mathrm{N}}$) to evaluate statistical significance by combining correlated p-values from multiple studies in a meta-analysis. The proposed method is simple in concept and flexible to various correlation structures. Our theoretical investigation and simulation studies demonstrated that our proposed method performs well in terms of Type I error, statistical power, computing efficiency (regardless of the sample size), and statistical significance estimation accuracy. Real applications in large-scale GWASs and TWASs for rheumatoid arthritis and asthma facilitated efficient identification of critical genomic regions, such as the MHC region, and genes associated with rheumatoid arthritis and asthma, not reported in the previous GWASs or TWASs. We developed Pbine (https://github.com/Yinchun-Lin/Pbine) for meta-analysis based on a combination of p-values from multiple studies. Our method can combine p-values from more than two studies with different sample sizes and precision so as to different levels of importance and information. The incorporation of unequal weights into a p-value combination for more than two studies has been implemented into Pbine.

The results in our simulation studies and real data analyses demonstrated that our method outperforms Fisher’s method. We discussed the weakness of the decorrelation method – an order-noninterchangeable property. Although $p_{\mathrm{D}}$ can be calculated in either an ascending order or a descending order of p-values, we showed that p-values of these two procedures in the decorrelation method violate the uniformity property under a null distribution – the ascending order method ($p_{\mathrm{D}\mathrm{A}}$) tends to have more false negative and the descending order method ($p_{\mathrm{D}\mathrm{D}}$) have more false positive, particularly at the case with a high between-study correlation of p-values (Fig. S3). When we applied $p_{\mathrm{D}\mathrm{A}}$ and $p_{\mathrm{D}\mathrm{D}}$ in the meta-GWAS and meta-TWAS for rheumatoid arthritis, we did find a number of false-positive and false-negative findings (Table S2).

In addition to the methods discussed in this paper, studies have reported other p-value combination methods [30]. Some of these methods depend on p-value independency assumptions [31], [32], parametric assumptions [33], [34], and mathematical approximations such as Satterthwaite’s approximation [35], [36]. These methods may be efficient in computation. However, when their assumptions are violated, their performance is negatively affected by inflated Type I error, particularly when significance level $\mathrm{\alpha }$ is low [37]. In addition, several methods have been developed on the basis of a generalization of Fisher’s product p-value method, such as the weighted [38], truncated [15], and rank-truncated [39] product p-value methods. Our method can be generalized to more complicated cases.

CRediT authorship contribution statement

Yin-Chun Lin: Methodology, Software, Formal analysis, Writing – original draft, Writing – review & editing. Yu-Jen Liang: Data curation, Resources. Hsin-Chou Yang: Conceptualization, Methodology, Writing – original draft, Writing – review & editing, Resources, Supervision, Funding acquisition.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: