Context Matters: Recovering Human Semantic Structure from Machine Learning Analysis of Large‐Scale Text Corpora

Abstract

Applying machine learning algorithms to automatically infer relationships between concepts from large‐scale collections of documents presents a unique opportunity to investigate at scale how human semantic knowledge is organized, how people use it to make fundamental judgments (“How similar are cats and bears?”), and how these judgments depend on the features that describe concepts (e.g., size, furriness). However, efforts to date have exhibited a substantial discrepancy between algorithm predictions and human empirical judgments. Here, we introduce a novel approach to generating embeddings for this purpose motivated by the idea that semantic context plays a critical role in human judgment. We leverage this idea by constraining the topic or domain from which documents used for generating embeddings are drawn (e.g., referring to the natural world vs. transportation apparatus). Specifically, we trained state‐of‐the‐art machine learning algorithms using contextually‐constrained text corpora (domain‐specific subsets of Wikipedia articles, 50+ million words each) and showed that this procedure greatly improved predictions of empirical similarity judgments and feature ratings of contextually relevant concepts. Furthermore, we describe a novel, computationally tractable method for improving predictions of contextually‐unconstrained embedding models based on dimensionality reduction of their internal representation to a small number of contextually relevant semantic features. By improving the correspondence between predictions derived automatically by machine learning methods using vast amounts of data and more limited, but direct empirical measurements of human judgments, our approach may help leverage the availability of online corpora to better understand the structure of human semantic representations and how people make judgments based on those.

1. Introduction

Understanding the underlying structure of human semantic representations is a fundamental and longstanding goal of cognitive science (Murphy, 2002; Nosofsky, 1985, 1986; Osherson, Stern, Wilkie, Stob, & Smith, 1991; Rogers & McClelland, 2004; Smith & Medin, 1981; Tversky, 1977), with implications that range broadly from neuroscience (Huth, De Heer, Griffiths, Theunissen, & Gallant, 2016; Pereira et al., 2018) to computer science (Bojanowski, Grave, Joulin, & Mikolov, 2017; Mikolov, Yih, & Zweig, 2013; Rossiello, Basile, & Semeraro, 2017; Toutanova et al., 2015) and beyond (Caliskan, Bryson, & Narayanan, 2017). Most theories of semantic knowledge (by which we mean the structure of representations used to organize and make decisions based on prior knowledge) propose that items in semantic memory are represented in a multidimensional feature space, and that key relationships among items—such as similarity and category structure—are determined by distance among items in this space (Ashby & Lee, 1991; Collins & Loftus, 1975; DiCarlo & Cox, 2007; Landauer & Dumais, 1997; Nosofsky, 1985, 1991; Rogers & McClelland, 2004; Jamieson, Avery, Johns, & Jones, 2018; Lambon Ralph, Jefferies, Patterson, & Rogers, 2017; although see Tversky, 1977). However, defining such a space, establishing how distances are quantified within it, and using these distances to predict human judgments about semantic relationships such as similarity between objects based on the features that describe them remains a challenge (Iordan et al., 2018; Nosofsky, 1991). Historically, similarity has provided a key metric for a wide variety of cognitive processes such as categorization, identification, and prediction (Ashby & Lee, 1991; Nosofsky, 1991; Lambon Ralph et al., 2017; Rogers & McClelland, 2004; but also see Love, Medin, & Gureckis, 2004, for an example of a model eschewing this assumption, as well as Goodman, 1972; Mandera, Keuleers, & Brysbaert, 2017, and Navarro, 2019, for examples of the limitations of similarity as a measure in the context of cognitive processes). As such, understanding similarity judgments between concepts (either directly or via the features that describe them) is broadly thought to be critical for providing insight into the structure of human semantic knowledge, as these judgments provide a useful proxy for characterizing that structure.

The best efforts to date to define theoretical principles (e.g., formal metrics) that can predict semantic similarity judgments from empirical feature representations (Iordan et al., 2018; Gentner & Markman, 1994; Maddox & Ashby, 1993; Nosofsky, 1991; Osherson et al., 1991; Rips, 1989) capture less than half the variance observed in empirical studies of such judgments. At the same time, a comprehensive empirical determination of the structure of human semantic representation via similarity judgments (e.g., by evaluating all possible similarity relationships or object feature descriptions) is impossible, given that human experience encompasses billions of individual objects (e.g., millions of pencils, thousands of tables, all different from one another) and tens of thousands of categories (Biederman, 1987) (e.g., “pencil,” “table,” etc.). That is, one obstacle of this approach has been a limitation in the amount of data that can be collected using traditional methods (i.e., direct empirical studies of human judgments). Recently, however, the availability of vast amounts of data from the internet, and machine learning algorithms for analyzing those data, have presented the opportunity to study at scale, albeit less directly, the structure of semantic representations, and the judgments people make using these. This approach has shown promise: work in cognitive psychology and in machine learning on natural language processing (NLP) has used large amounts of human generated text (billions of words; Bojanowski et al., 2017; Mikolov, Chen, Corrado, & Dean, 2013; Mikolov, Sutskever, Chen, Corrado, & Dean, 2013; Pennington, Socher, & Manning, 2014) to create high‐dimensional representations of relationships between words (and implicitly the concepts to which they refer) that may provide insights into human semantic space. These approaches generate multidimensional vector spaces learned from the statistics of the input data, in which words that appear together across different sources of writing (e.g., articles, books) become associated with “word vectors” that are close to one another, and words that share fewer lexical statistics, such as less co‐occurrence are represented as word vectors farther apart. A distance metric between a given pair of word vectors can then be used as a measure of their similarity. This approach has met with some success in predicting categorical distinctions (Baroni, Dinu, & Kruszewski, 2014), predicting properties of objects (Grand, Blank, Pereira, & Fedorenko, 2018; Pereira, Gershman, Ritter, & Botvinick, 2016; Richie et al., 2019), and even revealing cultural stereotypes and implicit associations hidden within the documents (Caliskan et al., 2017). However, the spaces generated by such machine learning methods have remained limited in their ability to predict direct empirical measurements of human similarity judgments (Mikolov, Yih, et al., 2013; Pereira et al., 2016) and feature ratings (Grand et al., 2018). Nevertheless, this work suggests that the multidimensional representations of relationships between words (i.e., word vectors) can be used as a methodological scaffold to describe and quantify the structure of semantic knowledge and, as such, can be used to predict empirical human judgments.

Despite these different avenues, neither the “top‐down” theoretically principled approaches, nor “bottom‐up” data‐driven approaches have yet provided consistently accurate predictions of human judgments regarding the similarity relationships between objects or their features. Here, we present a novel method that addresses this challenge, by leveraging the idea that context exerts a critical influence on how people use semantic representations to make judgments based on them. This is supported by a long tradition of literature in cognitive psychology, showing that human semantic judgments are influenced by (among many other factors) the domain‐level semantic context in which these judgments are made (e.g., Dillard, Palmer, & Kinney, 1995; Gentner, 1982; Goldstone, Medin, & Halberstadt, 1997; Medin & Shaffer, 1978; Miller & Charles, 1991; Nosofsky, 1984), including when evaluating similarity relationships (Barsalou, 1982; McDonald & Ramscar, 2001; Medin, Goldstone, & Gentner, 1993; Forrester, 1995; Keßler et al., 2007; also see Supplementary Experiments 1—4 & Supplementary Fig. 1). This influence can include task demands (e.g., instructions provided by experimenters), incidental factors related to the circumstances of the task, and/or features of the items to be judged, as well as more subtle effects related to the sequence in which items are perceived and learned (Carvalho & Goldstone, 2017). For example, when asked to judge the similarity between a bear and a bull among other animals, people may focus on their physical characteristics as objects in a natural context (e.g., size), leading to the judgment that they are similar; however, in the context of financial markets, they may focus instead of the items’ economic value, leading to the judgment that they are very different. Furthermore, this observed contextual influence on human semantic judgments manifests implicitly and automatically in natural environments (i.e., with no requirement for external prompts, such as asking someone to think about the “nature” domain when evaluating the relationship between two animals) but accounting for this phenomenon remains difficult in laboratory studies.

The idea that context plays an important role in evaluating semantic relationships has also been exposed in current state‐of‐the‐art NLP models, which show that taking local contextual influences into account (i.e., the other 10–20 words that surround a given word) can improve the performance on tasks such as question answering and ambiguous pronoun comprehension (Cheng & Kartsaklis, 2015; Devlin, Chang, Lee, & Toutanova, 2019; Peters et al., 2018). Here, we extend this idea by implementing a method designed to also take broader forms of context into account. We assume that when people are generating the text corpora available on the internet (e.g., magazine articles, Wikipedia entries, etc.), their use of words is heavily influenced by the context in which they are writing. Here, we present a method for augmenting training data used by machine learning models to also take into account this type of global, domain‐level semantic context (the topic or domain being considered in the writings, e.g., National Geographic vs. Wall Street Journal). To do so, we introduce domain‐level semantic contextual constraints (which are intended to parallel the contextual constraints thought to be in effect for the human authors when they generated those text corpora) in the construction of the text corpora from which the high‐dimensional word embedding spaces are learned. More specifically, we sought to impose the effects of implicit attention to context hypothesize above by manipulating the domain of articles included in the contextually‐constrained (CC) training corpora, instead of having attention built in as a process model in the embedding models’ training optimization procedure. Accordingly, we predicted that training machine learning algorithms on such CC corpora and then using the resulting embeddings to infer semantic representations and relationships would yield results that align more closely with empirical measurements made directly from humans. We tested this approach in three experiments.

The first two experiments demonstrate that embedding spaces learned from CC text corpora substantially improve the ability to predict empirical measures of human semantic judgments within their respective domain‐level contexts (pairwise similarity judgments in Experiment 1 and item‐specific feature ratings in Experiment 2), despite being trained using two orders of magnitude less data than state‐of‐the‐art NLP models (Bojanowski et al., 2017; Devlin et al., 2019; Mikolov, Chen, et al., 2013; Mikolov, Sutskever, et al., 2013; Pennington et al., 2014). In the third experiment, we describe “contextual projection,” a novel method for taking account of the effects of context in embedding spaces generated from larger, standard, contextually‐unconstrained (CU) corpora, in order to improve predictions regarding human behavior based on these models. Finally, we show that combining both approaches (applying the contextual projection method to embeddings derived from CC corpora) provides the best prediction of human similarity judgments achieved to date, accounting for 60% of total variance (and 90% of human interrater reliability) in two specific domain‐level semantic contexts.

2. Methods

2.1. Generating word embedding spaces

We generated semantic embedding spaces using the continuous skip‐gram Word2Vec model with negative sampling as proposed by Mikolov, Sutskever, et al. (2013) and Mikolov, Chen, et al. (2013), henceforth referred to as “Word2Vec.” We chose Word2Vec because this type of model has been shown to be on par with, and in some cases superior to other embedding models at matching human similarity judgments (Pereira et al., 2016). Word2Vec hypothesizes that words that appear in similar local contexts (i.e., in a “window size” of a similar set of 8–12 words) tend to have similar meanings. To encode this relationship, the algorithm learns a multidimensional vector associated with each word (“word vectors”) that can maximally predict other word vectors within a given window (i.e., word vectors from the same window are placed close to each other in the multidimensional space, as are word vectors whose windows are highly similar to one another).

We trained four types of embedding spaces: (a) contextually‐constrained (CC) models (CC “nature” and CC “transportation”), (b) context‐combined models, and (c) contextually‐unconstrained (CU) models. CC models (a) were trained on a subset of English language Wikipedia determined by human‐curated category labels (metainformation available directly from Wikipedia) associated with each Wikipedia article. Each category contained multiple articles and multiple subcategories; the categories of Wikipedia thus formed a tree in which the articles themselves are the leaves. We constructed the “nature” semantic context training corpus by collecting all articles belonging to the subcategories of the tree rooted at the “animal” category; and we constructed the “transportation” semantic context training corpus by combining the articles from the trees rooted at the “transport” and “travel” categories. This procedure involved entirely automated traversals of the publicly available Wikipedia article trees with no explicit author intervention. To avoid topics unrelated to natural semantic contexts, we removed the subtree “humans” from the “nature” training corpus. Furthermore, to ensure that the “nature” and “transportation” contexts were non‐overlapping, we removed training articles that were labeled as belonging to both the “nature” and “transportation” training corpora. This yielded final training corpora of approximately 70 million words for the “nature” semantic context and 50 million words for the “transportation” semantic context. The combined‐context models (b) were trained by combining data from each of the two CC training corpora in varying amounts. For the models that matched training corpora size with the CC models, we selected proportions of the two corpora that added up to approximately 60 million words (e.g., 10% “transportation” corpus + 90% “nature” corpus, 20% “transportation” corpus + 80% “nature” corpus, etc.). The canonical size‐matched combined‐context model was obtained using a 50%–50% split (i.e., approximately 35 million words from the “nature” semantic context and 25 million words from the “transportation” semantic context). We also trained a combined‐context model that included all training data used to generate both the “nature” and the “transportation” CC models (full combined‐context model, approximately 120 million words). Finally, the CU models (c) were trained using English language Wikipedia articles unrestricted to a particular category (or semantic context). The full CU Wikipedia model was trained using the full corpus of text corresponding to all English language Wikipedia articles (approximately 2 billion words) and the size‐matched CU model was trained by randomly sampling 60 million words from this full corpus.

The primary factors controlling the Word2Vec model were the word window size and the dimensionality of the resulting word vectors (i.e., the dimensionality of the model's embedding space). Larger window sizes resulted in embedding spaces that captured relationships between words that were farther apart in a document, and larger dimensionality had the potential to represent more of these relationships between words in a vocabulary. In practice, as window size or vector length increased, larger amounts of training data were required. To build our embedding spaces, we first conducted a grid search of all window sizes in the set (8, 9, 10, 11, 12) and all dimensionalities in the set (100, 150, 200) and selected the combination of parameters that yielded the highest agreement between similarity predicted by the full CU Wikipedia model (2 billion words) and empirical human similarity judgments (see Section 2.3). We reasoned that this would provide the most stringent possible benchmark of the CU embedding spaces against which to evaluate our CC embedding spaces. Accordingly, all results and figures in the manuscript were obtained using models with a window size of nine words and a dimensionality of 100 (Supplementary Figs. 2 & 3).

All models were trained using the “genism” Python library's implementation of the Word2Vec model (Rehurek & Sojka, 2010). Aside from window size and dimensionality, all other parameters were kept as the default values from the original Word2Vec publications (Mikolov, Chen, et al., 2013; Mikolov, Sutskever, et al., 2013): an initial learning rate of 0.025, elimination of words that appear fewer than five times in the training corpus, a 0.001 threshold for downsampling frequently occurring words, an exponent of 0.75 for shaping the negative sampling distribution, five negative samples per positive sample, and the skip‐gram training algorithm. Given that the final value of the loss function optimized during training is not comparable across networks and/or across datasets/training corpora (Mikolov, Chen, et al., 2013; Mikolov, Sutskever, et al., 2013), we trained every network for a fixed number of iterations. The resulting vocabulary sizes for each embedding space we constructed were: 148K words for the CC “nature” model, 110K words for the CC “transportation” model, 204K words for the combined context models (canonical & full), 342K words for the CU Wikipedia full model, and 125K words for the CU Wikipedia subset model.

For each type of model (CC, combined‐context, CU), we trained 10 separate models with different initializations (but identical hyperparameters) to control for the possibility that random initialization of the weights may impact model performance. Cosine similarity was used as a distance metric between two learned word vectors. Subsequently, we averaged the similarity values obtained for the 10 models into one aggregate mean value. For this mean similarity, we performed bootstrapped sampling (Efron & Tibshirani, 1986) of all the object pairs with replacement to evaluate how stable the similarity values are given the choice of test objects (1,000 total samples). We report the mean and 95% confidence intervals of the full 1,000 samples for each model evaluation (Efron & Tibshirani, 1986).

We also compared against two pre‐trained models: (a) the BERT transformer network (Devlin et al., 2019) generated using a corpus of 3 billion words (English language Wikipedia and English Books corpus); and (b) the GloVe embedding space (Pennington et al., 2014) generated using a corpus of 42 billion words (freely available online: https://nlp.stanford.edu/projects/glove/). The pre‐trained GloVe model had a dimensionality of 300 and a vocabulary size of 400K words. For this model, we perform the sampling procedure detailed above 1,000 times and reported the mean and 95% confidence intervals of the full 1,000 samples for each model evaluation. The BERT model was pre‐trained on a corpus of 3 billion words comprising all English language Wikipedia and the English books corpus. The BERT model had a dimensionality of 768 and a vocabulary size of 300K tokens (word‐equivalents). For the BERT model, we generated similarity predictions for a pair of text objects (e.g., bear and cat) by selecting 100 pairs of random sentences from the corresponding CC training set (i.e., “nature” or “transportation”), each containing one of the two test objects, and comparing the cosine distance between the resulting embeddings for the two words in the highest (last) layer of the transformer network (768 nodes). The average similarity across the 100 pairs represented one BERT “model” (we did not retrain BERT). The procedure was then repeated 10 times, analogously to the 10 separate initializations for each of the Word2Vec models we built. Finally, similar to the CC Word2Vec models, we averaged the similarity values obtained for the ten BERT “models” and performed the bootstrapping procedure 1,000 times and report the mean and 95% confidence interval of the resulting similarity prediction for the 1,000 total samples.

Finally, we compared the performance of our CC embedding spaces against the most comprehensive concept similarity model available, based on estimating a similarity model from triplets of objects (Hebart, Zheng, Pereira, Johnson, & Baker, 2020). We compared against this dataset as it represents the largest scale attempt to date to predict human similarity judgments in any form and because it generates similarity predictions for all the test objects we selected in our study (all pairwise comparisons between our test stimuli shown below are included in the output of the triplets model).

2.2. Object and feature testing sets

To test how well the trained embedding spaces aligned with human empirical judgments, we constructed a stimulus test set comprising 10 representative basic‐level animals (bear, cat, deer, duck, parrot, seal, snake, tiger, turtle, and whale) for the nature semantic context and 10 representative basic‐level vehicles (airplane, bicycle, boat, car, helicopter, motorcycle, rocket, shuttle, submarine, truck) for the transportation semantic context (Fig. 1b). We also selected 12 human‐relevant features independently for each semantic context that have been previously shown to explain object‐level similarity judgments in empirical settings (Iordan et al., 2018; McRae, Cree, Seidenberg, & McNorgan, 2005; Osherson et al., 1991). For each semantic context, we collected six concrete features (nature: size, domesticity, predacity, speed, furriness, aquaticness; transportation: elevation, openness, size, speed, wheeledness, cost) and six subjective features (nature: dangerousness, edibility, intelligence, humanness, cuteness, interestingness; transportation: comfort, dangerousness, interest, personalness, usefulness, skill). The concrete features comprised a reasonable subset of features used throughout prior work on explaining similarity judgments, which are commonly listed by human participants when asked to describe concrete objects (Osherson et al., 1991; Rosch, Mervis, Gray, Johnson, & Boyes‐Braem, 1976). Little data have been collected about how well subjective (and potentially more abstract or relational [Gentner, 1988; Medin et al., 1993]) features can predict similarity judgments between pairs of real‐world objects. Prior work has shown that such subjective features for the nature domain can capture more variance in human judgments, compared to concrete features (Iordan et al., 2018). Here, we extended this approach to identifying six subjective features for the transportation domain (Supplementary Table 4).

Fig 1.

Generating contextually‐constrained (CC) embedding spaces and testing their predictions of human similarity judgments. (a) Model training. We generated contextually‐constrained (CC) embedding spaces using training sets composed of Wikipedia articles considered relevant to each semantic context (“nature”∼70M words, “transportation”∼ 50M words). Similarly, we trained contextually‐unconstrained (CU) models with the training set of all English language Wikipedia articles (∼2B words), as well as a size‐matched subset of this corpus (∼60M words). We compared the performance of these models to a CU pre‐trained BERT transformer network (∼3B words corpus) and against GloVe, a CU pre‐trained embedding space trained on the Common Crawl corpus (∼42B words). We also compared against a recent, large‐scale CU machine learning model (Hebart et al., 2020; ∼1.5M empirical comparisons). (b) To test models’ prediction of human similarity judgments, we selected 10 representative basic‐level objects for each context (10 animals and 10 vehicles) and collected human‐reported similarity judgments between all pairs of objects in each context (45 pairs per context). (c) We computed Pearson correlation between human empirical similarity judgments (all 45 pairwise comparisons within each semantic context, averaged across participants) and similarity predicted by each embedding model (cosine distance between embedding vectors corresponding to each object in each model). Error bars show 95% confidence intervals for 1,000 bootstrapped samples of the test‐set items (see Section 2.7 for details). All differences between CC models in their preferred context and other models are statistically significant, p ≤ .004.

For each of the twenty total object categories (e.g., bear [animal], airplane [vehicle]), we collected nine images depicting the animal in its natural habitat or the vehicle in its normal domain of operation. All images were in color, featured the target object as the largest and most prominent object on the screen, and were cropped to a size of 500 × 500 pixels each (one representative image from each category is shown in Fig. 1b).

2.3. Human behavioral experiments

To collect empirical similarity judgments, we recruited 139 participants (45 female, 108 right‐handed, mean age 31.5 years) through the Amazon Mechanical Turk online platform in exchange for $1.50 payment (expected rate $7.50/hour). Prior work has shown that for this type of task, interparticipant reliability should be high for a cohort of at least 20 participants (Iordan et al., 2018). Participants were asked to report the similarity between every pair of objects from a single semantic context (e.g., all pairwise combinations of 10 vehicles or all pairwise combinations of 10 animals) on a discrete scale of 1 to 5 (1 = not similar; 5 = very similar). In each trial, the participant was shown two randomly selected images from each category side‐by‐side and was given unlimited time to report a similarity judgment. Each participant made 45 comparisons (all pairwise combinations of 10 categories from a single randomly chosen semantic context) presented in a random order. In a pilot experiment (Supplementary Experiment 6), we ran both a text‐only version and an image‐only version of this task using the set of 10 test categories from the nature domain. We found that the correspondence between ratings obtained in the two versions was extremely high (r = .95), which suggests that such similarity ratings likely reflect semantic distinctions between items independent of stimulus modality, rather than purely visual or textual differences. To maximize salience for the online behavioral task employed in the current experiment, we chose to present participants with images, rather than words.

To ensure high‐quality judgments, we limited participation only to Mechanical Turk workers who had previously completed at least 1,000 HITs with an acceptance rate of 95% or above. We excluded 34 participants who had no variance across answers (e.g., choosing a similarity value of 1 for every object pair). Prior work has shown that for this type of task interparticipant reliability should be high (Iordan et al., 2018); therefore, to exclude participants whose response may have been random, we correlated the responses of each participant with the average of the responses for every other participant and calculated the Pearson correlation coefficient. We then iteratively removed the participant with the lowest Pearson coefficient, stopping this procedure when all remaining participants had a Pearson coefficient greater than or equal to 0.5 to the rest of the group. This excluded an additional 12 participants, leading to a final tally of n = 44 participants for the nature semantic context and n = 49 participants for the transportation semantic context.

To collect empirical feature ratings, we recruited 915 participants (392 female, 549 right‐handed, mean age 33.4 years) through the Amazon Mechanical Turk online platform in exchange for $0.50 payment (expected rate $7.50/hour). Prior work has shown that for this type of task interparticipant reliability should be high for a cohort of at least 20 participants per feature (Iordan et al., 2018). Participants were asked to rank every object from a single semantic context (e.g., all 10 vehicles or all 10 animals) along a randomly chosen context‐specific dimension (e.g., “How fast/slow is this vehicle?”) on a discrete scale of 1 to 5 (1 = low feature value, e.g., “slow;” 5 = high feature value, e.g., “fast”). In each trial, the participant was shown three randomly selected images from a total of nine possible images representing the object, as well as the name of the object (e.g., “bear”) and given unlimited time to report a feature rating. Each participant ranked all 10 objects, presented in a random order, from a single randomly chosen context along a single randomly chosen dimension.

We used an analogous procedure as in collecting empirical similarity judgments to select high‐quality responses (e.g., restricting the experiment to high performing workers and excluding 210 participants with low variance responses and 124 participants with answers that correlated poorly with the average response). This resulted in 18–33 total participants per feature (see Supplementary Tables 3 & 4 for details).

All participants had normal or corrected‐to‐normal visual acuity and provided informed consent to a protocol approved by the Princeton University Institutional Review Board.

2.4. Predicting similarity judgments from embedding spaces

To predict similarity between two objects in an embedding space, we computed the cosine distance between the word vectors corresponding to each object. We used cosine distance as a metric for two main reasons. First, cosine distance is a commonly reported metric used in the literature that allows for direct comparison to previous work (Baroni et al., 2014; Mikolov, Chen, et al., 2013; Mikolov, Sutskever, et al., 2013; Pennington et al., 2014; Pereira et al., 2016). Second, cosine distance disregards the length or magnitude of the two vectors being compared, taking into account only the angle between the vectors. Some studies (Schakel & Wilson, 2015) have demonstrated a relationship between the frequency with which a word appears in the training corpus and the length of the word vector. Because this frequency relationship should not have any bearing on the semantic similarity of the two words, using a distance metric such as cosine distance that ignores magnitude/length information is prudent.

2.5. Contextual projection: Defining feature vectors in embedding spaces

To generate predictions for object feature ratings using embedding spaces, we adapted and extended a previously used vector projection method first employed by Grand et al. (2018) and Richie et al. (2019). These prior approaches manually defined three separate adjectives for each extreme end of a particular feature (e.g., for the “size” feature, adjectives representing the low end are “small,” “tiny,” and “minuscule,” and adjectives representing the high end are “large,” “huge,” and “giant”). Subsequently, for each feature, nine vectors were defined in the embedding space as the vector differences between all possible pairs of adjective word vectors representing the low extreme of a feature and adjective word vectors representing the high extreme of a feature (e.g., the difference between word vectors “small” and “huge,” word vectors “tiny” and “giant,” etc.). The average of these nine vector differences represented a one‐dimensional subspace of the original embedding space (line) and was used as an approximation of its corresponding feature (e.g., the “size” feature vector). The authors originally dubbed this method “semantic projection,” but we will henceforth refer to it as “adjective projection” to distinguish it from a variant of this method that we implemented, and that can also be considered a form of semantic projection, as detailed below.

By contrast to adjective projection, the feature vectors endpoints of which were unconstrained by semantic context (e.g., “size” was defined as a vector from “small,” “tiny,” “minuscule” to “large,” “huge,” “giant,” regardless of context), we hypothesized that endpoints of a feature projection may be sensitive to semantic context constraints, similarly to the training procedure of the embedding models themselves. For example, the range of sizes for animals may be different than that for vehicles. Thus, we defined a new projection technique that we refer to as “contextual semantic projection,” in which the extreme ends of a feature dimension were chosen from relevant vectors corresponding to a particular context (e.g., for nature, word vectors “bird,” “rabbit,” and “rat” were chosen for the low end of the “size” feature and word vectors “lion,” “giraffe,” and “elephant” for the high end). Similarly to adjective projection, for each feature, nine vectors were defined in the embedding space as the vector differences between all possible pairs of an object representing the low and high ends of a feature for a given context (e.g., the vector difference between word “bird” and word “lion,” etc.). Then, the average of these new nine vector differences represented a one‐dimensional subspace of the original embedding space (line) for a given context and was used as the approximation of its corresponding feature for items in that context (e.g., the “size” feature vector for nature).

To avoid overfitting, and given the high interrater reliability observed for test object feature ratings (r = .68–.92), the contextual projection endpoints for each feature and context were chosen by the experimenters as reasonable examples of out‐of‐sample objects representative of the low/high value on their corresponding feature in that context (i.e., distinct from the 10 test objects used for each semantic context). All objects used as endpoints across each feature and semantic context are shown in Supplementary Table 5 (nature semantic context) and Supplementary Table 6 (transportation semantic context).

Once a feature subspace was defined (either by adjective or contextual projection), the rating of an object with respect to that feature was calculated by projecting the vector representing the object in the original embedding space onto the one‐dimensional feature subspace for each context, which resulted in a scalar value (overall range across all models, features, and contexts: [−0.6, 0.4]):

$$\mathrm{ratin}{g}_{\mathrm{obje}\mathrm{ct}}=\frac{\mathrm{feat}\mathrm{ur}{e}^T\mathrm{obje}\mathrm{ct}}{\left|\left|\mathrm{feat}\mathrm{ure}\right|\right|}$$

To illustrate the relationship with cosine distance in the original embedding space, we note that the difference between the feature ratings of two words is then equivalent to the normalized cosine distance between the vector difference of those two words in the original embedding space and the corresponding context‐specific feature vector:

$$\begin{array}{ccc}\hfill \mathrm{dist}\left(objec{t}_1,objec{t}_2\right)& =& {\displaystyle \frac{featur{e}^T\left(objec{t}_1-objec{t}_2\right)}{\left|\left|feature\right|\right|}=}\hfill \\ \hfill & =& cosineDist\left(objec{t}_1-objec{t}_2,feature\right)·\left|\left|objec{t}_1-objec{t}_2\right|\right|\hfill \end{array}$$

2.6. Using contextual projection to improve contextually‐unconstrained embeddings

To test whether contextual projection may help improve predictions of human similarity judgments from CU embeddings, we used a two‐step procedure. First, given a 100‐dimensional CU embedding space, we used contextual projection to generate 12 human‐relevant feature vectors for each of our two semantic contexts (nature and transportation). Second, for each semantic context and its corresponding 12‐dimensional feature subspace, we used a separate linear regression procedure to learn optimal weights for each context‐relevant feature that together best predicted empirical similarity judgments. To evaluate this projection and regression procedure, we performed cross‐validated out of sample prediction of human similarity judgments by repeatedly selecting one of the 10 test objects in each semantic context (e.g., “snake”) and learning regression weights that best predicted human similarity judgments using a CU embedding space (i.e., dimensionality reduction from a 100‐dimensional CU embedding space to a 12‐dimensional contextually‐ and human‐relevant 12 feature subspace defined through contextual projection). To estimate the weights, we used only empirical trials (pairwise similarity judgments) that did not involve the left‐out test object (36 out of 45 trials per feature: 80% of the empirical data). Subsequently, we used the learned regression weights to make new predictions on the left‐out 20% of the judgments (9 out of 45 trials per feature, each comparison between the left‐out object and the other nine test objects for that particular semantic context).

2.7. Statistics

For the non‐pre‐trained models, we averaged over n = 10 different learned embedding representations (10 different initial conditions) to obtain a mean similarity prediction for each type of model. All error bars reported were 95% confidence intervals using 1,000 bootstrapped samples of the test‐set items with replacement. For each model comparison in each condition, we used a non‐parametric statistical significance estimation procedure to obtain p‐values based on the aforementioned bootstrap sampling (Efron & Tibshirani, 1986): to compare two models, we sampled a correlation value from each one and computed the difference, repeating 1,000 times, once for each bootstrapped sample to obtain a distribution of differences; we then estimated the p‐value of the difference between the two models as 1 minus the proportion of values in this distribution that fell above zero. All correlation values reported are Pearson r correlation coefficients.

3. Results

3.1. Experiment 1: Predictions by embedding models of empirical similarity judgments are highly sensitive to the semantic context(s) of articles in their training sets

Word embedding spaces are generated by training machine learning models on large corpora of text, often using deep neural network algorithms. This approach is typically applied to the largest corpora available, on the assumption that larger datasets will provide more accurate estimation of the underlying semantic structure. However, aggregating across multiple domain‐level semantic contexts (e.g., National Geographic and Wall Street Journal) may dilute the sensitivity of resulting embedding spaces to contextually‐constrained human semantic judgments. Thus, we hypothesized that (a) contextually‐constraining the corpora used to train machine learning algorithms to particular domains would improve their ability to predict empirical similarity judgments; and that (b) cross‐contextual contamination in the training set of embedding models (i.e., including articles from multiple distinct semantic contexts) would induce a misalignment between distances in embedding spaces and human similarity judgments, hence lower performance despite increasing the amount of training data.

To test our hypotheses, we collected two sets of Wikipedia articles related to two distinct domain‐level semantic contexts (Fig. 1a): “nature” (∼70 million words) and “transportation” (∼50 million words) and trained corresponding embedding spaces for each set using continuous skip‐gram Word2Vec models with negative sampling (Mikolov, Sutskever, et al., 2013; Mikolov, Chen, et al., 2013). We refer to these models as “CC” (CC nature and CC transportation), since they take into account both local (word‐ and sentence‐level) and global (domain‐ and discourse‐level) context; we refer to other types of word embedding models (trained by us or pre‐trained) as “CU,” as they were not explicitly trained on CC corpora, although some may take into account more local context during training.

We compared our two CC embedding spaces to a CU Word2Vec embedding space trained on all English language Wikipedia articles (∼2 billion words) and to a CU embedding space trained on a random subset of this training corpus, size‐matched to the CC embedding spaces (∼60 million words). We also tested the performance of two additional existing, state‐of‐the‐art, pre‐trained CU models: GloVe (Pennington et al., 2014) and BERT (Devlin et al., 2019). BERT was trained on English language Wikipedia and English Books, ∼3 billion words, is sensitive to local word context (i.e., the 10–20 words that surround a particular concept), and has been shown to outperform Word2Vec embeddings on several human‐related cognitive tasks involving prediction of semantic knowledge; however, BERT has not been previously tested on its ability to match human similarity judgments. GloVe was trained on the enormous Common Crawl corpus (∼42 billion words) and thus provided insight into the role of corpus size on making predictions about human judgments. Finally, we compared our performance against a recent CU object similarity model (Hebart et al., 2020), which is the most comprehensive attempt, to date, of using machine learning models and large‐scale empirical data to predict relationships between semantic concepts.

To test how well each embedding space could predict human similarity judgments, we selected two representative subsets of ten concrete basic‐level objects commonly used in prior work (Iordan et al., 2018; Brown, 1958; Iordan, Greene, Beck, & Fei‐Fei, 2015; Jolicoeur, Gluck, & Kosslyn, 1984; Medin et al., 1993; Osherson et al., 1991; Rosch et al., 1976) and commonly associated with the nature (e.g., “bear”) and transportation context domains (e.g., “car”) (Fig. 1b). To obtain empirical similarity judgments, we used the Amazon Mechanical Turk online platform to collect empirical similarity judgments on a Likert scale (1–5) for all pairs of 10 objects within each context domain. To obtain model predictions of object similarity for each embedding space, we computed the cosine distance between word vectors corresponding to the 10 animals and 10 vehicles. To assess how well each embedding space can account for human judgments of pairwise similarity, we calculated the Pearson correlation between that model's predictions and empirical similarity judgments.

For animals, estimates of similarity using the CC nature embedding space were highly correlated with human judgments (CC nature r = .711 ± .004; Fig. 1c). By contrast, estimates from the CC transportation embedding space and the CU models could not recover the same pattern of human similarity judgments among animals (CC transportation r = .100 ± .003; Wikipedia subset r = .090 ± .006; Wikipedia r = .152 ± .008; Common Crawl r = .207 ± .009; BERT r = .416 ± .012; Triplets r = .406 ± .007; CC nature > CC transportation p < .001; CC nature > Wikipedia subset p < .001; CC nature > Wikipedia p < .001; nature > Common Crawl p < .001; CC nature > BERT p < .001; CC nature > Triplets p < .001). Conversely, for vehicles, similarity estimates from its corresponding CC transportation embedding space were the most highly correlated with human judgments (CC transportation r = .710 ± .009). While similarity estimates from the other embedding spaces were also highly correlated with empirical judgments (CC nature r = .580 ± .008; Wikipedia subset r = .437 ± .005; Wikipedia r = .637 ± .005; Common Crawl r = .510 ± .005; BERT r = .665 ± .003; Triplets r = .581 ± .005), the ability to predict human judgments was significantly weaker than for the CC transportation embedding space (CC transportation > nature p < .001; CC transportation > Wikipedia subset p < .001; CC transportation > Wikipedia p = .004; CC transportation > Common Crawl p < .001; CC transportation > BERT p = .001; CC transportation > Triplets p < .001). For both nature and transportation contexts, we observed that the state‐of‐the‐art CU BERT model and the state‐of‐the art CU triplets model performed approximately half‐way between the CU Wikipedia model and our embedding spaces that should be sensitive to the effects of both local and domain‐level context. The fact that our models consistently outperformed BERT and the triplets model in both semantic contexts suggests that taking account of domain‐level semantic context in the construction of embedding spaces provides a more sensitive proxy for the presumed effects of semantic context on human similarity judgments than relying exclusively on local context (i.e., the surrounding words and/or sentences), as is the practice with existing NLP models or relying on empirical judgements across multiple broad contexts as is the case with the triplets model.

Furthermore, we observed a double dissociation between the performance of the CC models according to context: predictions of similarity judgments were most substantially improved by using CC corpora specifically when the contextual constraint aligned with the category of objects being judged, but these CC representations did not generalize to other contexts. This double dissociation was robust across multiple hyperparameter choices for the Word2Vec model, such as window size, the dimensionality of the learned embedding spaces (Supplementary Figs. 2 & 3), and the number of independent initializations of the embedding models’ training procedure (Supplementary Fig. 4). Moreover, all results we reported involved bootstrap sampling of the test‐set pairwise comparisons, indicating that the difference in performance between models was reliable across item choices (i.e., particular animals or vehicles chosen for the test set). Finally, the results were robust to the choice of correlation metric used (Pearson vs. Spearman, Supplementary Fig. 5) and we did not observe any obvious trends in the errors made by networks and/or their agreement with human similarity judgments in the similarity matrices derived from empirical data or model predictions (Supplementary Fig. 6).

To further test the idea that embedding models are highly sensitive to the semantic contexts present in their training sets, we also evaluated the extent to which cross‐contextual contamination induces a misalignment between distances in embedding spaces and human similarity judgments. We generated new combined‐context embedding spaces using different proportions of the training data from each of the two semantic contexts (nature and transportation; Fig. 2a), both matching for the size of the CC models’ training set (60M words; canonical combined‐context model), as well as using all available training data from the two semantic contexts (120M words; full combined‐context model).

Fig 2.

Combined‐context models more poorly predict similarity judgments. (a) Combined‐context embedding spaces were generated by using training data from the nature and transportation semantic contexts in different proportions (60M words, e.g., 10%–90%, 50%–50%, etc.). A full combined‐context embedding space was also generated using all available training data from both semantic contexts (120M words). (b) When combining training data from two semantic contexts at different ratios (in increments of 10% training data for each context, e.g., 10% nature and 90 transportation, 20% nature and 80% transportation, etc.), the resulting combined‐context embeddings recover a proportional amount of information from their preferred/non‐preferred semantic contexts. (c) The canonical and full combined‐context models produced distances between concepts that were less aligned with human judgments in both the nature and the transportation semantic contexts, respectively, compared to the corresponding CC embedding spaces. Errors signify 95% confidence intervals 1,000 bootstrapped samples of the test‐set items (see Section 2.7 for details).

As predicted, combined‐context embedding spaces’ performance was intermediate between the preferred and non‐preferred CC embedding spaces in predicting human similarity judgments: as more nature semantic context data were used to train the combined‐context models, the alignment between embedding spaces and human judgments for the animal test set improved; and, conversely, more transportation semantic context data yielded better recovery of similarity relationships in the vehicle test set (Fig. 2b). We illustrated this performance difference using the 50% nature–50% transportation embedding spaces in Fig. 2(c), but we observed the same general trend regardless of the ratios (nature context: combined canonical r = .354 ± .004; combined canonical < CC nature p < .001; combined canonical > CC transportation p < .001; combined full r = .527 ± .007; combined full < CC nature p < .001; combined full > CC transportation p < .001; transportation context: combined canonical r = .613 ± .008; combined canonical > CC nature p = .069; combined canonical < CC transportation p = .008; combined full r = .640 ± .006; combined full > CC nature p = .024; combined full < CC transportation p = .001).

Crucially, we observed that when using all training examples from one semantic context (e.g., nature, 70M words) and adding new examples from a different context (e.g., transportation, 50M additional words), the resulting embedding space performed worse at predicting human similarity judgments than the CC embedding space that used only half of the training data. This result strongly suggests that the contextual relevance of the training data used to generate embedding spaces can be more important than the amount of data itself. Contrary to common practice, adding more training examples may, in fact, degrade performance if the extra training data are not contextually relevant to the relationships of interest (in this case, similarity judgments among items).

Together, these results strongly support the hypothesis that human similarity judgments can be better predicted by incorporating domain‐level contextual constraints into the training procedure used to build word embedding spaces. Although the performance of the two CC embedding models on their respective test sets was not equal, the difference cannot be explained by lexical features such as the number of possible meanings assigned to the test words (Oxford English Dictionary [OED Online, 2020], WordNet [Miller, 1995]), the absolute number of test words appearing in the training corpora, or the frequency of test words within the corpora (Supplementary Fig. 7 & Supplementary Tables 1 & 2), although the latter has been shown to potentially impact semantic information in word embeddings (Richie & Bhatia, 2021; Schakel & Wilson, 2015). However, it remains possible that more complex and/or distributional characteristics of the words in each domain‐specific corpus may be mediating factors that impact the quality of the relationships inferred between contextually relevant target words (e.g., similarity relationships). Indeed, we observed a trend in WordNet meanings toward greater polysemy for animals versus vehicles that may help partially explain why all models (CC and CU) were able to better predict human similarity judgments in the transportation context (Supplementary Table 1).

Furthermore, the performance of the combined‐context models suggests that combining training data from multiple semantic contexts when generating embedding spaces may be responsible in part for the misalignment between human semantic judgments and the relationships recovered by CU embedding models (which are usually trained using data from many semantic contexts). This is consistent with an analogous trend observed when humans were asked to perform similarity judgments across multiple interleaved semantic contexts (Supplementary Experiments 1–4 and Supplementary Fig. 1).

3.2. Experiment 2: Contextual projection captures reliable information about interpretable object feature ratings from contextually‐constrained embeddings

A leading theory of semantic representation (and a potential basis for how similarity judgments are made) suggests that objects can be described by a varying number of feature dimensions, which are largely assumed to be recognizable and simple (e.g., size, shape, location, function, etc.; Iordan et al., 2018; Nosofsky, 1991). However, it remains possible that the true underlying representation may instead be composed of more abstract combinations of such simple features, and/or other perhaps uninterpretable features. This would be consistent with most machine learning models, in which embeddings based on large‐scale, unconstrained corpora generally do not yield interpretable features, even when they generate results that capture some aspects of human performance (Mikolov, Sutskever, et al., 2013; Richie et al., 2019). One potential explanation for this fact may be that domain‐level contextual constraints play an important role in emphasizing particular features when these are being rated by humans, whereas this contextual influence is weakened when generating CU embedding spaces (cf. Experiment 1b). To evaluate this possibility, we tested whether CC embedding spaces would yield feature ratings for individual objects that are more closely aligned to humans on intuitively recognizable dimensions (e.g., size), as well as more relevant to predicting empirical similarity judgments.

To test how well embedding spaces could predict human feature ratings, we identified 12 context‐relevant features for each of the two semantic contexts used in Experiment 1 (see Section 2.2 for details) and we used the Amazon Mechanical Turk platform to collect ratings of each of those features for the 10 test objects in their associated contexts; that is, the 10 animals were rated on the 12 nature features and the 10 vehicles were rated on the 12 transportation features (Likert scales 1–5 were used for all features and objects). A full list of features for each semantic context is given in Supplementary Tables 3 and 4.

To generate feature ratings from embedding spaces, we used a novel “contextual semantic projection” approach. For a given feature (e.g., size), a set of three “anchor” objects was chosen that corresponded to the low end of the feature range (e.g., “bird,” “rabbit,” “rat”) and a second set of three anchor objects was chosen that corresponded to the high end of the feature range (e.g., “lion,” “giraffe,” “elephant”). The word vectors for these anchor objects were used to generate a one‐dimensional subspace for each feature (e.g., “size” line, see Section 2.5 for details). Test objects (e.g., “bear”) were projected onto that line and the relative distance between each word and the low‐/high‐end object represented a feature rating prediction for that object. To ensure generality and avoid overfitting, the anchor objects were out‐of‐sample (i.e., distinct from the 10 test objects used for each semantic context) and were chosen by experimenter consensus as reasonable representatives of the low/high value on their corresponding feature.

Crucially, by selecting different endpoints in each semantic context for features common across the two semantic contexts (e.g., “size”), this method allowed us to make feature ratings predictions in a manner specific to a particular semantic context (nature vs. transportation). For example, in the nature context, “size” was measured as the vector from “rat,” “rabbit,” etc., to “elephant,” “giraffe,” etc. (animals in the training, but not in the testing set) and in the transportation context as the vector from “skateboard,” “scooter,” etc. to “spaceship,” “carrier,” etc. (vehicles not in the testing set). By contrast, prior work using projection techniques to predict feature ratings from embedding spaces (Grand et al., 2018; Richie et al., 2019) has used adjectives as endpoints, ignoring the potential influence of domain‐level semantic context on similarity judgments (e.g., “size” was defined as a vector from “small,” “tiny,” “minuscule” to “large,” “huge,” “giant,” regardless of semantic context). However, as we argued above, feature ratings may be impacted by semantic context much as—and perhaps for the same reasons as—similarity judgments. To test this hypothesis, we compared our contextual projection technique to the adjective projection technique with regard to their ability to consistently predict empirical feature ratings. A complete list of the contextual and adjective projection endpoints used for each semantic context and each feature is listed in Supplementary Tables 5 and 6.

We found that both projection techniques were able to predict human feature ratings with positive correlation values, suggesting that feature information can be recovered from embedding spaces via projection (Fig. 3 & Supplementary Fig. 8). However, contextual projection predicted human feature ratings much more reliably than adjective projection on 18 out of 24 features and was tied for best performance for an additional 5 out of 24 features. Adjective projection performed best on a single nature feature (dangerousness in the nature context). Furthermore, across both semantic contexts, using CC embedding spaces (with either projection method), we were able to predict human feature ratings better than using CU embedding spaces for 13 out of 24 features and were tied for best performance for an additional 9 out of 24 features. CU embeddings performed best on only two nature context features (cuteness and dangerousness). Finally, we observed that all models were able to predict empirical ratings somewhat better on concrete features (average r = .570) compared to subjective features (average r = .517). This trend was somewhat enhanced for CC embedding spaces (concrete feature average r = .663, subjective feature average r = .530). This suggests that concrete features may be more easily captured and encoded by automated methods (e.g., embedding spaces), compared to subjective features, despite the latter likely playing a significant role in how humans evaluate similarity judgments (Iordan et al., 2018). Finally, our results were not sensitive to the initialization conditions of the embedding models used for predicting feature ratings or item‐level effects (Supplementary Fig. 8 includes 95% confidence intervals for 10 independent initializations of each model and 1,000 bootstrapped samples of the test‐set items per model). Together, our results suggest that CC embedding spaces, when used in conjunction with contextual projection, were the most consistent and accurate in their ability to predict human feature ratings compared to using CU embedding spaces and/or adjective projection.

Fig 3.

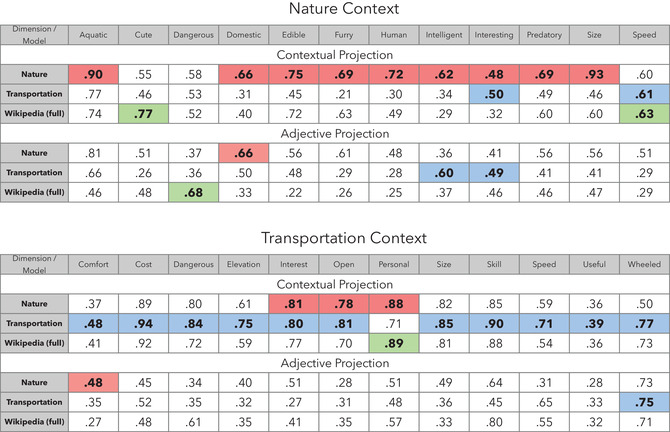
Contextual projection recovers human feature ratings. Pearson correlations between predicted feature ratings using the contextual and adjective projection methods for items in the nature context (animals) and items in the transportation context (vehicles); and empirically obtained human feature ratings for corresponding semantic contexts. Across both nature and transportation semantic contexts, using contextual projection generated ratings that were better aligned with human judgments compared to other models and projection methods for 18 out of the 24 features considered and tied for best for an additional 5 out of 24 features. Furthermore, contextually‐constrained embeddings (using either projection method) predicted feature ratings best on 13 out of 24 features and were tied for best performance for an additional 9 out of 24 features. Significance testing was done using 10 independent initializations of the model training procedure and 1,000 bootstrapped samples of the test‐set items each (Supplementary Fig. 8). Bolding and highlights indicate best (or tied for best) performing model in each column (red—contextually‐constrained nature; blue—contextually‐constrained transportation; green—contextually‐unconstrained).

To test whether the effects of cross‐contextual contamination in the training sets of embedding models extends to the prediction of feature ratings, we used contextual projection in conjunction with our canonical combined‐context embedding space generated in Experiment 1b (50% nature–50% transportation, 60M words). This procedure yielded feature predictions that were less well aligned with human feature ratings, compared to the CC models for the relevant semantic context, but better aligned than the CC models for the irrelevant context, or the CU models (Fig. 4 & Supplementary Fig. 9).

Fig 4.

Combined‐context embedding spaces recover feature ratings less well than CC embedding spaces. Pearson correlation between predicted feature ratings using contextual projection applied to the canonical combined‐context embedding space (50% nature – 50% transportation, 60M words) and empirical human feature ratings. Across both contexts, CC embeddings were best aligned with human judgments on 15 out of the 24 features considered, while the combined‐context embeddings were best or tied for best for only 7 out of 24. Significance testing was done using 10 independent initializations of the model training procedure and 1,000 bootstrapped samples of the test‐set items each (Supplementary Fig. 9). Bolding and highlights indicate best (or tied for best) performing model in each column (red—contextually‐constrained nature; purple—context‐combined; blue—contextually‐constrained transportation; green—contextually‐unconstrained).

Together, the findings of Experiment 2 support the hypothesis that contextual projection can recover reliable ratings for human‐interpretable object features, especially when used in conjunction with CC embedding spaces. We also showed that training embedding spaces on corpora that include multiple domain‐level semantic contexts substantially degrades their ability to predict feature values, even though these types of judgments are easy for humans to make and reliable across individuals, which further supports our contextual cross‐contamination hypothesis.

3.3. Experiment 3: Using contextual projection to improve prediction of human similarity judgments from contextually‐unconstrained embeddings

CU embeddings are built from large‐scale corpora comprising billions of words that likely span hundreds of semantic contexts. Currently, such embedding spaces are a key component of many application domains, ranging from neuroscience (Huth et al., 2016; Pereira et al., 2018) to computer science (Bojanowski et al., 2017; Mikolov, Yih, et al., 2013; Rossiello et al., 2017; Toutanova et al., 2015) and beyond (Caliskan et al., 2017). Our work suggests that if the goal of these applications is to solve human‐relevant problems, then at least some of these domains may benefit from employing CC embedding spaces instead, which would better predict human semantic structure. However, retraining embedding models using different text corpora and/or collecting such domain‐level semantically‐relevant corpora on a case‐by‐case basis may be expensive or difficult in practice. To help alleviate this problem, we propose an alternative approach that uses contextual feature projection as a dimensionality reduction technique applied to CU embedding spaces that improves their prediction of human similarity judgments.

Previous work in cognitive science has attempted to predict similarity judgments from object feature values by collecting empirical ratings for objects along different features and computing the distance (using various metrics) between those feature vectors for pairs of objects. Such methods consistently explain about a third of the variance observed in human similarity judgments (Maddox & Ashby, 1993; Nosofsky, 1991; Osherson et al., 1991; Rogers & McClelland, 2004; Tversky & Hemenway, 1984). They can be further improved by using linear regression to differentially weigh the feature dimensions, but at best this additional approach can only explain about half the variance in human similarity judgments (e.g., r = .65, Iordan et al., 2018).

Here, we test the hypothesis that human similarity judgments can be better predicted from CU embedding spaces by using contextually relevant features (cf. Experiment 2) together with the regression methods employed in cognitive psychology experiments that attempt to predict similarity between objects based on such features (Peterson, Abbott, & Griffiths, 2018). For a given embedding space, we first used contextual projection to construct a 12‐dimensional subspace corresponding to the 12 object features identified for that particular semantic context in Experiment 2 (see Supplementary Tables 3 and 4 for details on features and endpoints). Second, we used linear regression to learn an optimal set of weights between the original (e.g., 100‐dimensional) CU embedding space and the reduced 12‐dimensional subspace that maximized the new (projected) word vectors’ ability to predict human similarity judgments. To perform and evaluate this two‐step dimensionality reduction procedure, we used cross‐validated out of sample training and prediction: we repeatedly selected 1 of the 10 test objects in each semantic context (e.g., snake) to leave out and learned regression weights that best predicted human similarity judgments in the empirical trials that did not involve the left‐out object (36 out of 45 trials per feature; 80% of the empirical data). Then, we used the learned weights to make new predictions on the left‐out 20% of the judgments (9 out of 45 trials per feature, each comparison between the left‐out object and the other nine test objects for the semantic context).

The contextual projection and regression procedure significantly improved predictions of human similarity judgments for all CU embedding spaces (Fig. 5; nature context, projection & regression > cosine: Wikipedia p < .001; Common Crawl p < .001; transportation context, projection & regression > cosine: Wikipedia p < .001; Common Crawl p = .008). By comparison, neither learning weights on the original set of 100 dimensions in each embedding space via regression (Supplementary Fig. 10; analogous to Peterson et al., 2018), nor using cosine distance in the 12‐dimensional contextual projection space, which is equivalent to assigning the same weight to each feature (Supplementary Fig. 11), could predict human similarity judgments as well as using both contextual projection and regression together. These results suggest that the improved accuracy of combined contextual projection and regression provide a novel and more accurate approach for recovering human‐aligned semantic relationships that appear to be present, but previously inaccessible, within CU embedding spaces.

Fig 5.

Contextual projection and linear regression significantly improve recovery of human similarity judgments from embedding spaces (CC and CU). Contextual projection was used to generate 12‐dimensional subspaces for each embedding space corresponding to the 12 features for each semantic context. Linear regression was then used to learn an optimal mapping between the original embedding space and the 12‐dimensional feature subspace that best predicted human similarity judgments. Graphs show Pearson correlation between human similarity judgments and out‐of‐sample, cross‐validated predicted similarity values obtained using the projection and regression procedure (80% data used for training, 20% used for testing; averaged across 5 cross‐validation folds). (a) Nature semantic context. (b) Transportation semantic context. Error bars show 95% confidence intervals for 1,000 total bootstrapped samples of the test‐set items (see Section 2.7 for details). All differences between “projection and regression” bars and corresponding “cosine” bars are statistically significant, p ≤ .020.

Finally, if people differentially weight different dimensions when making similarity judgments, then the contextual projection and regression procedure should also improve predictions of human similarity judgments from our novel CC embeddings. Our findings not only confirm this prediction (Fig. 5; nature context, projection & regression > cosine: CC nature p = .030, CC transportation p < .001; transportation context, projection & regression > cosine: CC nature p = .009, CC transportation p = .020), but also provide the best prediction of human similarity judgments to date using either human feature ratings or text‐based embedding spaces, with correlations of up to r = .75 in the nature semantic context and up to r = .78 in the transportation semantic context. This accounted for 57% (nature) and 61% (transportation) of the total variance present in the empirical similarity judgment data we collected (92% and 90% of human interrater variability in human similarity judgments for these two contexts, respectively), which showed substantial improvement upon the best previous prediction of human similarity judgments using empirical human feature ratings (r = .65; Iordan et al., 2018). Remarkably, in our work, these predictions were made using features extracted from artificially‐built word embedding spaces (not empirical human feature ratings), were generated using two orders of magnitude less data that state‐of‐the‐art NLP models (∼50 million words vs. 2–42 billion words), and were evaluated using an out‐of‐sample prediction procedure. The ability to reach or exceed 60% of total variance in human judgments (and 90% of human interrater reliability) in these specific semantic contexts suggests that this computational approach provides a promising future avenue for obtaining an accurate and robust representation of the structure of human semantic knowledge.

4. Discussion

Our results support the hypothesis that efforts using machine learning methods applied to large‐scale text corpora to study how semantic knowledge is organized can benefit not only by taking local context into account (as previous approaches have done), but also by taking domain‐level semantic context into account. Specifically, we showed that doing so can reliably improve prediction of empirically measured human semantic similarity judgments and object feature ratings. We showed that this can be done by incorporating domain‐level contextual constraints both in the construction of the training corpora (Experiments 1–2) and/or in the methods used to extract relational information from contextually‐unconstrained embedding spaces (Experiment 3). For the latter, we described a novel, computationally tractable method (contextual projection) that we successfully applied to (a) predicting accurate feature ratings for human‐relevant dimensions of objects; and (b) improving the ability of contextually‐unconstrained embedding models to predict human similarity judgments.

From a psychological and cognitive science perspective, discovering reliable mappings between data‐driven approaches and human judgments may help improve long‐standing models of human behavior for tasks such as categorization, learning, and prediction. Understanding how people carry out such tasks can benefit by the ability to reliably estimate similarity between concepts, identify features that describe them, and characterize how attention may impact these measurements—efforts that, for practical reasons, have so far focused on either artificially‐built examples (e.g., sets of abstract shapes) or small‐scale subsets of cognitive space (Iordan et al., 2018; Goldstone et al., 1997; Maddox & Ashby, 1993; Nosofsky, 1985; Nosofsky, Sanders, & McDaniel, 2018; Osherson et al., 1991). Our work suggests that such efforts can benefit by the use of machine learning models trained on large‐scale corpora, by taking domain‐level information into account when constructing such corpora and/or interpreting the relationships among representations within them.

It is important to acknowledge that the results we report focus on a narrow set of stimuli (20 objects) representing only two semantic contexts (nature and transportation), involving a simple task (similarity judgments), and comparisons of performance to artificial neural networks of a particular form trained on a particular type of materials (words). The extent to which our findings generalize to other semantic domains, tasks, and types of models or data used to train them (e.g., images) remains a subject for future work. Nevertheless, we believe that our findings reflect a fundamental feature of human cognitive function: the influence of context on semantic processing, and, in particular, on similarity judgments. Decades of work have suggested that both attention and context play an important role in similarity judgments, and that such judgments are a fundamental building block for higher level cognitive processes (e.g., categorization and inference; Ashby & Lee, 1991; Nosofsky, 1991; Rogers & McClelland, 2004; Lambon Ralph et al., 2017). While some have challenged the generality of this claim (e.g., see Love et al. (2004) for an example of a model eschewing this assumption, as well as Goodman (1972), Mandera et al. (2017), and Navarro (2019) for examples of the limitations of similarity as a measure in the context of cognitive processes), at the least this debate highlights the potential value of developing more powerful tools for studying the structure of human semantic knowledge. The work we have presented here contributes to this goal by leveraging the development of machine learning methods to study semantic structure at scale, and by bringing these into closer contact with what is observed from human performance.

Our selection of two particular semantic domains (nature and transportation) highlights another important set of questions: what defines the forms of context of which people may make use, what is their scope, and how can they be determined empirically? While many may seem intuitively evident, such as the two we used, there are no doubt countless others, that may vary by degree, interact with one another, and be used in subtle ways. For example, while it may seem odd to ask which is more similar to a car, a dog or a wolf, many people would respond “dog,” suggesting that domesticity was used as the context for the judgment. Similarly, text corpora can be “carved” in multiple ways (for example, by selecting different root nodes in the Wikipedia article tree) and exploring such carvings remains an interesting direction for future work. Additionally, how representations of context are invoked for a particular use remains an important focus of work. For some domains, previous work has shown that exposure to relevant content—either for humans (e.g., judgments pertaining to different corpora, Kao, Ryan, Dye, & Ramscar, 2010; also see Supplementary Experiments 1–4) or for computational models (e.g., bioinformatics, Pakhomov, Finley, McEwan, Wang, & Melton, 2016)—may improve performance for tasks or applications that involve those domains specifically. Crucially, our work shows evidence that this phenomenon extends beyond restricted, highly specialized application domains (such as biomedical research) to simple forms of semantic judgments involving common basic‐level concepts (e.g., “dog”). As noted above, contextual effects on relationships can be subtle (both when accounting for and independent of word homonymy) and models designed to estimate them may or may not always benefit from context‐dependent information (Peterson et al., 2018; Richie & Bhatia, 2021). As such, the automatic identification of relevant semantic domains, as well as quantifying the interaction between semantic judgments (e.g., similarity relationships) across domains, is an important direction for future work. Additionally, the contextual projection method we put forward and its reliance on object exemplars, rather than adjectives (Grand et al., 2018; Richie et al., 2019) to reliably predict relative human feature ratings, suggests a potential future application in the development of a computational, embedding‐based, scalable account of semantics for gradable adjectives both within a particular context, as well as in a context‐independent manner (Toledo & Sassoon, 2011).

From a neuroscience perspective, it is unlikely that humans retrain their long‐standing semantic representations every time a new task demands it; instead, attention is thought to alter the context in which learned semantic structure is processed, both in behavior and in the brain (Bar, 2004; Çukur, Nishimoto, Huth, & Gallant, 2013; Miller & Cohen, 2001; Rosch & Lloyd, 1978). Recent advances in neuroimaging have allowed embedding‐based neural models of semantics to probe how concepts are processed across the human brain (Huth et al., 2016; Huth, Nishimoto, Vu, & Gallant, 2012) and to generate decoders of mental representations that can predict human behavior from neural responses (Pereira et al., 2018). Thus, increasing alignment between such embedding spaces and human semantic structure will help further our understanding of the structural underpinnings of semantic knowledge (Keung, Osherson, & Cohen, 2016; Lambon Ralph et al., 2017). As such, our results suggest a novel neuroscientific avenue for investigating the mechanisms of how context dynamically shifts human behavior and neural responses across large‐scale semantic structure.

From a natural language processing (NLP) perspective, embedding spaces have been used extensively as a primary building block, under the assumption that these spaces represent useful models of human syntactic and semantic structure. By substantially improving alignment of embeddings with empirical object feature ratings and similarity judgments, the methods we have presented here may aid in the exploration of cognitive phenomena with NLP. Both human‐aligned embedding spaces resulting from CC training sets, and (contextual) projections that are motivated and validated on empirical data, may lead to improvements in the performance of NLP models that rely on embedding spaces to make inferences about human decision‐making and task performance. Example applications include machine translation (Mikolov, Yih, et al., 2013), automatic extension of knowledge bases (Toutanova et al., 2015), text summarization (Rossiello et al., 2017), and image and video captioning (Gan et al., 2017; Gao et al., 2017; Hendricks, Venugopalan, & Rohrbach, 2016; Kiros, Salakhutdinov, & Zemel, 2014).

In this context, one important finding of our work concerns the size of the corpora used to generate embeddings. When using NLP (and, more broadly, machine learning) to investigate human semantic structure, it has generally been assumed that increasing the size of the training corpus should increase performance (Mikolov , Sutskever, et al., 2013; Pereira et al., 2016). However, our results suggest an important countervailing factor: the extent to which the training corpus reflects the influence of the same relational factors (domain‐level semantic context) as the subsequent testing regime. In our experiments, CC models trained on corpora comprising 50–70 million words outperformed state‐of‐the‐art CU models trained on billions or tens of billions of words. Furthermore, our CC embedding models also outperformed the triplets model (Hebart et al., 2020) that was estimated using ∼1.5 million empirical data points. Together, this demonstrates that data quality (as measured by contextual relevance) may be just as important as data quantity (as measured by total number of training words) when building embedding spaces intended to capture relationships salient to the specific task for which such spaces are employed. This finding may provide further avenues of exploration for researchers building data‐driven artificial language models that aim to emulate human performance on a plethora of tasks.

Recently, new approaches have been proposed that aim to incorporate contextual influences into artificial language models, such as BERT (Devlin et al., 2019), ELMO (Peters et al., 2018), and multisense embeddings (Cheng & Kartsaklis, 2015). Although such models have been shown to perform well on natural language tasks such as question answering, next sentence prediction, and ambiguous pronoun comprehension, these models focus on the effects of local context (i.e., the 10–20 words that surround a particular concept or the encompassing paragraph). By comparison, our approach also takes into account the effects of global, discourse‐level semantic effects (e.g., the topic or domain being considered in the writings). For example, BERT (Devlin et al., 2019) is considered state of the art for the tasks listed above and outperformed the context‐free Word2Vec and GloVe embedding models at predicting empirical similarity judgments. However, it could not match the performance of our CC models, despite using significantly more training data than our Word2Vec embedding models (3 billion vs. 50–70 million words, Fig. 1). This provides strong evidence that predictions of NLP models can be further improved by taking additional account of global, discourse‐level context. This is consistent with observations from studies in cognitive science over the past 40 years (Barsalou, 1982; Dillard et al., 1995; Forrester, 1995; Gentner, 1982; Keßler et al., 2007; Medin & Shaffer, 1978; Medin et al., 1993; Miller & Charles, 1991; Nosofsky, 1984; Goldstone et al., 1997; McDonald & Ramscar, 2001).

More broadly, the methods and findings we report here may help strengthen the link between human semantic space (how we organize knowledge and use it to interact with the world) and machine learning methods meant to automate tasks useful and directly relevant to humans (e.g., NLP). Improvements in predicting similarity between concepts in specific semantic contexts, as well as an efficient method of increasing the prediction performance of existing embedding models for predicting empirical semantic judgments (contextual projection), together validate a set of computational tools that allow for more accurate and robust representations of human semantic knowledge. These advances are likely to be helpful in the future in understanding the underlying structure of human semantic representations and in efforts to build artificial systems that can emulate and/or better interact with semantic representations.

Author contributions

M.C.I. and J.D.C. designed the study. M.C.I. and T.G. collected and analyzed the data with input from C.T.E., N.M.B., and J.D.C. M.C.I., T.G., and J.D.C wrote the manuscript with input from C.T.E. and N.M.B.

Competing interest statement

The authors have no conflicts to disclose.

Open Research Badges

This article has earned Open Data and Open Materials badges. Data are available at https://osf.io/v8qge/?view_only=c745eddd500a40fb8ef8285d701c20e2 and materials are available at https://osf.io/v8qge/?view_only=c745eddd500a40fb8ef8285d701c20e2.

Supporting information

Supplementary Figure 1. Semantic Context Influences Empirical Similarity Judgments.

Supplementary Figure 2. Nature Context – Correlation Between Human Similarity Judgments and Contextually‐Constrained Embedding Spaces for Varying Word2Vec Model Training Parameters: Syntactic Word Window Size 8—12, Dimensionality 100‐200.

Supplementary Figure 3. Transportation Context – Correlation Between Human Similarity Judgments and Contextually‐Constrained Embedding Spaces for Varying Word2Vec Model Training Parameters: Syntactic Word Window Size 8— 12, Dimensionality 100‐200.

Supplementary Figure 4. Number of Initializations for Each Model Does Not Change Prediction Results.

Supplementary Figure 5. Using Spearman Instead of Pearson Correlation Does Not Alter the Performance Gap Between Contextually‐Constrained and Contextually‐Unconstrained Embedding Models

Supplementary Figure 6. Similarity Matrices for Main Models in Fig. 1.

Supplementary Figure 7. Word Frequency Differences for Animals and Vehicles Between Training Corpora Do Not Influence Relative Performance of Models.

Supplementary Figure 8. Confidence Intervals for Feature Ratings Predictions.

Supplementary Figure 9. Confidence Intervals for Feature Rating Predictions for the Combined‐Context Models.

Supplementary Figure 10. Using Regression in the Original Embedding Space (Similar to Peterson et al., 2018) Yields Lower Prediction Performance for All Embedding Spaces Compared to the Projection and Regression Procedure (All Differences Between Results Shown in This Figure and Corresponding Results in Fig. 5 Are Significant).

Supplementary Figure 11. Contextual Projection and Regression Performs Better Than Using Cosine Distance in the 12‐Dimensional Contextual Projection Space.

Supplementary Figure 12. Empirical Semantic Similarity Judgments are Modality Independent.

Supplementary Table 1. Number of Meanings for Test Objects in Both Semantic Contexts (OED: Oxford English Dictionary).

Supplementary Table 2. Number of Occurrences of Test Objects in Frequency‐Matched Text Corpora (Supplementary Experiment 5 & Supplementary Fig. 7)

Supplementary Table 3. List of Features Selected for Nature Semantic Context.

Supplementary Table 4. List of Features Selected for Transportation Semantic Context.

Supplementary Table 5. Feature Endpoints for Adjective and Contextual Projection Methods – Nature Semantic Context.

Supplementary Table 6. Feature Endpoints for Adjective and Contextual Projection Methods – Transportation Semantic Context