Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2019 Sep 6;124(9):7413–7424. doi: 10.1029/2019JA026830

Pluto's Interaction With Energetic Heliospheric Ions

P Kollmann 1,✉, M E Hill 1, R C Allen 1, R L McNutt Jr 1, L E Brown 1, N P Barnes 2, P Delamere 2, G Clark 1, G B Andrews 1, N Salazar 1, J Westlake 1, G Romeo 1, J Vandegriff 1, M Kusterer 1, D Smith 1, K Nelson 1, S Jaskulek 1, R B Decker 1, A F Cheng 1, S M Krimigis 1,3, C M Lisse 1, D G Mitchell 1, H A Weaver 1, H A Elliott 4,5, E Fattig 4, G R Gladstone 4, P W Valek 4, S Weidner 4, J Kammer 4, F Bagenal 6, M Horanyi 6, D Kaufmann 6, A Harch 6, C B Olkin 6, M R Piquette 6, J R Spencer 6, L A Young 6, K Ennico 7, M E Summers 8, S A Stern 6
PMCID: PMC9285724  PMID: 35860291

Abstract

Pluto energies of a few kiloelectron volts and suprathermal ions with tens of kiloelectron volts and above. We measure this population using the Pluto Energetic Particle Spectrometer Science Investigation (PEPSSI) instrument on board the New Horizons spacecraft that flew by Pluto in 2015. Even though the measured ions have gyroradii larger than the size of Pluto and the cross section of its magnetosphere, we find that the boundary of the magnetosphere is depleting the energetic ion intensities by about an order of magnitude close to Pluto. The intensity is increasing exponentially with distance to Pluto and reaches nominal levels of the interplanetary medium at about 190R P distance. Inside the wake of Pluto, we observe oscillations of the ion intensities with a periodicity of about 0.2 hr. We show that these can be quantitatively explained by the electric field of an ultralow‐frequency wave and discuss possible physical drivers for such a field. We find no evidence for the presence of plutogenic ions in the considered energy range.

Keywords: Pluto, pickup ions, wave, New Horizons

Key Points

  • Pluto forms a wake for energetic heliospheric ions

  • Waves cause ion intensity oscillations in the wake

1. Introduction

Pluto was first visited in 2015 (Stern et al., 2015, 2018) by the New Horizons mission (Stern et al., 2018; Young et al., 2008), which was also the first time its space environment was sampled in situ (Bagenal et al., 2016). The dwarf planet has a tenuous N 2‐dominated atmosphere with a surface pressure of 12 μbar (Hinson et al., 2017). In the exosphere, CH4 becomes the dominating species (Young et al., 2018). Atmospheric ions were detected already around closest approach (Zirnstein et al., 2016), and the ion escape rate (McComas et al., 2016) was found to be only about an order of magnitude below the ion escape of Mars and Venus (Dong et al., 2017; Kollmann et al., 2016).

What makes Pluto special compared to other bodies that have been studied with energetic particle instrumentation is that it is embedded in a distinct and relatively dense population of energetic heliospheric ions, namely, interstellar pickup ions in the kiloelectron volt energy range and their suprathermal tail ranging to hundreds of kiloelectron volts (Kollmann et al., 2019). We will abbreviate this population as IPS (interstellar pickup and suprathermal) ions. IPS ions become more abundant beyond a few astronomical units. The closest analog measurements were probably the flyby of Cassini near Saturn's moon Titan while it was embedded in the solar wind and H pickup ions from Saturn's exosphere (Bertucci et al., 2015). However, the gyrodradii of these pickup ions were similar to the obstacle size and the flyby did not cross through the wake of Titan.

The gyroradii of 10 keV interstellar He+ pickup ions, as we will study them here, is 200R P (Pluto radius defined here as 1R P =1,188.3 km; Nimmo et al., 2017), much larger than the size of the obstacle. (The exact value depends on the magnetic field that can be estimated from Voyager measurements, Bagenal et al., 2015, or modeling, Barnes et al., 2019.) Despite their density being lower than the solar wind, at least interstellar H+ pickup ions are thought to play an important role in determining the shape of Pluto's heavy ion tail (Barnes et al., 2019).

In this paper we follow up on the IPS ion observations described in (Bagenal et al., 2016). We discuss the overall interaction of Pluto with its environment in section 3 and then focus in section 4 on observations in the wake that can be interpreted as showing energetic particle signatures of ultralow‐frequency (ULF) waves.

2. Data Set

2.1. Instrumentation

We use data from the PEPSSI instrument (Pluto Energetic Particle Spectrometer Science Investigation) (Kollmann et al., 2019; McNutt et al., 2008). PEPSSI measures ions with energies from a few kiloelectron volts to about a MeV. Here we only use measurements from the time‐of‐flight system of the instrument. While time‐of‐flight‐only measurements have ambiguity in determining ion species, the species and energy dependent detection efficiency of PEPSSI works out in a way that the count rates in the heliosphere, outside of Pluto, are dominated by heliospheric He+ (Kollmann et al., 2019). All measurements presented here are therefore assumed to be He+.

PEPSSI measures particles with six angular sectors, labeled S0 to S5. Their look direction is determined by the spacecraft attitude. We only use data from Sectors S0 and S1 here because these are the sectors with the highest instrument‐intrinsic efficiencies. We quantify look direction with a vector through the center of each sector. Each sector has a field of view of 12°×30°.

The PEPSSI instrument provides two data products. We will use “event data” to create ion spectra with high energy resolution (e.g., Figure 3 below). These data are based on recordings of the full measurement of single ions. As not all measurements can be stored like this, we need to bin the data in time, reducing the time resolution. For high time resolution (e.g., Figure 4 below), we therefore use the “rate channels” that record all measured ions with high time but limited energy resolution. Rate channels have names like L09 or J02 as they will be mentioned in some figure captions together with explanations on what they measure.

Figure 3.

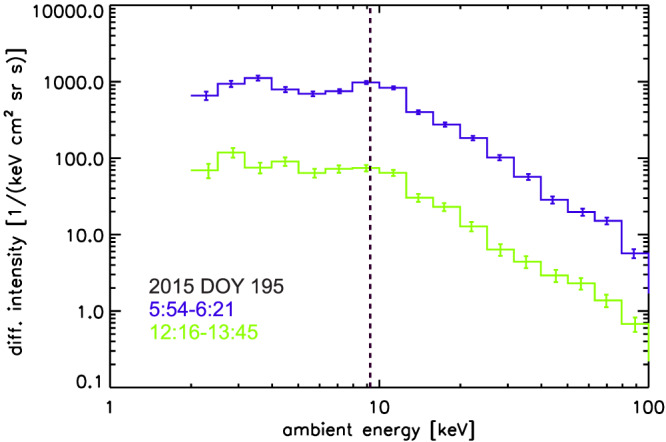
jgra55188-fig-0003

Open in a new tab

He+ energy spectra upstream of Pluto (blue) and within Pluto's wake (green). The spectra are shown in the spacecraft frame. It can be seen that the Pluto interaction mostly affects the overall amplitude but only barely the spectral shape. Measurements are taken with a cone angle of 34° to the Sun. The vertical dashed line shows the expected interstellar pickup ion cutoff energy based on the upstream solar wind measurements, the observation angle, and assuming the ions are He+. Error bars show the Poisson error of the event data counts. DOY = day of year.

Figure 4.

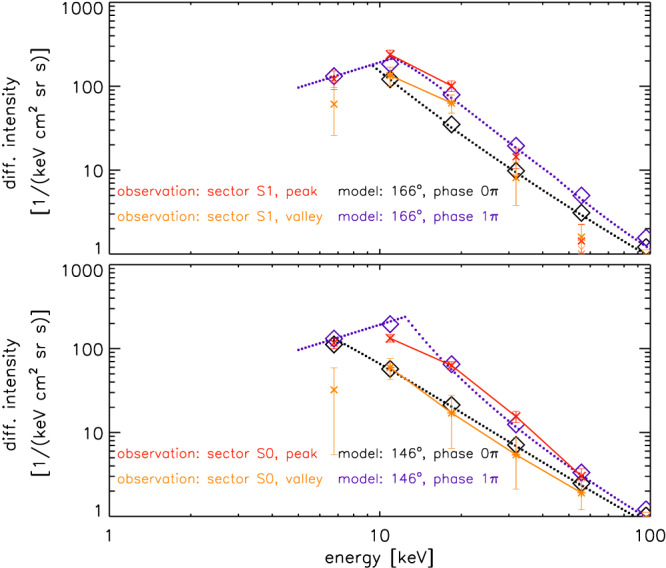
jgra55188-fig-0004

Open in a new tab

Energy spectra measured at a peak within Pluto's energetic particle wake (red x symbols) and in a valley (orange x symbols) for two different ion velocity directions (two panels). The ion velocity direction is opposite to the instrument look direction, meaning that an ion direction of 146° and a look direction of 34° are labeling the same spacecraft attitude. Either number labels measurements by sector S0 (lower panel), which is measuring further from the Sun than the other used sector, S1 (upper panel). We only connect data points with lines that are reliable in the sense that the Poisson error bars are small and where the bars of peak and valley do not overlap. Blue and black dotted curves: Model spectra assuming a time‐varying electric field (section 4.2). Blue and black diamonds = averages of the model spectra over the energy range that is also used for the measurements.

2.2. Coordinate System

We use the Pluto Solar Heliographic (PSH) coordinate system where the positive x axis is pointing from Pluto to the Sun (meaning that values in wake are negative), y is perpendicular to the Sun's spin axis and the x axis (therefore roughly in the ecliptic), and z completes the right‐handed system (and points roughly in the direction of the Sun's spin axis). In the following, we assume cylindrical symmetry and use the cylindrical distance that we define as ρ=yPSH2+zPSH2. For large values, the radial distance r=xPSH2+yPSH2+zPSH2 is approximately equal to the distance x PSH along the tail.

Vector directions in this coordinate system can be expressed through the cone angle α, which is the angle between the look direction L→ of the considered sector and the x axis: α=arccos((x→·L→)/(xL)). The distributions we usually observe only depend on the cone angle. A full description of the look direction requires the clock angle β, which is the angle between the projection of L→ into the yz plane and the z axis: β=arctan(yPSH/zPSH).

We have to distinguish between look direction of the instrument and the direction of the observed particle. Their vectors point in opposite directions. The nominal orientation of PEPSSI's most sensitive sector has a look direction cone angle of 34°. The particles observed by this sector have a cone angle of 180° minus the previous value, in our case 146°.

3. Pluto's Overall Interaction

We do not find evidence for any plutogenic ions in the energy range of our instrument (see section 3.3). The bulk of heavy ions originating from Pluto is found at <1 keV (McComas et al., 2016). What we observe instead is that Pluto is modifying the distribution of IPS ions in the interplanetary medium that we are observing through the measurement of He+. This modification includes a deflection of the ion bulk flow direction (section 3.1) and the formation of an energetic particle wake (section 3.2.)

Figure 1 shows an overview of the IPS ion measurements around the Pluto flyby. There are several abrupt apparent changes in intensity. Most result from changes in the spacecraft attitude that change the look direction of the instrument. To avoid confusion, we color code the intensities according to the current look direction. Only times with the same color can be compared.

Figure 1.

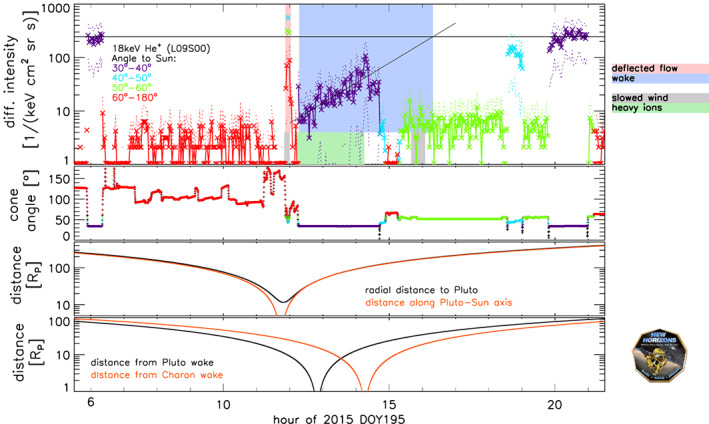
jgra55188-fig-0001

Open in a new tab

Overview of interstellar pickup and suprathermal ion measurements around Pluto. We only show data from a single sector of the Pluto Energetic Particle Spectrometer Science Investigation (PEPSSI) for clarity. This sector points into different look directions as a function of time, depending on the changing spacecraft attitude. (first panel) The x symbols and colored solid lines show intensities dominated by 18‐keV He+ ions. The color coding marks measurements at different cone angles relative to the Sun. Dashed lines indicate the Poisson error envelope of the intensities. Black lines show the average IPS intensity in the solar wind and an extrapolation of the Pluto wake intensity. The crossing point is an estimate when New Horizons passed the magnetic boundary of the Pluto wake. Blue and red shaded areas call out two regions discussed in section 3.1 and 3.2. Gray and green shading provide context, showing regions observed at lower energies than discussed in this paper (McComas et al., 2016). (second panel) Cone angle of the measurement shown in the first panel. (third panel) x PSH coordinate (orange) of New Horizons and the radial distance r to Pluto (black). (fourth panel) Cylindrical distance ρ of New Horizons to the wake center axis of Pluto (black) and of Charon (orange). PSH = Pluto Solar Heliographic coordinate system; DOY = day of year.

3.1. Deflection

Well before and after the Pluto encounter (<12 and >16 hr UTC), we observe nominal IPS intensities in the solar wind (dark blue data points in the first panel of Figure 1). Further observations in the interplanetary medium show that these intensities decrease with increasing angle relative to the flow direction (compare different colors outside of the Pluto interaction region of ≈12–16 hr UTC in Figure 1), as it is expected for particles moving away from the Sun. Around 11:56 UTC, at a radial distance of about 13R P , we observe the opposite behavior: intensities are increasing despite a look direction further away from the Sun (red shaded area). This behavior is consistent with the bulk flow direction of the energetic ions being deflected, roughly in the direction of the PEPSSI aperture (Bagenal et al., 2016). This deflection indicates a clear interaction of Pluto with IPS ions.

The apparent short duration and abrupt onset of the deflection is a bias resulting from the spacecraft attitude. The actual onset of the deflection might be more upstream and its extent might be gradual. Based on these measurements, we therefore do not know if Pluto is creating a sharp boundary of energetic ions, like a bow shock does to plasma, or if it is gradual, like a magnetopause to energetic ions.

The gray shading in Figure 1 illustrates that the time of slowed solar wind coincides with the deflection of energetic particles. The period of gradual solar wind slowing has been suggested to indicate the bow shock location (McComas et al., 2016).

3.2. Wake

We show the nominal ion intensities in the interplanetary medium as a horizontal black line in the first panel of Figure 1. After closest approach to Pluto, the intensities are reduced by over an order of magnitude compared to that nominal level. We interpret this as New Horizons entering the wake of Pluto. We use the term “wake” here because it describes the observation of IPS ions. This wake is by definition different from the magnetotail (or other regions set up mainly by the plasma) even though their volumes may roughly coincide: The wake is observed directly after the deflection (section 3.1), maybe close to the location of the bow shock. We are able to constrain its extent along the x axis; see below, but not along ρ.

The fact that the intensity is decreasing in the wake relative to the heliosphere informs us of the nature of the interaction between Pluto and its environment. If Pluto and its atmosphere were only slightly conducting, the interaction would be similar to, for example, Earth's Moon. A wake would form but given that the interstellar pickup ions, similar to suprathermal solar wind, are hot and relatively isotropic, this wake would refill closely behind the body (Clack et al., 2004; Halekas et al., 2011). Even the magnetopause of a magnetized body is not a sharp boundary to energetic ions (Cohen et al., 2016; Krupp et al., 2002; Mauk et al., 2016). The interaction of Pluto with IPS ions is therefore surprisingly strong.

The ion intensity in the wake is exponentially refilling with increasing radial distance to Pluto. The intensity does not go through a minimum around the time when New Horizons passes ρ=0; therefore, there is no evidence for a ρ dependence of the intensity. We observe the refilling over about 100R P . The intensity is still reduced at 14:42 UTC, when the spacecraft is changing to an attitude with low count rates. This is only observational bias and does not bear information on the extent of the wake. To determine this extent, we extrapolate the intensity increase before the attitude change up to the nominal solar wind values. This allows us to estimate the point where the wake vanishes because it becomes indistinguishable from the interplanetary medium, which occurs at x W =190R P for all y and z. This is the end of the wake along the Pluto‐Sun axis from the perspective of IPS ions. Note that New Horizons not necessarily traversed the wake until its end but may have left it to the side beforehand. Plutogenic plasma ions disappear at 14:15 UTC (McComas et al., 2016), suggesting that New Horizons left at least the heavy ion tail and potentially also the energetic particle wake. As our extrapolation mostly uses measurements before that time, this exit does not affect the estimate of the extent of the wake. There is no evidence in the measurements of whether the edge of the energetic particle wake is abrupt or gradual.

Figure 2 shows a zoom into the region of the wake. The first to third panels show particle intensities, and the fourth panel shows the clock angle of the instrument look direction. It can be seen that the ion intensities are independent on the clock angle of the observation. This means that the ion velocity distribution is symmetric around the Sun direction, as in the interplanetary medium. The oscillations in the ion intensities that are also visible in the figure are discussed in section 4.

Figure 2.

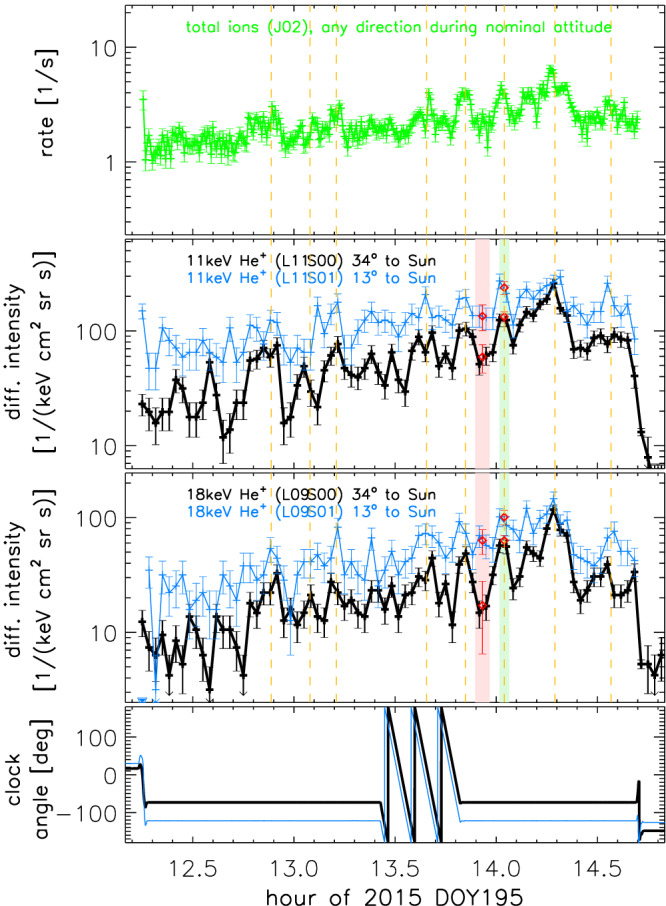
jgra55188-fig-0002

Open in a new tab

Zoom of Figure 1 into the energetic particle wake of Pluto. It can be seen that the interstellar pickup and suprathermal ion intensities increase exponentially and have oscillations superimposed. (first panel) Sum of all ions at all energies and directions that are detected by the Pluto Energetic Particle Spectrometer Science Investigation (PEPSSI) as a function of time. (second and third panels) He+ ion intensities for two different energies (middle and lower panel) and different look directions (different colors). Error bars are Poisson errors. vertical dashed lines = locations of the major peaks of the oscillation to guide the eye; vertical shaded areas = averaging ranges for a typical peak (green shading) and valley (red shading); red points = average respective intensities. (fourth panel) Cone angle of the two sectors shown. It can be seen that there is no correlation between cone angle and intensities, meaning that the ion distribution is symmetric around the Sun direction. The clock angle (not shown) is constant during this time period. DOY = day of year.

The measurements shown in Figure 1 for 12–15 hr UTC are for ions that reach the instrument from an angle of 34°. Particles observed at x PSH≈100R P (14 hr UTC) did pass Pluto at a cylindrical distance of ρ≈60R P , meaning that they were never close to the nose of the magnetosphere. Whatever mechanism is depleting the IPS ions is therefore not only acting close to Pluto. We suggest that along the entire cylindrical wake, until distance x W , there is some magnetic boundary that has the net effect of only letting a fraction of the overall ion distribution enter into the wake. We use the term “magnetic boundary” here as we currently do not want to imply formation mechanisms, as would be the case when using terms like magnetosheath, magnetic barrier, or magnetopause.

There are two prototype cases on how the magnetic boundary could prevent particles from entering the wake. It may be achieved by deflecting particles from large cone angles (that in the interplanetary medium have low intensities in the spacecraft frame) to smaller cone angles (explaining the small intensities at small angles). The smallest cone angles (which would have the highest intensities if they could enter the wake of Pluto) are entirely prevented from entering the wake. The deflection needs to be symmetric around the Sun direction, because the observed distribution shows this symmetry. This is different from the deflection close to Pluto (section 3.1) where the deflected flux points into a certain clock angle. The second option is that the boundary scatters away a fraction of particles, independent of their direction. Both mechanisms are able to explain the decreased intensities.

3.3. Decoupling From Plasma

Even though the overall amplitude of the energy spectra in the interplanetary medium and within the wake differ by over an order of magnitude, the spectral shapes are very similar (Figure 3), including the energy of the pickup ion cutoff. When measured in the spacecraft frame, as shown here, the pickup ion cutoff is at twice the bulk speed. Normally, the bulk speed of the interstellar pickup ions is the same as of the solar wind. As there is little solar wind entering the wake and all plasma is moving with low bulk speeds in this region (McComas et al., 2016), the interstellar pickup ions are therefore now moving independent of the solar wind plasma and the low energy plutogenic ions.

The similarity in spectral shape also suggests that the IPS ion composition in the wake is very similar to the surrounding heliosphere. We will therefore assume in the following analysis that the composition is identical to the heliosphere in the considered energy range of several kiloelectron volts to tens of kiloelectron volts. Our assumption is supported by the fact that spectra of plutogenic ions are observed to peak at hundreds of electron volts, so that no strong contributions are expected at the tens of kiloelectron volt energies discussed here.

4. Waves in the Wake

4.1. Observation

Figure 2 shows a zoom into the region of the wake. It can be seen that the intensities are oscillating with a period of ≈0.2 hr. The intensity peaks occur at the same time for all energies, meaning that there is no dispersion. We average the intensities at one peak and one valley and show their spectra in Figure 4. It can be seen that the contrast between peak and valley decreases with increasing energy and decreasing angle toward the Sun.

We suggest that the observed oscillations are a result of a local interaction with the oscillating electric field of an ULF wave, for example, through a drift resonance (Zong et al., 2008). Acceleration through an electric field increases the energy of a particle, while the phase space density (PSD) is conserved. Because energetic particle spectra are overall decreasing with energy, the acceleration then yields an increased PSD at a given energy compared to before the acceleration. Depending on wave phase, the field can also decelerate the particles, leading to a decrease in PSD at a given energy.

The acceleration needs to occur locally at the observation site; otherwise ions of different energies would disperse, and the intensity peak at the higher energies would run ahead of the peak at the lower energies.

4.2. Physical Model

We will now calculate if there is an electric field that would be able to quantitatively reproduce the observations discussed above in section 4.1. If such a field exists and is of a reasonable order of magnitude, this supports our interpretation of the data. We propose mechanisms to drive such an electric field in section 4.3.

We assume that the electric field E→ is described as

E→=E0→cos(k→·r→−ωt)=E0cos2πxλx+yλy+zλz−vwvsλ (1)

E0→ is the amplitude and initial direction of the electric field. k→ is the wave vector that is chosen to be perpendicular to the phase speed vector v→w of the wave, as it follows from Maxwell's equations in a near vacuum. λ=2π/k is the wavelength and λ i its components in PSH coordinates. v w is the phase speed and ω=kv w the angular frequency of the wave.

While r→ is generally an arbitrary location and t is an arbitrary time, we connect these two quantities here through the particle velocity v→ (with its components v i and the total speed v) and the traversed distance s of the particle. Therefore, the right‐hand side of equation (1) provides the electric field at the location of the particle during a certain wave phase. In order to compare the maximum effect that the field can have on the particle, we repeat the same calculations with a phase shifted of π.

The velocity v x of the considered particle changes over every chosen step Δx according to the energy change

ΔWx=ExΔxq (2)

imposed by the electric field and the charge q=+1e of the He+ ion. The step size in the y and z directions is determined by Δi=v i ΔT with ΔT=Δx/v x and allows us to calculate energy and speed change in the respective directions. We start out with the ion velocity vectors that were observed while New Horizons was at r→=(−100,10,5)RP and numerically calculate how v→ was changing backward in time.

After the ion leaves the assumed wake of Pluto (described in equation (3) below), the field is set to 0 and the particle energy and velocity are kept constant. In reality, there might be additional deflection at the magnetic boundary.

We assume that the region in which the electric field is operating is coinciding with the wake. Due to the lack of measurement constraints, we also assume that the wake is symmetric around the x axis. We estimate the cross section ρ t of the wake as a function of distance x PSH to Pluto. For this, we use the location of the observed deflection (section 3.1) together with the location where New Horizons leaves the heavy ion tail (McComas et al., 2016). These two points uniquely constrain the parameters of a linear function describing ρ(x PSH):

ρt/RP=−0.063(xPSH/RP)+9.1 (3)

With the now derived relation between the observed, final energy to the initial energy, we can calculate how the electric field distorts an assumed initial spectrum. Because our tracing does not account for any effect of the magnetic boundary, our initial distribution is taken inside the magnetic boundary. We assume that this distribution has a similar shape to normal heliospheric spectra. The assumed PSD f is isotropic in the solar wind frame, which moves with v b =400 km/s.

f=f0(|v→−vb→|/vb)2γ−2 (4)

We use here the PSD f in velocity space (particles per volume in real and in velocity space, not momentum space) that is related to the differential intensity j (particles per time, area, energy interval, and solid angle) through f=(m/v 2)j with the particle mass m. f 0 is a constant. Above the pickup ion cutoff, at |v→−vb→|>vb in the solar wind frame, we assume γ=−1.5, consistent with observations (Fisk & Gloeckler, 2012; Hill & Hamilton, 2010; Kollmann et al., 2019) and γ=+1 below the pickup cutoff.

Overall, we are now left with an optimization problem. To get started, we chose λ=2,800R P and v w =400 km/s based on theory (section 4.3). The results are not sensitive to λ as long as λ is much larger than the size of the system. We then vary E→ and the direction of k→ until the modeled spectra match the observed spectra. As our main concern here is to test if an electric field may be able in principle to explain the data; it is sufficient for our purposes to find a local minimum of the model‐data difference, and we do not need to test if there are ambiguities in the solution or whether we have found the optimum solution.

In Figure 4 we compare measured and modeled spectra. It can be seen that the model can reproduce the main features of the measurement, namely, that the intensity difference between energies decreases with energy (compare spectra within one panel) and that the difference between wave phases changes with particle direction (intensities vary more with phase for the lower panel).

The parameters for the model include an electric field of E=8×104 V/m. For comparison, the convective electric field of the upstream solar wind is 6×105 V/m (as it can be calculated from the frozen‐in condition based on the average magnetic field (Bagenal et al., 2015) and upstream solar wind speed (Bagenal et al., 2016).) The optimum cone angle of the electric field is 82°, and its clock angle is −8°. The propagation direction of the wave is described by the cone angle 170° and clock angle −15°. Example ion trajectories are shown in Figure 5. Examples on how the field changes the energy of the ion are shown in Figure 6.

Figure 5.

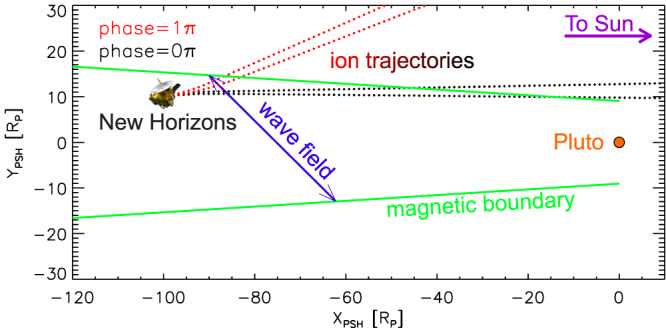
jgra55188-fig-0005

Open in a new tab

Sketch of the geometry and wave interaction in Pluto's wake. Locations are shown as projections on the x y plane of the Pluto Solar Heliographic (PSH) coordinate system, essentially looking down on Pluto's magnetosphere. The Sun direction is on the right. We show the location of New Horizons when observing the selected intensity peak and valley. Green = outline of the magnetic boundary of the wake; dotted lines = trajectories of the detected ions for the two considered look directions. Red and black curves are for two wave phases where the direction of the electric field is opposite. It can be seen that the electric field changes the trajectories of the ions. The electric field vector in the x y plane is shown as a blue line. Each arrowhead is for one of the wave phases shown here. Note that particularly the ions shown in red enter the wake from the side without ever being close to Pluto.

Figure 6.

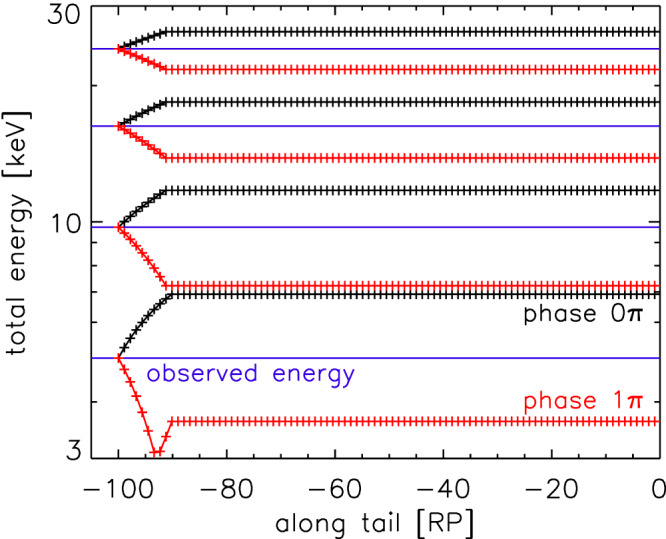
jgra55188-fig-0006

Open in a new tab

Energy change along Pluto's wake for ions with different starting energies (blue horizontal lines). All ions shown here are observed coming from a cone angle of 166°. It can be seen that the ions either lose (red) or gain (black) energy, depending on the wave phase. The x axis shows the x PSH coordinate of the ions. All ions start at x PSH=−100R P , because this is the location we are studying here, and change their energy over about 10R P until they leave the wake. PSH = Pluto Solar Heliographic coordinate system.

Overall, we find that the observed intensity oscillations can indeed be quantitatively explained with an oscillating electric field. This field shifts ion intensity spectra to lower or higher energies, depending on wave phase, which results in intensity changes when observing fixed energies.

4.3. Wave Drivers

Planetary magnetospheres show a large variety of waves, some of which may have electric field components that may explain the electric field inferred in section 4.2. A wave that might match the observed periodicity is the bi‐ion wave (Sauer et al., 1996, 1998). Such a wave grows in the presence of a flow shear as for example between upstream solar wind plasma and freshly created pickup ions. The pickup ion flow is directed parallel to the electric field. Because the gyroradius is usually much larger than the considered scale, the magnetic field does not play a role for the pickup ion motion.

At Pluto, bi‐ion waves show in simulations as a result of plutogenic pickup ions (Barnes et al., 2019; Delamere, 2009). Most of the wave power is between the gyrofrequency of upstream protons and pickup heavies, which are at 0.1 and 2.9 hr, respectively, based on the parameters found at Pluto (Bagenal et al., 2015; McComas et al., 2016). Given that the observed periodicity of ≈0.2 hr is indeed within this range, it is therefore well possible that the electric field discussed in section 4.2 is the result of such bi‐ion waves resulting from the plutogenic ions.

There exist a variety of other wave modes. Another wave that is important at unmagnetized planets is, for example, the lower hybrid wave (Shapiro et al., 1995) that may be able to accelerate pickup ions on scales smaller than their gyroradius, as it is needed at Pluto. A resonance between the IPS ions and any wave may be a mere coincidence. Another explanation is that the observed interstellar ions are actually driving the wave that is affecting them. A further mechanism for how an ion population can drive a wave is through the modified ion‐Weibel instability. This kind of wave grows in the presence of a charged particle beam (Chang et al., 1990; Fried, 1959). Examples are found at Mars (Sauer et al., 1997) and comet 67P/Churyumov‐Gerasimenko (Meier et al., 2016; Richter et al., 2015, 2016). IPS ions do not create a current in the heliosphere as all species, ions, and electrons, are moving with the same bulk speed. When the solar wind encounters Pluto, most solar wind plasma is excluded from the wake (Bagenal et al., 2016, 2019). IPS ions are also affected, but a fraction of them are able to enter the wake (Figure 1) while roughly maintaining their bulk speed (section 3.3, Figure 3). We suggest that these ions are driving a current that can be calculated as

j=qnvb (5)

with the IPS ion bulk speed v b and density n.

Based on the current, we are able to estimate the periodicity of the modified ion‐Weibel instability that can then be compared with observations. We assume that a magnetic field with amplitude B 0 and an electric field with amplitude E 0 oscillate perpendicular to each other and to the wave vector. We then find from Ampere's law (Fried, 1959; Richter et al., 2015)

j=B0k⊥μ0 (6)

where k ⊥ is the wave number perpendicular to the current and μ 0 is the natural constant. In principle, equation (6) can be generalized to account for the time dependence of the electric field that we found in section 4.2. However, the resulting displacement current is six orders of magnitude less than the term in equation (6) that scales with B 0, which means that it is the magnetic, not the electric field, that determines the periodicity.

Based on the dispersion relation and the direction of maximum wave growth, we assume (Chang et al., 1990; Meier et al., 2016; Richter et al., 2015)

ω=k‖vb (7)

where the ion bulk speed v b and the wave phase speed v w are approximately the same.

The components of the wave vector are related through the angle θ between k→ and j→.

k⊥k‖=tan(θ) (8)

New Horizons is roughly moving in the direction of the ion bulk speed. We can therefore relate k ‖ with the observed periodicity T through

2π/k‖=λ‖=vwT (9)

Inserting equations (6), (7), (8), (9) into each other, we get

T=2B0πtan(θ)jμ0vb (10)

We assume that the magnetic field oscillations are on the order of the background field, B 0=0.15 nT (Bagenal et al., 2015), because this is what is observed by Rosetta at 67P (Richter et al., 2015). For the cone angle we use θ=12° based on section 4.2.

We calculate the current through equation (5). The bulk speed used is the upstream solar wind speed, v b =403 km/s (Bagenal et al., 2016). We calculate the density n by transforming the measurements after entering the wake of Pluto into the frame moving with v b (Kollmann et al., 2019) in which the distribution is approximately isotropic (Gloeckler et al., 1997; Kollmann et al., 2019). After integrating over such a distribution we find j=1×10−11Am−2.

With these values, we find a periodicity of 0.1 hr, which is close to the observed period of 0.2 hr (section 4.1).

Plutogenic pickup ions are also expected to drive the modified ion‐Weibel instability (Sauer et al., 1997). The average current of plutogenic pickup ions is 2 orders of magnitude higher than the current from heliopsheric IPS ions, which could drive the wave and lead to an equivalently shorter periodicity that would be too short to be reliably observed. However, the parameters of the plutogenic ions are highly variable and decrease with distance to Pluto (McComas et al., 2016). Particularly in the region toward the end of the wake where we observe the most prominent oscillations, the Pluto ion density is about 2 orders of magnitude lower, making their current comparable with the IPS current.

There might be other mechanisms that also drive electric field oscillations. Two of the largest intensity peaks coincide with the passage of the geometrical shadows of Pluto and Charon (fourth panel of Figure 1). This suggests an additional interaction that has not been accounted for and that may drive the formation of the neighboring peaks.

4.4. Discussion

Given that our model assuming an electric field wave works out quantitatively and there are mechanisms that could drive this wave, we conclude that waves are indeed shaping the IPS ion distribution in Pluto's wake. Comet 67P/Churyumov‐Gerasimenko has been referred to as “the singing comet” (Glassmeier, 2017; Meier et al., 2016; Richter et al., 2016) thanks to its ULF waves for which we now also find evidence at “singing Pluto.”

By using energetic particle signatures we are able to infer properties of a varying electric field, which will induce a magnetic field, even though New Horizons is not able to directly measure electric or magnetic fields. PEPSSI measurements can be used to further constrain models of Pluto's environment.

5. Summary

We use measurements of energetic heliospheric ions, namely, IPS ions with energies of a few kiloelectron volts to tens of kiloelectron volts, to study the interaction of Pluto with the interplanetary medium. Our main findings are summarized below. A visualization of these findings is also shown in Figure 7.

  • Pluto deflects the bulk flow direction of heliospheric IPS ions (section 3.1).

  • The wake of Pluto shows depleted intensities of heliospheric IPS ions (Figure 1). The ion removal occurs not just at the nose of magnetosphere but also has to happen across the magnetic boundary of the wake (section 3.2 and Figure 5).

  • The bulk speed and IPS ion composition in Pluto's wake is similar to the upstream conditions (Figure 3). We find no evidence for plutogenic pickup ions in the kiloelectron volt energy range (section 3.3).

  • IPS ion intensities in the wake of Pluto are oscillating with a period of about 0.2 hr (Figure 2).

  • The oscillations are consistent with being the result of an electric field wave that is accelerating and decelerating ions, depending on wave phase. Because the intensity spectrum is energy dependent, this results in the observed changes in IPS ion intensity (section 4.2 and Figure 4).

  • The origin of the electric field wave may be the modified ion‐Weibel instability driven by the observed energetic IPS ions or a bi‐ion wave driven by low energy plutogenic pickup ions (section 4.3).

  • The wake that Pluto carves out of the IPS ion population extends ≈190R P downstream beyond which the intensities become indistinguishable from those in the interplanetary medium (section 3.2 and Figure 1).

Figure 7.

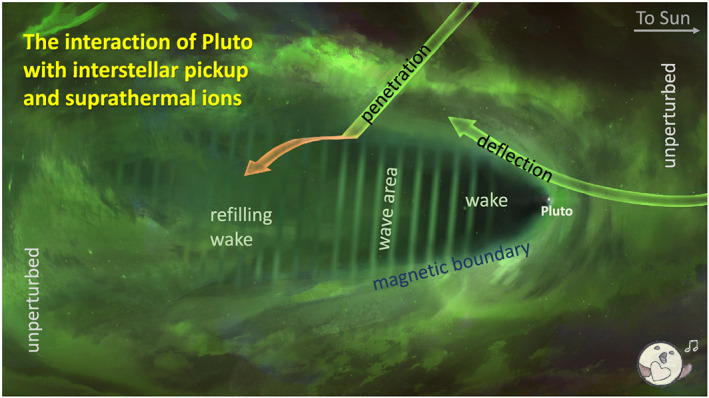
jgra55188-fig-0007

Open in a new tab

Summary sketch of the interaction between Pluto and the interplanetary medium. Pluto is embedded in a medium of interstellar pickup ions with kiloelectron volt energies and suprathermal ions with energies of tens of kiloelectron volts and above. These IPS (interstellar pickup and suprathermal) ions are shown in green to emphasize their extrasolar origin. Pluto is illustrated as a bright dot. The Sun is to the right of the figure. The primary effect of Pluto on IPS ions is that it depletes their intensities and forms a wake in the antisunward direction that is illustrated in black. The wake gradually refills with distance to Pluto until the intensities become indistinguishable from the unperturbed interplanetary medium (left and right areas). We find no evidence for energetic ions of plutogenic origin. Pluto is “singing” in the sense that there is an electric field wave acting within the wake that affects the observed IPS ion intensities. We symbolize this wave through the stripe pattern in the wake even though in reality the wavelength is larger than the length of the wake. IPS ions have the highest intensities when coming from the sunward direction (when measured in the Pluto or spacecraft frame) but can generally come from any direction. The ions are deflected (green arrows) from their original direction near the magnetic boundary that encompasses the wake. Ions that penetrate into the wake (red arrow) are further deflected by the electric field wave. The boundary of the energetic particle wake might be less sharp than plasma boundaries such as a bow shock or magnetic barrier. Sketch illustrated by Mike Yakovlev (JHU/APL).

Acknowledgments

This work was supported by NASA New Horizons funding through contract NAS5‐97271/Task Order 30. New Horizons/PEPSSI data are publicly available through NASA's planetary data archive (McNutt, 2017). We thank M. M. Yakovlev (JHU/APL) and H. Kollmann for graphics support.

Kollmann, P. , Hill, M. E. , Allen, R. C. , McNutt Jr, R. L. , Brown, L. E. , Barnes, N. P. , et al. (2019). Pluto's interaction with energetic heliospheric ions. Journal of Geophysical Research: Space Physics, 124, 7413–7424. 10.1029/2019JA026830

References

  1. Bagenal, F. , Delamere, P. A. , Elliott, H. A. , Hill, M. E. , Lisse, C. M. , McComas, D. J. , McNutt Jr, R. L. , Richardson, J. D. , Smith, C. W. , & Strobel, D. F. (2015). Solar wind at 33 AU: Setting bounds on the Pluto interaction for New Horizons. Journal of Geophysical Research: Planets, 120, 1497–1511. 10.1002/2015JE004880 [DOI] [Google Scholar]
  2. Bagenal, F. , Horányi, M. , McComas, D. J. , McNutt, R. L. , Elliott, H. A. , Hill, M. E. , Brown, L. E. , Delamere, P. A. , Kollmann, P. , Krimigis, S. M. , Kusterer, M. , Lisse, C. M. , Mitchell, D. G. , Piquette, M. , Poppe, A. R. , Strobel, D. F. , Szalay, J. R. , Valek, P. , Vandegriff, J. , Weidner, S. , Zirnstein, E. J. , Stern, S. A. , Ennico, K. , Olkin, C. B. , Weaver, H. A. , Young, L. A. , Gladstone, G. R. , Grundy, W. M. , McKinnon, W. B. , Moore, J. M. , Spencer, J. R. , Andert, T. , Andrews, J. , Banks, M. , Bauer, B. , Bauman, J. , Barnouin, O. S. , Bedini, P. , Beisser, K. , Beyer, R. A. , Bhaskaran, S. , Binzel, R. P. , Birath, E. , Bird, M. , Bogan, D. J. , Bowman, A. , Bray, V. J. , Brozovic, M. , Bryan, C. , Buckley, M. R. , Buie, M. W. , Buratti, B. J. , Bushman, S. S. , Calloway, A. , Carcich, B. , Cheng, A. F. , Conard, S. , Conrad, C. A. , Cook, J. C. , Cruikshank, D. P. , Custodio, O. S. , Dalle Ore, C. M. , Deboy, C. , Dischner, Z. J. B. , Dumont, P. , Earle, A. M. , Ercol, J. , Ernst, C. M. , Finley, T. , Flanigan, S. H. , Fountain, G. , Freeze, M. J. , Greathouse, T. , Green, J. L. , Guo, Y. , Hahn, M. , Hamilton, D. P. , Hamilton, S. A. , Hanley, J. , Harch, A. , Hart, H. M. , Hersman, C. B. , Hill, A. , Hinson, D. P. , Holdridge, M. E. , Howard, A. D. , Howett, C. J. A. , Jackman, C. , Jacobson, R. A. , Jennings, D. E. , Kammer, J. A. , Kang, H. K. , Kaufmann, D. E. , Kusnierkiewicz, D. , Lauer, T. R. , Lee, J. E. , Lindstrom, K. L. , Linscott, I. R. , Lunsford, A. W. , Mallder, V. A. , Martin, N. , Mehoke, D. , Mehoke, T. , Melin, E. D. , Mutchler, M. , Nelson, D. , Nimmo, F. , Nunez, J. I. , Ocampo, A. , Owen, W. M. , Paetzold, M. , Page, B. , Parker, A. H. , Parker, J. W. , Pelletier, F. , Peterson, J. , Pinkine, N. , Porter, S. B. , Protopapa, S. , Redfern, J. , Reitsema, H. J. , Reuter, D. C. , Roberts, J. H. , Robbins, S. J. , Rogers, G. , Rose, D. , Runyon, K. , Retherford, K. D. , Ryschkewitsch, M. G. , Schenk, P. , Schindhelm, E. , Sepan, B. , Showalter, M. R. , Singer, K. N. , Soluri, M. , Stanbridge, D. , Steffl, A. J. , Stryk, T. , Summers, M. E. , Tapley, M. , Taylor, A. , Taylor, H. , Throop, H. B. , Tsang, C. C. C. , Tyler, G. L. , Umurhan, O. M. , Verbiscer, A. J. , Versteeg, M. H. , Vincent, M. , Webbert, R. , Weigle, G. E. , White, O. L. , Whittenburg, K. , Williams, B. G. , Williams, K. , Williams, S. , Woods, W. W. , & Zangari, A. M. (2016). Pluto's interaction with its space environment: Solar wind, energetic particles, and dust. Science, 351, aad9045. 10.1126/Science.aad9045 [DOI] [PubMed] [Google Scholar]
  3. Barnes, N. P. , Delamere, P. A. , Strobel, D. F. , Bagenal, F. , McComas, D. J. , Elliott, H. A. , Valek, P. , Weaver, H. A. , Ennico, K. , Young, L. A. , & Stern, S. A. (2019). Constraining the IMF at Pluto using New Horizons SWAP data and hybrid simulations. Journal of Geophysical Research: Space Physics, 124, 1568–1581. 10.1029/2018JA026083 [DOI] [Google Scholar]
  4. Bertucci, C. , Hamilton, D. C. , Kurth, W. S. , Hospodarsky, G. , Mitchell, D. , Sergis, N. , Edberg, N. J. T. , & Dougherty, M. K. (2015). Titan's interaction with the supersonic solar wind. Geophysical Research Letters, 42, 193–200. 10.1002/2014GL062106 [DOI] [Google Scholar]
  5. Chang, C. L. , Wong, H. K. , & Wu, C. S. (1990). Electromagnetic instabilities attributed to a cross‐field ion drift. Physical Review Letters, 65, 1104–1107. 10.1103/PhysRevLett.65.1104 [DOI] [PubMed] [Google Scholar]
  6. Clack, D. , Kasper, J. C. , Lazarus, A. J. , Steinberg, J. T. , & Farrell, W. M. (2004). Wind observations of extreme ion temperature anisotropies in the lunar wake. Geophysical Research Letters, 31, L06812. 10.1029/2003GL018298 [DOI] [Google Scholar]
  7. Cohen, I. J. , Mauk, B. H. , Anderson, B. J. , Westlake, J. H. , Sibeck, D. G. , Giles, B. L. , Pollock, C. J. , Turner, D. L. , Fennell, J. F. , Blake, J. B. , Clemmons, J. H. , Jaynes, A. N. , Baker, D. N. , Craft, J. V. , Spence, H. E. , Niehof, J. T. , Reeves, G. D. , Torbert, R. B. , Russell, C. T. , Strangeway, R. J. , Magnes, W. , Trattner, K. J. , Fuselier, S. A. , & Burch, J. L. (2016). Observations of energetic particle escape at the magnetopause: Early results from the MMS Energetic Ion Spectrometer (EIS). Geophysical Research Letters, 43, 5960–5968. 10.1002/2016GL068689 [DOI] [Google Scholar]
  8. Delamere, P. A. (2009). Hybrid code simulations of the solar wind interaction with Pluto. Journal of Geophysical Research, 114, A03220. 10.1029/2008JA013756 [DOI] [Google Scholar]
  9. Dong, Y. , Fang, X. , Brain, D. A. , McFadden, J. P. , Halekas, J. S. , Connerney, J. E. P. , Eparvier, F. , Andersson, L. , Mitchell, D. , & Jakosky, B. M. (2017). Seasonal variability of Martian ion escape through the plume and tail from MAVEN observations. Journal of Geophysical Research: Space Physics, 122, 4009–4022. 10.1002/2016JA023517 [DOI] [Google Scholar]
  10. Fisk, L. A. , & Gloeckler, G. (2012). Particle acceleration in the heliosphere: Implications for astrophysics. Space Science Reviews, 173, 433–458. 10.1007/s11214-012-9899-8 [DOI] [Google Scholar]
  11. Fried, B. D. (1959). Mechanism for instability of transverse plasma waves. Physics of Fluids, 2, 337–337. 10.1063/1.1705933 [DOI] [Google Scholar]
  12. Glassmeier, K. H. (2017). Interaction of the solar wind with comets: A Rosetta perspective. Philosophical Transactions of the Royal Society of London Series A, 375, 20160256. 10.1098/rsta.2016.0256 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gloeckler, G. , Fisk, L. A. , & Geiss, J. (1997). Anomalously small magnetic field in the local interstellar cloud. Nature, 386, 374–377. 10.1038/386374a0 [DOI] [Google Scholar]
  14. Halekas, J. S. , Angelopoulos, V. , Sibeck, D. G. , Khurana, K. K. , Russell, C. T. , Delory, G. T. , Farrell, W. M. , McFadden, J. P. , Bonnell, J. W. , Larson, D. , Ergun, R. E. , Plaschke, F. , & Glassmeier, K. H. (2011). First results from ARTEMIS, a new two‐spacecraft lunar mission: Counter‐streaming plasma populations in the lunar wake. Space Science Reviews, 165, 93–107. 10.1007/s11214-010-9738-8 [DOI] [Google Scholar]
  15. Hill, M. E. , & Hamilton, D. C. (2010). Interim report on the power law index of interplanetary suprathermal ion spectra. AIP Conference Proceedings, 1302, 58–63. 10.1063/1.3529991 [DOI] [Google Scholar]
  16. Hinson, D. P. , Linscott, I. R. , Young, L. A. , Tyler, G. L. , Stern, S. A. , Beyer, R. A. , Bird, M. K. , Ennico, K. , Gladstone, G. R. , Olkin, C. B. , Pätzold, M. , Schenk, P. M. , Strobel, D. F. , Summers, M. E. , Weaver, H. A. , & Woods, W. W. (2017). Radio occultation measurements of Pluto's neutral atmosphere with New Horizons. Icarus, 290, 96–111. 10.1016/j.icarus.2017.02.031 [DOI] [Google Scholar]
  17. Kollmann, P. , Brandt, P. C. , Collinson, G. , Rong, Z. J. , Futaana, Y. , & Zhang, T. L. (2016). Properties of planetward ion flows in Venus' magnetotail. Icarus, 274, 73–82. 10.1016/j.icarus.2016.02.053 [DOI] [Google Scholar]
  18. Kollmann, P. , Hill, M. E. , McNutt Jr. R. L., Brown, L. E. , Allen, R. C. , Clark, G. , Andrews, B. , Salazar, N. , Westlake, J. , Romeo, G. , Vandegriff, J. , Kusterer, M. , Smith, D. , Jaskulek, S. , Decker, R. , Cheng, A. F. , Krimigis, S. M. , Lisse, C. M. , Mitchell, D. G. , Weaver, H. A. , Delamere, P. , Elliott, H. A. , Fattig, E. , Gladstone, G. R. , Valek, P. W. , Weidner, S. , Bagenal, F. , Horányi, M. , Kammer, J. A. , Kaufmann, D. , Olkin, C. B. , Piquette, M. R. , Spencer, J. R. , Steffl, A. J. , Stern, S. A. , Young, L. A. , Ennico, K. , Linscott, I. R. , Strobel, D. F. , Summers, M. E. , & Romeo, G. (2019). Suprathermal ions in the outer heliosphere. The Astrophysical Journal, 876(1), 46. 10.3847/1538-4357/ab125f [DOI] [Google Scholar]
  19. Krupp, N. , Woch, J. , Lagg, A. , Espinosa, S. A. , Livi, S. , Krimigis, S. M. , Mitchell, D. G. , Williams, D. J. , Cheng, A. F. , Mauk, B. H. , McEntire, R. W. , Armstrong, T. P. , Hamilton, D. C. , Gloeckler, G. , Dandouras, J. , & Lanzerotti, L. J. (2002). Leakage of energetic particles from Jupiter's dusk magnetosphere: Dual spacecraft observations. Geophysical Research Letters, 29(15), 1736. 10.1029/2001GL014290 [DOI] [Google Scholar]
  20. Mauk, B. H. , Cohen, I. J. , Westlake, J. H. , & Anderson, B. J. (2016). Modeling magnetospheric energetic particle escape across Earth's magnetopause as observed by the MMS mission. Geophysical Research Letters, 43, 4081–4088. 10.1002/2016GL068856 [DOI] [Google Scholar]
  21. McComas, D. J. , Elliott, H. A. , Weidner, S. , Valek, P. , Zirnstein, E. J. , Bagenal, F. , Delamere, P. A. , Ebert, R. W. , Funsten, H. O. , Horanyi, M. , McNutt Jr, R. L. , Moser, C. , Schwadron, N. A. , Strobel, D. F. , Young, L. A. , Ennico, K. , Olkin, C. B. , Stern, S. A. , & Weaver, H. A. (2016). Pluto's interaction with the solar wind. Journal of Geophysical Research: Space Physics, 121, 4232–4246. 10.1002/2016JA022599 [DOI] [Google Scholar]
  22. McNutt, R. (2017). New Horizons raw PEPSSI Pluto Cruise. NASA Planetary Data System: Small bodies node https://pdssbn.astro.umd.edu/holdings/nh-x-pepssi-2-plutocruise-v2.0/dataset.html
  23. McNutt, R. L. , Livi, S. A. , Gurnee, R. S. , Hill, M. E. , Cooper, K. A. , Andrews, G. B. , Keath, E. P. ; , Krimigis, S. M. , Mitchell, D. G. , Tossman, B. , Bagenal, F. , Boldt, J. D. , Bradley, W. , Devereux, W. S. , Ho, G. C. , Jaskulek, S. E. , Lefevere, T. W. , Malcom, H. , Marcus, G. A. , Hayes, J. R. , Moore, G. T. , Perry, M. E. , Williams, B. D. , Wilson, P. , Brown, L. E. , Kusterer, M. B , & Vandegriff, J. D. (2008). The Pluto Energetic Particle Spectrometer Science Investigation (PEPSSI) on the New Horizons Mission. Space Science Reviews, 140, 315–385. 10.1007/s11214-008-9436-y [DOI] [Google Scholar]
  24. Meier, P. , Glassmeier, K. H. , & Motschmann, U. (2016). Modified ion‐Weibel instability as a possible source of wave activity at comet 67P/Churyumov‐Gerasimenko. Annales Geophysicae, 34, 691–707. 10.5194/angeo-34-691-2016 [DOI] [Google Scholar]
  25. Nimmo, F. , Umurhan, O. , Lisse, C. M. , Bierson, C. J. , Lauer, T. R. , Buie, M. W. , Throop, H. B. , Kammer, J. A. , Roberts, J. H. , McKinnon, W. B. , Zangari, A. M. , Moore, J. M. , Stern, S. A. , Young, L. A. , Weaver, H. A. , Olkin, C. B. , & Ennico, K. (2017). Mean radius and shape of Pluto and Charon from New Horizons images. Icarus, 287, 12–29. 10.1016/j.icarus.2016.06.027 [DOI] [Google Scholar]
  26. Richter, I. , Auster, H. U. , Berghofer, G. , Carr, C. , Cupido, E. , Fornaçon, K. H. , Goetz, C. , Heinisch, P. , Koenders, C. , Stoll, B. , Tsurutani, B. T. , Vallat, C. , Volwerk, M. , & Glassmeier, K. H. (2016). Two‐point observations of low‐frequency waves at 67P/Churyumov‐Gerasimenko during the descent of PHILAE: Comparison of RPCMAG and ROMAP. Annales Geophysicae, 34, 609–622. 10.5194/angeo-34-609-2016 [DOI] [Google Scholar]
  27. Richter, I. , Koenders, C. , Auster, H. U. , Frühauff, D. , Götz, C. , Heinisch, P. , Perschke, C. , Motschmann, U. , Stoll, B. , Altwegg, K. , Burch, J. , Carr, C. , Cupido, E. , Eriksson, A. , Henri, P. , Goldstein, R. , Lebreton, J.‐P. , Mokashi, P. , Nemeth, Z. , Nilsson, H. , Rubin, M. , Szegö, K. , Tsurutani, B. T. , Vallat, C. , Volwerk, M. , & Glassmeier, K. H. (2015). Observation of a new type of low‐frequency waves at comet 67P/Churyumov‐Gerasimenko. Annales Geophysicae, 33, 1031–1036. 10.5194/angeo-33-1031-2015 [DOI] [Google Scholar]
  28. Sauer, K. , Bogdanov, A. , Baumgärtel, K. , & Dubinin, E. (1996). Bi‐ion discontinuities at weak solar wind massloading. Physica Scripta Volume T, 63, 111–118. 10.1088/0031-8949/1996/T63/017 [DOI] [Google Scholar]
  29. Sauer, K. , Dubinin, E. , Baumgärtel, K. , & Tarasov, V. (1998). Low‐frequency electromagnetic waves and instabilities within the Martian bi‐ion plasma. Earth, Planets, and Space, 50, 269–268. 10.1186/BF03352113 [DOI] [Google Scholar]
  30. Sauer, K. , Dubinin, E. , & Baumgärtel, K. (1997). Bi‐ion structuring in the magnetosheath of Mars—Theoretical modeling. Advances in Space Research, 20, 137. 10.1016/S0273-1177(97)00523-1 [DOI] [Google Scholar]
  31. Sauer, K. , Lipatov, A. , Baumgärtel, K. , & Dubinin, E. (1997). Solar wind‐Pluto interaction revised. Advances in Space Research, 20, 295. 10.1016/S0273-1177(97)00551-6 [DOI] [Google Scholar]
  32. Shapiro, V. D. , Szegö, K. , Ride, S. K. , Nagy, A. F. , & Shevchenko, V. I. (1995). On the interaction between the shocked solar wind and the planetary ions on the dayside of Venus. Journal of Geophysical Research, 100, 21,289–21,306. 10.1029/95JA01831 [DOI] [Google Scholar]
  33. Stern, S. A. , Bagenal, F. , Ennico, K. , Gladstone, G. R. , Grundy, W. M. , McKinnon, W. B. , Moore, J. M. , Olkin, C. B. , Spencer, J. R. , Weaver, H. A. , Young, L. A. , Andert, T. , Andrews, J. , Banks, M. , Bauer, B. , Bauman, J. , Barnouin, O. S. , Bedini, P. , Beisser, K. , Beyer, R. A. , Bhaskaran, S. , Binzel, R. P. , Birath, E. , Bird, M. , Bogan, D. J. , Bowman, A. , Bray, V. J. , Brozovic, M. , Bryan, C. , Buckley, M. R. , Buie, M. W. , Buratti, B. J. , Bushman, S. S. , Calloway, A. , Carcich, B. , Cheng, A. F. , Conard, S. , Conrad, C. A. , Cook, J. C. , Cruikshank, D. P. , Custodio, O. S. , Dalle Ore, C. M. , Deboy, C. , Dischner, Z. J. B. , Dumont, P. , Earle, A. M. , Elliott, H. A. , Ercol, J. , Ernst, C. M. , Finley, T. , Flanigan, S. H. , Fountain, G. , Freeze, M. J. , Greathouse, T. , Green, J. L. , Guo, Y. , Hahn, M. , Hamilton, D. P. , Hamilton, S. A. , Hanley, J. , Harch, A. , Hart, H. M. , Hersman, C. B. , Hill, A. , Hill, M. E. , Hinson, D. P. , Holdridge, M. E. , Horanyi, M. , Howard, A. D. , Howett, C. J. A. , Jackman, C. , Jacobson, R. A. , Jennings, D. E. , Kammer, J. A. , Kang, H. K. , Kaufmann, D. E. , Kollmann, P. , Krimigis, S. M. , Kusnierkiewicz, D. , Lauer, T. R. , Lee, J. E. , Lindstrom, K. L. , Linscott, I. R. , Lisse, C. M. , Lunsford, A. W. , Mallder, V. A. , Martin, N. , McComas, D. J. , McNutt, R. L. , Mehoke, D. , Mehoke, T. , Melin, E. D. , Mutchler, M. , Nelson, D. , Nimmo, F. , Nunez, J. I. , Ocampo, A. , Owen, W. M. , Paetzold, M. , Page, B. , Parker, A. H. , Parker, J. W. , Pelletier, F. , Peterson, J. , Pinkine, N. , Piquette, M. , Porter, S. B. , Protopapa, S. , Redfern, J. , Reitsema, H. J. , Reuter, D. C. , Roberts, J. H. , Robbins, S. J. , Rogers, G. , Rose, D. , Runyon, K. , Retherford, K. D. , Ryschkewitsch, M. G. , Schenk, P. , Schindhelm, E. , Sepan, B. , Showalter, M. R. , Singer, K. N. , Soluri, M. , Stanbridge, D. , Steffl, A. J. , Strobel, D. F. , Stryk, T. , Summers, M. E. , Szalay, J. R. , Tapley, M. , Taylor, A. , Taylor, H. , Throop, H. B. , Tsang, C. C. C. , Tyler, G. L. , Umurhan, O. M. , Verbiscer, A. J. , Versteeg, M. H. , Vincent, M. , Webbert, R. , Weidner, S. , Weigle, G. E. , White, O. L. , Whittenburg, K. , Williams, B. G. , Williams, K. , Williams, S. , Woods, W. W. , Zangari, A. M. , & Zirnstein, E. (2015). The Pluto system: Initial results from its exploration by New Horizons. Science, 350, aad1815. 10.1126/Science.aad1815 [DOI] [PubMed] [Google Scholar]
  34. Stern, S. A. , Grundy, W. M. , McKinnon, W. B. , Weaver, H. A. , & Young, L. A. (2018). The Pluto System after New Horizons. Annual Review of Astronomy and Astrophysics, 56, 357–392. 10.1146/annurev-astro-081817-051935 [DOI] [Google Scholar]
  35. Stern, S. A. , Weaver, H. A. , Spencer, J. R. , & Elliott, H. A. (2018). The New Horizons Kuiper Belt extended mission. Space Science Reviews, 214, 77. 10.1007/s11214-018-0507-4 [DOI] [Google Scholar]
  36. Young, L. A. , Stern, S. A. , Weaver, H. A. , Bagenal, F. , Binzel, R. P. , Buratti, B. , Cheng, A. F. , Cruikshank, D. , Gladstone, G. R. , Grundy, W. M. , Hinson, D. P. , Horanyi, M. , Jennings, D. E. , Linscott, I. R. , McComas, D. J. , McKinnon, W. B. , McNutt, R. , Moore, J. M. , Murchie, S. , Olkin, C. B. , Porco, C. C. , Reitsema, H. , Reuter, D. C. , Spencer, J. R. , Slater, D. C. , Strobel, D. , Summers, M. E. , Tyler, G. L. (2008). New Horizons: Anticipated Scientific Investigations at the Pluto System. Space Science Reviews, 140, 93–127. 10.1007/s11214-008-9462-9 [DOI] [Google Scholar]
  37. Young, L. A. , Kammer, J. A. , Steffl, A. J. , Gladstone, G. R. , Summers, M. E. , Strobel, D. F. , Hinson, D. P. , Stern, S. A. , Weaver, H. A. , Olkin, C. B. , Ennico, K. , McComas, D. J. , Cheng, A. F. , Gao, P. , Lavvas, P. , Linscott, I. R. , Wong, M. L. , Yung, Y. L. , Cunningham, N. , Davis, M. , Parker, J. W. , Schindhelm, E. , Siegmund, O , Stone, J. , Retherford, K. , & Versteeg, M. (2018). Structure and composition of Pluto's atmosphere from the New Horizons solar ultraviolet occultation. Icarus, 300, 174–199. 10.1016/j.icarus.2017.09.006 [DOI] [Google Scholar]
  38. Zirnstein, E. J. , McComas, D. J. , Elliott, H. A. , Weidner, S. , Valek, P. W. , Bagenal, F. , Stern, S. A. , Ennico, K. , Olkin, C. B. , Weaver, H. A. , & Young, L. A. (2016). Interplanetary magnetic field sector from Solar Wind around Pluto (SWAP) measurements of heavy ion pickup near Pluto. The Astrophysical Journal Letters, 823, L30. 10.3847/2041-8205/823/2/L30 [DOI] [Google Scholar]
  39. Zong, Q. , Wang, Y. , Yang, B. , Fu, S. , Pu, Z. , Xie, L. , & Fritz, T. A. (2008). Recent progress on ULF wave and its interactions with energetic particles in the inner magnetosphere. Science in China Series E: Technological Sciences, 51(10), 1620–1625. 10.1007/s11431-008-0253-z [DOI] [Google Scholar]

Articles from Journal of Geophysical Research. Space Physics are provided here courtesy of Wiley

RESOURCES