Dependency of R₂ and R₂* relaxation on Gd‐DTPA concentration in arterial blood: Influence of hematocrit and magnetic field strength

Abstract

Dynamic susceptibility contrast (DSC) MRI is clinically used to measure brain perfusion by monitoring the dynamic passage of a bolus of contrast agent through the brain. For quantitative analysis of the DSC images, the arterial input function is required. It is known that the original assumption of a linear relation between the R₂ ^(*) relaxation and the arterial contrast agent concentration is invalid, although the exact relation is as of yet unknown. Studying this relation in vitro is time‐consuming, because of the widespread variations in field strengths, MRI sequences, contrast agents, and physiological conditions. This study aims to simulate the R₂ ^(*) versus contrast concentration relation under varying physiological and technical conditions using an adapted version of an open‐source simulation tool. The approach was validated with previously acquired data in human whole blood at 1.5 T by means of a gradient‐echo sequence (proof‐of‐concept). Subsequently, the impact of hematocrit, field strength, and oxygen saturation on this relation was studied for both gradient‐echo and spin‐echo sequences. The results show that for both gradient‐echo and spin‐echo sequences, the relaxivity increases with hematocrit and field strength, while the hematocrit dependency was nonlinear for both types of MRI sequences. By contrast, oxygen saturation has only a minor effect. In conclusion, the simulation setup has proven to be an efficient method to rapidly calibrate and estimate the relation between R₂ ^(*) and gadolinium concentration in whole blood. This knowledge will be useful in future clinical work to more accurately retrieve quantitative information on brain perfusion.

Abbreviations used

AIF

arterial input function

CA

contrast agent

CBF

cerebral blood flow

CBV

cerebral blood volume

DCE

dynamic contrast‐enhanced

DSC

dynamic susceptibility contrast

FOV

field of view

MTT

mean transit time

RBC

red blood cell

SD

standard deviation

SO₂

oxygen saturation

1. INTRODUCTION

Dynamic susceptibility contrast (DSC) MRI is a clinically commonly used method to measure cerebral perfusion by monitoring the dynamic passage of a bolus of contrast agent through the brain. To obtain quantitative information, determination of the arterial input function (AIF) is required, which represents the input of the contrast agent from a supplying artery into the tissue of interest. The AIF is used for calculating the residue function via deconvolution of the concentration‐time profile in the tissue. ¹ From the residue function and the concentration‐time profile, important features such as the cerebral blood volume (CBV), cerebral blood flow (CBF), and the mean transit time (MTT) can be estimated.

The AIF concentration‐time profile is generally calculated from the R₂ ^(*) relaxation time curve obtained in a large feeding artery, where in common practice a linear relationship is assumed. ² However, the relation between R₂ ^(*) and Gd concentration ([Gd]) in whole blood is different from the relation in brain tissue. ³ Most literature focusing on susceptibility‐induced R₂ ^(*) changes has focused on the relation in brain tissue either by means of simulations or by analytical models. These studies are therefore focusing on magnetic susceptibility changes in the microvasculature, which are also governing the MRI‐signal changes of the BOLD effect. ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ A strong correlation between hematocrit and R₂* has been shown for in vitro studies ⁹ and a linear correlation has been verified in animal models. ¹⁰ A study conducted by Blockley et al. ¹¹ showed the dependency of the R₁ and R₂* relaxivities of ProHance, Vasovist, and deoxyhemoglobin on field strength, where the measurements were performed in whole blood. Previous in vitro experiments showed the existence of a quadratic relation between R₂* and [Gd] in human whole blood for a gradient‐echo sequence and it was shown that this relation was strongly dependent on the hematocrit value. ² , ¹² On the other hand, for spin‐echo sequences, the relation is more variable over a range of vessel sizes due to its microvascular sensitivity. ¹³ However, the relationship in whole blood, and for much larger susceptibilities than those induced by deoxyhemoglobin, are less well studied. Recently, a bilinear model was proposed to explain the relation between hematocrit, oxygen extraction fraction, and R₂. ⁴ Even more recently, a paper by Li and van Zijl ¹⁴ proposed a model that incorporates both the effects of exchange between compartments as well as the effects of diffusion through the local magnetic field gradients, where the influence of the hematocrit and oxygen saturation was studied. Wilson et al. ¹⁵ also included the transmembrane water exchange in their model to investigate the transverse relaxation in oxygenated human whole blood. In addition, Thulborn et al. ¹⁶ experimentally validated the hematocrit dependence for oxygen saturation‐dependent changes in R₂ in whole blood. However, the influence of the hematocrit value on the spin‐echo signal is currently unknown for susceptibility changes beyond those induced by de‐oxygenated blood. ¹⁷ Finally, for the previous simulation studies, the codes are not available to other researchers to apply these for their experimental conditions.

Typical DSC‐MRI sequences have a single echo time that is optimized for monitoring the passage of contrast agent through the tissue. However, this echo time is too long to reliably measure the contrast agent concentration inside an artery due to saturation effects. ¹⁸ , ¹⁹ , ²⁰ Hence, the current approach is to measure the AIF outside the artery, although this only allows measurements of the shape and not the amplitude of the AIF. The use of multiple echo sequences and combined gradient‐ and spin‐echo sequences for DSC‐MRI makes it more feasible to measure the AIF within an artery. ¹ , ²¹ , ²² , ²³ For measurement of the AIF inside an artery it is important to consider the relation between R₂ ^(*) and Gd concentration in arterial blood, as opposed to previous studies, which focused on the microvascular level or on measurements outside the artery. ¹⁸

Clinically, DSC‐MRI is often performed at different field strengths, along with different contrast agents and MRI sequences, and under varying physiological conditions, such as hematocrit and oxygen saturation. Therefore, in vitro assessment of the relationship between R₂ ^(*) and [Gd] under all these conditions is very time‐consuming and impractical, especially because such measurements need to be performed in flowing, human whole blood at body temperature, requiring about 1–2 L of blood per condition. As a solution, when sufficiently validated, simulations could provide information about this relation in a time‐efficient manner. Therefore, the aims of this study were twofold:

(1) To develop and validate an adapted open‐source simulation setup for the blood signal in a DSC acquisition and to compare the simulations with the previously measured quadratic relation between the R₂* relaxation and [Gd] in whole blood for gradient‐echo sequences (proof‐of‐concept). In this part of the study, the influence of the shape of red blood cells (RBCs) and their orientation with respect to the modeled plane was also estimated.

(2) To estimate the influence on this relation of the static magnetic field strength (1.5, 3, and 7 T), the sequence type (gradient‐echo vs. spin‐echo), and the physiological condition (hematocrit and oxygen saturation [SO₂] values).

2. METHODS

DSC‐MRI dynamically follows the passage of contrast agent, which is usually injected intravenously. The contrast agent causes an increase in field inhomogeneities due to susceptibility differences between the intravascular and extravascular compartments in tissue, as well as between plasma and RBCs in whole blood, which can be visualized as a drop in the MRI signal magnitude on T₂‐weighted images. The signal time curves are converted to ΔR₂ ^(*) relaxation curves, which are subsequently used for the calculation of concentration time curves. The relation between ΔR₂ ^(*) and contrast concentration in tissue has been studied in previous research for both gradient‐echo and spin‐echo sequences by means of Monte Carlo simulations ¹³ as well as analytical models. ³ , ⁴ , ⁶ In this study we will make use of the same physics principles and MRI contrast agent properties to study the relaxivity in human whole blood.

2.1. Implementation

The processes that need to be considered for studying the relation between ΔR₂ ^(*) and [Gd] in whole blood are the susceptibility‐induced field changes, which depend on the main magnetic field strength, the diffusion of water within these field changes, the MRI sequence parameters, but also the hematocrit and shape of the RBCs. These processes are taken into account in the open‐source dynamic contrast‐enhanced (DCE) simulation tool of Pannetier et al., ⁵ which we therefore have taken as a starting point for our simulation setup. To allow simulating whole blood, the geometry of the simulation tool was adjusted as illustrated in Figure 1A,B. In the original tool, a two‐dimensional (2D) geometry was used, which included by default five vessels with a certain permeability, and that allowed leakage of contrast agent into the surrounding extracellular extravascular space (Figure 1A). In our model, the “vessels” represent RBCs and the number can be adjusted to simulate different hematocrit values, while the “extracellular extravascular space” corresponds to blood plasma (Figure 1B). The RBCs are modeled to have an impermeable wall for the contrast agent to only allow contrast agent in the blood plasma. The water molecules can diffuse freely throughout the 2D lattice. The water diffusion is incorporated by convolving the magnetization distribution with a diffusion kernel. Next to the change of geometry, the simulation tool was adapted for DSC simulations by adjusting the input parameters accordingly (Table 1).

FIGURE 1.

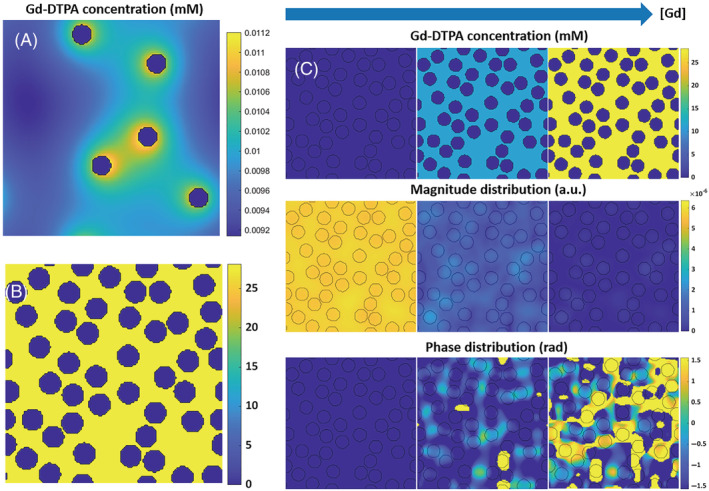
Adaptations to the dynamic contrast‐enhanced (DCE) simulation tool: (A) whereas in the original tool five vessels are simulated with a certain permeability and contrast agent (CA) is leaking into the surrounding extracellular extravascular space, in our model (B) the “vessels” represent the red blood cells with zero permeability, while the extracellular extravascular space corresponds to the blood plasma. (C) Linearly increasing [CA], resulting in phase and magnitude changes and dephasing, which were finally summed over the simulated space, thereby inducing more dephasing for gradient‐echo sequences

TABLE 1.

Overview of simulation parameters

Type	Parameter	Value
Lattice	Dimension	256 x 256 pixels
	Size	70 x 70 μm2
RBCs	Radius	3.5 μm (circular RBCs) 24
	Minimum interspace	0.55 μma
	Number	Varying with hematocrit (46 RBCs for hematocrit of 36%)
	Magnetic susceptibility	−0.736*10−6 ppm cgs (assuming Y = 100%) 17
	T 1	1 sb
	T 2	Varying with field strength (200/117/50*10−3 s for B0 of 1.5/3/7 T) 14
	Proton concentration	0.7
Blood plasma	Magnetic susceptibility	−0.722*10−6 ppm cgs 17
	T 1	1 sb
	T 2	Varying with field strength (1,194/500/304*10−3 s for B0 of 1.5/3/7 T) 14
	Proton concentration	0.95
Contrast agent	r 1 (T 1 relaxivity)	0 mM−1 s‐1b
	r 2 (T 2 relaxivity)	Varying with field strength (4.6/5.2/4.8 mM−1 s−1 for B0 of 1.5/3/7 T) 25 , 26
	Diffusivity	48.5*10−11 m2 s−1 (default Dfree) 5
	Permeability	0 s‐1
	Magnetic susceptibility	4π*2.55*10−8 mM−1 2
MRI	TE	20*10−3/40*10−3 s (gradient‐echo/spin‐echo)
	TR	1 s
	Excitation time	0 s
	FA	90°/90°–180° (gradient‐echo/spin‐echo)
	Phase angle	0°
	Static magnetic field	Varying (1.5/3/7 T)
Other	Water diffusivity	760*10−12 m2 s−1 (default Dfree) 5

^a to prevent overlap of red blood cells (RBCs).

^b to minimize T1 effects to reflect complete refreshment of flowing blood.

Because we are using the vessels of the DCE simulation tool to represent RBCs, the blood volume fraction corresponds to the hematocrit value, although the water fractions in the blood plasma and RBCs have to be accounted for due to the difference in protein content. Previous literature reported water fractions of 0.95 and 0.7 for blood plasma and RBCs, respectively. ²⁷ In the original setup, the field of view (FOV) depended on the defined blood volume fraction, the number of vessels and their radius. However, we assumed a fixed FOV in our simulation model to allow studying the influence of the hematocrit value. The ΔR₂ ^(*) relaxation is calculated from the MRI signal magnitude using the following equation:

$$∆{\mathrm{R}}_2^{*}\left(\mathrm{t}\right)=-\frac{1}{\mathrm{TE}}*\ln \left(\left|\frac{\mathrm{S}\left(\mathrm{t}\right)}{{\mathrm{S}}_{\text{base}}}\right|\right),$$ (1)

where S_base is the mean baseline signal magnitude after reaching the steady state. For the contrast agent concentration, a linear increase is simulated, as illustrated in Figure 1C. Because the rise in contrast concentration is relatively slow (a total increase of 18 mM in 30 s) compared with the T₁ relaxation time (1 s), such a quasi‐static approximation is valid. The increasing contrast agent concentration induces susceptibility‐induced field changes. Diffusion through the magnetic field inhomogeneities results in dephasing and thus causes a drop in the MRI signal magnitude, as shown in Figure 1C. Summation over the complete simulation area will finally induce additional signal decrease due to dephasing. Because we are focusing on a large artery, where a high blood flow can be presumed and thus a complete refreshment of flowing blood, spin history effects will be minimal. Therefore, we assumed that T₁ effects of the contrast agent can be neglected, which was performed by using a zero T₁ relaxivity (r₁) of the contrast agent and T₁ relaxation times of 1 s for blood plasma as well as RBCs. Note that the specified relaxation time of 1 s only scales the final magnetization, which will cancel out when calculating ΔR₂ ^(*).

2.2. Validation

To validate the simulation model, we compared the output of our simulations with a previously measured ΔR₂* versus [Gd‐DTPA] relation acquired in vitro at 1.5 T using flowing human whole blood with a hematocrit value of 36%. ² The in vitro data were previously used for determination of the accuracy of a partial volume correction method for measurement of the AIF. It was shown that using the in vitro‐determined relation between ΔR₂* and [Gd‐DTPA] improved the in vivo reproducibility of the AIF measurements. ² The measured in vitro relation between the relaxation and contrast concentration appeared to follow a quadratic dependency according to the equation:

$$∆{\mathrm{R}}_2^{*}=\mathrm{a}*{\left[\mathrm{Gd}\right]}^2+\mathrm{b}*\left[\mathrm{Gd}\right],$$ (2)

where the in vitro measurements ² provided for the two parameters: a = 574*10⁻⁶ (ms*mM^{2 )−1} and b = 7.6*10⁻³ (ms*mM)⁻¹.

To allow validation with the in vitro data (proof‐of‐concept), the simulation parameters were set similar to those of the in vitro experiment. Table 1 summarizes these simulation parameters. The simulation was performed five times with a nonfixed seed for RBC positioning to obtain the mean and standard deviation (SD) and thereby also a reflection on how dependent the simulations are on the exact location of the RBCs.

RBCs are known to be “disc‐shaped” and, to deepen our understanding of the model, the simulation setup was tested with three types of RBCs to validate the influence of their shape and the orientation with respect to the modeled plane (Figure 2):

1. Circular RBCs with a radius of 3.5 μm (Figure 2A). ²⁴

2. Ellipsoidal RBCs with radii of 4.5 and 2.72 μm, which keeps the surface area of the ellipses and thus also the number of RBCs within the simulation volume equal to that of the first settings. The RBCs are aligned in two different directions, as shown in Figure 2B,C. For both orientations, and in fact all our simulations, all cells are pointing in the same direction, because in a large artery the RBCs are aligned with the blood flow in the direction of least resistance. ²⁸

3. Ellipsoidal RBCs with radii of 3.5 and 1.25 μm in, respectively, the x ‐and y‐direction (Figure 2D). ²⁴ This better represents the in vivo conditions, but implies a smaller surface area, and thus more RBCs are needed to achieve a similar hematocrit value.

FIGURE 2.

Different red blood cell (RBC) configurations used for simulations shown in Figure 4. (A) Circular RBCs (step 1), (B) Ellipsoidal RBCs aligned in the horizontal direction (step 2), (C) Ellipsoidal RBCs aligned in the vertical direction (step 2), and (D) Ellipsoidal RBCs with a smaller surface area (step 3)

The magnetic field distortions induced by susceptibility changes were calculated using a Fourier‐based approach ²⁹ , ³⁰ adapted in 2D, where these distortions were averaged over three orthogonal orientations of the modeled plane with respect to the main magnetic field to approach a three‐dimensional (3D) situation. ⁵

2.3. Application of the simulation model: influence of sequence type, hematocrit, B₀, and SO₂

The simulation model was subsequently employed to study four important questions that are relevant to interpretation of DSC‐MRI data: (1) What is the influence of the MRI sequence (gradient‐echo vs. spin‐echo) on the ΔR₂ ^(*) relation in general? (2) What is the influence of the hematocrit value? (3) What is the influence of the magnetic field strength? (4) What is the influence of blood oxygen saturation?

By default, a gradient‐echo sequence is incorporated in the DCE simulation tool of Pannetier et al. In the current study, an additional ideal spin‐echo sequence was created by inserting a 180° refocusing pulse at TE/2 into the sequence. The simulation was performed with hematocrit values of 10%, 20%, 30%, 40%, and 45% to investigate the R₂ ^(*) dependency for both gradient‐echo and spin‐echo sequences. Subsequently, the curves were fitted to a second‐order polynomial defined as ΔR₂ ^(*) = a*[Gd]² + b*[Gd] to study the dependency on hematocrit value in more detail. In addition, field strengths of 1.5, 3, and 7 T were used with the corresponding literature values for the T₂ relaxivity (r₂) of the contrast agent and the calculated values for the field strength‐dependent T₂ relaxation times of blood plasma and RBCs, using the analytical equations from Li and van Zijl. ¹⁴ (Table 1). Finally, the simulation was performed for the extreme SO₂ value of 0% and values within the physiological range of 60%, 80%, 90%, 95%, and 100%. The SO₂ was indirectly defined by the RBC susceptibility using the following relation ¹⁷ :

$${\mathrm{\chi }}_{\mathrm{RBC}}=-0.736*{10}^{-6}+\left(1-\mathrm{Y}\right)*0.264*{10}^{-6},$$ (3)

where Y is the oxygen saturation.

3. RESULTS

3.1. Validation

Figure 3A shows both the previously observed ΔR₂* versus [Gd] relation in vitro, ² as well as the resulting relation from the simulations. For most concentrations the simulation data overlapped with the in vitro data, with the in vitro data positioned around the minimum of the simulation range. The results also showed an increasing SD with increasing [Gd], which might suggest that the dephasing effect due to magnetic field inhomogeneities became more dependent on the exact configuration of the RBCs. In addition, the orientation of the RBCs with respect to the modeled plane was studied for both gradient‐echo and spin‐echo sequences by varying the shape and surface area of the RBCs (Figure 3B,C).

FIGURE 3.

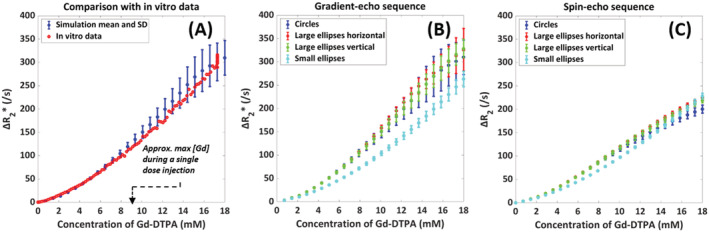
Simulation data (blue) for arterial blood with a hematocrit value of 36% and field strength of 1.5 T for a gradient‐echo sequence with TE = 20 ms, TR = 1 s, and FA = 90° in comparison with in vitro data (red), including the mean and SD over the different red blood cell (RBC) configurations (A). The in vitro data are from van Osch et al. ² The dashed arrow indicates the approximate maximum contrast concentration during a single dose injection. (B) and (C) show the influence of magnetic field direction on the relation between [Gd‐DTPA] and ΔR₂ ^(*) in arterial blood by simulating different shape and surface areas of the RBCs, including the mean and SD over the different RBC configurations. The large ellipses and circles are equal in surface area and are different from the small ellipses. The number of small ellipses was higher to achieve the same hematocrit value for all different RBC types. The results are shown for both gradient‐echo (B) and spin‐echo (C) sequences. The blue curve for the circles in (B) is equal to the results in (A)

The shape and orientation of the RBCs seemed to have limited influence on the results, except for small deviations at higher [Gd], while changing the surface area of the RBCs had a larger effect, as shown in Figure 3B,C. Moreover, these effects seemed more pronounced for gradient‐echo than for spin‐echo sequences (Figure 3B,C).

3.2. Application of the simulation model

In general, higher relaxation rates were observed for the gradient‐echo sequence, as expected, because spin‐echo refocuses the phase accrual for static spins as well as the mean phase accrual for diffusing spins. This can be seen in the following sections, which illustrate the influence of the hematocrit, field strength, and oxygen saturation. A more detailed discussion on the influence of the sequence type is provided in Figure S1.

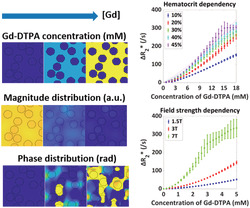
3.2.1. Influence of hematocrit

The dependency on the hematocrit at 1.5 T is depicted in Figure 4, from which it can be seen that the relaxivity increased with hematocrit for both the gradient‐echo and spin‐echo sequences. For the gradient‐echo sequence, the 30%, 40%, and 45% hematocrit curves were overlapping, especially at higher concentrations, while for the spin‐echo sequence, all the curves were leveling off at higher concentrations and the standard deviations were significantly smaller. To study the hematocrit dependency in more detail, the curves were fitted to a second‐order polynomial, and the numerical fit results are provided in Table 2. The increasing value of a indicates an increasing amount of quadraticity for the gradient‐echo sequence from a hematocrit value of 10% to 20%, while the a values for higher hematocrit were lower. For the spin‐echo sequence, the a values were more variable and there was no clear increase in the amount of quadraticity.

FIGURE 4.

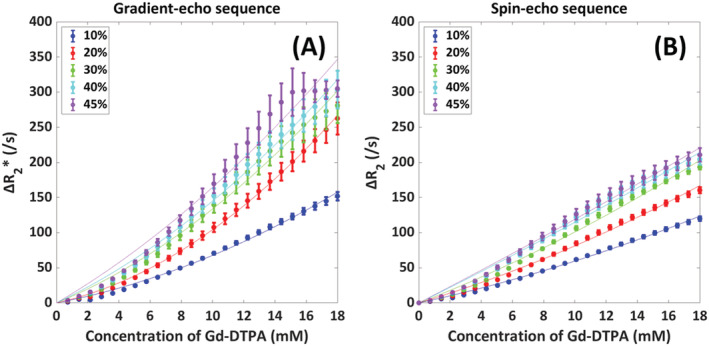
Influence of hematocrit value (10%, 20%, 30%, 40%, 45%) on the relation between [Gd‐DTPA] and ΔR₂ ^(*) in arterial blood with the mean and SD as calculated over five different red blood cell configurations. The resulting fits to a second‐order polynomial, defined as ΔR₂ ^(*) = a*[Gd]² + b*[Gd], are depicted by the thin solid lines. The results are shown for both gradient‐echo (A) and spin‐echo (B) sequences

TABLE 2.

Numerical fit results for the dependency of ΔR₂ ^(*) versus [Gd] on hematocrit value. The curves were fitted to a second‐order polynomial defined as ΔR₂ ^(*) = a*[Gd]²  + b*[Gd]

Sequence type	Hematocrit	a	b	Adjusted R2
Gradient‐echo sequence	10%	0.249	4.28	0.996
	20%	0.548	4.95	0.999
	30%	0.424	9.14	0.991
	40%	0.394	10.6	0.994
	45%	0.350	13.0	0.975
Spin‐echo sequence	10%	0.113	4.83	0.997
	20%	0.144	6.69	0.995
	30%	0.148	8.62	0.993
	40%	0.0524	11.0	0.990
	45%	0.0439	11.5	0.991

3.2.2. Influence of magnetic field strength

The field strength dependency for a hematocrit value of 36% is illustrated in Figure 5, which shows an increasing relaxivity with field strength. This is in agreement with previous literature. ¹² The shape of both the 1.5 and 3 T was quadratic, in contrast to the shape of the 7 T curve. In addition, the SD for the gradient‐echo 7 T curve was highly fluctuating for concentrations above 3 mM. The observed signal for the separate runs at 7 T was close to zero, which explains those fluctuations. It is commonly assumed that the effect of the contrast agent scales is approximately linearly with the field strength. Therefore, we scaled the concentration according to the field strength, as illustrated in Figure 5C,D. The results show that the simulations closely approximated this expectation, but we see some small deviations, which are especially visible for the spin‐echo sequence. These deviations point to a slightly sublinear relation between the effective relaxivity and magnetic field strength.

FIGURE 5.

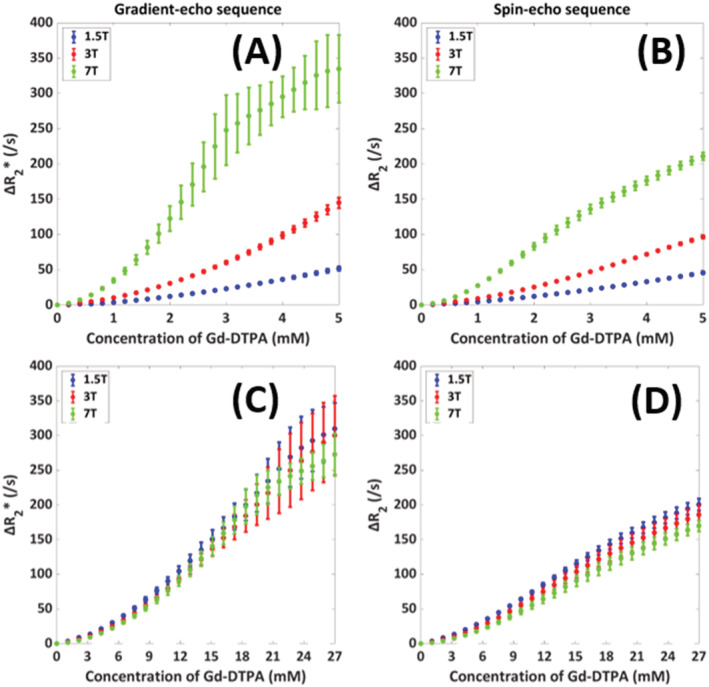
Influence of field strength (1.5, 3, and 7 T) on the relation between [Gd‐DTPA] and ΔR₂ ^(*) in arterial blood with the mean and SD as calculated over five different RBC configurations. In (A) and (B), the x‐axis shows the concentration of Gd‐DTPA, while in (C) and (D) the concentration was scaled by the field strength to allow for a better comparison of the shape of the relation. The results are shown for both gradient‐echo (A and C) and spin‐echo (B and D) sequences

3.2.3. Influence of blood oxygen saturation

Finally, Figure 6 shows the dependency on the SO₂ of the RBCs at 1.5 T. The SO₂ appears to have only a minor effect on the relation, that is, the effect of SO₂ was overwhelmed by the higher magnetic susceptibility of the contrast agent.

FIGURE 6.

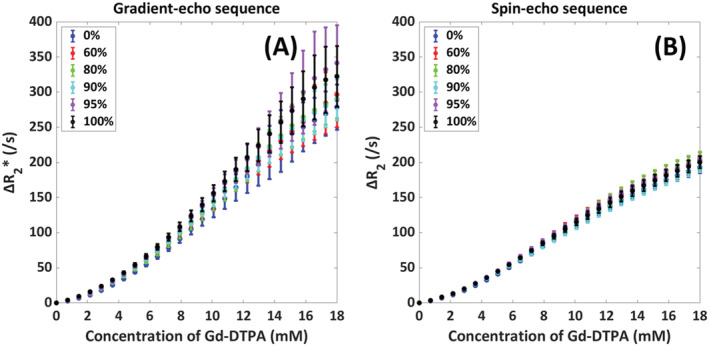
Influence of SO₂ value (0%, 60%, 80%, 90%, 95%, 100%) on the relation between [Gd‐DTPA] and ΔR₂ ^(*) in arterial blood with the mean and SD as calculated over five different red blood cell configurations. The results are shown for both gradient‐echo (A) and spin‐echo (B) sequences

4. DISCUSSION

For quantitative analysis of DSC‐MRI data, measurement of the AIF is required. The common practice of assuming a linear relation between ΔR₂ ^(*) and contrast agent concentration has previously been shown to be invalid. Most literature has focused on the relation between ΔR₂ ^(*) and the concentration of contrast agent in brain tissue, more specifically on magnetic susceptibility changes in microvasculature, because those are also governing the BOLD effect. ⁴ , ¹³ , ³¹ Moreover, most of the in vitro measurements in whole blood were focused on gradient‐echo sequences. Also, for the previous studies the code was not made public, making it more difficult to use it for other conditions in future simulation studies. By adapting the DCE simulation tool of Pannetier et al., we provide a simple simulation setup to estimate the relation between ΔR₂ ^(*) and contrast agent concentration in whole blood for different MRI sequences, field strengths, and physiological conditions such as hematocrit and oxygen saturation. Within the simulation tool we varied the distribution of RBCs to provide an estimate of the main measurement error of the simulation setup. To support our idea of performing open‐source science, the adapted simulation code will be made publicly available on GitHub.

The aim of this study consisted of two parts, namely: (1) the development and validation, and (2) the application of the simulation tool. First, the DCE simulation tool was adapted for intra‐arterial DSC‐MRI measurements. Because we are focusing on the AIF in a large artery, where fresh inflow can be assumed, spin history effects are minimal and therefore T₁ effects of the contrast agent were neglected in the simulations. The validity of the simulations was tested by comparison of the results with previously acquired in vitro data in human whole blood. The results from the validation part show a close agreement of the simulations and in vitro data. This shows the applicability of our adapted simulations for investigating the relation between ΔR₂ ^(*) and contrast agent concentration. In the next step, the dependency on orientation was investigated by varying the shape and surface area of the RBCs (large‐scale orientation of the vessel with respect to the main magnetic field and modeled plane), as well as the orientation of the RBCs (small‐scale orientation). The shape dependency of susceptibility differences upon R₂ has been studied by Kiselev and Novikov ³² for spheres and disks with a varying height‐to‐radius ratio. In our case the height‐to‐radius ratio (although in 2D) for the ellipses was 1.65 and we compared these results with circles with an equal surface area. In line with Kiselev and Novikov, ³² we observed that the relaxivity for these spheres and ellipses was quite similar. When changing the surface area, while keeping the hematocrit equal, we observed more profound changes in relaxivity. The resulting dependency on RBC shape and surface area suggests that the vessel orientation with respect to the main magnetic field (large‐scale orientation) might matter, because the disc‐shaped RBCs are known to orientate in a similar fashion in flowing blood. It should be kept in mind that the orientation of the vessel will also have a macroscopic effect on the magnetic field within the artery, which is the cause of the orientation dependency of phase‐based AIF measurement. This is, however, a global change in magnetic field, and it will not affect the magnitude of the signal.

Subsequently, the simulation tool was applied to study the dependencies of ΔR₂ ^(*) on hematocrit value, field strength, and oxygen saturation value. The main new observations of our study are threefold: (1) not only gradient‐echo (ΔR₂*) relaxivity, but also spin‐echo (ΔR₂) relaxivity in fully oxygenated whole blood is nonlinearly dependent on the hematocrit; (2) the shape of the ΔR₂ ^(*) is dependent on the magnetic field strength; and (3) the influence of the SO₂ on the relation between ΔR₂ ^(*) and [Gd] in fully oxygenated blood is only minor.

Nonlinear dependency on hematocrit for the spin‐echo sequence can be partly explained by nonrefocused phase accumulation due to water diffusion effects through the RBC‐induced magnetic field inhomogeneities. In addition, the fraction of RBCs plays a role; more RBCs result in larger consecutive areas where no contrast is present and thus less signal loss occurs in those areas. Boxerman et al. ¹³ studied the relation for a spin‐echo sequence in rat tissue, and their results also showed a diverse nonlinear profile. Our simulations were only compared with gradient‐echo and not with spin‐echo measurements, which should be considered a limitation of our study, especially because it is more challenging to perform simulations for spin‐echo sequences. For the gradient‐echo sequence, the dependency on hematocrit value has been observed in previous studies. Akbudak et al. ¹² used a blood phantom system to study hematocrit values of 0%, 30%, and 40%. The linear behavior of the ΔR₂* versus [Gd] curve at low hematocrit is in line with this previous study and confirms the expectation that the relation is mainly influenced by the linearly increasing contrast agent concentration. For the higher hematocrit values, their results showed a quadratic dependency on hematocrit and, in contrast to our results, there was a clear distinction between the results for hematocrit values of 30% and 40%. The difference with this study is that our simulations extended until 18 mM, whereas Akbudak et al.’s maximum concentration was 10 mM. Previous literature on DSC‐MRI AIF measurements report a blood concentration of 18 mM for a double dose of Gd‐based contrast. ³ , ³³ Clinically, frequently a single dose is used for gradient‐echo sequences, while for spin‐echo sequences a double dose is injected. ³⁴ When looking at a concentration of 10 mM in our results, the 40% curve is close to what Akbudak et al. observed, whereas our simulations for 30% hematocrit show significantly higher ΔR₂*. An explanation for these differences with the in vitro observation could be found in the positioning of the RBCs; in the blood phantom study a blood pump was used to pump the blood around, to resemble as closely as possible the conditions in a large artery. Real flow of RBCs will result in more random positioning and orientation, as well as potential shape changes of RBCs, compared with the simulation conditions in which static RBC arrangements were assumed, which is a less realistic scenario. ²⁸ Additionally, the number of RBCs simulated is much lower than in an actual large artery, which is expected to affect the variability, albeit not the mean of simulations. To overcome this limitation, we repeated the simulations with different distributions of RBCs to determine the sensitivity to this distribution. Nevertheless, dynamical changes of the RBC distribution within the echo time are not incorporated.

The second main finding concerns the field strength dependency of the shape of the ΔR₂ ^(*) curves. The relaxivity increases with field strength, which is in accordance with general expectations and previous literature. ³ , ¹¹ , ¹² Comparison with Blockley et al. ¹¹ shows slightly lower values for the relaxivity, especially for a field strength of 3 T. A clear difference with Blockley et al. is that the experimental data used to validate our simulations were only acquired at 1.5 T, whereas the experiments in Blockley et al. were performed at 1.5, 3, and 7 T. A possible explanation for the different values is the contrast agent that is used in both studies, which each have a slightly different transverse relaxivity. The most obvious difference is the equalization point of the plasma and RBC susceptibilities, which is not visible in our results. The reason for this is that most of our simulations were performed for an SO₂ of 100%, whereas this effect will only be visible at lower oxygen saturation values (Figure S2). In addition, we obtained a larger separation between the curves of 1.5 and 3 T compared with the previously obtained results of Akbudak et al. ¹² Because those results are for hematocrit values of 30% and 40%, our results with a hematocrit of 36% over all field strengths were expected to fall in between those two curves. However, the simulation curve for a field strength of 3 T lies significantly above both curves obtained in vitro. To enhance the visibility of differences in the shape of the relation, we scaled the concentration according to the field strength to correct for an expected linear relation. The results show a small additional effect, which indicates a slightly sublinear dependency. The shape of the 7 T appears sigmoidal opposed to the quadratic shape at 1.5 and 3 T. This is in contrast to the expected exponential behavior from the previous study conducted by Blockley et al. ¹¹ The cause of this nonexponential behavior is probably digitization noise of the simulations, where we are running into limits of the precision of the simulations when approaching the zero signal level. From our results we could observe a quite significantly increased SD for higher concentrations of contrast agent, as calculated over different RBC configurations, especially for gradient‐echo. This finding was further evaluated and the results are provided in Figure S1.

The final main observation is related to the influence of the SO₂ of the blood, which appeared to have almost no influence on the relation between ΔR₂ ^(*) and [Gd]. A likely reason for this is that the contrast agent‐induced susceptibility changes of the blood plasma are much larger than the de‐oxygenated hemoglobin‐induced changes. Therefore, a change in the RBC oxygen saturation is hardly visible in the resulting relation. For an SO₂ of 95%, the susceptibility of the RBCs and the plasma is equal. When the SO₂ drops below 95%, the susceptibilities of the RBCs and plasma will equalize at a specific concentration of Gd, while above this value they will only diverge. For the extreme case of 0% SO₂, the equalization point is around 0.8 mM [Gd], which would only lead to a small offset of the curve. Blockley et al. ¹¹ have demonstrated this equalization point, which corresponded to a minimum in the parabolic dependency of R₂* versus contrast concentration. The most important difference between this previous paper in comparison with our study is the low maximum concentration of the contrast agent that was used in their study. To compare our simulations with their results, we performed an additional simulation for an SO₂ of 0% and a high field strength of 7 T, where we used a maximum contrast concentration of 3 mM (Figure S2). From our results we could see a similar effect, where a minimum was visible for the dependency of ΔR₂ ^(*) versus contrast concentration, corresponding to the expected equalization point of the blood plasma and RBC susceptibilities. Differences in the obtained values are hypothesized to originate from the difference in contrast agent that was used, our simulations compared with in vitro data in Blockley et al., and in our case ΔR₂ ^(*) was displayed on the y‐axis instead of R₂* in Blockley et al. The dependency of the relation on TE was also simulated, see supplemental information (Figure S3).

In general, our results confirm that the intravascular R₂* is determined predominantly by R₂ at low field (1.5 T), which is in agreement with previous literature. ⁷ , ⁸

The main limitation of this study is that we used a 2D simulation space, for which the shape and size of the RBCs is determined by the orientation of the vessel with respect to the main magnetic field. In a large artery the RBCs are aligned with the blood flow in the direction of the least resistance. ²⁸ For this reason, all cells were simulated in the same direction, where the two most extreme directions were chosen to study the influence of the RBC orientation with respect to the main magnetic field. Furthermore, when taking a cross‐sectional view, the RBCs appear as biconcave disks, but when looking at the top of the vessel, the RBCs appear to be circular shaped. However, repeating the simulations with different shapes showed some, albeit relatively minor, influences, while the relative size of the RBCs (with constant hematocrit) seems to be more important. Nevertheless, instead of biconcave disks we only considered ellipsoidal RBCs, which is a clear simplification and will have a different effect on the magnetic field gradients around the cells. In the current simulations the magnetic field perturbations are calculated as the average over three orthogonal directions, which might explain the limited influence of the RBC orientation. 3D simulations with biconcave RBCs are a possible extension of the simulation tool, although the total calculation time would severely limit its applicability, which was the reason to stay with 2D simulations. The fact that our 2D simulations yielded highly comparable results with the in vitro data shows that this approach was not too unrealistic.

The next limitation to consider is that we focused on a single intra‐arterial voxel without considering the surroundings of the vessel. Hereby, we focused on the local structure and did not take the macrostructure of the artery into account. Therefore, we also only report the influence on the magnitude of the MRI signal, because phase changes are governed by the macrostructure of the artery. This is an important limitation, because phase measurements of the AIF are potentially a better approach than amplitude‐based measurements. For example, it was shown by Akbudak et al. that phase‐based AIF measurements are unaffected (or at least less affected) by the hematocrit. ¹²

Another limitation of this study is the large and unphysiological range of hematocrit values that were simulated. We decided to broaden the range of hematocrit values compared with what is typically observed in vivo, which could provide us with more insight into the signal behavior. Also, the maximum achievable hematocrit value was 45% due to limitations in the RBC positioning in the current simulation setup (i.e. RBCs are put at random locations within the simulation grid one at a time, with a minimum interspace to prevent overlap between cells).

A further limitation is that at high concentrations and high field strength, deviations are observed, which most likely can be attributed to digitization noise. These data should be interpreted with care. Furthermore, the simulations of this study use a relatively small FOV. However, some additional simulations showed similar findings for a larger FOV of 210 μm² compared with our standard FOV of 70 μm² (data not shown). It should also be recognized that we calculated the mean and SD to obtain a measure of the simulation error by using only five different RBC configurations, whereas in vivo the distribution of RBCs will depend on the local flow conditions and would also be dynamically changing due to (pulsatile) blood flow. Other RBC distributions as well as dynamic changes of these could also be incorporated in the simulation tool; however, based upon the good correspondence with the in vitro data, we kept the positioning of RBCs similar in the simulation tool, as originally proposed for the vessel locations. The choice of Gd‐DTPA as the contrast agent was intended as a starting point for our study and, by doing so, our results could be validated against the previous research of van Osch et al.² It should be recognized that this contrast agent is not widely used anymore, although other gadolinium‐based contrast agents have fairly similar properties. Finally, restrictions on water exchange between RBCs and plasma are currently not incorporated in the simulation; the water is allowed to diffuse freely throughout the total 2D simulation space. Previous literature has already addressed the relatively long lifetime of water inside the RBC, which would affect the exchange contribution to the transverse relaxation. ¹⁴ , ³⁵ Ideally, the permeability of the RBC membranes should be considered. Pannetier et al. ⁵ already suggested to model the water diffusion in the same manner as the constrained diffusion of the contrast agent, but this would lead to a severe time penalty for performing the simulations. Despite those limitations, the adjusted 2D simulation setup has opened new possibilities in the development of a general model containing the influence of both the technical and physiological parameters on the relation between ΔR₂ ^(*) and [Gd]. This model could eventually be applied in vivo to allow for a determination of the AIF that is more specific for the patient and MRI characteristics, thereby improving the accuracy of the quantitative analysis of the DSC data.

5. CONCLUSIONS

We have shown the applicability of our adapted simulation setup for rapidly calibrating and estimating the relation between ΔR₂ ^(*) and [Gd]. The results from this study confirmed the nonlinear relationship between ΔR₂ ^(*) and [Gd] in human whole blood and showed its dependency on the hematocrit and field strength for both gradient‐echo and spin‐echo sequences. The dependency on the vessel orientation with respect to the main magnetic field suggests that future research on the conversion to 3D simulations could lead to a more realistic model. Also, the use of other vascular arrangements would be of interest for future studies to broaden our knowledge. In conclusion, this study provides useful insights leading towards more accurate AIF estimation, enabling improved quantitative information on brain perfusion.

Supporting information

Figure S1. Comparison of the relation between [Gd‐DTPA] and ΔR₂ ^(*) in arterial blood for gradient‐echo and spin‐echo sequences with a hematocrit value of 36% and field strength of 1.5 T (A) and the relative SD (SD divided by mean) as calculated for 15 different configurations of RBCs (B)

Figure S2. Simulation data for a hematocrit of 36% and a field strength of 7 T at low contrast concentrations, which illustrates the equalization point of plasma and RBC susceptibilities around 0.8mM. The results are shown for both gradient‐echo (A) and spin‐echo (B) sequences

Figure S3. Simulation data for a hematocrit of 36% and a field strength of 1.5 T illustrating the TE dependency for both gradient‐echo (A) and spin‐echo sequences (B) and the relative SD (SD divided by mean) as calculated for 5 different configurations of RBCs (C&D)

van Dorth D, Venugopal K, Poot DHJ, et al. Dependency of R₂ and R₂* relaxation on Gd‐DTPA concentration in arterial blood: Influence of hematocrit and magnetic field strength. NMR in Biomedicine. 2022;35(5):e4653. doi: 10.1002/nbm.4653