Abstract
The Gravity Recovery and Climate Experiment Follow‐On (GRACE‐FO), launched May 22, 2018 and collecting science data since June 2018, is extending the 15‐year data record of Earth mass change established by its predecessor GRACE mission (2002–2017). The GRACE‐FO satellites carry onboard a novel technology demonstration instrument for intersatellite ranging, the Laser Ranging Interferometer (LRI), in addition to the microwave interferometer (MWI) carried on GRACE. The LRI has out‐performed its in‐orbit performance requirements both in terms of accuracy as well as the duration of tracking. Here, we compare and validate LRI‐based gravity solutions for January 2019 to September 2020 against the MWI solutions. The comparison between the two sets of gravity solutions shows great similarities in general and nearly perfect consistency at a large hydrologic basin spatial scale (100,000 km2 and above), commonly viewed as the spatial resolution established by GRACE. The comparison in the spectral domain shows differences at the higher degrees of the spectrum, with lower error in the zonal and near zonal terms for the LRI solutions. We conclude that the LRI observations can be used to recover time‐varying gravity signals to at least the level of accuracy established by the MWI‐based solutions. This is a promising finding, especially when considering the benefits of using the LRI over the MWI, such as the great stability of the instrument and the low occurrence of instrument reboot events.
Keywords: GRACE‐FO, laser ranging interferometer, KBR, inter‐satellite ranging system, gravity recovery
Key Points
Gravity solutions are estimated from the laser ranging interferometer observations on board the Gravity Recovery and Climate Experiment Follow‐On satellites
Some modifications are needed when applying estimation procedures initially developed for the microwave interferometer to this new observation type
These new gravity solutions are comparable to the gravity solutions derived from the microwave interferometer observations at 270 km spatial scale
1. Introduction
The GRACE Follow‐On mission (GRACE‐FO), a US‐German collaboration between NASA and German Research Centre for Geosciences (GFZ), fulfills the need to extend the 15‐year mass change observation record of the NASA/DLR Gravity Recovery and Climate Experiment mission (GRACE). The twin GRACE‐FO satellites were launched on May 22, 2018 from Vandenberg Air Force Base, California, sharing a ride with five Iridium‐Next satellites aboard a Space‐X Falcon‐9 (Kornfeld et al., 2019). GRACE (Tapley, Bettadpur, et al., 2004), which was in operation between 2002 and 2017, provided invaluable observations of the variations of the Earth's gravity field and mass transport. GRACE has transformed the fields of geodesy and Earth sciences by providing measurements of gravity field variations at a spatial resolution never attained before on a global scale. The pair of GRACE satellites flew in tandem in a near‐polar orbit, roughly 200 km apart. They carried on‐board a K‐band microwave interferometer (MWI) ranging system which enables measurements of the variations in the intersatellite distance at a micrometer precision. When combined with GPS measurements, along with the non‐gravitational accelerations and rotations recorded by the onboard accelerometers and star cameras, the K/Ka‐band ranging (KBR) system observes the variations in the gravitational force experienced by the satellites by measuring the effects of the gravity on the relative inter‐satellite range. During its 15‐year lifetime (2002–2017), the global scientific community has come to rely on GRACE observations for monitoring the effects of climate change (Tapley et al., 2019), the evolution of the cryosphere (Gunter et al., 2010), oceans (Bonin & Save, 2020; Chen et al., 2019; Landerer et al., 2015), hydrology cycles, including flood and drought (Girotto & Rodell., 2019; Scanlon et al., 2016), and tectonic events (Ghobadi‐Far, Han, Allgeyer et al., 2020) among others. Though the GRACE‐FO mission was designed to be a continuation of GRACE, many of the onboard instruments and sensors have been upgraded based on the knowledge acquired during the GRACE mission (Landerer, Flechtner, Save et al., 2020). While the main satellite‐to‐satellite (SST) tracking instrument on board GRACE‐FO is still the K/Ka‐band MWI, the twin satellites also carry on‐board a secondary ranging system intended as a technology demonstration for future missions. The Laser Ranging Interferometer (LRI) is the first of its kind to operate between two distant satellites.
The LRI has met its in‐orbit performance requirements such as laser link acquisition, uninterrupted science data collection, and noise level performance and it has exceeded expectations with regards to its ranging accuracy (Abich et al., 2019). We present in this study how the LRI ranging measurements can be successfully used for gravity recovery through a process similar to the one devised for the traditional KBR‐based gravity solutions. We conclude that it is possible to recover the same gravity signal by using the SST‐ranging observations from either the KBR or the LRI. This result goes far beyond the requirements of the LRI and supports the notion that an LRI‐based inter‐satellite ranging system is a sound technology for future gravity missions. We first provide a presentation of the LRI instrument and its ranging measurement. Next, we detail the gravity estimation process. The description begins with an exhaustive list of the background models used for the equation of motions, the gravitational and non‐gravitational forces. We then give an overview of the NASA Jet Propulsion Laboratory (JPL) instrument observation products involved in the gravity estimation. These are the observations from the LRI, the GPS receiver, the accelerometers, and the star cameras on board each satellite. Regarding the estimation process itself, we focus on the modifications needed to the processing schemes originally designed for the KBR solutions that were necessary due to the differences in the KBR and LRI measurements characteristics. These modifications include a change in the parametrization of the estimation problem and a change in the weighting strategy of the various types of ranging observations. The final discussion will provide a validation of the LRI gravity solutions through a comparison to the KBR solutions, both in the geospatial and spectral domains. We will show that the same signals are recovered globally but that differences exist at the higher degree harmonics of the spectrum as well as in the estimate of the Earth's dynamic oblateness coefficient C20. One final consideration will show that the comparison of the KBR and LRI post‐estimation residual errors are consistent with each other both temporally and geospatially, except for a larger noise level in the KBR residuals due to a larger instrument noise.
2. LRI Instrument
The LRI instrument on‐board of each satellite includes an optical cavity that generates a laser beam with a wavelength of 1,064.5 nm. The local laser beam out of the cavity is first directed to a beam splitter. Through the beam splitter, 10% of the local laser beam is then directed to a differential wave front sensor (phasemeter) consisting of a four‐quadrant photo array for the detection of the heterodyne (or beat) frequency. The other 90% of the local laser beam is directed to a triple mirror assembly (TMA). The three mirrors of the TMA are equivalent to a retroreflector with a vertex at the center of mass of the satellite and redirect the local beam to the other satellite. A Fast Steering Mirror (FSM) outside of the optical cavity actively compensates for the satellite's attitude fluctuation around the line of sight and ensures a precise beam pointing based on the photo‐array readings. The LRI phasemeters record the phase differentials, at a 10 Hz sampling rate on each of their four quadrants.
One satellite operates as the laser source, and the other as the transponder. The source sends to the transponder a beam, whose frequency is stabilized by the optical cavity. The energy of the incoming beam at the transponder is too weak to be directly sent back again to the source. Instead, the optical transponder cavity generates its own beam, phase‐locked with the incoming beam from the source, which is then sent back to the source. Additionally, a constant 10 MHz tone, or phase ramp, is added to the transponder's phase. Because the local laser beam is phase‐locked with the incoming laser beam, their phases cancel each other in the phase differential observation. Thus, the phase differential between the incoming beam and the local beam observed by the transponder's phasemeter is exactly the phase ramp. Conversely, the source observes the beat note between its local beam and the incoming beam from the transponder, whose phase corresponds to the one at the source from one round‐trip ago plus the ramping phase added to the transponder's beam. The gravity field variations cause continuous variations in the distance between the two satellites, leading to a Doppler shift which effectively contains information on gravity field variations. Because of the round‐trip nature of the LRI measurements, the phase differential recorded at the source contains twice the Doppler shift, once for each leg of the trip. The range inferred from the source and transponder phasemeters measurements is called the Two‐Way Range (TWR). It is different from the KBR Dual‐One‐Way Range (DOWR) where the local wave front is mixed with the incoming wave front from the other satellite after traveling the inter‐satellite distance only once. The KBR differential phase measurements on each satellite are of the same nature and both contain the gravity signal by way of the Doppler shift. Both GRACE‐FO satellites can operate as either LRI transponder or source and both have been enabled in each mode at some point in the mission. The satellite labeled as GRACE‐FO 2 (GF2) was operating as the source from the beginning of the mission until December 13, 2018. GRACE‐FO 1 (GF1) has been operating as the source since that date and up to the time of writing.
The in‐orbit performance of the LRI has exceeded the instrument requirements. The LRI carrier‐to‐noise ratio was evaluated in‐orbit at 88dB‐Hz, well above its 70dB‐Hz operational minimum requirement. The LRI range data noise at frequencies where it can be directly evaluated (frequencies greater than 30 mHz, beyond which gravity cannot be observed) has also surpassed its requirements: in‐orbit performance has shown a noise level of 10 nm/√Hz at 40 mHz compared to the 80 nm/√Hz requirement at that same frequency (Abich et al., 2019).
3. Estimation Process
The spherical harmonic coefficients (SHC) of the Earth's gravity field are estimated using the variational method (Cassel, 2013; Kang et al., 2020). Best known a priori models for the orbital dynamics are used to predict the orbit and to calculate the observation residuals. A differential correction process, including adjustment of optimal data weights, is used to obtain a monthly mean adjustment to the background gravity model. The sequence of such corrections provides the needed information for improvements to the mean Earth gravity models and for the evaluation of time‐variable mass flux in the Earth system.
The reference frame definition and dynamic models used in these steps are described in Section 3.1. Section 3.2 discusses the instrument observations data: the LRI ranging system, accelerometers, star cameras, and GPS receivers. These are the Level‐1B (L1B) V04 products provided by NASA JPL, which are available on the PO.DAAC portal (GRACE‐FO, 2019). Finally, the estimation procedure is presented in Sections 3.3, 3.4, 3.5.
3.1. Reference System and Background Models
The background models and reference frame definition used for orbit propagation broadly comply with the IERS Conventions (2010) and it is 2018 update (IERS Conventions, 2018). The models are summarized in Table 1. Complete details are provided in the CSR GRACE‐FO L2 Processing Standards Document RL06 (Save, 2019).
Table 1.
Summary of Models Used in CSR Release‐06 Gravity Estimation Process
| Models | Definition | Description |
|---|---|---|
| Equations of motion: | ||
| Inertial Earth‐centered ref. frame | IERS‐2010 | Polar motion, precession, nutation, and sideral rotation; reference epoch: J2000.0. |
| Earth‐fixed Earth‐centered ref. frame | IGS‐14 | |
| Gravitational Accelerations: | ||
| Mean gravity field | GGM05C | Complete to degree 360; degree 1 set to 0;secular change not modeled. |
| Solid Earth Tides | IERS‐2010 | Anelastic Earth; zero‐tide system: permanent tide in set to 4.201e−9. |
| Ocean Tides | Cartwright and Tayler (1971) | Tidal arguments and amplitudes/phases. |
| GOT4.8 | Diurnal/semi‐diurnal. | |
| Ray and Cartwright (1994) | Periods > monthly: self‐consistent equilibrium model. | |
| Egbert and Ray (2003) | Mm and Mf. | |
| FES2004 | Mtm and Msm. | |
| Petrovskaya et al. (2001) | Ellipsoidal correction. | |
| Atmospheric and Oceanic Variability | AOD1B RL06 | 3 hourly time series, degree/order 180. |
| Solid Earth Pole Tide | IERS C04 | Anelastic Earth polar motion. |
| IERS‐2010 | Anelastic Earth mean polar motion. | |
| Ocean Pole Tide | IERS C04 | Self‐consistent equilibrium model of Desai. |
| N‐Body Perturbations | JPL DE‐430 | Direct and indirect 3rd body point‐mass perturbations; Sun and Moon indirect J2 effect. |
| General Relativistic Perturbations | IERS‐2010 | |
| Non‐Gravitational Accelerations: | ||
| Accelerations from accelerometers | L1B ACT | JPL V04 acceleration product (transplant). |
| LIB SCA | JPL V04 attitude product (star camera + IMU); used to rotate accelerations. | |
The gravitational accelerations are the sum of direct planetary gravitational attraction and geopotential accelerations. All geopotential accelerations are represented using a spherical harmonic expansion with time‐variable coefficients. The total accelerations are computed as the sum of the Earth‐fixed gradient of the geopotential rotated to the inertial frame, and the tabular non‐gravitational accelerations rotated from the satellite to the inertial frame. The model for the orientation of the Earth‐fixed reference relative to the inertial reference, including the polar motion, follows the IERS‐2010 conventions. The total accelerations are used for the integration of equations of motion.
The GGM05C static field is used as the mean gravity field, with the degree 1 coefficients set to 0, consistent with the origin of the reference frame being the center of the mass of the Earth system. Solid Earth and ocean tidal contributions to the geopotential are computed as specified in IERS‐2010 conventions. The solid Earth contributions are computed for the anelastic Earth model. Corrections to specific spherical harmonic coefficients are computed and added to the mean field coefficients. The non‐tidal variability in the atmosphere and oceans is removed by using the 3‐hr AOD1B Release‐06 product (Dobslaw, Bergmann‐Wolf, Dill, Poropat, Thomas et al., 2017). It is based on analysis and forecast data of the operational high‐resolution global numerical weather prediction (NWP) model from the European Centre for Medium‐Range Weather Forecasts (ECMWF) and ocean bottom pressure from an unconstrained simulation of the Max Planck Institute global ocean general circulation model MPIOM (Jungclaus et al., 2013) consistently forced with ECMWF atmospheric data (Dobslaw, Bergmann‐Wolf, Dill, Poropat, & Flechtner, 2017). The solid earth pole tide contributions are computed as corrections to spherical harmonic coefficients and , from an anelastic Earth model to scale the difference between the epoch pole position and a linear mean pole, as specified in IERS‐2010 conventions. The self‐consistent equilibrium model of Desai is used for the ocean pole tide contributions, with the same polar motion time series as for the solid Earth pole tide.
The third body perturbations, based on the JPL DE‐430 ephemerides, are directly computed as accelerations acting on the spacecraft. They include the direct and indirect effects evaluated using point‐mass formulas. The indirect J2 effects are also included in the Sun and Moon perturbations. Finally, the general relativistic contributions to the accelerations and light propagation are computed as specified in the IERS‐2010 conventions.
3.2. Measurements
3.2.1. LRI Observations
The gravity field solutions presented in this study were created using the V04 LRI1B range‐rate observations (GRACE‐FO, 2019). Using range rate observations for SST information is a similar choice as the one made for the definitive monthly KBR solution (Landerer, Flechtner, Save et al., 2020). Range‐rate has been routinely used by the scientific community to derive gravity fields, though it has been shown that, given the right parametrization and weighting scheme, the gravity fields can also be estimated from either range or range acceleration observations (Smith, 2018; Tregoning et al., 2017; Wallace, 2005). Due to onboard issues in 2018, the LRI was not operating in science mode during most of that year and only collected science data for a couple of brief periods, none of them amounting to a full calendar month. Again, from February 7, 2019 to March 18, 2019 the LRI did not collect science data. Since then, the LRI has been continuously operating in science mode except for a few brief outages (Landerer, Flechtner, Bettadpur, et al., 2020). This paper will exclusively focus on 19 LRI solutions from January 2019 to September 2020 and excluding February and March 2019.
The LRI ranging observations are contained in the LRI1B product, which is delivered in a similar format as the KBR1B, with the exception of a few fields that are either not applicable to the LRI observations or whose definition differs (Wen et al., 2019). The LRI1B observations (range, range rate, and range acceleration) are already corrected in time (datation bias, filter delay, and daily LRI time bias) and in amplitude: a scaling factor is applied to correct for the uncertainty in laser frequency which may vary as laser cavity environment changes (Wen et al., 2019). The light‐time corrections which account for the fact that the two satellites are moving while the ranging signal is traveling are also provided in the LRI1B product and need to be added to the observations before processing. Because of the different nature of the ranging measurement (TWR vs. DOWR), the light time corrections for the LRI and the KBR observations are not identical. Finally, the KBR1B and LRI1B products also differ in their sampling rates, at 0.2 and 0.5 Hz respectively.
The Level‐1A (L1A) LRI observations, that is the phase differentials from the photo‐array, exhibit an occasional unexpected type of errors that manifest as discontinuities in the phase differentials registered at both satellites. Figures 1a and 1b show the running difference between consecutive phase differential observations at the source and transponder satellites as they are reported in the LRI1A product. This quantity helps illustrate the continuity anomalies in the LRI observations, identified as “phase jumps”. Since the phasemeter at the transponder satellite only observes the added phase ramp, the difference between consecutive phase differential observations, in the absence of data gap should be constant—of the order of a few thousandths of a phase cycle. Because of the nature of the LRI measurements, a discontinuity in the phase differential observed on one satellite can be due to a discontinuity in the phase of the beam from the either satellite. Figure 1a shows a typical phase jump on the order a hundred phase cycles; Figure 1b shows a jump three orders of magnitude larger. The latter type of phase jumps is rather infrequent―no more than a few per month―and has been labeled as “mega phase jumps”. Phase jumps appear to be linked to roll thrust activations (Abich et al., 2019) that occur several times per revolution to compensate for the loss of magnetorquer control authority in the roll direction around the magnetic equator. Consequently, simply editing out the phase jump observations is not an option since these are not randomly distributed around the globe. The nearly systematic deletion of data at the magnetic equator would skew the estimation of the gravity field. Instead, the phase jumps have been largely modeled out by JPL in the 1A‐to‐1B process which converts the LRI1A phase differentials into the LRI1B ranging observations. Though the procedure has proven successful at removing most phase jumps, some are only partially removed. A CRN temporal filter is applied to the phase differential observations in the 1A‐to‐1B process. Any remnants of these discontinuities passed through the temporal filter will appear in the LRI1B ranging observations as an oscillation of approximately 40–60 s, tapered on each end. The signature of the phase jumps in the LRI1B last much longer than the LRI1A phase differential anomaly itself because of the “smearing” effect of the temporal filtering. The resulting oscillations in the LRI1B ranging data are easily identified in the range rate “prefit” residuals, which are the difference between the LRI1B range rates and the range rates computed from the satellites' precise reference orbits. Figure 1c illustrates the signature in the range rate prefits of the typical phase jump from Figure 1a. This signature is two orders of magnitude greater than the variability of the range rates and needs to be edited out of the LRI ranging observations prior to the gravity estimation. The editing is currently performed manually by simply removing from the LRIB data the records matching a phase jump signature. On the other hand, Figure 1d illustrates the signature of the mega phase jump from Figure 1b. Here, the resulting range rate outliers are commensurate to the range rate variability and do not require editing. Experiments removing the smaller signatures in the LRI1B such as in Figure 1b have shown that the resulting LRI gravity solutions are not sensitive to them; they are therefore left in. It can be surprising that the larger anomaly in the LRI1A data may lead to a smaller outlier in LRI1B, and vice versa. This is a consequence of the current phase jump removal procedure in the 1A‐to‐1B process which may only partially remove some large phase jumps in LRI1A and may miss some of the small ones.
Figure 1.
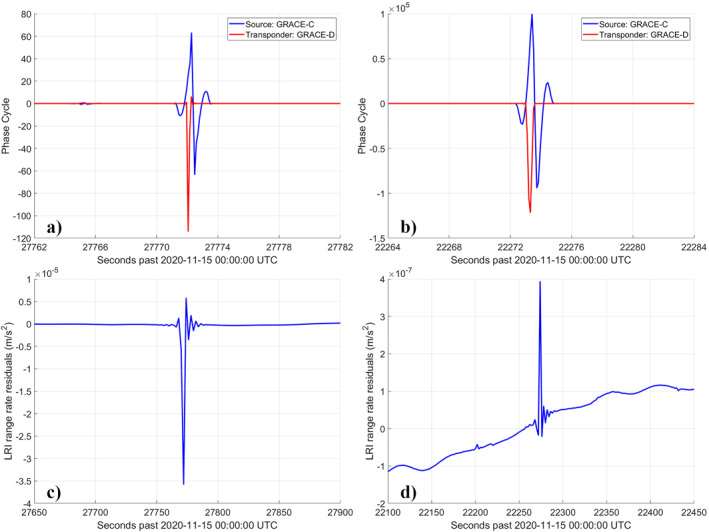
Running difference between consecutive phase differential values illustrating a typical phase jump (a), and a “mega phase jump” (b). Signatures of these phase jumps in the laser ranging interferometer range rate prefit residuals: some are quite large and must be edited out (c); others are small enough and can be left in the satellite to satellite data (d).
As of this writing, efforts are underway at JPL to completely remove phase jumps signatures from the LRI1B product but currently, the user must edit the LRI1B data prior to gravity field estimation. Early tests show that these fixes will improve data handling/screening strategies, but they will not significantly impact the gravity field estimates or science inference compared to the current LRI1B product when processed with proper editing.
3.2.2. GPS Observations
The precise GRACE‐FO orbit determination is carried out using the ionosphere‐free double‐differenced (DD) combination of the L1 and L2 carrier phase observations. The GRACE‐FO GPS observations are given in NASA JPL's V04 GPS1B product and ground station GPS data from a subset of IGS ground stations selected based on the stations' performance and the global geographical distribution of the selected stations subset. The GPS antennas onboard the GRACE‐FO satellites are the connecting modules between a GPS satellite and GRACE‐FO GPS receivers. Because the point at which the GPS signal is received (or phase center) by the GRACE‐FO antenna varies with the elevation and azimuth of the GPS satellite, a correction needs to be applied to the GPS observations to compensate for this offset in order to achieve sufficient accuracy in the orbit determination of the satellites (Haines et al., 2004). To that end, we use the map of the phase center variations, determined as a function of elevation and azimuth, provided by NASA JPL. For the orbit adjustment and the gravity estimation steps, the GPS DD observations are down‐sampled to a 2‐min sampling rate, unless the orbit adjustment step requires a more rapid sampling rate to achieve orbit convergence. In a few such cases, the GPS DD observations are used at a 30‐s sampling rate instead.
3.2.3. Satellite Acceleration and Attitude
The non‐gravitational linear accelerations used for orbit propagation are taken from a new product called ACT1B. The ACT1A/B products were created to mitigate the presence of spurious spikes and jumps in the accelerometer observations (McCullough et al., 2019). The calibrated linear accelerations in ACT1A/B are obtained after the thruster signatures are replaced with a calibrated thrust model. The remaining large spurious spikes unrelated to thruster firings are removed and replaced by linearly interpolating over the resulting data gap. Additionally, the noise characteristics of GF2's accelerometer changed a few weeks into the mission exhibiting frequent bias jumps severely deteriorating the quality of the measurements. Since then, the ACT1A/B products for GF2 are based on a time‐shifted transplant of the GF1 thrust‐free accelerations with the GF2 thrust signatures restored via the thrust model.
The attitude data product SCA1B is similar to the one from GRACE (Case et al., 2010). However, each GRACE‐FO satellite has onboard three star‐trackers and four Inertial Measurements Units (IMUs), while GRACE only had two star‐trackers and no functional IMUs. This allows for smoother transitions in the attitude data when one or more star camera heads are experiencing either Moon‐ or Sun‐blinding. Furthermore, the star‐trackers observations are combined with the IMU observations through a Kalman filter, further reducing the noise of the attitude data in the production of SCA1B.
3.3. Variational Method and Least Square Estimate
Let a set of observations be given and for the estimation of an ‐dimensional state vector , which contains the set of variables required to describe the system at any time and the unknown constant parameters used to define the dynamic model and the measurement model. The non‐linear observation equation is written as:
| (1) |
where G is a function of a set of n parameters X to be estimated, and represent the random noise. In order to solve this nonlinear problem, Equation 1 must be linearized. The linearized observation equation is given as follows (Tapley, Schutz, & Born, 2004):
| (2) |
where is the linearized state vector with respect to , which represents the best a priori knowledge of the system state parameters, are the linearized observations (also called “prefit” residuals), and contains the partial derivatives of G in a matrix form evaluated at epoch along the reference solution . Note that Equation 2 features a different linearized state vector at each epoch . These time‐dependent state vectors are however not arbitrary but result from variations in the parameters of the problem, that is the initial conditions and the force model. Using the classic variational method, the linearized state vector at epoch is related to the initial conditions at epoch via the following equation:
| (3) |
is the state transition matrix and contains the partial derivatives of the state vector at epoch with respect to its initial conditions. The particulars of the state transition matrix for the gravity estimation from SST data have been detailed by Bettadpur and McCullough (2017). Combining Equations 2 and 3, the linearized equations can then be written as:
| (4) |
Given an observation weight matrix , the weighted least square method selects the estimate of which minimizes the following performance index:
| (5) |
Finally, the least square solution, or best estimate of the linearized state vector which minimizes the performance index , is expressed as:
| (6) |
The least square solution contains the estimates of all the system unknown linearized parameters and variables at epoch . The details of the parameters estimated in our solutions are given in the following section. The details of the strategy for the determination of the weight matrix is described in Section 3.5. For the solutions presented in this study, the estimation of is performed in one step and the estimation procedure used does not include any constraint or regularization applied to the solution.
3.4. Parametrization
The basic organization of the estimation problem starts with the definition of an “arc”, which is the duration for which the satellite orbit initial conditions are adjusted. A “batch” is defined as a collection of arcs for which a single adjustment of the mean gravity field is performed. All gravity solutions presented in this study result from estimation carried out in batches of one calendar month, made up of a collection of daily arcs. We apply a “parameter leveling” (Gunter, 2004) approach to the gravity field coefficients and other necessary parameters being estimated. In this approach, the parameters are divided into three categories: (a) the local parameters estimated using one type of observation and over only one arc or a portion thereof, or a “sub‐arc” (in other words partial derivatives with respect to this parameter are only written for one data set over one arc or its sub‐arc), (b) the common parameters estimated using all types of observations but over one arc or sub‐arc only, and (c) the global parameters estimated using all types of observations across all arcs. Over the years of reprocessing of the GRACE data, some of these parameters have proven very effective in reducing error in the gravity solution (Kim, 2000). The CSR‐RL06 parametrization used for GRACE solutions was adopted for both the KBR and LRI GRACE‐FO gravity solutions, with the exception of the accelerometer scale matrix coefficients now being estimated as global parameters rather than common parameters. The complete list of the parameters being adjusted in the least square estimation process is given in Table 2. All the parameters in Table 2 are estimated together at once.
Table 2.
Summary of Parametrization Used in CSR Release‐06 GRACE‐FO Gravity Estimation Process
| Parameter type | Description | Solve span and Remarks |
|---|---|---|
| Orbit arc length (common) | Satellite initial conditions | Estimated once per arc for each satellite. |
| Dynamical parameters (common) | Accelerometer bias | Includes a constant bias and a bias rate for each satellite. |
| Terms are estimated once per arc in the accelerometer x and z directions. | ||
| Terms are estimated every 3 hr in the accelerometer y direction (sub‐arc). | ||
| Observation parameters (local) | GPS double difference ambiguity | Estimated per combination and per pass. |
| GPS troposphere zenith delay correction | One parameter per station estimated every 2.5 hr (sub‐arc). | |
| SST range rate corrections (KBR or LRI) | Includes a constant bias, a bias rate, and a once‐per‐revolution periodic bias term. | |
| All terms are estimated once per revolution (sub‐arc). | ||
| LRI‐specific range rate corrections | Estimated once per arc. | |
| LRI scale and LRI time bias corrections. | ||
| Does not apply to KBR observations (except for one experiment mentioned in Section 4.2). | ||
| Accelerometer scales (global) | Full accelerometer scale matrix | Estimated once per batch. |
| 9 individual components are estimated for each satellite. | ||
| Gravity field parameters (global) | Spherical Harmonic Coefficients | Estimated once per batch. |
| Solutions used in this study are estimated up to degrees 60, 120 and 180 |
The local parameters for the SST range rate (KBR or LRI) are a bias, a bias rate, and a once‐per‐revolution periodic bias term. All three parameters are estimated once per orbit period. The local parameters for the GPS observations are the double‐differenced ambiguity (one parameter per combination and per pass) and a tropospheric delay (one parameter per station per 2.5 hr).
The common parameters are, for each spacecraft, the initial position and velocity vectors, an acceleration bias and bias rate in the along‐track and radial directions estimated daily, an acceleration bias and bias rate in the cross‐track direction estimated every 3 hr.
Finally, the global parameters are the gravity coefficients and a full three‐by‐three acceleration scale matrix for each satellite. The purpose of the scale matrix, is three‐fold: scaling the accelerations observations, representing the “crosstalk” between the accelerometers' axes and corrects for misalignment of the accelerometer with respect to the satellite science reference frame:
| (7) |
where , and are the linear accelerations recorded by the accelerometer proof mass along the roll, pitch and yaw axes (Kim, 2000). The common parameters for the acceleration bias terms are added to the scaled accelerations from Equation 7.
In the case of the LRI solutions, two additional LRI local parameters are estimated once per arc: one accounts for possible error in the LRI Time Bias correction, the other for possible error in the LRI Scale correction.
| (8) |
The LRI corrections are already applied to the LRI1B observations. However, the presence of large phase jumps in the LRI1A product can severely affect the accuracy of these corrections estimated in the L1A‐to‐L1B processing. For most monthly solutions and with the exception of the degree 2 coefficients which will be discussed later, we find that estimating adjustments to these corrections do not bring significant change to the solutions given the parametrization previously described. On the other hand, some months such as March 2020 can contain several large phase jumps, which negatively impacted the LRI1B observations on seven separate days. As a result, the solutions for such months are noticeably improved by the estimation of the adjustments to the LRI corrections.
3.5. Weighting Scheme
Both the KBR and LRI unconstrained gravity solutions are obtained using a weighted least squares estimation (LSE) technique, where weights are determined through an iterative numerical method. In the estimation of the gravity field from GRACE or GRACE‐FO data, we are combining different types of observations, namely the GPS double differenced observations from each satellite and the SST observations from one (as is the case in this study) or more instruments. The levels of accuracy are different for each type of observation, it is therefore not realistic to weigh each data type equally. In addition, variations within a given observation type (due to instrument errors or malfunctions) can cause one set of measurements to be less accurate than another. Additionally, systemic effects that are improperly modeled can present themselves as systemic errors. Although the observation noise information is commonly used to design default weights for the observation data in the weighted LSE, the a priori noise assessment of GPS and SST data are generally not adequate to select the best weights for these data sets. Instead, the weights are estimated following the method described by Tapley and Born (1971) and refined by Yuan (1991). The goal of the method is to determine the weights that maximize the joint probability density function of the generalized observation error, which is assumed to be Gaussian. If the observation data is grouped by type and by estimation arc, with a total number of q groups, and their associated observation errors assumed to be independent, then the joint probability density function can be written as:
| (9) |
where is the set of observations in the kth group, is the weight matrix associated with the observations in the kth group, and is the matrix composed of the rows from the matrix , defined in Equation 5, that correspond to the observations in the kth group. For the estimation of the LRI solutions presented here, the three types of observations are the double differenced GPS observations for each satellite and the SST observations, therefore q is equal to 3 times the number of arcs included in the monthly batch. The maximum likelihood problem is equivalent to minimizing the function defined as L = −ln(F) which can be written as:
| (10) |
In our estimation process, a diagonal observation error covariance is used to weight each group of data, with all the observations within the kth group being weighted equally by the following weight matrix:
| (11) |
where is the a priori variance of the observation type over the considered arc. The assumption that the observation errors are uncorrelated within the kth group is made implicitly by the use of a diagonal matrix. Additionally, if the errors are not sufficiently known or modeled, the a priori values do not adequately represent the observation error. This can lead to incorrect weights for one or several data types to the detriment of the others. The weight scaling factor is to be determined so that it satisfies the minimum condition of the function L. With such a definition of the matrices , Equation 10 can be written as:
| (12) |
Then the first order optimal conditions (conditions on the first derivatives of L) are:
| (13) |
| (14) |
Equation 13 leads to the usual least square estimate from Equation 6, which in the case of grouped observations can be re‐written as (Kang et al., 2020):
| (15) |
Equation 14 leads to the expression of the weight scaling factors:
| (16) |
The Hessian matrix of the function L is always positive definite if the sum of the observation groups' normal matrices, , is positive definite (Yuan, 1991). Since the weight matrices are defined as diagonal matrices of positive numbers, the normal matrix of each observation group is positive definite, hence their sum is positive definite. As a result, the second order optimal conditions (conditions on the seconds derivatives of L) are always satisfied and the weight scaling factors on Equation 16 are optimum.
Because the optimal weight factors are a function of the least square estimate, they cannot be estimated simultaneously. Rather, they are obtained through an iterative procedure. The initial weight scaling factors are set equal to some initial guess (though they could also be set to 1) and the least square estimate is computed as per Equation 15. The new weight scaling factors are then obtained using Equation 16 and the new weights are updated according to Equation 11, where are now the diagonal elements of the weight matrix from the previous iteration. The process is repeated until the convergence of the weight values is achieved.
The weights thus derived are the mathematical optimum of the joint probability function F of the generalized error, but only under the assumptions that the error is Gaussian, independent across different observations groups, and uncorrelated within each group. These assumptions represent a simplification of the system and they are not true in practice. In particular, we know that observation errors will be time‐correlated if their systemic part is not adequately handled; this is especially true for the double differenced GPS observation error which is poorly modeled. Without any regularization procedure applied, the least‐square estimate will then minimize the maximum likelihood function, distributing both stochastic and systemic errors across the parameters, regardless of how the systemic errors may distort the estimates of the parameters. Furthermore, the GPS observations do not contribute to the whole gravity field spectrum uniformly, but rather mostly contribute to the very low degrees and sectoral components of the gravity field while the SST contribution are informing the rest of the spectrum (McCullough, 2017). The direct consequence observed in the GRACE solutions was that the optimal weights obtained from Equation 16 tended to favor the low degrees and sectorals via the GPS observations to the detriment of the rest of the spectrum. Starting with GRACE Release 05 gravity solutions, an upper bound was imposed to the GPS observations weights. By imposing a maximum weight on the GPS observations, we trade‐off gravity field error at the low degree for lower error in the rest of the spectrum. Through heuristic experiments, it was found that a maximum weight corresponding to a minimum sigma value of 2.12 cm gives the best compromise for the KBR solutions (Kang et al., 2020). Without this upper bound applied, the GPS optimal weights for the GRACE‐FO KBR solutions would usually be found at values corresponding to sigma values of about 8–9 mm.
To devise and evaluate the relative performance of various weighting strategies, we rely on changes to the “Degree Difference Variance” (DDV) of the resulting gravity solutions with changing data weights. The DDV is a commonly used criterion for the relative “goodness” of gravity solutions in the spherical harmonic domain (Kim, 2000). For a given degree, n, of the gravity solution, the DDV value is defined as:
| (17) |
where and are the spherical harmonic coefficients of degree n and order m for the gravity solution and mean background gravity field. Up to approximately degree 30, the deviation of a gravity solution from the mean field is mainly attributed to change in the gravity signal, while the solution error at these degrees is believed to represent a much smaller portion of the variance.
Conversely, at mid to high degrees, the deviation is mostly attributed to an error in the estimate and not the actual gravity signal. Consequently, a lower DDV curve at mid‐to‐high degrees signifies a lower error in the gravity solution. When comparing two gravity solutions obtained from the same observations but with different parametrization and/or weighting schemes, comparing their respective DDV curves helps identify the strategy that leads to the gravity solution with the lowest error. The DDV of the degree‐60 solutions is routinely used to evaluate the quality of a solution, with an emphasis on the lower to mid‐degrees which correspond to most research applications based on spatial domain representations. Higher degree solutions provide higher spatial resolution, while a degree‐60 solution can possibly alias some of these short wavelength signals into the lower degree harmonics. On the other hand, the higher resolutions come with added noise which necessitates more aggressive post‐processing filtering. Though they do not correspond to the highest spatial resolution, degree‐60 solutions are adequate for evaluating the relative performance of various solutions.
While the weighting strategy used for GRACE solutions was adopted for the GRACE‐FO KBR gravity fields, that strategy had to be modified for the gravity fields derived using the LRI data. Sampling experiments described hereafter showed that the 2.5‐times higher LRI observation sampling rate is the reason why the KBR solution weighting strategy cannot be applied to the LRI solutions.
To study the effect of the sampling rate on the weighting strategy we devised an experiment using the KBR1B and LRI1B data downsampled to their common epochs, equivalent to a 0.1 Hz sampling rate. The downsampling does alias the original frequencies greater than the folding frequency of 0.05 Hz into the frequencies lower than the folding frequency. We, therefore, expect increased noise at lower frequencies in the downsampled data sets, thus some degradation of both the KBR and LRI resulting solutions. However, the goal of the sampling experiment is to compare the relative goodness of two solutions derived from SST observations with the identical sampling rate and not their absolute goodness nor their relative goodness compared to the fully sampled solutions. Figure 2a shows the September 2019 DDV curves with respect to the mean field GGM05C for KBR and LRI solutions obtained after downsampling both sets of SST observations to their common sample times (0.1 Hz sampling rate) and using the 2.12 cm lower bound for the GPS sigma. When the KBR and LRI solutions are estimated using SST observations with the same sampling rate, applying the same GPS weighting strategies to both solutions leads to comparable DDV curves. Next, Figure 2b shows KBR and LRI solutions for that same month, using the full rate data (0.2 Hz for KBR and 0.5 Hz for LRI). In this case, using the same GPS weighting strategies leads to an LRI DDV curve higher than the KBR one for degrees 30 and above. This suggests that when combined with the full‐rate LRI data, the GPS data is underweighted with a minimum sigma set at 2.12 cm. Finally, Figure 2c shows the result of increasing the GPS data weight (i.e., lowering its sigma) while using the full‐rate LRI data; the KBR solution is the same as in Figure 2b. In this third strategy, the GPS data is assigned a fixed weight corresponding to a sigma value of 3.16 mm for the LRI solution. Because the optimal sigmas corresponding to the GPS optimal weights never drop that low, it is equivalent to imposing an upper bound to the sigmas which are smaller than the GPS optimal sigmas, or in other words imposing a lower bound on the weights which is greater than the GPS optimal weights, effectively upweighting the GPS data. These two different strategies applied respectively to the KBR (minimum sigma set at 2.12 cm) and LRI (fixed sigma set at 3.16 mm) solutions lead to commensurate DDV curves, especially reducing differences between the KBR and LRI DDV curves at the mid‐degree range (30–45), as shown on Figure 2c. By upweighting the GPS data, we compensate for the LRI higher sampling rate which leads to relative weights overly favoring the LRI data in the previous case.
Figure 2.
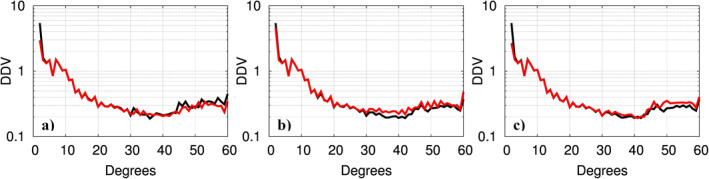
Unitless Degree Difference Variance (DDV) up to degree 60 with respect to GGM05C mean field: K/Ka‐band ranging (KBR) solution in black; laser ranging interferometer (LRI) solution in red. (a) 10‐s downsampled solutions with 2.12 cm lower bound for the GPS error covariance. (b) fully sampled solutions with a 2.12 cm lower bound for the GPS error covariance. (c) fully sampled solutions with 2.12 cm lower bound for the GPS error covariance applied to the KBR solution and 3.16 mm fixed GPS error covariance applied to the LRI solution.
The value of 3.16 mm for the GPS sigma used for the LRI solutions is based on weighting calibration experiments performed using June and July 2019 as test cases for which a range of values for the GPS sigma was applied. The value of 3.16 mm was found to be a convex minimum in the DDV sense and was adopted for the whole suite of LRI monthly solutions. Figure 3 shows the effect of increasing the value of the GPS fixed weights on the DDV curves at mid and higher degrees for July 2019 LRI solution (only degrees 20 to 60 are plotted for readability). Two DDV curves are also plotted as baselines for comparison: the Release‐06 July 2019 KBR solution (in red) and the LRI solution computed with the same upper bound applied the GPS weights like the one used for the KBR solution (in green). The quality of this LRI solution is visibly much poorer than the KBR solution, with a large variance value near the resonant degree 45. The goal of this calibration experiment is to tune the constraint on the GPS weight so that the DDV curve of the LRI solution is as low (or lower) as the KBR one. In Figure 3a, it can be observed that as the value of the fixed weights applied to the GPS observations increases, the quality of the LRI solutions improves for degrees 30 to 60, with the error spike near degree 45 disappearing. These solutions are labeled “gps_2.0” through “gps_10.0” and correspond to the following decreasing equivalent sigma values (in millimeters): 7.07, 5.77, 5.00, 4.47, and 3.16. Figure 3b shows the DDV for the next experimental value for the GPS fixed weights, labeled “gps_20.0”, corresponding to an equivalent sigma of 2.24 mm. We see a pronounced degradation in quality at degrees 48 and beyond while not bringing much improvement to the 20–47 mid‐degrees. Finally, Figure 3c shows that continuing to increase the value of the GPS fixed weights progressively further degrades the LRI solution quality passed degree 48 while still not bringing improvement to the mid‐degrees. These solutions are labeled “gps_30.0” through “gps_50.0” and correspond to the following decreasing equivalent sigma values (in millimeters): 1.83, 1.58, and 1.41. The “inflection” point was therefore found to be for the solution labeled “gps_10.0” corresponding to sigma of 3.16 mm. The GPS weighting strategy adopted at the CSR is directly dependent on the estimation method and on the characteristics of the GPS observations (2‐min sampling rate, double‐differenced observations). This strategy is likely not suitable if a different estimation method and/or type of GPS observations is used (different sampling rates and/or undifferenced observations). The key finding of the GPS weighting experiment in Figure 2 is that a GPS weighting strategy that was designed for a KBR‐based gravity solution may need to be re‐evaluated when using LRI observations.
Figure 3.
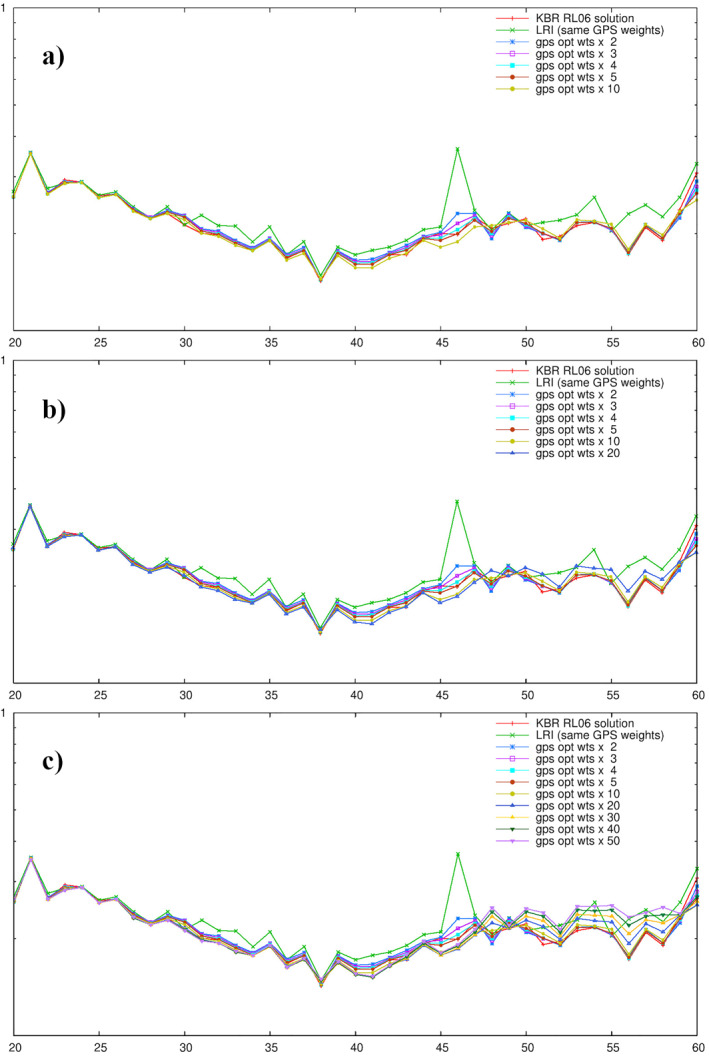
Effect of the GPS fixed weights on the degree difference variance (DDV) of the laser ranging interferometer (LRI) solutions at mid and high degrees (20–60). Results are shown for the test case of July 2019. The K/Ka‐band ranging (KBR) DDV (red) and the DDV for the LRI solution (green) estimated with the same weighting strategy as the KBR solution are also plotted for comparison. The GPS weights are fixed to (a) 2 times the a priori weights to 10 times the a priori weights, then (b) 20 times the a priori weights, and finally (c) 30 times the a priori weights to 50 times the a priori weights.
Finally, it was observed that the SST optimal weights when applied to the LRI solutions would sometimes favor a handful of days over all others in the monthly batch by assigning weights up to several orders of magnitude larger to these specific SST observations than for the rest of days. This effectively reduces a gravity solution to just a few days' worth of SST observations and completely degrades its quality. This behavior is not currently well‐understood and was never seen with the KBR solutions, whether they be GRACE or GRACE‐FO solutions. To mitigate this unwanted effect, a lower bound of 25.8 nm/s is applied to the LRI sigma preventing the LRI SST weights from increasing.
4. Results
4.1. Geospatial and Temporal Representations of LRI Gravity Solutions
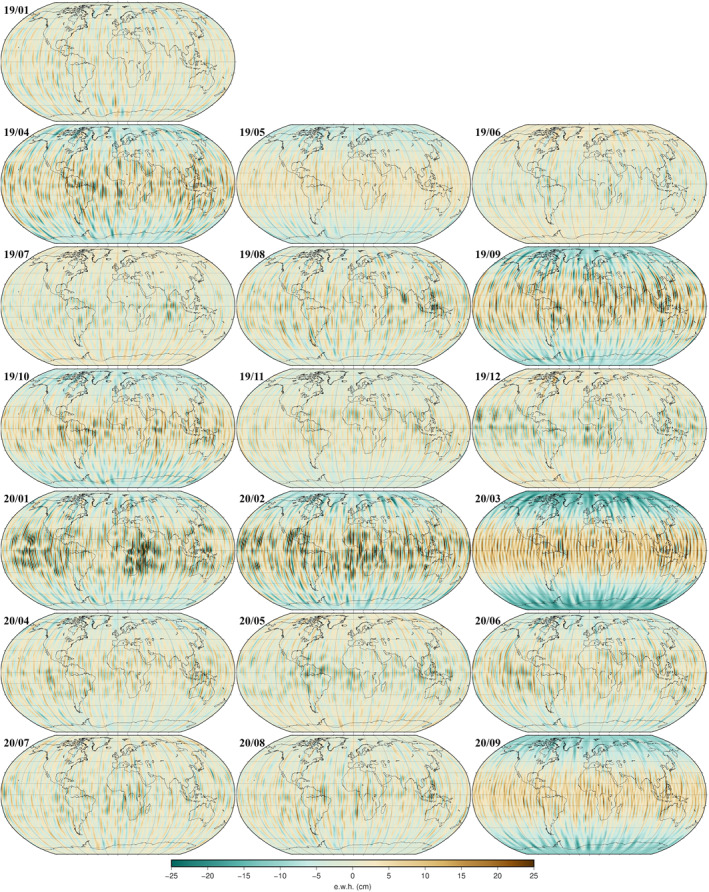
A total of 19 monthly gravity field solutions were computed using a full calendar month of LRI observations. Figure 4 presents the geographical projections of these gravity solutions—estimated up to degree and order 120—as maps of equivalent water height (ewh). The mean gravity field GGM05C has been removed and the contribution of the C20 harmonic has been set to zero (the C20 estimate would otherwise dominate the map representation and hide the smaller geographic deviations from the mean field). A DDK3 anisotropic filter (Kusche, 2007) is applied to the projections to remove the North‐South striations characteristic of the GRACE and GRACE‐FO unconstrained solutions which can be in part explained by the over‐sampling of the gravity signal's low frequency (Peidou & Pagiatakis, 2020).
Figure 4.

The CSR 120‐degree laser ranging interferometer gravity solutions are shown as equivalent water heights (unit in cm). The GGM05C mean field has been removed and the C20 deviations from the mean are set to 0. A DDK3 filter is applied (February 2019 and March 2019 not available).
The series of monthly projections in Figure 4 features some of the familiar large hydrological signals. These include the annual wet and dry cycle over the Amazonian region, the wet season in the Sub‐Saharan region from August to December, as well as the water storage cycle of the Ganges‐Brahmaputra water basin with a low in February‐June and a peak in August‐November. Another interesting signal is the exceptionally dry summer across central Europe in 2019 (Boergens et al., 2020; Xu et al., 2020). The dry spell, attributed to temperatures that exceeded the record‐breaking temperatures of 2003, can be seen stretching from July through November 2019. The variations in total water storage (TWS) anomaly obtained from both the LRI and KBR solutions are compared to those computed from NOAA's NLDAS hydrology model (Xia et al., 2012). The GRACE‐FO solutions are represented by a 0.5‐degree grid of values generated after several corrections and post‐processing are applied to the spherical harmonic solutions. First, the C20 and C30 coefficients were replaced with NASA TN‐14 (Loomis et al., 2020) values. Then the GGM05C mean field and rates from the ICE‐6G_D (Peltier et al., 2018) glacial isostatic adjustment (GIA) model are removed. Degree 1 coefficients from NASA TN‐13 (Landerer, 2020) are added. The same corrections are applied to the GRACE solutions (GRACE, 2018) for comparison. Finally, a 2004–2009 mean, based on GRACE's best years, is removed and a DDK3 filter is applied before generating the spatial grids. The fluxes out of the NLDAS model (precipitation less evapotranspiration and runoff) are accumulated over the whole GRACE/GRACE‐FO span as a proxy to the TWS anomalies. The NLDAS grids are averaged up from their native 0.125° to match the GRACE‐FO 0.5‐degree grids. Finally, the same 2004–2009 mean removed from the GRACE and GRACE‐FO TWS is removed from the NLDAS grids. We choose to present results for TWS anomalies rather than fluxes because it is the commonly preferred quantity. It should however be noted that hydrological models tend to underestimate large interannual trends of water storage compared to GRACE/GRACE‐FO (Scanlon et al., 2018). Consequently, the longer the time span considered for comparison between model and satellite data, the worse the comparison metrics may become. For the TWS anomaly results discussed below, this caveat means that the comparison statistics between GRACE/GRACE‐FO and NLDAS may appear better for GRACE‐FO than for GRACE in basins where NLDAS underestimate the interannual signal over the much longer span of the GRACE mission.
Figure 5 shows the TWS anomalies summed over four of the 18 large hydrologic units (HU2) as defined by the USGS Watershed Boundary Dataset (USGS, 2020b). In general, the TWS anomaly signals are well recovered by the GRACE‐FO LRI solutions over these larger basins: out of the 18 HU2 regions, 15 have a correlation factor, r, with the NLDAS time series greater than 0.8, 10 of them exceeding 0.9. The remaining three HU2 regions show a correlation factor between 0.72 and 0.8. Furthermore, all 18 regions show a correlation factor between the LRI‐ and the KBR‐derived TWS anomaly series are greater than 0.96, (10 of them >0.99). The GRACE‐FO solution's performance over these basins is also on par with the GRACE solutions when compared to NLDAS, though some of GRACE TWS anomaly statistics with respect to NLDAS may be negatively impacted by the longer time span over which they are computed. This can be seen in the third panel on Figure 5 showing the TWS anomaly for the Great Lakes region (HU‐04). The NLDAS time series does not capture the water level rise of the Great Lakes since 2013, whereas the GRACE/GRACE‐FO TWS time series was shown to correlate with in situ water level gauges, with a 6‐month lead (Argus et al., 2020). The first two panels show the TWS anomalies computed over the Pacific Northwest (HU‐17) and the Texas‐Gulf (HU‐12) regions. The former region shows no strong interannual signal over the GRACE/GRACE‐FO time span; the interannual signal of the latter region is adequately modeled in the NLDAS accumulated flux time series. In both cases, it can be observed that the correlation factors for the GRACE and GRACE‐FO solutions with respect to NLDAS are of comparable quality, all exceeding 0.9. The last panel shows the TWS anomaly for the Rio Grande region (HU‐13). This region corresponds to the poorer agreement between the GRACE‐FO KBR and LRI estimates, with still a 0.96 correlation factor between them. It is also a region where NLDAS seems to overestimate the recovery following the 2011–2014 drought. The model also appears to under‐represent the seasonal variability of the TWS anomaly from 2015 to 2020. It can be concluded that, at a spatial scale of 100,000 km2 and above, the GRACE‐FO LRI and the KBR solutions perform equally well and consistently with the GRACE solutions.
Figure 5.
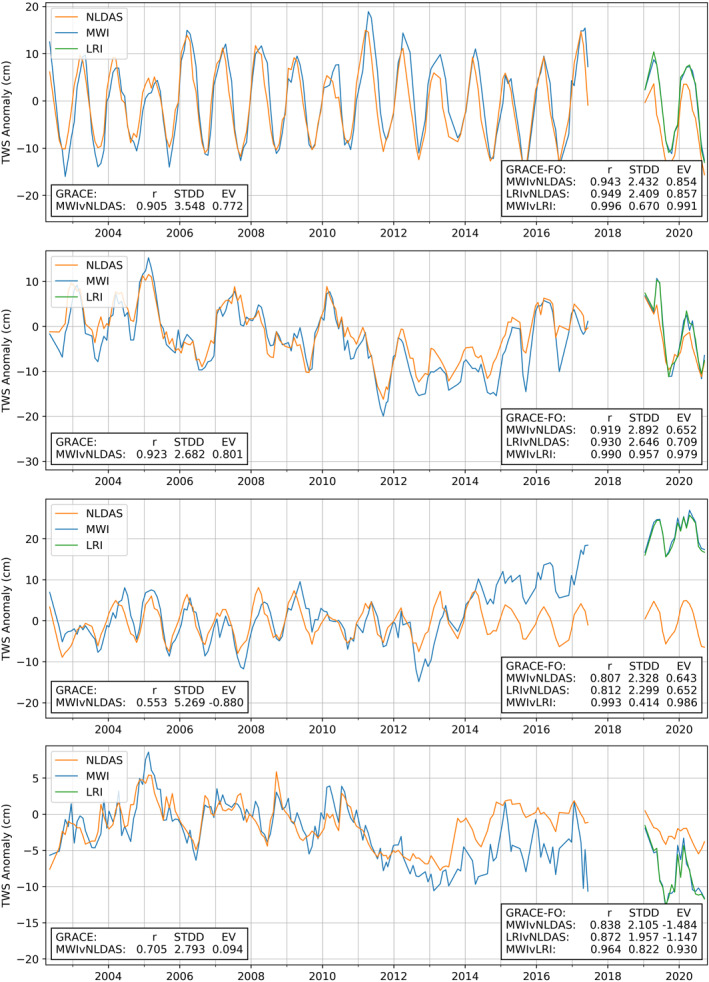
Total water storage anomalies computed as flux accumulation from NLDAS (orange), and directly from the Gravity Recovery and Climate Experiment/ Gravity Recovery and Climate Experiment‐Follow On (GRACE‐FO) K/Ka‐band ranging (blue) and laser ranging interferometer GRACE‐FO (green) monthly solutions over several USGS hydrologic units (HU2). A 2004–2009 mean is removed from all time series. From top to bottom: Pacific Northwest region, Texas‐Gulf region, Great Lakes region, and Rio Grande region.
Figure 6 illustrates the performance of the two sets of GRACE‐FO gravity solutions at a smaller spatial scale. The maps of the explained variance (EV) and correlation of the GRACE‐FO TWS anomalies against the NLDAS grid show the same geophysical patterns for KBR and LRI, though some of the finest details may differ slightly.
Figure 6.
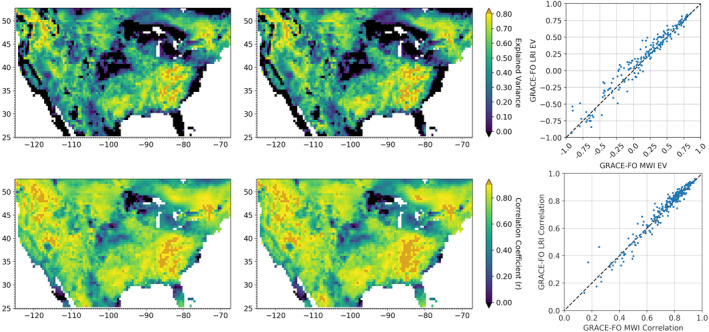
Comparison of the K/Ka‐band ranging and laser ranging interferometer Gravity Recovery and Climate Experiment‐Follow On solutions against NLDAS. Top panels: explained variance, color scale from 0 to 0.8. Bottom panels: correlation, color scale from 0 to 0.9. Left panels: KBR versus NLDAS. Center panels: LRI versus NLDAS. Right panels: regression of the LRI versus NLDAS statistics (y‐axis) against the KBR versus NLDAS statistics (x‐axis) for all the USGS hydrological units (HU4).
The correlation factor and variance explained between the two GRACE‐FO solutions sets both exceed 0.9 over the continental US. The comparison of these two statistics computed over subregions (HU4) of the previous larger hydrologic units is presented as regressions plots. The comparison over HU4 regions also confirms that both sets of GRACE‐FO solutions perform at the same level. The HU4 regions, as defined by the USGS National Hydrography Dataset (USGS, 2020a), range from around 5,000 to 110,000 km2 in size, most of them lying right at the resolvable spatial bound from GRACE and GRACE‐FO data. It is therefore important to note that the regression plots comparing the expected variance and correlation values from the KBR and LRI GRACE‐FO solutions show strong agreement but some of the low values are to be expected over regions too small to be adequately observed by GRACE‐FO.
To identify the disparities in the spatial domain between the KBR and the LRI solutions, it may be preferable to look at the map of the difference between the solutions. The two sets of solutions are differenced in the spherical harmonic domain and then projected as water layer maps with a 270 km Gaussian smoothing. Though some level of smoothing is necessary for the analysis, a Gaussian kernel is applied rather than a DDK filter, which would filter the very features we are interested in. The difference in C20 contributions is included since the difference is not large enough to mask the higher degree details. The projections of the difference between LRI and KBR solutions are presented in Figure 7. The main finding is the absence of an actual geographical signal in these maps, meaning that at that level of smoothing the same gravity signal is captured by both solutions. The two only remaining features are the difference in C20 estimates and the North‐South residual striations, which indicates differences in the commission error of the two solutions, in other words, differences in the propagation of the observation error into the gravity estimate. The difference in commission errors comes from both using different types of SST data and differences in the estimation strategies.
Figure 7.
Difference between K/Ka‐band ranging and laser ranging interferometer CSR 120‐degree solutions shown as equivalent water heights (unit in cm). C20 is included. A 270 km Gaussian smoothing is applied (Feb 2019 and March 2019 not available).
The months of January and February 2020 stand out from the rest of the maps with North‐South striations of greater intensity. There were two separate “bit flip” events in each of these months that caused the GRACE‐FO satellites to switch to fail‐safe mode, each time causing an approximately weeklong science data gap in both KBR and LRI observations. The quality of the solutions from either instrument was likely degraded due in part to the decrease in the amount of SST observations. This is illustrated by the monthly global RMS presented in Figure 8. The monthly global RMS is computed for each monthly solution by removing the GGM05C mean field and projecting the spherical harmonic expansion from degree 15 (first resonant degree) to degree 120 and applying the same 270 km Gaussian filter. These global RMS are different from the global ocean RMS that will be discussed next. By excluding the lowest degrees, we reduce the large geographic signals, such as the ones over the icesheets, so that they do not drown out the temporal variations of the North‐South striations in the monthly RMS. The degradation of the solutions' quality over the first two months of 2020 is commensurate for both instruments, each going from a global RMS of 15–18 cm ewh. At the same time, we observe the global RMS of the difference between the LRI and KBR solutions increasing as well from 4 to 8 cm ewh (shown in blue on Figure 8, C20 excluded).
Figure 8.
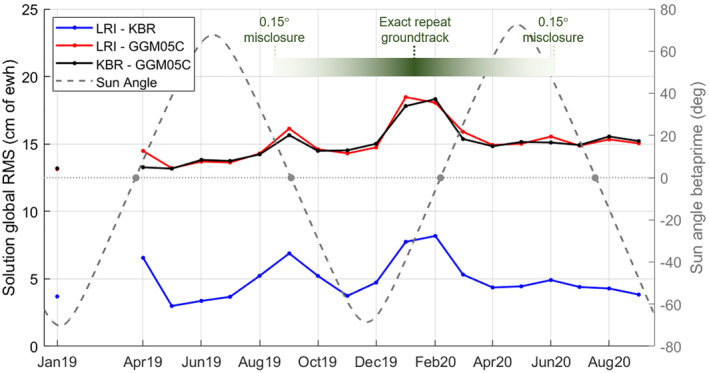
Monthly global RMS of the laser ranging interferometer‐K/Ka‐band ranging (LRI‐KBR) solution difference maps shown in Figure 7, C20 is excluded (blue) and Sun angle beta’ (gray). For comparison, the RMS of the difference of the solutions from each instrument and GGM05C, excluding all coefficients of degrees lesser than 15 are also shown (red: LRI, black: KBR). The green band represents a timeline of the evolution of the near‐repeat groundtrack misclosure.
Another such event can be seen from August to October 2019. There was no data loss during these months, however, the angle β’ representing the angle between the orbit plane and the Sun direction was approaching zero. Higher instrument noise has been observed when the Sun is in the orbit plane, especially in the accelerometer measurements, and is the topic of ongoing studies at CSR and JPL. Figure 8 shows that the degradation in the LRI and KBR solutions during that period is lower than during January‐February 2020, which also corresponds to another transition through a β’ = 0 orientation. However, the difference between the LRI and KBR solutions is similar to the one seen in early 2020. This suggests that the sensitivities to the β’ = 0 orientation of the LRI and KBR instruments themselves are comparable and that the difference in the solutions comes from the different estimation strategies. The KBR and LRI parametrizations and possibly the weighting strategies are likely distributing the same level of error differently through the gravity harmonic spectrum, and therefore geospatially. These spectral differences will be discussed further in the following section.
Finally, we note that the β’ = 0 during summer 2020 did not exhibit any visible degradation in either the gravity fields or an increased difference between the LRI and the KBR solution. We postulate that the effect of the added instrument noise mostly affects the quality of the gravity solutions when the satellites are flying in a repeat or near‐repeat orbit. The GRACE‐FO satellites passed through an 11‐day/167‐revolution repeat orbit from late January to early February 2020. This repeat orbit results in a groundtrack with ascending equatorial crossings about 2° apart, reducing the observability of the gravity field harmonic decomposition. The satellites remained in the vicinity of this repeat orbit, within a groundtrack misclosure of 0.15° at the equator, from late August 2019 to late June 2020. The poorer global coverage of a near‐repeat orbit not only reduces observability, it also has the disadvantage of geospatially “packing” observations errors such as the ones seen at β’ = 0.
The last metric based on the geospatial representation to be considered for the assessment of the gravity solutions is the ocean RMS values. Because the oceans are devoid of gravity signals of large magnitude as can be found on land (glaciers, ice sheets, Amazon, etc), they represent a large portion of the globe of relatively low signal amplitude, which is ideal for the evaluation of the gravity solutions overall noise level, and its stability through time. The global ocean RMS are evaluated using the spherical harmonic expansion of the gravity solutions up to degree 60. To assess the noise level of the solutions over the oceans, we remove from them a long period signal computed as a 12‐parameter fit of the KBR solutions over the entire GRACE/GRACE‐FO span. The 12 parameters account for a bias, a trend, and the sine and cosine of the following five periods: annual, semi‐annual, 161.04 days, 1,400 days, and 2,800 days. The C20 and C30 coefficients are set to zero before computing the residuals between the gravity solution and the 12‐parameter fit and a 300‐km Gaussian smoothing kernel is applied. The global ocean RMS is computed as the root mean square of the residuals over the global open ocean, excluding a 300 km buffer region along the coastlines. Figure 9 shows the ocean RMS for both the LRI and KBR solutions from January 2019 to September 2020. For comparison purposes, the ocean RMS for the GRACE solutions is also presented; these GRACE solutions were computed using an estimation strategy comparable to the one presented in this study (except for the parametrization of the accelerometer scale matrix). We observe that ocean RMS values from the GRACE‐FO KBR and LRI solutions remain within a couple of millimeter ewh of each other, with the exception of the April 2019 solution where the largest difference in the ocean RMS values reaches 6 mm ewh. The GRACE‐FO ocean RMS values range from 2.5 to 4 cm ewh, with an approximately semi‐annual variation which is likely linked to the β’‐sensitivity of the GRACE‐FO system. Except for this semi‐annual variation, the GRACE‐FO ocean RMS values are comparable to the ones obtained in 2011–2012 from the GRACE solutions.
Figure 9.
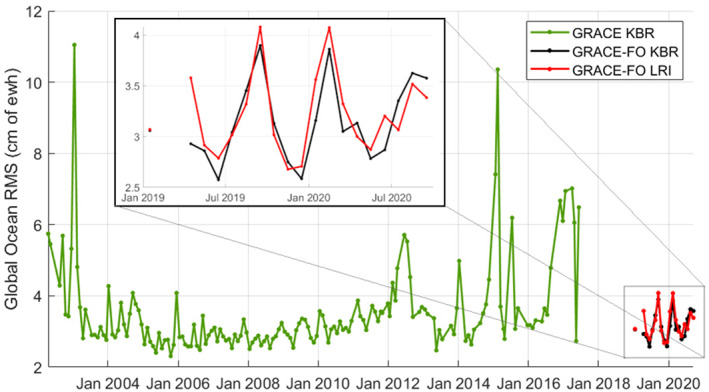
Monthly ocean RMS time series for Gravity Recovery and Climate Experiment (GRACE) and GRACE‐Follow On mission solutions. A 12‐parameter fit is subtracted from the degree‐60 solutions, C20 and C30 are set to zero, 300‐km Gaussian smoothing is applied.
4.2. Spectral Representation of the LRI Gravity Solutions
The LRI gravity estimates are obtained in the spectral domain as spherical harmonic expansion up to degree and order 60, 96, 120, and 180. The higher the maximum degree, the higher the corresponding spatial resolution, but also the higher the noise which requires a more aggressive filtering strategy, in turn decreasing the spatial resolution. In the spectral domain, however, it is possible to extract insight and information from higher degree solutions.
The degree‐60 solutions are routinely used to evaluate the quality of a solution, with an emphasis on the lower to mid‐degrees which correspond to most research applications using geographic grids. Figure 10 shows the degree‐60 DDV curves comparison between the LRI and the KBR for all 19 months for which and LRI solution was computed. The DDV curve represents a degree‐wise quantification of the deviation of a solution with respect to the mean field, here GGM05C. Though a monthly gravity solution may exhibit some strong localized geographic signals with respect to the mean field, this does not translate to a strong power associated to a particularly high degree, since the associated spherical harmonic functions are defined over the whole sphere. Therefore, the DDV curve of an error‐free gravity solution would be expected to decrease as the degree increases. Conversely, the greater the DDV at mid and high degree (degree 30–40 and above), the poorer the solution.
Figure 10.
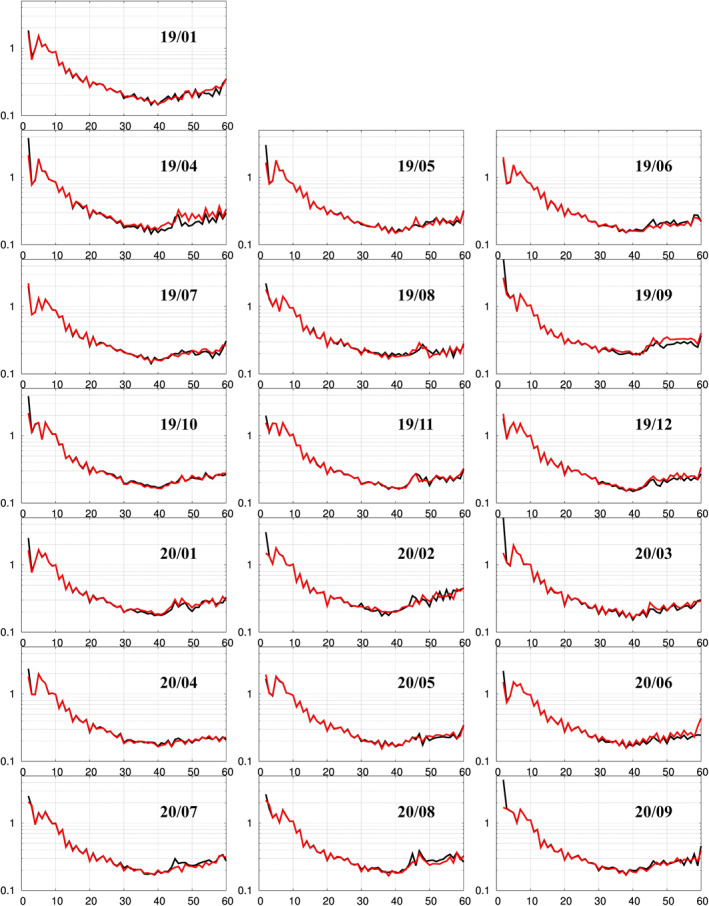
Degree Difference Variance (DDV) up to degree 60 with respect to GGM05C mean field. K/Ka‐band ranging solutions in black; laser ranging interferometer solutions in red. Unitless logarithmic y‐axis ranges from 0.1 to 5 (February 2019 and March 2019 are not available).
With this in mind, we can conclude from Figure 10 that the LRI and KBR monthly solutions are of comparable quality degree‐wise. Both sets of solutions show degradation of quality at degree 45 due to the geopotential coefficients of resonant order 45 which persists across most months in either LRI or KBR, with the exception of January, July, and October 2019, as well as the second quarter and September of 2020. It has been suggested that the GRACE solutions suffer from sub‐Nyquist sampling artifacts, reminiscent of the Moiré fringes in optical physics (Peidou & Pagiatakis, 2020), though the causes for this sampling degradation are not identified. These artifacts result in approximately 90 North‐South striations along the equator (before smoothing) in the GRACE gravity solutions. These conclusions can be extended to GRACE‐FO since the sampling of observation along the groundtracks is a feature common to both missions (even if the groundtracks themselves are different). These striations can be linked back to sectorial (spherical harmonic coefficient for which the degree and order are equal) and near sectorial harmonics of roughly degree 45 which explain, at least in part, the resonance at degree 45 on the DDV curve. It is of note, however, that some months show a stronger resonance in either the LRI or the KBR solution, while the other solution shows a weaker or no resonance.
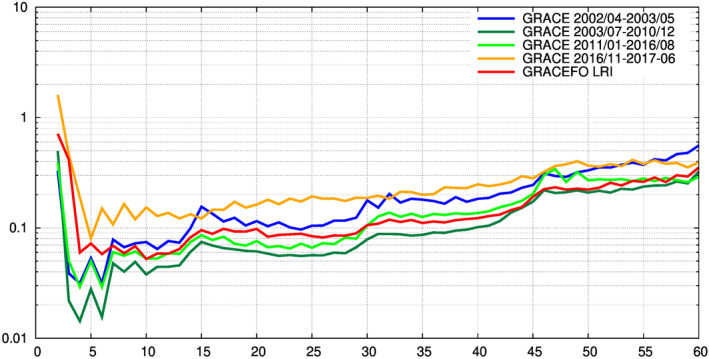
Figure 11 shows a DDV comparison of the overall quality of the LRI solutions compared to the overall quality of the GRACE KBR solutions across the four distinct noise regimes experienced during the mission (Save, 2020). The degree differences in Figure 11 are computed with respect to the monthly mascon fields, which are used as a proxy to the true signal in the context of the comparison of the LRI solutions against the GRACE solutions. The use of the mascons as a reference field, instead of a mean field such as GGM05C, is necessary when averaging over such long periods; the interannual trend in the gravity signal would not allow the comparison between spectra of solutions separated by multiple years. Each line shown in Figure 11 represents the rms of the DDV values over stretches of time, as labeled. The GRACE‐FO LRI errors for degree 2–6 are superior to the ones of the GRACE solutions across all noise regimes, except for the “single accelerometer” months (yellow line). This can be at least partially explained by some mismodeling in the transplant acceleration from the ACT1B product. From degree 6 up to the first resonant degree 15, the errors of the LRI solutions are comparable to GRACE second‐best noise regime (light green) and smaller past degree 30; the LRI solutions errors are however higher from degree 15 to degree 30. The LRI solutions errors remain larger than that of GRACE best noise regime (dark green) up to degree 43, but they are comparable beyond that point for the higher degrees.
Figure 11.
Triangular plots showing the absolute values of the estimated gravity coefficients with respect to the coefficients derived from the monthly CSR mascons (up to degree and order 180). Left panels: K/Ka‐band ranging solutions from Gravity Recovery and Climate Experiment. Right panels: laser ranging interferometer solutions. The top panels show relatively good months, while the bottom panels show months with a slight degradation in the solutions qualities.
The DDV curves only present a degree‐wise aggregated view of the gravity solutions spectra. By looking at their full spectra, it is possible to identify some crucial differences between the two sets of solutions that are lost in the aggregation of the DDV curves. Figure 12 shows triangular spectral representations of the gravity coefficients of LRI and KBR solutions with low error, May 2020, and high error, February 2020, according to the DDV curves. For comparison purposes, solutions for GRACE are also provided: January 2008 represents a low error month within the best noise regime period (dark green line on Figure 11), while December 2013 represents a month with higher error within the second‐best GRACE noise regime (light green line on Figure 11). The values plotted are the absolute values of the coefficients from the full 180‐degree solutions with respect to the coefficients derived from the CSR mascons fields to allow a comparison with GRACE. The positive order values along the y‐axis correspond to the C nm harmonic coefficients, while the negative order values correspond to the S nm coefficients. Overall, the same broad scale patterns can be observed in GRACE‐FO KBR and LRI representations. The deviations from the mascon fields are larger at the low degree where the temporal gravity signal mostly resides, then decrease in the mid degrees to increase again rapidly around degree 80–100. The solutions error also increases along the sectorial and near sectorial coefficients. Errors in this region of the spectrum can be associated with North‐South striations. It can also be observed that GRACE‐FO KBR and LRI solutions suffer from the same order resonances, though their intensity may vary slightly between both sets; such order resonances appear as horizontal lines in Figure 12. These order resonances are the result of resonant frequencies in the satellites' orbital osculating elements, or “germinal” orbital frequencies. The germinal frequencies are then propagated to many spherical harmonics of the same order, and nearby orders, in the expansion formulation of the gravity potential (Casotto, 1990; Rosborough & Tapley, 1987). It is therefore expected to find their signatures in both the KBR and LRI solutions' spectra. The difference in intensity, though very subtle, may be indicative of the respective sensitivity of the LRI and KBR gravity estimation processes (parametrization, observation rate, weighing strategy). However, the main difference between the triangle plots of the LRI and KBR solution sets are the lower deviations from the mascon fields for the zonal (order 0) and near zonal coefficients of the LRI gravity solutions at degree 120 and beyond. This is indicative of the LRI solutions being more effective at resolving the higher degree zonal and near zonal terms of the gravity field than the KBR ones. This is a testament to the low‐level noise in the LRI observations, which will be discussed further in Section 4.3, allowing for much finer resolution in the along‐track direction. Though our current estimation method as well as error sources from other instruments do not permit us to translate this improvement from the spectral domain to the spatial domain in Level‐2 products, these results are very meaningful, especially in the context of future gravity mission discussions.
Figure 12.
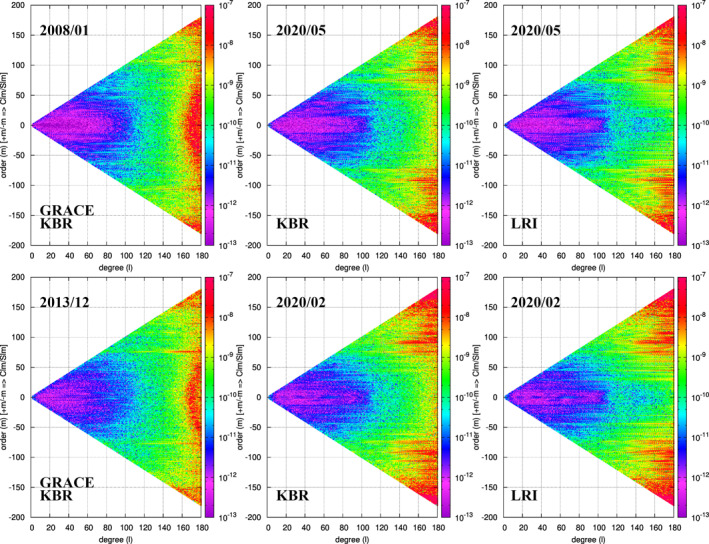
Triangular plots showing the absolute values of the estimated gravity coefficients with respect to the coefficients derived from the monthly CSR mascons (up to degree and order 180). Left panels: K/Ka‐band ranging (KBR) solutions from Gravity Recovery and Climate Experiment. Center panels: KBR solutions from GRACE Follow‐On Mission. Right panels: laser ranging interferometer solutions. The top panels show relatively good months, while the bottom panels show months with degradation in the quality of the solutions.
Another important difference between both solution sets is the estimated values for the C20 coefficient. As can be observed in Figure 11, the error in degree 2 dominates the low degree error. It is well‐known that the C20 term was not well observed by GRACE. The C20 time series from GRACE includes an unexpected 161‐day periodic signal. Ocean tide aliasing effects once proposed as a possible source of this signal were disproven and a more likely source was suggested to be the thermal effects in the accelerometer observations, probably linked to the β’ angle between the orbit plane and the direction to the Sun (Cheng & Ries, 2017). It has since become the norm to replace the GRACE estimate of C20 with one based on Satellite Laser Ranging (SLR) before using the GRACE gravity field solution in geophysics applications. The same limitations seem to affect the GRACE‐FO mission and the replacement of the C20 term was recommended again in Technical Note 14 (TN‐14), which provides the recommended replacement estimate values for both GRACE and GRACE‐FO (Loomis et al., 2020).
The top panel shown in Figure 13 shows the C20 time series for both the GRACE‐FO KBR and LRI solutions with respect to GGM05C. A prediction based on a fit of the CSR GRACE solutions is shown as best guess of the expected estimates. The values provided in TN‐14 are also provided for comparison. The LRI estimates of the C20 term are slightly better than the ones obtained from KBR. This is probably due to the estimation of the LRI scale and time bias correction adjustment. These terms are designed to correct errors in the LRI measurements that will manifest themselves as once and twice per revolution signals. Because of the geometry of the spherical harmonic function associated with it, the C20 term is naturally sensitive to errors with a twice per revolution signature. Consequently, the LRI correction parameters are expected to be highly correlated with C20. Their estimates are likely absorbing part of the twice per revolution error otherwise left in the C20 estimate. Experiments performed at the CSR showed that applying an LRI‐like parametrization to the GRACE‐FO KBR gravity estimation improved the C20 estimates of the KBR solution. The same experiment was conducted for the GRACE solutions but led to a degradation of the C20 estimate. We postulate that the twice per revolution error being absorbed by the LRI parameters likely relates to the error in the thrust modeling in the ACT1B product, which is largest during the roll thrust at the crossing of the magnetic equator. Such error was not an issue during the GRACE mission which would explain why the alternate parametrization did not have the intended effect. This being said, the LRI estimates still show some sizable discrepancies with respect to the SLR estimates, especially from December 2019 onward. Consequently, it is advised to replace the C20 term in LRI solutions as well. Furthermore, the LRI‐like parametrization experiments for the KBR solutions also showed an increase in the estimator's formal error of the C20 estimates, which is to be expected when estimating highly correlated parameters. We note however that the effect was more drastic for GRACE solutions where the C20 formal errors were multiplied by a factor 3 to 5, while they only increase by 30%–40% for the GRACE‐FO KBR solutions. We can infer from these results that the absorption of systemic errors by the LRI correction parameters likely also comes at the cost of an increase of the C20 formal error, though this cost has not been evaluated.
Figure 13.
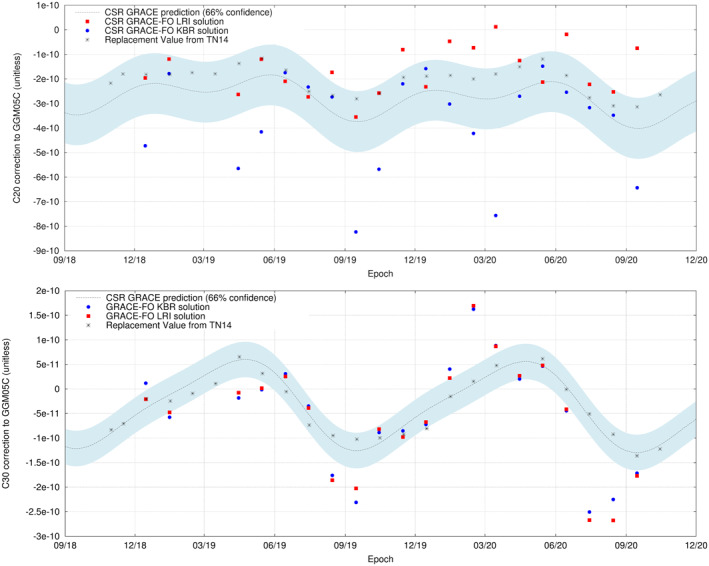
C20 (top) and C30 (bottom) estimates from CSR monthly RL06 K/Ka‐band ranging and laser ranging interferometer (LRI) degree‐60 gravity solutions with respect to GGM05C (only the months where an LRI solution is available are plotted). The blue‐ribbon curve shows the predicted values based on a fit of the Gravity Recovery and Climate Experiment solutions which include a constant term, a trend, and an annual signal with a 66% confidence interval. For comparison, the replacement values recommended in NASA Goddard's TN14 are also provided.
In addition, the estimation of the C30 term has also proven to be unreliable for GRACE‐FO. This may correspond to the use of transplanted acceleration data for one of the satellites. A similar degradation of C30 is seen during the last few months of the GRACE mission when it was flying in single accelerometer mode (Loomis et al., 2020). TN‐14 also recommends replacing the C30 estimate with one based on SLR in GRACE‐FO KBR solutions. The bottom panel of Figure 13 shows the C30 time series for both the GRACE‐FO KBR and LRI solutions with respect to GGM05C, along with a GRACE‐based prediction and the TN‐14 estimates. This time, there is very little difference between the LRI and the KBR estimates.
Efforts are currently underway at JPL to create an enhanced ACT1B product. It is expected that a better ACT transplant product will improve the estimation of the C20 and C30 terms for both the KBR and LRI solutions. However, until this new data set is released and its effect on C20 and C30 assessed, it is necessary to follow the TN‐14 recommendations and replace the two estimates with the SLR‐based ones in the KBR and LRI solutions alike.
4.3. Postfit Residuals in the Temporal Domain
The range rate postfit residuals are another measure of the quality of the gravity solutions. They are defined as:
| (18) |
where is the least square estimate defined in Equation 15, are the linearized SST observations and contains the rows of H defined in Equation 5 that correspond to the SST observations. The postfits represent the residual observations after adjustment of the gravity coefficients and the other parameters. Consequently and by definition, the posfit residuals not only contain the errors arising from inadequacy in the estimation process, but they also contain system errors that are poorly modeled and instrument noise, both appearing in the postfits via the term . Figure 14a shows a snapshot in time of the LRI and KBR postfit residuals for one revolution on May 10, 2020. The two postfits time series align perfectly and their comparison is dominated by the high‐frequency noise in the KBR postfit residuals, which can be linked back to the lower precision of the MWI instrument compared to the LRI. Small sub‐monthly signals of the order of a tenth of a micron per second are clearly visible in the postfit residuals from both instruments to a level that was never attained by GRACE, the postfits of which were dominated by noise. This is the direct result of the lower noise in GRACE‐FO MWI instrument and the unprecedented low observation noise of the LRI instrument. Though the full exploitation of such precise observations may be difficult in Level‐2 global gravity products, along track analysis using Level‐1B LRI observations have already successfully been conducted to reveal short‐wavelength gravitational perturbations previously undetected or mismodeled (Ghobadi‐Far, Han, McCullough et al., 2020).
Figure 14.
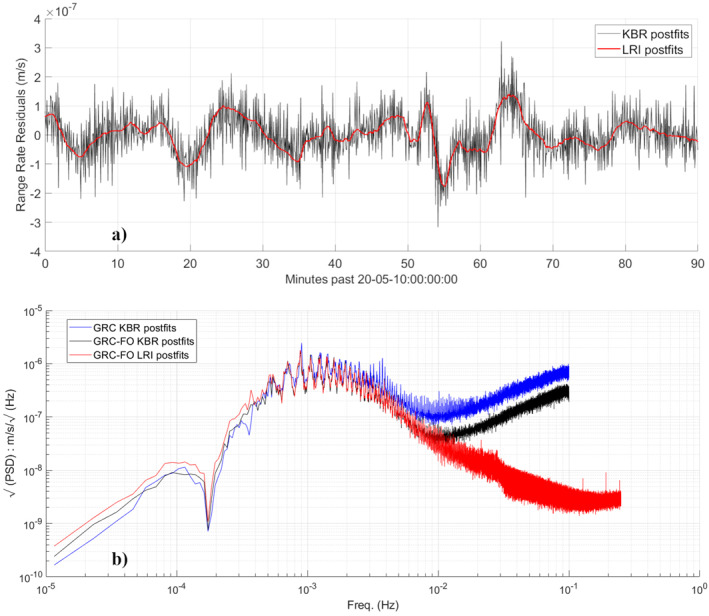
(a) K/Ka‐band ranging (KBR) (black) and laser ranging interferometer (LRI) (red) range rate postfit residuals for the first orbital revolution of May 10, 2020. (b) Averaged periodograms of the KBR and LRI range rate postfit residuals for the 17 data‐gap free days of the May 2020 solutions. The averaged periodogram of the GRACE KBR range rate postfit residuals for 17 data‐gap free days over January–February 2013 is given for comparison.
Figure 14b shows the periodograms of the KBR and LRI residuals, with Nyquist frequencies of 100 mHz for KBR and 250 mHz for LRI. These periodograms were computed as the average of 17 individual periodograms from the 17 days in May 2020 that did not contain any data gap in either the LRI or the KBR observations. The purpose of averaging multiple periodograms is to reduce the scatter in the high frequency band of the spectrum and reveal possible frequency peaks and features that would otherwise be hidden within the scatter. A periodogram of GRACE KBR range rate postfit residuals from 17 gap‐free days is also provided for comparison. The GRACE‐FO KBR periodogram starts flattening around 8 mHz and starts rising after 10 mHz, corresponding to the MWI observation noise. The differences between the GRACE‐FO residuals at low frequencies can be explained by the adjustments to the LRI1B scale and time bias corrections contained in the estimate term of the LRI residuals which mostly affects the low frequencies up to twice‐per‐revolution, corresponding to roughly 0.35 mHz. Past that frequency, the LRI periodogram follows the KBR one up to 8 mHz. The LRI residuals spectrum density continues to decrease past 10 mHz before flattening softly around 170 mHz. Two distinctive features can be seen in the LRI high frequency band. We can first notice a bulge at 30 mHz. At the time of writing, the origin of the bulge is not understood but has been observed in the LRI postfits of other monthly solutions as well. This feature is being investigated at the CSR and JPL. Second, three small frequency spikes can be seen toward the end of the spectrum at 128 mHz, 192 and 244 mHz, all corresponding to a few microseconds. We postulate that these frequencies relate to an error introduced in the L1A‐to‐L1B conversion from phase to range rate. The L1A phase observations are given at a sampling rate close to, but not exactly equal to, 10 Hz and there are some systematic irregularities in the time intervals between phase observations. During the L1A‐to‐L1B process, the phase observations are converted using a smoothing interpolator to range rate observations with an exact sampling rate of 0.5 Hz. Some interpolator errors are likely to occur with a distinctive temporal pattern matching the time interval irregularities in the L1A phase observations. This hypothesis has not been investigated in further detail at the time of writing.
The size of the GRACE‐FO postfit residuals is consistent throughout the solutions. Figure 15 shows the daily root mean square of the range rates posfit residuals (postfit rms) for the GRACE solutions and for GRACE‐FO KBR and LRI solutions. For GRACE‐FO, both the KBR and LRI postfit rms show the same monthly variations, with variation amplitude four times as large for LRI than for KBR, while the LRI postfit rms values remain, on average, half that of the KBR: 40 nm/s for the former against 80 nm/s for the latter. Regardless of the SST instrument, the GRACE‐FO postfit rms are much smaller than the ones obtained for the GRACE RL06 solutions which are of the order of 150–200 nm/s before 2016 and increase to 300–500 nm/s by the end of 2017 when the GRACE satellites operated in single accelerometer mode.
Figure 15.
Daily rms of the K/Ka‐band ranging (KBR) (black) and laser ranging interferometer (red) range rate postfit residuals. The daily rms of the Gravity Recovery and Climate Experiment KBR (blue) range rate postfit residuals are given for the whole mission for comparison.
4.4. Postfit Residuals in the Geospatial Domain
The quality of data fit during gravity field model estimation is routinely assessed in map form, with the most desirable outcome being an absence of any geographical coherence in the postfit residuals and the areas of large signals. However, careful consideration is needed in this case since the observations (or observation residuals) are functions of the orbital coordinates, which are themselves coherent with the gravity field variations. The Theory of Geographically Correlated Orbit Perturbations (TGCOP) was pioneered at UTCSR (Rosborough, 1986; Rosborough & Tapley, 1987) for quantifying the impact of coherence of the radial orbit perturbations with the static gravity field upon oceanographic inferences using the TOPEX/Poseidon radar altimeter data. The theory was directly extended to time‐variable gravity field effects (Bettadpur & Eanes, 1994), quantifying the influence of coherence of the radial orbit perturbations due to gravity variations from ocean tides on the determination of ocean tide models from radar altimeters. The principles can be also extended to the case of SST since the intersatellite range variations are a linear function of radial and transverse orbit perturbations and the inter‐satellite separation (Kim, 2000); and at any location, both radial and transverse orbit perturbations are coherent with the time‐variable geospatial processes that cause gravity field variations.
In this study, we invoke the TGCOP for the limited purpose of qualitative and comparative analyses for the goodness of fit. The analysis need not be limited to ground‐track crossover locations, and data residuals can be evaluated in geographic bins, separately for the ascending and descending tracks. The analysis is carried out using satellite‐to‐satellite range accelerations derived by numerical differentiation of the range‐rate residuals from gravity adjustments since, unlike the range rate, the range‐acceleration residuals are not masked by the relatively large residual (slow) orbit variations.
The prefits, , are the residuals of the observations relative to the best a priori model (“background”). They are expected to contain signals from time‐variable gravity due to unmodeled mass change. According to the TGCOP, the symmetric and skew‐symmetric components in the mathematical expressions of SST prefit residuals will be coherent in time with the geophysical processes that give rise to the residuals. Here, we designate the components as “symmetric” and “skew‐symmetric” in place of the “mean” and “variable” designation used in the TGCOP literature (Rosborough, 1986; Rosborough & Tapley, 1987). We deem the new designation to better represent the nature of the mathematical expressions of the prefits given in TGCOP while being less prone to misinterpretation in the context of time‐varying gravity fields (Rosborough worked in the context of a static field). Over one month, the average prefit residuals from the ascending tracks in a bin will equal the sum of the average of the symmetric and the skew‐symmetric parts, whereas the average prefit residuals from the descending tracks in that same bin will equal the difference of the average of the symmetric minus the skew‐symmetric parts.
We adjust the monthly “mean” gravity field using these prefit residuals. In complete analogy with the case of radial orbit perturbations (Bettadpur & Eanes, 1994; Rosborough & Tapley, 1987), the estimated gravity field parameters will adjust to minimize the symmetric part of the prefits, since this is the spatially coherent component (in phase) with the mean gravitational potential. The skew‐symmetric part, on the other hand, will not be adjusted by gravity field parameters as it is not is spatially coherent (out of phase) with the mean gravitational potential.
The signal adjusted to the gravity parameters is labeled “geofits”. As a result of the previous arguments, we may expect the sum of the averaged ascending and averaged descending geofits, labeled “A + D” geofits on Figure 16, to display geographically coherent signals that represent that month's adjustment to the background gravity model (“A + D” is effectively canceling out the skew‐symmetric part), while the difference of the averaged ascending minus averaged descending geofits, labeled “A‐D” geofits, should remain featureless (“A‐D” is effectively canceling out the symmetric part). This last statement is however not completely exact in practice because of the discrepancy between the basis functions used in the TGCOP to express the symmetric and skew‐symmetric components of the prefits and the Legendre polynomials used to express the gravity potential in spherical harmonics. The two sets of basis functions only noticeably differ at high latitude. Consequently, the “A‐D” geofits may still show signal at a high latitude where the symmetric component is not perfectly represented by Legendre polynomials, and thus not exactly canceled out in the “A‐D” averaging.
Figure 16.
Laser ranging interferometer (top row) and K/Ka‐band ranging (middle row) geofit range accelerations derived from the estimated geopotential monthly mean deviation from the GGM5G background model. A 25 mHz CRN temporal filter is applied. The data is averaged over 3‐degree bins; no additional spatial smoothing applied. First column: all data is averaged regardless of the direction of the satellites (“All”). Second column: the average value of the data from ascending tracks is added to the average value from descending tracks (“A + D”). Third column: the average value from descending tracks is subtracted from the average value from ascending tracks (“A‐D”). The bottom row displays the difference between the two first rows on a narrower color scale.
Figure 16 shows the LRI and KBR range‐accelerations geofits for the November 2019 solutions; these range‐acceleration geofits are obtained by smoothing and differentiating the range rate geofits using a 25 mHz temporal filter. The geofits are then averaged over 3‐degree bins. As expected, the maps of the geofits show a signal that is coherent with the mean gravity field and the difference between the KBR and LRI geofits only amounts to a few scattered speckles. The “A + D” geofits plots show approximately the same signal as the averaged geofits, with twice the amplitude. Finally, some signal coherent with the mean gravity field does appear at high latitudes in the “A‐D” geofits for both the LRI and the KBR because of the basis functions discrepancy previously described. At low and mid latitude where this discrepancy is not numerically significant, the “A‐D” geofits maps is devoid of signal.
The residual observations after gravity adjustment are labeled “postfits”. A map of “A + D” postfits should therefore show no signal coherence: all signals coherent with the monthly mean field should be adjusted by gravity field parameters. The “flatness” of the “A + D” postfits maps, therefore, shows the goodness of fit. If the “A + D” maps show residuals coherent with the gravity signals, this is normally due to a data misfit caused by inadequate parametrization or a priori constraints on the adjusted gravity parameters. The maps of “A‐D” postfits may display geographical coherent features other than the ones due the estimated monthly mean gravity field since we only adjust a mean gravity field over the time span under evaluation.
Figure 17 presents the geographical distribution of the 25 mHz‐smoothed LRI and KBR range‐acceleration postfits for the November 2019 solutions, obtained using the same CRN filter as the geofits, and averaged over the same 3‐degree bins. The maps of the averaged postfits, as well as the maps of the “A + D” postfits, show no apparent signals that are coherent with the mean gravity field, attesting to the adequacy of both the LRI and KBR solutions: all deviations from the background gravity model contained in the prefits at this spatial scale were correctly estimated and adjusted out the postfits. Here again, we observe very little difference between the LRI and KBR postfits and none of these differences are coherent with the mean gravity field. The “A‐D” postfits maps exhibit a horizontal band pattern for the LRI and KBR. This pattern is not well‐understood and was not seen on GRACE. The band pattern appears to intensify around the times when the Sun angle β’ approaches zero, possibly suggesting a system sensitivity to the Sun incidence that is not well modeled out of the prefits. Some geographically coherent signal is also visible in the “A‐D” postfits maps which can be interpreted as sub‐monthly time‐varying signal not captured by a monthly mean gravity estimate. This signal is the same in the LRI and KBR “A‐D” postfits, meaning that no solution is leaving out signal being captured by the other.
Figure 17.
Laser ranging interferometer (top row) and K/Ka‐band ranging (middle row) postfit range accelerations. A 25 mHz CRN temporal filter is applied. The data is averaged over 3‐degree bins; no additional spatial smoothing is applied. First column: all data is averaged regardless of the direction of the satellites (“All”). Second column: the average value of the data from ascending tracks is added to the average value from descending tracks (“A + D”). Third column: the average value from descending tracks is subtracted from the average value from ascending tracks (“A‐D”). The bottom row displays the difference between the two first rows on a narrower color scale.
5. Conclusions
The LRI instrument, intended as a technology demonstration instrument on board the GRACE‐FO satellites, has not only fulfilled its scientific requirements (Abich et al., 2019; Landerer, Flechtner, Save et al., 2020) but has also provided SST ranging data of the highest quality. It has made the recovery of the time‐varying gravity signal from this new data product possible through an estimation process similar to the one traditionally used for the monthly gravity solutions based on the KBR SST data. The LRI gravity estimation process employed at the CSR has been modified in two major ways to accommodate for the different nature of the LRI ranging observations. First, the parametrization of the estimation process has been altered to include two additional LRI‐related parameters: the adjustments to the scale and time‐bias corrections. Second, the weighting strategy of the double differenced GPS observations against the LRI SST observations has been revised to balance out the higher sampling rate of the LRI data. The LRI monthly gravity solutions show high consistency with their KBR counterparts. The comparison in the geographical domain shows that the same gravity signal is recovered from both sets at the GRACE spatial resolution (using a DDK3 filter) and over hydrological basins (USGS HU2, HU4). Furthermore, both sets show good correlations with the TWS anomalies from the NLDAS hydrology model over large basins (HU2). Comparison at the 270 km spatial scale only shows differences in the North‐South striations, which are thought to be linked to sub‐Nyquist sampling artifacts, and in the C20 coefficient. Though the North‐South striations in both sets of gravity solutions are not identical, they are equal in overall magnitude (in the global rms sense), suggesting that both estimation processes are equally sensitive to the sampling limitations. The difference in the C20 coefficient have been linked to the additional LRI‐related parameters that are believed to absorb some of the thrust mismodelling error along the magnetic equator in the GRACE‐FO accelerations product ACT1B, while at the same time increasing the C20 estimates formal errors of the solutions due to the correlation between the parameters. Comparison of the 180‐degree solutions from LRI and KBR reveals differences at the high degree zonals and near‐zonals, with smaller errors in the LRI solutions past degree 120. Finally, the SST postfits were analyzed as an additional quality assessment metric. The postfits from LRI and KBR are equivalent to each other, up to the KBR instrument noise frequency (approximately 10 mHz) where the spectral density of the KBR postfits starts increasing. Meanwhile, the spectrum of the LRI continues decreasing passed 10 mHz and nearly all the way to its Nyquist frequency thanks to the much lower instrument noise of the LRI. The comparative geographical analysis of the LRI and KBR postfits using the TGCOP approach also revealed that both sets of gravity solutions adequately capture the monthly gravity signal with the same overall efficiency.
We conclude that the LRI interferometer observations allows for the estimation of monthly time‐varying gravity field at least as well the microwave interferometer, with superior attributes in the spectral and temporal domains as a direct consequence of the higher precision of its observations. The resolution of the near zonal coefficients shown in this study as well as line‐of‐sight gravity analysis published by other research groups (Ghobadi‐Far, Han, McCullough et al., 2020) demonstrate the superiority of the LRI measurements over the ones of the MWI. These conclusions added to the benefits of using the LRI over the MWI, such as the great stability of the instrument itself and the low occurrence of instrument reboot events, make the LRI instrument an attractive technology for future gravity missions using intersatellite ranging as their primary observations.
Acknowledgments
The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing the computing resources that have contributed to the research results reported within this study. The authors also want to acknowledge JPL's GRACE‐FO L1 team and LRI team for their continuing collaboration. GRACE‐FO is a partnership between NASA and the Helmholtz Centre Potsdam GFZ German Research Centre for Geosciences. The twin GRACE‐FO spacecrafts are operated from the German Space Operations Center in Oberpfaffenhofen, Germany, under a GFZ contract with the German Aerospace Center. JPL manages the mission for NASA's Science Mission Directorate at NASA Headquarters in Washington. Caltech in Pasadena, California, manages JPL for NASA. This work was sponsored by JPL contract 1604489. Ellmer, Fahnestock, Landerer, McCullough, Wiese and Yuan's work represents research carried out at the Jet Propulsion Laboratory/California Institute of Technology, under a contract with the National Aeronautics and Space Administration.
Pie, N. , Bettadpur, S. V. , Tamisiea, M. , Krichman, B. , Save, H. , Poole, S. , et al. (2021). “Time variable Earth gravity field models from the first spaceborne laser ranging interferometer”. Journal of Geophysical Research: Solid Earth, 126, e2021JB022392. 10.1029/2021JB022392
Data Availability Statement
The LRI and KBR gravity field solutions created for the purpose of this study are publicly available from the Texas Data Repository: Pie (2021), "CSR GRACE‐FO LRI and KBR Gravity Solutions", https://doi.org/10.18738/T8/VZGGS2, Texas Data Repository, V1. The LRI and KBR solutions are consistently processed except for differences noted by the authors. Datasets for this research are available in these intext data citation references (GRACE‐FO, 2019; GRACE, 2018; Loomis et al., 2020; Landerer, 2020; Peltier et al., 2018; U.S. Geological Survey, 2020a, 2020b; Xia et al., 2012).
References
- Abich, K. , Abramovici, A. , Amparan, B. , Baatzsch, A. , Okihiro, B. B. , Barr, D. C. , et al. (2019). In‐orbit performance of the GRACE Follow‐on laser ranging interferometer. Physical Review Letters, 123(3). 10.1103/physrevlett.123.031101 [DOI] [PubMed] [Google Scholar]
- Argus, D. F. , Ratliff, B. , DeMets, C. , Borsa, A. A. , Wiese, D. N. , Blewitt, G. , et al. (2020). Rise of Great Lakes surface water, sinking of the upper Midwest of the United States, and viscous collapse of the forebulge of the former Laurentide ice sheet. Journal of Geophysical Research: Solid Earth, 125, e2020JB019739. 10.1029/2020JB019739 [DOI] [Google Scholar]
- Bettadpur, S. , & McCullough, C. (2017). The classical variational approach. In Naeimi M., & Flury J. (Eds.), Global gravity field modeling from satellite‐to‐satellite tracking data. Lecture notes in Earth system sciences (pp. 81–95): Springer. 10.1007/978-3-319-49941-3_3 [DOI] [Google Scholar]
- Bettadpur, S. V. , & Eanes, R. J. (1994). Geographical representation of radial orbit perturbations due to ocean tides: Implications for satellite altimetry. Journal of Geophysical Research: Oceans, 99(C12), 24883–24894. 10.1029/94JC02080 [DOI] [Google Scholar]
- Boergens, E. , Güntner, A. , Dobslaw, H. , & Dahle, C. (2020). Quantifying the Central European droughts in 2018 and 2019 with GRACE Follow‐On. Geophysical Research Letters, 47, e2020GL087285. 10.1029/2020GL087285 [DOI] [Google Scholar]
- Bonin, J. A. , & Save, H. (2020). Evaluation of sub‐monthly oceanographic signal in GRACE “daily” swath series using altimetry. Ocean Science, 16(2), 423–434. 10.5194/os-16-423-2020 [DOI] [Google Scholar]
- Cartwright, D. E. , & Tayler, R. J. (1971). New computations of the tide‐generating potential. Geophysical Journal International, 23(1), 45–73. 10.1111/j.1365-246X.1971.tb01803.x [DOI] [Google Scholar]
- Case, K. , Kruizinga, G. , & Wu, S. C. (2010). GRACE Level 1B data product user handbook, JPL D‐22027, GRACE 327‐733. Revision from https://PODAAC-tools.jpl.nasa.gov/drive/files/allData/grace/docs/Handbook_1B_v1.3.pdf [Google Scholar]
- Casotto, S. (1990). Spectral decomposition of geopotential, Earth and ocean tidal perturbations in linear satellite theory. Celestial Mechanics and Dynamical Astronomy, 50, 125–141. 10.1007/BF00051046 [DOI] [Google Scholar]
- Cassel, K. W. (2013). Variational methods with applications in science and engineering. Cambridge University Press. 10.1017/CBO9781139136860 [DOI] [Google Scholar]
- Chen, J. , Tapley, B. , Seo, K.‐W. , Wilson, C. , & Ries, J. (2019). Improved quantification of global mean ocean mass change using GRACE satellite gravimetry measurements. Geophysical Research Letters, 46, 13984–13991. 10.1029/2019gl085519 [DOI] [Google Scholar]
- Cheng, M. , & Ries, J. (2017). The unexpected signal in GRACE estimates of C20. Journal of Geodesy, 91, 897–914. 10.1007/s00190-016-0995-5 [DOI] [Google Scholar]
- Dobslaw, H. , Bergmann‐Wolf, I. , Dill, R. , Poropat, L. , & Flechtner, F. M. (2017). AOD1B description document. GFZ German Research Centre for Geosciences. Retrieved from https://PODAAC-tools.jpl.nasa.gov/drive/files/allData/grace/docs/AOD1B_PDD_RL06_v6.1.pdf [Google Scholar]
- Dobslaw, H. , Bergmann‐Wolf, I. , Dill, R. , Poropat, L. , Thomas, M. , Dahle, C. , et al. (2017). A new high‐resolution model of non‐tidal atmosphere and ocean mass variability for de‐aliasing of satellite gravity observations: AOD1B RL06. Geophysical Journal International, 211(1), 263–269. 10.1093/gji/ggx302 [DOI] [Google Scholar]
- Egbert, G. D. , & Ray, R. D. (2003). Deviation of long‐period tides from equilibrium: Kinematics and geostrophy. Journal of Physical Oceanography, 33, 822–839. [DOI] [Google Scholar]
- Ghobadi‐Far, K. , Han, S.‐C. , Allgeyer, S. , Tregoning, P. , Sauber, J. , Behzadpour, S. , et al. (2020). GRACE gravitational measurements of tsunamis after the 2004, 2010, and 2011 great earthquakes. Journal of Geodesy, 94(65). 10.1007/s00190-020-01395-3 [DOI] [Google Scholar]
- Ghobadi‐Far, K. , Han, S.‐C. , McCullough, C. M. , Wiese, D. N. , Yuan, D.‐N. , Landerer, F. W. , et al. (2020). GRACE Follow‐On laser ranging interferometer measurements uniquely distinguish short‐wavelength gravitational perturbations. Geophysical Research Letters, 47, e2020GL089445. 10.1029/2020GL089445 [DOI] [Google Scholar]
- Girotto, M. , & Rodell, M. (2019). Terrestrial water storage. In Maggioni V., & Massari C. (Eds.), Extreme hydroclimatic events and multivariate hazards in a changing environment (pp. 41–64). Elsevier. 10.1016/B978-0-12-814899-0.00002-X [DOI] [Google Scholar]
- GRACE . (2018). GRACE_GSM_L2_GRAV_CSR_RL06. Version 6.0. PO.DAAC. 10.5067/GRGSM-20C06 [DOI] [Google Scholar]
- GRACE‐FO . (2019). GRACE‐FO level‐1B Release version 4.0 from JPL in ASCII. Version 4. PO.DAAC. 10.5067/GFL1B-ASJ04 [DOI] [Google Scholar]
- Gunter, B. C. (2004). Computational methods and processing strategies for estimating Earth’s gravity field (Thesis Ph. D.). University of Texas at Austin. Retrieved from http://hdl.handle.net/2152/1318 [Google Scholar]
- Gunter, B. C. , Riva, R. E. M. , Urban, T. , Harpold, R. , Schutz, B. , Nagel, P. , & Helsen, M. (2010). Evaluation of GRACE and ICESat mass change estimates over Antarctica. In Mertikas S. (Ed.), Gravity, geoid and Earth observation. International association of geodesy Symposia (Vol. 135, pp. 563–569): Springer. 10.1007/978-3-642-10634-7_75 [DOI] [Google Scholar]
- Haines, B. , Bar‐Sever, Y. , Bertiger, W. , Desai, S. , & Willis, P. (2004). One‐centimeter orbit determination for Jason‐1: New GPS‐based strategies. Marine Geodesy, 27(1–2), 299–318. 10.1080/01490410490465300 [DOI] [Google Scholar]
- IERS Conventions . (2010). IERS Technical Note 36. In Petit G., & Luzum B. (Eds.), Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie (p. 179). Retrieved from https://www.iers.org/SharedDocs/Publikationen/EN/IERS/Publications/tn/TechnNote36/tn36.pdf [Google Scholar]
- IERS Conventions . (2018). Chapter 7 (updated): Displacement of reference points. Retrieved from https://iers-conventions.obspm.fr/content/chapter7/icc7.pdf [Google Scholar]
- Jungclaus, J. H. , Fischer, N. , Haak, H. , Lohmann, K. , Marotzke, J. , Matei, D. , et al. (2013). Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI‐Earth system model. Journal of Advances in Modeling Earth Systems, 5, 422–446. 10.1002/jame.20023 [DOI] [Google Scholar]
- Kang, Z. , Bettadpur, S. , Nagel, P. , Save, H. , Poole, S. , & Pie, N. (2020). GRACE‐FO precise orbit determination and gravity recovery. Journal of Geodesy, 94(85). 10.1007/s00190-020-01414-3 [DOI] [Google Scholar]
- Kim, J. (2000). Simulation study of a low‐low satellite‐to‐satellite tracking mission. Thesis (Ph. D.). University of Texas at Austin. 10.26153/tsw/12695 [DOI] [Google Scholar]
- Kornfeld, R. P. , Arnold, B. W. , Gross, M. A. , Dahya, N. T. , Klipstein, W. M. , Gath, P. F. , & Bettadpur, S. (2019). GRACE‐FO: The gravity recovery and climate experiment follow‐on mission. Journal of Spacecraft and Rockets, 56(3), 931–951. 10.2514/1.A34326 [DOI] [Google Scholar]
- Kusche, J. (2007). Approximate decorrelation and non‐isotropic smoothing of time‐variable GRACE‐type gravity field models. Journal of Geodesy, 81, 733–749. 10.1007/s00190-007-0143-3 [DOI] [Google Scholar]
- Landerer, F. W. (2020). Monthly estimates of degree‐1 (geocenter) gravity coefficients, generated from GRACE (04‐2002‐06/2017) and GRACE‐FO (06/2018 onward) RL06 solutions. Retrieved from https://PODAAC-tools.jpl.nasa.gov/drive/files/allData/grace/docs/TN-13_GEOC_CSR_RL06.txt [Google Scholar]
- Landerer, F. W. , Flechtner, F. M. , Bettadpur, S. , McCullough, C. , Save, H. & Dahle, C. (2020). GRACE‐FO mission status. GRACE/GRACE‐FO Science Team Meeting, online, 2020, October–29 Oct 2020, GSTM2020‐74. 10.5194/gstm2020-74 [DOI]
- Landerer, F. W. , Flechtner, F. M. , Save, H. , Webb, F. H. , Bandikova, T. , Bertiger, W. I. , et al. (2020). Extending the global mass change data record: GRACE Follow‐On instrument and science data performance. Geophysical Research Letters, 47, e2020GL088306. 10.1029/2020GL088306 [DOI] [Google Scholar]
- Landerer, F. W. , Wiese, D. N. , Bentel, K. , Boening, C. , & Watkins, M. M. (2015). North Atlantic meridional overturning circulation variations from GRACE ocean bottom pressure anomalies. Geophysical Research Letters, 42, 8114–8121. 10.1002/2015GL065730 [DOI] [Google Scholar]
- Loomis, B. D. , Rachlin, K. E. , Wiese, D. N. , Landerer, F. W. , & Luthcke, S. B. (2020). Replacing GRACE/GRACE‐FO C30 with satellite laser ranging: Impacts on Antarctic Ice Sheet mass change. Geophysical Research Letters, 47. 10.1029/2019GL085488 [DOI] [Google Scholar]
- McCullough, C. M. (2017). Gravity field estimation for next generation satellite missions. Thesis (Ph. D.). University of Texas at Austin. 10.15781/T2TH8BX4W [DOI] [Google Scholar]
- McCullough, C. M. , Harvey, N. , Save, H. , & Bandikova, T. (2019). Description of calibrated GRACE‐FO accelerometer data products (ACT), JPL D‐103863. Retrieved from https://PODAAC-tools.jpl.nasa.gov/drive/files/allData/gracefo/docs/GFO.ACT.JPL-D-103863.20190520.pdf [Google Scholar]
- Peidou, A. , & Pagiatakis, S. (2020). Stripe mystery in GRACE geopotential models revealed. Geophysical Research Letters, 47. 10.1029/2019GL085497 [DOI] [Google Scholar]
- Peltier, W. R. , Argus, D. F. , & Drummond, R. (2018). Comment on “An assessment of the ICE‐6G_C (VM5a) glacial isostatic adjustment model” by Purcell et al. Journal of Geophysical Research: Solid Earth, 123, 2019–2028. 10.1002/2016JB013844 [DOI] [Google Scholar]
- Petrovskaya, M. , Vershkov, A. , & Pavlis, N. (2001). New analytical and numerical approaches for geopotential modeling. Journal of Geodesy, 75, 661–672. 10.1007/s001900100215 [DOI] [Google Scholar]
- Pie, N. (2021). CSR GRACE‐FO LRI and KBR gravity solutions, version 1. Texas Data Repository. 10.18738/T8/VZGGS2 [DOI] [Google Scholar]
- Ray, R. D. , & Cartwright, D. E. (1994). Satellite altimeter observations of the Mf and Mm ocean tides, with simultaneous orbit corrections. In Schutz B. E., Anderson A., Froidevaux C., & Parke M. (Eds.), Gravimetry and Space techniques applied to Geodynamics and ocean dynamics. (pp. 69–78). AGU Books Board. 10.1002/9781118666647.ch6 [DOI] [Google Scholar]
- Rosborough, G. W. (1986). Satellite orbit perturbations due to the geopotential. Thesis (Ph. D.). University of Texas at Austin. 10.26153/tsw/12697 [DOI] [Google Scholar]
- Rosborough, G. W. , & Tapley, B. D. (1987). Radial, transverse and normal satellite position perturbations due to the geopotential. Celestial Mechanics, 40, 409–421. 10.1007/BF01235855 [DOI] [Google Scholar]
- Save, H. (2019). CSR Level‐2 processing standards document for Level‐2 product Release 06, CSR GRFO‐19‐01 (GRACE‐FO D‐103920). Retrieved from https://podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo/docs/GRACE-FO_L2-CSR_ProcStds_v1.1.pdf [Google Scholar]
- Save, H. (2020). Science operations report, GRACE/GRACE‐FO Science Team Meeting, online, 27–29 Oct 2020, GSTM2020–79. 10.5194/gstm2020-79 [DOI]
- Scanlon, B. R. , Zhang, Z. , Save, H. , Wiese, D. N. , Landerer, F. W. , Long, D. , et al. (2016). Global evaluation of new GRACE mascon products for hydrologic applications. Water Resources Research, 52, 9412–9429. 10.1002/2016wr019494 [DOI] [Google Scholar]
- Scanlon, B. R. , Zhang, Z. , Save, S. , Sun, A. Y. , Schmied, H. M. , van Beek, L. P. H. , et al. (2018). Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data. Proceedings of the National Academy of Sciences, 115(6), 1080–1089. 10.1073/pnas.1704665115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, M. S. (2018). Utilization of simulated GRACE inter‐satellite range‐accelerations to estimate Earth's gravity field. Thesis (M.S. in Aerospace Engineering). University of Texas at Austin. 10.26153/tsw/1302 [DOI] [Google Scholar]
- Tapley, B. D. , Bettadpur, S. , Watkins, M. , & Reigber, C. (2004). The gravity recovery and climate experiment: Mission overview and early results. Geophysical Research Letters, 31, L09607. 10.1029/2004GL019920 [DOI] [Google Scholar]
- Tapley, B. D. , & Born, G. H. (1971). Sequential estimation of the state and the observation‐error covariance matrix. AIAA Journal, 9(2), 212–217. 10.2514/3.6153 [DOI] [Google Scholar]
- Tapley, B. D. , Schutz, B. E. , & Born, G. H. (2004). Fundamentals of orbit determination. In Tapley B. D., Schutz B. E., & Born G. H. (Eds.), Statistical orbit determination (pp. 159–284). Elsevier Academic Press. 10.1016/B978-012683630-1/50023-0 [DOI] [Google Scholar]
- Tapley, B. D. , Watkins, M. M. , Flechtner, F. M. , Reigber, C. , Bettadpur, S. , Rodell, M. , et al. (2019). Contributions of GRACE to understanding climate change. Nature Climate Change, 9, 358–369. 10.1038/s41558-019-0456-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tregoning, P. , Purcell, A. P. , Allgeyer, S. , & McQueen, H. (2017). The role of range acceleration observations and regularisation in the estimation of sub‐monthly temporal gravity fields f rom GRACE observations. Poster presented at American geophysical union, Fall 2017, new Orleans, LA. Abstract G31B‐0403. Retrieved from https://agu.confex.com/agu/fm17/meetingapp.cgi/Paper/263271 [Google Scholar]
- U.S. Geological Survey . (2020a). National hydrography dataset for hydrologic unit (HU4). Retrieved from https://www.usgs.gov/core-science-systems/ngp/national-hydrography/access-national-hydrography-products [Google Scholar]
- U.S. Geological Survey . (2020b). Watershed boundary dataset for hydrologic unit (HU2). Retrieved from https://www.usgs.gov/core-science-systems/ngp/national-hydrography/access-national-hydrography-products [Google Scholar]
- Wallace, M. S. (2005). A comparison of range and range‐rate measurements for the generation of the GRACE gravity fields. Thesis (M.S. in Aerospace Engineering). University of Texas at Austin. 10.26153/tsw/13249 [DOI] [Google Scholar]
- Wen, H. Y. , Kruizinga, G. , Paik, M. , Landerer, F. W. , Bertiger, W. , Sakumura, C. , et al. (2019). GRACE‐FO Level‐1 data product user handbook, JPL D‐56935. Retrieved from https://podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo/docs/GRACE-FO_L1_Handbook.pdf [Google Scholar]
- Xia, Y. , Mitchell, K. , Ek, M. , Sheffield, J. , Cosgrove, B. , Wood, E. , et al. (2012). NCEP/EMC. In Mocko D. (Ed.), NLDAS Noah land Surface model L4 hourly 0.125 x 0.125 degree V002. NASA/GSFC/HSL. Goddard Earth Sciences Data and Information Services Center (GES‐DISC). 10.5067/47Z13FNQODKV [DOI] [Google Scholar]
- Xu, P. , Wang, L. , Liu, Y. , Chen, W. , & Huang, P. (2020). The record‐breaking heat wave of June 2019 in Central Europe. Atmospheric Science Letters, 21, e964. 10.1002/asl.964 [DOI] [Google Scholar]
- Yuan, D.‐N. (1991). The determination and error assessment of the Earth’s gravity field model. Thesis (Ph. D.). University of Texas at Austin. 10.26153/tsw/12696 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The LRI and KBR gravity field solutions created for the purpose of this study are publicly available from the Texas Data Repository: Pie (2021), "CSR GRACE‐FO LRI and KBR Gravity Solutions", https://doi.org/10.18738/T8/VZGGS2, Texas Data Repository, V1. The LRI and KBR solutions are consistently processed except for differences noted by the authors. Datasets for this research are available in these intext data citation references (GRACE‐FO, 2019; GRACE, 2018; Loomis et al., 2020; Landerer, 2020; Peltier et al., 2018; U.S. Geological Survey, 2020a, 2020b; Xia et al., 2012).


