Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2022 Apr 5;49(7):e2021GL097697. doi: 10.1029/2021GL097697

Can Surface Soil Moisture Information Identify Evapotranspiration Regime Transitions?

Jianzhi Dong 1,2,✉, Ruzbeh Akbar 1, Daniel J Short Gianotti 1, Andrew F Feldman 3,4, Wade T Crow 5, Dara Entekhabi 1,6
PMCID: PMC9286566  PMID: 35865657

Abstract

The transition of evapotranspiration between energy‐ and water‐limitation regimes also denotes a nonlinear change in surface water and energy coupling strength. The regime transitions are primarily dominated by available moisture in the soil, although other micro‐meteorological factors also play a role. Remotely sensed soil moisture is frequently used for detecting evapotranspiration regime transitions during inter storm dry downs. However, its sampling depth does not include the entire soil profile, over which water uptake is dominated by plant root distribution. We use flux tower, surface (θ s ; observations at 5 cm), and vertically integrated in situ soil moisture (θv; 0–50 cm) observations to address the question: Can surface soil moisture robustly identify evapotranspiration regime transitions? Results demonstrate that θ s and θ v are hydraulically linked and have synchronized evapotranspiration regime transitions. As such, θ s and θ v capture comparable statistics of evapotranspiration regime prevalence, which supports the utility of remote‐sensing θ s for large‐scale land‐atmosphere exchange analysis.

Key Points

  • Observation‐based analysis shows that surface and root zone soil moisture are consistent in evapotranspiration regime identification

  • During interstorm drydowns, surface soil moisture availability signifies the transition from energy‐ to water‐limited regime

  • We demonstrate the general reliability of earth‐orbit retrieved surface soil moisture for large‐scale land‐atmosphere interaction studies

1. Introduction

Soil moisture is the primary variable controlling land surface water and energy balance coupling (Dirmeyer et al., 2000; Entekhabi et al., 1996). Specifically, during extended periods without precipitation, soil moisture falls below a threshold value—leading to a transition from energy‐ to water‐limited evapotranspiration regimes (Feldman et al., 2020; Haghighi et al., 2018; Seneviratne et al., 2010). Under water‐limited regimes, evapotranspiration is reduced with decreased soil moisture, which results in increased sensible heating of the lower atmosphere (Berg et al., 2014; Seneviratne et al., 2010). As a result, the transitions between different evapotranspiration regimes regulate the development of the boundary layer at hydrometeorological timescales and the onset of heatwaves on hydroclimatological timescales (Feldman et al., 2019; Koster et al., 2019; Yuan et al., 2019).

Passive microwave remote sensing (radiometry) is used for sensing soil moisture dynamics at the global scale (Entekhabi et al., 2010; Kerr et al., 2010; Wagner et al., 1999). These data sets allow—for the first time—a global view of soil moisture dynamics, enabling identification of global distributions and transitions between energy‐ and water‐limited evapotranspiration regimes. For example, Denissen et al. (2020) uses the merged multi‐satellite European Space Agency Climate Change Initiative soil moisture product and FluxCOM evapotranspiration data set to quantify the spatial distribution of the threshold soil moisture values over Europe. Likewise, Crow et al. (2015) combine multisensory soil moisture and evapotranspiration products to estimate the overall coupling strength of evapotranspiration and soil moisture, which implicitly reflects the occurrence frequency of water‐limited regimes at a given location. This method is further employed for diagnosing numerical weather forecasting systems (Crow et al., 2020), land surface models (Dong et al., 2020), and Earth system models (Dong et al., 2022). Recently, Akbar, Gianotti, et al. (2018) demonstrate that L‐band retrieved soil moisture drydown patterns can be decoded to quantify daily evapotranspiration regime transitions. This approach is noteworthy since it only uses soil moisture data, which relaxes the requirement for high‐quality evapotranspiration data. Their soil moisture drydown analysis has been recently extended to the global scale and applied to flash drought monitoring (Sehgal et al., 2021a, 2021b).

All of these studies are based on remote sensing soil moisture measurements that have, at best, a sampling depth of less than ∼10 and ∼5 cm more typically (Njoku & Kong, 1977; Ulaby et al., 1978). They are thus essentially analyzing land‐atmosphere coupling processes using only the dynamics of surface soil moisture (θ s ). However, plant roots can reach to soil water storages at several tens of centimeters and for certain limited species, to tens of meters (Fan et al., 2017; Gao et al., 2014; Yang et al., 2016). Therefore, evapotranspiration can draw water from soil layers that are considerably deeper than the θ s sampling depth (Buitink et al., 2020; Green et al., 2019; Humphrey et al., 2021; Li et al., 2021). Based on this line of reasoning, the expectation is that θ s is likely biased in its representation of evapotranspiration regime transitions or overall land surface energy partitioning (Hirschi et al., 2014; Mueller & Seneviratne, 2012). Indeed, a recent study shows that θ s ‐based thresholds of soil moisture for separating energy and water limited regimes (denoted as θ ∗) are biased low versus those for root zone soil moisture (Buitink et al., 2020).

In contrast, recent studies argue that θ s and root zone soil moisture temporal dynamics are tightly correlated due to their hydraulic connectivity (Akbar, Short Gianotti, et al., 2018; Albergel et al., 2008; Dong & Crow, 2018; Short Gianotti et al., 2019) and, hence, tend to reflect similar surface energy balance information (Qiu et al., 2016, 2020).

Therefore, a natural question is whether evapotranspiration regime transitions are evident in remotely sensed θ s . Specifically, is deeper soil moisture information absolutely necessary to correctly identify the evapotranspiration regime transitions?

In order to address this question, we take an observation‐driven approach to assess evapotranspiration regime transitions (as deduced from flux tower measurements and in situ soil moisture sensors) based on θ s (measured at 5 cm depth) and a vertically integrated profile soil moisture (θ v , from 0 to 50 cm profile). We quantify the degree of consistency in evapotranspiration regime transitions based on these two soil moisture series at sites in the continental United States. In this way, we provide observational evidence for the consistency of θ s ‐ and θ v ‐based evapotranspiration regime transitions and clarify the utility of remotely sensed surface soil moisture for large‐scale land‐atmosphere exchange analysis.

2. Data and Method

Water‐ and energy‐limited evapotranspiration regimes are identified based on volumetric soil water content (θ) and a threshold value θ ∗, that is, as θ < θ ∗ and θ ≥ θ ∗, respectively. Approaches for determining θ ∗ and evapotranspiration regime transitions are outlined in Sections 2.1 and 2.2. Our analysis is entirely based on in situ observations. Given the general data availability, this study uses 0–50 cm vertically integrated soil moisture (θ v ) to represent root zone temporal dynamics. There are, of course, exceptions where certain plants have adapted to frequent water stress by extending roots into far deeper soil layers and approaching underground aquifers (Fan et al., 2017; Gao et al., 2014). Nonetheless, for most ecosystems, more than 75% of vegetation roots are located in the top 50 cm of the soil column (Zeng, 2001), and soil moisture availability above 30 cm is most responsible for vegetation dynamics (Li et al., 2021). Therefore, θ v is expected to be representative of the general vegetation root water stress conditions.

As noted above, to demonstrate the robustness of our findings, two independent approaches are employed for θ ∗ determination. The first approach is based on turbulent fluxes measured by eddy‐covariance systems and high‐quality soil moisture profile observations (Section 2.1). The second approach is based on soil moisture drydown analysis alone (Akbar et al., 2018), which can be extended to, far more numerous, soil moisture in situ measurement locations lacking colocated flux towers.

2.1. Flux‐Tower Based ET Regime Identification

Land surface partitioning of available energy for exchange with the overlying atmosphere can be characterized using the non‐dimensional evaporative fraction (EF)

EF=LELE+SH (1)

where LE and SH are daily mean latent and sensible heat fluxes (W/m2), respectively. Clearly, EF values are unstable when its denominator is close to zero. Therefore, only days with both LE and SH values greater than 1 W/m2 are considered in this study.

EF is affected by a number of environmental factors, but soil moisture status dominates the day‐to‐day EF variations, especially in water‐limited locations (Lu et al., 2016). Contrasting EF sensitivities to soil moisture variations are evident in the energy‐limited (θ ≥ θ ∗, zero slope) and water‐limited (θ < θ ∗, positive slope) regimes (Dirmeyer et al., 2000; Haghighi et al., 2018; Lu et al., 2016). Therefore, the threshold θ ∗ can be identified by fitting a piece‐wise linear function to the observed θ‐EF relationship. Once the θ ∗ value is determined, the temporal transitions of different ET regimes can be identified according to the variations of θ with respect to θ ∗.

Observations from the AmeriFlux US‐Ton site (38.43°N−120.96°W, see Figure 1 inset) located in California are used here for demonstration (Ma et al., 2016). This site is selected because it provides high‐quality LE, SH, and soil moisture profile observations (available at 5, 20, and 50 cm depths for the woody savanna site) throughout the extended 2000–2020 period. More importantly, this site is characterized by a Mediterranean climate with frequent evapotranspiration regime transitions. In addition, dry‐wet transitional climate conditions are typically associated with strong temporal variations in rooting depth, which maximize the difference of θ s ‐ and θ v ‐characterized vegetation water availability (Fan et al., 2017; Gao et al., 2014). Therefore, this site is ideal for rigorously testing the consistency of θ s ‐ and θ v ‐identified evapotransption regimes. Note that the US‐Ton site has observations for both grass and wood savanna land cover types. However, only top 20 cm soil moisture values are measured for the grass site and hence, we focus on observations from the woody savanna.

Figure 1.

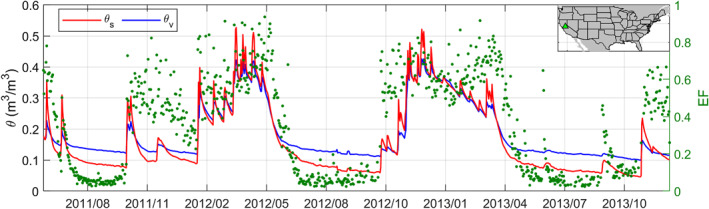
Figure 1

Open in a new tab

Example time series of θ s and θ v , and evaporative fraction (EF) at the US‐Ton site (Ma et al., 2016). The location of US‐Ton site is shown in the upper right map. Due to the relatively complete soil moisture profile measurement, flux tower and soil moisture observations for the woody savanna land cover type are used here for demonstration.

We acknowledge that the US‐Ton site is not representative of woody forest and humid climate conditions. However, as mentioned above, forest sites with complete soil moisture profile (top 50 cm) observations are very limited. In addition, humid regions dominated by energy‐limited regimes have limited value for characterizing the evapotranspiration regime fluctuations. Nonetheless, evapotranspiration regime analysis based on various land cover types and climate conditions are comprehensively analyzed based on high‐quality soil moisture networks in the following section.

2.2. Evapotranspiration Regime Identification From Soil Moisture Drydown Analysis

Soil moisture losses on nonprecipitation days are dominated by water‐ and energy‐limited evapotranspiration, and drainage dominated hydrological regimes, which can be quantified as a piecewise linear function (Laio et al., 2001). Therefore, once the functional form of soil moisture losses has been optimized, the associated θ ∗ values are also implicitly determined. In this study, the soil moisture drydown analysis is performed using the existing framework proposed by Akbar, Gianotti, et al. (2018).

Soil moisture profile observations from Soil Climate Analysis Network (SCAN) and U.S. Climate Reference Network (USCRN) are used for soil moisture loss analysis. Likewise, measurements at the 5 cm and 0–50 cm averaged daily soil moisture values are used for representing θ s and θ v temporal dynamics, respectively. We limit ourselves to sites with at least 5 years of available measurements during the 2010–2021 period. In addition, given θ s is theoretically more sensitive to meteorological forcing (Albergel et al., 2008), sites with θ v standard deviations higher than that of θ s are excluded. Overall, 114 stations are used and their spatial distributions are shown in Figure 3.

Figure 3.

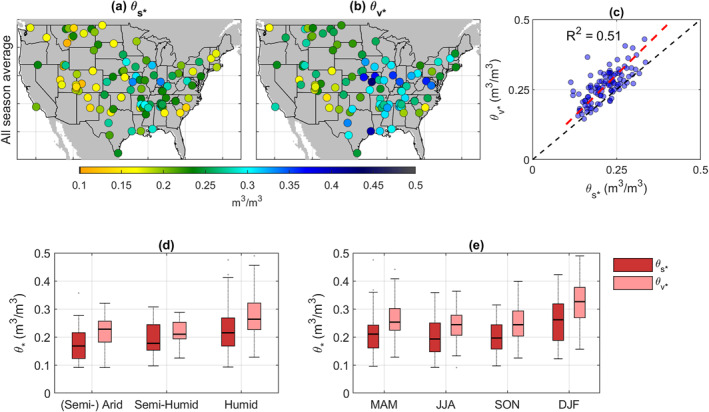
Figure 3

Open in a new tab

Spatial distribution of θ s ‐ and θ v ‐based θ ∗ estimates, denoted as θs∗ and θv∗, respectively (parts a and b). The spatial consistency of θs∗ and θv∗ is shown in c, with each symbol denoting θ ∗ estimates from a particular site. Red dashed line in part c denotes the relationship of θs∗ and θv∗ based on total least squares linear regression (slope is 1.18 and the intercept is 0.0076 m3/m3). The impacts of local climate and seasonality on θ ∗ are shown in parts d and e, respectively. Note that both θs∗ and θv∗ are estimated separately for each season and all‐season‐averages are presented in parts (a–d). The (Semi‐) Arid, Semi‐Humid, and Humid climate zones are classified as land areas with aridity index (calculated as the ratio of annual mean precipitation and potential evapotranspiration) lower than 0.5, 0.5–0.65, and higher than 0.65, respectively.

To minimize the impact of seasonal variations in vegetation and climate on soil moisture losses (Feldman et al., 2019; Haghighi et al., 2018; Sehgal et al., 2021b), soil moisture drydown analyses are performed separately for each season. Note that θ ∗ cannot be estimated for sites dominated by either water‐ or energy‐limited regimes. Figure S1 in Supporting Information S1 shows the stations that do not consistently reflect both regimes and, therefore, cannot be used to estimate θ ∗.

Soil moisture loss analysis requires high‐quality precipitation data to identify dry down time series. To do so, we use the global, daily 0.1‐degree Multi‐Source Weighted‐Ensemble Precipitation product (Beck et al., 2019). This product combines gauge‐based, remote‐sensing, and reanalyzed precipitation estimates. Therefore, it is more accurate than traditional gridded precipitation estimates over the continental US.

2.3. The Consistency of θ s and θ v Identified Evapotranspiration Regimes

To evaluate the general consistency of θ s ‐ and θ v ‐based evapotranspiration regime identification, two metrics are used. The first metric is the probability of θ ≤ θ ∗ (denoted as γ), which quantifies the incidence of the water‐limited regime

γ=nw/n (2)

where n w is the number of days when θ is lower than θ ∗ (i.e., water‐limited regime) and n is the total number of days with valid observations. The θ s ‐ and θ v ‐based γ values are calculated on site‐by‐site bases for each season, which are subsequently used for quantifying the consistency of θ s ‐ and θ v ‐based evapotranspiration regime identification.

In addition, a consistency metric π is defined and used to compare θ s and θ v estimated evapotranspiration regimes, calculated as

π=nc/n (3)

where n c is the number of days that θ s and θ v identify the same evapotranspiration regime. Clearly, π ranges from zero to one, and π = 1 indicates that θ s and θ v are identical in regime identification.

3. Results and Discussions

3.1. Flux Tower‐Based Analysis

Figure 1 shows an example times series of observed EF, θ s , and θ v . The demonstration is for a 2 year sub‐sample of the 20 years of US‐Ton flux tower and soil moisture sensor data. As expected, θ s and θ v dry‐wet temporal variabilities are tightly correlated (Short Gianotti et al., 2019). As a result, both θ s and θ v can capture similar intra‐ and inter‐seasonal variations of EF—reflecting the time‐varying control of soil moisture on land surface energy partitioning.

Interestingly, it is at least visually evident that θ s can be better suited in capturing the short‐term EF variations, compared to θ v . For instance, sharply increased EF is observed in September 2013—suggesting an increase in evapotranspiration water availability. Such evapotranspiration water availability change is clearly captured by θ s , but not by θ v . This may suggest that θ s is the primary water source for soil evaporation and canopy transpiration at this site, and subsurface soil moisture has limited evapotranspiration information. As a result, integrating soil moisture information from deeper soil layers may even degrade evapotranspiration information contained in θ s . This finding is consistent with a recent flux tower‐based study, which demonstrates that θ s tend to contain higher EF information than that of θ v , even sampled across various climate and vegetation conditions (Qiu et al., 2020).

Figure 2 provides a quantitative comparison of θ s ‐ and θ v ‐based evapotranspiration regime identification for the site shown in Figure 1. The scatterplot of observed θ s and EF demonstrate a clear nonlinear relationship, which signifies the transition of water‐ and energy‐limited evapotranspiration regimes as a function of soil water availability (Figure 2a). Based on this θ s ‐EF relationship, the optimal θ ∗ can be determined and used for quantifying the temporal variations of evapotranspiration regimes, defined as θs∗ (Figure 2a). Relative to θ s , θ v contains lower temporal dynamics and is typically wetter in dry months (Figure 1). Therefore, θv∗ is higher than that of θs∗ (Figure 2b), which is consistent with a previous study (Buitink et al., 2020).

Figure 2.

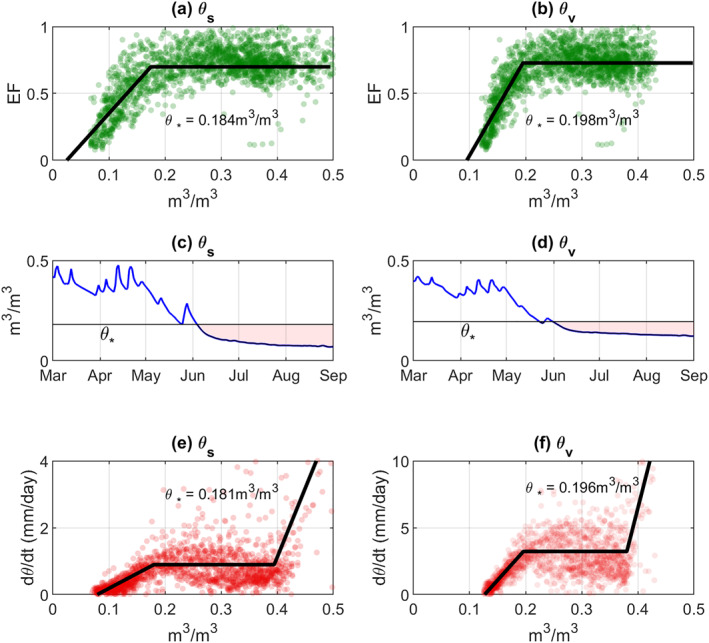
Figure 2

Open in a new tab

Evaporative fraction (EF) as a function of θ s (a) and θ v (b) at the Tonzi Ranch (US‐Ton) example site. Parts (c) and (d) are θ s ‐ and θ v ‐based evapotranspiration regime classification from March 2010 to September 2010 (with red shadings denote the water‐limited regime), respectively. The θ ∗ values, estimated solely based on soil moisture temporal dynamics via dry down analysis, are shown in parts (e) and (f). Observations during 2000–2020 March‐April‐May months are used for the θ ∗ analysis (i.e., parts a, b, e and f), with thick black lines indicating optimized hydrological regimes (Section 2.1).

However, the degree to which θ s and θ v capture the same evapotranspiration regime transitions (with π approaching 1) depends not only on the absolute value of the soil moisture threshold θ ∗, but also on the marginal probability distribution of the corresponding soil moisture time series. It is clear that both θ ∗ values and the statistical distributions of θ s and θ v are different. Ultimately, the question is whether landscape evapotranspiration regimes identified by θ s and θ v are mutually consistent?

To address this question, Figures 2c and 2d provide an illustrative example of θ s ‐ and θ v ‐based regimes identification. They show that θ s and θ v are equivalent in terms of capturing the onset and the development of evapotranspiration water stress, that is, the transition from an energy‐to water‐limited regime (see the red shaded area). As sampled across the entire 2000–2020 period, the binary consistency (π) of θ s ‐ and θ v ‐based regimes classification is 0.97. Therefore, it appears that although θ s and θ v time series contain systematic differences, their evapotranspiration regime identification is consistent. This implies a generally shape‐preserving transformation between surface and column‐average soil moisture dynamics at the daily timescale (Short Gianotti et al., 2019).

3.2. Soil Moisture Drydown Based Evapotranspiration Regime Identification

Soil moisture dry down analysis based evapotranspiration regime identification is illustrated in Figures 2e and 2f using the same US‐Ton site. The three segments of the piecewise linear function (defined by the state‐dependent loss rate of dθ/dt and θ) denote the water‐ and energy‐limited evapotranspiration and drainage dominated hydrological regimes, respectively. It is noteworthy that θ ∗ derived from θ‐EF relationship and dry down analysis are highly consistent (compare reported θ ∗ values in Figures 2a and 2e as well as Figures 2b and 2f). Comparisons of these two methods at additional sites can be found in Figure S2 in Supporting Information S1. These results suggest that soil moisture drydown analysis is a viable tool for evapotranspiration regime identification.

Figure 3 shows θ ∗ estimates over 114 soil moisture sites. For brevity, we focus on the seasonal average of θ ∗ estimates, and the temporal variability of θ ∗ is shown in Figure 3e. Both θs∗ and θv∗ demonstrate a clear west‐east gradient (Figures 3a and 3b), which reflects climatic influence on θ ∗ (Figure 3d). The geographic distributions of θs∗ and θv∗ are highly consistent, with a spatial correlation of 0.71 (coefficient of determination R 2 = 0.51, Figure 3c). However, there is a shift (bias) between θs∗ and θv∗ as evident in Figure 3c—indicating transitions typically occurring at lower θ s and higher θ v contents.

Although θ ∗ values and temporal dynamics contain systematic differences, θ s ‐ and θ v ‐based evapotransparition regimes are highly consistent. Across all seasons and all sites, the correlation of θ s ‐ and θ v ‐based γ (the incidence of water‐limited regime) is 0.72 and the relative difference is 8.5% (Figure 4a). Likewise, the spatially averaged binary consistency (π) of θ s ‐ and θ v ‐based evapotranspiration regime classification also exceeds 0.8 for all four seasons (Figure 4b). Given the uncertainties in soil moisture observations (Chen et al., 2016) and θ ∗ estimation (Akbar, Gianotti, et al., 2018), the consistency of θ s ‐ and θ v ‐based results are remarkable. Therefore, it appears that θ ∗ adjusts to the amplitude of soil moisture dynamics, which yields consistent evapotranspiration regime identification based on either θ s or θ v .

Figure 4.

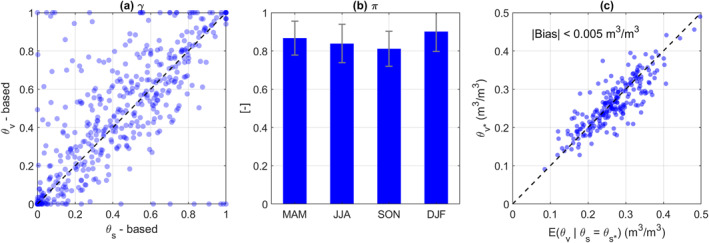
Figure 4

Open in a new tab

The consistency of θ s ‐ and θ v ‐based evapotranspiration regime identification as evaluated using both γ (a) and π (b). γ is the fraction of time spent in the water‐limited regime (integrating the moisture threshold and marginal distribution). π quantifies the consistency of θ s ‐ and θ v ‐identified day‐to‐day evapotranspiration regime transition. Note that part a includes γ values from all seasons and all sites. Error bars in part b denote the standard deviation of π across all available sites for a particular season. Part c shows the comparison of θ ∗ directly estimated by θ v drydown analysis (i.e., θv∗) and conditionally averaged θ v when θ s reaches θs∗.

Figure 4c provides a candidate explanation for the observed consistency between θ s and θ v ‐based evapotranspiration regime identification. The soil moisture profile during dry downs starts to deplete from the surface layer, due to the dual action of bare soil evaporation and transpiration by shallow roots near the surface (see Figure 1). Therefore, during inter‐storm dry downs, the onset of water stress should start from the surface and first become evident in the θ s time series. At this time, subsurface soil layers are likely still under the energy‐limited regime. Therefore, the start of the energy‐ to water‐limited regime transition of the soil profile is determined by the time when θ s drops to θs∗. The question is if the hydraulic connectivity in the profile results in a nearly synchronized transition of θ v to its threshold value (i.e., θv∗) as well.

The consistency that the transitions are closely coupled for the surface and the integrated profile can be quantified by assessing how close is θ v to its threshold θv∗ at the time θ s reaches its threshold θs∗, that is, whether θv∗=Eθv|θs=θs∗?

Figure 4c shows that Eθv|θs=θs∗ and θ v drydown analysis estimated θv∗ are highly consistent and unbiased. This directly explains why θ s ‐ and θ v ‐based evapotranspiration regime identification is so highly consistent.

Note that Figure 4 is not representative of cases with strongly decoupled surface and subsurface soil moisture dynamics (Scott et al., 2008). For instance, cases where θ s is constantly dominated by water‐limited regimes, whereas θ v indicates a wet and energy‐limited regime (see Figure S1 in Supporting Information S1). For those cases, θ s may be a better indicator of evapotranspiration regime—given that θ v cannot capture the water stress of soil evaporation or vegetation roots in the surface soil layer. Likewise, in nature, site‐dependent layered pedology, xeric plants with deep root taps, macropores and groundwater dynamics may complicate the connections of surface and subsurface hydraulic links (Kramer & Boyer, 1995). However, these conditions may be only applicable to very limited cases, given that θ s and θ v are broadly consistent in their classification of evapotranspiration regime transitions (Figures 2 and 4).

4. Conclusion

Transitions between water‐ and energy‐limited evapotranspiration regimes are the building blocks for large‐scale land‐atmosphere interaction, which, for example, have direct implications for hydroclimate extremes (e.g., heatwave and flash drought). Remotely sensed surface soil moisture information is now available at the global scale and has been used for such analysis. However, due to its limited representativeness of the soil moisture profile, the reliability of remotely sensed surface soil moisture for land‐atmosphere coupling analysis remains undefined. Here, we use observation‐driven approaches based on in situ soil moisture profile and flux tower observations to address the applicability of surface soil moisture for identifying the evapotranspiration regimes. As such, we seek to provide theoretical support for the application of remotely sensed surface soil moisture in large‐scale hydroclimatological and hydrometeorological analyses.

Based on the soil moisture—EF relationship and a soil moisture drydown analysis, we demonstrate that surface (at 5 cm, θ s ) and vertically integrated (0–50 cm, θ v ) soil moisture measurements are consistent in regards to their evapotranspiration regime classification. This is because the θ s is preferentially dried by evapotranspiration during drydowns. Hence, θ s determines the onset of evapotranspiration water stress and regime transitions. Therefore, the θ s and θ v dynamics essentially provide mutually useful information for quantifying evapotranspiration regime changes. Although this conclusion may be violated by cases with complex surface‐subsurface hydraulic links, it is supported and verified by a range of in situ observations across a range of climate, soil and vegetation conditions.

As such, we demonstrate that surface soil moisture, equivalent to that now available globally from Earth‐orbiting satellites (with over a decade of data), contains sufficient and reliable information for identifying landscape evapotranspiration regimes. Therefore, it highlights the value of remotely sensed soil moisture for monitoring the onset and the development of hydroclimate extremes, and its applicability for large‐scale land‐atmosphere interaction analysis.

Supporting information

Supporting Information S1

Click here for additional data file. (397.2KB, docx)

Acknowledgments

Authors with MIT affiliation thank NASA, which provided support in the form of a sponsored research grant (Subcontract No. 1510842). Jianzhi Dong is partly funded by National Natural Science Fundation of China (52179021). A. F. Feldman was supported by an appointment to the NASA Postdoctoral Program at the NASA Goddard Space Flight Center, administered by Universities Space Research Association under contract with NASA. USDA ARS is an equal opportunity employer.

Dong, J. , Akbar, R. , Short Gianotti, D. J. , Feldman, A. F. , Crow, W. T. , & Entekhabi, D. (2022). Can surface soil moisture information identify evapotranspiration regime transitions? Geophysical Research Letters, 49, e2021GL097697. 10.1029/2021GL097697

Data Availability Statement

The in situ soil moisture observations are available at: https://www.geo.tuwien.ac.at/insitu/data_viewer/ and https://www.ncei.noaa.gov/pub/data/uscrn/products/daily01/. The AmeriFlux data are available at: https://ameriflux.lbl.gov/data/data-availability/.

References

  1. Akbar, R. , Gianotti, D. J. S. , McColl, K. A. , Haghighi, E. , Salvucci, G. D. , & Entekhabi, D. (2018). Estimation of landscape soil water losses from satellite observations of soil moisture. Journal of Hydrometeorology, 19(5), 871–889. 10.1175/jhm-d-17-0200.1 [DOI] [Google Scholar]
  2. Akbar, R. , Short Gianotti, D. , McColl, K. A. , Haghighi, E. , Salvucci, G. D. , & Entekhabi, D. (2018). Hydrological storage length scales represented by remote sensing estimates of soil moisture and precipitation. Water Resources Research, 54, 1476–1492. 10.1002/2017wr021508 [DOI] [Google Scholar]
  3. Albergel, C. , Rüdiger, C. , Pellarin, T. , Calvet, J. C. , Fritz, N. , Froissard, F. , et al. (2008). From near‐surface to root‐zone soil moisture using an exponential filter: An assessment of the method based on in‐situ observations and model simulations. Hydrology and Earth System Sciences, 12, 1323–1337. 10.5194/hess-12-1323-2008 [DOI] [Google Scholar]
  4. Beck, H. E. , Wood, E. F. , Pan, M. , Fisher, C. K. , Miralles, D. G. , Van Dijk, A. I. J. M. , et al. (2019). MSWEP V2 global 3‐hourly 0.1 precipitation: Methodology and quantitative assessment. Bulletin of the American Meteorological Society, 100, 473–500. 10.1175/bams-d-17-0138.1 [DOI] [Google Scholar]
  5. Berg, A. , Lintner, B. R. , Findell, K. L. , Malyshev, S. , Loikith, P. C. , & Gentine, P. (2014). Impact of soil moisture–atmosphere interactions on surface temperature distribution. Journal of Climate, 27, 7976–7993. 10.1175/jcli-d-13-00591.1 [DOI] [Google Scholar]
  6. Buitink, J. , Swank, A. M. , van der Ploeg, M. , Smith, N. E. , Benninga, H.‐J. F. , van der Bolt, F. , et al. (2020). Anatomy of the 2018 agricultural drought in the Netherlands using in situ soil moisture and satellite vegetation indices. Hydrology and Earth System Sciences, 24, 6021–6031. 10.5194/hess-24-6021-2020 [DOI] [Google Scholar]
  7. Chen, F. , Crow, W. T. , Colliander, A. , Cosh, M. H. , Jackson, T. J. , Bindlish, R. , et al. (2016). Application of triple collocation in ground‐based validation of soil moisture active/passive (SMAP) level 2 data products. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 10, 489–502. 10.1109/JSTARS.2016.2569998 [DOI] [Google Scholar]
  8. Crow, W. T. , Gomez, C. A. , Sabater, J. M. , Holmes, T. , Hain, C. R. , Lei, F. , et al. (2020). Soil moisture–evapotranspiration overcoupling and L‐Band brightness temperature assimilation: Sources and forecast implications. Journal of Hydrometeorology, 21, 2359–2374. 10.1175/jhm-d-20-0088.1 [DOI] [Google Scholar]
  9. Crow, W. T. , Lei, F. , Hain, C. , Anderson, M. C. , Scott, R. L. , Billesbach, D. , & Arkebauer, T. (2015). Robust estimates of soil moisture and latent heat flux coupling strength obtained from triple collocation. Geophysical Research Letters, 42, 8415–8423. 10.1002/2015gl065929 [DOI] [Google Scholar]
  10. Denissen, J. M. C. , Teuling, A. J. , Reichstein, M. , & Orth, R. (2020). Critical soil moisture derived from satellite observations over Europe. Journal of Geophysical Research: Atmospheres, 125, e2019JD031672. 10.1029/2019jd031672 [DOI] [Google Scholar]
  11. Dirmeyer, P. A. , Zeng, F. J. , Ducharne, A. , Morrill, J. C. , & Koster, R. D. (2000). The sensitivity of surface fluxes to soil water content in three land surface schemes. Journal of Hydrometeorology, 1, 121–134. [DOI] [Google Scholar]
  12. Dong, J. , & Crow, W. T. (2018). Use of satellite soil moisture to diagnose climate model representations of European soil moisture‐air temperature coupling strength. Geophysical Research Letters, 45, 12–884. 10.1029/2018gl080547 [DOI] [Google Scholar]
  13. Dong, J. , Dirmeyer, P. A. , Lei, F. , Anderson, M. C. , Holmes, T. R. H. , Hain, C. , & Crow, W. T. (2020). Soil evaporation stress determines soil moisture‐evapotranspiration coupling strength in land surface modeling. Geophysical Research Letters, 47, e2020GL090391. 10.1029/2020gl090391 [DOI] [Google Scholar]
  14. Dong, J. , Lei, F. , & Crow, W. T. (2022). Land transpiration‐evaporation partitioning errors responsible for modeled summertime warm bias in the central United States. Nature Communications, 13, 1–8. 10.1038/s41467-021-27938-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Entekhabi, D. , Njoku, E. G. , O'Neill, P. E. , Kellogg, K. H. , Crow, W. T. , Edelstein, W. N. , et al. (2010). The soil moisture active passive (SMAP) mission. Proceedings of the IEEE, 98, 704–716. 10.1109/jproc.2010.2043918 [DOI] [Google Scholar]
  16. Entekhabi, D. , Rodriguez‐Iturbe, I. , & Castelli, F. (1996). Mutual interaction of soil moisture state and atmospheric processes. Journal of Hydrology, 184, 3–17. 10.1016/0022-1694(95)02965-6 [DOI] [Google Scholar]
  17. Fan, Y. , Miguez‐Macho, G. , Jobbágy, E. G. , Jackson, R. B. , & Otero‐Casal, C. (2017). Hydrologic regulation of plant rooting depth. Proceedings of the National Academy of Sciences, 114, 10572–10577. 10.1073/pnas.1712381114 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Feldman, A. F. , Short Gianotti, D. J. , Trigo, I. F. , Salvucci, G. D. , & Entekhabi, D. (2019). Satellite‐based assessment of land surface energy partitioning–soil moisture relationships and effects of confounding variables. Water Resources Research, 55, 10657–10677. 10.1029/2019wr025874 [DOI] [Google Scholar]
  19. Feldman, A. F. , Short Gianotti, D. J. , Trigo, I. F. , Salvucci, G. D. , & Entekhabi, D. (2020). Land‐atmosphere drivers of landscape‐scale plant water content loss. Geophysical Research Letters, 47, e2020GL090331. 10.1029/2020gl090331 [DOI] [Google Scholar]
  20. Gao, H. , Hrachowitz, M. , Schymanski, S. J. , Fenicia, F. , Sriwongsitanon, N. , & Savenije, H. H. G. (2014). Climate controls how ecosystems size the root zone storage capacity at catchment scale. Geophysical Research Letters, 41, 7916–7923. 10.1002/2014gl061668 [DOI] [Google Scholar]
  21. Green, J. K. , Seneviratne, S. I. , Berg, A. M. , Findell, K. L. , Hagemann, S. , Lawrence, D. M. , & Gentine, P. (2019). Large influence of soil moisture on long‐term terrestrial carbon uptake. Nature, 565, 476–479. 10.1038/s41586-018-0848-x [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Haghighi, E. , Short Gianotti, D. J. , Akbar, R. , Salvucci, G. D. , & Entekhabi, D. (2018). Soil and atmospheric controls on the land surface energy balance: A generalized framework for distinguishing moisture‐limited and energy‐limited evaporation regimes. Water Resources Research, 54, 1831–1851. 10.1002/2017wr021729 [DOI] [Google Scholar]
  23. Hirschi, M. , Mueller, B. , Dorigo, W. , & Seneviratne, S. I. (2014). Using remotely sensed soil moisture for land–atmosphere coupling diagnostics: The role of surface vs. root‐zone soil moisture variability. Remote Sensing of Environment, 154, 246–252. 10.1016/j.rse.2014.08.030 [DOI] [Google Scholar]
  24. Humphrey, V. , Berg, A. , Ciais, P. , Gentine, P. , Jung, M. , Reichstein, M. , et al. (2021). Soil moisture–atmosphere feedback dominates land carbon uptake variability. Nature, 592, 65–69. 10.1038/s41586-021-03325-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kerr, Y. H. , Waldteufel, P. , Wigneron, J.‐P. , Delwart, S. , Cabot, F. , Boutin, J. , et al. (2010). The SMOS mission: New tool for monitoring key elements of the global water cycle. Proceedings of the IEEE, 98, 666–687. 10.1109/jproc.2010.2043032 [DOI] [Google Scholar]
  26. Koster, R. D. , Schubert, S. D. , Wang, H. , Mahanama, S. P. , & DeAngelis, A. M. (2019). Flash drought as captured by reanalysis data: Disentangling the contributions of precipitation deficit and excess evapotranspiration. Journal of Hydrometeorology, 20, 1241–1258. 10.1175/jhm-d-18-0242.1 [DOI] [Google Scholar]
  27. Kramer, P. J. , & Boyer, J. S. (1995). Water relations of plants and soils. Academic press. [Google Scholar]
  28. Laio, F. , Porporato, A. , Ridolfi, L. , & Rodriguez‐Iturbe, I. (2001). Plants in water‐controlled ecosystems: Active role in hydrologic processes and response to water stress: II. Probabilistic soil moisture dynamics. Advances in Water Resources, 24, 707–723. 10.1016/s0309-1708(01)00005-7 [DOI] [Google Scholar]
  29. Li, W. , Migliavacca, M. , Forkel, M. , Walther, S. , Reichstein, M. , & Orth, R. (2021). Revisiting global vegetation controls using multi‐layer soil moisture. Geophysical Research Letters, 48, e2021GL092856. 10.1029/2021gl092856 [DOI] [Google Scholar]
  30. Lu, Y. , Dong, J. , Steele‐Dunne, S. C. , & van de Giesen, N. (2016). Estimating surface turbulent heat fluxes from land surface temperature and soil moisture observations using the particle batch smoother. Water Resources Research, 52, 9086–9108. 10.1002/2016wr018943 [DOI] [Google Scholar]
  31. Ma, S. , Baldocchi, D. , Wolf, S. , & Verfaillie, J. (2016). Slow ecosystem responses conditionally regulate annual carbon balance over 15 years in Californian oak‐grass savanna. Agricultural and Forest Meteorology, 228, 252–264. 10.1016/j.agrformet.2016.07.016 [DOI] [Google Scholar]
  32. Mueller, B. , & Seneviratne, S. I. (2012). Hot days induced by precipitation deficits at the global scale. Proceedings of the National Academy of Sciences, 109, 12398–12403. 10.1073/pnas.1204330109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Njoku, E. G. , & Kong, J. A. (1977). Theory for passive microwave remote sensing of near‐surface soil moisture. Journal of Geophysical Research, 82, 3108–3118. 10.1029/jb082i020p03108 [DOI] [Google Scholar]
  34. Qiu, J. , Crow, W. T. , Dong, J. , & Nearing, G. S. (2020). Model representation of the coupling between evapotranspiration and soil water content at different depths. Hydrology and Earth System Sciences, 24, 581–594. 10.5194/hess-24-581-2020 [DOI] [Google Scholar]
  35. Qiu, J. , Crow, W. T. , & Nearing, G. S. (2016). The impact of vertical measurement depth on the information content of soil moisture for latent heat flux estimation. Journal of Hydrometeorology, 17, 2419–2430. 10.1175/jhm-d-16-0044.1 [DOI] [Google Scholar]
  36. Scott, R. L. , Cable, W. L. , & Hultine, K. R. (2008). The ecohydrologic significance of hydraulic redistribution in a semiarid savanna. Water Resources Research, 44. 10.1029/2007wr006149 [DOI] [Google Scholar]
  37. Sehgal, V. , Gaur, N. , & Mohanty, B. P. (2021a). Global flash drought monitoring using surface soil moisture. Water Resources Research, 57(9), e2021WR029901. 10.1029/2021WR029901 [DOI] [Google Scholar]
  38. Sehgal, V. , Gaur, N. , & Mohanty, B. P. (2021b). Global surface soil moisture drydown patterns. Water Resources Research, 57, e2020WR027588. 10.1029/2020wr027588 [DOI] [Google Scholar]
  39. Seneviratne, S. I. , Corti, T. , Davin, E. L. , Hirschi, M. , Jaeger, E. B. , Lehner, I. , et al. (2010). Investigating soil moisture–climate interactions in a changing climate: A review. Earth‐Science Reviews, 99, 125–161. 10.1016/j.earscirev.2010.02.004 [DOI] [Google Scholar]
  40. Short Gianotti, D. J. , Salvucci, G. D. , Akbar, R. , McColl, K. A. , Cuenca, R. , & Entekhabi, D. (2019). Landscape water storage and subsurface correlation from satellite surface soil moisture and precipitation observations. Water Resources Research, 55, 9111–9132. 10.1029/2019wr025332 [DOI] [Google Scholar]
  41. Ulaby, F. T. , Batlivala, P. P. , & Dobson, M. C. (1978). Microwave backscatter dependence on surface roughness, soil moisture, and soil texture: Part I‐bare soil. IEEE Transactions on Geoscience Electronics, 16, 286–295. 10.1109/tge.1978.294586 [DOI] [Google Scholar]
  42. Wagner, W. , Lemoine, G. , & Rott, H. (1999). A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sensing of Environment, 70, 191–207. 10.1016/s0034-4257(99)00036-x [DOI] [Google Scholar]
  43. Yang, Y. , Donohue, R. J. , & McVicar, T. R. (2016). Global estimation of effective plant rooting depth: Implications for hydrological modeling. Water Resources Research, 52, 8260–8276. 10.1002/2016wr019392 [DOI] [Google Scholar]
  44. Yuan, X. , Wang, L. , Wu, P. , Ji, P. , Sheffield, J. , & Zhang, M. (2019). Anthropogenic shift towards higher risk of flash drought over China. Nature Communications, 10, 1–8. 10.1038/s41467-019-12692-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zeng, X. (2001). Global vegetation root distribution for land modeling. Journal of Hydrometeorology, 2, 525–530. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information S1

Click here for additional data file. (397.2KB, docx)

Data Availability Statement

The in situ soil moisture observations are available at: https://www.geo.tuwien.ac.at/insitu/data_viewer/ and https://www.ncei.noaa.gov/pub/data/uscrn/products/daily01/. The AmeriFlux data are available at: https://ameriflux.lbl.gov/data/data-availability/.

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES